14-17高数
高数课本课后必做习题

习题3—1
1、2、3、4、5、6、7、8、9、10、11、12、13、14
习题3—2
1(1)~(16)、2
习题3—3
1、3、4、5、7、10(1)~(3)
习题3—4
1、2、3(1)~(7)、5(1)~(5)、6、8(1)~(4)、9(1)~(6)、10(1)~(3)、12、13、14
习题2—3
1(1)~(12)、3(1)~(2)、4、10(1)~(2)
习题2—4
1(1)~(4)、2、3(1)~(4)、4(1)~(4)、5(1)~(2)、6、7(1)~(2)、8(1)~(4)
习题2—5
2、3(1)~(10)、4(1)~(8)
总习题二
1、2、3、6、7、8(1)~(5)、9(1)~(2)、11、12(1)~(2)、13、14。
1、2、4、5、6(1)~(2)、8、9、11、19。
第十章重积分(二重积分)
习题10—1
4(1)~(4)、5(1)~(4)
习题10—2
1(1)~(4)、2(1)~(4)、4(1)~(4)、5、6(1)~(6)、7、8、9、10、12(1)~(4)、13(1)~(4)、14(1)~(3)、15(1)~(4)
习题4—3
1~24
习题4—4
1~24
总习题四
1~40。
第五章定积分
习题5—1
10、11、12、13
习题5—2
2、3、4、5(1)~(3)、6(1)~(11)、9(1)~(2)、11、12、13
习题5—3
1(1)~(26)、2、3、4、5、6、7(1)~(13)
习题5—4
1(1)~(10)
总习题五
(word完整版)高数极限60题及解题思路.doc

高数极限 60 题1. 求数列极限 lim (sin n1 sin n ) 。
n2. 设 S nn k ,其中 b k (k 1)! ,求 lim S n 。
k1 b k n3. 求数列极限 lim (123 2n 1) ,其中q。
nqqnq14.求数列极限 lim [ n 24n 5 (n 1)] 。
n5. 求数列极限 lim (112 )(112 )...(112)。
n 23n6. 求极限 lim( x1)2(2x 1) 2 (3x 1)2 ... (10 x 1)2 。
x(10 x 1)(11x 1)7. 求极限 lim (4x 28x 5 2x 1) 。
x2e 3 x 3e2 x8. 讨论极限 lim3xx4e e2x。
9. 求极限 lim tan 2xtan( x) 。
x4410. 求极限 lim33x 2 2 。
x2x 211. 求极限 lim (1 2 x)5 (1 4 x) 3x。
x 012. 求极限 lim1 tan x 3 sin x 1 。
xx13. 讨论极限 lim2 2 cos x 。
x 0x14. 求数列极限 lim 2nsin2n 1。
n15.设x 1a 0,且 x n 1ax n ,证明: lim x n 存在,并求出此极限值。
n16. 设 x 12 ,且 x n 12 x n ,证明: lim x n 存在,并求出此极限值。
n17.设 x n 1 1 1 ... 1 ( n 为正整数),求证: lim x n 存在。
2 222 3 n n18. 求数列极限 lim2n。
nn!19. 求极限lim ln( 2 3e 2 x )3 x。
xln( 3 2e )20. 求极限 lim xx xx。
xx21. 无限循环小数 0.9 的值 (A) 不确定 (B) 小于 1 (C)等于 1 (D) 无限接近 1222. 求数列极限 lim (sec )n 。
nn23. 应用等价无穷小性质,求极限lim arctan(1x 01124.(1 4x)2(1 6x) 3 求极限 limx。
考研高数教材要做的题目和不考的章节

高等数学(同济大学第六版)考研课后习题要求做的题目(2(A)表示第2题的单数题;2(B)表示第2题的双数题)章节不要求掌握内容要求做的习题第一章第一节双曲函数4(B)、5、6、15、16第二节1第三节1、2、3、4第四节1、6、7第五节1(A)、3、4、5第六节柯西极限存在准则1(B)、2(A)、4第七节1、2、3、4第八节1、2、3、4、5第九节1、4、5、6第十节一致连续性1、2、3、5总习题一2、3、4、5、9、10、11、12、13第二章第一节6、7、8、11、12、13、15至20第二节2(B)、4、5、7(B)、8、9、10、11(B)、14第三节1(B)、3、4、9、11、12第四节参数方程所确定的函数的导数和相关变化率数三不要求1、2、3、4(A)、(数学一、数学二:7、8(B)、10、11、12)第五节微分在近似计算中应用1、2、3(B)总习题二1、2、3、6、7、10、11、14第三章第一节5、6、7、8、9、10、11、12、14第二节1(B)、3、4第三节1、3、4、5、6第四节3(B)、4、5、6、9(B)、11、12、13、14、15第五节1(B)、2、3、5、6、9、10、13第六节1、4第七节本节数三不要求1、2、3、4、5总习题三1至13、15、17、19、20第四章第一节2(B)、4、5、6、7第二节1(B)、2(B)第三节1、2至24单数第四节1、2至24单数总习题四1、2、3至40单数第五章第一节3、5、7、11、12、13(A)第二节1、2、3、4、5、6(A)、9至14第三节1(B)、2、3、5、6、7(B)第四节1(B)、2总习题五3、4、6、10、11、12、13、14第六章第一节第二节弧长数学三不要求1、2(B)、3、4、6、8、9、10、11、12、15、16(数学一、数学二:21、24、27、28)第三节本节数学三不要求4、5、6、7、10、11、12总习题六3、4、5、6、7第七章第一节3、5第二节例4.1(B)、2(B)、4第三节可化为齐次的方程1(A)、2(B)、3第四节例2. 伯努利方程(数学一1(B)、2(A)、3、4、8(B)要)第五节例4. 例6.1(B)、3本节数学三不要求第六节例2. 常数变易法3第七节例4. 例5.1(A)、2(B)、3第八节1(A)、6第九节本节数学二、数学三不要求1、2总习题七1、2、3(B)、7、8第八章第一节本章数学二、数学三不要求4、15、16第二节1、3、9、10第三节2、3、7、9(A)第四节3、4、5、8第五节1、2、3、5、6、8、9第六节2、4、5、7、8、9、13、15总习题八16、17、19、21第九章第一节平面点集第二节1(B)、4、6、9第三节全微分在近似计算中应用1、2、3、5第四节9、10、11、12、13第五节2、3、4、6、7、8、10、11第六节本节数学二、数学三不要求4、5、6、7、8、9、10、11、12第七节本节数学二、数学三不要求1、3、4、5、6、7、8、10第八节1、2、5、6、10、11、12总习题九2、9、10、11. (数学一:14、15、16、17、18)第十章第一节4(B)、5(B)第二节二重积分的换元法1、2、3、4、6、9、10、11、12、13、14、15第三节本节数学二、数学三不要求1、4、5、6、7、9、10、11、15第四节本节数学二、数学三不要求1、4(1)、5、7(1)、8总习题十1、2(B)、3、5、6. (数学一:8、9、10)第十一章第一节本章数学二、数学三不要求3第二节3、4、5第三节1、3、4(3)、5、6(B)、8(B)、9第四节5、6(B)第五节3第六节1第七节2总习题十一2、3、4、5、7第十二章第一节本章数学二不要求3、4第二节1(A)、2(B)、3(B)、4(B)、5(B)第三节1、2第四节2(A)、5、6第七节本节数学三不要求1(1)、2(2)、3、6第八节本节数学三不要求1(1)(3)、2(2)总习题十二1、2、3、4、5、7、8、9、10具体的重点知识点如下:1.极限计算(数列和函数极限,等价无穷小代换、泰勒公式、洛必达法则等),2.导数及其应用(方程根的问题、极值最值、拐点、凹凸性、渐近线、不等式的证明等),3.中值定理相关的证明,4.不定积分、定积分的计算(换元法、分部积分法、有理函数积分的计算,变限积分函数求导公式、牛顿-莱布尼兹公式的应用等),5.定积分的几何应用(微元法,平面图形的面积、旋转体的表面、弧长、旋转体的体积等),6.多元函数的微分法(偏导数的计算、条件极值为重点),7.二重积分的计算(数二、数三的必考题),8.微分方程(特定类型的方程求解,应用题等),9.级数(敛散性判断、级数求和、函数的幂级数展开,傅立叶级数(数一)),10.曲线曲面积分(数一必考,格林公式、高斯公式、斯托克斯公式的运用)。
17考研高数第三章 中值定理及应用(下)及不定积分概念

y
f ( x)
y
f ( x )
y
f ( x )
o
x
x
o
( A)
x
f ( x )
( B)
o
y
f ( x )
当x 0时, f ( x )单调增加,
y
则 f ( x ) 0, ( A)(C )不对
当x 0时,
f ( x )增 减 增,
o
(C )
x
o
( D)
x 则 f ( x)由正 负 正,
x a x a x a
f ( x) 3)斜渐近线: 如果 lim a , lim[ f ( x ) ax ] b, x x x
则y ax b为曲线的一条斜渐近线.
9
3 2 x 【y 2 x】 例12 曲线 y 的渐近线方程为 ________. 2 x 1 解 D : (, ). 没有铅直渐近线
x2 x2
则有铅直渐近线 x 0.
12
2 x x 1 x2 例15 曲线 y e arctan 的渐近线有( ( x 1)( x 2)
1
)
( A)1条; ( B )2条;
(C )3条;
( D )4条.
解 函数的间断点为: x 0, x -1, x 2 1 2 x x 1 x2 lim e arctan , x 0 ( x 1)( x 2)
又 lim f ( x ) lim ( x ln x A) ,
x x
又 lim f ( x ) lim ( x ln x A) A lim( x ln x )
x 0 x 0 x 0
13级课表汇总
测量学(1-6,9-10)第五教2-8
采1-4高数(15,17-18)
五教101
工1-3高数(11-16)
五教2-8
工1-3C语言程序设计(1-16)五教101
建123C语言程序设计A(1-8,11-18)五教109
测量学(1-6,9-10周)
采1-4中国近现代史纲要(1-6,9-15,17)一教302
五教203
采1-4普通物理学A(1-6,9-15,17)
四教一合班
安123线代(1-17)
四教七合班
安1-3C语言程序设计A(17-18)五教203
建123普通化学(1-8)
五教103
工123普通物理学B(1-10)五教101
建123线代(1-8)
四教四合班
采矿12英语(1-6,9-15,17-18)
五教101
建1-3C语言程序设计(15-18)
五教10
建123普通物理学(1-8)
五教203
工3英语(1-16)
五教104
第五六节
普通物理学B(1-10)
五教101
采1-4工业1-3形势与政策(15)五教2-2
建123普通化学(1-8)
五教203
安123普通物理学实验A(2-6)四教2楼
普通物理学实验A(12-16)四教2楼
五教205
安1-3普通物理学A(1-14)四教一合班
工1-3高数(3-16)
五教2-8
建123高数(1-8,11-17)
五教101
采1-4C语言程序设计(1-6,9-15,17-18)
五教2-5
安12英语(1-16)
高数 1.2.1极限概念

S 2 a 0
a0 q
S3 a0 a0 q a0 q 2
2 Sn a0 q n a a q a q 0 0 0 k 0 n 1
a qk
0
………
现在研究数列{sn}的收敛问题. 如果q 1时 n n a aq 2 n1 a aq , sn a aq aq aq 1 q 1 q 1 q
自变量趋向负无穷大时函数的极限
例 1. 2. 8
x
l i mx 2
0 .
2015 年 2 月 14日 1 1 时 3 9 分
自变量 x 趋向无穷大时函数的极限
(4) x→∞: | x | 无限地增大,如下例.
例 1. 2. 9
1 l i m x x
1 0 . 数列的极限 lim 0 为其特例. n n
lim y A.
x
读作 x 趋于□时函数y 的极限是A. x→□ 的六种不同情况: (1) x→a: a 为常数,如例 1. 2. 7 中x→0. (2) x→+∞: x 的值无限地增大,如例 1. 2. 8. (3) x→-∞: x 的值无限地减小,如下例 1. 2. 9.
下一张
2015 年 2 月 14日 1 1 时 3 9 分
当q 1时, 收敛 aq n 0 当q 1时, 发散
n
sn 不存在 , 此时级数也发散. 如果 q 1, lim n
综上所述
2015 年 2 月 14日 1 1 时 3 9 分
例 2.2.6 把循环小数 2.317 2.3171717 表示成
分数的形式 .
2015 年 2 月 14日 1 1 时 3 9 分
《高数》第1章

复合函数也可以由两个以上的函数复合而成.例 2 y 如: = ln 2 + x ,是由 y = ln u , u = v , v = 2 + x 2 三 个函数复合而成的. 个函数复合而成的. 指出下列函数的复合过程。 指出下列函数的复合过程。 y = cos x 2 , (2) = ln 2 sin x, (3) = e arctan y y ) (1) ) ) 解 (1) y = cos x 2由 y = cos u , u = x 2 复合而成 复合而成. 例2
在图形上,单调增加的函数的图象是随着x的增大而呈上升的 在图形上 , 单调增加的函数的图象是随着 的增大而呈上升的 曲线, 单调减少的函数, 其图象是随着x的增大而下降的曲 曲线 , 单调减少的函数 , 其图象是随着 的增大而下降的曲 线.
的定义域为D, (3)奇偶性:设f(x)的定义域为 ,对 ∀x ∈ D,如果 )奇偶性: 的定义域为 ( i) f ( − x ) = − f ( x ) ,则称该函数为奇函数; 则称该函数为奇函数; (ii) f ( − x ) = f ( x ) ,则称该函数为偶函数. 则称该函数为偶函数. 在图形上, 奇函数的图象关于原点对称 , 偶函数的 在图形上 , 奇函数的图象关于原点对称, 图象关于y 轴对称. 图象关于 轴对称.
21世纪高职高专精品教材 世纪高职高专精品教材
高等数学
上海交通大学出版社
第1章 函数、极限与连续 章 函数、
1.1 函数
1.1.1 1.1.2 1.1.3 1.1.4 一元函数 复合函数与反函数 基本初等函数 初等函数
1.1 函数
1.1.1 一元函数 1.一元函数的概念 定义1 是一个非空的实数集合, 定义1 设 D 是一个非空的实数集合,如果存在某种对 y 应规律 f , 使得对 ∀x ∈ D , 都有唯一的实数y 与之 对应, 对应,就称 f 确定了一个一元函数 f : D → f ( D ) ,通常 为自变量, 为函数(因变量) 记为 y = f ( x ) .称 x 为自变量, y 为函数(因变量), 为定义域, 称为值域. 为定义域,函数值的集合 f ( D ) 称为值域. D 如果对于确定的x 如果对于确定的 0 ∈ D ,通过对应规律 f ,函数 f (x) 有唯一确定的值 y0 与之对应,称 y0 为函数 与之对应, y = f (x) 在 x0 处的函数值,记为 处的函数值,
考研数学必做课后习题(同济)

高等数学课后习题解读总习题一:1是填空题,是考察与极限有关的一些概念,这个是很重要的,要掌握好。
而且几乎每章的总习题都设了填空题,均与这些章节的重要概念有关。
所以每章的总习题里的填空题所涉及的知识点,比如谁是谁的什么条件之类,务必要搞清楚。
2是无穷小的阶的比较3、4、5、6是与函数有关的题目,这个是学好高数的基础,但却不是高数侧重的内容,熟悉即可7用定义证明极限,较难,一般来说能理解极限的概念就可以了8典型题,求各种类型极限,重要,6个小题各代表一种类型,其实求极限的题目基本跳不出这六种框架了9典型题,选择合适的参数,使函数连续,用连续的定义即可10典型题,判断函数的间断点类型,按间断点的分类即可11较难的极限题,这里是要用到夹逼原理,此类题目技巧性强,体会一下即可12证明零点存在的问题,要用到连续函数介值定理,重要的证明题型之一,必需掌握13该题目给出了渐近线的定义以及求法,要作为一个知识点来掌握,重要综上,第一章总习题要着重掌握的是1、2、8、9、10、12、13题总习题二:1填空题,不多说了,重点2非常好的一道题目,考察了与导数有关的一些说法,其中的干扰项(B)(C)设置的比较巧妙,因为平时我们一般只注意到导数在某点存在的条件是左右导数都存在且相等,容易忽视另一个重要条件:函数必须要在该点连续,否则何来可导?而(B)(C)项的问题正是在于即使其中的极限存在,也不能保证函数在该点连续,因为根本就没出现f(a),所以对f(x)在a 处的情况是不清楚的。
而对(A)项来说只能保证右导数存在。
只有(D)项是能确实的推出可导的3物理应用现在基本不要求了4按定义求导数,不难,应该掌握5常见题型,判断函数在间断点处的导数情况,按定义即可6典型题,讨论函数在间断点处的连续性和可导性,均按定义即可7求函数的导数,计算层面的考察,第二章学习的主要内容8求二阶导数,同上题9求高阶导数,需注意总结规律,难度稍大,体会思路即可10求隐函数的导数,重要,常考题型11求参数方程的导数,同样是常考题型12导数的几何应用,重要题型13、14、15不作要求综上,第二章总习题需重点掌握的题目是1、2、4、5、6、7、8、10、11、12第三章的习题都比较难,需要多总结和体会解题思路总习题三1零点个数的讨论问题,典型题,需掌握2又一道设置巧妙的题目,解决方法有很多,通过二阶导的符号来判断函数增量与导数、微分的大小关系,07年真题就有一道题目由此题改造而来,需重点体会3举反例,随便找个有跳跃点的函数即可4中值定理和极限的综合应用,重要题目,主要从中体会中值定理的妙处5零点问题,可用反证法结合罗尔定理,也可正面推证,确定出函数的单调区间即可,此题非典型题6、7、8中值定理典型题,要证明存在零点,可构造适当的辅助函数,再利用罗尔定理,此类题非常重要,要细心体会解答给出的方法9非常见题型,了解即可10罗必达法则应用,重要题型,重点掌握11不等式,一般可用导数推征,典型题12、13极值及最值问题,需要掌握,不过相对来说多元函数的这类问题更重要些14、15、16不作要求17非常重要的一道题目,设计的很好,需要注意题目条件中并未给出f''可导,故不能连用两次洛必达法则,只能用一次洛必达法则再用定义,这是此题的亮点18无穷小的阶的比较,一是可直接按定义,二是可将函数泰勒展开,都能得到结果,此题考察的是如何判断两个量的阶的大小,重要19对凹凸性定义的推广,用泰勒公式展开到二阶可较方便的解决,此题可看作泰勒公式应用的一个实例,重在体会其思想20确定合适的常数,使得函数为给定的无穷小量,典型题,且难度不大综上,第三章总习题需要重点掌握的是1、2、4、6、7、8、10、11、12、13、17、18、20第四章没有什么可说的重点,能做多少是多少吧……积分的题目是做不完的。
高数作业习题

高等数学课程作业习题高等数学(第五版)上册(1-7章)作业P20 习题1-11,3,5,6(2)(4)(6)(8)(10),7(1)(3),8,10,11,12(2)(4)(6),13(1)(3)(5),14(2)(4)(6),15,16(1)(3)(5),17(2)(4),18,20。
P30习题1-21(1)(3)(5),3(2)(4),4,5,6。
P37习题1-31(1)(3),2(2),3,5,6,8,9。
P41习题1-41,2(2),4(1),5,6,7。
P48习题1-51,2,3.P55习题1-61,2,4(2)(3)(5)。
P57习题1-71,2,3,4.P64习题1-81(2),2(1)(2)(3),3,5。
681,3(1)(3)(5)(7),4(2)(4)(6),5。
P73习题1-102,3,4.P73总复习一1,2,3(2)(4),4,8(2)(4)(5)(6),9,10,11,12。
P85习题2-11,5,6,7(2)(4)(6),8,9,11,13,14,15,16,17,18。
P96习题2-21,2(2)(4)(6)(8)(10),3(1)(3),4,5,6(2)(4)(6)(8)(10),7(2)(4)(6)(8)(10),8(2)(4)(6)(8)(10),9(2)(4)(6)(8)(10),10(2)(4)(6)(8)(10)。
P101习题2-31(3)(5)(6)(11),2,3,4,6,8(1)(2),9(1)(3)。
P110习题2-41(1)(3),2,3(2)(4),4(1)(3),6,7,8(2)(4),9(1),10,12。
P122习题2-51,2,3(2)(4)(6)(8),4(1)(3)(5)(7),6,7(1),9(1)(2),10(1),11。
P124总习题二1,2,5,6,7(1)(3)(5),8(2),9(2),10,11(2),13。
1321,3,4,5,6,7,9,11,12,14,15。
同济高数第七版(上册)考研数学考纲
会〔数一数二
例1~5
习题6-3:
5, 11
总习题六
总结归纳本章的基本概念、基本定理、基本公式、基本方法
总习题六:
1, 2 , 4, 5, 6, 7, 9
第七章微分方程
7.1微分方程的基本概念
微分方程的阶、解、通解、
初始条件和特解
了解
例1,2
习题7-1:1<3><4>
2<2><4>, 3<2>, 4<3>,5<1>, 7
例12〔记住结论
习题5-3:
1〔4〔7〔10〔18
(19)〔21〔25〔26
2,5,6,7〔10〔11〔13
5.4反常积分
无穷限的反常积分
了解概念,会计算反常积分
例1~7
习题5-4:
1〔4〔8〔10
2,3〔记住结论,4
无界函数的反常积分
5.5反常积分的审敛法
不作要求
总习题五
总结归纳本章的基本概念、基本定理、基本公式、基本方法
基本定理、基本公式、基本方法
P70总习题一:
3,5,9〔2〔4〔6
(7)〔8,10,11,
12,13,14
第二章导数与微分
章节
教材内容
考纲要求
必做例题
必做习题
2.1导数
概念
导数的定义
理解[重点]
例1~6
P83习题2-1:
6,7,13,16〔2,
17,18,19
导数的物理意义
了解〔仅数学一数学二要求〔会用
6713162171819导数的物理意义了解仅数学一数学二要求会用导数描述物理量引例1导数的几何意义理解数一数二了解数三会求平面曲线的切线例89引例2导数的经济意义了解仅数三要求单侧导数以及单侧可导与可导的关系理解例7函数的可导性与连续性的关系理解重点例101122函数的求导法则函数的和差积商的求导法则掌握例115p94习题22
数二高数课后题(考研)

2012届钻石卡学员考研数学学习计划(基础阶段)数学二——高等数学第一单元学习计划——函数、极限、连续本计划对应教材:高等数学上册同济大学数学系编高等教育出版社第六版在第一单元中我们应当学习-—1.函数的概念及表示方法;2.函数的有界性、单调性、周期性和奇偶性;3.复合函数、分段函数、反函数及隐函数的概念;4.基本初等函数的性质及其图形;5.极限及左右极限的概念,极限存在与左右极限之间的关系;6.极限的性质及四则运算法则;7.极限存在的两个准则,会利用其求极限;两个重要极限求极限的方法;8.无穷小量、无穷大量的概念,无穷小量的比较方法,利用等价无穷小求极限;9.函数连续性的概念,左、右连续的概念,判断函数间断点的类型;10.连续函数的性质和初等函数的连续性,闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),会用这些性质。
第一单元调整学习计划第二单元学习计划——一元函数微分学本计划对应教材:高等数学上册同济大学数学系编高等教育出版社第六版在第一单元中我们应当学习——1.导数和微分的概念、关系,导数的几何意义、物理意义,会求平面曲线的切线方程和法线方程,函数的可导性与连续性之间的关系;2.导数和微分的四则运算法则,复合函数的求导法则,基本初等函数的导数公式,一阶微分形式的不变性;3.高阶导数的概念,会求简单函数的高阶导数;4.会求以下函数的导数:分段函数、隐函数、由参数方程所确定的函数、反函数;5.罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理、泰勒(Taylor)定理、柯西(Cauchy)中值定理,会用这四个定理证明;6.会用洛必达法则求未定式的极限;7.函数极值的概念,用导数判断函数的单调性,用导数求函数的极值,会求函数的最大值和最小值;8.会用导数判断函数图形的凹凸性,会求函数图形的拐点,会求函数的水平、铅直和斜渐近线;9.曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.第二单元学习计划调整任务第三单元学习计划——不定积分本计划对应教材:高等数学上册同济大学数学系编高等教育出版社第六版在第一单元中我们应当学习——1.原函数、不定积分的概念;2.不定积分的基本公式,不定积分的性质,不定积分的换元积分法与分部积分法;第三单元学习计划调整任务第四单元学习计划——定积分及其应用本计划对应教材:高等数学上册同济大学数学系编高等教育出版社第六版在第一单元中我们应当学习—-1.定积分的概念和性质,定积分中值定理;2.定积分的换元积分法与分部积分法;3.积分上限的函数的概念和它的导数,牛顿—莱布尼茨公式;4.反常积分的概念与计算;5.用定积分计算平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力,函数的平均值.第五单元学习计划——常微分方程本计划对应教材:高等数学上册 同济大学数学系编 高等教育出版社 第六版 在第一单元中我们应当学习——1. 微分方程及其阶、解、通解、初始条件和特解等概念;2. 变量可分离的微分方程及一阶线性微分方程的解法;3. 齐次微分方程的解法;4. 可降阶微分方程:()(),(,)(,)n yf x y f x y y f y y ''''''===和的解法;5. 线性微分方程解的性质及解的结构;6. 二阶常系数齐次线性微分方程的解法;7. 会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.第五单元学习计划调整任务第六单元——向量代数和空间解析几何(考研数学二不要求)第七单元学习计划——多元函数微分学本计划对应教材:高等数学上册同济大学数学系编高等教育出版社第六版在第一单元中我们应当学习—-1.二元函数的概念与几何意义;2.二元函数的极限与连续的概念,有界闭区域上连续函数的性质;3.多元函数偏导数和全微分的概念,全微分存在的必要条件和充分条件,全微分形式的不变性,会求全微分;4.多元复合函数一阶、二阶偏导数的求法;5.隐函数存在定理,计算多元隐函数的偏导数;6.多元函数极值和条件极值的概念,二元函数极值存在的必要条件、充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值.第七单元学习计划调整任务第八单元学习计划——重积分本计划对应教材:高等数学上册同济大学数学系编高等教育出版社第六版在第一单元中我们应当学习——1.二重积分的概念和性质,二重积分的中值定理;2.会利用直角坐标、极坐标计算二重积分.第八单元学习计划调整任务第九单元——曲线积分与曲面积分(考研数学二不要求)第十单元——无穷级数(考研数学二不要求)。
考研数学一高数下册范围

考研数学一高数下册范围答:第九章多元函数微分学及应用考试范围:1、两元函数极限的概念、存在性、求法与连续2、偏导数的定义与偏导数的求法及二阶偏导数3、二元函数可微分的判定及全微分的求法4、隐函数存在定理、求导方法及多元复合函数求导法则5、多元函数微分学的几何应用及方向导数与梯度(数一考试内容)6、多元函数的极值及其求法习题范围习题9-1:第2题、第6、7题习题9-2:第1题、第3题、第4题、第6题、第7题、第8、9题、习题9-3:第1题、第2题、第4题、第5题、习题9-4:第1、2、3、4题、第7题、第8、9、10题、第11题、第12、13题习题9-5:第1、3、4题、第5题、第6题、第7题、第8题、第9题、第11题习题9-6 (数学一考试内容):第4、5题、第6题、第7、8、9题第12题习题9-7 (数学一):第1、2题、第3题、第5、6题、第8题习题9-8:第1题、第2、3、4题、第11题总复习题九:第1题,第2题(数一)、第3题、第5题、第6题、第8题、第9题、第10题、第11题、第12题,第14、15、17题(数一) 第19题(数三),第20题(数一数二)第十章重积分(数二、三只考二重积分) .考试范围:1、二重积分的定义域性质2、二重积分的交换积分次序及二重积分的计算3、三重积分的性质、应用与三重积分的计算(数一考试内容)习题范围:刃題10-1:第4題、第5題可題10-2:第1題、第2題、第4、5題、第6題、第11、12題第13、14、、15題、第21題刃題10-3: (数学一考武内容)第1題、第4、5、6、7、8題、第9、10題第11、15題刃題10-4:第1、2題、第5題、第8題、第9題、第10、11題、第12、13題(数学一)忌ヲ題十:第1題、第2題、第3題、第4題、第5、6題第7題、第8題、第9題、第13題第十一章曲銭釈分与曲面釈分(数一)略第十ニ章无劣級数(数二不考)考武范国:1、常数級数的性貭与收斂性的判定(正項級数与交錯級数)2、冪級数的收斂区域与收斂半径的求法;3、函数展开成幂级数与幂级数和函数的求法4、傅里叶级数与三角级数、正弦余弦级数(数一考试内容)习题范围:习题12-1:第3题、第4题习题12-2:第1题、第2题、第3、4、5题习题12-3:第1题、第2题习题12-4:第3、4、5、6题习题12-7 (数一)第1题、第2题、第4题、第5题、题6题总习题十二:第1题、第2题、第3题、第5、6、7、8、9题第10题。
高数课本_同济六版

第一章函数与极限(考研必考章节,其中求极限是本章最重第二章要的内容,要掌握求极限的集中方法)第三章第四章第一节映射与函数(一般章节)第五章一、集合(不用看)二、映射(不用看)三、函数(了解)第六章注:P1--5 集合部分只需简单了解第七章P5--7不用看第八章P7--17 重点看一下函数的四大性态:单调、奇偶、周期、有界第九章P17--20 不用看第十章P21 习题1.1第十一章1、2、3大题均不用做第十二章4大题只需做(3)(5)(7)(8)第十三章5--9 均做第十四章10大题只需做(4)(5)(6)第十五章11大题只需做(3)(4)(5)第十六章12大题只需做(2)(4)(6)第十七章13做14不用做15、16重点做第十八章17--20应用题均不用做第二节数列的极限(一般章节本章用极限定义证的题目考纲不作要求,可不看)一、数列极限的定义(了解)二、收敛极限的性质(了解)二、P26--28 例1、2、3均不用证三、p28--29 定理1、2、3的证明不用自己证但要会理解四、P30 定理4不用看五、P30--31 习题1-2六、1大题只需做(4)(6)(8)七、2--6均不用做第三节(一般章节)(标题不再写了对应同济六版教材标题)一、(了解)二、(了解)二、P33--34 例1、2、3、4、5只需大概了解即可三、P35 例6 要会做例7 不用做四、P36--37 定理2、3证明不用看定理3’4”完全不用看五、六、p37习题1--3七、1--4 均做5--12 均不用做第四节(重要)第五节第六节一、无穷小(重要)二、无穷大(了解)第七节第八节 p40 例2不用做 p41 定理2不用证第九节 p42习题1--4第十节第十一节 1做 2--5 不全做 6 做 7--8 不用做第五节(注意运算法则的前提条件是各自存在)第六节p43 定理1、2的证明要理解第七节p44推论1、2、3的证明不用看第八节p48 定理6的证明不用看第九节p49 习题1--5第十节1题只需做(3)(6)(7)(8)(10)(11)(13)(14)第十一节2、3要做4、5重点做6不做第六节极限存在准则(重要) 两个重要极限(重要两个重要极限要会证明第七节第八节第九节p50 准则1的证明要理解第十节p51 重要极限一定要会独立证明(经典重要极限)第十一节第十二节p53另一个重要极限的证明可以不用看第十三节p55--56柯西极限存在准则不用看第十四节第十五节p56习题1--7第十六节第十七节1大题只做(1)(4)(6)第十八节2全做3不用做4全做,其中(2)(3)(5)重点做第七节(重要)第八节p58--59 定理1、2的证明要理解第九节p59 习题1--7 全做第十节第八节(基本必考小题)第九节p60--64 要重点看第八节基本必出考题第十节p64 习题1--8第十一节第十二节1、2、3、4、5要做其中4、5要重点做第十三节6--8不用做第九节(了解)第十节p66--67 定理3、4的证明均不用看第十一节p69 习题1--9第十二节1、2要做第十三节3大题只做(3)——(6)第十四节4大题只做(4)——(6)第十五节5、6均要重点做第十节(重要,不单独考大题,但考大题会用到)第十一节第十二节一、(重要)二、(重要)p72三、一致连续性(不用看)第十三节p74习题1--10第十四节1、2、3、5要做,要会用5的结论。
高等数学习题及解答 (2)

普通班高数作业(下)第六章 定积分1、根据定积分的几何意义,说明下列各式的正确性:(第二版P186:1;第三版P155:1) (1)0sin 20=⎰πxdx (4)⎰⎰=-11142xdxdx x2、不计算积分,比较下列各积分值的大小:(第二版P186:2;第三版P155:3) (4)⎰10dx e x与⎰102dx e x(5)⎰2sin πxdx 与⎰20πxdx(6)⎰-02cos πxdx 与⎰20cos πxdx3、利用定积分性质,估计下列积分值:(第二版P186:3;第三版P155:4) (1)⎰-=22dx eI xx (5)⎰--=2295dx xx I (6)⎰=20sin πdx x x I 4、求下列极限:(第二版P186:4;第三版P160:1)(2)211)1(1ln lim -+⎰→x dt t txx (3)⎰+→xt x dt t x 010)2sin 1(1lim (4)2210lim x x t x dt e ⎪⎭⎫⎝⎛⎰+∞→ (6)x x x dt e x xt x sin arctan lim 002⋅⋅-⎰-→5、求下列导数:(第二版P186:5;第三版P161:2)(1)⎰-32x x t dt e dx d (2)⎰-x tdt x t dxd 033sin )( 6、求证方程⎰--=π02cos 1ln dx x exx 在()∞+,0内有且仅有两个不同的实根。
(第二版P186:7;第三版P161:4)7、设)(x f 在[]b a ,上连续,且0)(>x f ,令⎰⎰+=xbxadt t f dt t f x F )(1)()(。
求证:(1)2)(≥'x F ;(2))(x F 在()b a ,内有且仅有一个零点。
(第二版P186:8;第三版P161:5)8、设)(x f 为连续函数,且存在常数a ,满足(1)⎰=+3)(15x adt t f x ,求)(x f及常数a 。
高数第十章答案

高数第十章答案【篇一:高等数学2第十章答案】=txt>1.根据二重积分的性质,比较下列积分的大小:(1)成;2223d与,其中积分区域是圆周(x?2)?(y?1)?2所围(x?y)d?(x?y)d????? dd(2)??ln(x?y)d?与??[ln(x?y)]d?,其中d是三角形闭区域,三顶点分别为(1,0),dd2(1,1),(2,0);2.利用二重积分的性质估计下列积分的值:(1)i?22sinxsinyd?,其中d?{(x,y)|0?x??,0?y??};??d(2)i?2222,其中d?{(x,y)|x?y?4}.(x?4y?9)d???d(3).i?d,其中d?{(x,y)|0?x?1,0?y?2}解 ?f?x,y??,积分区域的面积等于2,在d上f?x,y?的最大值m?14?x?y?0?,最小值m?1?5?x?1,y?2? 故0.4?i?0.5习题10-2二重积分的计算法1.计算下列二重积分:(1)??(x2?y2)d?,其中d?{(x,y)||x|?1,|y|?1};d(2)??sinyd?,其中d是由y?x,y2?x所围成的闭区域. dy解:??sinyd??dy?10dy?ysinyy2ydx?1?sin1 2.画出积分区域,并计算下列二重积分:(1)??ex?yd?,其中d?{(x,y)||x|?y?1}d(2)22(x?y?x)d?,其中d是由直线y?2,y?x及y?2x所围成的闭区域。
??d3.化二重积分i???f(x,y)d?为二次积分(分别列出对两个变量先后次序不同的两个二次d积分),其中积分区域d是:(1)由直线y?x及抛物线y2?4x所围成的闭区域;(2)由直线y?x,x?2及双曲线y?1(x?0)所围成的闭区域。
x4.求由曲面z?x2?2y2及z?6?2x2?y2所围成的立体的体积。
5.画出积分区域,把积分22其中积分区域d是: ??f(x,y)dxdy表示为极坐标形式的二次积分, d(1){(x,y)|x?y?2x};(2){(x,y)|0?y?1?x,0?x?1}6.化下列二次积分为极坐标形式的二次积分:(1?2dxxfdy;【篇二:高等数学2第十章答案_62010】=txt>1.根据二重积分的性质,比较下列积分的大小:(1)成;2223d与,其中积分区域是圆周(x?2)?(y?1)?2所围(x?y)d?(x?y)d????? dd(2)??ln(x?y)d?与??[ln(x?y)]d?,其中d是三角形闭区域,三顶点分别为(1,0),dd2(1,1),(2,0);2.利用二重积分的性质估计下列积分的值:(1)i?22sinxsinyd?,其中d?{(x,y)|0?x??,0?y??};??d(2)i?2222,其中d?{(x,y)|x?y?4}.(x?4y?9)d???d(3).i?d,其中d?{(x,y)|0?x?1,0?y?2}解f?x,y??,积分区域的面积等于2,在d上f?x,y?的最大值1m??x?y?0?,最小值m???x?1,y?2? 45故0.4?i?0.5习题10-2二重积分的计算法1.计算下列二重积分:(1)22(x?y)d?,其中d?{(x,y)||x|?1,|y|?1};??d(2)??xcos(x?y)d?,其中d是顶点分别为(0,0),(?,0)和(?,?)的三角形闭区域。
日本古代令制国石高数

28
29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46
地区 京畿 京畿 京畿 京畿 京畿 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东海道 东山道 东山道 东山道 东山道 东山道 东山道 东山道
17.7 18.6 19.4 16.8 27 24.4 6.2 18.4 12.6 36.6 20.26 33.6 26.6 14 41.8 31 34.1 17 28 17.5 0.53 1.6
山口
6
51 山阳道 长门
山口
6
52 南海道 纪伊
和歌山、三重
7
53 南海道 淡路
兵库
2
54 南海道 阿波
德岛
9
55 南海道 赞岐
香川
11
56 南海道 伊予
爱媛
14
57 南海道 土佐
高知
7
58 西海道 筑前
福冈
15
59 西海道 筑后
福冈
10
60 西海道 丰前
大分
8
61 西海道 丰后
大分
8
62 西海道 肥前
郡数 8 15 15 3 13 4 15 2 8 8 14 7 4 3 8 21 4 11 12 11 13 18 4 10 14 9 54
12
3 12 4 4 4 7 3 6 5 8 7 6 10 6 4 14 7 11
47 山阳道 备中
2021年重庆专升本高数真题答案

重庆市2021年普通高校专升本选拔考试《高等数学》试 题(回忆版)一、单项选择题(本大题共8小题,每小题4分,满分32分)1.当0→x 时,下列为无穷小量是( C )。
A.sin 1xB.cos xC.sin x 2D. arccos x 2.若级数∑1n p+1∞n=1收敛,则p 的取值范围为( C )。
A. (1,+∞)B. [1,+∞)C. (0,+∞)D. [0,+∞)3.设平面π1: x-5y+2z+1=0,π2:2x-2y+2z+1=0 ,π3:4x+2y+3z-1=0,则下列关系式正确的是( C )。
A. π1⊥π2B. π1∥π2C. π1⊥π3D. π1∥π34.下列广义积分发散的是( D )。
A. ∫11+x 2ⅆx +∞0 B. ∫√1−x 210 C. ∫e −x ⅆx +∞0 D. ∫ln x xⅆx +∞1 5.求微分方程y ′′+4y ′−5y =0通解是( A )。
A. y =C 1ⅇx +C 2ⅇ−5x B. y =C 1ⅇ−x +C 2ⅇ5xC. y =(C 1+C 2x )ⅇxD. y =(C 1+C 2x )ⅇ5x6. ∫[f (x )−f (−x )]cos x ⅆx =a−a ( D )。
A. f (a )B. 2f (a )C. 2f (a )cos aD.07.已知AB =O 则,下列说法正确的是( C )。
A. A =O 或B =OB. r (A )+r (B )=0C. |A |=0或|B |=0D. r (A )+r (B )=m 8.设A,B 为两个随机事件,则下列等式正确的是( A )。
A. (A ∪B )−B =AB. (A ∪B )∪B =AC. A ∪B ̅̅̅̅̅̅̅̅=A ̅∩B ̅D. A ∪B ̅=AB ̅∪A B 二、填空题(本大题共4小题,每小题4分,满分16分)9.极限lim n→∞sin nx n= 0 。
10. f (x )=∫ⅇt 2ⅆt x 20,则f ′(1)= 2e 。
高职类学生成绩大数据与生源类型相关性分析及对策研究
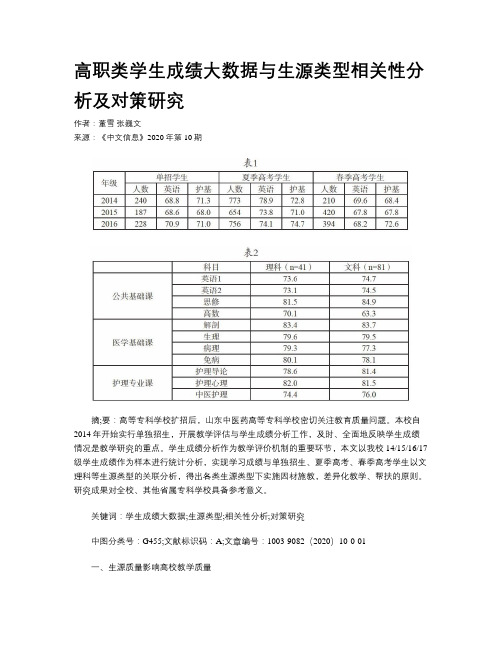
高职类学生成绩大数据与生源类型相关性分析及对策研究作者:董雪张巍文来源:《中文信息》2020年第10期摘;要:高等专科学校扩招后,山东中医药高等专科学校密切关注教育质量问题。
本校自2014年开始实行单独招生,开展教学评估与学生成绩分析工作,及时、全面地反映学生成绩情况是教学研究的重点。
学生成绩分析作为教学评价机制的重要环节,本文以我校14/15/16/17级学生成绩作为样本进行统计分析,实现学习成绩与单独招生、夏季高考、春季高考学生以文理科等生源类型的关联分析,得出各类生源类型下实施因材施教,差异化教学、帮扶的原则。
研究成果对全校、其他省属专科学校具备参考意义。
关键词:学生成绩大数据;生源类型;相关性分析;对策研究中图分类号:G455;文献标识码:A;文章编号:1003-9082(2020)10-0-01一、生源质量影响高校教学质量教学工作一直是学校的中心工作,全面提高教学质量是学校的首要任务。
其中高校教学质量的高低受到多种因素的影响,其中主要的影响因素有师资力量、生源类型与类型、学风建设、教学方法等。
对影响因素进行精细化分析,能够理性的挖掘教学质量受各影响要素影响的程度,并以提高教学质量为目标,抓学风建设为手段,研究不同的影响要素下的差异化教学方式,提升教学认知水平。
山东中医药高等专科学校从2014年开始实行单独招生,目前学校有三种生源,单独招生学生,夏季高考学生,春季高考学生;同时学校招生时文理兼收(除药学以外)。
在日常教学过程中,对不同生源学生学习能力都会有主观的认识评价,利用大数据分析手段,通过客观的学生成绩数据分析,实现生源类型对学生成绩影响的相关性分析工作是教学评价机制的首要任务。
进一步研究不同生源类型下,实施差异化教学方式是提高学生成绩、升学率、就业率的关键。
二、生源类型与学生成绩相关性分析学习成绩是高校生源质量评价体系里的重要内容。
现以本校护理专业2014-2017级护理系学生为研究对象,对多维生源类型学生的主要科目考试成绩进行分析,挖掘内在的规律。
高数

1.已知b a ,为常数,3122lim2=-++∞→x bx ax x ,则=a _ ,=b _ ; 解 ∞→x 时极限值存在且值为3,则分子、分母x 的最高次幂应相同,所以0=a ,那么 32122lim 122lim 122lim 2==-+=-+=-++∞→∞→∞→b xx b x bx x bx ax x x x ,所以6=b . 2.0=x 是xxx f sin )(=的 __ 间断点; 解 0=x 时,函数xx x f sin )(=无定义,但1sin lim0=→x xx ,极限存在,所以0=x 是xxx f sin )(=的可去间断点. 3.2x =是221()32x f x x x -=-+的 间断点;解:无穷.4.1x =是221()32x f x x x -=-+的 间断点;解:可去。
5.0=x 是10100 xe x y x x x ⎧<⎪⎪==⎨⎪>⎪⎩的____ 间断点;解:可去。
6.()()2211lim 1sin1x x x →--=________________.解:07.1lim arctan x x x →∞=________________. 解:08.sin cos limx x xx→∞+= _______________.解:09.2121lim 11x x x →⎛⎫- ⎪--⎝⎭ = ______________. 解:12-10.cos limx x xx→∞-=______________.解:111.(1)lim 1n n n →∞⎡⎤-+⎢⎥⎣⎦ =______________. 解:112.limx →∞=______________.解:013.1lim1x x →-=______________.14.1lim tan x x x →∞=______________. 解:115.1lim 2sin2x xx →+∞=______________. 解:116.21sin (1)lim 1x x x →--=______________. 解:017.()1lim 12xx x →-=______________.解:2e -18.22lim 1x x x +→∞⎛⎫+ ⎪⎝⎭=______________.解:2e19.121lim 21x x x x +→∞-⎛⎫ ⎪+⎝⎭=______________.解:1e -20.11lim 1x x x x +→∞-⎛⎫ ⎪+⎝⎭=______________.解:1e -21.11lim 11x x x +→∞⎛⎫- ⎪+⎝⎭=______________.解:1e -22.12lim 121x x x +→∞⎛⎫- ⎪+⎝⎭=______________.解:1e -23.01cos limsin x xx x→-=______________.解:1224.lim 0)x a +→≠=______________.25.2lim cos 3x x π→=______________.解:126.()22lim 21x x x →-+=____________.解:7选择题1.下列极限存在的是( )(A) xx 4lim ∞→; (B) 131lim 33-+∞→x x x ; (C) x x ln lim 0+→; (D) 11sin lim 1-→x x .解析 (A)04lim =-∞→x x ,+∞=+∞→x x 4lim , 所以xx 4lim ∞→不存在;(B)311311lim 131lim 3333=-+=-+∞→∞→xx x x x x ,极限存在;(C)-∞=+→x x ln lim 0,所以x x ln lim 0+→不存在; (D)1→x 时,01→-x ,∞→-11x ,所以11sin lim 1-→x x 不存在.2.已知615lim=-+∞→x ax x ,则常数=a ( ).(A) 1; (B) 5 ; (C) 6 ; (D) -1.解析 C 611515lim ==-+=-+∞→a xx a x ax x ,所以 6=a . 3.xx f 12)(=在0=x 处 ( ).(A) 有定义; (B) 极限存在; (C) 左极限存在; (D) 右极限存在. 解析 C 因xx f 12)(=,在0=x 处无定义,02lim )(lim 100==--→→xx x x f ,即xx f 12)(=在0=x 处左极限存在, +∞==++→→xx x x f 102lim )(lim ,即xx f 12)(=在0=x 处右极限不存在, 由极限存在的充要条件,可知函数xx f 12)(=在0=x 处的极限不存在.4.当+∞<<x 0时,xx f 1)(=( D ). (A)有最大值与最小值; (B)有最大值无最小值;(C)无最大值有最小值; (D)无最大值无最小值. 解析 xx f 1)(=在()+∞,0上是连续函数,图形如下:所以当+∞<<x 0时,xx f 1)(=无最大值与最小值. 5.函数2()2x f x x +=+的连续区间是( )A []2,2-B ()2,-+∞C ),2()2,(∞+---∞D (,2)-∞-解: (C) 因为02≠+x ,即2-≠x ,所以连续区间是),2()2,(∞+---∞ ;6.0x =为函数sin 2()xf x x=的( ) A 连续点 B 跳跃间断点C 可去间断点D 第二类间断点 解:(C)0≠x 时函数有意义,而2222sin lim 2sin lim)(lim 000=⋅==→→→xxx x x f x x x ,所以0=x 为函数的可去间断点.7.下列各式中,正确的是 .A.B.2πarctan lim -=∞→x xC.D.解D 参见基本初等函数的图像,得到:0sin lim 0=→x x .8.设 则 _____________.A.1- B 1C.0D.不存在解 B 由函数图像及极限存在的判定定理得:1lim lim 11==+-→→x x x x ,因此, 1lim ()1x f x →=. 9.若 存在, 不存在,则下列命题正确的是____________ .A.存在 B. 不存在C.存在D. 与具体函数有关解.B . 由极限的四则运算法则,若)(lim 0x f x →存在,)(lim 0x g x →不存在,)]()([lim 0x g x f x ±→ 不存在.10.极限=________________.A.5B.C.D.解A .)10(lim 2x x x x -++∞→=xx x x x x ++-++∞→22210)10(lim=xx x x +++∞→21010lim=11/1010lim2+++∞→x x =5.11.=__________________.A.B.C.D.61解C . 330lim 3sin 2x x x →=301211lim ().3sin 2824x x x →⋅⋅= 12.=__________________.A.B.C.2πD.解. B . =∞→x x x 1t a n l i m=∞→x x x 11t a n lim .11c o s111s i nlim =⋅∞→xx x x 13.xx x 10)21(lim -→=_____________.A.1e- B.2eC.2e- D.e解C . xx x 10)21(lim -→ =)2(21])2(1[lim -⋅-→-+xx x =.e 1214.当 ,___________无穷小量?A.高阶B.低阶C.等价D.同阶解D .=→x x x 2sin 3tan lim0=⋅→x x x x x 2sin 33tan 223lim 0⋅→x x x 2sin 2lim 230=→xx x 33tan lim023, 由无穷小的比较的定义,两者为同阶无穷小.15.函数11)(++=x x x f 的连续区间是_____________.A.[1-,1]B.(1-,+)∞C. D.解C . 因11)(++=x x x f 是初等函数,则求其连续区间就是求其定义域,则1-≠x ,即),1()1,(∞+---∞ 为函数的定义区间,即为函数的连续区间.16.若41,1,()1,1,x x f x x a x ⎧-≠⎪=-⎨⎪=⎩ 为___________时,在 处连续.A.B. 4C.1-D.1解B . 因为 =--→11lim41x x x ()()=-+-+→111)1(lim 21x x x x x ()(),411lim 21=++→x x x 由连续定义,所以 ()()41lim 1===→a f x f x .17.=_____________.A.B.C.2πD.解D .]ln tan [ln lim 0x x x -→==→xx x tan lnlim 0=→xx x tan limln 00tan limln 0=→xx x .判断题1. 若函数)(x f 在0x 处极限存在,则)(x f 在0x 处连续. ( × )解析 函数在一点连续,要求函数在该点极限存在,且极限值等于该点函数值.如函数⎩⎨⎧=≠=,0,1,0,)(x x x x f 0lim )(lim 00==→→x x f x x ,即函数)(x f 在0=x 处极限存在;但1)0(0)(l i m 0=≠=→f x f x ,所以函数⎩⎨⎧=≠=0,1,0,)(x x x x f 在0=x 处不连续. 2. 分段函数必有间断点. ( × )解析 分段函数不一定有间断点.如函数⎩⎨⎧<-≥=0,,0,)(x x x x x f 是分段函数,()0lim )(lim 00=-=--→→x x f x x ,0lim )(lim 0==++→→x x f x x ,所以0)(lim 0=→x f x ;又因为0)0(=f ,即)0()(lim 0f x f x =→,所以函数)(x f 在0=x 处连续,无间断点.3. x 3tan 与x 3sin 是0→x 时的等价无穷小. ( √ )解析 13cos 1lim 3sin 3tan lim00==→→xx x x x ,由等价无穷小的定义,x 3tan 与x 3sin 是0→x 时的等价无穷小.4. 无界函数不一定是无穷大量. ( √ )解析 无穷大必无界,但反之不真.如函数x x x f cos )(=,当∞→x 时是无界函数;但若取2ππ2+=n x ,∞→x (∞→n )时0cos )(==x x x f ,不是无穷大量. 5. 因为0lim()x xf x →存在,所以()f x 在0x 点必须有定义;( )解:(×)函数在一点的极限与函数在该点有无定义无关.6. 当0x x →时,函数在0x 的极限值不一定是0()f x ;解:(√)函数的极限是函数值无限接近的一个常数,不一定是该点的函数值.7. 无穷小量就是很小的数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年福建省普通高校专升本招生考试高等数学 试卷(考试时间120分钟,满分150分)考生答题注意事项:1、答题前,考生务必在试卷、答题卡规定的地方填写自己的准考证号、姓名。
考生要认真核对答题卡粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致。
2、本试卷分为两部分,第一部分为选择题,第二部分为非选择题。
选择题每小题选出答案后,用2B 铅笔将答题卡上的相应代码涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案代码。
非选择题用0.5毫米黑色签字笔在答题卡上书写作答,在试卷上作答无效。
3、考试结束后,考生必须将试卷和答题卡一并交回。
4、合理安排答题空间,超出答题区域无效。
第一部分 选择题一、单项选择题(本大题共1 0小题,每小题5分,共50分。
在每小题列出的四个备选项中只有一个是符合题目要求的,请选出并将答题卡上对应的答案代码涂黑,错涂、多涂或未涂均不得分)1.若()()()=⎪⎩⎪⎨⎧≥<≤--<-=2,2,1,22,0,2,1f f x x x x f 则【 】 A .-1 B .0 C .1 D .22.当x →0时,无穷小tan2x 是x 的【 】 A .高阶无穷小B .低阶无穷小C .等价无穷小D .同阶非等价无穷小3.下列各式中正确的是【 】A .B .()exx x 221lim =++∞→ C .2021lim e x xx =⎪⎭⎫ ⎝⎛++→ D .()e x xx =+→1lim 04.函数exy 2015=的一阶导函数='y 【 】 A . e 2015xB .2015xe 2015xC .2015e 2015xD .2015e x5.曲线x y 3=在区间()+∞,0上【 】A .单调上升且是凹的B .单调上升且是凸的C .单调下降且是凹的D .单调下降且是凸的6.下列函数在区间[-1,1]上满足罗尔中值定理所有条件的是【 】 A .y=2x+1B .y=|x|-1C .y=x 2 + 1D .y=112-x7.已知()()=+=⎰x f C x dx x f 则,sin 【 】A .sinxB .-sinxC .cosxD .-cosx8.点(1,2,3)关于x 轴的对称点是【 】 A .(-1,-2,-3)B .(1,-2,-3)C .(-1,2,-3)D .(-1,-2,3)9.二阶常系数齐次线性微分方程06'''=-+y y y 的通解是【 】 A .x xe C eC y 2231--+=B .x xe C eC y 2231+=-C .x xe C eC y 2231-+=D .x xe C eC y 2231+=10.设()c bx ax x x f +++=23,0x 是方程()0=x f 的最小的根,则必有【 】 A .()0'0<x fB .()0'0>x fC .()0'0≤x fD .()0'0≥x f第二部分 非选择题二、填空题(本大题共6小题,每小题5分,共30分。
把答案填在答题卡的相应位置上) 11.函数()()21ln x x f -=的连续区间为 .12.极限()=--→11sin lim21x x x . 13.曲线⎩⎨⎧==te y t x 3在t=1处的切线方程是 . 14.()=+-⎰dx x 3sin 2115 . e xx x 221lim =⎪⎭⎫⎝⎛+∞→15.=∞-⎰dx e x1 .16.记costdt t -0)()(χχχ⎰=Φ,则)('χΦ= . 三、计算题(本大题共6小题,每小题7分,共42分。
请在答题卡上作答) 17.求极限xxx 211cos 1lim 0+--→.18.已知函数()⎪⎩⎪⎨⎧=∈≠+=02,,,sin 2x Z k k x xax x x f ,π在点x=0处连续,求a 的值.19.已知函数()x y y =由方程22x xy e y=+确定,求()x y '.20.求定积分dx xnx 111e +⎰.21.求过直线L :12312zy x =-=-与平面π:022=-++z y x 的交点,且与直线L 垂直的平面方程.22.求常微分方程x xy y 22'=+的通解.四、应用题(本大题共2小题,每小题11分,共22分。
请在答题卡上作答) 23.已知平面图形D 由曲线xe y =,x y =,0=x ,1=x 围城. (1)求D 的面积A ;(2)求D 绕x 轴旋转一周所得旋转体的体积V.24.设A 生活区位于一直线河AC 的岸边,B 生活区与河岸的垂足C 相距2km ,且A 、B 生活区相距29km.现需要再、在河岸边修建一个水厂D (如图所示),向A 、B 生活区供水.已知从水厂D 向A 、B 生活区铺设水管的费用分别是30万元/km 和50万元/km ,求当水厂D 设在离C 多少km 时,才能使铺设水管的总费用最省?五、应用题(本大题共2小题,每小题11分,共22分。
请在答题卡上作答)25.设函数()⎪⎩⎪⎨⎧=≠+=.0,0,0,1sin 22x x xx xx f (1)证明()0=x x f 在处可导;(2)讨论是否存在点0=x 的一个邻域,使得()x f 在该领域内单调,并说明理由.CA2kmD B29km2015年福建省普通高校专升本招生考试高等数学 试卷参考答案一、选择题 1.B2.D3.A4.C5.A6.C7.C8.B9.B10.A二、填空题11.),1()1,(+∞--∞ 12.0.5 13.323e x e y +=14.615.e16.x sin三、计算题 17.0 18.2 19.xe yx y y 222+-=20.121.022=-++z y x 22.21x ce y -+=四、应用题 23.231-e )(;⎪⎭⎫ ⎝⎛-652122e π)( 24.0450)5(3045'''22>验证求到令,,目标函数,,为设y y x x y x BD x DA x CD =++-=+=-=结论:23=x五、证明题 25.思路2101sin2lim 0)0()(lim 1200=-+=--→→x x x x x f x f x x )用导数的定义证明:( (2)不存在2016年福建省专升本高等数学标准答案一、单项选择题(本大题共10小题,每小题5分,共50分)1. C. 2. C. 3. B. 4. C. 5. D. 6. A. 7. B. 8. B. 9. D. 10. A.二、填空题(本大题共6小题,每小题5分,共30分)11.22+sin x . 12.1. 13.21x +. 14.3. 15. 2. 16.1-.三、计算题(本大题共6小题,每小题7分,共42分)17.解:原式2202sin 12lim6124x xx →==⋅; 另解:原式0sin 1lim 66x x x →==. 18. 解:直线的方向向量是{}112m =-,由题意知,平面的法向量就是直线的方向向量,即{}112n m ==-;又平面过点(1,1,2)-,所以,平面方程为(1)2(1)(2)0x y z -++--=,即230x y z +-+=.19.解:1yy e y ''+=⋅,11yy e '=-. 20.解:原式1111()(1)1x x x x xd e xe e dx e e e e ==-=-=--=⎰⎰.21.解:232y x ax '=+,62y x a ''=+;由题意知,11620a b a ++=-⎧⎨+=⎩,31a b =-⎧⎨=⎩.22.解:111dy dx y x =--,1ln ln(1)y x C =--+,1C y x =-,(1C C e =). 四、应用题(本大题共2小题,每小题11分,共22分)23. 解: 设总利润为()L x ,由题意得()()()L x q P x C q =⋅-(420)(30000100)2qq q =--+2320300002q q =--,(0,)x ∈+∞, ()320L x q '=-,令()0L x '=,得320q =.依题意,最大利润存在,且驻点唯一. 所以,当生产320件时,获得的利润最大,此时产品的价格260P =元.24.解:220cos sin 1S xdx x ππ===⎰; 220cos x V xdx ππ=⎰222001cos 21(sin 2)2224x dx x x πππππ+==+=⎰. 五、证明题(本大题共1小题,每小题6分,共6分)25.证明(1)由题意知,220()0x x f x x x ⎧≥⎪=⎨-<⎪⎩,因为00()(0)lim lim 00x x f x f x x ++→→-==-,00()(0)lim lim 00x x f x f x x --→→-=-=-;所以,函数()f x 在0x =处可导,且(0)0f '=;(2)当0x >时,()20f x x '=>,所以函数()f x 在(0,)+∞内单调递增;当0x <时,()20f x x '=->,所以函数()f x 在(,0)-∞内单调递增; 且(0)0f '=,所以,函数()f x 在(,)-∞+∞内单调递增.版权所有 翻印必究 212017高数真题答案1-10:DCCBA DACBC;11. 3; 12. 2; 13. 1,+2⎛⎫∞ ⎪⎝⎭; 14. 1; 15. 0; 16. 1-; 17.解:原式211lim 1x x x →-=-()()121lim 1x x x →'-='-11lim 2x x →=12=; 18.解:由()20y e x y '++=,得20y ey y ''⋅++=,即21y y e -'=+,故01y y ='=-,因此切线方程:1y x=-; 19.解:(2ln 4y x x '⎡⎤'=+⎢⎥⎣⎦2244x x x x '=+++22144x x x ⎛⎫=++++24x =+20.解:原式()()1420121212x d x =++⎰()3420122123x =⋅⋅+263=; 21.解:将直线的参数方程21321x t y t z t =+⎧⎪=+⎨⎪=-⎩代入平面方程可得4t =-,所以交点为:()7,10,5---; 22.解:由公式法:()()1P x Q x ==,所以dx dx y e C e -⎛⎫⎰⎰=+ ⎪⎝⎭()x x e C e -=+; 23. 面积()2212A y y dy -⎡⎤=+-⎣⎦⎰92=, ()()2222211=3V V V h r rR R y dy -=-++-⎰ππ台圆内3372=2155-=πππ72=5π; 24. 解:(1) []0,2D :,()()26661f x x x x x '=-=-,令()0f x '=,得10x =、21x =,比大小:()01f =、()10f =、()25f =,综上可得:最小值为()10f =; (2) (),D -∞+∞:,()()2666f x x kx x x k '=-=-,令()0f x '=,得10x =、2x k =, 由0k >,得()0f k <,即()1,k ∈+∞.。
