圆锥的体积练习题(完美打印版)

合集下载

(完整版)圆锥的体积练习题

圆锥的体积练习题一、填空：1、等底等高的圆柱和圆锥，圆柱体的体积是90立方米，那么圆锥的体积是（）立方米。

2、等底等高的圆柱和圆锥，圆锥的体积是9立方米，圆柱体的体积是（）立方米。

3、等底等高的圆柱和圆锥，圆柱体的体积是33立方米，那么圆锥的体积是（）立方米。

二、判断。

①圆锥的体积等于圆柱体积的。

（）②两个体积相等的等底圆柱和圆锥，圆锥的高一定是圆柱高的3倍。

（）③一个圆锥形物体，底面积是a 平方米，高是b 米，它的体积是ab 立方米。

（）④把一根圆体木头，削成一个最大的圆锥体，削去体积是圆锥体积的2倍。

（）⑤圆柱体的体积一定比圆锥体的体积大（）⑥圆锥的体积等于和它等底等高圆柱体积的三分之一。

（）⑦正方体、长方体、圆锥体的体积都等于底面积×高。

（）⑧一个圆柱的体积是27立方米，和它等底等高的圆锥的体积是9立方米。

（）三、求下列各圆锥的体积：（1）底面周长是9.42米，高是1.8米；（2）底面半径是4厘米，高是21厘米；（3）底面直径是6分米，高是6分米；四、解决问题。

①一堆圆锥形的煤堆，底面半径是1.5 米，高是1.2 米。

如果每立方米煤约重1.4 吨，这堆煤有多少吨？②有一块正方体的木材，它的棱长是9分米，把这块木料加工成一个最大的圆锥体，被削去的体积是多少？③在打谷场上，有一个近似于圆锥的小麦堆，测得底面直径是4米，高是1.2米。

每立方米小麦约重735千克，这堆小麦约有多少千克？（得数保留整千克）④一个圆锥形沙堆，底面周长是25.12米，高1.5米，每立方米的沙重1.5吨，这堆沙有多少吨？⑤把一块底面半径2厘米、高6厘米的圆柱形泥巴捏成一个与圆柱底面相等的圆锥形。

请你算出它的高。

1．把圆柱的侧面沿高剪开，得到一个( )，这个( )的长等于圆柱底面的( )，宽等于圆柱的( )，所以圆柱的侧面积等于( )一、圆柱体积。

1. 求下面各圆柱的体积。

（1）底面积0.6平方米，高0.5米（2）底面半径是3厘米，高是5厘米。

六年级下学期数学圆锥的体积完整版题型总结带详细答案

圆锥的体积重要题型同步巩固及提升圆锥的体积公式是：（V=1/3Sh ）知识点强化：1、判断：（1）、圆锥的体积是圆柱的体积的1/3（×）（2）、一个圆锥的底面半径扩大3倍，它的体积也扩大3倍。

（×）（3）、一个正方体与一个圆锥的底面积和高都相等，这个正方体的体积是圆锥的体积的1/3。

（×）（4）、把一个圆柱削成一个圆锥，这个圆锥的体积是圆柱体积的1/3. （×）（5）、圆锥的体积比与他等底等高的圆柱的体积小2/3。

（√）2、填空（1）等底等高的圆柱和圆锥的体积相差16立方分米，这个圆柱的体积是（24）立方分米，这个圆锥的体积是（8 ）立方分米。

（2）等底等高的圆柱和圆锥的体积的和是96立方分米，这个圆柱的体积是（72）立方分米，这个圆锥的体积是（24 ）立方分米。

（3）等底等高的圆柱和圆锥，圆柱的体积比圆锥的体积多24立方分米，圆柱的体积是（36）立方厘米，圆锥的体积是（12 ）立方厘米。

例题强化拔高：例题1、在一个底面直径是20cm的圆柱形玻璃杯中放着一个底面直径为6cm，高20cm的圆锥形铁锤，铅锤没入水中，当铅锤从水中取出后，杯中的水将下降多少？（π取3.14.）铁锤的体积：3.14×（6÷2）×（6÷2）×20÷3=188.4（立方厘米）玻璃杯的底面积：3.14×（20÷2）×（20÷2）=314（平方厘米）水下降的高度：188.4÷314=0.6（厘米）例2、一个圆柱体形状的木棒，沿着底面直径竖直切成两部分，已知这两部分的表面积之和比圆柱体的表面积大2000cm2,则这个圆柱体木棒的侧面积是多少？dh=2000÷2=1000（平方厘米）侧面积=πdh=1000×3.14=3140(平方厘米)例3、一个底面直径是12cm的圆锥形木块，把它分成形状大小完全相同的两个木块后，表面积比原来增加了120cm2，这个圆锥形木块的体积是多少？增加的面积是两个三角形一个三角形的面积：120÷2=60（平方厘米）高：60×2÷12=10（厘米）半径：12÷2=6（厘米）体积：：1/3×3.14×6×6×10=376.8（立方厘米）例4、把一个底面直径是20cm的装有一些水的圆柱形玻璃杯，已知杯中水面距离杯口3cm，若将一个圆锥形铅垂完全浸入杯中，水会溢出20ml，求铅垂的体积。

圆锥体积练习题及答案

圆锥体积练习题及答案一、选择题1. 一个圆锥的底面半径为3cm，高为4cm，则该圆锥的体积是：A. 9πcm³B. 24πcm³C. 36πcm³D. 48πcm³答案：C2. 一个圆锥体的半径和高分别为r和h，如果将该圆锥的半径和高都增加到原来的2倍，则新圆锥的体积是原来的几倍？A. 4倍B. 6倍C. 8倍D. 16倍答案：D3. 一个圆锥的体积为400πcm³，底面半径为8cm，求该圆锥的高。

A. 5cmB. 10cmC. 15cmD. 20cm答案：D4. 若一个圆锥的体积为1000cm³，底面半径为r，则该圆锥的高等于多少？A. 10cmB. 20cmC. 30cmD. 40cm答案：A5. 一个圆锥的体积为125πcm³，高为10cm，求该圆锥的底面半径。

A. 2cmB. 3cmC. 4cmD. 5cm答案：B二、填空题1. 一个圆锥的底面直径为6cm，高为8cm，其体积为______cm³。

答案：48π2. 一个圆锥的底面半径为5cm，高为12cm，其体积为______cm³。

答案：100π3. 一个圆锥的体积为1000cm³，底面半径为10cm，则其高为______cm。

答案：104. 若一个圆锥的体积为2000πcm³，底面半径为15cm，则其高为______cm。

答案：85. 一个圆锥的体积为144πcm³，底面半径为6cm，则其高为______cm。

答案：8三、解答题1. 一个圆锥的体积为300πcm³，底面半径为4cm，求该圆锥的高。

解：已知圆锥的体积为300πcm³，底面半径为4cm。

圆锥体积的公式为V = (1/3)πr²h，代入已知数据可得：300π = (1/3)π(4)²h300π = (1/3)π(16)h300 = (1/3) × 16h900 = 16hh = 900 ÷ 16h ≈ 56.25所以，该圆锥的高约为56.25cm。

2022-2023学年人教版数学六年级下册圆锥的体积练习题(含答案)

原来的体积可表示为：
现在的体积表示为：
故答案为：C
【点睛】本题主要考查了圆柱体积公式的灵活运用。
10．C
【分析】圆柱的体积＝圆柱的底面积×圆柱的高，圆锥的体积＝圆锥的底面积×圆锥的高× ，假设圆柱的高是1，圆锥的高则是4，圆柱的底面积是2，则圆锥的底面积是1，即可得出圆柱的体积∶圆锥的体积＝（2×1）∶（1×4× ），再根据比的基本性质进行化简即可得出答案。
23．如图，圆锥形容器中装有水40升，水面高度是这个容器的一半，这个容器最多能装水多少升？
24．用一块长18.84分米，宽5分米的长方形铁皮做一个高5分米的圆柱形水桶的侧面，再配一个底做成圆柱形水桶。做这样一个水桶还需要多少平方分米的铁皮？这个水桶最多可盛水多少升？
25．用铁皮制作一个有盖的圆柱形铁桶，底面半径是3dm，高是6dm。
【详解】A．圆柱的体积是圆锥体积的3倍，所以原说法错误；
B．圆柱的体积比圆锥体积多2倍，所以原说法错误；
C．圆锥的体积是圆柱体积的，所以原说法错误；
D．圆锥的体积比圆柱体积少，所以原说法正确。
故答案为：D
【点睛】本题考查圆柱和圆锥的体积关系，等底等高的圆柱的体积是圆锥体积的3倍。
13．C
【分析】把圆柱形木料截成3个小圆柱，表面积增加了4个底面的面积，其中一个底面的面积＝增加的表面积÷4；原来这根木料的体积＝底面积×高。
【详解】36÷3＝12（厘米）
【点睛】掌握圆柱、圆锥等体积等底时，它们高的关系是解题的关键。
【详解】解：设有水部分底面半径为r，则
r∶4＝5∶7
7r＝20
r＝
3×42×3＋3×42×7× －3× ×5×
＝144＋112－3× ×5×
＝256－

六年级数学下册圆柱和圆锥的体积及答案练习题苏教版

（苏教版）六年级数学下册圆柱和圆锥的体积班级______姓名______一、圆柱体积。

1. 求下面各圆柱的体积。

（1）底面积0.6平方米，高0.5米（2）底面半径是3厘米，高是5厘米。

（3）底面直径是8米，高是10米。

（4）底面周长是25.12分米，高是2分米。

2. 有两个底面积相等的圆柱，第一个圆柱的高是第二个圆柱的4/7。

第一个圆柱的体积是24立方厘米，第二个圆柱的的体积比第一个圆柱多多少立方厘米？3. 在直径0.8米的水管中，水流速度是每秒2米，那么1分钟流过的水有多少立方米？4. 牙膏出口处直径为5毫米，小红每次刷牙都挤出1厘米长的牙膏。

这支牙膏可用36次。

该品牌牙膏推出的新包装只是将出口处直径改为6毫米，小红还是按习惯每次挤出1厘米长的牙膏。

这样，这一支牙膏只能用多少次？5. 一根圆柱形钢材，截下1.5米，量得它的横截面的直径是4厘米。

如果每立方厘米钢重7.8克，截下的这段钢材重多少千克？（得数保留整千克数。

）6. 把一个棱长6分米的正方体木块，削成一个最大的一圆柱体，这个圆柱的体积是多少立方分米？7. 右图是一个圆柱体，如果把它的高截短3厘米，它的表面积减少94.2平方厘米。

这个圆柱体积减少多少立方厘米？二、圆锥体积。

1.选择题。

（1）一个圆锥体的体积是a 立方米，和它等底等高的圆柱体体积是( )。

① 31a 立方米 ② 3a 立方米 ③ 9立方米（2）把一段圆钢切削成一个最大的圆锥体，圆柱体体积是6立方米，圆锥体体积是( )立方米。

① 6立方米 ② 3立方米 ③ 2立方米2.判断对错。

（1）圆柱的体积相当于圆锥体积的3倍。

………（）（2）一个圆柱体木料，把它加工成最大的圆锥体，削去的部分的体积和圆锥的体积比是 2 ：1。

………（）（3）一个圆柱和圆锥等底等高，体积相差21立方厘米，圆锥的体积是7立方厘米。

………（）3.填空。

（1）一个圆柱体积是18立方厘米，与它等底等高的圆锥的体积是（）立方厘米。

《圆锥的体积》练习题

圆锥的体积练习题姓名：学号：1.填一填。

（1）准备等底等高的圆柱形容器和圆锥形容器各一个，将圆锥形容器装满沙子，再倒入圆柱形容器，（）次能倒满。

或将圆柱形容器装满水，再倒入圆锥形容器，能将圆锥形容器倒满（）次。

因为圆柱的体积＝（）×（），所以圆锥的体积＝（），用字母表示圆锥的体积计算公式是（）。

（2）一个圆柱和一个圆锥等底等高，如果圆锥的体积是9dm3，那么圆柱的体积是（）；如果圆柱的体积是9dm3，那么圆锥的体积是（）。

（3）下图中，圆锥（）的体积与圆柱的体积相等。

（4）一个圆锥的底面直径和高都是6cm，那么这个圆锥的体积是（）cm3。

（5）一个圆锥的体积是15.7m3，底面积是3.14m2，那么它的高是（）m。

（6）将24个圆锥形铁块熔化后，可以重新铸成和原来圆锥形铁块等底等高的圆柱形铁块（）个。

（损耗忽略不计）（7）圆柱底面半径是圆锥底面半径的3倍，它们的高相等，那么圆柱体积是圆锥体积的（）倍。

（8）一个圆锥形沙堆，底面积是12m2，高是1.5m，用这堆沙铺在长8m、宽5m的长方体跳远坑中，厚（）m。

（9）一个圆锥的底面半径是3cm，高是6cm，它的体积是（）cm³；与这个圆锥等底等高的圆柱的体积是（）cm³。

（10）一个圆锥的底面周长是18.84dm，高是5dm，它的体积是（）dm³。

（11）把一个体积为94.2cm³的圆柱木料削成个最大的圆锥，这个圆锥的体积是（）cm³，削去部分的体积是（）cm³。

（12）一个圆柱与一个圆锥的底面积相等，体积也相等。

若圆锥的高是1.8dm，则圆柱的高是（）dm；若圆柱的高是1.8dm，则圆锥的高是（）dm。

2.有一堆圆锥形的沙子，底面直径是12m，高是5m。

（1）这堆沙子有多少立方米？（2）如果把这堆沙子以3cm的厚度铺在宽10m的路上，能铺多长的路？3.计算下面圆锥的体积。

4.一个圆锥形路障警示标志如下图，这个路障标志的体积约是多少立方厘米？5.把一个体积是282.6cm³的铁块熔铸成一个底面半径为6cm的圆锥形机器零件，圆锥形零件的高是多少厘米？6.如图，先将甲容器注满水，再将甲容器中的水倒入空的乙容器中，这时乙容器中的水面有多高？7.把一个横截面是正方形的长方体木块削成个最大的圆锥。

锥体体积练习题

锥体体积练习题问题1. 高为9cm，底面积为16cm²的圆锥的体积是多少？2. 一张圆形硬纸板直径为50cm，从它的一个边缘开始割开，沿着直径割下一个扇形，另一个扇形面积为$\frac{3}{4}$圆面积。

将剩下的部分折成一个圆锥，求这个圆锥的高和体积3. 圆锥的底半径为r，母线长L，求圆锥的体积4. 底面为直径为50cm的圆锥的高为80cm，一层面积为4cm²的涂料要刷两遍，每遍比上一遍多用涂料$\frac{1}{6}$。

那么需用多少只4cm宽的刷子？5. 钢球是由两个半球熔接而成，每个半球的半径均为5cm，则整个钢球的体积为多少？解答1. 圆锥体积公式为$V=\frac{1}{3}S_hh$，其中$S_h$为底面积，$h$为高。

代入数据可得：$V=\frac{1}{3}\times16\times9=48(cm^3)$。

2. 设所割扇形的圆心角为$2\theta$，则可得$\frac{3}{4}\pir^2=\frac{1}{2}\pi r^2\sin\theta$，解得$\sin\theta=\frac{3}{8}$。

圆锥的底直径为50cm，半径为25cm，所以底圆周长为$C=2\pir=50\pi$，剩余部分的周长为$\frac{3}{4}\times2\pir=\frac{3}{4}\times25\pi$。

将剩余部分展开，可看作是圆锥的侧面积，所以有$C=2\pi r=L\sin\theta+\pi r$，带入数据计算可得$L=15.92$，以及圆锥的高$h=r\cos\theta$，带入数据计算可得$h=24.34$。

所以圆锥的体积为$V=\frac{1}{3}\times\pi r^2\timesh=3026(cm^3)$。

3. 圆锥体积公式为$V=\frac{1}{3}\pi r^2h$。

设底面半径为$r$，母线长为$L$，则分解出一个等腰三角形，可得$h=\sqrt{L^2-r^2}$，带入圆锥体积公式，可得$V=\frac{1}{3}\pi r^2\sqrt{L^2-r^2}$。

人教版六年级数学下册圆柱与圆锥体积专项练习题精选

人教版六年级数学下册圆柱与圆锥体积专项练习题精选1.把圆柱的侧面沿着高剪开，得到一个矩形，这个矩形的长等于圆柱底面的周长，宽等于圆柱的高，所以圆柱的侧面积等于底面周长乘以高。

2.单位换算：1升=1000毫升=1立方分米=1000立方厘米1平方米=平方分米，1公顷=平方米415平方厘米=41.5平方分米，4.5立方米=4500立方分米2.4立方分米=2400毫升，4070立方分米=4.07立方米3立方分米40立方厘米=3040立方厘米325立方米=立方分米，5380毫升=5.38升380毫升3.基础练：1.将4个棱长为1分米的正方体拼成一个长方体，这个长方体的表面积是20平方分米，体积是4立方分米。

2.一个圆柱底面半径2分米，侧面积是113.04平方分米，这个圆柱体的高是9分米。

4.把一根圆柱形木料截成3段，表面积增加了45.12平方厘米，这根木料的底面积是15.04平方厘米。

5.一个圆柱体的底面半径为r，侧面展开图形是一个正方形。

圆柱的高是r根2.6.一个圆柱的底面周长是12.56厘米，高是6厘米，那么底面半径是2厘米，底面积是4平方厘米，侧面积是75.36平方厘米，体积是50.24立方厘米。

7.一个圆柱和一个圆锥的底面积相等，高也相等，那么圆柱的体积是圆锥的3倍，圆柱的体积的2/3就等于圆锥的体积。

8.一个圆柱体和一个圆锥体的底面积和体积分别相等，已知圆柱体的高6厘米，那么圆锥体的高是4厘米。

9.等底等高的圆柱和圆锥的体积相差16立方米，这个圆柱的体积是32立方米，圆锥的体积是16立方米。

10.一个体积为60立方厘米的圆柱，削成一个最大的圆锥，这个圆锥的体积是40立方厘米。

11.圆柱的底面半径是3厘米，体积是6.28立方厘米，这个圆柱的高是2厘米。

12.一个圆柱体高4分米，体积是40立方分米，比与它等底的圆锥体的体积多10立方分米。

这个圆锥体的高是6分米。

13.把一段圆钢切削成一个最大的圆锥体，切削掉的部分重8千克，这段圆钢重16千克。

圆锥的体积典型例题及答案

圆锥的体积答案典题探究例1．圆锥的体积是它等底等高圆柱体积的，所以圆柱的体积比它等底等高的圆锥体积大．×．（判断对错）考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：因为一个圆柱的体积是与它等底等高的圆锥体积的3倍，所以圆柱体积比与它等底等高的圆锥体积大2倍．解答：解：因为一个圆柱的体积是与它等底等高的圆锥体积的3倍，所以圆柱体积比与它等底等高的圆锥体积大：（3﹣1）÷2=2倍．故答案为：×．点评：此题是考查圆柱、圆锥的关系，要注意圆柱和圆锥在等底等高的条件下体积有3倍或的关系．例2．如果圆柱体积是圆锥体积的3倍，那么它们一定等底等高．√．（判断对错）考点：圆锥的体积．专题：立体图形的认识与计算．分析：因为等底等高的圆柱体的体积是圆锥体体积的3倍，所以如果圆柱体积是圆锥体积的3倍，那么它们一定等底等高．据此解答即可．解答：解：因为等底等高的圆柱体的体积是圆锥体体积的3倍，所以如果圆柱体积是圆锥体积的3倍，那么它们一定等底等高．说法正确．故答案为：√．点评：本题要结合圆柱的体积和圆锥的体积计算公式进行判断．例3．一个圆锥体的底面半径是3分米，高是6分米，它的体积是56.52立方分米．考点：圆锥的体积．专题：立体图形的认识与计算．分析：圆锥的体积公式：V=sh=πr2h，已知底面半径是3分米，高是6分米．据此解答．解答：解：×3.14×32×6=×3.14×9×6=56.52（立方分米）答：它的体积是56.52立方分米．故答案为：56.52．点评：本题主要考查了学生对圆锥体积公式的掌握．例4．一个圆锥和一个圆柱等底等高，它们的体积相差20立方厘米，那么圆柱的体积是30立方厘米．考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：等底等高的圆柱的体积是圆锥体积的3倍，因此它们的体积差除以2就是圆锥的体积，用圆锥的体积乘3就是圆柱的体积．解答：解：20÷2=10（立方厘米）；10×3=30（立方厘米）．答：圆柱的体积是30立方厘米．故答案为：30立方厘米．点评：本题考查的目的是使学生理解掌握：等底等高的圆柱与圆锥之间的体积关系，即等底等高的圆柱是圆锥体积的3倍．据出关系可以解决有关的实际问题．例5．一个圆柱形橡皮泥，底面积是12平方厘米，高是5厘米．如果把它捏成同样高的圆锥，这个圆锥的底面积是多少？考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：压轴题；立体图形的认识与计算．分析：根据题意可知，圆柱形橡皮泥捏成圆锥形后，体积不变，根据v=sh，所以先求出橡皮泥的体积，然后根据“s=v×3÷h”求出圆锥的高．解答：解：橡皮泥的体积：12×5=60（cm3），圆锥的高：60×3÷5=36（cm2）；答：圆锥的底面积是36厘米2．点评：此题主要考查圆柱的体积公式及有关圆锥体积公式的应用．例6．把三角形ABC沿着边AB或BC分别旋转一周，得到两个圆锥（如图1、图2），（单位：厘米）谁的体积大？大多少立方厘米？考点：圆锥的体积．专题：压轴题．分析：由图1可知，圆锥的底面半径是3厘米，高是6厘米，由图2可知，圆锥的底面半径是6厘米，高是3厘米，利用公式解答即可．解答：解：（1）3.14×32×6÷3=3.14×9×6÷3=56.52（立方厘米）；（2）3.14×62×3÷3=3.14×36×3÷3=113.04（立方厘米）；113.04﹣56.52=56.52（立方厘米）；答：图2的体积大，大56.52立方厘米．点评：此题主要考查圆锥体积的计算，可以直接利用公式解答．演练方阵A档（巩固专练）一．选择题（共15小题）1．（•长寿区）一个圆柱体和一个圆锥体的底面积相等，圆锥的高是圆柱高的3倍．则圆锥的体积（）圆柱的体积．A．小于B．等于C．大于D．无选项考点：圆锥的体积；圆柱的侧面积、表面积和体积．分析：根据题干，设圆柱和圆锥的底面积相等是S，设圆柱的高是h，则圆锥的高是3h，由此利用圆柱和圆锥的体积公式求出它们的体积即可解答．解答：解：设圆柱和圆锥的底面积相等是S，设圆柱的高是h，则圆锥的高是3h，圆柱的体积是：Sh，圆锥的体积是：S×3h=Sh，所以圆柱的体积与圆锥的体积相等．故选：B．点评：此题考查了圆柱与圆锥的体积公式的灵活应用．2．（•北京模拟）如果一个圆锥体的底面半径扩大2倍，高缩小为原来的一半，它的体积是原来体积的（）A．2倍B．一半C．不变考点：圆锥的体积．分析：根据圆锥的体积公式，v=sh÷3，圆锥体的底面半径扩大2倍，它的底面积就扩大4倍，因为圆的半径扩大2倍圆的面积就扩大4倍，高缩小为原来的一半，由此得解．解答：解：圆锥体的底面半径扩大2倍，它的底面积就扩大4倍，又知高缩小为原来的一半，由此得此它的体积就扩大2倍．故选A．点评：此题的解答主要根据因数与积的变化规律来解答，3．（•福田区模拟）一个圆柱和一个圆锥的底面直径相等，圆锥的高是圆柱的3倍，圆锥的体积是12立方分米，圆柱的体积是（）立方分米．A．12B．36C．4考点：圆锥的体积；圆柱的侧面积、表面积和体积．分析：一个圆柱和一个圆锥的底面直径相等，则它们的底面积就相等，根据圆柱和圆锥的体积公式即可解答．解答：解：一个圆柱和一个圆锥的底面直径相等，则它们的底面积就相等，圆柱的体积=底面积×高，圆锥的体积=×底面积×高，圆锥的高是圆柱的3倍，所以圆柱和圆锥的体积相等，也是12立方分米．故选：A．点评：此题考查了圆柱与圆锥的体积公式的灵活应用．4．（•临川区模拟）用一个高是30厘米的圆锥体容器装满水，倒入和它等底等高的圆柱体容器中，水的高度是（）厘米．A．10B．90C．20考点：圆锥的体积；圆柱的侧面积、表面积和体积；立体图形的容积．分析：由于水的体积没变，倒入和它等底等高的圆柱体容器中，水在圆柱体的容器的高是圆锥高的，由此解答即可．解答：解：30×=10（厘米）；答：水的高是10厘米；故选：A．点评：此题考查的目的是，理解和掌握等底等高圆柱和圆锥，圆锥的体积是圆柱体积的．5．（•广州模拟）大小两个圆柱的高相等，大圆柱的半径是小圆柱半径的2倍，大小两个圆柱的体积比是（）A．1：2B．1：4C．4：1D．2：1考点：圆锥的体积；比的意义；圆柱的侧面积、表面积和体积．分析：根据圆柱体的体积公式，v=sh，再利用因数与积的变化规律即可解答．解答：解：两个圆柱的高相等，大圆柱的半径是小圆柱半径的2倍，因为圆的半径扩大2倍圆的面积就扩大4倍，由此得出大圆柱的体积是小圆柱的4倍，即大小两个圆柱的体积比是：4：1．故选：C．点评：此题主要考查圆柱和圆锥的体积计算，及圆的半径扩大2倍圆的面积就扩大4倍．6．（•保靖县）右图中圆锥体积是圆柱体积的，那么圆锥的高是（）cm．A．2B．6C．18考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：根据题干可得：圆柱与圆锥的底面积相等，圆锥体积是圆柱体积的；因为等底等高的圆锥的体积是圆柱的体积的，由此可得这个圆柱与圆锥的高相等．解答：解：根据题干分析可得：圆柱与圆锥的底面积相等，圆锥体积是圆柱体积的；因为等底等高的圆锥的体积是圆柱的体积的，由此可得这个圆柱与圆锥的高相等，也是6厘米．故选：B．点评：此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用．7．（•和平区）一个圆柱和一个圆锥，底面积和高分别相等．若圆柱的体积是2.4立方米．则圆锥的体积是（）立方米．A．0.8B．3.6C．4.8D．7.2考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：根据题意，根据圆锥的体积等于与它等底等高的圆柱体积的，已知圆柱的体积是2.4立方米，据此解答．解答：解：2.4×=0.8（立方米），答：圆锥的体积是0.8立方米．故选：A．点评：此题主要根据等底等高的圆锥的体积是圆柱体积的，再根据一个数乘分数的意义，用乘法解答．8．（•北京）把一个圆柱削成一个和它等底等高的圆锥，削去部分的体积是圆柱体积的（）A．3倍B．2倍C．考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：因为圆柱的体积等于和它等底等高的圆锥体积的3倍，所以削去部分的体积是圆锥体积的2倍，是圆柱的体积的（1﹣）；据此解答即可．解答：解：由分析可知：把一个圆柱形的木块削成一个和它等底等高的圆锥，削去部分体积是这个圆柱体积的：1﹣=．答：削去部分的体积是圆柱体积的．故选：C．点评：此题利用“圆柱的体积等于和它等底等高的圆锥体积的3倍”这一知识点来解答．9．（•铁山港区模拟）如果圆锥体的底面半径扩大2倍，高不变，那么这个圆锥体的体积扩大（）倍．A．2B．4C．8考点：圆锥的体积；积的变化规律．专题：立体图形的认识与计算．分析：根据圆锥的底面积和体积公式和积的变化规律即可判断．解答：解：（1）圆锥的底面积=πr2，底面半径扩大2倍，根据积的变化规律可得：圆锥的底面积就扩大2×2=4倍，（2）圆锥的体积=×底面积×高，高一定时，根据积的变化规律可得：底面积扩大4倍，圆锥的体积就扩大4倍，故选：B．点评：此题考查了积的变化规律在圆锥的体积公式中的灵活应用．10．（•宝安区）一个圆柱和一个圆锥的体积和底面积分别相等，圆柱的高与圆锥的高的比是（）A．1：1B．1：2C．1：3D．3：1考点：圆锥的体积；比的意义；圆柱的侧面积、表面积和体积．专题：比和比例；立体图形的认识与计算．分析：根据圆柱的体积公式V=sh，圆锥的体积公式V=sh，当圆柱和圆锥的体积、底面积分别相等时，圆柱的高是圆锥的高的，由此求出圆柱的高，进而做出选择．解答：解：因为，圆柱的体积公式V=sh，圆锥的体积公式V=sh，所以，当圆柱和圆锥的体积、底面积分别相等时，圆柱的高是圆锥的高的，故选：C．点评：此题主要考查了利用圆柱与圆锥的体积公式，推导出在体积、底面积分别相等时，圆柱的高与圆锥的高的关系．11．（•广汉市模拟）一个长方体和一个圆锥体的底面积和高分别相等，长方体体积是圆锥体积的（）A．3倍B．2倍C．D．无法确定考点：圆锥的体积；圆柱的侧面积、表面积和体积．分析：长方体的体积=底面积×高；圆锥的体积=×底面积×高，由此公式即可得出长方体体积与圆锥的体积的倍数关系．解答：解：长方体的体积=底面积×高；圆锥的体积=×底面积×高，若它们的底面积和高分别相等，则：长方体的体积是圆锥的体积的3倍，故选：A．点评：此题考查了长方体和圆锥的体积公式的灵活应用，得出结论：等底等高的长方体体积是圆锥的体积的3倍．12．（•天河区）一个圆柱和一个圆锥等底等高，圆柱的体积是240立方厘米，圆锥的体积是（）立方厘米．A．640B．800C．720D．80考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：由圆锥体积公式的推导可知，当一个圆柱和一个圆锥等底等高时，则圆锥的体积应是圆柱体积的；也就是说，把圆柱的体积看作单位“1”，是3份，圆锥的体积是1份，已知圆柱体积是240立方厘米，用240除以3即得圆锥的体积．解答：解：一个圆柱和一个圆锥等底等高，那么圆锥体积是圆柱体积的；圆锥的体积：240÷3=80（立方厘米）；答：圆锥的体积是80立方厘米．故选：D．点评：此题是考查圆柱、圆锥的关系，要明确等底等高的圆柱和圆锥体积有3倍或的关系．13．（•东兰县模拟）把一团圆柱体橡皮泥揉成与它等底的圆锥体，高将（）A．扩大3倍B．缩小3倍C．扩大6倍D．缩小6倍考点：圆锥的体积；圆柱的侧面积、表面积和体积．分析：根据题意知道，在捏橡皮泥的过程中，它的总体积不变，再根据等底等高的圆锥形和圆柱形的关系，即可得到答案．解答：解：根据等底等高的圆锥形的体积是圆柱形体积的，又因为，在捏橡皮泥的过程中，它的总体积不变，所以，把一团圆柱体橡皮泥揉成与它等底的圆锥体，高将扩大3倍；故选：A．点评：解答此题的关键是，根据题意，结合等底等高的圆锥形的体积是圆柱形体积的，即可得到答案．14．（•宿城区模拟）一个圆柱与一个圆锥体体积相等，底面积也相等．已知圆柱的高是9厘米，则圆锥的高是（）厘米．A．3B．9C．27D．54考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：根据圆柱的体积公式V=sh及圆锥的体积公式V=sh，知道当圆柱和圆锥的底面积和体积相等时，圆柱的高与圆锥的高的比是1：3，再根据圆柱的高为9厘米，由此即可求出圆锥的高．解答：解：因为，圆柱的体积公式是：V=sh，则h=圆锥的体积公式是：V=sh，则h=圆柱和圆锥的底面积和体积相等时圆柱的高与圆锥的高的比是：=：1：3圆锥的高为：9×3=27（厘米）答：圆锥的高为27厘米．故选：C．点评：解答此题的关键是，根据圆柱和圆锥的体积公式，得出圆柱和圆锥的高的关系．15．（•广州）底面积相等的圆柱和圆锥，它们的体积比是2：1，圆锥的高是9厘米，圆柱的高是（）厘米．A．3B．6C．9考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：平面图形的认识与计算．分析：由圆柱和圆锥的体积公式可得：圆柱的高：圆锥的高=2：3，由此即可解决．解答：解：由底面积相等的圆柱和圆锥的体积比是2：1可得：圆柱的高：圆锥的高=2：3，设圆柱的高为x厘米，根据题意可得：x：9=2：33x=2×93x=18x=6；答：圆柱的高是6厘米．故选：B．点评：此题是考查圆柱与圆锥体积公式的综合应用，利用公式的各种变换即可解决问题．二．填空题（共13小题）16．一个圆锥的高一定，它的底面半径和体积不成比例．考点：圆锥的体积；辨识成正比例的量与成反比例的量．分析：因为圆的半径和圆的面积不成比例，所以圆锥的底面半径和体积也不成比例．解答：解：根据公式：v=sh，因为圆的半径和圆的面积不成比例，所以圆锥的底面半径和体积也不成比例．故答案为：不成．点评：解答此题关键是判断圆的半径和面积不成比例．17．（•上高县模拟）圆锥的底面半径扩大3倍，高缩小3倍后，圆锥的体积不变．×．（判断对错）考点：圆锥的体积；积的变化规律．专题：立体图形的认识与计算．分析：圆锥的体积=πr2h，设原来圆锥的半径为2，高为3，则变化后的圆锥的半径为6，高为1，由此利用公式分别计算出它们的体积即可解答．解答：解：设原来圆锥的半径为2，高为3，则变化后的圆锥的半径为6，高为1，原来圆锥的体积是：×22×3=（）×4=4π变化后的圆锥的体积是：π×62×1×1=12π4π：12π=即变化后圆锥的体积是原来体积的，所以本题错误．故答案为：×．点评：此题考查了圆锥的体积公式的灵活应用．18．（•蓝田县模拟）一个圆柱体和一个圆锥体的底面积和体积分别相等，已知圆柱体的高4厘米，那么圆锥体的高是12厘米．考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：根据圆柱的体积公式V=sh及圆锥的体积公式V=sh，知道当圆柱和圆锥的底面积和体积相等时，圆柱的高与圆锥的高的比是1：3，再根据圆柱的高为4厘米，由此即可求出圆锥的高．解答：解：因为，圆柱的体积公式是：V=sh圆锥的体积公式是：V=sh圆柱和圆锥的底面积和体积相等时圆柱的高与圆锥的高的比是1：3圆锥的高为：4×3=12（厘米）答：圆锥的高为12厘米．故答案为：12．点评：解答此题的关键是，根据圆柱和圆锥的体积公式，得出圆柱和圆锥的高的关系．19．（•肃州区模拟）一个圆锥与一个长方体的底面积相等，高也相等，则长方体体积是圆锥体体积的3倍．√．（判断对错）考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：长方体的体积=底面积×高；圆锥的体积=×底面积×高，由此公式即可得出长方体体积与圆锥的体积的倍数关系．解答：解：长方体的体积=底面积×高；圆锥的体积=×底面积×高，若它们的底面积和高分别相等，则：长方体的体积是圆锥的体积的3倍．故答案为：√．点评：此题考查了长方体和圆锥的体积公式的灵活应用，得出结论：等底等高的长方体体积是圆锥的体积的3倍．20．圆柱体的体积是3立方米，与它等底等高的圆锥体体积是9立方米．×（判断对错）考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：平面图形的认识与计算．分析：等底等高的圆锥的体积是圆柱体积的，把圆柱的体积看作单位“1”，根据一个数乘分数的意义，用乘法求出圆锥的体积，然后与9立方米进行比较即可．据此判断．解答：解：3×=1（立方米），答：与它等底等高的圆锥体体积是1立方米．故答案为：×．点评：此题主要考查等底等高的圆锥与圆柱体积直接关系的灵活运用．21．如图，把直角三角形以直角边为轴快速旋转一周，得到的立体图形的体积最大是50.24立方厘米．（π取3.14）考点：圆锥的体积；作旋转一定角度后的图形．专题：立体图形的认识与计算．分析：根据圆锥的定义，把一个直角三角形以直角边为轴快速旋转一周，得到的立体图形是圆锥体，要使得到的圆锥的体积最大，也就是以3厘米的直角边为轴旋转，即得到的圆锥的底面半径是4厘米，高是3厘米，根据圆锥的体积公式：v=sh，把数据代入公式解答即可．解答：解： 3.14×42×3，= 3.14×16×3，=50.24（立方厘米）；答：得到的立体图形的体积最大是50.24立方厘米．故答案为：50.24．点评：此题考查的目的是理解圆锥的定义，掌握圆锥体积的计算方法．22．一个圆锥体，高扩大2倍，底面半径缩小2倍，体积大小不变．×．考点：圆锥的体积．专题：立体图形的认识与计算．分析：设原圆锥的底面半径为2r，高为h，则变化后的圆锥的底面半径为r，高为2h，由此根据圆锥的体积公式分别求出变化前后的圆锥的体积，即可解答．解答：解：设原圆锥的底面半径为2r，高为h，则变化后的圆锥的底面半径为r，高为2h，则：原来圆锥的体积是：×π×（2r）2×h=πr2h；变化后的圆锥的体积是：×π×r2×2h=πr2h；所以变化前后的体积之比是：πr2h：πr2h=2：1；答：一个圆锥体，高扩大2倍，底面半径缩小2倍，则体积会缩小2倍．故答案为：×．点评：此题主要考查了圆锥的体积公式的计算应用，分别求出这个圆锥变化前后的体积即可解答．23．把一个圆柱体剥成一个最大的圆锥，剥去部分的体积是圆锥体积的2倍．√（判断对错）考点：圆锥的体积．专题：立体图形的认识与计算．分析：根据把“一个圆柱体剥成一个最大的圆锥”，实际是把一个圆柱体切削成一个和它等底等高的圆锥；根据等底等高的圆锥体是圆柱体的，得出剥去部分的体积是圆柱的，即剥去部分是圆锥体积的2倍．解答：解：由分析可知：把一个圆柱体剥成一个最大的圆锥，剥去部分的体积是圆锥体积的2倍；故答案为：√．点评：解答此题的关键是，知道如何把一个圆柱体剥成一个最大的圆锥，得出剥成的圆锥与圆柱的关系，进而得出剥去部分的体积与圆柱的关系．24．高1米，底面周长是18.84米的圆锥形沙堆的体积是9.42立方米．考点：圆锥的体积．专题：立体图形的认识与计算．分析：沙堆的形状是圆锥形的，由底面周长是18.84米先求得底面半径，再利用圆锥的体积计算公式V=πr2h求得体积，问题得解．解答：解：×3.14×（18.84÷3.14÷2）2×1=×3.14×32×1=3.14×3=9.42（立方米）；答：这个圆锥形沙堆的体积是9.42立方米．故答案为：9.42．点评：此题主要考查圆锥的体积计算公式V=πr2h，运用公式计算时不要漏乘．25．（•北京）圆锥的体积等于与它等底等高的圆柱的体积的三分之一．考点：圆锥的体积．专题：立体图形的认识与计算．分析：圆锥的体积等于等底等高的圆柱体积的，据此解答即可．解答：解：圆锥的体积等于与它等底等高的圆柱的体积的三分之一．故答案为：等底等高．点评：此题考查的目的是使学生牢固掌握圆柱和圆锥的体积之间的关系．26．（•紫金县）把圆柱体削成一个最大的圆锥体，圆锥体体积是削去部分的．正确．（判断对错）考点：圆锥的体积．分析：根据等底等的圆柱体与圆锥的体积关系，圆锥的体积是圆柱体体积的，由此得出答案．解答：解：把圆柱体的体积看作“1”，与它等底等高的圆锥的体积是圆柱体的，削求部分是圆柱体的．1﹣=；÷=×=；答：圆锥体体积是削去部分的．故答案为：正确．点评：此题考查的你的在于理解和掌握圆柱体与圆锥体积之间的关系，及圆锥的体积计算．27．（•福田区模拟）圆锥的底面半径是6厘米，高是20厘米，它的体积是0.0007536立方米．考点：圆锥的体积．分析：圆锥的体积=πr2h，由此代入数据即可计算出这个圆锥的体积．解答：解：×3.14×62×20，=×3.14×36×20，=753.6（立方厘米），=0.0007536（立方米），答：它的体积是0.0007536立方米．故答案为：0.0007536．点评：此题考查了圆锥的体积公式的计算应用，要求学生熟记公式即可解答．28．（•贵州模拟）如图，旋转一周所得图形的体积是37.68立方厘米．考点：圆锥的体积．专题：立体图形的认识与计算．分析：旋转一周所得图形是一个圆锥，该圆锥的底面半径是3厘米，高是4厘米，进而根据“圆锥的体积=πr2h”进行解答即可．解答：解：×3.14×32×4=9.42×4=37.68（立方厘米）；答：体积是37.68立方厘米；故答案为：37.68．点评：解答此题应根据圆锥的特征和圆锥的体积计算方法V=πr2h进行解答．B档（提升精练）一．选择题（共15小题）1．（•安徽模拟）圆柱和圆锥的底面积、体积分别相等，圆锥的高是圆柱的高的（）A．B．C．2倍D．3倍考点：圆锥的体积；圆柱的侧面积、表面积和体积．专题：立体图形的认识与计算．分析：根据圆柱的体积公式，V=sh=πr2h，与圆锥的体积公式，V=sh=πr2h，知道在底面积和体积分别相等时，圆柱的高是圆锥的高的，即圆锥的高是圆柱高的3倍，据此解答即可得到答案．解答：解：因为，圆柱的体积是：V=πr2h1，圆锥的体积是：V=πr2h2，πr2h1=πr2h2，所以，h1=h2，即h2=3h1．故答案为：D．点评：此题主要是利用圆柱与圆锥的体积公式，推导出在底面积和体积分别相等时，圆柱的高与圆锥的高的关系．2．（•广州模拟）把底面积是18平方厘米，高是2厘米的圆柱形零件削成最大的圆锥，削成的圆锥体积是（）立方厘米．A．12B．18C．24D．36考点：圆锥的体积．分析：根据题意，削成的最大圆锥的底面积是18平方厘米，高是2厘米，可直接利用圆锥的体积公式计算即可得到答案．解答：解：×18×2，=6×2，=12（立方厘米）；答：削成最大的圆锥体积是12立方厘米．故选：A．点评：此题主要考查的是圆锥的体积公式：V=sh．3．（•高碑店市）圆锥体的底面积和高都扩大到原来的2倍，则体积扩大到原来的（）倍．A．．2B．、4C．、8考点：圆锥的体积．专题：立体图形的认识与计算．分析：根据圆锥的体积公式=底面积×高×，根据积的变化规律可知，圆锥体的底面积和高都扩大到原来的2倍，那么体积就会扩大到原来的（2×2）倍，列式解答即可得到答案．解答：解：2×2=4，答：圆锥体的底面积和高都扩大到原来的2倍，则体积扩大到原来的4倍．故选：B．点评：此题主要考查的是圆锥体的体积公式和积的变化规律的应用．4．（•福田区模拟）一个圆锥体的底面半径扩大3倍，高缩小3倍，则体积（）A．扩大3倍B．扩大6倍C．缩小3倍D．不变考点：圆锥的体积．分析：设原圆锥的底面半径为r，高为3h，则变化后的圆锥的底面半径为3r，高为h，由此根据圆锥的体积公式分别求出变化前后的圆锥的体积，即可解答．解答：解：设原圆锥的底面半径为r，高为3h，则变化后的圆锥的底面半径为3r，高为h，则：原来圆锥的体积是：×π×r2×3h=πr2h；变化后的圆锥的体积是：×π×（3r）2×h=3πr2h；。

北师大版六年级下册数学《圆锥的体积》一课一练(含答案)

六年级下册数学一课一练-1.4圆锥的体积一、单选题1.一个圆锥的体积是n立方厘米，和它等底等高的圆柱体的体积是（）立方厘米。

A. nB. 2nC. 3nD. 4n2.图中瓶底的面积和圆锥杯口的面积相等，将瓶子中的液体导入圆锥杯中，能倒满（）杯。

A. 2B. 3C. 4D. 63.一个圆锥的体积是36立方厘米，底面积是12平方厘米，高是（）厘米．A. 9B. 6C. 34.一个圆柱和一个圆锥的体积相等，高也相等．圆锥和圆柱底面积的比是( )A. 3∶1B. 1∶3C. 1∶15.体积相等的圆柱和圆锥，如果它们的底面积相等，那么圆锥的高应是圆柱高的（）A. 3倍B. 6倍C.D.二、判断题6.圆柱的体积等于圆锥体积的3倍。

7.圆锥体积是圆柱体积的三分之一．8.一个圆锥的底面积是一个圆柱底面积的3倍，它们的高相等，则它们的体积也相等。

9.圆锥体积是圆柱体积的10.等底等高的圆柱和长方体的体积相等．三、填空题11.一个圆柱形瓶子的高是2h，一个圆锥形杯子的底面积与圆柱的底面积相等，高是h，那么一瓶水倒入杯子中，能倒________杯．12.一个圆柱和一个圆锥的底面积相等，体积也相等，圆柱的高是3cm，圆锥的高是________cm。

13.等底等高的圆柱和圆锥，体积之差是3.2立方分米，圆柱的体积是________立方分米。

14.一个圆柱和一个圆锥等底等高，它们的体积的差是50立方厘米，它们的体积的和是________立方厘米．15.一个圆锥与一个圆柱的底面积和体积都相等，圆柱的高是4分米，圆锥的高是________分米。

四、解答题16.一个圆锥形沙堆，高1.2m，底面周长是18.84m，每立方米沙约重1.7吨。

这堆沙约重多少吨？（结果保留整数）五、综合题17.解答．（1）三角形顶点A用数对表示是________．（2）如果AC=4厘米，BC=3厘米，AB=5厘米，把三角形绕C点顺时针每次旋转90°，转动一圈后，A 点走过的图形是________形，它的面积是________平方厘米．（3）将三角形按3：1放大，画出放大后的图形．（4）把这个图形绕AC轴旋转一圈形成的物体是________形，体积是________立方厘米．六、应用题18.在一个从里面量底面半径4厘米、高18厘米的圆柱形玻璃缸中，放入一个圆锥形铁块，铁块底面半径3厘米、高8厘米。

2022-2023学年人教版数学六年级下册圆锥的体积练习题(含解析)

【详解】底面周长：2×3.14×2
＝6.28×2
＝12.56（cm）
表面积：2×3.14×2×3＋2×3.14×22
＝6.28×2×3＋2×3.14×4
＝37.68＋25.12
＝62.8（cm2）
3.14×22＝12.56（cm2）
体积：12.56×3＝37.68（cm3）
圆锥体积：37.68× ＝12.56（cm3）
2022-2023学年人教版数学六年级下册圆锥的体积练习题
学校:___________姓名：___________班级：____________
一、选择题
1．在学习圆柱的体积计算公式时，是把圆柱转化为（）推导出来的。
A．正方体B．长方体C．长方形
2．一个长方形，如果它的长扩大到原来的3倍，宽不变，那么它的面积就会扩大到原来的（）倍。
③圆柱有无数条高，圆锥只有一条高。④5的倍数一定是合数。
A．①③B．②④C．②③D．②③④
12．一个圆柱和一个圆锥等底等高，圆锥的体积比圆柱的体积少0.8立方分米，那么圆柱的体积是（）立方分米。
A．0.4B．0.8C．1.2D．2.4
13．圆锥的底面半径和高都扩大到原来的2倍，它的体积扩大到原来的（）倍。
四、解答题
21．有一段钢可做一个底面直径6厘米，高9厘米的圆锥体零件。如果把它改制成高是6厘米的圆柱体零件，零件的底面积是多少平方厘米？
22．一堆煤呈圆锥形，底面直径是2m，高是1.5m。已知每立方米的煤重1.2t，这堆煤大约有多少吨？（得数保留整数）
23．甲乙两人比赛400米跑，甲离终点100米时，乙刚好跑到中点，照这样的速度，乙跑到终点时，比甲正好慢25秒，甲平均每秒跑多少米？
A．3B．6C．9

(完整版)圆锥的体积练习题及答案

六年级数学下册圆锥的体积一、填空 1.把一个体积是18立方厘米的圆柱削成一个最大的圆锥，削成的圆锥体积是（）立方厘米。

2.一个圆柱和一个圆锥的体积和底面积相等，圆锥的高是9厘米，圆柱的高是（）厘米。

3.圆锥的底面半径是3厘米，体积是6.28立方厘米，这个圆锥的高是（）厘米。

4.一个棱长是4分米正方体容器装满水后，倒入一个底面积是12平方分米的圆锥体容器里正好装满，这个圆锥体的高是（）分米。

二、判断 1.一个圆柱与一个圆锥的底面积和体积相等，那么圆锥的高是圆柱高的。

（）13 2.把一个圆柱削成一个圆锥，这个圆锥的体积是圆柱体积的。

（）13 3.圆柱体积比与它等底等高的圆锥体的体积大2倍。

（）4.圆锥的底面周长是12.56分米，高是4分米，它的体积是（）立方分米。

三、选择　1.把一段圆钢切削成一个最大的圆锥体，切削掉的部分重8千克，这段圆钢重（）千克。

①24　②16　③12　④8 2.一个圆柱体积比一个与它等底等高的圆锥体的体积大（） ① ②1　③2倍　④3倍23 3.一个底面直径是27厘米，高9厘米的圆锥体木块，分成形状大小完全相同的两个木块后，表面积比原来增加（）平方厘米。

①81　②243　③121.5　④125.6四、应用题1.一根圆柱形钢管，长30厘米，外直径是长的，管壁厚1厘米，已知每立方厘米的钢15重7.8克，这根钢管重多少千克？2.一辆货车箱是一个长方体，它的长是4米，宽是1.5米，高是4米，装满一车沙，卸后沙堆成一个高是0.5米的圆锥形，它的底面积是多少平方米？参考答案一、填空1.6立方厘米。

2.3厘米。

3. 厘米。

234.16分米。

二、判断1.×2.×3.√4.×三、选择1.①2.③3.③四、应用题1. 外直径：30× ＝6（厘米）外半径：156÷2＝3（厘米）内直径：6－1－1＝4（厘米）内半径：4÷2＝2（厘米）体积：3.14×（3×3－2×2）×30＝471（立方厘米）重量：7.8×471＝3673.8（克）答：这根钢管重3673.8克。

六年级数学下册典型例题系列之第三单元：圆锥体积的生活实际问题专项练习(解析版)

2021-2022学年六年级数学下册典型例题系列之第三单元：圆锥体积的生活实际问题专项练习（解析版）1．一个圆锥形沙堆，底面周长是6.28米，高是90厘米，每立方米沙重2吨，这堆沙约有多少吨？【解析】90厘米＝0.9米6.28÷3.14÷2＝1（厘米）3.14×1²×0.9÷3×2＝0.942×2＝1.884（吨）答：这堆沙约有1.884吨。

2．一个圆锥形小麦堆的底面周长为12.56m，高是3m。

如果每立方米小麦的质量为700kg，这堆小麦的质量为多少千克？【解析】半径：12.56÷3.214÷2＝4÷2＝2（米）1×3.14×22×3×7003＝3.14×4×700＝3.14×2800＝8792（千克）答：这堆小麦的质量为8792千克。

3．一堆煤成圆锥形，高3米，底面周长为31.4米。

这堆煤的体积是多少？如果每立方米煤重1.4吨，这堆煤重多少吨？【解析】1×3.14×（31.4÷3.14÷2）2×33＝3.14×52＝78.5（立方米）78.5×1.4＝109.9（吨）答：这堆煤的体积是78.5立方米；这堆煤重109.9吨。

4．张大伯家收成的稻谷堆成一个圆锥形，量得底面周长为18.84m，高2m，已知每立方米稻谷重0.55吨，这堆稻谷重多少吨？【解析】13×3.14×（18.84÷3.14÷2）2×2×0.55＝13×3.14×9×2×0.55＝9.42×2×0.55＝18.84×0.55＝10.362（吨）答：这堆稻谷重10.362吨。

圆锥体积应用题及答案

圆锥体积应用题及答案圆锥体积应用题及答案圆锥体积应用题及答案一、填空：1、5.4平方分米＝（）平方厘米； 1.05立方米＝（）升；240立方厘米＝（）立方分米； 10.01升＝（）毫升。

2、圆柱的上、下两面都是（）形，而且大小（）；圆柱的高有（）条，圆锥的高有（）条。

3、一个圆柱体，如果把它的高截短了3厘米，表面积就减少了94.2平方厘米，体积就减少（）立方厘米。

4、一个圆锥的底面积是40平方厘米，高12分米，体积是（）立方厘米。

5、一个圆柱的底面半径是3分米，高2分米，它的侧面积是（），表面积是（），体积是（）。

6、一个圆柱的底面周长6.28厘米，高是3厘米，它的体积是（）立方厘米。

7、一个圆柱和一个圆锥等底等高，如果圆柱的体积是18立方分米，那么圆锥的体积是（）立方分米；如果圆锥的体积是18立方分米，那么圆柱的体积是（）立方分米；如果它们的体积相差18立方分米，那么圆锥的体积是（）立方分米，圆柱的体积是（）立方分米。

8、把棱长为2分米的正方体木块，削成一个最大的圆锥，圆锥的体积约是（）立方分米。

（结果保留两位小数）9、在一个高24厘米的圆锥形量杯里装满了水，如果将这些水倒入与它底面积相等的圆柱形量杯中，水面高（）厘米。

10、一根长4米，横截面半径为2分米的圆柱形木料截成同样长的5段，表面积比原来增加（）平方分米。

二、选择题：1、右图中的正方体、圆柱和圆锥底面积相等，高也相等。

下面哪句话是正确的？（）A、圆柱的体积比正方体的体积小一些。

B、圆锥的体积是正方体的13 。

C、圆柱体积与圆锥体积相等。

2、一个圆柱和一个圆锥的底面直径相等，圆锥的高是圆柱的3倍，圆锥的体积是15立方分米，圆柱的体积是（）立方分米。

A、45B、15C、53、圆柱的底面半径和高都乘3，它的'体积应乘（）。

A、3B、6C、9D、274、用一根小棒粘住直角三角形的一条直角边，旋转一周，这个三角形转动后产生的图形是（）。

六年级下册数学试题-第5周圆锥的体积整理和复习(含答案)人教版

六年级第5周一级监测卷监测内容：圆锥的体积整理和复习时间：40分钟满分100分一、填一填。

（每空3分，共27分）（1）圆锥的体积等于和它（）的圆柱体积的31，所以圆锥的体积＝（），用字母表示为（）。

（2）一个圆柱和一个圆锥等底等高。

若圆柱的体积是15.9dm 3，则圆锥的体积是（）dm 3；若圆锥的体积是15.9dm 3，则圆柱的体积是（）dm 3。

（3）圆锥形容器高18厘米，容器中盛满水。

如果将水全部倒入与它等底的圆柱形容器中，则水高为( )厘米。

（4）一个圆锥的底面周长是6.28厘米,高是9厘米,这个圆锥的体积是( )立方厘米。

（5）自来水管的内直径是2厘米,水管内水的流速是10厘米/秒。

一位同学刷牙时没有关水龙头,10分钟浪费( )升水。

二、填表。

（每空3分，共12分）三、选择。

（将正确答案的序号填在括号里）（每题5分，共15分）1.一个圆锥的体积是18立方米，底面积是18平方米，它的高是（）。

A.1mB.2mC.3mD.6m2.等底等高的长方体、正方体、圆柱的体积相比较（）。

A. 正方体的体积大B. 长方体的体积大C. 圆柱的体积大D. 一样大3.圆柱的底面半径为r ，高为h ，表示它的表面积的式子是（）。

A. 2πr hB. 2πr 2＋2πr hC.πr 2＋2πr hD. πr 2h四、解决问题。

（共46分）1.一个圆柱形油桶,从里面量,底面半径是40厘米,高是60厘米。

(1)如果1升柴油重0.85千克,这个油桶可装柴油多少千克?（6分）(2)做这样一个油桶,至少需要铁皮多少平方分米? （得数保留整数）（6分）2.李伯伯家的小麦丰收了,他把小麦放在院子里堆成了圆锥形,底面周长是12.56m，高是1.8m。

(1)如果每立方米小麦重750千克,那么这堆小麦重多少千克?（6分）(2)李伯伯家有0.5公顷麦田,平均每公顷产小麦多少千克?（6分）(3)如果每千克小麦售价为3.5元,这些小麦能卖多少钱？（6分）3.一个圆锥形沙堆，底面半径是2m，高是1.5m，用这堆沙在5m宽的小路上铺4cm厚的路面，可以铺几米?（8分）4.有一个底面直径是10cm的圆柱形容器,容器内盛了一些水,把一个底面周长是18.84cm的圆锥放入容器内(圆锥全部浸入水中),容器的水面升高了0.9cm,这个圆锥的高是多少厘米?(容器厚度忽略不计)（8分）六年级第5周二级监测卷监测内容：圆柱的体积、圆锥的认识时间：40分钟满分100分一、填一填。

圆柱、圆锥表面积与体积练习题

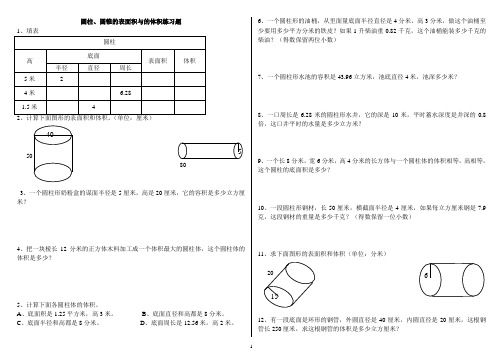
圆柱、圆锥的表面积与的体积练习题2、计算下面图形的表面积和体积。

（单位：厘米）803、一个圆柱形奶粉盒的谋面半径是5厘米，高是20厘米，它的容积是多少立方厘米？4、把一块棱长12分米的正方体木料加工成一个体积最大的圆柱体，这个圆柱体的体积是多少？5、计算下面各圆柱体的体积。

A 、底面积是1.25平方米，高3米。

B 、底面直径和高都是8分米。

6、一个圆柱形的油桶，从里面量底面半径直径是4分米，高3分米，做这个油桶至少要用多少平方分米的铁皮？如果1升柴油重0.82千克，这个油桶能装多少千克的柴油？（得数保留两位小数）7、一个圆柱形水池的容积是43.96立方米，池底直径4米，池深多少米？8、一口周长是6.28米的圆柱形水井，它的深是10米，平时蓄水深度是井深的0.8倍，这口井平时的水量是多少立方米？9、一个长8分米，宽6分米，高4分米的长方体与一个圆柱体的体积相等，高相等，这个圆柱的底面积是多少？10、一段圆柱形钢材，长50厘米，横截面半径是4厘米，如果每立方厘米钢是7.9克，这段钢材的重量是多少千克？（得数保留一位小数）11、求下面图形的表面积和体积（单位：分米）12、有一段底面是环形的钢管，外圆直径是40厘米，内圆直径是20厘米，这根钢圆柱的体积练习二1、一个圆柱的底面半径是6厘米，高是2分米，求这个圆柱的体积。

2、小刚有一个圆柱形的水杯，水杯的底面半径是5厘米，高是10厘米，有资料显示：每人每天的正常饮水量大约是1升，小刚一天要喝几杯水？3、一个圆柱形水桶，底面直径和高都是40厘米，用这个水桶容积的85%装水，每升水重1千克，桶中的水大约有多少千克？4、一个底面半径是10米的圆柱形蓄水池，能蓄水2512立方米，若再挖深2米，可蓄水多少立方米？5、一个圆柱形油桶，内底面直径是40厘米，高是50厘米，它的容积是多少升？如果1升柴油重0.85千克，这具油桶可装柴油多少千克？（得数保留整千克）6、一个圆柱形玻璃杯底面半径是10厘米，里面装不水，水的高度是12厘米，把一小块铁块放进杯中，水上升到15厘米，这块铁块重多少克？（每立方厘米铁重7.8克）7、下图是一个长15厘米，宽6厘米、高15个底面半径为5厘米的圆柱形空洞，求这个零件的体积。

(完整版)人教版小学数学六年级下册圆锥的认识及其体积练习题

人教版小学数学六年级下册《圆锥的认识及其体积》练习题教课目的：1、认识圆锥，圆锥的高和侧面，掌握圆锥的特点，会看圆锥的平面图，会正确丈量圆锥的高。

2、探究出圆锥体积和圆柱体积之间的关系，初步掌握圆锥体积的计算公式，并能运用公式正确地计算圆锥的体积，解决实质生活中相关圆锥体积计算的简单问题。

3、培育学生的自主探究意识，激发学生激烈的求知欲念。

教课重、难点：1、正确理解圆锥的构成。

2、正确探究出圆锥体积和圆柱体积之间的关系。

教课内容：圆锥的认识及其体积的应用【知识点解说】1.圆锥的特点：（1）圆锥有一个极点，它的底面是一个圆。

（2）圆锥有一个曲面，这个曲面叫做侧面。

（3）从圆锥的极点究竟面圆心的距离叫做高。

沿着曲面上的线都不是圆锥的高。

（4）因为圆锥只有一个极点，因此圆锥只有一条高。

（5）圆锥的侧面睁开后是一个扇形 .2. 圆锥的体积：1 ×圆柱的体积＝1×底面积×高，字母公式：V＝1 Sh圆锥的体积＝3 3 3【稳固练习】一. 填空1. 一个圆柱和一个圆锥的底面积和高分别相等，圆锥的体积是圆柱体积的（），圆柱的体积是圆锥体积的（）．2. 一个圆锥体底面直径和高都是 6 厘米，它的体积是 () 立方厘米。

3. 一个圆锥体的底面周长是 12.56 分米 , 高是 6 分米 , 它的体积是 ( ) 立方分米。

4. 等底等高的圆柱和圆锥的体积相差16 立方米，这个圆柱的体积是（）立方米，圆锥的体积是（）立方米。

5. 一个圆锥的体积是 7.2 立方米，与它等底等高的圆柱的体积是（）立方米。

6. 将棱长为 6 分米的正方体木块，削成一个最大的圆锥体，这个圆锥的体积是（）立方分米，一共削去（）立方分米的木材7.. 一个圆柱和圆锥等底等高，它们的体积一共60 立方厘米，那么，圆柱的体积是（）立方厘米，圆锥的体积是（）立方厘米。

8. 一个圆柱的底面半径是 3 厘米，高是 2 厘米，这个圆柱的底面周长是（）厘米，底面积是（）平方厘米，侧面积是（）平方厘米，表面积是（）平方厘米，体积是（）立方厘米，和它等底等高的圆锥的体积是（）立方厘米。

(完整版)圆锥的表面积和体积练习题精选

(完整版)圆锥的表面积和体积练习题精选一、选择题1. 设一圆锥的底面直径为8cm，高为10cm，求它的体积。

A. 115.34cm^3B. 134.66cm^3C. 146.78cm^3D. 156.56cm^32. 圆锥的底面半径为6cm，高为8cm，求圆锥的表面积。

A. 188.5cm^2B. 201.6cm^2C. 211.2cm^2D. 227.2cm^23. 一个圆锥的体积为100cm^3，高为10cm，求它的底面半径。

A. 1cmB. 2cmC. 3cmD. 4cm4. 圆锥的底面半径为12cm，高为16cm，求圆锥的表面积。

A. 1027.2cm^2B. 1095.6cm^2C. 1159.04cm^2D. 1224.8cm^25. 设一圆锥的体积为314cm^3，底面半径为5cm，求它的高。

A. 10cmB. 14cmC. 16cmD. 20cm二、计算题1. 一个圆锥的半径为3cm，它的侧面积是多少？2. 圆锥的底面直径为12cm，高为9cm，求它的体积。

3. 一个圆锥的底面半径为4cm，它的体积是20cm^3，求它的高。

4. 圆锥的底面半径为8cm，侧面积为120cm^2，求它的高。

5. 设一个圆锥的高为10cm，底面半径为6cm，求它的体积。

以上是关于圆锥的表面积和体积的练题精选。

希望能帮助你加深对此概念的理解和掌握。

Note: The document above is a practice exercise focusing on the surface area and volume of cones. It includes multiple-choice questions and calculations for further practice.。

圆锥体的体积练习题

圆锥体的体积练习题一、选择题1. 下列关于圆锥体体积的公式，正确的是：A. V = πr²hB. V = 1/3πr²hC. V = 2πr²hD. V = 1/2πr²h2. 一个圆锥体的底面半径为3cm，高为4cm，其体积为：A. 12π cm³B. 36π cm³C. 48π cm³D. 144π cm³3. 两个圆锥体的底面半径和高都相等，它们的体积关系是：A. 一定相等B. 不一定相等C. 第一个圆锥体体积大于第二个D. 第一个圆锥体体积小于第二个二、填空题1. 圆锥体的体积公式是V = ________ πr²h。

2. 一个圆锥体的底面半径为5cm，高为10cm，其体积是________ cm³。

3. 若圆锥体的体积为30π cm³，底面半径为3cm，则圆锥体的高为 ________ cm。

1. 已知圆锥体的底面半径为7cm，高为14cm，求圆锥体的体积。

2. 已知圆锥体的体积为54π cm³，高为9cm，求圆锥体的底面半径。

3. 一个圆锥体的底面直径为10cm，高为8cm，求圆锥体的体积。

4. 两个圆锥体的体积分别为36π cm³和64π cm³，它们的底面半径和高都相等，求这两个圆锥体的底面半径和高。

四、应用题1. 某车间有一个圆锥形铁块，其底面半径为10cm，高为20cm，求该铁块的体积。

2. 一个圆锥形沙堆，底面半径为4m，高为3m，求这堆沙的体积。

3. 有一块圆锥形土地，其底面直径为16m，高为10m，求这块土地的体积。

五、判断题1. 圆锥体的体积与它的底面半径成正比。

（）2. 如果两个圆锥体的底面半径相等，那么它们的高也一定相等。

（）3. 圆锥体的体积是圆柱体体积的三分之一，当它们的底面半径和高都相等时。

（）4. 圆锥体的体积可以通过测量其斜高来计算。

圆锥的体积练习题3

圆锥的体积练习题一、求圆锥的体积：1、底面半径是4厘米，高是5厘米。

2、底面直径是12厘米，高是4厘米。

3、底面周长是12.56分米，高是6分米。

二、应用题：1、一圆锥形的沙堆，底面直径是6米，高1.8米，它的体积是多少？2、一圆锥形的沙堆，底面周长是6.28米，高1.2米。

若把它在宽5米的公路上铺2厘米厚，能铺多长？3、一个圆锥和一个圆柱等底等高，圆柱比圆锥的体积大48立方分米，求圆柱和圆锥的体积各是多少？4、把一个底面周长是25.12分米，高是9分米的圆柱木料削成一个最大的圆锥体，这个圆锥的体积是多少分米？5、将一个体积为42.39立方分米的圆柱形零件熔铸成一个底面直径为12分米的圆锥体零件，圆锥的高是多少？6、将一个棱长为6分米的正方体木块切削成一个最大的圆锥体，应削去多少木料？三、提高内容：1、将一个底面半径是4分米，高6分米的圆柱体零件熔铸成一个底面直径为4分米的圆锥形零件，求圆锥零件的高是多少分米？2、一个圆锥和一个圆柱等体积等高，已知圆柱的底面周长是12.56分米，圆锥的底面积是多少？3、一个直角三角形的三条边分别为3厘米、4厘米、5厘米，沿它的一条直角边为轴旋转一周，可得什么图形？体积最小是多少？体积最大是多少？四、发展内容：1、一个长方体木块，长55厘米，宽40厘米，高30厘米，将其加工成一个最大的圆锥体木块，圆锥的体积是多少？2、一圆锥形的底面半径和高都等于正方体的棱长，已知正方体的体积是30立方厘米，圆锥的体积是多少？3、圆柱的体积是圆锥的2倍，圆柱的高与圆锥的高的比是2：5，圆锥的底面积与圆柱的底面积的比是多少？五，练习题一填空1、一个圆柱和一个圆锥的底面积和高分别相等，圆锥的体积是圆柱体积的（），圆柱的体积是圆锥体积的（）．2、一个圆柱的体积是15立方厘米，与它等底等高的圆锥的体积是（）立方厘米．3一个圆锥的体积是7.2立方米，与它等底等高的圆柱的体积是（）立方米．4、圆锥的底面半径是6厘米，高是20厘米，它的体积是（）立方米．5、等底等高的圆柱和圆锥的体积相差16立方米，这个圆柱的体积是（）立方米，圆锥的体积是（）立方米．6、等底等高的一个圆柱和一个圆锥的体积和是96立方分米，圆柱的体积是（）立方分米，圆锥的体积是（）立方分米．二、判断1、圆锥的体积是等于圆柱体积的．（）2、圆锥的体积比与它等底等高的圆柱体积小．（）3、一个圆锥的底面半径扩大3倍，它的体积也扩大3倍．（）4、一个正方体和一个圆锥体的底面积和高都相等，这个正方体体积是圆锥体积的3倍．（）三、选择1、一个圆柱和一个圆锥的底面直径相等，圆锥的高是圆柱的3倍，圆锥的体积是12立方分米，圆柱的体积是（）立方分米．①12 ②36 ③4 ④82、一个圆锥的体积是12立方厘米，底面积是4平方厘米，高是（）厘米．①3②6 ③9 ④123、一个圆锥的体积是n立方厘米，和它等底等高的圆柱体的体积是（）立方厘米．①n ②2n ③3n ④四、应用题1、一堆圆锥形黄沙，底面周长是25.12米，高1.5米，每立方米的黄沙重1.5吨，这堆沙重多少吨？2、把一个横截面为正方形的长方体，削成一个最大的圆锥体，已知圆锥体的底面周长6.28厘米，高5厘米，长方体的体积是多少？一、填空1、把一个体积是18立方厘米的圆柱削成一个最大的圆锥，削成的圆锥体积是（）立方厘米．2、一个圆柱和一个圆锥的体积和底面积相等，圆锥的高是9厘米，圆柱的高是（）厘米．3、圆锥的底面半径是3厘米，体积是6.28立方厘米，这个圆锥的高是（）厘米．4、一个棱长是4分米正方体容器装满水后，倒入一个底面积是12平方分米的圆锥体容器里正好装满，这个圆锥体的高是（）分米．5．把圆柱切开、再拼起来，能得到一个（）。