第十五章工具变量估计与TSLS-3
计量经济学-工具变量

利用E(zii)=0,在大样本下可得到:
~1
zi yi zi xi
关于0 的估计,仍用~0 Y ~1X 完成。
这种求模型参数估计量的方法称为工具变 量法(instrumental variable method),相应的估 计 量 称 为 工 具 变 量 法 估 计 量 ( instrumental variable (IV) estimator)。
CONSP 0 1GDPP 由于:居民人均消费支出(CONSP)与人 均国内生产总值(GDPP)相互影响,因此,
容易判断GDPP与同期相关(往往是 正相关),OLS估计量有偏并且是非一致的
(低估截距项而高估计斜率项 )。
OLS估计结果:
(13.51) (53.47) R2=0.9927 F=2859.23 DW=0.5503 SSR=23240.7
用OLS估计模型,相当于用xi去乘模型两边、对i求 和、再略去xii项后得到正规方程:
xi yi 1 xi2
解得:
ˆ1
xi yi xi2
(*)
由于Cov(Xi,i)=E(Xii)=0,意味着大样本下: (xii)/n0
表明大样本下:
ˆ1
xi yi xi2
2. 工具变量并没有替代模型中的解释变量, 只是在估计过程中作为“工具”被使用。
上述工具变量法估计过程可等价地分解成下 面的两步OLS回归:
第一步,用OLS法进行X关于工具变量Z的回归:
Xˆ i ˆ0 ˆ1Zi
Yˆi ~0 ~1 Xˆ i
容易验证仍有:
~1
zi yi zi xi
如果用GDPPt-1为工具变量,可得如下工具 变量法估计结果:
第15章-工具变量

Cov( z, y) 1Cov( z, x) Cov( z, u)
现在,在式 (15.4) 中 Cov(z,u)=0 与式(15.5) 中 Cov(z,x)≠0 的假定下 ,我们可以解出 1 为:
Cov( z, y ) 1 Cov( z, x)
(15.9)
[注意到,若 z 与 x 不相关,即 Cov(z,x)=0,这 个简单的代数关系便不成立。]方程 (15.9)表 明, 1 是 z 和 y 之间的总体协方差除以 z 和 x 之间的总体协方差,这说明 1 被识别了。 给定一个随机样本,我们用对应样本量来估 计总体量。
score 0 1skipped u
(15.8)
其中,score 是期末考试成绩, skipped 是该 学期逃课的总次数。
当然,我们可能担心 skipped 与 u 中其他因素 相关:越有能力而又积极的学生可能逃课也越 少。因而 score 对 skipped 的简单回归,可能 不会给出逃课之因果效应的可靠估计。
这样一来 , 我们便把 abil 放人误差项中,而 只留下简单回归模型: Log(wage) =β 0+β 1educ+u (15.1 ) 其中,u 包含 abil。当然,如果用 OLS 估计 方程 (15.1) ,若 educ 与 abil 相关,则得到 的结果将是 1 的有偏而又不一致估计量。
即使能获得,如果我们的兴趣在于变量的影响, 而该变量又不随时间而变化,它对于我们也几 无用处:一阶差分或固定效应估计排除了不随 时间而变化的变量。 此外,迄今为止我们所研 究的面板数据方法,还不能解决与解释变量相 关的时变(即随着时间而不断变化的)遗漏变 量问题。
在本章,我们对内生性问题采用了一种不同的 方法。你将看到如何用工具变量法 (IV)来解决 一个或多个解释变量的内生性问题。就应用计 量经济学中线性方程的估计而言,两阶段最小 二乘法 (2SLS 或 TSLS)的受欢迎程度仅次于普 通最小二乘。
工具变量(IV):估计与检验

用到 i E zi x 为对称矩阵
-1
秩条件r i E zi x =k意味着工具变量w i与内生解释 变量x i相关,若不相关,则秩条件无法满足。证略
阶条件:zi中至少包含k个变量 根据是否满足阶条件可分为三种情况:
1 不可识别:工具变量个数少于内生解释变量个数 2 恰好识别:工具变量个数等于内生解释变量个数 3 过度识别:工具变量个数多于内生解释变量个数
解释变量内生性检验
Hausman 检验
寻找工具变量的方法:几个实例
方法 例子
由来
经典假设 所有的解释变量Xi与随机误差项彼此 之间不相关。
Cov (u i , X i ) 0
若解释变量Xi和ui相关,则OLS估计量是非一致 的,也就是即使当样本容量很大时,OLS估计量 也不会接近回归系数的真值。 造成误差项与回归变量相关(内生性)的原因 很多,但我们主要考虑如下几个方面: • 遗漏变量变量 • 变量有测量误差 • 双向因果关系。
1、矩估计(Method of Moments,MM)
首先以一个例子来说明矩估计方法:假设随机变量 x N , 2 ,其中, 2为待估参数。因为有两 个待估参数,故需要使用以下两个总体矩条件: 一阶中心矩:E x =
2 2 二阶中心矩:E x =Var x + E x = + 2 2
可以引入工具变量w t 来解决内生变量问题。一个有 效的工具变量应满足以下两个条件: (1)相关性:工具变量与内生解释变量相关,即 Cov w t,p t 0,p t为内生解释变量 (2)外生性:工具变量与扰动项不相关,即 Cov w t, t =0
二、工具变量法作为一种矩估计
09_模型设定偏差、随机解释变量和工具变量

回归系数的 OLS 估计量为:
β = ( X ' X )−1 X 'Y = ( X ' X )−1 X ' ( X β + ε ) = β + ( X ' X )−1 X 'ε
当 X 与扰动项不相关时,
p lim 1 X 'ε = 0 N
假设
p lim
1 N
X
'X
=
ΣX
存在,并且非奇异(逆矩阵存在),
估计也依然是无偏的,因此所建立的假设检验(t 和 F 检验)依然 有效。
加入多余变量的模型的参数的估计值为:
将 Y 的实际模型代入得:
两边取期望得:
厦门大学国际经济与贸易系 胡朝霞
6
2) 但是,回归系数的 OLS 估计量的方差不是最小方差的(大于 真实模型相应估计量的方差),因此 OLS 估计量是非有效的估计 量,即非 BLUE 估计量。它将导致回归系数估计量的精度下降, 并可能拒绝显著的解释变量。
ห้องสมุดไป่ตู้
E
(β
* 2
)
=
β2
+
β3 iβ32
=
β2
+
β3
cov( X 2 , X3 ) var( X 2 )
≠
β2
E(β 1*) = β1 + β3 i( X3 − β32 X 2 ) ≠ β1
β*
当β3 与 cov(X2,X3)的符号相同时, 2 将平均上偏;异号时,将
平均下偏。
2)如果被省略了变量 X3 与真实模型中的变量 X2 的相关系数为 0(即
1.残差的分析
残差的分析不仅可以用于自相关和异方差的鉴别,还可用于遗漏 变量和不正确的函数形式的诊查。
工具变量(IV):估计与检验_图文_图文

• 3。Wright考虑了几个可能的工具变量; 其中一个是天气。例如,某牧场的降雨量低 于平均值会使牧草减少从而减少给定价格时 黄油的产量(会使供给曲线向左移动而使均 衡价格上升),因此牧场地区降雨量满足工 具变量相关性的条件。但牧场地区降雨量对 黄油的需求没有直接影响,因此牧场地区降 雨量与ui的相关系数为零;也就是牧场地区 降雨量满足工具变量外生性条件。
• 例如具休考虑黄油的需求弹性估计问题 :
根据11个均衡样本点估计的方程究竟是需求函数还是 供给函数?两者都不是。由于这些点是由需求和供给 两者的变化确定的,因此用OLS拟合这些点的直线既 不是需求曲线也不是供给曲线的估计。
利用这些样本点估计出来的OLS拟合线是需求曲 线还是供给曲线,都不是!两个极端的情况如图 :
• 工具变量的外生性:若销售税是外生的,则必 须与需求方程中的误差无关;即销售税必然只 是通过价格间接影响香烟的需求。这看上去是 合理的:主要是因为不同州选择了不同的销售 额、收入、财产和其他公共财政事业的混合税 收,所以不同州的一般销售税是不同的。其中 关于公共财政的选择受到政治考量的驱使而不 是受香烟需求有关的因素影响。
工具变量(IV):估计与检验_图文_图文.ppt
• 由来
• 估计
– 矩估计(不好)
– 2SLS (最常用) – GMM(异方差自相关);LIML(若IV)
• 工具变量有效imum eigenvalue statistic,最小特征值统计量,用于多内 生解释变量
• 相关性条件:
• 1. 当包含一个内生变量但有多个工具变量时,工具 变量相关性的条件为给定W时至少有一个Z对预测X 是有用的(相关的)。
• 2. 当包含多个内生变量时,不但要排除完全多重共 线性问题,而且工具变量必须提供关于这些变量外生 性变动的足够信息,以分离出它们各自对Y的效应。
第15章-工具变量讲解

这样一来 , 我们便把 abil 放人误差项中,而 只留下简单回归模型: Log(wage) =β 0+β 1educ+u (15.1 ) 其中,u 包含 abil。当然,如果用 OLS 估计 方程 (15.1) ,若 educ 与 abil 相关,则得到 的结果将是 1 的有偏而又不一致估计量。
第15章 工具变量估计与两阶段最小二乘法
在本章中,我们进一步研究多元回归模型中的 内生解释变量 (endogenous explanatory Variables) 问题。在第 3 章中,我们推导出遗漏一个重要变 量时 OLS 估计量的偏误,在第 5 章中,我们说明 了在遗漏变量(omitted variables)的情况下,OLS 通 常是不一致的。
举例来说,考虑成年劳动者的工资方程中存 在无法观测之能力因素的问题。一个简单的 模型为: log(wage)=β 0+β 1educ+β 2abil+e 其中,e 是误差项。
在第 9 章中,我们证明了在某些假定下,如 何用诸如 IQ 的代理变量代替能力,从而通过 以下回归可得到一致估计量 log(wage)对 educ,IQ 回归 然而假定不能得到适当的代理变量(或它不 具备足以获取 1 一致估计量所需的性质)。
我们一开始先说明,在存在遗漏变量的情况 下,如何用 IV 法获得一致估计量。此外, IV 至少能在某些假定下用于解决变量误差 (errors-in-variables)问题。下一章将证明运 用 IV 法如何估计联立方程模型。
我们对工具变量估计的论述严格遵照我们在 第 1 篇中对普通最小二乘的推导,其中假定 我们有一个来自潜在总体的随机样本。这个 起点很合人意,因为除了简化符号之外,它 还强调用潜在总体来表述对 IV 估计所做的重 要假定 (正如用 OLS 时一样)。
内生性与工具变量估计方法
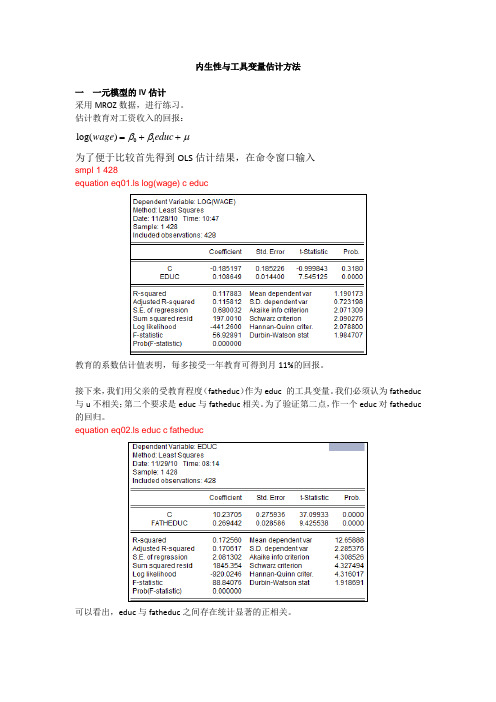
内生性与工具变量估计方法一 一元模型的IV 估计采用MROZ 数据,进行练习。
估计教育对工资收入的回报:01log()wage educ ββμ=++为了便于比较首先得到OLS 估计结果,在命令窗口输入smpl 1 428equation eq01.ls log(wage) c educ教育的系数估计值表明,每多接受一年教育可得到月11%的回报。
接下来,我们用父亲的受教育程度(fatheduc )作为educ 的工具变量。
我们必须认为fatheduc 与u 不相关;第二个要求是educ 与fatheduc 相关。
为了验证第二点,作一个educ 对fatheduc 的回归。
equation eq02.ls educ c fatheduc可以看出,educ 与fatheduc 之间存在统计显著的正相关。
采用fatheduc 作为educ 的工具变量,进行工具变量回归。
equation eq03.tsls log(wage) c educ @ fatheducIV 估计量的标准误是OLS 标准误的2.5倍,这在我们的意料之中。
二 多元模型的IV 估计 采用card 数据,进行练习。
估计教育对工资收入的回报:012log()var wage educ Control iables βββμ=+++为了便于对照,先做OLS 回归 Smpl 1 3010Equation eq01.ls log(wage) c educ exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669在这个例子中,受教育程度的工具变量是标志着一个人是否在一所四年制大学附近成长的虚拟变量(nearc4)。
为了验证受教育程度与该虚拟变量的偏相关性,先做educ对nearc4以及其他所有外生变量的回归:Equation eq02.ls educ c nearc4 exper expersq black smsa south smsa66 reg662 reg663 reg664 reg665 reg666 reg667 reg668 reg669Nearc4的系数估计值意味着,在其他因素固定的情况下,曾住在大学附近的人所受的教育比不在大学附近长大的人平均多出约1/3年。
工具变量法~

工具变量法一、工具变量法的主要思想在无限分布滞后模型中,为了估计回归系数,通常的做法是对回归系数作一些限制,从而对受限的无限分布滞后模型进行估计。
在这里,考伊克模型、适应性期望模型与部分调整模型给出了很好的解决此类问题的思路。
经过变换,新的模型中,随机扰动项的表达式为:考伊克模型:1t t t v u u λ-=- (01λ<< ,λ为衰减率) (1.1); 适应性期望模型:1(1)t t t v u u λ-=--(01λ<< ,λ为期望系数)(1.2);部分调整模型:(1)t t v u γ=-(01γ≤< ,1γ-为调整系数) (1.3)。
t u 为原无限分布滞后模型中的扰动项,t v 为变换后的扰动项。
在原模型中的随机扰动项满足经典假设的前提下,部分调整模型也满足经典假设,但是考伊克模型与适应性期望模型的随机扰动项由于存在原随机扰动项的滞后项,也就是说考伊克模型与适应性期望模型的解释变量1t Y - 势必与误差项t v 相关,因此,可能会出现上述两个模型的最小二乘估计甚至是有偏的这样严重的问题。
那么,我们是否可以找到一个与1t Y -高度相关但与t v 不相关的变量来替代1t Y -?在这里,一个可行的估计方法就是工具变量法。
在讨论工具变量法之前,我们先来了解一下外生变量和内生变量。
一般来说:一个回归模型中的解释变量有的与随机扰动项无关,我们称这样的解释变量为外生变量;而模型中有的解释变量与随机扰动项相关,我们可称这样的解释变量为内生解释变量。
内生解释变量的典型情况之一就是滞后应变量为解释变量的情形,如上述考伊克模型与适应性期望模型中的1t Y -。
外生解释变量:回归模型中的解释变量与随机扰动项无关; 内生解释变量:回归模型中的解释变量与随机扰动项无关;了解了内生变量和外生变量的概念,我们接着讨论工具变量法的主要思想:工具变量法和普通最小二乘法是模型参数估计的两类重要方法,在多元线性回归模型中,如果出现解释变量与随机误差项相关(即出现内生变量)时,其回归系数的普通最小二乘估计是非一致的,这时就需要引入工具变量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y=b0+b1x+u 正确方程估计: ^ ˆ 2 ˆ AVar(b1 ) 2
SSTx Rx, z
n
ˆ
2
n
i 1
ˆ ˆ ( yi b0 b1, IV x1 ) n2
TSLS中第二阶段的方差估计:
ˆ
2
i 1
ˆ ˆ ˆ ( yi b0 b1, IV x1 ) n2
可以根据第一种度量写出模型 用test2作为test1的工具变量估计 同样可以用test2作为能力度量构建模型,用test1 作为工具变量进行估计。 两种方式g(wage)=b0+b1educ+b2exper+b3exper2+(b4/g1) test1+(u-e1/g1)
ŷ2相当于把y2中与z1不相关的部分e已经剔除了。 TSLS估计量的方差通常较大!【爱】核心用户 By微0渺 上传
多个内生变量(阶条件和秩条件)
y1=b0+b1y2+b2y3+b3z1+b4z2+b5z3+u 阶条件:
除z1, z2和z3外,至少还应存在两个外生变量,分别 作为内生解释变量y2和y3的工具变量。 被排斥的外生变量至少与结构方程中包含的内生解 释变量一样多。【爱】核心用户 By微0渺 上传
多重共线性与TSLS
TSLS中共线性问题更加严重:
结构方程: y1=b0+b1y2+b2z1+u TSLS中第二阶段的方程: y1=b0+b1ŷ2+b2z1+v ŷ2和z1的相关程度一定大于y2和z1的相关程度
ˆ ˆ ˆ ˆ y2 0 1z1 2 z2 e y2 e
n ˆ ˆ ˆ ( y1i b 0 b1 y2i b 2 z1i ) 0 i 1 n ˆ ˆ ˆ z1i ( y1i b 0 b1 y2i b 2 z1i ) 0 i 1 n ˆ ˆ ˆ ˆ y2i ( y1i b 0 b1 y2i b 2 z1i ) 0 i 1
第一阶段回归为:
ˆ ˆ ˆ ˆ ˆ y2 0 1z1 2 z2 3 z3
工具变量的相关性检验: H0: 2=3=0 第二阶段,用ŷ2代替内生变量y2【爱】核心用户 By微0渺 上传
多重工具变量时的IV估计
矩条件:
E(u)=0;E(z1u)=0;E(z2u)=0; E(z3u)=0 四个方程,三个未知参数 ŷ2是z1, z2和z3的线性组合: E(ŷ2 u)=0
ˆ ˆ ˆ ˆ y2 0 1z1 2 z2 e y2 e【爱】核心用户 By微0渺 上传
多重工具变量
对于一个内生解释变量,有不止一个外生变量 可作为工具变量 结构方程: y1=b0+b1y2+b2z1+u y2的工具变量有两个:z2和z3 TSLS方法:
秩条件(工具变量的相关性)【爱】核心用户 By微0渺 上传测量误差问题的IV解决办法
考虑模型:
y=b0+b1x1*+b2x2+u 假定:Cov(x1*, u) = 0; Cov(x2, u) = 0 x1*不可观测,一种可观测度量为x1 :
x1 = x1*+e1
测量误差问题: y=b0+b1x1+b2x2+(u-b1e1)
内生性检验与过度识别约束检验
内生性检验
考虑模型: y1=b0+b1y2+b2z1+b2z2+u 检验y2的内生性,外生变量z1, z2, z3, z4 基本思想:
Biblioteka 若y2内生,OLS估计量不一致,TSLS估计量一致 若y2外生,OLS估计量和TSLS估计量都一致 比较OLS估计值和TSLS估计值的差异:
TSLS的理论解释
用 ŷ2代替内生变量y2意味着: y1=b0+b1(ŷ2+e)+b2z1+u =b0+b1ŷ2+b2z1+(b1e+u) 第二阶段回归得到b0和b1一致估计量的条件:
Cov(z1, b1e+u) = 0 Cov(ŷ2, b1e+u) = 0
为什么满足?
外生变量:Cov(z1, u) = 0; Cov(z2, u) =0 第一阶段回归: Cov(z1, e) = 0; Cov(z2, e) =0
若差异小,两者都具有一致性,外生 若差异大,内生【爱】核心用户 By微0渺 上传
用 ŷ2作为y2的工具变量
IV估计量与TSLS估计量等同【爱】核心用户 By微0渺 上传
应用中的注意事项:
对于估计值,利用Eviews的TSLS选项和分别作两阶 段OLS回归等同; 对于标准差,应该使用TSLS选项,若分别作两阶段 的OLS回归,第二阶段的标准差不准确。 以简单回归为例:
两个例子:
调查工人收入时,雇主可以提供第二种度量 调查家庭收入时,夫妻双方可以给出两种度量【爱】核心用户 By微0渺 上传
关于个人能力的处理:
log(wage)=b0+b1educ+b2exper+b3exper2+b4abil+u 若有两种测试指标作为能力的度量:
test1=g1abil+e1 test2=d1abil+e2
Cov(x1, u-b1e1) 0 OLS估计量是不一致的。【爱】核心用户 By微0渺 上传
y=b0+b1x1+b2x2+(u-b1e1) 若存在x1*的另一种可观测度量z1
z1 = x1*+a1 z1 可以作为x1的工具变量:
Cov(z1, x1) = Cov(x1*+a1, x1*+e1) 0 Cov(z1, u-b1e1) = Cov(x1*+a1, u-b1e1) = 0
