初三数学重点难点几何题及答案
初三数学变态难的几何压轴题

由于几何压轴题难度较大,对于不同的学生来说,感受的难度可能会不同,因此没有具体的题目可以作为“初三数学变态难的几何压轴题”。
不过,以下题目可以作为几何压轴题的代表之一,供您参考:
1. 三角形ABC中,AB=AC,D是BC上一点,E是AC上一点,AD=AE,角BAD=30度,求角EDC的度数。
2. 圆O的半径为10cm,A是圆O上一点,B是OA的中点,点P从点O出发,以每秒2cm的速度沿圆周连续运动一周回到O点,则当PA与OB垂直时,P点在圆周上共运动了____________秒。
3. 已知抛物线y=-x^2+4x+m-1与x轴只有一个交点,则m=_______.
4. 已知关于x的一元二次方程 x^2 + 2(k - 1)x + k^2 - 1 = 0 有两个不相等的实数根。
希望以上题目对您提高数学水平有所帮助。
同时建议咨询数学老师或查阅相关教辅练习资料,获取更具针对性的题目。
初中数学经典几何题及答案解析

4e d c 经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CEBO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1F经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.FPDE CBAAPCBACBPDEDCA A CBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
初中数学经典几何题及答案,附知识点及结论总结
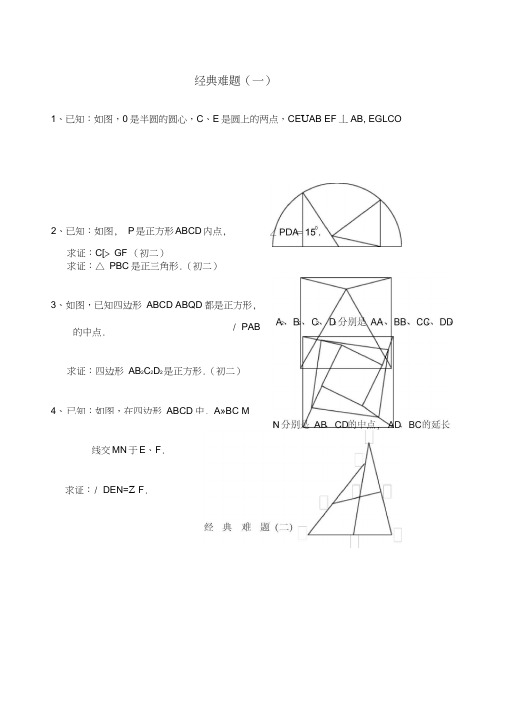
经典难题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CE U AB EF丄AB, EGLCO2、已知:如图, P是正方形ABCD内点,求证:C[> GF (初二)求证:△ PBC是正三角形.(初二)3、如图,已知四边形ABCD ABQD都是正方形,/ PAB的中点.求证:四边形AB2C2D2是正方形.(初二)4、已知:如图,在四边形ABCD中, A»BC M线交MN于E、F.求证:/ DEN=Z F .1、已知:△ ABC中,H为垂心(各边高线的交点),0为外心,且OM L BC于M(1) 求证:AH= 20M经典难题(三)求证:CE= CF.(初二)求证:AE= AF.(初二) 3、设P 是正方形ABCD-边BC 上的任一点,PF 丄AP,求证:P 心PF.(初二)2、设MN 是圆0外一直线,过0作0A ±MN 于A ,自A 引圆的两条直线,交圆于 B 、C 及D E ,直线EB 及CD 分别交MN 于P 、Q.求证:A 吐AQ (初二)3、如果上题把直线 MN 由圆外平移至圆内,设MN 是圆0的弦,过 MN 的中点A 任作两弦BC DE 设CD EB 分别交MN 于P 、Q.求证:A 吐AQ (初二)4、如图,分别以厶ABC 的 AC 和BC 为一边,在△ ABC 的外侧作正方ACDE 和正方形CBFG 点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二1、如图,四边形ABC 助正方形,DE// AC ,AE= AC ,AE 与 CD 相交于 F .2、如图,四DE// AC ,且 CE= CA线EC 交DA 延长线,CEE4、如图,PC切圆0于C, AC为圆的直径,PEF为圆的割线,AE AF与直线PO相交于B、D.求求:/ APB的度数.(初二)2、设P是平行四边形ABCM部的一点,且/ PBA^Z求证:/ PAB=Z PCB (初二)3、设ABC助圆内接凸四边形,求证:AB- CM AD- BO AC- BD (初三)4、平行四边形ABC冲,设E、F分别是BC AB上的一点,AE与QF相交且AE= CF.求证:/ DPA F Z DPC (初二)经典难题(五)1、设P 是边长为1的正△ ABC 内任一点,L = PA + PB + PC ,求证:< L V 2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA + PB+ PC 的最小值.~C DB ADA / DCA CB GFHkZCAC B°,Z EBAC3、P 为正方形ABCD 内的一点,并且 PA = a , P 吐2a , PO 3a ,求正方形的边长.4、如图,△ ABC 中,/ ABC=ZACB= 80°, D E 分别是 AB =20°,求/ BED 勺度数. 经典难题(一)1.如下图做GH L AB,连接EQ 由于GOF 四点共圆,所以/ 即厶GHI ^A OGE 可得匹GQ =CO,又 CO=EQ 所以 CD=G 得证。
(完整版)中考数学几何综合压轴题初三难题训练(真题附答案)

中考数学几何综合压轴题初三难题训练1. (2015金华中考)如图,正方形 ABCD 和正三角形 AEF 都内接于eO , EF 与BC , CD 分别相交 于点G , H ,则-EF 的值是()GHA.——B. 2C. . 3D. 222.(2015遵义中考)将正方形 ABCD 绕点A 按逆时针方向旋转 30°,得正方形 AB 1GD 1,B^!交CD 于点E , AB 3,则四边形A^ED 的内切圆半径为()D ,E 分别是OA ,OB 的中点,则图中影阴部分的面积为 ___________ cm 2 .A. D.3. (2015遵义中考)如图,在圆心角为90°的扇形OAB 中,半径 OA 2cm ,C 为弧AB 的中点,6Di到E ,且有 EBD CAB • (1) 求证:BE 是eO 的切线;(2 )若BC 3 , AC 5,求圆的直径 AD 及切线BE 的长.5. (2016岳阳中考)数学活动 旋转变换(1) 如图①,在 VABC 中, ABC 130°,将VABC 绕点C 逆时针旋转500得到VABC ,连接 BB ,求ABB 的大小;(2) 如图②,在 VABC 中, ABC 150° , AB 3, BC 5,将VABC 绕点C 逆时针旋转 60° 得到VABC ,连接BB ,以A 为圆心,AB 长为半径作圆.(I)猜想:直线 BB 与e A 的位置关系,并证明你的结论; (H)连接AB ,求线段AB 的长度;(3)如图③,在 VABC 中, ABC 90° 180° , AB m , BC n ,将VABC 绕点 C 逆180°得到VABC ,连接AB 和BB ,以A 为圆心,AB 长为半与角 满足什么条件时,直线 BB 与e A 相切,请说明理由,并求此条件下线段AB 的长度(结果用角或角 的三角函数及字母 m , n 所组成的式子表示)时针旋转2角度0° 2径作圆,问:角6. (2016成都中考)如图,在RtVABC中,ABC 90°,以CB为半径作eC,交AC于点D,交AC 的延长线于点E,连接BD , BE .(1)求证:VABD s VAEB ;AB 4(2)当一—时,求tanE ;BC 3BE父于点F .(3 )在(2 )的条件下,作BAC的平分线,与7. (2016苏州中考)如图,在矩形ABCD中,AB 6cm , AD 8cm •点P从点B出发,沿对角线BD向点D匀速运动,速度为4cm/s,过点P作PQ BD交BC于点Q,以PQ为一边作正方形PQMN,使得点N落在射线PD上,点O从点D出发,沿DC向点C匀速运动,速度为3cm/s,以O为圆心,0.8cm为半径作圆O,点P与点O同时出发,设它们的运动时间为t (单位:s)(0 t 8)•3(1)如图,连接DQ,当DQ平分BDC时,t的值为.(2)如图,连接CM,若VCMQ是以CQ为底的等腰三角形,求t的值;(3)请你继续连行探究,并解答下列问题:①证明:在运动过程中,点O始终在QM所在直线的左侧;②如图3,在运动过程中,当QM与圆O相切时,求t的值;并判断此时PM与圆O是否也相切?说明理由.8. (2015扬州中考)如图,已知 eO 的直径AB 12cm , AC 是eO 的弦,过点 延长线于点P ,连接BC •(1) 求证: PCA B ;(2) 已知 P 400 ,点Q 在优弧ABC 上,从点A 开始逆时针运动到点 重合),当VABQ 与VABC 的面积相等时,求动点 Q 所经过的弧长.C 作eO 的切线交BA 的C 停止(点Q 与点C 不9. ( 2015大庆中考)如图, 四边形ABCD 内接于eO ,ADPBC P 为BD 上一点,APB BAD . (1) 证明:AB CD ;(2) 证明:DP BD AD BC ; (3) 证明:BD 2 AB 2 AD BC .10. (2015武汉中考)如图,AB是eO的直径,ABT 4^ , AT AB •(1)求证:AT是eO的切线;(2)连接OT交e O于点C,连接AC,求tan TAC的值.11. (2016随州中考)如图,AB是eO的弦,点C为半径OA的中点,过点C作CD OA交弦AB 于点E,连接BD,且DE DB •(1)判断BD与eO的位置关系,并说明理由;5(2)若CD 15 , BE 10 , ta nA -,求eO 的直径.1212. (2015德州中考)如图,eO的半径为1 , A, P , B , C是eO上的四个点, APC CPB 60°•(1) 判断VABC的形状:;(2) 试探究线段PA,PB,PC之间的数量关系,并证明你的结论;(3) 当点P位于的什么位置时,四边形APBC的面积最大?求出最大面积.13. (2016淮安中考)问题背景:如图1,在四边形 ADBC 中, ACB形,所以CE . 2CD ,从而得出结论:AC BC . 2CD •(1) 简单应用:在图1中,若AC 2 , BC 2 2,则CD •(2) 如图3, AB 是eO 的直径,点 C 、D 在e 上,AD BD ,若AB 13, BC 12,求CD 的 长. (3) 拓展规律:如图 4 , ACB ADB 90° , AD BD ,若 AC m , BC n m n ,求 CD 的长(用含m , n 的代数式表示)1(4 )如图5 , ACB 90° , AC BC ,点P 为AB 的中点,若点E 满足AE 1AC ,3CE CA ,点Q 为AE 的中点,则线段 PQ 与AC 的数量关系是.ADB 90° , A D BD ,探究线段 AC,BC,CD 之间的数量关系•小吴同学探究此问题的思路是:将 VBCD 绕点D ,逆时针旋转 90°到 VAED 处,点 B,C 分别落在点 A,E 处(如图2),易证点 C,A,E 在同一条直线上,并且VCDE 是等腰直角三角li14. (2015宜昌中考)如图,四边形ABCD为菱形,对角线AC , BD相交于点E , F是边BA延长线上一点,连接EF,以EF为直径作eO,交边DC于D,G两点,AD分别与EF,GF交于I , H两占八、、♦(1)求FDE的度数;(2)试判断四边形FACD的形状,并证明你的结论;(3)当G为线段DC的中点时,(i)求证:FD FI ;(ii)设AC 2m, BD 2n,求eO的面积与菱形ABCD的面积之比.15. (2015株洲中考)已知AB是圆O的切线,切点为B,直线AO交圆O于C , D两点,CD 2 , DAB 30°,动点P在直线AB上运动,PC交圆O于另一点Q .(1)当点P运动到使Q , C两点重合时(如图1),求AP的长;(2)点P在运动过程中,有几个位置(几种情况)使VCQD的面积为丄?(直接写出答案)21(3)当使VCQD的面积为丄,且Q位于以CD为直径的的上半圆上,CQ QD时(如图2),2求AP的长.第11页(共29页)第12页(共29页)第一部分 1.C【解析】如图,连接 AC 、BD 、OF ,其中AC 与EF 交于点I . QAO 是EAF 的角平分线,OAF 60o 2 30o .QOA OF ,OFA OAF 30° ,COF 60° ,BD CO 2 1 1 GH BD 2r r , 2 2竺3 3 .GH r作 DAB 1与 AB 1C 1的角平分线交于点 O ,过O 作OF AB 1 , 则 OAF 30° , AB 1O 4^ ,答案EF 3 o r 2 23r . QAO 2OI ,OI -r , CI 21 r r2 FI r sin60°GH CI 11 r , 22.B 【解析】设eO 的半径为r ,则 OF r ,第13页(共29页)故B i FOF 〔OA , 2 设B i Fx , 则AF :丄3 x , 故 3 2 x 2 2 x 2 2x ,解得x3 -,负值舍去. 2 四边形AB iE D 的内切圆半径为宁-第二部分3. n 1二2 2 2 【解析】连接0C ,过C 点作CF OA 于F •Q 半径OA 2cm , C 为A B 的中点,D 、E 分别是OA 、OB 的中点, OD OE 1cm , OC 2cm , AOC 4^ •CF . 2 • 鸟白图形ACDS 扇形OACS VOCD 2 45 n 221 2 1 23601 n2 2 cm . 2 2Q S VODE 〔OD 2 1 OE cm 2 2S 阴影S 扇形OAB S 空白图形ACD S VODE90 n 221 2 1—n ------ —360 2 2 21 —n _! 12 cm . 2 2 2第三部分4. (1)如图,连接OB .第14页(共29页)QBD BC ,CAB BAD .Q EBD CAB ,BAD EBD .QAD 是eO 的直径,ABD 90o , OA BO .BAD ABO .EBD ABO .OBE EBD OBD ABD OBD ABD 90°.Q 点B 在e O 上,BE 是eO 的切线.(2)如图,设圆的半径为 R ,连接CD .QAD 为eO 的直径,ACCD 90° .QBC BD ,OB CD .OB PAC .QOA OD ,1 5 OF AC .2 2Q 四边形ACBD 是圆内接四边形,BDE ACB .Q DBE ACB ,VDBE s VCAB . DB DEAC BC .3DE 5 3 .DEQ OBE OFD 90 ,DF PBE .QR 0 ,R 3.QBE 是eO 的切线,5. (1)如图①中, QVA BC 是由VABC 旋转得到,ABC ABC 130°,CB CBCBB CBB ,Q BCB 50o ,CBB CB B 650,ABB ABC BB C 65° .(2 )(1)结论:直线 BB ,是e A 的切线. 理由:如图②中,150°,CB CB ,Q ABC ABC CBB CBB ,Q BCB 60° ,CBB CB B 60° ,ABB ABC BBC 90° .AB BB ,直线BB ,是e A 的切线.(H) Q 在 RtVABB 中,Q AB B 90° , BB BC 5 , AB AB 3,AB AB 2 BB 2 34 .(3 )如图③中,当 180°时,直线BB ,是e A 的切线 理由:Q ABC ABC ,CB CB ,OF OB ODOEBE JDE AE * 2 3 3\5 5 3 115(3)解法一:在 RtVABC 中, -AC 2 BG -AB 2 11BG 即 5x BG 4x 3x ,解得BG 2 2 12 x . 590°.AB BB ,直线BB ,是e A 的切线.在VCBB 中QCB CB n , BCB 2 ,BB 2 nsin ,在 RtVA BB 中,AB . BB 2 AB 2 ,m 2 4n 2si n 26. (1) QDE 为e C 的直径,DBE 90° . 又 Q ABC 90° ,DBE DBC 90° , CBE DBC 90° ,ABD CBE .又QCB CE ,CBE E , ABD E .又 Q BAD EAB ,VABD ^VAEB .(2 )由(1)知,VABD s VAEB 在 RtVDBE 中,BD 1 tanEBE 2CBB CBB ,Q BCB 2 ,CBB ABB CB B 180° 2-------------? 2ABC BBC90°180° 90°BD BE ABAEABQ - BC设 AB 4x ,贝U CE 在 RtVABC 中,AB CB 3x .5x ,AE AC CE 5x 3x 8x BD BE AB AE 4x8xQAF 是 BAC 的平分线, BF AB 4x 1 FHEF 2BG BE 32 2 12 8FH BG一x x3 3 5 5 1又 Qta nE2EH 2FH 16 x ,5AM AE EM24 x ・ 5 在 RtVAHF 中, 2 2 AH HF AF 1 2 3即 224 x5e C 的半径是3xQAF 平分 BAC , FE AE 8x 2AE 于 H , 【解析】解法二:如图 2过点A 作EB 延长线的垂线,垂足为点在 VBAE 中,有 1 2 3 E 180°90° 90° , 4 2 E 45 ,VGAF 为等腰直角三角形8.5 L ,AFeC 的半径是NG BN a ,CG 3 a ,4 NC BC 9 a,4BH 9a, 5AB 3a , AC AG 3a ,tan NAC NG AG sin NAC 10105a ,4 15 a,4 13由( 2) 可知, AE 8x , tanEAG AE 于点M , 解法三:AE 于点G ,FM BAC 的平分线,QAF 是AE 10 .在 RtVDBE 中,设 BP 4t ,则 PQ 3t , BQ 5t .Q DQ 平分 BDC , QC CD , QP BD .CQ PQ 3t .QCQ 8 5t.3t 8 5t ,即 t 1.(2)如图,过点M 作ME BC 于点E .在 RtVAFM 中, FM AF sin NAC 2 卫互,AM 10 5 3 10 5 在 RtVEFM 中, EM FM tanE2 10 QBH a,5 EH 18 a, 5 DE 9 a ,2 DC 9 a ,4 AD 3 a,2 又QAE DE3 a 2 9 a2 9a,10 106DC 3.1087. (1)【解析】由题意可VBPQ s VBCD .DH AE10 ,a在 RtVABD 中,AB 6cm , AD 8cm ,BD 10cm .由 BPQ BCD , QBP DBC ,得 VPBQ ^VCBD .PB PQ BQBC CD BD .Q PB 4t ,PQ 3t , BQ 5t .Q MQ MC ,1 1 QE CE —QC - 8 5t2 2Q VMEQ s VDCB , EQ BCMQ BD1 -8 5t 23t40t 49(3)如图1,设QM 所在直线交CD 于点F . ① Q VQCF s VBCD , CF CDCQ CB CF 68 5t 8E15 -t , DF 4 又DO 3t , DO DF CF 6 ,即点O 始终在QM 所在直线的左侧.②如图,设MQ与eO相切时,切点我G,连接OG ,OG BCOF BD,0.88吗3t 10,4丄4t3当t -时,正方形PQMN的边长为3解法一:连接MO并延长交PQ于点贝U VMOG s VMHQ ,OG MGHQ MQ,260.815HQ4,HQ241328PH13 °HK14 213HK HQ .点O不在PMQ的平分线上,当QM1与eO相切时,PM与eO【解析】解法二:连接OM , OP ,Q SVMPQ SVMOQ S VPOQ S VPOM ,则VOGF s VBCD ,534 , QF-,FG3 5 .H,过点H作HK PM于点K不相切.OQ,设点O到MP的距离为h ,1 4 0.8 1 344142 h 8 .2 2 152h7 20.8 .15当QM与eO相切时,PM与eO不相切QAB是eO的直径,ACB 1 2 90o,又PC是eO的切线,PCO PCA 1 90°,2 PCA.又OC OB .2 B,PCA B .(2) Q P 40°,AOC 50°.QAB 12,AO 6 .AOQ 130°时,VABQ与VABC的面积相等,优弧ABQ所对的圆心角为230°时,VABQ与VABC的面积相等,13n31803180当BOQ 50°时,即9. (1) Q AD PBC ,ADB DBC ,AB DC ,AB CD .(2) Q APB BAD , BAD BCD 180° , APBBCD APD ,Q ADB CBD .VADPWDBC ,AD DPBD BC ,DP BD AD BC .QBD 2DE 2 BE 2, DE 2 CD 2 CE 2 ,2 BD 2CD 2 BE 2 CE 2AB 2 BE CE BE CEAB 2 AD BC.10. (1) QAB AT ,ATB B 45°.BAT 90° .AT 是eO 的切线.(2 )设eO 半径为r ,延长TO 交eO 于D ,连接AD .点Q 所经过的弧长 230 n 6 180 23 n3AAPD 180° , (3)如图,过点D 作DE BC 交BC 于E .QCD是直径,CAD BAT 90°.TAC OAD D . 又ATC DTA,VTAC s VTDA.TA TCTD AT .TA2TC TD , 即4r2 TC TC 2r 解得TC 5 1r.tan TAC tan DACADTCAT.5 1 r2r51211. (1)连接OB .QOB OA, DE DB ,A OBA, DEB ABD.QCD OA,A AEC A DEB 90°,OBA ABD 90°,OB BD ,BD是eO的切线;(2)如图,过点D作DG BE于G .QDE DB,1EG -BE 5,2GDE A,VACE s VDGE,QVACE s VDGE12. (1)等边三角形(2) PA PB PC .证明:如图,在PC上截取PD PA,连接AD .PA AD , PAD 60o.Q BAC 60o,PAB DAC .Q APC 60o,VPAD是等边三角形.Q ACE DGE 90°, AEC GED ,tan EDG tanAEGDG5—,即DG 12 .12在RtVEDG 中,DE .DG2 EG213. QCD 15, DECE 2 .13 ,ACDGCEGE,AC CE DGGE245e O的直径2OA 4AD96QAB AC ,VPAB 也VDAC .PB DC .QPD DC PC ,PA PB PC .(3)当点P 为A B 的中点时,四边形 APBC 面积最大.理由如下:如图,过点 P 作PE AB ,垂足为E , 过点C 作CF AB ,垂足为F ,四边形APBC 面积最大. Qe O 的半径为1,其内接正三角形的边长AB 31S 四边形APBC 匚 2 32 3 . 13. (1) CD 3(2)连接 AC 、BD 、AD ,Q AB 是eO 的直径,ADB ACB 90° ,Q A D B D ,AD BD ,将VBCD 绕点D ,逆时针旋转90°到VAED 处,如图3 ,EADDBC , Q DBCDAC 180° , EADDAC 180° , E 、A 、C 三点共线,Q AB 13,BC 12,由勾股定理可求得: AC 5 ,Q BC AE ,CE AE AC 17,2 AB PE ,S VABC 1AB CF . 2S 四边形APBC 1 — AB PE 2 Q 当点P 为A B 的中点时, CF . PE CF PC , PC 为eO 直径, Q S VPABQ EDA CDB ,EDA ADC CDB ADC ,即 EDCADB 90° ,Q CD ED , VEDC 是等腰直角三角形,CE 2CD ,17近 CD 2(3)以AB 为直径作eO ,连接OD 并延长交eO 于点D 1 , 连接D 1A ,D 1B , D 1C ,如图D 1C又Q 0D 是eO 的直径,DCD 1 90o ,Q AC m , BC n由勾股定理可求得: 2 2 DQ AB2 n22PQ = -^」AC • 614.( 1)QEF 为eO 的直径,FDE 90° .(2)四边形FACD 为平行四边形•理由如下:QABCD 为菱形,AB PCD , AC BD ,AEB 90° • 又 FDE 90o ,AC PFD •四边形FACD 为平行四边形.(3)(i )如图,连接GE •由(2)的证明过程可知: ACBC ■ 2D 1C ,ABm 2 2 Q D 1C 2 CD 2 2 D 1D 2CD m 2 n 2CD (4)Q 在RtVDEC 中,G 为CD 的中点,EG DG ,弧DG 弧EG ,1 2.又EF 为eO 的直径,FGE 90° ,FG EG .QG 为DC 中点,E 为AC 中点,GE 为VDAC 的中位线,EG PAD . FGADF l HDFHI 90o . 1 3 24 90o , 3 4 ,FD FI .(ii ) Q 菱形ABCD , AE CE m , BE DE nQ 四边形FACD 为平行四边形,FD AC 2m FIQ FD PAC , 3 8 .又34 7, 78 , EI EA m . 在 RtVFDE 中,FE 2 FD 2 DE 2 ,3m $ 2m $ n 2,解得,n 5m .2 3m9 2 1 S eo n 测,S 菱形ABCD — 2m 2n 2mn 2 4 2 S e O : S 菱形ABCD 9 n m 2:2 5m 2葺5. 4 4015. (1) QAB 是圆O 的切线,OBA 90o .2 5m 2 ,QRtVOBA中,CD 2, DAB 30°,OB 1 ,OB OC AC 1 .Q当点P , C运动到Q , C两点重合时,PC为圆O的切线,PCA 90°,Q DAB 30°, AC 1 ,AP -A/3•3(2)有4个位置使VCQD的面积为-•21【解析】由于CD的长度2,而S VCQD1, 故CD上的高的长度为-,从而如下图,我们可得到答案.2(3)过点Q作QN AD于点N,过点P作PM AD于点M •QNQCD是圆O的直径,CQD 90°• 易证VQCN s VDQN •QN CNDN QNQN2 CN DN .1x 2 x4解得X i 2 3, x22QCQ QD ,CNCNQN易证VPMC s VQNC .易得列空2 3MP QNCM 2 3 MP .在RtVAMP中易得AM 3MP , QAM CM AC 1,2,3 MP . 3MP 1 ,MP 3 14 ,薦1AP2MP21 2.又QCB CE,3 E .。
几何难题中考压轴题带含及详细解析

几何难题精选解答题〔共 30 小题〕1 .〔2021 ?河南〕如图 1,在 Rt △ABC 中,∠B=90 °,BC=2AB=8 ,点 D、E 分别是边 BC、AC 的中点,连接DE,将△EDC 绕点 C 按顺时针方向旋转,记旋转角为α.〔1〕问题发现①当α=0 °时, = ;②当α=180 °时, = .〔2〕拓展研究试判断:当 0°≤α<360 °时,的大小有无变化?请仅就图 2 的状况给出证明.〔3〕问题解决当△EDC 旋转至 A,D,E 三点共线时,直接写出线段 BD 的长.2.〔2021 ?济南〕如图 1 ,在△ABC 中,∠ACB=90 °,AC=BC ,∠EAC=90 °,点M 为射线 AE 上任意一点〔不与 A 重合〕,连接 CM ,将线段 CM 绕点 C 按顺时针方向旋转 90 °获取线段CN ,直线 NB 分别交直线 CM 、射线 AE 于点 F、D.〔1〕直接写出∠ NDE 的度数;〔2〕如图 2、图 3,当∠EAC 为锐角或钝角时,其他条件不变,〔 1〕中的结论可否发生变化?若是不变,采用其中一种状况加以证明;若是变化,请说明原由;〔3〕如图 4,假设∠EAC=15 °,∠ACM=60 °,直线CM 与 AB 交于 G,BD= ,其他条件不变,求线段 AM的长.3 .〔2021 ?岳阳〕直线 m ∥n ,点 C 是直线 m 上一点,点 D 是直线 n 上一点, CD 与直线 m 、n 不垂直,点 P 为线段 CD 的中点.〔1〕操作发现:直线 l ⊥m ,l⊥n,垂足分别为 A、B,当点 A 与点 C 重合时〔如图①所示〕,连接 PB,请直接写出线段 PA 与 PB 的数量关系:.〔2〕猜想证明:在图①的状况下,把直线 l 向上平移到如图②的地址,试问〔 1〕中的 PA 与 PB 的关系式可否依旧成立?假设成立,请证明;假设不成立,请说明原由.〔3〕延伸研究:在图②的状况下,把直线 l 绕点 A 旋转,使得∠ APB=90 °〔如图③所示〕,假设两平行线 m 、n 之间的距离为 2k .求证: PA ?PB=k ?AB.4 .〔2021 ?重庆〕在△ABC 中,AB=AC ,∠A=60 °,点D 是线段 BC 的中点,∠EDF=120 °,DE 与线段 AB 相交于点 E.DF 与线段 AC 〔或 AC 的延伸线〕订交于点 F.〔1〕如图 1,假设 DF⊥AC,垂足为 F,AB=4 ,求 BE 的长;〔2〕如图 2,将〔1 〕中的∠EDF 绕点 D 顺时针旋转必然的角度, DF 仍与线段 AC 订交于点 F.求证:BE+CF= AB;〔3〕如图 3,将〔 2〕中的∠EDF 连续绕点 D 顺时针旋转必然的角度,使 DF 与线段 AC 的延伸线订交于点 F,作 DN ⊥AC 于点 N ,假设 DN ⊥AC 于点 N ,假设 DN=FN ,求证: BE+CF= 〔BE﹣CF〕.5 .〔2021 ?烟台〕【问题提出】如图①,△ ABC 是等腰三角形,点 E 在线段 AB 上,点 D 在直线 BC 上,且 ED=EC ,将△BCE 绕点 C 顺时针旋转 60°至△ACF 连接 EF试证明: AB=DB+AF【类比研究】〔1〕如图②,若是点 E 在线段 AB 的延伸线上,其他条件不变,线段 AB ,DB,AF 之间又有怎样的数量关系?请说明原由〔2〕若是点 E 在线段 BA 的延伸线上,其他条件不变,请在图③的基础大将图形补充完满,并写出 AB ,DB ,AF 之间的数量关系,不用说明原由.6 .〔2021 ?莆田〕在 Rt△ACB 和 Rt △AEF 中,∠ACB= ∠AEF=90 °,假设点P 是 BF 的中点,连接 PC,PE.特别发现:如图 1,假设点 E,F 分别落在边 AB,AC 上,那么结论: PC=PE 成立〔不要求证明〕.问题研究:把图 1 中的△AEF 绕着点 A 顺时针旋转.〔1〕如图 2,假设点 E 落在边 CA 的延伸线上,那么上述结论可否成立?假设成立,请恩赐证明;假设不成立,请说明原由;〔2〕如图 3,假设点 F 落在边 AB 上,那么上述结论可否依旧成立?假设成立,请恩赐证明;假设不成立,请说明原由;〔3〕记 =k ,当 k 为何值时,△ CPE 总是等边三角形?〔请直接写出 k 的值,不用说明原由〕7 .〔2021 ?襄城区模拟〕如图,正方形 ABCO 的边 OA 、OC 在坐标轴上,点 B 坐标为〔3,3〕.将正方形 ABCO绕点 A 顺时针旋转角度α〔 0°<α<90 °〕,获取正方形 ADEF ,ED 交线段 OC 于点 G,ED 的延伸线交线段 BC于点 P,连 AP 、AG .〔1〕求证:△AOG ≌△ADG ;〔2〕求∠PAG 的度数;并判断线段 OG 、PG、BP 之间的数量关系,说明原由;〔3〕当∠1= ∠2 时,求直线 PE 的解析式;〔4〕在〔3〕的条件下,直线 PE 上可否存在点 M ,使以 M 、A、G 为极点的三角形是等腰三角形?假设存在,请直接写出 M 点坐标;假设不存在,请说明原由.8 .〔2021 ?重庆校级一模〕,四边形 ABCD 是正方形,点 P 在直线 BC 上,点 G 在直线 AD 上〔P、G 不与正方形极点重合,且在 CD 的同侧〕, PD=PG ,DF⊥PG 于点 H,DF 交直线 AB 于点 F,将线段 PG 绕点 P逆时针旋转 90 °获取线段P E,连接 EF.〔1〕如图 1,当点 P 与点 G 分别在线段 BC 与线段 AD 上时,假设 PC=1 ,计算出 DG 的长;〔2〕如图 1,当点 P 与点 G 分别在线段 BC 与线段 AD 上时,证明:四边形 DFEP 为菱形;〔3〕如图 2,当点 P 与点 G 分别在线段 BC 与线段 AD 的延伸线上时,〔2〕的结论:四边形 DFEP 为菱形可否依旧成立?假设成立,请给出证明;假设不成立,请说明原由.9 .〔2021 ?房山区二模〕在△ ABC 中,AB=BC=2 ,∠ABC=90 °,BD 为斜边 AC 上的中线,将△ ABD 绕点 D 顺时针旋转α〔0°<α<180 °〕获取△EFD,其中点 A 的对应点为点 E,点 B 的对应点为点 F.BE 与 FC 订交于点 H.〔1〕如图 1,直接写出 BE 与 FC 的数量关系:;〔2〕如图 2,M 、N 分别为 EF、BC 的中点.求证: MN= ;〔3〕连接 BF,CE,如图 3,直接写出在此旋转过程中,线段 BF、CE 与 AC 之间的数量关系:.10 .〔2021 ?衢州校级模拟〕图 1 是边长分别为 4 和 2 的两个等边三角形纸片 ABC 和 ODE 叠放在一起〔 C与 O 重合〕.〔1〕操作:固定△ ABC ,将△0DE 绕点 C 顺时针旋转 30 °后获取△ODE ,连接 AD 、B E,CE 的延伸线交 AB 于 F 〔图 2〕;研究:在图 2 中,线段 BE 与 AD 之间有怎样的大小关系?试证明你的结论.〔2〕在〔 1〕的条件下将的△ ODE ,在线段 CF 上沿着 CF 方向以每秒 1 个单位的速度平移,平移后的△ CDE 设为△PQR,当点 P 与点 F 重合时停止运动〔图 3〕研究:设△PQR 搬动的时间为 x 秒,△PQR 与△ABC 重叠局部的面积为 y,求 y 与 x 之间的函数解析式,并写出函数自变量 x 的取值范围.〔3〕将图 1 中△0DE 固定,把△ABC 沿着 OE 方向平移,使极点 C 落在 OE 的中点 G 处,设为△ABG ,尔后将△ABG 绕点 G 顺时针旋转,边 BG 交边 DE 于点 M ,边 AG 交边 DO 于点 N ,设∠BGE= α〔30 °<α<90 °〕;〔图4 〕研究:在图 4 中,线段 ON ?EM 的值可否随α的变化而变化?若是没有变化,请你求出 ON ?EM 的值,若是有变化,请你说明原由.11 .〔2021 ?武义县模拟〕〔 1 〕将矩形 OABC 放在平面直角坐标系中,极点 O 为原点,极点 C、A 分别在 x轴和 y 轴上, OA=8 ,OC=10 ,点 E 为 OA 边上一点,连接 CE,将△EOC 沿 CE 折叠.①如图 1,当点 O 落在 AB 边上的点 D 处时,求点 E 的坐标;②如图 2,当点 O 落在矩形 OABC 内部的点 D 处时,过点 E 作 EG∥x 轴交 CD 于点 H,交 BC 于点 G,设 H〔m ,n 〕,求 m 与 n 之间的关系式;〔2〕如图 3,将矩形 OABC 变为边长为 10 的正方形,点 E 为 y 轴上一动点,将△ EOC 沿 CE 折叠.点 O 落在点 D 处,延伸 CD 交直线 AB 于点 T,假设 = ,求 AT 的长.12 .〔2021 ?石家庄校级模拟〕如图 1,在菱形 ABCD 中,AC=6 ,BD=6 ,AC,BD 订交于点 O .〔1〕求边 AB 的长;〔2〕如图 2,将一个足够大的直角三角板 60 °角的极点放在菱形 ABCD 的极点 A 处,绕点 A 左右旋转,其中三角板 60 °角的两边分别于边 BC,CD 订交于 E,F,连接 EF 与 AC 订交于点 G.①判断△AEF 是哪一种特别三角形,并说明原由;②旋转过程中可否存在线段 EF 最短,假设存在,求出最小值,假设不存在,请说明原由.13 .〔2021 春 ?泰安校级期中〕如图,正方形 OEFG 绕着边长为 30 的正方形 ABCD 的对角线的交点 O 旋转,边 OE、OG 分别交边 AD 、AB 于点 M 、N .〔1〕求证: OM=ON ;〔2〕设正方形 OEFG 的对角线 OF 与边 AB 订交于点 P,连接 PM .假设 PM=13 ,试求 AM 的长;〔3〕连接 MN ,求△AMN 周长的最小值,并指出此时线段 MN 与线段 BD 的关系.14 .〔2021 ?天津〕在平面直角坐标系中, O 为原点,点 A〔﹣2 ,0〕,点 B〔0,2〕,点 E,点 F 分别为 OA ,OB 的中点.假设正方形 OEDF 绕点 O 顺时针旋转,得正方形 OE ′D′F′,记旋转角为α.〔Ⅰ〕如图①,当α =90 °时,求AE′,BF′的长;〔Ⅱ〕如图②,当α =135 °时,求证AE′=BF ′,且AE′⊥BF′;〔Ⅲ〕假设直线 AE′与直线BF′订交于点P,求点 P 的纵坐标的最大值〔直接写出结果即可〕.15 .〔2021 春 ?青山区期末〕正方形 ABCD 和正方形 EBGF 共极点 B,连 AF,H 为 AF 的中点,连 EH,正方形 EBGF 绕点 B 旋转.〔1〕如图 1,当 F 点落在 BC 上时,求证: EH= FC;〔2〕如图 2,当点 E 落在 BC 上时,连 BH ,假设 AB=5 ,BG=2 ,求 BH 的长;〔3〕当正方形 EBGF 绕点 B 旋转到如图 3 的地址时,求的值.16 .〔2021 ?盐城〕阅读资料如图①,△ABC 与△DEF 都是等腰直角三角形,∠ACB= ∠EDF=90 °,且点 D 在 AB 边上,AB、EF的中点均为 O ,连接 BF、CD 、CO ,显然点 C、F、O 在同一条直线上,可以证明△ BOF≌△COD ,那么 BF=CD .解决问题〔1〕将图①中的 Rt△DEF 绕点 O 旋转获取图②,猜想此时线段 BF 与 CD 的数量关系,并证明你的结论;〔2〕如图③,假设△ ABC 与△DEF 都是等边三角形, AB 、EF 的中点均为 O ,上述〔 1 〕中的结论依旧成立吗?如果成立,请说明原由;如不成立,央求出 BF 与 CD 之间的数量关系;〔3〕如图④,假设△ABC 与△DEF 都是等腰三角形, AB 、EF 的中点均为 0,且顶角∠ACB= ∠EDF= α,请直接写出的值〔用含α的式子表示出来〕17 .〔2021 ?梅州〕用如图①,②所示的两个直角三角形〔局部边长及角的度数在图中已标出〕,完成以下两个研究问题:研究一:将以上两个三角形如图③拼接〔 BC 和 ED 重合〕,在 BC 边上有一动点 P.〔1〕当点 P 运动到∠CFB 的角均分线上时,连接 AP,求线段 AP 的长;〔2〕当点 P 在运动的过程中出现 PA=FC 时,求∠PAB 的度数.研究二:如图④,将△ DEF 的极点 D 放在△ABC 的 BC 边上的中点处,并以点 D 为旋转中心旋转△ DEF,使△DEF 的两直角边与△ ABC 的两直角边分别交于 M 、N 两点,连接 MN .在旋转△DEF 的过程中,△ AMN 的周长可否存在有最小值?假设存在,求出它的最小值;假设不存在,请说明原由.18 .〔2021 ?营口〕如图,点 P 是⊙O 外一点, PA 切⊙O 于点 A,AB 是⊙O 的直径,连接 OP ,过点 B 作 BC∥OP 交⊙O 于点 C,连接 AC 交 OP 于点 D .〔1〕求证: PC 是⊙ O 的切线;〔2〕假设 PD= ,AC=8 ,求图中阴影局部的面积;〔3〕在〔 2〕的条件下,假设点 E是的中点,连接 CE,求 CE 的长.19 .〔2021 ?永州〕问题研究:〔一〕新知学习:圆内接四边形的判判断理:若是四边形对角互补,那么这个四边形内接于圆〔即若是四边形 EFGH 的对角互补,那么四边形 EFGH 的四个极点 E、F、G、H 都在同个圆上〕.〔二〕问题解决:⊙ O 的半径为 2,AB ,CD 是⊙O 的直径. P 是上任意一点,过点 P 分别作 AB,CD 的垂线,垂足分别为 N,M .〔1〕假设直径 AB⊥CD,关于上任意一点 P〔不与 B、C 重合〕〔如图一〕,证明四边形 PMON 内接于圆,并求此圆直径的长;〔2〕假设直径 AB⊥CD ,在点 P〔不与 B、C 重合〕从 B 运动到 C 的过程中,证明 MN 的长为定值,并求其定值;〔3〕假设直径 AB 与 CD 订交成 120 °角.①当点 P 运动到的中点 P1 时〔如图二〕,求 MN 的长;②当点 P〔不与 B、C 重合〕从 B 运动到 C 的过程中〔如图三〕,证明 MN 的长为定值.〔4〕试问当直径 AB 与 CD 订交成多少度角时, MN 的长取最大值,并写出其最大值.20 .〔2021 ?盘锦〕如图 1,△ABC 和△AED 都是等腰直角三角形,∠ BAC= ∠EAD=90 °,点B 在线段 AE 上,点C 在线段 AD 上.〔1〕请直接写出线段 BE 与线段 CD 的关系:;〔2〕如图 2,将图 1 中的△ABC 绕点 A 顺时针旋转角α〔 0<α<360 °〕,①〔1〕中的结论可否成立?假设成立,请利用图 2 证明;假设不成立,请说明原由;②当 AC= ED 时,研究在△ABC 旋转的过程中,可否存在这样的角α,使以 A、B、C、D 四点为极点的四边形是平行四边形?假设存在,请直接写出角α的度数;假设不存在,请说明原由.21 .〔2021 ?旭日〕问题:如图〔 1〕,在 Rt△ACB 中,∠ACB=90 °,AC=CB ,∠DCE=45 °,试试究AD 、DE、EB 满足的等量关系.[研究发现 ]小聪同学利用图形变换,将△ CAD 绕点 C 逆时针旋转 90°获取△CBH,连接 EH,由条件易得∠ EBH=90 °,∠ECH= ∠ECB+ ∠BCH= ∠ECB+ ∠ACD=45 °.依照“边角边〞,可证△ CEH ≌,得 EH=ED .在 Rt△HBE 中,由定理,可得 BH 2+EB 2=EH 2,由 BH=AD ,可得 AD 、DE、EB 之间的等量关系是.[实践运用 ]〔1〕如图〔 2 〕,在正方形 ABCD 中,△AEF 的极点 E、F 分别在 BC、CD 边上,高 AG 与正方形的边长相等,求∠EAF 的度数;〔2〕在〔 1〕条件下,连接 BD ,分别交 AE、AF 于点 M 、N ,假设 BE=2 ,DF=3 ,BM=2 ,运用小聪同学探究的结论,求正方形的边长及 MN 的长.22 .〔2021 ?自贡〕在△ABC 中,AB=AC=5 ,cos ∠ABC= ,将△ABC 绕点 C 顺时针旋转,获取△ A1B1C.〔1〕如图①,当点 B1 在线段 BA 延伸线上时.①求证: BB1∥CA 1;②求△AB1C 的面积;〔2〕如图②,点 E 是 BC 边的中点,点 F 为线段 AB 上的动点,在△ ABC 绕点 C 顺时针旋转过程中,点 F 的对应点是 F1,求线段 EF1 长度的最大值与最小值的差.23 .〔2021 ?吉林〕两个三角板 ABC,DEF,按以以下图的地址摆放,点 B 与点 D 重合,边 AB 与边 DE 在同一条直线上〔假设图形中所有的点,线都在同一平面内〕.其中,∠C= ∠DEF=90 °,∠ABC= ∠F=30 °,AC=DE=6cm .现固定三角板 DEF,将三角板 ABC 沿射线 DE 方向平移,当点 C 落在边 EF 上时停止运动.设三角板平移的距离为 x〔cm 〕,两个三角板重叠局部的面积为 y〔cm 2〕.〔1〕当点 C 落在边 EF 上时, x= cm ;〔2〕求 y 关于 x 的函数解析式,并写出自变量 x 的取值范围;〔3〕设边 BC 的中点为点 M ,边 DF 的中点为点 N .直接写出在三角板平移过程中,点 M 与点 N 之间距离的最小值.24 .〔2021 ?汕尾〕在 Rt△ABC 中,∠A=90 °,AC=AB=4 ,D,E 分别是边 AB ,AC 的中点,假设等腰 Rt△ADE绕点 A 逆时针旋转,获取等腰 Rt△AD 1E1,设旋转角为α〔 0<α≤180 °〕,记直线 BD1 与 CE1 的交点为 P.〔1〕如图 1,当α=90 °时,线段BD 1 的长等于,线段 CE1 的长等于;〔直接填写结果〕〔2〕如图 2,当α=135 °时,求证:BD 1=CE 1,且 BD1⊥CE1;〔3〕求点 P 到 AB 所在直线的距离的最大值.〔直接写出结果〕25 .〔2021 ?赤峰〕如图,四边形 ABCD 是边长为 2,一个锐角等于 60°的菱形纸片,小芳同学将一个三角形纸片的一个极点与该菱形极点 D 重合,按顺时针方向旋转三角形纸片,使它的两边分别交 CB、BA〔或它们的延长线〕于点 E、F,∠EDF=60 °,当CE=AF 时,如图 1 小芳同学得出的结论是 DE=DF .〔1〕连续旋转三角形纸片,当 CE≠AF 时,如图 2 小芳的结论可否成立?假设成立,加以证明;假设不成立,请说明原由;〔2〕再次旋转三角形纸片,当点 E、F 分别在 CB、BA 的延伸线上时,如图 3 请直接写出 DE 与 DF 的数量关系;〔3〕连 EF,假设△DEF 的面积为 y ,CE=x ,求 y 与 x 的关系式,并指出当 x 为何值时, y 有最小值,最小值是多少?26 .〔2021 ?海南〕如图,菱形 ABCD 中,点 P 是 CD 的中点,∠BCD=60 °,射线AP 交 BC 的延伸线于点 E,射线 BP 交 DE 于点 K,点 O 是线段 BK 的中点.〔1〕求证:△ADP ≌△ECP;〔2〕假设 BP=n ?PK,试求出 n 的值;〔3〕作 BM 丄 AE 于点 M ,作 KN 丄 AE 于点 N,连接 MO 、NO ,如图 2 所示,请证明△MON 是等腰三角形,并直接写出∠ MON 的度数.27 .〔2021 ?丹东〕在正方形 ABCD 中,对角线 AC 与 BD 交于点 O;在 Rt△PMN 中,∠MPN=90 °.〔1〕如图 1,假设点 P 与点 O 重合且 PM ⊥AD 、PN ⊥AB ,分别交 AD 、AB 于点 E、F,请直接写出 PE 与 PF 的数量关系;〔2〕将图 1 中的 Rt△PMN 绕点 O 顺时针旋转角度α〔 0 °<α<45 °〕.①如图 2,在旋转过程中〔 1〕中的结论依旧成立吗?假设成立,请证明;假设不成立,请说明原由;②如图 2,在旋转过程中,当∠ DOM=15 °时,连接EF,假设正方形的边长为 2,请直接写出线段 EF 的长;③如图 3,旋转后,假设 Rt△PMN 的极点 P 在线段 OB 上搬动〔不与点 O 、B 重合〕,当 BD=3BP 时,猜想此时PE 与 PF 的数量关系,并给出证明;当 BD=m ?BP 时,请直接写出 PE 与 PF 的数量关系.28 .〔2021 ?成都〕 AC ,EC 分别是四边形 ABCD 和 EFDC 的对角线,点 E 在△ABC 内,∠CAE+ ∠CBE=90 °.〔1〕如图①,当四边形 ABCD 和 EFCG 均为正方形时,连接 BF.〔i〕求证:△CAE∽△CBF;〔ii 〕假设 BE=1 ,AE=2 ,求 CE 的长;〔2〕如图②,当四边形 ABCD 和 EFCG 均为矩形,且 = =k 时,假设 BE=1 ,AE=2 ,CE=3 ,求 k 的值;〔3〕如图③,当四边形 ABCD 和 EFCG 均为菱形,且∠ DAB= ∠GEF=45 °时,设BE=m ,AE=n ,CE=p ,试试究 m ,n,p 三者之间满足的等量关系.〔直接写出结果,不用写出解答过程〕29 .〔2021 ?锦州〕如图①,∠ QPN 的极点 P 在正方形 ABCD 两条对角线的交点处,∠ QPN= α,将∠QPN 绕点P 旋转,旋转过程中∠ QPN 的两边分别与正方形 ABCD 的边 AD 和 CD 交于点 E 和点 F〔点 F 与点 C,D 不重合〕.〔1〕如图①,当α =90 °时,DE,DF,AD 之间满足的数量关系是;〔2〕如图②,将图①中的正方形 ABCD 改为∠ADC=120 °的菱形,其他条件不变,当α =60 °时,〔1〕中的结论变为 DE+DF= AD ,请给出证明;〔3〕在〔2〕的条件下,假设旋转过程中∠ QPN 的边 PQ 与射线 AD 交于点 E,其他条件不变,研究在整个运动变化过程中, DE,DF ,AD 之间满足的数量关系,直接写出结论,不用加以证明.30 .〔2021 ?绵阳〕如图 1,矩形 ABCD 中,AB=4 ,AD=3 ,把矩形沿直线 AC 折叠,使点 B 落在点 E 处,AE交 CD 于点 F,连接 DE.〔1〕求证:△DEC≌△EDA;〔2〕求 DF 的值;〔3〕如图 2,假设 P 为线段 EC 上一动点,过点 P 作△AEC 的内接矩形,使其极点 Q 落在线段 AE 上,定点 M 、N 落在线段 AC 上,当线段 PE 的长为何值时,矩形 PQMN 的面积最大?并求出其最大值.几何难题精选 (1) 旋转圆四边形参照答案与试题解析一.解答题〔共 30 小题〕1 .〔2021 ?河南〕如图 1,在 Rt △ABC 中,∠B=90 °,BC=2AB=8 ,点 D、E 分别是边 BC、AC 的中点,连接DE,将△EDC 绕点 C 按顺时针方向旋转,记旋转角为α.〔1〕问题发现①当α=0 °时, = ;②当α=180 °时, = .〔2〕拓展研究试判断:当 0°≤α<360 °时,的大小有无变化?请仅就图 2 的状况给出证明.〔3〕问题解决当△EDC 旋转至 A,D,E 三点共线时,直接写出线段 BD 的长.【考点】几何变换综合题.【专题】压轴题.【解析】〔1〕①当α=0 °时,在Rt △ABC 中,由勾股定理,求出 AC 的值是多少;尔后依照点 D、E 分别是边BC、AC 的中点,分别求出 AE、BD 的大小,即可求出的值是多少.②α=180 °时,可得AB ∥DE,尔后依照,求出的值是多少即可.〔2〕第一判断出∠ ECA= ∠DCB ,再依照,判断出△ECA∽△DCB,即可求出的值是多少,进而判断出的大小没有变化即可.〔3〕依照题意,分两种状况:①点 A,D,E 所在的直线和 BC 平行时;②点 A ,D,E 所在的直线和 BC 订交时;尔后分类谈论,求出线段 BD 的长各是多少即可.【解答】解:〔 1〕①当α=0 °时,∵Rt △ABC 中,∠B=90 °,∴AC= ,∵点D、E 分别是边 BC、AC 的中点,∴,∴.②如图 1,,当α=180 °时,可得 AB∥DE,∵,∴ = .故答案为:.〔2〕如图 2,,当 0°≤α<360 °时,的大小没有变化,∵∠ECD= ∠ACB ,∴∠ECA= ∠DCB ,又∵,∴△ECA∽△DCB ,∴.〔3〕①如图 3 ,,∵AC=4 ,CD=4 ,CD ⊥AD ,∴AD= = ,∵AD=BC ,AB=DC ,∠B=90 °,∴四边形 ABCD 是矩形,∴.②如图 4,连接 BD,过点 D 作 AC 的垂线交 AC 于点 Q ,过点 B作 AC 的垂线交 AC 于点 P,,∵AC=4 ,CD=4 ,CD ⊥AD ,∴AD= = ,∵点D、E 分别是边 BC、AC 的中点,∴DE= =2 ,∴AE=AD ﹣DE=8 ﹣2=6 ,由〔2〕,可得,∴BD= = .综上所述, BD 的长为 4 或.【谈论】〔1〕此题主要观察了几何变换综合题,观察了解析推理能力,观察了分类谈论思想的应用,观察了数形结合思想的应用,要熟练掌握.〔2〕此题还观察了相似三角形、全等三角形的判断和性质的应用,要熟练掌握.〔3〕此题还观察了线段长度的求法,以及矩形的判断和性质的应用,要熟练掌握.2.〔2021 ?济南〕如图 1 ,在△ABC 中,∠ACB=90 °,AC=BC ,∠EAC=90 °,点M 为射线 AE 上任意一点〔不与 A 重合〕,连接 CM ,将线段 CM 绕点 C 按顺时针方向旋转 90 °获取线段CN ,直线 NB 分别交直线 CM 、射线 AE 于点 F、D.〔1〕直接写出∠ NDE 的度数;〔2〕如图 2、图 3,当∠EAC 为锐角或钝角时,其他条件不变,〔 1〕中的结论可否发生变化?若是不变,采用其中一种状况加以证明;若是变化,请说明原由;〔3〕如图 4,假设∠EAC=15 °,∠ACM=60 °,直线CM 与 AB 交于 G,BD= ,其他条件不变,求线段 AM的长.【考点】几何变换综合题.【专题】压轴题.【解析】〔1〕依照题意证明△ MAC ≌△NBC 即可;〔2〕与〔 1〕的证明方法相似,证明△ MAC ≌△NBC 即可;〔3〕作 GK ⊥BC 于 K,证明 AM=AG ,依照△MAC ≌△NBC ,获取∠BDA=90 °,依照直角三角形的性质和条件求出 AG 的长,获取答案.【解答】解:〔 1〕∵∠ACB=90 °,∠MCN=90 °,∴∠ACM= ∠BCN ,在△MAC 和△NBC 中,,∴△MAC ≌△NBC ,∴∠NBC= ∠MAC=90 °,又∵∠ACB=90 °,∠EAC=90 °,∴∠NDE=90 °;〔2〕不变,在△MAC ≌△NBC 中,,∴△MAC ≌△NBC ,∴∠N= ∠AMC ,又∵∠MFD= ∠NFC,∠MDF= ∠FCN=90 °,即∠NDE=90 °;〔3〕作 GK⊥BC 于 K,∵∠EAC=15 °,∴∠BAD=30 °,∵∠ACM=60 °,∴∠GCB=30 °,∴∠AGC= ∠ABC+ ∠GCB=75 °,∠AMG=75 °,∴AM=AG ,∵△MAC ≌△NBC ,∴∠MAC= ∠NBC ,∴∠BDA= ∠BCA=90 °,∵BD= ,∴AB= + ,AC=BC= +1 ,设 BK=a ,那么 GK=a ,CK= a,∴a+ a= +1 ,∴a=1 ,∴KB=KG=1 ,BG= ,AG= ,∴AM= .【谈论】此题观察的是矩形的判断和性质以及三角形全等的判断和性质,正确作出辅助线、利用方程的思想是解题的重点,注意旋转的性质的灵便运用.3 .〔2021 ?岳阳〕直线 m ∥n ,点 C 是直线 m 上一点,点 D 是直线 n 上一点, CD 与直线 m 、n 不垂直,点 P 为线段 CD 的中点.〔1〕操作发现:直线 l ⊥m ,l⊥n,垂足分别为 A、B,当点 A 与点 C 重合时〔如图①所示〕,连接 PB,请直接写出线段 PA 与 PB 的数量关系: PA=PB .〔2〕猜想证明:在图①的状况下,把直线 l 向上平移到如图②的地址,试问〔 1〕中的 PA 与 PB 的关系式可否依旧成立?假设成立,请证明;假设不成立,请说明原由.〔3〕延伸研究:在图②的状况下,把直线 l 绕点 A 旋转,使得∠ APB=90 °〔如图③所示〕,假设两平行线 m 、n 之间的距离为 2k .求证: PA ?PB=k ?AB.【考点】几何变换综合题.【专题】压轴题.【解析】〔1〕依照三角形 CBD 是直角三角形,而且点 P 为线段 CD 的中点,应用直角三角形的性质,可得 PA=PB ,据此解答即可.〔2〕第一过 C 作 CE⊥n 于点 E,连接 P E,尔后分别判断出 PC=PE 、∠PCA= ∠PEB、AC=BE ;尔后依照全等三角形判断的方法,判断出△ PAC∽△PBE,即可判断出 PA=PB 依旧成立.〔3〕第一延伸 AP 交直线 n 于点 F,作 AE⊥BD 于点 E,尔后依照相似三角形判断的方法,判断出△AEF∽△BPF,即可判断出 AF ?BP=AE ?BF,再个 AF=2PA ,AE=2k ,BF=AB ,可得 2PA ?PB=2k .AB,因此 PA?PB=k ?AB,据此解答即可.【解答】解:〔 1〕∵l⊥n,∴BC⊥BD,∴三角形 CBD 是直角三角形,又∵点 P 为线段 CD 的中点,∴PA=PB .〔2〕把直线 l 向上平移到如图②的地址, PA=PB 依旧成立,原由以下:如图②,过 C 作 CE⊥n 于点 E,连接 P E,,∵三角形 CED 是直角三角形,点 P 为线段 CD 的中点,∴PD=PE ,又∵点 P 为线段 CD 的中点,∴PC=PD ,∴PC=PE ;∵PD=PE ,∴∠CDE= ∠PEB,∵直线 m ∥n ,∴∠CDE= ∠PCA ,∴∠PCA= ∠PEB,又∵直线 l⊥m ,l⊥n,CE⊥m ,CE⊥n ,∴l∥CE,∴AC=BE ,在△PAC 和△PBE 中,∴△PAC≌△PBE,∴PA=PB .〔3〕如图③,延伸 AP 交直线 n 于点 F,作 AE⊥BD 于点 E,,∵直线 m ∥n ,∴,∴AP=PF ,∵∠APB=90 °,∴BP⊥AF,又∵AP=PF ,∴BF=AB ;在△AEF 和△BPF 中,∴△AEF∽△BPF,∴,∴AF ?BP=AE ?BF,∵AF=2PA ,AE=2k ,BF=AB ,∴2PA ?PB=2k .AB ,∴PA?PB=k ?AB .【谈论】〔1〕此题主要观察了几何变换综合题,观察了解析推理能力,观察了分类谈论思想的应用,观察了数形结合思想的应用,观察了从图象中获守信息,并能利用获取的信息解答相应的问题的能力.〔2〕此题还观察了直角三角形的性质和应用,要熟练掌握.〔3〕此题还观察了全等三角形的判断和性质的应用,以及相似三角形的判断和性质的应用,要熟练掌握.4 .〔2021 ?重庆〕在△ABC 中,AB=AC ,∠A=60 °,点D 是线段 BC 的中点,∠EDF=120 °,DE 与线段 AB 相交于点 E.DF 与线段 AC 〔或 AC 的延伸线〕订交于点 F.〔1〕如图 1,假设 DF⊥AC,垂足为 F,AB=4 ,求 BE 的长;〔2〕如图 2,将〔1 〕中的∠EDF 绕点 D 顺时针旋转必然的角度, DF 仍与线段 AC 订交于点 F.求证:BE+CF= AB;〔3〕如图 3,将〔 2〕中的∠EDF 连续绕点 D 顺时针旋转必然的角度,使 DF 与线段 AC 的延伸线订交于点 F,作 DN ⊥AC 于点 N ,假设 DN ⊥AC 于点 N ,假设 DN=FN ,求证: BE+CF= 〔BE﹣CF〕.【考点】几何变换综合题;全等三角形的判断与性质;等边三角形的判断与性质;锐角三角函数的定义.【专题】压轴题.【解析】〔1〕如图 1,易求得∠B=60 °,∠BED=90 °,BD=2 ,尔后运用三角函数的定义即可求出 BE 的值;〔2〕过点 D 作 DM ⊥AB 于 M ,作 DN ⊥AC 于 N,如图 2,易证△MBD ≌△NCD ,那么有 BM=CN ,DM=DN ,进而可证到△ EMD ≌△FND ,那么有 EM=FN ,即可获取 BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD×cos60 °=BD= BC= AB;〔3〕过点 D 作 DM ⊥AB 于 M ,如图 3.同〔1〕可得:∠B= ∠ACD=60 °,同〔2〕可得: BM=CN ,DM=DN ,EM=FN .由 DN=FN 可得 DM=DN=FN=EM ,进而可得BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM ,B E﹣CF=BM+EM ﹣CF=BM+NF ﹣CF=BM+NC=2BM .尔后在 Rt△BMD 中,运用三角函数即可获取 DM= BM ,即 BE+CF= 〔B E﹣CF〕.【解答】解:〔 1〕如图 1,∵AB=AC ,∠A=60 °,∴△ABC 是等边三角形,∴∠B= ∠C=60 °,BC=AC=AB=4 .∵点D 是线段 BC 的中点,∴BD=DC= BC=2 .∵DF⊥AC,即∠AFD=90 °,∴∠AED=360 °﹣60 °﹣90 °﹣120 °=90 °,∴∠BED=90 °,∴BE=BD ×cos ∠B=2 ×cos60 °=2 × =1 ;〔2〕过点 D 作 DM ⊥AB 于 M ,作 DN ⊥AC 于 N,如图 2,那么有∠AMD= ∠BMD= ∠AND= ∠CND=90 °.∵∠A=60 °,∴∠MDN=360 °﹣60 °﹣90 °﹣90 °=120 °.∵∠EDF=120 °,∴∠MDE= ∠NDF .在△MBD 和△NCD 中,,∴△MBD ≌△NCD ,∴BM=CN ,DM=DN .在△EMD 和△FND 中,,∴△EMD ≌△FND ,∴EM=FN ,∴BE+CF=BM+EM+CF=BM+FN+CF=BM+CN=2BM=2BD ×cos60 °=BD= BC= AB ;〔3〕过点 D 作 DM ⊥AB 于 M ,如图 3.同〔1〕可得:∠B= ∠ACD=60 °.同〔2〕可得: BM=CN ,DM=DN ,EM=FN .∵DN=FN ,∴DM=DN=FN=EM ,∴BE+CF=BM+EM+CF=CN+DM+CF=NF+DM=2DM ,BE﹣CF=BM+EM ﹣CF=BM+NF ﹣CF=BM+NC=2BM .在 Rt△BMD 中,DM=BM ?tanB= BM ,∴BE+CF= 〔BE﹣CF〕.【谈论】此题主要观察了等边三角形的判断与性质、四边形的内角和定理、全等三角形的判断与性质、三角函数的定义、特别角的三角函数值等知识,经过证明三角形全等获取 BM=CN ,DM=DN ,EM=FN 是解决此题的关键.5 .〔2021 ?烟台〕【问题提出】如图①,△ ABC 是等腰三角形,点 E 在线段 AB 上,点 D 在直线 BC 上,且 ED=EC ,将△BCE 绕点 C 顺时针旋转 60°至△ACF 连接 EF试证明: AB=DB+AF【类比研究】〔1〕如图②,若是点 E 在线段 AB 的延伸线上,其他条件不变,线段 AB ,DB,AF 之间又有怎样的数量关系?请说明原由〔2〕若是点 E 在线段 BA 的延伸线上,其他条件不变,请在图③的基础大将图形补充完满,并写出 AB ,DB ,AF 之间的数量关系,不用说明原由.【考点】几何变换综合题.【专题】压轴题.【解析】第一判断出△ CEF 是等边三角形,即可判断出 EF=EC,再依照 ED=EC ,可得 ED=EF ,∠CAF= ∠BAC=60 °,因此∠EAF= ∠BAC+ ∠CAF=120 °,∠DBE=120 °,∠EAF= ∠DBE;尔后依照全等三角形判断的方法,判断出△EDB ≌△FEA ,即可判断出 BD=AE ,AB=AE+BF ,因此 AB=DB+AF .〔1〕第一判断出△CEF 是等边三角形,即可判断出 EF=EC,再依照 ED=EC ,可得 ED=EF ,∠CAF= ∠BAC=60 °,因此∠EFC= ∠FGC+ ∠FCG,∠BAC= ∠FGC+ ∠FEA,∠FCG= ∠FEA,再依照∠FCG= ∠EAD ,∠D= ∠EAD,可得∠D= ∠FEA;尔后依照全等三角形判断的方法,判断出△ EDB≌△FEA,即可判断出 BD=AE ,EB=AF ,进而判断出AB=BD ﹣AF 即可.〔2〕第一依照点 E 在线段 BA 的延伸线上,在图③的基础大将图形补充完满,尔后判断出△ CEF 是等边三角形,即可判断出 EF=EC ,再依照 ED=EC ,可得 ED=EF ,∠CAF= ∠BAC=60 °,再判断出∠ DBE= ∠EAF,∠BDE= ∠AEF;。
【中考冲刺】初三数学培优专题 25 平面几何的最值问题(含答案)(难)

平面几何的最值问题阅读与思考几何中的最值问题是指在一定的条件下,求平面几何图形中某个确定的量(如线段长度、角度大小、图形面积)等的最大值或最小值. 求几何最值问题的基本方法有:1.特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,再进行一般情形下的推证.2.几何定理(公理)法:应用几何中的不等量性质、定理.3.数形结合法等:揭示问题中变动元素的代数关系,构造一元二次方程、二次函数等.例题与求解【例1】在Rt △ABC 中,CB =3,CA =4,M 为斜边AB 上一动点.过点M 作MD ⊥AC 于点D ,过M 作ME ⊥CB 于点E ,则线段DE 的最小值为 .(四川省竞赛试题)解题思路:四边形CDME 为矩形,连结CM ,则DE = CM ,将问题转化为求CM 的最小值.【例2】如图,在矩形ABCD 中,AB =20cm ,BC =10cm .若在AC ,AB 上各取一点M ,N ,使BM +MN 的值最小,求这个最小值.(北京市竞赛试题)ADMN解题思路:作点B 关于AC 的对称点B ′,连结B ′M ,B ′A ,则BM = B ′M ,从而BM +MN = B ′M +MN .要使BM +MN 的值最小,只需使B ′M 十MN 的值最小,当B ′,M ,N 三点共线且B ′N ⊥AB 时,B ′M +MN 的值最小.【例3】如图,已知□ABCD ,AB =a ,BC =b (b a ),P 为AB 边上的一动点,直线DP 交CB 的延长线于Q .求AP +BQ 的最小值. (永州市竞赛试题)PDA BQ解题思路:设AP =x ,把AP ,BQ 分别用x 的代数式表示,运用不等式以ab b a 222≥+或a +b ≥2ab(当且仅当a =b 时取等号)来求最小值. 【例4】阅读下列材料:问题 如图1,一圆柱的底面半径为5dm ,高AB 为5dm ,BC 是底面直径,求一只蚂蚁从A 点出发沿圆柱表面爬行到C 点的最短路线. 小明设计了两条路线:图2图1摊平沿AB 剪开ACBBA路线1:侧面展开图中的线段AC .如图2所示.设路线l 的长度为l 1,则l 12 =AC 2=AB 2 +BC 2 =25+(5π) 2=25+25π2. 路线2:高线AB 十底面直径BC .如图1所示.设路线l 的长度为l 2,则l 22 = (BC +AB )2=(5+10)2 =225.∵l 12 – l 22 = 25+25π2-225=25π2-200=25(π2-8),∴l 12 >l 22 ,∴ l 1>l 2 . 所以,应选择路线2.条路线才能使蚂蚁从点A 出发沿圆柱表面爬行到C 点的路线最短. (衢州市中考试题)解题思路:本题考查平面展开一最短路径问题.比较两个数的大小,有时比较两个数的平方比较简便.比较两个数的平方,通常让这两个数的平方相减.【例5】如图,已知边长为4的正方形钢板,有一个角锈蚀,其中AF =2,BF =1.为了合理利用这块钢板,将在五边形EABCD 内截取一个矩形块MDNP ,使点P 在AB 上,且要求面积最大,求钢板的最大利用率. (中学生数学智能通讯赛试题)NME DAB解题思路:设DN =x ,PN =y ,则S =xy .建立矩形MDNP 的面积S 与x 的函数关系式,利用二次函数性质求S 的最大值,进而求钢板的最大利用率.【例6】如图,在四边形ABCD 中,AD =DC =1,∠DAB =∠DCB =90°,BC ,AD 的延长线交于P ,求AB ·S △P AB 的最小值. (中学生数学智能通讯赛试题)1ABD解题思路:设PD =x (x >1),根据勾股定理求出PC ,证Rt △PCD ∽Rt △P AB ,得到PCPACD AB ,求出AB ,根据三角形的面积公式求出y =AB ·S △P AB ,整理后得到y ≥4,即可求出答案.能力训练A 级1.如图,将两张长为8、宽为2的矩形纸条交叉,使重叠部分是一个菱形.容易知道当两张纸条垂直时,菱形的周长有最小值,那么菱形周长的最大值是 . (烟台市中考试题)2.D 是半径为5cm 的⊙O 内一点,且OD =3cm ,则过点O 的所有弦中,最短的弦AB = cm . (广州市中考试题)3.如图,有一个长方体,它的长BC =4,宽AB =3,高BB 1=5.一只小虫由A 处出发,沿长方体表面爬行到C 1,这时小虫爬行的最短路径的长度是 . (“希望杯”邀请赛试题)DD 1第1题图 第3题图 第4题图 第5题图4.如图,在△ABC 中,AB =10,AC =8,BC =6,经过点C 且与边AB 相切的动圆与CB ,CA 分别相交于点E ,F ,则线段EF 长度的最小值是( ) (兰州市中考试题)A .42B .4. 75C .5D .4. 85.如图,圆锥的母线长OA =6,底面圆的半径为2.一小虫在圆锥底面的点A 处绕圆锥侧面一周又回到点A ,则小虫所走的最短距离为( ) (河北省竞赛试题) A .12B .4πC .62D .636.如图,已知∠MON = 40°,P 是∠MON 内的一定点,点A ,B 分别在射线OM ,ON 上移动,当△P AB 周长最小时,∠APB 的值为( ) (武汉市竞赛试题) A .80° B .100° C .120° D .140° 7.如图, ⌒AD 是以等边三角形ABC 一边AB 为半径的四分之一圆周,P 为AD 上任意一点.若AC =5,则四边形ACBP 周长的最大值是( ) (福州市中考试题) A .15B .20C .15+52D .15+55NM NMAOPBDCBCA DBA PE第6题图 第7题图 第8题图 8.如图,在正方形ABCD 中,AB =2,E 是AD 边上一点(点E 与点A ,D 不重合),BE 的垂直平分线交AB 于M ,交DC 与N .(1) 设AE =x ,四边形ADNM 的面积为S ,写出S 关于x 的函数关系式.(2) 当AE 为何值时,四边形ADNM 的面积最大?最大值是多少? (山东省中考试题)9.如图,六边形ABCDEF 内接于半径为r 的⊙O ,其中AD 为直径,且AB =CD =DE =F A . (1) 当∠BAD =75°时,求⌒BC 的长; (2) 求证:BC ∥AD ∥FE ;(3) 设AB =x ,求六边形ABCDEF 的周长l 关于x 的函数关系式,并指出x 为何值时,l 取得最大值.10.如图,已知矩形ABCD 的边长AB =2,BC =3,点P 是AD 边上的一动点(P 异于A 、D ).Q 是BC边上任意一点.连结AQ,DQ,过P作PE∥DQ交于AQ于E,作PF//AQ交DQ于F.(1) 求证:△APE∽△ADQ;(2) 设AP的长为x,试求△PEF的面积S△PEF关于x的函数关系式,并求当P在何处时,S△PEF取得最大值?最大值为多少?(3) 当Q在何处时,△ADQ的周长最小?(须给出确定Q在何处的过程或方法,不必证明)(无锡市中考试题)B Q11.在等腰△ABC中,AB=AC=5,BC=6.动点M,N分别在两腰AB,AC上(M不与A,B重合,N不与A,C重合),且MN∥BC.将△AMN沿MN所在的直线折叠,使点A的对应点为P.(1)当MN为何值时,点P恰好落在BC上?(2)设MN=x,△MNP与等腰△ABC重叠部分的面积为y,试写出y与x的函数关系式,当x为何值时,y的值最大,最大值是多少?(宁夏省中考试题)B CAB级1.已知凸四边形ABCD中,AB+AC+CD= 16,且S四边彤ABCD=32,那么当AC= ,BD= 时,四边形ABCD面积最大,最大值是.(“华杯赛”试题)2.如图,已知△ABC的内切圆半径为r,∠A=60°,BC=23,则r的取值范围是.(江苏省竞赛试题)DBAB CAA第2题图第3题图第4题图第5题图3.如图⊙O的半径为2,⊙O内的一点P到圆心的距离为1,过点P的弦与劣弧⌒AB组成一个弓形,则此弓形面积的最小值为.4.如图,△ABC的面积为1,点D,G,E和F分别在边AB,AC,BC上,BD<DA,DG∥BC,DE ∥AC ,GF ∥AB ,则梯形DEFG 面积的最大可能值为 .(上海市竞赛试题)5.已知边长为a 的正三角形ABC ,两顶点A ,B 分别在平面直角坐标系的x 轴,y 轴的正半轴上滑动,点C 在第一象限,连结OC ,则OC 的最大值是 .(潍坊市中考试题)6.已知直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD =2,BC =DC =5,点P 在BC 上移动,则当P A + PD 取最小值时,△APD 中边AP 上的高为( ) (鄂州市中考试题)A .17172B .17174C .17178D .3QADBCA BDCPP第6题图 第7题图 第8题图7.如图,正方形ABCD 的边长为4cm ,点P 是BC 边上不与点B ,C 重合的任意一点,连结AP ,过点P 作PQ ⊥AP 交DC 于点Q .设BP 的长为x cm ,CQ 的长为y cm . (1) 求点P 在BC 上运动的过程中y 的最大值;(2) 当y =41cm 时,求x 的值. (河南省中考试题)8.如图,y 轴正半轴上有两点A (0,a ),B (0,b ),其中a >b >0.在x 轴上取一点C ,使∠ACB 最大,求C 点坐标. (河北省竞赛试题)9.如图,正方形ABCD 的边长为1,点M ,N 分别在BC ,CD 上,使得△CM N 的周长为2.求: (1) ∠MAN 的大小;(2) △MAN 的面积的最小值. (“宇振杯”上海市竞赛试题)10,如图,四边形ABCD 中,AD = CD ,∠DAB =∠ACB =90°,过点D 作DE ⊥AC 于F ,DE 与AB相交于点E .(1) 求证:AB ·AF =CB ·CD ; (2)已知AB =15cm ,BC =9cm ,P 是射线DE 上的动点,设DP =x cm(x >0),四边形BCDP 的面积为y cm 2. ①求y 关于x 的函数关系式;②当x 为何值时,△PBC 的周长最小?求出此时y 的值.(南通市中考试题)MNExCB第6题图 第7题图 第8题图 第9题图11.如图,已知直线l :k kx y 42-+=(k 为实数).(1) 求证:不论k 为任何实数,直线l 都过定点M ,并求点M 的坐标;(2) 若直线l 与x 轴、y 轴的正半轴交于A ,B 两点,求△AOB 面积的最小值.(太原市竞赛试题)12.如图,在Rt △ABC 中,∠C =90°,BC =2,AC =x ,点F 在边AB 上,点G ,H 在边BC 上,四边形EFGH 是一个边长为y 的正方形,且AE =AC . (1) 求y 关于x 的函数解析式;(2) 当x 为何值时,y 取得最大值?求出y 的最大值.(上海市竞赛试题)平面几何的最值问题例1125提示:当CM ⊥AB 时,CM 值最小,CM =125AC BC AB ⋅= 例2 如图,B ′M +MN 的最小值为点B ′到AB 的距离B ′F ,BE =45AB BCAC⋅=cm ,BB ′=85cm ,AE =()2222204585AB BE --=.在△ABB ′中,由12BB ′•AE =12AB •B ′F ,得B ′F =16cm .故BM +MN 的最小值为16cm . 例3 由△APD ∽△BPQ ,得AP AD BP BQ =,即BQ =()b a x AD BP AP x-⋅=,∴AP +BQ =x +ab b x -.∵x +ab x ≥2ab x ab x ⋅=仅当x =abx即x ab ,上式等号成立.故当AP ab ,AP +BQ 最小,其最小值为ab-b .例4 ⑴22125l π=+,22l =49,l 1<l 2,故要选择路线l 较短. ⑵()2221l h r π=+,()2222l h r =+,()2221244l l r r h π⎡⎤-=--⎣⎦.当r =244h π-时,2212l l =,当r >244h π-时,2212l l >,当r <244hπ-时,2212l l <. 例5 设DN =x ,PN =y ,则S =xy ,由△APQ ∽△ABF ,得()41242y x -=--即x =10-2y ,代入S =xy 得S =xy =y (10-2y ),即S =-2252522y ⎛⎫-+ ⎪⎝⎭,因3≤y ≤4,而y =52不在自变量y 的取值范围内,所以y =52不是极值点,当y =3时,S (3)=12,当y =4时,S (4)=8,故S max =12.此时,钢板的最大利用率21214212-⨯⨯=80%. 例6 设PD =x (x >1),则PC 21x -,由R t △PCD ∽△P AB ,得AB =21CD PA PC x ⋅=-y =AB •S △P AB ,则y =12AB ×P A ×AB =()()2121x x +-,求y 的最小值,有下列不同思路:①配方:y =21212242121x x x x --++=+--1221x x -=-x =3时,y 有最小值4.②运用基本不等式:y =122221x x -++≥- 321221x x -⋅-+2=4,∴当12x -=21x -,即当x =3时,y 有最小值4. ③借用判别式,去分母,得x 2+2(1-y )x +1+2y =0,由△=4(1-y )2-4(1+2y )=4y (y -4)≥0,得y ≥4,∴y 的最小值为4. A 级1. 17 提示:当两张纸条的对角重合时,菱形周长最大.2. 83.74 4. D 5. D 6. B7. C 提示:当点P 与点D 重合时,四边形ACBP 的周长最大.8. (1)连结ME ,过N 作NF ⊥AB 于F ,可证明Rt △EB A ≌Rt △MNF ,得MF =AE =x. ∵ME 2=AE 2+AM 2,故MB 2=x 2+AM 2,即(2-AM )2=x 2+AM 2,AM =1-14x 2,∴S =2AM DN +×AD =2AM AF+×2=AM +AM +MF =2 AM +AE =2(1-14x 2)+x =-12x 2+x +2.(2)S =-12(x 2-2 x +1)+52=-12(x -1)2+52. 故当AE =x =1时,四边形ADNM 的面积最大,此时最大值为52. 9. (1)BC 长为23rπ. (2)提示:连结BD . (3)过点B 作BM ⊥AD 于M ,由(2)知四边形ABCD为等腰梯形,从而BC =AD -2 AM =2r -2 AM . 由△BAM ∽△DAB ,得AM =2AB AD =22x r ,∴BC =2r-2x r . 同理,EF =2 r -2x r . l =4 x +2(2 r -2x r )=-xr(x -r )2+6 r (0<x 2 r ). . 当x =r时,l 取得最大值6 r .10. (1)∵∠APE =∠ADQ ,∠AEP =∠AQD ,∴△APE ∽△ADQ . (2)由△APE ∽△ADQ ,△PDF ∽△ADQ ,S △PEF =12S □PEQF ,得S △PEF =-13x 2+x =-13(x -32)2+34. 故当x =32时,即P 是AD 的中点时,S △PEF 取得最大值,(3)作A 关于直线BC 的对称点A′,连结DA′交BC 于Q ,则这个Q 点就是使△ADQ 周长最小的点,此时Q 是BC 的中点.11. (1)点P 恰好在BC 上时,由对称性知MN 是△ABC 的中位线,∴当MN =12BC =3时,点P 在BC 上. (2)由已知得△ABC 底边上的高h =225-3=4. ①当0<x ≤3时,如图1,连结AP 并延长交BC 于点D ,AD 与MN 交于点O .由△AMN ∽△ABC ,得AO =23x ,y =S △PMN =S △AMN =12·x ·23x =13x 2即y =13x 2. 当=3时,y 的值最大,最大值是3. ②当3<x <6时,如图2,设△PMN 与BC 相交于点E ,F ,AP 与BC 相交于D . 由①中知AO =23x ,∴AP =43x ,∴PD =AP -AD =43x -4,∵△PEF ∽△ABC . ,∴PEFABC S S ∆∆=(PD AD )2=(4434x -)2,即PEF ABC S S ∆∆=2-3)9x (. ∵S △ABC =12,∴S △PEF =43(x -3)2. ∴y =S △AMN -S △PEF =13x 2-43(x -3)2=-x 2+8x -12=-(x -4)2+4. 故当x =4时,y 的最大值为4. 综上,当x =4时,y 的值最大,最大值为4. B 级1. 8 2 32 提示:当∠CAB =∠ACD =90°时,四边形ABCD 的面积达到最大值.2. 0<r ≤1 提示:设BC =a ,CA =b ,AB =c ,b +c =3(r +1),又12bc sin60°=S △ABC =12(a +b +c )r ,即12bc ·32=12[33r +1)]r ,. bc =4r (r +2). b ,c 为方程x 2-3r +1)x +4r (r +2)=0的两个根,由△≥0,得(r +1)≤22. 因r >0,r +1>0,故r +1≤2,即0<r ≤1. 3.249π3提示:过P 作垂直于OP 的弦AB ,此时弓形面积最小. 4.13 提示:设AD AB =x ,则BD BA =1-x =CG CA ,ADGABCS S ∆∆=x 2,BDE ABC S S ∆∆=(1-x )2=CFG ABC S S ∆∆,S 梯形DEFG=1―x 2―2(1-x )2=-3(x -23)2+13.5. 312+a 提示:当OA =OB 时,OC 的长最大.6. C7. (1)由Rt △ABP ∽Rt △PCQ ,得BP CQ =AB CP ,即x y =44x -,y =-14(x -2)2+1(0<x <4). 当x =2时, y 最大值=1cm. (2)由14=-14(x -2)2+1,得x =(2+3)cm 或(2-3)cm. 8. 当过A ,B 两点的圆与x 轴正半轴相切时,切点C 为所求. 作O′D ⊥A B 于D . ,O′D 2= O′B 2-BD 2=2()2a b +-2()2a b -=ab ,O′D =ab 故点C 坐标为(ab ,0).9. (1)如图,延长CB 到L ,使BL =DN ,则Rt △ABL ≌Rt △ADN ,得AL =AN ,∠1=∠2,又∵N =2―CN ―CM =DN +BM =BL +BM =ML ,且AM =AM ,∠NAL =∠DAB =90°. ∴△AMN ≌△AML ,故∠MAN =∠MAL=902=45°. (2)设CM =x ,CN =y ,MN =z ,则2222222,2,x y z x y z x y z x y z ++==--⎧⎧⇔⎨⎨+=+=⎩⎩,于是,(2―y ―z )2+y 2=z 2. 整理得2y 2+(2z -4)y +(4-4z )=0. ∵y >0,故△=4(z -2)2-32(1-z )≥0,即(z +2+22)(z +2-22)≥0. 又∵z >0,故z ≥22-2,当且仅当x =y =2-2时等号成立. 由于S △AMN =S △AML =12·ML ·AB =12 MN ×1=2z ,因此,△AMN 的面积的最小值为2-1.10. (1)提示:证明△ADF ∽△BAC . (2)①AB =15,BC =9,∠ACB =90°,∴AC 22AB BC -=2215912-=,∴CF =AF =6,∴()()19632702y x x x =+⨯=+>.②∵BC =9(定值),∴△PBC 的周长最小,就是PB +PC 最小,由(1)知,点C 关于直线DE 的对称点是点A ,所以PB +PC =PB +P A ,故只要求PB +P A 最小.显然当P 、A 、B 三点共线时PB +P A 最小,此时DP =DE ,PB +P A =AB .由(1),角∠ADF =∠F AE ,∠DF A =∠ACB =90°,得△DAF ∽△ABC .EF ∥BC ,得AE =BE =12AB =152,EF =92.∴ AF ∶BC =AD ∶AB ,即6∶9=AD ∶15,∴AD =10.Rt △ADF 中,AD =10,AF =6,∴DF =8.∴DE =DF +FE =8+92=252. ∴当x =252时,△PBC 的周长最小,此时y =1292. 11.(1)令k =1,得y =x +2;令k =2,得y =2x +6,联立解得x =4,y =2,故定点(4,2). (2)取x =0,得OB =2-4k (k <0),取y =0,得OA =()420k k k-<.于是△ABO 的面积()()114224022k S OA OB k k k-==-<,化简得()28820k S k +-+=.由()28640S ∆=--≥得2160S S -≥,故S ≥16.将S =16代入上述方程,得k =12-.故当k =12-,S 值最小. 12.(1)如图,延长EF 交AC 于点D ,DF ∥BC ,Rt △ADF ∽Rt △ACB ,AE =AC =x ,()2222DE x x y xy y =--=-22xy y y x y x -+-=,2x -2y -xy =22x xy y -,两边平方整理得(x 2+2x +2)y 2-(x 3+2x 2+4x )y +2x 2=0.解得2222x y x x =++(y =x 舍去) . (2)由(1)22122222y x x ==+++≤ .当且仅当2x x =,即2x =,上式等号成立.故当2x =,y 去最大21.。
中考复习初中数学几何证明经典试题(含答案)
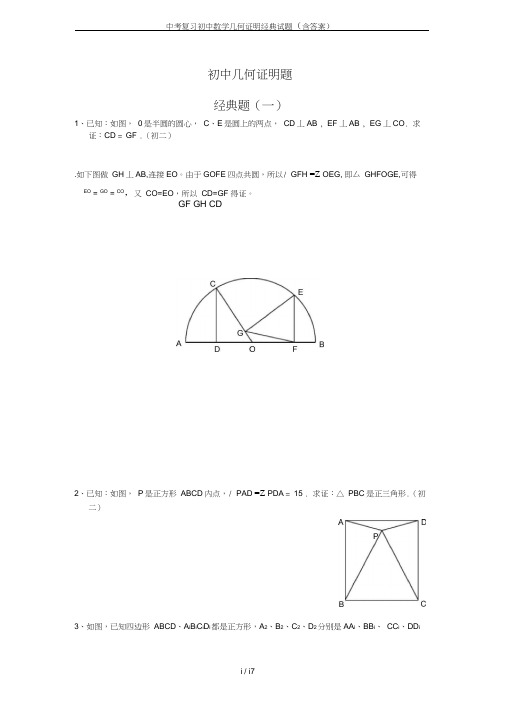
初中几何证明题经典题(一)1、已知:如图,0是半圆的圆心,C、E是圆上的两点,CD丄AB , EF丄AB , EG丄CO. 求证:CD = GF .(初二).如下图做GH丄AB,连接EO。
由于GOFE四点共圆,所以/ GFH =Z OEG, 即厶GHFOGE,可得EO = GO = CO,又CO=EO,所以CD=GF 得证。
GF GH CD2、已知:如图,P是正方形ABCD内点,/ PAD =Z PDA = 15°. 求证:△ PBC是正三角形.(初二)3、如图,已知四边形ABCD、A i B i C i D i都是正方形,A2、B2、C2、D2分别是AA i、BB i、CC i、DD i的中点.及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP = AQ .(初二)3、如果上题把直线 MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN P 、Q .4、 1、求证:四边形 A 2B 2C 2D 2是正方形.(初二)已知: 求证: 如图,在四边形 的延长线交 / DEN = Z△ ABC 中, MN F .ABCD 中,AD = BC , M 、N 分别是 AB 、CD 的中点,AD 、BC 于E 、F .经典题(二)已知: (1) 求证:AH = 20M ;(2) 若/ BAC = 60°,求证:H 为垂心 (各边高线的交点),0为外心,且 0M 丄BC 于M . AH = A0 .(初二)2、设MN 是圆O 外一直线,过O 作OA 丄MN 于A ,自A 引圆的两条直线,交圆于DCGN求证:AP = AQ .(初二)ECAM NP4、如图,分别以厶 ABC 的AC 和BC 为一边,在△ ABC 的外侧作正方形 ACDE 和正方形 CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于 AB 的一半.(初二)经典题(二)1、如图,四边形 ABCD 为正方形, 求证:CE = CF .(初二)2、如图,四边形 ABCD 为正方形,DE // AC ,且CE = CA ,直线EC 交DA 延长线于F . 求证:AE = AF .(初二)DE // AC , AE = AC , AE 与 CD 相交于 F .FEAD1、设P 是边长为1的正△ ABC 内任一点,4、如图,PC 切圆0于C , AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于3、设ABCD 为圆内接凸四边形,求证: AB • CD + AD • BC = AC • BD .(初三)B 、D .求证: AB = DC , BC = AD .(初三)1、已知:△ ABC 是正三角形,P 是三角形内一点 求:/ APB 的度数.(初二)2、设P 是平行四边形 ABCD 内部的一点,且/求证:/ PAB = Z PCB .(初二)4、平行四边形 ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE = CF .求证:/ DPA =Z DPC .(初二)AO DB EFC求证:4、如图,△ ABC 中,/ ABC =Z ACB = 80°, D、E 分别是AB、AC 上的点,/ DCA = 30°, / EBA = 20°,求/ BED 的度数. LiB C经典题(一)1•如下图做GH丄AB,连接E0。
初中数学:20道经典几何难题(附答案),练熟后中考成绩不下130

初中数学:20道经典几何难题(附答案),练熟后中考成绩不
下130
老师们都喜欢说语文者得天下,得作文者得语文!可是对于初中数学来说,几何在数学学习和考试中的地位和作文在语文考试中的地位比起来,恐怕只有过之而无不及!所以我们也可以说初中数学是:得几何者得数学!、一来是几何几乎承包初中数学半壁江山,68%的核心考点都出自几何!而且,“几何”问题不仅是初中数学的重点,到了高中数学学习中也占很大比重!如果初中几何知识没学好,那么等到高中继续学习几何知识时,一定会遇到更大的难度!但是不管怎么说,初中的几何其实难度还是不大的。
初中三年也是塑造孩子的抽象思维的最佳时期。
如果在此时,不能够通过数学几何,来对孩子的抽象思维能力进行一点训练,那到了高中,恐怕更加地更不上了。
为此,小课堂整理了这份初中几何必考的20道经典题汇总资料,我希望各位家长朋友可以为自己的孩子收藏一份,哪怕孩子对于初中几何知识掌握并不是十分熟练和牢固,可是多做一些题目,对于孩子们理解和掌握几何知识还是有非常大的帮助,何况这些题目都是初中数学考试中经常出现的题目!。
初三数学立体几何基础练习题及答案

初三数学立体几何基础练习题及答案练习题1:1. 计算一个边长为4cm的正方体的体积和表面积。
2. 已知一个正方体的体积为64cm³,求其边长。
3. 一个正方体的表面积为96cm²,求其边长。
4. 一个正方体的边长为10cm,求其体积和表面积。
练习题2:1. 已知一个立方体的体积为27cm³,求其边长。
2. 一个立方体的表面积为54cm²,求其体积和边长。
3. 一个立方体的体积为125cm³,求其表面积和边长。
4. 已知一个立方体的表面积为150cm²,求其体积和边长。
练习题3:1. 已知一个圆柱体的底面半径为3cm,高度为8cm,求其体积和侧面积。
2. 一个圆柱体的体积为72π cm³,底面半径为4cm,求其高度和侧面积。
3. 一个圆柱体的侧面积为96π cm²,底面半径为3cm,求其高度和体积。
4. 已知一个圆柱体的高度为6cm,侧面积为48π cm²,求其底面半径和体积。
答案:练习题1:1. 该正方体的体积为64cm³,表面积为96cm²。
2. 该正方体的边长为4cm。
3. 该正方体的边长为4cm。
4. 该正方体的体积为1000cm³,表面积为600cm²。
练习题2:1. 该立方体的边长为3cm。
2. 该立方体的体积为27cm³,边长为3cm。
3. 该立方体的表面积为150cm²,边长为5cm。
4. 该立方体的体积为250cm³,边长为5cm。
练习题3:1. 该圆柱体的体积为72π cm³,侧面积为48π cm²。
2. 该圆柱体的高度为4cm,侧面积为64π cm²。
3. 该圆柱体的高度为8cm,体积为288π cm³。
4. 该圆柱体的底面半径为2cm,体积为72π cm³。
初中数学经典几何题及答案
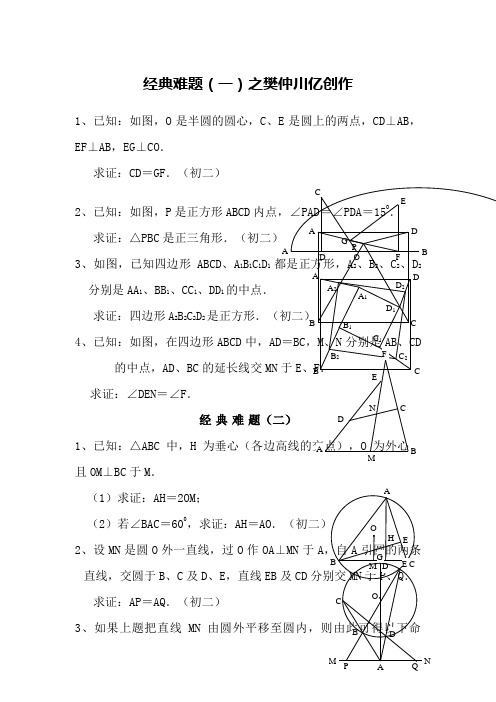
经典难题(一)之樊仲川亿创作1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C2D 24、已知:如图,在四边形ABCD 中,AD 的中点,AD 、BC 的延长线交MN 求证:∠DEN =∠F .经典难1、已知:△ABC 中,H 且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A 直线,交圆于B 、C 及D 、E ,直线EB 及CD 求证:AP =AQ .(初二)3、如果上题把直线MN题:设MN 是圆O 的弦,过MN CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 方形ACDE 和正方形CBFG ,点P 是EF求证:点P 到边AB 的距离等于AB经典难1、如图,四边形ABCD 为正方形,DE ∥交于F .求证:CE =CF 2、如图,四边形ABCD 交DA 延长线于F .求证:AE =AF 3、设P 是正方形ABCD DCE .求证:PA =PF 4、如图,PC 切圆O 于AF 与直线PO 相交于B 1、已知:△ABC 4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB+PC 的最小值.3、P 为正方形ABCD 内的一点,而且PA =a ,PB =正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E的点,∠DCA =300,∠EBA =200,求∠BED APC B P ADCBCBD A F PDE CBAAPC B经典难题(一)⊥AB,连接EO。
初中数学经典几何题及答案,附知识点及结论总结
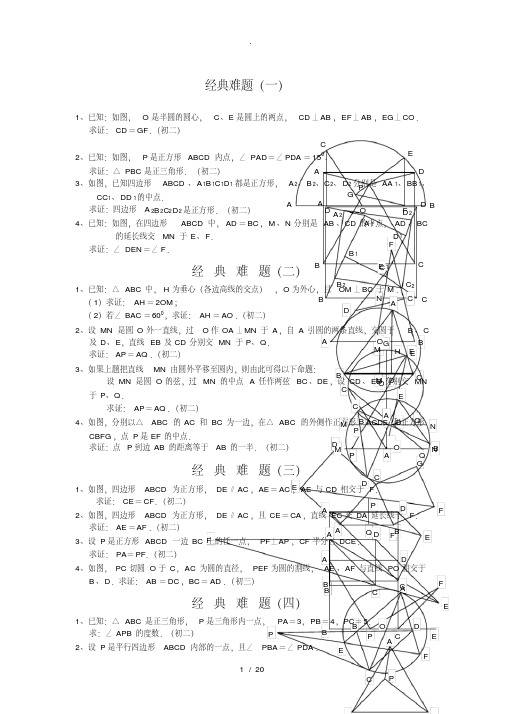
P C G FBQ A D E 经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150.求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.(初二)经典难题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典难题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .APCDBAF G CE B O D D 2 C 2B 2 A 2 D 1C 1B 1C BD A A 1 A N FE C D MB · AD HE M C B O ·GAO D B E CQ P NM ·O Q PB DEC NM ·ADAFD EC BED ACBF F E P CB A ODB FAEP A求证:∠PAB=∠PCB.(初二)3、设ABCD为圆内接凸四边形,求证:AB·CD+AD·BC=AC·BD.(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典难题(一)1.如下图做GH⊥AB,连接EO。
初三数学重点难点几何题及答案
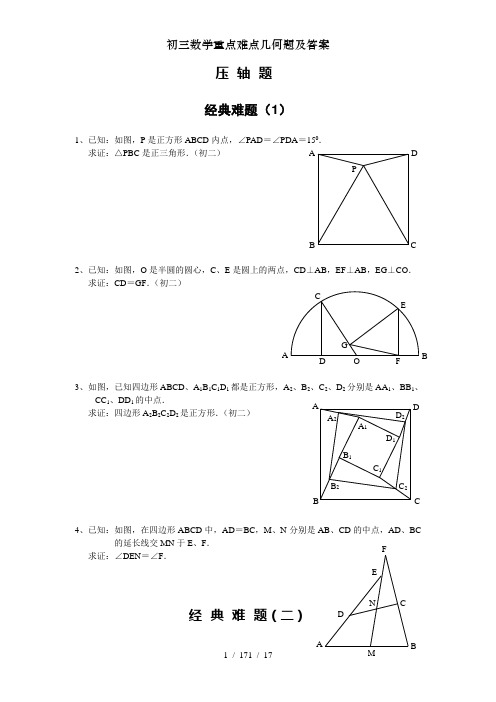
压轴题 经典难题(1)1、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)2、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 A FG CEBO D A P C D BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
初中数学经典几何题(难)及答案分析

经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA .求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)1、设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.AP CB ACBPDEDCB A A CBPD1.如下图做GH⊥AB,连接EO。
初三数学重点难点试卷答案

一、选择题1. 答案:B解析:本题考查了二次函数的性质。
由于a=1>0,所以二次函数的图像开口向上,对称轴为y轴,顶点坐标为(0,-1)。
因此,当x=2时,y的值最小,为-1。
2. 答案:C解析:本题考查了圆的性质。
根据圆的定义,圆上任意一点到圆心的距离都相等,即半径相等。
因此,ABCD为圆的直径,且AC=BD,所以ABCD是矩形。
3. 答案:A解析:本题考查了三角函数的定义。
根据正弦函数的定义,sinA=对边/斜边。
在直角三角形ABC中,∠A=30°,所以sinA=1/2。
4. 答案:D解析:本题考查了不等式的解法。
将不等式两边同时乘以-1,得到-3x > 6。
再将不等式两边同时除以-3,注意不等号方向改变,得到x < -2。
5. 答案:B解析:本题考查了一元二次方程的解法。
将方程两边同时除以x+1,得到x-2=3。
将方程两边同时加上2,得到x=5。
二、填空题6. 答案:2π解析:本题考查了圆的周长公式。
圆的周长公式为C=2πr,其中r为圆的半径。
题目中给出了圆的半径为2,所以周长为2π×2=4π。
7. 答案:3解析:本题考查了勾股定理。
在直角三角形ABC中,根据勾股定理,A B²=AC²+BC²。
已知AC=5,BC=4,代入公式得到AB²=5²+4²=41,所以AB=√41。
8. 答案:-1解析:本题考查了函数的奇偶性。
函数f(x)在x=0处的函数值为f(0)=0,且f(-x)=-f(x),所以函数f(x)是奇函数。
根据奇函数的性质,f(0)=0。
9. 答案:-2解析:本题考查了一元二次方程的解法。
将方程x²-5x+6=0进行因式分解,得到(x-2)(x-3)=0。
解得x=2或x=3,所以方程的解为x=-2。
10. 答案:12解析:本题考查了几何图形的面积计算。
根据长方形的面积公式,面积S=长×宽。
初中数学经典几何题及答案-附知识点及结论总结
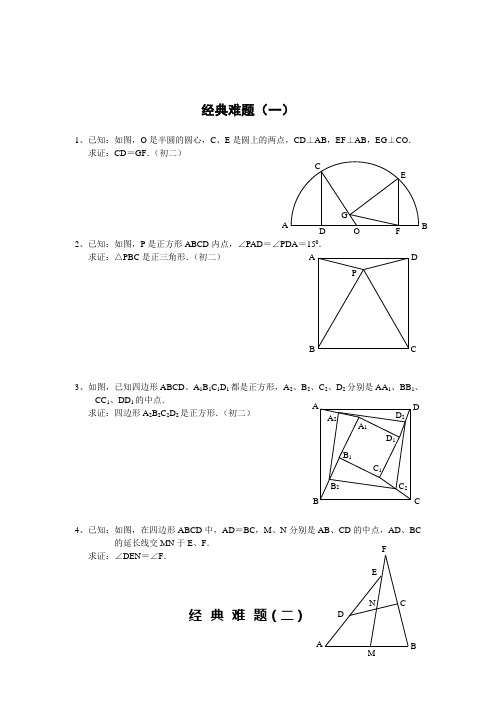
经典难题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)A P C DB A FG CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 内任一点,L =≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC0,∠EBA =200,求∠BED 的度数.经典难题(一)1.如下图做GH ⊥AB,连接EO 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
压轴题 经典难题(1)1、已知:如图,P 是正方形ABCD 点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)2、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典难题(二)D 2 C 2B 2 A 2 D 1C 1 B 1 C B DA A 1A FG CE B O D A P C D BF1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典难 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC 求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,D .求证:AB =DC ,BC =AD .(初三)经典难1、已知:△ABC 是正三角形,P求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆接凸四边形,求证:AB ·CD +AD ·BC =AC ·4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二) 经典难题(五)1、设P 是边长为1的正△ABC 任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.4、如图,△ABC 中,∠ABC =∠ACB =800,D 、E 分别是AB 、AC 上的点,∠DCA =300,∠EBA =200,求∠BED 的度数.FP DE CBAA PC BAC BPDEDA ACBPD经典难题(一)1.如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2. 如下图做△DGC使与△ADP全等,可得△PDG为等边△,从而可得△DGC≌△APD≌△CGP,得出PC=AD=DC,和∠DCG=∠PCG=150所以∠DCP=300 ,从而得出△PBC是正三角形3.如下图连接BC1和AB1分别找其中点F,E.连接C2F与A2E并延长相交于Q点,连接EB2并延长交C2Q于H点,连接FB2并延长交A2Q于G点,由A2E=12A1B1=12B1C1= FB2 ,EB2=12AB=12BC=F C1 ,又∠GFQ+∠Q=900和∠GE B2+∠Q=900,所以∠GE B2=∠GFQ又∠B2FC2=∠A2EB2,可得△B2FC2≌△A2EB2,所以A2B2=B2C2,又∠GFQ+∠HB2F=900和∠GFQ=∠EB2A2 ,从而可得∠A2B2 C2=900 ,同理可得其他边垂直且相等,从而得出四边形A2B2C2D2是正方形。
4.如下图连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=∠F,∠QNM=∠DEN和∠QMN=∠QNM,从而得出∠DEN=∠F。
经典难题(二)1.(1)延长AD到F连BF,做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)连接OB,OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证。
3.作OF⊥CD,OG⊥BE,连接OP,OA,OF,AF,OG,AG,OQ。
由于22AD AC CD FD FD AB AE BE BG BG,由此可得△ADF≌△ABG,从而可得∠AFC=∠AGE。
又因为PFOA与QGOA四点共圆,可得∠AFC=∠AOP和∠AGE=∠AOQ,∠AOP=∠AOQ,从而可得AP=AQ。
4.过E,C,F 点分别作AB 所在直线的高EG ,CI ,FH 。
可得PQ=2EGFH。
由△EGA ≌△AIC ,可得EG=AI ,由△BFH ≌△CBI ,可得FH=BI 。
从而可得PQ=2AI BI=2AB,从而得证。
经典难题(三)1.顺时针旋转△ADE ,到△ABG ,连接CG. 由于∠ABG=∠ADE=900+450=1350从而可得B ,G ,D 在一条直线上,可得△AGB ≌△CGB 。
推出AE=AG=AC=GC,可得△AGC为等边三角形。
∠AGB=300,既得∠EAC=300,从而可得∠A EC=750。
又∠EFC=∠DFA=450+300=750.可证:CE=CF。
2.连接BD作CH⊥DE,可得四边形CGDH是正方形。
由AC=CE=2GC=2CH,可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150,又∠FAE=900+450+150=1500,从而可知道∠F=150,从而得出AE=AF。
3.作FG⊥CD,FE⊥BE,可以得出GFEC为正方形。
令AB=Y ,BP=X ,CE=Z ,可得PC=Y-X 。
tan∠BAP=tan∠EPF=XY=ZY X Z,可得YZ=XY-X2+XZ,即Z(Y-X)=X(Y-X) ,既得X=Z ,得出△ABP≌△PEF ,得到PA=PF ,得证。
经典难题(四)1.顺时针旋转△ABP 600,连接PQ ,则△PBQ是正三角形。
可得△PQC是直角三角形。
所以∠APB=1500。
2.作过P点平行于AD的直线,并选一点E,使AE∥DC,BE∥PC.可以得出∠ABP=∠ADP=∠AEP,可得:AEBP共圆(一边所对两角相等)。
可得∠BAP=∠BEP=∠BCP,得证。
3.在BD取一点E,使∠BCE=∠ACD,既得△BEC∽△ADC,可得:BE BC =ADAC,即AD•BC=BE•AC,①又∠ACB=∠DCE,可得△ABC∽△DEC,既得AB AC =DEDC,即AB•CD=DE•AC,②由①+②可得: AB•CD+AD•BC=AC(BE+DE)= AC·BD ,得证。
4.过D 作AQ ⊥AE ,AG ⊥CF ,由ADE S=2ABCDS=DFCS,可得:2AE PQ =2AE PQ,由AE=FC 。
可得DQ=DG ,可得∠DPA =∠DPC (角平分线逆定理)。
经典难题(五)1.(1)顺时针旋转△BPC 600 ,可得△PBE 为等边三角形。
既得PA+PB+PC=AP++PE+EF 要使最小只要AP ,PE ,EF 在一条直线上, 即如下图:可得最小L=;(2)过P点作BC的平行线交AB,AC与点D,F。
由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最大L< 2 ;由(1)和(2)既得:≤L<2 。
2.顺时针旋转△BPC 600,可得△PBE为等边三角形。
既得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小PA+PB+PC=AF。
既得AF=213(1)42= 23=4232=2(31)2 = 2(31)2 =62。
3.顺时针旋转△ABP 900 ,可得如下图:既得正方形边长L = 2222(2)()22a = 522a 。
4.在AB 上找一点F ,使∠BCF=600 ,连接EF ,DG ,既得△BGC 为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE ≌△ACF , 得到BE=CF , FG=GE 。
推出 : △FGE 为等边三角形 ,可得∠AFE=800 ,既得:∠DFG=400 ①又BD=BC=BG ,既得∠BGD=800 ,既得∠DGF=400 ② 推得:DF=DG ,得到:△DFE ≌△DGE , 从而推得:∠FED=∠BED=300 。
