2021届绵阳一诊 理科数学试题
四川省绵阳2023-2024学年高三上学期一诊模拟(三)数学(理科)试题含解析

绵阳2021级高三上期一诊模拟(三)数学(理科)试题(答案在最后)时间:120分钟,满分:150分本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的).1.集合{}2|60A x x x =--<,集合{}2|lo 1g B x x =<,则A B ⋃=A.()2,3- B.(),3-∞ C.()2,2- D.()0,2【答案】A 【解析】【分析】先由二次不等式的解法得{}|23A x x =-<<,由对数不等式的解法得{}|02B x x =<<,再结合集合并集的运算即可得解.【详解】解不等式260x x --<,解得23x -<<,则{}|23A x x =-<<,解不等式2log 1x <,解得02x <<,即{}|02B x x =<<,即A B ⋃=()2,3-,故选:A.【点睛】本题考查了二次不等式的解法及对数不等式的解法,重点考查了集合并集的运算,属基础题.2.复数z =)A.1B.-1C.iD.-i【答案】B 【解析】【分析】根据复数的运算即可化简复数,然后根据虚部的概念即可求解.【详解】()()()21i 1i 1i 1i z -===-+-,∴虚部为-1.故选:B3.以下说法正确的有()A.“24-<<x ”是“22150x x --<”的必要不充分条件B.命题“01x ∃>,0ln(1)0x -≥”的否定是“1x ∀≤,ln(1)0x -<”C.“2b ac =”是“,,a b c ”成等比数列的充分必要条件D.设,R a b ∈,则“0a ≠”是“0ab ≠”的必要不充分条件【答案】D 【解析】【分析】根据充分、必要条件、存在量词命题的否定等知识确定正确答案.【详解】A 选项,()()2215530x x x x --=-+<,解得35x -<<,所以“24-<<x ”是“22150x x --<”的充分不必要条件,A 选项错误.B 选项,因为由0ln(1)0x -≥,得011x -≥,即02x ≥,所以命题“01x ∃>,0ln(1)0x -≥”的否定是“1x ∀>,2x <”,B 选项错误.C 选项,当0a b c ===时,有2b ac =,但此时“,,a b c ”不是等比数列;当“,,a b c ”成等比数列时,有b ca b=,即2b ac =,所以“2b ac =”是“,,a b c ”成等比数列的必要不充分条件,C 选项错误.D 选项,当0,0a b ≠=时,有0ab =;当0ab ≠时,有0,0a b ≠≠;所以“0a ≠”是“0ab ≠”的必要不充分条件,所以D 选项正确.故选:D.4.古代数学家刘徽编撰的《重差》是中国最早的一部测量学著作,也为地图学提供了数学基础,根据刘徽的《重差》测量一个球体建筑的高度,已知点A 是球体建筑物与水平地面的接触点(切点),地面上B ,C 两点与点A 在同一条直线上,且在点A 的同侧,若在B ,C 处分别测量球体建筑物的最大仰角为60°和20°,且BC =100m ,则该球体建筑物的高度约为()(cos10°≈0.985)A.45.25mB.50.76mC.56.74mD.58.60m【答案】B 【解析】【分析】数形结合,根据三角函数解三角形求解即可;【详解】设球的半径为R ,,tan10RAB AC ==,100tan10R BC =-=,25250.760.985R R ==故选:B.5.已知2sin 63πθ⎛⎫+= ⎪⎝⎭,则sin 26πθ⎛⎫-= ⎪⎝⎭()A.19-B.19C.9-D.9【答案】A 【解析】【分析】由22()266πππθθ+-=+,结合诱导公式、二倍角余弦公式可得2sin(22sin ()166ππθθ-=+-,即可求值.【详解】由题意有:22()266πππθθ+-=+,∴2cos(2sin(2cos 2()12sin ()26666πππππθθθθ+-=--=+=-+,又2sin 63πθ⎛⎫+= ⎪⎝⎭,∴1sin 269πθ⎛⎫-=- ⎪⎝⎭.故选:A.6.如图所示的程序框图的输出结果为()A.20142015B.12015C.20152016D.12016【答案】C 【解析】【分析】运行程序,根据裂项求和法求得正确答案.【详解】运行程序,0,1S i ==,判断否,1101212S =+=⨯⨯,2i =,判断否,11,31223S i =+=⨯⨯,……以此类推,111,2016122320152016S i =+++=⨯⨯⨯ ,判断是,输出111122320152016S =+++⨯⨯⨯ 1111112015112232015201620162016=-+-++-=-=.故选:C7.已知函数ππ()sin()22f x x ωϕϕ⎛⎫=+-<< ⎪⎝⎭在3π7π,88⎛⎫ ⎪⎝⎭内单调递减,3π8x =是函数()f x 的一条对称轴,且函数π8y f x ⎛⎫=+⎪⎝⎭为奇函数,则7π24f ⎛⎫= ⎪⎝⎭()A.32B.1- C.12D.32【答案】D 【解析】【分析】利用正弦型函数的对称性、奇偶性、单调性进行求解即可.【详解】因为函数()f x 在3π7π,88⎛⎫⎪⎝⎭内单调递减,3π8x =是函数()f x 的一条对称轴,所以有7π3π17π3π12π2882882T ωω-≤⇒-≤⋅⇒≤,所以()()3ππ2πZ 182k k ωϕ⋅+=+∈,因为ππsin 88y f x x ωωϕ⎛⎫⎛⎫=+=++ ⎪ ⎪⎝⎭⎝⎭是奇函数,所以()()ππZ 28m m ωϕ+=∈,由()()12-可得:()422k m ω=-+,而2ω≤,所以2ω=±,当2ω=时,()()2ππZ πZ 84m m m m πϕϕ+=∈⇒=-∈,因为ππ22ϕ-<<,所以π4ϕ=-,即π()sin(24f x x =-,当3π7π,88x ⎛⎫∈⎪⎝⎭时,ππ3π2,422x ⎛⎫-∈ ⎪⎝⎭,显然此时函数单调递减,符合题意,所以7π7πππ3()sin(2)sin 2424432f =⨯-==;当2ω=-时,()()2πππZ πZ 84m m m m ϕϕ-+=∈⇒=+∈,因为ππ22ϕ-<<,所以π4ϕ=,即π()sin(2)4f x x =+,当3π7π,88x ⎛⎫∈ ⎪⎝⎭时,()π2π,2π4x +∈,显然此时函数不是单调递减函数,不符合题意,故选:D8.设等比数列{}n a 的公比为q ,其前n 项和为n S ,前n 项积为n T ,且满足条件11a >,202220231a a >⋅,20222023(1)(1)0a a -⋅-<则下列选项正确的是()A.{}n a 为递增数列B.202220231S S +<C.2022T 是数列{}n T 中的最大项D.40451T >【答案】C 【解析】【分析】根据等比数列的通项公式和前n 项和公式、数列的单调性等知识对选项进行分析,从而确定正确答案.【详解】由20222023(1)(1)0a a -⋅-<可得:20221a -和20231a -异号,即202220231010a a ->⎧⎨-<⎩或202220231010a a -<⎧⎨->⎩.而11a >,202220231a a >⋅,可得2022a 和2023a 同号,且一个大于1,一个小于1因为11a >,所有20221a >,20231a <,即数列{}n a 的前2022项大于1,而从第2023项开始都小于1.对于A :公比202320221a q a =<,因为11a >,所以11n n a a q -=为减函数,所以{}n a 为递减数列.故A 不正确;对于B :因为20231a <,所以2023202320221a S S =<-,所以202220231S S +>.故B 错误;对于C :等比数列{}n a 的前n 项积为n T ,且数列{}n a 的前2022项大于1,而从第2023项开始都小于1,所以2022T 是数列{}n T 中的最大项.故C 正确;对于D :24044404512340444045123404511111()()()T a a a a q a q a qa q a α+++=== 404520224045202240451142020534()a q a q a ⨯===,因为20231a <,所以404520231a <,即40451T <.故D 错误.故选:C9.如图,ABC 的外接圆圆心为O ,2AB =,3AC =,则AO BC ⋅=()A.52B.32C.3D.2【答案】A 【解析】【分析】根据给定条件,分别求出AO AB ⋅ 、AO AC ⋅即可求解作答.【详解】因ABC 的外接圆圆心为O ,2AB =,3AC =,由圆的性质得1||cos ,||2AO AO AB AB 〈〉=,有21||||cos ,||22AO AB AO AB AO AB AB ⋅=〈〉==,同理219||22AO AC AC ⋅== ,所以5()2AO BC AO AC AB AO AC AO AB ⋅=⋅-=⋅-⋅= .故选:A【点睛】方法点睛:求两个向量的数量积的方法:利用定义;利用向量的坐标运算;利用数量积的几何意义.具体应用时可根据已知条件的特征来选择,同时要注意数量积运算律的应用.10.已知实数0x >,则函数x y x =的值域为()A.(0,)+∞B.(1,)+∞ C.1,e ∞⎛⎫+ ⎪⎝⎭D.1ee ,∞-⎛⎫+ ⎪⎝⎭【答案】D 【解析】【分析】x y x =的两边同时取自然对数得到()ln ln 0y x x x =>,令()()ln 0f x x x x =>,求导得到其单调性,求出()()ln 0f x x x x =>的值域,求出答案.【详解】对x y x =的两边同时取自然对数得,()ln ln 0y x x x =>,令()()ln 0f x x x x =>则()1ln f x x '=+,令()0f x ¢>,解得1e x >,令()0f x '<,解得10ex <<,故()()ln 0f x x x x =>在10,e ⎛⎫ ⎪⎝⎭上单调递减,在1,e⎛⎫+∞ ⎪⎝⎭上单调递增,故()()ln 0f x x x x =>在1ex =上取得极小值,也是最小值,且1111ln e e e ef ⎛⎫==- ⎪⎝⎭,故()()ln 0f x x x x =>的值域为1,e ⎡-+∞⎫⎪⎢⎣⎭,所以xy x =的值域为1e e ,-⎛⎫+∞ ⎪⎝⎭.故选:D11.若函数()y f x =满足()()2f a x f a x b ++-=,则说()y f x =的图象关于点(),a b 对称,则函数...1220212022()12320222023x x x x x f x x x x x x ++++=++++++++++的对称中心是()A.(1011,2022)- B.()1011,2022 C.(1012,2023)- D.()1012,2023【答案】C 【解析】【分析】求出定义域,由定义域的对称中心,猜想1012a =-,计算出(1012)(1012)4046f x f x --++-=,从而求出对称中心.【详解】函数定义域为{|1, 2...,...2022,2023}x x x x x ≠-≠-≠-≠-,定义域的对称中心为(1012,0)-,所以可猜1012a =-,则.10121011101010091010(1012)101110101009101010.11.x x x x xf x x x x x x -+-+-+++-+=+++++-+-+-+++,.10121011101010091010(1012)101110101009101010.11.x x x x xf x x x x x x----------=+++++--------1012101110101009101010111010101..091001011.x x x x x x x x x x+++--=++++++++--,故(1012)(1012)f x f x -+--+101010121009101110121010101110111010101010111011x x x x x x x x x x x x ++++-+-⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪=++++-+-⎝⎭⎝⎭⎝⎭ 622023404=⨯=所以()y f x =的对称中心为(1012,2023)-,故选:C .12.已知函数()f x 及其导函数()f x '定义域均为R ,记()()1g x f x '=+,且(2)(2)4f x f x x +--=,()3g x +为偶函数,则()()717g g '+=()A.0B.1C.2D.3【答案】C 【解析】【分析】对(2)(2)4f x f x x +--=两边同时求导,结合函数的周期和偶函数的性质进行求解即可.【详解】因为()3g x +为偶函数,()()1g x f x '=+,所以()()44f x f x ''+=-+,对(2)(2)4f x f x x +--=两边同时求导,得(2)(2)4f x f x ''++-=,所以有(4)()4(4)()4(4)()4(8)(),f x f x f x f x f x f x f x f x ''''''''++-=⇒-+-=⇒++=⇒+=所以函数()f x '的周期为8,在(2)(2)4f x f x ''++-=中,令0x =,所以(2)2f '=,因此()()()171822g f f ''===,因为()3g x +为偶函数,所以有()()()()()()()3373311g x g x g g x g x g ''=-⇒=--⇒=-'+-'+,()()()()()()()(8)()7171712f x f x g x g x g x g x g g ''''''+=⇒+=-⇒+=-⇒=-,由()()1,2可得:()70g '=,所以()()7172g g '+=,故选:C【点睛】关键点睛:本题的关键是对(2)(2)4f x f x x +--=两边同时求导,再利用赋值法进行求解.第Ⅱ卷(非选择题,共90分)二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上.13.已知(2,),(3,1)a b λ=-=,若()a b b +⊥ ,则a = ______.【答案】【解析】【分析】根据题意求得(1,1)a b λ+=+ ,结合向量的数量积的运算公式求得λ的值,得到a的坐标,利用向量模的公式,即可求解.【详解】因为(2,),(3,1)a b λ=-= ,可得(1,1)a b λ+=+,又因为()a b b +⊥,可得()(1,1)(3,1)310b b a λλ=+⋅=++=⋅+ ,解得4λ=-,所以(2,4)a =-- ,所以a ==故答案为:14.若“[]01,4x ∃∈使20040x ax -+>”为假命题,则实数a 的取值范围为___________.【答案】[5,)+∞【解析】【分析】将问题转化为“4≥+a x x在[]1,4上恒成立”,再利用对勾函数的单调性求得最值,从而得解.【详解】因为“[]01,4x ∃∈使20040x ax -+>”为假命题,所以“[]1,4x ∀∈,240x ax -+≤”为真命题,其等价于4≥+a x x在[]1,4上恒成立,又因为对勾函数()4f x x x=+在[]1,2上单调递减,在[]2,4上单调递增,而()()145f f ==,所以()max 5f x =,所以5a ≥,即实数a 的取值范围为[5,)+∞.故答案为:[5,)+∞.15.设矩形()ABCD AB BC >的周长为12,把ABC 沿AC 向ADC △折叠,AB 折后交DC 于点M ,则ADM △的面积最大值为___________.【答案】27-【解析】【分析】作图,令ABC 折叠后对应为AEC △,且AB x =(36x <<),易得ADM CEM ≅ ,再设,AM a DM x a ==-且2a x a >>,勾股定理列方程得186a x x=+-,最后应用三角形面积公式、基本不等式求面积最大值,注意取值条件.【详解】如下图,ABC 折叠后对应为AEC △,令AB x =且36x <<,则6BC x =-,由图知:AD BC EC ==,90D E ∠=∠=︒,AMD CME ∠=∠,则ADM CEM ≅ ,所以,DM EM AM CM ==,而AB AE AM EM AM DM ==+=+,令,AM a DM x a ==-且2a x a >>,则222AD DM AM +=,所以22218(6)()6x x a a a x x -+-=⇒=+-,则186DM x =-,则13183(6)(1)273()27272ADM S AD DM x x x x =⋅=--=-+≤-- ,当且仅当x =所以ADM △的面积最大值为27-故答案为:27-16.若存在两个不等的正实数x ,y ,使得()()e e x yx y x y t -+-=-成立,则实数t 的取值范围为___________.【答案】),2l 2(n2-∞-【解析】【分析】对已知等式进行变形,构造新函数,利用导数判断函数的单调性,结合题意进行求解即可.【详解】()()22e e e e x y x y x y x xt y yt x y t ⇒-+==--++--,构造函数()()2e 0mf m m mt m =-+>,所以原问题等价于存在两个不等的正实数x ,y ,使得()()f x f y =,显然函数()f m 不是正实数集上的单调函数,()()e 20m f m m t m '=-+>,设()()()e 20e 2m mg m m m g m '=->⇒=-,当ln 2m >时,()()0,g m g m '>单调递增,当0ln 2m <<时,()()0,g m g m '<单调递减,故()()min ln 22ln 2g m g ==-,当2ln 20t -+≥时,即ln 22t ≥-时,()()0,f m f m '≥单调递增,所以不符合题意;当2ln 20t -+<时,即ln 22t <-时,显然存在0m ,使得()00f m '=,因此一定存在区间()()00,0m m εεε-+>,使得()f m '在()()0000,,,m m m m εε-+上异号,因此函数()f m 在()()0000,,,m m m m εε-+上单调性不同,因此一定存在两个不等的正实数x ,y ,使得()()e e x yx y x y t -+-=-成立,故答案为:),2l 2(n2-∞-【点睛】关键点睛:本题的关键是由()()e e x y x y x y t -+-=-构造函数()()2e 0mf m m mt m =-+>.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.设等差数列{}n a 前n 项和n S ,11a =,满足()1252n n S n a +=++,N*n ∈.(1)求数列{}n a 的通项公式;(2)记21n n n n b S S ++=,设数列{}n b 的前n 项和为n T ,求证516<n T .【答案】(1)21n a n =-(2)证明见解析【解析】【分析】(1)根据等差数列的通项公式进行求解即可;(2)利用等差数列前n 项和公式,结合裂项相消法进行求解即可.【小问1详解】依题意有()121252a a a +=++,11a = ,23a ∴=,又{}n a 为等差数列,设公差为d ,212d a a ∴=-=,()12121n a n n ∴=+-=-.【小问2详解】由(1)可得()21212n n n S n+-==,22221111(2)4(2)n n b n n n n ⎛⎫+∴==- ⎪++⎝⎭12111413b ⎛⎫=- ⎪⎝⎭,222111424b ⎛⎫=- ⎪⎝⎭,322111435b ⎛⎫=- ⎪⎝⎭,L ,1221114(1)(1)n b n n -⎛⎫=- ⎪-+⎝⎭,221111155144(1)(2)4416n T n n ⎛⎫∴=+--<⨯= ⎪++⎝⎭.18.已知函数()322f x x ax bx =-++(1)若其图象在点()()1,1f 处的切线方程为10x y -+=,求a ,b 的值;(2)若1是函数()f x 的一个极值点,且函数()f x x 在[]2,3上单调递增,求实数a 的取值范围.【答案】(1)1a =,0b =(2),(7,332)⎛⎤ ⎥⎝-∞⎦【解析】【分析】(1)由题意()132f a b =-+=,且()1321f a b '=-+=,由此即可得解.(2)一方面:由题意()1320f a b '=-+=,且()232f x x ax b '=-+至少有两个零点(否则()f x 单调递增没有极值点);另一方面:由题意3222()22220f x x ax x a x x x '--⎛⎫=--=≥ ⎪⎝⎭在[]2,3上恒成立,分离变量即可;结合两方面即可得解.【小问1详解】点()()1,1f 在切线10x y -+=上,()132f a b ∴=-+=,①()232f x x ax b '=-+,()1321f a b '=-+=,②联立①②解得1a =,0b =.【小问2详解】依题意有()232f x x ax b '=-+,()1320f a b '=-+=,23b a =-,且()()22412234690a a a a ∆=--=-+>,3a ∴≠;又2()223f x x ax a x x =-++-,3222()2222f x x ax x a x x x '--⎛⎫=--= ⎪⎝⎭,则[]2,3x ∈时,32220x ax --≥,即3222x a x -≤,令3222()x g x x-=,23x ≤≤,求导得34()20g x x '=+>,所以()g x 单调递增,min 7()(2)2a g x g ∴≤==;又3a ≠,所以a 的取值范围为,(7,332)⎛⎤ ⎥⎝-∞⎦ .19.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若sin sin sin sin a b B C c A B ++=-.(1)求角A 的大小;(2)若D 为BC 上一点,BAD CAD ∠=∠,3AD =,求4b c +的最小值.【答案】(1)2π3A =(2)27【解析】【分析】(1)利用正弦定理化简已知条件,结合余弦定理求得正确答案.(2)利用三角形的面积公式列方程,结合基本不等式求得4b c +的最小值.【小问1详解】依题意,sin sin sin sin a b B C c A B++=-,由正弦定理得222,a b b c a b bc c c a b ++=-=+-,222c b a bc +-=-,所以2221cos 022b c a A bc +-==-<,所以A 是钝角,所以2π3A =.【小问2详解】1π23BAD CAD A ∠=∠==,ABC ABD ACD S S S =+ ,所以12π1π1πsin 3sin 3sin 232323bc c b =⋅⋅+⋅⋅,即()333,1b c bc c b bc c b +=+=+=,所以()3312344151527b c b c b c c b c b ⎛⎫+=++=++≥+ ⎪⎝⎭,当且仅当()123,293b c c b c b bc c b ⎧=⎪==⎨⎪=+⎩时等号成立.20.已知向量π2cos ,23a x θ⎛⎫⎛⎫=+-- ⎪ ⎪⎝⎭⎝⎭ ,ππ2cos ,1062b x θθ⎛⎫⎛⎫⎛⎫=----<< ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ ,设()2f x a b =⋅+ ,且()f x 的图象关于点π,012⎛⎫ ⎪⎝⎭对称.(1)若3tan 2x =,求()f x 的值;(2)若函数()g x 的图象与函数()f x 的图象关于直线π8x =对称,且()g x 在区间5π,12t ⎡⎤-⎢⎥⎣⎦上的值域为[]1,2-,求实数t 的取值范围.【答案】(1)117(2)ππ,124轾犏-犏臌【解析】【分析】(1)根据平面向量数量积的坐标表示公式,结合正弦的二倍角公式、正弦型函数的对称性、同角的三角函数关系式、两角差的正弦公式进行求解即可;(2)根据函数的对称性,结合正弦型函数的性质进行求解即可.【小问1详解】ππππ()24cos cos 224cos sin 3633f x a b x x x x θθθθ⎛⎫⎛⎫⎛⎫⎛⎫=⋅+=-+----+=-+-+- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2ππ2sin 222sin 2233x x θθ⎛⎫⎛⎫=-+-=-- ⎪ ⎪⎝⎭⎝⎭若()f x 的图象关于点π,012⎛⎫ ⎪⎝⎭对称,则()ππ2πZ 63k k θ--=∈,()π2πZ 6k k θ∴-=+∈,()ππZ 212k k θ=--∈.π12θ∴=-,()2sin 26πf x x ⎛⎫∴=- ⎪⎝⎭.若tan 2x =,则2222sin cos 2tan sin 2sin cos 1tan 7x x x x x x x ===++,同理可得1cos 27x =.πππ4331111()2sin 22sin 2cos cos 2sin 2666147f x x x x ⨯⎛⎫⎛⎫∴=-=-=⨯ ⎪ ⎪⎝⎭⎝⎭;【小问2详解】若函数()g x 的图象与()f x 的图象关于直线π8x =对称,则ππππ()2sin 22sin 24463g x f x x x ⎛⎫⎛⎫⎛⎫⎛⎫=-=--=-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.因为5π12x t -≤≤,所以7πππ22633x t -≤-≤-,而()g x 在5π,12t ⎡⎤-⎢⎥⎣⎦上的值域为[]1,2-,则π12sin 223x ⎛⎫-≤--≤ ⎪⎝⎭,即π22sin 213x ⎛⎫-≤-≤ ⎪⎝⎭,因为7π5π2sin 2sin 166⎛⎫-== ⎪⎝⎭,所以πππ2236t -≤-≤,ππ124t ∴-≤≤,故t 的取值范围为ππ,124轾犏-犏臌21.已知函数()e cos sin x a f x x x +=+-.(1)当0a =时,讨论()f x 在()0,∞+上的单调性;(2)当0x >时,()0f x ≥,求实数a 的取值范围.【答案】(1)()f x 在()0,∞+上单调递增.(2)π,2⎡⎫⎪∞⎢⎣+⎭-【解析】【分析】(1)由导数与单调性的关系求解,(2)参变分离后转化为求()()sin cos ,0,ex x x x x ϕ∞-=∈+的最大值.【小问1详解】当0a =时,()()e cos sin ,e sin cos xx f x x x f x x x =+-=--'.令()e sin cos x h x x x =--,则当π,2x ⎡⎫∈+∞⎪⎢⎣⎭时,2e e 2,sin cos 2x x x π≥>+<,从而()e sin cos 0xh x x x =-->成立;当π0,2x ⎡⎫∈⎪⎢⎣⎭时,()πe cos sin e 4x x h x x x x ⎛⎫=-+=+- ⎪⎝⎭',此时有[)πe 1,14x x ⎛⎫≥-∈- ⎪⎝⎭,从而()()0,h x h x '≥在π0,2⎡⎫⎪⎢⎣⎭上单调递增,()()00h x h ≥=,故当0,0a x =≥时,()0f x '≥恒成立,函数()f x 在()0,∞+上单调递增.【小问2详解】法一:(分离参数法)e cos sin 0x a x x ++-≥,则sin cos e e axx x -≥.令()()sin cos ,0,e x x x x x ϕ∞-=∈+,则()()2cos ,0,e x x x x ϕ∞=∈+'.故()x ϕ在π0,2⎛⎫ ⎪⎝⎭上单调递增,在π3π+2π,+2π22k k ⎛⎫ ⎪⎝⎭上单调递减,在3π52π,π2π22k k ⎛⎫++ ⎪⎝⎭上单调递增,其中k ∈N ,又ππ2π22k ϕϕ⎛⎫⎛⎫≥+ ⎪ ⎪⎝⎭⎝⎭,故π21e e a ≥.故实数a 的取值范围是π,2⎡⎫⎪∞⎢⎣+⎭-.法二:由()0f x ≥对()0,x ∈+∞恒成立,得π02f ⎛⎫≥ ⎪⎝⎭,即2e 10a π-≥,亦即2a π≥-.下面证明:当2a π≥-时,()0f x ≥对()0,x ∈+∞恒成立.当π2a ≥-时,()2e cos sin e cos sin x x a f x x x x x π-+=+-≥+-,令()2e cos sin x g x x x π-=+-,则()22e sin cos e 4x x g x x x x πππ--⎛⎫=--=+ ⎪⎝⎭'.当π0,2x ⎛⎫∈ ⎪⎝⎭时,2e 14x x ππ-⎛⎫<+> ⎪⎝⎭,所以()0g x '<,当π,π2x ⎛⎫∈ ⎪⎝⎭时,2e 14x x ππ-⎛⎫>+< ⎪⎝⎭,所以()0g x '>,当()π,x ∈+∞时,22e e 24x x πππ-⎛⎫>>+< ⎪⎝⎭,所以()0g x '>,所以()g x 在π0,2⎛⎫ ⎪⎝⎭上单调递减,在π,2x ⎛⎫∈+∞ ⎪⎝⎭上单调递增,故当π2a ≥-时,()()π02f x g x g ⎛⎫≥≥= ⎪⎝⎭对()0,x ∈+∞恒成立.综上:实数a 的取值范围是π,2⎡⎫⎪∞⎢⎣+⎭-.(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.选修4-4:坐标系与参数方程22.如图,在极坐标系Ox 中,圆O 的半径为2,半径均为1的两个半圆弧12,C C 所在圆的圆心分别为1π1,2O ⎛⎫ ⎪⎝⎭,23π1,2O ⎛⎫ ⎪⎝⎭,M 是半圆弧1C 上的一个动点,N 是半圆弧2C 上的一个动点.(1)若2π3O ON ∠=,求点N 的极坐标;(2)若点K 是射线()π03θρ=≥与圆O 的交点,求MOK 面积的取值范围.【答案】(1)11π1,6⎛⎫ ⎪⎝⎭(2)30,2⎛⎤ ⎥⎝⎦【解析】【分析】(1)根据图形关系可确定1ρ=,极角11π6θ=,由此可得点N 的极坐标;(2)利用θ表示出OM 和MOK ∠,代入三角形面积公式,结合三角恒等变换知识可化简得到1πsin 226MOK S θ⎛⎫=-+ ⎪⎝⎭ ,结合正弦型函数值域可求得结果.【小问1详解】由2π3O ON ∠=知:21O O ON ==,6πAON ∠=,∴点N 的极角为π11π2π66-=,∴点N 的极坐标为11π1,6⎛⎫ ⎪⎝⎭.【小问2详解】由题意知:2OK =,π2sin π2OM θθ⎛⎫=≤< ⎪⎝⎭,π3MOK θ∠=-,1πsin 2sin sin 23MOK S OK OM MOK θθ⎛⎫∴=⋅∠=- ⎪⎝⎭21112sin sin cos sin cos cos 2sin 222222θθθθθθθθ⎛⎫=-==-- ⎪ ⎪⎝⎭1πsin 226θ⎛⎫=-+ ⎪⎝⎭,π,π2θ⎡⎫∈⎪⎢⎣⎭ ,π7π13π2,666θ⎡⎫∴+∈⎪⎢⎣⎭,π1sin 21,62θ⎛⎫⎡⎫∴+∈- ⎪⎪⎢⎝⎭⎣⎭,30,2MOK S ⎛⎤∴∈ ⎥⎝⎦.选修4-5:不等式选讲23.选修4-5:不等式选讲已知函数()2f x x a =-+,()4g x x =+,a R ∈.(1)解不等式()()f x g x a <+;(2)任意x R ∈,2()()f x g x a +>恒成立,求a 的取值范围.【答案】(1)()1,-+∞(2)()2,3-【解析】【分析】(1)由于不等式可24x x -<+,可平方后求解;(2)不等式()()2f x g x a +>可化为224a a x x -<-++,利用不等式的三角不等式求得24x x -++的最小值,然后解不等式可得a 的范围.【详解】(1)不等式()()f x g x a <+即24x x -<+,两边平方得2244816x x x x -+<++,解得1x >-,所以原不等式的解集为()1,-+∞.(2)不等式()()2f x g x a +>可化为224a a x x -<-++,又()()24246x x x x -++≥--+=,所以26a a -<,解得23a -<<,所以a 的取值范围为()2,3-.【点睛】本题考查绝对值不等式的问题,解绝对值不等式常用方法是根据绝对值的定义去绝对值符号后再求解,如果对两边均非负的不等式可平方去绝对值符号.绝对值三角不等式在求含绝对值的最小值时用处较大,而且是常用方法.。
高中级第一次诊断性考试数学理科四川省各地市一诊高三数学试题集三[整理四]四(共10页)
![高中级第一次诊断性考试数学理科四川省各地市一诊高三数学试题集三[整理四]四(共10页)](https://img.taocdn.com/s3/m/23a3299850e79b89680203d8ce2f0066f5336487.png)
高中(gāozhōng)2021级第一次诊断性考试数学〔理工类〕本套试卷分为试题卷和答题卷两局部,其中试题卷由第I卷〔选择题〕和第II卷〔非选择题〕组成,一共4页;答题卷一共4页。
满分是150分,在在考试完毕之后以后将答题卡和答题卷一起交回。
第I卷〔选择题,一共60分〕考前须知:1、答第1卷前,所有考生必须将本人的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2、每一小题在选出答案以后,用铅笔把答题卡上对应题目之答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案,不能答在试题卷上。
3、参考公式:假如事件A、B互斥,那么P〔A+B〕=P〔A〕+P〔B〕;假如事件A、B互相HY,那么P〔A·B〕=P〔A〕·P〔B〕;假如事件A在一次试验中发生的概率为P,那么n次HY重复试验中恰好发生k次的概率:。
一、选择题:本大题一一共12小题,每一小题5分,一共60分。
在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的,把它选出来填涂在答题卡上。
1. 复数A. 0B. 1C. iD.2. “m>1,n>1”是“log m n>0”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件3. 与函数有一样图象的一个函数是A. B.C. D.4. 某公司(ɡōnɡ sī)有N个员工,下设假设HY门,现采用分层抽样方法从全体员工中抽取一个容量为n的样本〔N是n的正整数倍〕。
某部门被抽取了m个员工,那么这一部门的员工数为A. B. C. D.5. 命题“假设a,b都是奇数,那么a+b是偶数〞的逆否命题是A. 假设a+b不是偶数,那么a,b都不是奇数B . 假设a+b不是偶数,那么a,b不都是奇数C. 假设a+b是偶数,那么a,b都是奇数D. 假设a+b是偶数,那么a,b不都是奇数6. 设函数在点x = 0处连续,那么a的值是A. 0B.C.D. 17. 假设存在,那么a的值是1A. 0B. 1C. -1 D.28. 设随机变量服从正态分布N(0,1),记,那么以下结论不正确的选项是A. B.C. D.9. 函数的图象具有的特征:①原点O〔0,0〕是它的对称中心;②最低点是〔1,2a〕;③y轴是它的一条渐进线。
四川省绵阳市2024届高三一模数学(理)试题含解析

2021级高三一诊模拟考试数学(理)试题(三)(答案在最后)一、单选题1.已知集合{}21,Z A x x k k ==-∈,{}41,Z B x x k k ==+∈,则()A.A B A =B.A B B ⋃=C.()R B A ⋂=∅ðD.()R A B ⋂=∅ð【答案】C 【解析】【分析】通过推理得到B 是A 的真子集,从而根据交集,并集和补集的概念进行计算,对四个选项一一进行判断正误.【详解】{}{}{}21,Z 41,Z 41,Z A x x k k x x k k x x k k ==-∈==+∈⋃=-∈,故B 是A 的真子集,故A B B = ,A B A ⋃=,()R B A ⋂=∅ð,(){}41,Z R A B x x k k ⋂==-∈≠∅ð,故A ,B ,D 均错误,C 正确.故选:C.2.已知a ,b ,c 满足c <b <a ,且ac <0,那么下列选项中一定成立的是()A.ab >acB.c (b -a )<0C.cb 2<ab 2D.ac (a -c )>0【答案】A 【解析】【分析】根据已知条件,求得,c a 的正负,再结合b c >,则问题得解.【详解】由c <b <a 且ac <0,知c <0且a >0.由b >c ,得ab >ac 一定成立,即A 正确;因为0,0c b a <-<,故()0c b a ->,故B 错误;若0b =时,显然不满足22cb ab <,故C 错误;因为0,0ac a c -,故()0ac a c -<,故D 错误.故选:A .【点睛】本题考查不等式的基本性质,属简单题.3.若等比数列{}n a 满足232a a +=,246a a -=,6a =().A.32-B.8- C.8D.64【答案】A 【解析】【分析】根据条件先求出数列的首项和公比,即可求出.【详解】设数列{}n a 的公比为q ,2231132411+26a a a q a q a a a q a q ⎧+==⎨-=-=⎩,解得2q =-,11a =,()55611232a a q ∴==⨯-=-.故选:A.4.下列命题正确的是()A.命题“p q ∧”为假命题,则命题p 与命题q 都是假命题B.命题“若x y =,则sin sin x y =”的逆否命题为真命题C.若0x 使得函数()f x 的导函数()00f x '=,则0x 为函数()f x 的极值点;D.命题“0x ∃∈R ,使得20010x x ++<”的否定是:“x ∀∈R ,均有210x x ++<”【答案】B 【解析】【分析】根据复合命题的真假判断A ,根据四种命题的关系判断B ,根据极值的定义判断C ,根据命题的否定判断D .【详解】对于A :命题“p q ∧”为假命题,则命题p 与命题q 至少有一个假命题,故A 错误;对于B :命题“若x y =,则sin sin x y =”显然为真命题,又原命题与逆否命题同真同假,故B 正确;对于C :若0x 使得函数()f x 的导函数()00f x '=,如果两侧的导函数的符号相反,则0x 为函数()f x 的极值点;否则,0x 不是函数()f x 的极值点,故C 错误;对于D :命题“存在0R x ∃∈,使得20010x x ++<”的否定是:“对任意R x ∀∈,均有210x x ++≥”.故D错误.故选:B .5.设0.70.362,log 4,4a b c ===,则()A.c a b >>B.a c b>> C.b c a>> D.b a c>>【答案】B 【解析】【分析】根据指数函数、对数函数的性质计算可得;【详解】解:因为()0.30.320.6422==,00.60.71212222=<<<=,所以1a c >>因为66610log log 4g 1lo 6=<<=所以01b <<,所以ac b >>.故选:B6.若向量a ,b 满足2a = ,()26a b a +⋅=,则b 在a 方向上的投影为()A.1 B.12C.12-D.-1【答案】B 【解析】【分析】先利用向量数量积的运算求得a b ⋅ ,再利用投影的定义求解即可.【详解】因为2a = ,()26a b a +⋅=,所以226a b a +⋅= ,即2622a b +⋅= ,则1a b ⋅= ,故b 在a 方向上的投影1cos ,2a b b a b a ⋅==.故选:B .7.函数()()100ln 0e exxx f x x -=≠-的大致图象是()A. B.C.D.【答案】A 【解析】【分析】利用排除法,先判断函数的奇偶性,再取特殊值验证即可【详解】因为()100ln 100ln ()e ee exxxxx x f x f x ---==-=---,所以()f x 为奇函数,所以函数图象关于原点对称,所以排除CD ,因为(1)0f =,1111eeee1100ln 1100e0e e ee ef ---⎛⎫==< ⎪⎝⎭--,所以排除B ,故选:A8.已知角α的终边落在直线2y x =-上,则22cos2sin23sin ααα++的值为()A.25-B.25C.±2D.45【答案】B 【解析】【分析】根据角α终边的位置得到tan 2α=-,然后将22cos 2sin 23sin ααα++转化为2222tan tan 1tan ααα+++再代入求值即可.【详解】角α的终边落在直线2y x =-上,所以tan 2α=-,2222222cos 2sin 2sin cos 3sin 2cos 2sin 23sin cos cos αααααααααα-++++=+22222cos 2sin cos sin cos sin αααααα++=+2222tan tan 1tan ααα++=+24414-+=+25=.故选:B.9.函数()sin()(0,0,0)f x A x A ωϕωπϕ=+>>-<<的部分图象如图所示,为了得到()sin g x A x ω=的图象,只需将函数()y f x =的图象()A .向左平移6π个单位长度B.向左平移12π个单位长度C.向右平移6π个单位长度D.向右平移12π个单位长度【答案】B 【解析】【分析】根据函数图象得到()f x 、()g x 的解析式,然后利用图象平移的结论进行图象平移即可.【详解】根据图象可得2A =,周期T π=,因为2T πω=,所以2ω=,()()2sin 2f x x ϕ=+,将,23π⎛⎫⎪⎝⎭代入()f x 可得()2222sin 2332k k πππϕϕπ⎛⎫=+⇒+=+∈ ⎪⎝⎭Z ,解得()26k k πϕπ=-+∈Z ,因为0πϕ-<<,所以6πϕ=-,所以()2sin 26f x x π⎛⎫=- ⎪⎝⎭,()2sin 2g x x =,因为()2sin 212f x x π⎛⎫=- ⎪⎝⎭,所以()f x 向左平移12π个单位长度即可得到()g x 的图象.故选:B.10.过点()3,0作曲线()e xf x x =的两条切线,切点分别为()()11,x f x ,()()22,x f x ,则12x x +=()A.3-B.C.D.3【答案】D【解析】【分析】求出函数的导函数,设切点坐标为()000,ex x x ,即可得到切线方程,依题意关于0x 的方程200330x x -++=有两个不同的解1x 、2x ,利用韦达定理计算可得.【详解】因为()e x f x x =,所以()()1e xf x x '=+,设切点坐标为()000,e x x x ,所以()()0001e xf x x '=+,所以切线方程为()()00000e1e x x y x x x x -=+-,所以()()00000e1e 3x x x x x -=+-,即()02033e 0x x x -++=,依题意关于0x 的方程()20033e0x x x -++=有两个不同的解1x 、2x ,即关于0x 的方程200330x x -++=有两个不同的解1x 、2x ,所以123x x +=.故选:D11.已知函数()sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为π,若()f x m =在[0,)π上有两个实根a ,b ,且||3a b π->,则实数m 的取值范围是()A.1,02⎛⎫-⎪⎝⎭B.10,2⎛⎫ ⎪⎝⎭C.1,12⎛⎫ ⎪⎝⎭D.11,22⎛⎫-⎪⎝⎭【答案】D 【解析】【分析】由题设可得()sin(26f x x π=+,将问题转化为在132[,)666t x πππ=+∈上sin y t =与y m =有两个交点且交点横坐标之差2||3a b t t π->,应用数形结合确定m 的取值范围.【详解】由题设,2T ππω==,则2ω=,即()sin(2)6f x x π=+,又()f x m =在[0,)π上有两个实根a ,b ,且||3a b π->,[0,)π上,132[,)666t x πππ=+∈,则sin y t =的图象如下:∴要使||3a b π->,则对应2||2||3a b t t a b π-=->,∴当1122m -<<时,()f x m =有两个交点且||3a b π->.故选:D12.已知定义在R 上的奇函数()f x 满足()()20f x f x -+=,当(]0,1x ∈时,()2log f x x =-.若函数()()sin F x f x x π=-在区间[]1,m -上有10个零点,则实数m 的取值范围是()A.[)3.5,4 B.(]3.5,4 C.(]5,5.5 D.[)5,5.5【答案】A 【解析】【分析】根据题意可知()f x 和()sin πx 都是周期为2的周期函数,因此可将()()()sin πF x f x x =-的零点问题转换为()f x 和()sin πx 的交点问题,画出函数图形,找到交点规律即可找出第10个零点坐标,而m 的取值范围就在第10个零点和第11个零点之间.【详解】由()()()()()2022f x f x f x f x f x -+=⇒=--=-得()f x 是一个周期为2的奇函数,当(]0,1x ∈时,()2log f x x =-,因此211log 122f ⎛⎫=-=⎪⎝⎭,()10f =因为()f x 是奇函数,所以()00f =,112⎛⎫-=- ⎪⎝⎭f ,()10f -=且()()sin πg x x =的周期为2π2πT ==,且()10g -=,112g ⎛⎫-=- ⎪⎝⎭,()00g =,112g ⎛⎫= ⎪⎝⎭,()10g =求()()()sin πF x f x x =-的零点,即是()f x 与()g x 的交点,如图:为()f x 与()g x 在[]1,1-区间的交点图形,因为()f x 与()g x 均为周期为2的周期函数,因此交点也呈周期出现,由图可知()F x 的零点周期为12,若在区间[]1,m -上有10个零点,则第10个零点坐标为()3.5,0,第11个零点坐标为()4,0,因此3.54m ≤<.故选:A【点睛】思路点睛:函数的零点问题,往往可以转化为常见函数的交点的个数问题,而图象的刻画需结合函数的奇偶性、周期性等来处理.二、填空题13.若x ,y 满足约束条件21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩,则23z x y =-的最小值为______.【答案】5-【解析】【分析】先作出可行域,将目标函数23z x y =-化为2133y x z =-,要求z 的最小值,则需求直线2133y x z =-在y 轴上的截距的最大值,由图可得答案.【详解】由x ,y 满足约束条件21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩作出可行域,如图由2121x y x y +=⎧⎨+=-⎩,解得()1,1A -由210x y x y +=⎧⎨-=⎩,解得11,33C ⎛⎫ ⎪⎝⎭由2100x y x y ++=⎧⎨-=⎩,解得11,33B ⎛⎫-- ⎪⎝⎭将目标函数23z x y =-化为2133y x z =-,则z 表示直线2133y x z =-在y 轴上的截距的13-倍.要求z 的最小值,则需求直线2133y x z =-在y 轴上的截距的最大值.由图可知,当目标函数过点()1,1A -时,直线2133y x z =-在y 轴上的截距的最大值.此时z 的最小值为()21315z =⨯--⨯=-故答案为:5-14.当7,66x ππ⎡⎤∈⎢⎥⎣⎦时,函数23sin 2cos y x x =--的值域为________.【答案】728⎡⎤⎢⎥⎣⎦【解析】【分析】由7,66x ππ⎡⎤∈⎢⎥⎣⎦,求得1sin [,1]2x ∈-,化简2172(sin )48y x =-+,结合二次函数的性质,即可求解.【详解】因为7,66x ππ⎡⎤∈⎢⎥⎣⎦,可得1sin [,1]2x ∈-,又由222173sin 2cos 3sin 2(1sin )2(sin 48y x x x x x =--=---=-+,当1sin 4x =,取得最小值min 78y =;当1sin 2x =-或sin 1x =,取得最大值min 2y =,即函数的值域为728⎡⎤⎢⎥⎣⎦,.故答案为:728⎡⎤⎢⎥⎣⎦,.【点睛】本题主要考查了函数的值域的求解,其中解答中熟记三角函数的基本关系式和正弦函数的性质,以及二次函数的图象与性质是解答的关键,属于基础题.15.已知函数()()2e ,1lg 2,1x x f x x x -⎧≤⎪=⎨+>⎪⎩,则不等式()11f x +<的解集为______.【答案】()0,7【解析】【分析】分别在11x +≤和11x +>的情况下,结合指数和对数函数单调性可解不等式求得结果.【详解】当11x +≤,即0x ≤时,()()2111e e 1x x f x -+-+==<,10x ∴-<,解得:1x >(舍);当11x +>,即0x >时,()()1lg 31f x x +=+<,0310x ∴<+<,解得:37x -<<,07x ∴<<;综上所述:不等式()11f x +<的解集为()0,7.故答案为:()0,7.16.数列{}n a 的前n 项和为n S ,23nn n a S +=,数列{}n b 满足()()211332n bn n a a n N *++=-∈,则数列{}n b 的前10项和为______.【答案】65【解析】【分析】由,n n a S 的递推式可得121323n n n a a +++-=⨯,结合已知条件有1n b n =+,即可求数列{}n b 的前10项和.【详解】由23nn n a S +=知:11123n n n a S ++++=,则1112233n n n n n n a S a S ++++--=-,得1323nn n a a +-=⨯,∴121323n n n a a +++-=⨯,而()()211332n bn n a a n N *++=-∈,∴1n b n =+,故数列{}n b 的前10项和为1010(211)652T ⨯+==,故答案为:65.【点睛】关键点点睛:,n n a S 递推式的应用求条件等式中因式213n n a a ++-的表达式,进而求数列{}n b 的通项,最后求{}n b 前10项和.三、解答题17.在ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,向量()2,1m b = ,()2,cos n a c C =- ,且//m n.(1)求角B 的大小;(2)若点M 为BC 中点,且AM AC =,求sin BAC ∠.【答案】(1)π3B =;(2)sin 7BAC ∠=.【解析】【分析】(1)利用向量共线的坐标表示,再利用正弦定理边化角及和角的正弦公式求解作答.(2)取CM 中点D ,连接AD ,利用直角三角形边角关系及正弦定理求解作答.【小问1详解】向量()2,1m b = ,()2,cos n a c C =- ,且//m n,于是2cos 2b C a c =-,在ABC 中,由正弦定理,得2sin cos 2sin sin B C A C =-,即2sin cos 2sin()sin 2sin cos 2cos sin sin B C B C C B C B C C =+-=+-,整理得2cos sin sin B C C =,又sin 0C ≠,因此1cos 2B =,而0πB <<,所以π3B =.【小问2详解】取CM 中点D ,连接AD ,由AM AC =,得AD CM ⊥,令CD x =,而点M 为BC 中点,则3BD x =,由(1)知π3B =,于是AD =,AC =,在ABC中,由正弦定理知4πsin sin 3x BAC =∠,所以sin 7BAC ∠=.18.已知数列{}n a 是公差不为零的等差数列,11a =,其前n 项和为n S ,数列{}n b 前n 项和为n T ,从①1a ,2a ,5a 成等比数列,2n n T b -=,②53253S S -=,1122n n T -⎛⎫=- ⎪⎝⎭,这两个条件中任选一个作为已知条件并解答下列问题.(1)求数列{}n a ,{}n b 的通项公式;(2)求数列n n a b ⎧⎫⎨⎬⎩⎭的前n 项和n M .【答案】(1)条件选择见解析;21n a n =-,112n n b -⎛⎫ ⎪⎝⎭=;(2)()2323nn M n =-⋅+.【解析】【分析】(1)选条件①:设数列{}n a 的公差为d ,根据等比中项的性质建立方程,解之可求得公差d ,由等差数列的通项公式求得n a ,再由2n n T b -=,112n n T b --=-两式相减得数列{}n b 是首项为1,公比为12的等比数列,根据等比数列的通项公式求得n b ;选条件②:由已知得等差数列{}n a 的公差为2d =,由等差数列的通项公式求得n a ,再由1112n n n n b T T --⎛⎫=-= ⎪⎝⎭求得n b ,注意1n =时是否满足;(2)由(1)可得:()1212n nna nb -=-⋅,由错位相减法可求得n M .【详解】解:(1)选条件①:设数列{}n a 的公差为d ,由1a ,2a ,5a 成等比数列,可得:2215a a a =,即()2114d d +=+,解得:2d =或0d =(舍),所以()12121n a n n =+-=-,∵2n n T b -=,∴112n n T b --=-,2n ≥,两式相减整理得:112n n b b -=,2n ≥,又当1n =时,有112T b =-,解得:11b =,∴数列{}n b 是首项为1,公比为12的等比数列,∵112n n b -⎛⎫ ⎪⎝⎭=;选条件②:∵5332253S S a a -=-=,∴等差数列{}n a 的公差为2d =,又11a =,∴()12121n a n n =+-=-,又∵1122n n T -⎛⎫=- ⎪⎝⎭,∴当2n ≥时,有1112n n n n b T T --⎛⎫=-= ⎪⎝⎭,又当1n =时,有111T b ==,也适合上式,∵112n n b -⎛⎫ ⎪⎝⎭=;(2)由(1)可得:()1212n nna nb -=-⋅,∴·()0121123252212n n M n -=⨯+⨯+⨯+⋅⋅⋅+-⋅,又()()12121232232212n n n M n n -=⨯+⨯+⋅⋅⋅+-⋅+-⋅,两式相减得:()()()21232121222212121212n n n nn M n n ---=+++⋅⋅⋅+--⋅=+--⋅-整理得:()2323nn M n =-⋅+.19.设()2sin cos cos 4f x x x x π⎛⎫=-+⎪⎝⎭.(Ⅰ)求()f x 的单调区间;(Ⅱ)在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫==⎪⎝⎭,求ABC ∆面积的最大值.【答案】(Ⅰ)单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(Ⅱ)ABC ∆面积的最大值为234+【解析】【详解】试题分析:(Ⅰ)首先利用二倍角公式化简函数()f x 的解析式,再利用正弦函数的单调性求其单调区间;(Ⅱ)首先由02A f ⎛⎫= ⎪⎝⎭结合(Ⅰ)的结果,确定角A 的值,然后结合余弦定理求出三角形ABC ∆面积的最大值.试题解析:解:(Ⅰ)由题意知()1cos 2sin 2222x x f x π⎛⎫++ ⎪⎝⎭=-sin 21sin 21sin 2222x x x -=-=-由222,22k x k k Z ππππ-+≤≤+∈可得,44k x k k Z ππππ-+≤≤+∈由3222,22k x k k Z ππππ+≤≤+∈可得3,44k x k k Z ππππ+≤≤+∈所以函数()f x 的单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(Ⅱ)由1sin 0,22A f A ⎛⎫=-=⎪⎝⎭得1sin 2A =由题意知A 为锐角,所以cos 2A =由余弦定理:2222cos a b c bc A =+-可得:2212b c bc+=+≥即:2bc ≤当且仅当b c =时等号成立.因此12sin 24bc A +≤所以ABC ∆面积的最大值为24考点:1、诱导公式;2、三角函数的二倍角公式;3、余弦定理;4、基本不等式.20.已知()()3223,f x x ax bx aa b R =+++∈.(Ⅰ)若()f x 在=1x -时有极值0,求a ,b 的值;(Ⅱ)若()()6xg x f x b a e '=-+⋅⎡⎤⎣⎦,求()g x 的单调区间.【答案】(Ⅰ)2a =,9b =;(Ⅱ)答案见解析.【解析】【分析】(Ⅰ)求出导函数()f x ',由题意可得2310630a ab b a ⎧+--=⎨-+=⎩,解方程组求出a ,b 的值,再验证是否在=1x -是否取得极值即可.(Ⅱ)由题意求出()()()322xg x x x a e '=++⋅,讨论1a =、1a >或1a <,利用导数与函数单调性之间的关系即可求解.【详解】解:(Ⅰ)由题意得()236f x x ax b '=++,则2310630a ab b a ⎧+--=⎨-+=⎩,解得:13a b =⎧⎨=⎩或29a b =⎧⎨=⎩,经检验当1a =,3b =时,函数()f x 在=1x -处无极值,而2a =,9b =满足题意,故2a =,9b =;(Ⅱ)()()()26322xxg x f x b a e x ax a e'=-+⋅=++⋅⎡⎤⎣⎦故()()()322xg x x x a e '=++⋅,故1a =时,()0g x '≥,函数()g x 在R 上递增,当1a >时,函数()g x 在(),2-∞-a 递增,在()2,2a --递减,在()2,-+∞递增,当1a <时,函数()g x 在(),2-∞-递增,在()2,2a --递减,在()2,a -+∞递增.21.已知函数()ln f x x x =-.(1)求证:()1f x ≤-;(2)若函数()()()0ex xg x af x a =+>有两个零点,求a 的取值范围.【答案】(1)证明见解析(2)10ea <<【解析】【分析】(1)求出()1xf x x-'=,讨论其符号后可得函数的单调性,结合原函数的最值可得不等式成立.(2)求出()g x ',讨论其符号后可得函数的单调性,根据零点的个数可得最值的符号,从而可得a 的取值范围,注意利用零点存在定理验证.【小问1详解】()1xf x x-'=,则当01x <<时,()0f x ¢>,当1x >时,()0f x ¢<,故()f x 在()0,1上为增函数,在()1,+∞上减函数,故()()max 11f x f ==-即()1f x ≤-.【小问2详解】()ln e x x g x a x ax =-+,故()()()1111e e xx a x x a g x x x x --⎛⎫'=+=-+ ⎪⎝⎭,因为0,0a x >>,故10ex a x +>,所以当01x <<时,()0g x ¢>,当1x >时,()0g x ¢<,故()g x 在()0,1上为增函数,在()1,+∞上减函数,因为函数()g x 有两个零点,故()()max 110e g x g a ==-+>即10ea <<,又当10ea <<时,对任意10e a x -<<,有:ln ln ln 10ex xa x ax a x x a x -+<+<+<,故此时()g x 在()0,1上有且只有一个零点.下证:当e x >时,总有2ln x x >成立,设()2ln S x x x =-,则()20x S x x-'=>,故()S x 在()e,+∞上为增函数,故()()e e 20S x S >=->,即2ln x x >成立.故当e x >时有2e x x >.由(1)可得ln e e x xx x a x ax a -+≤-+,故当11(e)x a a >>时,11ln 0e x x axa x ax a x x--+<-+=<,故此时()g x 在()1,+∞上有且只有一个零点.综上,当()g x 有两个零点时,10ea <<.22.数学中有许多寓意美好的曲线,在极坐标系中,曲线:sin3()C ρθρ=∈R 被称为“三叶玫瑰线”(如图所示).(1)当[0,)θπ∈,求以极点为圆心,22为半径的圆与三叶玫瑰线交点的极坐标;(2)设点P 是由(1)中的交点所确定的圆M 上的动点,直线:cos 24l πρθ⎛⎫+= ⎪⎝⎭,求点P 到直线l 的距离的最大值.【答案】(1)2223211,,,,,2122424212ππππ⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭;(2)322.【解析】【分析】(1)由sin 322ρθρ=⎧⎪⎨=⎪⎩可得2sin 32θ=,然后解出θ的值即可;(2)将圆M 和直线l 的极坐标方程转化为直角坐标方程,然后可求出答案.【详解】(1)由sin 322ρθρ=⎧⎪⎨=⎪⎩可得2sin 32θ=,所以324k πθπ=+或()3324k k Z πθπ=+∈所以2312k ππθ=+或()234k k Z ππθ=+∈因为[0,)θπ∈,所以311,,,124412ππππθ=所以交点的极坐标为2223211,,,,,,,2122424212ππππ⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭(2)由(1)可得圆M 的极坐标方程为22ρ=,转化为直角坐标方程为2212x y +=直线:cos 24l πρθ⎛⎫+= ⎪⎝⎭的直角坐标方程为2x y -=所以点P 到直线l 23222+=23.已知函数()|1||2|f x x x =-++.(1)求不等式()5f x ≤的解集;(2)若不等式()21f x x ax ≥-+的解集包含[]1,1-,求实数a 的取值范围.【答案】(1)[] 3,2-;(2)[]1,1-.【解析】【分析】(1)分类讨论,求解不等式即可;(2)将问题转化为二次函数在区间上恒成立的问题,列出不等式组即可求得.【详解】(1)当2x ≤-时,()5f x ≤等价于215x --≤,解得[]3,2x ∈--;当21x -<<时,()5f x ≤等价于35≤,恒成立,解得()2,1x ∈-;当1x ≥时,()5f x ≤等价于215x +≤,解得[]1,2x ∈;综上所述,不等式的解集为[]3,2-.(2)不等式()21f x x ax ≥-+的解集包含[]1,1-,等价于()21f x x ax ≥-+在区间[]1,1-上恒成立,也等价于220x ax --≤在区间[]1,1-恒成立.则只需()22g x x ax =--满足:()10g -≤且()10g ≤即可.即120,120a a +-≤--≤,解得[]1,1a ∈-.【点睛】本题考查绝对值不等式的求解,以及二次函数在区间上恒成立的问题,属综合基础题.。
四川省绵阳市高中2021届高三第一学期第一次诊断性考试数学(理)试题 含答案

nHH
nB
a opuv
/
口 3
飞·
-π
fo
、‘,/
(1)求角 C 的大小;
(2)若cosB = __!_, c = 7,求 AB 边 上的高. 7 理科数学试题第 3 页(共 4 页)
20. (12分)
己知函数 f(x)是定义在R 上的奇函数,当 x<O 时, f(x)= 兰兰 +1. x
(1)求函数 f(x) 的解析式: (2)若对于任意实数x,不等式 f(e勺+ 2af(ex)二三0恒成立,求实数α的取值范围.
时cosα=
A. _!_ 2
B. 丘二1
c. 一)一3
D. 豆1
。n+ 11.数列{αn}满足
一1一=一2一一一 1 2 αn+I αn
,α2
L.
1
=一
5
,α4=一19
,数列{
bn}的前n项和为品,若bn
=αna
n+!'
4
则便不等式
S“n
>
一
27
成立的n的最小值为
A. 11
B. 12
c. 13
D. 14
p
极向上的活力.某公司设计方案如图,等腰今PMN 的顶点P
在半径为20m的大①0上,点 M, N在半径为lOm的小①O
上,圆心。与点P都在弦 MN的同侧.设弦 MN 与对应劣弧
所围成的弓形面积为S, LOPM 与 LOPN 的面积之和为S1,
ζMON=2α,当S1-S的值最大时,该设计方案最美,则此
2.下列函数中,既是奇函数又是增函数的是
A.y=tan.x
B.y=ln.x
C.y=x3
高考模拟练习—四川省绵阳市2021-2022学年高三上学期诊断性考试理科数学试题(含答案解析)

……○…………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________……○…………内…………○…………装…………○…………订…………○…………线…………○…………四川省绵阳市2021-2022学年高三上学期理科数学试题试卷副标题考试范围:xxx ;考试时间:100分钟;命题人:xxx题号 一 二 三 总分 得分注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明 评卷人 得分一、单选题 1.设集合{(,)|}A x y y x ==,2{(,)|}B x y y x ==,则集合A B 的元素个数为( ) A .0B .1C .2D .32.二项式52x x ⎛⎫- ⎪⎝⎭的展开式中,3x 的系数为( )A .10-B .15-C .10D .153.如图,茎叶图记录了甲、乙两个家庭连续9个月的月用电量(单位:度),根据茎叶图,下列说法正确的是( )A .甲家庭用电量的中位数为33B .乙家庭用电量的极差为46C .甲家庭用电量的方差小于乙家庭用电量的方差D .甲家庭用电量的平均值高于乙家庭用电量的平均值4.已知角α的终边过点3)A ,则cos 6πα⎛⎫+= ⎪⎝⎭( )A .12-B .0C .12D 35.已知双曲线2222:1x y E a b-=(0a >,0b >)的焦距为4,两条渐近线互相垂直,则E的方程为( ) A .221x y -=B .22122x y -=C .22144x y -=D .22188x y -=6.已知平面向量a ,b 不共线,46AB a b =+,3BC a b =-+,3CD a b =+,则( ) A .A ,B ,D 三点共线 B .A ,B ,C 三点共线 C .B ,C ,D 三点共线D .A ,C ,D 三点共线7.函数()f x 是定义域为R 的偶函数,当[1,0]x ∈-时,1()e 1ex f x a =++,若(1)1f =,则(0)f =( ) A .eB .e -C .1eD .1e-8.已知直线10x y +-=与圆()()22:21C x y m -+-=相交于A ,B 两点,若AB =则m =( ) A B .5C .3D .49.第24届冬季奥林匹克运动会将于2022年在北京举办,为了解某城市居民对冰雪运动的关注情况,随机抽取了该市100人进行调查统计,得到如下22⨯列联表:下列说法正确的是( )参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.附表:A .有99%以上的把握认为“关注冰雪运动与性别有关”B .有99%以上的把握认为“关注冰雪运动与性别无关”C .在犯错误的概率不超过0.1%的前提下,认为“关注冰雪运动与性别无关”D .在犯错误的概率不超过0.1%的前提下,认为“关注冰雪运动与性别有关”10.已知,m n 为整数,且,[1,5]m n ∈,设平面向量(,)a m n =与(2,1)b =-的夹角为θ,则,2πθπ⎡⎫∈⎪⎢⎣⎭的概率为( )A .932B .964C .425D .62511.已知函数()2()ln f x x a x x =--,若不等式()0f x >有且仅有2个整数解,则实数a 的取值范围是( )A .ln 2ln 3,66⎡⎫⎪⎢⎣⎭ B .ln 2ln 3,66⎛⎤⎥⎝⎦ C .ln 2,6⎛⎤-∞ ⎥⎝⎦ D .ln 2ln 3,33⎛⎫⎪⎝⎭12.已知1F ,2F 分别为椭圆()2222:10x yE a b a b+=>>的左,右焦点,E 上存在两点A ,B使得梯形12AF F B (其中c 为半焦距),且123AF BF =,则E 的离心率为( ) A B C .12D 第II 卷(非选择题)请点击修改第II 卷的文字说明 二、填空题 13.设i 是虚数单位,若复数z 满足i 6i z z ⋅=+,则复数z 的虚部为______.14.现从4名男志愿者和3名女志愿者中,选派2人分别去甲、乙两地担任服务工作,若被选派的人中至少有一名男志愿者,则不同的选派方法共有___________种.(用数字作答)15.已知,A B 为抛物线2:4C x y =上的两点,2()1,M -,若AM MB =,则直线AB 的方程为_________.16.已知函数()sin f x x x =,下列关于函数()f x 的说法正确的序号有________. ①函数()f x 在73,62ππ⎡⎤⎢⎥⎣⎦上单调递增;②2π是函数()f x 的周期; ③函数()f x 的值域为[2,1]-;④函数()f x 在[2,2]ππ-内有4个零点.三、解答题 17.已知数列{}n a 为公差大于0的等差数列,2315a a ⋅=,且1a ,4a ,25a 成等比数列. (1)求数列{}n a 的通项公式; (2)设11n n n b a a +=⋅,数列{}n b 的前n 项和为n S ,若2041m S =,求m 的值.18.某通讯商场推出一款新手机,分为甲、乙、丙、丁4种不同的配置型号.该商场对近期售出的100部该款手机的情况进行了统计,绘制如下表格:(1)每售出一部甲、乙、丙、丁配置型号的手机可分别获得利润600元、400元、500元、450元,根据以上100名消费者的购机情况,求该商场销售一部该款手机的平均利润; (2)该商场某天共销售了4部该款手机,每销售一部该款手机的型号相互独立,其中甲配置型号手机售出的数量为X ,将样本频率视为概率,求X 的概率分布列及期望. 19.在ABC 中,角,,A B C 的对边分别为,,a b c ,其中b =(sin )cos sin cos a C B B C -=.(1)求角B 的大小;(2)求ABC 周长的取值范围.20.已知函数2()(2)e x f x x ax x =---.(1)当12a =-时,求函数()f x 的极值;(2)若曲线()f x 在()2,1-上任意一点处切线的倾斜角均为钝角,求实数a 的取值范围. 21.已知椭圆()2222:10x y E a b a b +=>>的右焦点为F ,点A ,B 分别为右顶点和上顶点,点O 为坐标原点,11e OF OA FA+=,OAB e 为E 的离心率. (1)求椭圆E 的方程;(2)过点O 异于坐标轴的直线与E 交于M ,N 两点,射线AM ,AN 分别与圆22:4C x y +=交于P ,Q 两点,记直线MN 和直线PQ 的斜率分别为1k ,2k ,问12k k 是否为定值?若是,求出该定值;若不是,请说明理由.22.在直角坐标系xOy 中,曲线C 的参数方程为2sin 2cos ,1cos 2sin x y αααα=++⎧⎨=+-⎩(α为参数),以坐标原点为极点,x 轴正半轴为极轴建立的极坐标系中,直线l 的方程是cos 13πρθ⎛⎫+= ⎪⎝⎭. (1)求曲线C 的普通方程和直线l 的直角坐标方程;(2)若点A 的坐标为()2,0,直线l 与曲线C 交于P ,Q 两点,求11AP AQ+的值. 23.已知函数()f x =(1)当2m =时,求函数()f x 的定义域;(2)设函数()f x 的定义域为M ,当12m >-时,1[,]2m M -⊆,求实数m 的取值范围.………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________………内…………○…………装…………○…………订…………○…………线…………○…………参考答案:1.C 【解析】 【分析】集合为点集,交集的元素个数等与函数y x =与2y x 图象交点个数,作图可解.【详解】如图,函数y x =与2y x 图象有两个交点,故集合A B 有两个元素.故选:C2.A 【解析】 【分析】首先求出二项式展开式的通项,再令523-=r 求出r ,再代入计算可得; 【详解】解:二项式52x x ⎛⎫- ⎪⎝⎭展开式的通项为()55215522rr r r r r r T C x C x x --+⎛⎫=-=- ⎪⎝⎭,令523-=r ,解得1r =,所以()113325210T C x x =-=-,故3x 的系数为10-; 故选:A 3.C 【解析】 【分析】根据给定茎叶图,逐项分析计算,再判断作答. 【详解】对于A ,由茎叶图知,甲家庭用电量的中位数为32,A 不正确; 对于B ,由茎叶图知,乙家庭用电量的极差56-11=45,B 不正确; 对于C ,甲家庭用电量的平均数112232425323337415027799x ++++++++==,乙家庭用电量的平均数211233438394042515633499x ++++++++==,甲家庭用电量的方差2222211277277277277[(12(23)(24(25)99999s =-+-+-+- 2222227727727727727781936(32)(33)(37(41(50)]99999729+-+-+-+-+-=, 乙家庭用电量的方差2222221334334334334[(11(23)(34)(3899999s =-+-+-+- 22222334334334334334119628(39)(40)(42(51)(56]99999729+-+-+-+-+-=, 显然81936119628729729<,即甲家庭用电量的方差小于乙家庭用电量的方差,C 正确; 对于D ,由C 选项的计算知27733499<,甲家庭用电量的平均值低于乙家庭用电量的平均值,D 不正确. 故选:C 4.B 【解析】 【分析】根据三角函数定义求出sin α和cos α,利用余弦的和角公式即可求cos 6πα⎛⎫+ ⎪⎝⎭.【详解】 由题可知1sin 2αα==, ∴111cos sin 06222πααα⎛⎫+=-=-= ⎪⎝⎭.故选:B. 5.B 【解析】 【分析】根据题意,得到a =b ,再根据2c =,由222+=a b c 即可求出答案. 【详解】双曲线2222:1x y E a b-=的渐近线方程为b y x a =±由两条渐近线互相垂直,则221b b b a a a-⨯=-=-,所以a b =又双曲线E 的焦距为4,则22224242a b a ⎛⎫+=== ⎪⎝⎭,解得a =所以双曲线E 的方程为:22122x y -=故选:B 6.D 【解析】 【分析】根据给定条件逐项计算对应三点确定的某两个向量,再判断是否共线作答. 【详解】平面向量a ,b 不共线,46AB a b =+,3BC a b =-+,3CD a b =+, 对于A ,3(3)6BD BC CD a b a b b =+=-+++=,与AB 不共线,A 不正确; 对于B ,因46AB a b =+,3BC a b =-+,则AB 与BC 不共线,B 不正确; 对于C ,因3BC a b =-+,3CD a b =+,则BC 与CD 不共线,C 不正确; 对于D ,46(3)393AC AB BC a b a b a b CD =+=++-+=+=,即//AC CD , 又线段AC 与CD 有公共点C ,则A ,C ,D 三点共线,D 正确. 故选:D 7.C 【解析】 【分析】根据函数是偶函数知f (-1)=f (1)=1,由此求出a 的的值即可计算. 【详解】由题可知f (-1)=f (1)=1, 则11e 11ea -++=,得a =-1,∴()1e 1ex f x =-++,∴f (0)=1e .故选:C. 8.B 【解析】 【分析】先求出圆心到直线的距离,再利用弦心距、半径和弦长的关系列方程可求出m 的值 【详解】圆()()22:21C x y m -+-=的圆心(2,1)C 0m >), 则圆心(2,1)C 到直线10x y +-=的距离为d ==因为AB = 所以222+=,解得5m =,故选:B 9.A 【解析】 【分析】根据给定数据及参考公式计算2K 的观测值,再与临界值表比对判断作答. 【详解】依题意,2K 的观测值为22100(45202510)8.129 6.63570305545K ⨯-⨯=≈>⨯⨯⨯, 所以有99%以上的把握认为“关注冰雪运动与性别有关”,A 正确,B 不正确; 而犯错误的概率不超过1%,不能确定犯错误的概率不超过0.1%的情况,C ,D 不正确. 故选:A 10.D 【解析】 【分析】依题意可得1cos 0θ-<≤,再根据向量夹角的坐标表示得到不等式,再用列举法列出所有可能结果,再根据古典概型的概率公式计算可得;【详解】解:因为平面向量(,)a m n =与(2,1)b =-的夹角为θ,且,2πθπ⎡⎫∈⎪⎢⎣⎭,所以1cos 0θ-<≤,即10m -<≤+,所以20m n <-≤,因为,m n 为整数,且,[1,5]m n ∈,(,)a m n =,所以a 共有5525⨯=种可能,又因为20m n -≤,]5[1n ∈,,所以1m =或2,①当1m =时,由20m n -≤,即20n -≤,所以2n =或3或4或5,满足题意;②当2m =时,由20m n -≤,即40n <-≤,所以4n =或5,满足题意;故()1,2a =或()1,3或()1,4或()1,5或()2,4或()2,5共6种情况符合题意,所以,2πθπ⎡⎫∈⎪⎢⎣⎭的概率为625; 故选:D 11.A 【解析】 【分析】转化()0f x >有且仅有2个整数解为()>-2ln x a x x 有两个整数解,画出()==-2()ln ,()g x x h x a x x 两个函数的图像,数形结合列出不等关系控制即得解【详解】由题意,()0f x >有且仅有2个整数解即()-->2ln 0x a x x有两个整数解,即()>-2ln xa x x 有两个整数解令()==-2()ln ,()g x x h x a x x(1)当0a =时,ln 0x >即1x >,有无数个整数解,不成立;(2)当0a <时,如图所示,()>-2ln x a x x 有无数个整数解,不成立;………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________………内…………○…………装…………○…………订…………○…………线…………○…………(3)当0a >时,要保证()()g x h x >有两个整数解如图所示,(3)(3)(4)(4)g h g h >⎧⎨≤⎩即ln3(93)ln 4(164)a a >-⎧⎨≤-⎩,解得ln 2ln 366a ≤< 故选:A 12.D 【解析】 【分析】根据123AF BF =,可得12AF BF ∕∕,则12,AF BF 为梯形12AF F B 的两条底边,作21F P AF ⊥垂足为P ,则22PF c ,从而可求得1245AF F ∠=︒再结合123AF BF =建立a ,b ,c 的关系即可得出答案.………外…………○…………装…………○…………订…………○…………线…………○学校:___________姓名:___________班级:___________考号:___________………内…………○…………装…………○…………订…………○…………线…………○解:因为123AF BF =,所以12AF BF ∕∕,则12,AF BF 为梯形12AF F B 的两条底边, 作21F P AF ⊥于点P ,则21F P AF ⊥,因为梯形12AF F B 的高为2c ,所以22PF c =, 在12Rt F PF 中,122F F c =,则2112222PF F F PF c PF =-==,即1245PF F ∠=︒,设1AF x =,则22AF a x =-,在12AF F △中由余弦定理,得22AF =221122AF F F +-112cos 45AF F F ,即222(2)422a x x c cx -=+-,解得2122b AF x ac ==-, 同理2222b BF x a c ==+, 又123AF BF =,所以22322a c a c+=-, 即222a c =,所以22c e a ==. 故选:D.13.-3 【解析】根据给定等式结合复数的除法运算直接计算作答. 【详解】因i 6i z z ⋅=+,则(1i)6i z -+=,于是得6i 6i(1i)66i33i 1i (1i)(1i)2z ---====--+-+--, 所以复数z 的虚部为-3. 故答案为:-3 14.36 【解析】 【分析】依题意分两种情况讨论,①选一名男志愿者与一名女志愿者,②选两名男志愿者,按照分步乘法计数原理与分类加法计数原理计算可得; 【详解】解:依题意分两种情况讨论,①选一名男志愿者与一名女志愿者,则有11243224C C A =种选派方法;②选两名男志愿者,则有224212C A =种选派方法;综上可得一共有241236+=种选派方法; 故答案为:36 15.230x y +-= 【解析】 【分析】由于AM MB =可得M 为中点,则121224x x y y +=-⎧⎨+=⎩,根据点差法即可求得直线AB 的斜率,从而得方程. 【详解】设()()1122,,,A x y B x y 又()1,2M -,因为AM MB =,所以121224x x y y +=-⎧⎨+=⎩,又2211224,4x y x y ==,则22121244x x y y -=-,得1212442y y x x x x -+==--则直线AB 的斜率为12k =-,故直线AB 的方程为()1212y x -=-+,化简为230x y +-=.联立24230x yx y ⎧=⎨+-=⎩,可得2260x x +-=280∆=>,直线与抛物线有两个交点,成立故答案为:230x y +-=. 16.①③④ 【解析】 【分析】①化简解析式,求出3x π+范围,根据正弦函数的单调性即可判断;②根据奇偶性举特例验证f (x +2π)与f (x )关系即可;③分类讨论求出f (x )解析式,研究在x ≥0时的周期性,再求出值域即可; ④根据值域和单调性讨论即可. 【详解】∵函数()sin f x x x =,定义域为R ,()()()sin sin f x x x x x f x -=--==,∴()f x 为偶函数.当73,62x ππ⎡⎤∈⎢⎥⎣⎦时,cos 0x <,()sin 2sin 3f x x x x π⎛⎫=+=+ ⎪⎝⎭,311326x πππ⎡⎤+∈⎢⎥⎣⎦,,此时正弦函数为增函数,故①正确;∵sin 0333f πππ⎛⎫== ⎪⎝⎭,∴033f f ππ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,而52333f f f ππππ⎛⎫⎛⎫⎛⎫-+==- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,∴2π不是函数()f x 的周期,故②错误;当022x k ππ⎡⎫∈+⎪⎢⎣⎭,或32222k k ππππ⎡⎫++⎪⎢⎣⎭,,k ∈Z 时,cos cos x x =, 此时()sin 2sin 3f x x x x π⎛⎫==- ⎪⎝⎭,当32222x k k ππππ⎡⎫∈++⎪⎢⎣⎭,,k ∈Z 时,cos cos x x =-,此时()sin 2sin 3f x x x x π⎛⎫==+ ⎪⎝⎭,故0x 时,2π是函数的一个周期, 故考虑[]0,2x π∈时,函数的值域,当02,π⎡⎤∈⎢⎥⎣⎦x 时,()2sin 3f x x π⎛⎫=- ⎪⎝⎭,,336x πππ⎡⎤-∈-⎢⎥⎣⎦,此时()f x 单调递增,();f x ⎡⎤∈⎣⎦ 当3,22x ππ⎛⎫∈ ⎪⎝⎭时,()2sin 3f x x π⎛⎫=+ ⎪⎝⎭,53,362x πππ⎛⎫+∈ ⎪⎝⎭,此时()f x 单调递减, ()()2,1f x ∈-;当322x ππ⎡⎤∈⎢⎥⎣⎦,时,()2sin 3f x x π⎛⎫=- ⎪⎝⎭,75,363x πππ⎡⎤-∈⎢⎥⎣⎦,此时()2,f x ⎡∈-⎣, 综上可知,()[]2,1f x ∈-,故③正确;由③知,02,π⎡⎤∈⎢⎥⎣⎦x 时,()002f f π⎛⎫⋅< ⎪⎝⎭,且函数单调递增,故存在一个零点,当726x ππ⎡⎤∈⎢⎥⎣⎦,时,7026f f ππ⎛⎫⎛⎫⋅< ⎪ ⎪⎝⎭⎝⎭,且函数单调递减,故存在一个零点, 其他区域无零点,故当[]0,2x π∈时,函数有2个零点,∵函数为偶函数,∴函数()f x 在[]2,2ππ-内有4个零点.故④正确; 故答案为:①③④. 17.(1)21n a n =- (2)20m = 【解析】 【分析】设数列{}n a 的公差为d ,0d >,根据2315a a ⋅=,且1a ,4a ,25a 成等比数列求出1,a d ,从而可求出数列{}n a 的通项公式;(2)求出数列{}n b 的通项公式,再利用裂项相消法可求出数列{}n b 的前n 项和为n S ,从而可得出答案. (1)………外…………○…………装…………○…………订…………○…………线…………○…………学校:___________姓名:___________班级:___________考号:___________………内…………○…………装…………○…………订…………○…………线…………○…………解:设数列{}n a 的公差为d ,0d >, 因为1a ,4a ,25a 成等比数列,2315a a ⋅=,所以241252315a a a a a ⎧=⋅⎨⋅=⎩,即()()()()211111324215a d a a d a d a d ⎧+=+⎪⎨++=⎪⎩,解得112a d =⎧⎨=⎩或(舍去),所以21n a n =-; (2) 解:()()111111212122121n n n b a a n n n n +⎛⎫===- ⎪⋅-+-+⎝⎭,所以111111111121335212122121n S nn n n n ⎛⎫⎛⎫=-+-++-=-= ⎪ ⎪-+++⎝⎭⎝⎭, 又2041m S =,即202141m m =+,所以20m =. 18.(1)475(2)分布列见解析,1EX = 【解析】 【分析】(1)根据给定频数表直接计算平均数作答.(2)由题意,X 服从二项分布,即1~(4,)4X B ,根据二项分布的概率公式和期望公式即得解 (1)依题意,25600404001550020450475100x ⨯+⨯+⨯+⨯==,所以该商场销售一部手机的平均利润为475元. (2)该商场每销售一部手机,该手机为甲配置型号手机的概率为2511004=, 由题意,甲配置型号手机售出的数量为X 服从二项分布,即1~(4,)4X B ,则X 所有可能取值为0,1,2,3,4,4413()()((0,1,2,3,4)44k k kP X k C k -===,故X 的分布列为:由二项分布的期望公式:1414EX np ==⨯=.19.(1)3π (2)(【解析】 【分析】(1)利用两角和的正弦公式及诱导公式得到cos sin a B A =,再由正弦定理得到1sin cos b B B=,即可得到tan B ,即可得解; (2)利用余弦定理及基本不等式得到03ac <≤,再根据()222233a c a c ac ac +=++=+求出a c +的取值范围,即可得解;(1)解:因为()sin cos sin cos a C B B C -=,即cos sin cos sin cos a B C B B C -=,所以()cos sin cos sin cos sin a B C B B C C B =+=+,即cos sin a B A =,所以1sin cos a A B=,又sin sin a bA B=,b =1sin cos b B B =,所以sin tan cos B B b B ===()0,B π∈,所以3B π=;(2)解:因为3B π=、b =2222cos b a c ac B =+-,即223a c ac =+-,即2232a c ac ac +=+≥当且仅当a c ==03ac <≤,所以()222233a c a c ac ac +=++=+,所以()2312a c <+≤a c +≤,所以ABCC≤,即三角形的周长的取值范围为(20.(1)()f x 在1x =处取极小值且极小值为()11e 2f =--.(2)213e 124a -+-≤≤【解析】 【分析】(1)求出函数的导数,讨论其符号后可得函数的极值.(1)曲线()f x 在()2,1-上任意一点处切线的倾斜角均为钝角即为(1)e 210x x ax ---<对任意的()2,1x ∈-恒成立,参变分离后可求参数的取值范围. (1)当12a =-时,21()(2)e 2xf x x x x =-+-,故()()()(1)e 11e 1x xf x x x x =-+-=-+',当1x <时,()0f x '<;1x >时,()0f x '>, 故()f x 在1x =处取极小值且极小值为()11e 2f =--.(2)()(1)e 21x f x x ax =-'--,因为曲线()f x 在()2,1-上任意一点处切线的倾斜角均为钝角, 故()0f x '<对任意的()2,1x ∈-恒成立, 即(1)e 210x x ax ---<对任意的()2,1x ∈-恒成立. 当0x =时,0(01)e 20120a --⨯-=-<,此时a R ∈, 当01x <<时,即(1)e 12x x a x -->对任意01x <<恒成立,设()(1)e 1x x g x x--=,则()()22222213e 11e 124e (1)e 10xx x x x x x x x g x x x x ⎡⎤⎛⎫-++⎢⎥ ⎪-++⎝⎭--+⎢⎥⎣⎦'===>, 故()g x 在0,1上为增函数,故()()11g x g <=-,故21a ≥-即12a ≥-.当20x -<<时,即(1)e 12x x a x --<对任意21x -<<-恒成立,同理有()g x 在()2,0-上为增函数,故()()23e 122g x g -+>-=,故23e 122a -+≤即23e 14a -+≤,综上,有213e 124a -+-≤≤. 【点睛】思路点睛:含参数的不等式的恒成立问题,可以通过对原函数的分类讨论求出参数的取值范围,也可以通过参变分离后结合导数求出新函数的值域或范围,从而得到参数的取值范围. 21.(1)22142x y +=(2)12k k 为定值23【解析】 【分析】(1)根据11eOF OA FA+=,OAB ,求得,a b ,即可得出答案; (2)设点001122(,),(,),(,)M x y P x y Q x y ,则点00(,)N x y --,根据,M N 在椭圆E 上,可得12AM AN k k ⋅=-,设直线AM 的方程为2x my =+,则直线AN 的方程为22x y m =-+,分别联立222,1,42x my x y =+⎧⎪⎨+=⎪⎩,222,4,x my x y =+⎧⎨+=⎩求得,,M P Q 三点的坐标,从而可得出结论. (1) 解:因为11e OF OA FA +=,所以11e c a a c +=-, 又2221,2OABcSab e a b c a====+, 联立可得2,a b ==所以椭圆E 的方程为22142x y +=; (2)解:设点001122(,),(,),(,)M x y P x y Q x y ,则点00(,)N x y --, 由题意得(2,0)A , 因为,M N 在椭圆E 上,所以2200142x y +=,则220042x y =-,所以220000220000122422y y y y x x x y ---⋅===-----, 即12AM AN k k ⋅=-,设直线AM 的方程为2x my =+,则直线AN 的方程为22x y m=-+, 联立222,1,42x my x y =+⎧⎪⎨+=⎪⎩消x 得22(2)40m y my ++=,由,A M 在椭圆E 上,所以0242m y m =-+,所以20024222m x my m -=+=+, 所以012022y m k x m ==-, 联立222,4,x my x y =+⎧⎨+=⎩消x 得22(1)40m y my ++=, 由点,A P 在圆C 上,所以1241m y m =-+,所以21122221m x my m-=+=+,同理:22222828,44m m y x m m -==++, 所以22124221(36)342y y m m mk x x m m -+===---, 所以2122222233k m m k m m -=⋅=-, 即12k k 为定值23. 【点睛】本题考查了椭圆的几何性质,考查了直线与椭圆的位置关系,考查了定值问题,考查了数据分析能力和数学运算能力,运算量比较大,有一定的难度.22.(1)曲线C 的普通方程为()()22215x y -+-=;直线l 的直角坐标方程为20x -= 【解析】 【分析】………外…………○…………装…………○…………订…………○…………线…………○………… 学校:___________姓名:___________班级:___________考号:___________………内…………○…………装…………○…………订…………○…………线…………○………… (1)直接消去参数α,可得到曲线C 的普通方程,先cos 13πρθ⎛⎫+= ⎪⎝⎭化简,然后利用极坐标与直角坐标的关系可得到直线l 的直角坐标方程; (2)由(1)可得直线l 的倾斜角,设出直线l 的参数方程,代入到曲线C 的直角坐标方程,可得关于t 的一元二次方程,设点A ,B 对应的参数分别为12,t t ,根据韦达定理,可得1212,t t t t +表达式,结合t 的几何意义,即可得答案.(1) 由2sin 2cos 1cos 2sin x y αααα=++⎧⎨=+-⎩ 可得 将上式分别平方,然后相加可得()()22215x y -+-= 由cos 13πρθ⎛⎫+= ⎪⎝⎭可得cos cos sin sin 133ππρθθ⎛⎫-= ⎪⎝⎭ 即13cos sin 12ρθθ=,则320x y -= (2) 由(1)可知直线l 36π,且点()2,0A 在直线l 上, 所以直线l 的参数方程为:2cos 6sin 6x t y t ππ⎧=+⎪⎪⎨⎪=⎪⎩,即3212x y t ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数) 将直线l 的参数方程代入曲线C 的普通方程,整理得240t t --= 设点A ,B 对应的参数分别为12,t t ,则12121,4t t t t +==- 则()2121212121212121241111t t t t t t t t AP AQ t t t t t t t t +-+-+=+===11617+==23.(1)(,1][5,)-∞-⋃+∞; (2)1124m -<≤-. 【解析】 【分析】 (1)将2m =代入,列出不等式,再解含绝对值符号的不等式作答.(2)利用给定条件去掉绝对值符号,转化成恒成立的不等式,分离参数构造函数推理作答. (1) 当2m =时,()f x 21220x x --+-≥, 当2x -≤时,不等式化为:12220x x -++-≥,解得1x ≤,则有2x -≤, 当122x -<≤时,不等式化为:12220x x ----≥,解得1x ≤-,则有21x -<≤-; 当12x >时,不等式化为:21220x x ----≥,解得5x ≥,则有5x ≥, 综上得:1x ≤-或5x ≥, 所以函数()f x 的定义域为(,1][5,)-∞-⋃+∞. (2) 因当12m >-时,1[,2m M -⊆,则对1[,2x m ∀∈-,210x x m m --+-≥成立, 此时,210x -≤,0x m +≥,则210120x x m m x x m m --+-≥⇔----≥231m x ⇔≤-+, 于是得1[,]2x m ∀∈-,231m x ≤-+成立,而函数31y x =-+在1[,2m -上单调递减, 当12x =时,min 12y =-,从而得122m ≤-,解得14m ≤-,又12m >-,则1124m -<≤-, 所以实数m 的取值范围是1124m -<≤-.。
2021届绵阳一诊 理科数学(Word版含答案)
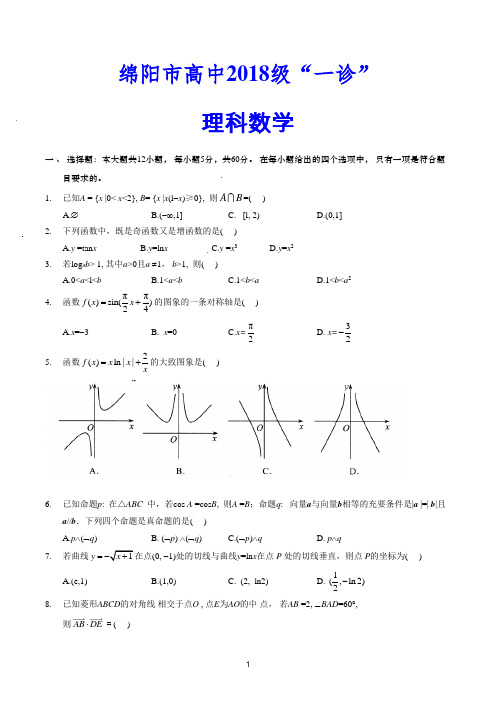
绵阳市高中2018级“一诊”理科数学一 、 选择题:本大题共12小题, 每小题5分,共60分。
在每小题给出的四个选项中, 只有一项是符合题目要求的。
1. 已知A = {x |0< x <2}, B = {x |x (l -x )≥0}, 则B A =( )A.∅B.(-∞,1]C. [l, 2)D.(0,1]2. 下列函数中,既是奇函数又是增函数的是( )A.y =tan xB.y =ln xC.y =x 3D.y =x 23. 若log a b > 1, 其中a >0且a ≠1, b >1, 则( )A.0<a <l<bB.1<a <bC.1<b <aD.1<b <a 24. 函数ππ()sin()24f x x =+的图象的一条对称轴是( )A.x =-3B. x =0C.x=π2D. x=32-5. 函数2()ln ||f x x x x=+的大致图象是( )6. 已知命题p : 在△ABC 中,若cos A =cos B , 则A =B ;命题q : 向量a 与向量b 相等的充要条件是|a |=| b |且a //b .下列四个命题是真命题的是( ) A.p ∧(⌝q )B. (⌝p ) ∧(⌝q )C.(⌝p )∧qD. p ∧q7. 若曲线1y x =-+在点(0, -1)处的切线与曲线y =ln x 在点 P 处的切线垂直,则点 P 的坐标为( )A.(e,1)B.(1,0)C. (2, ln2)D. 1(,ln 2)2-8. 已知菱形ABCD 的对角线 相交于点O , 点E 为AO 的中 点, 若AB =2, ∠BAD =60°,则AB DE ⋅=( )A.-2B. 12-C. 72-D.129. 若a <b < 0, 则下列不等式中成立的是( )A. 11a b a <- B. 11a b b a+>+C.11b b a a -<-D. (1)(1)a b a b ->-10. 某城市要在广场中央的圆形地面设计 一块浮雕,彰显城市积极向上的活力.某公司设计方案如图, 等腰△PMN 的顶点P 在半径为20m 的大⊙O 上,点M , N 在半径为10m 的小⊙O 上, 圆心O 与点P 都在弦MN 的同侧. 设弦MN 与对应劣弧所围成的弓形面积为S , △OPM 与△OPN 的面积之和为S 1,∠MON =2α, 当S 1-S 的值最大时,该设计方案最美, 则此时cos α=( ) A.12B.512- C.32D.212- 11. 数列{a n }满足21121n n n a a a ++=-,2411,59a a ==,数列{b n }的前n 项和为S n ,若b n =a n a n +1,则使不等式427n S >成立的n 的最小值为( ) A. 11 B. 12C. 13D. 1412. 若1823,23a b +==,则以下 结论正确的有( ) ①b -a <1 ②112a b+> ③34ab > ④22b a > A.1个B.2个C.3个D.4个二、填空题:本大题共4小题, 每小题5分, 共20分.13. 已知向量a =(l, 0), b =(l, 1), 且a +λb 与a 垂直,则实数λ= .14. 若实数x ,y 满足0,,22,x x y x y ≥⎧⎪≤⎨⎪+≥⎩则z =2x +y 的最大值为 .15. 已知sin x +cos y =14, 则sin x -sin 2y 的最大值为 . 16. 若函数f (x )=(x 2 +ax +2a )e x 在区间(-2, 1)上恰有一个极值点,则实数a 的取值范围为 .三、解答题:共70分。
四川省绵阳2023-2024学年高三上学期10月月考(一诊模拟)理科数学试题含解析

绵阳南山高2021级高三(上)一诊模拟考试理科数学(答案在最后)注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将答题卡交回.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集U =R ,集合{}220A x x x =-<,{}1B x x =>,则()UA B = ð()A.{}12x x << B.{}12x x ≤< C.{}01x x << D.{}01x x <≤【答案】D 【解析】【分析】先解一元二次不等式,化简集合A,再利用数轴进行集合的补集和交集运算可得.【详解】解一元二次不等式化简集合A,得{|02}A x x =<<,由{|1}B x x =>得{|1}U C B x x =≤,所以(){|01}U A C B x x ⋂=<≤.故选D.【点睛】本题考查了一元二次不等式的解法,集合的交集和补集运算,用数轴运算补集和交集时,注意空心点和实心点的问题,属基础题.2.若复数5i43iz =-,则z =()A.34i 55+ B.34i 55-+ C.34i 55-- D.34i 55-【答案】C 【解析】【分析】由复数的四则运算结合共轭复数的概念求解.【详解】由()5i 43i 5i 34i43i 2555z +===-+-,得34i 55z =--.故选:C3.设n S 是等差数列{}n a 的前n 项和,若25815a a a ++=,则9S =()A.15B.30C.45D.60【答案】C 【解析】【分析】根据等差数列的性质求出5a ,再根据等差数列前n 项和公式即可得解.【详解】由题意得2585315a a a a ++==,所以55a =,所以()199599452a a S a +===.故选:C.4.已知命题p :x ∃∈R ,使得2210ax x ++<成立为真命题,则实数a 的取值范围是()A.(],0-∞ B.(),1-∞ C.[)0,1 D.(]0,1【答案】B 【解析】【分析】由一次函数和二次函数的图象和性质,知当0a ≤时,命题为真命题,当0a >时,需0∆>,最后综合讨论结果,可得答案.【详解】命题p 为真命题等价于不等式2210ax x ++<有解.当0a =时,不等式变形为210x +<,则12x <-,符合题意;当0a >时,Δ440a =->,解得01a <<;当a<0时,总存在x ∃∈R ,使得2210ax x ++<;综上可得实数a 的取值范围为(),1-∞.故选:B5.在△ABC 中,AD 为BC 边上的中线,E 为AD 的中点,则EB =A.3144AB AC -B.1344AB AC -C.3144+AB AC D.1344+AB AC 【答案】A 【解析】【分析】分析:首先将图画出来,接着应用三角形中线向量的特征,求得1122BE BA BD =+,之后应用向量的加法运算法则-------三角形法则,得到BC BA AC =+,之后将其合并,得到3144BE BA AC =+ ,下一步应用相反向量,求得3144EB AB AC =-,从而求得结果.【详解】根据向量的运算法则,可得()111111222424BE BA BD BA BC BA BA AC=+=+=++1113124444BA BA AC BA AC=++=+,所以3144EB AB AC =-,故选A.【点睛】该题考查的是有关平面向量基本定理的有关问题,涉及到的知识点有三角形的中线向量、向量加法的三角形法则、共线向量的表示以及相反向量的问题,在解题的过程中,需要认真对待每一步运算.6.执行如图所示的程序框图,若输出的a 的值为17,则输入的最小整数t 的值为()A.9B.12C.14D.16【答案】A 【解析】【分析】根据流程框图代数进行计算即可,当进行第四次循环时发现输出的a 值恰好满足题意,然后停止循环求出t 的值.【详解】第一次循环,2213a =⨯-=,3a t =>不成立;第二次循环,2315a =⨯-=,5a t =>不成立;第三次循环,2519a =⨯-=.9a t =>不成立;第四次循环,29117a =⨯-=,17a t =>,成立,所以917t <≤,输入的最小整数t 的值为9.故选:A7.纯电动汽车是以车载电源为动力,用电机驱动车轮行驶,符合道路交通、安全法规各项要求的车辆,它使用存储在电池中的电来发动.因其对环境影响较小,逐渐成为当今世界的乘用车的发展方向.研究发现电池的容量随放电电流的大小而改变,1898年Peukert 提出铅酸电池的容量C 、放电时间t 和放电电流I 之间关系的经验公式:C I t λ=,其中λ为与蓄电池结构有关的常数(称为Peukert 常数),在电池容量不变的条件下,当放电电流为15A 时,放电时间为30h ;当放电电流为50A 时,放电时间为7.5h ,则该萻电池的Peukert 常数λ约为()(参考数据:lg20.301≈,lg30.477≈)A.1.12 B.1.13C.1.14D.1.15【答案】D 【解析】【分析】根据题意可得1530507.5C λλ=⨯=⨯,再结合对数式与指数式的互化及换底公式即可求解.【详解】由题意知1530507.5C λλ=⨯=⨯,所以50304157.5λ⎛⎫== ⎪⎝⎭,两边取以10为底的对数,得10lg 2lg23λ=,所以2lg220.3011.151lg310.477λ⨯=≈≈--.故选:D .8.若cos 0,,tan 222sin παααα⎛⎫∈= ⎪-⎝⎭,则tan α=()A.15B.C.3D.3【答案】A 【解析】【分析】由二倍角公式可得2sin 22sin cos tan 2cos 212sin αααααα==-,再结合已知可求得1sin 4α=,利用同角三角函数的基本关系即可求解.【详解】cos tan 22sin ααα=- 2sin 22sin cos cos tan 2cos 212sin 2sin αααααααα∴===--,0,2πα⎛⎫∈ ⎪⎝⎭ ,cos 0α∴≠,22sin 112sin 2sin ααα∴=--,解得1sin 4α=,215cos 1sin 4αα∴=-=,sin 15tan cos 15ααα∴==.故选:A.【点睛】关键点睛:本题考查三角函数的化简问题,解题的关键是利用二倍角公式化简求出sin α.9.函数π()412sin 2x xf x x -⎛⎫=-⋅⋅+ ⎪⎝⎭的大致图象为()A.B. C.D.【答案】D 【解析】【分析】对函数化简后,利用排除法,先判断函数的奇偶性,再取特殊值判断即可【详解】因为()|22|cos x x f x x -=-⋅,()22cos()()xx f x x f x --=-⋅-=,所以()f x 为偶函数,所以函数图象关于y 轴对称,所以排除A ,C 选项;又1(2)4cos 204f =-<,所以排除B 选项,故选:D .10.设函数π()sin 3f x x ω⎛⎫=+⎪⎝⎭在区间(0,π)恰有三个极值点、两个零点,则ω的取值范围是()A.513,36⎫⎡⎪⎢⎣⎭B.519,36⎡⎫⎪⎢⎣⎭C.138,63⎛⎤ ⎥⎝⎦D.1319,66⎛⎤ ⎥⎝⎦【答案】C【解析】【分析】由x 的取值范围得到3x πω+的取值范围,再结合正弦函数的性质得到不等式组,解得即可.【详解】解:依题意可得0ω>,因为()0,x π∈,所以,333x πππωωπ⎛⎫+∈+ ⎪⎝⎭,要使函数在区间()0,π恰有三个极值点、两个零点,又sin y x =,,33x ππ⎛⎫∈⎪⎝⎭的图象如下所示:则5323ππωππ<+≤,解得13863ω<≤,即138,63ω⎛⎤∈ ⎥⎝⎦.故选:C .11.已知函数()1ex x f x +=.若过点()1,P m -可以作曲线()y f x =三条切线,则m 的取值范围是()A.40,e ⎛⎫ ⎪⎝⎭B.80,e ⎛⎫ ⎪⎝⎭C.14,e e ⎛⎫- ⎪⎝⎭D.18,e e ⎛⎫ ⎪⎝⎭【答案】A 【解析】【分析】切点为0001,e x x x +⎛⎫ ⎪⎝⎭,利用导数的几何意义求切线的斜率,设切线为:()000001e ex x x x y x x +--=-,可得()021ex x m +=,设()()21exx g x +=,求()g x ',利用导数求()g x 的单调性和极值,切线的条数即为直线y m =与()g x 图象交点的个数,结合图象即可得出答案.【详解】设切点为0001,e x x x +⎛⎫ ⎪⎝⎭,由()1e x x f x +=可得()()2e e 1e ex x xx x x f x -⋅+-==',所以在点0001,e x x x +⎛⎫ ⎪⎝⎭处的切线的斜率为()00e x x kf x -'==,所以在点0001,e x x x +⎛⎫ ⎪⎝⎭处的切线为:()000001e ex x x x y x x +--=-,因为切线过点()1,P m -,所以()0000011e ex x x x m x +--=--,即()021ex x m +=,即这个方程有三个不等根即可,切线的条数即为直线y m =与()g x 图象交点的个数,设()()21e xx g x +=,则()()()2222211e e xxx x x x g x +-++'-+==由()0g x '>可得11x -<<,由()0g x '<可得:1x <-或1x >,所以()()21exx g x +=在(),1-∞-和()1,+∞上单调递减,在()1,1-上单调递增,当x 趋近于正无穷,()g x 趋近于0,当x 趋近于负无穷,()g x 趋近于正无穷,()g x 的图象如下图,且()41eg =,要使y m =与()()21e xx g x +=的图象有三个交点,则40em <<.则m 的取值范围是:40,e ⎛⎫ ⎪⎝⎭.故选:A.12.已知函数()323,0,31,0x x f x x x x ->⎧=⎨-+≤⎩,函数()()()g x f f x m =-恰有5个零点,则m 的取值范围是()A.()3,1- B.()0,1 C.[)1,1- D.()1,3【答案】C【分析】由题意可先做出函数()f x 的大致图象,利用数形结合和分类讨论,即可确定m 的取值范围.【详解】当0x ≤时,()233f x x ¢=-.由()0f x ¢>,得1x <-,由()0f x '<,得10-<≤x ,则()f x 在(]1,0-上单调递减,在(),1-∞-上单调递增,故()f x 的大致图象如图所示.设()t f x =,则()m f t =,由图可知当3m >时,()m f t =有且只有1个实根,则()t f x =最多有3个不同的实根,不符合题意.当3m =时,()m f t =的解是11t =-,23t =.1f x t =()有2个不同的实根,2f x t =()有2个不同的实根,则()t f x =有4个不同的实根,不符合题意.当13m ≤<时,()m f t =有3个不同的实根3t ,4t ,5t ,且()321t ∈--,,(]41,0t ∈-,[)52,3t ∈.3f x t =()有2个不同的实根,4f x t =()有2个不同的实根,5f x t =()有3个不同的实根,则()t f x =有7个不同的实根,不符合题意.当11m -≤<时,()m f t =有2个不同的实根6t ,7t ,且()631t ∈--,,[)71,2t ∈.6f x t =()有2个不同的实根,7f x t =()有3个不同的实根,则()t f x =有5个不同的实根,符合题意.当3<1m -<-时,()m f t =有2个不同的实根8t ,9t ,且()831t ∈--,,()901t ∈,,8f x t =()有2个不同的实根,9f x t =(),有2个不同的实根,则()t f x =有4个不同的实根,不符合题意.当3m ≤-时,()m f t =有且只有1个实根,则()t f x =最多有3个不同的实根,不符合题意,综上,m 的取值范围是[)1,1-.【点睛】方法点睛:对于函数零点问题,若能够画图时可作出函数图像,利用数形结合与分类讨论思想,即可求解.本题中,由图看出,m 的讨论应有3m =,13m ≤<,11m -≤<,3<1m -<-,3m ≤-这几种情况,也是解题关键.二、填空题:本大题共4小题,每小题5分,共20分.13.已知向量()()3,1,1,0,a b c a kb ===+ .若a c ⊥,则k =________.【答案】103-.【解析】【分析】利用向量的坐标运算法则求得向量c的坐标,利用向量的数量积为零求得k 的值【详解】()()()3,1,1,0,3,1a b c a kb k ==∴=+=+,(),33110a c a c k ⊥∴⋅=++⨯= ,解得103k =-,故答案为:103-.【点睛】本题考查平面向量的坐标运算,平面向量垂直的条件,属基础题,利用平面向量()()1122,,,p x y q x y ==垂直的充分必要条件是其数量积12120x x y y +=.14.如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点,从A 点测得M 点的仰角60MAN ∠=︒,C 点的仰角45CAB ∠=︒以及75MAC ∠=︒;从C 点测得60MCA ∠=︒.已知山高200BC =m ,则山高MN =______m .【答案】300【解析】【分析】先求,AC AMC ∠,由正弦定理得sin sin MCA AMCAM AC∠∠=,最后由sin MN AM MAN =⋅∠可求.【详解】由题意,sin BCAC CAB==∠m ,18045AM C M AC M CA ∠=︒-∠-∠=︒,由正弦定理得2sin sin 22MCA AMC AM AM AC AM ∠∠=⇒=⇒=m ,所以sin 3002MNAM MAN =⋅∠==m.故答案为:30015.已知等比数列{}n a 的前3项和为25168,42a a -=,则6a =___________.【答案】3【解析】【分析】设等比数列{}n a 的公比为q ,根据已知条件利用等比数列的定义计算可得12q =,196a =,即可求得6a 的值.【详解】解:设等比数列{}n a 的公比为q ,0q ≠,由题意1q ≠,因为前3项和为168,故()3112311681a q a a a q-++==-,又()43251111a a a q a q a q q-=-=-,所以12q =,196a =,则561196332a a q ==⨯=.故答案为:3.16.已知函数()y f x =是R 的奇函数,对任意x R ∈,都有(2)()(2)f x f x f -=+成立,当12,,1[]0x x ∈,且12x x ≠时,都有()()12120f x f x x x ->-,有下列命题①(1)(2)(3)(2019)0f f f f ++++= ②直线5x =-是函数()y f x =图象的一条对称轴③函数()y f x =在[7,7]-上有5个零点④函数()y f x =在[7,5]--上为减函数则结论正确的有____________.【答案】①②④【解析】【分析】根据题意,利用特殊值法求得()20f =,进而分析得到1x =时函数()f x 的一条对称轴,,函数()f x 时周期为4的周期函数,且函数()f x 在[1,1]-上单调递增,据此结合选项,逐项判定,即可求解.【详解】由题意,函数()y f x =是R 的奇函数,则()00f =,对任意x R ∈,都有(2)()(2)f x f x f -=+成立,当2x =,有()()0220f f ==,即()20f =,则有(2)()f x f x -=,即1x =时函数()f x 的一条对称轴,又由()f x 为奇函数,则(2)()f x f x -=--,即()()2f x f x +=-,可得()()()42f x f x f x +=-+=,所以函数()f x 时周期为4的周期函数,当12,,1[]0x x ∈,且12x x ≠时,都有()()12120f x f x x x ->-,可函数()f x 在[1,1]-上单调递增,对于①中,由()()2f x f x +=-,则(1)(2)(3)(4)0f f f f +++=,所以(1)(2)(3)(2019)504[(1)(2)(3)(4)]f f f f f f f f ++++=+++ ()(1)(2)(3)20f f f f +++==,所以①正确;对于②中,由1x =时函数()f x 的一条对称轴,且函数()f x 时周期为4的周期函数,则直线5x =-是函数()y f x =图象的一条对称轴,所以②正确;对于③中,函数()y f x =在[7,7]-上有7个零点,分别为6,4,2,0,2,4,6---,所以C 错误;对于④中,函数()y f x =在[1,1]-上为增函数且周期为4,可得()y f x =在[5,3]--上为增函数,又由5x =-是函数()y f x =图象的一条对称轴,则函数()y f x =在[7,5]--上为减函数,所以④正确.故答案为:①②④三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分.17.已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象,如图所示.(1)求函数()f x 的解析式;(2)将函数()f x 的图象向右平移3π个单位长度,再将得到的图象上各点的横坐标缩短为原来的12,纵坐标不变,得到函数()g x 的图象,当0,3x π⎡⎤∈⎢⎥⎣⎦时,求函数()g x 的值域.【答案】(1)()323f x x π⎛⎫=+ ⎪⎝⎭(2)332⎡-⎢⎣【解析】【分析】(1)根据正弦型函数的图像求三角函数的解析式,根据最大值求出A ,由最小正周期求出ω,并确定ϕ.(2)根据平移后得到新的正弦型函数解析式,由函数解析式求出函数值域.【小问1详解】解:根据函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象可得3A =1252632ππππω=-=⋅,所以2ω=.再根据五点法作图可得23πϕπ⋅+=,所以3πϕ=,()323f x x π⎛⎫=+ ⎪⎝⎭.【小问2详解】将函数()f x 的图象向右平移3π个单位后,可得323sin 2333y x x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎢⎥⎝⎭⎝⎭⎣⎦的图象,再将得到的图象上各点的横坐标缩短为原来的12,纵坐标不变,得到函数()343g x x π⎛⎫=- ⎪⎝⎭的图象.由0,3x π⎡⎤∈⎢⎥⎣⎦,可得4,33x πππ⎡⎤-∈-⎢⎥⎣⎦又 函数()g x 在50,24π⎡⎤⎢⎥⎣⎦上单调递增,在5,243ππ⎡⎤⎢⎥⎣⎦单调递减∴3(0)2g =-,524g π⎛⎫= ⎪⎝⎭03g π⎛⎫= ⎪⎝⎭∴3()4,32g x x π⎛⎫⎡=-∈- ⎪⎢⎝⎭⎣∴函数()g x 在0,3π⎡⎤⎢⎥⎣⎦的值域32⎡-⎢⎣.18.已知数列{}n a 的前n 项和为n S ,313log 1log n n b b +-=,且()1122n n n a a a n +-=+≥.339S b ==,414b a =.(1)求数列{}n a 和{}n b 的通项公式;(2)若11n n n c a b ++=⋅,求数列{}n c 的前n 项和n T .【答案】(1)13n n b -=,21n a n =-(2)13n n T n +=⋅【解析】【分析】(1)根据对数运算得13n nb b +=,利用等比数列定义求通项公式,利用等差中项判断数列{}n a 为等差数列,建立方程求出公差,从而可得{}n a 的通项;(2)利用错位相减法计算即可.【小问1详解】∵313log 1log n n b b +-=,∴313log log (3)n n b b +=,则13n nb b +=,所以{}n b 为等比数列,又39b =,得11b =,所以13n n b -=,由112n n n a a a +-=+知{}n a 是等差数列,且41427b a ==,39S =,∴111327339a d a d +=⎧⎨+=⎩,得11a =,2d =.∴21n a n =-.【小问2详解】因为21n a n =-,13n n b -=,所以()11213nn n n c a b n ++=⋅=+,所以()()1231335373213213n n n T n n -=⋅+⋅+⋅+⋅⋅⋅+-⋅++⋅则()()23413335373213213n n n T n n +=⋅+⋅+⋅+⋅⋅⋅+-⋅++⋅上面两式作差得()223123232323213n n n T n +-=+⋅+⋅+⋅⋅⋅+⋅-+⋅()()111913922132313n n n n n -++⎛⎫- ⎪=+-+⋅=-⋅ ⎪-⎝⎭,∴13n n T n +=⋅19.记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=.(1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠.【答案】(1)证明见解析;(2)7cos 12ABC ∠=.【解析】【分析】(1)根据正弦定理的边角关系有ac BD b=,结合已知即可证结论.(2)方法一:两次应用余弦定理,求得边a 与c 的关系,然后利用余弦定理即可求得cos ABC ∠的值.【详解】(1)设ABC 的外接圆半径为R ,由正弦定理,得sin sin ,22b c R ABC C R==∠,因为sin sin BD ABC a C ∠=,所以22b c BD a R R ⋅=⋅,即BD b ac ⋅=.又因为2b ac =,所以BD b =.(2)[方法一]【最优解】:两次应用余弦定理因为2AD DC =,如图,在ABC 中,222cos 2a b c C ab+-=,①在BCD △中,222()3cos 23b a b b a C +-=⋅.②由①②得2222223(3b a bc a b ⎡⎤+-=+-⎢⎥⎣⎦,整理得22211203a b c -+=.又因为2b ac =,所以2261130a ac c -+=,解得3c a =或32c a =,当22,33c c a b ac ===时,333c c a b c +=+<(舍去).当2233,22c c a b ac ===时,22233()722cos 31222c c ABC c c c +⋅-==⋅∠.所以7cos 12ABC ∠=.[方法二]:等面积法和三角形相似如图,已知2AD DC =,则23ABD ABC S S =△△,即21221sin sin 2332b ac AD A B BC ⨯=⨯⨯∠∠,而2b ac =,即sin sin ADB ABC ∠=∠,故有ADB ABC ∠=∠,从而ABD C ∠=∠.由2b ac =,即b c a b =,即CA BA CB BD=,即ACB ABD ∽,故AD AB AB AC =,即23b c c b =,又2b ac =,所以23c a =,则2227cos 212c a b ABC ac +-==∠.[方法三]:正弦定理、余弦定理相结合由(1)知BD b AC ==,再由2AD DC =得21,33AD b CD b ==.在ADB 中,由正弦定理得sin sin AD BD ABD A=∠.又ABD C ∠=∠,所以s 3sin n 2i C b A b =,化简得2sin sin 3C A =.在ABC 中,由正弦定理知23c a =,又由2b ac =,所以2223b a =.在ABC 中,由余弦定理,得222222242793cos 221223a a a a c b ABC ac a +--⨯∠+===.故7cos 12ABC ∠=.[方法四]:构造辅助线利用相似的性质如图,作DE AB ∥,交BC 于点E ,则DEC ABC △∽△.由2AD DC =,得2,,333c a a DE EC BE ===.在BED 中,2222(()33cos 2323BED a c b a c -=⋅∠+⋅.在ABC 中222cos 2a a BC c A b c+-=∠.因为cos cos ABC BED ∠=-∠,所以2222222()()3322233a c b a c b a c ac +-+-=-⋅⋅,整理得22261130a b c -+=.又因为2b ac =,所以2261130a ac c -+=,即3c a =或32a c =.下同解法1.[方法五]:平面向量基本定理因为2AD DC =,所以2AD DC =uuu r uuu r .以向量,BA BC 为基底,有2133BD BC BA =+ .所以222441999BD BC BA BC BA =+⋅+ ,即222441cos 999b ac c ABC a ∠=++,又因为2b ac =,所以22944cos ac a ac ABC c ⋅∠=++.③由余弦定理得2222cos b a c ac ABC =+-∠,所以222cos ac a c ac ABC =+-∠④联立③④,得2261130a ac c -+=.所以32a c =或13a c =.下同解法1.[方法六]:建系求解以D 为坐标原点,AC 所在直线为x 轴,过点D 垂直于AC 的直线为y 轴,DC 长为单位长度建立直角坐标系,如图所示,则()()()0,0,2,0,1,0D A C -.由(1)知,3BD b AC ===,所以点B 在以D 为圆心,3为半径的圆上运动.设()(),33B x y x -<<,则229x y +=.⑤由2b ac =知,2BA BC AC ⋅=,2222(2)(1)9x y x y ++-+=.⑥联立⑤⑥解得74x =-或732x =≥(舍去),29516y =,代入⑥式得36||||6,32a BC c BA b =====,由余弦定理得2227cos 212a cb ABC ac +-∠==.【整体点评】(2)方法一:两次应用余弦定理是一种典型的方法,充分利用了三角形的性质和正余弦定理的性质解题;方法二:等面积法是一种常用的方法,很多数学问题利用等面积法使得问题转化为更为简单的问题,相似是三角形中的常用思路;方法三:正弦定理和余弦定理相结合是解三角形问题的常用思路;方法四:构造辅助线作出相似三角形,结合余弦定理和相似三角形是一种确定边长比例关系的不错选择;方法五:平面向量是解决几何问题的一种重要方法,充分利用平面向量基本定理和向量的运算法则可以将其与余弦定理充分结合到一起;方法六:建立平面直角坐标系是解析几何的思路,利用此方法数形结合充分挖掘几何性质使得问题更加直观化.20.已知函数()()e xf x a a x =+-.(1)讨论()f x 的单调性;(2)证明:当0a >时,()32ln 2f x a >+.【答案】(1)答案见解析(2)证明见解析【解析】【分析】(1)先求导,再分类讨论0a ≤与0a >两种情况,结合导数与函数单调性的关系即可得解;(2)方法一:结合(1)中结论,将问题转化为21ln 02a a -->的恒成立问题,构造函数()()21ln 02g a a a a =-->,利用导数证得()0g a >即可.方法二:构造函数()e 1x h x x =--,证得e 1x x ≥+,从而得到2()ln 1f x x a a x ≥+++-,进而将问题转化为21ln 02a a -->的恒成立问题,由此得证.【小问1详解】因为()()e x f x a a x =+-,定义域为R ,所以()e 1xf x a '=-,当0a ≤时,由于e 0x >,则e 0x a ≤,故()0e 1xf x a -'=<恒成立,所以()f x 在R 上单调递减;当0a >时,令()e 10xf x a '=-=,解得ln x a =-,当ln x a <-时,()0f x '<,则()f x 在(),ln a -∞-上单调递减;当ln x a >-时,()0f x ¢>,则()f x 在()ln ,a -+∞上单调递增;综上:当0a ≤时,()f x 在R 上单调递减;当0a >时,()f x 在(),ln a -∞-上单调递减,()f x 在()ln ,a -+∞上单调递增.【小问2详解】方法一:由(1)得,()()()ln min 2ln ln ln e1a f a a x a f a a a --+=++=+=,要证3()2ln 2f x a >+,即证2312ln 2ln a a a ++>+,即证21ln 02a a -->恒成立,令()()21ln 02g a a a a =-->,则()21212a g a a a a-'=-=,令()0g a '<,则02a <<;令()0g a '>,则2a >;所以()g a 在0,2⎛⎫ ⎪ ⎪⎝⎭上单调递减,在,2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增,所以()2min 1ln ln 02222g a g ⎛⎫⎛==--= ⎪ ⎪ ⎪⎝⎭⎝⎭,则()0g a >恒成立,所以当0a >时,3()2ln 2f x a >+恒成立,证毕.方法二:令()e 1x h x x =--,则()e 1x h x '=-,由于e x y =在R 上单调递增,所以()e 1xh x '=-在R 上单调递增,又()00e 10h '=-=,所以当0x <时,()0h x '<;当0x >时,()0h x '>;所以()h x 在(),0∞-上单调递减,在()0,∞+上单调递增,故()()00h x h ≥=,则e 1x x ≥+,当且仅当0x =时,等号成立,因为()2ln 22()e e e ln 1x x x a f x a a x a a x a x x a a x +=+-=+-=+-≥+++-,当且仅当ln 0x a +=,即ln x a =-时,等号成立,所以要证3()2ln 2f x a >+,即证23ln 12ln 2x a a x a +++->+,即证21ln 02a a -->,令()()21ln 02g a a a a =-->,则()21212a g a a a a-'=-=,令()0g a '<,则02a <<;令()0g a '>,则2a >;所以()g a 在0,2⎛⎫ ⎪ ⎪⎝⎭上单调递减,在,2⎛⎫+∞ ⎪ ⎪⎝⎭上单调递增,所以()2min 1ln ln 02222g a g ⎛⎫⎛==--= ⎪ ⎪ ⎪⎝⎭⎝⎭,则()0g a >恒成立,所以当0a >时,3()2ln 2f x a >+恒成立,证毕.21.已知函数()()ln 1e x f x x ax -=++(1)当1a =时,求曲线()y f x =在点()()0,0f 处的切线方程;(2)若()f x 在区间()()1,0,0,-+∞各恰有一个零点,求a 的取值范围.【答案】(1)2y x=(2)(,1)-∞-【解析】【分析】(1)先算出切点,再求导算出斜率即可(2)求导,对a 分类讨论,对x 分(1,0),(0,)-+∞两部分研究【小问1详解】()f x 的定义域为(1,)-+∞当1a =时,()ln(1),(0)0e x x f x x f =++=,所以切点为(0,0)11(),(0)21e xx f x f x ''-=+=+,所以切线斜率为2所以曲线()y f x =在点(0,(0))f 处的切线方程为2y x=【小问2详解】()ln(1)e xaxf x x =++()2e 11(1)()1e (1)e x x x a x a x f x x x '+--=+=++设()2()e 1x g x a x =+-1︒若0a >,当()2(1,0),()e 10x x g x a x ∈-=+->,即()0f x '>所以()f x 在(1,0)-上单调递增,()(0)0f x f <=故()f x 在(1,0)-上没有零点,不合题意2︒若10a -≤≤,当,()0x ∈+∞,则()e 20x g x ax '=->所以()g x 在(0,)+∞上单调递增所以()(0)10g x g a >=+≥,即()0f x '>所以()f x 在(0,)+∞上单调递增,()(0)0f x f >=故()f x 在(0,)+∞上没有零点,不合题意3︒若1a <-(1)当,()0x ∈+∞,则()e 20x g x ax '=->,所以()g x 在(0,)+∞上单调递增(0)10,(1)e 0g a g =+<=>所以存在(0,1)m ∈,使得()0g m =,即()0'=f m 当(0,),()0,()x m f x f x '∈<单调递减当(,),()0,()x m f x f x '∈+∞>单调递增所以当(0,),()(0)0x m f x f ∈<=,令(),1,e x x h x x =>-则1(),1,e x x h x x -'=>-所以()x x h x e =在()1,1-上单调递增,在()1,+∞上单调递减,所以()1()1e h x h ≤=,又e e 10a -->,e 1e 10e e a a f a -⎛⎫-≥-+⋅= ⎪⎝⎭,所以()f x 在(,)m +∞上有唯一零点又(0,)m 没有零点,即()f x 在(0,)+∞上有唯一零点(2)当()2(1,0),()e 1x x g x a x∈-=+-设()()e 2x h x g x ax '==-()e 20x h x a '=->所以()g x '在(1,0)-单调递增1(1)20,(0)10eg a g ''-=+<=>所以存在(1,0)n ∈-,使得()0g n '=当(1,),()0,()x n g x g x '∈-<单调递减当(,0),()0,()x n g x g x '∈>单调递增,()(0)10g x g a <=+<又1(1)0eg -=>所以存在(1,)t n ∈-,使得()0g t =,即()0f t '=当(1,),()x t f x ∈-单调递增,当(,0),()x t f x ∈单调递减,当()1,0x ∈-,()()1e h x h >-=-,又e 1e 10a -<-<,()e e 1e e 0a f a a -<-=而(0)0f =,所以当(,0),()0x t f x ∈>所以()f x 在(1,)t -上有唯一零点,(,0)t 上无零点即()f x 在(1,0)-上有唯一零点所以1a <-,符合题意所以若()f x 在区间(1,0),(0,)-+∞各恰有一个零点,求a 的取值范围为(,1)-∞-【点睛】方法点睛:本题的关键是对a 的范围进行合理分类,否定和肯定并用,否定只需要说明一边不满足即可,肯定要两方面都说明.(二)选考题:共10分.请考生在第22、23题中任选一题做答.如果多做,则按所做的第一题记分.选修4—4:坐标系与参考方程22.在直角坐标系xOy 中,曲线M 的方程为24y x x =-+,曲线N 的方程为9xy =,以坐标原点O 为极点,x 轴的正半轴为极轴,建立极坐标系.(1)求曲线M ,N 的极坐标方程;(2)若射线00π:(0,02l θθρθ=≥<<与曲线M 交于点A (异于极点),与曲线N 交于点B ,且||||12OA OB ⋅=,求0θ.【答案】(1)π4cos 02ρθθ⎛⎫=≤≤⎪⎝⎭;2sin 218ρθ=(2)π4【解析】【分析】(1)根据极坐标与直角坐标的互化公式,即可求解曲线M 和N 的极坐标方程;(2)将0θθ=代入曲线M 和N的方程,求得||OB ρ==0||4cos OA ρθ==,结合题意求得0tan 1θ=,即可求解.【小问1详解】解:由y =224(0)y x x y =-+≥,即224(04,0)x y x x y +=≤≤≥,又由cos sin x y ρθρθ=⎧⎨=⎩,可得2π4cos (0)2ρρθθ=≤≤,所以曲线M 的极坐标方程为π4cos 02ρθθ⎛⎫=≤≤⎪⎝⎭.由9xy =,可得2cos sin 9ρθθ=,即2sin 218ρθ=,即曲线N 的极坐标方程为2sin 218ρθ=.【小问2详解】解:将0θθ=代入2sin 218ρθ=,可得||OB ρ==将0θθ=代入4cos ρθ=,可得0||4cos OA ρθ==,则||||OA OB ⋅=,因为||||12OA OB ⋅=,所以0tan 1θ=,又因为0π02θ<<,所以0π4θ=.选修4—5:不等式选讲23.已知函数()121f x x x =++-.(1)求不等式()8f x <的解集;(2)设函数()()1g x f x x =--的最小值为m ,且正实数a ,b ,c 满足a b c m ++=,求证:2222a b c b c a++≥.【答案】(1)7,33⎛⎫- ⎪⎝⎭(2)证明见详解【解析】【分析】(1)分段讨论去绝对值即可求解;(2)利用绝对值不等式可求得2m =,再利用基本不等式即可证明.【小问1详解】由题意可得:()31,11213,1131,1x x f x x x x x x x -≥⎧⎪=++-=--<<⎨⎪-+≤-⎩,当1x ≥时,则()318f x x =-<,解得23x ≤<;当11x -<<时,则()38f x x =-<,解得11x -<<;当1x ≤-时,则()318f x x =-+<,解得713x -<≤-;综上所述:不等式()8f x <的解集为7,33⎛⎫-⎪⎝⎭.【小问2详解】∵()()1112g x f x x x x =++---≥=,当且仅当[]1,1x ∈-时等号成立,∴函数()g x 的最小值为2m =,则2a b c ++=,又∵22a b a b +≥=,当且仅当2a b b =,即a b =时等号成立;22b c b c +≥=,当且仅当2b c c =,即b c =时等号成立;22c a c a +≥=,当且仅当2c a a =,即a c =时等号成立;上式相加可得:222222a b c b c a a b c b c a ⎛⎫⎛⎫⎛⎫+++++≥++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,当且仅当a b c ==时等号成立,∴2222a b c a b c b c a ++≥++=.。
2021届四川省绵阳市高三第一次诊断性考试数学(理)试题word版含解析

2021届四川省绵阳市高三上学期开学考试数学(文)试题一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合}32|{<<-=x x A ,}05|{2<-∈=x x Z x B ,则=B A ( ) A .}2,1{ B .}3,2{ C .}3,2,1{ D .}4,3,2{ 【答案】A2.已知命题p :01,2>+-∈∀x x R x ,则p ⌝为( )A .01,2>+-∉∀x x R x B .01,0200≤+-∉∃x x R x C .01,2≤+-∈∀x x R x D .01,0200≤+-∈∃x x R x【答案】D 【解析】试题分析:p ⌝为01,0200≤+-∈∃x x R x ,选D.考点:命题的否定【方法点睛】(1)对全称(存在性)命题进行否定的两步操作:①找到命题所含的量词,没有量词的要结合命题的含义加上量词,再进行否定;②对原命题的结论进行否定.(2)判定全称命题“∀x ∈M ,p(x)”是真命题,需要对集合M 中的每个元素x ,证明p(x)成立;要判定一个全称命题是假命题,只要举出集合M 中的一个特殊值x 0,使p(x 0)不成立即可.要判断存在性命题是真命题,只要在限定集合内至少能找到一个x =x 0,使p(x 0)成立即可,否则就是假命题.3.《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织二十八尺,第二日、第五日、第八日所织之和为十五尺,则第九日所织尺数为( ) A .8 B .9 C .10 D .11 【答案】B考点:等差数列4.若实数y x ,满足⎪⎩⎪⎨⎧≥≤+≥-010y y x y x ,则y x z +=2的最大值为( )A .0B .1C .2D .23 【答案】C 【解析】试题分析:可行域为一个三角形ABC 及其内部,其中11(0,0),(1,0),(,)22A B C ,所以直线y x z +=2过点B 时取最大值2,选C. 考点:线性规划【易错点睛】线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一,准确无误地作出可行域;二,画目标函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三,一般情况下,目标函数的最大或最小值会在可行域的端点或边界上取得. 5.设命题p :1)21(<x ,命题q :1ln <x ,则p 是q 成立的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B 【解析】6.2016年国庆节期间,绵阳市某大型商场举行“购物送券”活动.一名顾客计划到该商场购物,他有三张商场的优惠券,商场规定每购买一件商品只能使用一张优惠券.根据购买商品的标价,三张优惠券的优惠方式不同,具体如下:优惠券A :若商品标价超过100元,则付款时减免标价的10%; 优惠券B :若商品标价超过200元,则付款时减免30元;优惠券C :若商品标价超过200元,则付款时减免超过200元部分的20%.若顾客想使用优惠券C ,并希望比使用优惠券A 或B 减免的钱款都多,则他购买的商品的标价应高于( )A .300元B .400元C .500元D .600元 【答案】B 【解析】试题分析:设购买的商品的标价为x ,则(200)20%10%;(200)20%30;400,350400x x x x x x -⨯>⋅-⨯>⇒>>⇒>,选B.考点:不等式应用7.要得到函数)(2cos 32sin )(R x x x x f ∈+=的图象,可将x y 2sin 2=的图象向左平移( ) A .6π个单位 B .3π个单位 C .4π个单位 D .12π个单位【答案】A 【解析】试题分析:因为()sin 2322sin(2)3f x x x x π=+=+,所以可将x y 2sin 2=的图象向左平移3=26ππ,选A.考点:三角函数图像变换【思路点睛】三角函数的图象变换,提倡“先平移,后伸缩”,但“先伸缩,后平移”也常出现在题目中,所以也必须熟练掌握.无论是哪种变形,切记每一个变换总是对字母x 而言. 函数y =Asin(ωx +φ),x ∈R 是奇函数⇔φ=k π(k ∈Z);函数y =Asin(ωx +φ),x ∈R 是偶函数⇔φ=k π+π2(k ∈Z);函数y =Acos(ωx +φ),x ∈R 是奇函数⇔φ=k π+π2(k ∈Z);函数y =Acos(ωx +φ),x ∈R 是偶函数⇔φ=k π(k ∈Z).8.已知αθθsin 2cos sin =+,βθ2sin 22sin =,则( ) A .αβcos 2cos = B .αβ22cos 2cos=C .02cos 22cos =+αβD .αβ2cos 22cos = 【答案】D9.已知定义在),0[+∞上的函数)(x f 满足)(2)1(x f x f =+,当)1,0[∈x 时,x x x f +-=2)(,设)(x f 在),1[n n -上的最大值为)(*N n a n ∈,则=++543a a a ( )A .7B .87C .45D .14 【答案】A 【解析】 试题分析:23412345113111111(),()2(),(2)2()1,2()2,2()4,242222222a f a f f a f f a f a f ======+======,所以3451247a a a ++=++=,选A.考点:函数性质【思路点睛】(1)运用函数性质解决问题时,先要正确理解和把握函数相关性质本身的含义及其应用方向. (2)在研究函数性质特别是奇偶性、周期、对称性、单调性、最值、零点时,要注意用好其与条件的相互关系,结合特征进行等价转化研究.如奇偶性可实现自变量正负转化,周期可实现自变量大小转化,单调性可实现去f “”,即将函数值的大小转化自变量大小关系10.在ABC ∆中,81cos =A ,4=AB ,2=AC ,则A ∠的角平分线D A 的长为( ) A .22 B .32 C .2 D .1 【答案】C考点:余弦定理11.如图,矩形ABCD 中,2=AB ,1=AD ,P 是对角线AC 上一点,25AP AC =,过点P 的直线分别交DA 的延长线,AB ,DC 于N E M ,,.若DA m DM =,DC n DN =)0,0(>>n m ,则n m 32+的最小值是( ) A .56 B .512 C .524 D .548【答案】C 【解析】 试题分析:232555AP AC DP DA DC =⇒=+,设DP xDM yDN =+,则1x y +=,又DP mxDA ynDC =+,所以3232,15555mx ny m n==⇒+=,因此321941942423(23)()(12)(122)55555n m n m m n m n m n m n m n +=++=++≥+⋅=,当且仅当23m n =时取等号,选C.考点:向量表示,基本不等式求最值【易错点睛】在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.12.若函数144)(234+-++=x ax x x x f 的图象恒在x 轴上方,则实数a 的取值范围是( )A .)(2,+∞B .)(1,+∞C .),213(+∞-D .),212(+∞- 【答案】A二、填空题(每题4分,满分20分,将答案填在答题纸上)13.若向量)0,1(=a ,)1,2(=b ,)1,(x c =满足条件b a -3与c 垂直,则=x . 【答案】1 【解析】试题分析:(3)0(1,1)(,1)01a b c x x -⋅=⇒-⋅=⇒= 考点:向量垂直【方法点睛】平面向量数量积的类型及求法(1)求平面向量数量积有三种方法:一是夹角公式a ·b =|a ||b |cos θ;二是坐标公式a ·b =x 1x 2+y 1y 2;三是利用数量积的几何意义.(2)求较复杂的平面向量数量积的运算时,可先利用平面向量数量积的运算律或相关公式进行化简. 14.在公差不为0的等差数列}{n a 中,831=+a a ,且4a 为2a 和9a 的等比中项,则=5a . 【答案】13考点:等差数列 15.函数x x a x f ln )(=的图象在点))(,(22e f e 处的切线与直线x ey 41-=平行,则)(x f 的极值点是 . 【答案】e 【解析】 试题分析:2(1ln )()a x f x x -'=,所以244(12)1()1a f e a e e -'==-⇒=,因此)(x f 的极值点是1ln 0,x x e -== 考点:导数几何意义,函数极值【思路点睛】(1)求曲线的切线要注意“过点P 的切线”与“在点P 处的切线”的差异,过点P 的切线中,点P 不一定是切点,点P 也不一定在已知曲线上,而在点P 处的切线,必以点P 为切点.(2)利用导数的几何意义解题,主要是利用导数、切点坐标、切线斜率之间的关系来进行转化.以平行、垂直直线斜率间的关系为载体求参数的值,则要求掌握平行、垂直与斜率之间的关系,进而和导数联系起来求解.16.)(x f 是定义在R 上的偶函数,且0≥x 时,3)(x x f =.若对任意的]32,12[+-∈t t x ,不等式)(8)3(x f t x f ≥-恒成立,则实数t 的取值范围是 .【答案】3-≤t 或1≥t 或0t = 【解析】试题分析:由题意得0x <时,3()()f x f x x =-=-,即3()||f x x =,因此33(3)8()|3|8|||3|2||f x t f x x t x x t x -≥⇒-≥⇒-≥,当0t =时,x R ∈,满足条件;当0t >时,5tx t x ≥≤-或,要满足条件,需2123150t t t t t t ⎧-≥+≤-⎪⇒≥⎨⎪>⎩或;当0t <时,5tx x t ≥-≤或,要满足条件,需2123350t t t tt t ⎧-≥-+≤⎪⇒≤-⎨⎪<⎩或;综上实数t 的取值范围是3-≤t 或1≥t 或0t = 考点:不等式恒成立【思路点睛】求参数取值范围常用的方法和思路(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决;(3)数形结合法:先对解析式变形,在同一平面直角坐标系中,画出函数的图象,然后数形结合求解.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知函数)2||,0,0)(sin()(πϕωϕω<>>+=A x A x f 的图象(部分)如图所示.(1)求函数)(x f 的解析式; (2)若),(30πα∈,且34)(=παf ,求αcos .【答案】(1))6sin(2)(ππ+=x x f (2)6215+考点:求三角函数解析式,给值求值【方法点睛】已知函数sin()(A 0,0)y A x B ωϕω=++>>的图象求解析式(1)max min max min,22y y y y A B -+==. (2)由函数的周期T 求2,.T πωω=(3)利用“五点法”中相对应的特殊点求ϕ.18.设数列}{n a 的前n 项和为n S ,已知)(12*N n a S n n ∈-=.(1)求数列}{n a 的通项公式;(2)若对任意的*N n ∈,不等式92)1(-≥+n S k n 恒成立,求实数k 的取值范围. 【答案】(1)12-=n n a (2))643[∞+, 【解析】试题分析:(1)由和项求通项,要注意分类讨论:当1n =时,11a S =;当1n =时,11a S =解得11=a ;当2n ≥时,1n n n a S S -=-化简得12-=n n a a ;最后根据等比数列定义判断数列}{n a 为等比数列,并求出等比数列通项(2)先化简不等式,并变量分离得k ≥nn 292-,而不等式恒成立问题一般转化为对应函数最值问题,即k ≥nn 292-的最大值,而对数列最值问题,一般先利用相邻两项关系确定其增减性:令n nn b 292-=,则1112211292272+++-=---=-n nn n n nn n b b ,所以数列先增后减,最后根据增减性得最值取法:n b 的最大值是6436=b .试题解析:(1)令111121a a S n =-==,,解得11=a .……………………………2分 由12-=n n a S ,有1211-=--n n a S ,两式相减得122--=n n n a a a ,化简得12-=n n a a (n ≥2), ∴ 数列}{n a 是以首项为1,公比为2 的等比数列,∴ 数列}{n a 的通项公式12-=n n a .……………………………………………6分考点:由和项求通项,根据数列单调性求最值【方法点睛】给出S n 与a n 的递推关系求a n ,常用思路是:一是利用S n -S n -1=a n (n ≥2)转化为a n 的递推关系,再求其通项公式;二是转化为S n 的递推关系,先求出S n 与n 之间的关系,再求a n . 应用关系式a n =⎩⎪⎨⎪⎧S 1,n =1,S n -S n -1,n ≥2时,一定要注意分n =1,n ≥2两种情况,在求出结果后,看看这两种情况能否整合在一起. 19.在ABC ∆中,角C B A ,,所对的边分别为c b a ,,,已知12=c ,64=b ,O 为ABC ∆的外接圆圆心. (1)若54cos =A ,求ABC ∆的面积S ; (2)若点D 为BC 边上的任意一点,1134DO DA AB AC -=+,求B sin 的值. 【答案】(11442(2)552sin =B 【解析】考点:向量投影,正弦定理【思路点睛】三角函数和平面向量是高中数学的两个重要分支,内容繁杂,且平面向量与三角函数交汇点较多,向量的平行、垂直、夹角、数量积等知识都可以与三角函数进行交汇.不论是哪类向量知识与三角函数的交汇试题,都会出现交汇问题中的难点,对于此类问题的解决方法就是利用向量的知识将条件转化为三角函数中的“数量关系”,再利用三角函数的相关知识进行求解.20.已知函数x x x x f cos sin )(+=.(1)判断在)(x f 区间)3,2(上的零点个数,并证明你的结论;(参考数据:4.12≈,4.26≈)(2)若存在)2,4(ππ∈x ,使得x kx x f cos )(2+>成立,求实数k 的取值范围.【答案】(1)有且只有1个零点(2)π22<k (2)由题意等价于x x x cos sin +x kx cos 2+>,整理得x x k sin <.…………7分 令x x x h sin )(=,则2sin cos )(xx x x x h -=', 令x x x x g sin cos )(-=,0sin )(<-='x x x g ,∴g(x)在)24(ππ,∈x 上单调递减, …………………………………………9分 ∴0)14(22)4()(<-⨯=<ππg x g ,即0sin cos )(<-=x x x x g , ∴0sin cos )(2<-='xx x x x h ,即x x x h sin )(=在)24(ππ,上单调递减, ……11分 ∴ππππ2242244sin)(==<x h ,即π22<k . ………12分 考点:函数零点,利用导数研究不等式有解【方法点睛】利用函数零点的情况求参数值或取值范围的方法(1)利用零点存在的判定定理构建不等式求解.(2)分离参数后转化为函数的值域(最值)问题求解.(3)转化为两熟悉的函数图象的上、下关系问题,从而构建不等式求解.21.已知函数1ln )(2-+=ax x x f ,e e x g x-=)(.(1)讨论)(x f 的单调区间;(2)若1=a ,且对于任意的),1(+∞∈x ,)()(x f x mg >恒成立,求实数m 的取值范围. 【答案】(1)a ≥0时,)(x f 的单调递增区间是)0(∞+,; 0<a 时,)(x f 的单调递增区间是)210(a-,;单调递减区间是)21(∞+-,a.(2)m ≥e 3.②当em 30<<时,令x x q x me x p x 2)(1)(=-=,. 显然x me x p x 1)(-=在)1[∞+,上单调递增,∴2131)1()(min =-⨯<-==e e me p x p . 由x x q 2)(=在)1[∞+,单调递增,于是2)(min =x q .∴min min )()(x q x p <. 于是函数xme x p x 1)(-=的图象与函数x x q 2)(=的图象只可能有两种情况: 若)(x p 的图象恒在)(x q 的图象的下方,此时)()(x q x p <,即0)(<'x h ,故)(x h 在)1(∞+,单调递减,又0)1(=h ,故0)(<x h ,不满足条件. 若)(x p 的图象与)(x q 的图象在x>1某点处的相交,设第一个交点横坐标为x0,当)1(0x x ,∈时,)()(x q x p <,即0)(<'x h ,故)(x h 在)1(0x ,单调递减,又0)1(=h ,故当)1(0x x ,∈时,0)(<x h .∴)(x h 不可能恒大于0,不满足条件.……9分③当m ≥e 3时,令x x me x x 21)(--=ϕ,则21)(2-+='xme x x ϕ. ∵x ∈)1(∞+,,∴21)(2-+='xme x x ϕ>2-x me ≥0123>=-⋅e e , 故x xme x x 21)(--=ϕ在x ∈)1(∞+,上单调递增, 于是033211)1()(=-⨯>--=>e e me x ϕϕ,即0)(>'x h , ∴)(x h 在)1(∞+,上单调递增,∴0)1()(=>h x h 成立. 综上,实数m 的取值范围为m ≥e3.………………………………………12分考点:利用导数求函数单调区间,利用导数求参数取值范围【方法点睛】利用导数解决不等式恒成立问题的“两种”常用方法(1)分离参数法:将原不等式分离参数,转化为不含参数的函数的最值问题,利用导数求该函数的最值,根据要求得所求范围.一般地,f(x)≥a 恒成立,只需f(x)min ≥a 即可;f(x)≤a 恒成立,只需f(x)max ≤a 即可.(2)函数思想法:将不等式转化为某含待求参数的函数的最值问题,利用导数求该函数的极值(最值),然后构建不等式求解.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4-4:坐标系与参数方程以直角坐标系的原点O 为极点,x 轴非负半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为θθρcos 4sin 2=.(1)求曲线C 的直角坐标方程;(2)若直线l 的参数方程为⎪⎪⎩⎪⎪⎨⎧+=+=t y t x 511521(t 为参数),设点)1,1(P ,直线l 与曲线C 相交于B A ,两点,求||||PB PA +的值.【答案】(1)24y x =(2)415∴1544)(2122121=-+=-=+t t t t t t PB PA .……………………………10分考点:极坐标方程化为直角坐标方程,直线参数方程几何意义23.(本小题满分10分)选修4-5:不等式选讲已知函数)(|1||1|)(R a a x x x f ∈+--+=.(1)若1=a ,求不等式0)(≥x f 的解集;(2)若方程()f x x =有三个实数根,求实数a 的取值范围.【答案】(1))21[∞+-,(2)11a -<< (2)由方程x x f =)(可变形为11+--+=x x x a .令⎪⎩⎪⎨⎧>-≤≤---<+=+--+=,,,,,,12111211)(x x x x x x x x x x h 作出图象如右. ………………………8分于是由题意可得11a -<<.…………10分考点:绝对值定义【名师点睛】含绝对值不等式的解法有两个基本方法,一是运用零点分区间讨论,二是利用绝对值的几何意义求解.法一是运用分类讨论思想,法二是运用数形结合思想,将绝对值不等式与函数以及不等式恒成立交汇、渗透,解题时强化函数、数形结合与转化化归思想方法的灵活应用,这是命题的新动向.。
