武汉理工大学2004年数学分析

合集下载

武汉理工大学-历年真题清单

武汉理工大学研招办经济学院西方经济学（含微观、宏观经济学）2007——2009经济学（含微观、宏观经济学）1997——2000，2002——2006（2002——2004，2006有答案）宏观经济学2004——2006（2004有答案）货币银行学2004——2007（2004有答案）国际贸易概论1998——2000，2002——2009（2002——2004有答案）国际金融学2002，2004——2009（2002，2004有答案）国际市场营销2002财政学2007产业经济学2002，2006——2009（2002有答案）电子商务概论2008——2009运输经济学2002——2009区域经济学2007人力资源管理2007管理学概论2004——2007（2004有答案）管理学原理1997——2000，2002——2009（2002——2004有答案）微机原理及应用1997——2000，2002——2007概率论与数理统计2001——2009复试科目：国际贸易学2003加试科目：国际金融学2003；国际市场营销学2003复试科目：产业经济学2003复试科目：数量经济学专业复试2003文法学院伦理学基础综合2007——2009伦理学原理2007——2009伦理学2002——2005民法学2007民商法学2008——2009民商法学综合2007——2009经济法学2002，2004——2009经济法综合2007——2009法学综合2002——2006知识产权2007知识产权法2002——2005法理学与知识产权法2004——2005社会心理学2002心理学2002思想政治教育学原理与方法2002——2009中国化的马克思主义2007——2009马克思主义基本原理及其发展2007——2009马克思主义基本原理2007马克思主义哲学原理2002——2009新闻传播专业综合考试（含广告学、编辑出版学）2004——2005出版发行综合2006——2009广告学综合2006——2009传播学原理2004——2009专业综合（教育学、运动训练学）2007体育教育综合（运动生理学、运动训练学）2008——2009运动生理学2007复试科目：综合复试2003；复试（科技法方向）2003加试科目：专业加试2003；加试（科技法方向）2003高等教育研究所教育学2002——2006，2008——2009教育管理学2002——2006，2008——2009复试科目：综合复试2003加试科目：教育学2003；教育心理学2003外国语学院二外日语2002——2009二外法语2002——2009二外德语2002——2009二外俄语2003——2009基础英语2001——2009（注：其中2002，2003，2005年的试卷名称为“综合英语”）英语语言学2001——2003，2006——2009（2001有答案）语言学及英美文学2004——2005英美文学2007——2009英语写作2002复试科目：外国语言学及应用语言学专业复试2003艺术与设计学院设计艺术学专业综合（含设计艺术史论、工业设计及其理论、环境艺术设计及其理论、视觉传播艺术设计、动画艺术设计及其理论、数字艺术设计及其理论）2008——2009美术学专业综合2008——2009艺术学专业综合2008——2009设计艺术学专业史论2003——2006，2008——2009 美术学专业史论2008——2009艺术学专业史论2008——2009音乐艺术研究专业综合（报考艺术管理方向）2009 视觉传播艺术设计基础2007速写与焦墨山水画2005速写与花卉白描2005——2006速写与人物写生画2005——2006速写与色彩人物写生2005，2007速写与泥塑人物写生2007速写与素描人物写生2005速写与水彩或水粉画创作2005速写与装饰画创作2005——2006中外美术史2002，2005，2007中国美术史专题2006中国画创作基础2007艺术美术专业基础2007美术史论2005——2007美术理论2004艺术学概论2007艺术设计史基础2004——2005，2007艺术史论基础2007艺术设计史论基础2003，2006艺术设计理论2002艺术设计史2002专业史论2007艺术设计学“专业设计基础”2002专业设计2002信息设计基础2004——2005动画创作基础2004——2006艺术管理专业基础2004——2005，2007艺术教育专业基础2007民艺专业基础2004 ——2005民间美术2007民间艺术设计及其原理2006设计基础理论与设计基础表达2002环境艺术设计基础2006——2007环境艺术设计与公共艺术创作专业基础2002动画与数字化设计艺术基础2007动画设计与数码设计基础2002系统设计及传播艺术基础2002系统设计及传播艺术理论2002工业设计理论2002工业设计基础2004——2007数码设计理论2002数码艺术设计基础2003中外建筑史2002动画创作理论2002动画创作基础2003环境艺术设计2002环境艺术设计基础2004——2005公共艺术创作与设计2002公共艺术设计基础2006卡通画创作2002专业设计（计算机艺术设计）2002专业设计（系统设计及传播艺术设计）2002环境艺术设计专业方向（环境艺术设计基础）2003设计艺术学专业工业设计方向设计基础2003平面设计基础2003——2005平面艺术设计基础2006现代美术与公共艺术设计基础2003设计管理2006设计基础（展示设计及理论方向）2006信息设计基础2006影视艺术设计基础2006音乐艺术研究2007复试科目：艺术与设计学院复试2003加试科目：艺术与设计学院加试2003理工学院材料力学1997——2000，2002——2009弹性力学2002——2004，2007理论力学2002——2009工程力学2004微机原理及应用1997——2000，2002——2007微机原理（即：微型计算机原理）1997——2000，2002——2004 岩石力学1997——2000，2002岩体力学2003——2007（注：2003年有两种）结构力学2002——2009量子力学2004——2009物理光学2002，2004——2009电磁场与电磁波2004电磁场理论2005——2009概率论与数理统计2001——2009数值分析2002，2004——2007高等代数2001——2009数学分析2002——2009常微分方程2002——2007线性代数2002普通物理2002——2009运筹学2002——2008（注：2002年试卷有两种）物理化学2002——2009有机化学2002——2007无机化学2002——2009化学原理2008——2009基础无机化学2007物理化学原理2007高等数学2007，2009高等数学（工）2002——2006，2008高等数学（二）2004高等数学（文）2003——2005复试科目：应用化学专业复试2003复试科目：应用数学专业复试2003复试科目：固体力学专业复试2003资源与环境工程学院物理化学2002——2009材料力学1997——2000，2002——2009岩石力学1997——2000，2002岩体力学2003——2007（注：2003年有两种）岩石力学与工程2004——2009矿山岩石力学2002无机化学2002——2009浮选2002固体废物处理工程2002水污染控制工程2002大气污染控制工程2002化工基础2002——2007化工原理2002——2009（注：2002年称“环境化工原理”）采矿学2002安全工程学2007——2009爆破工程2002——2009（注：2003年称“凿岩爆破”）流体力学2002——2004胶体化学2003——2009结晶矿物学2003——2006环境学概论2004——2009环境化学2004——2007环境流体力学2002，2005——2007环境工程微生物学2005——2006环境生物学2005——2007矿物加工工程专业复试科目：综合复试2003采矿工程专业复试科目：专业复试2003环境工程专业复试科目：环境工程专业复试2003；加试科目：环境工程专业加试2003材料科学与工程学院材料科学基础2002——2009普通物理2002——2009材料力学1997——2000，2002——2009医学综合一（含生物化学、无机化学）2008——2009医学综合二（含生物化学、高分子化学）2008医学综合三（含生物化学、组织学）2008——2009医学综合2002，2004细胞生物学2002——2007组织学2002——2007物理光学2002，2004——2009计算机在材料科学中的应用2007计算机在材料中的应用2004——2005工程材料2002——2007生物化学2002——2007物理化学2002——2009有机化学2002——2007无机化学2002——2009陶瓷工艺原理2002玻璃工艺原理2002复合材料工艺2002铸造合金及其熔炼2002塑性成型原理2002材料成型原理2003——2009焊接冶金2002金属热处理2002金属材料学2007固体物理2002——2009聚合物加工原理与工艺2002胶凝材料学2002无机非金属材料工学2002，2004——2009金属学及热处理2002硅酸盐物理化学2002高分子化学及物理2002高分子化学2003——2009金属学原理2002——2007材料物理与化学专业复试科目：综合复试2003；加试科目：物理化学2003；材料学院同等学历加试2003材料学专业复试科目：综合复试2003；加试科目：物理化学2003；材料学院同等学历加试2003材料加工工程专业复试科目：综合复试2003；加试科目：物理化学2003；材料学院同等学历加试2003生物医学工程专业复试科目：生物医学工程专业复试2003；加试科目：生物化学2003；组织学2003机电工程学院材料力学1997——2000，2002——2009机械原理1997——2000，2002——2009机械设计1997——2000，2002——2009控制工程基础2002——2009统计质量管理2005——2009传感器原理2003——2009传感检测技术2002——2003传感技术1997——2000传感与检测技术2002电子技术基础2002——2009微机原理及应用1997——2000，2002——2007人机工程学2002——2006机电工程学院2003年同等学历考研加试题（测试技术）机电工程学院2003年同等学历考研加试题（机械原理）机电工程学院2003年同等学力考研加试题（机械设计）机电工程学院2003级硕士研究生复试试题汽车工程学院材料力学1997——2000，2002——2009理论力学2002——2009汽车理论基础2002——2009发动机原理2002——2009摩托车理论与结构设计2002汽车运用工程2002——2009汽车运输工程2002——2003工程热力学2002——2008汽车运输学2003——2005，2007交通运输学2006汽车营销与策划2009汽车市场学2004——2008动力机械及工程专业复试科目：动力机械及工程复试2003；加试科目：发动机构造2003；发动机原理2003车辆工程专业复试科目：综合复试2003；加试科目：汽车构造2003；汽车理论2003载运工具运用工程专业复试科目：综合复试2003自动化学院电路1997——2000，2002——2009电工技术基础2002电工原理2003——2006控制理论基础2002自动控制原理1997——2000，2002——2009信号处理技术2002——2005（注：2002——2003年称“信号分析与处理”）传感技术1997——2000传感与检测技术2002传感检测技术2002——2003传感器原理2003——2009电机及拖动基础2001电力电子技术（一）2007电力电子技术2002——2006，2008——2009微机原理及接口技术2002——2009数字电路2003——2009逻辑设计2004——2006电力电子与电力传动专业复试科目：电力电子与电力传动专业复试2003检测技术与自动化装置专业复试科目：检测技术与自动化装置专业复试2003 控制理论与控制工程专业复试科目：控制理论与控制工程专业复试2003；加试科目：自动控制原理2003；微机原理及接口技术2003计算机科学与技术学院数据结构1997——2000，2002——2008操作系统1998——2000，2002——2008计算机组成原理2002——2007微机原理及应用1997——2000，2002——2007C语言2007微机原理（即：微型计算机原理）1997——2000，2002——2004离散数学2002——2006计算机网络1999——2000，2002软件工程2002——2006数据库原理2002编译原理2002计算机原理2002计算方法2003——2005复试科目：计算机应用技术、计算机软件与理论专业2003加试科目：微机原理及应用2003；数据库应用2003信息工程学院数据结构1997——2000，2002——2008信号与系统1999——2000，2002——2009信号与线性系统2002——2006物理光学2002，2004——2008光纤光学2007现代光学2006高频电路2002微机原理及应用1997——2000，2002——2007微机原理（即：微型计算机原理）1997——2000，2002——2004 脉冲与数字电路1999——2000，2002电子技术基础2002——2009高频电子线路1999——2000，2002微机原理及其通信接口2003——2009信号分析与处理2002——2008传感技术1997——2000电路1997——2000，2002——2009数字信号处理1999——2000，2002，2009土木工程与建筑学院材料力学1997——2000，2002——2009传热学2002——2007中外建筑史2002——2009建筑历史2004——2007建筑设计2002——2004，2008——2009建筑设计（1）2005——2007建筑设计（2）2005——2007规划设计2007——2008城市规划原理2003——2009建筑结构抗震设计2007抗震结构设计2004结构力学2002——2009工程项目管理2008——2009建筑施工与工程项目管理2003——2007建筑施工技术2002建筑工程经济与企业管理2002工程热力学2002——2009土质学与土力学2002——2007水分析化学2002——2005水分析与物理化学2006——2007水力学与水泵2002——2007水力学与水分析化学2008——2009土力学2002——2009建筑构造2002岩石力学1997——2000，2002岩体力学2003——2007（注：其中2003年有两种）钢筋混凝土结构2002，2006——2009混凝土结构原理2003钢筋砼结构2005土力学与基础工程2002结构动力学2002结构设计原理2002（第1种），2002（第2种），2005——2007桥梁工程2002给水工程2002排水工程2002路基路面工程2002，2005——2007工程地质学2004——2006美学2004建筑设计及其理论专业复试科目：建筑设计2003；建筑设计知识2003；加试科目：中外建筑史2003结构工程专业复试科目：结构工程2003；综合复试（建筑工程施工技术、建设工程项目管理方向）2003；加试科目：施工组织学2003；建筑经济与企业管理2003；结构力学2003；混凝土结构2003桥梁与隧道工程专业复试科目：桥梁与隧道工程专业复试2003；加试科目：桥梁与隧道工程专业加试Ⅰ2003；桥梁与隧道工程专业加试Ⅱ2003岩土工程专业复试科目：综合复试2003市政工程专业复试科目：专业复试2003交通学院高等数学2007，2009高等数学（工）2002——2006，2008高等数学（二）2004交通运输装备2005——2007桥梁设计与施工2005，2007第三方物流理论与实践2007现代物流与运输2005——2006物流学2006现代物流学2002，2007——2009运输经济学2002——2009路基路面工程2002，2005——2007工程热力学2002——2009结构分析2008——2009理论力学2002——2009土质学与土力学2002——2006材料力学1997——2000，2002——2009施工组织及概预算2004土工原理与计算2008——2009公路工程施工组织及概预算2003信号与系统1999——2000，2002——2009微机原理及应用1997——2000，2002——2007运筹学2002——2009（注：2002年试卷有两种）船舶结构力学2002，2004——2009船舶原理2002——2009船舶设计原理2002——2009流体力学2002——2004，2006——2008环境学导论2002国际航运经济与政策2002——2004计算机辅助船体建造2002船舶技术经济学2002传热学2002——2007国际集装箱运输与多式联运2002——2004港口管理（运输企业管理学）2002——2005港口企业管理学2007运输企业管理学2006道路勘测设计2002船舶强度与结构设计2002——2007环境质量评价2002交通环境工程地质与应用2002声学基础2002，2006航运管理2002——2006（注：2002年有两种）结构设计原理2002（第1种），2002（第2种），2005——2007计算机辅助船舶设计2002船舶营运管理2007船舶建造工艺学2003——2007船机制造工艺学2002结构力学计算2008——2009结构力学与结构电算2003——2007运动生物力学2004划船运动概论2004船体振动学2006液压原理与控制2002机械制造工艺学2002流体力学专业复试科目：流体力学2003；加试科目：流体力学2003，工程热力学和传热学、水力学2003工程力学专业复试科目：理论力学2003道路与铁道工程专业复试科目：道路与铁道工程2003，桥梁工程2003；加试科目：土力学2003交通运输规划与管理专业复试科目：综合复试2003；加试科目：交通运输设备概论2003船舶与海洋结构物设计制造专业复试科目：综合复试2003；加试科目：船舶与海洋工程学2003结构工程专业复试科目：结构综合2003；加试科目：钢结构2003航运学院船舶管理2002——2009航运管理2002——2006（注：2002年有两种）航海学2002船舶操纵与避碰2002——2006航海气象学与海洋学2004，2006——2007（注：2007年试卷共3页，缺第2页）物理海洋数字计算2008信号与系统1999——2000，2002——2009能源与动力学院电力电子技术2008——2009电力电子技术（二）2006——2007测试技术2007A卷，2007B卷工程热力学与传热学2006——2009机械振动学2006热能与动力机械制造工艺学2006——2007轮机自动化2007——2009智能运输系统概论2006——2009专业综合（含工程热力学、传热学、内燃机原理）2005专业综合（含工程热力学、传热学、机械设计）2005专业综合（含自动控制理论、测试技术、计算机技术）2005专业综合（含自动控制理论、电工电子技术、计算机控制技术）2005专业综合（含机械设计、测试技术、自动控制理论）2005工程热力学2002——2009机械设计1997——2000，2002——2009船舶柴油机2009内燃机原理2007A卷，2007B卷内燃机原理2002——2004，2006传热学2002——2007自动控制理论2003——2004，2006——2007自动控制原理1997——2000，2002——2009动力机械制造与维修2009船舶动力装置原理与设计2002船舶建造工艺学2003——2007船机制造工艺学2002船舶机械制造与修理2003——2004船舶管理2002——2009机械制造工艺学2002轮机工程专业复试科目：轮机工程2003；加试科目：内燃机学2003；轮机概论2003；工程热力学和传热学2003载运工具运用工程专业复试科目：载运工具运用工程2003管理学院管理学原理1997——2000，2002——2009（2002——2004有答案）管理经济学基础2005——2007管理信息系统2002——2007（2002——2004部分有答案）概率论与数理统计2001——2009线性代数2002线性代数与概率统计2003——2009会计学原理1997——2000，2002——2009（2002——2004有答案）（注：1998年共3页，缺P3）技术经济学2002——2009（2002——2004部分有答案）运筹学2002——2009（注：2002年试卷有两种）现代工业管理2003——2004（2003——2004部分有答案）公司理财原理2002——2009（2002——2004有答案）（注：2002年称“财务管理学”，2003——2004称“公司财务管理”）项目管理2005——2007企业管理学2002（2002有答案）生产管理学2002（2002部分有答案）市场营销学2001(2001有答案)技术创新管理2003（2003部分有答案）工商管理硕士（MBA）专业复试科目：MBA专业综合课2003；加试科目：市场学2003；投资学2003会计学专业复试科目：财务会计与管理会计2003；加试科目：财务管理2003；会计学2003管理科学与工程专业复试科目：企业管理概论2003；加试科目：管理经济学2003；企业管理学2003技术经济及管理专业复试科目：投资分析2003；加试科目：产业经济学2003；投资学2003企业管理专业复试科目：市场营销与生产管理2003；加试科目：市场学2003；管理学原理2003系统工程专业复试科目：系统工程概论与线性规划2003；加试科目：概率统计2003；线性代数2003政治与行政学院邓小平理论和“三个代表”重要思想2007——2009邓小平理论2002——2006马克思主义哲学原理2002——2009政治学原理2007——2009西方哲学史2007——2009西方政治思想史2008——2009中外政治思想2007高等数学（文）2003——2004思想政治教育理论与方法2002——2005，2007科学技术史2002——2007中共党史2002——2009自然辩证法2002——2009中国近代史2002科学技术哲学专业复试科目：综合复试2003；加试科目：马克思主义哲学原理2003；现代科技导论2003中共党史专业复试科目：综合复试2003；加试科目：政治学原理2003；中国近代史2003物流工程学院机械设计基础2005——2009机械工程基础2004机械CAD基础2006起重运输机械2005——2009起重机械2002物流信息技术2005——2009物流学2006现代物流学2002，2007管理学基础2005——2009画法几何2002——2003，2005——2007材料力学1997——2000，2002——2009理论力学2002——2009机械原理1997——2000，2002——2009机械设计1997——2000，2002——2009电子技术基础2002——2009微机原理及应用1997——2000，2002——2007工程材料2002——2007工程力学2004运筹学2002——2009（注：2002年试卷有两种）运筹学与系统工程2004计算机应用基础与计算机技术基础2004仓储技术与设备2006——2007自动识别技术2007CAD/CAM技术2002液压原理与控制2002机械制造工艺学2002机电一体化技术2002液压技术2002机械制造及自动化专业复试科目：机械制造及自动化专业复试2003；面试科目：机械制造专业2003机械电子工程专业复试科目：机械电子工程专业复试2003；面试科目：机械一体化技术（机电专业）2003机械设计及理论专业复试科目：机械设计及理论专业复试2003化学工程学院制药化学2005——2009化工原理2005——2009药物分析2005——2007物理化学2006——2007。

2004年高考湖北卷理科数学试题及答案

2004年普通高等学校招生湖北卷理工类数学试题一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的. 1．与直线042=+-y x 的平行的抛物线2x y =的切线方程是（） A ．032=+-y x B ．032=--y xC ．012=+-y xD ．012=--y x2．复数ii 31)31(2++-的值是（）A ．－16B ．16C ．41-D ．i 4341- 3．已知)(,11)11(22x f xx x x f 则+-=+-的解析式可取为（） A ．21xx+ B ．212xx+-C ．212xx+ D ．21xx+-4．已知,,为非零的平面向量. 甲：则乙,:,=⋅=⋅（） A ．甲是乙的充分条件但不是必要条件 B ．甲是乙的必要条件但不是充分条件 C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件5．若011<③b a <；④2>+baa b 中，正确的不等式有（）A ．1个B ．2个C ．3个D ．4个6．已知椭圆191622=+y x 的左、右焦点分别为F 1、F 2，点P 在椭圆上，若P 、F 1、F 2是一个直角三角形的三个顶点，则点P 到x 轴的距离为（）A ．59 B ．3 C ．779 D ．49 7．函数]1,0[)1(log )(2在++=x a x f a 上的最大值和最小值之和为a ，则a 的值为（）A ．41 B ．21 C ．2D ．48．已知数列{n a }的前n 项和),,2,1]()21)(1(2[])21(2[11=+---=--n n b a S n n n 其中a 、b 是非零常数，则存在数列{n x }、{n y }使得（） A ．}{,n n n n x y x a 其中+=为等差数列，{n y }为等比数列 B ．}{,n n n n x y x a 其中+=和{n y }都为等差数列C ．}{,n n n n x y x a 其中⋅=为等差数列，{n y }都为等比数列D ．}{,n n n n x y x a 其中⋅=和{n y }都为等比数列9．函数1)(2++=x ax x f 有极值的充要条件是（）A ．0>aB ．0≥aC ．0<aD ．0≤a10．设集合044|{},01|{2<-+∈=<<-=mx mx R m Q m m P 对任意实数x 恒成立}，则下列关系中成立的是（） A ．P Q B ．Q PC ．P=QD ．P Q=11．已知平面βα与所成的二面角为80°，P 为α、β外一定点，过点P 的一条直线与α、β所成的角都是30°，则这样的直线有且仅有（）A ．1条B ．2条C ．3条D ．4条12．设)(t f y =是某港口水的深度y （米）关于时间t （时）的函数，其中240≤≤t .经长期观察，函数)(t f y =的图象可以近似地看成函数)sin(ϕω++=t A k y 的图象.下面的函数中，最能近似表示表中数据间对应关系的函数是（）A ．]24,0[,6sin 312∈+=t t y πB ．]24,0[),6sin(312∈++=t t y ππC ．]24,0[,12sin312∈+=t t y πD ．]24,0[),212sin(312t t y ππ++=二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上.13．设随机变量ξ的概率分布为====a k a ak P k则为常数,,2,1,,5)( ξ . 14．将标号为1，2，…，10的10个球放入标号为1，2，…，10的10个盒子内，每个盒内放一个球，则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有( )种.（以数字作答）15．设A 、B 为两个集合，下列四个命题： zz ①A B ⇔对任意B x A x ∉∈有, ②A B ⇔=B A③A B ⇔A⊇B④A B ⇔存在B x A x ∉∈使得,其中真命题的序号是 .（把符合要求的命题序号都填上） 16．某日中午12时整，甲船自A 处以16km/h 的速度向正东行驶，乙船自A 的正北18km处以24km/h 的速度向正南行驶，则当日12时30分时两船之间距间对时间的变化率是 km/h.三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）已知)32sin(],,2[,0cos 2cos sin sin 622παππααααα+∈=-+求的值.18．（本小题满分12分）如图，在棱长为1的正方体ABCD —A 1B 1C 1D 1中，点E 是棱BC 的中点，点F 是棱 CD 上的动点.（I ）试确定点F 的位置，使得D 1E ⊥平面AB 1F ；（II ）当D 1E ⊥平面AB 1F 时，求二面角C 1—EF —A 的大小（结果用反三角函数值表示）.AC A 1C 119．（本小题满分12分）如图，在Rt △ABC 中，已知BC=a ，若长为2a 的线段PQ 以点A 为中点，问与的夹角θ取何值时CQ BP ⋅的值最大？并求出这个最大值.A BC20．（本小题满分12分）直线12:1:22=-+=y x C kx y l 与双曲线的右支交于不同的两点A 、B.（I ）求实数k 的取值范围；（II ）是否存在实数k ，使得以线段AB 为直径的圆经过双曲线C 的右焦点F ？若存在，求出k 的值；若不存在，说明理由.21．（本小题满分12分）某突发事件，在不采取任何预防措施的情况下发生的概率为0.3，一旦发生，将造成 400万元的损失. 现有甲、乙两种相互独立的预防措施可供采用. 单独采用甲、乙预防措施所需的费用分别为45万元和30万元，采用相应预防措施后此突发事件不发生的概率为0.9和0.85. 若预防方案允许甲、乙两种预防措施单独采用、联合采用或不采用，请确定预防方案使总费用最少. （总费用．．．=采取预防措施的费用+发生突发事件损失的期望值.） 22．（本小题满分14分）已知.,2,1,1,}{,011 =+==>+n a a a a a a a nn n 满足数列（I ）已知数列}{n a 极限存在且大于零，求n n a A ∞→=lim （将A 用a 表示）；（II ）设;)(:,,2,1,1A b A b b n A a b n nn n n +-==-=+证明（III ）若 ,2,121||=≤n b n n 对都成立，求a 的取值范围.2004年普通高等学校招生湖北卷理工类数学试题参考答案一、选择题1．D 2．A 3．C 4．B 5．B 6．D 7．B 8．C 9．B 10．A 11．D 12．A 二、填空题13．4 14．240 15．（4） 16．－1.6 三、解答题17．本小题考三角函数的基本公式以及三角函数式的恒等变形等基础知识和基本运算技能，满分12分. 解法一：由已知得：0)cos sin 2)(cos 2sin 3(=-+αααα 0cos sin 20cos 2sin 3=-=+⇔αααα或由已知条件可知).,2(,2,0cos ππαπαα∈≠≠即所以 .32tan ,0tan -=∴<αα于是3sin2cos 3cos2sin )32sin(παπαπα+=+.tan 1tan 123tan 1tan sin cos sin cos 23sin cos cos sin )sin (cos 23cos sin 22222222222αααααααααααααααα+-⨯++=+-⨯++=-+= 代入上式得将32tan -=α..3265136)32(1)32(123)32(1)32()32sin(222即为所求+-=-+--⨯+-+--=+πα解法二：由已知条件可知所以原式可化为则,2,0cos παα≠≠AC A 1C 1..32tan .0tan ),,2(.0)1tan 2)(2tan 3(.02tan tan 62下同解法一又即-=∴<∴∈=-+=-+ααππααααα18．本小题主要考查线面关系和正方体等基础知识，考查空间想象能力和推理运算能力，满分12分. 解法一：（I ）连结A 1B ，则A 1B 是D 1E 在面ABB 1A ；内的射影∵AB 1⊥A 1B ，∴D 1E ⊥AB 1，于是D 1E ⊥平面AB 1F ⇔D 1E ⊥AF. 连结DE ，则DE 是D 1E 在底面ABCD 内的射影.∴D 1E ⊥AF ⇔DE ⊥AF.∵ABCD 是正方形，E 是BC 的中点. ∴当且仅当F 是CD 的中点时，DE ⊥AF ，即当点F 是CD 的中点时，D 1E ⊥平面AB 1F.…………6分（II ）当D 1E ⊥平面AB 1F 时，由（I ）知点F 是CD 的中点. 又已知点E 是BC 的中点，连结EF ，则EF ∥BD. 连结AC ，设AC 与EF 交于点H ，则CH ⊥EF ，连结C 1H ，则CH 是 C 1H 在底面ABCD 内的射影. C 1H ⊥EF ，即∠C 1HC 是二面角C 1—EF —C 的平面角.在Rt △C 1CH 中，∵C 1C=1，CH=41AC=42， ∴tan ∠C 1HC=224211==CH C C . ∴∠C 1HC=arctan 22，从而∠AHC 1=22arctan -π. 故二面角C 1—EF —A 的大小为22arctan -π.解法二：以A 为坐标原点，建立如图所示的空间直角坐标系（1）设DF=x ，则A （0，0，0），B （1，0，0），D （0，1，0），A 1（0，0，1），B （1，0，1），D 1（0，1，1），E )0,21,1(，F （x ，1，0）BFAB E D CD F x x D AF E D F AB E D AB E D AB E D x AF AB E D 111111111111,.21210,011)0,1,(),1,0,1(),1,21,1(平面的中点时是故当点即平面于是即⊥==-⇔=⋅⇔⇔⊥⊥=-=⋅∴==--=∴（1）当D 1E ⊥平面AB 1F 时，F 是CD 的中点，又E 是BC 的中点，连结EF ，则EF ∥BD. 连结AC ，设AC 与EF 交于点H ，则AH ⊥EF. 连结C 1H ，则CH 是C 1H 在底面ABCD 内的射影.∴C 1H ⊥EF ，即∠AHC 1是二面角C 1—EF —A 的平面角.31898983||||cos ).0,43,43(),1,41,41(),0,43,43(),1,1,1(11111-=⨯-=⋅=∠∴--==HC HA AHC HC H C.31arccos .31arccos )31arccos(11----=-=∠ππ的大小为故二面角即A EF C AHC19．本小题主要考查向量的概念，平面向量的运算法则，考查运用向量及函数知识的能力，满分12分.)()(,,,.0,:AC AQ AB AP CQ BP AC AQ CQ AB AP BP AQ AP -⋅-=⋅∴-=-=-==⋅∴⊥ 解法一.cos 2121)(222222θa a a a AC AB AP a APAB AC AP a AC AB AQ AB AC AP AQ AP +-=⋅+-=⋅+-=-⋅--=⋅+⋅--=⋅+⋅-⋅-⋅=.0.,)(0,1cos 其最大值为最大时方向相同与即故当⋅==θθ解法二：以直角顶点A 为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系..)()())(().2,2(),,(),,(),,().,(),,(.||,2||),,0(),0,(),0,0(,||||22by cx y x b y y x c x y x b c b y x y c x y x Q y x P a BC a PQ b C c B A b AC c AB -++-=--+--=⋅∴--=-=---=-=∴--====则的坐标为设点且则设.0,,)(0,1cos .cos .cos .||||cos 2222其最大值为最大时方向相同与即故当a a a by cx a bycx BC PQ ⋅==+-=⋅∴=-∴-=⋅=θθθθθ20．本小题主要考查直线、双曲线的方程和性质，曲线与方程的关系，及其综合应用能力，满分12分.解：（Ⅰ）将直线整理得后的方程代入双曲线的方程,12122=-+=y x C kx y l.022)2(22=++-kx x k ……①依题意，直线l 与双曲线C 的右支交于不同两点，故.22.022022,0)2(8)2(,0222222-<<-⎪⎪⎪⎩⎪⎪⎪⎨⎧>->-->--=∆≠-k k k k k k k k 的取值范围是解得（Ⅱ）设A 、B 两点的坐标分别为),(11y x 、),(22y x ，则由①式得⎪⎪⎩⎪⎪⎨⎧-=⋅-=+.22,22222221k x x kk x x ……② 假设存在实数k ，使得以线段AB 为直径的圆经过双曲线C 的右焦点F （c,0）. 则由FA ⊥FB 得：.0)1)(1())((.0))((21212121=+++--=+--kx kx c x c x y y c x c x 即整理得.01))(()1(221212=+++-++c x x c k x x k ……③把②式及26=c 代入③式化简得 .066252=-+k k解得))(2,2(566566舍去或--∉-=+-=k k可知566+-=k 使得以线段AB 为直径的圆经过双曲线C 的右焦点. 21．本小题考查概率的基本知识和数学期望概念及应用概率知识解决实际问题的能力，满分12分.解：①不采取预防措施时，总费用即损失期望为400×0.3=120（万元）；②若单独采取措施甲，则预防措施费用为45万元，发生突发事件的概率为1－0.9=0.1，损失期望值为400×0.1=40（万元），所以总费用为45+40=85（万元） ③若单独采取预防措施乙，则预防措施费用为30万元，发生突发事件的概率为1－0.85=0.15，损失期望值为400×0.15=60（万元），所以总费用为30+60=90（万元）； ④若联合采取甲、乙两种预防措施，则预防措施费用为45+30=75（万元），发生突发事件的概率为（1－0.9）（1－0.85）=0.015，损失期望值为400×0.015=6（万元），所以总费用为75+6=81（万元）.综合①、②、③、④，比较其总费用可知，应选择联合采取甲、乙两种预防措施，可使总费用最少.22．本小题主要考查数列、数列极限的概念和数学归纳法，考查灵活运用数学知识分析问题和解决问题的能力，满分14分.解：（I ）由两边取极限得对且存在nn n n n n a a a A a A a 1),0(lim ,lim 1+=>=+∞→∞→ .24,0.24,122++=∴>+±=+=a a A A a a A A a A 又解得（II ）.11,11Ab a A b a a a A b a n n n n n n ++=++=+=++得由都成立对即 ,2,1)(.)(11111=+-=+-=++-=++-=∴++n A b A b b A b A b A b A A b A a b n n n n n n n n （III ）.21|)4(21|,21||21≤++-≤a a ab 得令.,2,121||,23.23,14.21|)4(21|22都成立对时现证明当解得 =≤≥≥≤-+∴≤-+∴n b a a a a a a n n （i ）当n=1时结论成立（已验证）.（ii ）假设当那么即时结论成立,21||,)1(kk b k k n ≤≥= k k k k k A b A A b A b b 21||1|)(|||||1⨯+≤+=+ 故只须证明.232||,21||1成立对即证≥≥+≤+a A b A A b A k k .212121||,23.2||,1212||||.2,14,23,422411222++=⨯≤≥≥+≥-≥-≥+∴≥∴≤-+≥-+=++=k k k k k k k b a A b A b A A b A a a a a a a a A 时故当即时而当由于即n=k+1时结论成立.根据（i ）和（ii ）可知结论对一切正整数都成立.故).,23[,2,121||+∞=≤的取值范围为都成立的对a n b n ns=|BC|=. s′=.。

华中科技大学数学分析部分考研真题PDF

a a
b
x
5.设 f n ( x)( n = 1,2,...) 是区间 [a, b] 上的连续函数，当 n → +∞ 时， f n ( x) 在 [a, b] 上一致收敛于函数 f ( x ) ，每个 f n ( x) 在 [a, b] 上均有零点，证明： f ( x) 在 [a, b] 上至少有一个零点.
上一致收敛于 f ( x). 证明：至少存在一点 x0 ∈ [a, b], 使得 f ( x0 ) ≥ 0. 二.2005 年数学分析真题
eA − eA 1.设 an > 0 ( n = 1,2,...), ∑ an = 1, An = ∑ ak , 求极限 lim e . n →∞ A − Ae n =1 k =1 n n −1
∞ n
n n −1
2.设 f ( x) 在区间 [0,1] 上有二阶连续导数，f (0) = f (1) = 0, f ′( x) ≤
8 8 , f ′′( x) ≤ , 试给出 5 5
f ( x ) (0 ≤ x ≤ 1) 的一个估计.
3. 设 f ( x ) 在区间 [0，∞ ) 上可微且恒大于零， f (0) = 1,
2.设 f (t ) 为连续函数，证明： 3.设反常积分
1
∫
b
a
dy ∫ ( y − x) n f ( x) dx =
a x →∞
y
1 b (b − x ) n +1 f ( x ) dx. ∫ a n +1
∞ 0
∫
∞
0
f ( x) dx 绝对收敛且 lim f ( x ) = 0, 证明 ∫ f 2 ( x) dx 收敛. x df ( x) 存在且有限，证明： dx

2004年武汉理工大学管理学院管理学原理(代码418)考研真题(含部分答案)【圣才出品】

2004年武汉理工大学管理学院管理学原理（代码418）考研真题（含部分答案）武汉理工大学2004年研究生入学考试试题科目名称：管理学原理科目代码：418一、名词解释(每题5分，共25分)1．计划答：计划是对组织在未来一段时间内的目标和实现目标途径的策划与安排。

计划分为正式计划和非正式计划。

在管理学中，计划具有两重含义：其一是指计划管理工作。

管理学家一致认为，计划是最重要的管理职能之一。

其二是指以规划、预算等为主体的具体的计划形式。

它们是实施计划管理职能的书面文件。

2．反馈控制答：反馈控制又称事后控制、成果控制，指在一个时期的生产经营活动已经结束以后，对本期的资源利用状况及其结果进行总结。

主要包括财务分析、成本分析、质量分析以及职工成绩评定等内容。

这类控制主要是分析工作的执行结果，将其与控制标准相比较，发现已经发生或即将出现的偏差，分析其原因和对未来的可能影响，及时拟定纠正措施并予以实施，以防止偏差继续发生或防止其今后再度发生。

其优点是：（1）反馈控制为管理者提供了关于计划的效果究竟如何的真实信息。

如果反馈显示标准与现实之间只有很小的偏差，说明计划的目标是达到了；如果偏差很大，管理者就应该利用这一信息是新计划指定得更有效。

（2）反馈控制可以增强员工的积极性。

因为人们希望获得评价他们绩效的信息，而反馈正好提供了这样的信息。

反馈控制的主要缺点在于：只能事后发挥作用。

任何供以反馈分析的结果都是既定的、不能改变的结果，惟一的作用是为以后类似的工作提供警戒与参考。

而且，偏差发生与被发现并得到纠正之间有较长一段时滞，这必然对偏差纠正的效果发生很大影响。

但是在许多情况下，反馈控制是唯一可用的控制手段。

3．程序性决策答：程序性决策是指按既定的程序所进行的决策。

对于经常发生的需要决策的问题，可以制定一个例行程序，凡遇到这一类问题，就按照既定程序进行决策。

活动程序化有两个作用：（1）作为组织控制系统的组成部分，可使控制更为容易，从而提高控制效率；（2）作为组织协调系统的组成部分，可提高组织的专业化水平。

武汉理工大学2004年数学分析

武汉理工大学 2004 年硕士研究生入学考试试题课程: 数学分析（共1 页，共 7 大题，答题时不必抄题，标明题目序号）一、计算下列各题（10′×6=60分）1. 计算 xx e xx /220)1(lim +-→2. 计算 I =dx x x n ⎰π0sin ,其中 n 为正整数。

3. 计算 dxdy y x D)(22⎰⎰+, 其中D 是椭圆区域 1422≤+y x 4. 设 f(x) 连续,Ω为空间区域⎩⎨⎧≤≤≤+10222z t y x ,dv y x f z t F )]([)(222++=⎰⎰⎰Ω,求)('t F 5. 设s(a)是曲线 y=ax 2 ( a>0 ) 在y=1下方的一段弧长,求)(lim a s a +∞→ 6. 计算曲线积分22yx ydx xdy I L +-=⎰，其中L 是圆周2)1(22=+-y x ，取逆时针方向。

二. （15分）设f(x) 有三阶连续导数,且3/10))(1(lim e xx f x x x =++→,求)0(),0(),0('''f f f 三. （15分）证明:在光滑曲面F (x,y,z) = 0上离原点最近的点处的法线必过原点。

四. （15分）计算第二类曲面积分 ⎰⎰∑+dxdy y x e z 22, 其中Σ为由锥面22y x z += 和z=1,z=2所围立体整个表面外侧。

五. （15分）将函数⎰-=xt x dt e x f 022)(展开成 x 的幂级数。

六. （15分）设f ( x )为定义在),(∞-∞上的实函数, ],[b a x ∈∀存在x 的邻域,使得f ( x )在该邻域上有界, 证明f ( x )在[a, b]上有界。

七. （15分）以下两题任选一题，且仅选一题1. 讨论正项级数∑∞=++1)/1()2ln(n n n a n ( a > 0 ) 的敛散性。

欢迎报考武汉理工大学

413
数据结构
《数据结构》
严蔚敏
清华大学出版社
414
信号分析与处理
《数字信号处理》
姚天任
华中科技大学出版社第二版
《信号与系统》
郑君里
高等教育出版社第二版
415
技术经济学
《技术经济学》
杨青
胡艳
武汉理工大学出版社2003
《投资评价》
杨青
中国经济出版社2000
416
智能运输系统概论
《智能运输系统概论》
《微观经济学》
高鸿业
高鸿业
周军
周军
中国经济出版社
中国经济出版社
武汉理工大学出版社
武汉理工大学出版社
458
发动机原理
《内燃机学》
周龙保等
机械工业出版社
459
工程热力学
《工程热力学》
沈维道
高等教育出版社
460
汽车理论基础
《汽车理论》
余志生
机械工业出版社，2003
461
汽车市场学
《汽车营销》
张国方
人民交通出版社2003年
401
管理学概论
《管理学》
许庆瑞
高等教育出版社
《管理学》
徐国华等
清华大学出版社
《管理学原理与方法》
周三多
复旦大学出版社
402
材料力学
《材料力学》
孙训芳
高等教育出版社，第三版
403
理论力学
《理论力学》
哈尔滨工业大学编
高等教育出版社，第五版
404
机械原理
《机械原理》
《机械原理》
郑文伟
孙恒
高等教育出版社，第七版

(NEW)武汉理工大学管理学院《881运筹学》历年考研真题汇编(含部分答案)

8．互为对偶的两个线性规划问题的解存在关系 A．原问题无可行解，对偶问题也无可行解 B．对偶问题有可行解，原问题可能无可行解 C．若最优解存在，则最优解相同 D．一个问题无可行解，则另一个问题具有无界解
9．有m个产地n个销地的平衡运输问题模型具有特征 A．有mn个变量m+n个约束 B．有m+n个变量mn个约束 C．有mn个变量m+n－1约束 D．有m+n－1个基变量，mn－m－n－1个非基变量
5．线性规划可行域的顶点一定是( ) A．基本可行解 B．非基本解 C．非可行解 D．最优解
6.X是线性规划的基本可行解则有( ) A．X中的基变量非零，非基变量为零 B．X不一定满足约束条件 C．X中的基变量非负，非基变量为零 D．X是最优解
7．互为对偶的两个问题存在关系( )
A．原问题无可行解，对偶问题也无可行解 B．对偶问题有可行解，原问题也有可行解 C．原问题有最优解解，对偶问题可能没有最优解 D．原问题无界解，对偶问题无可行解
Hale Waihona Puke 目录第一部分武汉理工大学管理学院881运筹学历年考研真题 2014年武汉理工大学管理学院881运筹学考研真题（回忆版） 2013年武汉理工大学管理学院881运筹学考研真题（回忆版） 2010年武汉理工大学管理学院881运筹学考研真题（含答案） 2009年武汉理工大学管理学院881运筹学考研真题（含答案） 2008年武汉理工大学管理学院879运筹学考研真题（含答案） 2007年武汉理工大学管理学院409运筹学考研真题（含答案） 2006年武汉理工大学管理学院409运筹学考研真题（含答案） 2005年武汉理工大学管理学院409运筹学考研真题（含答案） 2004年武汉理工大学管理学院409运筹学考研真题（含答案） 2003年武汉理工大学管理学院运筹学考研真题（含答案） 2002年武汉理工大学管理学院运筹学考研真题（含答案）

华中师大04年数学分析

华中师范大学2004年研究生入学考试试题（数学分析）一、求下列极限（共50分，第1、2小题各10分，第3、4小题各15分）1、21sin 0lim(cos )x x x →；2、lim n →∞； 3、74lim x x →∞+-； 4、1lim sin (sin)2n n k k n nππ→∞=∑。

二、（15）设f(x),g(x)在[a,b]上连续，在(a,b)内可导，若12,x x 是f(x)在区间[a,b]上的两个零点，证明：存在[,]a b ξ∈，使得'()()'()f fg ξξξ+=三、（15）设f(x)在[a,b](b>a>0)上连续，在(a,b)内可导，证明：在（a,b ）内存在,ξη 使 2.'()'().f f a b ηηξ=四、（15）设f(x)在[a,b]上黎曼可积，证明：()f x e在[a,b]上也是黎曼可积的。

五、（15）设'()(1,2,3,n f x n =…）在[a,b]上连续，函数g(x)在[a,b]上也连续，且对[a,b]中任意的12,x x 和正整数n 有1212|()()|||n n M f x f x x x n-≤- （M>0为常数）证明：lim ().'()0b n n a g x f x dx →+∞=⎰六、（15）设()n f x （n=1,2,3…）在[a,b]上连续，且{()}n f x 在[a,b]上一致收敛与f(x)。

证明：1）存在M>0，使对任何自然数n 有|()|,|()|n f x M f x M ≤≤及2）若F(x)为-∞+∞（，）上连续函数，则(())n F f x 一致收敛于F(f(x)).七、（10）设函数f(x)在闭区间[-1，1]上具有三阶连续导数，且 f(-1)=0,f(1)=1,f '(0)=0,证明在（-1，1）内至少存在一点ξ 使得(3)()3fξ=。

2004年普通高等学校招生全国统一考试数学(文科类)(湖北卷)

2004年普通高等学校招生全国统一考试数学(文科类)(湖北卷)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设B A Q x x x B N k k x x A ⋂∈≤∈+==则},,6|{),,15|{等于 ( )A.{1,4}B.{1,6}C.{4,6}D.{1,4,6}2.已知点M(6,2)和M 2(1,7).直线y ＝mx —7与线段M 1M 2的交点M 分有向线段M 1M 2的比为3:2,则m 的值为( )A.23-B.32-C.41 D.4 3.已知函数)(,31)(x f x x f 则处的导数为在=的解析式可能为( )A.)1(3)1()(2-+-=x x x fB.)1(2)(-=x x fC.2)1(2)(-=x x fD.1)(-=x x f4.两个圆0124:0222:222221=+--+=-+++y x y x C y x y x C 与的公切线有且仅有( )A.1条B.2条C.3条D.4条5.若函数的图象经过第二且)10(1)(≠>-+=a a b a x f x、三、四象限,则一定有( )A.010><>b a 且C.010<<b a 且6.四面体ABCD 四个面的重心分别为E 、F 、G 、H,则四面体EFGH 的表面积与四面体ABCD 的表面积的比值是 ( )A.271B.161 C.91 D.81 7.已知,,为非零的平面向量.甲:则乙,:,=⋅=⋅( )A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件8.已知4254)(,252-+-=≥x x x x f x 则有( )A.最大值45B.最小值45 C.最大值1 D.最小值11111--n n则存在数列{n x }、{n y }使得 ( )A.}{,n n n n x y x a 其中+=为等差数列,{n y }为等比数列B.}{,n n n n x y x a 其中+=和{n y }都为等差数列C.}{,n n n n x y x a 其中⋅=为等差数列,{n y }都为等比数列D.}{,n n n n x y x a 其中⋅=和{n y }都为等比数列10.若,111ba <<则下列结论中不．正确的是 ( )A.a b b a log log >B.2|log log |>+a b b aC.1)(log 2<a bD.|log log ||log ||log |a b a b b a b a +>+11.将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子里,每个盒内放一个球,恰好3个球的标号与其在盒子的标号不．一致的放入方法种数为( )A.120B.240C.360D.72012.设)(t f y =是某港口水的深度y(米)关于时间t(时)的函数,其中240≤≤t .下表是该港口某一天从0时至经长期观观察,函数)(t f y =的图象可以近似地看成函数)sin(ϕω++=t A k y 的图象.在下面的函数中,最能近似表示表中数据间对应关系的函数是( )A.]24,0[,6sin 312∈+=t t y πB.]24,0[),6sin(312∈++=t t y ππC.]24,0[,12sin312∈+=t t y πD.]24,0[),212sin(312t t y ππ++=二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 13.Tan2010°的值为 . 14.已知n xx )(2121-+的展开式中各项系数的和是128,则展开式中x 5的系数是 .(以数字作答)15.某校有老师200人,男学生1200人,女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n的样本；已知从女学生中抽取的人数为80人,则n ＝. 16.设A 、B 为两个集合,下列四个命题: ①A B ⇔对任意B x A x ∉∈有, ②A B ⇔=B A③A B ⇔AB ④AB ⇔存在B x A x ∉∈使得,其中真命题的序号是 .(把符合要求的命题序号都填上)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.已知)32sin(],,2[,0cos 2cos sin sin 622παππααααα+∈=-+求的值.18.(本小题满分12分) 如图,在棱长为1的正方体ABCD —A 1B 1C 1D 1中,AC 与BD 交于点E,CB 与CB 1交于点F. (I)求证:A 1C ⊥平BDC 1；(II)求二面角B —EF —C 的大小(结果用反三角函数值表示).19.(本小题满分12分)如图,在Rt△ABC中,已知BC＝a.若长为2a的线段PQ以点A为中点,问与的夹角θ取何值时的值最大？并求出这个最大值.20.(本小题满分12分)直线12:1:22=-+=y x C kx y l 与双曲线的右支交于不同的两点A 、B.(Ⅰ)求实数k 的取值范围；(Ⅱ)是否存在实数k ,使得以线段AB 为直径的圆经过双曲线C 的右焦点F ？若存在,求出k 的值；若不存在,说明理由.21.(本小题满分12分)为防止某突发事件发生,有甲、乙、丙、丁四种相互独立的预防措施可供采用,单独采用甲、乙、丙、预防方案可单独采用一种预防措施或联合采用几种预防措施,在总费用不超过120万元的前提下,请确定一个预防方案,使得此突发事件不发生的概率最大.22.(本小题满分14分)已知c bx x x g b x x f c b ++=+=>->2)()(,0,1的图象与函数函数的图象相切. (Ⅰ)求b 与c 的关系式(用c 表示b)；(Ⅱ)设函数),()()()(+∞-∞=在x g x f x F 内有极值点,求c 的取值范围.2004年普通高等学校招生全国统一考试数学(文科类)(湖北卷)参考答案一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 13.3314.35 15.192 16.④ 17.本小题考三角函数的基本公式以及三角函数式的恒等基础知识和基本运算技能,满分12分. 解法一:由已知得:0)cos sin 2)(cos 2sin 3(=-+αααα0cos sin 20cos 2sin 3=-=+⇔αααα或由已知条件可知).,2(,2,0cos ππαπαα∈≠≠即所以 .32tan ,0tan -=∴<αα于是3sin2cos 3cos2sin )32sin(παπαπα+=+.tan 1tan 123tan 1tan sin cos sin cos 23sin cos cos sin )sin (cos 23cos sin 22222222222αααααααααααααααα+-⨯++=+-⨯++=-+= 代入上式得将32tan -=α..3265136)32(1)32(123)32(1)32()32sin(222即为所求+-=-+--⨯+-+--=+πα解法二:由已知条件可知所以原式可化为则,2,0cos πα≠≠a..32tan .0tan ),,2(.0)1tan 2)(2tan 3(.02tan tan 62下同解法一又即-=∴<∴∈=-+=-+ααππααααα18.本小题主要考查线面关系和正方体等基础知识,考查空间想象能力和推理能力.满分12分. 解法一:(Ⅰ)∵A 1A ⊥底面ABCD,则AC 是A 1C 在底面ABCD 的射影. ∵AC ⊥BD.∴A 1C ⊥BD.同理A 1C ⊥DC 1,又BD ∩DC 1＝D, ∴A 1C ⊥平面BDC 1....,22的平面角是二面角同理C EF B BHC EF CH EF BH BF BE --∠∴⊥⊥∴==又E 、F 分别是AC 、B 1C 的中点,.31arccos .31arccos )31arccos(31464621)46()46(2cos ,,.4623..21//222221----=-=∠∴-=⨯⨯-+=⋅-+=∠∆===∆∆∴∴=ππ的大小为故二面角得由余弦定理中于是在故是两个全等的正三角形与C EF B BHC CHBH BC CH BH BHC BCH BF CH BH CEF BEF AB EF解法二:(Ⅰ)以点C 为坐标原点建立如图所示的空间直角坐标系,则C(0,0,0). D(1,0,0),B(0,1,0),A 1(1,1,1),C 1(0,0,1),D 1(1,0,1).,,.011,011).1,0,1(),0,1,1(),,1,1,1(11111111111BDC C A D DC BD DC CA BD CA DC CA CA DC CA 平面又即⊥∴=⋂⊥⊥=+-=⋅=-=⋅∴-=-==∴(Ⅱ)同(I)可证,BD 1⊥平面AB 1C..31arccos .31331||||,cos ),1,1,1(),1,1,1(.,1111111111---=⨯=⋅>=<∴--=---=><π的大小为故二面角的平面角补角的大小就是所求二面角则C EF B B D C A D A D A D A19.本小题主要考查向量的概念,平面向量的运算法则,考查运用向量及函数知识的能力,满分12分.)()(,,,.0,:AC AB AC AB -⋅-=⋅∴-=-=-==⋅∴⊥ 解法一 .cos 21)(22223θa a a a APAB AC AP a AC AB AQ AB AC AP AQ AP +-=⋅+-=-⋅+-=⋅+⋅--=⋅+⋅-⋅-⋅=.0.,)(0,1cos 其最大值为最大时方向相同与即故当CQ ⋅==θθ解法二:以直角顶点A 为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角坐标系..)()())(().2,2(),,(),,(),,().,(),,(.||,2||),,0(),0,(),0,0(,||,||22by cx y x b y y x c x y x b c b y x y c x y x Q y x P a BC a PQ b C c B A b AC c AB -++-=--+--=⋅∴--=-=---=-=∴--====则的坐标为设点且则设.0,,)(0,1cos .cos .cos .cos 2222其最大值为最大时方向相同与即故当a a CQ BP a by cx abycx ⋅==+-=⋅∴=-∴-==θθθθθ 20.本小题主要考查直线、双曲线的方程和性质,曲线与方程的关系,及其综合应用能力,满分12分. 解:(Ⅰ)将直线整理得后的方程代入双曲线的方程,12122=-+=y x C kx y l.022)2(22=++-kx x k ……①依题意,直线l 与双曲线C 的右支交于不同两点,故.022022,0)2(8)2(,0222222⎪⎪⎪⎩⎪⎪⎪⎨⎧>->-->--=∆≠-k k k k k k(Ⅱ)设A 、B 两点的坐标分别为),(11y x 、),(22y x ,则由①式得⎪⎪⎩⎪⎪⎨⎧-=⋅-=+.22,22222221k x x k k x x ……② 假设存在实数k,使得以线段AB 为直径的圆经过双曲线C 的右焦点F(c,0).则由FA ⊥FB 得:.0)1)(1())((.0))((21212121=+++--=+--kx kx c x c x y y c x c x 即整理得 .01))(()1(221212=+++-++c x x c k x x k ……③ 把②式及26=c 代入③式化简得 .566).)(2,2(566566.066252的右焦点为直径的圆经过双曲线使得以可知舍去或解得C AB k k k k k +-=--∉-=+-==-+ 21.本小题考查概率的基础知识以及运用概率知识解决实际问题的能力,满分12分.解:方案1:单独采用一种预防措施的费用均不超过120万元.由表可知,采用甲措施,可使此突发事件不发生的概率最大,其概率为0.9.方案2:联合采用两种预防措施,费用不超过120万元,由表可知.联合甲、丙两种预防措施可使此突发事件不发生的概率最大,其概率为1—(1—0.9)(1—0.7)＝0.97.方法3:联合采用三种预防措施,费用不超过120万元,故只能联合乙、丙、丁三种预防措施,此时突发事件不发生的概率为1—(1—0.8)(1—0.7)(1—0.6)＝1—0.024＝0.976.综合上述三种预防方案可知,在总费用不超过120万元的前提下,联合使用乙、丙、丁三种预防措施可使此突发事件不发生的概率最大.22.本小题考查导数、切线、极值等知识及综合运用数学知识解决问题的能力.满分14分.解:(Ⅰ)依题意,令.21,12),()(b x b x x g x f -==+'='故得 .21,0,1.4)1(),221()21(2c b c b c b b g b f +-=∴>->=+-=- 得由于 (Ⅱ).43)(.)(2)()()(22223c b bx x x F bc x c b bx x x g x f x F +++='++++==:)(,0)(,0).3(4)(1216.043,0)(022222的变化如下且有一个实根则若则即令x F x x F c b c b b c b bx x x F '='=∆-=+-=∆=+++='于是0x x =不是函数)(x F 的极值点.)()(,0)(,02121x F x x x x x F '<='>∆且有两个不相等的实根则若的变化如下:由此,)(,)(21x F x x x F x x 是函数的极大值点是函数==的极小值点. 综上所述,当且仅当.),()(,0上有极值点在函数时+∞-∞=∆x F ).,347()347,0(.3473470.321321,21.330)3(42+∞+⋃-+>-<<>+-<+-∴+-=>-<>-=∆的取值范围是故所求或解之得或或得由c c c c c c c c b c b c b c b。

武汉大学649数学分析2004年(回忆版)考研专业课真题试卷

x x f ( ) + (2 x − 3 y 2 ) f ( xy ) + xy (1 − y 2 ) f ' ( xy ) 2 y y
二、设 x1 > 0，x= n +1 证明：
3(1 + xn ) ， (n 1, 2,3...) ，证明： lim xn 存在，并求出极限 = n →∞ 3 + xn
∑ arctan 2k
∞
1
2
5.
+ + + ... A(π ) 5 ！ 9! 13! = 4 8 12 π π 1 π B(π ) + + + + ... 3! 7！ 11! 15! eπ − e −π π A( x) − π 3 B( x) = sin x A(π ) −x ⇒ x = π 4π −π= π 2 − e e 3 B (π ) e − e π A( x) + π B ( x) = 2 4π 3
( x , y ) → (0,0)
lim
y y 1 + ( )2 x
≤
( x , y ) → (0,0)
lim = y 0
（2）可微性
∂f y3 = ∂x ( x 2 + y 2 ) x 2 + y 2 ∂f x3 = ∂y ( x 2 + y 2 ) x 2 + y 2 ( x, y ) = (ky, y ) 1 ∂f )3 显然不连续 =( 2 ∂x k +1 同样 ∂f 不连续。所以不可微 ∂y
6.
1+
π4
π8
π 12
= 设：F ( x , y) Fy' ( x, y ) =

考研真题

武汉理工大学2004年研究生入学考试试题课程数据结构资料来源:/info/zyk/20120511/7293.html（共3页，共3 题，答题时不必抄题，标明题目序号）请将所有的答案以小题号(1)—(28)的顺序写在答题纸上，1．在供选择的答案中选择1—4个正确的答案（60分，每小题３分）（1）数据结构研究的内容涉及。

A. 数据如何组织B. 数据如何存储C. 数据的运算如何实现D. 算法用什么语言来描述（2）将长度为n的单链表接在长度为m的单链表之后的算法的时间复杂度为：A．O（m+n） B.O(n) C.O(m) D.O(m*n)（3）i=1; j=n; x=r[1];while ( i<j ){ while (i<j && r[j] >=x) j--;r[i]=r[j];while (i<j && r[i] <=x) i++;r[i]=r[j];}r[j]=x;上述程序段的时间复杂度为：A．O(n） B.O(n2) C.O(1) D.O(nlog2n)（4）队列的“先进先出”特性是指。

A. 最后插入队列中的元素总是最后被删除B. 当同时进行插入、删除操作时，总是插入操作优先C. 每当有删除操作时，总要先做一次插入操作D. 每次从队中删除的总是最早插入的元素（5）在一个具有n个顶点的有向图中，所有顶点的入度之和与所有顶点的出度之和的差为：A．10 B.20 C. 0 D.5（6）树的后序遍历序列与其对应的二叉树（以孩子-兄弟链存储的二叉树）的遍历序列是一致的。

A．前序遍历 B.中序遍历 C. 后序遍历 D.层次遍历（7）下列关于二叉树遍历的叙述中, 正确的有:A. 若一个结点是某二叉树中序的最后一个结点, 则必是该二叉树的前序最后一个结点.B. 若一个结点是某二叉树前序的最后一个结点, 则必是该二叉树的中序最后一个结点.C. 若一个叶子是某二叉树中序的最后一个结点, 则必是该二叉树的前序最后一个结点.D. 若一个叶子是某二叉树前序的最后一个结点, 则必是该二叉树的中序最后一个结点.（8）将一组无序的数据重新排列成有序序列, 其方法有:A.拓扑排序B.快速排序C.堆排序D.基数排序（9）已知某二叉树的结点的后序序列是BDECA, 中序序列是BADCE, 则前序序列是: A.AEDCB B.ABCDE C. CDABC D.BDECA（10）对{05,46,13,55,94,17,42 }进行基数排序, 一趟排序的结果是:A.05,46,13,55,94,17,42B. 05,13,17,42,46,55,94C.42,13,94,05,55,46,17D. 05,13,46,55,17,42,94（11）每个结点的度或者为0或者为2的二叉树称为正则二叉树。

武汉理工大学专业课考研参考书目

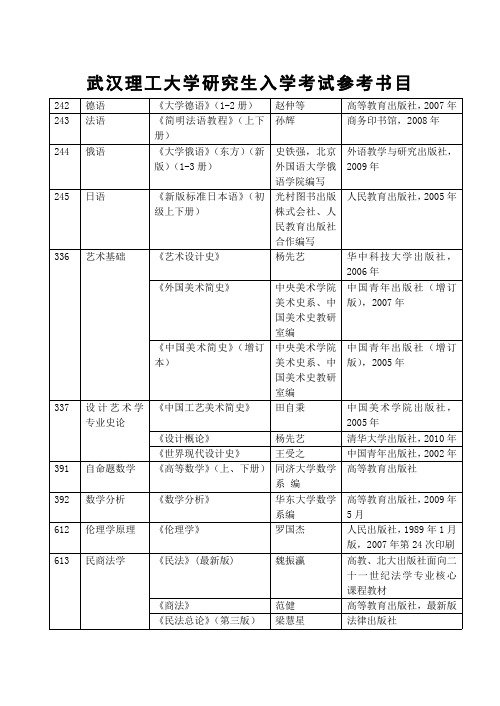
武汉理工大学研究生入学考试参考书目242德语《大学德语》（1-2册）赵仲等高等教育出版社，2007年243法语《简明法语教程》（上下册）孙辉商务印书馆，2008年244俄语《大学俄语》（东方）（新版）（1-3册）史铁强，北京外国语大学俄语学院编写外语教学与研究出版社，2009年245日语《新版标准日本语》（初级上下册）光村图书出版株式会社、人民教育出版社合作编写人民教育出版社，2005年336艺术基础《艺术设计史》杨先艺华中科技大学出版社，2006年《外国美术简史》中央美术学院美术史系、中国美术史教研室编中国青年出版社（增订版），2007年《中国美术简史》（增订本）中央美术学院美术史系、中国美术史教研室编中国青年出版社（增订版），2005年337设计艺术学专业史论《中国工艺美术简史》田自秉中国美术学院出版社，2005年《设计概论》杨先艺清华大学出版社，2010年《世界现代设计史》王受之中国青年出版社，2002年391自命题数学《高等数学》（上、下册）同济大学数学系编高等教育出版社392数学分析《数学分析》华东大学数学系编高等教育出版社，2009年5月612伦理学原理《伦理学》罗国杰人民出版社，1989年1月版，2007年第24次印刷613民商法学《民法》(最新版)魏振瀛高教、北大出版社面向二十一世纪法学专业核心课程教材《商法》范健高等教育出版社，最新版《民法总论》（第三版）梁慧星法律出版社614经济法学《经济法学》漆多俊高等教育出版社615马克思主义基本原理及其发展《马克思主义发展史》顾海良武汉大学出版社，2006年《回到文本——马克思主义经典文献解读》朱喆、杨金洲武汉理工大学出版社，2009年616传播学原理《传播学教程》郭庆光中国人民大学出版社《传播学引论》（增补版）李彬新华出版社，2003.8617体育教育专业综合《运动生理学》王瑞元人民体育出版社，2003.6《运动训练学》田麦久高等教育出版社，2006.7618教育学《新编教育学教程》叶澜华东师范大学出版社，2006年619基础英语《新编英语教程》1-6册李观仪上海外语教育出版社，2008年620设计艺术学专业史论《中国工艺美术简史》田自秉中国美术学院出版社，2005年《艺术设计史》杨先艺华中科技大学出版社，2006年《世界现代设计史》王受之中国青年出版社。

(完整word版)2004-2010华中师范大学数学分析考研真题

2004年数学分析1.求下列极限(共50分,第1,2小题各10分,第3,4小题各15分)(1)21sinlim(cos )xx x →(2)n(3)74lim x x →∞- (4)1lim sin(sin)2nn k k n nππ→∞=∑ 2.(15)设)(),(x g x f 在],[b a 上连续,在),(b a 内可导,若12,x x 是)(x f 在区间],[b a 上的两个零点，证明：存在[,]a b ξ∈，使得'()()'()0f f g ξξξ+=3.(15)设)(x f 在)0](,[>>a b b a 上连续,在),(b a 内可导,证明:在),(b a 内存在,ξη使ba f f ⋅'⋅=')()(2ηηξ.4.(15)设)(x f 在],[b a 上黎曼可积,证明:()f x e在],[b a 上也是黎曼可积的.5.(15)'()(1,2,3,n f x n =…）在],[b a 上连续,函数)(x g 在],[b a 上也连续,且对],[b a 中任意的12,x x 和正整数n ,有1212|()()|||n n Mf x f x x x n -≤-(0>M ),证明:lim ().'()0bn n ag x f x dx →+∞=⎰.6.(15)设()n f x ( ,2,1=n )在],[b a 上连续,且{()}n f x 在],[b a 上一致收敛与)(x f .证明:(1)存在0>M ,使对任何自然数n ,有|()|,|()|n f x M f x M ≤≤及. (2)若)(x F 为-∞+∞（，）上连续函数,则(())n F f x 一致收敛于))((x f F .7.(10)设函数)(x f 在闭区间]1,1[-上具有三阶连续导数,且0)0(,1)1(,0)1(='==-f f f ,证明:在)1,1(-内至少存在一点ξ,使得(3)()3fξ=.8.(15)函数),(y x F 在点00(,)x y 的某个邻域内有连续的二阶偏导数,且00000000(,)0,'(,)0,'(,)0,''(,)0x y xx F x y F x y F x y F x y ==><,证明:由方程),(y x F 确定的隐函数()y f x =在0x 点取得极小值.2005年数学分析1.求下列极限或指定函数的值:(1)1!2!3!!lim !n n n →∞++++(10分) (2)lim 62n n→∞(10分)(3)132lim [().2x x x x x e →+∞-+(10分) (4)设)(x f 在0=x 的邻域二阶可导,且130()lim(1)x x f x x e x→++=,求(0),'(0),''(0)f f f 的值.(15分) 2.(15)设函数)(),(x g x f 在],[b a 上可导,且在),(b a 上'()0g x ≠,证明:存在)()'()(,)()()'()f a f f a bg g b g ξξξξξ-∈=-(使.3.(15)设函数()f x 在]4,2[上有连续的一阶导函数,且(2)(4)0f f ==,证明：4242max |'()||()|x f x f x dx ≤≤≥⎰.4.(13)设有方程.sin (01)x m q x q =+<<.若0101,.sin ,,sin ,,n n x m x m q x x m q x +==+=+证明:{}n x 收敛; 设lim n n x l →+∞=,再证明l 是方程.sin x m q x =+的唯一解.5.(13)证明:函数项级数11((1))x nn x e nn ∞=-+∑在任何有穷区间[,]a b 上一致收敛.6.(13)设()f x 在[,]a b 上二阶可导,且''()0f x >,证明:1()()2baa b f f x dx b a +≤-⎰. 7.(13)设12,,,,n a a a 均为常数,证明:函数项级数101..!xn t n n a t e dt n ∞-=∑⎰在[,]a b 上一致收敛. 8.(13)设()f x 在[,]a b 上黎曼可积，()0,f x c ≥≥用可积准则证明：函数ln ()f x 在[,]a b 上黎曼可积.9.(10)设()f x 在[,]a b 上具有连续的二阶导数,证明:在(,)a b 内存在ξ,使得31()()()().''()224baa b f x dx b a f b a f ξ+=-+-⎰2006年数学分析1.(30) (1)111sin)1(sin lim121----→x x e x x . (2) 设x x a x y +=,求y '. (3)dx xx ⎰+ln 1ln ln . (4)设yx y x y x f y arcsin)1(),(2-+=,求)1,(x f x '. (5)dxdy e y x y xD22)(+⎰⎰+,其中}1),{(22≤+=y x y x D . (6) 求⎰-=Lydx ydy x I cos sin ,其中L 是从点)0,0(O 到点)0,(πA 的正弦曲线有x y sin =.2.(20)设)(x f 在(,)a +∞上可导,且'()f x 在(,)a +∞上有界,证明:(1) )(x f 在(,)a +∞上一致连续.(2)()lim ()lim ()x x af a f x f x ++→∞→=存在，但不一定存在.(3)若)(lim x f x +∞→存在，且)(lim )(lim x f x f ax x +→+∞→=，则)(x f '在(,)a +∞上至少有一个零点。

武汉理工大学2004年研究生入学考试试题

武汉理工大学2004年研究生入学考试试题课程材料科学基础（共3页，共十题，答题时不必抄题，标明题目序号，相图不必重画，直接做在试题纸上）一、判断下列叙述是否正确？若不正确，请改正（30分）1. 结晶学晶胞是反映晶体结构周期性的最小重复单元。

2. 热缺陷是温度高于绝对零度时，由于晶体组成上的不纯净性所产生的一种缺陷。

3. 晶面指数通常用晶面在晶轴上截距的互质整数比来表示。

4. 固溶体是在固态条件下，一种物质以原子尺寸溶解在另一种物质中所形成的单相均匀的固体。

5. 扩散的推动力是浓度梯度，所有扩散系统中，物质都是由高浓度处向低浓度处扩散。

6. 初次再结晶的推动力是晶界过剩的自由焓。

7. 在热力学平衡条件下，二元凝聚系统最多可以3相平衡共存，它们是一个固相、一个液相和一个气相。

8. 临界冷却速率是形成玻璃所需要的最小冷却速率，临界冷却速率越大越容易形成非晶体。

9. 马氏体相变是一种无扩散性相变，相变时成分发生变化但结构不变。

10.在临界温度、临界压力时，化学势及其一阶偏导数连续，二阶偏导数不连续的相变为二级相变，发生二级相变时，体系的体积和热焓发生突变。

11.驰豫表面是指在平行于表面的方向上原子间距不同于该方向上晶格内部原子间距的表面。

12.固态反应包括界面化学反应和反应物通过产物层的扩散等过程，若化学反应速率远大于扩散速率，则动力学上处于化学动力学范围。

二、ZnS 的一种结构为闪锌矿型结构，已知锌离子和硫离子半径分别为r Zn 2+=0.068nm ，r s 2-0.156nm ，原子质量分别为65.38和32.06。

1. 画出其晶胞结构投影图；2. 计算ZnS 的晶格常数；3. 试计算ZnS的晶体的理论密度。

（15分）三、FeO结构属于NaCl型结构，其中氧的摩尔分数 x=0.52，晶格常数为0.429nm，由于存在正离子缺位，所以对应地存在一部分Fe3+离子。

试计算1.这种氧化铁中Fe2+/Fe3+离子比值2.这种氧化铁的密度。

华中科技大学2004年《数学分析》试题答案

证明：
，
若收敛，则
即收敛。
若不收敛，同理可知不收敛。
10．设，在上连续，（），当时，在上一致收敛于．证明：至少存在一点，使得．
证明：
当时，在上一致收敛于，则，并且在上连续，从而在上取得最大值，设为。
若对任意的，均有，则，因此
矛盾，因此至少存在一点，使得．
华中科技大学2004年《数学分析》试题
(试题由博士论坛之硕博之路版主hfg1964录入)
以下每题15分
1．设，（），（）．求级数之和．
解：
2．设，（）．证明（）．此估计式能否改进？
3．设有处处连续的二阶偏导数，．证明
．
证明：
4．设在上连续，在内可微，存在唯一点，使得，
6．求，是取反时针方向的单位圆周．
解：的参数方程：
7．设是连续正值函数，
．
证明（）是严格单调减函数．
证明：
因此，（）是严格单调减函数
8．设级数收敛，证明
．
证明：
由收敛知，在上一致收敛，从而，
因此在上一致收敛，则分收敛级数收敛．
．设，（），
，证明是在上的最大值．
证明：反证法，假设不是在上的最大值。
由于，存在，当时，
考察闭区域，显然：
由已知在上连续，从而在上取得最大值，设为。
显然在上，总有，因而必有：。
当时，，因此是在上的最大值。由假设，。
这与已知矛盾，可知假设不真。
5．设处处有．证明：曲线位于任一切线之上方，且与切线有唯一公共点．

历年高考数学真题-2004年普通高等学校招生全国统一考试湖北卷文科数学试题及答案

2004年普通高等学校招生湖北卷文史类数学试题一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．设B A Q x x x B N k k x x A ⋂∈≤=∈+==则},,6|{),,15|{等于（）A ．{1,4}B ．{1,6}C ．{4,6}D ．{1,4,6}2．已知点M （6，2）和M 2（1，7）.直线y=mx —7与线段M 1M 2的交点M 分有向线段M 1M 2的比为3：2，则m 的值为（）A ．23-B ．32-C ．41D ．4 3．已知函数)(,31)(x f x x f 则处的导数为在=的解析式可能为（）A ．)1(3)1()(2-+-=x x x fB ．)1(2)(-=x x fC ．2)1(2)(-=x x fD ．1)(-=x x f4．两个圆0124:0222:222221=+--+=-+++y x y x C y x y x C 与的公切线有且仅有（）A ．1条B ．2条C ．3条D ．4条5．若函数的图象经过第二且)10(1)(≠>-+=a a b a x f x 、三、四象限，则一定有（）A ．010><>b a 且C ．010<<b a 且6．四面体ABCD 四个面的重心分别为E 、F 、G 、H ，则四面体EFGH 的表面积与四面体ABCD 的表面积的比值是（）A ．271 B ．161 C ．91 D ．817．已知c b a ,,为非零的平面向量. 甲：则乙,:,c b c a b a =⋅=⋅ （）A ．甲是乙的充分条件但不是必要条件B ．甲是乙的必要条件但不是充分条件C ．甲是乙的充要条件D ．甲既不是乙的充分条件也不是乙的必要条件8．已知4254)(,252-+-=≥x x x x f x 则有（）A ．最大值45 B ．最小值45 C ．最大值1 D ．最小值19．已知数列{n a }的前n 项和),,2,1]()21)(1(2[])21(2[11 =+---=--n n b a S n n n 其中a 、b 是非零常数，则存在数列{n x }、{n y }使得（）A ．}{,n n n n x y x a 其中+=为等差数列，{n y }为等比数列B ．}{,n n n n x y x a 其中+=和{n y }都为等差数列C ．}{,n n n n x y x a 其中⋅=为等差数列，{n y }都为等比数列D ．}{,n n n n x y x a 其中⋅=和{n y }都为等比数列10．若,111ba <<则下列结论中不．正确的是（）A ．a b baloglog >B ．2|loglog|>+a b baC ．1)(log2<a bD ．|loglog||log||log |a b a b ba b a+>+11．将标号为1，2，…，10的10个球放入标号为1，2，…，10的10个盒子里，每个盒内放一个球，恰好3个球的标号与其在盒子的标号不．一致的放入方法种数为（）A ．120B ．240C ．360D ．72012．设)(t f y =是某港口水的深度y （米）关于时间t （时）的函数，其中240≤≤t .下表是该港口某一天从0时至24时记录的时间t 与水深y 的关系：经长期观观察，函数)(t f y =的图象可以近似地看成函数)sin(ϕω++=t A k y 的图象.在下面的函数中，最能近似表示表中数据间对应关系的函数（）A ．]24,0[,6sin 312∈+=t t y π B ．]24,0[),6sin(312∈++=t t y ππC ．]24,0[,12sin312∈+=t t y πD ．]24,0[),212sin(312t t y ππ++=二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. 13．Tan2010°的值为 .14．已知n xx )(2121-+的展开式中各项系数的和是128，则展开式中x 5的系数是 .（以数字作答）15．某校有老师200人，男学生1200人，女学生1000人.现用分层抽样的方法从所有师生中抽取一个容量为n 的样本；已知从女学生中抽取的人数为80人，则n= .16．设A 、B 为两个集合，下列四个命题：①A ⊄B ⇔对任意B x A x ∉∈有, ②A ⊄ B ⇔=B A φ③A ⊄B ⇔AB ④A ⊄ B ⇔存在B x A x ∉∈使得,其中真命题的序号是 .（把符合要求的命题序号都填上）三、解答题：本大题共6小题，共74分. 解答应写出文字说明，证明过程或演算步骤. 17．（本小题满分12分）已知)32sin(],,2[,0cos 2cos sin sin 622παππααααα+∈=-+求的值.18．（本小题满分12分）如图，在棱长为1的正方体ABCD —A 1B 1C 1D 1中，AC 与BD 交于点E ，CB 与CB 1交于点F.（I ）求证：A 1C ⊥平BDC 1；（II ）求二面角B —EF —C 的大小（结果用反三角函数值表示）.BDB 1D19．（本小题满分12分）如图，在Rt △ABC 中，已知BC=a .若长为2a 的线段PQ 以点A 为中点，问BC PQ 与的夹角θ取何值时CQ BP ⋅的值最大？并求出这个最大值.A BC20．（本小题满分12分）直线12:1:22=-+=y x C kx y l 与双曲线的右支交于不同的两点A 、B.（Ⅰ）求实数k 的取值范围；（Ⅱ）是否存在实数k ，使得以线段AB 为直径的圆经过双曲线C 的右焦点F ？若存在，求出k 的值；若不存在，说明理由.21．（本小题满分12分）为防止某突发事件发生，有甲、乙、丙、丁四种相互独立的预防措施可供采用，单独采用甲、乙、丙、丁预防措施后此突发事件不发生的概率（记为P ）和所需费用如下表：120万元的前提下，请确定一个预防方案，使得此突发事件不发生的概率最大.22．（本小题满分14分）已知c bx x x g b x x f c b ++=+=>->2)()(,0,1的图象与函数函数的图象相切.（Ⅰ）求b 与c 的关系式（用c 表示b ）；（Ⅱ）设函数),()()()(+∞-∞=在x g x f x F 内有极值点，求c 的取值范围.2004年普通高等学校招生湖北卷文史类数学试题参考答案一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的.1．D 2．D 3．A 4．B 5．C 6．C 7．B 8．D 9．C 10．D 11．B 12．A 二、填空题：本大题共4小题，每小题4分，共16分.把答案填在题中横线上. 13．33 14．35 15．192 16．④17．本小题考三角函数的基本公式以及三角函数式的恒等基础知识和基本运算技能，满分12分.解法一：由已知得：0)cos sin 2)(cos 2sin 3(=-+αααα 0cos sin 20cos 2sin 3=-=+⇔αααα或由已知条件可知).,2(,2,0cos ππαπαα∈≠≠即所以.32tan ,0tan -=∴<αα于是3sin2cos 3cos2sin )32sin(παπαπα+=+.tan 1tan 123tan 1tan sin cos sin cos 23sin cos cos sin )sin (cos 23cos sin 22222222222αααααααααααααααα+-⨯++=+-⨯++=-+=代入上式得将32tan -=α ..3265136)32(1)32(123)32(1)32()32sin(222即为所求+-=-+--⨯+-+--=+πα解法二：由已知条件可知所以原式可化为则,2,0cos πα≠≠aBDB 1D ..32tan .0tan ),,2(.0)1tan 2)(2tan 3(.02tan tan 62下同解法一又即-=∴<∴∈=-+=-+ααππααααα18．本小题主要考查线面关系和正方体等基础知识，考查空间想象能力和推理能力.满分12分.解法一：（Ⅰ）∵A 1A ⊥底面ABCD ，则AC 是A 1C 在底面ABCD 的射影. ∵AC ⊥BD.∴A 1C ⊥BD.同理A 1C ⊥DC 1,又BD ∩DC 1=D, ∴A 1C ⊥平面BDC 1.（Ⅱ）取EF 的中点H ，连结BH 、CH ， ...,22的平面角是二面角同理C EF B BHC EF CH EF BH BF BE --∠∴⊥⊥∴==又E 、F 分别是AC 、B 1C 的中点，.31arccos .31arccos)31arccos(31464621)46()46(2cos ,,.4623..21//222221----=-=∠∴-=⨯⨯-+=⋅-+=∠∆===∆∆∴∴=ππ的大小为故二面角得由余弦定理中于是在故是两个全等的正三角形与C EF B BHC CH BH BCCHBHBHC BCH BF CH BH CEF BEF AB EF解法二：（Ⅰ）以点C 为坐标原点建立如图所示的空间直角坐标系,则C(0,0,0). D(1,0,0),B(0,1,0),A 1(1,1,1),C 1(0,0,1),D 1(1,0,1)BP.,,.011,011).1,0,1(),0,1,1(),,1,1,1(11111111111BDC C A D DC BD DC CA BD CA DC CA BD CA DC BD CA 平面又即⊥∴=⋂⊥⊥=+-=⋅=-=⋅∴-=-==∴（Ⅱ）同（I ）可证，BD 1⊥平面AB 1C. .31arccos.31331,cos ),1,1,1(),1,1,1(.,11111111---=⨯=⋅>=<∴--=---=><π的大小为故二面角的平面角补角的大小就是所求二面角则C EF B B D C A B D C A B D C A B D D A19．本小题主要考查向量的概念，平面向量的运算法则，考查运用向量及函数知识的能力，满分12分.)()(,,,.0,:AC AQ AB AP CQ BP AC AQ CQ AB AP BP AQ AP AC AB AC AB -⋅-=⋅∴-=-=-==⋅∴⊥ 解法一 .cos 21)(22223θa a BCPQ a AC AB AP a APAB AC AP a AC AB AQ AB AC AP AQ AP +-=⋅+-=-⋅+-=⋅+⋅--=⋅+⋅-⋅-⋅=.0.,)(0,1cos 其最大值为最大时方向相同与即故当CQ BP BC PQ ⋅==θθ解法二：以直角顶点A 为坐标原点，两直角边所在直线为坐标轴建立如图所示的平面直角坐标系..)()())(().2,2(),,(),,(),,().,(),,(.||,2||),,0(),0,(),0,0(,||,||22by cx y x b y y x c x CQ BP y x PQ b c BC b y x CQ y c x BP y x Q y x P a BC a PQ b C c B A b AC c AB -++-=--+--=⋅∴--=-=---=-=∴--====则的坐标为设点且则设.0,,)(0,1cos .cos .cos .cos 2222其最大值为最大时方向相同与即故当CQ BC BC PQ a a CQ BP a by cx aby cx BC PQ ⋅==+-=⋅∴=-∴-=⋅=θθθθθ20．本小题主要考查直线、双曲线的方程和性质，曲线与方程的关系，及其综合应用能力，满分12分.解：（Ⅰ）将直线整理得后的方程代入双曲线的方程,12122=-+=y x C kx y l.022)2(22=++-kx x k……①依题意，直线l 与双曲线C 的右支交于不同两点，故.22.022022,0)2(8)2(,0222222-<<-⎪⎪⎪⎩⎪⎪⎪⎨⎧>->-->--=∆≠-k k k k k k k k 的取值范围是解得（Ⅱ）设A 、B 两点的坐标分别为),(11y x 、),(22y x ，则由①式得 ⎪⎪⎩⎪⎪⎨⎧-=⋅-=+.22,22222221k x x kk x x ……②假设存在实数k ，使得以线段AB 为直径的圆经过双曲线C 的右焦点F （c,0）. 则由FA ⊥FB 得：.0)1)(1())((.0))((21212121=+++--=+--kx kx c x c x y y c x c x 即整理得.01))(()1(221212=+++-++c x x c k x x k……③把②式及26=c 代入③式化简得.566).)(2,2(566566.066252的右焦点为直径的圆经过双曲线使得以可知舍去或解得C AB k k k k k+-=--∉-=+-==-+21．本小题考查概率的基础知识以及运用概率知识解决实际问题的能力，满分12分. 解：方案1：单独采用一种预防措施的费用均不超过120万元.由表可知，采用甲措施，可使此突发事件不发生的概率最大，其概率为0.9.方案2：联合采用两种预防措施，费用不超过120万元，由表可知.联合甲、丙两种预防措施可使此突发事件不发生的概率最大，其概率为 1—(1—0.9)(1—0.7)=0.97.方法3：联合采用三种预防措施，费用不超过120万元，故只能联合乙、丙、丁三种预防措施，此时突发事件不发生的概率为1—（1—0.8）(1—0.7)(1—0.6)=1—0.024=0.976.综合上述三种预防方案可知，在总费用不超过120万元的前提下，联合使用乙、丙、丁三种预防措施可使此突发事件不发生的概率最大.22．本小题考查导数、切线、极值等知识及综合运用数学知识解决问题的能力.满分14分.解：（Ⅰ）依题意，令.21,12),()(b x b x x g x f -==+'='故得.21,0,1.4)1(),221()21(2c b c b c b b g b f +-=∴>->=+-=- 得由于（Ⅱ）.43)(.)(2)()()(22223c b bx x x F bc x c b bx x x g x f x F +++='++++==:)(,0)(,0).3(4)(1216.043,0)(022222的变化如下且有一个实根则若则即令x F x x F c b c b b c b bx x x F '='=∆-=+-=∆=+++='于是0x x =不是函数)(x F 的极值点. )()(,0)(,02121x F x x x x x F '<='>∆且有两个不相等的实根则若的变化如下：由此，)(,)(21x F x x x F x x 是函数的极大值点是函数==的极小值点. 综上所述，当且仅当.),()(,0上有极值点在函数时+∞-∞=∆x F ).,347()347,0(.3473470.321321,21.330)3(42+∞+⋃-+>-<<>+-<+-∴+-=>-<>-=∆的取值范围是故所求或解之得或或得由c c c c c c c c b c b c b c b。