1线段射线直线的概念 及性质
直线射线和线段的认识与应用

直线射线和线段的认识与应用直线、射线和线段是几何学中常见的基本概念。
它们在数学中被广泛应用于各种领域,如几何形状、图形推导以及问题解决等。
本文将详细介绍直线、射线和线段的定义、性质、认识及其实际应用。
一、直线的认识与应用直线是最基本的几何概念之一。
它没有开始和结束的点,可以延伸到无穷远。
直线的定义非常简洁,它由无数个点组成,而且这些点是无穷多的。
直线可以用于表示两个点之间的最短距离,也可用于构造其他图形、研究线性方程等。
在实际生活中,我们常常使用直线进行测量和规划。
例如,在建筑和工程领域,直线用于绘制平面图、地图等。
此外,直线的概念也应用于物理、经济、统计学等学科中的数据分析和模型推导。
二、射线的认识与应用射线是直线的一种特殊形式,它有一个起点,但没有终点。
射线的定义非常具体,它由起点和向一个方向无限延伸的直线组成。
射线在几何学中有广泛的应用。
一方面,射线可用于测量和定位。
在导航中,我们可以利用射线确定特定位置的方位角。
另一方面,射线也可以用于解决图形推导和证明问题。
在解析几何学中,射线可以用于表示直线上的点的坐标。
三、线段的认识与应用线段是由两个端点连接而成的直线部分。
与直线和射线不同,线段有一个确定的长度,它在两个端点之间有开始和结束的点。
线段在几何学中被广泛应用于测量、构造和推导。
当我们需要测量距离或长度时,可以使用线段进行测量。
在建筑设计中,线段可以用于规划建筑物的尺寸和位置。
此外,线段也可以用于解决几何问题,如证明图形的相似性、角的平分线等。
四、直线、射线和线段的区别与联系直线、射线和线段在定义和性质上有明显的区别,但它们也存在着联系和关联。
首先,直线是最基本的几何概念,它没有开始和结束的点,可以无限延伸。
而射线是直线的一种特殊形式,它有一个起点但没有终点,可以向一个方向无限延伸。
线段则不同,它有一个明确的长度,有明显的开始和结束的点。
其次,直线和射线具有相似的性质,都是由无穷多个点组成。
直线、射线、线段(基础)知识讲解

直线、射线、线段(基础)知识讲解责编:杜少波【学习目标】1.理解直线、射线、线段的概念,掌握它们的区别和联系;2. 利用直线、线段的性质解决相关实际问题;3.利用线段的和差倍分解决相关计算问题.【要点梳理】要点一、直线1.概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始概念,直线常用“一根拉得紧的细线”、“一张纸的折痕”等实际事物进行形象描述.2. 表示方法:(1)可以用直线上的表示两个点的大写英文字母表示,如图1所示,可表示为直线AB(或直线BA).(2)也可以用一个小写英文字母表示,如图2所示,可以表示为直线l.3.基本性质:经过两点有一条直线,并且只有一条直线.简单说成:两点确定一条直线.要点诠释:直线的特征:(1)直线没有长短,向两方无限延伸.(2)直线没有粗细.(3)两点确定一条直线.(4)两条直线相交有唯一一个交点.4.点与直线的位置关系:(1)点在直线上,如图3所示,点A在直线m上,也可以说:直线m经过点A.(2)点在直线外,如图4,点B在直线n外,也可以说:直线n不经过点B.要点二、线段1.概念:直线上两点和它们之间的部分叫做线段.2.表示方法:(1)线段可用表示它两个端点的两个大写英文字母来表示,如图所示,记作:线段AB或线段BA.(2)线段也可用一个小写英文字母来表示,如图5所示,记作:线段a.3. “作一条线段等于已知线段”的两种方法:法一:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a.法二:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a的长度,再画一条等于这个长度的线段.4.基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.如图6所示,在A ,B 两点所连的线中,线段AB 的长度是最短的.要点诠释:(1)线段是直的,它有两个端点,它的长度是有限的,可以度量,可以比较长短.(2)连接两点间的线段的长度,叫做这两点的距离. (3)线段的比较:①度量法:用刻度尺量出两条线段的长度,再比较长短.②叠合法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.5.线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如图7所示,点C 是线段AB 的中点,则12AC CB AB ==,或AB =2AC =2BC .要点诠释:若点C 是线段AB 的中点,则点C 一定在线段AB 上.要点三、射线1.概念:直线上一点和它一侧的部分叫射线,这个点叫射线的端点.如图8所示,直线l 上点O 和它一旁的部分是一条射线,点O 是端点.l2.特征:是直的,有一个端点,不可以度量,不可以比较长短,无限长.3.表示方法:(1)可以用两个大写英文字母表示,其中一个是射线的端点,另一个是射线上除端点外的任意一点,端点写在前面,如图8所示,可记为射线OA .(2)也可以用一个小写英文字母表示,如图8所示,射线OA 可记为射线l . 要点诠释:(1)端点相同,而延伸方向不同,表示不同的射线.如图9中射线OA ,射线OB 是不同的射线.(2)端点相同且延伸方向也相同的射线,表示同一条射线.如图10中射线OA 、射线OB 、射线OC 都表示同一条射线.要点四、直线、射线、线段的区别与联系1.直线、射线、线段之间的联系(1)射线和线段都是直线上的一部分,即整体与部分的关系.在直线上任取一点,则可将直线分成两条射线;在直线上取两点,则可将直线分为一条线段和四条射线.(2)将射线反向延伸就可得到直线;将线段一方延伸就得到射线;将线段向两方延伸就得到直线. 图6 图7图8 图9 图102.三者的区别如下表要点诠释:(1)联系与区别可表示如下:(2)在表示直线、射线与线段时,勿忘在字母的前面写上“直线”“射线”“线段”字样.【典型例题】类型一、相关概念1.下列说法中,正确的是( )A.射线OA与射线AO是同一条射线B.线段AB与线段BA是同一条线段C.过一点只能画一条直线D.三条直线两两相交,必有三个交点【答案】B【解析】射线OA的端点是O,射线AO的端点是A,所以射线OA与射线AO不是同一条射线,故A 错误;过一点能画无数条直线,所以C错误;三条直线两两相交,有三个交点或一个交点(三条直线相交于一点时),所以D错误;线段AB与线段BA是同一条线段,所以B正确.【总结升华】直线和线段用两个大写字母表示时,与字母的前后顺序无关,但射线必须是表示端点的字母写在前面,不能互换.举一反三:【变式1】以下说法中正确的是()A.延长线段AB到C B.延长射线ABC.直线AB的端点之一是A D.延长射线OA到C【答案】A【变式2】如图所示,请分别指出图中的线段、射线和直线的条数,并把它们分别表示出来.【答案】解:如下图所示,在直线上点A左侧和点C右侧分别任取点X和Y.图中有6条射线:射线AX、射线AY、射线BX、射线BY、射线CX、射线CY.有3条线段:线段AB(或BA)、线段BC(或CB)、线段AC(或CA)有1条直线:直线AC(或AB,BC).类型二、有关作图2.如图所示,线段a,b,且a>b.用圆规和直尺画线段:(1)a+b;(2)a-b.【答案与解析】解:(1) 画法如图(1),画直线AF,在直线AF上画线段AB=a,再在AB的延长线上画线段BC=b,线段AC就是a与b的和,记作AC=a+b.(2) 画法如图(2),画直线AF,在直线AF上画线段AB=a,再在线段AB上画线段BD=b,线段AD 就是a与b的差,记作AD=a-b.【总结升华】在画线段时,为使结果更准确,一般用直尺画直线,用圆规量取线段的长度.举一反三:【变式1】如图,C是线段AB外一点,按要求画图:(1)画射线CB;(2)反向延长线段AB;(3)连接AC,并延长AC至点D,使CD=AC.【答案】解:【高清课堂:直线、射线、线段397363 按语句画图3(3)】【变式2】用直尺作图:P 是直线a 外一点,过点P 有一条线段b 与直线a 不相交.【答案】解:类型三、有关条数及长度的计算3.如图,A 、B 、C 、D 为平面内任意三点都不在同一条直线上的四点,那么过其中两点,可画出 条直线.【思路点拨】根据两点确定一条直线即可计算出直线的条数.【答案】6条直线【解析】由两点确定一条直线知,点A 与B,C,D 三点各确定一条直线,同理点B 与C 、D 各确定一条直线,C 与D 确定一条直线,综上:共有直线:3+2+1=6(条).【总结升华】平面上有n 个点,其中任意三点不在一条直线上,则最多确定的直线条数为:(1)123...(1)2n n n -++++-=. 举一反三:【变式1】如图所示,已知线段AB 上有三个定点C 、D 、E .(1)图中共有几条线段?(2)如果在线段CD 上增加一点,则增加了几条线段?你能从中发现什么规律吗?【答案】解:(1)线段的条数:4+3+2+1=10(条);(2)如果在线段CD 上增加一点P ,则P 与其它五个点各组成一条线段,因此,增加了5条线段. (注解:若在线段AB 上增加一点,则增加2条线段,此时线段总条数为1+2;若再增加一点,则又增加了3条线段,此时线段总条数为1+2+3;…;当线段AB 上增加到n 个点(即增加n -2个点)时,线段的总条数为1+2+……+(n -1)=21n(n -1) .) 【变式2】)如图直线m 上有4个点A 、B 、C 、D ,则图中共有________条射线.【答案】84.(2016春•启东市月考)已知点C 在线段AB 上,线段AC=7cm ,BC=5cm ,点M 、N 分别是AC 、BC 的中点,求MN 的长度.【思路点拨】根据M 、N 分别为AC 、BC 的中点,根据AC 、BC 的长求出MC 与CN 的长,由MC+CN 求出MN 的长即可.【答案与解析】解:∵AC=7cm ,BC=5cm ,点M 、N 分别是AC 、BC 的中点,∴MC=AC=3.5cm ,CN=BC=2.5cm ,则MN=MC+CN=3.5+2.5=6(cm ).【总结升华】此题考查了线段的和差,熟练掌握线段中点定义是解本题的关键.【高清课堂:直线、射线、线段397363画图计算例2】举一反三:【变式】在直线l 上按指定方向依次取点A 、B 、C 、D ,且使AB :BC :CD=2:3:4,如图所示,若AB 的中点M 与CD 的中点N 的距离是15cm ,求AB 的长.【答案】解:依题意,设AB =2x cm ,那么BC =3x cm ,CD =4x cm .则有:MN=BM+BC+CN= x+3x+2x=15 解得:52x = 所以AB=2x =5252⨯=cm. 类型四、最短问题5.(2015•新疆)如图所示,某同学的家在A 处,星期日他到书店去买书,想尽快赶到书店,请你帮助他选择一条最近的路线( )A .A →C →D →B B . A →C →F →BC . A →C →E →F →BD .A →C →M →B【答案】B .【解析】根据两点之间的线段最短,可得C、B两点之间的最短距离是线段CB的长度,所以想尽快赶到书店,一条最近的路线是:A→C→F→B.【总结升华】“两点之间线段最短”在实际生活中有广泛的应用,此类问题要与线段的性质联系起来,这里线段最短是指线段的长度最短,连接两点的线段的长度叫做两点间的距离,线段是图形,线段长度是数值.举一反三:【变式】 (1)如图1所示,把原来弯曲的河道改直,A、B两地间的河道长度有什么变化?(2)如图2,公园里设计了曲折迂回的桥,这样做对游人观赏湖面风光有什么影响?与修一座直的桥相比,这样做是否增加了游人在桥上行走的路程?说出上述问题中的道理.【答案】解:(1)河道的长度变小了.(2)由于“两点之间,线段最短”,这样做增加了游人在桥上行走的路程,有利于游人更好地观赏湖面风光,起到“休闲”的作用.。
直线、射线、线段(基础)知识点讲解

直线、射线、线段(基础)知识讲解
【学习目标】
1.理解直线、射线、线段的概念,掌握它们的区别和联系;
2. 利用直线、线段的性质解决相关实际问题;
3.利用线段的和差倍分解决相关计算问题.
【要点梳理】
要点一、直线
1.概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始概念,直线常用“一根拉得紧的细线”、“一张纸的折痕”等实际事物进行形象描述.
2. 表示方法:(1)可以用直线上的表示两个点的大写英文字母表示,如图1所示,可表示为直线AB(或直线BA).
(2)也可以用一个小写英文字母表示,如图2所示,可以表示为直线l.
3.基本性质:经过两点有一条直线,并且只有一条直线.简单说成:两点确定一条直线.要点诠释:
直线的特征:(1)直线没有长短,向两方无限延伸.
(2)直线没有粗细.
(3)两点确定一条直线.
(4)两条直线相交有唯一一个交点.
4.点与直线的位置关系:
(1)点在直线上,如图3所示,点A在直线m上,也可以说:直线m经过点A.
(2)点在直线外,如图4,点B在直线n外,也可以说:直线n不经过点B.
要点二、线段
1.概念:直线上两点和它们之间的部分叫做线段.
2.表示方法:
(1)线段可用表示它两个端点的两个大写英文字母来表示,如图所示,记作:线段AB或线段BA.
(2)线段也可用一个小写英文字母来表示,如图5所示,记作:线段a.
3. “作一条线段等于已知线段”的两种方法:
法一:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC上截取AB=a.
法二:用刻度尺作一条线段等于已知线段.例如:可以先量出线。
直线射线线段定义

直线射线线段定义直线、射线、线段是我们学习数学中最基础的概念之一,它们是我们进行几何学和代数学计算的基础。
在这篇文章中,我们将深入探讨这三个概念的定义、特点以及它们在数学中的应用。
一、直线的定义直线是一条无限延伸的线段,它没有起点和终点,可以无限延伸。
在几何学中,直线通常表示为一条粗细为零的线段,它具有以下特点:1. 直线上的任意两点都可以用一条直线连接起来。
2. 直线上的任意一点到另外一点的距离是无限的。
3. 直线可以被任意延伸。
4. 直线没有宽度和长度,只有方向。
在数学中,我们通常用字母小写字母l来表示直线。
直线的长度是无限的,因此我们通常不会计算直线的长度,而是通过直线上的两个点来计算它们之间的距离。
二、射线的定义射线是起点固定、延伸方向唯一的线段,它可以无限延伸,但只有一个起点。
射线的特点如下:1. 射线上的点到起点的距离是有限的。
2. 射线只有一个起点和一个无限远的终点。
3. 射线可以被任意延伸。
在数学中,我们通常用大写字母表示射线,如AB表示从点A开始向B方向延伸的射线。
三、线段的定义线段是由两个点A和B之间的线段组成,它有起点和终点,长度是有限的。
线段的特点如下:1. 线段上的任意两点可以用一条线段连接起来。
2. 线段的长度是有限的。
3. 线段的起点和终点是固定的。
在数学中,我们通常用小写字母表示线段,如ab表示由点a和点b组成的线段。
四、直线、射线、线段的应用直线、射线、线段在几何学和代数学中都有广泛的应用。
在几何学中,我们可以通过这些概念来计算和描述各种图形的形状和大小,如平面图形、立体图形等。
在代数学中,我们可以通过直线、射线、线段来描述和计算各种函数的性质,如一次函数、二次函数等。
另外,在实际生活中,直线、射线、线段也有许多应用,如建筑设计、道路规划、电路设计等。
在建筑设计中,直线、射线、线段可以用来描述建筑物的形状和大小,帮助建筑师规划建筑物的结构和布局。
在道路规划中,直线、射线、线段可以用来描述道路的走向和长度,帮助交通规划师规划道路的走向和布局。
初中数学《直线、射线、线段》知识全解

《直线、射线、线段》知识全解
课标要求
理解直线线段射线的概念及表示方法,区别它们之间的相同点与不同点,理解公理两点之间线段最短.
教材从线段的应用实例开始学习,提出直线、射线、线段表示方法,特性,点与直线的位置关系.在画图的过程中总结直线性质.本节学习的重点是线段,通过多种不同的方法比较线段的大小、引出中点的定义,两点的距离以及线段的性质.
内容解析
(1)直线、射线、线段的特性
端点数延伸性能否度量画法表示
线段2个不延伸可度量
线段AB、线段
BA
线段a
射线1个
向一个方向
无限延伸不可度量
射线OA
直线无端点
向两个方向
无限延伸
不可度量
直线AB(直线
BA)
直线l
(2)
经过两点有一条直线,并且只有一条直线,也就是“两点确定一条直线”.
(3)线段的性质
两点之间,线段最短.
(4)两点的距离:连接两点间的线段的长度.
(5)线段的中点:在线段上,把线段分成两条相等线段的点.
重点难点
本节内容的重点是理解直线性质,会用字母表示图形和根据语言描述图形,画一条线段,比较两条线段的长短,在现实情境中了解线段的性质.难点是根据语言描述画出图形,尺规作图.
教法导引
从学生已有的知识出发,激发学生的兴趣,利用小组交流、讨论的方式将问题解释清楚.学法建议
按照思考、交流、总结、应用的步骤学习.。
线段,射线,直线的表示方法

线段,射线,直线的表示方法
各种图形表示方法:
直线:一个小写字母或两个大写字母,但前面必须加“直线”两字,如:直线l,直线m;直线AB,直线CD。
例:直线l;直线AB。
射线:一个小写字母或端点的大写字母。
和射线上的一个大写字母,前面必须加“射线”两字。
如:射线a;射线OA。
例:射线AB。
线段:用表示端点的大写字母表示,如线段AB;用一个小写字母表示,如线段a。
例:线段AB;线段a。
1、基本概念:
直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。
一条直线可以用一个小写字母表示。
线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。
一条线段可用它的端点的两个大写字母来表示。
射线:直线上一点和它一旁的部分叫做射线。
这个点叫做射线的端点。
一条射线可以用端点和射线上另一点来表示。
注意:(1)线和射线无长度,线段有长度。
(2)直线无端点,射线有一个端点,线段有两个端点。
2、基本性质:
直线的性质:过两点有且只有一条直线,即两点确定一条直线。
线段的性质:两点之间线段最短。
射线线段直线的定义

射线线段直线的定义射线、线段和直线是几何学中常见的概念,它们在数学和物理学中都有广泛的应用。
本文将分别从射线、线段和直线的定义、特性以及应用等方面进行介绍和阐述。
我们来了解一下射线的概念。
射线是由一个起点和一个方向组成的几何图形,它是无限延伸的,没有终点。
射线通常用一条带有箭头的直线段表示,箭头所指的方向就是射线的方向。
射线的起点叫做原点或起点,而射线上的任意一点都可以看作是其终点。
射线的长度没有限制,可以无限延伸。
接下来,我们来了解一下线段的概念。
线段是由两个端点和它们之间的所有点组成的几何图形,它是有限长度的。
线段通常用一条不带箭头的直线段表示,两个端点分别表示线段的起点和终点。
线段的长度是有限的,起点和终点之间的所有点都属于线段。
我们来了解一下直线的概念。
直线是由无数个点一起组成的几何图形,它是无限延伸的。
直线通常用一条带有箭头的直线段表示,箭头所指的方向就是直线的方向。
直线上的点可以无限延伸,直线没有起点和终点。
射线、线段和直线都有其独特的特性和应用。
首先,射线的无限延伸性使得它在几何学中常常用于表示方向。
在物理学中,射线被广泛应用于光学研究和光线追踪等领域。
其次,线段的有限长度使得它在几何学中常常用于表示距离。
在工程学中,线段被广泛应用于测量和建模等领域。
最后,直线的无限延伸性使得它在几何学中常常用于表示无限性。
在数学中,直线被广泛应用于解析几何和线性代数等领域。
除了以上的基本定义和特性之外,射线、线段和直线还有一些重要的性质。
例如,两条射线可以相交,相交的点称为交点。
线段也可以相交,如果两个线段的交点在它们的内部,则称其为内部交点,如果交点在它们的延长线上,则称其为外部交点。
直线与直线之间可以平行、相交或重合。
如果两条直线没有交点,则称其为平行线;如果两条直线有且只有一个交点,则称其为相交线;如果两条直线完全重合,则称其为重合线。
在几何学中,射线、线段和直线是一些基本的概念,它们在数学和物理学中有着广泛的应用。
线段,射线,直线的区别和联系

线段,射线,直线的区别和联系
区别:直线没有端点,可以沿两端无限延长,也就是说直线没有长度。
射线有一个端点,仅能沿一端无限延长,也没有长度。
线段有两个端点,不能延长,有长度。
联系:线段是直线上两点间的部分,射线是直线上一点向一侧无限延伸的部分,它们都是直线的一部分。
同一平面的两条直线有3种位置关系:平行、相交、垂直(其中垂直是相交的特殊情况)。
基本概念:
1、直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。
一条直线可以用一个小写字母表示。
2、线段:直线上两个点和它们之间的部分叫做线段,这两个点叫做线段的端点。
一条线段可用它的端点的两个大写字母来表示。
3、射线:直线上一点和它一旁的部分叫做射线。
这个点叫做射线的端点。
一条射线可以用端点和射线上另一点来表示。
直线 射线 线段
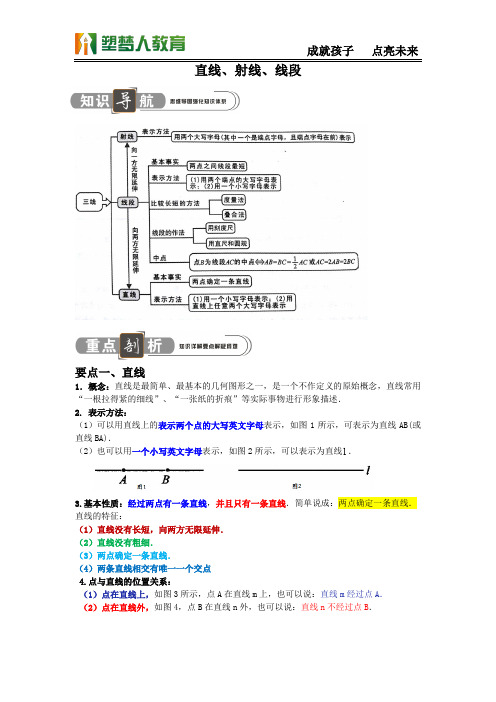
直线、射线、线段要点一、直线1.概念:直线是最简单、最基本的几何图形之一,是一个不作定义的原始概念,直线常用“一根拉得紧的细线”、“一张纸的折痕”等实际事物进行形象描述.2. 表示方法:(1)可以用直线上的表示两个点的大写英文字母表示,如图1所示,可表示为直线AB(或直线BA).(2)也可以用一个小写英文字母表示,如图2所示,可以表示为直线l.3.基本性质:经过两点有一条直线,并且只有一条直线.简单说成:两点确定一条直线.直线的特征:(1)直线没有长短,向两方无限延伸.(2)直线没有粗细.(3)两点确定一条直线.(4)两条直线相交有唯一一个交点4.点与直线的位置关系:(1)点在直线上,如图3所示,点A在直线m上,也可以说:直线m经过点A.(2)点在直线外,如图4,点B在直线n外,也可以说:直线n不经过点B.要点二、线段1.概念:直线上两点和它们之间的部分叫做线段.2.表示方法:(1)线段可用表示它两个端点的两个大写英文字母来表示,如图所示,记作:线段AB 或线段BA .(2)线段也可用一个小写英文字母来表示,如图5所示,记作:线段a .3. “作一条线段等于已知线段”的两种方法:法一:用圆规作一条线段等于已知线段.例如:下图所示,用圆规在射线AC 上截取AB =a .法二:用刻度尺作一条线段等于已知线段.例如:可以先量出线段a 的长度,再画一条等于这个长度的线段.4.基本性质:两点的所有连线中,线段最短.简记为:两点之间,线段最短.如图6所示,在A ,B 两点所连的线中,线段AB 的长度是最短的.要点剖析:(1)线段是直的,它有两个端点,它的长度是有限的,可以度量,可以比较长短. (2)连接两点间的线段的长度,叫做这两点的距离. (3)线段的比较:①度量法:用刻度尺量出两条线段的长度,再比较长短.②叠合法:利用直尺和圆规把线段放在同一条直线上,使其中一个端点重合,另一个端点位于重合端点同侧,根据另一端点与重合端点的远近来比较长短.5.线段的中点:把一条线段分成两条相等线段的点,叫做线段的中点.如图7所示,点C 是线段AB 的中点,则12AC CB AB ==,或AB =2AC =2BC .要点剖析:若点C 是线段AB 的中点,则点C 一定在线段AB 上图6 图71.概念:直线上一点和它一侧的部分叫射线,这个点叫射线的端点.如图8所示,直线l 上点O 和它一旁的部分是一条射线,点O 是端点.l2.特征:是直的,有一个端点,不可以度量,不可以比较长短,无限长. 3.表示方法:(1)可以用两个大写英文字母表示,其中一个是射线的端点,另一个是射线上除端点外的 任意一点,端点写在前面,如图8所示,可记为射线OA .(2)也可以用一个小写英文字母表示,如图8所示,射线OA 可记为射线l . 要点剖析:(1)端点相同,而延伸方向不同,表示不同的射线.如图9中射线OA ,射线OB 是不同的射线.(2)端点相同且延伸方向也相同的射线,表示同一条射线.如图10中射线OA 、射线OB 、射线OC 都表示同一条射线.要点四、直线、射线、线段的区别与联系1.直线、射线、线段之间的联系(1)射线和线段都是直线上的一部分,即整体与部分的关系.在直线上任取一点,则可将直线分成两条射线;在直线上取两点,则可将直线分为一条线段和四条射线.(2)将射线反向延伸就可得到直线;将线段一方延伸就得到射线;将线段向两方延伸就得到直线.2.三者的区别如下表要点剖析:图8 图9 图10(1)联系与区别可表示如下:(2)在表示直线、射线与线段时,勿忘在字母的前面写上“直线”“射线”“线段”字样.命题点一:计算图形中的直线、射线、线段的条数例1.如图,(1)能用字母表示的直线有_____条,它们是___________________________(2)能用字母表示的线段有_____条,它们是___________________________(3)在直线EF上能用字母表示的射线有_____条,它们是_______________________例2。
1.线段、射线、直线的概念 及性质

学习目标
1.结合实例弄清线段、射线、直线的概念及 它们之间的联系与区别. 2.知道“两点确定一条直线”.
重点:线段、射线、直线的概念、区别.
:下面的图形你认识吗?
线段 射线
直线
问题导学
1、自学课本106页议一议前面给出的例子,归 纳线段、射线、直线的概念。
小结:
小结:(直线的性质)
⑴ 经过一点有 无条数直线; ⑵ 经过两点有 一条直线,并且只有一条直线。
解释:
⑵中的“有”是存在的意思,“只有”是唯一的 意思,也就是说“两点确定一条直线”。
问:
1、要把一根木条用钉子固定在木板上, 要求用尽可能少的钉子,问至少要几颗 钉子?
导学测评
1、判断下列说法是否正确.
来表示.
表示线段的两个字母 没有顺序!
2)小结射线的表示方法
O
A
表示为: 射线OA 。
射线的表示方法:
用它的端点和射线上的另一点来表
示,其中,表示 端点的字母必须写在
另一个字母的 前面 .
表示射线的两个字母是 有顺序的!
1、怎样表示图中的射线?
OA
表示为:射线OA
2、怎样表示图中的射线?
O
B
表示为:射线OB
问题(二):我们可以用什么方式表 示一条线段?射线?直线?
1、小组合作完成课本106页议一议的内容, 归纳线段、射线、直线的表示方法。
1)小结线段的表示方法
A
B 表示为:线段 AB(或线段BA)
a
表示为: 线段 a
小结:线段有两种表示方法:
1.用它的 两个端点的大写字母 的来表示;
2.用 一个小写字母
七年级几何第一讲:直线、射线、线段

七年级几何第一讲:直线、射线、线段一、直线、射线、线段的基本概念及性质1、直线(1) 思考:经过一点可以得到几条直线?经过两点可以得到几条直线?直线公理:经过两点有一条直线,并且只有一条直线,简述为:两点确定一条直线(2) 直线的表示方法:①l;②AB(3) 点和直线的位置关系:点在直线上;点在直线外2、射线(1) 射线的概念:直线上的一点和它一旁的部分叫做射线,这个点叫做射线的端点(2) 射线的表示方法3、线段(1) 线段的概念:直线上的两个点和它们之间的部分叫做线段,这两个点叫做线段的端点(2) 线段公理:所有连接两点的线中,线段最短,即两点之间线段最短(3) 线段的表示方法:如图1,用两个大写字母表示,记作线段AB或线段BA;或用一个小写字母表示,记作线段a注:①线段AB和线段BA是同一条线段;②连接AB就是画以A、B为端点的线段;③延长线段AB是指按从A到B的方向延长(4) 线段的中点及等分点的概念:例1.如果线段AB=10cm,MA+MB=14cm,那么下列说法中正确的是()A.M点在线段AB上B.M点在直线AB上C.M点在直线AB外D.M点可能在直线AB上,也可能在直线AB外例2.下列四个图中的线段(或直线、射线)能相交的是()A.(1)B.(2)C.(3)D.(4)例3.观察图形,下列说法正确的个数是()(1) 直线BA和直线AB是同一条直线(2) 射线AC和射线AD是同一条射线(3)AB+BD>AD(4) 三条直线两两相交时,一定有三个交点A.1个B.2个C.3个D.4个二、几何计数问题例4.如图,点A、B、C、D是直线L上的四点.已知点E是直线L外的一点.则图中的线段有_________条,三角形有_________个例5.观察图①,由点A和点B可确定_________条直线观察图②,由不在同一直线上的三点A、B和C最多能确定_________条直线(1) 动手画一画图③中经过A、B、C、D四点的所有直线,最多共可作_________条直线(2) 在同一平面内任三点不在同一直线的五个点最多能确定_________条直线、n 个点(n ≥2)最多能确定_________条直线例6.观察下列图形,并阅读下面相关文字:则n 条直线最多有___________个交点例7.① 如图1直线l 上有2个点,则图中有2条可用图中字母表示的射线,有1条线段② 如图2直线l 上有3个点,则图中有________条可用图中字母表示的射线,有_______条线段 ③ 如图3直线上有n 个点,则图中有________条可用图中字母表示的射线,有________条线段 ④ 应用③中发现的规律解决问题:某校七年级共有6个班进行足球比赛,准备进行循环赛(即每两队之间赛一场),预计全部赛完共需________场比赛有关线段的计算专题一:直接求线段长度 例1.(2013·江岸)如图,已知AD =21DB ,E 是BC 的中点,BE =51AC =2cm ,求线段AB 和DE 的长练1.(2013·硚口)如图,线段AD 上有两个点C 、B ,AB =3CB ,M 、N 分别是线段AB 和线段CD 的中点,若AB =12cm ,MN =10cm ,则线段AD 的长为( ) A .20 cmB .21 cmC .22 cmD .24 cm练2.(2014·武汉三初12月月考)已知:如图,点C 为线段AB 的中点,点E 为线段AB 上的点,点D 为线段AE 的中点,若线段AB =15,CE =4.5,求线段DE练3.(2014·江岸期末)已知线段AB =6cm ,延长AB 至点C ,使BC =AB ,反向延长线段AB 至D ,使AD =21AB (1) 按题意画出图形,并求出CD 的长(2) 若M 、N 分别是AD 、BC 的中点,求MN 的长练4.(2013·洪山)已知线段AB 的长度是a cm ,线段BC 的长度比线段AB 的长度的2倍多5 cm ,线段AD 的长度比线段BC 长度2倍少5 cm (1) 求线段CD 的长度(用含a 的代数式表示) (2) 当a =15时,求线段CD 的长练5.(2014·东湖开发区)如图(1),长方形纸片ABCD ,点E 、F 分别在边AB 、CD 上,连接EF ,将∠BEF 对折,点B 落在直线EF 上的点B ′处,得折痕EM ;将AEF 对折,点A 落在直线EF 上的A ′处,得折痕EN(1) 若A ′F ∶FB ′∶B ′E =2∶3∶1且FB ′=6,求线段EB 的长度 (2) 如图(2),若F 为边DC 的一点,BE =83AB ,长方形ABCD 的面积为48,求三角形FEB 的面积专题二:作图并求线段长度例2.(2013·洪山)已知线段AB =3cm ,反向延长线段AB 到C ,使BC =53AB ,D 是BC 的中点,则线段AD 的长为( )cm A .12B .1C .52D .4练1.(2014·硚口期末)根据条件画出图形,并解答问题:(1) 已知三条直线a 、b 、c ,且直线a 、c 相交于点B ,直线b 、c 相交于点A ,直线a 、b 相交于点C ,点D 在线段AC 上,点E 在线段DC 上,请你按已知画出图形 (2) 在(1)的基础上,若AD 的2倍比AE 少4,且AE =16,试求DE 的长练2.(2014·东湖开发区)如图,说明题.如图,已知四个点A 、B 、C 、D(1) 画射线AD ;(2) 画线段BC ;(3) 画∠ACD ;(4) 画出一点P ,使P 到点A 、B 、C 、D 的距离之和最小,并说明理由练3.(2013·硚口)如图,同一平面内有五个点A 、B 、C 、D 、E ,位置如图所示,按下列要求解答:(1) 画直线AB(2) 连接DA 并延长DA 至点M ,使AM =2DA(3) 在平面内是否存在一点P ,使P A +PE +PC +PD 最小?若存在,在图中画出点P ,并简要说明理由;若不存在,直接回答不存在专题三、线段条数问题例3.(2014·江汉期末)将线段AB 延长至C ,再将线段AB 反向延长至D ,则图中线段一共有( ) A .8条B .7条C .6条D .5条练1.(2014·武昌期末)如图,C 为线段AB 延长线上一点,D 为线段BC 上一点,CD =2BD ,E 为线段AC 上一点,CE =2AE (1) 若AB =18,BC =21,求DE 的长(2) 若AB =a ,求DE 的长(用含a 的代数式表示) (3) 若图中所有线段的长度之和是线段AD 长度的7倍,则ACAD的值为专题四、多选项问题1.(2013·江岸)已知点A 、B 、C 是同一条直线上的三个不同点,下列论断:① 若点C 为线段AB 的中点,则AC =BC ;② 若AC =BC ,则点C 为线段AB 的中点;③ 若点C 为线段AB 的中点,则AB =2BC ;④ 若AB =2BC ,则点C 为线段AB 的中点,其中正确的有( ) A .①②③B .①②③④C .②③④D .①③④2.(2014·东湖开发区)如图所示,B 在线段AC 上,且BC =3AB ,D 是线段AB 的中点,E 是BC 的三等分点,则下列结论:① EC =31AE ;② DE =5BD ;③ BE =21(AE +BC );④ AE =56(BC-AD ),其中正确结论的有( ) A .①②B .①②④C .②③④D .①②③④3.(2014·武汉三初12月月考)如图,C 为射线AB 上一点,AB =30,AC 比BC 的41多5,P 、Q 两点分别从A 、B 两点同时出发,分别以2单位/秒和1单位/秒的速度在射线AB 上沿AB 方向运动,运动时间为t 秒,M 为BP 的中点,N 为QM 的中点,以下结论:① BC =2AC ;② AB =4NQ ;③ 当PB =21BQ 时,t =12,其中正确结论的个数是( ) A .1B .2C .3D .4针对练习1.(2012·武昌期末)四位同学做“读语句画图”练习.甲同学读语句“直线经过A ,B ,C 三点,且点C 在点A 与点B 之间”,画出图形(1);乙同学读语句“两条线段AB ,CD 相交于点P ”画出图形(2);丙同学读语句“点P 在直线l 上,点Q 在直线l 外”画出图形(3);丁同学读语句“点M 在线段AB 的延长线上,点N 在线段AB 的反向延长线上”画出图形(4).其中画的不正确的是( )A .甲同学B .乙同学C .丙同学D .丁同学2.(2012·武昌期末)如图,点C ,D 在线段AB 上,AC =31AB ,CD =21CB ,若AB =3,则图中所有线段长的和是( ) A .6B .8C .10D .123.(2012·青山期末)如图,线段AB =9cm ,C 、D 、E 分别为线段AB (端点A ,B 除外)上顺次的三个不同的动点,图中所有线段的和等于40cm ,则下列结论一定成立的是( ) A .CD =1cm B .CE =2cm C .CE =3cm D .DE =2cm4.(2012·江岸区)已知:如图,点C 为线段AB 的中点,点E 为线段AB 上的点,点D 为线段AE 的中点(1) 若线段AB =a ,CE =b ,|a -15|+(b -4.5)2=0,求a 、b (2) 如图1,在(1)的条件下,求线段DE (3) 如图2,若AB =15,AD =2BE ,求线段CE5.(2011·江岸区)如图,已知线段AB ,点C 在AB 的延长线上,AC =35BC ,D 在AB 的反向延长线上,BD =53DC (1) 在图上画出点C 和点D 的位置(2) 设线段AB 长为x ,则BC =________,AD =________(用含x 的代数式表示) (3) 若AB =12 cm ,求线段CD 的长6.(2012·青山期末)已知m 、n 满足|m -12|+(n -m +10)2=0 (1) 求m 、n 的值(2) 已知线段AB =m ,在直线AB 上取一点P ,恰好是AP =nPB ,点Q 为BP 的中点,求线段AQ 的长7.已知方程5m -6=4m 的解也是关于x 的方程2(x -3)-n =4的解 (1) 求m 、n 的值(2) 已知线段AB =m ,在直线AB 上取一点P ,恰好使PBAP=n ,点Q 为PB 的中点,求线段AQ 的长。
直线射线与线段的区别

直线射线与线段的区别直线、射线和线段是几何学中常见的概念,它们都属于直线的一种表示形式,但在长度和方向上有所不同。
下面将详细讨论直线、射线和线段的区别。
1. 直线:直线是无限延伸的,由无数个点组成,可以在两个方向上无限延长。
直线没有起点和终点,用两个箭头表示。
直线可以用字母表示,例如L 或 AB。
2. 射线:射线是起始于一个点,无限延伸出去的直线部分。
射线有一个起点,但没有终点,只能沿一个方向延伸。
射线一般用起点和延伸方向上的任意一点表示,例如 AB。
3. 线段:线段是直线的一部分,它有一个起点和一个终点。
线段是有限长度的,不能无限延伸。
线段可以用两个点表示,例如 AB。
直线、射线和线段之间的区别可以通过以下几个方面来理解:1. 长度:直线是无限长的,没有具体的长度。
射线也是无限长的,但只是其中的一部分。
线段则是有限长度的。
2. 方向:直线可以在两个方向上延长,没有具体的方向。
射线从一个起点出发,只有一个方向。
线段有一个起点和一个终点,给出了具体的方向。
3. 表示方法:直线可以用一个字母或写出任意两个点表示。
射线可以用一个起点和其中的一个点表示。
线段需要用两个点来确定起点和终点。
4. 实际应用:直线常用于表示平行或垂直关系,例如平行线的性质。
射线常用于表示方向或光的传播路径。
线段常用于表示有限的长度或距离。
总结起来,直线没有起点和终点,可以在两个方向上无限延长;射线有一个起点但没有终点,只能沿一个方向延伸;线段有一个起点和一个终点,是有限长度的。
了解它们的区别有助于我们在几何学和数学问题中的应用和理解。
线段、射线、直线知识点总结及习题

M O a线段、射线、直线【知识要点】知识点1、线段、直线、射线的概念:线段:一段拉直的棉线可近似地看作线段,线段有两个端点。
线段的画法:(1)画线段时,要画出两个端点之间的部分,不要画出向任何一方延伸的情况.(2)以后我们说“连结 ”就是指画以A 、B 为端点的线段.射线:将线段向一个方向无限延长,就形成了射线,射线有一个端点。
如手电筒、探照灯射出的光线等。
射线的画法:画射线 一要画出射线端点 ;二要画出射线经过一点,并向一旁延伸的情况.直线:将线段向两个方向无限延长就形成了直线,直线没有端点。
如笔直的铁轨等。
直线的画法:用直尺画直线,但只能画出一部分,不能画端点。
知识点2、线段、直线、射线的表示方法:(1) 点的记法:用一个大写英文字母(2) 线段的记法:①用两个端点的字母来表示 ②用一个小写英文字母表示 如图:记作线段AB 或线段BA , 记作线段a ,与字母顺序无关 此时要在图中标出此小写字母(3) 射线的记法:用端点及射线上一点来表示,注意端点的字母写在前面如图:记作射线OM,但不能记作射线MO(4) 直线的记法:①用直线上两个点来表示 ②用一个小写字母来表示如图:记作直线AB 或直线BA , 记作直线l与字母顺序无关。
此时要在图中标出此小写字母知识点3、线段、射线、直线的区别与联系:联系:三者都是直的,线段向一个方向延长可得到射线,线段向两个方向延长可得到直线,故射线、线段都是直线的一部分,线段是射线的一部分。
区别:直线可以向两方延伸,射线可以向一方无限延伸,线段不能延伸,三者的区别见下表:BA BAlB AaMOBAkB A名称图形表示方法界限端点长度线段线段AB(或线段BA)(字母无序)线段a 两方有界两个有射线射线AB(字母有序) 一方有界,一方无限一个无直线直线AB(或直线BA)(字母无序)直线l 两方无限无无知识点4、直线的基本性质(重点)(1)经过一点可以画无数条直线(2)经过两点只可以画一条直线直线的基本性质:经过两点有且只有一条直线(也就是说:两点确定一条直线)注:“确定”体现了“有”,又体现了“只有”。
直线射线与线段的绘制与性质

直线射线与线段的绘制与性质直线、射线和线段是我们在几何学中经常遇到的基本概念,它们在几何图形的描述和分析中起着重要的作用。
本文将介绍直线、射线和线段的绘制方法以及它们的性质。
一、直线的绘制与性质直线是由无数个点组成的无限延伸的线段,在几何学中经常用一条箭头表示。
绘制直线的方法有多种,以下是其中的两种常见方法:方法一:通过给出两个点绘制直线。
我们可以首先在纸上任选两个点A和B,然后用直尺将两点连接起来,得到一条直线AB。
直线的性质之一是,通过直线上的任意两点,都可以画出一条直线。
方法二:通过给出一个点和一条与之垂直的线绘制直线。
我们可以在纸上先给出一个点A,然后用直尺将另一条与之垂直的线段BC绘制在点A附近,这样就得到了一条直线AB,其中B为直线AB上的任意一点。
除了以上绘制直线的方法,直线还有以下性质:1. 直线上的任意两点可以通过直线连接起来。
2. 直线没有起点和终点,是无限延伸的。
3. 直线的方向唯一,可以用一条箭头表示。
二、射线的绘制与性质射线是由一个起点和无限延伸的线段组成的,常用一条带箭头的线段表示。
绘制射线的方法如下:方法一:通过给出一个起点和一个与之垂直的直线绘制射线。
我们可以在纸上先给出一个起点A,然后用直尺将一个与之垂直的直线BC 绘制在起点A附近,这样就得到一条射线AB。
射线的性质如下:1. 射线有一个起点,但是没有终点,是无限延伸的。
2. 射线的方向唯一,可以用一条箭头表示。
3. 经过射线上的任意两点,都可以画出一条射线。
三、线段的绘制与性质线段是有两个端点组成的有限长度线段,常用一条不带箭头的线段表示。
绘制线段的方法如下:方法一:通过给出线段的两个端点绘制线段。
我们可以在纸上给出线段的两个端点A和B,然后用直尺将这两个点连接起来,这样就得到了线段AB。
线段的性质如下:1. 线段有起点和终点,是有限长度的。
2. 线段的两个端点唯一确定了线段的位置。
3. 线段的长度可以通过两个端点在数轴上的位置计算得到。
直线、射线、线段知识点总结(含例题)

直线、射线、线段知识点1.直线(1)定义:一点在空间沿着一个方向及它的相反方向运动,所形成的图形就是直线.(2)直线公理:经过两点___________直线,并且___________直线.简单说成:___________.(3)表示方法:直线AB或直线a.(4)当两条不同的直线有一个公共点时,我们就称这两条直线___________,这个公共点叫做它们的___________.2.射线(1)定义:直线上的一点和它一旁的部分叫做射线.(2)特征:是直的,有一个端点,不可以度量,不可以比较长短,无限长.(3)表示方法:射线AB或射线a.3.线段(1)定义:直线上两个点和它们之间的部分叫做线段.(2)特征:线段是直的,它有两个端点,它的长度是有限的,可以度量,可以比较长短.(3)表示方法:线段AB或线段a.(4)两点的所有连线中,___________最短.简单说成:两点之间,___________.(5)连接两点间的___________,叫做这两点的距离.4.方法归纳:(1)过一点的直线有___________;直线是是向___________方向无限延伸的,无端点,不可度量,不能比较大小;(2)要注意区别直线公理与线段的性质:直线公理是指___________,线段的性质是指两点之间线段最短;在线段的计算过程中,经常涉及线段的性质、线段的中点以及方程思想.(3)延伸与延长是不同的,线段不能___________,但可以___________,直线和射线能___________,但是不能___________;(4)直线和线段用两个大写字母表示时,与字母的前后顺序___________,但射线必须是表示端点的字母写在前面,不能互换;(5)直线中“有且只有”中的“有”的含义是___________,“只有”的含义是,“有且只有”与“确定”的意义相同;(6)射线:一要确定___________,二要确定___________,二者缺一不可.K知识参考答案:1.(2)有一条,只有一条,两点确定一条直线;(4)相交,交点3.(4)线段,线段最短;(5)线段的长度4.(1)无数条,两个(2)两点确定一条直线(3)延伸,延长,延伸,延长(4)无关(5)存在性,唯一性(6)端点,延伸方向K—重点(1)直线公理;(2)线段的性质K—难点直线、射线、线段的概念K—易错直线、射线、线段的联系和区别一、直线、射线、线段【例1】下列说法中正确的个数为①射线OP和射线PO是同一条射线;②连接两点的线段叫两点间的距离;③两点确定一条直线;④若AC=BC,则C是线段AB的中点.A.1个B.2个C.3个D.4个【答案】A【解析】①射线OP端点是O,从O向P无限延伸,射线PO端点是P,从P向O无限延伸,所以不是同一条射线,故①错误;【名师点睛】(1)直线、射线、线段的表示方法①直线:用一个小写字母表示,如:直线l,或用两个大写字母(直线上的)表示,如直线AB.②射线:是直线的一部分,用一个小写字母表示,如:射线l;用两个大写字母表示,端点在前,如:射线OA.注意:用两个字母表示时,端点的字母放在前边.③线段:线段是直线的一部分,用一个小写字母表示,如线段a;用两个表示端点的字母表示,如:线段AB(或线段BA).(2)点与直线的位置关系:①点经过直线,说明点在直线上;②点不经过直线,说明点在直线外.二、直线的性质(1)直线公理:经过两点有且只有一条直线.简称:两点确定一条直线.(2)经过一点的直线有无数条,过两点就唯一确定,过三点就不一定了.【例2】平面上有四点,过其中每两点画出一条直线,可以画直线的条数为A.1或4 B.1或6C.4或6 D.1或4或6【答案】D【解析】如图所示:分别根据四点在同一直线上、三点在同一条直线上、任意三点均不在同一条直线上描出各点,再根据两点确定一条直线画出各直线可知:平面上有四点,过其中每两点画出一条直线,可以画直线的条数为1或4或6.故选D.三、线段的性质线段公理:两点的所有连线中,可以有无数种连法,如折线、曲线、线段等,这些所有的线中,线段最短.简单说成:两点之间,线段最短.【例3】把一条弯曲的公路改为直路,可以缩短路程,其理由是A.两点之间,线段最短B.两点确定一条直线C.线段有两个端点D.线段可以比较大小【答案】A【解析】把一条弯曲的公路改为直路,其理由是:两点之间,线段最短.故选A.四、两点之间的距离(1)两点间的距离连接两点间的线段的长度叫两点间的距离.(2)平面上任意两点间都有一定距离,它指的是连接这两点的线段的长度,学习此概念时,注意强调最后的两个字“长度”,也就是说,它是一个量,有大小,区别于线段,线段是图形.线段的长度才是两点的距离.可以说画线段,但不能说画距离.【例4】已知线段AB=8cm,在线段AB的延长线上取一点C,使线段AC=12cm,那么线段AB和AC中点的距离为A.2cm B.3cm C.4cm D.5cm【答案】A五、比较线段的长短(1)比较两条线段长短的方法有两种:度量比较法、重合比较法.就结果而言有三种结果:AB>CD、AB=CD、AB<CD.(2)线段的中点:把一条线段分成两条相等的线段的点.(3)线段的和、差、倍、分及计算做一条线段等于已知线段,可以通过度量的方法,先量出已知线段的长度,再利用刻度尺画条等于这个长度的线段,也可以利用圆规在射线上截取一条线段等于已知线段.【例5】如图,四条线段中,最短和最长的一条分别是A.ac B.bdC.ad D.bc【答案】B【解析】通过观察测量比较可得:d线段长度最长,b线段最短.故选B.。
小学数学点知识归纳直线线段与射线的概念

小学数学点知识归纳直线线段与射线的概念直线、线段和射线是数学中基本的几何概念,它们在几何学中经常被用到。
本文将对直线、线段和射线的概念进行归纳和解释,并介绍它们在小学数学中的应用。
一、直线的概念直线是由无数个点按一定方向无限延伸而成的,它没有起点和终点。
直线通常用两个点来表示,如AB表示直线的一个方向,BA表示同一直线的相反方向。
在几何坐标系中,直线可以用斜率和截距来表示。
斜率表示直线的倾斜程度,截距表示直线与坐标轴的交点。
直线具有很多性质和定理,在几何学中被广泛应用。
二、线段的概念线段是直线上的一段有限长度的部分,它有起点和终点。
线段的长度是有限的,可以通过两点的距离来计算。
线段通常用起点和终点的字母表示,如AB表示线段的方向,BA表示同一线段的相反方向。
线段的长度可以用数值来表示,比如AB=5cm表示线段AB的长度为5厘米。
线段是直线的一个部分,具有直线的性质,但是长度有限。
三、射线的概念射线是直线上的一部分,它有一个起点但没有终点。
射线是由起点出发,按照一定方向无限延伸而成的。
射线通常用起点和通过的一个字母来表示,如OA表示从O点出发的射线。
射线的方向可以用箭头来表示,箭头指向表示射线的无限延伸方向。
射线具有直线的性质,但是只有一个起点。
直线、线段和射线在小学数学中常被用到,它们有以下几个重要应用:1. 图形绘制:在画图纸、图形几何等问题中,我们常常需要用直线、线段和射线来绘制和构造图形。
比如,我们可以用线段来表示多边形的边,用直线来表示两个点之间的最短路径。
2. 测量长度:线段是有限长度的,可以用来测量物体的长度。
学生可以通过利用尺子等工具,在实际问题中测量线段的长度。
比如,可以通过测量文具的长度来学习和比较不同物体的大小。
3. 方向标示:直线、线段和射线有明确的方向,可以用来表示物体的方向。
比如,我们可以用箭头来表示公园的出口方向,用射线来表示一条直线上的行走方向。
4. 判断相互关系:直线、线段和射线之间有很多相互关系,学生可以通过观察和比较它们的性质来判断它们之间的关系。
七年级直线线段射线知识点

七年级直线线段射线知识点在七年级数学中,直线、线段和射线是非常重要的知识点,它们被广泛应用于几何学和数学分析的各个领域。
本文将介绍七年级直线、线段和射线的相关知识点,以帮助读者更好地理解这些概念。
文章分为三个部分:直线、线段和射线。
一、直线1. 定义直线可以看做是一条无限延伸的线。
在数学中,通常把直线看做是由无数个点组成的几何形状,它没有任何弯曲以及开始和结束的点。
直线通常用两个点来描述,在坐标系中,由两个点可以确定唯一的一条直线。
2. 符号表示直线可以用大写字母L来表示。
3. 相关术语(1) 线段:直线上的两个点之间构成的部分称为线段。
(2) 射线:以一点为端点,从这个点开始向外延伸的部分称为射线。
(3) 垂线:与直线相交,并且与直线垂直的线称为垂线。
(4) 平行线:在同一平面内没有交点的线称为平行线。
二、线段1. 定义线段是指直线上的两个端点之间的有限部分。
与直线相比,线段有明显的起点和终点。
线段同时也是基本的几何图形之一。
2. 符号表示线段一般用小写字母表示,例如ab表示由a点和b点两个端点所构成的线段,也可以用符号“ ”表示,即ab。
3. 相关术语(1) 线段长度:线段长度是指线段的长度,可以用两个端点之间的距离来表示。
(2) 等长线段:两个线段的长度相等,则称这两个线段是等长的。
(3) 中点:一条线段的中点是指在这条线段上距离两个端点相等的点,连接中点和端点的线称为线段的中线。
三、射线1. 定义射线是在一点上开始向外延伸的线段。
射线有一个起点,但没有终点,它是无限延伸的。
2. 符号表示射线可以用大写字母表示,例如AB表示以A为起点,沿着B 方向延伸的射线。
3. 相关术语(1) 射线长度:射线没有长度,但可以用起点和某个点之间的距离来表示。
(2) 直角:射线与直线相交时,垂直于直线的射线称为直角。
(3) 角度:两条射线之间的夹角称为角度,以度(°)或弧度(rad)来度量。
总结在本文中,我们讲解了七年级数学中关于直线、线段和射线的概念、表示方法以及相关术语。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小结:(直线的性质)
⑴ 经过一点有 无条数直线; ⑵ 经过两点有 一条直线,并且只有一条直线。
解释:
⑵中的“有”是存在的意思,“只有”是唯一的 意思,也就是说“两点确定一条直线”。
问:?
1、要把一根木条用钉子固定在木板上, 要求用尽可能少的钉子,问至少要几颗 钉子?
导学测评
1、判断下列说法是否正确.
A
B
C
× (6)直线AB 和直线AC表示的不是同一条直线; ( ) √ (7) 线段BC和线段CB表示的是同一条线段 ( ) × (8) 射线AC 和射线CA表示的是同一条射线。 ( )
2、归纳线段、射线、直线之间的区别与联系?
名
图形
称
表示方法
线A
段
a
B 线段AB 线段 a
延伸 端点 长度可 方向 个数 否度量
(1)画一条 2cm 的直线 .
( ×)
(2)如图,直线 AB和直线AC表示的是同
( √)
一条直线 .
A BC
(3)如图,射线OA和射线OB表示的是同一条射线 . ( √)
OA B
(4) 直线、射线、线段都有两个端点;
( )×
√ (5)直线和射线可以延伸,线段不能延伸; ( )
请观察图形作出判断:
不能延伸 两个 可以
射
线O
A
射线OA 一方延伸
一个 不可以
直
C
D
直线CD
两方延伸
无 不可以
线
m
直线 m
归纳小结
1、什么是线段?射线?直线?
2、直线的性质是什么? 3、线段、射线、直线之间有何区别与联系?
表示为:射线OB
3、怎样表示图中的射线?
O
C
表示为:射线OC
4、怎样表示图中以O为端点的射线?
OA B C
可以表示为射线OA,也可以表示为射线 OB或射线OC.
同一条射线可以有 不同的表示方法!
3)小结直线的表示方法
M
N
表示为 :直线 MN( 或直线NM) 。
a
表示为: 直线 a 。
直线有两种表示方法: 1.用这条直线上的 两个 大写字母来表示; 2.用 一个 小写字母来表示.
问题(二):我们可以用什么方式表 示一条线段?射线?直线?
1、小组合作完成课本106页议一议的内容, 归纳线段、射线、直线的表示方法。
1)小结线段的表示方法
A
B 表示为:线段 AB( 或线段BA)
a
表示为: 线段 a
小结:线段有两种表示方法:
1.用它的 两个端点的大写字母 的来表示;
2.用 一个小写字母
表示直线的两个字母 没有顺序!
1A
B 记作:直线AB ( √ )
2O
P
记作:射线PO ( × )
3a
b 记作:直线ab ( × )
4A
B 记作:线段BA ( √ )
问题(三):直线的性质是什么?
问:⑴ 过一点O 可以画几条直线?
O
这告诉我
⑵过两点A、B 可以画几条直线? 们一个什 么道理? A B
①有 两个 端点的直线叫线段; ②将一条线段向 一个 方向就形成了射线; ③将一条线段向 两个 方向无限延伸就形成了直线
问:
2、理解线段、射线、直线的概念应注意些什么?
(线段有 两个 端点,不能延伸)
射线
(射线有 一个 端点,可以向一个方向无限延伸)
直线
(直线 两个 端点,可以向两个方向无限延伸)
来表示.
表示线段的两个字母 没有顺序!
2)小结射线的表示方法
O
A
表示为 : 射线OA 。
射线的表示方法:
用它的端点和射线上的另一点来表
示,其中,表示 端点的字母必须写在
另一个字母的 前面 .
表示OA
表示为:射线OA
2、怎样表示图中的射线?
O
B
1.线段、射线、直线的概念 及性质
学习目标
1.结合实例弄清线段、射线、直线的概念及 它们之间的联系与区别. 2.知道“两点确定一条直线”.
重点:线段、射线、直线的概念、区别.
:下面的图形你认识吗?
线段 射线
直线
问题导学
1、自学课本106页议一议前面给出的例子,归 纳线段、射线、直线的概念。
小结:
