认识三角形2
认识三角形(二)习题

认识三角形(二) 同步练习题A组一、填空题1.已知三角形的三边分别为2,a,4,那么a的取值范围是______.2.(1)已知a,b,c是△ABC的三边长,a,b满足|a-7|+(b-1)2=0,c为奇数,则c=______.(2)已知a,b,c为△ABC的三条边,化简|a+b-c|-|b-a-c|=______.3.(1)一个三角形的两边长为3 cm和2 cm,第三边长为奇数,则第三边的长为______cm.(2)已知三角形的三边长分别是3,x,9,则化简|x-5|+|x-13|=______.4.(1)若等腰三角形中有两边长分别为2和5,则这个三角形的周长为______.(2)若等腰三角形两边长分别为3和5,则它的周长为______.二、选择题5.下列长度的三条线段,能组成三角形的是( )A.4 cm,5 cm,9 cm B.8 cm,8 cm,15 cmC.5 cm,5 cm,10 cm D.6 cm,7 cm,14 cm6.若要植一块三角形草坪,两边长分别是20米和50米,则这块草坪第三边长不能为( )A.60米B.50米C.40米D.30米7.长度分别为2,3,3,4的四根细木棒首尾相连,围成一个三角形(木棒允许连接,但不允许折断),得到的三角形的最长边长为( )A.4 B.5 C.6 D.7三、解答题9.由下列长度的三条线段能组成三角形吗?请说明理由(1)10 cm,12 cm,21 cm;(2)5 cm,5 cm,10 cm;(3)5.4 cm,7.2 cm,11 cm;(4)(k+1) cm,(k+2) cm,(2k+2) cm(k>0).10.(1)如图,已知△ABC.①若AB=4,AC=5,则BC边的取值范围是______;②D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.(2)已知△ABC中,三边长分别为a,b,c,且满足a=b+2,b=c+1.①试说明b一定大于3;②若这个三角形周长为22,求a,b,c.B组一、填空题11.(1)有长度分别为10 cm,7 cm,5 cm和3 cm的四根铁丝,选其中三根组成三角形,则有______种选法.(2)等腰三角形的周长是27 cm,一腰上的中线将周长分为5∶4两部分,则这个等腰三角形的底边长为______.13.已知四边形ABCD的四边分别为a,b,c,d,若a=3,b=4,d=10,则c的取值范围是______.15.△ABC中,三边之比为3:4:5,且最长边为10m,则△ABC周长为_____cm.18.有两根小棒分别长2厘米和4厘米.要围成一个等腰三角形,第三根小棒的长度应该是____厘米.二、解答题30.如图所示,D是△ABC的边AC上任意一点(不含端点),连结BD,请判断AB+BC+AC与2BD的大小关系,并说明理由.。
西南师大版数学四年级下册 第4单元 认识三角形(2) 教案

认识三角形(二)教学内容知识与技能:知道三角形任意两条边的和大于第三边;并会判断指定长度的三条线段能否围成三角形。
过程与方法:探究三角形三边的关系,根据三角形三边的关系解释生活中的现象;提高运用数学知识解决实际问题的能力;提高观察、思考、抽象概况能力和动手操作能力。
情感与态度:积极参与探究活动,在活动中获得成功的体验,培养学习的兴趣。
重点、难点重点在观察、操作、比较和分析中发现三角形三条边的关系。
难点应用三角形三边的关系解决实际生活中的问题。
情境导入找出图示中的三角形。
由三条线段围成的图形叫做三角形。
三角形的三边长度存在怎样的数量关系?两点之间线段最短探究新知(图示)把一根吸管任意剪成3段,能围成一个三角形吗?先做一做,在合同伴交流。
动手做一做:将多根吸管剪成不同的3段。
测出长度。
围成一圈。
通过图示,我们可以得出什么结论:当两根吸管的长度和等于第三根吸管时,不能围成三角形。
当两根吸管的长度和小于第三根吸管时,不能围成三角形。
当两根吸管的长度和大于第三根吸管时,能围成三角形。
剪一剪,围一围,填写下表。
当三条线段中的任意两条之和大于第3条边时,这三条线段才能围成三角形。
也可以说三角形任意两边之和大于第3边。
一个三角形的3个内角和是多少度?所有三角形的内角和都是180°吗?怎样去验证一下呢?拿起你的量角器,量一量每个三角形三个内角的度数吧!将三角形的三个角撕下来,拼到一起,你能发现什么?这三个内角拼在一起正好是一个平角,说明三角形的内角和是180°。
课堂练习三角形的一个内角为80°,另外两个角可能是多少度?三角形内角和是180°,除了这个80°的角,剩下两个角的度数和为:180°-80°=100°。
课堂小结1.三角形任意两边的内角和不能小于第三边。
2.三角形的内角和为180°。
7.4认识三角形(2)

A
C
B
F
C
如上所示,线段 AF 就是△ABC 的中线 3 1)三角形的中线必为线段 2)三角形的中线必平分对边 如上所示,线段 AF 是△ABC 的中线
1 必有:BF=CF= 2 BC
3)三角形有三条中线 例:做出下列三角形的三条角平分线 教师先做示范,然后再让学生自行画出 其余两个 锐角三角形
A
七、平面图形的认识(二) ---- [教案] 课 题 7.4 认识三角形(2) 教学目标 重 难 点 点 1 知道三角形高、中线、角平分线的定义 2 会做任意三角形高、中线、角平分线 会做任意三角形高、中线、角平分线 会做任意三角形高、中线、角平分线 讲练结合、探索交流 活 动 课型
课时 分配
本课(章节)需 2 本 节 课 为 第 2 为 本 学期总第
课时 课时 课时
教学方法 教 师
新授课
教具
投影仪
学 生 活 动
一 三角形的高 1 复习:过点 A 做 BC 的垂线,垂足为 D
A
A
B
C
B
C
A
A
B
C
2 在黑板上做△ABC,过点 A 做对边 BC B C D 的垂线,垂足为 D,我们 就将线段 AD 称为△ABC 的高 3 高的定义:在三角形中,从一个顶点向它的对边所在的直线做垂线,顶 点与垂 足之间的线段称为三角形的高 例如在上图中,我们从△ABC 的一个顶点出发,向它对边 BC 所在 的直线作垂线,垂足为 D,线段 AD 就是三角形的高 注:1)三角形的高必为线段 2)三角形的高必过顶点垂直于对边 3)三角形有三条高 为了将这三条高加以区别,我们把 AD 称为 BC 边上的高 例:做出下列三角形的三条高 1 锐角三角形: A 可由教师先做示范,然后再让学生自行画出 其余两个
认识三角形(2)

初中数学七年级下册 苏科版
回 顾 思思考 考 回顾
你还记得 “过一点画已知直线的垂线” 吗?
画法
过三角形 的一个顶点,你能画出 它的对边的垂线吗?
0 42 5 3 4 5 1 2
3
4
5
6
A
B
C
0
1
2 0 3 1 4 205 31
0 1 2 3 4 5
0 1 2 3 4 5 7
B
D
C3
做一做
锐角三角形的三条高
每人准备一个锐角三角形纸片。 (1) 你能画出这个三角形的三条高吗? (2) 你能用折纸的办法得到它们吗? (3) 这三条高之间有怎样的位置关系? 将你的结果与同伴进行交流. 锐角三角形的三条高是 在三角形的内部还是外部? 锐角三角形的三条高交于同一点. 锐角三角形的三条高 都在三角形的内部。
17
C D
A
折痕AD即为三角形的∠A的角平分线。
B
10
三形的角平分线的定义
以前所学的“角平分线 ”是一条射线, “三角形的角平分线” 还是射线 吗? 在三角形中,一个内角 B 的平分线与它的对边相交, 这个角的顶点与交点之间的 线段叫三角形的角平分线。 线段 注意
!
A 1 2
D ∠1=∠2 图5−10
p126
折、画钝角三角形的三条高
在纸上画出一个钝角三角形。 (2) 你能折出钝角三角形的 A 三条高吗? 你能画出钝 角三角形的三条高吗? 为了便于折出BC边上的高, 需要把CB延长。 为了便于折出AB边上的高, 需要把AB延长。 D D B B A
F F C C
E F D B E
BC边上的高是在三角形的 内部还是外部? 外部 AB边上的高呢?
初中数学精品试题:认识三角形(二)

C B A (第6题) 1.1 认识三角形(二)A 组1.如图,CD ⊥AB ,则图中直角三角形有( )A .1个B .2个C .3个D .4个2.如图,在△ABC 中,∠B=60°,AD 是△ABC 的角平分线,∠DAC=31°,则∠C 的度数为( )A .58°B .60°C .62°D .92°3.在△ABC 中,D 为BC 上的一点,且S △ABD =S △ACD ,则AD 为△ABC 的( )A .高B .角平分线C .中线D .不能确定4.如图,在△ABC 中,BO ,CO 分别是∠ABC ,∠ACB 的平分线,∠A =50°,则∠BOC 等于( )A .110°B .115°C .120°D .130°5.下面四个图形中,线段BE 是△ABC 的高的图是( )A .B .C .D .6.如图,在△ABC 中,AB =5厘米,BC =3厘米,BM 为中线,则△ABM 与 △BCM 的周长之差是 厘米.★7.如图,在△ABC 中,点D 、E 、F 分别为BC 、AD 、CE 的中点.若S △BFC =1,则S △ABC = . 8.如图, 在△ABC 中, 请作图:①画出△ABC 的一条角平分线CD ;②画出△ABC 中AC 边上的中线BE ;③画出△ABC 中BC 边上的高AF .9.如图,在△ABC 中,AB=AC ,AC 边上的中线BD 将这个三角形的周长分为15cm 和6cm 两部分,求三角形三边的长。
(第1题) (第2题) (第4题) (第7题)B 组★10.如图,在△ABC 中,AB =AC ,P 是BC 边上任意一点,PF ⊥AB 于 点F ,PE ⊥AC 于点E ,BD 为△ABC 的高线,BD =8,求PF +PE 的值.11.如图,在△ABC 中,BO 、CO 分别是∠ABC 、∠ACB 的平分线.(1)若∠ABC=60°,∠ACB=50°,求∠BOC 的度数.(2)若∠A=60°,求∠BOC 的度数.(3)若∠A =α,求∠BOC 的度数(用α的代数式表示).★12.如图,在△ABC 中,E 为BC 上一点,EC =2BE ,D 为AC 的中点. 设△ABC ,△ADF ,△BEF 的面积分别为,,,BEF ADF ABC S S S △△△若12=ABC S △,则BEF ADF S S △△-=_______.★13.如图,在△ABC 中,AD 是BC 边上的高线,AE 是△ABC 的角平分线.若α=∠B ,)(βαβ<=∠C ,用含βα,的代数式表示∠EAD .2。
初中数学_认识三角形(2)教学设计学情分析教材分析课后反思

七年级的学生思维活跃,模仿能力强。
对新知事物满怀探求的欲望,同时他们也具备了一定的学习能力,在老师的指导下,能针对某一问题展开讨论并归纳总结,但受年龄特征的影响,他们知识迁移能力不强推理能力还需进一步培养。
通过做三角形我发现并不是任意三条木条就一定能钉成一个三角形,三角形的构成是有条件的。
”这对整节课起到了画龙点晴的作用。
整节教学活动通过讨论、精讲、合理利用模型,让学生动手操作、自主探究、合作交流达到了预期目的。
本节课实在小学初步认识三角形的基础上,又具体介绍了三角形的有关概念和三角形三边的关系。
它既是上学期所学线段和角的延续,又是后继学习全等三角形和四边形的基础。
在知识体系中具有承上启下的作用。
认识三角形(2)评测练习独立尝试1、有两边相等的三角形叫做等腰三角形。
2、三边都相等的三角形是等边三角形,也叫正三角形。
3、三角形的三边关系:(1)三角形任意两边之和第三边;(2)三角形任意两边之差第三边。
4、下面各组数分别表示三条线段的长度,试判断以它们为边是否能组成三角形。
(1)1:4:5 (2)3:3:5(3)3x、5x、7x(x为正数)(4)三条线段长度之比为4:7:6仔细阅读课本第85、86页①记住等边三角形的概念。
②记住等腰三角形的概念。
③记住等边三角形三边关系定理。
三角形是学生们平日里接触较多的一种图形,在低年级就已经直观认识过,因而本课的重点就放在三角形的稳定性、定义和分类上。
所学重难点都是由学生在操作中获得的,不是由老师讲出来,硬塞给学生。
这样做,学生就会主动参与学习,落到实处,效果也好。
在整个课堂里,老师只是充当一个参与者、引导者。
课堂总结也是通过老师的引导,由学生做出归纳,这样效果要比由老师包办好。
从这节课可以看出:一、有效地激发了学生的兴趣,促进学生主动参与。
从学生的生活入手,让学生感受三角形与生活的密切联系,从而激发学生学习三角形的热情,变“要我学”为“我要学”。
二、改变数学学习方式,引导学生经历过程。
认识三角形2

3、一个三角形最多有______个锐角,至少有 _______个锐角
问题:
通过画图我们可以发现:锐角三角形的 三条中线、三条角平分线、三条高都交于一 点,并且这些交点都在三角形的________部
B
D
E
C
如果∠ADC=90°,那么线段AD 是△ABC的___
2、如图,AD、AM、AH分别是△ABC的角 平分线、中线、高。 (1)因为AD是△ABC的角平分线,所以 1 ∠___=∠____= ∠_____
2
(2) 因为AM是△ABC的中线,所以 A ___=____= 1 _____
2
(3)因为AH是△ABC 的高,所以 ∠___=∠____=90° B
M D H
C
3、如图,BD=DE=EF=FC。
AD是△____的中线,
____是△AEC的中线,
AE是△____和△_____的中线。
A
B
D
E
F
C
4、已知: AD、AE是△ABC中线和高。 AB=5cm,AC=3cm, (1)求△ABD与△ACD的周长之差; (2)写出△ABD与△ACD的面积关系, A 并说明理由
钝角三角形的三条中线、三条角平分线、 三条高________,并且三条高的交点在三 角形的________部
直角三角形的三条中线、三条角平分线、三 条高________ ,并且三条高的交点就是三角 形的________.
1、点D是△ABC的BC边上的一点。 如果BD=CD,那么线段AD是 △ABC的___ 如果∠BAD=∠CAD,那么线段 AD是△ABC的_____
1.1认识三角形(2)

问题导学:
直角三角形可以用符号 “Rt△”表示,直角三角形 ABC可以写成“Rt△ABC”. 把直角所对的边称为直角三 角形的斜边, 夹直角的两条 边称为直角边.
C
直 角 边A
直角边 B
直角三角形有许多性质,你能发现它的两个 锐角之间有什么关系吗?
直角三角形的两个锐角互余.
自学检测:
如图,在△ABC中,D为BC上的一点, ∠ADB=90°,∠1=∠B。若按角分类,△ABC 是什么形状的三角形?为什么?
A 2
1
B
D
C
巩固练习: 认一认:将下面的这些三角形进行分类
④
①
锐角三角形
直角三角形
钝角三角形
③⑤
① ④ ⑥
②⑦
巩固练习:
1、在△ABC中∠A:∠B:∠C=1:2:3,则 △ABC是( B ) A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
2、判断: (1)一个三角形的三个内角可以都小于 60°; ( × ) (2)一个三角形最多只能有一个内角是钝 角或直角; ( √ )
1.1认识三角形(2)
温故互查:(二人小组完成)
1、三角形的定义
? ?。
由不在同一直线上的三条线段,首尾顺次相接 所组成的图形叫做三角形.
2、三角形的三个内角有什么关系
三角形三个内角的和等于180
在△ABC中,∠A+∠B+∠C=1800
问题导学:
(1)下图中小明所拿三角形被遮住的两个内 角是什么角?小颖的呢?试着说明理由.
∠A+∠B+∠C+∠D+∠E+∠F= A B C H D G F 360 度
M
E
认识三角形(2)练习

认识三角形(2)练习一.目标导航1.通过观察、想象、推理、交流等活动,发展空间观念、推理能力和有条理地表达能力;2.能证明出“三角形内角和等于180°”,能发现“直角三角形的两个锐角互余”;3.按角将三角形分成三类.二.基础过关1.一个三角形的三个内角分别为α,α-1,α+1(α>1°),•则这个三角形三个内角的度数分别为()A.44°,45°,91°B.49°,59°,69°C.59°,60°,61°D.30°,60°,90°2.给定下列条件,不能判定三角形是直角三角形的是()A.∠A+∠B=∠C B.∠A:∠B:∠C=1:2:3C.2∠A=3∠B=4∠C D.∠A-∠B=∠C3.如图所示,AB∥CD,∠A=55°,∠C=80°,则∠M等于()A.55°B.25°C.35°D.15°4.在△ABC中,若∠A=78°36′,∠B=57°36°,则∠C=_______.5.已知在Rt△ABC中,∠C=90°,∠BAC=30°,AB=10,那么BC=_______.6.如图所示,将一幅直角三角板叠在一起,使直角顶点重合于点O,使∠AOB+∠DOC=_______.3题图6题图10题图7.在一个三角形中,最多有______个锐角,有______个直角,有_______个钝角.8.•在直角三角形中,•有一个锐角是另一个锐角2•倍,•则这两个锐角的度数是_________.9.在△ABC中,∠A:∠B=5:7,∠C-∠A=10°,则∠C=________.三.能力提升10.如图所示,∠1+∠2+∠3+∠4+∠5的度数为()A.180°B.360°C.220°D.300°11.如图所示,△ABC为直角三角形,∠ACB=90°,与∠1互余的角有()A.∠B B.∠A C.∠BCD和∠A D.∠BCD11题图13题图14题图12.三角形中,最大的内角不能小于()A.30°B.60°C.90°D.45°13.如图所示,AB∥CD,∠E=130°,∠F=70°,则∠1+∠2=_______,∠3+ ∠4=_______.14.如图所示,平面上放着等距离的10个点,把这些点作为三角形的顶点,•可作_____个等边三角形.15.如图所示,按规定,一块模板中AB,CD的延长线应相交成85°的角,因交点不在板上,不便测量,工人师傅连接AC,测得∠BAC=32°,∠DCA=65°,此时AB,CD的延长线相交成的角是否符合规定?为什么?15题图16.如图所示,AB⊥BC,DC⊥BC,若∠DBC=45°,∠A=70°,求∠D,∠AED,∠BFE的度数.16题图17.如图所示,AB∥CD,AD∥BC,∠1=65°,∠2=55°,求∠C的度数.17题图四.聚沙成塔如图(1)所示,有一个五角形ABCDE,你能说明∠A+∠B+∠C+∠D+∠E=180•°吗?如图(2)所示,如图(3)所示,如果B点向右移动到AC上或AC的另一侧时,•上述结论是否仍然成立呢?分别说明理由.。
7.4.2认识三角形(2)课课练及答案(苏科版七年级下)pfd版
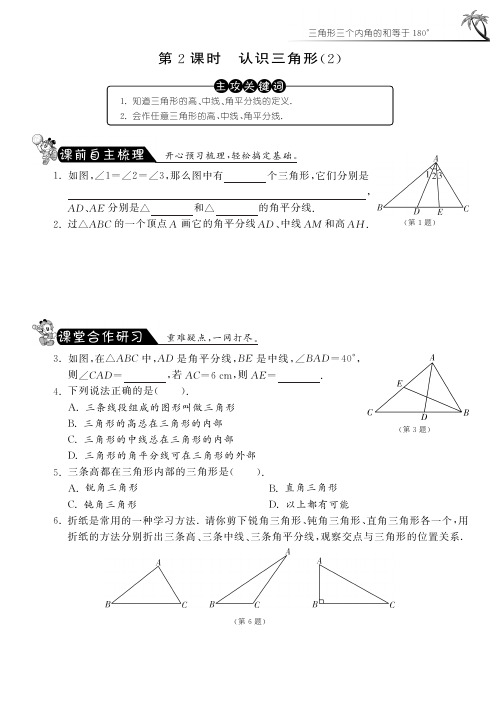
三角形三个内角的和等于180ʎ第2课时㊀认识三角形(2)㊀1.知道三角形的高㊁中线㊁角平分线的定义.2.会作任意三角形的高㊁中线㊁角平分线.㊀开心预习梳理,轻松搞定基础.(第1题)1.如图,ø1=ø2=ø3,那么图中有㊀㊀㊀㊀个三角形,它们分别是㊀,A D ㊁A E 分别是ә㊀㊀㊀㊀和ә㊀㊀㊀㊀的角平分线.2.过әA B C 的一个顶点A 画它的角平分线A D ㊁中线AM 和高AH .㊀重难疑点,一网打尽.(第3题)3.如图,在әA B C 中,A D 是角平分线,B E 是中线,øB A D =40ʎ,则øC A D =㊀㊀㊀㊀,若A C =6c m ,则A E =㊀㊀㊀㊀.4.下列说法正确的是(㊀㊀).A.三条线段组成的图形叫做三角形B .三角形的高总在三角形的内部C .三角形的中线总在三角形的内部D.三角形的角平分线可在三角形的外部5.三条高都在三角形内部的三角形是(㊀㊀).A.锐角三角形B .直角三角形C .钝角三角形D.以上都有可能6.折纸是常用的一种学习方法.请你剪下锐角三角形㊁钝角三角形㊁直角三角形各一个,用折纸的方法分别折出三条高㊁三条中线㊁三条角平分线,观察交点与三角形的位置关系.(第6题)七年级数学(下)㊀源于教材,宽于教材,举一反三显身手.(第7题)7.如图,A B ʊC D ,直线E F 与A B ㊁C D 分别相交于E ㊁F 两点,E P 平分øA E F ,过点F 作F P ʅE P ,垂足为P ,若øP E F =30ʎ,则øP F C =㊀㊀㊀㊀.8.能把一个三角形分成两个面积相等部分的是(㊀㊀).A.中线B .高C .角平分线D.以上都不是9.如图是3ˑ4的正方形网格(每个小正方形的边长为1),点A ㊁B ㊁C ㊁D ㊁E ㊁F ㊁G 七点在格点上.请解答下列各题:(1)在图(1)中画一个面积为1的直角三角形;(三角形的顶点从以上七点中选择)(2)在图(2)中画一个面积为12的钝角三角形.(三角形的顶点从以上七点中选择)(第9题)㊀瞧,中考曾经这么考!10.(2012 山东德州)不一定在三角形内部的线段是(㊀㊀).A.三角形的角平分线B .三角形的中线C .三角形的高D.三角形的中位线11.(2012 黑龙江绥化)若等腰三角形两边长分别为3和5,则它的周长是㊀㊀㊀㊀.第2课时㊀认识三角形(2)1.6㊀әA B D㊁әA B E㊁әA B C㊁әA D E㊁әA D C㊁әA E C㊀B A E㊀A C D2.如图:(第2题)3.40ʎ㊀3c m㊀4.C㊀5.A㊀6.略7.60ʎ㊀8.A㊀9.略㊀10.C㊀11.11或13。
认识三角形 (2)

教学过程:一、导入同学们,请观察这张图片,你能从图片里找到三角形吗?对,在这里。
想一想,你在生活中的哪些地方还见到过三角形?指名说说。
今天我们就一起来认识一下三角形。
(板书:三角形的认识)二、探究2、请在纸上画一个三角形,不要画的太小哦。
请你到前面来,在黑板上画一个三角形。
同学们,我们像刚才一样,将三条线段首尾相接围成的图形就是一个三角形。
(课件)3、下面老师要看看谁的眼睛最亮,(课件)认真观察,下面哪一幅图是三角形?为什么?(第3是三角形,因为只有它是由三条线段首尾相接围成的,其他都不是。
)说的真好,三条线段必须要首尾相接,才能围成三角形。
围成三角形的三条线段叫做三角形的边,线段的端点叫做三角形的顶点,每两条边之间的夹角叫做三角形的角。
请大家在自己刚才画好的三角形上标出三角形的边,顶点和角。
同桌探究交流,你找出了几条边,几个顶点,几个角?完成的同学用端正的坐姿告诉老师。
请你到前面来,在老师三角形上标出所有的边、角和顶点。
给大家说说,你的想法。
(三角形有三条边,三个顶点,三个角。
)孩子你真棒,谢谢你,请回座位。
5、大家请看,方格纸上有4个点,从这4个点中任选3个作为顶点,都能画一个三角形吗?你有什么发现?哪三个点可以,哪三个点不可以,为什么?请在答题纸上第2题中画一画,和同桌互相说一说你的发现。
有小组已经完成了,请你给大家说说你们小组的发现。
(B.C.D三点不可以画一个三角形,因为这三个点在一条直线上。
)所以我们发现在同一条直线上的三个点不能画一个三角形。
6、同学们,请看这幅图,你知道图中画的是什么吗?这是一个人字梁,是建造房屋时房顶的结构,你能量出图中人字梁的高度吗?你量的是哪条线段?它和底边有什么样的位置关系?请看答题纸上第3题,想一想,量一量,同桌交流你的发现。
指名回答。
(量的是中间最高的那条线段,它和底边互相垂直。
)7、如果我们把人字梁所表示的三角形画下来,就可以这样表示出它的高和底。
(课件出示三角形的高和底)从三角形的一个顶点到对边的垂直线段是三角形的高,这条对边是三角形的底。
认识三角形(2)

任意画一个锐角△ABC,请你画出BC边上的高. A
友情提示:
垂直的记号; 垂足的字母. C B D 三角形高线的说法:AD是Δ ABC的高;AD是Δ ABC中BC边 上的高;AD垂直于BC,垂足为D;∠ADB=∠ADC=90°. (1)锐角三角形有几条高?你能把它们都画出来吗? (2)这三条高之间有怎样的位置关系?将你的结果与同伴进 行交流. (3)锐角三角形的三条高是在三角形的内部还是外部? (4)你能用折纸的方法得到这三条高吗?
1.如图: (1)AC是哪些三角形的边? (2)若AB⊥CD,垂足为D,则CD是哪些三角形的高? (3)若E是BC中点,则AE是哪个三角形的中线?
A D B
A M B C ( 第 2题 )
F
E C ( 第 1题 )
2. 如图,已知BM是Δ ABC的中线,AB=5cm, BC=3cm,Δ ABM与Δ BCM周长差是多少?Δ ABM与 Δ BCM的面积有什么关系?
A
B
D E
F
C
课堂作业
1.如图(1), (1)当 = 时, AD是△ABC的中线. (2)当 = 时,ED是△BEC的角平分线. (3)当AD⊥BC时,BD是△ 的高,又是△
A E
图(1) 图(2)
的高.
A
B
D
C
B
C
2.如图(2),在△ABC中,分别画出中线AD、角平分线BE、 高CF.
课后探究
(3)尝试:小组内分工合作,分别画出 锐角三角形、直角三角形、钝角三角形 的3条角平分线. (4)三角形的3条角平分线之间有什么关 系?请将你的发现结果与同学交流.
三角形的三条角平分线都在三 角形的内部,并且交于一点.
1.1 认识三角形 第2课时 浙教版数学八年级上册课件(共24张PPT)

三角形 的高线
从三角形的一个顶 点向它的对边所在 的直线作垂线,顶点
B
和垂足之间的线段
A
∵AD是△ABC的BC上的高线.
∴AD⊥BC
D C ∠ADB=∠ADC=90°.
再见
2
3
4
5
6
7
8
9 10
01 23 4 5
D
C
新课讲解
一个三角形的高线共有几条?总的结高(三:在夹条三钝)角角形的的两外边部上. 因此必须先把它们的边
请画出下面三角形的高线,你延发长现,再了画什它么们?的高.
A
A
F E
B
D
CC
D B
B
A D
CE F
新课讲解
三角形的高线 总结
高 锐角三角形
直角三角形
新课讲解
一个三角形有几条角平分线? (三条) 请画出下面三角形的角平分线,你发现了什么?
三角形的三条角平分线交于一点. 称之为三角形的内心.
做一做
如图,AE是△ABC的角平分线.已知∠B=45°, ∠ C=60°,
求下列角的大小.
C
(1) ∠BAE (2) ∠AEB
E
解(:1)∵AE是△ABC的角平分线
EO D
B
C
(3)当∠A= x 时,求∠BOC的度数 (用含x代数式表示).
变式:将上体中的角平分线改为高线,∠BOC和∠A又会有什么 数量关系?
做一做
A
4.如图,已知:△ABC中,BD、CE分别
是△ABC的两条高线,AC=4,BD=5,CE=3,
EOD
求AB.
B
C
一展身手
A 5.课本P9,探究活动
11.1认识三角形(2)

1.请同学们按照四人小组用你所想到的方法求出三角形的内角和。2.按小组汇报。
(1)老师刚才看到许多同学都是用量角器进行测量,那咱们来看看他们量的结果如何。
我们先来看锐角三角形(贴锐角三角形)。
哪些同学测量的是锐角三角形的内角?请两名同学分别说说三个内角分别是多少?内角和是多少?
我们再来看直角三角形(贴直角三角形)。
(A)带①去(B)带②去(C)带③去(D)带①和②去
五、小结:
六、作业布置:
七、板书设计:
八、课后反思
中点中点
同学们,通过拼和折,你们能得到一个什么结论?
结论:三角形的内角和等于180度(板书)
那,刚才我们量的结果中,为什么有的不是180度呢(引导学生说出“误差”)
三、巩固练习。(课件展示)
1、求出三角形各个角的度数。(有图)
(1)找三边相等。
(2)我是等腰三角形,顶角是96度。
(3)我是直角三角形,我有一个锐角是40度。(引导学生总结求直角三角形中锐角的方法)
(2)拼一拼。
剪下三个内角拼一拼,每种三角形的三个内角拼在一起分别能形成一个平角,即是180度,我们就可以说三角形的内角和是180度。(学生边汇报电脑边演示)
(1)(2)(3)
(3)折一折。
先找出三角形一个内角两条边的中点,再把两点连接起来,沿着这条线往下折,角的顶点刚好与对边重合,然后再把其它两个内角折起来,也能形成一个平角。从而可以证明三角形的内角和就是180度。
11.1认识三角形(二)
教学目标
知识目标:通过测量、撕拼、折叠等方法,探索和发现三角形三个内角的度数和等于180度。
能力目标:已知三角形两个角的度数,会求出第三个角的度数。
1.1认识三角形(2)

是△ABC的角平分线.已知∠BAC=82°∠C=40°,与
求∠DAE的大小。
高
解: ∵
AE是BC边上的角平分线, 且∠BAC=82°
1
∴ ∠EAC= ∠BAC=41°
2
Hale Waihona Puke ∵ AD是△ABC的高,B
A DE
线 有 关 C的
例∴ 1∠你ADC=还90°有其他解法吗?
计
算 ∵ ∠DAC+ ∠ADC+ ∠C =180° ((三根角形据三什内角么的?和)等于180°)
直角三角形的三条高
A
F
交于直角顶点。
议一议:
DB
C
钝角三角形的三条高
交于一点吗?
E
它们所在的直线交于一点吗? O
钝 角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
12
高 条数
位置
锐角三角形
3
都在三角 形内部
垂足 交点
在相应顶点的 对边上
在三角形内部
图形
A
B
C
直角三角形 3
直角边上的高分别 与另一条直角边重 合,还有一条高在 三角形内部
三角形的三条中线会交于同一 点,称之为三角形的重心.
如图,过△ABC的顶点A,
你能画它对边BC的垂线吗?
A
通过两个问题的引出,教师
引导学生回忆过一个已知点
画已知直线的垂线的方法,
B
并总结画图的规律:
D
C
一落,二靠,三画。
记垂足为D,线段AD即为:三角形的高。
在三角形中,过一个顶点作它对边的垂线段,
①是直角的顶点 ②在斜边上
在直角顶点
第七章 第6课时 认识三角形(2)

第6课时认识三角形(2)【基础巩固】1.在下列各图的△ABC中,正确画出AC边上的高的图形是()2.(2012.德州)不一定在三角形内部的线段是( )A.三角形的角平分线B.三角形的中线C.三角形的高D.三角形两边中点的连线3.(2012.哈尔滨)一个等腰三角形的两边长分别为5和6,则这个等腰三角形的周长是____.4.如图,在△ABC中,AD是角平分线,AH是高,CE是中线,(1)若∠BAD=40°,则∠CAD=_______°,∠CAB=________°;(2)若AB=6 cm,则AE=_______cm,BE=_______cm;(3)∠_______=∠_______=90°,写出图中直角三角形_____________________.5.如图,AD⊥BC于D,图中以AD为高的三角形有_______个,它们分别是_______.6.利用直角三角板分别画出下列三角形的三条高.【拓展提优】7.(2012.巴中)三角形的下列线段中能将三角形的面积分成相等两部分的是( ) A.中线B.角平分线 C.高D.两边中点的连线8.如图,AD⊥BC,GC⊥BC,CF⊥AB,D、C、F是垂足,下列说法中错误的是( )A.△ABC中,AD是BC边上的高B.△ABC中,GC是BC边上的高D.△GBC中,GC是BC边上的高D.△GBC中,CF是BG边上的高9.如图,△ABC中,∠ACB=90°,CD⊥AB,其中可以作为三角形的高的线段有()A.2条B.3条C.4条D.5条10.如图,已知AB⊥BC,EF⊥BC,CD⊥AD.(1)在△ABC中,BC边上的高是_______;(2)在△AEC中,AE边上的高是_______;(3)在△FEC中,EC边上的高是_______.11.等腰三角形的腰长是10,一腰上的中线将三角形的周长分成差为4的两部分,则等腰三角形的底边长是________.12.作图:(1)画出图中△ABC的高AD(标注出点D的位置);(2)画出把△ABC沿射线AD方向平移2 cm后得到的△A1B1C1;(3)根据“图形平移”的性质,得BB1=_______cm,AC与A1C1的关系是:_______.13.如图,已知△ABC.(1)画中线AD.(2)画△ABD的高BE及△ACD的高CF.量一量,比较BE和CF的大小.14.把△ABC的面积分成三等份.(用刻度尺画准,3种方法)参考答案【基础巩固】1.C 2.C 3.16或174.(1)4080 (2)3 3 (3)AHB AHC △ABH、△ACH、△ADH 5.6 △ABE,△ABD,△ABC,△AED,△AEC,△ADC6.略【拓展提优】7.A 8.B 9.D 10.(1)AB(2)CD (3)EF 11.6或14 12.(1)略(2)略(3)2平行13.略,相等14.略。
浙教版初中数学八年级上册1.1认识三角形2

三、自主学习
1.把一个角分成两个相等的
线叫做这个角的平分线。在三
A
角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点
之间的
叫做三角形的
。一个三角形共有
条角平
分线,它们相交于
点。
2.已知如图(1),AD 是△ABC 的平分线,
①则
=
1
=
,②若∠BAC=800,则∠
2
BAD=
, ∠CAD=
。
B
2cm。你能求出 AB 的长吗?
A
B
D
C
2.如图在三角形 ABC 中,AD 是三角形 ABC 的高,AE 是∠BAC 的角平分线. 已知∠ BAC=82°, ∠ C=40°,(1)求∠ DAE 的大小.(2)若 AE 是中线且 BC=10,AD=4,图中有面积 相等的三角形吗?面积是多少?
A
B DE
均在三角形的 ,三条高的延长线也相交于 点。
四、合作学习
合作学习一
5.在三角形中,连结一个顶点与它对边
的线段,叫做这个三角形的
共有 条中线,它们相交于
点。
6.已知如图(2),AD 是△ABC 中 BC 是的中线,
则①BD ②S△ABD
DC
1
S△ADC
S△ABC,
2
1
BC,
2
③若 BC=8cm,则 BD=
C
七、总结反思 通过本节课的学习,你知道了哪些新知识?有什么新方法?还有什么不明白的地方和问题? 新知识: 新方法: 不明白处和问题:
相信自己,就能走向成功的第一步 教师不光要传授知识,还要告诉学生学会生活。数学思维可以让
他们更理性地看待人生
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 三条线段的长度分别为:
(1)3cm、4cm、5cm; (2)8cm、7cm、15cm;
(3)13cm、12cm、20cm; (4)5cm、5cm、11cm;
能组成三角形的有( B )组。
A、1
B、2
C、3
D、4
2.三角形的两边长分别为3和5,第三边 的长可以是8吗?可以是2吗?
3.在△ABC中,a=4, b=2,若第三边
1.分别量出下面三个三角形的三边长 度,并填入空格内:
⑴a=______; ⑵a=______; b=______; b=______; c=______; c=______;
⑶a=______; b=______; c=______;
2. 计算每个三角形的任意两边之差,并与第三边比较, 你能得到什么结论?
B C (2)在一个三角形中,任意两边之和与第三边的长 度有怎样的关系? 三角形任意两边之和大于第三边
三角形 边的性质
三角形任意两边之和大于 第三边。
a+b>c
C
a+c>ห้องสมุดไป่ตู้ b+c>a
⑴ ⑵ C
b
A
a c
B
能否用以前学过的知识来解释? B 两点之间,线段最短!
A
⑶
在三角形中,任意两边之 和大于第三边,那么任意 两边之差与第三边的长度 有怎样的关系呢?
1.有两边相等的三角形叫等腰三角形;
顶角
腰 底角
腰 底角
底边
2.有三边相等的三角形叫等边三角形;
也叫正三角形
⑴元宵节的晚上,房梁上亮起了彩灯,装有黄色 彩灯的电线与装有红色彩灯的电线哪根长呢?说 说你的理由。 利用你发现的规律填空: A AB+AC > BC;
AC+BC
> AB;
AB+BC > AC;
1、有两根长度分别为5cm和8cm的木棒,取一根木棒,
与原来的两根木棒摆成三角形,你准备取多长的木棒?
2、有两根长度分别为5cm和8cm的木棒,取一根木 棒,与原来的两根木棒摆成三角形,则第三根木棒最 长不能超过多少?最短不能少于多少?
第三根木棒大于3cm,小于13cm.
三角形第三边的取值范围是: 两边之差<第三边<两边之和
c的长是偶数,求c的长。
姚明一步能走3米吗?现在你能做出回答 了吗?
姚明身高为 2.26米, 他的 腿长大约为1.2 米,他一步(两 脚着地时两脚 的间距)能迈 3米吗?
P67 习题3.2 第2、3题
三角形 边的性质
三角形任意两边之差小于 第三边。
C
b-a<c
c-a<b c-b<a
A
b c
a
B
例1 有两根长度分别为5cm和8cm的木棒,用长度为
2cm的木棒与它们能摆成三角形吗?为什么?
长度为13cm的木棒呢?
解: 取长度为2cm的木棒时,由于2+5=7
<8,出现了两边之和小于第三边的
情况,所以它们不能摆成三角形。 取长度为13cm的木棒时,由于5+8=13=13 (第三边),出现了两边之和等于第三边的 情况,所以它们也不能摆成三角形。
有人说他一步能走3米,你相信吗?
知识再现:
锐角三角形 ————所有内角都是锐角的三角形 直角三角形 ————有一个内角是直角的三角形 钝角三角形 ————有一个内角是钝角的三角形
①
②
③
④
⑤
④
⑤
锐角三角形
⑥
直角三角形 ③ ⑥
⑦ ⑦ 钝角三角形
⑤
② ⑦
①
②
③
④
⑤
⑥
⑦
这些三角形中,有等腰三角形吗?
