认识三角形(2)答案
中考《三角形认识》复习练习题及答案

中考数学复习专题练习认识三角形一、选择题:1、一定在△ABC内部的线段是()A.锐角三角形的三条高、三条角平分线、三条中线B.钝角三角形的三条高、三条中线、一条角平分线C.任意三角形的一条中线、二条角平分线、三条高D.直角三角形的三条高、三条角平分线、三条中线2、有5根小木棒,长度分别为2cm、3cm、4cm、5cm、6cm,任意取其中的3根小木棒首尾相接搭三角形,可搭出不同的三角形的个数为()A.5个 B.6个 C.7个 D.8个3、如图,AD是△ABC中∠BAC的角平分线,DE⊥AB于点E,S△ABC=7,DE=2,AB=4,则AC长是()A.3 B.4 C.6 D.54、如图,一副分别含有30°和45°角的两个直角三角板,拼成如下图形,其中∠C=90°,∠B=45°,∠E=30°,则∠BFD的度数是( )A.15° B.25° C.30° D.10°5、如图,在△ABC中,∠ACB=100°,AC=AE,BC=BD,则∠DCE的度数为()A.20° B.25° C.30° D.40°6、一个多边形少加了一个内角时,它的度数和是1310°,则这个内角的度数为()A.120° B.130° C.140° D.150°7、已知一个等腰三角形两内角的度数之比为1:4,则这个等腰三角形顶角的度数为()A.20°或100° B.120° C.20°或120° D.36°8、一个正多边形的每个内角都等于140°,那么它是正()边形A.正六边形 B.正七边形 C.正八边形 D.正九边形9、如图所示,小华从A点出发,沿直线前进10米后左转24°,再沿直线前进10米,又向左转24°,…,照这样走下去,他第一次回到出发地A点时,一共走的路程是()A.140米 B.150米 C.160米 D.240米10、如图,已知点D是△ABC的重心,连接BD并延长,交AC于点E,若AE=4,则AC的长度为()A.6 B.8 C.10 D.1211、.光线a照射到平面镜CD上,然后在平面镜AB和CD之间来回反射,光线的反射角等于入射角.若已知∠1=52°,∠3=70°,则∠2是( )A.52° B.61° C.65° D.70°12、如图,在四边形ABCD中,E、F分别是AB、AD的中点.若EF=2,BC=5,CD=3,则tanC等于()A. B. C. D.二、填空题:13、a、b、c为三角形的三条边,则= .14、如图,△ABC的两条高线AD、BE交于点F,∠BAD=45°,∠C=60°,则∠BFD的度数为15、如果将长度为a﹣2,a+5和a+2的三根线段首尾顺次相接可以得到一个三角形,a取值范围是.16、一个三角形的两边长为8和10,若另一边为a,当a为最短边时,a的取值范围是;当a为最长边时,a的取值范围是 .17、已知△ABC 的三边长 a、b、c,化简│a+b-c│-│b-a-c│的结果是 .18、将一副三角尺按如图所示的方式放置,使含30°角的三角尺的短直角边和含45°角的三角尺的一条直角边重合,则∠1的度数是.19、如图,∠2+∠3+∠4=320°,则∠1= .20、如图,七星形中∠A+∠B+∠C+∠D+∠E+∠F+∠G= .21、如图,将∠BAC沿DE向∠BAC内折叠,使AD与A′D重合,A′E与AE重合,若∠A=30°,则∠1+∠2= .22、如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数为.23、如图,已知矩形ABCD,一条直线将该矩形ABCD分割成两个多边形,若这两个多边形的内角和分别为M和N,则M+N= _.24、如图,一个面积为50平方厘米正方形与另一个小正方形并排放在一下起,则△ABC面积是平方厘米.三、简答题:25、如图,在△ABC中,AB=AC,AC边上的中线把三角形的周长分为24cm和30cm两部分,求三角形各边的长.26、如图,AD为△ABC的中线,BE为△ABD的中线,(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;(2)作出△BED的BD边上的高;(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?27、(1)如图,在△ABC中,∠B=40°,∠C=80°,AD⊥BC于D,且AE平分∠BAC,求∠EAD的度数.(2)上题中若∠B=40°,∠C=80°改为∠C>∠B,其他条件不变,请你求出∠EAD与∠B、∠C之间的数列关系?并说明理由.28、如图,∠O=30°,任意裁剪的直角三角形纸板两条直角边所在直线与∠O的两边分别交于D、E两点.(1)如图1,若直角顶点C在∠O的边上,则∠ADO+∠OEB= 度;(2)如图2,若直角顶点C在∠O内部,求出∠ADO+∠OEB的度数;(3)如图3,如果直角顶点C在∠O外部,求出∠ADO+∠OEB的度数.29、如图(甲),D是△ABC的边BC的延长线上一点.∠ABC、∠ACD的平分线相交于P1.(1)若∠ABC=80°,∠ACB=40°,则∠P1的度数为;(2)若∠A=α,则∠P1的度数为;(用含α的代数式表示)(3)如图(乙),∠A=α,∠ABC、∠ACD的平分线相交于P1,∠P1BC、∠P1CD的平分线相交于P2,∠P2BC、∠P2CD的平分线相交于P3依此类推,则∠Pn的度数为(用n与α的代数式表示)30、阅读下列材料:某同学遇到这样一个问题:如图1,在△ABC中,AB=AC,BD是△ABC的高.P是BC边上一点,PM,PN分别与直线AB,AC垂直,垂足分别为点M,N.求证:.他发现,连接AP,有,即.由AB=AC,可得.他又画出了当点P在CB的延长线上,且上面问题中其他条件不变时的图形,如图2所示.他猜想此时BD,PM,PN之间的数量关系是:.请回答:(1)请补全以下该同学证明猜想的过程;证明:连接AP.∵,∴.∵AB=AC,∴.(2)参考该同学思考问题的方法,解决下列问题:在△ABC中,AB=AC=BC,BD是△ABC的高.P是△ABC所在平面上一点,PM,PN,PQ分别与直线AB,AC,BC垂直,垂足分别为点M,N,Q.①如图3,若点P在△ABC 的内部,则BD,PM,PN,PQ之间的数量关系是:;②若点P在如图4所示位置,利用图4探究得出此时BD,PM,PN,PQ之间数量关系是:.31、已知锐角△ABC中,CD、BE分别是AB、AC边上的高,M是线段BC的中点,连接DM、EM.(1)若DE=3,BC=8,求△DME的周长;(2)若∠A=60°,求证:∠DME=60°;(3)若BC2=2DE2,求∠A的度数.参考答案1、A.2、C.3、A.4、A.5、D.6、B.7、C.8、D.9、B.10、B.11、B.12、B.13、答案为:2a.14、答案为:60° 15、答案为:a>5.16、答案为:2<a≤8,10≤a<18.17、答案为:2b-2c. 18、答案为:75°.19、答案为:40°.20、答案为:180°.21、答案为:60°.22、答案为:40°.23、答案为:360°或540°或720°.24、答案为25.25、解:设AB=AC=2,则AD=CD=,(1)当AB+AD=30,BC+CD=24时,有2=30,∴ =10,2 =20,BC=24-10=14.三边长分别为:20 cm,20 cm,14 cm.(2)当AB+AD=24,BC+CD=30时,有=24,∴ =8,,BC=30-8=22.三边长分别为:16 cm,16 cm,22 cm.26、解:(1)∵∠BED是△ABE的一个外角,∴∠BED=∠ABE+∠BAD=15°+35°=50°。
七年级新思维24-认识三角形

24.认识三角形问题解决例1 (江苏省竞赛题)在△ABC 中,高BD 和CE 所在直线相交于O 点,若△ABC 不是直角三角形,且∠60A =°,则∠BOC =_______度. 【答案】当ABC △为锐角三角形时,∠60BOC =°.例2 (北京市竞赛题)如图,将纸片△ABC 沿着DE 折叠压平,则( ).A .∠A =∠1+∠2B .∠A =12(∠1+∠2)C .∠A =13(∠1+∠2) D .∠A =14(∠1+∠2)【答案】B 180B C AED ADE A ∠+∠=∠+∠=︒-∠,又1B C AED ADE ∠+∠+∠+∠+∠+2∠=360︒,得2(180)12360A ︒-∠+∠+∠=︒,化简得1(12)2A ∠=∠+∠.例3 (1)如图①,AD BC ⊥于D AE ,平分∠BAC ,试探寻∠DAE 与∠C 、∠B 的关系. (2)如图,②,若将点A 在AE 上移动到F ,FD BC ⊥于D ,其他条件不变,那么∠EFD 与∠C 、∠B 是否还有(1)中的关系?请说明理由. (3)请你提出一个类似的问题.B D CE E 图①图②AFB D AC【答案】(1)∠1();2DAE C B =∠-∠(2)过A 作AG BC ⊥于G ,则1();2EFD EAG C B ∠=∠=∠-∠(3)略例4 如图①,已知A 为x 轴负半轴上一点,B 为x 轴正半轴上一点,(02)(32)C D --,,,. (1)求△BCD 的面积;(2)如图②,若AC BC ⊥,作∠CBA 的平分线交CO 于P ,交CA 于Q ,判断∠CPQ 与∠CQP 的大小关系,并证明你的结论;(3)如图③,若∠ADC =∠DAC ,点B 在x 轴正半轴上运动,∠ACB 的平分线CE 交DA 的延长线于点E ,在B 点的运动过程中,EABC∠∠的值是否变化?若不变,求出其值;若变化,请说明理由.12EBD AC图①图②图③【答案】(1)3BCD S =△ (2)可证明.CPQ CQP ∠=∠(3)CD ∥AB ,可证明1122ABCE ABC ABC ∠∠==∠∠为定值. 例5 在三角形纸片内有2008个点,连同三角形纸片的3个顶点,共有2011个点,在这些点中,没有三点在一条直线上.问:以这2011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形? (天津市竞赛题)解法一 我们不妨先退一步,考察三角形内有一个点、两个点、三个点…的简单情形,有下表所示的关系:不难发现,这个点必落在已连好的某一个小三角形内,它与该三角形的三个顶点可得到三个小三角形,从而增加了两个小三角形,于是可以推出,当三角形内有2008个点时,连接可得到小三角形的个数为:3+2×(2008-1)=4017(个).解法二 整体核算法.设连线后把原三角形分割成n 个小三角形,则它们的内角和为180°·n ,又因为原三角形内每一个点为小三角形顶点时,能为小三角形提供360°的内角,2008个点共提供内角2008×360°,于是得方程1803602008180n =⨯+,解得4017n =,即这2008个点能将原三角形纸片分割成4017个小三角形. 角平分线角平分线是联系角与角之间关系的纽带,当角平分线与三角形相遇可生成内涵上有关联性、解法上有共通性的组图.例6 (1)如图①,已知△ABC 中的两内角平分线交于P 点,两外角平分线交于M 点,一内角平分线与一外角平分线交于N 点.试分别探究∠BPC 、∠M 、∠N 与∠A 关系; (2)如图②,在凹四边形ABCD 中,已知∠ABD 与∠ACD 的平分线交于点E , 求证:2A DE ∠+∠∠=.y y x x PNBM ACBDA CE图①图②分析与解 (1)∠90BPC =°+11190.222A M A N A ∠∠=︒-∠∠=∠,,(2)凹四边形ABCD 形似“规形”,易证∠BDC =∠A +∠B +∠C . 图②可分解为两个“规形”,BE CE 、分别平分∠ABD 、∠ACD ,∴可设∠ABE =∠DBE =x ,∠ACE =∠DCE =y . 由(1)得∠E =∠A +x y +, ① ∠D =∠E +x y +, ② ②-①得,∠D –∠E =∠E –∠A , ∴∠E =2A D∠+∠. 数学冲浪知识技能广场 1.(2012年山东省烟台市中考题)一副三角形叠在一起如图放置,最小锐用的顶点D 恰好放在等腰直角三角板的斜边AB 上,BC 与DE 交于点M .若∠ADF =100°,则∠BM D =_______度. 【答案】851MF EBDAC(第1题)(第2题)2.(湖北省荆州市中考题)一副三角板,如图所示叠放在一起,则图中∠1的度数为_______. 【答案】75° 3.(新疆乌鲁木齐市中考题)如图,△ABC 中,∠80A =°,剪去∠A =80°,剪去∠A 后,得到四边形BCED ,则∠1+∠2=_______. 【答案】260°EBD A C21(第3题)(第4题)4.(广西桂林市中考题)如图,在△ABC 中,∠A =α,∠ABC 的平分线与∠ACD 的平分线交于点1A ,得∠1;A ∠1A BC 的平分线与∠1ACD 的平分线相交于点2A ,得∠2A ;…,2008A BC ∠的平分线与∠2008A CD 的平分线相交于点2009A ,得∠2009A ,则∠2009A =_______.【答案】20092α5.(“希望杯”邀请赛试题)如图,△ABC 中,∠A 、∠B 、∠C 的外角分别记为αβγ、、.若345αβγ=∶∶∶∶,则∠A ∶∠B ∶∠C =( ). A .3∶2∶1 B .1∶2∶3 C .3∶4∶5 D .5∶4∶3【答案】AγβαBA C(第5题)(第6题)PBMAC6.(“希望杯”邀请赛试题)如图,BP 是△ABC 中∠ABC 的平分线,CP 是∠ACB 的邻补角的平分线.若∠20ABP =︒,∠50ACP =°,则∠A +∠P =( ). A .70° B .80° C .90° D .100° 【答案】C 7.(内蒙古呼和浩特市中考题)在等腰△ABC 中,AB AC =,一边上的中线BD 将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为( ). A .7 B .11 C .7或11 D .7或10 【答案】C 8.(武汉市选拔赛试题)如图,△ABC 中,∠ABD =∠DBE =∠EBC ,∠ACD =∠DCE =∠ECB ,若∠145BEC =°,则∠BDC 等于( ). A .100° B .105° C .110° D .115° 【答案】CC(第8题)A B OM (第9题)EBD A CN9.如图,已知射线OM 与射线ON 互相垂直,B A 、分别为OM ON 、上一动点,∠ABM 、∠BAN 的平分线交于C .问:B A 、在OM ON 、上运动过程中,∠C 的度数是否改变?若不改变,求出其值;若改变,说明理由.【答案】190452C AOB ∠=︒-∠=︒,为一定值.10.如图①,已知△ABC 中,∠ABC =∠ACB D ,为BC 边上一点,E 为直线AC 上一点,且∠ADE =∠AED .(1)求证:∠2BAD =∠CDE ,(2)如图②,若D 在BC 的反向延长线上,其他条件不变,(1)中的结论是否仍成立?证明你的结论.DE CB(第10题)A图①图②B EAC【答案】(1)证明略;(2)(1)中的结论仍然成立 思维方法天地11.在△ABC 中,∠50A =°,高BE CF 、交于O ,且O 不与B C 、重合,则∠BOC 的度数为_______. 【答案】50130︒︒或 12.(“希望杯”邀请赛试题)如图,已知∠45C =°,∠45B =°+2α,∠45BAC =°+3α,AE 平分∠BAD ,则∠CAE =_______. 【答案】126︒ 13.(河南省竞赛题)如图,BP 平分∠ABC 交CD 于F ,DP 平分∠ADC 交AB 于E ,AB 与CD 相交于G ,如果∠4A =2°,∠38C =°,那么∠P 的度数为_______.【答案】40︒ 如图,由对顶三角形性质得122122A P A C ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩, 解得∠40P =°.14.如图,已知△ABC 中,∠A =∠ACB ,CP 平分∠ACB BD CD ,、分别为△ABC 的两外角的平分线,给出下列结论:①;CP CD ⊥②∠90D =°–12A ∠;③PD ∥AC .其中正确结论的个数是( ). A .0 B .1 C .2 D .3 【答案】D(第12题)EDAG 21B E CF P(第13题答案)DA(第13题)(第14题)F B A C FGC D E PDAP EB15.(江苏省竞赛题)如图,∠31ABC =°,又∠BAC 的平分线AE 与∠FCB 的平分线CE 相交于E 点,则∠AEC 为( ).A .14.5°B .15.5°C .16.5°D .20° 【答案】B(第15题)(第16题)E GFEBDACF B DA C16.如图,△ABC 中,∠90BAC =°,AD BC ⊥,∠ABC 的平分线BE 交AD 于点F ,AG 平分∠DAC .给出下列结论:①∠BAD =∠C ;②∠AEF =∠AFE ;③∠EBC =∠C ; ④AG EF ⊥.其中正确的结论是( ).A .②③④B .①③④C .①②④D .①②③ 【答案】C17.平面内的四条线段AB BC CD DA 、、、首尾顺次连接,已知∠24ABC =°, ∠42ADC =°.(1)如图①,若∠BAD 与∠BCD 的平分线交于点M ,求∠AMC 的值;(2)如图②,点E 在BA 的延长线上,∠DAE 的平分线和∠BCD 的平分线交于点N ,求∠ANC 的值.【答案】(1)可证明1()33.2AMC ABC ADC ∠=∠+∠=︒(2)可证明1(180)1232ANC B D ∠=︒+∠+∠=︒.NM 图①图②(第18题)(第17题)BD ACEBDA C GEB D A CF18.如图,在△BCD 中,BE 平分∠DBC 交CD 于F ,延长BC 至G CE ,平分∠DCG ,且EC DB 、的延长线交于A 点,若∠30A =°,∠75DFE =°.(1)求证:∠DFE =∠A +∠D +∠E ; (2)求∠E 的度数;(3)若在图中作∠CBE 与∠GCE 的平分线交于1E ,作∠1CBE 与∠1GCE 的平分线交于2E ,作∠2CBE 与∠2GCE 的平分线交于3E ,依此类推,∠n CBE 与∠n GCE 的平分线交于1n E +,请用含有n 的式子表示∠1n E +的度数.【答案】(1)略;(2)2D E ∠=∠,代入(1)得15;E ∠=︒(3)122113022n n n E D +++∠=∠=⋅︒. 应用探究乐园19.把一副学生用三角板(30°、60°、90°和45°、45°、90°)如图①放置在平面直角坐标系中,点A 在y 轴正半轴上,直角边AC 与y 轴重合,斜边AD 与y 轴重合,直角这AE 交x 轴于F ,斜边AB 交x 轴于G O ,是AC 中点,8AC =. (1)把图①中的Rt △AED 绕A 点顺时针旋转α度得图②,此时△AGH 的面积是10,△AHF 的面积是8,分别求F H B 、、三点的坐标;(2)如图③,设∠AHF 的平分线和∠AGH 的平分线交于点M ,∠EFH 的平分线和∠FOC 的平分线交于点N ,当△AED 绕A 点转动时,∠N +∠M 的值是否会改变,若改变,请说明理由,若不改变,请求出其值.(第19题)图①图②图③【答案】(1)(50)(10)(84)F H B ---,,,,,. (2)22.57597.522M N M N αα∠=︒+∠=︒-∠+∠=︒,,,故M N ∠+∠的值不会改变.20.(2012年山洪省青岛市中考题)问题提出 以n 边形的n 个顶点和它内部的m 个点,共(m n +)个点作为顶点,可把原n 边形分割成多少个互不重叠的小三角形?问题探究 为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:探究一:以△ABC 的三个顶点和它内部的1个点P ,共4个点为顶点,可把△ABC 分割成多少个互不重叠的小三角形?如图①,显然,此时可把△ABC 分割成3个互不重叠的小三角形.探究二:以△ABC 的三个顶点和它内部的2个点P Q ,,共5个点为顶点,可把△ABC 分割成多少个互不重叠的小三角形?在探究一的基础上,我们可看作在图①△ABC 的内部,再添加1个点,那么点Q 的位置会有两种情况:一种情况,点Q 在图①分割成的某个小三角形内部,不妨假设点Q 在△PAC 内部,如图②; 另一种情况,点Q 在图①分割成的小三角形的某条公共边上,不妨假设点Q 在PA 上,如图③.显然,不管哪种情况,都可把△ABC 分割成5个互不重叠的小三角形. 探究三:以△ABC 的三个顶点和它内部的3个点P Q R ,,共6个点为顶点,可把△ABC 分割成_______个互不重叠的小三角形,并在图④中画出一种分割示意图.探究四:以△ABC 的三个顶点和它内部的m 个点,共(3m +)个顶点,可把△ABC 分割成_______个互不重叠的小三角形.探究拓展:以四边形的4个顶点和它内部的m 个点,共(4m +)个顶点,可把四边形分割成_______个互不重叠的小三角形.问题解决 以n 边形的n 个顶点和它内部的m 个点,共(m n +)个顶点,可把△ABC 分割成_______个互不重叠的小三角形.实际应用 以八边形的8个顶点和它内部的2012个点,共2020个顶点,可把八边形分割成多少个互不重叠的小三角形?(要求列式计算)图④图①图②图③CABABAC【答案】7 分割示意图:(答案不唯一). 探究四:32(1)21m m +-+或 探究拓展:42(1)22m m +-+或 问题解决:2(1)22n m m n +-+-或实际应用:把82012n m ==,代入上述代数式,得2222012824024824030m n +-=⨯+-=+-=.BC A。
小学数学四年级-认识三角形和四边形(经典例题含答案)
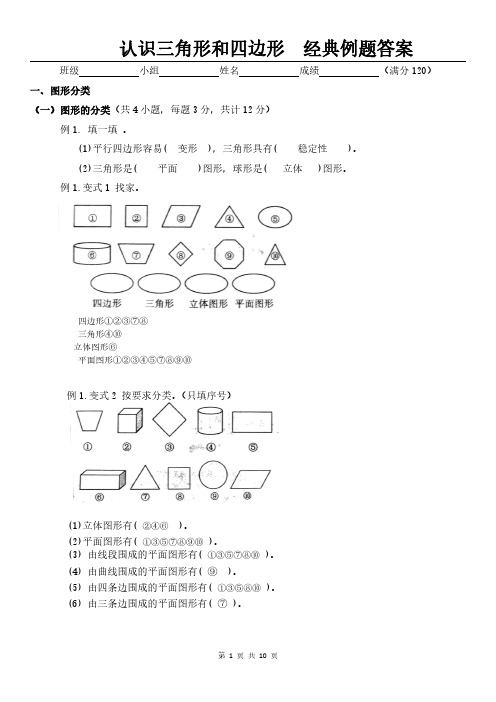
认识三角形和四边形经典例题答案班级小组姓名成绩(满分120)一、图形分类(一)图形的分类(共4小题,每题3分,共计12分)例1.填一填。
(1)平行四边形容易(变形),三角形具有(稳定性)。
(2)三角形是(平面)图形,球形是(立体)图形。
例1.变式1找家。
四边形①②③⑦⑧三角形④⑩立体图形⑥平面图形①②③④⑤⑦⑧⑨⑩例1.变式2按要求分类。
(只填序号)(1)立体图形有(②④⑥)。
(2)平面图形有(①③⑤⑦⑧⑨⑩)。
(3)由线段围成的平面图形有(①③⑤⑦⑧⑩)。
(4)由曲线围成的平面图形有(⑨)。
(5)由四条边围成的平面图形有(①③⑤⑧⑩)。
(6)由三条边围成的平面图形有(⑦)。
例1.变式3哪种围篱笆的方法更牢固?为什么?答:第二种方法更牢固,利用了三角形的稳定性(二)理解三角形的稳定性和四边形的不稳定性及其在生活中的运用(共4小题,每题3分,共计12分)例2.观察下面物体,你发现了什么?答:发现生活中的物品都是由图形构成的,三角形能起到很好的固定作用例2.变式1数一数,下面图中各有几个三角形。
104例2.变式2从一块长方形木板上锯掉一块宽为20厘米的长方形木条,剩下的木板为一个正方形,周长为180厘米,求原来长方形木板的周长和锯下的长方形木条的周长。
原:(180÷4+20+180÷4)×2=220(厘米)锯:(20+180÷4)×2=130(厘米)答:原来长方形木板的周长是220厘米,锯下的长方形木条的周长是130厘米.例2.变式3自行车的三角形车架是利用了三角形的(稳定性)特性.例3.填一填。
(1)三个角都是(锐)角的三角形是锐角三角形,有(一)个角是(直角)的三角形是直角三角形,有(一)个角是(钝角)的三角形是钝角三角形。
(2)有(两)条边相等的三角形是等腰三角形,(三)条边都相等的三角形是等边三角形。
例3.变式1分类。
(1)锐角三角形有(①⑤⑥)。
北师大四年级下册讲义第四讲 认识三角形和四边形(二)(含答案)

第四讲认识三角形和四边形(二)知识点四三角形边的关系1、三角形任意两边之和大于第三边。
2、根据上述知识点判断所给的已知长度的三条线段能否围成三角形。
如果能围成三角形,能围成一个什么样的三角形。
知识精讲四例1.三角形两边之和()第三边A.大于B.小于C.等于例2 .1,2,3厘米的三根火柴()围成三角形A.能B.不能例3.若等腰三角形的两边长分别为3和7,则它的周长为________。
例4.若等腰三角形的两边长分别是3和4,则它的周长为________。
例5.长为10、7、5、3的四跟木条,选其中三根组成三角形有________种选法。
例6.三角形的周长是24cm,三边长是三个连续的自然数,则三边长为________。
例7.在△ABC中,若a=3,b=5,则第三边c的取值范围是________。
例8.△ABD中,△B的对边是________。
例9.如果三条线段的比:(1)5:20:30;(2)5:10:15;(3)3:3:5(4)3:4:5;(5)5:5:10。
那么其中可以构成三角形的比有________。
例10.等腰三角形腰长10厘米,周长24厘米,底长________厘米。
例11.等腰三角形可以分为________、________、________。
例12.三角形按边分类可以分为________、________。
例13.已知等腰三角形的两边长分别为4,9,求它的周长例14.一个等腰三角形,周长为20cm,一边长6cm,求其他两边长参考答案1.【答案】A【考点】三角形的特性【解析】【解答】三角形两边之和大于第三边。
【分析】考查了三角形的特性。
2.【答案】B【考点】三角形的特性【解析】【解答】两边之和大于第三边才能围成三角形【分析】考查了三角形的特性3.【答案】17【考点】三角形的特性【解析】【解答】由两边之和大于第三边,另外一边只能是7,周长17厘米【分析】考察了三角形的特性4.【答案】10或11【考点】三角形的特性【解析】【解答】由两边之和大于第三边,另外一边可能是3或4【分析】考察了三角形的特性5.【答案】2【考点】三角形的特性【解析】【解答】3+5+7,5+7+10,一共两种【分析】考察了三角形的特性6.【答案】7cm ,8cm ,9cm【考点】三角形的特性【解析】【解答】其中一边必为24÷3=8,所以剩下两边是7和9【分析】考察了三角形的特性7.【答案】2到8【考点】三角形的特性【解析】【解答】根据两边之和大于第三边,两边只差小于第三边判断【分析】考察了三角形的特性8.【答案】AD【考点】三角形的特性【解析】【解答】画出三角形,来判断【分析】考察了三角形的特性9.【答案】(3),(4)【考点】三角形的特性【解析】【解答】根据两边之和大于第三边,两边只差小于第三边判断【分析】考察了三角形的特性10.【答案】4【考点】三角形的特性【解析】【解答】24-10-10=4厘米【分析】考察了三角形的特性11.【答案】等腰直角三角形;等腰锐角三角形;等腰钝角三角形【考点】三角形的特性【解析】【解答】等腰三角形的三种分类【分析】考察了三角形的特性12.【答案】等腰三角形;等边三角形【考点】三角形的特性【解析】【解答】三角形的分类【分析】考察了三角形的特性13.【答案】解:另外一边根据边的关系,只能是9,9+9+4=22答:它的周长是22【考点】三角形的特性【解析】【分析】考察了三角形的特性14.【答案】解:如果一边6厘米为腰时,则其他两边一个是腰6厘米,别一边是:20-6X2=8厘米;如果一边6厘米为底边时,则两个腰都是:(20-6)÷2=7厘米【考点】三角形的特性【解析】【分析】考察了三角形的特性对应练习一、选择题1.三角形两边之差()第三边A.大于B.小于C.等于2 .5,6,7厘米的三根火柴()围成三角形A.能B.不能3.有3厘米和4厘米的火柴,加上()厘米的火柴后能围成三角形A.6B.7C.8二、判断题4.三条线段一定能围成三角形5.三角形任意两边之和一定大于第三边6.三角形的三边长可以相等7.用四根一样的火柴棒可以围成一个三角形8.三角形任意两边之差大于第三边三、应用题9.三角形两边长为5厘米,8厘米,求第三边边长10.有木条4根,长度为12厘米,10厘米,8厘米,4厘米,选其中三根组成三角形,则选择的种数有哪几种11.三角形两边长为2厘米和7厘米,第三边长是奇数,第三边长多少?对应练习答案解析部分一、选择题1.【答案】B【考点】三角形的特性【解析】【解答】三角形两边之差小于第三边。
认识三角形(2)

拓展提高A与 的差为20 ∠ A与∠B 的差为200,求∠B。 ABC中 80° 2、在△ABC中, ∠ A= 80°, ∠C, 的度数。 ∠B= ∠C,求∠C的度数。
3、已知三角形三个内角的度数之比为 、 1:2:3,求这三个内角的度数 : : ,求这三个内角的度数.
ABC
A
C B
中,∠A=45°∠B=30°, ,∠A=45°∠B=30° 求∠C的度数。 的度数。
解:∵∠A+∠B+∠C=180° (三角形三个内角的和等于180°) ∵∠A+∠B+∠C=180° 三角形三个内角的和等于180° ∴ ∠C=180°-( ∠A+∠B) 180° = 180°-(45°+ 30°) 180° (45° 30° = 105° 105°
例2 在△ ABC中,∠A是∠B的2倍,∠C比 ∠A+∠B大12°,判断△ ABC的形状。 °
拓展:在△ ABC中, ∠C= ∠ABC=2 ∠A, 拓展 BD⊥AC, 求∠DBC度数。
1. 三角形三个内角的和等于180°。 即:△ABC中, ∠A +∠B +∠C=180 ° 2、三角形按内角的大小可分为: 、三角形按内角的大小可分为: 锐角三角形 直角三角形
6、观察下面的三角形,并把它们的标号 、观察下面的三角形, 填入相应的圈内。 填入相应的圈内。
①
②
③
④
⑤ 锐角三角形 ③ ⑤
⑥ 直角三角形 ① ④⑥
⑦ 钝角三角形 ② ⑦
思考: 思考:
在三角形中,最多有几个锐角? 在三角形中,最多有几个锐角? 几个钝角?几个直角呢? 几个钝角?几个直角呢? 那最少有几个锐角呢? 那最少有几个锐角呢?
A
钝角三角形
1.1认识三角形(2)

问题导学:
直角三角形可以用符号 “Rt△”表示,直角三角形 ABC可以写成“Rt△ABC”. 把直角所对的边称为直角三 角形的斜边, 夹直角的两条 边称为直角边.
C
直 角 边A
直角边 B
直角三角形有许多性质,你能发现它的两个 锐角之间有什么关系吗?
直角三角形的两个锐角互余.
自学检测:
如图,在△ABC中,D为BC上的一点, ∠ADB=90°,∠1=∠B。若按角分类,△ABC 是什么形状的三角形?为什么?
A 2
1
B
D
C
巩固练习: 认一认:将下面的这些三角形进行分类
④
①
锐角三角形
直角三角形
钝角三角形
③⑤
① ④ ⑥
②⑦
巩固练习:
1、在△ABC中∠A:∠B:∠C=1:2:3,则 △ABC是( B ) A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定
2、判断: (1)一个三角形的三个内角可以都小于 60°; ( × ) (2)一个三角形最多只能有一个内角是钝 角或直角; ( √ )
1.1认识三角形(2)
温故互查:(二人小组完成)
1、三角形的定义
? ?。
由不在同一直线上的三条线段,首尾顺次相接 所组成的图形叫做三角形.
2、三角形的三个内角有什么关系
三角形三个内角的和等于180
在△ABC中,∠A+∠B+∠C=1800
问题导学:
(1)下图中小明所拿三角形被遮住的两个内 角是什么角?小颖的呢?试着说明理由.
∠A+∠B+∠C+∠D+∠E+∠F= A B C H D G F 360 度
M
E
专题2-2 认识三角形(拓展提高)(解析版)

专题2.2认识三角形(拓展提高)一、单选题1.一个三角形的两边长分别为2和5,且第三边长为整数,这样的三角形的周长最大值是()A.10 B.11 C.12 D.13【答案】D【分析】先根据三角形的三边关系定理求得第三边的取值范围;再根据第三边是整数,从而求得周长最大时,对应的第三边的长.【详解】解:设第三边为a,根据三角形的三边关系,得:5-2<a<5+2,即3<a<7,∵a为整数,∴a的最大值为6,则三角形的最大周长为6+2+5=13.故选:D.【点睛】此题考查了三角形的三边关系:三角形两边之和大于第三边,两边之差小于第三边.2.如图,在△ABC中,AB=5,AC=8,CD=3BD,点E是AC的中点,BE、AD交于点F,则四边形DCEF 的面积的最大值是().A.10cm2B.9cm2C.8cm2D.7cm2【答案】B【分析】连接CF,设S△BFD=a,根据CD=3BD,点E是AC的中点,得出S△CFD=3a,S△ABF=S△CBF=4a,S△ABD=5a,即可得出S△ADC=15a,S△AFC=12a,S△ABC=20a,进而得出S四边形DCEF=9a,从而得出S四边形DCEF=920S△ABC,当△ABC的面积取最大值时,四边形DCEF的面积的最大,求得△ABC的面积的最大值,即可求得结果.【详解】解:连接CF,设S △BFD =a ,∵CD =3BD ,∴S △CFD =3a ,S △ADC =3S △ABD ,∵点E 是AC 的中点,∴S △ABE =S △CBE ,S △AFE =S △CFE ,∴S △ABF =S △CBF =4a ,∴S △ABD =5a ,∴S △ADC =15a ,∴S △AFC =12a ,S △ABC =20a ,∴S △EFC =6a ,∴S 四边形DCEF =9a ,∴S 四边形DCEF =920S △ABC , ∵在△ABC 中,AB =5,AC =8,∴S △ABC 的最大值为:12×5×8=20,∴四边形DCEF 的面积的最大值是9(cm 2),故选:B .【点睛】本题考查了三角形的面积,根据等高的三角形面积的比等于它们底的比,得出S 四边形DCEF =920S △ABC 是解题的关键.3.如图,直线a ∥b ,在Rt △ABC 中,点C 在直线a 上,若∠1=58°,∠2=24°,则∠B 的度数为( )A .56°B .34°C .36°D .24°【答案】A 【分析】利用平行线的性质,三角形的外角的性质求出∠A 即可解决问题. 【详解】解:如图,∵a ∥b ,∴∠1=∠3=58°,∵∠3=∠2+∠A , ∴∠A =58°-24°=34°, ∵∠ACB =90°, ∴∠B =90°-34°=56°, 故选:A .【点睛】本题考查平行线的性质,三角形的外角的性质,三角形的内角和定理等知识,解题的关键是熟练掌握基本知识.4.如图,ABC 面积为1,第一次操作:分别延长AB ,BC ,CA 至点1A ,1B ,1C ,使1A B AB =,1B C BC =,1C A CA =,顺次连接1A ,1B ,1C ,得到111A B C △,则111A B C △的面积是( )A .4B .7C .10D .13【答案】B 【分析】根据题意,连接A 1C ,得到11A BC ABC S S ∆∆==,则11122A B B A BC S S ∆∆==,然后同理可求112C B C S ∆=,12AAC S ∆=,即可得到答案. 【详解】解:连接A 1C ,如图∵AB =A 1B ,∴△ABC 与△A 1BC 的面积相等, ∵△ABC 面积为1, ∴11A BC S ∆=.∵BB 1=2BC , ∴11122A B B A BC S S ∆∆==,同理可得,112C B C S ∆=,12AAC S ∆=, ∴11122217A B C S ∆=+++=; 故选:B .【点睛】本题考查了三角形的面积,三角形的中线问题,此题属规律性题目,解答此题的关键是找出相邻两次操作之间三角形面积的关系,再根据此规律求解即可.5.如图,在△ABC 中,∠A =78°,∠EBD =∠EDB ,DF 平分∠EDC ,则∠BDF 的度数为( )A .35°B .39°C .40°D .45°【答案】B 【分析】设,BDF x EBD y ∠=∠=,利用外角性质求出2AED y ∠=,利用角平分线性质得到EDF CDF x y ∠=∠=+,根据三角形内角和定理得到180A ADE AED ∠+∠+∠=︒,即可求出答案. 【详解】解:设,BDF x EBD y ∠=∠=,∵∠EBD =∠EDB , ∴2AED y ∠=,∵DF 平分∠EDC ,∴EDF CDF x y ∠=∠=+, ∴180(22)ADE x y ∠=︒-+,∵180A ADE AED ∠+∠+∠=︒,∠A =78°, ∴78180(22)2180x y y ︒+︒-++=︒, 解得39x =︒, 故选:B .【点睛】此题考查三角形内角和定理,角平分线的性质定理,外角的性质,读懂图形理解各角之间的位置关系是解题的关键.6.如图,将一副三角尺按图中所示位置摆放,点F 在AC 上,其中90ACB ∠=︒,60ABC ∠=︒,90EFD ∠=︒,45DEF ∠=︒,//AB DE ,则AFD ∠的度数是( )A .15︒B .30C .45︒D .60︒【答案】A 【分析】设AB 与EF 交于点M ,根据//AB DE ,得到45AMF E ∠=∠=︒,再根据三角形的内角和定理求出结果.【详解】解:设AB 与EF 交于点M , ∵//AB DE , ∴45AMF E ∠=∠=︒,∵90ACB ∠=︒,60ABC ∠=︒, ∴30A ∠=︒, ∴1803045105AFM ∠=︒-︒-︒=︒, ∵90EFD ∠=︒,∴AFD ∠=15︒, 故选:A .. 【点睛】此题考查平行线的性质,三角形的内角和定理,熟记平行线的性质并应用是解题的关键. 二、填空题7.如图,在ABC 中,80A ∠=︒,30C ∠=︒,将CDE △沿DE 折叠得到C DE ',则12∠+∠等于__________________度.【答案】50°.【分析】连接DG ,将∠ADG+∠AGD 作为一个整体,根据三角形内角和定理来求解.【详解】解:连接DG ,根据折叠的性质,得:30C C '==︒∠∠,()()()12180'180'180180301808050C ADG AGD C A ∠+∠=︒-∠-∠+∠=︒-∠-︒-∠=︒-︒-︒-︒=︒故答案为:50°.【点睛】本题考查折叠的性质和三角形的内角和定理,解题的关键是作出辅助线帮助求解,熟练掌握基本知识,属于中考常考题型.8.如图,在ABC 中,80A ∠=︒,高BE 和CH 的交点为O ,则∠BOC =______ 【答案】100︒【分析】由BE 、CF 是△AB C 的高可得90BHC AEB ∠=∠=︒,根据三角形内角和定理可得∠ABE 的度数,进而可求出∠BOH 的度数,根据平角的定义即可得答案.【详解】∵BE 和CH 为ABC 的高, ∴90BHC AEB ∠=∠=︒, ∵80A ∠=︒,∴在ABE △中,180180908010ABE AEB A ∠=︒-∠-∠=︒-︒-︒=︒,在BHO △中,180180901080BOH BHO HBO ∠=︒-∠-∠=︒-︒-︒=︒, ∴180********BOC BOH ∠=︒-∠=︒-︒=︒. 故答案为:100︒.【点睛】本题考查三角形内角和定理,任意三角形的内角和等于180°,熟练掌握三角形内角和定理是解题关键.9.如图,△ABC 中,∠BDC =90°,BE 、CE 分别平分∠ABD 和∠ACD ,BF 、CF 分别平分∠ABE 和∠ACE ,若∠A =40°,则∠F =__°.【答案】52.5.【分析】利用三角形内角和、角平分线的性质求出∠FBC+∠FCB的度数,问题即可解决.【详解】解:∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°,∵∠BDC=90°,∴∠DBC+∠DCB=90°,∴∠ABD+∠ACD=140°﹣90°=50°,∵BE、CE分别平分∠ABD和∠ACD,BF、CF分别平分∠ABE和∠ACE,∴∠FBD+∠FCD=34×50°=37.5°,∴∠FBC+∠FCB=37.5°+90°=127.5°,∴∠F=180°﹣127.5°=52.5°,故答案为52.5.【点睛】本题考查三角形内角和定理,角平分线的定义等知识,关键是熟练掌握这些基本知识,这是基本的题型.10.如图,△ABC中,BE、CD分别平分∠ABC、∠ACB,并相交于点O,∠BOC=140°,则∠A=__°.【答案】100【分析】先根据BO平分∠ABC,CO平分∠ACB,可得∠ABC=2∠1,∠ACB=2∠2,再根据三角形内角和定理计算出∠1+∠2的度数,进而得到∠ABC+∠ACB,即可算出∠A的度数.【详解】解:如图,∵BO平分∠ABC,CO平分∠ACB,∴∠ABC=2∠1,∠ACB=2∠2,∵∠BOC=140°,∴∠1+∠2=180°﹣140°=40°,∴∠ABC+∠ACB=2×40°=80°,∴∠A=180°﹣80°=100°,故答案为:100【点睛】本题考查了角的平分线及三角形内角和定理,熟练掌握角的平分线与三角形内角和定理是解题的关键.11.如图,矩形ABCD的对角线AC,BD相交于点O,∠AOB=70°,则∠ACB的大小为____.【答案】35°【分析】根据矩形的性质和等腰三角形的性质求得∠BAO的度数,再根据直角三角形的两锐角互余求解即可.【详解】解:∵四边形ABCD是矩形,对角线AC,BD相交于点O,∴OA=OB,∠ABC=90°,又∵∠AOB=70°,∴∠BAO=∠ABO=12(180°﹣70°)=55°,∴∠ACB=90°﹣∠BAO=90°﹣55°=35°.故答案为:35°.【点睛】本题考查矩形的性质、等腰三角形的性质、直角三角形的两锐角互余,熟练掌握矩形的性质和等腰三角形的性质是解答的关键.12.如图,∠CAD和∠CBD的平分线相交于点P.请写出∠C、∠D、∠P的数量关系____________.【答案】2∠P=∠D+∠C【分析】根据三角形的外角性质、角平分线的定义得到12∠CAD+∠P=12∠CBD+∠C,12∠CAD+∠D=12∠CBD+∠P,两式相减整理即可.【详解】解:∵∠BF A=∠P AC+∠P,∠BF A=∠PBC+∠C,∴∠P AC+∠P=∠PBC+∠C,∵∠CAD和∠CBD的平分线相交于点P,∴∠P AC=∠P AD=12∠CAD,∠PBC=∠PBD=12∠CBD,∴12∠CAD+∠P=12∠CBD+∠C①,∵∠DEP=∠P AD+∠D,∠DEP=∠EBP+∠P,∴12∠CAD+∠D=12∠CBD+∠P②,①﹣②,得∠P﹣∠D=∠C﹣∠P,整理得,2∠P=∠D+∠C,故答案为:2∠P=∠D+∠C.【点睛】本题考查角平分线定义,三角形外角性质,以及等式的性质,掌握角平分线定义,三角形外角性质,以及等式的性质是解题关键.13.如图,点O是ABCD的对称中心,点E为BC边的中点,点F为AD边上的点,且13DF AD.若12,S S 分别表示AOE △和CDF 的面积,则1S 与2S 之间的等量关系是______.【答案】1234S S = 【分析】根据三角形性质可得S 1=14ABC S , S 2=13ADC S ,根据平行四边形性质可得 ABC ADC S S =,然后可以得到解答. 【详解】解:如图,连结OC ,则A 、O 、C 三点在同一直线上,∵O 是AC 中点,E 是BC 中点,∴S 1=11112224AEC ABC ABC S S S =⨯=,∵DF =13AD , ∴S 2=13ADC S , ∴S 1:S 2=113434=:, 即1234S S =, 故答案为1234S S =. 【点睛】本题考查三角形与平行四边形的综合应用,熟练掌握三角形中线的性质及平行四边形的对称性是解题关键.14.下图是可调躺椅示意图(数据如图),AE 与BD 的交点为C ,且A ∠,B ,E ∠保持不变.为了舒适,需调整D ∠的大小,使110EFD ∠=︒,则图中D ∠应___________(填“增加”或“减少”)___________度.【答案】减少 10【分析】先通过作辅助线利用三角形外角的性质得到∠EDF 与∠D 、∠E 、∠DCE 之间的关系,进行计算即可判断.【详解】解:∵∠A +∠B =50°+60°=110°, ∴∠ACB =180°-110°=70°, ∴∠DCE =70°, 如图,连接CF 并延长,∴∠DFM =∠D +∠DCF =20°+∠DCF ,∠EFM =∠E +∠ECF =30°+∠ECF ,∴∠EFD =∠DFM +∠EFM =20°+∠DCF+30°+∠ECF=50°+∠DCE=50°+70°=120°,要使∠EFD =110°,则∠EFD 减少了10°,若只调整∠D 的大小,由∠EFD =∠DFM +∠EFM =∠D +∠DCF +∠E +∠ECF =∠D +∠E +∠ECD =∠D +30°+70°=∠ D +100°,因此应将∠D 减少10度;故答案为:①减少;②10.【点睛】本题考查了三角形外角的性质,同时涉及到了三角形的内角和与对顶角相等的知识;解决本题的关键是理解题意,读懂图形,找出图形中各角之间的关系以及牢记公式建立等式求出所需的角,本题蕴含了数形结合的思想方法. 三、解答题15.已知ABC 中,AD BC ⊥于点D ,AE 平分BAC ∠,过点A 作直线//GH BC ,且60GAB ∠=︒,40C ∠=︒.(1)求ABC 的外角CAF ∠的度数;(2)求DAE ∠的度数.【答案】(1)100°;(2)10°【分析】(1)根据平行线的性质、对顶角相等计算即可;(2)根据角平分线的定义得到∠BAE =40°,根据平行线的性质求出∠GAD =90°,结合图形计算,得到答案.【详解】解:(1)∵GH ∥BC ,∠C =40°,∴∠HAC =∠C =40°,∵∠F AH =∠GAB =60°,∴∠CAF =∠HAC +∠F AH =100°;(2)∵∠HAC =40°,∠GAB =60°, ∴∠BAC =80°,∵AE 平分∠BAC , ∴∠BAE =40°,∵GH ∥BC ,AD ⊥BC , ∴∠GAD =90°, ∴∠BAD =90°-60°=30°,∴∠DAE =∠BAE -∠BAD =10°.【点睛】本题考查的是三角形的外角性质、三角形内角和定理、角平分线的定义、平行线的性质,掌握三角形内角和定理、平行线的性质是解题的关键.16.如图,ABC 中,80,30,BAC C BP ∠=︒∠=︒平分ABC ∠,点D 为射线BP 上一动点.(1)连接AD ,若//AD BC ,求ADB ∠的度数;(2)连接DC ,若DC 所在的直线垂直于ABC 的一边,则所有满足条件的BDC ∠的度数为__________.【答案】(1)35°;(2)125°或25°或55°【分析】(1)根据三角形内角和得到∠ABC ,根据角平分线的定义得到∠ABP ,再利用平行线的性质得到∠ADB ;(2)分1D C AB ⊥,2D C AC ⊥,3D C BC ⊥三种情况分别求解.【详解】解:(1)∵80BAC ∠=︒,30C ∠=︒, ∴70ABC ∠=︒,∵BP 平分ABC ∠, ∴35ABP CBP ∠=∠=︒, ∵//AD BC , ∴35ADB CBP ∠=∠=︒.(2)①当1D C AB ⊥时,延长1CD 至E ,90BEC ∠=︒,135ABD ∠=︒, ∴11125BDC BEC ABD ∠=∠+∠=︒, ②当2D C AC ⊥时,223090120BCD ACB ACD ∠=∠+∠=︒+︒=︒, ∴221801803512025BD C CBP BCD ∠=︒-∠-∠=︒-︒-︒=︒,③当3D C BC ⊥时,390BCD ∠=︒,35CBP ∠=︒, ∴33180180359055BD C CBP BCD ∠=︒-∠-∠=︒-︒-︒=︒.【点睛】本题考查了平行线的性质,角平分线的定义,三角形内角和,垂直的定义,解题的关键是灵活运用所学知识,同时分类讨论解决问题.17.给出三个多项式26,2,2A x x B x C x =-+=-=+.(1)计算:A B -;(2)计算:()B C A B ⋅⋅-;(3)分别比较A 与B 、A 与C 的大小,并说明理由;(4)若22x -<<时,A 、B 、C 能否作为同一个三角形的三边长?请说明理由.【答案】(1)24x +;(2)416x -;(3)A B >;A C >,理由见解析;(4)不能;证明见解析【分析】(1)计算A -B ,去括号,合并同类项即可;(2)将A ,B ,C 代入,利用整式的混合运算法则计算即可;(3)分别计算A -B 和A -C ,根据结果比较即可;(4)计算B +C ,将A 利用完全平方公式变形,比较B +C 和A 的结果可得.【详解】解:(1)()262A B x x x -=-+--262x x x =-+-+24x =+;(2)()B C A B ⋅⋅-()()()2224x x x =-++()()2244x x =-+416x =-;(3)A 与B ,2440A B x -=+≥>, ∴A B >,A 与C ,()262A C x x x -=-+-+262x x x =-+--224x x =-+()213x =-+, ∵10x -≥, ∴30A C -≥>, 故A C >;(4)不能作为同一个三角形的三边长,∵224x x -++==B +C ,221232364244A x x x ⎛⎫=-+=-+≥> ⎪⎝⎭, ∴B C A +<,故A 、B 、C 不能同时作为同一个三角形的三边长.【点睛】本题考查了整式的混合运算,三角形的三边关系,完全平方公式,平方差公式,解题的关键是掌握整式的大小比较方法的使用.18.如图,在ABC 中,90,BAC AD BC ∠=︒⊥于点,D AE 平分,50DAC B ∠∠=︒,求BAD ∠和AEC ∠的度数.【答案】∠BAD =40°,∠AEC =115°【分析】先由三角形内角和定理求出∠C 的度数,再由直角三角形的性质即可求出∠BAD 的度数;在△ADC 中,由∠ADC =90°,∠C =40°可得出∠DAC 的度数,再由角平分线的性质即可求出∠DAE 的度数,再由直角三角形的性质求出∠AED 的度数,由两角互补的性质即可得出∠AEC 的度数.【详解】解:在△ABC 中,∵∠BAC =90°,∠B =50°,∴∠C =90°-∠B =40°,∵AD ⊥BC 于点D ,∴∠BAD =90°-∠B =40°;在△ADC 中,∵∠ADC =90°,∠C =40°,∴∠DAC =90°-∠C =50°,∵AE 平分∠DAC ,∴∠DAE =12∠DAC =25°, 在△DAE 中,∵∠ADE =90°,∠DAE =25°,∴∠AED =90°-∠DAE =65°,∴∠AEC =180°-∠AED =180°-65°=115°.【点睛】本题考查的是三角形内角和定理、角平分线的性质及两角互补的性质,熟知三角形的内角和是180°是解答此题的关键.19.如图,将一张三角形纸片ABC 的一角折叠,使得点A 落在四边形BCDE 的外部A '的位置且A '与点C 在直线AB 的异侧,折痕为DE ,已知90C ∠=︒,30A ∠=︒.(1)求12∠-∠的度数;(2)若保持A DE '的一边与BC 平行,求ADE ∠的度数.【答案】(1)60°;(2)45°或30°【分析】(1)先求出∠B 的度数,在根据四边形内角和求出∠1+∠BFD 的度数,由∠BFD =∠A ′FE 和∠A ′的度数可求出答案.(2)分EA '∥BC 和DA '∥BC 两种情况讨论.当DA '∥BC 时,先求出∠A ′DA =90°,再根据折叠可得出∠ADE =45°;当EA '∥BC 时,根据平行线的性质求出∠2=∠ABC =60°,由(1)得出∠1=120°,再根据折叠可求出∠ADE 的度数.【详解】解:(1)由折叠可知,30A A '∠=∠=︒在A EF '△中,2180A A FE ''∠+∠+∠=︒2180150A AFE A FE ''∴∠=︒-∠-∠=︒-∠在ABC 中,18060B C A ∠=︒-∠-∠=︒在四边形BCDF 中,1360C B BFD ∠+∠+∠+∠=︒1360210C B BFD BFD ∴∠=︒-∠-∠-∠=︒-∠ 因为BFD A FE '∠=∠1221015060∴∠-∠=︒-︒=︒(2)①当//DA BC '时,90ADA ACB '∠=∠=︒ ADE 沿DE 折叠A DE ' 1452ADE A DE ADA ''∴∠=∠=∠=︒②当//EA BC '时,260ABC ∠=∠=︒由(1)知,1260∠-∠=︒,1260120∴∠=∠+︒=︒,ADE 沿DE 折叠A DE '()11801302ADE A DE ADA ''∴∠=∠=∠=︒-∠=︒综上,∠ADE 的度数为:45°或30°.【点睛】本题考查了翻折变换的性质,三角形的一个外角等于与它不相邻的两个内角的和,三角形的内角和等于180°,平行线的性质,属于综合题,但难度不大.熟记性质准确识图是解题的关键.20.先阅读下面的内容,再解答问题.(阅读)例题:求多项式2222613m mn n n ++-+的最小值.解;()()2222222226132694()(3)4m mn n n m mn nn n m n n ++-+=+++-++=++-+,∵22()0,(3)0m n n +≥-≥ ∴多项式2222613m mn n n ++-+的最小值是4.(解答问题)(1)请写出例题解答过程中因式分解运用的公式是____________;(2)已知a 、b 、c 是ABC 的三边,且满足2210841a b a b +=+-,求第三边c 的取值范围; (3)求多项式2224369x xy y y -+--+的最大值. 【答案】(1)完全平方公式;(2)1<c <9;(3)18【分析】(1)根据完全平方公式解答;(2)利用完全平方公式把原式变形,根据偶次方的非负性分别求出a 、b ,根据三角形的三边关系计算,得到答案;(3)利用完全平方公式把原式变形,根据偶次方的非负性解答即可.【详解】解:(1)例题解答过程中因式分解运用的公式是完全平方公式, 故答案为:完全平方公式;(2)a 2+b 2=10a +8b -41,a 2-10a +25+b 2-8b +16=0,(a -5)2+(b -4)2=0.∵(a -5)2≥0,(b -4)2≥0,∴a -5=0,b -4=0,∴a =5,b =4,∴5-4<c <5+4,即1<c <9;(3)原式=2222426918x xy y y y --+---+ =()()222226918x xy y y y ---++++ =()()222318x y y +---+∵-2(x -y )2≤0,-(y +3)2≤0,∴多项式2224369x xy y y -+--+的最大值是18. 【点睛】本题考查的是配方法的应用,掌握完全平方公式、偶次方的非负性是解题的关键.。
7.4.2认识三角形(2)课课练及答案(苏科版七年级下)pfd版
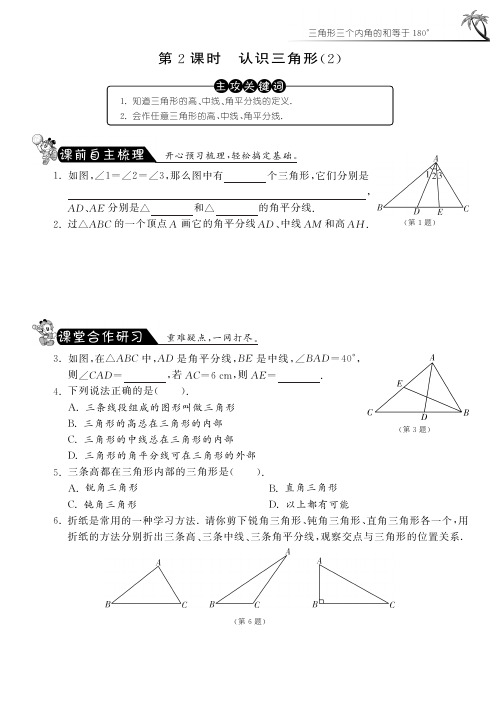
三角形三个内角的和等于180ʎ第2课时㊀认识三角形(2)㊀1.知道三角形的高㊁中线㊁角平分线的定义.2.会作任意三角形的高㊁中线㊁角平分线.㊀开心预习梳理,轻松搞定基础.(第1题)1.如图,ø1=ø2=ø3,那么图中有㊀㊀㊀㊀个三角形,它们分别是㊀,A D ㊁A E 分别是ә㊀㊀㊀㊀和ә㊀㊀㊀㊀的角平分线.2.过әA B C 的一个顶点A 画它的角平分线A D ㊁中线AM 和高AH .㊀重难疑点,一网打尽.(第3题)3.如图,在әA B C 中,A D 是角平分线,B E 是中线,øB A D =40ʎ,则øC A D =㊀㊀㊀㊀,若A C =6c m ,则A E =㊀㊀㊀㊀.4.下列说法正确的是(㊀㊀).A.三条线段组成的图形叫做三角形B .三角形的高总在三角形的内部C .三角形的中线总在三角形的内部D.三角形的角平分线可在三角形的外部5.三条高都在三角形内部的三角形是(㊀㊀).A.锐角三角形B .直角三角形C .钝角三角形D.以上都有可能6.折纸是常用的一种学习方法.请你剪下锐角三角形㊁钝角三角形㊁直角三角形各一个,用折纸的方法分别折出三条高㊁三条中线㊁三条角平分线,观察交点与三角形的位置关系.(第6题)七年级数学(下)㊀源于教材,宽于教材,举一反三显身手.(第7题)7.如图,A B ʊC D ,直线E F 与A B ㊁C D 分别相交于E ㊁F 两点,E P 平分øA E F ,过点F 作F P ʅE P ,垂足为P ,若øP E F =30ʎ,则øP F C =㊀㊀㊀㊀.8.能把一个三角形分成两个面积相等部分的是(㊀㊀).A.中线B .高C .角平分线D.以上都不是9.如图是3ˑ4的正方形网格(每个小正方形的边长为1),点A ㊁B ㊁C ㊁D ㊁E ㊁F ㊁G 七点在格点上.请解答下列各题:(1)在图(1)中画一个面积为1的直角三角形;(三角形的顶点从以上七点中选择)(2)在图(2)中画一个面积为12的钝角三角形.(三角形的顶点从以上七点中选择)(第9题)㊀瞧,中考曾经这么考!10.(2012 山东德州)不一定在三角形内部的线段是(㊀㊀).A.三角形的角平分线B .三角形的中线C .三角形的高D.三角形的中位线11.(2012 黑龙江绥化)若等腰三角形两边长分别为3和5,则它的周长是㊀㊀㊀㊀.第2课时㊀认识三角形(2)1.6㊀әA B D㊁әA B E㊁әA B C㊁әA D E㊁әA D C㊁әA E C㊀B A E㊀A C D2.如图:(第2题)3.40ʎ㊀3c m㊀4.C㊀5.A㊀6.略7.60ʎ㊀8.A㊀9.略㊀10.C㊀11.11或13。
七年级数学下册《认识三角形》练习题及答案解析(北师大版)
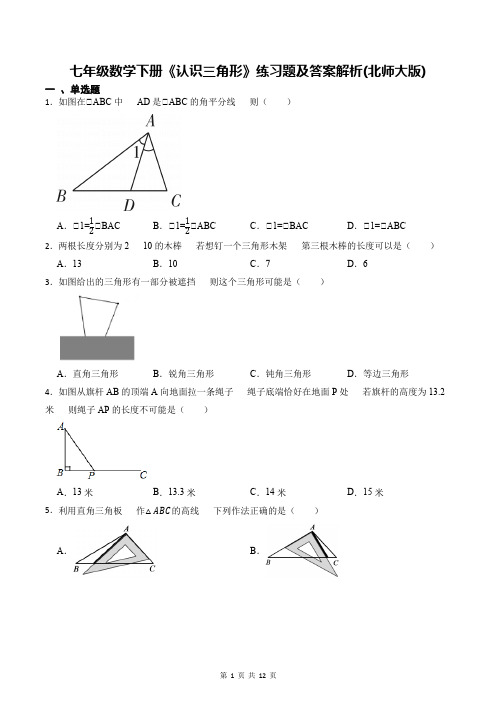
七年级数学下册《认识三角形》练习题及答案解析(北师大版) 一、单选题1.如图在△ABC中AD是△ABC的角平分线则()A.△1=12△BAC B.△1=12△ABC C.△1=△BAC D.△1=△ABC2.两根长度分别为2 10的木棒若想钉一个三角形木架第三根木棒的长度可以是()A.13B.10C.7D.63.如图给出的三角形有一部分被遮挡则这个三角形可能是()A.直角三角形B.锐角三角形C.钝角三角形D.等边三角形4.如图从旗杆AB的顶端A向地面拉一条绳子绳子底端恰好在地面P处若旗杆的高度为13.2米则绳子AP的长度不可能是()A.13米B.13.3米C.14米D.15米5.利用直角三角板作△ABC的高线下列作法正确的是()A.B.C.D.6.若一个直角三角形其中一个锐角为40° 则该直角三角形的另一个锐角是()A.60°B.50°C.40°D.30°7.如图AD BE CF是△ABC的三条中线则下列结论正确的是()A.BC=2AD B.AB=2AF C.AD=CD D.BE=CF8.如图用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限)不计螺丝大小其中相邻两螺丝的距离依次为3 4 5 7 且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框则任意两个螺丝间的距离的最大值为()A.9B.8C.7D.69.将一个三角形纸片剪开分成两个三角形这两个三角形不可能()A.都是直角三角形B.都是钝角三角形C.都是锐角三角形D.是一个直角三角形和一个钝角三角形10.如图若△ABC的三条内角平分线相交于点I 过I作DE△AI分别交AB AC于点D E 则图中与△ICE一定相等的角(不包括它本身)有()个.A.1B.2C.3D.4二、填空题11.如图AD AE分别是△ABC的角平分线和高∠B=50°∠C=70°则∠BAD=度∠EAD=度.12.已知三角形三边长分别为2 x 13 若x为正整数则这样的三角形有个.13.已知△ABC中△A=12△B=13△C 则△ABC是三角形.14.同一平面内有A B C三点A B两点之间的距离为5cm点C到直线AB 的距离为2cm且△ABC为直角三角形则满足上述条件的点C有个.三、作图题15.用圆规和直尺作图:已知△AOB(如图)求作:△AOB的平分线OC.(要求保留作图痕迹不写作法和证明过程).四解答题16.如图AD是△BAC的平分线CE是△ADC边AD上的高若△BAC=80° △ECD=25° 求△ACB的度数.17.已知a b c是△ABC的三边长若b=2a−1c=a+5且△ABC的周长不超过20cm 求a范围.18.如图在△ABC中AD△BC 垂直为D △1=△B △C=67° 求△BAC的度数19.如图所示图中共有多少个三角形?请写出这些三角形并指出所有以E为顶点的角.20.如图在△ABC中CE BF是两条高若△A=70° △BCE=30° 求△EBF与△FBC的度数.21.如图求△A+△B+△C+△D+△E的大小.22.如图1 AB与CD相交于点O 若△D=38° △B=28° △DAB和△BCD的平分线AP和CP 相交于点P 并且与CD AB分别相交于M N.试求:(1)△P 的度数;(2)设△D=α △B=β △DAP= 13 △DAB △DCP= 13 △DCB 其他条件不变 如图2 试问△P 与△D △B 之间存在着怎样的数量关系(用α β表示△P ) 直接写出结论.参考答案1.【答案】A【解析】【解答】解:∵AD 是△ABC 的角平分线 ∴△1=12△BAC故答案为:A.【分析】根据角平分线的定义求解即可.2.【答案】B【解析】【解答】解:设第三边的长度为x则10−2<x <10+2 即8<x <12 则x =10符合题意 故答案为:B.【分析】设第三边的长度为x 根据三角形中任意两边之和大于第三边 任意两边之差小于第三边 列出不等式组 求解可得x 的取值范围 从而一一判断即可得出答案.3.【答案】B【解析】【解答】解:由图形可得:该三角形为锐角三角形.故答案为:B.【分析】观察图形可知:图中的三角形有两个锐角 且第三个角也小于90° 据此可判断出三角形的形状.4.【答案】A【解析】【解答】解:∵旗杆的高度为AB =13.2米又∵AP >AB∴绳子AP 的长度不可能是:13米. 故答案为:A.【分析】直角三角形的性质:斜边大于直角边 据此解答即可.5.【答案】C【解析】【解答】解:由三角形的高线的定义可知:A 作法不符合题意 不符合题意;B 作法不符合题意 不符合题意;C 作法符合题意 符合题意;D 作法不符合题意 不符合题意; 故答案为:C .【分析】根据高线的定义逐项判断即可。
认识三角形(2)

任意画一个锐角△ABC,请你画出BC边上的高. A
友情提示:
垂直的记号; 垂足的字母. C B D 三角形高线的说法:AD是Δ ABC的高;AD是Δ ABC中BC边 上的高;AD垂直于BC,垂足为D;∠ADB=∠ADC=90°. (1)锐角三角形有几条高?你能把它们都画出来吗? (2)这三条高之间有怎样的位置关系?将你的结果与同伴进 行交流. (3)锐角三角形的三条高是在三角形的内部还是外部? (4)你能用折纸的方法得到这三条高吗?
1.如图: (1)AC是哪些三角形的边? (2)若AB⊥CD,垂足为D,则CD是哪些三角形的高? (3)若E是BC中点,则AE是哪个三角形的中线?
A D B
A M B C ( 第 2题 )
F
E C ( 第 1题 )
2. 如图,已知BM是Δ ABC的中线,AB=5cm, BC=3cm,Δ ABM与Δ BCM周长差是多少?Δ ABM与 Δ BCM的面积有什么关系?
A
B
D E
F
C
课堂作业
1.如图(1), (1)当 = 时, AD是△ABC的中线. (2)当 = 时,ED是△BEC的角平分线. (3)当AD⊥BC时,BD是△ 的高,又是△
A E
图(1) 图(2)
的高.
A
B
D
C
B
C
2.如图(2),在△ABC中,分别画出中线AD、角平分线BE、 高CF.
课后探究
(3)尝试:小组内分工合作,分别画出 锐角三角形、直角三角形、钝角三角形 的3条角平分线. (4)三角形的3条角平分线之间有什么关 系?请将你的发现结果与同学交流.
三角形的三条角平分线都在三 角形的内部,并且交于一点.
初一数学第七章 平面图形认识(二) 第6课时 认识三角形练习题(附答案)

第七章 平面图形认识(二)第6课时 认识三角形一、选择题1.(2011·来宾)已知一个三角形的两边长分别是2和3,则下列数据中,可作为第三边的长的是【 】A .1B .3C . 5D .72.下列哪组数据能构成三角形的三边 【 】A .1cm 、2cm 、3cmB .2cm 、3cm 、4cmC .4cm 、4cm 、9cmD .1cm 、2cm 、4cm3.一个三角形三边长分别为3、4、x ,则x 的取值范围是 【 】A .x >2B .x <5C .3<x <5D .1<x <74.(2012·义乌)三角形的两边长分别为3和5,第三边长是偶数,则第三边长可以是 【 】A .2B . 3C . 4D .85.若三角形的三边长分别为3,4,x -1,则x 的取值范围是 【 】A .0<x <8B .2<x <8C .0<x <6D .2<x <66.下列说法中正确的是 【 】A .有且只有一条直线垂直于已知直线B .互相垂直的两条线段一定相交C .从直线外一点到这条直线的垂线段,叫做这点到这条直线的距离D .三角形的高、中线、角平分线都是线段7.三角形的高线是 【 】A .直线B .线段C .射线D .三种情况都可能8.在三角形中,交点一定在三角形内部的有①三角形的三条高线 ②三角形的三条中线 ③三角形的三条角平分线 ④三角形的外角平分线 【 】A .①②③④B .①②③C .①④D .②③9.下列说法中:①三条线段组成的图形叫做三角形;②三角形的角平分线是射线;③三角形的三条高所在的直线相交于一点,这一点不在三角形的内部,就在三角形的外部;④三角形的三条中线相交于一点,且这点一定在三角形的内部.其中正确的有 【 】A .4个B .3个C .2个D .1个10.三角形的下列四种线段中一定能将三角形分成面积相等的两部分的是 【 】A .角平分线B .中位线C .高D .中线二、填空题11.(2012·金华)已知三角形的两边长为4,8,则第三边的长度可以是_________(写出一个即可).12.(2012·柳州)如果三角形的两条边长分别为23cm 和10cm ,第三边与其中一边的长相等,那么第三边的长为_________.12.若一个边长都是整数的三角形周长是15cm ,则满足条件的三角形有_________种.14.小明有两根3cm 、7cm 的木棒,他想以这两根木棒为边做一个等腰三角形,还需再选用一根_________. 长的木棒15.已知:在△ABC 中,AB =3,AC =7,BC 长是正整数,当△ABC 的周长最大时,此时BC 的长为_________.16.如果三角形的三条高的交点落在一个顶点上,那么它的形状是 _________.17.已知BD 是△ABC 的一条中线,△ABD 与△BCD 的周长分别为24,17,则AB -BC 的长是_________.18.如图,AD 、BE 、CF 是ABC ∆的3条中线,若AF =2cm ,则AB =____cm ,若BD =5cm ,则BC =____cm , 若AE =2cm ,则AC =____cm .则ABC ∆的周长是_______cm .F E D C B A 第19题A B C F E D 第20题 第18题19.如图,在△ABC 中,AD 是高,AE 是角平分线,BF 是中线,则∠ =∠ =90o ;∠ =∠ =BAC 21; = =12AC . 20.如图,(1)△ABC 的边BC 上的高是 ;(2)△ADC 的边DC 上的高是 ;(3)△EBC 的边EC 上的高是 ;(4)AB =2cm ,CF =2cm ,△ABC 的面积S =_____ cm 2.三、解答题21.(2013·新疆)等腰三角形的两边长分别为3和6,求这个等腰三角形的周长22.已知a 、b 、c 是△ABC 的三边长,化简|a +b -c |+|a -b -c |23.已知三角形的两边a =3,b =7,第三边是c ,且a <b <c ,求c 的取值范围?24.小亮家离学校1千米,小明家离学校3千米,如果小亮家与小明家相距x 千米,那么求x 的取值范围?25.如图,线段AB =CD ,AB 与CD 相交于•,且∠A •C =60°,CE 是由AB 平移所得,判断AC +BD 与AB 的大小关系?并说明理由。
浙教版八年级数学上《第1章三角形的初步认识》单元测试(2)含答案解析

《第1章三角形的初步认识》一、填空题1.已知三角形的两边分别为4和9,则此三角形的第三边可能是()A.4 B.5 C.9 D.132.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于()A.50° B.30° C.20° D.15°3.如图所示,△ACB≌A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20° B.30° C.35° D.40°4.长为9,6,5,4的四根木条,选其中三根组成三角形,选法有()A.1种B.2种C.3种D.4种5.尺规作图是指()A.用直尺规范作图B.用刻度尺和圆规作图C.用没有刻度的直尺和圆规作图D.直尺和圆规是作图工具6.如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=()A.50° B.40° C.70° D.35°7.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是()A.45° B.54° C.40° D.50°8.一副三角板如图叠放在一起,则图中∠α的度数为()A.75° B.60° C.65° D.55°9.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC ∥AB,则∠BAD的度数为()A.30° B.35° C.40° D.50°10.如图所示,△ABC与△BDE都是等边三角形,AB<BD.若△ABC不动,将△BDE绕点B旋转,则在旋转过程中,AE与CD的大小关系为()A.AE=CD B.AE>CD C.AE<CD D.无法确定二、认真填一填11.若三角形的两边长分别为3、4,且周长为整数,这样的三角形共有个.12.如图,在△ABC 和△DEF 中,已知:AC=DF ,BC=EF ,要使△ABC ≌△DEF ,还需要的条件可以是 .(只填写一个条件)13.若△ABC ≌△DEF ,且∠A=110°,∠F=40°,则∠E= 度.14.在△ABC 中,∠A :∠B :∠C=1:2:3,则∠A= ,∠C= .15.如图,在△ABC 中,∠B=60°,∠C=40°,AD ⊥BC 于D ,AE 平分∠BAC ;则∠DAE= .16.如图,D 、E 分别是△ABC 边AB 、BC 上的点,AD=2BD ,BE=CE ,设△ADC 的面积为S 1,△ACE 的面积为S 2,若S △ABC =6,则S 1﹣S 2的值为 .17.如图,将纸片△ABC 沿DE 折叠,点A 落在点P 处,已知∠1+∠2=100°,则∠A 的大小等于 度.18.如图,△ABC 中,∠BAC=100°,EF ,MN 分别为AB ,AC 的垂直平分线,如果BC=12cm ,那么△FAN 的周长为 cm ,∠FAN= .三、解答题19.如图,点A、C、D、B 四点共线,且AC=DB,∠A=∠B,∠E=∠F.求证:DE=CF.20.如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明.21.如图,在△ABC中,∠B=40°,∠C=110°.(1)画出下列图形:①BC边上的高AD;②∠A的角平分线AE.(2)试求∠DAE的度数.22.作图,如图已知三角形ABC内一点P(1)过P点作线段EF∥AB,分别交BC,AC于点E,F(2)过P点作线段PD使PD⊥BC垂足为D点.23.如图,在△ABC中,AD平分∠BAC,AD的垂直平分线EF交BC的延长线于点F,连接AF,求证:∠CAF=∠B.24.如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC.25.如图,在长方形ABCD中,AB=8cm,BC=6cm,点E是CD的中点,动点P从A点出发,以每秒2cm 的速度沿A→B→C→E运动,最终到达点E.若设点P运动的时间是t秒,那么当t取何值时,△APE 的面积会等于10?26.(14分)课本拓展旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?1.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?2.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C= ;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案.3拓展提升:(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)《第1章三角形的初步认识》参考答案与试题解析一、填空题1.已知三角形的两边分别为4和9,则此三角形的第三边可能是()A.4 B.5 C.9 D.13【考点】三角形三边关系.【分析】根据三角形的第三边大于两边之差,而小于两边之和求得第三边的取值范围,再进一步选择.【解答】解:根据三角形的三边关系,得第三边大于5,而小于13.故选C.【点评】本题考查了三角形的三边关系,即三角形的第三边大于两边之差,而小于两边之和,此题基础题,比较简单.2.如图,将三角尺的直角顶点放在直尺的一边上,∠1=30°,∠2=50°,则∠3的度数等于()A.50° B.30° C.20° D.15°【考点】平行线的性质;三角形的外角性质.【专题】计算题.【分析】首先根据平行线的性质得到∠2的同位角∠4的度数,再根据三角形的外角的性质进行求解.【解答】解:根据平行线的性质,得∠4=∠2=50°.∴∠3=∠4﹣∠1=50°﹣30°=20°.故选:C.【点评】本题应用的知识点为:三角形的外角等于与它不相邻的两个内角的和.两直线平行,同位角相等.3.如图所示,△ACB≌A′CB′,∠BCB′=30°,则∠ACA′的度数为()A.20° B.30° C.35° D.40°【考点】全等三角形的性质.【分析】根据全等三角形性质求出∠ACB=∠A′CB′,都减去∠A′CB即可.【解答】解:∵△ACB≌A′CB′,∴∠ACB=∠A′CB′,∴∠ACB﹣∠A′CB=∠A′CB′﹣∠A′CB,∴∠ACA′=∠BCB′,∵∠BCB′=30°,∴∠ACA′=30°,故选B.【点评】本题考查了全等三角形性质的应用,注意:全等三角形的对应角相等.4.长为9,6,5,4的四根木条,选其中三根组成三角形,选法有()A.1种B.2种C.3种D.4种【考点】三角形三边关系.【专题】常规题型.【分析】要把四条线段的所有组合列出来,再根据三角形的三边关系判断能组成三角形的组数.【解答】解:四根木条的所有组合:9,6,5和9,6,4和9,5,4和6,5,4;根据三角形的三边关系,得能组成三角形的有9,6,5和9,6,4和6,5,4.故选:C.【点评】本题考查了三角形的三边关系,熟记三角形的任意两边之和大于第三边,两边之差小于第三边是解题的关键.5.尺规作图是指()A.用直尺规范作图B.用刻度尺和圆规作图C.用没有刻度的直尺和圆规作图D.直尺和圆规是作图工具【考点】作图—尺规作图的定义.【分析】根据尺规作图的定义作答.【解答】解:根据尺规作图的定义可知:尺规作图是指用没有刻度的直尺和圆规作图.故选C.【点评】尺规作图是指用没有刻度的直尺和圆规作图.6.如图,BE、CF都是△ABC的角平分线,且∠BDC=110°,则∠A=()A.50° B.40° C.70° D.35°【考点】三角形内角和定理;角平分线的定义.【分析】根据数据线的内角和定理以及角平分线的定义,可以证明.【解答】解:∵BE、CF都是△ABC的角平分线,∴∠A=180°﹣(∠ABC+∠ACB),=180°﹣2(∠DBC+∠BCD)∵∠BDC=180°﹣(∠DBC+∠BCD),∴∠A=180°﹣2(180°﹣∠BDC)∴∠BDC=90°+∠A,∴∠A=2(110°﹣90°)=40°.故选B.【点评】注意此题中的∠A和∠BDC之间的关系:∠BDC=90°+∠A.7.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE的大小是()A.45° B.54° C.40° D.50°【考点】平行线的性质;三角形内角和定理.【分析】根据三角形的内角和定理求出∠BAC,再根据角平分线的定义求出∠BAD,然后根据两直线平行,内错角相等可得∠ADE=∠BAD.【解答】解:∵∠B=46°,∠C=54°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣46°﹣54°=80°,∵AD平分∠BAC,∴∠BAD=∠BAC=×80°=40°,∵DE∥AB,∴∠ADE=∠BAD=40°.故选:C.【点评】本题考查了平行线的性质,三角形的内角和定理,角平分线的定义,熟记性质与概念是解题的关键.8.一副三角板如图叠放在一起,则图中∠α的度数为()A.75° B.60° C.65° D.55°【考点】三角形的外角性质;三角形内角和定理.【分析】因为三角板的度数为45°,60°,所以根据三角形内角和定理即可求解.【解答】解:如图,∵∠1=60°,∠2=45°,∴∠α=180°﹣45°﹣60°=75°,故选A.【点评】本题利用三角板度数的常识和三角形内角和定理,熟练掌握定理是解题的关键.9.如图,在△ABC中,∠CAB=70°,将△ABC绕点A逆时针旋转到△ADE的位置,连接EC,满足EC ∥AB,则∠BAD的度数为()A.30° B.35° C.40° D.50°【考点】旋转的性质.【分析】根据两直线平行,内错角相等可得∠ACB=∠CAB,根据旋转的性质可得AC=AE,∠BAC=∠DAE,再根据等腰三角形两底角相等列式求出∠CAE,然后求出∠DAB=∠CAE,从而得解.【解答】解:∵CE∥AB,∴∠ACB=∠CAB=75°,∵△ABC绕点A逆时针旋转到△AED,∴AC=AE,∠BAC=∠DAE,∴∠CAE=180°﹣70°×2=40°,∵∠CAE+∠CAD=∠DAE,∠DAB+∠CAD=∠BAC,∴∠DAB=∠CAE=40°.故选C.【点评】本题考查了旋转的性质,平行线的性质,等腰三角形两底角相等的性质,熟记各性质并求出∠DAB=∠CAE是解题的关键.10.如图所示,△ABC与△BDE都是等边三角形,AB<BD.若△ABC不动,将△BDE绕点B旋转,则在旋转过程中,AE与CD的大小关系为()A.AE=CD B.AE>CD C.AE<CD D.无法确定【考点】全等三角形的判定与性质;等边三角形的性质.【分析】本题可通过证△ABE和△CBD全等,来得出AE=CD的结论.两三角形中,已知了AB=BC、BE=BD,因此关键是证得∠ABE=∠CBD;由于△ABC和△BED都是等边三角形,因此∠EBD=∠ABC=60°,即∠ABE=∠CBD=120°,由此可得证.【解答】解:∵△ABC与△BDE都是等边三角形,∴AB=BC,BE=BD,∠ABC=∠EBD=60°;∴∠ACB+∠CBE=∠EBD+∠CBE=120°,即:∠ABE=∠CBD=120°;∴△ABE≌△CBD;∴AE=CD.故选A.【点评】本题考查了全等三角形的判定与性质,等边三角形的性质,当出现两个等边三角形时,一般要利用等边三角形的边和角从中找到一对全等三角形.二、认真填一填11.若三角形的两边长分别为3、4,且周长为整数,这样的三角形共有 5 个.【考点】三角形三边关系;一元一次不等式组的整数解.【分析】设第三边的长为x,根据三角形的三边关系的定理可以确定x的取值范围,进而得到答案.【解答】解:设第三边的长为x,则4﹣3<x<4+3,所以1<x<7.∵x为整数,∴x可取2,3,4,5,6.故答案为5.【点评】此题主要考查了三角形的三边关系,关键是掌握三角形三边关系定理:三角形两边之和大于第三边.三角形的两边差小于第三边.12.如图,在△ABC和△DEF中,已知:AC=DF,BC=EF,要使△ABC≌△DEF,还需要的条件可以是AB=DE .(只填写一个条件)【考点】全等三角形的判定.【专题】开放型.【分析】根据“SSS”添加条件.【解答】解:若加上AB=DE,则可根据“SSS”判断△ABC≌△DEF.故答案为AB=DE.【点评】本题考查了全等三角形的判定:判定方法有“SSS”、“SAS”、“ASA”、“AAS”.13.若△ABC≌△DEF,且∠A=110°,∠F=40°,则∠E= 30 度.【考点】全等三角形的性质.【分析】根据全等三角形的性质得出∠D=∠A=110°,∠C=∠F=40°,进而得出答案.【解答】解:∵△ABC≌△DEF,∠A=110°,∠F=40°,∴∠D=∠A=110°,∠C=∠F=40°,∴∠DEF=180°﹣110°﹣40°=30°.故答案为:30;【点评】此题主要考查了全等三角形的性质,利用其性质得出对应角相等是解题关键.14.在△ABC中,∠A:∠B:∠C=1:2:3,则∠A= 30°.,∠C= 90°..【考点】三角形内角和定理.【分析】有三角形内角和180度,又知三角形内各角比,从而求出.【解答】解:由三角形内角和180°,又∵∠A:∠B:∠C=1:2:3,∴∠A=180°×=30°,∠C=180°×=90°.故填:30°,90°.【点评】本题考查三角形内角和定理,结合已知条件,从而很容易知道各角所占几分之几.而解得.15.如图,在△ABC中,∠B=60°,∠C=40°,AD⊥BC于D,AE平分∠BAC;则∠DAE= 10°.【考点】三角形内角和定理;三角形的外角性质.【分析】根据∠B=60°,∠C=40°可得∠BAC的度数,AE平分∠BAC,得到∠BAE和∠CAE的度数,利用外角的性质可得∠AED的度数,再根据垂直定义,得到直角三角形,在直角△ABD中,可以求得∠DAE的度数.【解答】解:∵∠C=40°,∠B=60°,∴∠BAC=180°﹣40°﹣60°=80°,∵AE平分∠BAC,∴∠BAE=∠CAE=40°,∴∠AED=80°,∵AD⊥BC于D,∴∠ADC=90°,∴∠DAE=180°﹣80°﹣90°=10°,故答案为:10°.【点评】本题主要考查角平分线的定义和垂直的定义,外角性质,三角形内角和定理,综合利用各定理及性质是解答此题的关键.16.如图,D 、E 分别是△ABC 边AB 、BC 上的点,AD=2BD ,BE=CE ,设△ADC 的面积为S 1,△ACE 的面积为S 2,若S △ABC =6,则S 1﹣S 2的值为 1 .【考点】三角形的面积.【专题】压轴题.【分析】根据等底等高的三角形的面积相等求出△AEC 的面积,再根据等高的三角形的面积的比等于底边的比求出△ACD 的面积,然后根据S 1﹣S 2=S △ACD ﹣S △ACE 计算即可得解.【解答】解:∵BE=CE ,∴S △ACE =S △ABC =×6=3,∵AD=2BD ,∴S △ACD =S △ABC =×6=4,∴S 1﹣S 2=S △ACD ﹣S △ACE =4﹣3=1.故答案为:1.【点评】本题考查了三角形的面积,主要利用了等底等高的三角形的面积相等,等高的三角形的面积的比等于底边的比,需熟记.17.如图,将纸片△ABC 沿DE 折叠,点A 落在点P 处,已知∠1+∠2=100°,则∠A 的大小等于 50 度.【考点】三角形内角和定理;翻折变换(折叠问题).【分析】根据已知求出∠ADP+∠AEP=360°﹣(∠1+∠2)=260°,根据折叠求出∠ADE+∠AED=×260°=130°,根据三角形内角和定理求出即可.【解答】解:∵∠1+∠2=100°,∴∠ADP+∠AEP=360°﹣(∠1+∠2)=260°,∵将纸片△ABC沿DE折叠,点A落在点P处,∴∠ADE=∠ADP,∠AED=∠AEP,∴∠ADE+∠AED=×260°=130°,∴∠A=180°﹣(∠ADE+∠AED)=50°,故答案为:50.【点评】本题考查了三角形的内角和定理和折叠的性质的应用,注意:三角形的内角和等于180°,题目比较好,难度适中.18.如图,△ABC中,∠BAC=100°,EF,MN分别为AB,AC的垂直平分线,如果BC=12cm,那么△FAN的周长为12 cm,∠FAN= 20°.【考点】线段垂直平分线的性质.【分析】由EF,MN分别为AB,AC的垂直平分线,可得AF=BF,AN=CN,即可得△FAN的周长等于BC;又由∠BAC=100°,求得∠BAF+∠CAN=∠B+∠C=180°﹣∠BAC=80°,继而求得答案.【解答】解:∵EF,MN分别为AB,AC的垂直平分线,∴AF=BF,AN=CN,∴△FAN的周长为:AF+FN+AN=BF+FN+CN=BC=12cm;∴∠BAF=∠B,∠CAN=∠C,∵△ABC中,∠BAC=100°,∴∠BAF+∠CAN=∠B+∠C=180°﹣∠BAC=80°,∴∠FAN=∠BAC﹣(∠BAF+∠CAN)=20°.故答案为:12,20°.【点评】此题考查了线段垂直平分线的性质以及等腰三角形的判定与性质.此题难度不大,注意掌握数形结合思想与转化思想的应用.三、解答题19.如图,点A、C、D、B 四点共线,且AC=DB,∠A=∠B,∠E=∠F.求证:DE=CF.【考点】全等三角形的判定与性质.【专题】证明题.【分析】根据条件可以求出AD=BC,再证明△AED≌△BFC,由全等三角形的性质就可以得出结论.【解答】证明:∵AC=DB,∴AC+CD=DB+CD,即AD=BC,在△AED和△BFC中,∴△AED≌△BFC.∴DE=CF.【点评】本题考查了线段的数量关系,全等三角形的判定及性质的运用,解答时证明△AED≌△BFC 是解答本题的关键.20.如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.(1)从图中任找两组全等三角形;(2)从(1)中任选一组进行证明.【考点】全等三角形的判定.【专题】证明题.【分析】(1)根据题目所给条件可分析出△ABE≌△CDF,△AFD≌△CEB;(2)根据AB∥CD可得∠1=∠2,根据AF=CE可得AE=FC,然后再证明△ABE≌△CDF即可.【解答】解:(1)△ABE≌△CDF,△AFD≌△CEB;(2)∵AB∥CD,∴∠1=∠2,∵AF=CE,∴AF+EF=CE+EF,即AE=FC,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS).【点评】此题主要考查了三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.21.如图,在△ABC中,∠B=40°,∠C=110°.(1)画出下列图形:①BC边上的高AD;②∠A的角平分线AE.(2)试求∠DAE的度数.【考点】作图—复杂作图.【分析】(1)利用直角三角板一条直角边与BC重合,沿BC平移使另一直角边过A画BC边上的高AD即可;再根据角平分线的做法作∠A的角平分线AE;(2)首先计算出∠BAE的度数,再计算出∠BAD的度数,利用角的和差关系可得答案.【解答】解:(1)如图所示:(2)在△ABC中,∠BAC=180°﹣11°﹣40°=30°,∵AE平分∠BAC,∴∠BAE=∠BAC=15°,在Rt△ADB中,∠BAD=90°﹣∠B=50°,∴∠DAE=∠DAB﹣∠BAE=35°.【点评】此题主要考查了复杂作图,以及角的计算,关键是正确画出图形.22.作图,如图已知三角形ABC内一点P(1)过P点作线段EF∥AB,分别交BC,AC于点E,F(2)过P点作线段PD使PD⊥BC垂足为D点.【考点】作图—基本作图.【分析】(1)根据过直线外一点作已知直线平行线的方法作图即可;(2)利用直角三角板,一条直角边与BC重合,沿BC平移,使另一条直角边过点P画垂线即可.【解答】解:如图所示:.【点评】此题主要考查了基本作图,关键是掌握利用直尺做平行线的方法.23.如图,在△ABC中,AD平分∠BAC,AD的垂直平分线EF交BC的延长线于点F,连接AF,求证:∠CAF=∠B.【考点】线段垂直平分线的性质.【专题】证明题.【分析】EF垂直平分AD,则可得AF=DF,进而再转化为角之间的关系,通过角之间的平衡转化,最终得出结论.【解答】证明:∵EF垂直平分AD,∴AF=DF,∠ADF=∠DAF,∵∠ADF=∠B+∠BAD,∠DAF=∠CAF+∠CAD,又∵AD平分∠BAC,∴∠BAD=∠CAD,∴∠CAF=∠B.【点评】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.24.如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC.【考点】全等三角形的判定与性质;角平分线的性质.【专题】证明题.【分析】在AB上截取ME=BN,证得△BND≌△EMD,进而证得∠DBN=∠MED,BD=DE,从而证得BD平分∠ABC.【解答】解:如图所示:在AB上截取ME=BN,∵∠BMD+∠DME=180°,∠BMD+∠BND=180°,∴∠DME=∠BND,在△BND与△EMD中,,∴△BND≌△EMD(SAS),∴∠DBN=∠MED,BD=DE,∴∠MBD=∠MED,∴∠MBD=∠DBN,∴BD平分∠ABC.【点评】本题考查了三角形全等的判定和性质,等腰三角形的判定和性质.25.如图,在长方形ABCD中,AB=8cm,BC=6cm,点E是CD的中点,动点P从A点出发,以每秒2cm 的速度沿A→B→C→E运动,最终到达点E.若设点P运动的时间是t秒,那么当t取何值时,△APE 的面积会等于10?【考点】一元一次方程的应用;三角形的面积.【专题】几何动点问题.【分析】分为三种情况讨论,如图1,当点P在AB上,即0<t≤4时,根据三角形的面积公式建立方程求出其解即可;如图2,当点P在BC上,即4<t≤7时,由S△APE =S四边形AECB﹣S△PCE﹣S△PAB建立方程求出其解即可;如图3,当点P在EC上,即7<t≤9时,由S△APE==10建立方程求出其解即可.【解答】解:如图1,当点P在AB上,即0<t≤4时,∵四边形ABCD是矩形,∴AD=BC=6,AB=CD=8.∵AP=2t,∴S△APE=×2t×6=10,∴t=.如图2,当点P在BC上,即4<t≤7时,∵E是DC的中点,∴DE=CE=4.∵BP=2t﹣8,PC=6﹣(2t﹣8)=14﹣2t.∴S=(4+8)×6﹣×(2t﹣8)×8﹣(14﹣2t)×4=10,解得:t=7.5>7舍去;当点P在EC上,即7<t≤9时,PE=18﹣2t.∴S△APE=(18﹣2t)×6=10,解得:t=.总上所述,当t=或时△APE的面积会等于10.【点评】本题考查了矩形的性质的运用,三角形的面积公式的运用,梯形的面积公式的运用.解答时灵活运用三角形的面积公式求解是关键.26.课本拓展旧知新意:我们容易证明,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?1.尝试探究:(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?2.初步应用:(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,∠1=130°,则∠2﹣∠C= 50°;(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请利用上面的结论直接写出答案∠P=90°﹣∠A .3拓展提升:(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)【考点】三角形的外角性质;三角形内角和定理.【专题】探究型.【分析】(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;(2)根据(1)的结论整理计算即可得解;(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;(4)延长BA、CD相交于点Q,先用∠Q表示出∠P,再用(1)的结论整理即可得解.【解答】解:(1)∠DBC+∠ECB=180°﹣∠ABC+180°﹣∠ACB=360°﹣(∠ABC+∠ACB)=360°﹣(180°﹣∠A)=180°+∠A;(2)∵∠1+∠2=∠180°+∠C,∴130°+∠2=180°+∠C,∴∠2﹣∠C=50°;(3)∠DBC+∠ECB=180°+∠A,∵BP、CP分别平分外角∠DBC、∠ECB,∴∠PBC+∠PCB=(∠DBC+∠ECB)=(180°+∠A),在△PBC中,∠P=180°﹣(180°+∠A)=90°﹣∠A;即∠P=90°﹣∠A;故答案为:50°,∠P=90°﹣∠A;(4)延长BA、CD于Q,则∠P=90°﹣∠Q,∴∠Q=180°﹣2∠P,∴∠BAD+∠CDA=180°+∠Q,=180°+180°﹣2∠P,=360°﹣2∠P.【点评】本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质并读懂题目信息是解题的关键.。
1.1认识三角形(2)

是△ABC的角平分线.已知∠BAC=82°∠C=40°,与
求∠DAE的大小。
高
解: ∵
AE是BC边上的角平分线, 且∠BAC=82°
1
∴ ∠EAC= ∠BAC=41°
2
Hale Waihona Puke ∵ AD是△ABC的高,B
A DE
线 有 关 C的
例∴ 1∠你ADC=还90°有其他解法吗?
计
算 ∵ ∠DAC+ ∠ADC+ ∠C =180° ((三根角形据三什内角么的?和)等于180°)
直角三角形的三条高
A
F
交于直角顶点。
议一议:
DB
C
钝角三角形的三条高
交于一点吗?
E
它们所在的直线交于一点吗? O
钝 角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
12
高 条数
位置
锐角三角形
3
都在三角 形内部
垂足 交点
在相应顶点的 对边上
在三角形内部
图形
A
B
C
直角三角形 3
直角边上的高分别 与另一条直角边重 合,还有一条高在 三角形内部
三角形的三条中线会交于同一 点,称之为三角形的重心.
如图,过△ABC的顶点A,
你能画它对边BC的垂线吗?
A
通过两个问题的引出,教师
引导学生回忆过一个已知点
画已知直线的垂线的方法,
B
并总结画图的规律:
D
C
一落,二靠,三画。
记垂足为D,线段AD即为:三角形的高。
在三角形中,过一个顶点作它对边的垂线段,
①是直角的顶点 ②在斜边上
在直角顶点
三角形的认识学案例题解析答案

三角形的认识教学目的1、认识三角形的角、边以及角平分线、中线和高线;2、会根据边的关系判断能否组成三角形,以及会画角平分线、中线和高线;3、利用三角形的性质解决问题。
教学内容一.【知识梳理】知识点一:认识三角形1.概念:由不在同一条直线上的三条线段首尾顺序相接所组成的图形叫三角形。
“三角形”用符号“△”表示。
如图:顶点是A,B,C的三角形记做“△ABC”∠A, ∠B, ∠C是在三角形,由相邻两边组成的角,称为“三角形的内角”,简称“三角形的角”。
线段AB ,BC,CA是三角形的三条边。
2.知识回顾(1)、三角形三个内角和等于180°(2)、三角形按内角的大小进行分类三个内角都是锐角的三角形是“锐角三角形”(3)、三角形有一个内角是直角的三角形是“直角三角形”有一个内角是钝角的三角形是“钝角三角形”(4)、三角形任何两边的和大于第三边(5)、三角形任何两边之差小于第三边例题一:(一)填空题。
1、在△ABC中,∠A=40°,∠B=∠C,则∠C=.2、小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形,那么他选的三根木棒的长度分别是3、三角形的一边为5 cm,一边为7 cm,则第三边的取值范围是4、△ABC中,若∠A=35°,∠B=65°,则∠C=;若∠A=120°,∠B=2∠C,则∠C=。
(二)选择题1.如果三角形的三个内角的度数比是2:3:4,则它是( )A.锐角三角形B.钝角三角形;C.直角三角形D.钝角或直角三角形2.若三角形中最大内角是60°,则这个三角形是( ) A 、不等边三角形B 、等腰三角形C 、等边三角形D 、不能确定3.已知△ABC 中,∠A=2(∠B+∠C),则∠A 的度数为( )A.100°B.120°C.140°D.160°4.在下列条件中:①∠A+∠B=∠C ,②∠A ∶∠B ∶∠C=1∶2∶3,③∠A=90°-∠B ,④∠A=∠B=½ ∠C 中,能确定△ABC 是直角三角形的条件有( )A .1个 B. 2个 C. 3个 D. 4个小结:1、判断能组成三角形的三条线段只需满足较小两边之和大于最大边,或最大边与任意较小边之差小于第三边即可;2、三角形的内角之和满足180°即可知识点二:三角形的高线定义:过一个三角形的顶点向它的对边所在直线作垂线,顶点与垂足之间的线段叫做三角形的高。
三角形的初步认识能力提升测试卷(二)及答案

三角形的初步认识能力提升测试卷(二)及答案以下是查字典数学网为您引荐的三角形的初步看法才干提升测试卷(二)及答案,希望本篇文章对您学习有所协助。
三角形的初步看法才干提升测试卷(二)及答案一、选择题(共10小题,每题3分,共30分)温馨提示:每题四个答案中只要一个是正确的,请把正确的答案选出来!1.一个三角形的两边长区分是2cm和9cm,第三边的长是一个奇数,那么第三边长为( )A、5cm B、7cm C、9cm D、11cm2.如图,点P是BAC的平分线AD上一点,PEAC于点E.PE=3,那么点P到AB的距离是( )A.3B.4C.5D.63.关于三角形的内角,以下判别中不正确的选项是( );A.至少有两个锐角B.最多有一个直角C.必有一个角大于600D.至少有一个角不小于6004.以下四组中一定是全等三角形的是( );A.两条边对应相等的两个锐角三角形B.面积相等的两个钝角三角形C.斜边相等的两个直角三角形D.周长相等的两个等边三角形5. 如图,在ABC中,BC边上的垂直平分线交AC于点D,AB=3,AC=7,BC=8,那么ABD的周长为( )A.10B.11C.15D.126、一个三角形的两个内角区分为55和65,这个三角形的外角不能够是( )A、115B、120C、125D、1307、如图,在锐角△ABC中,CD、BE区分是AB、AC边上的高,且CD、BE相交于一点P,假定A=50,那么BPC=( )A、150B、130C、120D、1008、用12根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余、堆叠和折断,那么能摆出不同的三角形的个数是( )A、1B、2C、3D、49.如图,在△ABC中,D、E区分是AC、BC边上的点,假定△ADB≌△EDB≌△EDC,那么C的度数为( )A、15B、20C、25D、3010.在△ABC中,A=2B=4C,那么△ABC为( )A.锐角三角形B.钝角三角形C.直角三角形D.都有能够二、填空题(共6小题,每题4分,共24分)温馨提示:填空题必需是将最繁复最正确的答案填在空格处!11.在△ABC中,有两条边长区分是2 cm ,5 cm,那么第三边的范围是_________.假定三边中有两边相等,那么△ABC的周长为cm.12.三角形的三边长区分是3、x、9,那么化简 = ;13.如图,在ABC中,AD是BC边上的中线,AB=7 cm ,AC=5cm,那么ABD和ACD的周长差为 cm.14、设△ABC的三边为a、b、c,化简15、三角形的两边长区分是3cm和7cm,第三边长是偶数,那么这个三角形的周长为___________cm;16、如图,把矩形ABCD沿AM折叠,使D点落在BC上的N点处,假设AD= cm,DM=5cm,DAM=30,那么AN=_____cm,NM=______cm,BNA=_________度;三、解答题(共8题,共66分)温馨提示:解答题必需将解答进程清楚地表述出来!17(此题8分).如图,ABC中,C,D,E,F区分在AB,BC,AC上,且, ;求证: .证明:∵DEC=BDE( )DEC=DEF+FEC 又∵DEF=B(),______=______(等式性质).在△EBD与△FCE中,______=______(已证),______=______(),C(),△EBD≌△FCE ( )ED=EF ( ).18、(此题8分).如图,在△ABC中,AE是BC边上的高,AD 是角平分线,B=42,C=68.(1)求DAE的度数;(2)假定B= ,C= ,用含的代数式表示DAE.19、(此题8分)如图,点E、A、B、F在同一条直线上,AD与BC交于点O,CAE=DBF,AC=BD.说出CAD=DBC的理由。
七年级下数学 认识三角形(2)检测题(含答案)

1.如果一个三角形的两边长分别为 3 和 6,则第三边长可能是(
)
A.3
B.6
C.3 或 6
D.12 或 15
2.为估计池塘两岸 A、B 间的距离,杨阳在池塘一侧选取了一点 P,测得 PA
=16 m,PB=12m,那么 AB 间的距离不可能是(
)
A.5 m B.15 m C.20 m
因此另两4,即三边长为 4,4,8.此时不能构成三角形;
②当 x=5x-12 时,x=3,即三边长为 3,2,3,其周长为 8;
③当 2x-4=5x-12 时,x=8,即三边长为8,4,4,不能构成三角形.
3
333
故三角形周长为 8.
14.解:
②腰长为 8,则底边长为:20-8×2=4,底边长为 8cm,另一个腰长为 4cm,能构成三角形.
因此另两边长为 8cm、4cm 或 6cm、6cm.
(2)①底边长为 4,则腰长为:(20-4)÷2=8,所以另两边的长为 8cm,8cm,能构成三角形;
②腰长为 4,则底边长为:20-4×2=12,底边长为 12cm,另一个腰长为 4cm,不能构成三角形.
形呢?通过尝试,列表如下.
火柴棒数
3
5
6
…
示意图
…
形状
等边三角形
等腰三角形
等边三角形
…
问:(1)4 根火柴棒能搭成三角形吗?
(2)8 根、12 根火柴棒分别能搭成几种不同形状的三角形? 并画出它们的示意图.
解:
4.1 认识三角形(2) 答案
1.(B) 2.(D) 3.(D) 4.(C) 5.(A) 6.(C) 7.(B)
5.已知三角形的三边长为 3、8、x,若 x 为偶数,则 x 的值有(
七年级数学下册《认识三角形》例题解析(含答案)

《认识三角形》例题解析例1(1)已知:如图1,D是BC上一点,∠C=62°,∠CAD=32°,则∠ADB=_______度.(2)(黑龙江)一个三角形的两边长分别为3和7,且第三边长为整数,这样的三角形的周长最小值是()A.14B.15C.16D.17(3)用7根火柴首尾顺次连接摆成一个三角形,能摆成不同的三角形的个数为________.解:(1)∠ADB=∠CAD+∠C=32°+62°=94°.故应填94°.(2)∵这个三角形第三边应满足4<x<10,∴最小边为5.则周长最小值为3+5+7=15.故应选B.(3)7根火柴可分为:1,1,5;1,2,4;1,3,3;2,2,3四种,其中能摆成三角形的是:1,3,3;2,2,3两种.故应填2.评析:第(3)小题要分类讨论,并要用三角形三边关系来检验每种情况能否构成三角形.例2如图2,在△ABC中,AD平分∠BAC,BE是高,∠BAC=60°,∠EBC=20°,试求∠ADC的度数.解:因为∠BAC=60°,AD平分∠BAC,所以∠BAD=30°.又因为BE是高,所以∠ABE=30°.而∠EBC=20°,所以∠ABD=50°.所以∠ADC=∠ABD+∠BAD=50°+30°=80°.评析:解这类题目要明确所求的角属于哪一个三角形的内角或外角,抓住题目中存在的等量关系列式计算即可.有时运用列方程解会更简捷.例3如图3,已知:在直角三角形ABC中,∠A=90°,BP平分∠ABC,若CP平分∠ACB且交BP于P,求∠BPC的度数.解:因为BP、CP分别平分∠ABC、∠ACB,所以∠PBC=12∠ABC,∠PCB=12∠ACB.因为∠BPC=180°-(∠PBC+∠PCB),又∠ABC+∠ACB=180°-∠A,所以∠BPC=180°-12(∠ABC+∠ACB)=90°+12∠A.即∠BPC=90°+12×90°=135°.跟踪练习:1.如图4所示,∠1和∠2是A、B两木板与地面的夹角,∠3是两木板间的夹角.若∠3=110°,则∠2-∠1=________.2.如图5,三角形纸片ABC中,∠A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为______.3.如图7,已知DE分别交△ABC的边AB、AC于D、E,交BC的延长线于F,∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.4.如图8,BP、CP分别平分△ABC的内角∠ABC和外角∠ACD,BP、CP交于P点,若∠A=80°,试求∠P的度数.参考答案:1.702.603.874.40。
