万有引力与航天PPT 演示文稿
合集下载
万有引力与航天PPT课件

专题整合
1.地球表面,万有引力约等于物体的重力,由 GMRm2 =mg; ①可以求得地球的质量 M=gGR2; ②可以求得地球表面的重力加速度 g=GRM2 ;
③得出一个代换式GM=gR2,该规律也可以应用到其他
星球表面.
2.应用万有引力等于向心力的特点,即 GMr2m=mvr2=mω2r =m(2Tπ)2r,可以求得中心天体的质量和密度. 3.应用 GMr2m=mvr2=mω2r=m(2Tπ)2r 可以计算做圆周运动天
两颗卫星环月的运行均可视为匀速圆周运
动,运行轨道如图1所示.则( )
A.“嫦娥二号”环月运行的周期比“嫦娥一号”大
图1
B.“嫦娥二号”环月运行的线速度比“嫦娥一号”小
C.“嫦娥二号”环月运行的向心加速度比“嫦娥一号”大
D.“嫦娥二号”环月运行的向心力与“嫦娥一号”相等
解析 根据万有引力提供向心力 GMr2m=mvr2=m4Tπ22r=ma 可得,v= GrM,T= 4GπM2r3,a=GrM2 ,又“嫦娥一号”的轨道半径大于嫦娥二号
第六章 万有引力与航天
学案8 章末总结
网络构建
专题整合
自我检测
网络构建
万Hale Waihona Puke 有 引 力 与 航 天人类对 行星运 动规律 的认识
地心说
日心说
第一定律 轨道
开普勒行星运动定律第二定律 面积
第三定律 周期
定律 定律 定律
万有引力定律的发现
万
内容:自然界中任何两个物体都相互吸引,引力的方向在
有 引 力 与 航
万 有 引 力 定 律
它们的 连线 上,引力的大小与物体的 质量m1和m2
的乘积 成正比、与 它们之间距离r的二次方 成反比
万有引力与航天PPT课件

A.每颗星做圆周运动的角速度为 3
Gm L3
B.每颗星做圆周运动的加速度与三星的质量无关
C.若距离 L 和每颗星的质量 m 都变为原来的 2 倍,则周期变为原来的 2 倍
D.若距离 L 和每颗星的质量 m 都变为原来的 2 倍,则线速度变为原来的 4 倍
物 理 第六章 万有引力与航天
必修2
网络构建
第六章 万有引力与航天
网络构建
专题突破
体验高考
章末自测
两种特殊卫星 1.近地卫星 沿半径约为地球半径的轨道运行的地球卫星,其发射速度与环绕速度相等, 均等于第一宇宙速度 7.9 km/s。 2.同步卫星 运行时相对地面静止,T=24 h;同步卫星只有一条运行轨道,它一定位于赤 道正上方,且距离地面高度约为 h=3.6×104 km,运行时的速率 v≈3.1 km/s。
D.由上述
B
和
C
中给出的公式,知卫星运行的线速度将减小到原来的
2 2
物理 必修2
第六章 万有引力与航天
网络构建
专题突破
体验高考
章末自测
解析: 对于不同轨道上的人造地球卫星,其角速度 ω= GrM3 不同,所以
由公式 v=ωr,不能得到卫星线速度 v 跟 r 成正比关系的结论,它的决定式为 v
=
GrM,A 错误;同理,F=mvr2中卫星运行速度 v 是变量,向心力 F 跟 r 成
日”。1970 年 4 月 24 日我国首次成功发射的人造卫星东方红一号,目前仍然在
椭圆轨道上运行,其轨道近地点高度约为 440 km,远地点高度约为 2 060 km;1984
年 4 月 8 日成功发射的东方红二号卫星运行在赤道上空 35 786 km 的地球同步轨
《万有引力和航天》课件

航天技术的发展
火箭技术
详细了解火箭技术的发展,从早期的火箭 到现代可重复使用的火箭。
空间食品
了解在长时间太空任务中如何满足宇航员 的营养需求。
太空服
探索太空服的演变,以及它们在航天任务 中扮演的关键角色。
太空探测器
探索太空探测器的进步并了解它们在探索 太阳系和宇宙的重要作用。
中国的航天事业
发射记录
探索牛顿对物理学的其他重大贡献,以 及他对科学的影响。
万有引力与天体运动
行星运动
解释为什么行星绕着太阳旋转,并探索其他天 体的运动。
引力波
了解近年来关于引力波发现的突破和其对对宇 宙观测的重要意义。
太空的万有引力应用
1
卫星导航系统
揭示卫星导航系统如何利用万有引力定律提供精准的定位和导航服务。
2
月球探测任务
了解通过万有引力利用月球探测任务进行地质和科学研究的重要性。
3
太空望远镜
探索使用太空望远镜在宇宙中观测和研究的前沿。
航天的历史
人造卫星
回顾第一颗人造卫星的发 射,标志着航天的开端。
阿波罗登月计划
探索人类首次登上月球的 历史时刻和阿波罗任务的 成就。
国际空间站
了解国际合作下建造和运 营国际空间站的重要性。
《万有引力和航天》PPT 课件
万有引力和航天是关于宇宙和人类探索的精彩主题。这个课件将带您深入了 解万有引力的概念、航天的历史以及未来太空探索的挑战和可能性。
万有引力的概念
探索万有引力的基础知识,包括引力的定义和万有引力定律的公式。
牛顿的贡献
1 万有引力定律
2 力学的奠基人
了解牛顿对万有引力定律的贡献和他的 思考过程。
四章第4单元 万有引力与航天(64张ppt)

[尝试解题] 因各小行星到太阳中心的距离不同,皆大于地球到太 v2 Mm 2π 2 阳中心的距离,根据万有引力公式 G r2 =m r =m( T ) r =ma,知太阳对各小行星的引力不相同,各小行星绕太阳 GM 运动的周期均大于一年,则选项 A、B 错误,由 a= r2 和 GM v = r ,r 越小,a 越大,r 越大,v 越小,则选项 C 正
万有引力定律
[想一想]
(1)开普勒行星运动定律不仅适用于行星绕太阳运动,
也适用于卫星绕地球运动,若一颗卫星绕地球做椭圆轨道运
动,则它在近地点和远地点的速度大小关系如何? (2)请根据万有引力定律和牛顿第二定律分析地球表面上 不同质量的物体的重力加速度大小关系。
提示: (1)由于卫星与地球的连线在单位时间内扫过 的面积相等,故卫星在近地点的速度大于在远地点的速 度。
[例1]
(2012· 浙江高考)如图4-4-1所示,在火星
与木星轨道之间有一小行星带。假设该带中的小行星只 受到太阳的引力,并绕太阳做匀速圆周运动。下列说法 正确的是( )
图 4- 4- 1
A.太阳对各小行星的引力相同 B.各小行星绕太阳运动的周期均小于一年 C.小行星带内侧小行星的向心加速度值大于外 侧小行星的向心加速度值 D.小行星带内各小行星圆周运动的线速度值大 于地球公转的线速度值
2
确,D 错误。 [答案] C
(1)不同轨道上运行的卫星的加速度、线速度、角 速度、周期可以比较大小,但不同轨道上卫星的质量
及所受的万有引力大小无法比较。
(2)要熟记经常用到的常数,如地球自转一周为一 天,绕太阳公转一周为一年,月球绕地球公转一周为 一月(27.3天)等。
天体质量和密度的估算
(1)利用天体表面的重力加速度 g 和天体半径 R。 Mm gR2 由于 G R2 =mg,故天体质量 M= G ,天体密度 ρ M M 3g = V =4 =4πGR。 3 π R 3 (2)通过观察卫星绕天体做匀速圆周运动的周期 T 和
第4节---万有引力定律与航天(超好用)PPT优秀课件

地 球同步卫星与现在的相比( A )
A.距地面的高度变大 B.向心加速度变大
C.线速度变大
D.角速度变大
2.(单选)(2015·高考福建卷)如图,若两颗人造卫星 a 和 b 均绕地球做匀速圆周运动,a、b 到地心 O 的距离分别为
r1、r2,线速度大小分别为 v1、v2,则( A )
A.vv12=
23
远地点---速度小,动能小
卫星变轨原理
使卫星v2加 ,使 m 速 R22 v到 GM R2 m
卫星在圆 轨道运行 速度V1
R
1
2
V2
mv12 R
G
Mm R2
2021/5/26
F引
θ>900
v减
小
24
(单选)(2014·高考山东卷)2013 年 我国相继完成“神十”与“天宫”对接、 “嫦娥”携“玉兔”落月两大航天工程. 某航天爱好者提出“玉兔”回家的设想: 如图,将携带“玉兔”的返回系统由月球 表面发射到 h 高度的轨道上,与在该轨道绕月球做圆周运动的飞 船对接,然后由飞船送“玉兔”返回地球.设“玉兔”质量为 m, 月球半径为 R,月面的重力加速度为 g 月.以月面为零势能面,“玉 兔”在 h 高度的引力势能可表示为 Ep=RGMR+mhh,其中 G 为引力 常量,M 为月球质量.若忽略月球的自转,从开始发射到对接完 成需要对“玉兔”做的功为( D )
引力势能
②同一圆轨道卫星动能、势能、 机械能变化吗?
③相同质量不同圆轨道卫星动能、 势能、机械能有什么关系?
④同一椭圆轨道卫星动能、势能、 机械能变化吗?如何变化?
2021/5/26
18
(单选)(2014·高考天津卷)研究表明,地球自转在
万有引力与航空航天 嫦娥探月精品PPT课件

运载火箭
发射到环绕月球的示意图
与嫦娥一号的比较
进入实验轨道拍照
嫦娥三号(未发射)
祝同学们学习进步 勇攀高峰!
ng, this course is expected to bring you value and help
为方便学习与使用课件内容,课件可以在下载后自由编辑, 请根据实际情况调整
第一宇宙速度: v=7.9km/s 第二宇宙速度: v=11.2km/s 第三宇宙速度: v=16.7km/s
运载火箭 工作原理
中国运载火箭家族
发射地点
中国探月工程
嫦娥一号
嫦娥二号
嫦娥三号
嫦娥一号
“嫦娥一号”月球探测卫星于2007年10月24日在西昌 卫星发射中心由“长征三号甲”运载火箭发射升空。 运行在距月球表面200千米的圆形极轨道上执行科 学探测任务。
万有引力与航空航天
----嫦娥探月
阿波罗8号从月球返航的途 中,当地面控制中心问及“是 谁在驾驶”的时候,指令长这 样回答:“我想现在是牛顿在 驾驶”
万有引力:
F
G
Mm r2
其中,F为力,G为引力常量,M、m 为物体的质量,r为两物体之间的距离。
三个宇宙速度
牛顿在思考万有引力定律时就曾想过,从高山上水平抛出 物体,速度一次比一次大,落地点也就一次比一次远。如 果速度足够大,物体就不再落回地面,它将绕地球运动, 成为人造地球卫星,那么这个速度应该有多大?
在嫦娥一号上搭载了8种24台科学探测仪器, 重130千克,即微波探测仪系统、γ射线谱仪、 X射线谱仪、激光高度计、太阳高能粒子探测 器、太阳风离子探测器、CCD立体相机、干涉 成像光谱仪。
2009年3月1日16时13分,嫦娥一号卫星在控制下成 功撞击月球。为我国月球探测的一期工程,划上 了圆满句号。
万有引力与航天(共64张PPT)
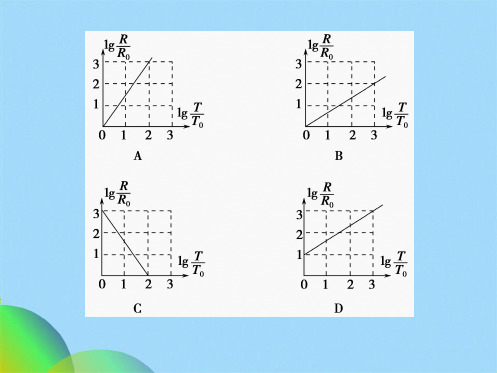
( ).
A.同步卫星运行速度是第一宇宙速度的n1倍 B.同步卫星的运行速度是地球赤道上随地球自转的物体
速度的1n倍
C.同步卫星运行速度是第一宇宙速度的
1倍 n
D.同步卫星的向心加速度是地球表面重力加速度的
n1倍
解析 设地球半径为 R,质量为 M,则第一宇宙速度 v1= GRM,根据万有引力等于向心力得同步卫星的运行速度 v=
GM R
C.沿 c 运动的物体初速度一定大于第二宇宙速度
D.沿 d 运动的物体初速度一定大于第三宇宙速度
解析 b 是贴近地球表面的圆,沿此轨迹运动的物体满足
GMRm2 =mvR2,解得 v=
GRM,或满足 mg=mvR2,解得 v=
gR,以上得到的两个速度均为第一宇宙速度,发射速度小
于第一宇宙速度则不能成为人造卫星,如 a,故 A、B 正确; 发射速度大于第一宇宙速度而小于第二宇宙速度,卫星的轨
万有引力定律及其应用 Ⅱ(考纲要求)
【思维驱动】
(单选)关于万有引力公式 F=Gmr1m2 2,以下说法中正确的是 ( ).
A.公式只适用于星球之间的引力计算,不适用于质量较小
的物体
B.当两物体间的距离趋近于0时,万有引力趋近于无穷大
C.两物体间的万有引力也符合牛顿第三定律
D.公式中引力常量G的值是牛顿规定的
于太阳和地球连线的延长线上,一飞行器 处于该点,在几乎不消耗燃料的情况下与 地球同步绕太阳做圆周运动,则此飞行器 的
( ).
图5-3-3
A.线速度大于地球的线速度 B.向心加速度大于地球的向心加速度 C.向心力仅由太阳的引力提供 D.向心力仅由地球的引力提供 解析 飞行器与地球同步绕太阳做圆周运动,所以ω飞= ω地,由圆 周运动线速度和角速度的关系v=rω得v飞>v地,选项A正确;由 公式a=rω2知,a飞>a地,选项B正确;飞行器受到太阳和地球的 万有引力,方向均指向圆心,其合力提供向心力,故C、D选项 错.
万有引力与航天PPT教学课件

gR2
Rh
T 2
(R h)3 gR 2
例8、我国于2007年10月24日发射的“嫦娥一号”探月卫星简化
后的路线示意图如图所示。卫星由地面发射后,经过发射轨道进
入停泊轨道,然后在停泊轨道经过调速后进入地月转移轨道,再
次调速后进入工作轨道,卫星开始对月球进行探测。已知地球与
月球的质量之比为a,卫星的停泊轨道与工作轨道的半径之比为b,
例12、宇航员在一星球表面上的某高处,沿水平方向抛出一小球。
经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离
为L。若抛出时初速度增大到2倍,则抛出点与落地点之间的距离
为 3L 。已知两落地点在同一水平面上,该星球的半径为R,万
有引力常数为G。求该星球的质量M
2 3LR 2 M 3Gt 2
⑵如两质量分布均匀的球体:
m1 球心
球心 m2
r
无论球体的大小相对于r大小不能忽略也好, 可以忽略也罢,它们的万有引力大小都可以用 F= Gm1m2/r2 求解,r为 两球心 之间的距离。
例3、下列说法符合史实的是( C ) A.牛顿发现了行星的运动规律 B.开普勒发现了万有引力定律 C.卡文迪许第一次在实验室里测出了万有引力常量 D.牛顿发现了海王星和冥王星
必修第七章 万有引力与航天
一、开普勒行星运动定律
1、开普勒第一定律(轨道定律):所有的行星绕 太阳运动 的 轨道都是 椭圆 , 太阳 处在所有椭圆的一个 焦 点 上。
2、开普勒第二定律(面积定律):对任意一个行星来说,它
与 太阳的
连线在 相等的时 间
内扫过
的 相等的面积 。(即近日点速率最大,远日点速率最小)
的半径R0之比r/R0=60。设卫星表面的重力加速度为g,则在卫星
(完整版)万有引力与航天 课件PPT

课堂探究
【突破训练 3】已知地球质量为 M,半径为
R,自转周期为 T,地球同步卫星质量为
m,力常量为 G.有关同步卫星,下列
表述正确的是
( BD )
A.卫星距地面的高度为
3
GMT2 4π2
B.卫星的运行速度小于第一宇宙速度
C.卫星运行时受到的向心力大小为
Mm G R2 D.卫星运行的向心加速度小于地球表面 的重力加速度
上信息下列说法正确的是
()
A.月球的第一宇宙速度为 gr
B.“嫦娥四号”绕月运行的速度为
gr2 R
C.万有引力常量可表示为ρ3Tπ2rR33
D.“嫦娥四号”必须减速运动才能返回地球
课堂探究
【突破训练 2】2013 年 6 月 13 日,神州十号与天宫一号成功实现自 动交会对接.对接前神州十号与天宫一号都在各自的轨道上做匀
卫星运行参量的比较和运算
为r,运行速率为v1,向心加速度为a1;地球 解析指导
赤道上的物体随地球自转的向心加速度为a2, 求比值→找到物理量的联系点
第一宇宙速度为v2,地球半径为R,则下列
比值正确的是( AD)
A. a1 r
a2 R
B. a1 ( R )2
a2 r
C. v1 r
v2 R
D. v1 R
时,弹簧测力计的示数为 N.已知引
力常量为 G,则这颗行星的质量为
(B )
mv2 A. GN
Nv2 C.Gm
mv4 B. GN
Nv4 D.Gm
考点定位
天体质量的计算
解析指导
表面附近→轨道半径=星球 半径
卫星绕行星运动:
G
M 行m卫 R2
m卫
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例4、如图1所示,在半径为R=20cm,质量为M=168kg的均匀铜球 上,挖去一个球形空穴,空穴的半径为R/2,并且跟铜球相切,在 铜球外有一个质量为m=lkg可视为质点的小球,这个小球位于连接 铜球的中心跟空穴中心的直线上,并且在靠近空穴一边,两个球心 相距d=2m,试求它们之间的吸引力。
F 2.41 109 N
a3 GM 即 2 K ( M为中心天体质量) 2 T 4 K是一个与行星无关的常 量,仅与 中心天体有关
长轴 短 轴
பைடு நூலகம்
例1、1990年4月25日,科学家将哈勃天文望远镜送上距地球表面约 600 km的高空,使得人类对宇宙中星体的观测与研究有了极大的进 展。假设哈勃望远镜沿圆轨道绕地球运行。已知地球半径为 6.4×106m,利用地球同步卫星与地球表面的距离为3.6×107m这一事 实可得到哈勃望远镜绕地球运行的周期。以下数据中最接近其运行 周期的是 ( B ) A.0.6小时 B.1.6小时 C. D.24小时 3 4.0小时 例2、关于开普勒行星运动的公式 a =k,以下理解正确的是 AD A.k是一个与行星无关的常量 T2 B.若地球绕太阳运转轨道的半长轴为R地,周期为T地;月球绕地球 3 3 运转轨道的长半轴为R月,周期为T月,则 R月 R地 2 2 C.T表示行星运动的自转周期 T地 T月 D.T表示行星运动的公转周期
图1
例5、由于万有引力定律和库仑定律都满足平方反比律,因此引力 场和电场之间有许多相似的性质,在处理有关问题时可以将它们进 行类比.例如电场中反映各点电场强弱的物理量是 电场强度,其 F 定义式为 E q 在引力场中可以有一个类似的物理量用来反映 各点引力场 的强弱.设地球质量为M,半径为R,地球表面处重力 加速度为g,引力常量为G,如果一个 质量为m的物体位于距地心 AD 2R处的某点,则下列表达式中能反映该点引力场强弱的是( ) g M Mm m G G 2 2 2 A. (2 R) B. G C . D. 4 (2 R) (2 R)
必修第七章
一、开普勒行星运动定律
万有引力与航天
1、开普勒第一定律(轨道定律):所有的行星绕 太阳运动 的 轨道都是 椭圆 , 太阳 处在所有椭圆的一个 焦 点 上。 2、开普勒第二定律(面积定律):对任意一个行星来说,它 太阳的 与 连线在 相等的时 间 内扫过 相等的面积 。 (即近日点速率最大,远日点速率最小) 的 3、开普勒第三定律(周期定律):所有行星的轨道的半长 三次 方 周期 二 次 方 的比值都相等。 轴的 跟它的公转 的
三、万有定律的应用
1、讨论重力加速度g随离地面高度 Mm h的变化情况: 物体的重力近似 M mg G 为地球对物体的引力,即 。所以重力加速度 g G , ( R h) 2 ( R h) 2 可见,g随h的 增大而减小 。 2、估算中心天体的质量的基本思路: (1)从环绕天体出发:通过观测环绕天体运动的 周期T和轨道半径r ; 就可以求出中心天体的质量M (2)从中心天体本身出发:只要知道中心天体的表面重力加速度g和半径R , 就可以求出中心天体的质量M。 3、求解卫星的有关问题:在高考试题中,应用万有引力定律解 题的知识常集中于两点: 一是天体运动的向心力来源于天体之间的万有引力。 2 Mm v2 4 r 2 G 2 ma m m r m 向 r r T2 即 ; Mm 二是地球对物体的万有引力近似等于物体的重力,即G 2 mg 从而得出 GM gR2 (黄金代换,不考虑地球自转)。 R
GM Mm a ( g ) 4)由 G 2 ma向 ( g ) 可得: 向 2 r r
例6、两颗人造卫星A、B绕地球作圆周运动,周期之比为TA:TB =1:8,则轨道半径之比和运动速率之比分别为 D A、RA:RB=4:1 VA:VB=1:2 B、 RA:RB= 4:1 VA:VB=2:1 C、 RA:RB=1:4 VA:VB=1:2 D、 RA:RB=1:4 VA:VB=2:1 例7、 2003年10月15日,我国神舟五号载人飞船成功发射。标志 着我国的航天事业发展到了很高的水平。飞船在绕地球飞行的第5 圈进行变轨,由原来的椭圆轨道变为距地面高度为h的圆形轨道。 已知地球半径为R,地面处的重力加速度为g.求: (1)飞船在上述圆轨道上运行的速度v; (2)飞船在上述圆轨道上运行的周期T.
重心
m2
们的万有引力大小就 可以用 F= Gm1m2/r2 求解。
⑵如两质量分布均匀的球体:
m1 球心 r 无论球体的大小相对于r大小不能忽略也好, 球心
m2
可以忽略也罢,它们的万有引力大小都可以用
F= Gm1m2/r2 求解,r为 两球心 之间的距离。
例3、下列说法符合史实的是( C ) A.牛顿发现了行星的运动规律 B.开普勒发现了万有引力定律 C.卡文迪许第一次在实验室里测出了万有引力常量 D.牛顿发现了海王星和冥王星
r>>物体本身大小 3、适用条件:适用于 质 点 间的相互作用 均匀球体 4、万有引力定律的推导: 牛二+开三+牛三
⑴如两形状不规则的物体:
m1 重心 r ①如果物体的大小相对于r大小不能忽略时,它 们的万有引力大小就 不能 用 F= Gm1m2/r2 求解。 ②如果物体的大小相对于r大小可以忽略时,它
小结 : R地球 T地球
3 2
R火星 T火星
3
2
R土星 T土星
3
2
GM 相等的原因: 同一中心天体(太阳) 2 4
二、万有引力定 律 1、内容:自然界中 任 何 两个物体都是 相互吸引 的 ,引力 的大小跟这两个物体的质量 m1和m2的乘 积 成正比,跟它 们的 距离的二次方 成反比。
m1m2 11 2 2 2、公式:F G 2 G=6.67259 10 N m / kg 叫引力常量 r
人造地球卫星运动的v、ω、T、a与轨道半径r的关系
讨论:
Mm v2 1)由 G 2 m r r
可得:v
GM r
GM r3
r越大,v越小。 r越大,ω越小。 r越大,T越大。 r越大,a向(g/)越小。
Mm 2 G m r 可得: 2)由 2 r
2
Mm r3 2 T 2 3)由 G 2 m r 可得: r GM T
