高中物理 万有引力与航天精品课件.ppt
合集下载
万有引力与航天PPT课件

A.每颗星做圆周运动的角速度为 3
Gm L3
B.每颗星做圆周运动的加速度与三星的质量无关
C.若距离 L 和每颗星的质量 m 都变为原来的 2 倍,则周期变为原来的 2 倍
D.若距离 L 和每颗星的质量 m 都变为原来的 2 倍,则线速度变为原来的 4 倍
物 理 第六章 万有引力与航天
必修2
网络构建
第六章 万有引力与航天
网络构建
专题突破
体验高考
章末自测
两种特殊卫星 1.近地卫星 沿半径约为地球半径的轨道运行的地球卫星,其发射速度与环绕速度相等, 均等于第一宇宙速度 7.9 km/s。 2.同步卫星 运行时相对地面静止,T=24 h;同步卫星只有一条运行轨道,它一定位于赤 道正上方,且距离地面高度约为 h=3.6×104 km,运行时的速率 v≈3.1 km/s。
D.由上述
B
和
C
中给出的公式,知卫星运行的线速度将减小到原来的
2 2
物理 必修2
第六章 万有引力与航天
网络构建
专题突破
体验高考
章末自测
解析: 对于不同轨道上的人造地球卫星,其角速度 ω= GrM3 不同,所以
由公式 v=ωr,不能得到卫星线速度 v 跟 r 成正比关系的结论,它的决定式为 v
=
GrM,A 错误;同理,F=mvr2中卫星运行速度 v 是变量,向心力 F 跟 r 成
日”。1970 年 4 月 24 日我国首次成功发射的人造卫星东方红一号,目前仍然在
椭圆轨道上运行,其轨道近地点高度约为 440 km,远地点高度约为 2 060 km;1984
年 4 月 8 日成功发射的东方红二号卫星运行在赤道上空 35 786 km 的地球同步轨
人教版高中物理必修二第六章《万有引力与航天》精品课件(共58张PPT)

(3)不仅从事运动学研究还从事天体力学的研究
开普勒对天上运动的研究与伽利略对地上运动的研 究一起为牛顿定律及其世界体系的建立奠定了基础。
托勒密 (约90—168) 哥白尼(1473—1543) 第谷(1546—11630) 笛卡尔(1596-1650) 胡克(1635-1703) 牛顿(1643—1727) 哈雷 (1656-1742) 卡文迪许(1731-1810)
物理必修2
第六章 《万有引力与航天》
一、本章教材概述:
(1)从知识结构上看,本章教材是应用牛顿运动定律 和曲线运动的知识研究天体运动。牛顿运动定律和万有引 力定律构成了牛顿力学的核心内容。 本章前三节内容充分展现了万有引力定律发现的科学 过程,也向我们展现了前辈科学家富有创造而又严谨的科 学思维。教学中可以充分利用这些材料进行物理学史及物 理研究方法教育,培养学生的科学素养进而发展学生的科 学思维能力。
似的视为圆运动 (2)规律:根据圆周运动的相关规律写出
动力学方程
v2 F m r
(3)周期:注意到圆周运动线速度与周期间 2r 的关系 v T
(4)向心力表达式: (5)开普勒第三定律 r与T之间的相关性,消T
3 m r 2 F 4 T 2 r2
r3 k 2 T
二、本章知识结构
开普勒三定律 天体运动
天体质量
天体密度
双星 万有引力定律
环绕速度 运行周期
牛顿运动定律
人造地球卫星 宇宙速度
重力加速度 同步卫星
三、教学建议
课时分配建议 第一 第一节 单元 第二节
第三节 行星的运动 太阳与行星间的引力 万有引力定律 万有引力理论的成就 宇宙航行 3课时 1课时 1课时 1课时 万有引力定律的 建立过程。
开普勒对天上运动的研究与伽利略对地上运动的研 究一起为牛顿定律及其世界体系的建立奠定了基础。
托勒密 (约90—168) 哥白尼(1473—1543) 第谷(1546—11630) 笛卡尔(1596-1650) 胡克(1635-1703) 牛顿(1643—1727) 哈雷 (1656-1742) 卡文迪许(1731-1810)
物理必修2
第六章 《万有引力与航天》
一、本章教材概述:
(1)从知识结构上看,本章教材是应用牛顿运动定律 和曲线运动的知识研究天体运动。牛顿运动定律和万有引 力定律构成了牛顿力学的核心内容。 本章前三节内容充分展现了万有引力定律发现的科学 过程,也向我们展现了前辈科学家富有创造而又严谨的科 学思维。教学中可以充分利用这些材料进行物理学史及物 理研究方法教育,培养学生的科学素养进而发展学生的科 学思维能力。
似的视为圆运动 (2)规律:根据圆周运动的相关规律写出
动力学方程
v2 F m r
(3)周期:注意到圆周运动线速度与周期间 2r 的关系 v T
(4)向心力表达式: (5)开普勒第三定律 r与T之间的相关性,消T
3 m r 2 F 4 T 2 r2
r3 k 2 T
二、本章知识结构
开普勒三定律 天体运动
天体质量
天体密度
双星 万有引力定律
环绕速度 运行周期
牛顿运动定律
人造地球卫星 宇宙速度
重力加速度 同步卫星
三、教学建议
课时分配建议 第一 第一节 单元 第二节
第三节 行星的运动 太阳与行星间的引力 万有引力定律 万有引力理论的成就 宇宙航行 3课时 1课时 1课时 1课时 万有引力定律的 建立过程。
万有引力与航天(共64张PPT)
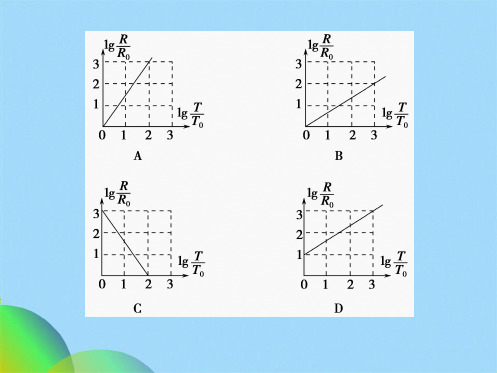
( ).
A.同步卫星运行速度是第一宇宙速度的n1倍 B.同步卫星的运行速度是地球赤道上随地球自转的物体
速度的1n倍
C.同步卫星运行速度是第一宇宙速度的
1倍 n
D.同步卫星的向心加速度是地球表面重力加速度的
n1倍
解析 设地球半径为 R,质量为 M,则第一宇宙速度 v1= GRM,根据万有引力等于向心力得同步卫星的运行速度 v=
GM R
C.沿 c 运动的物体初速度一定大于第二宇宙速度
D.沿 d 运动的物体初速度一定大于第三宇宙速度
解析 b 是贴近地球表面的圆,沿此轨迹运动的物体满足
GMRm2 =mvR2,解得 v=
GRM,或满足 mg=mvR2,解得 v=
gR,以上得到的两个速度均为第一宇宙速度,发射速度小
于第一宇宙速度则不能成为人造卫星,如 a,故 A、B 正确; 发射速度大于第一宇宙速度而小于第二宇宙速度,卫星的轨
万有引力定律及其应用 Ⅱ(考纲要求)
【思维驱动】
(单选)关于万有引力公式 F=Gmr1m2 2,以下说法中正确的是 ( ).
A.公式只适用于星球之间的引力计算,不适用于质量较小
的物体
B.当两物体间的距离趋近于0时,万有引力趋近于无穷大
C.两物体间的万有引力也符合牛顿第三定律
D.公式中引力常量G的值是牛顿规定的
于太阳和地球连线的延长线上,一飞行器 处于该点,在几乎不消耗燃料的情况下与 地球同步绕太阳做圆周运动,则此飞行器 的
( ).
图5-3-3
A.线速度大于地球的线速度 B.向心加速度大于地球的向心加速度 C.向心力仅由太阳的引力提供 D.向心力仅由地球的引力提供 解析 飞行器与地球同步绕太阳做圆周运动,所以ω飞= ω地,由圆 周运动线速度和角速度的关系v=rω得v飞>v地,选项A正确;由 公式a=rω2知,a飞>a地,选项B正确;飞行器受到太阳和地球的 万有引力,方向均指向圆心,其合力提供向心力,故C、D选项 错.
《万有引力定律》万有引力与宇宙航行PPT优质课件

27
[针对训练3] 同步卫星距离地面的高度约为地球半径的6倍,那么,某卫星在同步轨道 上运行时受到的引力是它在地面上受到的引力的n倍,则n等于( )
A.7 解析
1
1
B.49
C.36
D.49
该卫星在同步轨道上受到的万有引力 F1=G(6RM+mR)2=G49MRm2 ,该卫星在
地面上受到的万有引力 F2=GMRm2 ,n=FF12=419,故 B 正确,A、C、D 错误。 答案 B
23
核心要点二 万有引力定律的简单应用 1.任何两个物体间都存在着万有引力,但 F=Gmr1m2 2有其适用范围,在计算万有引
力的大小时注意判断是否符合适用条件。 2.在应用万有引力定律表达式 F=Gmr1m2 2进行有关计算时,r 是指两质点(或两球心,
或质点与球心)之间的距离,而不是两物体(球)之间的距离。
理的热情。
2
知识点一 行星与太阳间的引力 [观图助学]
(1)为什么苹果从树上落向地面而不飞上天空?
(2)在我们周围物体都要受到地球引力的作用,那么地球也受到太阳的引力作用 吗?为什么地球不会落到太阳的表面,而是环绕太阳转动?
3
1.推导过程 如右图所示,设行星的质量为m,速度为v,行星与太阳间的距离为r,则行星绕太 v2 阳做匀速圆周运动的向心力为F=____m__r____①
25
解析 根据 F=GMRm2 ,可得FF太月阳=MM太月阳·RR太22月阳,代入数据可知,太阳对地球上相同质 量海水的引力远大于月球对其的引力,则 A 正确,B 错误;由于月心到不同区域海 水的距离不同,所以引力大小有差异,C 错误,D 正确。 答案 AD
26
[针对训练2] 如图所示,两球间的距离为r,两球的质量分布均
(完整版)万有引力与航天 课件PPT

课堂探究
【突破训练 3】已知地球质量为 M,半径为
R,自转周期为 T,地球同步卫星质量为
m,力常量为 G.有关同步卫星,下列
表述正确的是
( BD )
A.卫星距地面的高度为
3
GMT2 4π2
B.卫星的运行速度小于第一宇宙速度
C.卫星运行时受到的向心力大小为
Mm G R2 D.卫星运行的向心加速度小于地球表面 的重力加速度
上信息下列说法正确的是
()
A.月球的第一宇宙速度为 gr
B.“嫦娥四号”绕月运行的速度为
gr2 R
C.万有引力常量可表示为ρ3Tπ2rR33
D.“嫦娥四号”必须减速运动才能返回地球
课堂探究
【突破训练 2】2013 年 6 月 13 日,神州十号与天宫一号成功实现自 动交会对接.对接前神州十号与天宫一号都在各自的轨道上做匀
卫星运行参量的比较和运算
为r,运行速率为v1,向心加速度为a1;地球 解析指导
赤道上的物体随地球自转的向心加速度为a2, 求比值→找到物理量的联系点
第一宇宙速度为v2,地球半径为R,则下列
比值正确的是( AD)
A. a1 r
a2 R
B. a1 ( R )2
a2 r
C. v1 r
v2 R
D. v1 R
时,弹簧测力计的示数为 N.已知引
力常量为 G,则这颗行星的质量为
(B )
mv2 A. GN
Nv2 C.Gm
mv4 B. GN
Nv4 D.Gm
考点定位
天体质量的计算
解析指导
表面附近→轨道半径=星球 半径
卫星绕行星运动:
G
M 行m卫 R2
m卫
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【解析】 根据开普勒第三定律,Ta32=恒量,当圆轨道的半径 R 与 椭圆轨道的半长轴 a 相等时,两卫星的周期相等,故选项 A 错误;卫星 沿椭圆轨道运行且从近地点向远地点运行时,万有引力做负功,根据动 能定理,知动能减小,速率减小;从远地点向近地点移动时动能增加, 速率增大,且两者具有对称性,故选项 B 正确;所有同步卫星的运行周 期相等,根据 GMr2m=m(2Tπ)2r 知,同步卫星轨道的半径 r 一定,故选项 C 错误;根据卫星做圆周运动的向心力由万有引力提供,可知卫星运行的 轨道平面过某一地点,轨道必过地心,但轨道不一定重合,故北京上空 的两颗卫星的轨道可以不重合,选项 D 错误.
表面上所受重力应是在地球表面上所受重力的 8 倍,选项 C 错误;第一宇宙速度
v= GRM,因此,该外星球上第一宇宙速度是地球上第一宇宙速度的 2 倍,选
项 D 正确.
【答案】 D
1.(2012·石家庄模拟)当卫星绕地球运动的轨道半径为 R 时,线速度 为 v,周期为 T.下列变换符合物理规律的是( )
2.计算时应注意的问题 (1)由于环绕天体的质量m被约分,因此不能求出它的质量和密 度. (2)环绕天体的轨道半径r等于中心天体的半径R加上环绕天体离 中心天体表面的高度h,即r=R+h. (3)当环绕天体在中心天体表面绕行时,轨道半径r=R.
(2012·北京四中模拟)已知下列数据: (1)地面附近物体的重力加速度g; (2)地球半径R; (3)月球与地球的两球心间的距离r; (4)卫星环绕地球运动的第一宇宙速度v1; (5)月球绕地球运动的周期T1; (6)地球绕太阳运动的周期T2; (7)万有引力常量G. 试选取适当的数据估算地球的质量.(要求给出三种方法)
2.对航天器的变轨问题,要抓住其在确定轨道上运行时机械能守恒, 在不同轨道上运行时其机械能不同,轨道半径越大机械能越大.
3.航天器经过同一点的加速度大小如何变化,可根据所受万有引力 的大小来确定.
近期我国发射了一颗“北斗”二代卫星,假设发射过程要经
过两次变轨,从如图 2-2-2 所示的近地轨道 1 经椭圆转移轨道 2 到达工 作轨道 3,P、Q 两点均可近似认为是两圆弧的切点(r3>r2>r1,其中 r1 为 圆轨道 1 的半径,r2 为椭圆轨道 2 的半长轴,r3 为圆轨道 3 的半径),则下 列关于卫星有关量的推理及结论正确的是( )
A.由 GMr2m=ma 可知在切点 P 处,卫 星在 1、2 轨道上的加速度 a 相同
B.由 a=vr2且在 P 点 r2>r1 及 v2<v1, 故加速度 a1>a2
C.由 a=vr2推出 v= ar,且在 Q 点 a3=a2 及 r3=r2,故 v3= v2 D.由 GMr2m=mvr2且在 Q 点有 r3>r2,故 v3<v2
零.矿井底部和地面处的重力加速度大小之比为( )
A.1-Rd
B.1+Rd
C.R-R d2
D.R-R d2
【解析】 设地球的密度为 ρ,地球的质量为 M,根据万有引力定 律可知,地球表面的重力加速度 g=GRM2 .地球质量可表示为 M=34πR3ρ. 因质量分布均匀的球壳对球壳内物体的引力为零,所以矿井下以(R-d) 为半径的地球的质量为 M′=43π(R-d)3ρ,解得 M′=R-R d3M,则矿 井底部处的重力加速度 g′=GR-M′d2, 则矿井底部处的重力加速度和地 球表面的重力加速度之比为gg′=1-Rd,选项 A 正确.
第2讲 万有引力与航天
1.估算中心天体的质量和密度的常见思路 (1)利用中心天体表面的重力加速度g和天体半径R,质量为m的物体 在天体表面受到的重力近似等于万有引力,即GMRm2 =mg可得天体质量M =gGR2,进而求得ρ=MV =34πMR3=4π3GgR. (2)利用环绕天体的轨道半径r、周期T,GMr2m=m4Tπ22r即M=4GπT2r23. 若环绕天体绕中心天体表面做匀速圆周运动时,轨道半径r=R,则 ρ=43πMR3=G3Tπ2.
【答案】 A
1.人造卫星的线速度、角速度、周期与轨道半径的关系 做匀速圆周运动的卫星所受的万有引力完全提供所需向心力,即 F 引 =F 向, 即 GMr2m=mvr2=mrω2=m4Tπ22r=man,可推导出:
v=
GM r
ω= T=2π
GM
v减小
r3 r3
⇒当
r
增大时ωT增减大小
GM
an减小
量为 M,半径为 R,由牛顿第二定律可得 GRM+mh2=m(R+h)(2Tπ)2,解得 T=2π(R
+h)
RG+Mh,由于不知道该外星球的同步卫星的高度和地球同步卫星的高度之
间的大小关系,所以不能确定该外星球的同步卫星周期和地球同步卫星周期之间
的关系,选项 A 错误;设外星球的人造卫星的环绕速度为 v,则 GMr2m=mvr2,解
GRM+mh2=m(R+h)(2Tπ)2, 其中 T=nt , 解得 M=4π2n2GRt2+h3, 又因土星体积 V=34πR3, 所以 ρ=MV =3πnG2tR2R+3 h3,故 D 正确.
【答案】 D
3.(2012·新课标全国高考)假设地球是一半径为 R、质量分布均匀的
球体.一矿井深度为 d.已知质量分布均匀的球壳对壳内物体的引力为
【解析】 探测器变轨后轨道半径变大,根据 GMr2m=ma 可知其加 速度变小,选项 A 错误;探测器变轨过程中要在远地点向运动后方喷气, 使其动能增加,选项 B 错误、C 正确;由于探测器变轨后轨道半径变大, 可知其周期变大,选项 D 错误.
【解析】 根据牛顿第二定律,卫星的加速度取决于其受到的万有 引力,由 GMr2m=ma 知,在 P 点 a1=a2,在 Q 点 a2=a3,A 项正确;GMr2m =mvr2是物体做圆周运动的条件,只适用于圆周运动,故 D 项错误;在 P 点由近地圆轨道 1 变轨到椭圆轨道 2 必须加速,即 v2>v1,所以 B 项中 “v2<v1”的假设错误,B 项错误;C 项中椭圆轨道 2 在 Q 点的半径应是 椭圆轨道在 Q 点的一小段圆弧的半径,r3>r2,由椭圆轨道 2 变轨到轨道 3 需加速,则 v3>v2,C 错误.
【解析】 行星做圆周运动的向心力由万有引力提供:GMr2m= mr(2Tπ)2,v=r(2Tπ),其中M为被该行星环绕的恒星的质量,v为该行星的 线速度,T为该行星的运动周期,故C、D正确.
【答案】 CD
2.如图 2-2-1 所示,是美国的“卡西尼”号探测器经过长达 7 年 的“艰苦”旅行,进入绕土星飞行的轨道,若“卡西尼”号探测器在半 径为 R 的土星上空离土星表面高 h 的圆形轨道上绕土星飞行,环绕 n 周 飞行时间为 t,已知引力常量为 G,则下列关于土星质量 M 和平均密度 ρ 的表达式正确的是( )
得 v= GrM,因外星球质量是地球质量的 2 倍,所以绕该外星球的人造卫星的 运行速度大于以相同轨道半径绕地球的人造卫星的运行速度,选项 B 错误;物体
在外星球表面上所受的重力等于外星球对它的万有引力大小,即 mg=GMRm2 ,因
外星球质量是地球质量的 2 倍,半径是地球半径的一半,因此某物体在该外星球
【解析】 同步卫星的周期为 24 h,根据角速度 ω=2Tπ可知,同步卫
星的角速度小,A 项错误;根据GMr2m=mvr2=mr(2Tπ)2=ma 向得 T=
4GπM2r3,v=
GrM,a 向=GrM2 ,因同步卫星的周期 24 小时大于 GPS 导
航系统的周期 12 小时,所以同步卫星的轨道半径大,线速度小,向心加
【答案】 B
3.(2012·洛阳模拟)我国正在建立的北斗导航系统建成后,将有 助于减少我国对GPS导航系统的依赖.北斗导航系统中有几颗卫星 是地球同步卫星,GPS导航系统是由周期约为12 h的卫星群组成.则 北斗导航系统中的同步卫星与GPS导航卫星相比( )
A.同步卫星的角速度大 B.同步卫星的轨道半径大 C.同步卫星的线速度大 D.同步卫星的向心加速度大
【答案】 见解析
1.(2012·青岛模拟)美国宇航局2011年12月5日宣布,他们发现 了太阳系外第一颗类似地球的、能适合居住的行星——“开普勒22b”,它每290天环绕着一颗类似于太阳的恒星运转一周.若万有 引力常量已知,下列选项中的信息能求出该行星的轨道半径的是 ()
A.该行星表面的重力加速度 B.该行星的密度 C.该行星的线速度 D.被该行星环绕的恒星的质量
速度小,B 项正确,C、D 项错误.
【答案】 B
1.提供天体做圆周运动的向心力是该天体受到的万有引力,F 供= GMr2m,天体做圆周运动需要的向心力是 F 需=mvr2.当 F 供=F 需时,天体在 圆轨道上正常运行;当 F 供>F 需时,天体做近心运动;当 F 供<F 需时,天 体做离心运动.
正确;同理,RT23=R64′T23,R′=4R,选项 B 正确;由万有引力公式和向
心力公式可得:GMRm2 =mRv2,v=
GMR ,即vv′=
2RR,v′= 22v,
选项 C 错误;同理,vv/2= RR′,R′=4R,由圆周运动周期公式可得:
T=2πvR,TT′=Rv′′×Rv=8,T′=8T,选项 D 错误.
【答案】 AB
2.(2012·北京高考)关于环绕地球运动的卫星,下列说法正确的是 ()
A.分别沿圆轨道和椭圆轨道运行的两颗卫星,不可能具有相同的 周期
B.沿椭圆轨道运行的一颗卫星,在轨道不同位置可能具有相同的 速率
C.在赤道上空运行的两颗地球同步卫星,它们的轨道半径有可能 不同
D.沿不同会 重合
【答案】 A
1.(2012·孝感模拟)“嫦娥一号”探月器发射时在绕地球运行中, 进行了四次变轨,其中有一次变轨是提高近地点的高度,使之从距 地200 km上升到距地600 km,这样既提高了探测器飞行高度,又减 慢了探测器经过近地点的速度,于是增长了测控时间,关于这次变 轨下列说法正确的是( )
