单自由度振动系统固有频率及阻尼的测定-实验报告
实验指导书及实验报告-自由衰减法测量单自由度系统的固有频率和阻尼比

实验报告1:自由衰减法测量单自由度系统的固有频率和阻尼比姓名:刘博恒学号:1252227专业:车辆工程(汽车) 班级:12级日期:2014年12月25日组内成员张天河、刘嘉锐、刘博恒、马力、孙贤超、唐鑫一、实验目的1.了解单自由度自由衰减振动的有关概念。
2.学会用数据采集仪记录单自由度系统自由衰减振动的波形。
3.学会根据自由衰减振动波形确定系统的固有频率和阻尼比。
二、实验原理由振动理论可知,一个单自由度质量-弹簧-阻尼系统,其质量为m(kg),弹簧刚度为K(N m⁄),粘性阻尼系数为r(N∙m s⁄)。
当质量上承受初始条件(t=0时,位移x=x0,速度ẋ=ẋ0)激扰时,将作自由衰减振动。
在弱阻尼条件下其位移响应为:x=Ae−nt sin(√p2−n2t+φ)式中:n=r2m为衰减系数(rad/s)p=√Km为固有圆频率(rad/s)A=√ẋ02+2nẋ0x0+p2x02p2−n2为响应幅值(m)φ=tan−1x0√p2−n2ẋ0+nx0为响应的相位角(rad)引入:阻尼比ξ=np对数衰减比δ=ln A1A3则有:n=δT d而T d=1f d =√p2−n2f d=p d2π=√p2−n22π为衰减振动的频率,p d=√p2−n2为衰减振动的圆频率。
在计算对数衰减比时,考虑到传感器的误差及系统本身迟滞,振动的平衡点位置可能不为0,因此可以使用相邻周期的峰峰值来代替振幅值计算,即δ=ln A1+A2A3+A4。
从衰减振动的响应曲线上可直接测量出δ、T d,然后根据n=δT d 可计算出n;T d=1f d=√p2−n2计算出p;ξ=np可计算出ξ;n=r2m计算出r;f0=p2π=12π√Km计算出无阻尼时系统的固有频率f0;T0=1f =2π∙√mK计算出无阻尼时系统的固有周期T0。
三、实验方法1)将系统安装成单自由度无阻尼系统,在质量块的侧臂有一个“测量平面”,用于电涡流传感器拾振。
阻尼振动实验报告

阻尼振动实验报告篇一:阻尼振动与受迫振动实验报告阻尼振动与受迫振动实验报告一、实验目的(一)观察扭摆的阻尼振动,测定阻尼因数。
(二)研究在简谐外力矩作用下扭摆的受迫振动,描绘扭摆在不同阻尼的情况下的共振曲线(即幅频特性曲线)。
(三)描绘外加强迫力矩与受迫振动之间的位相随频率变化的特性曲线(即相频特性曲线)。
(四)观测不同阻尼对受迫振动的影响。
二、实验仪器扭摆(波尔摆)一套,秒表,数据采集器,转动传感器。
三、实验任务1、调整仪器使波耳共振仪处于工作状态。
2、测量最小阻尼时的阻尼比ζ和固有角频率ω0。
3、测量其他2种或3种阻尼状态的振幅,并求ζ、τ、Q和它们的不确定度。
4、测定受迫振动的幅频特性和相频特性曲线。
四、实验步骤1、打开电源开关,关断电机和闪光灯开关,阻尼开关置于“0”档,光电门H、I可以手动微调,避免和摆轮或者相位差盘接触。
手动调整电机偏心轮使有机玻璃转盘F上的0位标志线指示0度,亦即通过连杆E和摇杆M使摆轮处于平衡位置。
然后拨动摆轮使偏离平衡位置150至200度,松开手后,检查摆轮的自由摆动情况。
正常情况下,震动衰减应该很慢。
2、开关置于“摆轮”,拨动摆轮使偏离平衡位置150至200度后摆动,由大到小依次读取显示窗中的振幅值θj;周期选择置于“10”位置,按复位钮启动周期测量,停止时读取数据10Td。
并立即再次启动周期测量,记录每次过程中的10Td的值。
(1)逐差法计算阻尼比ζ;(2)用阻尼比和振动周期Td计算固有角频率ω0。
3、依照上法测量阻尼(2、3、4)三种阻尼状态的振幅。
求出ζ、τ、Q和它们的不确定度。
4、开启电机开关,置于“强迫力”,周期选择置于“1”,调节强迫激励周期旋钮以改变电机运动角频率ω,选择2个或3个不同阻尼比(和步骤3中一致),测定幅频和相频特性曲线,注意阻尼比较小(“0”和“1”档)时,共振点附近不要测量,以免振幅过大损伤弹簧;每次调节电机状态后,摆轮要经过多次摆动后振幅和周期才能稳定,这时再记录数据。
实验11:单自由度系统强迫振动的幅频特性、固有频率及阻尼比的测定

2.5kg,上下都可以放,由于速度传感器不能倒置,只能把
质量块放到梁的下面,传感器安装在简支梁的中部。
2、 开机进入 DASP2000 标准版软件的主界面,选择单通道按
钮。进入单通道示波状态进行波形和波谱同时示波。
3、 把 ZJ-601A 型振动教学试验仪的频率按钮用手动搜索一下
梁当前的共振频率,调节放大倍数到“1”档,不要让共振
无量纲的加速度响应,将上式对时间 t 再微分一次,
������0���⁄���̈������=- ������������2 sin(������������ − ������)=- β∝ sin(������������ − ������)
振动幅度最大的频率叫共振频率������������、������������,有阻尼时共振频 率为
������������=������√1 − ������2 或������������ = ������√1 − ������2 ω、f— —固有频率; D——阻尼比。 由于阻尼比较小,所以一般认为:������������ = ω 根据幅频特性曲线:
在
D<1
时,共振处的动力放大系数|������������������������ |=2������√11−������2
有阻尼的强迫振动,当经过一定时间后,只剩下强迫振动部分,
有阻尼强迫振动的振幅特性:������
=
√(1−������2
1 )2+4������2
������2=������������������������
当干扰力确定后,由力产生的静态位移������������������就可随之确定,而强迫
振动的动态位移与频率比 u 和阻尼比 D 有关,这种关系即表现为幅
振动系统固有频率的测量

一、实验目的1、了解和熟悉共振前后利萨如图形的变化规律和特点;2、学习用“共振法”测试机械振动系统的固有频率(幅值判别法和相位判别法);3、学习用“锤击法”测试机械振动系统的固有频率(传函判别法);4、学习用“自由衰减振动波形自谱分析法”测试振动系统的固有频率(自谱分析法)。
二、实验装置框图图1 实验装置框图三、实验原理对于振动系统,经常要测定其固有频率,最常用的方法就是用简谐力激振,引起系统共振,从而找到系统的各阶固有频率。
另一种方法是锤击法,用冲击力激振,通过输入的力信号和输出的响应信号进行传函分析,得到各阶固有频率。
以下对这两种方法加以说明:1、简谐力激振简谐力作用下的强迫振动,其运动方程为:方程式的解由这两部分组成:式中常数由初始条件决定:,其中:代表阻尼自由振动基,代表阻尼强迫振动项。
自由振动周期:,强迫振动项周期:由于阻尼的存在,自由振动基随时间不断得衰减消失。
最后,只剩下后两项,也就是通常讲的定常强动,即强迫振动部分:通过变换可写成:式中:,设频率比代入公式则振幅:,滞后相位角:因为为弹簧受干扰力峰值作用引起的静位移,所以振幅A可写成:其中称为动力放大系数:动力放大系数β是强迫振动时的动力系数即动幅值与静幅值之比。
这个数值对拾振器和单自由度体系的振动的研究都是很重要的。
当,即强迫振动频率和系统固有频率相等时,动力系数迅速增加,引起系统共振,由式:可知,共振时振幅和相位都有明显变化,通过对这两个参数进行测量,我们可以判别系统是否达到共振动点,从而确定出系统的各阶振动频率。
(一)幅值判别法在激振功率输出不变的情况下,由低到高调节激振器的激振频率,通过示波器,我们可以观察到在某一频率下,任一振动量(位移、速度、加速度)幅值迅速增加,这就是机械振动系统的某阶固有频率。
这种方法简单易行,但在阻尼较大的情况下,不同的测量方法的出的共振动频率稍有差别,不同类型的振动量对振幅变化敏感程度不一样,这样对于一种类型的传感器在某阶频率时不够敏感。
振动实验报告讲解

振动实验报告讲解振动与控制系列实验姓名:李⽅⽴学号:201520000111电⼦科技⼤学机械电⼦⼯程学院实验1 简⽀梁强迫振动幅频特性和阻尼的测量⼀、实验⽬的1、学会测量单⾃由度系统强迫振动的幅频特性曲线。
2、学会根据幅频特性曲线确定系统的固有频率f 0和阻尼⽐。
⼆、实验装置框图图3.1表⽰实验装置的框图图3-1 实验装置框图KCX图3-2 单⾃由度系统⼒学模型三、实验原理单⾃由度系统的⼒学模型如图3-2所⽰。
在正弦激振⼒的作⽤下系统作简谐强迫振动,设激振⼒F 的幅值B 、圆频率ωo(频率f=ω/2π),系统的运动微分⽅程式为:扫频信号源动态分析仪计算机系统及分析软件打印机或绘图仪简⽀梁振动传感器激振器⼒传感器质量块M或 M F x dt dxdt x d M F x dt dx n dtx d FKx dt dx C dtx d M /2/222222222=++=++=++ωξωω(3-1)式中:ω—系统固有圆频率ω =K/Mn ---衰减系数 2n=C/M ξ---相对阻尼系数ξ=n/ωF ——激振⼒ )2sin(sin 0ft B t B F πω== ⽅程①的特解,即强迫振动为:)2sin()sin(0?π?ω-=-=f A A x (3-2)式中:A ——强迫振动振幅--初相位20222024)(/ωωωn M B A +-=(3-3)式(3-3)叫做系统的幅频特性。
将式(3-3)所表⽰的振动幅值与激振频率的关系⽤图形表⽰,称为幅频特性曲线(如图3-3所⽰):3-2 单⾃由度系统⼒学模型 3-3 单⾃由度系统振动的幅频特性曲线图3-3中,Amax 为系统共振时的振幅;f 0为系统固有频率,1f 、2f 为半功率点频率。
振幅为Amax 时的频率叫共振频率f 0。
在有阻尼的情况下,共振频率为:221ξ-=f f a (3-4) 当阻尼较⼩时,0f f a =故以固有频率0f 作为共振频率a f 。
阻尼和固有频率的测量

时,
,而且与阻尼大小无关,系统处
于相位共振状态,可以方便的识别出系统的固有频率 ;在幅频图上,
当
时,
达到极大值,且
,故可以识别出阻尼系
数。
2021/5/9
22
8.3.2 实频图与虚频图
频响函数的实部和虚部分别为
其图形如图13所示。在实部图上,利用半功率点
法可以识别出系统的相对阻尼系数
,
时虚部达到极大值,实部为0,系统处于共振状
应为
图1 单自由度系统模型
(1)
衰减系数
2021/5/9
2
响应曲线如图2所示。 结论:
频率,
为衰减振动的周期, 为衰减振动的圆频率。
2021/5/9
为衰减振动的
3
2021/5/9
图2 弱阻尼衰减振动的响应曲线
4
从图2衰减振动的响应曲线上可直接测量出
,然后根
据
可计算出 n ;
计算出 p; 可计算出
阻尼系数和固有频率
的测量
2021/5/9
1
8.1 阻尼系数的测量
8.1.1 自由振动衰减法
图1所示的一个单自由度质量---弹簧----
阻尼系统,其质量为m (kg),弹簧刚度系
数为k (N/m),粘性阻尼系数为r (N. m
/s)。当质量上承受初始条件t=0时,位
移
,速度
激励时,将做
自由衰减振动。在弱阻尼条件下其位移响
态,可识别出系统的固有频率。
2021/5/9
图13频响函数的实部与虚部图
23
8.3.2 Nyquist图
以频响函数的实部为横坐标, 虚部为纵坐标,绘出频响函数矢量 随频率的变化图,这些变化矢量的 端点轨迹图称为Nyquist图,图形 方程为:
单自由度振动系统固有频率及阻尼的测定实验报告(精)

单自由度振动系统固有频率及阻尼的测定实验报告一、实验目的1、掌握测定单自由度系统固有频率、阻尼比的几种常用方法2、掌握常用振动仪器的正确使用方法二、实验内容1、记录水平振动台的自由衰减振动波形2、测定水平振动台在简谐激励下的幅频特性3、 测定水平振动台在简谐激励下的相频特性4、 根据上面测得的数据,计算出水平振动台的固有频率、阻尼比三、实验原理由台面、支撑弹簧片及电磁阻尼器组成的水平振动台(见图四),可视为单自由度系统,它在瞬时或持续的干扰力作用下,台面可沿水平方向振动。
1、 衰减振动:用一橡皮锤沿水平方向敲击振动台,系统获得一初始速度而作自由振动,因存在阻尼,系统的自由振动为振幅逐渐减小的衰减振动。
阻尼越大,振幅衰减越快。
选x 为广义坐标,根据记录的曲线可分析衰减振动的周期d T ,频率d f ,对数减幅系数δ及阻尼比ζ,有i t T d ∆=, dd T f 1= )ln(111+=i X X iδd nT =, πδδπδζ2422≈+= 其中∆t 为i 个整周期相应的时间间隔,1X 和1+i X 为相隔i 个周期的振幅。
2、 强迫振动的幅频特性测定:保持功放的输出电流幅值不变,即保持激振力力幅不变,缓慢地由低频2Hz 到高频40Hz 改变激振频率,用相对式速度拾振器检测速度振动量,再经过积分处理后得到位移量,由测试数据可描绘出一条振幅频率特性曲线而根据该测试曲线可由如下关系式估算系统的固有频率n f 及阻尼比ζ nf≈m f , 021B B m =ζ 或 ζm f ff 212-≈ 其中m f 为振幅达到最大m B 时的激振频率;0B 为零频率的相应振幅(约等于f =2Hz 时的振幅);1f 和2f 为振幅m B B 707.0=的对应频率,即半功率点频率。
改变阻尼大小重新进行频率扫描可获得一组相应于不同阻尼比的幅频特性曲线。
四、实验装置测试系统如图四所示,其部分仪器的原理及功能说明如下:1、实验装置:振动台系统由台面、支撑弹簧片及电磁阻尼器组成,台面可沿水平面纵轴方向振动。
单自由度振动系统固有频率及阻尼的测定-实验报告

1
DC 输出:0~30V,2A
PAB 32~2A KIKUSUI(日本)
7
微型计算机
1
内部有 A/D、D/A 插卡
通用型
-3-
五.实验步骤
1. 打开微型计算机,运行进入“单自由度系统”程序。 2. 单击“设备虚拟连接”功能图标,进入设备连接状态,参照图六对显示试验设备进行联
线。连线完毕后,单击“连接完毕”,如连接正确,则显示“连接正确”,即可往下进 行,否则重新连接,直至连接正确。 3. 接通阻尼器励磁及功率放大器电源,调励磁电流为某一定值(分别为������ = 0.6A, 0.8A, 1.0A) 4. 测定自由衰减振动: 单击“自由衰减记录”功能图标,进入如图七显示界面。单击 (Start)键,开始测试。由 一电脉冲沿水平方向突然激励振动台,微机屏幕上显示自由衰减曲线。用鼠标调节光标 的位置,读出有关的数据。改变周期数 i 的数值,即可直接显示相应的周期和频率。 5. 测定幅频特性和相频特性: 单击“简谐激励振动”功能图标,按图八所示,单击“信号输入显示框中的频率,将弹、 出一个对话框,可以直接输入激励频率。也可单击频率的单步步进键进行激励调节。单 击 (Start)键,开始测试,开始强迫振动幅频特性和相频特性测量,其中2Hz~15Hz内大致 相隔1Hz设一个测点;15Hz~30Hz 内每隔5Hz设一个测点。 在显示检测框显示力信号和相应信号波形,以便观察信号的质量。幅值比显示振动位移
注:由于实验时间所限,加之读数难度较大,在������������ 附近没有加密测量相频点。这是实验中的失误。
-5-
七.实验数据处理
1. 根据自由衰减振动记录的有关数据,分析计算系统的固有圆频率������������及阻尼比ζ。
振动系统固有频率实验报告

汕头大学实验报告h学习觀讎輔解繃诚竝X学获嗣法脱翩固有孵腹理与方法;幅蓟别腳融判别法)3>学和击刼试嗣靈翻解桶理与方歯借酬别法)三、买验原理对于振动索竈負営要测定其固有频騒辭用的方法就是用删力®^ 到系统的各阶同有解.另一种方決是用锤击法,用冲击力滋扳衣汀1 的力信号和細狮鮒号进疔传酚飙得昭阶国有频転L蒯力激振由附力作用下的强迫翩]系统,其运动方程划mx+Cx+Kx = f sin w J方程式的腰乩勺+兀这二部分紇成; 血=严((?1 co叫f+G in⑴詁)式巾CD rj =UJ Jl-D*Hk團3阻思强址扳动G 甘数E H 初始条件决定 = A sin cu/+ cos to/+ 牝讣;芍代表迥尼n 由振动基•心代表阻尼强迫振动项.自由振动取周期T D =—强述振动项周期7;=—co f由于阻尼的存在,自白振动基随时间不斷地袁减泊先•最后.只剩下后两项.也就是通常讲的定离强动、 只廻卞强追振动部分.即(CD 2 -CD ;)- +牝硏 3沁」+(co 亍心 F + 4 Jco :沏叭'设频率比“二吳C1)则振幅」_g/co7(1-»2)2 +4w :D =g (co 一 軸;)辺垃变换可写成式申茸中x = A siiX 3 / — 屮)£ = Deo 代入上式2Dit(p = __rI -tr因为=FJm/K/m =^ =兀戲弹簧受干扰力峰值作用引起的静位移,所戏扛幅A跡写成■4 — -(X . — P-T ..J(1 一屮尸+4八"其中P称为动力放大系数=--- ------ --------/1_宀十北莎动力放大系数卩是遥迫抚动讨的动力系敌即动枠童与醴堀坐Z比.这几霞置就拾压器杆舉白白度体系的报动的研究都是很重要的「当k = H即强迫ftU黑;车和系统固有频率相等时,动力系数迅屢增加.引起系统共振,由式x = J sin( lx) / - (p)可知:・共抵寸捱幅和贰位擀有明显的变化.遞垃对这炖个参数进行削亘.我们可以判别系统星否达到共抿动点,从iru确崖出系统列各阶推动頻丰•・1)幅隹判丸法在濒抿功車撞岀不变的駕况下、由低到戲诣节黴报器妁激扼數憲*通过示波器.我们可以观察到在某一频率下.任一振动量速度、血逮度)躺蛍迅速増加,这就是机械振动泵统的某阶固有频率. 建即方注简单•易,厂口在阻尼较大的情况下.不同的测st方法得出的共振动频率稍有差别,不同类型的抿动呈对摄幅变化敏感程度不一样.这样对于一种类型的传感蒂在其阶频率时不够敏感.2)相位判别法再位判法是Hi推并撫时持竦的雄位值以及共掘动前后柑位变化址■申所梃击来的一种共撫判貳法□在简潸力津振的错况下,用片'位法来判迄共振是一珅较为敏感的方也*而且共报足的頻泰就是系统的无阳尼固有频部.可以排琛阻尼因責的彩响’Si报估号呀;F = Tsin toZ 位移估号为:j?= Ksinf tor -cp)速度‘舌号为T y=tjFcos(a)r -p)加速度怙兮为: y - -w;} sin(CDZ一tp)(1)位移判别共fti埒飯推动怙号卷入到采集仪的第一迈道4|【'(讪)•位移传感器就出信号或通辽2 J违0 1型匪动教学牧积分档愉汨金为(2移酣倍号输入到第二通道(即Y轴)•此讨阿通道的信号分别为’戲报伯号戈h F=Fsin^住坯估弓为:y =Fsingf-tp)共撮时,如=⑷八(P二一・X轴信号和Y轴信号的相位差为K/2,根据利萨如图原理可知.屏慕匕的图象将适一个正暂區U当⑴賂大于⑴耗或冏小于他」,區象榔将白正鴉岡变为斜巒列,耳变化过程噩下图所示B闵此医躱圧煞商雾睦恢变为正碉囿的頻幸就是抿动体的嵐有频率.罩小乜移判别共戎拘利我如昌形(2) 速嗖判别共抿用滋抿佶号撞入到采集仪的第一通道<UI:X轴).速度传痣梆检出唱号或通过2 J吨0 1躺动教学仅积分档績出量为速度的伯号轮入到第二通道(即y轴人此时两辿道的伯号分别为:徽振倍号为’ F = Fsm^t遠度们弓为:y -(U ¥ casfujr )忑標时・<p = -・\轴信号和¥轴伯号的相位差沟匚,2’根据利萨幼图原理可知,屏幕上的图彖应是一条貞线*当3晤大于或略小于时.医彖都绍白.直线变为斜巒岡.具变化过程如下图所示.因此图姣:弓魁林圜变为直线的频率就是按动体的底有锲車.■»S 5用洼度判别共娠的剧萨扫:划形(3)加速度判别共撫将4嫌信号输入到采集仪的第一通道(即X 轴W 度传感器输出伯号输入到第二通道(即Y 轴). 此时两邇道的信号分别为:眾据信号为’ F=Fsin (i>f加速嘍悩 v A : y = -to ;Y sin ( sr -u j共掘时* tn =UJ ^(p = -. X 轴信号和Y 轴悄号的相位差>j;t 2.根据利萨幼圏原理可知.屏幕上的图躱应是一个正喘側.当CD 瞪大于(叭或略小于CD 」,1胡彖都將日正稠圆变为斜嘀恻.其变化过 程虻下圧萨乐.因就圏象由铁箭圜变为正咂岡的叔率就是摄动体的氏订臧誑=羊鬥 I;「二戈’一 ―一 .< ;9 峯 T2s 传函内虬也I 毁事响应雷歡判别 ——动力放大系数判别祛)通常我们认为振动系统为线性系统,用一特定已知的滋振力.以可控的方法来滋励踣构.同时测豐 输入和输出信号.通过传函分析,得到系统固有频率.响应与澈振力之间的关系可用导纳表示, y = A=厂 2尹 厂妒半F ^(1 - I ;2)2 +4D 2U 2 丨■『Y 的奩义就是蝠竺为I 的澈唏力靳产生的响应”硏:究¥与澈耐力之问的关岳.就可得到系统的频响 特性曲线.在共抿頻率F 的导纳值迅逑增大.从而可以判别幹阶共掘鹤率. 皿、实验步骤一、幅值判别法测量L 安裝仪器耙电动接粒式激撮器安装在底庫上,调节电动接鎚式激振器高度;让接傩头就简支梁产生一定的预 压力,使澈扳杆上的红线与激摄动器朋面平齐为宜.把藏报器的信号输入朗圳连接线接到ZJV60]A^ 撮动載学试验仪的功放输出接口上.把带厳座的加速度传療器故在简支樂匕输出僧号接到ZJY601A 型振动截学试验仪的加速度传感 器输入瑞.功能档住拔至殛囿档的aM 度。
振动系统固有频率的测试实验报告
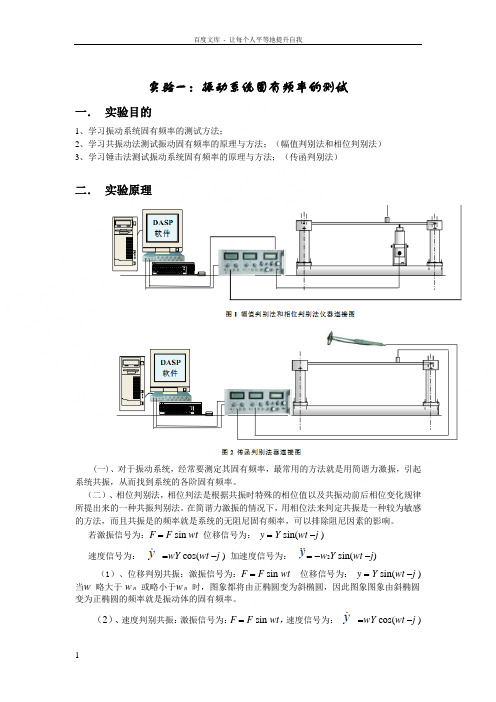
实验一:振动系统固有频率的测试一.实验目的1、学习振动系统固有频率的测试方法;2、学习共振动法测试振动固有频率的原理与方法;(幅值判别法和相位判别法)3、学习锤击法测试振动系统固有频率的原理与方法;(传函判别法)二.实验原理(一)、对于振动系统,经常要测定其固有频率,最常用的方法就是用简谐力激振,引起系统共振,从而找到系统的各阶固有频率。
(二)、相位判别法,相位判法是根据共振时特殊的相位值以及共振动前后相位变化规律所提出来的一种共振判别法。
在简谐力激振的情况下,用相位法来判定共振是一种较为敏感的方法,而且共振是的频率就是系统的无阻尼固有频率,可以排除阻尼因素的影响。
若激振信号为:F = F sin wt 位移信号为:y = Y sin(wt -j )速度信号为:=wY cos(wt -j ) 加速度信号为:= -w2Y sin(wt -j)(1)、位移判别共振:激振信号为:F = F sin wt 位移信号为:y = Y sin(wt -j ) 当w 略大于w n或略小于w n时,图象都将由正椭圆变为斜椭圆,因此图象图象由斜椭圆变为正椭圆的频率就是振动体的固有频率。
(2)、速度判别共振:激振信号为:F = F sin wt,速度信号为:=wY cos(wt -j )当w 略大于w n或略小于w n时,图象都将由直线变为斜椭圆,因此图象由斜椭圆变为直线的频率就是振动体的固有频率。
(3)、加速度判别共振:激振信号F = F sin wt,加速度信号= -w2Y sin(wt -j) 共振时,屏幕上的图象应是一个正椭圆。
因此图象由斜椭圆变为正椭圆的频率就是振动体的固有频率。
(三)、另一种方法是用锤击法,用冲击力激振,通过输入的力信号和输出的响应信号进行传函分析,得到各阶固有频率。
响应与激振力之间的关系可用导纳表示:Y 的意义就是幅值为1 的激励力所产生的响应。
研究Y 与激励力之间的关系,就可得到系统的频响特性曲线。
振动系统固有频率的测试实验报告

实验一:振动系统固有频率的测试一.实验目的1、学习振动系统固有频率的测试方法;2、学习共振动法测试振动固有频率的原理与方法;(幅值判别法和相位判别法)3、学习锤击法测试振动系统固有频率的原理与方法;(传函判别法)二.实验原理(一)、对于振动系统,经常要测定其固有频率,最常用的方法就是用简谐力激振,引起系统共振,从而找到系统的各阶固有频率。
(二)、相位判别法,相位判法是根据共振时特殊的相位值以及共振动前后相位变化规律所提出来的一种共振判别法。
在简谐力激振的情况下,用相位法来判定共振是一种较为敏感的方法,而且共振是的频率就是系统的无阻尼固有频率,可以排除阻尼因素的影响。
若激振信号为:F = F sin wt 位移信号为:y = Y sin(wt -j )速度信号为:=wY cos(wt -j ) 加速度信号为:= -w2Y sin(wt -j)(1)、位移判别共振:激振信号为:F = F sin wt 位移信号为:y = Y sin(wt -j ) 当w 略大于w n或略小于w n时,图象都将由正椭圆变为斜椭圆,因此图象图象由斜椭圆变为正椭圆的频率就是振动体的固有频率。
(2)、速度判别共振:激振信号为:F = F sin wt,速度信号为:=wY cos(wt -j ) 当w 略大于w n或略小于w n时,图象都将由直线变为斜椭圆,因此图象由斜椭圆变为直线的频率就是振动体的固有频率。
(3)、加速度判别共振:激振信号F = F sin wt,加速度信号= -w2Y sin(wt -j) 共振时,屏幕上的图象应是一个正椭圆。
因此图象由斜椭圆变为正椭圆的频率就是振动体的固有频率。
(三)、另一种方法是用锤击法,用冲击力激振,通过输入的力信号和输出的响应信号进行传函分析,得到各阶固有频率。
响应与激振力之间的关系可用导纳表示:Y 的意义就是幅值为1 的激励力所产生的响应。
研究Y 与激励力之间的关系,就可得到系统的频响特性曲线。
阻尼运动实验报告

竭诚为您提供优质文档/双击可除阻尼运动实验报告篇一:《阻尼振动与受迫振动》实验报告《阻尼振动与受迫振动》实验报告工程物理系核41崔迎欢20XX011787一.实验名称:阻尼振动与受迫振动二.实验目的1.观测阻尼振动,学习测量振动系统基本参数的方法;2.研究受迫振动的幅频特性和相频特性,观察共振现象;3.观测不同阻尼对受迫振动的影响。
三..实验原理1.有粘滞阻尼的阻尼振动弹簧和摆轮组成一振动系统,设摆轮转动惯量为J,粘滞阻尼的阻尼力矩大小定义为角速度dθ/dt与阻尼力矩系数γ的乘积,弹簧劲度系数为k,弹簧的反抗力矩为-kθ。
忽略弹簧的等效转动惯量,可得转角θ的运动方程为d2?d?J2k??0dtdt记ω0为无阻尼时自由振动的固有角频率,其值为ω0k/J,定义阻尼系数β=γ/(2J),则上式可以化为:d2?d??2??k??02dtdt2小阻尼即?2??0?0时,阻尼振动运动方程的解为??tiexp(??t)cos??i(*)?由上式可知,阻尼振动角频率为?d?阻尼振动周期为Td?2?2.周期外力矩作用下受迫振动的解在周期外力矩mcosωt激励下的运动方程和方程的通解分别为dd2?d?J2k??mcos?tdtdt??tiexp???t?cos??i??mcos??t?这可以看作是状态(*)式的阻尼振动和频率同激励源频率的简谐振动的叠加。
一般t>>τ后,就有稳态解??tmcos??t稳态解的振幅和相位差分别为?m???arctan2??22?0??其中,φ的取值范围为(0,π),反映摆轮振动总是滞后于激励源支座的振动。
3.电机运动时的受迫振动运动方程和解弹簧支座的偏转角的一阶近似式可以写成??tmcos?t式中αm是摇杆摆幅。
由于弹簧的支座在运动,运动支座是激励源。
弹簧总转角为t?mcos?t。
于是在固定坐标系中摆轮转角θ的运动方程为d2?d?J2k?mcos?t??0dtdt也可以写成d2?d?J2k??k?mcos?tdtdt于是得到2?m?由θm的极大值条件??m0可知,当外激励角频率??m有极大值系统发生共振,θ?,称为阻尼比。
振动实验报告1

振动实验报告1实验⼀振动系统固有频率的测试⼀、实验⽬的:1、学习振动系统固有频率的测试⽅法;2、学习共振动法测试振动固有频率的原理与⽅法;3、学习锤击法测试振动系统固有频率的原理与⽅法;⼆、实验原理1、简谐⼒激振1)幅值判别法在激振功率输出不变的情况下,由低到⾼调节激振器的激振频率,通过⽰波器,我们可以观察到在某⼀频率下,任⼀振动量(位移、速度、加速度)幅值迅速增加,这就是机械振动系统的某阶固有频率。
这种⽅法简单易⾏,但在阻尼较⼤的情况下,不同的测量⽅法得出的共振动频率稍有差别,不同类型的振动量对振幅变化敏感程度不⼀样,这样对于⼀种类型的传感器在某阶频率时不够敏感。
2)相位判别法相位判法是根据共振时特殊的相位值以及共振动前后相位变化规律所提出来的⼀种共振判别法。
在简谐⼒激振的情况下,⽤相位法来判定共振是⼀种较为敏感的⽅法,⽽且共振是的频率就是系统的⽆阻尼固有频率,可以排除阻尼因素的影响。
A.位移判别共振将激振动信号输⼊到采集仪的第⼀通道(即X 轴),位移传感器输出信号或通过ZJY-601A 型振动教学仪积分档输出量为位移的信号输⼊到第⼆通道(即Y 轴),此时两通道的信号分别为激振信号为:位移信号为:共振时,,X 轴信号和Y 轴信号的相位差为p / 2,根据利萨如图原理可知,屏幕上的图象将是⼀个正椭圆。
当w 略⼤于n w 或略⼩于n w 时,图象都将由正椭圆变为斜椭圆,其变化过程如下图所⽰。
因此图象图象由斜椭圆变为正椭圆的频率就是振动体的固有频率。
B.速度判别共振将激振信号输⼊到采集仪的第⼀通道(即X 轴),速度传感器输出信号或通过ZJY-601A 型振动教学仪积分档输出量为速度的信号输⼊到第⼆通道(即Y 轴),此时两通道的信号分别为:激振信号为:速度信号为:共振时,,X 轴信号和Y 轴信号的相位差为p / 2。
根据利萨如图原理可知,屏幕上的图象应是⼀条直线。
当w 略⼤于n w 或略⼩于n w 时,图象都将由直线变为斜椭圆,其变化过程如下图所⽰。
振动系统固有频率的测试实验报告

实验一:振动系统固有频率的测试一. 实验目的1、学习振动系统固有频率的测试方法;2、 学习共振动法测试振动固有频率的原理与方法;(幅值判别法和相位判别法)3、 学习锤击法测试振动系统固有频率的原理与方法;(传函判别法)二. 实验原理(一)、对于振动系统,经常要测定其固有频率,最常用的方法就是用简谐力激振,引起 系统共振,从而找到系统的各阶固有频率。
(二)、相位判别法,相位判法是根据共振时特殊的相位值以及共振动前后相位变化规律 所提出来的一种共振判别法。
在简谐力激振的情况下,用相位法来判定共振是一种较为敏感 的方法,而且共振是的频率就是系统的无阻尼固有频率,可以排除阻尼因素的影响。
若激振信号为:F = F sinwt位移信号为:y €Y sin (wt-j )■ ■ ■速度信号为:丁 €wY cos (wt -j )加速度信号为:」=w 2Y sin (wt -j )(1)、位移判别共振:激振信号为:F = F sin wt 位移信号为:y =F sin (wt -j ) 当w略大于w n 或略小于⑷“时,图象都将由正椭圆变为斜椭圆,因此图象图象由斜椭圆 变为正椭圆的频率就是振动体的固有频率。
(2)、速度判别共振:激振信号为:F = F sin wt ,速度信号为:「=wY cos (wt -j ) 当w略大于w n或略小于⑷“时,图象都将由直线变为斜椭圆,因此图象由斜椭圆变为直线的 频率就是振动体的固有频率。
(3)、加速度判别共振:激振信号F = F sin wt ,加速度信号、=w 2Y sin (wt -j )共振时, 屏幕上的图象应是一个正椭圆。
因此图象由斜椭圆变为正椭圆的频率就是振动体的 固有频率。
(三)、 另一种方法是用锤击法,用冲击力激振, 通过输入的力信号和输出的响应信号 进行传函分析, 得到各阶固有频率。
响应与激振力之间的关系可用导纳表示:Y 的意义就是幅值为也的激励力所产生的响应。
机械实验之振动参数的测定

振器能起到隔振作用的最低频率。
2.4 实验操作注意点
1)信号源的输出电流不能太大,一般取在200~300毫安之间,激振头的 最大输入电流为500毫安。
2)由于信号源的粗调旋钮自身比较小,调节比较灵敏,同时信号源显示 又存在一定的迟延,所以很不容易调节,需要特别的耐心
2.5有可能出现的问题
在实验的过程中,有于测振仪自身没有调零功能,因此,有时会出 现零漂较大的情况(达到0.04mm),而主动隔振在加上空气阻尼器的时 候振幅也很小,所以误差相对较大,甚至导致实验失败。
C)绘出振动波形图波峰和波谷的两根包络线,然后设定,并读出个波形所
经历的时间t,量出相距i个周期的两振幅 , 20 。按公式计算 tgx0d/(x•0nx0)和 n/0
2)用强迫振动法测量
tg
x0d
•
/(x0
nx0)和
n/0
A)加速度传感器置于简支梁上,其输出端接信号采集分析仪,用来测量简支 梁的振动幅值
2.5 实验的其他方法
在测系统的阻尼比时还可以采用放大系数法
在简谐激振力作用
1下,有阻尼单自由度系统的放大系数
为:
共振时, 1/ 2, 1/ 2
即: 1 y静 2 2y动
放大系数 是指激振力作用时的振幅与静力作用时最大位移的比 值,所以有
1
A1 i
3.分析总结
3.1 实验体会
1) 信号发生器在调定到一定的频率微调旋钮由于比较时会发生一些困 难,主要因素如下:
主动隔振效率: 0 2
讨论:1)当 a 1 时, A2 A1 , 1 ,隔振器没有隔振效果
0 时,即 2 共振
2)当
A2 时 A1
,/ 隔0 振器才发生作用
实验一单自由度振动系统固有频率及阻尼比的测定

实验二 刚性转子动平衡实验一、实验目的(1) 掌握刚性转子动平衡的基本原理和步骤; (2) 掌握虚拟基频检测仪和相关测试仪器的使用; (3) 了解动静法的工程应用。
二、实验内容采用两平面影响系数法对一多圆盘刚性转子进行动平衡三、实验原理工作转速低于最低阶临界转速的转子称为刚性转子,反之称为柔性转子。
本实验采取一种刚性转子动平衡常用的方法—两平面影响系数法。
该方法可以不使用专用平衡机,只要求一般的振动测量,适合在转子工作现场进行平衡作业。
根据理论力学的动静法原理,一匀速旋转的长转子,其连续分布的离心惯性力系,可向质心C 简化为过质心的一个力R (大小和方向同力系的主向量∑=iS R )和一个力偶M (等于力系对质心C 的主矩CiΜS m M ==∑)(),见图一。
如果转子的质心恰在转轴上且转轴恰好是转子的惯性主轴,即转轴是转子的中心惯性主轴,则力R 和力偶矩M C 的值均为零。
这种情况称转子是平衡的;反之,不满足上述条件的转子是不平衡的。
不平衡转子的轴与轴承之间产生交变的作用力和反作用力,可引起轴承座和转轴本身的强烈振动,从而影响机器的工作性能和工作寿命。
图一 转子系统与力系简化刚性转子动平衡的目标是使离心惯性力系的主向量和主矩的值同时趋近于零。
为此,先在转子上任意选定两个截面I 、II (称校正平面),在离轴线一定距离1r 、2r (称校正半径),与转子上某一参考标记成夹角1θ、2θ处,分别附加一块质量为1m 、2m 的重块(称校正质量)。
如能使两质量1m 和2m 的离心惯性力(其大小分别为211ωr m 和222ωr m ,ω为转动角速度)正好与原不平衡转子的离心惯性力系相平衡,那么就实现了刚性转子的动平衡。
两平面影响系数法的过程如下;(1)在额定的工作转速或任选的平衡转速下,检测原始不平衡引起的轴承或轴颈A 、B 在某方位的振动量11010ψ∠=V V 和22020ψ∠=V V ,其中10V 和20V 是振动位移(也可以是速度或加速度)的幅值,1ψ和2ψ是振动信号对于转子上参考标记有关的参考脉冲的相位角。
振动系统固有频率的测试实验原理、方法和报告

振动系统固有频率的测试一、实验目的1、学习振动系统固有频率的测试方法;2、学习共振动法测试振动固有频率的原理与方法二、实验装置简图图2-11、简支梁2、加速度传感器3、接触式激振器三、实验仪器简介请参照实验一《简谐振动幅值测量》内介绍。
四、实验原理1、幅值判别法在激振功率输出不变的情况下,由低到高调节激振器的激振频率,通过示波器可以观察到在某一频率下,任一振动量(位移、速度、加速度)幅值迅速增加,这就是机械振动系统的某阶固有频率。
这种方法简单易行,但在阻尼较大的情况下,不同的测量方法得出的共振频率稍有差别,不同类型的振动量对振幅变化敏感程度不一样,这样对于一种类型的传感器在某阶频率时不够敏感。
2、相位判别法相位判别法时根据共振时特殊的相位值以及共振前后相位变化规律所提出来的一种共振判别法。
在简谐力激振的情况下,用相位法来判定共振是一种较为敏感的方法,而且共振时的频率就是系统的无阻尼固有频率,可以排除阻尼因素的影响。
激振信号为:F=F sinωt位移信号为:x=x0sin(ωt+φ)速度信号为:v=ωx0cos(ωt+φ)加速度信号为:a=-ω2x0sin(ωt+φ)1)位移判别共振将激振信号输入到采集仪的第一通道(即X轴),位移传感器输出信号或通过振教仪积分档输出量为位移的信号输入到第二通道(即Y轴),此时两通道的信号分别为:激振信号为:F=F sinωt位移信号为:x=x0sin(ωt+φ)共振时,ω=ωn,φ=π/2,X轴信号和Y轴信号的相位差为π/2,根据莉萨如图原理可知,屏幕上的图形将是一个正椭圆。
当ω略大于ωn或略小于ωn时,图像都将由正椭圆变为斜椭圆,其变化过程如图2-2所示。
因此图像由斜椭圆变为正椭圆的频率就是振动体的固有频率。
ω<ωnω=ωnω>ωn图2-2用位移判别共振的莉萨如图形2)速度判别共振将激振信号输入到采集仪的第一通道,速度传感器输出信号或通过振教仪积分档输出量为速度的信号输入到第二通道(即Y轴),此时两通道的信号分别为:激振信号为:F=F sinωt速度信号为:v=ωx0cos(ωt+φ)共振时,ω=ωn,φ=π/2,X轴信号和Y轴信号的相位差为π/2,根据莉萨如图原理可知,屏幕上的图形将是一条直线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4、根据相频特性的测试数据,在同一图上绘出几条相位差频率( 特性曲线,由此分析阻尼的影响并计算系统的固有频率及阻尼比。
5、根据实验现象和绘制的幅频、相频特性曲线,试分析对于不同阻尼的振动系统,几种固有频率和阻尼比测量方法的优劣以及原因。
首先,在水平振动台面上不加任何重物,测量系统在自由衰减振动时的固有频率;之后在水平振动台面上放置一个质量已知的砝码,再次测量系统在自由振动时的固有频率。记录两次测得的固有频率,并根据其估算水平振动台面的等效质量。
4、测定自由衰减振动特性:
撤去水平振动台面上的砝码,调整励磁电流至0.6A。继续使用“自由衰减记录”功能进行测试。操作方法与步骤3基本相同,但需按照数据记录表的提示记录衰减振动的峰值、对应时间和周期数i等数据,以计算系统的阻尼。
假设实验使用的单自由度振动系统中,水平振动台面的等效质量为 ,系统的等效刚度为 ,在无阻尼或阻尼很小时,系统自由振动频率可以写作 。这一频率容易通过实验的方式测得,我们将其记作 ;此时在水平振动台面上加一个已知质量 ,测得新系统的自由振动频率为 。则水平振动台面的等效质量为 可以通过以下关系得到: 。
、 的意义同拾振器。但对激振器说, 的值表示单位电流产生的激振力大小,称为力常数,由厂家提供。JZ-1的力常数约为5N/A。频率可变的简谐电流由信号发生器和功率放大器提供。
4、计算机虚拟设备:
在计算机内部,插有A/D、D/A接口板。按照单自由系统按测试要求,进行专门编程,完成模拟信号输入、显示、信号分析和处理等功能。
6、教师签名的原始数据表附在实验报告最后,原始数据记录纸在实验课上提供,必须每人交一份,可以采用复印、拍照打印等方式进行复制。原始数据上要写清所有人的姓名学号,不得使用铅笔记录。
七、参考资料
1清华大学理论力学教研组编.第十三章质点沿直线的振动—§13-1~§13-3.《理论力学》(第四版).
2范钦珊主编.第14章振动—§14-1~14-3.《工程力学教程(Ⅲ)》.
图六自由衰减记录波形显示界面
图七简谐激励强迫振动显示界面
振幅
相位差
其中 , 。
1、衰减振动:
用手沿水平方向轻轻敲击振动台,系统获得一个初始速度而作自由振动,因存在阻尼,系统的自由振动为振幅逐渐减小的衰减振动。阻尼越大,振幅衰减越快。
为了便于观察和分析运动规律,采用电动式相对速度拾振器将机械振动信号变换为与速度成比例的电压信号,该电压信号经过计算机A/D和积分处理,得到与运动位移成比例的数字量,并显示运动位移随时间变化的波形。改变阻尼的大小可观察衰减振动波形的相应变化。
在显示检测框显示力信号和相应信号波形,以便观察信号的质量。幅值比显示振动位移与力的有效值比B。精确测出幅值振幅 的最大值 及对应的频率 ,并精确找出与振幅 对应的频率 和 。相位差显示振动位移与力信号相位差 。精确测出相位差 时的频率 。由于相频特性在 邻近变化大,应加密测点。
6、改变阻尼器励磁电流值(分别为1.0A、0.8A),重复步骤4、5。
为磁隙的磁感应强度 ;l为线圈在磁隙中有效长度(m); 的值表示对应于单位速度的感应电势,称为拾振器的名义灵敏度,由厂家提供。CD-2拾振器的名义灵敏度约为30V/m/s或30mV/mm/s。
图五相对式速度拾振器结构简图
3、电磁激振器:
JZ-1型电磁激振器与CD-2型相对式速度拾振器在结构上甚至尺寸上都完全相同,只是二者互为逆变换器。拾振器的作用是将机械能转换为电能。为获得高的名义灵敏度,线圈通常用很细的铜线绕成很多圈。激振器的作用是将电能转换为机械能,为生产较大推力,线圈选用较粗的铜线绕成,以便允许通过较强的电流。设电流为 (A或mA),产生的激振力为 ,则
五、实验步骤
1、打开微型计算机,运行进入“单自由度系统”程序。
2、接通阻尼器励磁及功率放大器电源,调励磁电流至0A。
3、估算水平振动台面的等效质量:
单击“自由衰减记录”功能图标,进入如图六显示界面。单击(Start)键的同时,沿水平方向轻轻敲击振动台,微机屏幕上显示自由衰减曲线。用鼠标将光标的位置调节到波峰(或波谷处),读出有关的数据。改变周期数i的数值,即可直接显示相应的周期和频率。为提高测量精度,实验中应选取尽量多的周期数值。
5、根据上面测得的数据,计算出水平振动台的固有频率、阻尼比
三、实验原理
单自由度振动系统是一种简单且常见的振动系统模型。本实验中的振动系统由台面、支撑弹簧片及电磁阻尼器组成的水平振动台(见图四),可视为单自由度系统,它在瞬时或持续的干扰力作用下,台面可沿水平方向振动。
与之前常见的质量弹簧系统不同,本实验中单自由度振动系统的等效质量、刚度均属于未知量。且通过观察不难发现,银白色的水平振动台面无法单独取出以测量质量。这一系统反应了大多数实际振动系统的特性——即难以分别得到其准确的等效质量、刚度的数值,再通过理论计算得到固有频率。因此通过实验的方式直接测量系统整体的固有频率成为一种非常重要而可靠的研究手段,同时系统的等效质量和刚度,也可以由测量结果推导得出。
当单自由度振动系统具有粘滞阻尼时,自由振动微分方程的标准形式为 ,式中 为广义坐标, 为阻尼系数, , 为广义阻力系数, 为等效质量; 为固有的圆频率, , 为等效刚度。在阻尼比 的小阻尼情况下,运动规律为 ,式中 , 由运动的起始条件决定, 。
具有粘滞阻尼的单自由度振动系统,在广义简谐激振力 作用下,系统强迫振动微分方程的标准形式为 ,式中 。系统稳态强迫振动的运动规律 ,式中
图二强迫振动的幅频特性曲线图三强迫振动的相频特性曲线
由相频特性求阻尼比的原理如下:
其中 , —激振频率, —固有频率。由于
故有 即
即在相位共振点( , )附近,取一小段频率区间△f求出相应的相位变化 即可由下式确定阻尼比 (参看图三):
对于单自由度小阻尼系统, 。
四、实验装置
测试系统如图四所示,其部分仪器的原理及功能说明如下:
单自由度振动系统固有频率及阻尼的测定
一、实验目的
1、掌握测定单自由度系统固有频率、阻尼比的几种常用方法
2、掌握常用振动仪器的正确使用方法
二、实验内容
1、根据单自由度系统固有频率公式,估算水平振动台面的等效质量
2、记录水平振动台的自由衰减振动波形
3、测定水平振动台在简谐激励下的幅频特性
4、测定水平振动台在简谐激励下的相频特性
1、实验装置:
振动台系统由台面、支撑弹簧片及电磁阻尼器组成,台面可沿水平面纵轴方向振动。铝质台面在电磁阻尼器的磁隙中运动时,产生与运动速度成正比的电涡流阻尼,调节阻尼电磁铁的励磁电流可改变阻尼的大小。
表一实验设备名称
序号
名称
主要技术指标
1
单自由度实验装置
固有频率:约10Hz
阻尼比:0.01~0.20可变
5、测定幅频特性和相频特性:
保持励磁电流不变。单击“简谐激励振动”功能图标,按图七所示,单击“信号输入显示框中的频率,将弹出一个对话框,可以直接输入激励频率。也可单击频率的单步步进键进行激励调节。
打开信号发生器,输出正弦信号后,单击屏幕上的(Start)键,开始测试,开始强迫振动幅频特性和相频特性测量,测量中必须随时保持信号发生器的频率与计算机上显示的频率一致。其中2Hz—15Hz内大致相隔1Hz设一个测点;15Hz—30Hz内每隔5Hz设一个测点。
六、实验报告要求
1、简述实验目的、内容、装置及实验步骤,叙述实验原理,实验报告的文字部分必须手写。本次实验报告中叙述实验目的、内容、原理、装置及实验步骤的部分不建议超过3页。严禁照抄实验指导书和往届实验报告!
2、根据自由衰减振动记录的有关数据,估算水平振动台面的等效质量,计算系统的固有频率及阻尼比,此部分计算过程需手写。
2、相对式速度拾振器:
CD-2型相对式速度拾振器原理结构简图如图五所示,它由磁路系统、线圈、弹簧片、连接杆、顶杆和限幅箱等六部分组成。其中,线圈、连接杆和顶杆构成拾振器的可动部分,磁钢和钢质外壳构成带有环形磁隙的磁路系统。使用时,传感器外壳用安装座固定在基座上,顶杆借助拱形簧片的变形恢复力压紧在测量对象上,从而带动线圈相对环形磁隙以相对速度 振动,因而切割磁力线而产生感应电势,其开路电压的大小为
保持功放的输出电流幅值不变,即保持激振力幅值不变,缓慢地由低频2Hz到高频30Hz改变激振频率,用相对式速度拾振器检测速度振动量,再经过积分处理后得到位移量,由测试数据可描绘出一条振幅频率特性曲线(图二)。
而根据该测试曲线可由如下关系式估算系统的固有频率 及阻尼比
,
其中 为振幅达到最大 时的激振频率,即共振频率; 和 为振幅 的对应频率,即半功率点频率。
在自由衰减振动测试中,单击“自由衰减记录”功能键,可以实现波形记录、光标读数等功能,此时显示界面如图六所示。
在强迫振动的幅频特性和相频特性的测试中,单击“简谐激励振动”程序,可以实现信号发生器(产生一个可调节频率的正弦信号)、积分、电压表(完成两个信号有效值比)、波形显示等功能。显示界面如图七所示。
改变阻尼大小重新进行频率扫描可获得一组相应于不同阻尼比的幅频特性曲线。
3、强迫振动的相频特性测定:
在进行频率扫描的同时,如将激振力信号和拾振器的检测信号(正比于振动速度)分别接到计算机A/D并进行处理,可得到振动位移对激振力的相位差 。由测试数据可描绘出相位差频率特性曲线如图三。 时所对应的频率即为系统的固有频率,用 表示。
2
相对式速度拾振器
工作频率:2-500Hz
位移:3mm峰峰值
3
电磁激振器
最大激振力:2N
频率:2~1000Hz
4
阻尼励磁电源及
信号跟随器
最大电流输出1.5A
5
信号发生பைடு நூலகம்及
功率放大器
频率范围1Hz-6MHz,频率分辨率0.01Hz
