高等教育大学本科课件 材料力学 第3章 轴向拉压变形
合集下载
材料力学第3章 轴向拉压变形

Fy 0 :FN1 sin 30 FN3 sin 30 F
(2) 变形协调方程
Δl2 Δl1 Δl3 Δl2 tan30 sin 30 sin 30 tan30
秦飞 编著《材料力学》 第3章 轴向拉压变形
31
3.4 拉压杆静不定问题的解法
例题3-5
(3) 利用物性关系,用力表示变形协调方程
切
B点水平位移:
线 代
圆
Fa
弧
Bx BB1 l1 EA ()
B点铅垂位移:
By
BB'
l2 sin 45
l1
tan
45
(1
2
2) Fa EA
()
秦飞 编著《材料力学》 第3章 轴向拉压变形
19
3.3 桁架的节点位移
例题3-3
图示托架,由横梁AB与斜撑杆CD所组成,并承受集中载荷
2
3.1拉压杆的轴向变形与横向变形
轴向应变: l 胡克定律: FN
l
E EA
所以得到: l FNl EA
(拉压杆胡克定律)
l FNl EA
EA为拉压刚度,只与材料和横截面面积有关。
秦飞 编著《材料力学》 第3章 轴向拉压变形
3
3.1拉压杆的轴向变形与横向变形
(2)补充方程-变形协调方程(compatibility equation)
l1
tan
l2
sin
l3
秦飞 编著《材料力学》 第3章 轴向拉压变形
25
3.4 拉压杆静不定问题 解法
(3)物性(物理)关系
l1
FN1l1 E1 A1
(2) 变形协调方程
Δl2 Δl1 Δl3 Δl2 tan30 sin 30 sin 30 tan30
秦飞 编著《材料力学》 第3章 轴向拉压变形
31
3.4 拉压杆静不定问题的解法
例题3-5
(3) 利用物性关系,用力表示变形协调方程
切
B点水平位移:
线 代
圆
Fa
弧
Bx BB1 l1 EA ()
B点铅垂位移:
By
BB'
l2 sin 45
l1
tan
45
(1
2
2) Fa EA
()
秦飞 编著《材料力学》 第3章 轴向拉压变形
19
3.3 桁架的节点位移
例题3-3
图示托架,由横梁AB与斜撑杆CD所组成,并承受集中载荷
2
3.1拉压杆的轴向变形与横向变形
轴向应变: l 胡克定律: FN
l
E EA
所以得到: l FNl EA
(拉压杆胡克定律)
l FNl EA
EA为拉压刚度,只与材料和横截面面积有关。
秦飞 编著《材料力学》 第3章 轴向拉压变形
3
3.1拉压杆的轴向变形与横向变形
(2)补充方程-变形协调方程(compatibility equation)
l1
tan
l2
sin
l3
秦飞 编著《材料力学》 第3章 轴向拉压变形
25
3.4 拉压杆静不定问题 解法
(3)物性(物理)关系
l1
FN1l1 E1 A1
材料力学课件-第10讲 第三章 轴向拉压变形(4)

几个基本概念
算例 已知:F=100 kN,l=500 mm,[st]=150 MPa, [sc] = 100 MPa, A1 = A3,密度 r = 7.85103 kg/m3 试:按桁架重量最轻要求,确定A1,A2 与A3
பைடு நூலகம்
1. 应力分析
解静不定
2. 最轻重量设计
由于杆长制造误差或温度变化,结构在未受载时已存在的应力,分别称为初应力(或称预应力)与热应力。
解:(1)平衡方程(设各杆受拉)
代入物理方程
(2)协调方程
例:3杆制造误差长 ,1、2杆 ,3杆 ,求各杆内力
规律观察:
设 由温度变化引起:
解答成为(比较预应力与热应力)
解答:
为拉压刚度, 伸长为正,缩短为负。
(变截面、变轴力杆),
(阶梯形杆)
泊松比
★拉压与剪切应变能概念
§3-5 简单拉压静不定问题
*静不定问题:
*静定问题 :
*静不定度:未知力数与有效平衡方程数之差。
一度静不定
A
F
1
2
3
静定问题
由静力平衡方程可确定全部未知力(包括支反力与内力)的问题。
根据静力平衡方程不能确定全部未知力的问题。
2、几何方面
3、物理方面
4、支反力计算
何时
问题 :
补充方程:
解1:1、静力学方面
例:求杆两端的支反力。
2、物理方面
3、求解
解2:1、几何方面
例:求杆右端的支反力。
4、由平衡方程
例:各杆拉压刚度EA,杆1,2 长l
解:1、画变形图(画法2,教材P72图为画法1)
设节点C位移至C’,过C’点向三杆作垂线
算例 已知:F=100 kN,l=500 mm,[st]=150 MPa, [sc] = 100 MPa, A1 = A3,密度 r = 7.85103 kg/m3 试:按桁架重量最轻要求,确定A1,A2 与A3
பைடு நூலகம்
1. 应力分析
解静不定
2. 最轻重量设计
由于杆长制造误差或温度变化,结构在未受载时已存在的应力,分别称为初应力(或称预应力)与热应力。
解:(1)平衡方程(设各杆受拉)
代入物理方程
(2)协调方程
例:3杆制造误差长 ,1、2杆 ,3杆 ,求各杆内力
规律观察:
设 由温度变化引起:
解答成为(比较预应力与热应力)
解答:
为拉压刚度, 伸长为正,缩短为负。
(变截面、变轴力杆),
(阶梯形杆)
泊松比
★拉压与剪切应变能概念
§3-5 简单拉压静不定问题
*静不定问题:
*静定问题 :
*静不定度:未知力数与有效平衡方程数之差。
一度静不定
A
F
1
2
3
静定问题
由静力平衡方程可确定全部未知力(包括支反力与内力)的问题。
根据静力平衡方程不能确定全部未知力的问题。
2、几何方面
3、物理方面
4、支反力计算
何时
问题 :
补充方程:
解1:1、静力学方面
例:求杆两端的支反力。
2、物理方面
3、求解
解2:1、几何方面
例:求杆右端的支反力。
4、由平衡方程
例:各杆拉压刚度EA,杆1,2 长l
解:1、画变形图(画法2,教材P72图为画法1)
设节点C位移至C’,过C’点向三杆作垂线
材料力学 ppt课件
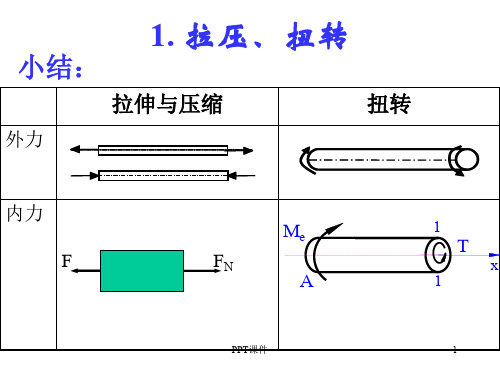
③应力分析:画危险面应力分布图,叠加;
④强度计算:建立危险点的强度条件,进行强度
计算。
PPT课件
20
2、两相互垂直平面内的弯曲
有棱角的截面
max
Mz Wz
My Wy
[ ]
圆截面
max
M
2 z
M
2 y
[ ]
W
3、拉伸(压缩)与弯曲
有棱角的截面
max
FN ,max A
(4)确定最大剪力和最大弯矩
3、弯曲应力与强度条件
(1)弯曲正应力
My
I PPT课件 z
12
M max Wz
yt,max yc,max
Oz y
PPT课件
t,max
Myt,max Iz
c,max
Myc,max Iz
13
(2)梁的正应力强度条件
M max
Wz
M
2 z
M
2 y
T
2
Mr4
M
2 z
M
2 y
0.75T
2
PPT课件
22
5、连接件的强度条件
剪切的强度条件
FS [ ]
AS
挤压强度条件
bs
Fbs Abs
[ bs ]
PPT课件
M z,max Wz
M y,max Wy
[ ]
圆截面
max
FN ,max A PPT课件
M max W
[ ]
21
4、弯曲与扭转
6+第三章+轴向拉压变形——材料力学课件PPT

FN21 2l 2EA
FN22l 2EA
FN23l 2EA
F 2l( 2 EA
1)
45 B A2
3、位移计算
F
W= FfBy 2
Vε
f By
2Fl( 2 EA
1)
8
第三章 轴向拉压变形
例:用能量法求A,C相对位移。
D
解:1、轴力分析
1
周边四杆轴力: 2
FN1 2 F
FA
2
C
F
杆2轴力: FN 2 F
2、应变能、外力功计算
B
Vε
4FN21l 2EA
FN22 2l 2EA
2 2 F 2l ,
2EA
W
1 2
F
A
/
C
,
3、位移计算 Vε W ,
(2 2)Fl
A/C
EA
9
➢ 总结:
第三章 轴向拉压变形
1、不用通过画变形图来确定节点的位移。 2、只能求解沿载荷作用线方向的位移。 3、同时作用有多个载荷时,无法求载荷的相应位移。
第三章 轴向拉压变形
上一讲回顾
★拉压杆变形
l FNl , EA 为拉压刚度, l伸长为正,缩短为负。
EA
l
l
FN ( x) EA( x)
dx(变截面、变轴力杆),l
n
i 1
EFiNAlii(阶梯形杆)
★拉压杆横向变形与泊松比
泊松比(0 0.5)
★叠加原理及其应用范围
★桁架小变形节点位移 1)按结构原始尺寸计算约束反力与内力; 2)由切线代圆弧的方法计算节点位移。
•应变能( V):构件因变形贮存能量。
•弹性体功能原理: Vε W (根据能量守恒定律) •功能原理成立条件:载荷由零逐渐缓慢增加,动能与 热能等的变化可忽略不计。
材料力学课件-第三章-轴向拉压变形

Δ
F
f
o
d
A
d
•弹性体功能原理:Vε W ,
f df
• 拉压杆应变能
2 FN l V ε 2 EA
Page28
BUAA
MECHANICS OF MATERIALS
*非线性弹性材料
F
f
•外力功计算
W fd
0
F W 2
•功能原理是否成立? •应变能如何计算计算?
dx
dz
dy
x
•单向受力体应变能
V v dxdydz dxdydz 2E
2
z
单向受力
Page30
BUAA
MECHANICS OF MATERIALS
2 dxdydz •单向受力体应变能 V v dxdydz 2E FN ( x ) •拉压杆 (x)= , dydz A A 2 FN ( x ) V dx (变力变截面杆) y 2 EA( x ) l 2 FN l dx (常应力等直杆) V dz 2 EA •纯剪应变能密度 dy dxdz dy dxdydz dVε 2 2 2 1 2 z v G 纯剪切
BUAA
MECHANICS OF MATERIALS
第三章
§3-1 §3-2 §3-3 §3-4
§3-5 §3-6
轴向拉压变形
引言 拉压杆的变形与叠加原理 桁架的节点位移 拉压与剪切应变能
简单拉压静不定问题 热应力与预应力
Page1
BUAA
MECHANICS OF MATERIALS
本章主要研究:
Page7
材料力学-3轴向拉压变形.

A
L1
B L1
L2 uB F
L2
vB
C B'
解:变形图如图2, B点位移至B'点,由图知:
vB
L1c tg
L2
sin
uB L1
例3:试定性画出图示结构中节点B的位移图。
1
2
α B
P
N2
N1
α B
P
1
2
α
α B’
B ΔL2 B2
例4 设横梁ABCD为刚梁,横截面面积为 76.36mm²的钢索绕过 无摩擦的定滑轮。设 P=20kN,试求刚索的应力和 C点的垂直 位移。设刚索的 E =177GPa。
由此可见:两解相同,即几个载荷同时作用所产生的总效果, 等于各载荷单独作用所产生的效果的总和。 ——力的叠加原理(线代数方程)
适用范围:(物理线性、几何线性、小变形)。 叠加原理:将复杂问题可化为许多简单问题叠加。
例1: 受拉空心圆杆内周长是变大还是变小,改变量多少? P
解:
E
P AE
4P D2 d 2
A1.5EAB 2EA C
D EA E EA F
4P
刚体
5P
2P
a
a
a
a
a
解:
§3-2 桁架的节点位移
一、 小变形放大图与位移的求法。 1、怎样画小变形放大图?
A
B
求各杆的变形量△Li ,如图;
L1
L2
C
变形图严格画法,图中弧线;
L2 P L1 C' C"
变形图近似画法,图中弧之切线。
2、写出图2中B点位移与两杆变形间的关系
A 76.36
A
建筑力学第3章轴向拉伸与压缩
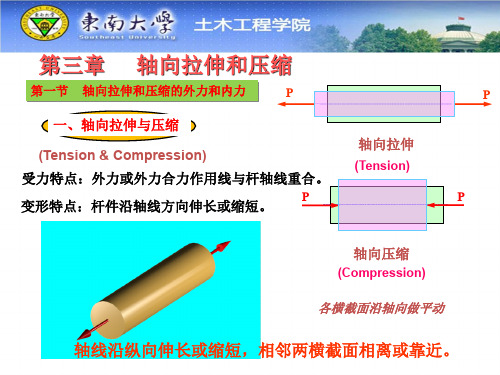
A
F
x
0
FN 1 cos 45 FN 2 0
FN 2 45° B
F
x
F
45°
y
0
B F
C
FN 1 sin 45 - F 0
FN 1 28.3kN FN 2 -20kN
A
2、计算各杆件的应力。
45°
C
B
FN 1 28.3 10 90MPa A1 20 2 4
斜截面上全应力:
p 0 cos
k
③pa 分解为:
p
P
P
p cos 0 cos 2
p sin 0 cossin
0
2
k
k
sin2
P
P
k
反映:通过构件上一点不同截面上应力变化情况。 当 = 0时, 当 = 90°时, 当 = ±45°时, 当 = 0,90°时,
Ⅱ段柱横截面上的正应力
FN 2 - 150 103 -1.1 MPa Ⅱ 2 A2 370
所以,最大工作应力为
max= = -1.1 MPa (压应力)
三、 轴向拉(压)杆斜截面上的应力
上述讨论的横截面上的正应力是今后强度计算的基础。 但不同的材料实验表明,拉(压)杆的破坏并不总是沿横截 面发生,有时确是沿斜截面发生的,为此,应进一步讨论斜 截面上的应力。为了全面分析拉(压)杆的强度,应研究它 斜截面上的应力情况。
解(1)、(2)曲线交点处:
30
60
B 31;PB 54.4kN
1 1
PB1 ,60 A /cos60/sin604601024/ 355.44kN
材料力学单辉祖第三章轴向拉压变形

o x
FN q
q
L
最大正应力发生在x = 0处
P
max
FN (0) P ql (0) A A
P
x
22
Example-变轴力杆
取长度为dx的微元体 由胡克定理知,微元体伸长为
FN ( x) d dx EA
FN ( x) P q(l x)
o x
FN
dx dFN对微段变形忽略
杆件在外力F2作用下 的伸长为
l
2P
P
3l P
2P
l2 P
FN 2 L 2 Pl EA EA
19
Example-多力杆
杆件的总伸长为
l l P l2 P
方法一答案
2 Pl l l1 l2 EA ()
2 Pl EA
2P
P
l
3l
20
Example-变轴力杆
B
60 0
F2 l
F1
l
C A
C"
D
C´ A´
几何关系
45
Example-Bracket
利用几何关系, 得A点垂直位移AA´
A 2CC CD 2 6.0 mm 0 sin 30
l B
600
F2
F1
l
C A
C"
D
C´ A´
几何关系
46
Example-零力杆
求A点的位移
*AB杆不受力不伸长,只转动
()
41
Example-Bracket
图示托架,AB为刚梁,CD为支撑杆,已知 F1=5kN,F2=10kN,l=1m,斜支撑CD为铝 管,弹性模量为E=70GPa,横截面面积为 A=440mm2,求刚梁AB端点A的铅垂位移。
FN q
q
L
最大正应力发生在x = 0处
P
max
FN (0) P ql (0) A A
P
x
22
Example-变轴力杆
取长度为dx的微元体 由胡克定理知,微元体伸长为
FN ( x) d dx EA
FN ( x) P q(l x)
o x
FN
dx dFN对微段变形忽略
杆件在外力F2作用下 的伸长为
l
2P
P
3l P
2P
l2 P
FN 2 L 2 Pl EA EA
19
Example-多力杆
杆件的总伸长为
l l P l2 P
方法一答案
2 Pl l l1 l2 EA ()
2 Pl EA
2P
P
l
3l
20
Example-变轴力杆
B
60 0
F2 l
F1
l
C A
C"
D
C´ A´
几何关系
45
Example-Bracket
利用几何关系, 得A点垂直位移AA´
A 2CC CD 2 6.0 mm 0 sin 30
l B
600
F2
F1
l
C A
C"
D
C´ A´
几何关系
46
Example-零力杆
求A点的位移
*AB杆不受力不伸长,只转动
()
41
Example-Bracket
图示托架,AB为刚梁,CD为支撑杆,已知 F1=5kN,F2=10kN,l=1m,斜支撑CD为铝 管,弹性模量为E=70GPa,横截面面积为 A=440mm2,求刚梁AB端点A的铅垂位移。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
步骤:1、分解载荷;
2、分段求变形;
2、求每种载荷作用下整
3、求代数和。
杆的变形;
3、叠加。
分段求变形
l FNi li FN ( x) dx EA l EA
叠加法
l FN (Fi ) li
EA
Page13
BUAA
两种方法的适用条件:
MECHANICS OF MATERIALS
—分段求变形法 对每一段独立求变形,然后在相加 —— 要求小变形条件
b
b
横向正应变
试验表明:在比例极限内,横向正应变与轴向正应变成正比
一般 与 符号相反。
定义:
泊松比
Page4
BUAA
MECHANICS OF MATERIALS
➢ 关于泊松比
1821年,纳维首次用分子理论研究各向同性弹性体 的 平1衡82问5题年,,其柯基西本把方纳程维中的只理包论含推一广个到弹各性向常异数性。弹性体,
作业:3-2, 3-4, 3-8
Page16
BUAA
MECHANICS OF MATERIALS
本讲内容
第三章 轴向拉压变形
§3-3 桁架的节点位移 §3-5 拉压静不定问题
Page17
BUAA
B
C B
C
MECHANICS OF MATERIALS
§3-3 桁架的节点位移
已知各杆EA, lAC, 角。求 节点A的位移 A
f ( x) kx
l ~ FN
F FN
AA
l FN l
EA
l
l
E
l FN l
EA
当函数是线性齐次函数时,叠加原理成立
1、线弹性:物理线性——应力与应变的关系 2、小变形:几何线性——用原始尺寸进行受力分析
(几组外力之间没有耦合作用)
Page15
BUAA
MECHANICS OF MATERIALS
P
精确分析方法:
1、轴力难以分析;
A
2、节点位置难以确定。
1833年,格林研究电磁波在弹性介质表面上的反射 与
折射时,首次用能量法证明,各向同性弹性材料的应 变许能多函人数进中行应试当验包来括验两证个泊弹松性比常为数1/。4的理论结论
维尔泰姆(1848):试验结果表明接近1/3; 基尔霍夫(1859):测出了三种钢材和两种黄铜, 1/4; 科尔纽(1869):光学干涉法测出玻璃=0.237;
0
l l FN ( x) dx 0 E( x) A( x)
Page11
BUAA
MECHANICS OF MATERIALS
➢ 叠加原理(力的独立作用原理)
P
3P
例:AB段和BC段的长度均为l,拉
A
B
C 压刚度为EA,求杆的总伸长。
P
A
B
C
l1
P 2l EA
l Pl
A
3P
B
C
l2
3 Pl EA
Page2
BUAA
MECHANICS OF MATERIALS
F
F
b
b1
l l1
➢ 拉压杆的轴向变形与胡克定律
l ~ FN
F FN
AA
l
l
E
l FN l
EA
拉压刚度
Page3
BUAA
MECHANICS OF MATERIALS
➢ 拉压杆的横向变形与泊松比
F
F
b
b1
l l1
b b1 b
1879年,马洛克测出了一系列材料的泊松比,指出泊松 比是独立的材料常数,否定了单常数理论。
Page6
BUAA
MECHANICS OF MATERIALS
➢ 关于横向变形的两点说明
F
F
b
b1
l l1
横向应变中的横向:横截面上任意一点沿面内任意方向
P
P
外径D和内径d如何变化?
泊松比:对于大多数各向同性材料0<<0.5 铜泡沫: =-0.39
Page7
BUAA
MECHANICS OF MATERIALS
常见材料的性能参数
对于各向同性材料,弹性模量E、泊松比 与剪切模量G
存在如下关系:
G E
2(1 )
Page8
BUAA
例题
MECHANICS OF MATERIALS
A (D2 d2) 4
A (D2 d 2 )(1 )2 4
EA
几个载荷同时作用所产生的总效果,等于各载荷单独作 用产生的效果的总和
Page12
BUAA
MECHANICS OF MATERIALS
➢ 两种方法的对比
P
3P
A
B
C
l FN l
EA
—分段求变形
—叠加原理
方法:分段求变形,将每段变形相加。
方法:分解载荷,将载荷作用效 果相加。
步骤:1、分段求轴力;(截面法)
0 EA
2EA
+ xΒιβλιοθήκη l FNi li FN ( x) dx EA l EA
Page10
BUAA
MECHANICS OF MATERIALS
例:杆绕CD轴匀速转动,求杆的总伸长。
l
C
dF ( ) 2(l )dm 2(l ) Ad
x
d
FN(x)
x
x
D FN ( x) 0 dFN ( ) x 2(l ) Ad
l FN l
EA
l
FNi li FN ( x) dx EA l EA
—叠加法
对每种载荷情况独立求解,然后将作用效果相加 —— 要求线弹性、小变形
Page14
BUAA
MECHANICS OF MATERIALS
➢ 从数学上理解叠加法
y f (x)
f ( x1 ) f ( x2 ) ?f ( x1 x2 )
BUAA
MECHANICS OF MATERIALS
第三章 轴向拉压变形
§3-1 引言 §3-2 拉压杆的变形与叠加原理
Page1
BUAA
MECHANICS OF MATERIALS
§3-2 拉压杆的变形与叠加原理
F
F
b
b1
l l1
杆件受轴向载荷时,其轴向与横向尺寸均发生变化。
纵向变形:杆件沿轴向或载荷方向的变形 横向变形:垂直于轴向或载荷方向的变形
当退化到各向同性弹性体时得到两个弹性常数。但柯 西认为纳维的单常数理论才是正确的。
1829年,泊松用纳维—柯西方法讨论板的平衡问题 时
指出,各向同性弹性杆受到单向拉伸,产生纵向应 变,同时会联带产生横向收缩,此横向应变为-x, 并证明=1/4。纳维—柯西—泊松的单常数理论
Page5
BUAA
MECHANICS OF MATERIALS
Page9
BUAA
MECHANICS OF MATERIALS
➢ 多力杆的变形
P
3P
A
B
C
l FN l
EA
分段求变形法
例:AB段和BC段的长度均为l,拉 压刚度为EA,求杆的总伸长。
P +
-
l Pl 2Pl Pl
2P
EA EA
EA
q
求dx段的变形
x
ql
FN(x)=qx
l l FN ( x)dx ql 2
