材料力学作业参考题解_轴向拉压
材料力学习题册答案-第2章-拉压

一、 选择题
1.图 1 所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将(
A.平动
B.转动
C.不动
D.平动加转动
D)
2.轴向拉伸细长杆件如图 2 所示,则正确的说法是 ( C )
A.1-1、2-2 面上应力皆均匀分布 B.1-1、2-2 面上应力皆非均匀分布 C. 1-1 面上应力非均匀分布,2-2 面上应力均匀分布 D.1-1 面上应力均匀分布,2-2 面上应力非均匀分布
30KN 1
300mm
l1 解:(1) 轴力图如下
2
400mm
l2
10KN
-
40KN
50KN 3
400mm
l3
10KN
+
10KN
(2)
(3)右端面的位移
=
= 即右端面向左移动 0.204mm。
8.一杆系结构如图所示,试作图表示节点 C 的垂直位移,设 EA 为常数。
A
30
C
30 ΔL2 60 ΔL1
CD 段:σ3= =
Pa=25MPa
2.图为变截面圆钢杆 ABCD,已知 =20KN, = =35KN, = =300mm, =400mm,
D
3
C
P3
2
,绘出轴力图并求杆的最大最小应力。
B
1 P2
A
P1
l3 解:
-
50KN
l2 15KN
l1
20KN
+
AB 段:σ1=
=
=176.9MPa
BC 段:σ2=
反力均匀分布,圆柱承受轴向压力 P,则基座剪切面的剪力
。ห้องสมุดไป่ตู้
材料力学1轴向拉压分析

1.衡。
设杆(A) qρ=(B)(C)(D)2.(A)(C)3. 在A和BA和点B(A) 0;(C) 45;。
4. 可在横梁(刚性杆)为A(A) [] 2A σ(C) []Aσ;5.(A)(C)6. 三杆结构如图所示。
今欲使杆3哪一种措施?(A) 加大杆3的横截面面积; (B) 减小杆3的横截面面积; (C) 三杆的横截面面积一起加大; (D) 增大α角。
7. 图示超静定结构中,梁AB 示杆1的伸长和杆2的缩短,(A) 12sin 2sin l l αβ∆=∆; (B) 12cos 2cos l l αβ∆=∆; (C) 12sin 2sin l l βα∆=∆; (D) 12cos 2cos l l βα∆=∆。
8. 图示结构,AC 为刚性杆,杆1(A) 两杆轴力均减小; (B) 两杆轴力均增大;(C) 杆1轴力减小,杆2轴力增大; (D) 杆1轴力增大,杆2轴力减小。
9. 结构由于温度变化,则:(A) (B) (C) (D) 10. 面n-n 上的内力N F 的四种答案中哪一种是正确的?(A) pD ; (B) 2pD;(C) 4pD ; (D) 8pD 。
11.的铅垂位移12. 截面的形状为13. 一长为l挂时由自重引起的最大应力14. 图示杆112A A >是N1F F 题1-141. D 2. D 3. C 4. B 5. B 6. B 7. C 8. C 9. B 10. B11. Fl EA ;12. ab;椭圆形 13. 22gl gl E ρρ, 14. >,= 15. 试证明受轴向拉伸的圆截面杆,其横截面沿圆周方向的线应变s ε等于直径的相对改变量d ε。
证:()s d πππd d ddddεε+∆-∆=== 证毕。
16. 如图所示,一实心圆杆1在其外表面紧套空心圆管2。
设杆的拉压刚度分别为11E A 和22E A 。
此组合杆承受轴向拉力F ,试求其长度的改变量。
材料力学第二章 轴 向拉压习题及答案

第二章轴向拉压一、选择题1.图1所示拉杆的外表面上有一斜线,当拉杆变形时,斜线将( D)A.平动B.转动C.不动D.平动加转动2.轴向拉伸细长杆件如图2所示,其中1-1面靠近集中力作用的左端面,则正确的说法应是( C)A.1-1、2-2面上应力皆均匀分布B.1-1、2-2面上应力皆非均匀分布C.1-1面上应力非均匀分布,2-2面上应力均匀分布D.1-1面上应力均匀分布,2-2面上应力非均匀分布(图1)(图2)3.有A、B、C三种材料,其拉伸应力—应变实验曲线如图3所示,曲线( B)材料的弹性模量E大,曲线( A )材料的强度高,曲线( C)材料的塑性好。
4.材料经过冷作硬化后,其( D)。
A.弹性模量提高,塑性降低B.弹性模量降低,塑性提高C.比例极限提高,塑性提高D.比例极限提高,塑性降低5.现有钢、铸铁两种杆材,其直径相同。
从承载能力与经济效益两个方面考虑,图4所示结构中两种合理选择方案是( A)。
A.1杆为钢,2杆为铸铁B.1杆为铸铁,2杆为钢C.2杆均为钢D.2杆均为铸铁(图3)(图4)(图5)6.在低碳钢的拉伸试验中,材料的应力变化不大而变形显著增加的是(B)。
A. 弹性阶段;B.屈服阶段;C.强化阶段;D.局部变形阶段。
7.铸铁试件压缩破坏(B)。
A. 断口与轴线垂直;B. 断口为与轴线大致呈450~550倾角的斜面;C. 断口呈螺旋面;D. 以上皆有可能。
8.为使材料有一定的强度储备,安全系数取值应( A )。
A .大于1; B. 等于1; C.小于1; D. 都有可能。
9. 等截面直杆在两个外力的作用下发生轴向压缩变形时,这对外力所具备的特点一定是等值、( C )。
A 反向、共线B 反向,过截面形心C 方向相对,作用线与杆轴线重合D 方向相对,沿同一直线作用10. 图6所示一阶梯形杆件受拉力P的作用,其截面1-1,2-2,3-3上的内力分别为N 1,N 2和N 3,三者的关系为( B )。
材料力学轴向拉压变形习题解

完美.格式.编辑习图第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a)解:(1)求指定截面上的轴力N^=FN22 = -2F F = -F(2)作轴力图轴力图如图所示。
(b)解:(1)求指定截面上的轴力N1JL =2FN2N—2F 2F =0(2)作轴力图N3J3二 F -2F 2F 二 F轴力图如图所示。
(c)解:(1)求指定截面上的轴力N1JL =2FN22 —F 2F =F(2)作轴力图N3「2F -F 2F =3F轴力图如图所示。
(d)解:(1)求指定截面上的轴力N L「F完美.格式.编辑N2Q 二-2F -qa F 二-2F a F 二-2F(2)作轴力图中间段的轴力方程为:N(x) = F - 匚x x (a,0]a轴力图如图所示。
完美.格式.编辑[习题2-2]试求图示等直杆横截面二-100M PaA 12 -2N 2 二 A 21-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积2A = 400mm ,试求各横截面上的应力。
N 3J3 =20 10-20=10(kN)(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力[习题2-3]试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积A = 200mm 2, A 2 = 300mm 2, A = 400mm 2,并求各横截面上的应力。
解:(1)求指定截面上的轴力N 1J = -20kNN 2/ =10-20 一10(kN)N 3; =20 10-20 = 10(kN) (2) 作轴力图轴力图如图所示。
(3) 计算各截面上的应力-20 1 03N2200mm-10 103N2300mm -—33.3MPa解:(1)求指定截面上的轴力 N 2‘ =10-20 一10(kN)Nu 3-20 10 N-A 400mm 2 N 2 2-10 10 N-A 2400 mm N 3 J310 103N _ A400mm 2»50M P a--25MPa25MPa23 J33 -3 N 3 -3 10 103N400mm2二25MPa]=357.62(kN)HI 川门[习题2-4]图示一混合屋架结构的计算简图。
材料力学典型题解

1轴向拉伸与压缩例1-1 如图所示的等截面直杆,受轴向力F 1=15kN ,F 2=10kN 的作用。
试分别求出杆件1-1、2-2截面的轴力,并画出轴力图。
F 2F 2C 22 22F 111 11B F 1AF RF RF N1F 1F N2F R F N10kN5kN图1-1解:(1)外力分析 先解除约束,画出杆件的受力图。
120,0xR FF F F = -+=∑得:()121510kN 5kN R F F F =-=-=(2)内力分析 外力F R 、F 1、F 2将杆件分为AB 段和BC 段,在AB 段,用1-1截面将杆件截分为两段,取左段为研究对象,右段对截面的作用力用F N1来代替。
假定内力F N1为正,列平衡方程10,0xN R FF F = +=∑得:15kN N R F F =-=-负号表示F N1的方向和假定方向相反,截面受压。
在BC 这一段,用任意2-2截面将杆件分为两段,取左段为研究对象,右段对左段截面的作用力用F N2来代替。
假定轴力F N2为正,有平衡方程2100xN R FF F F = +-=∑得: ()21515kN N R F F F =-+=-+=10kN (3)画轴力图由以上例题可以总结出求截面轴力的简捷方法:杆件任意截面的轴力F N (x )等于截面一侧所有外力的代数和。
即1nN i i F F ==∑,外力背离该截面的时取正,指向该截面时取负。
例1-2 如图所示为正方形截面阶梯杆,受力及尺寸如图所示。
试分析杆上1截面处和2截面处的正应力。
FF2hh12(a )FFF N 11122N hh σ==F F F N 1222244N h h σ==F F(b ) 图1-2解:先求出杆两截面处的轴力F N 1和F N 2,在用截面上的轴力除以相应的截面面积,如图(b )所示,不难求出σ1=F/h 2,σ2=F/(4h 2)。
例1-3 如图所示,斜杆AB 为直径d =20mm 的钢杆,载荷Q =15kN 。
材料力学典型例题与详解(经典题目)
所以石柱体积为
V3
=
G ρ
=
[σ ]A(l) − ρ
F
= 1×106 Pa ×1.45 m 2 −1000 ×103 N = 18 m3 25 ×103 N/m3
三种情况下所需石料的体积比值为 24∶19.7∶18,或 1.33∶1.09∶1。 讨论:计算结果表明,采用等强度石柱时最节省材料,这是因为这种设计使得各截面的正应 力均达到许用应力,使材料得到充分利用。 3 滑轮结构如图,AB 杆为钢材,截面为圆形,直径 d = 20 mm ,许用应力 [σ ] = 160 MPa ,BC 杆为木材,截面为方形,边长 a = 60 mm ,许用应力 [σ c ] = 12 MPa 。试计算此结构的许用载
= 1.14 m 2
A
2=
F+ρ [σ ] −
A1 l1 ρ l2
=
1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m 1×106 N/m 2 − 25×103 N/m3 × 5 m
= 1.31 m 2
A
3=
F
+ ρA1l1 + ρA2l2 [σ ] − ρ l3
= 1000 ×103 N + 25 ×103 N/m3 ×1.14 m 2 × 5 m + 25×103 N/m3 ×1.31 m 2 × 5 m = 1.49m 2 1×106 N/m 2 − 25 ×103 N/m3 × 5 m
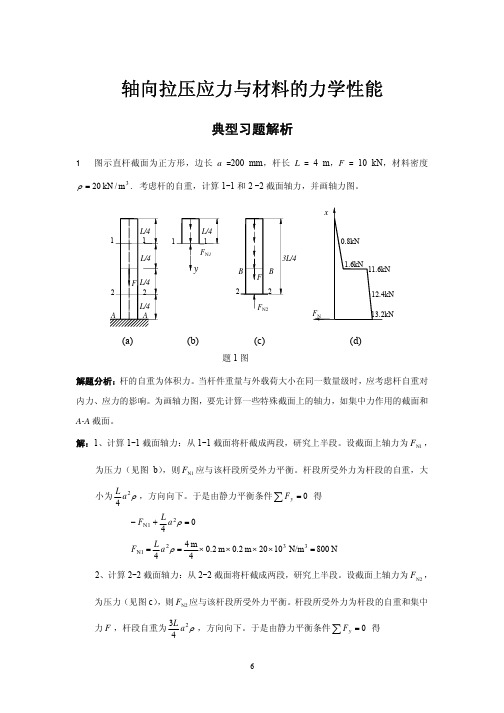
解:1、计算 1-1 截面轴力:从 1-1 截面将杆截成两段,研究上半段。设截面上轴力为 FN1 ,
为压力(见图 b),则 FN1 应与该杆段所受外力平衡。杆段所受外力为杆段的自重,大
《材料力学》第2章 轴向拉压变形 习题解

第二章轴向拉(压)变形[习题2-1] 试求图示各杆1-1和2-2横截面上的轴力,并作轴力图。
(a )解:(1)求指定截面上的轴力 FN =-11FF F N -=+-=-222(2)作轴力图轴力图如图所示。
(b )解:(1)求指定截面上的轴力 FN 211=-2222=+-=-F F N (2)作轴力图FF F F N =+-=-2233 轴力图如图所示。
(c )解:(1)求指定截面上的轴力 FN 211=-FF F N =+-=-222(2)作轴力图FF F F N 32233=+-=- 轴力图如图所示。
(d )解:(1)求指定截面上的轴力 FN =-11F F a aFF F qa F N 22222-=+⋅--=+--=-(2)作轴力图 中间段的轴力方程为: x aFF x N ⋅-=)(]0,(a x ∈轴力图如图所示。
[习题2-2] 试求图示等直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,试求各横截面上的应力。
2400mm A =解:(1)求指定截面上的轴力kNN 2011-=- )(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
(3)计算各截面上的应力MPa mm N A N 504001*********-=⨯-==--σMPa mm N A N 254001010232222-=⨯-==--σMPamm N A N 254001010233333=⨯==--σ[习题2-3] 试求图示阶梯状直杆横截面1-1、2-2和平3-3上的轴力,并作轴力图。
若横截面面积,,,并求各横截面上的应力。
21200mm A =22300mm A =23400mm A =解:(1)求指定截面上的轴力kNN 2011-=-)(10201022kN N -=-=-)(1020102033kN N =-+=-(2)作轴力图轴力图如图所示。
材料力学 中国建筑工业出版社第二章 轴向拉压习题答案

2-1a 求图示各杆指截面的轴力,并作轴力图。
(c ')(e ')(d ')N (kN)205455(f ')解:方法一:截面法(1)用假想截面将整根杆切开,取截面的右边为研究对象,受力如图(b)、(c)、(d)、(e)所示。
列平衡方程求轴力: (b) 图:)(20020011拉kN N NX =→=-→=∑(c) 图:)(5252002520022压kN N NX -=-=→=--→=∑(d) 图:)(455025200502520033拉kN N NX =+-=→=-+-→=∑(e) 图:)(540502520040502520044拉kN N NX =-+-=→=--+-→=∑(2)杆的轴力图如图(f )所示。
方法二:简便方法。
(为方便理解起见,才画出可以不用画的 (b ‘)、(c ‘)、(d ‘)、(e ‘) 图,作题的时候可用手蒙住丢弃的部份,并把手处视为固定端)(1)因为轴力等于截面一侧所有外力的代数和:∑=一侧FN 。
故:)(201拉kN N =)(525202压kN N -=-=)(455025203拉kN N =+-=)(5405025204拉kN N =-+-=(2)杆的轴力图如图(f ‘)所示。
2-2b 作图示杆的轴力图。
(c)图:(b)图:(3)杆的轴力图如图(d )所示。
2-5 图示两根截面为100mm ⅹ100mm 的木柱,分别受到由横梁传来的外力作用。
试计算两柱上、中、下三段的应力。
(b)(c)(d)(f)题2-5-N图(kN)6108.5N图(kN)326.5-解:(1)梁与柱之间通过中间铰,可视中间铰为理想的光滑约束。
将各梁视为简支梁或外伸梁,柱可视为悬臂梁,受力如图所示。
列各梁、柱的平衡方程,可求中间铰对各梁、柱的约束反力,计算结果见上图。
(2)作柱的轴力图,如(e)、(f)所示。
(3)求柱各段的应力。
解:(1)用1-1截面将整个杆切开,取左边部分为研究对象;再用x -x 截面整个杆切开,取右边部分为研究对象,两脱离体受力如图(b)、(c),建立图示坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
F
(a) 最大应力可能在1-1截面上或3-3截面上:
4A
(轴力图)
FN :
A F +
11
F A
3 3
3F 4A
3F
3 3
max 11
A 3F + +
3F
F 15 MPa A
(b) 等截面杆,最大应力在轴力最大的截 面上:
FN :
2F +
max 11
2
3F 2F + F +
2 2
FN :
3 3
+ A
FN1 FN2 FN3
3 3 2 2
1 1
F
(d) 如图取隔离体,有: FN1 = F FN2 = F-qa =0 FN3 = F-qa -2F = F-F -2F = -2F
q=F/a
q=F/a
F
F
可由受力与轴力图的特点,检查内力图: 轴力图在集中载荷作用处有突变,突变 值与集中力的大小相等;
FNAB
y FNAB A y
45 30
2
FNAC
FNAC x
1 3 25.622kN
F 18.117kN
(拉)
(拉)
求各杆变形(伸长):
F
FNACl AC 25.622103 1.6 l AC 1.104mm EAAC 210109 0.0152 / 4 FNABl AB 18.117103 2 l AB 1.078mm 9 2 EAAB 21010 0.012 / 4
l1
A
C
B l 2
B
2-6 图示结构中,为水平刚性杆,其他三杆材料相同,弹性模量均为E=210GPa。已知l=1m, A1=A2=100mm2,A3=150mm2,F=20kN。试求C点的水平位移和铅直位移。 解:用单位力法计算位移:
FN 1 FN 2
F 2
FN 3 0
FN 1
3F 45 MPa A
2-2 习题2-1图中的外力F=150N,横截面面积A=10mm2,长度a=150mm。试求各杆的最大 正应力,并指出所在截面。 解:先画出轴力图。
2 2
A
2F
F
1 1
2F
(c) 等截面杆,最大应力在轴力最大的截 面上:
3F
2F
FN : + F + +
max 2 2
A
FN 3
C
FN 2
B F
A l
1
3
2
计算C点竖直位移,加单位力如图:
C l/2
1 0 有: F F FN 3 0 2 0 0 0 3 FNi FNi li FN F l F F l Cy 1 N1 N 2 N 2 EA EA EA i 1 Fl 0.476(m m) ( ) 2 EA
0 N1 0 N2
F
B l/2
0 FN 1
0 FN 3
C
A
0 FN 2
B
1
计算C点水平位移,加单位力如图: 有:
0 0 0 FN FN 1 1 FN 2 0 3 2
0 FN 1
0 FN 3
C
A
0 FN 2
1
B
Cx
0 0 FNi FNi li FN F l Fl 1 N1 0.476(m m) () EA EA 2EA i 1 3
1 l
3
2
M A 0 FN 2
C A l/2
F
B l/2
FN 1
A
FN 3
FN 2
B F
l2
FN 2l 1010 1 0.476(m m) 9 6 EA 21010 10010
3
l3 0
变形后位置如图:
A
Cx Ax l1 0.476m m () Cy Ay l1 0.476m m ( )
2-8图示结构,已知外力F=35kN。钢圆杆AB和AC的直径分别为d1=12mm和d2=15mm,钢的弹 性模量E=210GPa。试求A点的铅直位移。 解:求各杆内力,如图取A点为对象,由平衡条件,有:
Fx 0 FNAB sin 45 FNAC sin 30 FNAC 2 FNAB Fy 0 FNAB cos 45 FNAC cos30 F
求位移,各杆变形与A点位移之间的几何关系如图:
l AC
A
l AB
A
x
有 整理得
AA Ay
A
l AC l AB A A tan 30 A A tan 45 A A cos30 cos 45 l AB l AC AA tan 30 1 tan 30 1.366m m cos30 cos 45
E
FB
求支反力
Fx 0 FAx 0
FAy
M B ( F ) 0 FAy
220 4 220 8 220 kN 12 220 4 220 8 M A ( F ) 0 FB 220 kN 12
求杆AC和CD的轴力:
A FAy
FNAE FNAC FNCE
由A点的平衡条件: FNAC 由C点的平衡条件: FNCD 由强度条件:
FAy
cos 45
2 220 311.13kN ( 拉 )
(拉)
FNAC cos45 220kN
l 2
FN ( y )
求地桩的缩短量δ:
y
l
FN ( y) F l 3 Fl d y y d y 0 EA l 3 EA 0 4 EA
l
8-1 图示各圆截面杆,材料的弹性系数E都相同,试计算各杆的应变能。 解: (b)
2 FN li F2 3l / 8 l/4 3l / 8 U [ ] 2 2 2 2Ei Ai 2E (2d ) / 4 d / 4 (2d ) / 4
F
3F FN1
N3
A
1 1
3F
3 3F 3 3 3
3F 3F 3F
FN2 F
2 2
2F 2F
FN :
2F +
3F + +
2-1 画以下各杆的轴力图,并求指定截面上的内力。 A 1 2 F 2F 2F (c) 如图取隔离体,有: 1 2 FN1 = 2F FN1 1 2F FN2 = 2F-F +2F= 3F 1 F 2F FN2 2 2F
2-9 图示为打入土中的混凝土地桩,顶端承受载荷F,并由作用于地桩的摩擦力所支持。设沿 地桩单位长度的摩擦力为 f,且 f =k y2,式中,k为常数。试求地桩的缩短δ 。已知地桩的横 截面面积为A,弹性模量为E,埋入土中的长度为l。 解:地桩所受外载为轴载,且在F和摩擦力共同作用下平衡。
l3 即: Fy ky dy F k F 0 0 3 3F 3F 则: k 3 f 3 y2 l l y Fy3 轴力方程为: FN ( y ) fdy 3 0 l
2-6 图示结构中,为水平刚性杆,其他三杆材料相同,弹性模量均为E=210GPa。已知l=1m, A1=A2=100mm2,A3=150mm2,F=20kN。试求C点的水平位移和铅直位移。 解:AB受力如图,由平衡条件:
Fx 0 FN 3 0
F 10 kN 2 F M 0 F 10 kN B N1 2 FN 1l 10103 1 有: l1 0.476(m m) 9 6 EA 21010 10010
解:求各杆内力及应力
FNAB FNBC
FNAB B FNBC F
F sin F cos sin
(拉) (压)
AB
BC
FNAB F AAB AAB sin F F cos NBC ABC ABC sin
由题义,各杆应力达到许用应力,则:
AAB
F [ ] sin
ABC
F cos [ ] sin
要求结构的总重量为最小即结构总体积最小,其体积为:
V AAB l AB ABC lBC
令:
F l F cos Fl 1 cos l [ ] sin cos [ ] sin [ ] sin cos sin
dV 0 d
得:
tan 2 54.74 54 44
即:两杆的夹角θ 值为 54 44
AAB 1 则: 3 ABC cos
两杆横截面面积的比值为
3
2-15 图示桁架结构,各杆都由两个相同的等边角钢相并而成。已知其许用应力[σ]=170MPa, 试选择杆AC和CD的角钢型号。 解:桁架结构各杆均为二力杆(拉压杆) FAx
在分布载荷作用处轴力图斜率的值等于 该处分布载荷的分布集度大小,则分布 载荷的起点和终点处为轴力图折点。
2F
F
+
FN :
2F
2-2 习题2-1图中的外力F=150N,横截面面积A=10mm2,长度a=150mm。试求各杆的最大 正应力,并指出所在截面。 解:先画出轴力图。
3
3F
3
2 2
F
2A
1 1
解:求横截面上的应力:
b F
F
h
F F 10103 100MPa A bh 5 20
求各斜截面上的应力:
由:
2
2
