人教版七年级数学下册《实数》全章复习与巩固(知识讲解及考点训练)

合集下载

实数(全章复习与巩固)(基础篇)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)

专题6.11 实数（全章复习与巩固）（基础篇）（专项练习）一、单选题1．4的算术平方根是（） A ．2±B ．2C ．2D 22．下列实数是无理数的是（） A 327-B ．13C ．3.14159D 63．下列说法不正确的是（） A ．0的平方根是0 B ．一个负数的立方根是一个负数 C ．﹣8的立方根是﹣2D ．8的算术平方根是24．若3m x y -和35n x y 的和是单项式，则()3m n +的平方根是（） A ．8B ．8-C ．4±D ．8±5．估计463 ） A ．3与4之间B ．4与5之间C ．5与6之间D ．6与7之间6．有一个数值转换器，原理如下：当输入的x 为64时，输出的y 是（）A ．22B ．32C ．23D ．87．如图，长方形内有两个相邻的正方形，面积分别为2和4，则阴影部分的面积为（）A ．22-2B ．2+2C ．2D ．28．若320a =10b =3c =，则a b c 、、的大小关系为（） A ．a c b <<B ．a b c <<C ．c<a<bD ．c b a <<9．若a 、b 为实数，则下列说法正确的是（）A aB ．有理数与无理数的积一定是无理数C ．若a 、b 均为无理数，则a b +一定为无理数D ．若a 为无理数，且()()220a b ++=，则2b =-10．下面是李华同学做的练习题，他最后的得分是（）姓名李华得分______填空题（评分标准，每道题5分）（1）16的平方根是4±（2）立方根等于它本身的数有0和1（3）38-的相反数是2（4）3=3--ππA ．5分B ．10分C ．15分D ．20分二、填空题11．16的平方根是___________． 12．计算327________．1321的相反数是__________，3.14π-=____________ 14．若实数a 、b 满足：2a b +，32a b．则()()a b a b +-的值是_____________．15．四个实数2-，023中，最小的实数是______． 16．实数a 在数轴上的位置如图，则|3a =_________．171032（填“＞”，“＜”或“=”）18．找规律填空：02，262103…，______（第n 个数）．三、解答题19．求下列各式中的x ： (1) 2481x =(2) ()3227x +=-20．计算(1) 20223113274-+-(2) 223(3)(3)1664---21．已知：9的平方根是3和5x +，y 13 (1) 求x y +的值；(2) 求22x y +的算术平方根．22．如图，长方形ABCD 的长为2cm ，宽为1cm ．（1）将长方形ABCD 进行适当的分割（画出分割线），使分割后的图形能拼成一个正方形，并画出所拼的正方形；（标出关键点和数据）（2）求所拼正方形的边长．23．【观察】请你观察下列式子．第111．第2132+=．第31353++．第413574+++=．第5135795++++．【发现】根据你的阅读回答下列问题： (1) 写出第7个等式．(2) 135(21)n +++++＝．(3) 利用（241220284452++++++24．阅读材料，完成下列任务：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π2等，而常用的“…”或者“≈”的表示方法都不够百分百准确．材料一：479<273<<， ∵1712<． 71的整数部分为1． 7172．材料二：我们还可以用以下方法求一个无理数的近似值．我们知道面积是2221>21x =+，可画出如图示意图．由图中面积计算，2211S x x =+⨯⋅+正方形，另一方面由题意知2S =正方形，所以22112x x +⨯⋅+=．略去2x ，得方程212x +=，解得0.5x =2 1.5．解决问题：(1) 85(2) 5（画出示意图，标明数据，并写出求解过程）参考答案1．C【分析】根据平方与开平方互为逆运算，可得一个正数的算术平方根．解：∵22＝4， ∵4的算术平方根是2；故选：C ．【点拨】本题考查了求一个数的算术平方根，平方与开平方互为逆运算是求一个正数的算术平方根的关键．2．D【分析】无理数即为无限不循环小数，初中阶段接触的无理数的表现形式主要有：∵开方开不尽的数；∵含有π的数；∵0.010010001...（每两个1之间依次多个0）这样的数；据此解答即可．解：A 3273--，属于整数，不是无理数，不符合题意； B 、13为分数，不是无理数，不符合题意；C 、3.14159为有限小数，不是无理数，不符合题意；D 6 故选：D ．【点拨】本题考查了无理数的定义以及求一个数的立方根，熟练掌握初中阶段无理数的主要表现形式是解本题的关键．3．D【分析】直接利用算术平方根、平方根、立方根的定义分析得出答案．解：A 、0的平方根是0，原说法正确，故此选项不符合题意；B 、一个负数的立方根是一个负数，原说法正确，故此选项不符合题意；C 、﹣8的立方根是﹣2，原说法正确，故此选项不符合题意；D 、8的算术平方根是2 故选：D ．【点拨】此题主要考查了算术平方根、平方根、立方根，熟练掌握算术平方根、平方根、立方根的定义是解题的关键．4．D【分析】根据题意可得3m x y -和35n x y 是同类项，从而得到3,1m n ==，再代入，即可求解．解：∵3m x y -和35n x y 的和是单项式， ∵3m x y -和35n x y 是同类项，∵3,1m n ==，∵()()333164m n +=+=， ∵()3m n +的平方根是8±．故选：D ．【点拨】本题主要考查了合并同类项，求一个数的平方根，熟练掌握根据题意得到3m x y -和35n x y 是同类项是解题的关键．5．C【分析】先把46332“夹逼法”即可求解．解：463232== ∵253236＜＜， ∵5326＜＜，故选：C【点拨】本题考查了无理数的估值问题，“夹逼法”的应用是解题的关键． 6．A解：由题中所给的程序可知：把64取算术平方根，结果为8， ∵8是有理数， ∵8 ∵y 82 故选A ． 7．A2，2，再根据阴影部分的面积等于矩形的面积减去两个正方形的面积进行计算．解：∵矩形内有两个相邻的正方形面积分别为 4 和 2， ∵2，2，∵阴影部分的面积(22224222=⨯--=．故选A ．【点拨】本题主要考查了算术平方根的应用，解题的关键在于能够准确根据正方形的面积求出边长.8．C10320的值的范围，再进行比较即可得出答案．解：82027<<， 32203∴<<，3104<<，320310<故选：A ．【点拨】本题考查了实数大小比较，估算无理数的大小，熟练掌握估算无理数的大小是解题的关键．9．D【分析】A a B 、有理数与无理数的积不一定是无理数，举例说明； C 、a 、b 均为无理数，a b +不一定还是无理数，举例说明；D 、利用两数相乘积为0，两因式中至少有一个为0求出b 的值，即可做出判断．解：A a 42=，错误；B 、有理数与无理数的积不一定是无理数，例如：020，错误；C 、a 、b 均为无理数，a b +不一定还是无理数，，例如：220-=，错误；D 、若a 为无理数，且()()220a b ++=，得到20a +≠，20b +=，解得：2b =-，正确，故选：D ．【点拨】此题考查了实数的运算，熟练掌握运算法则是解本题的关键． 10．B【分析】直接利用平方根、立方根、绝对值、相反数的性质分别判断得出答案．解：（1164=的平方根是2±，故此选项错误；（2）立方根等于它本身的数有0和1、 1-，故此选项错误；（3382--的相反数是2，故此选项正确；（4）()3=3=3----πππ，故此选项正确．李华最后得分为10分，故选：B ．【点拨】此题主要考查了实数的性质，绝对值的性质，平方根和立方根概念，正确化简各数是解题关键．11．4±【分析】根据平方根的定义即可求解．解：即：16的平方根是16=4± 故填：4±【点拨】此题主要考查平方根，解题的关键是熟知平方根的定义． 12．-3【分析】根据立方根的性质计算即可．解：327--3，故答案为：-3．【点拨】本题考查了立方根的性质，正数的立方根为正数，负数的立方根为负数，0的立方根为0，熟记立方根的性质是解题的关键．13． 12- 3.14π-【分析】根据相反数的定义及去绝对值符合号法则，即可求得． 21的相反数是)2112-=>3.14π，3.14<0π∴-，()3.14 3.14 3.14πππ∴-=--=-，故答案为：12 3.14π-．【点拨】本题考查了相反数的定义及去绝对值符合号法则，掌握和灵活运用相反数的定义及去绝对值符合号法则是解决本题的关键．14．32【分析】根据算术平方根和立方根的性质得到a +b =4，a －b =8，进而直接代入求解即可．解：∵实数a 、b 2a b +=32a b ，∵a +b =4，a －b =8， ∵()()a b a b +-=4×8=32，故答案为：32．【点拨】本题考查了算式平方根、立方根、代数式求值，理解算式平方根和立方根的性质是解答的关键．15．-2【分析】根据实数大小比较的方法解答即可．解：∵2-2<3， ∵最小的实数是-2 故答案为：-2．【点拨】本题考查了实数的大小比较，正数大于0，负数小于0，正数大于一切负数，两个负数，绝对值大的反而小．163a【分析】根据数轴上点的位置判断出3a 利用绝对值的代数意义化简即可得到结果．解：∵a ＜0，∵30a ＜，则原式3a ， 3a 17．>103>，进而即可求解．解：∵109>， 103>， 1032>，故答案为：>．10 18()21n -【分析】除第一个数外，其他数变成二次根式后，根号下面的数都是2的倍数，第二个数为2的1倍，第三个数为2的2倍，依此类推，第n 个数为2的()1n -倍，从而得出答案．解：由题意得：由题意得：第一项：00200==⨯=； 2212⨯ 第三项：24224=⨯= 6236=⨯……第n ()()2121n n ⨯-=-()21n -【点拨】本题考查了算术平方根，解题的关键是发现题目中数据的变化规律，要熟练掌握．19．(1)92x =± (2)5x =-【分析】（1）利用平方根解方程即可；（2）利用立方根解方程．（1）解：2481x =，∵2814x =， ∵81942x =±=±；（2）解：()3227x +=-，∵3227x +=-23x，解得：5x =-．【点拨】本题考查开方法解方程．熟练掌握平方根和立方根的定义，是解题的关键． 20．33 (2)8-【分析】（1）先计算乘方与开方，并去绝对值符号，再计算加减即可．（2）先计算开方与乘方，再计算加减即可．（1）解：原式13132=-+++33；（2）解：原式3344=---8=-．【点拨】本题考查实数的混合运算，求绝对值，平方根和立方根，熟练掌握实数运算法则是解题的关键．21．(1)5- 73【分析】（1）先根据平方根的意义可得350x ++=，从而求出x 的值，13值的范围，从而求出y 的值，然后代入式子中进行计算即可解答；（2）把x ，y 的值代入式子中求出22xy +的值，然后再利用算术平方根的意义，进行计算即可解答．（1）解：9的平方根是3和5x +， 350x ∴++=，解得：8x =-，91316<<，3134∴<<，y 133y ∴=，835x y ∴+=-+=-，x y ∴+的值为5-；（2）当8x =-，3y =时，2222(8)364973x y +=-+=+=，22x y ∴+73【点拨】本题考查了估算无理数的大小，平方根，熟练掌握估算无理数的大小是解题的关键．22．（1）分割方法不唯一，如图，见分析；（22cm .【分析】（1）根据AB=2AD ，可找到CD 的中点，即可分成两个正方形，再沿对角线分割一次，即可补全成一个新的正方形；（2）设拼成的正方形边长为cm x ，根据面积相等得到方程，即可求解．解：（1）如图，∵AB=2AD ，找到CD,AB 的中点，如图所示，可把矩形分割成4个等腰直角三角形，再拼成一个新的正方形；（2）设拼成的正方形边长为cm x ，根据题意得2122x =⨯=，∵2x2cm ．【点拨】此题主要考查实数性质的应用，解题的关键是根据图形的特点进行分割． 23．135791113++++++7 (2)n +1(3)14 【分析】（1）根据规律直接写出式子即可；（2135(21)n +++++n +1个式子，根据规律即可得；（3）41220283644524(1357891113)+++++++++++++利用规律即可得．（1）解：根据材料可知，第七个式子的被开方数为1+3+5+7+9+11+13， ∵第7135711137+++++，135711137+++++=；（2(21)1135(21)12n n n +++++++=+，故答案为：1n +；（3）解：根据（2）中的规律知， 11341220283644524(1357891113)4142++++++++++++++=．【点拨】本题考查了数字变化规律类，解题的关键是掌握是式子的规律．24．859 (2)2.25【分析】（1）根据材料一中的方法求解即可；（2）利用材料二中的方法画出图形，写出过程即可．（1）解：8185100<98510<<，859． 85859．（2）解：我们知道面积是5552>，52x =+，可画出如图示意图．由图中面积计算，2224S x x =+⨯+正方形，另一方面由题意知5S =正方形，所以2445x x ++=．略去2x ，得方程410x -=，解得0.25x =5 2.25．【点拨】本题考查了无理数的估算，解题关键是准确理解题目给出的方法，熟练进行计算．。

人教版七年级数学下册实数知识点总结

第一章实数考点一、实数的概念及分类（3分）1、实数的分类正有理数有理数零有限小数和无限循环小数实数负有理数正无理数无理数无限不循环小数负无理数整数包括正整数、零、负整数。

正整数又叫自然数。

正整数、零、负整数、正分数、负分数统称为有理数。

2、无理数在理解无理数时，要抓住“无限不循环”这一点，归纳起来有四类：（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等；（3）有特定结构的数，如0.1010010001…等；（4）某些三角函数，如sin60o 等（这类在初三会出现）考点二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数是一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a 与b 互为相反数，则有a+b=0，a=-b ，反之亦成立。

2、绝对值一个数的绝对值就是表示这个数的点与原点的距离，|a|≥0。

零的绝对值是它本身，若|a|=a ，则a ≥0；若|a|=-a ，则a ≤0。

正数大于零，负数小于零，正数大于一切负数，两个负数，绝对值大的反而小。

3、倒数如果a 与b 互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

零没有倒数。

考点三、平方根、算数平方根和立方根1、平方根如果一个数的平方等于a ，那么这个数就叫做a 的平方根（或二次方跟）。

一个数有两个平方根，它们互为相反数；零的平方根是零；负数没有平方根。

正数a 的平方根记做“a ”。

2、算术平方根正数a 的正的平方根叫做a 的算术平方根，记作“a ”。

正数和零的算术平方根都只有一个，零的算术平方根是零。

a （a ≥0） 0≥a==a a 2 ；注意a 的双重非负性：-a （a <0） a ≥03、立方根如果一个数的立方等于a ，那么这个数就叫做a 的立方根（或a 的三次方根）。

一个正数有一个正的立方根；一个负数有一个负的立方根；零的立方根是零。

实数(知识讲解)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)

专题6.7 实数（知识讲解）【学习目标】1. 了解无理数和实数的意义；2. 了解有理数的概念、运算法则在实数范围内仍适用 .【要点梳理】要点一、有理数与无理数有限小数和无限循环小数都称为有理数.无限不循环小数又叫无理数.特别说明：（1）无理数的特征：无理数的小数部分位数无限.无理数的小数部分不循环，不能表示成分数的形式.（2）常见的无理数有三种形式：①含π类.②看似循环而实质不循环的数，如：1.313113111…….5.要点二、实数有理数和无理数统称为实数. 1.实数的分类按定义分：实数⎧⎨⎩有理数：有限小数或无限循环小数无理数：无限不循环小数按与0的大小关系分：实数0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正有理数正数正无理数负有理数负数负无理数2.实数与数轴上的点一一对应.数轴上的任何一个点都对应一个实数，反之任何一个实数都能在数轴上找到一个点与之对应.要点三、实数大小的比较对于数轴上的任意两个点，右边的点所表示的实数总是比左边的点表示的实数大. 正实数大于0，负实数小于0，两个负数，绝对值大的反而小.要点四、实数的运算有理数关于相反数和绝对值的意义同样适合于实数.当数从有理数扩充到实数以后，实数之间不仅可以进行加、减、乘、除（除数不为0）、乘方运算，而且正数及0可以进行开平方运算，任意一个实数可以进行开立方运算.在进行实数的运算时，有理数的运算法则及运算性质等同样适用.【典型例题】类型一、实数➽➼概念的理解✬✬分类1．把下列各数写入相应的集合内：12-，22，364-，0.26，7π，0.10，5.12，33-，327+．(1) 有理数集合：{ }； (2) 正实数集合：{ }； (3) 无理数集合：{ } 【答案】(1) 12-，364-，0.26， 0.10，5.12(2) 22，0.26，7π，0.10，5.12，33-，327+(3) (3) 22，7π， 33-，327+【分析】（1）根据有理数的定义进行作答即可；（2）根据正数的定义进行判断即可；（3）根据无理数的定义进行判断即可．解：(1)有理数有：12-，3644-=-，0.26， 0.10，5.12故答案为：12-， 364-，0.26， 0.10，5.12(2)12-，3644-=-是负数，33-绝对值是正数正实数有：22，0.26，7π，0.10，5.12，33-，327+ 故答案为：22，0.26，7π，0.10，5.12，33-，327+ (3)无理数有：22， 7π， 33-，327+故答案为：22， 7π， 33-，327+【点拨】本题考查了实数的分类，即实数分为正实数，零，负实数；实数还可以分为有理数和无理数，有理数包括正数和分数，无理数是无线不循环小数，熟练掌握有理数、无理数的定义是解题的关键．举一反三：【变式1】把下列各数填入相应的集合内．32π、－5222034905380.3737737773…（相邻两个3之间的7逐次加1个），(1)有理数集合{…}(2)无理数集合{…}(3)负实数集合{… }【答案】(1) －52，49，0，38-(2) 32，π，2，203，-5，0.3737737773（3）－52，-5，38-.【分析】（1）根据有理数的定义进行判定即可得出答案；（2）根据无理数的定义进行判定即可得出答案；（3）根据负实数的定义进行判定即可得出答案．解：（1）有理数集合：{－52，49,0，38-…}（2）无理数集合：{32，π，2，203，-5，0.3737737773……}（3）负实数集合：{－52，-538-【点拨】本题主要考查了实数的分类，熟练掌握实数的分类进行求解是解决本题的关键.把下列各数序号分别填入相应的集合内：32① 14，10，①π-，①52-，15203①6-①38-①0.979779777···（相邻两个9之间7的个数逐次增加1）【答案】有理数集合：①①①；无理数集合：①①①①①①①；负实数集合：①①①①【分析】根据实数的性质即可分类．解：有理数为14，52-，38-；无理数为32，10，π-，15，203，6-，0.979779777···（相邻两个9之间7的个数逐次增加1）；负实数为π-，52-，38-，6-，①有理数集合：①①①；无理数集合：①①①①①①①；负实数集合：①①①①．【点拨】此题主要考查实数的分类，解题的关键是熟知实数的分类方法及特点．类型二、实数➽➼实数性质✬✬实数与数轴➽➼运算✬✬化简3 50.2-11-327825-3π-相反数倒数绝对值【分析】根据相反数、倒数、绝对值的定义依次即可得出答案．解：3 50.2-11-327825-3π-相反数350.21132-52-3π-倒数53-51111-2325--13π-绝对值350.2113252-3π-【点拨】本题考查实数的分类，立方根、分母有理化．对于分母中是二次根式的要分母有理化．举一反三：【变式1】实数a，b，c2a|a－b|＋|c－a|．【答案】a b c --+【分析】先判断0a b c <<<，进而得到0a b -<，0c a ->，再化简即可．解：由数轴上点的位置可得 0a b c <<<，①0a b -<，0c a ->， ①2a a b c a --+- a a b c a =-+-+-a b c =--+．【点拨】本题考查了求一个数的算术平方根，化简绝对值，整式的加减运算，实数与数轴，根据数轴及运算法则判断0a b -<，0c a ->是解本题的关键．【变式2】我们在学习“实数”时画了这样一个图，即“以数轴上的单位长为‘1’的线段作一个正方形，然后以原点O 为圆心，正方形的对角线长为半径画弧交数轴于点A ”，请根据图形回答下列问题：(1) 线段OA 的长度是多少?(要求写出求解过程) (2) 这个图形的目的是为了说明什么?(3) 这种研究和解决问题的方式体现了的数学思想方法(将下列符合的选项序号填在横线上)A ．数形结合B ．代入C ．换元D ．归纳【答案】(1) OA =2；(2)数轴上的点和实数是一一对应关系；(3)A【分析】（1）首先根据勾股定理求出线段OB 的长度，然后结合数轴的知识即可求解；（2）根据数轴上的点与实数的对应关系即可求解；（3）本题利用实数与数轴的对应关系即可解答．解：(1) OB 2＝12+12＝2①OB ＝2 ①OA ＝OB =2(2)数轴上的点和实数是一一对应关系(3) 这种研究和解决问题的方式，体现的数学思想方法是数形结合．故选A【点拨】本题主要考查了实数与数轴之间的关系，此题综合性较强，不仅要结合图形，还需要熟悉平方根的定义．也要求学生了解数形结合的数学思想．类型三、实数➽➼估算✬✬无理数的整数（小数）部分✬✬➽➼运算✬✬化简3．[阅读材料]459253，①151＜251的整数部分为15152(1)91的小数部分是．(2)已知a21b21a）3＋（b＋4）2的值．【答案】(1)91﹣9 (2)-43【分析】（1）估算出91的范围99110<<，可得到91的整数部分，进而得到91的小数部分；（2）估算出21的范围4215<<，可得到21的整数部分，进而得到21的小数部分，从而得到a，b的值，再求代数式的值即可．<<，(1)解：①8191100①99110<<，①91的整数部分是9，①91的小数部分91﹣9，故答案为：91﹣9；<<，(2)解：①162125①4＜21＜5，①21的整数部分是4，小数部分是21﹣4， ①a ＝4，b ＝21﹣4，①原式＝（﹣4）3+（21-4+4）2 ＝﹣64+21 ＝﹣43．∴代数式的值为43-．【点拨】本题考查了实数的大小比较，代数式求值，无理数估算知识．解题的关键在与正确的计算求值．举一反三：【变式1】比较下列各组数的大小：（1356；（2325-3-；（3513 【答案】（1）356<；（2）3253->-；（3）3512-> 【分析】（1）直接化简二次根式进而比较得出答案；（2）直接估算无理数的取值范围进而比较即可；（3）直接估算无理数的取值范围进而比较即可．解：（1）①366=，①356<；（2）①33252-<-<-，①3253->-；（3）①132<<，①13122<<， ①253<<， ①1512<-<， ①3512->．【点拨】本题主要考查了实数比较大小，正确估算无理数取值范围是解题关键．【变式2】2212221来表2（129的整数部分是，小数部分是；（2）如果55a，55b，求a5的值．【答案】（1）5，29﹣5；（2）35﹣2【分析】（1）估算29的近似值，即可得出29的整数部分和小数部分；（2）求出a、b的值，再代入计算即可．解：（1）①25＜29＜36，①5＜29＜6，①29的整数部分为5，小数部分为29﹣5，故答案为：5，29﹣5；（2）①2＜5＜3，①7＜5＋5＜8，①5＋5的小数部分a＝5＋5﹣7＝5﹣2，①2＜5＜3，①﹣3＜﹣5＜﹣2，①2＜5﹣5＜3，①5﹣5的整数部分为b＝2，①a＋5b＝5﹣2＋25＝35﹣2.【点拨】本题考查了无理数的估算，正确估算无理数的取值范围是解题的关键．类型四、实数➽➼实数的混合运算➼运算✬✬化简4．计算：（13325181276464 （23226511274⎛⎫-- ⎪⎝⎭【答案】（1）558；（2）112-．【分析】直接利用立方根的性质及平方根的性质分别化简，然后根据实数的运算法则求得计算结果解：（1）原式=519384-⨯- ，=152988-- ， =558（2）原式=3151274-+- ， =1134-+ ， =112-【点拨】此题主要考查了实数运算，正确化简各数是解题关键．举一反三：【变式1】计算题：（1）233111(2)2789⎛-+-⨯-- ⎝ （2238321253 【答案】（1）-3；（2）11【分析】（1）根据有理数的乘方，求一数的立方根和算术平方根进行计算；（2）根据求一数的立方根和算术平方根，化简绝对值，进行实数的混合运算．解：（1）原式11183111383⎛⎫=--⨯+⨯-=---=- ⎪⎝⎭；（2）2383212538235311--+-=-++-=．【点拨】本题考查了实数的混合运算，求一数的立方根和算术平方根，掌握实数的运算法则是解题的关键．【变式2】计算： (1)3112548(2) ()20223912712-【答案】(1)5 (2)22-【分析】对于（1），由1142=，255=，31182=，再计算即可；对于（2），由93=，(-1)2022=1，3273=，1221-=-，再计算即可．解：(1)原式=115522+-=；(2)原式=3132122--+-=-．【点拨】本题主要考查了实数的运算，求出各数的平方根和立方根是解题的关键．类型五、实数➽➼实数的运算➼程序设计✬✬新定义5．一个数值转换器，如图所示：(1) 当输入的x 为81时．输出的y 值是_________；(2) 若输入有效的x 值后，始终输不出y 值，请写出所有满足要求的x 的值； (3) 若输出的y 2，请写出两个满足要求的x 值．【答案】(1)3； (2)0x =，1； (3)4x =，2x =（答案不唯一）【分析】（1）根据运算规则即可求解；（2）根据0的算术平方根是0，1的算术平方根是1即可判断；（3）根据运算法则，进行逆运算即可求得无数个满足条件的数．（1）解：当81x =时，取算术平方根81=9，不是无理数，继续取算术平方根93=，不是无理数，继续取算术平方根得3，是无理数，所以输出的y 值为3；（2）解：当0x =，1时，始终输不出y 值．因为0，1的算术平方根是0，1，一定是有理数；（3）解：4的算术平方根为2，2的算术平方根是2，①4x =，2x =都满足要求．【点拨】本题考查了算术平方根的计算和无理数的判断，正确理解给出的运算方法是关键．举一反三：【变式】思考与探究：（1）在如图所示的计算程序中，若开始输入的数值是4，则最后输出的结果是___________．（2）在如图所示的计算程序中，若最后输出的结果是58，则开始输入的数值是___________．（3）按下面的程序计算，若开始输入的值x为正数，最后输出的结果为1621，则满足条件的x的不同值最多有多少个？【答案】（1）17；（2）6或－10；（3）6个【分析】（1）根据程序运算图可得算式4×3+5，按运算顺序进行求解即可；（2）设输入的数字为m，根据题意可得关于x的方程，解方程即可求得答案；（3）根据最后输出的结果，可计算出它前面的那个数，依此类推，可将符合题意的正数求出．解：（1）由题意得：4×3+5=17，故答案为：17；（2）设输入的数字为m，则有（m+2）2-6=58，解得：m=6或m=-10，故答案为：6或--10；（3）①最后输出的数为1621，①4[(x+5)-(-2)2]-3=1621，解得：x=405>0，又①4[(x+5)-(-2)2]-3=405，解得：x=101>0，又①4[(x+5)-(-2)2]-3=101，解得：x=25>0，又①4[(x+5)-(-2)2]-3=25，解得：x=6>0，又①4[(x+5)-(-2)2]-3=6，解得：x=54>0，又①4[(x+5)-(-2)2]-3=54，解得：x=116>0，又①4[(x+5)-(-2)2]-3=116，解得：x=1564-<0，（不符合题意） ①符合题意的正数最多有6个.【点拨】本题考查了程序运算，涉及了一元一次方程，利用平方根的解方程等知识，正确审题，弄清程序运算中的运算顺序，熟练掌握相关和运算法则和解题方法是解此类问题的关键．6．对于两个不相等的实数a 、b ，定义一种新的运算如下，(0)a b a b a b a b+*=+>-，如：323*2532+==-，求()654**的值．【答案】1【分析】根据已知条件先求出5*4的值，再求出6*（5*4）的值即可求出结果．解：①(0)a b a b a b a b +*=+>-， ①545*4354+==-， ①()636*5*46*3163+===-．【点拨】此题主要考查实数的运算，解题的关键是根据新定义运算法则进行求解．举一反三：【变式】定义新运算：对于任意实数a ，b ，都有2a b a b =+※，例如2747423=+=※．（1）求54※的值．（2）求(712※※的平方根．【答案】（1）21；（2）±4【分析】（1）根据定义新运算即可求54※的值；（2）根据定义新运算求()712※※的值，再计算平方根即可得出答案．解：（1）由定义新运算得：2545451621=+=+=※；（2）由定义新运算得：()7127(12)737916=+==+=※※※※， ①()712※※的平方根为164±=±．【点拨】本题考查新定义的有理数运算，掌握新定义的运算法则是解题的关键．类型六、实数➽➼实数的运算➼实际运用✬✬规律7．数学阅读是学生个体根据已有的知识经验，通过阅读数学材料建构数学意义和方法的学习活动，是学生主动获取信息，汲取知识，发展数学思维，学习数学语言的途径之一．请你先阅读下面的材料，然后再根据要求解答提出的问题：问题情境：设a ，b 是有理数，且满足2322+=-a b ab 的值．解：由题意得(3)(2)20-++a b ，①a ，b 都是有理数，①3,2a b -+也是有理数，2①30,20a b -=+=，①3,2a b ==-，①(2)36ab =-=-解决问题：设x ，y 都是有理数，且满足22585x y -+=+x y +的值．【答案】8或0【分析】根据题目中例题的方法，对所求式子进行变形，求出x 、y 的值，从而可以求得x +y 的值．解：①225845x y y -+=+，①（x 2-2y -8）+（y -4）5=0，①x 2-2y -8=0，y -4=0，解得，x =±4，y =4，当x =4，y =4时，x +y =4+4=8，当x=-4，y=4时，x+y=（-4）+4=0，即x+y的值是8或0．【点拨】本题考查实数的运算，解题的关键是明确题目中例题的解答方法，然后运用类比的思想解答所求式子的值．举一反三：【变式】如图1，有5个边长为1的小正方形组成的纸片，可以把它剪拼成一个正方形．（1）拼成的正方形的面积是，边长是；（2）仿照上面的做法，你能把下面这十个小正方形组成的图形纸，剪开并拼成一个大正方形吗？若能，在图2中画出拼接后的正方形，并求边长；若不能，请说明理由．【答案】（1）5；5（2）10【分析】（1）一共有5个小正方形，那么组成的大正方形的面积为5，边长为5的算术平方根；（2）一共有10个小正方形，那么组成的大正方形的面积为10，边长为10的算术平方根，在所给图形中截取两条长为10的且互相垂直的线段，进而拼合即可．解：（1）拼成的正方形的面积是：5，边长为：5．（2）如图所示，能，正方形的边长为10．【点拨】本题考查了图形的剪拼、勾股定理、正方形的面积和正方形的有关画图，巧妙地根据网格的特点画出正方形是解此题的关键.8．阅读下列材料：设：0.30.333x ==，①则10 3.333x =.①由①-①，得93x =，即13x =. 所以10.30.3333==. 根据上述提供的方法.把0.7•和1.3•化成分数，并想一想.是不是任何无限循环小数都可以化成分数？【答案】70.70.7779•=⋯=，41.33•=.任何无限循环小数都可以化成分数. 【分析】设0.70.777x ==⋯①则107.777x =⋯，①；由-②①，得97x =；由已知，得10.30.3333==，所以11.310.31.3=+=+任何无限循环小数都可以这样化成分数. 解：设0.70.777x ==⋯①则107.777x =⋯，①由①-①，得97x =，即79x =.所以70.70,7779=⋯=. 由已知，得10.30.3333==，所以141.310.3133=+=+=. 任何无限循环小数都能化成分数.【点拨】考核知识点：无限循环小数和有理数.模仿，理解材料是关键.举一反三：【变式】（2020春·山西太原·八年级太原师范学院附属中学校考阶段练习）阅读下列解题过程：231111()4422-===； 254221()9933-=； 279331()161644-===；… （111136-=________．（2）按照你所发现的规律，请你写出第n 个等式：________．（335799(1)(1)(1)(1)49162500----【答案】（1）56；（2）2211(1)1n n n n +-=++；（3）150 【分析】（1）仿照已知等式确定出所求即可；（2）归纳总结得到一般性规律，写出即可；（3）原式变形后，仿照上式得出结果即可．解：（1）11255136366-==；故答案为：56；（2）观察上面的解题过程，发现的规律为：2222221(1)211(1)(1)(1)1n n n n n n n n n ++---===++++，故答案为：2211(1)1n n n n +-=++；（3）35799(1)(1)(1)(1)49162500---- 149240149162500=⨯⨯⨯⨯ 12500=150=．【点拨】本题考查了实数的运算，规律型：数字的变化类，弄清题中的规律是解本题的关键．中考真题专练【1】（2020·重庆·统考中考真题）在整数的除法运算中，只有能整除与不能整除两种情况，当不能整除时，就会产生余数，现在我们利用整数的除法运算来研究一种数——“差一数”．定义：对于一个自然数，如果这个数除以5余数为4，且除以3余数为2，则称这个数为“差一数”．例如：14524÷=，14342÷=，所以14是“差一数”；19534÷=，但19361÷=，所以19不是“差一数”．（1）判断49和74是否为“差一数”？请说明理由；（2）求大于300且小于400的所有“差一数”．【答案】（1）49不是“差一数”，74是“差一数”，理由见分析；（2）314、329、344、359、374、389【分析】（1）直接根据“差一数”的定义计算判断即可；（2）解法一：根据“差一数”的定义可知被5除余4的数个位数字为4或9，被3除余2的数各位数字之和被3除余2，由此可依次求得大于300且小于400的所有“差一数”；解法二：根据题意可得：所求数加1能被15整除，据此可先求出大于300且小于400的能被15整除的数，进一步即得结果．解：（1）①49594÷=；493161÷=，①49不是“差一数”，①745144÷=；743242÷=，①74是“差一数”；（2）解法一：①“差一数”这个数除以5余数为4，①“差一数”这个数的个位数字为4或9，①大于300且小于400的符合要求的数为304、309、314、319、324、329、334、339、344、349、354、359、364、369、374、379、384、389、394、399，①“差一数”这个数除以3余数为2，①“差一数”这个数的各位数字之和被3除余2，①大于300且小于400的所有“差一数”为314、329、344、359、374、389．解法二：①“差一数”这个数除以5余数为4，且除以3余数为2，①这个数加1能被15整除，①大于300且小于400的能被15整除的数为315、330、345、360、375、390，①大于300且小于400的所有“差一数”为314、329、344、359、374、389．【点拨】此题主要考查了带余数的除法运算，第（2）题的解法一是用逐步增加条件的方法依此找到满足条件的所有数；解法二是正确得出这个数加1能被15整除，明确方法是关键．【2】（2019·重庆·统考中考真题）《道德经》中的“道生一，一生二，二生三，三生万物”道出了自然数的特征．在数的学习过程中，我们会对其中一些具有某种特性的数进行研究，如学习自然数时，我们研究了奇数、偶数、质数、合数等．现在我们来研究另一种特殊的自然数—“纯数”．定义；对于自然数n ，在计算n+（n +1）+（n +2）时，各数位都不产生进位，则称这个自然数n 为“数”，例如：32是”纯数”，因为计算32+33+34时，各数位都不产生进位；23不是“纯数”，因为计算23+24＋25时，个位产生了进位．（1）判断2019和2020是否是“纯数”？请说明理由；（2）求出不大于100的“纯数”的个数．【答案】（1）2019不是“纯数”，2020时“纯数”，见分析；（2）13个.【分析】（1）根据题目中的新定义可以解答本题，注意各数位都不产生进位的自然数才是“纯数”；（2）根据题意可以推出不大于100的“纯数”的个数，本题得以解决.解：（1）当2019n =时，12020n +=，22022n +=∵计算时，个位为90110++=，需要进位，∴2019不是“纯数”；当2020n =时，12021n +=，22022n +=∴个位为0123++=，不需要进位：十位为226++，不需要进位：百位为0000++=，不需要进位：千位为2226++=，不需要进位：∴2020是“纯数”；综上所述，2019不是“纯数”，2020时“纯数”.（2）由题意，连续的三个自然数个位不同，其他位都相同；并且，连续的三个自然数个位为0、1、2时，不会产生进位；其他位的数字为0、1、2、3时，不会产生进位；①当这个数为一位的自然数的时候，只能是0、1、2，共3个；②当这个数为二位的自然数的时候，十位只能为1、2、3，个位只能为0、1、2，共9个；③当这个数为100时，100是“纯数”；∴不大于100的“纯数”有39113++=个.【点拨】本题考查整式的加减、有理数的加法、新定义，解答本题的关键是明确题意，利用题目中的新定义解答.。

(完整word)新人教版七年级下册数学第六章实数知识点总结及阶梯练习,推荐文档

第六章实数知识网络:考点一、实数的概念及分类1、实数的分类厂正有理針3「育理数冲零卜有限卜数和王限値环外数宴埶齐L定有理割」厂正形里麹'IJ无理埶 Y 卜无限羽爾环扌觀L煲无理数」2、无理数在理解无理数时，要抓住“无限不循环”这一点，归纳起来有四类(1)开方开不尽的数，如、7,32等；(2)有特定意义的数，如圆周率n或化简后含有n的数，如\ +8等；3(3)有特定结构的数，如0.1010010001…等；(4)某些三角函数，如sin60。

等(这类在初三会出现)判断一个数是否是无理数，不能只看形式，要看运算结果，如16是有理数，而不是无理数。

3、有理数与无理数的区别(1)有理数指的是有限小数和无限循环小数，而无理数则是无限不循环小数；(2)所有的有理数都能写成分数的形式(整数可以看成是分母为1的分数)，而无理数则不能写成分数形式。

考点二、平方根、算术平方根、立方根1、概念、定义(1)如果一个正数x的平方等于a,即二'二，那么这个正数x叫做a的算术平方根。

(2)如果一个数的平方等于a,那么这个数就叫做a的平方根(或二次方跟)。

如果叮卫，那么x叫做(3)如果一个数的立方等于a,那么这个数就叫做a的立方根(或a的三次方根)。

如果厂亠x叫做a的立方根。

2、运算名称(1)求一个正数a的平方根的运算，叫做开平方。

平方与开平方互为逆运算。

(2)求一个数的立方根的运算，叫做开立方。

开立方和立方互为逆运算。

3、运算符号(1)正数a的算术平方根，记作“.可”。

(2)a(a>0)的平方根的符号表达为' ' 1 o(3)一个数a的立方根，用表示，其中a是被开方数，3是根指数。

4、运算公式(石『=谨(a^Q)口= _坯(注意：弦说明三次根号内的员号可以移到根号外面)4、开方规律小结(1)若a>0,则a的平方根是a, a的算术平方根，a;正数的平方根有两个，它们互为相反数,中正的那个叫它的算术平方根；0的平方根和算术平方根都是0;负数没有平方根。

人教版初中七年级数学下册第六单元《实数》知识点复习(含答案解析)

一、选择题1．下列各式计算正确的是（）A B = ±2 C = ±2 D ． A 解析：A【分析】根据平方根和立方根分别对四个选项进行计算即可．【详解】解：∵-1= 2= 2，，故只有A 计算正确；故选:A ．【点睛】本题考查的是平方根、算术平方根和立方根，计算的时候需要注意审题是求平方根还是算术平方根．2．下列各组数中，互为相反数的是（）A ．B ．2-与12-C ．()23-与23-D 解析：C【分析】根据绝对值运算、有理数的乘方运算、立方根、相反数的定义逐项判断即可得．【详解】A 、=不是相反数，此项不符题意；B 、2-与12-不是相反数，此项不符题意； C 、()223399,--=-=，则()23-与23-互为相反数，此项符合题意；D 2,2=-=-故选：C ．【点睛】本题考查了绝对值运算、有理数的乘方运算、立方根、相反数的定义，熟记各运算法则和定义是解题关键．3．已知122=，224=，328=，4216=，5232=，……，根据这一规律，20192的个位数字是（）A ．2B ．4C ．8D ．6C解析：C【分析】通过观察122=，224=，328=，4216=，，5232=…知，他们的个位数是4个数一循环，2，4，8，6，…因为2019÷4＝504…3，所以20192的个位数字与32的个位数字相同是8．【详解】解：仔细观察122=，224=，328=，4216=，，5232=…；可以发现他们的个位数是4个数一循环，2，4，8，6，…∵2019÷4＝504…3，∴20192的个位数字与32的个位数字相同是8．故答案是：8．【点睛】本题考查了尾数特征，解题的关键是根据已知条件，找出规律：2的乘方的个位数是每4个数一循环，2，4，8，6，…．4．下列实数220.010*******；； (相邻两个1之依次多一个0)；2，其中无理数有( )A ．2个B ．3个C ．4个D ．5个B解析：B【分析】根据无理数、有理数的定义即可判定选择项．【详解】4=-，是有理数；3.14是有限小数，是有理数；227是分数，是有理数；，0.010010001(相邻两个1之依次多一个0)2，是无理数，共3个，故选：B ．【点睛】本题考查了无理数的定义，注意无理数的三种形式：①开方开不尽的数，②无限不循环小数，③含有π的数．5．在0.010010001，3.14，π，1.51，27中无理数的个数是（）． A ．5个B ．4个C ．3D ．2个D解析：D【分析】根据无理数的概念解题，找出无理数的个数即可，无限不循环小数称为无理数；【详解】在0.010010001，3.14，π，1.51，27中无理数有π共2个，故选D ．【点睛】本题考查了无理数的概念，正确掌握无理数的概念是解题的关键；6 ）A ．8B ．8-C ．D ．± D 解析：D【分析】8=，再根据平方根的定义，即可解答．【详解】8=，8的平方根是±故选：D ．【点睛】8=．7．若1a >，则a ，a -，1a 的大小关系正确的是（） A ．1a a a >->B ．1a a a >->C ．1a a a >>-D ．1a a a ->> C 解析：C【分析】可以用取特殊值的方法，因为a ＞1，所以可设a=2，然后分别计算|a|，-a ，1a ，再比较即可求得它们的关系．【详解】解：设a=2，则|a|=2，-a=-2，112a =， ∵2＞12＞-2， ∴|a|＞1a＞-a ；故选：C ．【点睛】此类问题运用取特殊值的方法做比较简单．8．下列各数中，属于无理数的是（）A ．227B ．3.1415926C ．2.010010001D ．π3- D 解析：D【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．【详解】解：A 、227是有理数，故选项A 不符合题意； B 、3.1415926是有理数，故选项B 不符合题意；C 、2.010010001是有理数，故选项C 不符合题意；D 、π3-是无理数，故选项D 题意；故选：D ．【点睛】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．9．下列等式成立的是（）A ．±1B ＝±2C 6D 3A 解析：A【分析】分别根据算术平方根、立方根的定义逐一判断即可．【详解】A ．书写规范，故本选项符合题意；B.算术平方根只能是正数不能是负数，故本选项不合题意；C.立方根与被开方数符号一致，故本选项符合题意；D.33=27，27的立方根才等于3，故本选项不合题意．故选：A ．【点睛】本题主要考查了算术平方根与立方根的定义，熟练掌握算术平方根的性质是解答本题的关键．10．下列说法中：①0是最小的整数；②有理数不是正数就是负数；③﹣2π不仅是有理数，而且是分数；④237是无限不循环小数，所以不是有理数；⑤无限小数不一定都是有理数；⑥正数中没有最小的数，负数中没有最大的数；⑦非负数就是正数；⑧正整数、负整数、正分数、负分数统称为有理数；其中错误的说法的个数为（）A ．7个B ．6个C ．5个D ．4个B解析：B【分析】根据有理数的分类依此作出判断，即可得出答案．【详解】解：①没有最小的整数，所以原说法错误；②有理数包括正数、0和负数，所以原说法错误；③﹣2π是无理数，所以原说法错误； ④237是无限循环小数，是分数，所以是有理数，所以原说法错误； ⑤无限小数不都是有理数，所以原说法正确； ⑥正数中没有最小的数，负数中没有最大的数，所以原说法正确；⑦非负数就是正数和0，所以原说法错误；⑧正整数、负整数、正分数、负分数和0统称为有理数，所以原说法错误；故其中错误的说法的个数为6个．故选：B ．【点睛】本题考查了有理数的分类，认真掌握正数、负数、整数、分数、正有理数、负有理数、非负数的定义与特点是解题的关键．注意整数和正数的区别，注意0是整数，但不是正数．二、填空题11．把下列各数表示在数轴上，并把这些数按从大到小的顺序用“＞”连接起来． 0，327-，()2--，1--，9，22-画图见解析【分析】先把各数化简在数轴上表示出各数再根据在数轴上右边的数总比左边的数大把这些数按从大到小的顺序用＞连接起来【详解】解：在数轴上表示为：按从大到小的顺序用>连接为：【点睛】本题主要考查了解析：画图见解析，()239201272>-->>-->->- 【分析】先把各数化简，在数轴上表示出各数，再根据“在数轴上，右边的数总比左边的数大”把这些数按从大到小的顺序用“＞”连接起来．【详解】解：3273-=-，()22--=，11--=-，93=，224-=-，在数轴上表示为：按从大到小的顺序用>()239201272>-->>-->->-．【点睛】本题主要考查了实数的大小比较，解题的关键是准确在数轴上表示实数，并利用数轴对实数的大小进行比较．12．把下列各数的序号填入相应的括号内①-3，②π，，④-3.14，，⑥0，⑦227，⑧-1，⑨1.3，⑩1.8080080008…（两个“8”之间依次多一个“0”）．整数集合{ …}，负分数集合{ …}，正有理数集合{ …}，无理数集合{ …}．见解析【分析】先求出立方根再根据整数负分数正有理数无理数的定义即可得【详解】解析：见解析．【分析】先求出立方根，再根据整数、负分数、正有理数、无理数的定义即可得．【详解】3=-，13．求下列各式中x 的值（1）21(1)64x +-=；（2）3(1)125x -=．（1）；（2）【分析】（1）方程整理后利用平方根的性质开平方即可求解；（2）方程直接利用立方根的性质开立方即可求解；【详解】（1）解得：或；（2）解得：【点睛】本题主要考查解方程涉及到立方根平方根解解析：（1）132x =，272x =-；（2）6x = 【分析】（1）方程整理后，利用平方根的性质开平方即可求解；（2）方程直接利用立方根的性质开立方即可求解；【详解】（1）21(1)64x +-= 225(1)4x += 512x +=± 解得：32x =或72x =-；（2）3(1)125x -=15x -=解得：6x =．【点睛】本题主要考查解方程，涉及到立方根、平方根，解题的关键是熟练掌握开平方、开立方根的方法．14．定义：如果将一个正整数a 写在每一个正整数的右边，所得到的新的正整数能被a 整除，则这个正整数a 称为“魔术数”．例如：将2写在1的右边得到12，写在2的右边得到22，……，所得到的新的正整数的个位数字均为2，即为偶数，由于偶数能被2整除，所以2是“魔术数”．根据定义，在正整数3，4，5中，“魔术数”为____________；若“魔术数”是一个两位数，我们可设这个两位数的“魔术数”为x ，将这个数写在正整数n 的右边，得到的新的正整数可表示为()100n x +，请你找出所有的两位数中的“魔术数”是_____________．10202550【分析】①由魔术数的定义分别对345三个数进行判断即可得到5为魔术数；②由题意根据魔术数的定义通过分析即可得到答案【详解】解：根据题意①把3写在1的右边得13由于13不能被3整除故3 解析：10、20、25、50．【分析】①由“魔术数”的定义，分别对3、4、5三个数进行判断，即可得到5为“魔术数”； ②由题意，根据“魔术数”的定义通过分析，即可得到答案．【详解】解：根据题意，①把3写在1的右边，得13，由于13不能被3整除，故3不是魔术数；把4写在1的右边，得14，由于14不能被4整除，故4不是魔术数；把5写在1的右边，得15，写在2的右边得25，……由于个位上是5的数都能被5整除，故5是魔术数；故答案为：5；②根据题意，这个两位数的“魔术数”为x ，则1001001n x n x x+=+， ∴100n x为整数， ∵n 为整数， ∴100x为整数， ∴x 的可能值为：10、20、25、50；故答案为：10、20、25、50．【点睛】本题考查了新定义的应用和整数的特点，解题的关键是熟练掌握新定义进行解题．15．已知5的整数部分为a ，5-b ，则2ab b +=_________．【分析】求出的大小推出7＜＜8求出a 同理求出求出b 代入求出即可【详解】解：∵∴∴∴∴故答案为：【点睛】此题考查了无理数的大小的应用关键是确定和的范围解析：37-【分析】的大小，推出7＜5＜8，求出a ，同理求出253<-<，求出b ，代入求出即可．【详解】解：∵479<<， ∴23<<，32-<<- ∴758<+<，253<-<，∴7a =，523b =--=-，∴()(237337ab b b a b +=+=+=-．故答案为：37-【点睛】此题考查了无理数的大小的应用，关键是确定5和5-16．一个正数的两个平方根分别为27a -与34a -+，则这个正数为_______．169【分析】根据一个正数的两个平方根互为相反数求出a 的值就可以算出这个正数【详解】解：解得∴这个正数是故答案是：169【点睛】本题考查平方根解题的关键是掌握平方根的性质解析：169【分析】根据一个正数的两个平方根互为相反数，求出a 的值，就可以算出这个正数．【详解】解：()27340a a -+-+=，解得3a =-，()23713⨯--=-，∴这个正数是()213169-=．故答案是：169．【点睛】本题考查平方根，解题的关键是掌握平方根的性质．17．定义一种新运算；观察下列各式；131437=⨯+=()3134111-=⨯-=5454424=⨯+= ()4344313-=⨯-=（1）请你想一想：ab = ；（2）若a b ，那么a b b a （填“=”或“≠” ）；（3）先化简，再求值：()()2a b a b -+，其中1a =-，2b =．（1）4a+b ；（2）；（3）6a-3b-12【分析】（1）观察得到新运算等于第一个数乘以4加上第二个数据此列式即可；（2）根据新运算分别计算出与即可得到答案；（3）根据新运算分别化简再将ab 的值代解析：（1）4a+b ；（2）≠；（3）6a-3b ，-12【分析】（1）观察得到新运算等于第一个数乘以4，加上第二个数，据此列式即可；（2）根据新运算分别计算出a b 与b a 即可得到答案；（3）根据新运算分别化简再将a 、b 的值代入计算．【详解】（1）ab =4a+b ，故答案为：4a+b ；（2）a b =4a+b ，b a =4b+a ， ∵a b ， ∴a b ≠b a ，故答案为：≠；（3）()()2a b a b -+ =4（a-b ）+（2a+b ）=4a-4b+2a+b=6a-3b ，当1a =-，2b =时，原式=-6-6=-12．【点睛】此题考查新定义运算，整式的加减混合运算，正确理解新定义的运算规律并解决问题是解题的关键．18．若求若干个相同的不为零的有理数的除法运算叫做除方，如()()()()2223333÷÷-÷-÷-÷-，等。

人教版七年级实数知识点总结和压轴题练习(附答案解析)

初一实数所有知识点总结和常考题知识点：一、实数的概念及分类1、实数的分类正有理数有理数零有限小数和无限循环小数实数负有理数正无理数无理数无限不循环小数负无理数整数包括正整数、零、负整数。

正整数又叫自然数。

正整数、零、负整数、正分数、负分数统称为有理数。

2、无理数在理解无理数时，要抓住“无限不循环”这一时之，归纳起来有四类：（1）开方开不尽的数，如32,7等；（2）有特定意义的数，如圆周率π，或化简后含有π的数，如3π+8等；（3）有特定结构的数，如0.1010010001…等；二、实数的倒数、相反数和绝对值1、相反数实数与它的相反数时一对数（只有符号不同的两个数叫做互为相反数，零的相反数是零），从数轴上看，互为相反数的两个数所对应的点关于原点对称，如果a 与b 互为相反数，则有a+b=0，a=—b ，反之亦成立。

2、绝对值一个数的绝对值就是表示这个数的点与原点的距离，|a|≥0。

零的绝对值时它本身，也可看成它的相反数，若|a|=a ，则a≥0；若|a|=-a ，则a≤0。

正数大于零，负数小于零，正数大于一切负数，两个负数，绝对值大的反而小。

3、倒数如果a 与b 互为倒数，则有ab=1，反之亦成立。

倒数等于本身的数是1和-1。

零没有倒数。

4. 实数与数轴上点的关系：每一个无理数都可以用数轴上的一个点表示出来，数轴上的点有些表示有理数，有些表示无理数，实数与数轴上的点就是一一对应的，即每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都是表示一个实数。

三、平方根、算数平方根和立方根1、平方根（1）平方根的定义：如果一个数x 的平方等于a ，那么这个数x 就叫做a 的平方根．即：如果a x 2，那么x 叫做a 的平方根．（2）开平方的定义：求一个数的平方根的运算，叫做开平方．开平方运算的被开方数必须是非负数才有意义。

（3）平方与开平方互为逆运算：±3的平方等于9，9的平方根是±3（4）一个正数有两个平方根，即正数进行开平方运算有两个结果；一个负数没有平方根，即负数不能进行开平方运算（5）符号：正数a 的正的平方根可用a 表示，a 也是a 的算术平方根；正数a 的负的平方根可用-a 表示．（6）a x =2 <—> a x ±=a 是x 的平方 x 的平方是ax 是a 的平方根 a 的平方根是x2、算术平方根（1）算术平方根的定义：一般地，如果一个正数x 的平方等于a ，即a x =2，那么这个正数x 叫做a 的算术平方根．a 的算术平方根记为a ，读作“根号a”，a 叫做被开方数．规定：0的算术平方根是0.也就是，在等式a x =2 (x≥0)中，规定a x =。

数学人教版七年级下册实数全章复习

实数复习课教学目的：通过复习，使学生对本章的知识能得到熟练、巩固，并能灵活地运用实数知识去解决问题。

教学重点：熟练灵活运用有关的知识解决问题。

教学难点：熟练灵活运用有关的知识解决问题。

教学过程：一、知识框架平方根： 1、算术平方根：一个正数x 的平方等于a ，则正数x 叫做a 的算术平方根，记作2、平方根：一个数x 的平方等于a ，那么x 叫做a的平方根，记做3、求一个数的平方根的运算叫做数的开方 4、算术平方根与平方根的比较：立方根：1、一个数x 的立方等于a ，那么x 叫做a 的立方根2、一个正数的立方根是正数，一个负数的立方根是负数，0的立方根是0。

⎧⎧⎫⎨⎬⎪⎨⎩⎭⎪→⎩整数有理数有限小数或无限循环小数实数分数无理数无限不循环小数二、练习（一）、选择题： 1、在实数70107.081221.03、、、、－。

π中，其中无理数的个数为（）A 、1B 、2C 、3D 、4 2、16的算术平方根为（）A 、4B 、4±C 、2D 、2± 3、下列语句中，正确的是（）A 、无理数都是无限小数B 、无限小数都是无理数C 、带根号的数都是无理数D 、不带根号的数都是无理数 4、若a 为实数，则下列式子中一定是负数的是（） A 、2a - B 、2)1(+-a C 、2a -D 、)1(+--a5、下列说法中，正确的个数是（）（1）－64的立方根是－4；（2）49的算术平方根是7±；（3）271的立方根为31；（4）41是161的平方根。

A 、1B 、2C 、3D 、4 6. 估算728-的值在（）A. 7和8之间B. 6和7之间C. 3和4之间D. 2和3之间 7、下列说法中正确的是（）A 、若a 为实数，则0≥aB 、若a 为实数，则a 的倒数为a1C 、若y x 、为实数，且y x =，则y x =D 、若a 为实数，则02≥a8、若10<<x ，则x xx x 、、、12中，最小的数是（） A 、x B 、x1 C 、xD 、2x9、下列各组数中，不能作为一个三角形的三边长的是（）A 、1、1000、1000B 、2、3、5C 、222543、、D 、33364278、、（二）、填空题：1. 和数轴上的点一一对应.2. 若实数a b ，满足0a b a b +=，则________abab=． 3、如果2a =，3b =，那么2a b 的值等于． 4.有若干个数，依次记为123n a a a a ，，，，若112a =-，从第２个数起，每个数都等于1与它前面的那个数的差的倒数，则2005a =．5.比较大小：23- 0.02-；6. 如图，数轴上的两个点A B ，所表示的数分别是a b ，，在a b +，a b -，ab ，a b-中，是正数的有个．7.若3+x 是4的平方根，则=x ＿＿＿，若－8的立方根为1-y ，则y=________. 8、计算：2)4(3-+-ππ的结果是＿＿＿＿＿＿。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

《实数》全章复习与巩固（知识讲解）
【学习目标】
1.了解算术平方根、平方根、立方根的概念，会用根号表示数的平方根、立方根.
2.了解开方与乘方互为逆运算，会用平方运算求某些非负数的平方根，会用立方运算求某些数的立方根，会用计算器求平方根和立方根.
3.了解无理数和实数的概念，知道实数与数轴上的点一一对应，有序实数对与平面上的点一一对应；了解数的范围
由有理数扩大为实数后，概念、运算等的一致性及其发展变化.
4.能用有理数估计一个无理数的大致范围.
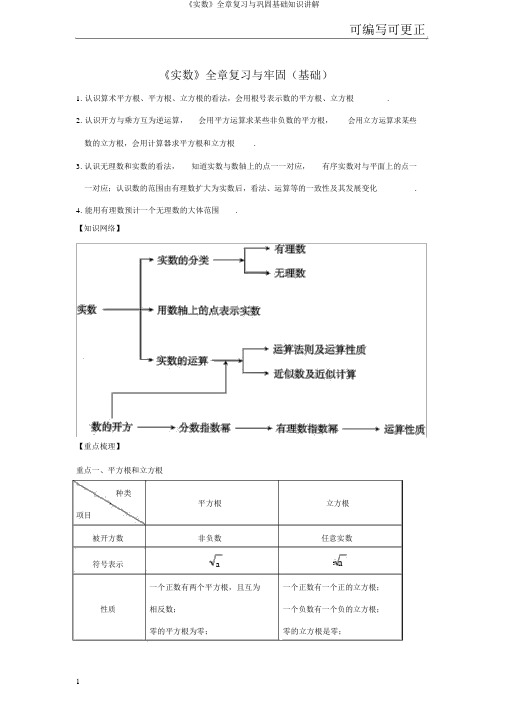
【知识网络】
【要点梳理】
要点一：平方根和立方根
要点二：实数
有理数和无理数统称为实数.
1.实数的分类
按定义分：
实数
按与0的大小关系分：
实数0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩
正有理数正数正无理数负有理数负数负无理数
要点诠释：（1）所有的实数分成三类：有限小数，无限循环小数，无限不循环小数．其中有限小数和无限循环
小数统称有理数，无限不循环小数叫做无理数．
（2
等；
②有特殊意义的数，如π；
③有特定结构的数，如0.1010010001…
（3）凡能写成无限不循环小数的数都是无理数，并且无理数不能写成分数形式.
（4）实数和数轴上点是一一对应的.
2.实数与数轴上的点一一对应.
数轴上的任何一个点都对应一个实数，反之任何一个实数都能在数轴上找到一个点与之对应.
3.实数的三个非负性及性质：
在实数范围内，正数和零统称为非负数。

我们已经学习过的非负数有如下三种形式：
（1）任何一个实数a 的绝对值是非负数，即|a |≥0；
（2）任何一个实数a 的平方是非负数，即≥0；
（3
().
非负数具有以下性质：
（1）非负数有最小值零；
（2）有限个非负数之和仍是非负数；
（3）几个非负数之和等于0，则每个非负数都等于0.
4.实数的运算： ⎧⎨⎩有理数：有限小数或无限循环小数
无理数：无限不循环小数2
a 0≥0a ≥
数a 的相反数是－a ；一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；0的绝对值是0. 有理数的运算法则和运算律在实数范围内仍然成立.实数混合运算的运算顺序：先乘方、开方、再乘除，最后算加减.同级运算按从左到右顺序进行，有括号先算括号里.
5.实数的大小的比较：
有理数大小的比较法则在实数范围内仍然成立.
法则1. 实数和数轴上的点一一对应，在数轴上表示的两个数，右边的数总比左边的数大；
法则2．正数大于0，0大于负数，正数大于一切负数，两个负数比较，绝对值大的反而小；
法则3. 两个数比较大小常见的方法有：求差法，求商法，倒数法，估算法，平方法.
【典型例题】
类型一、有关方根的问题
1、下列各式正确的是（）
A 7=-
B 3=±
C =
D 4=
【答案】D
举一反三：
【变式】如果m 有算术平方根，那么m 一定是（）
A ．正数
B ．0
C ．非负数
D ．非正数
【答案】C
2、观察下列各式，并用所得出的规律解决问题：
（1=1.414=14.14==0.1732=1.732=17.32…由此可见，被开方数的小数点每向右移动位，其算术平方根的小数点向移动位；
（2=2.236
7.071= ，= ；
（3=1=10=100…小数点变化的规律是：．
（4=2.154=4.642= ，= ．
【答案】（1）两，右，一；（2）0.7071，22.36；（3）被开方数的小数点向右（左）移三位，其立方根的小数点向右（左）移动一位；（4）21.54，﹣0.4642
类型二、与实数有关的问题 3、．把下列各数填入相应的集合中： 3.14，-2π，-917
，3100-， 0 ，1.212212221… ，3，0.151151115 无理数集合{ … }；
有理数集合{ … }；
非正数集合{ … }．【详解】由立方根的性质得：31000-<，
无理数集合{-2π
， 1.212212221…，…}；
有理数集合{3.14，0，0.151151115，… }；
非正数集合{-2π
，0，… }；
举一反三：
【变式】在实数0、π、、、﹣中，无理数的个数有（）
A ．1个
B ．2个
C ．3个
D ．4个
【答案】B ；
类型三、与实数有关计算
4、计算：
（1）⎛- ⎝；（2|1--
【答案】（1；（2）12-
解：（1）⎛ ⎝
=
；
（2|1--
=914+-
=12-举一反三：
【变式】计算：
（1）83237⎛⎫⨯-+ ⎪⎝⎭．（2
（3）221(12)332⎛⎫
-⨯-- ⎪⎝⎭．
【答案】（1）6
7；（2）4；（3）-11．
解：（1）8
3
237⎛
⎫
⨯-+ ⎪⎝⎭ =8
27-+ =6
7；
（2
+=-2+6
=4；
（3）22
1(12)332⎛⎫
-⨯-- ⎪⎝⎭ =1
(12)96-⨯-
=-2-9
=-11．
5、已知：（a+6）2+=0，则2b 2﹣4b ﹣a 的值为．
【答案】12．
解：∵（a+6）2+=0，
∵a+6=0，b 2﹣2b ﹣3=0，
解得，a=﹣6，b 2﹣2b=3，
可得2b 2﹣4b=6，
则2b 2﹣4b ﹣a=6﹣（﹣6）=12，
故答案为：12．
举一反三：
【变式1】实数a 、b 在数轴上所对应的点的位置如图所示：
化简＋∣a －b ∣＝ .
【答案】
2a
-1a 解：∵a ＜0＜b ,
∴a －b ＜0 ∴＋∣a －b ∣＝－a －(a －b )＝b －2a .
【变式2】实数在数轴上的位置如图所示，则的大小关系是：；
【答案】；类型四、实数综合应用
6、小燕在测量铅球的半径时，先将铅球完全浸没在一个带刻度的圆柱形小水桶中，拿出铅球时，小燕发现小水桶中的水面下降了1cm ，小燕量得小水桶的直径为12cm ，于是她就算出了铅球的半径．你知道她是如何计算的吗？请求出铅球的半径．（球的体积公式343
V r π=
，r 为球的半径．）【答案】3cm ．
【分析】设球的半径为r ，求出下降的水的体积，即圆柱形小水桶中下降的水的体积，最后根据球的体积公式列式求解即可．
解：设球的半径为r ，
小水桶的直径为12cm ，水面下降了1cm ， ∴小水桶的半径为6cm ，
∴下降的水的体积是π×62×1=36π(cm 3)，
即3
4363r ππ=，
解得：327r =，3r =，
答：铅球的半径是3cm ．
举一反三：
【变式】一个底为正方形的水池的容积是4863m ，池深1.5m ，求这个水池的底边长．
【答案】
解：设水池的底边长为x ，由题意得
答：这个水池的底边长为18m .
2a a 2,1,
,a a a a -21a a a a <<<-2 1.5486x ⨯=2324x =18x =。