将军饮马问题(讲)
八年级将军饮马问题例题讲解

八年级将军饮马问题例题讲解哎呀,今天咱们聊聊八年级的将军饮马问题,听名字就觉得特别有意思,对吧?咱们先来个开门见山,将军带着他的军队,经过一条河,得给马喝水。
这问题看似简单,但其实里面藏着不少小玄机,真的是个大考验,脑袋瓜得动一动。
想象一下,这将军带着一帮士兵,行军走到河边,嗨,口渴得不行,马儿们更是想喝水。
可是,问题来了,河边的水不深,能让马儿们喝到,但不让它们掉进水里。
将军一边心急如焚,一边得想办法。
怎么让这些马儿在喝水的时候不掉进河里呢?这时候就得用到一些小技巧了。
咱们可以想象一下,马儿们得排队,得一个一个地喝水。
将军心里想着,得控制好马儿的喝水速度,别让它们都挤在一起,这样容易出事。
也许能用一些方法,比如说把马儿们牵得远一些,慢慢地让它们喝,像是在参加比赛一样,嘿嘿,真是有意思的场景。
想想马儿们排成一队,乖乖的,一个个慢慢走过来喝水,真是可爱。
这时候就得算一算了,马儿们得喝多少水,每匹马喝水的速度又有多快。
嘿,可能是三两口就满足了,也可能是急着想喝个痛快,一口气喝个干净。
将军得根据情况来调整策略,真是够麻烦的。
不过,思来想去,最好的办法还是得让马儿们分批来,排着队,井然有序。
然后,咱们再来想象一下,如果马儿们不听话,乱跑,那可就麻烦了。
想象一下将军那个急得直挠头的样子,心里想着:这马儿也太不听话了!要不就得用点小办法,比如说放一块香饽饽在河边,吸引它们过来,嘿嘿,果然,马儿们就乖乖走过来喝水了。
就像小朋友看到喜欢的玩具一样,立马就冲过去了,真是太可爱了。
接着咱们来讨论一下,假设这条河不宽,马儿们很快就能喝到水,那将军得加快速度,不能让马儿们等太久。
想想那画面,马儿们都急得不行,口水都快流下来了,哈哈,真是个搞笑的场景。
将军这时候就得使出浑身解数,调整路线,确保马儿们能尽快喝水。
但是,事情总是没那么简单。
马儿喝水喝得急,可能还会打架,踩到脚,这可就不好了。
所以,将军得一边指挥,一边安抚,真是一场心力交瘁的战斗。
将军饮马(最完整讲义)
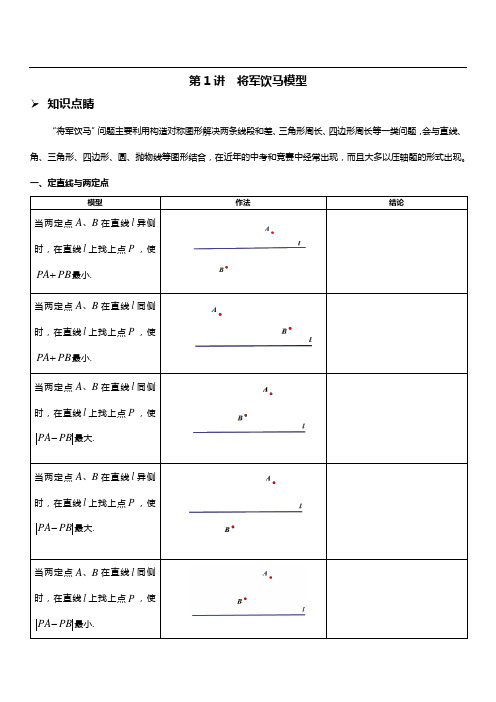
第1讲将军饮马模型➢知识点睛“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞赛中经常出现,而且大多以压轴题的形式出现。
一、定直线与两定点模型作法结论A、在直线l异侧当两定点B时,在直线l上找上点P,使PA+最小.PBA、在直线l同侧当两定点B时,在直线l上找上点P,使PA+最小.PBA、在直线l同侧当两定点B时,在直线l上找上点P,使PA-最大.PBA、在直线l异侧当两定点B时,在直线l上找上点P,使PA-最大.PBA、在直线l同侧当两定点B时,在直线l上找上点P,使PA-最小.PB二、角到定点模型作法结论点P 在AOB ∠的内部,在OA 上找一点M ,在OB 上找一点N ,使得PCD ∆周长最小.点P 在AOB ∠的内部,在OA 上找一点M ,在OB 上找一点N ,使得MN PN +最小.点Q P 、在AOB ∠的内部,在OA 上找一点M ,在OB 上找一点N ,使得四边形PMNQ 周长最小.点M 在AOB ∠的外部,在射线OA 上找一点P ,使PM 与点P 到射线OB 的距离和最小.点M 在AOB ∠的内部,在射线OA 上找一点P ,使PM 与点P 到射线OB 的距离和最小.点Q P 、分别在AOB ∠的边OB OA 、是,在OA 上找一点M ,在OB 上找一点N ,使得MQ MN PN ++最小.二、两定点一定长模型作法结论如图在直线l 上找上两点N M 、(M 在左),使NB MN AM ++最小,且d MN =.如图,21//l l ,21l l 、之间的距离为d ,在21l l 、上分别找N M 、两点,使1l MN ⊥,且NB MN AM ++最小.如图,21//l l ,43//l l ,21l l 、之间的距离为1d ,43//l l 之间的距离为2d ,在21l l 、上分别找N M 、两点,使1l MN ⊥,在43l l 、上分别找Q P 、两点,使3l PQ ⊥且QB PQ NP MN AM ++++最小.如图,在⊙O 上找一点N ,在直线l 找一点M ,使得MN AM +最小.➢ 精讲精练例1:如图,点P 是∠AOB 内任意一点,∠AOB =30°,OP =8,点M 和点N 分别是射线OA 和射线OB 上的动点,则△PMN 周长的最小值.P OBAMN例2:如图,正方形ABCD 的边长是4,M 在DC 上,且DM =1, N 是AC 边上的一动点,则△DMN 周长的最小值.例3:如图,在Rt △ABO 中,∠OBA =90°,A (4,4),点C 在边AB 上,且AC :CB =1:3,点D 为OB 的中点,点P 为边OA 上的动点,当点P 在OA 上移动时,使四边形PDBC 周长最小的点P 的坐标为( )A .(2,2)B .5(2,5)2C .8(3,8)3D .(3,3)第3题图 第4题图 第5题图例4:如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB 上的动点,则PC +PD 的最小值为( ) A .4B .5C .6D .7例5:如图,在等边△ABC 中,AB =6, N 为AB 上一点且BN =2AN , BC 的高线AD 交BC 于点D ,M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值是___________. PDCBAA BCDMNNMDCBA例6:如图,在Rt △ABD 中,AB =6,∠BAD =30°,∠D =90°,N 为AB 上一点且BN =2AN , M 是AD 上的动点,连结BM ,MN ,则BM +MN 的最小值.例7:如图,在Rt △ABC 中,∠ACB =90°,AC =6.AB =12,AD 平分∠CAB ,点F 是AC 的中点,点E 是AD 上的动点,则CE +EF 的最小值为( ) A .3 B .4 C . D .第7题图 第8题图 第9题图例8:如图,在锐角三角形ABC 中,BC =4,∠ABC =60°, BD 平分∠ABC ,交AC 于点D ,M 、N 分别是BD ,BC 上的动点,则CM +MN 的最小值是( ) A B .2 C .D .4例9:如图,在菱形ABCD 中,AC =BD =6,E 是BC 的中点,P 、M 分别是AC 、AB 上的动点,连接PE 、PM ,则PE +PM 的最小值是( ) A .6B .C .D .4.5NMDBA E AFCDBNM DCBAEPDCBAM例10:如图,矩形ABOC 的顶点A 的坐标为(-4,5),D 是OB 的中点,E 是OC 上的一点,当△ADE 的周长最小时,点E 的坐标是( ) A .4(0,)3B .5(0,)3C .(0,2)D .10(0,)3第10题图 第11题图 第12题图例11:如图,在矩形ABCD 中,AB =6,AD =3,动点P 满足13PAB ABCD S S ∆=矩形,则点P 到A 、B 两点距离之和PA +PB 的最小值为( ) A .B .C .D 例12:如图,矩形ABCD 中,AB =10,BC =5,点E 、F 、G 、H 分别在矩形ABCD 各边上,且AE =CG ,BF =DH ,则四边形EFGH 周长的最小值为( )A .B .C .D .例13:如图,∠AOB =60°,点P 是∠AOB 内的定点且OP M 、N 分别是射线OA 、OB 上异于点O 的动点,则△PMN 周长的最小值是( )A B C .6D .3第13题图 第14题图 CBH FGEDCB AA BMOPN例14:如图,∠AOB 的边OB 与x 轴正半轴重合,点P 是OA 上的一动点,点N (3,0)是OB 上的一定点,点M 是ON 的中点,∠AOB =30°,要使PM +PN 最小,则点P 的坐标为 .例15:如图,已知正比例函数y =kx (k >0)的图像与x 轴相交所成的锐角为70°,定点A 的坐标为(0,4),P 为y 轴上的一个动点,M 、N 为函数y =kx (k >0)的图像上的两个动点,则AM +MP +PN 的最小值为___________.第15题图例16:如图,在平面直角坐标系中,矩形ABCD 的顶点B 在原点,点A 、C 在坐标轴上,点D 的坐标为(6,4),E 为CD 的中点,点P 、Q 为BC 边上两个动点,且PQ =2,要使四边形APQE 的周长最小,则点P 的坐示应为______________.例17:如图,矩形ABCD 中,AD =2,AB =4,AC 为对角线,E 、F 分别为边AB 、CD 上的动点,且EF ⊥AC 于点M ,连接AF 、CE ,求AF +CE 的最小值.AB CD EFMx例18:如图,正方形ABCD 的面积是12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,求PD+PE 的最小值。
将军饮马(最完整讲义)

第1讲将军饮马模型➢知识点睛一、“将军饮马”问题主要利用构造对称图形解决两条线段和差、三角形周长、四边形周长等一类问题, 会与直线、角、三角形、四边形、圆、抛物线等图形结合, 在近年的中考和竞赛中经常出现, 而且大多以压轴题的形式出现。
二、定直线与两定点模型作法结论当两定点在直线异侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最小.当两定点在直线同侧时, 在直线上找上点, 使最大.当两定点在直线异侧时, 在直线上找上点, 使最大.当两定点在直线同侧时, 在直线上找上点, 使最小.二、角到定点模型作法结论点在的内部, 在上找一点, 在上找一点,使得周长最小.点在的内部, 在上找一点, 在上找一点,使得最小.点在的内部, 在上找一点, 在上找一点,使得四边形周长最小.点在的外部, 在射线上找一点, 使与点到射线的距离和最小.点在的内部, 在射线上找一点, 使与点到射线的距离和最小.点分别在的边是, 在上找一点, 在上找一点,使得最小.三、两定点一定长模型作法结论如图在直线上找上两点(在左), 使最小,且.如图, , 之间的距离为, 在上分别找两点, 使, 且最小.如图, , ,之间的距离为, 之间的距离为, 在上分别找两点, 使, 在上分别找两点, 使且最小.如图, 在⊙上找一点, 在直线找一点,使得最小.➢精讲精练例1: 如图, 点P是∠AOB内任意一点, ∠AOB=30°, OP=8, 点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值.例2: 如图, 正方形ABCD 的边长是4, M 在DC 上, 且DM=1, N 是AC 边上的一动点, 则△DMN 周长的最小值.A .例3: 如图, 在Rt △ABO 中, ∠OBA=90°, A (4,4), 点C 在边AB 上, 且AC:CB=1:3, 点D 为OB 的中点, 点P 为边OA 上的动点, 当点P 在OA 上移动时, 使四边形PDBC 周长最小的点P 的坐标为 B. ,C .,D .第3题图 第4题图 第5题图例4: 如图, 在△ABC 中, AC=BC, ∠ACB=90°, 点D 在BC 上, BD=3, DC=1, 点P 是AB 上的动点, 则PC+PD 的最小值为 A. 4 B. 5 C. 6 D. 7例5:如图, 在等边△ABC 中, AB=6, N 为AB 上一点且BN=2AN, BC 的高线AD 交BC 于点D, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值是___________.A BCDMN例6: 如图, 在Rt △ABD 中, AB=6, ∠BAD=30°, ∠D=90°, N 为AB 上一点且BN=2AN, M 是AD 上的动点, 连结BM, MN, 则BM+MN 的最小值.例7: 如图, 在Rt △ABC 中, ∠ACB=90°, AC=6. AB=12, AD 平分∠CAB, 点F 是AC 的中点, 点E 是AD 上的动点, 则CE+EF 的最小值为 A. 3 B. 4 C.D.第7题图 第8题图 第9题图A .例8: 如图, 在锐角三角形ABC 中, BC=4, ∠ABC=60°, BD 平分∠ABC, 交AC 于点D, M 、N 分别是BD, BC 上的动点, 则CM+MN 的最小值是B. 2C.D. 4例9: 如图, 在菱形ABCD 中, AC=, BD=6, E 是BC 的中点, P 、M 分别是AC.AB 上的动点, 连接PE 、PM, 则PE+PM 的最小值是A. 6B.C.D. 4.5E AFCDBNM DCBAEPDCBAMA .例10: 如图, 矩形ABOC 的顶点A 的坐标为(-4,5), D 是OB 的中点, E 是OC 上的一点, 当△ADE 的周长最小时, 点E 的坐标是B. C. D.第10题图 第11题图 第12题图例11: 如图, 在矩形ABCD 中, AB=6, AD=3, 动点P 满足, 则点P 到A.B 两点距离之和PA+PB 的最小值为A. B. C. D.例12: 如图, 矩形ABCD 中, AB=10, BC=5, 点E 、F 、G 、H 分别在矩形ABCD 各边上, 且AE=CG, BF=DH, 则四边形EFGH 周长的最小值为A. B. C. D.例13: 如图, ∠AOB=60°, 点P 是∠AOB 内的定点且OP=, 若点M 、N 分别是射线OA.OB 上异于点O 的动点, 则△PMN 周长的最小值是A. B. C. 6 D. 3第13题图 第14题图CBH FGEDCB AABMOPN例14: 如图, ∠AOB 的边OB 与x 轴正半轴重合, 点P 是OA 上的一动点, 点N (3,0)是OB 上的一定点, 点M 是ON 的中点, ∠AOB=30°, 要使PM+PN 最小, 则点P 的坐标为 .例15:如图, 已知正比例函数y=kx (k>0)的图像与x 轴相交所成的锐角为70°, 定点A 的坐标为(0, 4), P 为y 轴上的一个动点, M 、N 为函数y=kx (k>0)的图像上的两个动点, 则AM+MP+PN 的最小值为___________.第15题图例16: 如图, 在平面直角坐标系中, 矩形ABCD 的顶点B 在原点, 点A.C 在坐标轴上, 点D 的坐标为(6, 4), E 为CD 的中点, 点P 、Q 为BC 边上两个动点, 且PQ=2, 要使四边形APQE 的周长最小, 则点P 的坐示应为______________.例17:如图, 矩形ABCD 中, AD=2, AB=4, AC 为对角线, E 、F 分别为边AB 、CD 上的动点, 且EF ⊥AC 于点M,连接AF 、CE, 求AF+CE 的最小值.x例18: 如图, 正方形ABCD的面积是12, △ABE是等边三角形, 点E在正方形ABCD内, 在对角线AC上有一点P, 求PD+PE的最小值。
专题07 最值模型之将军饮马精讲练(11大模型)(解析版)

专题07最值模型之将军饮马精讲练(11大模型)学校:___________姓名:___________班级:___________考号:___________模型背景【模型来历】早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.【考点】两点之间线段最短,垂线段最短;三角形两边三边关系;轴对称;平行四边形--平移;【解题思路】学会化归,移花接木,化折为直【核心思想】共线与垂线段最短。
模型精讲一、两动一定型(2种模型):两定点到直线上一动点的距离和最小。
例1-1:如图1-1在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB最小.【证明】图1-2。
PA+PB的最小值即为线段AB的长度理由:在l上任取异于点P的一点P´,连接AP´、BP´,在△ABP’中,AP´+BP´>AB,即AP´+BP´>AP+BP ∴P为直线AB与直线l的交点时,PA+PB最小.图1-2lPABP'lAB图1-1反思:解决本题很简单,但却点明了将军饮马的解题思路。
【变式】例1-2 如图1-3,如图,定点A 和定点B 在定直线l 的同侧 要求:在直线l 上找一点P ,使得PA+PB 值最小 。
作法:图1-41.作A 关于直线CD 对称点A’。
2.连A’B 。
3.交点P 就是要求点。
连线长A’B 就是PA+PB 最小值。
【证明】:图1-5在l 上任取异于点P 的一点P´,连接AP´、BP´, 在△ABP’中,AP´+BP´>AB ,即AP´+BP´>AP+BP ∴P 为直线AB 与直线l 的交点时,PA+PB 最小.二、造桥选址,移花接木。
华东师大版八年级数学下册“将军饮马模型”专题讲义及解析

华东师大版八年级数学下册“将军饮马模型”专题讲义及解析华东师大版八年级数学下册“将军饮马模型”专题讲义及解析一、背景知识:据传说,古罗马时代有一位名叫XXX的学者,他精通数学和物理。
有一天,一位罗马将军前来请教他一个难题:每天他从军营A出发,先到河边饮马,然后再去河岸同侧的军营B开会,应该怎样走才能使路程最短?这个问题被称为“将军饮马”问题,据说XXX很快解决了它,从此这个问题流传至今。
二、将军饮马问题常见模型1.两定一动型:两个定点到一个动点的距离和最小例1:在一条定直线l上找一个动点P,使动点P到两个定点A和B的距离之和最小,即PA+PB最小。
作法:连接AB,与直线l的交点Q即为所求点,当动点P跑到点Q处时,PA+PB最小,且最小值等于AB。
原理:两点之间线段最短。
证明:连接AB,与直线l的交点Q,P为直线l上任意一点,在三角形PAB中,由三边关系可知:AP+PB≧AB(当且仅当PQ重合时取等)。
例2:在一条定直线l上找一个动点P,使动点P到两个定点A和B的距离之和最小,即PA+PB的和最小。
关键:找对称点。
作法:作定点B关于定直线l的对称点C,连接AC,与直线l的交点Q即为所求点,当动点P跑到点Q处时,PA+PB和最小,且最小值等于AC。
原理:两点之间,线段最短。
证明:连接AC,与直线l的交点Q,P为直线l上任意一点,在三角形PAC中,由三边关系可知:AP+PC≧AC(当且仅当PQ重合时取等)。
2.两动一定型例3:在∠XXX的内部有一点A,在OM上找一点B,在ON上找一点C,使得△BAC周长最短。
作法:作点A关于OM的对称点A’,作点A关于ON的对称点A’’,连接A’ A’’,与OM交于点B,与ON交于点C,连接AB,AC,△XXX即为所求。
原理:两点之间,线段最短。
例4:在∠XXX的内部有点A和点B,在OM上找一点C,在ON上找一点D,使得四边形ABCD周长最短。
作法:首先,我们作点A关于OM的对称点A',作点B关于ON的对称点B',然后连接A'B',交OM于点C,交ON于点D,最后连接AC和BD,四边形ABCD即为所求。
将军饮马专题ppt课件

第8题图
返回
1 综合训练
1. 如图,在矩形ABCD中,AB=2,AD=1,点E为AB的中点,M、N是CD上的两 动点,且MN=1,则EM+EN的最小值为____。
1 综合训练
2. 如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个 动点,则下列线段的长等于AP+EP最小值的是 ____。
之
间
,
线
段
最
短
2
用模型战试题
每一个试题都是模型,每一种模型都有方法
综合训练
针对训练1
2
1. 如图,等边△ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AB 边上一点,且AE=2,则线段EF+CF的最小值为( B ) A. 3 B. 2 3 C. 2 D. 2
第1题图
返回
2 针对训练2
两动一定型 2
例7
在∠MON的内部 有一点A,在OM上找 一点B,在ON上找一 点C,使得△BAC周长
最短.
在 OM上找一点C,在 ON上找一点D,使 得四边形ABCD周 长最短.
例9
在∠MON的内部 有一点A,在OM上 找一点B,在ON上 找一点C,使得AB +BC最短.
【传说】
早在古罗马时代,传说亚历山大城有一位精通数学 和物理的学者,名叫海伦.一天,一位罗马将军专程 去拜访他,向他请教一个百思不得其解的问题.
将军每天从军营A出发,先到河边饮马,然后再去 河岸同侧的军营B开会,应该怎样走才能使路程最短 ?这个问题的答案并不难,据说海伦略加思索就解决 了它.
从此以后,这个被称为“将军饮马”的问题便流传至 今.
A. 3 B. 2 3 C. 3 1 D. 3 2
将军饮马讲解

对“连”口诀最短路径问题
最短路径知识点三 ③双定双动:对“连”口诀:先对称后平移(先平移后对称),连接出最短 方法一:先对称后平移
技巧:作对称(同侧变异侧)---对称点平移定长线段(“一定两动”化“两定一动”)---连接两定点--动点反向平移定长线段---连接所得点.
对“连”口诀最短路径问题
最短路径知识点三 ③双定双动:对“连”口诀:先对称后平移(先平移后对称),连接出最短 方法二:先平移后对称
∴BC+AC = B’C+AC = B’A.
∴BC ’ +AC ’ = B’C ’ +AC ’
在△AB ’ C’中,AB ’ <C < BC ’ +AC ’ ,即AC+BC最小.
知识点
对“连”口诀 横批:对 勾 模 型
对
如图,在I上找一点P,使PA+PB最小
连
称
接
一
出
定
最
点
短
对“连”口诀最短路径问题
最短路径必考高频三大类型 ①双定单动:对“连”口诀:对称1动点,连接出最短 ②单定双动:对“连”口诀:双对称此定点,连接出最短 ③双定双动:对“连”口诀:先对称后平移(先平移后对称),连接出最短
对“连”口诀最短路径问题
最短路径必考知识点一 ①双定单动:对“连”口诀:对称1动点,连接出最短
定点双 对 称
连 接出最短
关键点:动点所在的直线为对称轴
对“连”口诀最短路径问题
最短路径知识点三 ③双定双动:对“连”口诀:先对称后平移(先平移后对称),连接出最短
问题:本题拓展为在直线l上找两个动点P、Q(PQ两动点间距离为定值),使得AP+PQ+BQ 的距离之和最短,又该如何处理呢?(“两动一定型”)
将军饮马问题讲义

将军饮马问题之阳早格格创做唐往诗人李颀的诗《古从军止》启头二句道:"黑日登山视烽火,薄暮饮马傍接河."诗中隐含着一个有趣的数教问题.如图所示,诗中将军正在瞅视烽火之后从山足下的A面出收,走到河边饮马后再到B面宿营.请问何如走才搞使总的路途最短?那个问题早正在古罗马时代便有了,传道亚历山大乡有一位粗通数教战物理的教者,名喊海伦.一天,一位罗马将军博程去考察他,背他请教一个百思不得其解的问题.将军每天从军营A出收,先到河边饮马,而后再去河岸共侧的B天启会,该当何如走才搞使路途最短?今后,那个被称为"将军饮马"的问题广大流传.将军饮马问题=轴对于称问题=最短距离问题(轴对于称是工具,最短距离是题眼).所谓轴对于称是工具,即那类问题最时常使用的搞法便是做轴对于称.而最短距离是题眼,也便表示着归类那类的题手段缘由.比圆题目时常会出现线段a+b 那样的条件大概者问题.一往出现不妨赶快偶像到将军问题,而后利用轴对于称解题.一.六大模型1.如图,曲线l 战l 的同侧二面A、B,正在曲线l 上供做一面P,使PA+PB 最小.2.如图,曲线l 战l 的共侧二面A、B,正在曲线l 上供做一面P,使PA+PB 最小.3.如图,面P 是∠MON 内的一面,分别正在OM,ON 上做面A,B.使△PAB 的周少最小.4.如图,面P,Q 为∠MON 内的二面,分别正在OM,ON 上做面A,B.使四边形PAQB 的周少最小.5.如图,面A 是∠MON 中的一面,正在射线ON 上做面P,使PA 取面P 到射线OM 的距离之战最小6. .如图,面A 是∠MON 内的一面,正在射线ON 上做面P,使PA 取面P 到射线OM 的距离之战最小罕睹问题最先明黑几个观念,动面、定面、对于称面.动面普遍便是题目中的所供面,即那个大概的面.定面即为题目中牢固的面.对于称的面,做图所得的面,需要连线的面.1. 怎么对于称,做谁的对于称?.简朴道所有题目需要做对于称的面,皆是题手段定面.大概者道惟有定面才不妨去做对于称的.(不决定的面做对于称式不意思的)那么做谁的对于称面?最先要粗确闭于对于称的对于象肯定是一条线,而不是一个面.那么是哪一条线?普遍而止皆是动面天圆曲线.2. 对于称完以去战谁对接?一句话:战其余一个定面贯串.千万于不克不迭战一个动面贯串.粗确一个观念:定面的对于称面也是一个定面.比圆模型二战模型三.3. 所供面怎么决定?最先一定要明黑,所供面末尾反应正在图上一定是个接面.本量便是咱们所绘曲线战已知曲线的接面.底下咱们去瞅瞅将军饮马取二次函数分离的问题:1.如图,扔物线y=ax2+bx+c通过A(1,0)、B(4,0)、C(0,3)三面.(1)供扔物线的剖析式;(2)如图,正在扔物线的对于称轴上是可存留面P,使得四边形PAOC的周少最小?若存留,供出四边形PAOC周少的最小值;若不存留,请证明缘由.【分解】(1)设接面式为y=a(x﹣1)(x﹣4),而后把C面坐标代进供出a=,于是得到扔物线剖析式为y=x2﹣x+3;(2)先决定扔物线的对于称轴为曲线x=,连结BC接曲线x=于面P,如图,利用对于称性得到PA=PB,所以PA+PC=PC+PB=BC,根据二面之间线段最短得到PC+PA最短,于是可推断此时四边形PAOC的周少最小,而后估计出BC=5,再估计OC+OA+BC即可.【解问】解:(1)设扔物线剖析式为y=a(x﹣1)(x﹣4),把C(0,3)代进得a•(﹣1)•(﹣4)=3,解得a=,所以扔物线剖析式为y=(x﹣1)(x﹣4),即y=x2﹣x+3;(2)存留.果为A(1,0)、B(4,0),所以扔物线的对于称轴为曲线x=,连结BC接曲线x=于面P,如图,则PA=PB,PA+PC=PC+PB=BC,此时PC+PA最短,所以此时四边形PAOC的周少最小,果为BC==5,所以四边形PAOC周少的最小值为3+1+5=9.【面评】原题考查了待定系数法供二次函数的剖析式:正在利用待定系数法供二次函数闭系式时,要根据题目给定的条件,采用妥当的要领设出闭系式,进而代进数值供解.普遍天,当已知扔物线上三面时,常采用普遍式,用待定系数法列三元一次圆程组去供解;当已知扔物线的顶面大概对于称轴时,常设其剖析式为顶面式去供解;当已知扔物线取x轴有二个接面时,可采用设其剖析式为接面式去供解.也考查了最短路径问题.2.(2015•上乡区一模)设扔物线y=(x+1)(x﹣2)取x轴接于A、C二面(面A正在面C的左边),取y轴接于面B.(1)供A、B、C三面的坐标;(2)已知面D正在坐标仄里内,△ABD是顶角为120°的等腰三角形,供面D的坐标;(3)若面P、Q位于扔物线的对于称轴上,且PQ=,供四边形ABQP周少的最小值.【考面】二次函数概括题.【分解】(1)令x=0,供出取y轴的坐标;令y=0,供出取x 轴的坐标;(2)分三种情况计划:①当AB为底时,若面D正在AB上圆;若面D正在AB下圆;②当AB为腰时,A为顶面时,③当AB为腰时,A为顶面时;小心解问即可.(3)当AP+BQ最小时,四边形ABQP的周少最小,根据轴对于称最短路径问题解问.【解问】解:(1)当x=0时,y=﹣;当y=0时,x=﹣1大概x=2;则A(﹣1,0),B(0,﹣),C(2,0);(2)如图,Rt△ABO中,OA=1,OB=,∴AB=2,∠ABO=30°,∠BAO=60°,∴△ABD是顶角为120°的等腰三角形.①当AB为底时,若面D正在AB上圆,由∠ABO=∠BAD=30°,AB=2,得D1(0,﹣),若面D正在AB下圆,由∠BAD=∠DBA=30°,AB=2,得D2(﹣1,﹣),②当AB为腰时,A为顶面时,∵∠DAB=120°,∠OAB=60°,AD=AB=2,∴面D正在y轴大概x轴上,若D正在y轴上,得D3(0,),若D正在x轴上,得D4(﹣3,0);③当AB为腰时,A为顶面时,若面D正在第三象限,∵∠DBO=150°,BD=2,得D5(﹣1,﹣2);若面D正在第四象限时,∵DB∥x轴,BD=2,得D6(2,﹣),∴切合央供的面D的坐标为(0,﹣),(﹣1,﹣),(0,),(﹣3,0),(﹣1,﹣2),(2,﹣);(3)当AP+BQ最小时,四边形ABQP的周少最小,把面B进取仄移个单位后得到B1(0,﹣),∵BB1∥PQ,且BB1=PQ,∴四边形BB1PQ是仄止四边形,∴BQ=B1P,∴AP+BQ=AP+B1P,要正在曲线x=上找一面P,使得AP+B1P最小,做面B1闭于曲线x=的对于称面,得B2(1,﹣),则AB2便是AP+BQ的最小值,AB2==,AB=2,PQ=,∴四边形ABQP的周少最小值是+2.【面评】原题考查了二次函数概括题,波及二次函数取x轴的接面、取y轴的接面、等腰三角形的本量、勾股定理等真量,存留性问题的出现使得易度删大.。
[精选]将军饮马问题(讲)资料
![[精选]将军饮马问题(讲)资料](https://img.taocdn.com/s3/m/cfa30963aa00b52acec7ca14.png)
类型一、基本模式类型二、轴对称变换的应用(将军饮马问题) 2、如图所示,如果将军从马棚M 出发,先赶到河 0A 上的某一位置 P ,再马上赶到河 0B 上的某一位置Q,然后立即返回校场 N.请为将军重新设计一条路线 (即选择点P 和Q ), 使得总路程M 卉PQ+ QN 最短.0B 上的某一位置 Q.请为将军设计一条路线(即选择点P 和Q ),使得总路程 M 卉PQ 最短.3、将军要检阅一队士兵,要求 (如图所示):队伍长为a ,沿河0B 排开(从点P 到点Q );将 军从马棚M 出发到达队头P ,从P 至Q 检阅队伍后再赶到校场 N.请问:在什么位置列队(即 选择点P 和Q ),可以使得将军走的总路程 皿卉PQ^ QN 最短?将军饮马问题【变式】如图所示,将军希望从马棚4.如图,点 边的距离之和最小,再马上赶到河P 至 U 0A5已知/ MON内有一点P, P关于OM ON的对称点分别是召和R, 隅分别交OM, ON于点A B,已知=15,则厶PAB的周长为(A. 15 B 7.5 C. 10 D. 246. 已知/ AOB试在/ AOB内确定一点P,如图,使P到OA OB的距离相等,并且到M N 两点的距离也相等•7、已知/ MON= 40 ° , P为/ MON内一定点,OM上有一点A, ON上有一点B,当△ PAB的周长取最小值时,求/ APB的度数.8. 如图,在四边形ABCD中,/ A= 90°, AD= 4,连接BD, BD丄CD / ADB=Z C.若P是BC边上一动点,贝U DP长的最小值为_______.练习1、已知点A在直线I夕卜,点P为直线I上的一个动点,探究是否存在一个定点B,当点P在直线I上运动时,点P与A、B两点的距离总相等,如果存在,请作出定点 B ;若不存在,请说明理由.A■2、如图,在公路a 的同旁有两个仓库 A 、B ,现需要建一货物中转站,要求到 A 、B 两仓 库的距离和最短,这个中转站 M 应建在公路旁的哪个位置比较合理?A.■BA■----------------------------------------------------- a3、 已知:A 、B 两点在直线I 的同侧, 在I 上求作一点 M ,使得|AM -BM |最小.4、 如图,正方形 ABCD 中,AB =8, M 是DC 上的一点,且 DM =2 , N 是AC 上的一动 点,求DN MN 的最小值与最大值.A B,在坐标轴上找两点 C 、D,使得四边形ABCD 勺周长最小。
最短路径(将军饮马)问题(知识梳理与考点分类讲解)(人教版)(教师版) 24-25学年八年级数学上册

专题13.10最短路径(将军饮马)问题(知识梳理与考点分类讲解)第一部分【知识点归纳】【模型一:两定交点型】如图1,直线l和l的异侧两点A.B,在直线l上求作一点P,使PA+PB 最小;图1【模型二:两定一动型】如图2,直线l和l的同侧两点A.B,在直线l上求作一点P,使PA+PB 最小(同侧转化为异侧);图2【模型三:一定两动型】如图3,点P是∠MON内的一点,分别在OM,ON上作点A,B。
使△PAB的周长最小。
图3【模型四:两定两动型】如图4,点P,Q为∠MON内的两点,分别在OM,ON上作点A,B。
使四边形PAQB的周长最小。
图4【模型五:一定两动(垂线段最短)型】如图5,点A是∠MON外的一点,在射线ON上作点P,使PA与点P到射线OM的距离之和最小。
图5【模型六:一定两动,找(作)对称点转化型】如图6,点A是∠MON内的一点,在射线ON 上作点P,使PA与点P到射线OM的距离之和最小。
图6【考点1】两定一动型;【考点2】一定两动(两点之间线段最短)型;【考点3】一定两动(垂线段最短)型;【考点4】两定两动型;【考点5】一定两动(等线段)转化型;.第二部分【题型展示与方法点拨】【考点1】两定一动型;【例1】(23-24八年级上·全国·课后作业)如图,在ABC ∆中,3,4AB AC ==,EF 垂直平分BC ,交AC 于点D ,则ABP 周长的最小值是()A .12B .6C .7D .8【答案】C 【分析】本题主要考查了,轴对称﹣最短路线问题的应用,解此题的关键是找出P 的位置.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,根据题意知点B 关于直线EF 的对称点为点C ,故当点P 与点D 重合时,AP BP +的值最小,即可得到ABP 周长最小.解:∵EF 垂直平分BC ,∴点B ,C 关于EF 对称.∴当点P 和点D 重合时,AP BP +的值最小.此时AP BP AC +=,∵3,4AB AC ==,ABP ∴ 周长的最小值是347AP BP AB AB AC ++=+=+=,故选:C .【变式】(23-24八年级上·广东广州·期中)如图,在ABC V 中,1216AB AC ==,,20BC =.将ABC V 沿射线BM 折叠,使点A 与BC 边上的点D 重合,E 为射线BM 上的一个动点,则CDE 周长的最小值.【答案】24【详解】设BM 与AC 的交点为点F ,连接AE ,DF 先根据折叠的性质可得12BD AB ==,DF AF =,DE AE =,BDF BAF ∠=∠,再根据两点之间线段最短可得当点E 与点F 重合时,CDE 周长最小,进而求解即可.解:如图,设BM 与AC 的交点为点F ,连接AE ,DF ,由折叠的性质得:12BD AB ==,DF AF =,DE AE =,BDF BAF ∠=∠,20128CD BC BD ∴=-=-=,CDE ∴ 周长8CD DE CE AE CE =++=++,要使CDE 周长最小,只需AE CE +最小,由两点之间线段最短可知,当点E 与点F 重合时,最小值为AC ,∴CDE 周长为:681624AC +=+=.故答案为:24.【点拨】本题考查了折叠的性质等知识点,熟练掌握折叠的性质是解题关键.【考点2】一定两动(两点之间线段最短)型;【例2】(23-24八年级上·湖北省直辖县级单位·期末)如图,45MON ∠=︒,P 为MON ∠内一点,A 为OM 上一点,B 为ON 上一点,当PAB 的周长取最小值时,APB ∠的度数为()A .45︒B .90︒C .100︒D .135︒【答案】B 【分析】本题主要考查了最短路线问题、四边形的内角和定理、轴对称的性质等知识点,掌握两点之间线段最短的知识画出图形是解题的关键.如图:作P 点关于OM ON 、的对称点A B ''、,连接A B '',此时PAB 的周长最小为A B '',求出A B ''即可.解:如图:作P 点关于OM ON 、的对称点A B ''、,然后连接A B '',∵点A '与点P 关于直线OM 对称,点B '与点P 关于ON 对称,∴A P OM B P ON A A AP B B BP ''''⊥⊥==,,,,∴A APA B BPB ''''∠=∠∠=∠,,∵A P OM B P ON ''⊥⊥,,∴180MON A PB ''∠+∠=︒,∴18045135A PB ''∠=︒-︒=︒,在A B P ''△中,由三角形的内角和定理可知:18013545A B ''∠+∠=︒-︒=︒,∴45A PA BPB ''∠+∠=︒,∴1354590APB ∠=︒-︒=︒.故选:B .【变式】(23-24八年级上·江苏无锡·期中)如图,45AOB ∠=︒,点M N 、分别在射线OA OB 、上,5MN =,15OMN S = ,点P 是直线MN 上的一个动点,点P 关于OA 的对称点为1P ,点P 关于OB 的对称点为2P ,连接1OP 、2OP 、12PP ,当点P 在直线MN 上运动时,则12OPP 面积的最小值是.【考点3】一定两动型(垂线段最短);【例3】(22-23八年级上·湖北武汉·期末)如图,在ABC V 中,3AB =,4BC =,5AC =,AB BC ⊥,点P 、Q 分别是边BC 、AC 上的动点,则AP PQ +的最小值等于()A .4B .245C .5D .275【答案】B 【分析】作A 过于BC 的对称点A ',过点A '作A Q AC '⊥,交AC 于点Q ,交BC 于点P ,根据对称可得:AP PQ A P PQ A Q ''+=+≥,得到当,,A P Q '三点共线时,AP PQ +最小,再根据垂线段最短,得到A Q AC '⊥时,A Q '最小,进行求解即可.解:作A 过于BC 的对称点A ',过点A '作A Q AC '⊥,交AC 于点Q ,交BC 于点P ,【变式】(23-24七年级下·陕西西安·阶段练习)如图,在Rt ABC △中,90ACB ∠=︒,3AC =,4BC =,5AB =,AD 是ABC V 的角平分线,若P Q 、分别是AD 和AC 边上的动点,则PC PQ +的最小值是.AD 是BAC ∠的平分线,1QAD Q AD∴∠=∠在AQD 与1AQ D 中【考点4】两定两动型;【例4】如图,已知24AOB ∠=︒,OP 平分AOB ∠,1OP =,C 在OA 上,D 在OB 上,E 在OP 上.当CP CD DE ++取最小值时,此时PCD ∠的度数为()A .36︒B .48︒C .60︒D .72︒【答案】D 【分析】作点P 关于OA 的对称点P',作点E 关于OB 的对称点'E ,连接'OP 、'PP 、'OE 、'EE 、''P E ,则由轴对称知识可知=''CP CD DE CP CD DE ++++,所以依据垂线段最短知:当''P C D E 、、、在一条直线上,且'''P E OE ⊥时,CP CD DE ++取最小值,根据直角三角形的两锐角互余及三角形外角的性质可以'P C PC =,'E D ED =,'1OP OP ==,=''CP CD DE CP CD DE ++++,'P OE ∠''P C D E 、、、在一条直线上,且''P E ''=9048=42OP E ∠︒-︒︒,'='''=7842CP P OP P OP E ∠∠-∠︒-︒=【答案】44βα-=︒【分析】本题考查轴对称—最短问题、三角形的内角和定理.三角形的外角的性质等知识,解题的关键是灵活运用所学知识解决问题.OQM OQM NQP '∴∠=∠=∠,OPQ ∠∴1(180)2PQN AOB α∠=︒-=∠+∠44βα∴-=︒,故答案为:44βα-=︒.【考点5】一定两动(等线段)转化型;【例5】(20-21八年级上·湖北鄂州·期中)如图,AD 为等腰△ABC 的高,其中∠ACB =50°,AC =BC ,E ,F 分别为线段AD ,AC 上的动点,且AE =CF ,当BF +CE 取最小值时,∠AFB 的度数为()A .75°B .90°C .95°D .105°【答案】C 【分析】先构造△CFH 全等于△AEC ,得到△BCH 是等腰直角三角形且FH=CE ,当FH+BF 最小时,即是BF+CE 最小时,此时求出∠AFB 的度数即可.解:如图,作CH ⊥BC ,且CH=BC ,连接HB ,交AC 于F ,此时△BCH 是等腰直角三角形且FH+BF 最小,∵AC=BC ,∴CH=AC ,∵∠HCB=90°,AD ⊥BC ,∴AD//CH ,∵∠ACB=50°,∴∠ACH=∠CAE=40°,∴△CFH ≌△AEC ,∴FH=CE ,∴FH+BF=CE+BF 最小,此时∠AFB=∠ACB+∠HBC=50°+45°=95°.故选:C .【点拨】本题考查全等三角形的性质和判定、等腰三角形的性质、最短路径问题,关键是作出辅助线,有一定难度.【变式】(23-24七年级下·四川宜宾·期末)在ABC V 中,80CAB ∠=︒,2AB =,3AC =,点E 是边AB 的中点,CAB ∠的角平分线交BC 于点D .作直线AD ,在直线AD 上有一点P ,连结PC 、PE ,则PC PE -的最大值是.∵CAB ∠的角平分线交∴FAP ∠∠=∵AP AP =,∴APF APE ≌∴PF PE =,第三部分【中考链接与拓展延伸】1、直通中考【例1】(2020·湖北·中考真题)如图,D 是等边三角形ABC 外一点.若8,6BD CD ==,连接AD ,则AD 的最大值与最小值的差为.【答案】12【分析】以CD 为边向外作等边三角形CDE ,连接BE ,可证得△ECB ≌△DCA 从而得到BE=AD ,再根据三角形的三边关系即可得出结论.解:如图1,以CD 为边向外作等边三角形CDE ,连接BE ,∵CE=CD ,CB=CA ,∠ECD=∠BCA=60°,∴∠ECB=∠DCA ,∴△ECB ≌△DCA (SAS ),∴BE=AD ,∵DE=CD=6,BD=8,∴8-6<BE<8+6,∴2<BE<14,∴2<AD<14.∴则AD 的最大值与最小值的差为12.故答案为:12【点拨】本题考查三角形全等与三角形的三边关系,解题关键在于添加辅助线构建全等三角形把AD 转化为BE 从而求解,是一道较好的中考题.【例2】(2020·新疆·中考真题)如图,在ABC V 中,90,60,4A B AB ∠=∠=︒=︒,若D 是BC 边上的动点,则2AD DC +的最小值为.在Rt DFC △中,30DCF ∠=︒,12DF DC ∴=,122()2AD DC AD DC +=+2()AD DF =+,∴当A ,D ,F 在同一直线上,即此时,60B ADB ∠=∠=︒,2、拓展延伸【例1】(23-24八年级上·江苏镇江·阶段练习)如图,AC 、BD 在AB 的同侧,点M 为线段AB 中点,2AC =,8BD =,8AB =,若120CMD ∠=︒,则CD 的最大值为()A .18B .16C .14D .12【答案】C 【分析】本题考查等边三角形的判定和性质,两点之间线段最短,解题的关键是学会添加常用辅助线,学会利用两点之间线段最短解决最值问题.如图,作点A 关于CM 的对称点A ',点B 关于DM 的对称点B ',证明'' A MB 为等边三角形,即可解决问题.解:如图,作点A 关于CM 的对称点A ',点B 关于DM 的对称点B ',∵120CMD ∠=︒,∴60∠+∠=︒AMC DMB ,∴60''∠+∠=︒CMA DMB ,∴60''∠=︒A MB ,∵MA MB MA MB ''===,∴'' A MB 为等边三角形∵14CD CA A B B D CA AM BD ''''<++=++=,∴CD 的最大值为14,故选:C .【例2】(22-23八年级上·湖北武汉·期末)如图,锐角ABC V 中,302A BC ∠=︒=,,ABC V 的面积是6,D 、E 、F 分别是三边上的动点,则DEF 周长的最小值是()A .3B .4C .6D .7∴AM AE AN ==,MF =∵BAC BAD DAC ∠=∠+∠∴MAN MAB BAD ∠=∠+∠∴(2MAN BAE EAC ∠=∠+∠。
将军饮马问题(讲)电子教案

将军饮马问题(讲)将军饮马问题类型一、基本模式类型二、轴对称变换的应用(将军饮马问题)2、如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短.【变式】如图所示,将军希望从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q.请为将军设计一条路线(即选择点P和Q),使得总路程MP+PQ最短.3、将军要检阅一队士兵,要求(如图所示):队伍长为a,沿河OB排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.请问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程MP+PQ+QN最短?4. 如图,点M在锐角∠AOB内部,在OB边上求作一点P,使点P到点M的距离与点P到OA边的距离之和最小5已知∠MON内有一点P,P关于OM,ON的对称点分别是和,分别交OM, ON于点A、B,已知=15,则△PAB 的周长为()A. 15 B 7.5 C. 10 D. 246. 已知∠AOB,试在∠AOB内确定一点P,如图,使P到OA、OB的距离相等,并且到M、N 两点的距离也相等.7、已知∠MON=40°,P为∠MON内一定点,OM上有一点A,ON上有一点B,当△PAB的周长取最小值时,求∠APB的度数.8. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥CD,∠ADB=∠C.若P是BC边上一动点,则DP长的最小值为______.练习1、已知点A在直线l外,点P为直线l上的一个动点,探究是否存在一个定点B,当点P 在直线l上运动时,点P与A、B两点的距离总相等,如果存在,请作出定点B;若不存在,请说明理由.2、如图,在公路a 的同旁有两个仓库A 、B ,现需要建一货物中转站,要求到A 、B 两仓库的距离和最短,这个中转站M 应建在公路旁的哪个位置比较合理?aBA3、 已知:A 、B 两点在直线l 的同侧, 在l 上求作一点M ,使得||AM BM -最小.4、如图,正方形ABCD 中,8AB =,M 是DC 上的一点,且2DM =,N 是AC 上的一动点,求DN MN +的最小值与最大值.NMD CB A5、如图,已知∠AOB 内有一点P ,试分别在边OA 和OB 上各找一点E 、F ,使得△PEF 的周长最小。
将军饮马问题(解析版)

将军饮马问题模型的概述:唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题:将军在观望烽火之后从山脚下的A点出发,走到河边让战马饮水后再到B 点宿营。
问如何行走才能使总的路程最短。
模型一(两点在河的异侧):将军在观望烽火之后从山脚下的A点出发,走到河边让战马饮水后再到B 点宿营,将在何处渡河使行走距离最短并求最短距离。
方法:如右图,连接AB,与线段L交于点M,在M处渡河距离最短,最短距离为线段AB的长。
模型二(两点在河的同侧):将军在观望烽火之后从山脚下的A点出发,需先走到河边让战马饮水后再到B点宿营,将在何处渡河使行走距离最短并求最短距离。
方法:如右图,作点B关于直线L的对称点B',连接AB',与直线L的交点即为所求的渡河点,最短距离为线段AB'的长。
模型三:如图,将军同部队行驶至P处,准备在此驻扎,但有哨兵发现前方为两河AB、BC的交汇处,为防止敌军在对岸埋伏需派侦察兵到河边观察,再返回P处向将军汇报情况,问侦察兵在AB、BC何处侦查才能最快完成任务并求最短距离。
数学描述:如图在直线AB、BC上分别找点M、N,使得∆PMN周长最小。
方法:如右图,分别作点P关于直线AB、BC的对称点P'、P'',连接P'P'',与两直线的交点即为所求点M、N,最短距离为线段P'P''的长。
模型四如图,深夜为防止敌军在对岸埋伏,将军又派一队侦察兵到河边观察,并叮嘱观察之后先去存粮位置点Q处查看再返回P处向将军汇报情况,问侦察在AB、BC何处侦查才能最快完成任务并求最短距离。
数学描述:如图在直线AB、BC上分别找点M、N,使得四边形PQNM周长最小。
方法:如右图,分别作点P、点Q关于直线AB、BC的对称点P'、Q',连接P'Q',与两直线的交点即为所求点M、N,最短距离为线段(PQ+P'Q')的长。
数学模型社团第16讲 将军饮马问题

数学模型社团第16讲 将军饮马问题早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题.将军每天从军营A 出发,先到河边饮马,然后再去河岸同侧的军营B 开会,应该怎样走才能使路程最短?这个问题的答案并不难,据说海伦略加思索就解决了它.从此以后,这个被称为“将军饮马”的问题便流传至今.“将军饮马”问题主要利用构造对称图形解决求两条线段和差、三角形周长、四边形周长等一类最值问题,会与直线、角、三角形、四边形、圆、抛物线等图形结合,在近年的中考和竞赛中经常出现,而且大多以压轴题的形式出现.【例1】(2019秋•丰台区期末)如图,在ABC ∆中,3AB =,4AC =,5BC =,EF 是BC 的垂直平分线,P 是直线EF 上的任意一点,则PA PB +的最小值是( )A .3B .4C .5D .6【例2】(2019秋•邳州市期末)如图,60AOB ∠=︒,点P 是AOB ∠内的定点且OP =点M ,N 分别是射线OA ,OB 上异于点O 的动点,则PMN ∆周长的最小值是( )A B C .3 D .6【例3】(2017•内江)如图,已知直线12//l l ,1l 、2l 之间的距离为8,点P 到直线1l 的距离为6,点Q 到直线2l 的距离为4,PQ =1l 上有一动点A ,直线2l 上有一动点B ,满足2AB l ⊥,且PA AB BQ ++最小,此时PA BQ += .【例4】(2020•河北区模拟)如图,在矩形ABCD 中,4AB =,5AD =,连接AC ,O 是AC 的中点,M 是AD 上一点,且1MD =,P 是BC 上一动点,则PM PO -的最大值为 .【同步训练】1.(2020•安徽模拟)Rt ABC ∆中,90ACB ∠=︒,4AC =,8BC =,D ,E 是AB 和BC 上的动点,连接CD ,DE ,则CD DE +的最小值为( )A .8B C D .3252.(2020•恩施州)如图,正方形ABCD 的边长为4,点E 在AB 上且1BE =,F 为对角线AC 上一动点,则BFE ∆周长的最小值为( )A.5B.6C.7D.8 3.(2020•绥化一模)如图所示,正方形ABCD的面积为12,ABE∆是等边三角形,点E在正方形内,在对角线AC上找到一点P,使PD PE+的和最小,则这个和的最小值是()A B C.3D4.(2020秋•常州期中)如图,45∠内部一条射线,点D为射线OCAOB∠=︒,OC为AOB上一点,OD E、F分别为射线OA、OB上的动点,则DEF∆周长的最小值是( )A B.2C.D.45.(2019秋•碑林区校级月考)在正方形ABCD中,8AD=,2DE=,F为直线BD上一点,G为BC的中点,||-的最大值为()EF GFA.6B.2C.D.6.(2020•黑龙江)如图,在边长为4的正方形ABCD中,将ABD∆沿射线BD平移,得到+的最小值为.∆,连接EC、GC.求EC GCEGF。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
类型一、基本模式类型二、轴对称变换的应用(将军饮马问题)2、如图所示,如果将军从马棚上的某一位置 Q ,然后立即返回校场Q ),使得总路程 MP +PQ + QN 最短.OB 上的某一位置 Q .请为将军设计一条路线 (即选择点P 和Q ),使得总路程 MP +PQ 最短.3、将军要检阅一队士兵,要求 (如图所示):队伍长为a ,沿河0B 排开(从点P 到点Q );将 军从马棚M 出发到达队头P,从P 至Q 检阅队伍后再赶到校场 N .请问:在什么位置列队(即将军饮马问题flM 出发,先赶到河 0A 上的某一位置 P ,再马上赶到河 0BN .请为将军重新设计一条路线 (即选择点P 和【变式】如图所示,将军希望从马棚 M 出发, 先赶到河OA 上的某一位置P ,再马上赶到河AOA 边的距离之和最小P 到练习1、已知点A 在直线 直线I 上运动时,点 请说明理由.I 外,点P 为直线I 上的一个动点,探究是否存在一个定点B ,当点P 在 P 与A 、B 两点的距离总相等,如果存在,请作出定点 B ;若不存在,5已知/ MON 内有一点P , P 关于OM , ON 的对称点分别是 百和均,分别交OM, ON于点A 、B,已知耳时=15,则^ PAB 的周长为(6. 已知/ AOB ,试在/ AOB 内确定一点 P ,如图,使 P 到OA 、OB 的距离相等,并且到 N 两点的距离也相等.7、已知/ MON = 40°, P 为/ MON 内一定点,OM 上有一点 A , ON 上有一点B ,当△ PAB 的周长取最小值时,A. 15B 7.5 C. 10D. 24求/ APB 的度数.8.如图,在四边形 ABCD 中,/ A = 90°, AD = 4,连接 BD , BD 丄 CD,/ ADB =/ C 若 P 是BC 边上一动点,则 DP 长的最小值为5、如图,已知/ AOB 内有一点P ,试分别在边 OA 和0B 上各找一点 E 、F ,使得△ PEF 的周 长最小。
试画出图形,并说明理由。
6、如图,直角坐标系中有两点 A 、B,在坐标轴上找两点 C D,使得四边形ABCD 的周长最小。
.A2、如图,在公路a 的同旁有两个仓库 A 、B ,现需要建一货物中转站,要求到 库的距离和最短,这个中转站 M 应建在公路旁的哪个位置比较合理?A 、B 两仓已知:A 、B 两点在直线I 的同侧, 在I 上求作一点M ,使得| AM BM |最小.如图,正方形 ABCD 中,AB 8, M 是DC 上的一点,且 DM 2 , N 是AC 上的一动 点,求DN MN 的最小值与最大值.MN7、如图,村庄 A 、B 位于一条小河的两侧,若河岸 a 、b 彼此平行,现在要建设一座与河岸 垂直的桥CD,问桥址应如何选择,才能使 A 村到B 村的路程最近?Jf g xp ,当X 为何值时,y 的值最小,并求出这个最小值.A(1, -3)、B(4, -1)、P(a,0)、N(a+2,0),当四边形 PABN 的周长最小ABCD 中,AB=CD=AD=2 / D=120°,点 E 、F 是底边 AD 与 BC 的中 EF 上找一点P ,使BP+AP 最短.9、在平面直角坐标系中, 时,求a 的值.10、如图,在等腰梯形 点,连接EF 在线段练习1、观察下列银行标志, O从图案看既是轴对称图形又是中心对称图形的有(A . 1个B . 2个 C. 3个D . 4个2、 以下图形中,既是轴对称图形,又是中心对称图形的是(A .等边三角形B .矩形C .等腰梯形3、 在下列四个图案中既是轴对称图形,又是中心对称图形的是 )D .平行四边形£4、在等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的个数为 (A. 1个B. 2个C. 3个D. 4个5、把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图甲).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中, 两个对应三角形(如图乙)的对应点所具有的性质是(A)对应点连线与对称轴垂直(C)对应点连线被对称轴垂直平分图甲口图乙( ) (B)对应点连线被对称轴平分(D)对应点连线互相平行6、对右图的对称性表述, 正确的是().A.轴对称图形 B .中心对称图形C.既是轴对称图形又是中心对称图形D.既不是轴对称图形又不是中心对称图形7、如图,△ A B' C是由△ ABC经过变换得到的,则这个变换过程是(A)平移(B)轴对称(C)旋转(D)平移后再轴对称ABCA'BB'BC&如图所示,四边形 OABC 是矩形,点A 、C 的坐标分别为(3, 0), ( 0, 1 ),点D 是线段1BC 上的动点(与端点 B 、C 不重合),过点D 作直线y = — — x + b 交折线OAB 于点E.2(1) 记^ ODE 的面积为S,求S 关于b 的函数关系式;(2) 当点E 在线段OA 上时,若矩形OABC 关于直线DE 的对称图形为四边形 OA 1B 1C 1,9、探究OA 1B 1C 1与矩形OABC 的重叠部分的面积是否发生变化,若不变,求出该重叠部分的面积;若改变,请说明理由.①若直线与折线 OAB 的交点在OA 上时,即此时 E (2b , 0)1 1--S= — OE • CO= — X 2b X 1 = b2②若直线与折线此时E ( 3, bl ),D (2b —2, 1)【答案】(1) 若直线经过点 若直线经过点 若直线经过点 由题意得B (3, 1). b = 32b= § 2b = 1A (3, 0)时,则B ( 3, 1 )时,则C (0 , 1 )时,则31<bW -,如图 25-a ,3 5 OAB 的交点在BA 上时,即一< b < -,如图2由题意知,DM // NE , DN// ME ,•四边形DNEM 为平行四边形 根据轴对称知,/ MED =/ NED又/ MDE =/ NED, •/ MED =/ MDE , • MD = ME ,;平行四边形 过点D 作DH 丄OA ,垂足为H ,i由题易知,tan / DEN=—, DH = i , • HE = l ,l设菱形DNEM 的边长为a ,则在RtA DHM 中,由勾股定理知:ll l5a(l a ) i ,- a -5• - S 四边形 DNEM = NE • DH =—4•••矩形OA i B i C i 与矩形OABC 的重叠部分的面积不发生变化,面积始终为•- S = S 矩一($△ OCD + & OAE + &DBE )i3 - [-(lb -i) l i 5 iX i + — X(5-lb ).(l b )+ - X 3(b3)] = |b b ll llb b l 3 2 5 2 (l )如图 形OABC 的重叠部分的面积即为四边形 本题答案由无锡市天一实验学校金杨建老师草制! 3,设O i A i 与CB 相交于点M , OA 与GB i 相交于点N , DNEM 的面积。
则矩形OA i B i C i 与矩DNEM 为菱形.io .如图,在平面直角坐标系中,△ABC (-i,3 )。
(i )画出△ ABC 关于x 轴对称的^ A i B i C i , (l )画出△ ABC 绕原点O 顺时针方向旋转(3)将^ A l B l C l 平移得到^ A 3B 3C 3,使点的三个顶点的坐标分别为A ( 0,i ),B (-i,i ), C,点C l 的对应点是C 3 (4, -i ),在坐标系中画出^并写出点C i 的坐标;90°后得到的^ A i B i C i ,并写出点 C 的坐标;, A l的对应点是A 3,点B l 的对应点是B 3A 3B 3C 3,并写出点 A 3, B 3的坐标。
【答案】(1)C1(-1,-3) (2)C2(3,1) (3)A3(2,-2),B3(2,-1) 11、分别按下列要求解答:(1)在图1中,将^ ABC先向左平移5个单位,再作关于直线AB的轴对称图形,经两次变换后得到△ A1B1 C.画出△ A1B1C1;.(2)在图2中,△ ABC经变换得到△ A2B2C2.描述变换过程【答案】(1)如图.(2)将^ ABC先关于点A作中心对称图形,再向左平移2个单位,得到△ A2B2C2.(变换过程不唯一)12径CD上找一点P,使BP+AP的值最小,并求BP+AP的最小值.径CD 上找一点P ,使BP+AP 的值最小,并求 BP+AP 的最小值. 12、(1)观察发现如题26(a)图,若点A , B 在直线I 同侧,在直线I 上找一点P ,使AP+BP 的值最小.做法如下:作点 B 关于直线I 的对称点B ,连接AB ,与直线I 的交点就是所求的点 P 再如题26(b)图,在等边三角形 ABC 中,AB=2,点E 是AB 的中点,AD 是高,在 AD 上 找一点P ,使BP+PE 的值最小.做法如下:作点 B 关于AD 的对称点,恰好与点 C 重合,连接CE 交AD 于一点,则这 点就是所求的点⑵实践运用已知O O 的直径CD 为4, AD 的度数为60°,点B 是A D 的中点,在直P,故BP+PE 的最小值为 A fi 题18(a)图 2 题18(b)图 如题26(c)图,题18(c)图(3)拓展延伸如题26(d)图,在四边形 ABCD 的对角线AC 上找一点P ,使/ APB=/APD.保留 作图痕迹,不必写出作法.所以/ AEB=15°,因为B 关于CD 的对称点所以/ BOE=60°, 所以△ OBE 为等边三角形, 所以/ OEB=60°, 所以/ OEA=45° 又因为OA=OE , 所以△ OAE 为等腰直角三角形,所以 AE=2j2.AC 于P 即可,13、如图所示,A 、B 两村之间有一条河,河宽为 要使AB 两村路程最近,请确定修桥的地点。
连接 OA 、OB 、OE ,连接AE 交CD与一点P , AP+BP 最短,因为 ,点B 是A D 的中点,a ,现要在河上修一座垂直于河岸的桥, (I (n)桥建在何处才能使 AB 两村到桥的距离相E , 0 I 0 fAD 的度数为60° (3)找B 关于AC 对称点E ,连DE 延长交C?。
