12.21第八讲. 数阵图进阶_

数阵图(三)(含详细解析)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．数阵图与数论【例 1】把0—9这十个数字填到右图的圆圈内，使得五条线上的数字和构成一个等差数列，而且这个等差数列的各项之和为55，那么这个等差数列的公差有种可能的取值．【考点】数阵图与数论【难度】3星【题型】填空【关键词】迎春杯，三年级，初赛，第8题【解析】设顶点分别为A 、B 、C 、D 、E ，有45+A +B +C +D +E =55，所以A +B +C +D +E =10，所以A 、B 、C 、D 、E 分别只能是0-4中的一个数字.则除之外的另外5个数（即边上的）为45-10=35.设所形成的等差数列的首项为a 1，公差为d .利用求和公式5（a 1＋a 1+4d ）2=55，得a 1+2d =11，故大于等于0+1+5=6，且为奇数，只能取7、9或11，而对应的公差d 分别为2、1和0.经试验都能填出来所以共有3中情况，例题精讲知识点拨教学目标5-1-3-3.数阵图公差分别为2、1、0.【答案】2种可能【例 2】将1~9填入下图的○中，使得任意两个相邻的数之和都不是3，5，7的倍数．【考点】数阵图与数论【难度】4星【题型】填空【解析】根据题意可知1的两边只能是3与7；2的两边只能是6与9；3的两边只能是1、5或8；4的两边只能是7与9．可以先将3—1—7--写出来，接下来7的后面只能是4，4的后面只能是9，9的后面只能是2，2的后面只能是6，可得：3—1—7—4—9—2—6--，还剩下5和8两个数．由于6814+=是7的倍数，所以接下来应该是5，这样可得：3—1—7—4—9—2—6—5—8—3．检验可知这样的填法符合题意．【答案】3—1—7—4—9—2—6—5—8—3【例 3】在下面8个圆圈中分别填数字l，2，3，4，5，6，7，8(1已填出)．从1开始顺时针走1步进入下一个圆圈，这个圆圈中若填n(n≤8)。

数阵图讲义

54321 776655443322117654321a首先我们观察下图：图中有4个大圆，每个圆周上都有四个数字，神奇的是，每个圆周上的四个数字之和都等于20。

不信，你就算算。

上面这幅图就是数阵图。

把给定的一些数按一定的要求或规律填在特定形状的图形中，这样的图形叫做数阵图。

数阵图绚丽迷人，变化多端，引人入胜。

常见的主要有三种：（1）辐射型（2）封闭型（3）复合型。

一般说来，数阵图主要讨论以下两个问题：（1）满足某种条件的填法是否存在；（2）在填法存在的情况下，把待定的数字补充完整。

这一讲我们学习辐射型数阵图。

【例1】把1～5这五个数分别填在下图中的方格中，使得横行三数之和与竖列三数之和都等于8。

【分析与解】这是辐射型数阵图。

你可能觉得这道题太简单了，七拼八凑就会写出正确答案。

可是，你明白其中的道理吗？下面我们就一起来探索其中的道理，只有弄清其中的道理，才可能解答更复杂巧妙的数阵图问题。

中间方格的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“中心数”。

用字母a 表示。

因为横行的三个数之和与竖列的三个数之和都等于8。

所以横行的三个数之和加上竖列的三个数之和为（8＋8=）16，即（1＋2＋3＋4＋5）＋a =8＋8，整理得：15＋a =16。

为什么还要加上a 呢？因为 a 是中心数，相加时一共被加了两次，其余各数均被加了一次。

在计算1＋2＋3＋4＋5时已计算了一次，所以最后还要加上a 。

解得：a =1求出了中心数。

其余各数就好填了。

如图所示。

【例2】把1～7这七个数分别填入下图的各个方格内，使每条线段上三个○内数的和相等。

654321c b a 【分析与解】首先，我们分析一下，这七个○内的数中，哪几个数是关键？由图我们看到，在计算每条线段上三个数的和的过程中，都要用到中心数。

另外，还要知道每条线段上三个数的和是几。

所以，确定中心数和每条线段上三个数的和是解答本题的关键。

为此，我们设图中的中心数为a ，每条线段上三个○内数的和为k ，则3k=（1＋2＋3＋4＋5＋6＋7）＋2a3k=28＋2a下面，我们利用上面得到的关系式3k=28＋2a 来确定中心数a 的值。

数阵图知识点总结

数阵图知识点总结数阵图在计算机科学中有很多应用，例如在图像处理中用来表示图像的像素信息，在数据库中用来存储和管理数据，还可以用来表示图形和网络的关系。

数阵图还可以用来做矩阵运算，包括加法、减法、乘法以及求逆等。

在算法和数据结构中，数阵图也是一个常见的数据结构，例如用来表示图形的邻接矩阵，解决网络流的最大流问题等。

数阵图可以用不同的方式表示和存储，例如用数组、链表、向量等数据结构来实现。

在不同的应用场景中，选择不同的表示和存储方式可以提高数据的访问效率和计算性能。

本文将从数阵图的基本定义、表示和存储、运算以及应用等方面进行介绍和总结。

1. 数阵图的基本定义数阵图可以定义为一个m行n列的二维数组，用来存储各种不同类型的数据。

在数学中，数阵图可以表示为一个m×n的矩阵，每个元素用Aij表示，其中i表示行号，j表示列号，Aij表示矩阵中第i行第j列的元素。

例如，一个3行4列的数阵图可以表示为：A11 A12 A13 A14A21 A22 A23 A24A31 A32 A33 A34在计算机科学中，数阵图也可以用数组、链表、向量等数据结构来表示和存储。

例如，可以用一维数组来表示一个m行n列的数阵图，数组的长度为m×n，其中每个元素对应矩阵中的一个元素。

也可以用链表来表示一个数阵图，每一行用一个链表节点来表示，节点中包含该行中的所有元素。

向量也是一种常见的数阵图表示方式，它可以用来表示稀疏矩阵，在稀疏矩阵中大部分元素为0，向量可以节省存储空间和提高计算性能。

2. 数阵图的表示和存储在计算机中，数阵图可以用不同的数据结构来表示和存储，选择不同的表示和存储方式可以根据实际应用场景来提高数据访问效率和计算性能。

常见的数阵图表示和存储方式包括数组、链表、向量等。

下面分别介绍各种方式的表示和存储方法：2.1 数组表示数组是一种连续存储的数据结构，可以用来表示和存储数阵图。

数组的优点是数据访问速度快，可以通过下标直接访问元素，缺点是数组的大小固定，不方便动态扩展。

第八讲(幻方与数阵图)

（提高）学案 1 在下图空格中填入 7 个自然数，使每行、每列、每一对角线三数之和为 90
23
57
40
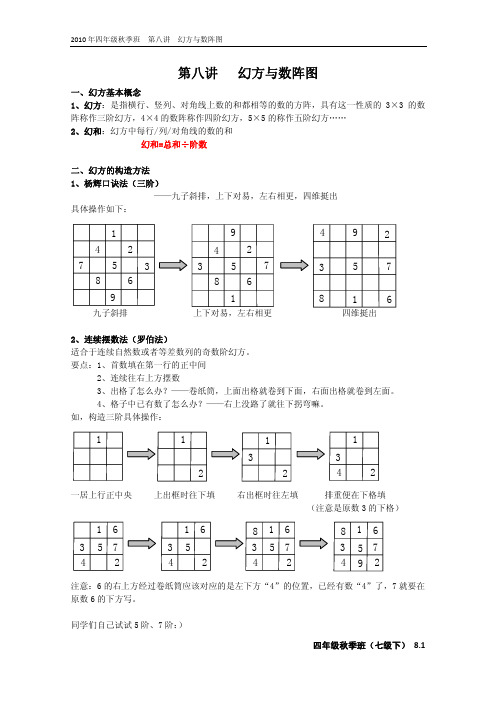
解析：告诉了幻和，先求中间数=90÷3=30
23 30
告诉了相邻 2 个棱块，一定能求对角角块=（23+57）÷2=40，得到右图
57
接下来就容易了吧？同学们自己计算吧！
（尖子）学案 1 按要求完成幻方
（1）只求 x
x
（2）如果中间格填入 100，请在（1）的基础上完成所有格的填数。
19
解析：想想窍门 2，95=（x+19）÷2，那么可算出 x=117
95
中间数是 100，可求出幻和是 300，其他的就好填了，同学们自己试试吧！
最后答案： 24 117 105 你填对了吗？
181 100 19
95 29 176
492 357
每个数加 3
7 12 5 6 8 10
816
11 4 9
先写出基本型
OK 啦
当然，本题并没有说用哪些数，所以答案很多，但是这种方法是不是更快呢？
拓展：请用 11.13.15.17.19.21.23.25.27 编制一个三阶幻方解析：这是一个等差数列，将它与基本型中的 1-9 对应好
11 13 15 17 19 21 23 25 27 对应 1 2 3 4 5 6 7 8 9
2010 年四年级秋季班第八讲幻方与数阵图
第八讲幻方与数阵图
一、幻方基本概念 1、幻方：是指横行、竖列、对角线上数的和都相等的数的方阵，具有这一性质的 3×3 的数阵称作三阶幻方，4×4 的数阵称作四阶幻方，5×5 的称作五阶幻方…… 2、幻和：幻方中每行/列/对角线的数的和

学而思四年级春季班数阵图进阶知识总结

数阵图，这一讲在初步的基础上，更加强化了如何更方便的填完整个数阵图：
算数和→找合适的线和→算出重复数→尝试枚举填完有了这个思路，在做数阵图题目时便更加的方便，不再会硬着头皮试半天。

★结合数论分析数和、线和、重复数的关系
如图，将1~8分别填入下面各圈中，使得每条线上的和均相等，问此时A 和B 的差值是多少？ A
B
【详解】
这类问题均要通过找数和、线和、重复数的关系：算出所有数的数和：123836+++
+= 上方两个交叉的线和2k ，加上下方一个横的线和k ，可以囊括所有的数，并且重复算了一次A ，则有：336k A -=
根据3k 是3的倍数，36也是3的倍数，可以得出，A 也是3的倍数，那么A 只有两种可能，要么是3，要么是6，之后算出线和k ，并填完数阵图，可以得出，无论A 是3还是6，A 、B 两个数的差都是4. 练习
数阵图进阶。

小学数学-数阵图讲解学习PPT文档25页

小学数学-数阵图讲解学习
6、纪律是自由的第一条件。——黑格尔 7、纪律是集体的面貌，集体的声音，集体的动作，集体的表情，集体的信念。 ——马卡连柯
8、我们现在必须完全保持党的纪律，否则一切都会陷入污泥中。 ——马克思 9、学校没有纪律便如磨坊没有水。— —夸美纽斯
10、一个人应该：活泼而守纪律，天真而不幼稚，勇敢而鲁莽，倔强而有原则，热情而不冲动，乐观而不盲目。 ——马克思
ቤተ መጻሕፍቲ ባይዱ
1、最灵繁的人也看不见自己的背脊。——非洲 2、最困难的事情就是认识自己。——希腊 3、有勇气承担命运这才是英雄好汉。——黑塞 4、与肝胆人共事，无字句处读书。——周恩来 5、阅读使人充实，会谈使人敏捷，写作使人精确。——培根

小学数学思维方法：幻方与数阵图

幻方与数阵图【知识要点】一、幻方在一个由若干个排列整齐的数组成的正方形中，图中任意一横行、一纵行及对角线的几个数之和都相等，具有这种性质的图表，称为“幻方”。

我国古代称为“河图”、“洛书”，又叫“纵横图”。

三阶幻方的性质：1.中心位置上的数等于幻和除以3；2.角上得数等于和它不相邻的两条边上的数的平均数；3.中心数两头的数之和等于中心数的2倍。

二、数阵图数阵图问题千变万化，这一类问题要求数阵中填入了一些数以后，能保证数阵中特定关系线（或关系区域）上的数的和相等，解决这类问题可以按以下步骤解决问题：第一步：从整体考虑，将要求满足相等的几个数字和全部相加，一般为n ×s 的形式。

第二步：从个体考虑，分别计算每一个位置数字相加的次数，将比较特殊的（多加或少加几次）位置数字用未知数表示，全部相加，一般为题目所给全部数字和×一般位置数字相加次数±特殊位置数字和×多加或少加次数的形式。

第三步：格局整体与个体的关系，列出等式即n ×s=题目所给全部数字和×一般位置数字相加次数±特殊位置数字和×多加或少加次数。

第四步：根据数论植树即整除性确定特殊位置数的取值即相对应的S 值。

第四步：根据确定的特殊位置数字及S 值进行数字分组及尝试。

【典型例题】一、幻方例1：如下图，将1—9填入3×3的方格表中，使得每行每列以及两条对角线上的三个数字之和都相等，你一共可以得到多少种填法？分析：首先，我们思考要填出一个三阶幻方，什么量的求出是最重要的？立刻我们就知道，那个所谓的“幻和”，即每行、每列、每条对角线三个数的和是最重要的量。

它是多少呢？如果我们按照行（按照列也一样）把幻方中的九个数加起来，那么它们的总和不就是3倍的“幻和”吗？而另一方面，我们也知道，由于1到9这九个数字都只各用了一次，所以3倍的的“幻和”第1题就等于1+2+3+4+5+6+7+8+9=45。

小学奥数数阵图

第十七周数阵图把一些数字按照一定的要求，排列成各种各样的图形，叫做数阵图。

数阵是由幻方演化出来的另一种数字图。

幻方一般均为正方形。

图中纵、横、对角线数字和相等。

数阵则不仅有正方形、长方形，还有三角形、圆、多边形、星形、花瓣形、十字形，甚至多种图形的组合。

变幻多姿，奇趣迷人。

一般按数字的组合形式，将其分为三类，即辐射型数阵、封闭型数阵、复合型数阵。

【解题技巧】数阵的分类：封闭型：封闭型数阵图的解题突破口，是确定各边顶点所应填的数。

为确定这些数，采用的方法是建立有关的等式，通过以最小值到最大值的讨论，来确定每条边上的几个数之和，再将和数进行拆分以找到顶点应填入的数，其余的数再利用和与顶点的数就容易被填出。

（1—6）辐射型：辐射型数阵图，解法的关键是确定中心数。

具体方法是：通过所给条件建立有关等式，通过整除性的讨论，确定出中心数的取值，然后求出各边上数的和，最后将和自然数分拆成中心数的若干个自然数之和，确定边上其他的数。

复合型：复合型数阵图，解题的关键是要以中心数和顶点数为突破口。

数阵的特点：每一条直线段或由若干线段组成的封闭线上的数字和相等。

它的表达形式多为给出一定数量的数字，要求填入指定的图中，使其具备数阵的特点。

解数阵问题的一般思路是：1.求出条件中若干已知数字的和。

2.根据“和相等”，列出关系式，找出关键数——重复使用的数。

3.确定重复用数后，对照“和相等”的条件，用尝试的方法，求出其他各数。

有时，因数字存在不同的组合方法，答案往往不是唯一的。

【铜牌例题】将2、3、4、5、6、7、8、9、10填入下图中的9个方格中，使每行、每列及对角线之和相等，小明已经填了5个数，请将其余4个数填入。

【答案】【解析】先根据最左边一列求出幻和，然后根据这个和和给出的数字逐步推算。

3+8+7=18；第二行中间的数是：18-8-4=6；第三行中间的数是：18-7-9=2；第一行第一个数是：18-4-9=5；第一行中间的数是：18-3-5=10；【举一反三1】（第十届走美杯初赛）小华需要构造一个3×3的乘积魔方，使得每行、每列、每条对角线上三个正整数的乘积都相等；现在他已经填入了2，3，6三个数，那当小华的乘积魔方构造完毕后，x等于______。

数阵图讲义——精选推荐

54321 776655443322117654321a首先我们观察下图：图中有4个大圆，每个圆周上都有四个数字，神奇的是，每个圆周上的四个数字之和都等于20。

不信，你就算算。

上面这幅图就是数阵图。

把给定的一些数按一定的要求或规律填在特定形状的图形中，这样的图形叫做数阵图。

数阵图绚丽迷人，变化多端，引人入胜。

常见的主要有三种：（1）辐射型（2）封闭型（3）复合型。

一般说来，数阵图主要讨论以下两个问题：（1）满足某种条件的填法是否存在；（2）在填法存在的情况下，把待定的数字补充完整。

这一讲我们学习辐射型数阵图。

【例1】把1～5这五个数分别填在下图中的方格中，使得横行三数之和与竖列三数之和都等于8。

【分析与解】这是辐射型数阵图。

你可能觉得这道题太简单了，七拼八凑就会写出正确答案。

可是，你明白其中的道理吗？下面我们就一起来探索其中的道理，只有弄清其中的道理，才可能解答更复杂巧妙的数阵图问题。

中间方格的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“中心数”。

用字母a 表示。

因为横行的三个数之和与竖列的三个数之和都等于8。

所以横行的三个数之和加上竖列的三个数之和为（8＋8=）16，即（1＋2＋3＋4＋5）＋a =8＋8，整理得：15＋a =16。

为什么还要加上a 呢？因为 a 是中心数，相加时一共被加了两次，其余各数均被加了一次。

在计算1＋2＋3＋4＋5时已计算了一次，所以最后还要加上a 。

解得：a =1求出了中心数。

其余各数就好填了。

如图所示。

【例2】把1～7这七个数分别填入下图的各个方格内，使每条线段上三个○内数的和相等。

654321cba【分析与解】首先，我们分析一下，这七个○内的数中，哪几个数是关键？由图我们看到，在计算每条线段上三个数的和的过程中，都要用到中心数。

另外，还要知道每条线段上三个数的和是几。

所以，确定中心数和每条线段上三个数的和是解答本题的关键。

为此，我们设图中的中心数为a ，每条线段上三个○内数的和为k ，则 3k=（1＋2＋3＋4＋5＋6＋7）＋2a3k=28＋2a下面，我们利用上面得到的关系式3k=28＋2a 来确定中心数a 的值。

四年级奥数之数阵图进阶

【今日讲题】例2，例3，例5 【讲题心得】 ______________________________________________ ______________________________________________ ______________________________________________ ______________________________________________ _____________________________________. 【家长评价】 ______________________________________________ ______________________________________________ ______________________________________________ ______________________________________________ _____________________________________. 2这七个数字，分别填入图中各个○内，使每条线段上的三个 ○内数的和都等于14.
【课前小练习】(★) 2．请将1、2、4、6这四个数填入到下图中各空白区域内，使得每请将这个数填到下图中各空白区域内，使得每个圆圈里的四个数字和都等于15. 3 5 7
【例2】(★★★) 把1～9这9个数分别填入下图的圆圈中，使得每条直线上的3个数的和都相等和都相等.
3
【铺垫】(★★)
9 7
把1至8分别填入图的八个方格内，使得各列上两个数之和都相等，各行四个数之和也相等.
知识大总结 1. 名词：重叠数、边和、圈和、数字和 1 名词：重叠数、边和、圈和、数字和. 2. 分类：放射型、封闭型、复合型 ⑴ 口诀：数边和，找重叠，列等式 ⑵ 利用整除关系. 3 3. 原则： ⑴ 一般之中寻找特殊般之中寻找特殊 ⑵ 重叠数尽量少. 1 5 9 7

(完整)小学三年级奥数--数阵图

数阵图（一）在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。

它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。

那么，到底什么是数阵呢？我们先观察下面两个图：左上图中有3个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于13。

右上图就更有意思了，1～9九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于15，不信你就算算。

上面两个图就是数阵图。

准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。

要排出这样巧妙的数阵图，可不是一件容易的事情。

我们还是先从几个简单的例子开始。

例1把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。

同学们可能会觉得这道题太容易了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。

下面我们就一起来分析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。

分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。

也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。

因为横行的三个数之和与竖列的三个数之和都等于9，所以(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。

重叠数求出来了，其余各数就好填了(见右上图)。

试一试：练习与思考第1题。

例2把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。

分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。

所以，必须先求出这个“和”。

根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。

数阵图(一)(含详细解析)

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类：1. 定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.3.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．模块一、封闭型数阵图【例 1】把1～8的数填到下图中，使每个四边形中顶点的数字和相等。

【考点】复合型数阵图【难度】3星【题型】填空【关键词】学而思杯，3年级，第6题【解析】例题精讲知识点拨教学目标5-1-3-1.数阵图87654321【答案】87654321【例 2】将1～8这八个自然数分别填入下图中的八个○内，使四边形每条边上的三个数之和都等于14，且数字1出现在四边形的一个顶点上.应如何填？（1）【考点】封闭型数阵图【难度】2星【题型】填空【解析】为了叙述方便，先在各圆圈内填上字母，如下图（2）.由条件得出以下四个算式：（2）h gf ed c baa+b+c=14（1）c+d+e=14 （2） e+f+g=14 （3）a+h+g=14 （4）由（1）+（3），得：a+b+c+e+f+g=28，（a+b+c+d+e+f+g+h ）-（d+h ）=28，d+h=（1+2+3+4+5+6+7+8）-28=8，由（2）+（4），同样可得b+f=8，又1，2，3，4，5，6，7，8中有1+7=2+6=3+5=8.又1要出现在顶点上，d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性，不妨设b=2，f=6，d=3，h=5. a ，c ，e ，g 可取到1，4，7，8若a=1，则c=14-（1+2）=11，不在1，4，7，8中，不行.若c=1，则a=14-（1+2）=11，不行. 若e=1，则c=14-（1+3）=10，不行. 若g=1，则a=8，c=4，e=7.说明：例题为封闭型数阵，由它的分析思考过程可以看出，确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】在如图6所示的○内填入不同的数，使得三条边上的三个数的和都是12，若A 、B 、C 的和为18，则三个顶点上的三个数的和是。

奥数知识点简单数阵图

简单数阵图一、辐射型数阵图从一个中心出发，向外作若干条射线，在每条射线上安放同样多个数，使其和是一个不变的数。

突破关键：确定中心数，多算的次数，公共的和。

先求重叠数。

数总和+中心数×重复次数＝公共的和×线数重叠部分=线总和-数总和/线总和=公共的和×线数数和：指所有要填的数字加起来的和中心数：指中间那数字，即重复计算那数字（重叠数）重复次数：中心数多算的次数，一般比线数少1公共的和：指每条直线上几个数的和线数：指算公共和的线条数例1、把1-5这五个数分别填在左下图中的方格中，使得横行三数与竖列三数之和都等于9。

例2、把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。

分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。

也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。

因为横行的三个数之和与竖列的三个数之和都等于9，所以：总和数=(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。

分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。

所以，必须先求出这个“和”。

根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。

例3、把1~5这五个数填入右图中的○里，使例4、将1~7这七个自然数填入左下图的每条直线上的三个数之和相等七个○内，使得每条边上的三个数之和都等于10。

分析与解：例1是知道每条直线上的三数之和，不知道重叠数；例2是知道重叠数，不知道两条直线上的三个数之和；本例是这两样什么都不知道。

但由例1、例2的分析知道，(1+2+3+4+5)+重叠数=每条直线三数之和×2，每条直线上三数之和=(15+重叠数)÷2。

趣味数学—数阵图与幻方

三年级奥数--数阵图与幻方知识框架一、数阵图定义及分类：定义：把一些数字按照一定的要求，排成各种各样的图形，这类问题叫数阵图.数阵：是一种由幻方演变而来的数字图.数阵图的种类繁多，这里只向大家介绍三种数阵图：即封闭型数阵图、辐射型数阵图和复合型数阵图.二、解题方法：解决数阵类问题可以采取从局部到整体再到局部的方法入手：第一步：区分数阵图中的普通点(或方格)和关键点(或方格)；第二步：在数阵图的少数关键点(一般是交叉点)上设置未知数，计算这些关键点与相关点的数量关系，得到关键点上所填数的范围；第三步：运用已经得到的信息进行尝试．这个步骤并不是对所有数阵题都适用，很多数阵题更需要对数学方法的综合运用．三、幻方起源：幻方也叫纵横图，也就是把数字纵横排列成正方形，因此纵横图又叫幻方．幻方起源于我国，古人还为它编撰了一些神话．传说在大禹治水的年代，陕西的洛水经常大肆泛滥，无论怎样祭祀河神都无济于事，每年人们摆好祭品之后，河中都会爬出一只大乌龟，乌龟壳有九大块，横着数是3行，竖着数是3列，每块乌龟壳上都有几个点点，正好凑成1至9的数字，可是谁也弄不清这些小点点是什么意思．一次，大乌龟又从河里爬上来，一个看热闹的小孩惊叫起来：“瞧多有趣啊，这些点点不论横着加、竖着加还是斜着加，结果都等于十五！”于是人们赶紧把十五份祭品献给河神，说来也怪，河水果然从此不再泛滥了．这个神奇的图案叫做“幻方”，由于它有3行3列，所以叫做“三阶幻方”，这个相等的和叫做“幻和”．“洛书”就是幻和为15的三阶幻方．如下图：987654321我国北周时期的数学家甄鸾在《算数记遗》里有一段注解：“九宫者，二四为肩，六八为足，左三右七，戴九履一，五居中央．”这段文字说明了九个数字的排列情况，可见幻方在我国历史悠久．三阶幻方又叫做九宫图，九宫图的幻方民间歌谣是这样的：“四海三山八仙洞，九龙五子一枝连；二七六郎赏月半，周围十五月团圆．”幻方的种类还很多，这节课我们将学习认识了解它们．四、幻方定义：幻方是指横行、竖列、对角线上数的和都相等的数的方阵，具有这一性质的33⨯的数阵称作三阶幻方，44⨯的数阵称作四阶幻方，55⨯的称作五阶幻方……如图为三阶幻方、四阶幻方的标准式样，98765432113414151612978105113216。

【数学培优课程】 PC 第1册第08讲数阵图(上) 教师版

第08讲数阵图（上）教学目标：1、学习辐射型数阵图的填写方法；2、了解数阵图的填写方法和技巧；3、模仿理财师，锻炼计算能力、逻辑思维能力。

教学重点：掌握几种典型数阵图的填法。

教学难点：学习如何确定数阵图的关键位置，快速准确地填写。

教学过程：【知识拓展】例1、把1～7这七个数填在雪花的七个花瓣。

（1）使每三个位于同一直线上的花瓣上的数之和等于10，应该如何填写？（2）如果只要求每三个位于同一直线上的花瓣上的数之和都等于14，应该如何填写？解析部分：第一步：先让学生理解（1）同一直线上的花瓣上三个数的和是10，那么三个和数的总和是10×3=30，在这个总和中，填在中心位置的数加了3次，而其余的数却只加了1次，中心数被多计算了2次；第二步：让学生知道因为七个数的和是1+2+3+4+5+6+7=28，那么中心数是（30-28）÷（3-1）=1，然后利用配对法填写其他的数。

第三步：让学生按照上面的方法填写（2）。

家长建议：1、家长可以让学生做一做：如果只要求每三个位于同一直线上的花瓣上的数之和都等于12，应该如何填写？2、家长可以让学生做一做：将2～8这七个自然数，填入左下图的七个圆圈中，使得每条边上的三个数之和都等于13。

参考答案：填写方式如下图所示：重叠数：【10×3-（1+2+3+4+5+6+7）】÷（3-1）=1；利用配对法填写其它的空。

（1）每三个位于同一直线上的花瓣上的数之和是10；（2）每三个位于同一直线上的花瓣上的数之和是14；例2、把7，8，9，10，11，12，13，14分别填入○里，使每一个大圆上的五个数之和等于50。

参考答案：【50×2-（7+8+9+10+11+12+13+14）】÷（2-1）=16÷1=16a+b=16=7+9，那么每个大圆圈剩下的3个圆圈内数的和是50-16=34，34=8+12+14=11+10+13。

【课本】四年级下第08讲_复杂数阵图

第八讲复杂数阵图较复杂的数阵图往往给人感觉可能性太多，不知道该怎么去试．而寻找特殊对象可以帮助我们从纷繁复杂的条件中找到最关键的环节进行突破．那什么样的对象在数阵图中可以算特殊呢？比如数阵图要填的若干数中最大或者最小的就算特殊；奇偶性与别的数不同的也算特殊；数阵图中重数最多或最少的空格也算特殊……一个对象只要有与众不同的地方就是特殊．至于什么样的特殊对解题有用，那还得看题目本身．但只要你有一双发现特殊的慧眼，总可以找到那个对解题最有用的“特殊”．例题1请将1～10填入图中的10个圆圈中（其中两个数已经填好），使得除了第一行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差．「分析」根据已有的数字9，图中哪两个圆圈已经可以填出来了？剩下的数中，谁最特殊？请将1~8填入下图的8个方格中，使得a 、b 、c 、d 四个方格中的数，恰好等于它上方与之有公共边的两个方格中所填数的差．其中b 填7．那么d 填几？接下来我们重点学习一下数阵图分析中与“重数分析”有关的一些方法．在已知全部填入数字的情况下，我们通常是把所有相同的和相加，通过对每一个数字的重复次数来找出其中的特殊重数，是解题的关键．例题2将1~9填入图中的九个圆圈内，使四条直线上三个圆圈内所填数之和都是15．「分析」如果把四条直线的和加起来，每个圆圈各加了多少次？它们的重数一样吗？哪个圆圈的重数比较特殊？这个重数特殊的位置必须填几？练习2把1~8这八个数填入下边的圆圈内，使得每条直线上的数之和都等于14．例题3把1~7这七个数填入下图中的方框中，使得每条直线上的三个数之和都相等．如果中心方框内填的数相等，那么就视为同一种填法．请填出所有的可能性．「分析」如果把三条直线的和加起来，每个方框各加了多少次？它们的重数一样吗？哪个方框的重数比较特殊？这个重数特殊的位置可以填几？有几种可能？把1~9这九个数填入图中的圆圈内，使得三条直线上的所有数之和都是相等．请至少填出两种情况．例题4将数字1，2，3，4，5，6，7填入图中的小圆圈内，使得每个圆周上的3个数之和与每条直线上的3个数之和都相等．「分析」如果把两个圆周的和与三条直线的和加起来，每个圆圈各加了多少次？它们的重数一样吗？哪个圆圈的重数比较特殊？这个重数特殊的位置必须填几？练习4如图所示，将数字1、2、3、4、5、6、7、8、9填入图中的小圆圈内，使得圆周上的4个数之和与每条直线上的3个数之和都相等，那么这个和是多少？前面几个例题只有一个特殊格，那么接下来我们来看一下有多个特殊格、多个重数的题目．例题5图中一共有10个方格，现在把10个连续的自然数填到里面（9是这10个自然数中第三大的），每个方格填一个．如果要求图中的3个22的正方形中的4个数加起来的和都相等，那么这个和最小可能是多少？请给出一种填法．「分析」如果把三个正方形“加起来”，共12个数相加，相当于把每个方格各加了几次？由此你能得到什么结论？下图中有三个圆环，将1～8填入图中的8个圆圈内，使得每个圆环上4个顶点的数字之和都相等．那么这个和最大可能是多少？请给出一种填法．「分析」把三个圆周和加起来，图中的8个○有几种不同的重数？由此你能得到什么结论？课堂内外阵中国古代作战是非常讲究阵法即作战队形的，称之为“布阵”．布阵得法就能充分发挥军队的战斗力，克敌制胜．中国古代军事史上有名的作战阵法有三种：八阵：战国时大军事家孙膑创造，据说是受了《易经》八卦图的启发，所以又称八卦阵．具体阵势是大将居中，四面各布一队正兵，正兵之间再派出四队机动作战的奇兵，构成八阵．八阵散布成八，复而为一，分合变化，又可组成六十四阵．当年诸葛亮还用石头在四川奉节布设过八阵的方位，作为教练将士演习阵法之用，名为“八阵图”．撒星阵：南宋名将岳飞破金兵“拐子马”的阵法．撒星阵的队形布列如星，连成一排的“拐子马”冲来时士兵散而不聚，使敌人扑空．等敌人后撤时散开的士兵再聚拢过来，猛力扑击敌人，并用刀专砍马腿，以破“拐子马”．鸳鸯阵：明代将领戚继光为抗击倭寇而创设的一种阵法．他把士兵分为三队，当敌人进到百步时第一队士兵发射火器；敌人进到六十步时士兵发射弩箭；敌人进到十步时第三队士兵用刀矛向敌人冲杀．这些变化反映了中国作战阵法从传统的方阵向多兵种的集团阵法演变的过程．作业1.请将2~9填入下图的8个方格中，使得a、b、c、d四个方格中的数，恰好等于它上方与之有公共边的两个方格中所填数的差．其中b填7．2.将数字1，3，5，7，9，11，13填入右上图中的小圆圈内，使得每个圆周上的3个数之和与每条直线上的3个数之和都相等．3.把1至10填入右图的圆圈内，使得每条直线上的4个数之和都等于23．4.将2至8填入右上图的圆圈中，使得每条直线上的所有数字之和都相等．5.图中一共有10个方格，现在把10个连续的自然数填到里面（9是这10个自然数中第三大的），每个方格填一个．如果要求图中的3个22的正方形中的4个数加起来的和都相等，那么这个和最大可能是多少？请给出一种填法．。