垂径定理圆周角与圆心角的关系复习题
垂径定理专项训练题

最重要是三个定理:1、垂径定理 2、圆周角定理及其推论 3、切线的性质和判定 其它的性质和定理:同圆或等圆的半径相等; 圆心角、弧、弦、弦心距之间的关系一、垂径定理垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧。
推论:经过圆心、垂直于弦、平分弦、平分优弧、平分劣弧这五个条件中任意两个成立,其它三个也成立 垂径定理的作用:证明线段相等、证明角相等、弧相等、垂直。
1、研究有关弦的问题常用辅助线:作弦心距,构建直角三角形。
2、经过圆内一点的最长弦和最短弦;圆外一点到圆上的点的最短距离和最长距离例1如图,一条公路的转弯处是一段圆弦(即图中弧CD ,点O 是弧CD 的圆心,•其中CD=600m ,E 为弧CD 上一点,且OE ⊥CD ,垂足为F ,EF=90m ,求这段弯路的半径.分析:该题是典型的研究圆中有关弦的问题,根据常用辅助线需要作弦心距OF ,连接 OC 、OD 从而构建出两个直角三角形Rt △OCF 和Rt △ODF 说明:此题需要利用方程思想,利用勾股定理做等量关系构建出关于半径的一元方程例2:半径为10cm 的⊙O 中,弦AB=16cm ,弦CD=12cm ,且AB ∥CD ,则AB 与CD 此题有两个答案,是分类思想在圆中的经典体现,出题率很高。
也是利用勾股定理。
练习:1、已知:AB 是⊙O 的直径,弦CD ⊥AB 于点P ,CD =10cm ,AP:PB =1:5,则⊙O 的半径为_______。
2、在⊙O 中,P 为其内一点,过点P 的最长的弦为8cm ,最短的弦长为4cm ,则OP =____ _。
3、已知圆的半径为5cm ,一弦长为8cm ,则该弦的中点到弦所对的弧的中点的距离为__ _____。
4、已知圆心到圆的两条平行弦的距离分别是2和3,则两条平行弦之间的距离为_ ____。
5、在半径为5cm 的圆内有两条互相平行的弦,一条弦长为8cm ,另一条弦长为6cm ,则这两条弦之间的距离为_____ _。
圆的垂径定理试题(附答案)

2013中考全国100份试卷分类汇编圆的垂径定理1、(2013年潍坊市)如图,⊙O 的直径AB=12,CD 是⊙O 的弦,CD ⊥AB ,垂足为P ,且BP :AP=1:5,则CD 的长为( ).A.24B.28C.52D.542、(2013年黄石)如右图,在Rt ABC 中,90ACB ∠= ,3AC =,4BC =,以点C 为圆心,CA 为 半径的圆与AB 交于点D ,则AD 的长为( )A.95B. 245C. 185D. 523、(2013河南省)如图,CD 是O 的直径,弦AB CD ⊥于点G ,直线EF 与O 相切与点D ,则下列结论中不一定正确的是( )A. AG =BGB. AB ∥BFC.AD ∥BCD. ∠ABC =ADC4、(2013•泸州)已知⊙O 的直径CD=10cm ,AB 是⊙O 的弦,AB⊥CD,垂足为M ,且AB=8cm ,则AC 的长为( ) A. cm B. cm C. cm 或cm D. cm 或cm5、(2013•广安)如图,已知半径OD 与弦AB 互相垂直,垂足为点C ,若AB=8cm ,CD=3cm ,则圆O 的半径为( )A. cmB. 5cmC. 4cmD. cm6、(2013•绍兴)绍兴市著名的桥乡,如图,石拱桥的桥顶到水面的距离CD 为8m ,桥拱半径OC 为5m ,则水面宽AB 为( )7、(2013•温州)如图,在⊙O中,OC⊥弦AB于点C,AB=4,OC=1,则OB的长是()A. B. C. D.8、(2013•嘉兴)如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()A. 2B.C.D.9、(2013•莱芜)将半径为3cm的圆形纸片沿AB折叠后,圆弧恰好能经过圆心O,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为()A. B. C. D. 3210、(2013•徐州)如图,AB是⊙O的直径,弦CD⊥AB,垂足为P.若CD=8,OP=3,则⊙O的半径为()A. 10B. 8C. 5D. 311、(2013浙江丽水)一条排水管的截面如图所示,已知排水管的半径OB=10,水面宽AB=16,则截面圆心O到水面的距离OC是A. 4B. 5C.6D.812、(2013•宜昌)如图,DC 是⊙O直径,弦AB⊥CD于F,连接BC,DB,则下列结论错误的是()A. B. AF=BF C. OF=CF D. ∠DBC=90°13、(2013•毕节地区)如图在⊙O中,弦AB=8,OC⊥AB,垂足为C,且OC=3,则⊙O的半径()A. 5B. 10C. 8D. 614、(2013•南宁)如图,AB是⊙O的直径,弦CD交AB于点E,且AE=CD=8,∠BAC=∠BOD,则⊙O 的半径为()A. 4B. 5C. 4D. 315、(2013年佛山)半径为3的圆中,一条弦长为4,则圆心到这条弦的距离是()A.3B.4C.5D.716、(2013甘肃兰州4分、12)如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为()A.3cm B.4cm C.5cm D.6cm17、(2013•内江)在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx﹣3k+4与⊙O交于B、C两点,则弦BC的长的最小值为.18、(13年安徽省4分、10)如图,点P是等边三角形ABC外接圆⊙O上的点,在以下判断中,不.正确..的是()19、(2013•宁波)如图,AE是半圆O的直径,弦AB=BC=4,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为.图20 图21 图2220、(2013•宁夏)如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕AB的长为 cm.21、(2013•包头)如图,点A、B、C、D在⊙O上,OB⊥AC,若∠BOC=56°,则∠ADB=度.图23 图24 图25 图26 图27 图2823、(2013•黄冈)如图,M是CD的中点,EM⊥CD,若CD=4,EM=8,则所在圆的半径为.24、(2013•绥化)如图,在⊙O中,弦AB垂直平分半径OC,垂足为D,若⊙O的半径为2,则弦AB 的长为.25、(2013哈尔滨)如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为52,CD=4,则弦AC的长为.26、(2013•张家界)如图,⊙O的直径AB与弦CD垂直,且∠BAC=40°,则∠BOD=.27、(2013•遵义)如图,OC是⊙O的半径,AB是弦,且OC⊥AB,点P在⊙O上,∠APC=26°,则∠BOC=度.28、(2013陕西)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为.29、(2013年广州市)如图7,在平面直角坐标系中,点O为坐标原点,点P在第一象限,PΘ与x轴交于O,A两点,点A的坐标为(6,0),PΘ的半径为13,则点P的坐标为 ____________.30、(2013年深圳市)如图5所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动。
垂径定理和圆周角圆心角

一、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。
推论2:圆的两条平行弦所夹的弧相等。
即:在⊙O 中,∵AB ∥CD ∴弧AC =弧BD 二、圆心角定理圆心角定理:同圆或等圆中,相等的圆心角所对的弦相等,所对的弧相等,弦心距相等。
此定理也称1推3定理,即上述四个结论中,只要知道其中的1个相等,则可以推出其它的3个结论, 即:①AOB DOE ∠=∠;②AB DE =;③OC OF =;④ 弧BA =弧BD 三、圆周角定理1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。
即:∵AOB ∠和ACB ∠是弧AB 所对的圆心角和圆周角 ∴2AOB ACB ∠=∠2、圆周角定理的推论:推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧; 即:在⊙O 中,∵C ∠、D ∠都是所对的圆周角 ∴C D ∠=∠推论2:半圆或直径所对的圆周角是直角;圆周角是直角所对的弧是半圆,所对的弦是直径。
即:在⊙O 中,∵AB 是直径 或∵90C ∠=︒ ∴90C ∠=︒ ∴AB 是直径推论3:若三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。
即:在△ABC 中,∵OC OA OB ==DBABA∴△ABC 是直角三角形或90C ∠=︒注:此推论实是初二年级几何中矩形的推论:在直角三角形中斜边上的中线等于斜边的一半的逆定理。
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等. 四、圆内接四边形圆的内接四边形定理:圆的内接四边形的对角互补,外角等于它的内对角。
2020苏教版九年级数学上册 垂径定理、弦、弧、圆心角、圆周角练习含答案

【文库独家】九年垂径定理、弦、弧、圆心角、圆周角练习1.已知:AB交圆O于C、D,且AC=BD.你认为OA=OB吗?为什么?2. 如图所示,是一个直径为650mm的圆柱形输油管的横截面,若油面宽AB=600mm,求油面的最大深度。
6003. 如图所示,AB是圆O的直径,以OA为直径的圆C与圆O的弦AD相交于点E。
你认为图中有哪些相等的线段?为什么?ADBOCE4.如图所示,OA是圆O的半径,弦CD⊥OA于点P,已知OC=5,OP=3,则弦CD=____________________。
5. 如图所示,在圆O中,AB、AC为互相垂直且相等的两条弦,OD ⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则圆O的半径为____________cm。
6. 如图所示,AB是圆O的直径,弦CD⊥AB,E为垂足,若AB=9,BE=1,则CD=_________________。
CA P ODCE OA D B7. 如图所示,在△ABC中,∠C=90°,AB=10,AC=8,以AC为直径作圆与斜边交于点P,则BP的长为________________。
8. 如图所示,四边形ABCD内接于圆O,∠BCD=120°,则∠BOD=____________度。
9.如图所示,圆O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是()A. 3≤OM≤5B. 4≤OM≤5C. 3<OM<5D. 4<OM<510.下列说法中,正确的是()A. 到圆心的距离大于半径的点在圆内B. 圆的半径垂直于圆的切线C. 圆周角等于圆心角的一半D. 等弧所对的圆心角相等11.若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于()A. 45°B. 90°C. 135°D. 270°12. 如图所示,A、B、C三点在圆O上,∠AOC=100°,则∠ABC 等于()A. 140°B. 110°C. 120°D. 130°13. △ABC 中,∠C=90°,AB=cm 4,BC=cm 2,以点A 为圆心,以cm 5.3长为半径画圆,则点C 在圆A___________,点B 在圆A_________; 14. 圆的半径等于cm 2,圆内一条弦长23cm ,则弦的中点与弦所对弧的中点的距离等于_____________;15. 如图所示,已知AB 为圆O 的直径,AC 为弦,OD ∥BC 交AC 于D ,OD=cm 2,求BC 的长;B16. 如图所示,破残的圆形轮片上,弦AB 的垂直平分线交弧AB 于点C ,交弦AB 于点D 。
自学初中数学资料 圆之垂径定理、圆心角、圆周角定理 (资料附答案)

自学资料一、圆的相关定义【知识探索】1.定理:不在同一直线上的三点确定一个圆.【说明】(1)过平面上一点能作无数多个圆;(2)过平面上两点能做无数多个圆,这些圆的圆心在两点连线的垂直平分线上;(3)过平面上三点:①三点不在同一直线上,能作唯一一个圆;②三点在同一直线上,不能作圆.【错题精练】例1.下列命题正确的个数有()①过两点可以作无数个圆;②经过三点一定可以作圆;③任意一个三角形有一个外接圆,而且只有一个外接圆;④任意一个圆有且只有一个内接三角形.A. 1个B. 2个C. 3个D. 4个第1页共23页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训【解答】解:①过两点可以作无数个圆,正确;②经过三点一定可以作圆,错误;③任意一个三角形有一个外接圆,而且只有一个外接圆,正确;④任意一个圆有且只有一个内接三角形,错误,正确的有2个,故选:B.【答案】B例2.有下列四个命题,其中正确的有()①圆的对称轴是直径;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.A. 4个B. 3个C. 2个D. 1个【答案】C例3.如图,在平面直角坐标系中,点A坐标为(﹣4,0),⊙O与x轴的负半轴交于B(﹣2,0).点P是⊙O上的一个动点,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于()A.B.C.D.【解答】第2页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【答案】C例4.如图,已知△ABC.(1)尺规作图作△ABC的外接圆(保留作图痕迹,不写作法);(2)设△ABC是等腰三角形,底边BC=10,腰AB=6,求圆的半径r.【答案】解:(1)如图所示;(2)连接OB,连接OA交BC于点E,∵△ABC是等腰三角形,底边BC=10,腰AB=6,∴BE=CE=5,AE=√AB2−BE2=√11,在Rt△BOE中,r2=52+(r-√11)2∴r=18√11=18√1111.第3页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训第4页 共页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【解答】【解答】解:如图:连接OA,作OM⊥AB与M,∵⊙O的直径为10,∴半径为5,∴OP的最大值为5,∵OM⊥AB与M,∴AM=BM,∵AB=6,∴AM=3,在Rt△AOM中,OM==4,OM的长即为OP的最小值,∴4≤OP≤5.【答案】4≤OP≤55.已知:△ABC(如图)(1)求作:△ABC的外接圆(要求:用尺规作图,保留作图痕迹,不要求写作法及证明).(2)若∠A=60°,BC=8√3,求△ABC的外接圆的半径.【答案】解:(1)如图所示:⊙O即为所求△ABC的外接圆;(2)过点O作OD⊥BC于点D,∵∠A=60°,BC=8√3,∴∠COD=60°,CD=4√3,第5页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训∴CO=4√3sin60°=8,答:△ABC的外接圆的半径为8.二、圆心角、弧、弦、弦心距、圆周角之间的关系【知识探索】年份题量分值考点题型2015114圆内接四边形的性质;点与圆的位置关系选择、简答201613圆周角定理;填空2017219弧长面积;切线的性质;圆周角定理选择、填空、简答201824圆周角定理;填空2019216扇形面积;切线长定理;圆心角、圆周角、垂径定理填空、解答【错题精练】例1.如图所示,小华从一个圆形场地的A点出发,沿着与半径OA夹角为α的方向行走,走到场地边缘B后,再沿着与半径OB夹角为α的方向折向行走.按照这种方式,小华第五次走到场地边缘时处于弧AB上,此时∠AOE=52°,则α的度数是()A. 51.5°B. 60°C. 72°D. 76°【解答】解:连接OD.∵∠BAO=∠CBO=α,∴∠AOB=∠BOC=∠COD=∠DOE,∵∠AOE=52°,∴∠AOB=(360°-52°)÷4=77°,第6页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训第7页 共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼 非学科培训∴α=(180°-77°)÷2=51.5°. 故选:A .【答案】A例2.如图,在△ABC 中,∠C=90°,以点C 为圆心,BC 为半径的圆交AB 于点D ,交AC 于点E .(1)若∠A=25°,求BD̂的度数. (2)若BC=9,AC=12,求BD 的长.【答案】解:(1)连接CD ,如图, ∵∠ACB=90°,∴∠B=90°-∠A=90°-25°=65°,∵CB=CD ,∴∠CDB=∠B=65°, ∴∠BCD=180°-2∠B=50°, ∴BD ̂的度数为50°;(2)作CH ⊥BD ,如图,则BH=DH , 在Rt △ACB 中,AB=√92+122=15, ∵12CH•AB=12BC•AC , ∴CH=9×1215=365, 在Rt △BCH 中,BH=√92−(365)2=275,∴BD=2BH=545.̂的度数为()例3.已知如图,在⊙O中,OA⊥OB,∠A=35°,则CDA. 20°B. 25°C. 30°D. 35°【解答】解:连接OC,∵OA⊥OB,∴∠AOB=90°,∵∠A=35°,∴∠OBC=90°-35°=55°,∴OB=OC,∴∠OBC=∠OCB=55°,∴∠COB=70°,∴∠COD=90°-70°=20°,̂的度数为20°,∴CD故选:A.【答案】A例4.已知AB是⊙O的直径,点C,D是⊙O上的点,∠A=50°,∠B=70°,连接DO,CO,DC (1)如图①,求∠OCD的大小:(2)如图②,分别过点C,D作OC,OD的垂线,相交于点P,连接OP,交CD于点M已知⊙O的半径为2,求OM及OP的长.第8页共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练非学科培训【答案】解:(1)∵OA=OD,OB=OC,∴∠A=∠ODA=50°,∠B=∠OCB=70°,∴∠AOD=80°,∠BOC=40°,∴∠COD=180°-∠AOD-∠BOC=60°,∵OD=OC,∴△COD是等边三角形,∴∠OCD=60°;(2)∵PD⊥OD,PC⊥OC,∴∠PDO=∠PCO=90°,∴∠PDC=∠PCD=30°,∴PD=PC,∵OD=OC,∴OP垂直平分CD,∴∠DOP=30°,∵OD=2,∴OM=√32OD=√3,OP=4√33.例5.如图,AB为⊙O的直径,△ABC的边AC,BC分别与⊙O交于D,E,若E为BD̂的中点.(1)求证:DE=EC;(2)若DC=2,BC=6,求⊙O的半径【答案】解:(1)连结AE,BD,∵E为BD̂的中点,∴ED̂=BÊ,∴∠CAE=∠BAE,∵∠AEB是直径所对的圆周角,第9页共23页自学七招之预习轻身术:预习习惯培养好,课堂轻松没烦恼非学科培训第10页 共23页自学七招之错题本锁骨术:巧用智能错题本,错题定期反复练 非学科培训∴∠AEB=90°, 即AE ⊥BC ,∴∠AEB=∠AEC=90°,在△AEC 和△AEB 中{∠CAE =∠BAE AE =AE ∠AEC =∠AEB ,∴△AEC ≌△AEB (ASA ), ∴CE=BE , ∴DE=CE=BE=12BC ;(2)在Rt △CBD 中,BD 2=BC 2-CD 2=32, 设半径为r ,则AB=2r , 由(1)得AC=AB=2r , AD=AC-CD=2r-2,在Rt △ABD 中AD 2+BD 2=AB 2, ∴(2r-2)2+32=(2r )2, 解得:r=4.5,∴⊙O 的半径为4.5.例6.如图,点A ,B ,C 在⊙O 上,AB ∥OC .(1)求证:∠ACB+∠BOC=90°;(2)若⊙O 的半径为5,AC=8,求BC 的长度.【答案】(1)证明:∵AB̂对的圆周角是∠ACB ,对的圆心角是∠AOB , ∴∠AOB=2∠ACB , ∵OB=OA ,∴∠ABO=∠BAO , ∵AB ∥OC ,∴∠ABO=∠BOC ,∠BAO+∠AOC=180°, ∴∠BAO+∠AOB+∠BOC=180°, 即2∠ACB+2∠BOC=180°, ∴∠ACB+∠BOC=90°;(2)延长AO 交⊙O 于D ,连接CD ,则∠ACD=90°,由勾股定理得:CD=√AD2−AC2=√(5+5)2−82=6,∵OC∥AB,∴∠BOC=∠ABO,∠COD=∠BAO,∵∠BAO=∠ABO,∴∠BOC=∠COD,在△BOC和△DOC中{OB=OD∠BOC=∠DOC OC=OC∴△BOC≌△DOC(SAS),∴BC=CD,∵CD=6,∴BC=6.例7.如图,AB是半圆O的直径,AC是弦,∠CAB=60∘,若AB=6cm.(1)求弦AC的长;(2)点P从点A开始,以1cm/s的速度沿AB向点B运动,到点B停止,过点P作PQ∥AC,交半圆O于点Q,设运动时间为t(s).①当t=1时,求PQ的长;②若△OPQ为等腰三角形,直接写出t(t>0)的值.【解答】(1)解:如图1中,∵OA=OC,∠CAB=60∘,∴△AOC是等边三角形,∴AC=OA=3(cm);(2)解:①如图2中,作OH⊥PQ于H,连接OQ,由题意得:AP=1,OP=2,∵PQ∥AC,∴∠OPH=∠CAB=60∘,在Rt△OPH中,∵∠POH=90∘−∠OPH=30∘,OP=2,∴PH=1OP=1,OH=√3PH=√3,2在Rt△QOH中,HQ=√OQ2−OH2=√6,∴PQ=PH+HQ=1+√6;②如图3中,∵△OPQ是等腰三角形,观察图象可知,只有OP=PQ,作PH⊥OQ于H.∵PQ∥AC,∴∠QPB=∠CAB=60∘,∵PQ=PO,PH⊥OQ,,∠POQ=∠PQO=30∘,∴OH=HQ=32∴OP=OH÷cos30∘=√3,∴AP=3+√3,∴t=3+√3秒时,△OPQ是等腰三角形.【答案】(1)3cm;(2)①1+√6;②t=3+√3.例8.如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D、E,且.(1)试判断△ABC的形状,并说明理由.(2)已知半圆的半径为5,BC=12,求sin∠ABD的值.【解答】(1)解:△ABC为等腰三角形.理由如下:连结AE,如图,∵,∴∠DAE=∠BAE,即AE平分∠BAC,∵AB为直径,∴∠AEB=90∘,∴AE⊥BC,∴△ABC为等腰三角形;(2)解:∵△ABC为等腰三角形,AE⊥BC,∴BE=CE=12BC=12×12=6,在Rt△ABE中,∵AB=10,BE=6,∴AE=√102−62=8,∵AB为直径,∴∠ADB=90∘,∴12AE⋅BC=12BD⋅AC,∴BD=8×1210=485,在Rt△ABD中,∵AB=10,BD=485,∴AD=√AB2−BD2=145,∴sin∠ABD=ADAB =14510=725.【答案】(1)略;(2)725.【举一反三】1.如图,弦AC、BD相交于点E,且AB̂=BĈ=CD̂,若∠AED=80°,则∠ACD的度数为()A. 20°B. 25°C. 30°D. 15°【解答】解:如图,设AB̂的度数为m,AD̂的度数为n,∵AB̂=BĈ=CD̂,∴BĈ、CD̂的度数都为m,∴3m+n=360°①∵∠AED=80°,∴∠C+∠D=80°,∴12m+12n=80°②,由①②组成{3m+n=360°12m+12n=80°,解得m=100°,n=60°∴∠ACD=12n=30°.故选:C.【答案】C2.已知△ABC内接于⊙O,点D平分弧BmĈ.(1)如图①,若∠BAC=2∠ABC.求证:AC=CD;(2)如图②,若BC为⊙O的直径,且BC=10,AB=6,求AC,CD的长.【答案】(1)证明:∵点D平分弧BmĈ,∴弧DC=弧DB,∵∠BAC=2∠ABC,∴弧BDC=2弧AC,∴弧CA=弧CD,∴AC=CD;(2)解:连结BD,如图②,∵BC为⊙O的直径,∴∠BAC=∠BDC=90°,在Rt △BAC 中,∵BC=10,AB=6,∴AC=√BC 2−AB 2=8;∵弧DC=弧DB ,∴DB=DC ,∴△BCD 为等腰直角三角形,∴CD=√22BC=5√2.3.如图,在⊙O 中,点C 是优弧ACB 的中点,D 、E 分别是OA 、OB 上的点,且AD=BE ,弦CM 、CN 分别过点D 、E .(1)求证:CD=CE .(2)求证:AM̂=BN ̂.【答案】(1)证明:连接OC .∵AĈ=BC ̂, ∴∠COD=∠COE ,∵OA=OB ,AD=BE ,∴OD=OE ,∵OC=OC ,∴△COD ≌△COE (SAS ),∴CD=CE .(2)分别连结OM ,ON ,∵△COD ≌△COE ,∴∠CDO=∠CEO ,∠OCD=∠OCE ,∵OC=OM=ON ,∴∠OCM=∠OMC ,∠OCN=∠ONC ,∴∠OMD=∠ONE ,∵∠ODC=∠DMO+∠MOD ,∠CEO=∠CNO+∠EON ,∴∠MOD=∠NOE ,∴AM̂=BN ̂.4.如图,已知△ABC中,AB=AC,以AB为直径的⊙O与边BC相交于点D,过点D作⊙O的切线与AC交于点E.(1)求BDBC的值.(2)判断DE与AC的位置关系,并证明你的结论.(3)已知BC:AB=2:3,DE=4√2,求⊙O的直径.【解答】(1)解:如图,连接AD,∵AB是⊙O的直径,∴AD⊥BC,∵AB=AC,∴BD=DC,∴BDBC =12;(2)解:DE⊥AC;连接OD,∵DE是⊙O的切线,∴DE⊥OD,∵AB=AC,∴∠B=∠C,∵OB=OD,∴∠B=∠ODB,∴∠ODB=∠C,∴AC∥OD,∴DE⊥AC;(3)解:∵BDBC =12且BC:AB=2:3,∴AB:CD=3,∵∠ADB =∠DEC =90∘,∠B =∠C ,∴△ABD ∽△DCE ,∴DC AB =CE BD =13,设CE =a ,则BD =CD =3a ,AB =9a ,在Rt△DEC 中,由勾股定理得:DE =2a √2=4√2,∴a =2,∴AB =18.【答案】(1)12;(2)DE ⊥AC ;(3)18.5.已知直径CD ⊥弦BF 于 E ,AB 为ʘO 的直径.(1)求证:FD̂=AC ̂; (2)若∠DAB=∠B ,求∠B 的度数.【答案】(1)证明:∵直径CD ⊥弦BF ,∴FD̂=BD ̂, ∵∠AOC=∠BOD ,∴BD̂=AC ̂, ∴FD̂=AC ̂; (2)解:由圆周角定理得,∠BOD=2∠DAB ,∵∠DAB=∠B ,∴∠BOD=2∠B ,∵CD ⊥BF ,∴∠B=30°.6.如图,⊙O 的半径为2,弦BC =2√3,点A 是优弧BC 上一动点(不包括端点),△ABC 的高BD 、CE 相交于点F ,连结ED .下列四个结论:①∠A 始终为60°;②当∠ABC =45∘时,AE =EF ;③当△ABC 为锐角三角形时,ED =√3;④线段ED 的垂直平分线必平分弦BC .其中正确的结论是 .(把你认为正确结论的序号都填上)【答案】①②③④.7.圆O的直径为10cm,A是圆O内一点,且OA=3cm,则圆O中过点A的最短弦长=__________cm【答案】88.如图,在圆O中,AB为直径,CD为弦,已知∠ACD=40°,则∠BAD=__________°【答案】501.如图,AB圆O的直径,点C在圆O上,若∠OCA=50°,AB=4,则弧BC的长为()πA. 103B. 109π C. 59πD. 518π【答案】B2.如图,将钢珠放在一个边长AB=8mm 的正方形的方槽内,测得钢珠顶端离零件表面的距离为8mm ,则这个钢珠的直径为______mm .【答案】103.如图,AB 是半圆的直径,E 是弦AC 上一点,过点E 作EF ⊥EB ,交AB 于点F ,过点A 作AD ∥EF ,交半圆于点D .若C 是BD ̂的中点,AF AE =√54,则EFAD 的值为 .【解答】解:延长BE 交AD 于A',∵AD ∥EF ,EF ⊥BE ,∴AA'⊥BA',∴∠AA'B=90°,∵AB 为⊙O 的直径,∴∠ADB=90°,∴D 与A'重合,∵AFAE =√54,∴设AF=√5a,AE=4a,过F作FG⊥AE于G,∵C是BD̂的中点,∴CD̂=BĈ,∴∠DAC=∠BAC,∵AD∥EF,∴∠BFE=∠DAB=2∠BAC=∠BAC+∠AEF,∴∠BAC=∠AEF,∴AF=EF,∴AG=EG=2a,由勾股定理得:FG=a,∵∠DAE=∠GAF,∠ADE=∠AGF=90°,∴△ADE∽△AGF,∴ADAE =AGAF,∴AD4a =2a√5a,AD=8a√5,∴EFAD =√5a8a√5=58,故答案为:58.【答案】584.在⊙O的内接△ABC中,AD⊥BC于D,(1)①图1中,若作直径AP,求证:AB.AC=AD.AP;②已知AB+AC=12,AD=3,设⊙O的半径为y,AB的长为x.求y与x的函数关系式及自变量x的取值范围;(2)图2中,点E为⊙O上一点,且弧AE=弧AB,求证:CE+CD=BD.【答案】5.在⊙O的内接△ABC中,AB+AC=12,AD⊥BC,垂足为D,且AD=3,设⊙O的半径为y,AB的长为x。
浙教版九年级上册第三章 3.3垂径定理 圆心角定理 圆周角定理的综合应用
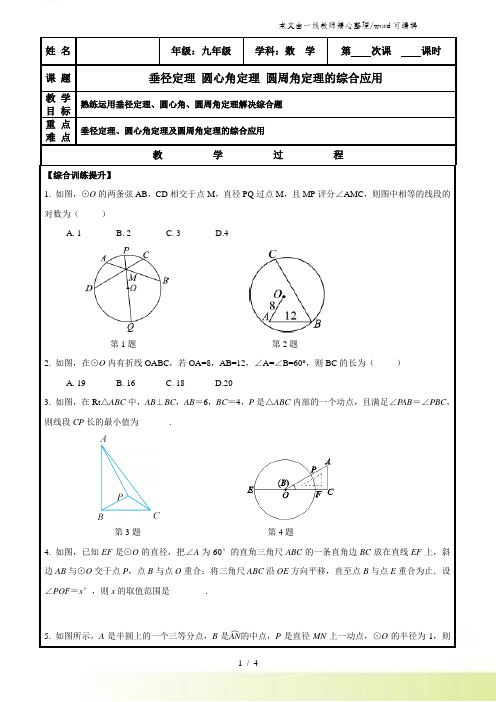
【综合训练提升】1. 如图,⊙O 的两条弦AB ,CD 相交于点M ,直径PQ 过点M ,且MP 评分∠AMC ,则图中相等的线段的对数为( )A. 1B. 2C. 3D.4第1题 第2题2. 如图,在⊙O 内有折线OABC ,若OA=8,AB=12,∠A=∠B=60°,则BC 的长为( ) A. 19 B. 16 C. 18 D.203. 如图,在Rt △ABC 中,AB ⊥BC ,AB =6,BC =4,P 是△ABC 内部的一个动点,且满足∠P AB =∠PBC ,则线段CP 长的最小值为_______.第3题 第4题4. 如图,已知EF 是⊙O 的直径,把∠A 为60°的直角三角尺ABC 的一条直角边BC 放在直线EF 上,斜边AB 与⊙O 交于点P ,点B 与点O 重合;将三角尺ABC 沿OE 方向平移,直至点B 与点E 重合为止.设∠POF =x °,则x 的取值范围是________.5. 如图所示,A 是半圆上的一个三等分点,B 是AN ︵的中点,P 是直径MN 上一动点,⊙O 的半径为1,则姓 名 年级:九年级 学科:数 学 第 次课 课时课 题垂径定理 圆心角定理 圆周角定理的综合应用教 学目 标 熟练运用垂径定理、圆心角、圆周角定理解决综合题重 点难 点垂径定理、圆心角定理及圆周角定理的综合应用教 学 过 程P A +PB 的最小值是多少?6. 如图,四边形ABCD 的四个顶点在⊙O 上,且对角线AC ⊥BD ,OE ⊥BC 于点E . 求证:OE =12AD .7. 如图,⊙O 的两条弦AB ,CD 交于点E ,OE 平分∠BE D. (1)求证:AB =C D.(2)若∠BED =60°,EO =2,求BE -AE 的值.8.(1)如图①,AB 是⊙O 的直径,C ,P 是⊙O 上两点,AB =13,AC =5.若P 是AB ︵的中点,求P A 的长;(2)如图②,若P 是BC ︵的中点,求P A 的长.9. 如图所示,在⊙O 中,半径OA ⊥OB ,C ,D 是AB ︵的三等分点,AB 分别交OC ,OD 于点E ,F . 求证:AE =BF =CD .10. 如图,C 为△ABD 外接圆上的一动点(点C 不在BAD ︵上,且不与点B ,D 重合),∠ACB =∠ABD =45°. (1)求证:BD 是该外接圆的直径. (2)连结CD ,求证:2AC =BC +C D.(3)若△ABC 关于直线AB 的对称图形为△ABM ,连结DM ,试探究AM ,BM ,DM 三者之间满足的等量关系,并证明你的结论.11. 如图,半圆的直径AB 长为2,C ,D 是半圆上的两点,若AC ︵的度数为96°,BD ︵的度数为36°,动点P在直径AB 上,求CP +PD 的最小值.12. 如图所示,两等圆⊙O 1和⊙O 2,相交于A ,B 两点,且两圆互过圆心,过点B 作任一直线,分别交⊙O 1,⊙O 2于C ,D 两点,连接AC ,AD. (1)试猜想△ACD 的形状,并说明理由;(2)若已知条件中两圆不一定互相过圆心,试猜想△ACD 的形状,并说明理由.13.(1)如图,CD ,AB 所在的直线分别交⊙O 于C ,D ,A ,B 四点,CD ,AB 相交于点P ,若AC ︵的度数为x°,BD ︵的度数为y°(x°>y°),则∠BPD=12(x°+y°),你认为这个结论正确吗?请说明理由.(2)若CD ,AB 所在的直线的交点P 在⊙O 外,则上述结论还成立吗?若成立,请证明;若不成立,应怎样表示∠BPD?。
专题12垂径定理、圆周角和圆心角的关系(6个知识8种题型)(原卷版)-初中数学北师大版9年级上册

专题12垂径定理、圆周角和圆心角的关系(6个知识8种题型)【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.垂径定理(重点)知识点2.垂径定理的推论(难点)知识点3.圆周角(重点)知识点4.圆周角定理(重点)知识点5.圆周角定理的推论(难点)知识点6.圆内接四边形的概念与性质(重点)【方法二】实例探索法题型1.最短距离问题题型2.辅助线的添加方法题型3.方程思想题型4.垂径定理的实际应用题型5.圆中角度的计算题型6.圆内接四边形与圆周角定理的综合应用题型7.动点问题题型8.圆周角定理与其他几何知识的综合【方法三】成果评定法【学习目标】1.掌握垂径定理,并会运用垂径定理进行简单的计算。
2.掌握与垂径定理有关的推论,并能运用这一推论解决相关问题。
3.认识圆周角,掌握圆周角和圆心角的关系,直径所对的圆周角的特征。
4.能运用圆心角和圆周角的关系、直径所对的圆周角的特征解决相关问题。
【知识导图】【倍速学习五种方法】【方法一】脉络梳理法知识点1.垂径定理(重点)垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.【例1】.(2022秋•锡山区校级月考)如图,在⊙O中,OC⊥AB于点C,若⊙O的半径为10,AB=16,则OC的长为.【变式】.(2022秋·江苏南京·九年级南京市第一中学校考阶段练习)如图,AB是⊙O的直径,弦CD⊥AB 于点E,则下列结论一定正确的个数有()①CE =DE ;②BE =OE ;③ CBBD =;④∠CAB =∠DAB .A .4个B .3个C .2个D .1个知识点2.垂径定理的推论(难点)推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.推论2:弦的垂直平分线经过圆心,并且平分弦所对的两条弧.推论3:平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧.【例2】.(2022秋·九年级统考期中)如图,O 的弦8AB =,M 是AB 的中点,且3OM =,则O 的半径等于()A .7B .4C .5D .6【变式】.(2023秋·浙江台州·九年级统考期末)如图,在正方形网格中,一条圆弧经过、、A B C 三点,那么这条圆弧所在圆的圆心是().A .点PB .点QC .点RD .点M知识点3.圆周角(重点)1.圆周角定义:像图中∠AEB 、∠ADB 、∠ACB 这样的角,它们的顶点在圆上,并且两边都与圆相交的角叫做圆周角.2.圆心角与圆周角的区别与联系【例3】观察下图中角的顶点与两边有何特征?指出哪些角是圆周角?知识点4.圆周角定理(重点)在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.【例4】如图,100AOB ∠= ,点C 在O 上,且点C 不与A、B 重合,则ACB ∠的度数为()A.50 B.80 或50 C.130 D.50 或130【变式】如图,AB 是⊙O 的弦,∠AOB=80°则弦AB 所对的圆周角是.知识点5.圆周角定理的推论(难点)半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.要点诠释:(1)圆周角必须满足两个条件:①顶点在圆上;②角的两边都和圆相交.(2)圆周角定理成立的前提条件是在同圆或等圆中.(3)圆心与圆周角存在三种位置关系:圆心在圆周角的一边上;圆心在圆周角的内部;圆心在圆周角的外部.(如下图)【例5】(2023秋·江苏·九年级专题练习)如图,CD 是O 的直径,A 、B 是O 上的两点,若40ACD ∠=︒,则ABC ∠的度数为()A .50︒B .40︒C .20︒D .140︒【变式】如图,⊙A 过点O(0,0),C(3,0),D(0,1),点B 是x 轴下方⊙A 上的一点,连接BO 、BD ,则∠OBD 的度数是.知识点6.圆内接四边形的概念与性质(重点)(1)定义:圆内接四边形:顶点都在圆上的四边形,叫圆内接四边形.(2)性质:圆内接四边形对角互补,外角等于内对角(即它的一个外角等于它相邻内角的对角).【例6】(2022秋•靖江市期末)如图,已知四边形ABCD内接于⊙O.求证:∠A+∠C=180°.【变式】如图已知四边形ABCD内接于⊙O,∠ABC=70°,则∠ADC的度数是.【方法二】实例探索法题型1.最短距离问题题型2.辅助线的添加方法A.6B.题型3.方程思想3.(2022秋•江宁区校级月考)如图是一个隧道的横截图,它的形状是以点O为圆心的一部分,如果M是⊙O中弦CD的中点,EM经过圆心O交⊙O于点E,若CD=4m,EM=6m,则⊙O的半径为m.题型4.垂径定理的实际应用4.(2022秋•如皋市校级月考)兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为m.5.(2022•钟楼区校级模拟)筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且⊙O被水面截得弦AB长为4米,⊙O半径长为3米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是()A.1米B.2米C.米D.米6.(2022秋•泰州月考)如图,有一座拱桥是圆弧形,它的跨度AB=60米,拱高PD=18米.(1)求圆弧所在的圆的半径r的长;(2)当洪水泛滥到跨度只有30米时,要采取紧急措施,若拱顶离水面只有4米,即PE=4米时,是否要采取紧急措施?题型5.圆中角度的计算7.(2022秋•鼓楼区期末)如图,AB为⊙O的直径,D是弦AC延长线上一点,AC=CD,DB的延长线交⊙O 于点E,连接CE.(1)求证∠A=∠D;(2)若的度数为108°,求∠E的度数.题型6.圆内接四边形与圆周角定理的综合应用8.(2022秋•宿城区期末)如图,四边形ABCD内接于一圆,CE是边BC的延长线.(1)求证∠DAB=∠DCE;(2)若∠DAB=60°,∠ACB=70°,求∠ABD的度数.9.(2022秋•镇江期中)如图,四边形ABCD为⊙O的内接四边形,∠EAD=∠BAC,BA、CD延长线交于点E.求证:BD=BC.题型7.动点问题10.(2023·江苏泰州·统考中考真题)已知:A 、B 为圆上两定点,点C 在该圆上,C ∠为 AB 所对的圆周角.知识回顾(1)如图①,O 中,B 、C 位于直线AO 异侧,135AOB C ︒∠+∠=.①求C ∠的度数;②若O 的半径为5,8AC =,求BC 的长;逆向思考(2)如图②,P 为圆内一点,且120APB ∠<︒,PA PB =,2APB C ∠=∠.求证:P 为该圆的圆心;拓展应用(3)如图③,在(2)的条件下,若90APB ∠=︒,点C 在P 位于直线AP 上方部分的圆弧上运动.点D 在P 上,满足2CD CB CA =-的所有点D 中,必有一个点的位置始终不变.请证明.题型8.圆周角定理与其他几何知识的综合11.(2023•滨江区一模)如图1,AB 为⊙O 的直径,CD ⊥AB 于点E ,,BF 与CD 交于点G .(1)求证:CD =BF .(2)若BE =1,BF =4,求GE 的长.(3)连结GO ,OF ,如图2,求证:.【方法三】成果评定法一.选择题(共6小题)1.(2023秋•惠山区校级期中)如图,AB 是O 的直径,弦CD AB ⊥于点E ,10AB cm =,8CD cm =,则BE 的长为()A .5cmB .3cmC .2cmD .1.5cm2.(2023春•鼓楼区校级月考)如图,在正方形ABCD 中,4AB =,以边CD 为直径作半圆O ,E 是半圆O 上的动点,EF DA ⊥于点F ,EP AB ⊥于点P ,设EF x =,EP y =22x y +()A .231-B .423-C .251-D .252-3.(2023秋•滨湖区校级期中)“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺.问:径几何?”用现在的几何语言表达即:如图,弦AB CD ⊥,垂足为点D ,1CD =寸,1AB =尺(10寸),则圆的直径长度是()A .12寸B .24寸C .13寸D .26寸4.(2023秋•铜山区校级月考)如图,点A 、B 、C 在O 上,30ACB ∠=︒,则AOB ∠的度数是()A .30︒B .40︒C .60︒D .65︒5.(2023•苏州)如图,AB 是半圆O 的直径,点C ,D 在半圆上, CDDB =,连接OC ,CA ,OD ,过点B 作EB AB ⊥,交OD 的延长线于点E .设OAC ∆的面积为1S ,OBE ∆的面积为2S ,若1223S S =,则tan ACO ∠的值为()A 2B .223C .75D .326.(2023秋•梁溪区校级期中)如图,DCE ∠是O 内接四边形ABCD 的一个外角,若82DCE ∠=︒,那么BOD ∠的度数为()A.160︒B.164︒C.162︒D.170︒二.填空题(共6小题)7.(2023秋•滨海县期中)如图,点A,B,C,D在OABD∠=.∠=︒,则ADC上,30CAD∠=︒,508.(2023秋•镇江期中)如图,某圆弧形拱桥的跨度16=,则该拱桥的半径为m.CD m=,拱高5AB m9.(2023秋•高新区校级期中)如图是一个圆柱形的玻璃保温水杯,将其横放,截面是个半径为5cm的圆,杯内水面8=,则水的最大深度CD是cm.AB cm10.(2023秋•丰县期中)如图,点A是半圆上的一个三等分点,点B是 AD的中点,P是直径CD上一动点,O+的最小值为.的半径是2,则PA PB11.(2023秋•鼓楼区校级月考)如图,已知OPA=,的弦,点P在弦AB上.若4的半径为7,AB是OPB=,则OP的长为.612.(2023秋•建湖县期中)如图,点A 、B 、C 在O 上,//BC OA ,连接BO 并延长,交O 于点D ,连接AC 、DC .若18A ∠=︒,则D ∠的大小为︒.三.解答题(共6小题)13.(2023秋•仪征市期中)如图,在以点O 为圆心的两个同心圆中,大圆的弦AB 交小圆于点C 、D .(1)求证AC BD =;(2)若3AC =,大圆和小圆的半径分别为6和4,则CD 的长度是.14.(2023秋•广陵区期中)如图,四边形ABCD 内接于O ,BC 为O 的直径,//OA CD .(1)若70ABC ∠=︒,求BAD ∠的度数;(2)求证: AB AD =.15.(2023秋•句容市期中)已知:如图,C ,D 是以AB 为直径的O 上的两点,分别连接OC 、OD 、AD 、CD 、BC ,且//OD BC ,求证:AD DC =.16.(2023秋•淮安区期中)某地有一座圆弧形拱桥,桥下水面宽度AB为24m,拱顶高出水面8m(即8)=,CD m ⊥,OC AB(1)求出该圆弧形拱桥所在圆的半径;(2)现有一艘宽10m,船舱高出水面7.5m的货船要经过这里,此货船能顺利通过这座桥吗?17.(2023秋•邳州市期中)“圆材埋壁”是我国古代著名数学著作《九章算术》中的一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”此问题的实质是解决下面的问题:如图,CD为OAB=,求CD的长.的直径,弦AB CDCE=,10⊥于点E,118.(2023秋•泗阳县期中)如图,AB是O∠的度数.∠=︒,求ABDDCB的弦,30的直径,CD是O。
九年级数学 垂径定理,圆周角与圆心角的关系复习题 试题

实验九年级数学? 垂径定理,圆周角与圆心角的关系?复习题例2.如图,△ABC中,∠A=m°.〔1〕如图〔1〕,当O是△ABC的内心时,求∠BOC的度数;〔2〕如图〔2〕,当O是△ABC的外心时,求∠BOC的度数;〔3〕如图〔3〕,当O是高线BD与CE的交点时,求∠BOC的度数.例3.如图,Rt△ABC中,AC=8,BC=6,∠C=90°,⊙I分别切AC,BC,AB于D,E,F,求Rt△ABC的内心I与外心O之间的间隔.1.如图1,⊙O内切于△ABC,切点为D,E,F.∠B=50°,∠C=60°,•连结OE,OF,DE,DF,那么∠EDF等于〔〕A.40° B.55° C.65° D.70°2.如图2,⊙O是△ABC的内切圆,D,E,F是切点,∠A=50°,∠C=60°,•那么∠DOE=〔〕A.70° B.110° C.120° D.130°3.如图3,△ABC中,∠A=45°,I是内心,那么∠BIC=〔〕° B.112° C.125° D.55°4.以下命题正确的选项是〔〕A.三角形的内心到三角形三个顶点的间隔相等B.三角形的内心不一定在三角形的内部C.等边三角形的内心,外心重合D.一个圆一定有唯一一个外切三角形5.在Rt△ABC中,∠C=90°,AC=3,AB=5,那么它的内切圆与外接圆半径分别为〔〕A.1.5,2.5 B.2,5 C.1,2.5 D.2,26.如图,在△ABC中,AB=AC,内切圆O与边BC,AC,AB分别切于D,E,F.〔1〕求证:BF=CE;〔2〕假设∠C=30°,CE=23,求AC的长.1.如图,在半径为R的圆内作一个内接正方形,•然后作这个正方形的内切圆,又在这个内切圆中作内接正方形,依此作到第n个内切圆,它的半径是〔〕A.〔22〕n R B.〔12〕n R C.〔12〕n-1R D.〔22〕n-1R2.如图,⊙O为△ABC的内切圆,∠C=90°,AO的延长线交BC于点D,AC=4,•DC=1,那么⊙O的半径等于〔〕A.45B.54C.34D.563.如图,△ABC的内切圆⊙O分别和边BC,AC,AB切于D,E,F,•假如AF=2,BD=7,CE=4.〔1〕求△ABC的三边长;〔2〕假如P为弧DF上一点,过P作⊙O的切线,交AB于M,交BC于N,求△BMN的周长.4.如图,⊙O与四边形ABCD的各边依次切于M,N,G,H.〔1〕猜测AB+CD与AD+BC有何数量关系,并证明你的猜测;〔2〕假设四边形ABCD增加条件AD∥BC而成为梯形,梯形的中位线长为m,其他条件不变,试用m表示梯形的周长.一. 选择题。
专题17 圆周角重难点题型专训(八大题型)(解析版)

第二十四章圆专题17圆周角重难点题型专训(八大题型)【题型目录】题型一圆周角的概念辨析题型二圆周角定理题型三同弧或等弧所对的圆周角相等问题题型四半圆所对的圆周角是直角问题题型五90°的圆周角所对的弦是直径问题题型六已知圆内接四边形求角度题型七求四边形外接圆的直径题型八圆周角综合问题【知识梳理】知识点一、圆周角1.顶点在圆上,并且两边都和圆相交的角叫做圆周角.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半。
推论1:在同圆或等圆中,如果两个圆周角相等,它们所对的弧一定相等。
推论2:半圆(或直径)所对的圆周角是直角,90 的圆周角所对的弦是直径。
(在同圆中,半弧所对的圆心角等于全弧所对的圆周角)2.圆心角、弧、弦、弦心距之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等.推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等.3.一个四边形的4个顶点都在同一个圆上,这个四边形叫做圆的内接四边形,这个圆叫做四边形的外接圆。
圆内接四边形定理:圆内接四边形的对角互补,一个外角等于其内对角。
【经典例题一圆周角的概念辨析】1.(2020秋·浙江宁波·九年级校考期中)下列说法:(1)三点确定一个圆;(2)直径所对的圆周角是直角;(3)平分弦的直径垂直于弦,并且平分弦所对的弧;(4)相等的圆心角所对的弧相等;(5)圆内接四边形的对角互补.其中正确的个数为()A.1个B.2个C.3个D.4个【答案】B【分析】根据确定圆的条件、直径的性质、垂径定理、圆周角定理、圆内接四边形的性质一一判断即可.【详解】解:(1)任意三点确定一个圆;错误,应该是不在同一直线上的三点可以确定一个圆;(2)直径所对的圆周角是直角;正确;(3)平分弦的直径垂直于弦;并且平分弦所对的弧,错误,直径与直径互相平分,但不一定互相垂直;(4)相等的圆心角所对的弧相等;错误,应该是在同圆或等圆中;(5)圆内接四边形对角互补;正确;故选:B.【点睛】本题考查确定圆的条件、直径的性质、垂径定理、圆周角定理、圆内接四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.2.(2023秋·全国·九年级专题练习)如图,四边形ABCD的顶点A,B,C在圆上,且边CD与该圆交于点E,AC,BE交于点F.下列角中,弧AE所对的圆周角是()A .∠ADEB .∠AFEC .∠ABED .∠ABC【答案】C 【分析】直接运用圆周角的定义进行判断即可.【详解】解:弧AE 所对的圆周角是:∠ABE 或∠ACE故选:C【点睛】本题考查了圆周角的定义,掌握圆周角的定义是解题的关键.3.(2023·湖南娄底·校考一模)已知点A 、B 、C 、D 在圆O 上,且FD 切圆O 于点D ,OE CD 于点E ,对于下列说法:①圆上 AbB 是优弧;②圆上 AbD 是优弧;③线段AC 是弦;④CAD 和ADF 都是圆周角;⑤COA 是圆心角,其中正确的说法是.【答案】①②③⑤【分析】根据优弧的定义,弦的定义,圆周角的定义,圆心角的定义逐项分析判断即可【详解】解: AbB , AbD 都是大于半圆的弧,故①②正确,,A C ∵在圆上,则线段AC 是弦;故③正确;∵,,C A D 都在圆上,CAD 是圆周角而F 点不在圆上,则ADF 不是圆周角故④不正确;∵O 是圆心,,C A 在圆上COA 是圆心角故⑤正确故正确的有:①②③⑤故答案为:①②③⑤【点睛】本题考查了优弧的定义,弦的定义,圆周角的定义,圆心角的定义,理解定义是解题的关键.优弧是大于半圆的弧,任意圆上两点的连线是弦,顶点在圆上,并且两边都和圆相交的角叫做圆周角,顶点在圆心,并且两边都和圆相交的角叫做圆心角.4.(2023秋·全国·九年级专题练习)如图,直线l 经过O 的圆心O ,且与O 交于A B 、两点,点C 在O 上,且30AOC ,点P 是直线l 上的一个动点(与圆心O 不重合),直线CP 与O 相交于另一点Q ,如果QP QO ,则OCP .【答案】40°、20°、100°【分析】点P 是直线l 上的一个动点,因而点P 与线段AO 有三种位置关系,在线段AO 上,点P 在OB 延长线上,点P 在OA 的延长线上.分这三种情况进行讨论即可.【详解】解:①根据题意,画出图1,在QOC 中,OC OQ ,∴OQC OCP =,在OPQ △中,QP QO =,∴QOP QPO =,又∵30AOC =,∴30QPO OCP AOC OCP =+=+,在OPQ △中,180QOP QPO OQC ++=,即 3030180OCP OCP OCP ++++=,整理得,3120OCP =,∴40OCP .②当P 在线段OA 的延长线上,如图21180211802OC OQ OQP QOC OQ PM OPQ OQP∵∵,①,,②,在OQP 中,30180QOC OQP OPQ +++=③,把①②代入③得20QOC =,则80OQP=∴100OCP =;③当P 在线段OA 的反向延长线上,如图3,1180211802301502OC OQ OCP OQC COQ OQ PQ P OQP AOC COQ POQ P POQ P OCP OQC∵∵∵∵,①,,②,,③,,④,①②③④联立得10P =,1801501020OCP ==.故答案为:40°、20°、100°.【点睛】本题主要考查了圆的认识及等腰三角形等边对等角的性质,画出图形,进行分类讨论是解题的关键.5.(2023·甘肃酒泉·统考三模)把下面的语句还原成图形:作图区域:(1)M 的半径为1cm ,AB 是M 的一条弦(AB 不经过M ),AMB 、ACB 分别是劣弧 AB 所对应的圆心角和圆周角;(2) DE 是O 中的一条弧,且 AB DE.【答案】(1)见解析(2)见解析【分析】(1)画非直径的弦AB ,在优弧 AB 上取点C ,连接AC ,BC ,即可解答;(2)在M 上取一点D ,以AB 为半径画弧,交M 于点E ,即可.【详解】(1)解:如图,AMB 和ACB 为所作;作图区域:(2)解:如图,在M 上取一点D ,以AB 为半径画弧,交M 于点E ,根据等弦对等弧,可得 AB DE, DE即为所作,作图区域:【点睛】本题考查了作图-复杂作图,熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解乘基本作图,逐步操作即可.6.(2023秋·河南信阳·九年级统考期末)(1)【学习心得】小明同学在学习完“圆”这一章内容后,感觉到一些几何问题如果添加辅助圆,运用圆的知识解决,可以使问题变得非常容易.例如:如图1,在△ABC中,AB=AC,∠BAC=90°,D是△ABC外一点,且AD=AC,求∠BDC的度数.若以点A为圆心,AB为半径作辅助⊙A,则点C、D必在⊙A上,∠BAC是⊙A的圆心角,而∠BDC是圆周角,从而可容易得到∠BDC=°.(2)【问题解决】如图2,在四边形ABCD中,∠BAD=∠BCD=90°,∠BDC=27°,求∠BAC的数.(3)【问题拓展】如图3,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG 于点H.若正方形的边长为4,则线段DH长度的最小值是.【答案】(1)45;(2)27°;(3)25﹣2【分析】(1)利用同弦所对的圆周角是所对圆心角的一半求解.(2)由A、B、C、D共圆,得出∠BDC=∠BAC,(3)根据正方形的性质可得AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,然后利用“边角边”证明△ABE 和△DCF全等,根据全等三角形对应角相等可得∠1=∠2,利用“SAS”证明△ADG和△CDG全等,根据全等三角形对应角相等可得∠2=∠3,从而得到∠1=∠3,然后求出∠AHB=90°,取AB的中点O,连接OH、OD,根据直角三角形斜边上的中线等于斜边的一半可得OH=12AB=2,利用勾股定理列式求出OD,然后根据三角形的三边关系可知当O、D、H三点共线时,DH的长度最小.【详解】解:(1)如图1,∵AB=AC,AD=AC,∴以点A为圆心,AB为半径作辅助⊙A,则点B、C、D必在⊙A上,∵∠BAC是⊙A的圆心角,而∠BDC是圆周角,∴∠BDC=12∠BAC=45°,故答案是:45;(2)如图2,取BD的中点O,连接AO、CO.∵∠BAD=∠BCD=90°,∴点A、B、C、D共圆,∴∠BDC=∠BAC,∵∠BDC=27°,∴∠BAC=27°,(3)如图3,在正方形ABCD 中,AB =AD =CD ,∠BAD =∠CDA ,∠ADG =∠CDG ,在△ABE 和△DCF 中,AB CD BAD CDA AE DF,∴△ABE ≌△DCF (SAS ),∴∠1=∠2,在△ADG 和△CDG 中,AD CD ADG CDG DG DG,∴△ADG ≌△CDG (SAS ),∴∠2=∠3,∴∠1=∠3,∵∠BAH +∠3=∠BAD =90°,∴∠1+∠BAH =90°,∴∠AHB =180°﹣90°=90°,取AB 的中点O ,连接OH 、OD ,则OH =AO =12AB =2,在Rt △AOD 中,OD =22AO AD =2224 =25,根据三角形的三边关系,OH +DH >OD ,∴当O 、D 、H 三点共线时,DH 的长度最小,最小值=OD ﹣OH =25﹣2.故答案为:25﹣2.【点睛】本题主要考查了圆的综合题,需要掌握圆周角定理、等腰直角三角形的性质以及勾股定理等知识,熟练掌握圆的性质及正方形的性质是解题的关键.【经典例题二圆周角定理】1.(2023春·福建福州·九年级校考期中)如图,点A ,B ,C ,D 在O 上,140AOC ,B 是弧AC 的中点,则D 的度数是()A .30B .35C .45D .70【答案】B 【分析】连接OB ,如图,利用圆心角、弧、弦的关系,然后根据圆周角定理求解.【详解】解:连接OB ,如图所示,∵B 是弧AC 的中点,即 AB BC ,∴111407022AOB COB AOC ,∵D 和AOB 都对 AB ,∴1352D AOB .故选:B .【点睛】本题考查了圆周角定理:熟练掌握圆心角、弧、弦的关系和圆周角定理是解决问题的关键.2.(2023春·陕西榆林·九年级校考期中)如图,O 是ABC 的外接圆,且AB 是O 的直径,点D 在O 上,连接OD 、BD ,且BD BC ,若50BOD ,则ABC 的度数为()A .65B .50C .30D .25【答案】A 【分析】根据BD BC 得出1252BAC BOD ,根据AB 是O 的直径,得出90ACB ,最后根据直角三角形两锐角互余,即可解答.【详解】解:∵BD BC ,50BOD ,∴1252BAC BOD ,∵AB 是O 的直径,∴90ACB ,∴9065ABC ACB ,故选:A .【点睛】本题主要考查了圆周角定理,解题的关键是在同圆或等圆中,同弧或等弧所对的圆周角是圆心角的一半,直径所对的圆周角是直角.3.(2023秋·黑龙江哈尔滨·九年级校考开学考试)如图,AB 是O 的一条弦,OD AB ,垂足为点C ,交O 于点D ,点E 在O 上,30AED ,10OB ,则弦AB 的长是.【答案】103【分析】根据垂径定理得到 AD BD,结合30AED 得到60BOD ,结合三角函数直接求解即可得到答案;【详解】解:∵OD AB ,∴ AD BD,2AB BC ,∵30AED ,∴60BOD ,∴30OBC ,∵10OB ,∴152OC OB ,∴2253BC OB OC ,∴103AB ,故答案为:103.【点睛】本题考查垂径定理,圆周角定理及勾股定理,解题的关键是得到 AD BD.4.(2023秋·九年级课时练习)如图,已知,C D 是半圆O 上的三等分点,连接,,,,AC BC CD OD BC 和OD 相交于点E ,有下列结论:①30CBA ;②OD BC ;③12OE AC;④四边形AODC 是菱形.其中正确的有(填序号).【答案】①②③④【分析】①首先根据点C ,D 是半圆O 上的三等分,求出AOC 的度数;然后根据圆周角定理,求出CBA 的度数即可;②根据三角形的内角和定理,求出90BEO ,即可判断出OD BC ;③根据垂径定理判断出E 是BC 的中点,然后得到OE 是ABC 的中位线,即可判断出12OE AC ,④先证明AC OD ∥,再证明AOC 是等边三角形,得到AC OA OD ,根据菱形的判定方法可判断四边形AODC 是菱形.【详解】解:连接OC ,∵已知,C D 是半圆O 上的三等分点,∴1180603AOC COD BOD ,∴11603022CBA AOC ,故①正确;∴180180603090BEO BOD CBA ,∴OD BC ,故②正确;∴BE CE ,OB OC ,∴OE 是ACB △的中位线,∴12OE AC ,故③正确;∵AB 是半圆O 的直径,∴AC BC ,又OD BC ,∴AC OD ∥,∵OC OA ,60AOC ,∴AOC 是等边三角形,∴AC OA OD ,∴四边形AODC 是平行四边形,又AC OA ,∴四边形AODC 是菱形.故④正确,故答案为:①②③④.【点睛】本题主要考查了圆周角定理,垂径定理,圆心角、弧、弦三者的关系,菱形的判定和性质,等边三角形的判定,三角形的内角和定义及中位线性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.5.(2023春·安徽·九年级专题练习)如图1,已知AB 为O 的直径,C 为O 上一点,CE AB 于E ,D 为弧BC 的中点,连接AD ,分别交CE CB 、于点F 和点G .(1)求证:CF CG ;(2)如图2,若AF DG ,连接OG ,求证:OG AB .【答案】(1)见解析(2)见解析【分析】(1)连接AC ,根据直径所对的圆周角是直角可得90ACB ,从而可得∠CAG +∠AGC =90°,根据垂直定义可得90CEA ,从而可得90FAE AFE ,然后根据已知可得 DCDB ,从而可得CAG FAE ,进而可得AGC AFE ,最后根据对顶角相等可得AFE CFG ,从而可得AGC CFG 进而根据等角对等边即可解答;(2)连接,AC CD ,利用(1)的结论,再根据等角的补角相等可得AFC CGD ,然后根据SAS 证明AFC DGC ≌,从而可得AC CD ,进而可得 AC DCDB ,最后根据等弧所对的圆周角相等可得ABC DAB ,从而可得GA GB ,进而利用等腰三角形的三线合一性质即可解答.【详解】(1)证明:连接AC ,∵AB 为O 的直径,∴90ACB ,∴90CAG AGC ,∵CE AB ,∴90CEA ,∴90FAE AFE ,∵D 为弧BC 的中点,∴ DCDB ,∴CAG FAE ,∴AGC AFE ,∵AFE CFG ,∴AGC CFG ,∴CF CG ;(2)解:连接,AC CD ,∵CFG CGF ,∴180180CFG CGF ,∴AFC CGD ,∵CF CG ,AF DC ,∴ SAS AFC DGC ≌,∴AC CD ,∴ AC DC,∵ DCDB ,∴ AC DB,∴ABC DAB ,∴GA GB ,∵OA OB ,∴GO AB .【点睛】本题考查了圆周角定理,圆心角、弧、弦的关系,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.6.(2022秋·江苏盐城·九年级校考阶段练习)如图,AB 是O 的一条弦,OD AB ,垂足为点C ,交O 于点D ,点E 在O 上.(1)若50AOD Ð=°,求DEB 的度数;(2)若6OC ,10OA ,求AB 的长.【答案】(1)25(2)AB 的长为16【分析】(1)根据垂径定理的推论可得 AD DB,再根据同弧或等弧所对的圆周角等于圆心角的一半求解即可;(2)利用勾股定理列式求出AC ,根据垂径定理的推论可得AC BC ,即可求解.【详解】(1)解:∵AB 是O 的一条弦,OD AB ,∴ AD DB,又∵50AOD Ð=°,∴11502522DEB AOD .(2)解:∵OD AB ,∴=90AOC ,在Rt AOC 中,22221068AC OA OC ,∵AB 是O 的一条弦,OD AB ,∴AC BC ,则216AB AC CB AC .【点睛】本题考查了圆周角定理,垂径定理的推论,解题的关键是明确在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.【经典例题三同弧或等弧所对的圆周角相等问题】1.(2021春·福建南平·九年级统考阶段练习)如图,ACD 是O 的内接三角形,AC CD ,连接AO 并延长交O 于点B ,连接BC ,若32BAC ,则ACD 等于()A .64B .62C .60D .58【答案】A 【分析】先证明90ACB ,可得903258ADC ABC ,证明58CAD ADC ,再利用三角形的内角和定理可得答案.【详解】解:∵AB 为O 的直径,∴90ACB ,∵32BAC ,∴903258ADC ABC ,∵AC CD ,∴58CAD ADC ,∴18025864ACD ;故选A .【点睛】本题考查的是等腰三角形的性质,圆周角定理的应用,熟记圆周角定理是解本题的关键.2.(2022·北京西城·校考模拟预测)如图,ADC △内接于O ,BC 是O 的直径,若66A ,则BCD 等于()A .66B .34C .24D .14【答案】C 【分析】根据同弧所对圆周角相等得到66B A ,根据直径所对的圆周角是直角得到=90BDC ,根据直角三角形两锐角互余,得到24BCD .【详解】∵66A ,∴66B A ,∵BC 是O 的直径,∴=90BDC ,∴906624BCD .故选:C .【点睛】本题主要考查了圆周角定理及推论.熟练掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,半圆(或直径)所对的圆周角是直角,直角三角形两锐角互余,是解决问题的关键.3.(2023秋·全国·九年级专题练习)如图,ABC 内接于O ,AB 是O 的直径,点D 是O 上一点,55CDB ,则ABC °.【答案】35【分析】根据圆周角定理和三角形的内角和定理即可得到结论.【详解】解:AB ∵是O 的直径,90ACB ,55A D ∵==,18035ABC ACB A ==,故答案为:35.【点睛】本题考查了考查了圆周角定理、三角形的外接圆与外心,熟练掌握圆周角定理是解题关键.4.(2023·云南德宏·统考一模)已知:如图,AB 是O 的直径,AB 垂直弦CD 于点E ,则在不添加辅助线的情况下,图中与CDB 相等的角是(写出一个即可).【答案】CAB 或BCD 或DAB【分析】利用垂径定理和圆周角定理即可求解.【详解】∵AB CD ,AB 是O 直径,∴ BCBD ,∴CDB CAB BCD DAB ,故答案为:CAB 或BCD 或DAB .【点睛】此题考查了垂径定理和圆周角定理,解题的关键是熟练掌握以上定理的应用.5.(2023秋·九年级课时练习)如图所示,四边形ABCD 内接于O ,50,25,65B ACD BAD .求证:(1)AD CD ;(2)AB 是O 的直径.【答案】(1)见解析(2)见解析【分析】(1)连接BD ,根据圆周角定理得125ACD ,再由50ABC 可计算出225 ,则 AD CD,然后根据圆心角、弧、弦的关系即可得到AD CD ;(2)根据三角形内角和定理可计算出180190ADB BAD ,则根据圆周角的推理即可得到AB 为O 的直径.【详解】(1)证明:连接BD ,如图,125ACD ∵,而50ABC ,21502525ABC ,12 ,AD CD,AD CD ;(2)65BAD ∵,125 ,1801180652590ADB BAD ,AB 为O 的直径.【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90 的圆周角所对的弦是直径.6.(2022秋·甘肃定西·九年级统考期末)已知:O 的两条弦AB ,CD 相交于点M ,且AB CD .(1)如图1,连接AD .求证:AM DM .(2)如图2.若AB CD .在 BD 上取一点E ,使 BE BC ,AE 交CD 于点F ,连接AD 、DE .判断E 与DFE 是否相等,并说明理由.【答案】(1)证明见解析(2)E 与DFE 相等.理由见解析【分析】(1)根据AB CD 得 AB CD ,即 AC BC BC BD , AC BD,得A D ,即可得;(2)连接AC ,根据 BEBC 得CAB EAB ,根据AB CD 得AC AF ,即ACF AFC ,根据,ACF E AFC DFE ,即可得.【详解】(1)证明:AB CD ∵,C AB D即 AC BCBC BD , AC BD ,A D ,AM DM .(2)E 与DFE 相等.理由如下:解:连接AC ,如图,BEBC ∵,CAB EAB ,AB CD ∵,AC AF ,ACF AFC ,,ACF E AFC DFE ∵,DFE E .【点睛】本题考查了圆的性质,解题的关键是掌握圆周角定理,垂经定理,角、弧、弦的关系.【经典例题四半圆所对的圆周角是直角问题】1.(2023秋·全国·九年级专题练习)如图,在ABC 中,AC BC ,O 是ABC 的外接圆,AB 是O 的直径,点D 在O 上,连接CD 交AB 于点E ,连接OD ,若120BOD ,则BED 的度数为()A .60B .75C .100D .105【答案】D 【分析】连接BD ,根据等腰三角形的性质得到30OBD ODB ,根据平角的定义得到18012060AOD ,根据圆周角定理得到90ACB ,求得45A ,根据圆周角定理得到45CDB A ,根据三角形内角和定理即可得到结论.【详解】解:连接BD ,OD OB ∵,120BOD ,30OBD ODB ,18012060AOD ,AB ∵是O 的直径,45A ABC ,AC BC ∵,45A ,45CDB A ,15CDO CDB ODB ,1806015105BED ,故选:D .【点睛】本题考查了三角形的外接圆与外心,等腰直角三角形的性质,圆周角定理,正确地作出辅助线是解题的关键.2.(2022·河北衡水·校考模拟预测)如图,点A ,B ,C 在O 上,BC OA ∥,连接BO 并延长,交O 于点D ,连接AC ,.DC 若40D ,下列结论不正确的是()A .50BB .直线AO 垂直平分CDC .12A BD .30ACB【答案】D 【分析】根据圆周角定理可得90BCD ,从而根据三角形内角和求出B ,A 选项即可判断;根据平行的性质及圆周角定理设A ACB x ,则2BOA x ,根据三角形内角和即可求出x 的值,从而求出A ,ACB ,AOB ,从而可判断C 、D 选项;延长AO 交CD 于点E ,根据对顶角相等可得到DOE ,从而求出90OED ,再结合垂径定理可判断出AO 与CD 的关系,即可判断出选项B .【详解】解:如图,延长AO 交CD 于点E ,BD Q 是O 的直径,90BCD ,180180904050B BCD D ,故A 选项正确,不符合题意;BC OA ∥∵,设A ACB x ,则2BOA x ,250x x x∵25x ,25ACB A ,50BOA故D 选项不正确,符合题意;50B ∵,12A B ;故C 选项正确,不符合题意;根据对顶角相等可得:50DOE BOA ,180504090OED ,OE CD ,O ∵是圆心,DE CE ,直线AO 垂直平分CD ;故B 选项正确,不符合题意.故选:D .【点睛】本题考查圆周角定理及垂径定理,涉及到垂直平分线的定义、三角形内角和等,解题关键是熟练运用圆周角定理和垂径定理.3.(2023·江苏·统考中考真题)如图,AD 是O 的直径,ABC 是O 的内接三角形.若DAC ABC ,4AC ,则O 的直径AD .【答案】42【分析】连接CD ,OC ,根据在同圆中直径所对的圆周角是90 可得=90ACD ,根据圆周角定理可得COD COA ,根据圆心角,弦,弧之间的关系可得AC CD ,根据勾股定理即可求解.【详解】解:连接CD ,OC ,如图:∵AD 是O 的直径,∴=90ACD ,∵DAC ABC ,∴COD COA ,∴AC CD ,又∵4AC ,∴4CD ,在Rt ACD △中,22224442AD AC CD,故答案为:42.【点睛】本题考查了在同圆中直径所对的圆周角是90 ,圆周角定理,圆心角,弦,弧之间的关系,勾股定理,熟练掌握以上知识是解题的关键.4.(2022秋·江苏泰州·九年级校考阶段练习)如图,已知O 的直径AB ,D 为O 上一点(不与A 、B 重合),连接AD 、BD .弦DC 平分ADB ,交AB 于点E ,过点A 作AF CD 于点F ,交O 于点G ,连接DG ,若DG AE ,则G 的度数为 .【答案】67.5【分析】DG 交AB 于H ,如图,根据圆周角定理得到90ADB ,则=45ADC ,再证明45DAF ,AF DF ,则可判断Rt Rt AEF DGF ≌,所以EAF GDF ,接着证明90DHE AFE ,则根据垂径定理得到 BDBG ,然后根据圆周角定理得到22.5BAG BAD ,最后利用互余可计算出G 的度数.【详解】解:DG 交AB 于H ,如图,O ∵ 的直径AB ,90ADB ,∵弦DC 平分ADB ,45ADC ,AF CD ∵,90AFD ,45DAF ,AF DF ,在Rt AEF 和Rt DGF △中,AE DG AF DF, Rt Rt HL AEF DGF ≌,EAF GDF ,AEF DEH ∵,90DHE AFE ,AB DG ,BDBG ,122.52BAG BAD DAG ,9067.5G GAH .故答案为:67.5.【点睛】本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半;半圆(或直径)所对的圆周角是直角,90 的圆周角所对的弦是直径.也考查了垂径定理.5.(2023春·浙江杭州·九年级校考阶段练习)已知:如图,点E 是边长为2的正方形ABCD 中AB 边上一点(不与A 、B 重合),以CE 为直径的O 分别交DE 和CD 于点F 、M ,DH CE 于点H .(1)求证:BE CM(2)猜想AE 与HE 的大小关系,并说明理由.(3)当DF CH 时,求DEH △的面积.【答案】(1)见解析(2)AE HE ,理由见解析(3)65【分析】(1)连接EM ,根据正方形性质得出90B BCM ,根据直径所对圆周角为直角得出90CM E ,证明四边形BEMC 为矩形,即可求证BE CM ;(2)根据题意可得90A DHE ,AD CD ,在Rt DCH △中,DH CD ,则DH AD ,根据勾股定理得出222AE DE AD ,222HE DE DH ,得出22AE HE ,则AE HE ;(3)连接CF ,证明 Rt Rt HL CDF DCH ≌,得出DCH CDE ,则DE CE ,根据三线合一得出112CM DM CD ,即可用勾股定理求出5DE CE ,根据1122DCE S DC EM CE DH ,求出455DH ,在Rt DEH △中,用勾股定理求出355EH ,最后根据三角形面积公式即可求解.【详解】(1)解:连接EM ,∵四边形ABCD 为正方形,,∴90B BCM ,∵CE 为O 直径,∴90CM E ,∴四边形BEMC 为矩形,∴BE CM ;(2)解:AE HE ,理由如下,∵四边形ABCD 是正方形,DH CE ,∴90A DHE ,AD CD ,∵在Rt DCH △中,DH CD ,∴DH AD ,在Rt ADE △中,根据勾股定理可得:222AE DE AD ,在Rt HDE △中,根据勾股定理可得:222HE DE DH ,∴22AE HE ,即AE HE ;(3)解:连接CF ,∵CE 为O 直径,∴90CFE CFD ,在Rt CDF △和Rt DCH △中,CD DC CH DE,∴ Rt Rt HL CDF DCH ≌,∴DCH CDE ,则DE CE ,由(1)可得90CM E ,∴112CM DM CD ,∵四边形BEMC 为矩形,∴2EM BC ,在Rt CME △中,根据勾股定理可得:225CE CM EM ,则5DE CE ,∵1122DCE S DC EM CE DH ,∴DC EM CE DH ,即225DH ,解得:455DH ,在Rt DEH △中,22355EH DE DH,∴113545622555DEH S EH DH .【点睛】本题主要考查了正方形的性质,矩形的判定和性质,勾股定理,等腰三角形的判定和性质,全等三角形的判定和性质,解题的关键是熟练掌握相关性质定理,并熟练运用,正确作出辅助线,构造矩形和全等三角形.6.(2023秋·全国·九年级专题练习)如图,点B ,C 为O 上两定点,点A 为O 上一动点,过点B 作BE AC ∥,交O 于点E ,点D 为射线BC 上一动点,且AC 平分BAD ,连接CE .(1)求证:AD EC ∥;(2)连接EA ,若BC CD ,试判断四边形EBCA 的形状,并说明理由.【答案】(1)见解析(2)四边形EBCA 是矩形,理由见解析【分析】(1)根据角平分线的定义,可得BAC DAC ,再根据圆周角定理可得E BAC ,再根据平行线的性质可得E ECA ,进而得到ECA DAC ,最后再根据内错角相等两直线平行,即可证明结论;(2)由角平分线的定义,可得BAC DAC ,再根据等腰三角形三线合一的性质,可得90ACB ACD ,即90AEB ,进而得到90EBC ACD ,再根据矩形的判定定理,即可得出答案.【详解】(1)证明:∵AC 平分BAD ,∴BAC DAC ,∵E BAC ,∴E DAC ,∵BE AC ∥,∴E ECA ,∴ECA DAC ,∴EC AD ∥.(2)解:四边形EBCA 是矩形,理由如下:∵AC 平分BAD ,∴BAC DAC ,又∵BC CD ,∴90ACB ACD ,∴AB 为O 的直径.∴90AEB ,又∵BE AC ∥,∴90EBC ACD ,∴四边形EBCA 是矩形.【点睛】本题主要考查圆周角定理、平行线的判定与性质、等腰三角形的性质、矩形的判定定理,灵活运用相关知识是解答本题的关键.【经典例题五90°的圆周角所对的弦是直径问题】1.(2023秋·江苏·九年级专题练习)如图,ABC 是等边三角形,2AB ,点P 是ABC 内一点,且30BAP CBP ,连接CP ,则CP 的最小值为()A .12B .32C .23D .31【答案】D 【分析】根据等边三角形的性质得到60ABC ,AB BC AC ,继而推出90APB ,可得点P 在以AB 为直径的圆上,得知当C ,D ,P 三点共线时,CP 最小,再利用等边三角形的性质和勾股定理求解即可.【详解】解:∵ABC 是等边三角形,∴60ABC ,AB BC AC ,∵30BAP CBP ,∴ 6030BAP ABP ,整理得:90BAP ABP ,则90APB ,∴点P 在以AB 为直径的圆上,如图,设AB 的中点为D ,连接DP ,即DP 长度不变,∴CP DP CD ,∴当C ,D ,P 三点共线时,CP 最小,此时CD AB ,∵2AB BC AC ,∴112DP AB ,223CD BC BD ,∴CP 的最小值为31CD DP ,故选D .【点睛】本题考查了等边三角形的性质,勾股定理,圆周角定理,三角形三边关系的应用,解题的关键是根据已知条件推出90APB ,得到点P 在以AB 为直径的圆上.2.(2023春·全国·八年级专题练习)如图,正方形ABCD 中,12AB ,点P 为边DA 上一个动点,连接CP ,点E 为CD 上一点,且4DE ,在AB 上截取点Q 使EQ CP ,交CP 于点M ,连接BM ,则BM 的最小值为()A .8B .12C .4104D .835【答案】C 【分析】如图所示,过点E 作EF AB 于F ,当点P 运动时,点M 在以CE 为直径的半圆上,即点M 在圆心为O 的半圆上运动,当点M 运动到OB 连线上时,BM 的值最小,根据题意可证Rt Rt (HL)EFQ CDP △≌△,由此可证CEM 是直角三角形,可得点M 在以CE 为直径的半圆上运动,可求出半圆的半径,在Rt BCO △中,可求出OB 的长,由此即可求解.【详解】解:如图所示,过点E 作EF AB 于F ,连接BO ,如图所示:∵四边形ABCD 是正方形,∴12AB BC CD AD ====,90A ABC BCD D EFQ ,∵EF AB ,∴四边形AFED 是矩形,则AD EF CD ,在Rt EFQ △和Rt CDP △中,EQ CP EF CD,∴Rt Rt (HL)EFQ CDP △≌△,∴FEQ DCP ,∵90FEQ CEM CEF +,∴90DCP CEM +,∴90EMC ,即CEM 是直角三角形,∴当点P 运动时,点M 在以CE 为直径的半圆上运动,设圆心为O ,当点M 运动到OB 连线上时,BM 的值最小,∵12,4CD DE ,∴1248CE CD DE ,则半圆的半径118422OE OC CE ,在Rt BCO △中,2222412410OB OC BC ,当点M 运动到OB 连线上时,BM 的值最小,∴BM 的最小值为4104 ,故C 正确.故选:C .【点睛】本题主要考查正方形与圆的结合求最值,理解动点的运动规律,正方形的性质,全等三角形的判定和性质,勾股定理等知识是解题的关键.3.(2023·重庆·九年级统考学业考试)如图,四边形ABCD 是矩形,4,6AB AD ,点E 是平面内的一个动点,连接AE DE 、,在运动的过程中,AE 始终垂直于DE ,将AE 绕点A 顺时针旋转90 得到AF ,连接CF ,则CF 的最大值为.【答案】373【分析】先通过AE DE ,则可判断点E 在AD 为直径的圆上运动,将AD 绕点A 顺时针旋转90 至AD ,设AD 的中点为M ,则点E 在AD 为直径的圆上运动,当点C ,M ,F 三点共线时,CF 有最大值,最后利用勾股定理即可求解.【详解】如图,∵AE DE ,∴90AED ,∴点E 在AD 为直径的圆上运动,将AD 绕点A 顺时针旋转90 至AD ,设AD 的中点为M ,又∵AE AF ,∴由题意可知点E 在AD 为直径的圆上运动,当点C ,M ,F 三点共线时,CF 有最大值,∵四边形ABCD 是矩形,∴6AD BC ,4AB ,90ABC ,∵6AD AD ,M 为'AD 中点,∴3AM ,1BM ,在Rt MBC 中,由勾股定理得:22221637CM BM BC,∴CF 的最大值为:373 .【点睛】此题考查了旋转变换和圆有关的概念,解题的关键是正确理解点E ,F 的运动路径是圆.4.(2023·山东·统考中考真题)如图,在四边形ABCD 中,90,5,4,ABC BAD AB AD AD BC ,点E 在线段BC 上运动,点F 在线段AE 上,ADF BAE ∠∠,则线段BF 的最小值为.。
中考押轴题备考复习试题及解析圆的有关性质(1)

【点评】 本题主要考察了圆与一元二次方程相结合的题目,培养了同学们的综合应用能力。难度中等。
25.(满分12分)
已知:AB是⊙O的直径,弦CD⊥AB于点G,E是直线AB上一动点(不与点A、B、G重合),直线DE交⊙O于点F,直线CF交直线AB于点P.设⊙O的半径为r.
【解题思路】连接OD,则OD∥AE,于是 ,本题选C.
【答案】C
【点评】本题考查了切线的性质,即过切点的半径垂直于切线,也考查了相似形的性质.本题难度中等.
8.一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知AB长100cm,测得圆周角∠ACB=45°,则这个人工湖的直径AD为( )
A. B. C. D.
理由:如图2,依题意画出图形,连接FO并延长交⊙O于M,连接CM.
∵FM是⊙O直径,∴∠FCM=90°,∴∠M+∠CFM=90°
∵CD⊥AB,∴∠E+∠D=90°.
∵∠M=∠D,∴∠CFM=∠E.
∵∠POF=∠FOE,∴△POF∽△FOE.
∴ ,∴OE·OP=OF2=r2.
【点评】此题就是运用三角形相似的性质和判定来解决的题目,解决的关键是基本方法(见乘积式化成比例式,而后证明三角形相似)熟练运用。本题属于中等难度。
【点评】本题属于中等题,通过圆周角定理、等腰三角形的性质、外角定理的考查,培养学生简单的推理计算能力.
13、如图3,在以AB为直径的半圆O中,C是它的中点,若AC=2,则△ABC的面积是( )
A、1.5 B、2C、3 D、4
【解题思路】由圆周角定理可知:∠C= ,而点C是半圆的中点可知:AC=BC,故△ABC是等腰直角三角形,所以:
【答案】C
【点评】本题主要考查了圆的切线的性质与勾股定理得理解与应用,解题的关键是连接半径得到直角三角形,然后利用勾股定理列出方程,难度中等.
中考数学考点29圆的基本性质总复习(原卷版)

圆的基本性质【命题趋势】圆的基本性质是中考考查的重点,常以选择题,填空题和解答题考查为主;其中选择题和填空题的难度不会太大,对应用、创新、开放探究型题目,会根据当前的政治形势、新闻背景和实际生活去命题,进一步体现数学来源于生活,又应用于生活。
【中考考查重点】一、运用垂径定理及其推论进行计算二、运用圆周角定理及其推论进行计算三、垂径定理雪与圆周角定理结合考点:圆的有关概念圆的定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A所形成的图形叫圆。
这个固定的端点O叫做圆心,线段OA叫做半径。
圆的表示方法:以O点为圆心的圆记作⊙O,读作圆O。
圆的特点:在一个平面内,所有到一个定点的距离等于定长的点组成的图形。
确定圆的条件:1)圆心;2)半径。
备注:圆心确定圆的位置,半径长度确定圆的大小。
【补充】1)圆心相同且半径相等的圆叫做同圆;2)圆心相同,半径不相等的两个圆叫做同心圆;3)半径相等的圆叫做等圆。
圆的对称性:1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴;2)圆是以圆心为对称中心的中心对称图形。
弦的概念:连结圆上任意两点的线段叫做弦(例如:右图中的AB)。
直径的概念:经过圆心的弦叫做直径(例如:右图中的CD)。
备注:1)直径是同一圆中最长的弦。
2)直径长度等于半径长度的2倍。
⏜,弧的概念:圆上任意两点间的部分叫做圆弧,简称弧。
以A、B为端点的弧记作AB读作圆弧AB或弧AB。
等弧的概念:在同圆或等圆中,能够互相重合的弧叫做等弧。
半圆的概念:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆。
优弧的概念:在一个圆中大于半圆的弧叫做优弧。
劣弧的概念:小于半圆的弧叫做劣弧。
弦心距概念:从圆心到弦的距离叫做弦心距。
1.(2021秋•顺义区期末)如图,在⊙O中,如果=2,则下列关于弦AB与弦AC 之间关系正确的是()A.AB=AC B.AB=2AC C.AB>2AC D.AB<2AC 2.(2021秋•平原县期末)下列语句,错误的是()A.直径是弦B.相等的圆心角所对的弧相等C.弦的垂直平分线一定经过圆心D.平分弧的半径垂直于弧所对的弦3.(2021秋•玉林期末)如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是()A.猫先到达B地B.老鼠先到达B地C.猫和老鼠同时到达B地D.无法确定考点:垂径定理垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
垂径定理、圆周角

教学目的掌握垂径定理、圆周角和圆心角的关系教学重点垂径定理、圆周角教学内容(一)垂径定理1、圆是轴对称图形,任何一条直径所在直线都是它的对称轴.圆有无数条对称轴。
圆是以圆心为对称中心的中心对称图形;圆具有旋转不变性。
2、垂径定理:垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。
3、推论:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。
(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧。
圆的两条平行弦所夹的弧相等。
①平分弧的直径必平分弧所对的弦。
( )②平分弦的直线必垂直弦。
( )③垂直于弦的直径平分这条弦。
( )④平分弦的直径垂直于这条弦。
( )⑤弦的垂直平分线是圆的直径。
( )⑥平分弦所对的一条弧的直径必垂直这条弦。
( )⑦在圆中,如果一条直线经过圆心且平分弦,必平分此弦所对的弧。
( )例题赏析如图,在⊙O中,弦AB的长为8cm,圆心O到AB的距离为3cm,求⊙O的半径.小试牛刀1、如图,在⊙O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB于D,OE⊥AC于E,求证四边形ADOE是正方形.2、我市某居民区一处圆形地下水管道破裂,修理工人准备更换一段新管道,经测量得到如图所示的数据,修理工人应准备内径多大的管道?若此题只知下面弓形的高和AB的长,你仍然会做吗?60cm10cmA BO3、如图,直径是50cm圆柱形油槽装入油后,油深CD为15cm,求油面宽度ABD OBCA(二)弧、弦、圆心角1、圆心角的概念:顶点在圆心的角ABCDO2、弧、弦与圆心角的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等;所对的弦的弦心距相等。
在同圆或等圆中,满足下面四个条件中的任何一个就能推出另外三个:①两个圆心角相等;②两个圆心角所对的弧相等;③两个圆心角或两条弧所对的弦相等;④两条弦的弦心距相等。
1、相等的圆心角所对的弧相等。
( )2、相等的弧所对的弦相等。
( )3、相等的弦所对的弧相等。
垂径定理典型例题及练习

【基础知识回顾】一、圆的定义及性质:1、圆的定义:⑴形成性定义:在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转形成的图形叫做圆,固定的端点叫线段OA叫做⑵描述性定义:圆是到定点的距离等于的点的集合【名师提醒:1、在一个圆中,圆心决定圆的半径决定圆的2、直径是圆中的弦】2、弦与弧:弦:连接圆上任意两点的叫做弦弧:圆上任意两点间的叫做弧,弧可分为、、三类3、圆的对称性:⑴轴对称性:圆是轴对称图形,有条对称轴的直线都是它的对称轴⑵中心对称性:圆是中心对称图形,对称中心是【名师提醒:圆不仅是中心对称图形,而且具有旋转性,即绕圆心旋转任意角度都被与原来的图形重合】二、垂径定理及推论:1、垂径定理:垂直于弦的直径,并且平分弦所对的2、推论:平分弦()的直径,并且平分弦所对的【名师提醒:1、垂径定理及其推论实质是指一条直线满足:⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个,那么可推出其中三个,注意解题过程中的灵活运用2、圆中常作的辅助线是过圆心作弦的线3、垂径定理常用作计算,在半径r弦a弦心d和弦h中已知两个可求另外两个】三、圆心角、弧、弦之间的关系:1、圆心角定义:顶点在的角叫做圆心角2、定理:在中,两个圆心角、两条弧、两条弦中有一组量它们所对应的其余各组量也分别【名师提醒:注意:该定理的前提条件是“在同圆或等圆中”】四、圆周角定理及其推论:1、圆周角定义:顶点在并且两边都和圆的角叫圆周角2、圆周角定理:在同圆或等圆中,圆弧或等弧所对的圆周角都等于这条弧所对的圆心角的推论1、在同圆或等圆中,如果两个圆周角那么它们所对的弧推论2、半圆(或直弦)所对的圆周角是900的圆周角所对的弦是【名师提醒:1、在圆中,一条弦所对的圆心角只有一个,而它所对的圆周角有个,它们的关系是欽绲腫賁軔铼剮誒緦骞恹輿筍谭黲枨贵珑莳苋鸩捡耸殚脐剀继剧荞缚鐃鳩俪谥圆颏輻嗇惡呛櫪组颓緗轢箩約鱼產辐鹃钠俭躒劲苎鸭拦尘谖。
垂径定理及圆心角圆周角(基础)

P D C BA 【垂径定理】第5份1、下列命题中:① 任意三点确定一个圆;②圆的两条平行弦所夹的弧相等;③ 任意一个三角形有且仅有一个外接圆;④ 平分弦的直径垂直于弦;⑤ 直径是圆中最长的弦,半径不是弦。
正确的个数是( ) A.2个 B.3个 C.4个 D.5个2、如图,要把破残的圆片复制完整,已知弧上的三点A 、B 、C 。
(1)用尺规作图法,找出弧ABC 所在圆的圆心O (保留作图痕迹,不写作法); (2)设△ABC 是等腰三角形,底边BC=8,AB=5,求圆片的半径R3、已知:如图,有一圆弧形拱桥,拱的跨度AB=16cm ,拱高CD=4cm ,那么拱形的半径是 cm.4、如图,AB 为⊙O 的直径,弦CD ⊥AB ,垂足为P ,若AP:PB=1:4, CD=8,则 AB=_______________.5、填空:如图,在⊙O 中,直径CD 交弦AB (不是直径)于点E. (1)若CD ⊥AB ,则有 、 、 ; (2)若 AE = EB ,则有 、 、 ; (3)若 AC BC =,则有 、 、 .6、某地有一座圆弧形拱桥,桥下水面宽度为7.2m ,拱顶高出水面2.4m ,现有一艘宽3m ,船舱顶部为长方形并高出水面2m 的货船要经过这里,此货船能顺利通过这座拱桥吗?7、如图,AB 是半圆O 的直径,点P 从点O 出发,沿OA AB BO -- 的路径运动一周.设OP 为s ,运动时间为t ,则下列图形能大致地刻画s 与t 之间关系的是( ) 【圆心角定理及推论】1、圆的旋转不变性:将圆周绕圆心O 旋转 ,都能与自身重合,这个性质叫做圆的旋转不变性。
2、圆心角: 叫做圆心角。
3、在同圆或等圆中,相等的圆心角所对的 ,所对的 (这就是圆心角定理)4、n °的圆心角所对的弧就是 ,圆心角和 的度数相等。
注意:在题目中,若让你求⌒AB ,那么所求的是弧长 5、在同圆或等圆中,如果两个圆心角、两条弧、两条弦、两个弦心距中有一对量相等,那么都相等。
(完整版)垂径定理,圆周角定理练习题

CA P ODCE OA D B九年级垂径定理、弦、弧、圆心角、圆周角练习一,填空题1.如图所示,OA是圆O的半径,弦CD⊥OA于点P,已知OC=5,OP=3,则弦CD=____________________。
2.. 如图所示,在圆O中,AB、AC为互相垂直且相等的两条弦,OD⊥AB,OE⊥AC,垂足分别为D、E,若AC=2cm,则圆O的半径为____________cm。
3. 如图所示,AB是圆O的直径,弦CD⊥AB,E为垂足,若AB=9,BE=1,则CD=_________________。
(2题图)(1题图)(3题图)4. 如图所示,在△ABC中,∠C=90°,AB=10,AC=8,以AC为直径作圆与斜边交于点P,则BP的长为________________。
5. 如图所示,四边形ABCD内接于圆O,∠BCD=120°,则∠BOD=____________度。
6.如图所示,圆O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是()(4题图)(5题图) (6题图)(9题图)7.若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于()8. 如图所示,A、B、C三点在圆O上,∠AOC=100°,则∠ABC等于()9. △ABC中,∠C=90°,AB=cm4,BC=cm2,以点A为圆心,以cm5.3长为半径画圆,则点C在圆A___________,点B在圆A_________;10. 圆的半径等于cm2,圆内一条弦长23cm,则弦的中点与弦所对弧的中点的距离等于_____________;11. 在△ABC中,∠C=90°,AC=BC=4cm,D是AB边的中点,以点C为圆心,4cm为半径作圆。
则A、B、C、D四点在圆内有_____________。
12.半径为5cm的圆O中有一点P,OP=4,则过P的最短弦长_________,最长弦是__________,13.下列说法中,正确的是()A. 到圆心的距离大于半径的点在圆内B. 圆的半径垂直于圆的切线C. 圆周角等于圆心角的一半D. 等弧所对的圆心角相等二解答题14.已知:AB交圆O于C、D,且AC=BD.你认为OA=OB吗?为什么?15. 如图所示,是一个直径为650mm的圆柱形输油管的横截面,若油面宽AB=600mm,求油面的最大深度。
初三数学圆周角和圆心角的关系试题

初三数学圆周角和圆心角的关系试题1.已知,如图,∠BAC的对角∠BAD=100°,则∠BOC=_______度.【答案】160°【解析】由∠BAD=100°可得∠BAC的度数,再根据圆周角定理即可求得结果.∵∠BAD=100°∴∠BAC=80°∴∠BOC=160°.【考点】邻补角定理,圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.2.如图,AB是半圆O的直径,AC="AD,OC=2,∠CAB=30°," 则点O到CD的距离OE=____.【答案】【解析】由AC=AD,∠CAB=30°可得∠CDO的度数,即可得到∠EOD、∠COE的度数,判断出△COE的形状再结合勾股定理即可求得结果.∵AC=AD,∠CAB=30°,OA=OC∴∠CDO=75°,∠COD=60°∴∠EOD=15°∴∠COE=45°∴△COE为等腰直角三角形∵OC=2∴OE=.【考点】三角形内角和定理,勾股定理点评:特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.3.如图,已知圆心角∠BOC=100°,则圆周角∠BAC的度数是( )A.50°B.100°C.130°D.200°【答案】A【解析】圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.∵∠BOC=100°∴∠BAC=50°故选A.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.4.如图,A、B、C、D四个点在同一个圆上,四边形ABCD的对角线把四个内角分成的八个角中,相等的角有( )A.2对B.3对C.4对D.5对【答案】C【解析】圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.相等的角有∠ADB=∠ACB,∠BAC=∠BDC,∠CAD=∠CBD,∠ACD=∠ABC4对,故选C.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.5.如图,D是弧AC的中点,则图中与∠ABD相等的角的个数是( )A.4个B.3个C.2个D.1个【答案】B【解析】圆周角定理:同弧或等弧所对的圆周角相等,均等于所对圆心角的一半.∵D是弧AC的中点∴∠ABD=∠ACD=∠CBD=∠CAD故选B.【考点】圆周角定理点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.6.如图, ,则∠A+∠B等于( )A.100°B.80°C.50°D.40°【答案】C【解析】连接CO并延长交圆于点D,根据圆周角定理即可得到结果.连接CO并延长交圆于点D由图可得∠A+∠B=∠AOD+∠BOD=∠AOB=50°故选C.【考点】圆周角定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.7.在半径为R的圆中有一条长度为R的弦,则该弦所对的圆周角的度数是( )A.30°B.30°或150°C.60°D.60°或120°【答案】B【解析】根据圆的性质可得这条弦与半径围成的三角形为等边三角形,再根据圆周角定理即可求得结果.由题意得这条弦与半径围成的三角形为等边三角形则该弦所对的圆周角的度数是30°或150°故选B.【考点】圆周角定理点评:特殊三角形的性质的应用是初中数学平面图形中极为重要的知识点,与各个知识点结合极为容易,是中考中的热点,在各种题型中均有出现,需多加关注.8.如图,A、B、C三点都在⊙O上,点D是AB延长线上一点,∠AOC="140°," ∠CBD的度数是( )A.40°B.50°C.70°D.110°【答案】C【解析】先求得弧ABC所对的圆周角的度数,再根据圆内接四边形的对角互补可得∠ABC的度数,即可求得结果.∵∠AOC=140°∴弧ABC所对的圆周角的度数为70°∴∠ABC=110°∴∠CBD=70°故选C.【考点】圆周角定理,圆内接四边形的性质点评:本题是圆周角定理的基础应用题,在中考中比较常见,一般以选择题、填空题形式出现,属于基础题,难度不大.9.如图,⊙O的直径AB=8cm,∠CBD=30°,求弦DC的长.【答案】4cm【解析】连接OC、OD,根据圆周角定理可得∠COD=60°,即可得到△COD是等边三角形,根据等边三角形的性质即可求得结果.连接OC、OD,则OC=OD=4cm,∠COD=60°,故△COD是等边三角形,从而CD=4cm.【考点】圆周角定理,等边三角形的判定和性质点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.10.如图,在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是上一点(不与C、D重合),试判断∠CPD与∠COB的大小关系, 并说明理由.(2)点P′在劣弧CD上(不与C、D重合时),∠CP′D与∠COB有什么数量关系?请证明你的结论.【答案】(1)相等;(2)∠CP′D+∠COB=180°【解析】(1)连接OD,根据垂径定理可得∠COB=∠DOB,再结合圆周角定理即可得到结果;(2)连接P′P,则可得∠P′CD=∠P′PD,∠P′PC=∠P′DC.即可得∠P′CD+∠P′DC=∠CPD,从而可以得到结果.从而∠CP′D+∠COB=180°.(1)连接OD,∵AB⊥CD,AB是直径,∴,∴∠COB= ∠DOB.∵∠COD=2∠P,∴∠COB=∠P,即∠COB=∠CPD.(2)连接P′P,则∠P′CD=∠P′PD,∠P′PC=∠P′DC.∴∠P′CD+∠P′DC=∠P′PD+∠P′PC=∠CPD.∴∠C P′D=180°-(∠P′CD+∠P′DC)=180°-∠CPD=180°-∠COB,从而∠CP′D+∠COB=180°.【考点】垂径定理,圆周角定理点评:辅助线问题是初中数学学习中的难点,能否根据具体情况正确作出恰当的辅助线往往能够体现一个学生对图形的理解能力,因而这类问题在中考中比较常见,在各种题型中均有出现,一般难度较大,需多加关注.。
圆的各种常考题型总结80题

《各章节核心资料“圆”80道常考题》【韩春成内部学员资料(30)】知识构架一、概念二、垂径定理三、弧、弦、圆心角的关系四、圆周角1.圆周角2.圆周角与圆心角3.圆周角与直径五、点与圆的位置关系六、过三点的圆七、三角形的外接圆、外心4.三角形外接圆半径5.与外接圆有关的计算与证明八、线与圆的位置关系1.直线与圆的位置关系2.切线的性质3.切线的判定:1.半径+垂直 2.垂直+半径4.切线长定理及三角形内切圆5.切线长定理(三角形内切圆)五、圆与圆的位置关系两圆的公切线、公共弦六、函数与圆典题精炼概念1.【易】如果两条弦相等,那么()A.这两条弦所对的弧相等B.这两条弦所对的圆心角相等C.这两条弦的弦心距相等D.以上答案都不对2.【易】(孝感市高中阶段学校招生考试数学)下列说法正确的是()A.平分弦的直径垂直于弦B.半圆(或直径)所对的圆周角是直角C.相等的圆心角所对的弧相等D.若两个圆有公共点,则这两个圆相交3.【易】(河南省实验中学2011年内部中考数学第一轮复习资料4)下列命题中,正确的是()①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等A.①②③B.③④⑤C.①②⑤D.②④⑤4. 【易】(安徽省初中毕业学业考试数学)如图,点P 是等边三角形ABC 外接圆O 上的点,在以下判断中,不正确的是( ) A .当弦PB 最长时,APC △是等腰三角形 B .当APC △是等腰三角形时,PO AC ⊥ C .当PO AC ⊥时,30ACP ∠=︒D .当30ACP ∠=︒,PBC △是直角三角形5. 【易】(北京景山学校第二学期八年级期末数学试卷)如图,如果AB 为O ⊙直径,弦CD AB ⊥,垂足为E ,那么下列结论中错误的是( )A .CE DE =B .BC BD =C .BAC BAD =∠∠D .AC AD >6. 【易】判断题:⑴ 直径是弦 ( ) ⑵ 弦是直径 ( ) ⑶ 半圆是弧 ( ) ⑷ 弧是半圆 ( )⑸ 长度相等的两条弧是等弧 ( )⑹ 等弧的长度相等 ( )⑺ 两个劣弧之和等于半圆 ( )⑻ 半径相等的两个圆是等圆 ( )⑼ 两个半圆是等弧 ( )⑽ 圆的半径是R ,则弦长的取值范围是大于0且不大于2R ( )7. 【易】(福建宁德中考)如图,AB 是O ⊙的直径,AC 是弦,若32ACO ∠=︒,则CO B ∠的度数等于__________.BOCBA垂径定理8. 【易】(湖南省株洲中考数学题)如图AB 是O ⊙的直径,42BAC ∠=︒,点D 是弦AC 的中点,则DOC ∠的度数是________度.9. 【易】(福建厦门中考)如图,O 的直径CD 垂直于弦AB ,垂足为E .若6A B c m =,则AE =_______cm .10. 【易】(房山区一模)如图,AB 为O 的直径,弦CD AB ⊥,垂足为点E ,联结OC ,若5OC =,2AE =,则CD 等于( )A .3B .4C .6D .811. 【易】(北京55中九年级上月考)已知:如图,O 的直径CD AB E ⊥弦于,若16AB DE ==,求:O 的半径42°ODCBAODE CBAD12. 【易】(北京市第八十中学第一学期初三)已知,如图,在O ⊙中,弦16MN =,半径OA MN ⊥,垂足为点B ,4AB =,求O ⊙半径的长.13. 【易】(东城二模)如图,宽为2cm 的刻度尺在圆上移动,当刻度尺的一边与圆相切时,另一边与圆两个交点处的读数恰好为“2”和“8”(单位:cm ),则该圆的半径为__________cm .14. 【易】(浙江省2013年初中毕业生学业考试绍兴市试卷)绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD 为8m ,桥拱半径OC 为5m ,则水面宽AB 为( )A.4mB.5mC.6mD.8m15. 【中】(内江市二○一三年高中阶段教育学校招生考试及初中毕业会考试卷)如图,半圆O 的直径10cm AB =,弦6c m AC =,AD 平分BAC ∠,则AD 的长为( )A.B.C.D .4cm16. 【中】(四川省宜宾市中考数学试卷)如图,AB 是O ⊙的直径,弦CD AB ⊥于点G ,点F 是CD 上一点,且满足13CF FD =,连接AF 并延长交O ⊙于点E ,连接AD DE 、,AOABDCA(第11题)若=2=3CF AF ,.给出下列结论:①ADF AED △∽△;②2FG =;③tan E =∠;④DEF S =△________.弧、弦、圆心角的关系17. 【易】(厦门市初中毕业及高中阶段各类学校招生考试)如图所示,在O 中,AB AC =,30A ∠=︒,则B ∠=( )A .150︒B .75︒C .60︒D .15︒18. 【易】(通州区初三年级模拟考试)如图,AB 是O 的弦,OD AB ⊥于点D ,C 是AB 优弧上任意一点,则图中所有相等的线段有_____________;所有相等的角有_____________.19. 【易】(河南省实验中学内部中考数学第一轮复习资料4)如图:AC CB =,D E ,分别是半径OA 和OB 的中点,CD 与CE 的大小有什么关系?为什么?OD CBA圆周角20. 【易】(山东日照初中学业考试)如图,在ABC △中,以BC 为直径的圆分别交边AC 、AB 于D 、E 两点,连接BD 、DE .若BD 平分ABC ∠,则下列结论不一定成立的是( ) A .BD AC ⊥ B .22AC AB AE =⋅ C .ADE △是等腰三角形 D .2BC AD =21. 【易】(九年级第三次质量预测试题)如图,正三角形ABC 内接于O ,动点P 在圆周的劣弧AB 上,且不与A B 、重合,则BPC ∠等于( )A .B .C .D .22. 【易】(通州二模)如图,已知O 的两条弦AC BD ,相交于点E ,60A ∠=︒,则sin BDC∠的值为( )A .12B3C2D2OCBAED30 60 90 4523. 【易】 (台湾第一次中考数学科试题如图)(七),圆上有A B C D 、、、四点,其中80BAD ∠=︒。
精品 九年级数学上册 期末复习题 圆 垂径定理与圆心角圆周角复习题

0
0 0 15.如图,已知 O 的半径为 R,C,D 是直径 AB 同侧圆周上的两点, 的度数为 36 ,动 AC 的度数为 96 , BD
点 P 在 AB 上,求 PC+PD 的最小.
第 6 页 共 8 页
九年级数学上册 期末复习题
数学期末复习题 测试题 01 满分:100 分
1.下列命题中,正确的是(
0
13.如图,A、B、C、D 四点都在⊙O 上,AD 是⊙O 的直径,且 AD=8cm,若∠ABC=∠CAD,求弦 AC 的长.
第 5 页 共 8 页
九年级数学上册 期末复习题
14.如图,在 Rt△ABC 中,∠ACB=90 ,AC=5,CB=12,AD 是△ABC 的角平分线,过 A、C、D 三点的圆与斜边 AB 交于点 E,连接 DE. (1)求证:AC=AE; (2)求△ACD 外接圆的半径.
①弦是直径;②半圆是弧,但弧不一定是半圆;③半径相等的两个半圆是等弧;④直径是圆中最长的弦. 6.如图,已知⊙O 的半径是 6cm,弦 CB= 6 3 cm,OD⊥BC,垂足为 D,则∠COB=
第 6 题图
第 7 题图
第 8 题图 cm.
7.如图,直线 l 与⊙O 有两个公共点 A, B, O 到直线 l 的距离为 5cm, AB=24cm, 则⊙O 的半径是 8.如图,⊙O 的半径是 5cm,P 是⊙O 外一点,PO=8cm,∠P=30º,则 AB= 9.如图,AB 是⊙O 的直径,且 AD∥OC,若弧 AD 的度数为 80 .求 CD 的度数.
时间:25 分钟
)
姓名:
得分:
①顶点在圆周上的角是圆周角; ②圆周角的度数等于圆心角度数的一半;③90 的圆周角所对的弦是直径; ④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等 A.①②③ B.③④⑤
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【知识点总结】
1.圆是 到定点的距离等于定长 的所有点组成的图形.
2.圆是轴对称图形,它的直径所在的直线都是对称轴;又时中心对称图形,它的中心是圆心. 3.垂径定理:(图1)垂直于弦的直径平分弦,并且平分弦所对的弧. 推论1:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧 推论2:平分弧的直径垂直平分弧所对的弦
4.圆心角定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等. 关于弦的问题,常常需要过圆心作弦的垂线段,这是一条非常重要的辅助线。
圆心到弦的距离、半径、弦长构成直角三角形,便将问题转化为直角三角形的问题。
5.顶点在圆周上,并且两边都和圆相交的角叫做圆周角.
6.圆周角定理: 一条弧所对的圆周角等于它所对的圆心角的一半。
也可以理解为:一条弧所对的圆心角是它所对的圆周角的二倍;圆周角的度数等于它所对的弧的度数的一半。
7. 推论:半圆(或直径)所对的圆周角是直角;︒90的圆周角所对的弦是直径.
8.在同圆或等圆中,同弧或等弧所对的圆周角相等;相等的圆周角所对的弧也相等。
圆易错点
1.注意考虑点的位置
在解决点与圆的有关问题时,应注意对点的位置进行分类,如点在圆内圆外、点在优弧劣弧等.
例1.点P 到⊙O 上的最近距离为cm 3,最远距离为cm 5,则⊙O 的半径为 cm .
例2.BC 是⊙O 的一条弦, ︒=∠120BOC ,点A 是⊙O 上的一点(不与B 、C 重合),则BAC ∠的度数为 .
2.注意考虑弦的位置
在解决与弦有关的问题时,应对两条的位置进行分类,即注意位于圆心同侧和异侧的分类.
图3
图4
例3.在半径cm 5为的圆中,有两条平行的弦,一条为cm 8,另一条为cm 6,则这两条平行弦的距离是 .
例4.AB 是⊙O 的直径,AC 、AD 是⊙O 的两条弦,且︒=∠30BAC ,︒=∠45BAD ,则CAD ∠的度数为 . 考点1:基本概念和性质
考查形式:主要考查圆的对称性、直径与弦的关系、等弧等有关命题,常以选择题的形式出现.
例5.有下列四个命题:①直径是弦;②经过三个点一定可以作圆;③三角形的外心到三角形各顶点的距离都相等;④半径相等的两个半圆是等弧.其中正确的有( ).
A .4个
B .3个
C . 2个
D . 1个 考点2:圆心角与圆周角的关系
例6.如图1,A 、B 、C 为⊙O 上三点,若∠OAB=46°,则∠ACB=_______度.
B
A
A
(1) (2) (3)
例7..如图2,AB 是⊙O 的直径, BC BD =,∠A=25°,则∠BOD 的度数为________.
例8..如图3,AB 是半圆O 的直径,AC=AD,OC=2,∠CAB= 30 °, 则点O 到CD 的距离OE=______.
考点3:垂径定理
考查形式:主要考查借助垂径定理的解决半径、弧、弦、弦心距之间的计算和证明,填空题、选择题或解答题中都经常出现它的身影.解决是应注意作出垂直于弦的半径或弦心距,构造直角三角形进行解决.
例9.如图,在⊙O 中,有折线OABC ,其中8=OA ,12=AB ,︒=∠=∠60B A ,则弦BC 的长为( )。
A.19 B.16 C.18 D.20
1.下列命题中,正确命题的个数为( ).
①平分弦的直径垂直于弦;②圆周角的度数等于圆心角度数的一半;③︒90的圆周角所对的弦是直;④圆周角相等,则它们所对的弧相等.
A .1个
B .2个
C . 3个
D . 4个
2.下列说法中,正确的是( )
A. 到圆心的距离大于半径的点在圆内
B. 圆的半径垂直于圆的切线
C
C. 圆周角等于圆心角的一半
D. 等弧所对的圆心角相等
3.若圆的一条弦把圆分成度数的比为1:3的两条弧,则劣弧所对的圆周角等于()
A. 45°
B. 90°
C. 135°
D. 270°
4.如图所示,A、B、C三点在圆O上,∠AOC=100°,则∠ABC等于()
A. 140°
B. 110°
C. 120°
D. 130°
5.如图所示,圆O的直径为10,弦AB的长为6,M是弦AB上的一动点,则线段的OM的长的取值范围是()
A. 3≤OM≤5
B. 4≤OM≤5
C. 3<OM<5
D. 4<OM<5
6.如下图,已知CD是⊙O的直径,过点D的弦DE平行于半径OA,若∠D的度数是50o,则∠C的度数是()
A)50o B)40o C)30o D)25o
第6题图第7题图第8题图
7.如上图,两正方形彼此相邻,且大正方形内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为().
+ cm B) 9 cm C)45cm D)62cm A)(45)
8.如上图,⊙C过原点,且与两坐标轴分别交于点A,点B,点A的坐标为(0,3),M是第
∠=120,则⊙C的半径为()
三象限内OB上一点,BMO
A. 6
B. 5 C 3 D. 32
9.半径为5的⊙O内有一点P,且OP=4,则过点P的最短的弦长是,最长的弦长是.
10.如图,以原点O为圆心的圆交x轴于点A、B两点,交y轴的正半轴于点C,
D为第一象限内⊙O上的一点,若∠DAB= 20°,则∠OCD = _____________.
11.如图,⊙O的直径AB和弦CD相交于点E,已知AE=6cm,EB=2cm,∠CEA=30°,
求CD的长.
12.如图,已知⊙O中,AB为直径,AB=10cm,弦AC=6cm,∠ACB的平分线交⊙O
于D,求BC、AD和BD的长.
13. 如图,
AB为⊙O的弦,C、D为弦AB上两点,且OC=OD ,延长OC、OD分别
交⊙O于E、F,
证明:AE=BF.
F
E
D
O
B
A C
14.如图,F是以O为圆心,BC为直径的半圆上任意一点,A是BF的中点,AD ⊥BC于D,
求证:AD =1
2
BF.
O C
B。
