设AE=x,DF=y,写出y关于x的函数关系式,并写出自变量x的取值范围;

合集下载

中考数学动点问题专题讲解(一)(建立动点问题的函数解析式)

所谓“动点型问题”是指题设图形中存在一个或多个动点 ,它们在线段、射线或弧线上运动的一类开放性题目 .解决这种问题的重点是动中求静 ,灵巧运用相关数学知识解决问题 .重点 :动中求静 .数学思想：分类思想函数思想方程思想数形联合思想转变思想着重对几何图形运动变化能力的观察从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，经过 “对称、动点的运动 ”等研究手段和方法，来研究与发现图形性质及图形变化，在解题过程中浸透空间看法和合情推理。

选择基本的几何图形，让学生经历研究的过程，以能力立意，观察学生的自主研究能力，促使培育学生解决问题的能力．图形在动点的运动过程中察看图形的变化状况，需要理解图形在不一样地点的状况，才能做好计算推理的过程。

在变化中找到不变的性质是解决数学 “动点 ”研究题的基本思路 ,这也是动向几何数学识题中最核心的数学实质。

二期课改后数学卷中的数学压轴性题正逐渐转向数形联合、动向几何、着手操作、实验研究等方向发展．这些压轴题题型众多、题意创新，目的是观察学生的剖析问题、解决问题的能力，内容包含空间看法、应企图识、推理能力等．从数学思想的层面上讲：（ 1）运动看法；（ 2）方程思想；（ 3）数形联合思想；（ 4）分类思想；（5）转变思想等．研究历年来各区的压轴性试题，就能找到今年中考数学试题的热门的形成和命题的动向，它有益于我们教师在教课中研究对策，掌握方向．只的这样，才能更好的培育学生解题修养，在素质教育的背景下更明确地表现课程标准的导向．本文拟就压轴题的题型背景和划分度丈量点的存在性和划分度小题办理手法提出自己的看法．专题一：成立动点问题的函数分析式函数揭露了运动变化过程中量与量之间的变化规律,是初中数学的重要内容 .动点问题反应的是一种函数思想,因为某一个点或某图形的有条件地运动变化 ,惹起未知量与已知量间的一种变化关系 ,这种变化关系就是动点问题中的函数关系 .那么 ,我们如何成立这种函数解析式呢下边联合中考试题举例剖析.一、应用勾股定理成立函数分析式例 1(2000 年·上海 )如图 1,在半径为 6,圆心角为 90°的扇形 OAB 的弧 AB 上,有一个动点 P,PH⊥ O A,垂足为 H,△ OPH 的重心为 G.(1)当点 P 在弧 AB 上运动时 ,线段 GO 、GP 、GH 中 ,有无长度保持不变的线段假若有 ,请指出这样的线段 ,并求出相应的长度 .(2)设 PH x ,GP y ,求 y 对于 x 的函数分析式，并写出函数的定义域(即自变量 x 的取值范围 ).(3)假如△ PGH 是等腰三角形 ,试求出线段 PH 的长 .解 :(1)当点 P 在弧 AB 上运动时 ,OP 保持不变 ,于是线段 GO 、GP 、GH中 ,有长度保持不变的线段，这条线段是GH=2NH=2 1 OP=2.B33 2P(2) 在 Rt △ POH中 ,OHOP 2 PH 236 x 2 ,∴yN11x 2.G xMHOH3622OM H A在 Rt △ MPH 中 ,图 1MPPH 2MH 2x 2 9 1 x 21 36 3 x 2.4 2∴ y =GP=2MP=136 3x 2 (0< x <6).33(3)△ PGH 是等腰三角形有三种可能状况 :① GP=PH时 , 1 36 3 2 x6x63x x , 解得 . 经查验 , 是原方程的根 ,且切合题意 .② GP=GH 时 ,题意 .1 x22 ,解得 x 0. 经查验 ,x 0是原方程的根 ,但不切合36 33③ PH=GH 时 , x 2 .综上所述 ,假如△ PGH 是等腰三角形 ,那么线段 PH 的长为6 或 2.本专题的主要特点是两个点在运动的过程中，直接或间接地结构了直角三角线，所以能够利用勾股定理去成立函数关系式 . 勾股定理是初中数学的重要定理，在运用勾股定理写函数分析式的过程中，主假如找边的等量关系，要擅长发现这种内在的关系，用代数式去表示这些边，达到解题的目的 . 因为是压轴题，有的先有铺垫，再写分析式；有的写好分析式后，再证明等腰三角形、相像三角形等，还有的再解一些与圆相关的体型 . 要仔细领悟，达到举一反三的目的 .1 切记勾股定理：在直角三角形中，两条直角边的平方和等于斜边的平方 .例题，扇形中∠ AOB=45°，半径 OB=2，矩形 PQRS 的极点 P 、 S 在半径 OA 上， Q 在半径 OB 上， R 在弧 AB 上，连结 OR.（ 1）当∠ AOR=30°时，求 OP 长（ 2）设 OP=x ，OS=y ，求 y 与 x 的函数关系式及定义域2 在四边形的翻折与旋转中，常常会应用到勾股定理，由此产生些函数分析式的问题，要娴熟掌握 .例题：如图，正方形 ABCD 中， AB=6，有一块含 45°角的三角板，把 45°角的极点放在 D 点，将三角板绕着点 D 旋转，使这个 45°角的两边与线段 AB 、 BC 分别订交于点 E 、 F （点 E 与点 A 、 B 不重合）（1）从几个不一样的地点，分别丈量AE、EF、 FC 的长，从中你能发现 AE、 EF、 FC的数目之间拥有如何的关系并证明你所获得的结论（2）设 AE=x，CF=y，求 y 与 x 之间的函数分析式，并写出函数的定义域（3）试问△ BEF的面积可否为 8 假如能，恳求出 EF的长；假如不可以，请说明原因 .3在一些特别的四边形中，如矩形、正方形，它们都是直角，菱形的对角线相互垂直，这些都有可能结构直角三角形，能够考虑用勾股定理写出函数的分析式.例题：如图，在菱形 ABCD中，AB=4，∠ B=60°，点 P是射线 BC上的一个动点，∠PAQ=60°，交射线 CD 于点 Q，设点 P 到点 B 的距离为 x， PQ=y（1）求证：三角形 APQ 是等边三角形（2）求 y 对于 x 的函数分析式，并写出它的定义域（3）假如 PD⊥ AQ，求 BP 的值4作底边上的高，能够结构直角三角形，利用勾股定理写函数的分析式例题：如图，等边△ABC的边长为 3，点 P、Q 分别是 AB、BC上的动点（点P、Q 与△ABC 的极点不重合），且AP=BQ， AQ、 CP 订交于点 E.（1）如设线段 AP 为 x，线段 CP为 y，求 y 对于 x 的函数分析式，并写出定义域（2）当△ CBP的面积是△ CEQ的面积的 2 倍时，求 AP 的长（3）点 P、Q 分别在 AB、BC 上挪动过程中， AQ 和 CP 可否相互垂直如能，请指出P 点的地点，请说明原因.5在解圆的题目时，首选的协助线是弦心距，它不单能够运用垂径定理，并且结构了直角三角形，为用勾股定理写函数分析式创建了条件.例题：如图，⊙ A 和⊙ B 是外离的两圆，两圆的连心线分别交⊙A、⊙ B 于 E、 F，点 P 是线段 AB 上的一动点（点P 不与 E、 F 重合）， PC切⊙ A 于点 C， PD 切⊙ B 于点 D，已知⊙A 的半径为 2 ，⊙ B 的半径为1，AB=5.（1）如设线段BP 的长为 x，线段 CP 的长为 y，求 y 对于 x 的函数分析式，并写出函数的定义域（2）假如 PC=PD，求 PB 的长（3）假如PC=2PD，判断此时直线CP与⊙ B 的地点关系，证明你的结论6 重申圆的首选协助线是弦心距，它不单能够均分弦，并且结构了直角三角形，为解题创建新思路 .例题：如图，在△ ABC中， AB=15,AC=20,cotA=2，P 是边 AB 上的一个动点，⊙P 的半径为定长 . 当点 P 与点 B 重合时，⊙ P 恰巧与边 AC 相切；当点 P 与点 B 不重合，且⊙ P 与边 AC 订交于点 M 和点 N 时，设 AP=x，MN=y.(1)求⊙ P 的半径(2)求 y 对于 x 的函数分析式，并写出它的定义域(3)当 AP=6 5时，试比较∠ CPN与∠ A 的大小，并说明原因阶梯题组训练1如图， E 是正方形 ABCD的边 AD 上的动点， F 是边 BC 延伸线上的一点，且 BF=EF，AB=12，设 AE=x，BF=y.（1）当△ BEF是等边三角形时，求BF 的长；（2）求 y 与 x 之间的函数分析式，并写出它的定义域；（3）把△ ABE 沿着直线 BE翻折，点 A 落在点 A′处，尝试究：△A′BF 可否为等腰三角形假如能，恳求出 AE 的长；假如不可以，请说明原因 .2如图，在△ ABC中，∠ACB=90°，∠ A=30°，D 是边 AC 上不与点 A、C 重合的随意一点，DE⊥ AB，垂足为点E， M 是 BD 的中点 .（1）求证： CM=EM;（2）假如 BC= 3设 AD=x， CM=y，求 y 与 x 的函数分析式，并写出函数的定义域；（3）当点 D 在线段 AC 上挪动时，∠ MCE 的大小能否发生变化假如不变，求出∠MCE 的大小；假如发生变化，说明如何变化.3 ABCD 中，对角线 AC⊥ AB， AB=15， AC=20，点 P 为射线 BC 上一动点， AP⊥ PM(点 M 与点B 分别在直线 AP 的双侧 )，且∠ PAM=∠ CAD，连结 MD.(1)当点 M 在 ABCD内时，如图，设 BP=x，AP=y，求 y 对于 x 的函数关系式，并写出函数定义域；(2) 请在备用图中画出切合题意的表示图，并研究：图中能否存在与△AMD 相像的三角形若存在，请写出并证明；若不存在，请说明原因；(3) 当△为等腰三角形时，求BP的长.4抛物线经过 A（2， 0）、 B（ 8， 0）、 C（0，16 3） . 3（1）求抛物线的分析式；（2）设抛物线的极点为P，把△ APB 翻折，使点 Pl 落在线段 AB 上（不与 A、 B 重合），记作 P′，折痕为 EF，设 AP′ =x，PE=y，求 y 对于 x 的函数关系式，并写出定义域；（3）当点 P′在线段 AB 上运动但不与 A、B 重合时，可否使△ EFP′的一边与 x 轴垂直若能，恳求出此时点P′的坐标；若不可以，请你说明原因.5 如图，矩形 ABCD中， AD=7， AB=BE=2，点 P 是 EC（包含 E、 C）上的动点，线段 AP 的垂直均分线分别交 BC、 AD 于点 F、 G，设 BP=x， AG=y.（1）四边形 AFPG是说明图形请说明原因；（2）求 y 与 x 的函数关系式；（3）假如分别以线段GP、 DC 为直径作圆，且使两圆外切，求x 的值 .6在梯形 ABCD中，ADE 为底边 BC 上一点，以点 E 为圆心， BE 为半径画⊙ E 交直线 DE于点F.（1）如图，当点 F 在线段 DE上时，设 BE=x，DF=y，试成立 y 对于 x 的函数关系式，并写出自变量 x 的取值范围；（2）当以 CD为直径的⊙ O 与⊙ E 相切时，求 x 的值；（3）连结 AF、 BF，当△ ABF 是以 AF 为腰的等腰三角形时，求x 的值 .7 如图，在正方形ABCD中， AB=1，弧 AC 是以点 B 为圆心， AB 长为半径的圆的一段弧，点E 是边 AD 上的随意一点（点 E 与点 A 、 D 不重合），过 E 作弧 AC 所在圆的切线，交 DC 于点F ，G 为切点 .（ 1）当∠ DEF=45°时，求证点 G 为线段 EF 的中点；（ 2）设 AE=x ， FC=y ，求 y 对于 x 的函数分析式，并写出函数的分析式；（ 3）将△ DEF 沿直线 EF 翻折后得△ D 1EF ，如图 2，当 EF=5时，议论△ AD 1D 与△ ED 1 F 是6否相像，假如相像，请加以证明；假如不相像，只需求写出结论，不要求写出原因.（ 2003 年上海第 27 题）二、应用比率式成立函数分析式例 2（ 2006 年·山东）如图 2,在△ ABC 中 ,AB=AC=1,点 D,E 在直线 BC 上运动 . 设 BD=x, CE=y .(1)假如∠ BAC=30° ,∠ DAE=105° ,试确立 y 与 x 之间的函数分析式；(2)假如∠ BAC 的度数为 ,∠ DAE 的度数为,当 ,知足如何的关系式时之间的函数分析式还成立试说明原因.解:(1)在△ ABC 中 ,∵ AB=AC,∠ BAC=30° ,∴∠ ABC=∠ACB=75° ,∴∠ ABD=∠ ACE=105° .∵∠ BAC=30°,∠ DAE=105° , ∴∠ DAB+∠ CAE=75° , 又∠ DAB+∠ ADB=∠ ABC=75° ,D∴∠ CAE=∠ ADB,B ∴△ ADB ∽△ EAC, ∴ABBD ,CEAC1 x1∴, ∴ y .y1x(2)因为∠ DAB+∠ CAE=,又∠ DAB+∠ ADB=∠ ABC=90,2且函数关系式成立 ,∴90 2 =, 整理得 90 .2 当90 时 ,函数分析式 y 1 2成立 .x例 3(2005 年·上海 )如图 3(1),在△ ABC 中 ,∠ ABC=90° ,AB=4,BC=3.点 O 是边 AC 上的一个动点 ,以点 O 为圆心作半圆 ,与边 AB 相切于点CD,交线段 OC 于点 E.作 EP ⊥ ED,交射线 AB 于点 P,交射线 CB 于点 F.,(1)中 y 与 xAEC图 2FBPD AE O3(1)(1)求证 : △ADE ∽△ AEP.PB (2)设 OA= x ,AP= y ,求 y 对于 x 的函数分析式 ,并写出它的定义域.F(3)当 BF=1 时 ,求线段 AP 的长 . D解:(1)连结 OD.依据题意 ,得 OD ⊥ AB,∴∠ ODA=90° ,∠ODA=∠ DEP.CA又由 OD=OE,得∠ ODE=∠ OED.∴∠ ADE=∠ AEP, ∴△ ADE ∽△E O AEP.3(2)(2) ∵ ∠ ABC=90 ° ,AB=4,BC=3, ∴ AC=5. ∵ ∠ ABC=∠ADO=90° , ∴ OD ∥ BC, ∴ODx , ADx ,35 4 5∴ OD= 3x ,AD=4x . ∴ AE=x 3x= 8x . 55 5 5∵△ ADE ∽△ AEP, ∴AEAD ,8 x 4 x1625∴55 .∴ y x ( 0 x).APAEy8 x 585(3)当 BF=1 时，①若 EP 交线段 ∵∠ ADE=∠ AEP, ∴∠ F=∠ PDE, CB 的延伸线于点 F,如图 3(1)，则 CF=4.∴∠ PDE=∠ PEC. ∵∠ FBP=∠ DEP=90°, ∠FPB=∠ DPE, ∴∠ F=∠ FEC, ∴ CF=CE.∴ 5-8x =4,得 x 5 .可求得 y 2 ,即 AP=2.5 8②若 EP 交线段 CB 于点 F,如图 3(2), 则 CF=2. 近似① ,可得 CF=CE. ∴ 5-8x =2,得 x 15 .5 8可求得 y6 ,即 AP=6.综上所述 , 当 BF=1 时 ,线段 AP 的长为 2 或 6.本专题研究在图形的运动变化过程中，存在平行或相像的三角形，利用比例式来成立函数关系式 . 难一些的题目此中的一个变量是比率式，一个变量是线段，也是利用相像或平行来结构比率式，进而写出函数的分析式 . 作为最后的一道压轴题，一般状况下写出分析式后还会有一个证等腰或相像或相切的题目，能够二次函数专题中的解题思想进行办理.1 由平行获得比率式，进而成立函数关系式.例题：如图，在△ ABC 中， AB=AC=4,BC=1AB ，点 P 是边 AC 上的一个点， AP= 1 PD ，22∠APD=∠ ABC ，连结 DC 并延伸交边 AB 的延伸线于点 E（1）求证：AD证明：△ ADE∽△ GFA （2）设 DE=x， BG=y，求 y 对于 x 的函数分析式及定义域（3）当 BH= 1时，求 DE的长43在学习利用相像比成立函数的分析式的时候，初中阶段的知识已经学了许多，对最后的压轴题的综合性的要求已经很高了. 一般会在写分析式前有一些证明或计算，写好分析式后再来一个证明等腰三角形或圆的地点关系等. 假如能够把一道复杂的压轴题拆分红几道小的题目，各个击破，难题也就变简单了.例题：如图，在Rt△ ABC中，∠ C=90°， sinB= 4，AC=4； D 是 BC的延伸线上一个动点，5∠EDA=∠B， AE(1) 找出图中的相像三角形，并加以证明(2)设 CD=x， AE=y，求 y 对于 x 的函数分析式，并写出函数的定义域(3)当△ ADE 为等腰三角形时，求 AE 的长4方才研究的写函数分析式都是在几何图形中进行的，下边来看在平面直角坐标系中如何写分析式 .例题：如图，在直角坐标系中的等腰梯形 AOCD 中，AD AD23例题：如图，在平面直角坐标系中，OC55点 A 的坐标为（ 1， 0），点 B、 C 的坐标分别为（ -1， 0）， C（ 0， b），且 0＜ b＜ 3， m 是经过点 B、 C 的直线，当点 C 在线段 OC上挪动时，过点 A 作 AD⊥m 于点 D.(1) 求点 D、 O 之间的距离S△BDA(2) 假如=ɑ，试求：ɑ与 b 的函数关系式及ɑ的取值范围S△BOC(3)当∠ ADO 的余切值为 2 时，求直线 m 的分析式(4)求此时△ ABD 与△ BOC重叠部分的面积6当我们学习到利用相像三角形的相像比来成立函数分析式的时候，初中阶段的知识已经学得差不多了，对于一些貌似很复杂的图形，只需能够分层求解，就能化繁为简.例题：如图，在边长为 6 的正方形ABCD的双侧如图作正方形BEFG、正方形 DMNK ，恰巧使得N、 A、 F 三点在向来线上，连结MF 交线段 AD 于点 P，连结 NP，设正方形BEFG 的边长为x，正方形DMNK 的边长为y.（1）求y对于x的函数关系式及自变量x 的取值范围（2）当△ NPF的面积为32 时，求 x 的值（3）以P为圆心，AP为半径的圆能够与以G 为圆心， GF 为半径的圆相切，若能恳求x 的值，若不可以，请说明原因练习：1. 如图，在三角形中， AB=AC=8，BC=10，点 D 、E 分别在 BC 、 AC 上（点 D 不与 B 、 C 重合），且∠ ADE=∠ B ，设 BD=x ， AE=y.（ 1）求 y 与 x 之间的函数分析式，并写出函数的定义域（ 2）点 D 在 BC 上的运动过程中，△ ADE 能否有可能成为一个等腰三角形若有可能，请求出当△ ADE 为等腰三角形时 x 的值 ;如不行能，请说明原因.2.在△ ABC 中， AB=4， AC=5， cosA= 3，点 D 是边 AC 上的点，点 E 是边 AB 上的点，且5知足∠ AED=∠ A ， DE 的延伸线交射线 CB 于点 F ，设 AD=x ， EF=y.（ 1）如图 1，用含 x 的代数式表示线段 AE 的长（ 2）如图 1，求 y 对于 x 的函数分析式及函数的定义域（3）连结 EC ，如图 2，求档 x 为什么值时，△AEC 与△ BEF 相像 .3.如图，在矩形 ABCD 中， AB=m （ m 是大于 0 的常数），BC=8，E 为线段 BC 上的动点（不与 B 、 C 重合） .连结 DE ，作 EF ⊥ DE ， EF 与射线 BA 交于点 F ，设 CE=x ， BF=y.(1) 求 y 对于 x 的函数关系式(2) 若 m=8，求 x 为什么值时， y 的值最大，最大值是多少(3) 若 y=12，要使△ DEF 为等腰三角形， m 的值应为多少m（1）已知在梯形 ABCD中， AD 如图， P 为 BC上的一点，且 BP=2. 求证：△ BEP∽△ CPD；（2）假如点 P 在 BC 边上挪动（点 P 与点 B、C 不重合），且知足∠ EPF=∠C， PF 交直线CD 与点 F，同时交直线 AD 于点 M ，那么（3）当点 F 在线段 CD 的延伸线上时，设 BP=x， DF=y，求 y 对于 x 的函数分析式，并写出函数的定义域；（4）当△DMF= 9 △ BEP时，求BP的长.S 4 S（1）如图，在四边形 ABCD中，∠ B=90°，AD 求 y 对于 x 的函数分析式，并写出定义域；（2）当 AD=11 时，求 AG 的长；（3）假如半径为EG 的⊙ E 与半径为FD 的⊙ F 相切，求这两个圆的半径.4. 如图，在半径为 5 的⊙ O 中，点A、 B 在⊙ O 上，∠ AOB=90°，点 C 是弧 AB 上的一个动点， AC与 OB 的延伸线订交于点D，设 AC=x， BD=y.(1) 求 y 对于 x 的函数分析式，并写出它的定义域；(2) 若⊙ O 与⊙ O 订交于点 A、 C，且⊙ O 与⊙ O 的圆心距为2，当 BD= OB 时，求⊙ O1 1 1 13 的半径；(3)能否存在点 C，使得△ DCB∽△ DOC 假如存在，请证明；假如不存在，请简要说明原因 .（ 1）已知∠ ABC=90°， AB=2，BC=3， ADPQ AD当 AD= 3，且点 Q 在线段 AB 上时，PC AB 2设点 B 、 Q 之间的距离为 x ，S △APQ=y ，此中 S △APQ 表示△ APQ 的面积， S △PBC 表示S △PBC△PBC 的面积，求 y 对于 x 的函数分析式，并写出函数定义域；（ 2）当 AD ＜ AB ，且点 Q 在线段 AB 的延伸线上时（如图 3 所示），求∠ QPC 的大小（. 2009上海第 25 题）三、应用求图形面积的方法成立函数关系式例 4（ 2004 年·上海）如图 ,在△ ABC 中 ,∠BAC=90° ,AB=AC=2 2 ,⊙ A 的半径为 1.若点O 在 BC 边上运动 (与点 B 、 C 不重合 ),设 BO= x ,△ AOC 的面积为y .(1)求 y 对于 x 的函数分析式 ,并写出函数的定义域 .A(2)以点 O 为圆心 ,BO 长为半径作圆 O,求当⊙ O 与⊙ A 相切时 , △AOC 的面积 .解:(1)过点 A 作 AH ⊥ BC,垂足为 H.∵∠ BAC=90°,AB=AC=2 2 , ∴BC=4,AH= 1 BC=2. ∴ OC=4- x .1OC AH ,2B OH C∵SAOC∴ yx4 ( 0 x4 ).图 82(2)①当⊙ O 与⊙ A 外切时 ,7在 Rt △AOH 中 ,OA= x 1,OH= 2x ,∴(x 1)2 22 (2 x)2 . 解得 x.67 17此时 ,△AOC 的面积y = 4 .6 6②当⊙ O 与⊙ A内切时 ,在 Rt△AOH 中 ,OA= x 1,OH= x 2 ,∴(x 1)2 22 (x 2) 2 . 解得 x 7 .7 1 2此时 ,△AOC 的面积y = 4 .2 2综上所述 ,当⊙ O 与⊙ A 相切时 ,△ AOC的面积为17或1.6 2例 2、【 09 广东】正方形 ABCD边长为 4， M 、N 分别是 BC、 CD 上的两个动点，当M 点在BC 上运动时，保持 AM 和 MN 垂直．（1）证明： Rt△ABM∽Rt△MCN；（2）设 BM=x，梯形 ABCN 的面积为 y，求 y 与 x 之间的函数关系式；当M 点运动到什么位置时，四边形 ABCN面积最大，并求出最大面积；（3）当 M 点运动到什么地点时 Rt△ABM∽Rt△AMN ，求此时 x 的值练习 1.如图，在△ ABC 中， BC=8， CA=AB、 AC、BC 上（点 E 与点 A、 B 不重合），连结求出 y 与 x 之间的函数表达式，并写出自变量，∠ C=60°， EF∥ BC，点 E、F、 DED、 DF。

相似三角形综合大题

相似三角形综合大题一．解答题（共30小题）1．（2012•昌平区二模)如图，在Rt△ABC中，∠ABC=90°，过点B作BD⊥AC于D，BE平分∠DBC,交AC于E，过点A作AF⊥BE于G，交BC于F，交BD于H．（1）若∠BAC=45°，求证：①AF平分∠BAC；②FC=2HD．(2)若∠BAC=30°，请直接写出FC与HD的等量关系．2．（2012•香坊区二模）已知:在△ABC中，∠ACB=90°,AC=2BC,D是线段AC上一点，E是线段CD上一点，过点D作DF⊥BE交BE的延长线于点F，连接CF．(1）当点D是线段AC的中点时(如图1)，求证：BF﹣DF=CF：（2）当点D与点A重合时,在线段EF上取点G，使GF=DF，连接DG并延长交CF于点H，交BC延长线相交于点P（如图2）,CH：HF=4:5,EG=，求PH的长．3．(2012•西青区一模）在△ABC中，∠ACB=90°，∠ABC=30°,将△ABC绕顶点C 顺时针旋转，旋转角为θ（0°＜θ＜180°），得到△A′B′C．（Ⅰ)如图①,当AB∥CB′时，设A′B′与CB相交于点D．证明：△A′CD是等边三角形；（Ⅱ)如图②,连接AA′、BB′，设△ACA′和△BCB′的面积分别为S1、S2．求证：S1:S2=1：3;（Ⅲ)如图③，设AC的中点为E，A′B′的中点为P，AC=a，连接EP．求当θ为何值时，EP的长度最大，并写出EP的最大值（直接写出结果即可)．4．（2012•南岗区校级二模）在△ABC中，已知∠BAC=45°，高线CD与高线AE 相交于点H,连接DE．（1）如图1,△ABC为锐角三角形时，求证:AE﹣CE=DE；（2）如图2，在（1)的条件下,作∠AEC的平分线交AC于点F，连接DF交AE于点G，若BD=CF，AE=6，求GH的长．5．（2012•徐汇区校级模拟）在△OAC中，∠AOC=90°，OB=6，BC=12，∠ABO+∠C=90°,M、N分别在线段AB、AC上．（1）填空:cosC=．(2)如图1,当AM=4，且△AMN与△ABC相似时，△AMN与△ABC的面积比为；（3)如图2，当MN∥BC时，将△AMN沿MN翻折，点A落在四边形BCNM所在平面的点为点E，EN与射线AB交于点F，设MN=x，△EMN与△ABC重叠部分的面积为y，求y关于x的函数解析式，并写出自变量的取值范围．6．（2012•道外区二模)已知：如图1，四边形ABCD中,∠ABC=∠ADC=90°，连接AC，tan∠CAD=，过点D作DE⊥AB，点E为垂足．（1)求证：AE+BC=DE；(2）连接BD，设BD与AC交于点F,DE与AC交于点G，若AG：FG=3：2,AE=6（如图2）,求线段BC的长．7．(2012•路南区一模）如图①,在△ABC中,AB=BC，∠ABC=120°，点P是线段AC上的动点（点P与点A、点C不重合），连接BP．将△ABP绕点P按顺时针方向旋转α角（0°＜α＜180°），得到△A1B1P，连接AA1，直线AA1分别交直线PB、直线BB1于点E,F．（1)如图①，当0°＜α＜60°时，在α角变化过程中，△APA1与△BPB1始终存在关系(填“相似”或“全等”），同时可得∠A1AP∠B1BP（填“=”或“＜”“＞”关系)．请说明△BEF与△AEP之间具有相似关系；（2）如图②，设∠ABP=β，当120°＜α＜180°时,在α角变化过程中，是否存在△BEF 与△AEP全等?若存在，求出α与β之间的数量关系；若不存在，请说明理由；(3)如图③，当α=120°时，点E、F与点B重合．已知AB=4，设AP=x,S=△A1BB1面积，求S关于x的函数关系式8．（2012•上虞市模拟）复习完“四边形”内容后，老师出示下题：如图1，直角三角板的直角顶点P在正方形ABCD的对角线BD上移动，一直角边始终经过点C，另一直角边交直线AB于点Q，连接QC．求证：∠PQC=∠DBC．（1）请你完成上面这道题；（2）完成上题后，同学们在老师的启发下进行了反思，提出许多问题，如：①如图2，若将题中的条件“正方形ABCD"改为“矩形ABCD”，其余条件都不变，是否仍能得到∠PQC=∠DBC？②如图3，若将题中的条件“正方形ABCD”改为“直角梯形ABCD”，其余条件都不变,是否仍能得到∠PQC=∠DBC？请你对上述反思①和②作出判断,在下列横线上填写“是"或“否"：①;②．并对①、②中的判断，选择其中一个说明理由．9．（2012•上海模拟）已知：在Rt△ABC中，∠C=90°,AC=4，∠A=60°，CD是边AB上的中线,直线BM∥AC,E是边CA延长线上一点，ED交直线BM于点F，将△EDC沿CD翻折得△E′DC，射线DE′交直线BM于点G．(1）如图1,当CD⊥EF时，求BF的值;（2）如图2,当点G在点F的右侧时；①求证：△BDF∽△BGD；②设AE=x,△DFG的面积为y，求y关于x的函数解析式,并写出x的取值范围; (3）如果△DFG 的面积为，求AE的长．10．（2012•道外区一模）已知：点P为正方形ABCD内部一点，且∠BPC=90°,过点P的直线分别交边AB、边CD于点E、点F．（1）如图1，当PC=PB时，则S△PBE、S△PCF S△BPC 之间的数量关系为；(2）如图2，当PC=2PB时，求证：16S△PBE+S△PCF=4S△BPG；（3）在（2）的条件下，Q为AD边上一点，且∠PQF=90°，连接BD，BD交QF 于点N，若S△bpc=80，BE=6．求线段DN的长．11．(2012•太原一模)如图1,已知四边形ABCD是正方形，对角线AC、BD相交于点E，以点E为顶点作正方形EFGH,使点A、D分别在EH和EF上，连接BH、AF．（1）判断并说明BH和AF的数量关系;（2)将正方形EFGH绕点E顺时针方向旋转θ（0°≤θ≤360°),设AB=a，EH=b，且a ＜2b．①如图2，连接AG，设AG=x，请直接写出x的取值范围;当x取最大值时,直接写出θ的值;②如果四边形ABDH是平行四边形,请在备用图中补全图形,并求a与b的数量关系．12．（2012•武汉模拟）（1)如图1，在△ABC中，点D，E在边BC上，BD：DE:CE=1：2：3,线段FG∥BC，分别交线段AD，AE于M、N两点,则有FM：MN：NG=（2)如图2，在△ABC中，∠BAC=90°，正方形DEGF的四个顶点有△ABC的三边上，线段FG分别交线段AD，AE于M、N两点，若BD=4，EC=9,求MN的长? （3)如图3，在△ABC中，∠BAC=90°，正方形DEGF的四个顶点在△ABC的三边所在的直线上,DA与EN的延长线分别交直线FG于M、N两点，求证：MN2=MF•NG．13．（2012•香坊区校级模拟）已知，等边△ABC中,D为BC上一点，DE∥AC交AB于C，M是AE上任意一点（M不与A、E重合），连DM，作DN平分∠MDC 交AC于N．（1）若BD=DC（如图1)，求证：EM+NC=DM；（2）在（1）的条件下，如图2，作DF⊥AC于F，若NF:FC=3：5，AM=4,连接MN将∠DMN沿MN翻折,翻折后的射线MD交AC于P,连接DP交MN于点Q，求PQ的长．14．（2012•香坊区一模)已知：在△ABC中，AB=AC，点P是BC上一点，PC=2PB，连接AP，作∠APD=∠B交AB于点D．连接CD,交AP于点E．(1）如图1,当∠BAC=90°时，则线段AD与BD 的数量关系为；（2）如图2，当∠BAC=60°时，求证：AD=BD；（3）在（2)的条件下，过点C作∠DCQ=60°交PA的延长线于点Q如图3，连接DQ，延长CA交DQ于点K，若CQ=．求线段AK的长．15．(2012秋•大丰市期末）探索绕公共顶点的相似多边形的旋转：（1）如图1，已知：等边△ABC和等边△ADE,根据(指出三角形的全等或相似），可得CE与BD的大小关系为：．（2）如图2，正方形ABCD和正方形AEFG，求：的值；（3）如图3,矩形ABCD和矩形AEFG，AB=kBC,AE=kEF，求：的值．（用k的代数式表示)16．(2012秋•东城区期末)如图1，在等腰直角△ABC中,∠BAC=90°，AB=AC=2，点E是BC边上一点，∠DEF=45°且角的两边分别与边AB，射线CA交于点P,Q．（1)如图2，若点E为BC中点，将∠DEF绕着点E逆时针旋转，DE与边AB交于点P，EF与CA的延长线交于点Q．设BP为x，CQ为y,试求y与x的函数关系式，并写出自变量x的取值范围；（2）如图3,点E在边BC上沿B到C的方向运动（不与B，C重合），且DE始终经过点A，EF与边AC交于Q点．探究：在∠DEF运动过程中，△AEQ能否构成等腰三角形，若能，求出BE的长；若不能，请说明理由．17．（2012秋•道外区期末）已知：△ACB与△DCE为两个有公共顶点C的等腰直角三角形，且∠ACB=∠DCE=90°，AC=BC,DC=EC．把△DCE绕点C旋转,在整个旋转过程中,设BD的中点为N，连接CN．(1）如图①，当点D在BA的延长线上时,连接AE，求证：AE=2CN；（2）如图②,当DE经过点A时,过点C作CH⊥BD，垂足为H，设AC、BD相交于F，若NH=4,BH=16，求CF的长．18．(2012春•泰兴市校级期中）在平面直角坐标系中,四边形ABOC是边长为1的正方形，其中点B、C分别在x轴和y轴上，点M为y轴负半轴上一动点，点N 为x轴正半轴上一动点,且∠NAM=45°．（1）试说明△OAN∽△OMA；（2）随着点N的变化，探求△OMN的面积是否发生变化？如果△OMN的面积不变，求出△OMN的面积;如果面积发生变化，请说明理由；(3）当△AMN为等腰三角形时，请求出点N的坐标．19．（2012秋•亭湖区校级期中）已知：如图，在直角梯形ABCD中,AD∥BC，∠B=90°,CD=8，BC=12，∠ACB=30°,E为BC边上一点，以BE为边作正△BEF，使正△BEF和梯形ABCD在BC的同侧．（l）当正△BEF的顶点F恰好落在对角线AC上时，求BE的长；（2)将（1）问中的正△BEF沿BC向右平移，记平移中的正△BEF为正△B′E′F′，当点E与点C重合时停止平移．设平移的距离为x，正△B′E′F′的边B′E′和E′F′分别与AC交于点M和点N，连接DM、DN:①设正△B′E′F′与△ABC重叠部分的面积为S,求S与x之间的函数关系式，并写出自变量x的取值范围，当DN取得最小值时,求出S的值；②是否存在这样的x,使三角形DMN是直角三角形？若存在,求出x的值；若不存在，请说明理由．20．（2012秋•江阴市校级期中）如果一个点能与另外两个点能构成直角三角形，则称这个点为另外两个点的勾股点．例如:矩形ABCD中，点C与A、B两点可构成直角三角形ABC,则称点C为A、B两点的勾股点．同样，点D也是A、B两点的勾股点．（1）在矩形ABCD中，AB=12，BC=6，边CD上A，B两点的勾股点的个数为个；（2）如图1，矩形ABCD中,AB=12，BC=6，DP=4，DM=8，AN=5．过点P作直线l平行于BC，点H为M、N两点的勾股点，且点H在直线l上，求PH的长；（3）如图2,矩形ABCD中，AB=12,BC=6，将纸片折叠，折痕分别与CD、AB交于点F、G，若A、E两点的勾股点为BC边的中点M,求折痕FG的长．21．（2012春•沧浪区校级期中)已知,正方形DEFG内接于△ABC中，且点E，F在BC上，点D，G分别在AB,AC上，（1)如图①，若△ABC是等腰直角三角形，AB=AC，∠A=90°，S△ADG=2,则S△ABC=．（2）如图②，若△ABC是直角三角形,∠A=90°，AB=4,AC=3，求正方形的边长．（3）如图③，若△ABC是任意三角形，S△ADG=1,S△BDE=3,S△FCG=1，则正方形的边长为．（4)如图④,若△ABC是任意三角形，求证：．22．(2012秋•哈尔滨月考)如图，△ABC和△CDE均为等边三角形，BC边上的中垂线AM 交BC边于点M．△CDE 绕着点C旋转，点D落在直线AM上(点D不与点A、M重合）时停止，△CDE在CD边的下方,连接BE．(1）如图1所示，当点D在线段AM上,求证：BE+DM=BC；（2）在（1）的条件下,设直线BE交直线AM于点N，如图2所示，若，且△CDE的面积为，求线段BN的长．23．（2012秋•南岗区校级月考）如图1,BD为矩形ABCD的对角线,∠DBC的平分线BE交DC于点E，DK ⊥BE交BE的延长线于K．（1）若tan∠DBC=，求证:BE=DK．（2）如图2，在（1)的条件下，∠BED绕点E顺时针旋转至∠B′ED′，∠B′ED′的两边分别交BD、DK于点I、L，若已知：DL：LK=5：3，IL=5，求IB的长？24．（2012秋•靖江市校级月考）等边△ABC的边长为2，P是BC边上的任一点（与B、C不重合)，连接AP，以AP为边向两侧作等边△APD和等边△APE，分别与边AB、AC交于点M、N，设BP=x．（如图1）（1）求证：AM=AN；（2）若BM=，求x的值;(3)连接DE，分别与边AB、AC交于点G、H（如图2）,当x取何值时，∠BAD=15°？并判断此时以DG、GH、HE这三条线段为边构成的三角形是什么特殊三角形，请说明理由．25．（2011•北塘区二模）如图1，在△ACD中,AC=2DC,AD=DC．(1）求∠C的度数；（2）如图2，延长CA到E，使AE=CD，延长CD到B，使DB=CE，AB、ED交于点O．求证:∠BOD=45°；(3）如图3，点F、G分别是AC、BC上的动点，且S△CFG=S四边形AFGB，作FM∥BC,GN∥AC，分别交AB于点M、N，线段AM、MN、NB能否始终组成直角三角形？给出你的结论，并说明理由．26．（2011•邯郸一模）(1)如图1，四边形ACDG与四边形ECBH都是正方形，且B，C，D在一条直线上，连接DE并延长交线段AB于点F．求证：AB=DE,AB⊥DE；(2）如果将（1）中的两个正方形换成两个矩形，如图2，且==，则AB与DE的数量关系与位置关系会发生什么变化？请说明你的看法和理由．(3）如果将（1）中的两个正方形换成两个直角三角形,如图3，∠BCE=∠ACD=90°,且=k，且请直接写出AB与DE的数量关系与位置关系．27．(2011•哈尔滨)已知：在△ABC中，BC=2AC，∠DBC=∠ACB，BD=BC，CD 交线段AB于点E．(1)如图1,当∠ACB=90°时，则线段DE、CE之间的数量关系为；（2）如图2，当∠ACB=120°时,求证：DE=3CE；（3）如图3,在（2）的条件下，点F是BC边的中点，连接DF，DF与AB交于G，△DKG和△DBG关于直线DG对称（点B的对称点是点K,延长DK交AB于点H．若BH=10，求CE的长．28．（2011•武汉模拟）在△ABC中，点D、E、F分别为边BC、AB、AC的中点，点G为线段DF上一点（点G不与D、F重合）,AG的延长线交BC于点K,交ED 的延长线于点H，连接BH．（1）如图1：若∠BAC=90°，写出图中所有与∠HBD相等的角，并选取一个给出证明．（2）如图2：若∠BAC≠90°，在(1)中与∠HBD相等的角中找出一个仍然与∠HBD 相等的角,并给出证明．29．（2011•黑龙江模拟）已知：如图，直角梯形ABCD中AD∥BC,∠A=90°，CD=CB=2AD．点Q是AB边中点，点P在CD边上运动，以点P为直角顶点作直角∠MPN，∠MPN的两边分别与AB边、CB边交于点M、N．（1）若点P与点D重合，点M在线段AQ上,如图(1）．求证：．（2）若点P是CD中点,点M在线段BQ上，如图（2)．线段MQ、CN、BC的数量关系是：,并证明你的猜想．30．(2011•南岗区校级三模）已知:梯形ABCD中，AD∥BC，∠ABC=90°，BE⊥CD 于点E．DP⊥CB于点P，连接AP、AE．（1）如图1，若∠C=45°，求证：AP=AE．（2）如图2，若∠C=60°,直接写出线段AP、AE的数量关系．（3)在（1）的条件下，将线段EA绕点E顺时针旋转得到线段EA′，使∠DEA′=∠DEA，直线EA′分别与线段BA延长线、线段BC交于点N、点K，已知AD=1，EK=．求线段NE的长．。

中考数学专题训练6：相似形中的一线三等角模型

中考数学专题训练6：相似形中的一线三等角模型【考点分析】三个相等的角的顶点在同一条直线上，那么就有一对三角形相似，这一结构称为“一线三等角”，如下图所示.此结构虽然不能直接作为定理使用，但因为其结构特殊，许多问题中常见，不妨引起重视.如图，∠A =∠CDE =∠B,则△ADE ∽△BCD ,因此EA :AD =BD :BC .例1.如图，在边长为2的等边△ABC 中，D 是BC 边上一点，E 、F 分别在AB 、AC 边上，且∠EDF =∠ABC . 已知BD =1，BE =31,求CF .例2．如图，等边△ABC 中，D 是BC 的中点，点E 、F 分别在边AB 、AC 上，且∠EDF =60°，找出图中的相似三角形，并证明之.练习：已知在等腰△ABC 中，AB=AC,D 是BC 的中点，∠EDF =∠B ,求证：△BDE ∽△DFE .例3. 如图，在梯形ABCD 中，AD ∥BC ，AB =CD =BC =6，AD =3.．点M 为边BC 的中点，以M 为顶点作∠EMF =∠B ，射线ME 交腰AB 于点E ，射线MF 交腰CD 于点F ，联结EF ．(1)求证：△MEF ∽△BEM ；(2)若△BEM 是以BM 为腰的等腰三角形，求EF 的长；(3)若EF ⊥CD ，求BE 的长．例4.在△ABC 中，AB =AC =8，BC =10，D 是BC 边上的一个动点，点E 在AC 边上，且∠ADE =∠C ．(1) 求证：△ABD ∽△DCE ；(2) 如果BD=x,AE=y ，求y 与x 的函数解析式，并写出自变量x 的取值范围；(3) 当点D 是BC 的中点时，试说明△ADE 是什么三角形，并说明理由．例5. 已知矩形ABCD 中，CD =2，AD =3，点P 是AD 上的一个动点，且和点A,D 不重合，过点P 作PE ⊥CP ，交边AB 于点E ,设PD=x,AE=y,，求y 关于x 的函数关系式，并写出x 的取值范围。

中考专题练习一线三等角

一线三等角(2 )当x何值时，y有最大值，最大值是多少？理论：略范例点睛1. 正方形ABCD边长为5，点P、Q分别在直线CB、DC上(点P不与点C、点B重合)，且保持/ APQ=90。

•当CQ=1时，写出线段BP的长3. (2007 •南京在梯形 ABCD 中，AD //BC,AB=DC=AD=6 ，/ABC=60。

，点 E、F 分别在线段AD、DC上(点E与点A、D不重合)，且/BEF=120。

，设AE=x , DF=y .(1 )求y与x的函数表达式；4. 女口图，Rt △ ABC 中,/ BAC=90 ° ,AB=AC=2 ，点D为BC边上动点(D不与B、C 重合)，/ ADE= 45 ° P E 交 AC 于点 E.(1)Z BAD与/ CD的大小关系为______ .请证明你的结论；(2)设 BD=x , AE=y，求y关于x的函数关系式，并写出自变量x的取值范围；(3)当厶A是等腰三角形时，求 AE的长；(4)是否存在x，使△DC的面积是厶ABD面积的2倍？若存在，求出x的值，若不存在，请说明理由.一.基础技能1. ( 2015?连云港)如图，在△ ABC中，ZBAC=60 ° ,Z ABC=90 °，直线I2//I3,丨1 与12之间距离是1 , 12与13之间距离是2 , 且l1 , l2 , l3分别经过点 A, B , C,则边 AC= .2. 如图，已知I1//I2//I3，相邻两条平行直线间的距离相等，若等腰直角△ ABC的三个项点分别在这三条平行直线上，则sina值是( )A. 1B. 6C._5D.J03 17 5 103. (2012 •苏州已知在平面直角坐标系中放置了 5个如图所示的正方形（用阴影表示），点B1在y轴上，点 C1、曰、E2、C2、E3、曰、C3在x轴上.若正方形 A1B1C1D1的边6.如图，将矩形纸片的两只直角分别沿EF、DF翻折，点B恰好落在AD边上的点B '处,点C恰好落在边 B'F上•若AE=3 , BE=5 ,___________________ __________________ I 则FC=长为 1，/B1C1O=60 ° , B1C1 //B2C2//B3C3, 则点A3到x轴的距离是（）4.如图，在边长为 9正三角形ABC中,BD=3，/ ADE=60。

初二几何证明题(精选多篇)

初二几何证明题(精选多篇)1如图，在△abc中，d是bc边上的一点，e是ad的中点，过点a作bc的平行线交be的延长线于f，且af=dccf．求证：d是bc的中点；如果ab=acadcf的形状，并证明你的结论aeb初二几何证明题 1.已知：如图，在△abc中，ad⊥bc，垂足为d，be⊥ac，垂足为e。

m为ab 中点，联结me,md、ed求证：角emd=2角dac证明：∵m为ab边的中点，ad⊥bc，be⊥ac，∴md=me=ma=mb∴△med为等腰三角形∵me=ma∴∠mae=∠mea∴∠bme=2∠mae ∵md=ma∴∠mad=∠mda,∴∠bmd=2∠mad,∵∠emd=∠bme-∠bmd=2∠mae-2∠mad=2∠dac2.如图，已知四边形abcd中，ad=bc,e、f分别是ab、cd中点，ad、bc的延长线与ef的延长线交于点h、d求证：∠ahe=∠bge证明：连接ac，作em‖ad交ac于m，连接mf.如下图：∵e是cd的中点，且em‖ad，∴em=1/2ad，m是ac的中点，又因为f是ab的中点∴mf‖bc，且mf=1/2bc.∵ad=bc，∴em=mf，三角形mef为等腰三角形，即∠mef=∠mfe.∵em‖ah，∴∠mef=∠ahf∵fm‖bg，∴∠mfe=∠bgf∴∠ahf=∠bgf.3.写出“等腰三角形两底角的平分线相等”的逆命题，并证明它是一个真命题这是经典问题,证明方法有很多种,对于初二而言,下面的反证法应该可以接受如图,已知bd平分∠abc,ce平分∠acb,bd=ce,求证:ab=ac证明:bd平分∠abc==>be/ae=bc/ac==>be/ab=bc/==>be=ab*bc/同理:cd=ac*bc/假设ab≠ac,不妨设ab>ac.....ab>ac==>bc+acac*bc==>ab*ab/>ac*bc/==>be>cdab>ac==>∠acb>∠abc∠bec=∠a+∠acb/2,∠bdc=∠a+∠abc/2==>∠bec>∠bdc过b作ce平行线,过c作ab平行线,交于f,连df则becf为平行四边形==>∠bfc=∠bec>∠bdc.....bf=ce=bd==>∠bdf=∠bfdcf=be>cd==>∠cdf>∠cfd==>∠bdf+∠cdf>∠bfd+∠cfd==>∠bdc>∠bfc...矛盾,从而假设不成立所以ab=ac。

等腰三角形分类讨论初三压轴题

中考热点3——等腰三角形分类讨论等腰三角形的分类讨论题多见于初三各级各类模拟考试甚至中考的压轴题中，由于这类题目都与图形运动有关，需要学生具有一定的想象能力、分析能力和运算能力，而这正是学生最缺乏的，理清这类题目的解题思路和解题策略将会等到在中考中获得高分的重要砝码。

等腰三角形分类讨论的解题思路粗分有两种，第一种：用含有字母的代数式分别表示等腰三角形的三条边，后用三条线段依次相等建立方程后求解，第二种：分别作出三种等腰三角形条件下图形，利用等腰三角形的有关性质和题目中的条件进行合理的转化后建立方程求解。

下面就常见的题型进行分析、归纳典型例题【例1】如图，在Rt △ABC 中，∠C =90°，54sin =B ，AC =4；D 是BC 的延长线上的一个动点，∠EDA =∠B ，AE ∥BC ．（1）找出图中的相似三角形，并加以证明；（2）设CD =x ，AE =y ，求y 关于x 的函数解析式，并写出函数的定义域；（3）当△ADE 为等腰三角形时，求AE 的长．【思路分析】思路一：用含有x 或者y 的代数式来表示等腰三角形的三条边长AD 、DE 、AE 三条线段依次相等建立方程后求解，显然AE 和DE 边都不方便用含含有x 或者y 的代数式表示。

思路二：分别作出三种等腰三角形条件下图形，利用第（1）题中证明的△ABD ∽△EDA 将等腰的条件转化到△ABD 中进行求解，最后带入定义域检验。

解：（1）∵AE ∥BC ∴∠EAD =∠ADB ，∠EDA =∠B ∴△ABD ∽△EDA （2）∵△ABD ∽△EDA ∴AEADAD BD = ∴y x x x 1616322+=++即3162++=x x y 0>x （3）情况一：当AE =AD 时AD =BD 即3162+=+x x67=x 情况二：DE =AE 时AB =AD ，AC ⊥BD BC =CD 即3=x情况三：AD =DE 时AB =BD 即53=+x2=x点评：将等腰三角形的条件进行适当转化，计算过程大大简化，既节约时间又提高正确率【例2】已知直线1l 的解析式63+=x y ，直线1l 与x 轴、y 轴分别交于点A 、B ，直线2l 经过B 、C 两点，E点C 的坐标为)0,8(.又知点P 在x 轴上从点A 向点C 移动，点Q 在直线2l 上从点C 向点B 移动.点P 、Q 同时出发，且移动的速度都为每秒1个单位长度，设移动时间为t 秒（100<<t ）（1）求直线2l 的解析式（2）当t 为何值时，△PCQ 是等腰三角形【思路分析】在直角坐标系中对等腰三角形进行讨论，依然遵循两大基本思路此题中PC 、QC 两条边长都方便用含有t 的代数式表示，而PQ 不易表示，将等腰三角形PQ =QC 和PC =PQ 两种情况，通过添加底边上的高转化为直角三角形，再用锐角三角比和相似三角形的方法进行求解则较易求得结果。

第24章专题06 相似三角形的性质重难点专练(学生版)

专题06 相似三角形的性质重难点专练第I 卷（选择题）一、单选题1．（2021·上海九年级专题练习）如图，在Rt ABC ∆中，90,BAC BA CA ∠=︒==D 为BC 边的中点，点E 是CA 延长线上一点，把CDE ∆沿DE 翻折，点C 落在C '处，EC '与AB 交于点F ，连接BC '．当43FA EA =时，BC '的长为（）AB ．CD ．第II 卷（非选择题）二、解答题2．（2021·上海中考真题）如图，在梯形ABCD 中，//,90,,AD BC ABC AD CD O ∠=︒=是对角线AC 的中点，联结BO 并延长交边CD 或边AD 于E ．（1）当点E 在边CD 上时，①求证：DAC OBC ∽；①若BE CD ⊥，求AD BC的值；（2）若2,3DE OE ==，求CD 的长．3．（2021·上海金山区·九年级二模）已知在①ABC 中，AB ＝AC＝①BAC ＝120°，①ADE 的顶点D 在边BC 上，AE 交BC 于点F （点F 在点D 的右侧），①DAE ＝30°．（1）求证：①ABF ①①DCA ；（2）若AD ＝ED ．①联结EC ，当点F 是BC 的黄金分割点（FC ＞BF ）时，求ABF FEC S S．①联结BE ，当DF ＝1时，求BE 的长．4．（2021·上海崇明区·九年级二模）已知：如图，梯形ABCD 中，AD ①BC ，AB ＝DC ，点E 在下底BC 上，①AED ＝①B ．（1）求证：CE •AD ＝DE 2；（2）求证：22CE ABADAE =．5．（2021·上海静安区·九年级二模）如图，已知半圆O 的直径AB ＝4，点P 在线段OA 上，半圆P 与半圆O 相切于点A ，点C 在半圆P 上，CO ①AB ，AC 的延长线与半圆O 相交于点D ，OD 与BC 相交于点E ．（1）求证：AD •AP ＝OD •AC ；（2）设半圆P 的半径为x ，线段CD 的长为y ，求y 与x 之间的函数解析式，并写出定义域；（3）当点E 在半圆P 上时，求半圆P 的半径．6．（2021·上海松江区·九年级二模）如图，已知在①ABC 中，BC ＞AB ，BD 平分①ABC ，交边AC 于点D ，E 是BC 边上一点，且BE ＝BA ，过点A 作AG ①DE ，分别交BD 、BC 于点F 、G ，联结FE ．（1）求证：四边形AFED 是菱形；（2）求证：AB 2＝BG •BC ；（3）若AB ＝AC ，BG ＝CE ，联结AE ，求ADE ABCS S ∆∆的值．7．（2021·上海九年级专题练习）（1）问题发现如图1，①ABC与①ADE都是等腰直角三角形，且①BAC＝①DAE＝90°，直线BD，CE交于点F，直线BD，AC交于点G．则线段BD和CE的数量关系是，位置关系是；（2）类比探究如图2，在①ABC和①ADE中，①ABC＝①ADE＝α，①ACB＝①AED＝β，直线BD，CE交于点F，AC与BD相交于点G．若AB＝kAC，试判断线段BD和CE的数量关系以及直线BD 和CE相交所成的较小角的度数，并说明理由；（3）拓展延伸如图3，在平面直角坐标系中，点M的坐标为（3.0），点N为y轴上一动点，连接MN．将线段MN绕点M逆时针旋转90得到线段MP，连接NP，OP．请直接写出线段OP长度的最小值及此时点N的坐标．8．（2021·上海九年级专题练习）（1）证明推断：如图（1），在正方形ABCD中，点E，Q分别在边BC ，AB 上，DQ AE ⊥于点O ，点G ，F 分别在边CD ，AB 上，GF AE ⊥．求证：FG AE =；（2）类比探究：如图（2），在矩形ABCD 中，23BC AB =将矩形ABCD 沿GF 折叠，使点A 落在BC 边上的点E 处，得到四边形EFGP ，EP 交CD 于点H ，连接AE 交GF 于点O ．试探究GF 与AE 之间的数量关系，并说明理由；（3）拓展应用：在（2）的条件下，连接CP ，若34BE BF =，GF =，求CP 的长． 9．（2021·上海九年级专题练习）如图，P 是正方形ABCD 边BC 上一个动点，线段AE 与AD 关于直线AP 对称，连接EB 并延长交直线AP 于点F ，连接CF ．（1）如图（1），①BAP ＝20°，直接写出①AFE 的大小；（2）如图（2），求证：BE CF ；（3）如图（3），连接CE ，G 是CE 的中点，AB ＝1，若点P 从点B 运动到点C ，直接写出点G 的运动路径长．10．（2021·上海宝山区·九年级期中）如图，在ABCD 中，BAD ∠的平分线交边BC 于点E ，交DC 的延长线于点F ，点G 在AE 上，联结,GD GDF F ∠=∠（1）求证：2AD DG AF =⋅；（2）连结BG ，如果BG AE ⊥，且6,9AB AD ==，求AF 的长．11．（2021·上海九年级专题练习）已知：如图，四边形ABCD 是菱形，点M 、N 分别在边BC 、CD 上，联结AM 、AN 交对角线BD 于E 、F 两点，且MAN ABD ∠=∠．（1）求证：2AB BF DE =⋅；（2）若BE DN DE DC=，求证：//EF MN ．12．（2021·上海九年级专题练习）如图，在ABC 中，90ABC ∠=︒，3AB =，4BC =，过点A 作射线//AM BC ，点D 、E 是射线AM 上的两点（点D 不与点A 重合，点E 在点D 右侧），连接BD 、BE 分别交边AC 于点F 、G ，DBE C ∠=∠．（1）当1AD =时，求FB 的长（2）设AD x =，FG y =，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结DG 并延长交边BC 于点H ，如果DBH △是等腰三角形，请直接写出AD 的长．13．（2021·上海闵行区·九年级一模）如图，在矩形ABCD 中，2AB =，1AD =，点E 在边AB 上（点E 与端点A 、B 不重合），联结DE ，过点D 作DF DE ⊥，交BC 的延长线于点F ，连接EF ，与对角线AC 、边CD 分别交于点G 、H ．设AE x =，DH y =．（1）求证：ADE CDF ∽△△，并求EFD ∠的正切值；（2）求y 关于x 的函数解析式，并写出该函数的定义域；（3）连接BG ，当BGE △与DEH △相似时，求x 的值．14．（2021·上海九年级专题练习）如图，已知正方形ABCD 中，BC ＝4，AC 、BD 相交于点O ，过点A 作射线AM ①AC ，点E 是射线AM 上一点，联结OE 交AB 边于点F ．以OE 为一边，作正方形OEGH ，且点A 在正方形OEGH 的内部，联结DH ．（1）求证：①HDO ①①EAO ；（2）设BF ＝x ，正方形OEGH 的边长为y ，求y 关于x 的函数关系式，并写出定义域；（3）联结AG ，当①AEG 是等腰三角形时，求BF 的长．15．（2021·上海九年级专题练习）如图，已知ABC 是等边三角形，点D 、E 分别在边BC 、AC 上，且CD CE =，联结DE 并延长至点F ，使EF AE =，联结AF ，CF ，联结BE 并延长交CF 于点G ．（1）求证：BC DF =；（2）若2BD DC =，求证：2GF EG =；16．（2021·上海九年级专题练习）如图，已知在Rt ABC 中，90ACB ∠=︒，4AC BC ==，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，EDB ADC ∠=∠，过点E 作EF AD ⊥，垂足为点G ，交射线AC 于点F ．（1）如果点D 为边BC 的中点，求DAB ∠的正切值；（2）当点F 在边AC 上时，设CD x =，CF y =，求y 关于x 的函数解析式及定义域；（3）联结DF 如果CDF 与AGE 相似，求线段CD 的长．17．（2020·上海市位育初级中学九年级期中）如图，在边长为10的正方形ABCD 中，内接有六个大小相同的正方形，点P ，Q ，M ，N 是落在大正方形边上的小正方形的顶点，则每个小正方形的面积为_____．18．（2021·上海）如图1，在Rt ABC 中，90,,C AC BC D ︒∠==是AB 边上一点，E 是在AC 边上的一个动点（与点A C 、不重合），,DF DE DF ⊥与射线BC 相交于点F ．（1）如图2，如果点D 是边AB 的中点，求证：DE DF =；（2）如果:AD DB k =，求:DE DF 的值；（3）如果6,:1:2AC BC AD DB ===，设,AE x BF y ==，求y 关于x 的函数关系式，并写出定义域；19．（2021·上海）如图，在Rt①ABC 中，①C=90°，AC=BC=6，点D 为AC 中点，点E 为边AB 上一动点，点F 为射线BC 上一动点，且①FDE=90°．（1）当DF//AB 时（图1），联结EF ，求DE ：DF 值；（2）当点F 在线段BC 上时（图2），设AE=x ，BF=y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结CE ，若①CDE 为等腰三角形，求BF 的长．20．（2021·上海）如图．已知在ABC ∆中.90,5,3ACB AB BC ︒∠===，点D 是边AB 上任意一点．连接DC ，过点C 作CE CD ⊥，垂足为点C ，连接DE ，使得EDC A ∠=∠，连接BE（1）求证：.AC BE BC AD ⋅=⋅（2）设AD x =，四边形BDCE 的面积为S ，求S 关于x 的函数解析式及x 的取值范围（3）当14BDE ABC S S ∆∆=，求CD 的值． 21．（2020·上海上外附中九年级月考）已知直角三角形斜边上的高为12，且斜边上的高把斜边分成3:4两段，则斜边上的中线长是__________22．（2021·上海九年级专题练习）如图，直角梯形OABC 的直角顶点O 是坐标原点，边OA 、OC 分别在x 轴、y 轴的正半轴上，OA//BC ，D 是BC 上一点，BD=0．25OA=根号2，AB=3，①OAB=45°，E 、F 分别是线段OA 、AB 上的两动点，且始终保持①DEF=45°（1）直接写出D 点的坐标；（2）设OE x =，AF y =，试确定y 与x 之间的函数关系；（3）当AEF ∆是等腰三角形时，将AEF ∆沿EF 折叠，得到A EF '∆，求A EF '∆与五边形OEFBC 重叠部分的面积23．（2020·上海市西南模范中学九年级月考）在平面直角坐标系中，四边形AOBC 的顶点O 是坐标原点，点B 在x 轴的负半轴上，且CB x ⊥轴，点A 的坐标为()0,6，在OB 边上有一点P ，满足AP =（l ）求P 点的坐标；（2）如果AOP 与APC △相似，且90PAC ∠=︒，求点C 的坐标．24．（2020·上海浦东新区·九年级月考）如图，梯形ABCD 中，AD//BC ，DC BC ⊥，且45B ∠=，1AD DC ==．点M 为边BC 上一动点，连接AM 并延长交射线DC 于点F ，作45FAE ∠=交射线BC 于点E 、交边DC 于点N ，联结EF ．（1）当:1:4CM CB =时，求CF 的长；（2）连接AC ，求证：2AC CE CF =⋅（3）设CM x =，CE y =，求y 关于x 的函数关系式，并写出定义域．25．（2021·上海九年级专题练习）如图，在Rt①ABC 中，①B ＝90°，AB ＝2，BC ＝1，点D ，E 分别是边BC ，AC 的中点，连接DE ．将①EDC 绕点C 按顺时针方向旋转，记旋转角为α．（1）①当α＝0°时，AE BD = ； ①当α＝180°时，AE BD= ；（2）试判断：当0°≤α＜360°时，AE BD 的大小有无变化？请仅就图2的情况给出证明．（3）当①EDC 旋转至A 、B 、E 三点共线时，直接写出线段BD 的长．26．（2020·上海市青浦区第一中学）在四边形ABCD 中，AB BC ⊥，AD 平行于BC ，3AB =，2AD =，点P 在线段AB 上，联结PD ，过点D 作PD DC ⊥，与BC 交于点C ，设AP 的长为x ．（1）当AP AD =时，求线段PC 的长；（2）设PDC ∆的面积为y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围；（3）当APD ∆与DPC ∆相似时，求线段BC 的长．27．（2021·上海九年级专题练习）如图，在直角梯形ABCD 中，//AB DC ，①DAB =90°，AB =8，CD =5，BC（1）求梯形ABCD 的面积；（2）联结BD ，求①DBC 的正切值．28．（2021·上海九年级专题练习）已知：如图，点E 为□ABCD 对角线AC 上的一点，点F 在线段BE 的延长线上，且EF=BE ，线段EF 与边CD 相交于点G ．（1）求证：DF //AC ；（2）如果AB=BE ，DG=CG ，联结DE 、CF ，求证：四边形DECF 是矩形．三、填空题29．（2021·上海九年级专题练习）如图，Rt ①ABC 中，AC ＝BC ＝3，D 为AB 中点，点E 在线段BC 上，且BE ＝2CE ，连接AE ，过点C 作CF ①AE ，垂足为F ，连接DF ，则DF 的长为_____．30．（2021·上海九年级专题练习）如图，等边①ABC 的边长为3，点D 在边AC 上，12AD =，线段PQ 在边BA 上运动，12PQ =，（1）若①ADQ ①①BPC ，则AQ ＝_____；（2）四边形PCDQ 面积的最大值为_____．31．（2021·上海九年级专题练习）如图，在ABC ∆中，AB BC =，AD BC ⊥于点D ，CE AB ⊥于点E ，点F 在DA 有延长线上，连接BF 交CE 延长线于点M ，tan 2DCA ∠=，:25:38BM MF =，若5EM =，则AF 的长为_____________．32．（2021·上海金山区·九年级一模）如图，在□ABCD 中，点E 在边BC 上，DE 交对角线AC 于F ，若2CE BE =，ABC ∆的面积等于15，那么FEC ∆的面积等于______．33．（2021·上海九年级一模）如图，在ABC 中，点D 是边BC 的中点，直线DF 交边AC 于点F ，交AB 的延长线于点E ，如果CF①CA=a①b ，那么BE①AE 的值为______．（用含a 、b 的式子表示）34．（2021·上海）如图，已知矩形纸片ABCD ，点E 在边AB 上，且1BE =，将CBE △沿直线CE 翻折，使点B 落在对角线AC 上的点F 处，联结DF ，如果点D,F,E 在同一直线上，则线段AE 的长为____．35．（2021·上海九年级专题练习）在Rt ABC ∆中，①C =90°，AC =2，BC =4，，点,D E 分别是边BC 、AB 的中点，将BDE ∆绕着点B 旋转，点,D E 旋转后的对应点分别为点,D E ''，当直线,D E ''经过点A 时，线段CD '的长为 ____________36．（2021·上海九年级专题练习）如图，AB 、CD 都是BD 的垂线，AB ＝4，CD ＝6，BD ＝14，P 是BD 上一点，联结AP 、CP ，所得两个三角形相似，则BP 的长是_____．37．（2021·上海九年级专题练习）如图，正方形纸片ABCD 的边长为4，E 是边CD 的中点，连接AE ，折叠该纸片，使点A 落在AE 上的G 点，并使折痕经过点B ，得到折痕BF ，点F 在AD 上，则GE 的长为_____．38．（2021·上海）如图，正方形ABCD 的对角线AC ，BD 相交于点O ，AB =E 为OC 上一点，2OE =，连接BE ，过点A 作AF BE ⊥于点F ，与BD 交于点G ，则EF 的长是______．39．（2021·上海九年级专题练习）如图，正方形ABCD 的对角线AC 上有一点E ，且4CE AE =，点F 在DC 的延长线上，连接EF ，过点E 作EG EF ⊥，交CB 的延长线于点G ，连接GF 并延长，交AC 的延长线于点P ，若10AB =，4CF =，则线段EP 的长是__________．40．（2020·上海上外附中九年级月考）如图，G 是ABC ∆的重心，延长BG 交AC 于点D ，延长CG 交AB 于点,,E P Q 分别是BCE ∆和BCD ∆的重心，则PQ BC=____________41．（2020·上海上外附中九年级月考）如图，P 是ABC ∆内一点，过点P 分别作直线平行于ABC ∆各边，形成三个小三角形面积分别为1233,12,27S S S ===，则ABC S ∆=__________42．（2020·上海上外附中九年级月考）如图，已知在ABC ∆中，60,CAB P ︒∠=为ABC ∆内一点且120,3,2APB APC AP BP ︒∠=∠===，则CP = ____________43．（2020·上海市西南模范中学九年级月考）已知，平行四边形ABCD 中，点E 是AB 的中点，在直线AD 上截取2AF FD =，连接EF ，EF 交AC 于G ，则AG AC=___________． 44．（2021·上海九年级专题练习）如图，在ABC 中，90ACB ∠=︒，AC BC =，点E 是边AC 上一点，以BE 为斜边往BC 侧作等腰Rt BEF △，连接,CF AF ，若6AB =，四边形ABFC 的面积为12，则AE =_________，AF =_________．45．（2021·上海）如图，在矩形ABCD 中， AB =3，BC =4，将矩形ABCD 绕点C 旋转，点A 、B 、D 的对应点分别为A’ 、B’、 D’，当A’ 落在边CD 的延长线上时，边A’ D’ 与边 AD 的延长线交于点F ，联结CF ，那么线段CF 的长度为____．46．（2021·上海九年级专题练习）如图，Rt①ABC 中，①BAC=90°，CE 平分①ACB ，点 D 在 CE 的延长线上，连接 BD ，过B 作BF①BC 交 CD 于点 F ，连接 AF ，若CF=2BD ，DE ：CE=5：8 ， BF =AF 的长为_________．47．（2021·上海九年级专题练习）如图，在矩形ABCD中，点E是边DC上一点，连结BE，将①BCE沿BE对折，点C落在边AD上点F处，BE与对角线AC交于点M，连结FM．若FM①CD，BC＝4．则AF＝_____48．（2021·上海）如图，在矩形ABCD中，AB＝3，AD＝4，将矩形ABCD绕着点B顺时针旋转后得到矩形A'BC'D'，点A的对应点A'在对角线AC上，点C、D分别与点C'、D'对应，A′D'与边BC交于点E，那么BE的长是_____．49．（2021·上海九年级专题练习）定义：如果三角形的两个内角①α与①β满足①α=2①β，那么，我们将这样的三角形称为“倍角三角形”．如果一个等腰三角形是“倍角三角形”，那么这个等腰三角形的腰长与底边长的比值为____．50．（2021·上海九年级专题练习）如图，在Rt①ABC中，①C＝90°，AC＝6，BC＝8，点D、E分别是边BC、AB上一点，DE①AC，BD＝，把①BDE绕着点B旋转得到①BD'E'（点D、E分别与点D'，E'对应），如果点A，D'、E'在同一直线上，那么AE'的长为_____．。

上海市青浦实验中学2022-2023学年八年级上学期期末数学试卷(含解析)

上海市青浦实验中学2022-2023学年八年级上学期期末数学试卷（解析版）一、填空题：（本大题共14题，每题2分，满分28分）1．方程x2＝3的根是．2．若一次函数图象与直线平行，且过点（0，2），则此一次函数的解析式是．3．当直线y＝（2﹣2k）x+k﹣3经过第二、三、四象限时，则k的取值范围是．4．函数的定义域是．5．在实数范围内因式分解：2x2+2x﹣1＝．6．已知函数，则f（6）＝．7．如果关于x的一元二次方程kx2+3x+4＝0有实数根，那么k的取值范围是．8．如果点（﹣3，a）、（﹣2，b）在反比例函数（k＜0）的图象上，那么a、b的大小关系是．（用“＜”号连接）9．某商场七月份的销售额为1000万元，八月份的销售额下降了20%，商场从九月份起改进经营措施，销售额稳步增长，十月份的销售额达到1352万元，如果每月的销售额增长率相同，设这个增长率为x，那么可列方程．10．如果过多边形的一个顶点共有8条对角线，那么这个多边形的内角和是度．11．在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，且AD＝5，AC＝10．则AB＝．12．如图所示，在平行四边形ABCD中，AB＝4cm，AD＝7cm，∠ABC的平分线BF交AD 于点E，交CD的延长线于点F，则DF＝cm．13．如图，平行四边形ABCD中，AE⊥BC，AF⊥CD，垂足分别是E、F，∠EAF＝60°，BE＝2，DF＝3，则平行四边形ABCD的周长为．14．已知两块相同的三角板如图所示摆放，点B、C、E在同一直线上，∠ABC＝∠DCE＝90°，∠ACB＝30°，AB＝2，将△ABC绕点C顺时针旋转一定角度α（0°＜α＜90°），如果在旋转的过程中△ABC有一条边与DE平行，那么此时△BCE的面积是．二、单项选择题：（本大题共4小题，每题3分，满分12分）15．下列一元二次方程中，有两个相等的实数根的方程是（）A．B．（x﹣2）2＝5C．x2+2x＝0D．16．已知一次函数y＝kx+b（k、b为常数）的图象如图所示，那么关于x的不等式kx+b＞0的解集是（）A．x＞0B．x＜0C．x＜2D．x＞2．17．下列说法正确的是（）A．一个人的体重与他的年龄成正比例关系B．圆的周长与直径成正比例关系C．周长一定时，长方形的长与宽成反比例关系D．车辆行驶的速度v一定时，行驶的路程s与时间t成反比例关系18．美国数学家伽菲尔德在1876年提出了证明勾股定理的一种巧妙方法，如图，在直角梯形ABCD中，AB∥CD，∠B＝90°，E是边BC上一点，且BE＝CD＝a，AB＝EC＝b．如果△ABE的面积为1，且a﹣b＝1，那么△ADE的面积为（）A．1B．2C．2.5D．5三、解答题：（本大题共有7题，第19、20题每题6分，第21、22、23题每题8分，第24、25题每题12分，满分60分）19．（6分）解方程：（x﹣1）2＝5﹣5x．20．（6分）用配方法解方程：x2﹣4x﹣2＝0．21．（8分）A、B两地相距45千米，甲骑电瓶车从A地出发前往B地，乙同时骑自行车从距离A地20千米的C地出发前往B地．图中的线段OP和线段MN分别反映了两人与A 地的距离y（千米）和行驶时间x（小时）的函数关系．根据图象提供的信息回答下列问题：（1）两人谁先到达B地？．（填“甲”或“乙”）（2）甲到达B地用了小时．（3）两人在出发多少小时后相遇？22．（8分）已知：如图，在矩形ABCD中，AB＝4，BC＝2．对角线AC的垂直平分线分别交AB、CD于点E、F．求线段CF的长．23．（8分）如图，已知△ABC中，∠C＝2∠B，AH⊥BC于点H，D是AC中点，DE∥AB，求证：EH＝AC．24．（12分）已知：如图，反比例函数的图象与直线y＝kx相交于点A，直线AC与x 轴交于点C（2，0），与y轴交于点B，点C是AB的中点．（1）求直线y＝kx的函数解析式；（2）求点C到直线OA的距离；（3）若点D是直线OA上一点，且△ABD是直角三角形，求点D的坐标．25．（12分）如图，在△ABC中，D是AB的中点，E是边AC上一动点，联结DE，过点D 作DF⊥DE交边BC于点F（点F与点B、C不重合），延长FD到点G，使DG＝DF，联结EF、AG，已知AB＝10，BC＝6，AC＝8．（1）求证：AC⊥AG；（2）设AE＝x，CF＝y，求y与x的函数解析式，并写出自变量x的取值范围；（3）当△BDF是以BF为腰的等腰三角形时，求AE的长．参考答案与试题解析一、填空题：（本大题共14题，每题2分，满分28分）1．方程x2＝3的根是x1＝，x2＝﹣．【分析】把方程两边开方即可．【解答】解：x2＝3，x＝±，所以x1＝，x2＝﹣．故答案为：x1＝，x2＝﹣．【点评】本题考查了解一元二次方程﹣直接开平方法：形如x2＝p或（nx+m）2＝p（p≥0）的一元二次方程可采用直接开平方的方法解一元二次方程．2．若一次函数图象与直线平行，且过点（0，2），则此一次函数的解析式是y＝﹣x+2．【分析】设一次函数的解析式是y＝kx+b，根据两直线平行求出k＝﹣，把点的坐标代入函数解析式，求出b即可．【解答】解：设一次函数的解析式是y＝kx+b，∵一次函数图象与直线y＝﹣x平行，∴k＝﹣，即y＝﹣x+b，∵一次函数的图象过点（0，2），∴代入得：2＝b，即y＝﹣x+2，故答案为：y＝﹣x+2．【点评】本题考查了两直线平行和用待定系数法求一次函数的解析式，能求出一次函数的解析式是解此题的关键．3．当直线y＝（2﹣2k）x+k﹣3经过第二、三、四象限时，则k的取值范围是1＜k＜3．【分析】根据一次函数y＝kx+b，k＜0，b＜0时图象经过第二、三、四象限，可得2﹣2k＜0，k﹣3＜0，即可求解；【解答】解：y＝（2﹣2k）x+k﹣3经过第二、三、四象限，∴2﹣2k＜0，k﹣3＜0，∴k＞1，k＜3，∴1＜k＜3；故答案为1＜k＜3；【点评】本题考查一次函数图象与系数的关系；掌握一次函数y＝kx+b，k与b对函数图象的影响是解题的关键．4．函数的定义域是．【分析】让被开方数为非负数列式求值即可．【解答】解：由题意得2x+1≥0，解得x≥﹣，故答案为x≥﹣．【点评】考查求函数自变量的取值；用到的知识点为：二次根式有意义，被开方数是非负数．5．在实数范围内因式分解：2x2+2x﹣1＝2（x+）（x+）．【分析】原式利用十字相乘法分解即可．【解答】解：原式＝2（x2+x﹣）＝2（x2+x+﹣﹣）＝2（x++）（x+﹣）＝2（x+）（x+），故答案为：2（x+）（x+）．【点评】本题考查了实数范围内分解因式，以及算术平方根，掌握因式分解的方法是关键．6．已知函数，则f（6）＝2．【分析】把x＝6代入计算即可．【解答】解：f（6）＝＝＝2，故答案为：2．【点评】本题考查函数值，理解函数值的定义是解决问题的前提，把x的值代入函数关系式按照关系式指明的运算进行计算是得出正确答案的关键．7．如果关于x的一元二次方程kx2+3x+4＝0有实数根，那么k的取值范围是k≤且k ≠0．【分析】利用一元二次方程的定义和判别式的意义得到k≠0且Δ＝32﹣4×k•4≥0，然后求出两不等式的公共部分即可．【解答】解：根据题意得k≠0且Δ＝32﹣4×k•4≥0，解得k≤且k≠0．故答案为：k≤且k≠0．【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac 有如下关系：当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根．8．如果点（﹣3，a）、（﹣2，b）在反比例函数（k＜0）的图象上，那么a、b的大小关系是a＜b．（用“＜”号连接）【分析】先根据反比例函数中k＜0判断出函数图象所在的象限及增减性，再根据各点横坐标的特点即可得出结论．【解答】解：∵反比例函数（k＜0）中k＜0，∴函数图象的两个分式分别位于二、四象限，且在每一象限内y随x的增大而增大，∵﹣3＜0，﹣2＜0，∴点（﹣3，a），（﹣2，b）位于第二象限，∴a＞0，b＞0，∵﹣3＜﹣2＜0，∴a＜b．故答案为：a＜b．【点评】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数的性质是解答此题的关键．9．某商场七月份的销售额为1000万元，八月份的销售额下降了20%，商场从九月份起改进经营措施，销售额稳步增长，十月份的销售额达到1352万元，如果每月的销售额增长率相同，设这个增长率为x，那么可列方程1000×（1﹣20%）（1+x）2＝1352．【分析】利用十月份的销售额＝八月份的销售额×（1+每月的销售额增长率）2，即可得出关于x的一元二次方程，此题得解．【解答】解：根据题意得1000×（1﹣20%）（1+x）2＝1352．故答案为：1000×（1﹣20%）（1+x）2＝1352．【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．10．如果过多边形的一个顶点共有8条对角线，那么这个多边形的内角和是1620度．【分析】从多边形一个顶点可作8条对角线，则这个多边形的边数是11，n边形的内角和可以表示成（n﹣2）•180°，代入公式就可以求出内角和．【解答】解：∵过多边形的一个顶点共有8条对角线，∴n﹣3＝8，∴n＝11，∴该多边形边数为11，∴（11﹣2）•180°＝1620°，∴这个多边形的内角和为1620°．故答案为：1620．【点评】本题主要考查了多边形的内角和公式，是需要熟记的内容，比较简单．11．在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，且AD＝5，AC＝10．则AB＝20．【分析】先根据CD⊥AB于D，AD＝5，AC＝10得到∠ACD＝30°，再利用同角的余角相等得到∠B＝∠ACD＝30°，所以AB＝2AC＝20．【解答】解：如图，∵CD⊥AB于D，AD＝5，AC＝10，∴∠ACD＝30°，∵CD⊥AB于D，∴∠B+∠BCD＝90°，又∠ACD+∠BCD＝90°，∴∠B＝∠ACD＝30°，∵AC＝10，∴AB＝2AC＝20．故答案为：20．【点评】本题考查了直角三角形30°所对的直角边等于斜边的一半，解题的关键是掌握直角三角形的这条性质．12．如图所示，在平行四边形ABCD中，AB＝4cm，AD＝7cm，∠ABC的平分线BF交AD 于点E，交CD的延长线于点F，则DF＝3cm．【分析】由BF平分∠ABC得到∠ABE＝∠CBE，又由平行四边形两组对边分别平行可以推出∠ABE＝∠BFC，然后可以得到BC＝CF，从而求出DF．【解答】解：∵BF平分∠ABC，∴∠ABE＝∠CBE，又∵AB∥CD，∴∠ABE＝∠BFC，∴∠CBE＝∠BFC，∴BC＝CF，∴DF＝CF﹣CD＝BC﹣AB＝7﹣4＝3．故答案为：3．【点评】此题主要利用利用平行四边形的性质：平行四边形的两组对边分别相等；平行四边形两组对边分别平行．13．如图，平行四边形ABCD中，AE⊥BC，AF⊥CD，垂足分别是E、F，∠EAF＝60°，BE＝2，DF＝3，则平行四边形ABCD的周长为20．【分析】由平行四边形的性质得AB∥CD，AD∥BC，AB＝CD，AD＝BC，再证∠BAE＝∠DAF＝30°，然后由含30°角的直角三角形的性质得AB＝2BE＝4，AD＝2DF＝6，即可解决问题．【解答】解：∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，AB＝CD，AD＝BC，∵AE⊥BC，AF⊥CD，∴∠AEB＝∠AFD＝90°，AF⊥AB，AE⊥AD，∴∠BAF＝∠DAE＝90°，∵∠EAF＝60°，∴∠BAE＝∠DAF＝90°﹣60°＝30°，∴AB＝2BE，AD＝2DF∵BE＝2，DF＝3，∴CD＝AB＝4，BC＝AD＝6，∴▱ABCD的周长＝2（AB+BC）＝2×（4+6）＝20，故答案为：20．【点评】此题考查了平行四边形的性质、含30°角的直角三角形的性质等知识，熟练掌握平行四边形的性质是解题的关键．14．已知两块相同的三角板如图所示摆放，点B、C、E在同一直线上，∠ABC＝∠DCE＝90°，∠ACB＝30°，AB＝2，将△ABC绕点C顺时针旋转一定角度α（0°＜α＜90°），如果在旋转的过程中△ABC有一条边与DE平行，那么此时△BCE的面积是或3．【分析】分两种情况画图讨论：如图1，当AC∥DE时，如图2，当BC∥DE时，利用含30度角的直角三角形即可解决问题．【解答】解：如图1，当AC∥DE时，过点B作BF⊥EC延长线于点F，根据题意可知：∠DEC＝60°，∠ACB＝30°，∵AC∥DE，∴∠ACF＝∠DEC＝60°，∴∠BCF＝30°，∵AB＝2，∴BC＝AB＝2，∴BF＝BC＝，∴△BCE的面积＝CE•BF＝2×＝；如图2，当BC∥DE时，过点B作BG⊥EC延长线于点G，∵BC∥DE，∴∠BCG＝∠DEC＝60°，∵BC＝AB＝2，∴BG＝BC＝3，∴△BCE的面积＝CE•BG＝2×3＝3．综上所述：△BCE的面积是或3．故答案为：或3．【点评】本题考查了旋转的性质，平行线的性质，三角形的面积，含30度角的直角三角形的性质，关键是利用分类讨论思想解决问题．二、单项选择题：（本大题共4小题，每题3分，满分12分）15．下列一元二次方程中，有两个相等的实数根的方程是（）A．B．（x﹣2）2＝5C．x2+2x＝0D．【分析】先把四个方程化为一般式，再计算各方程的根的判别式的值，然后根据根的判别式的意义进行判断．【解答】解：A．x2﹣x+＝0，∵Δ＝（﹣1）2﹣4×1×＝0，∴方程有两个相等的实数根；B．x2﹣4x﹣1＝0，∵Δ＝（﹣4）2﹣4×（﹣1）＝20＞0，∴方程有两个不相等的实数根；C．x2+2x＝0，∵Δ＝22﹣4×1×0＝4，∴方程有两个不相等的实数根；D．2x2﹣x+1＝0，∵Δ＝（﹣）2﹣4×2×1＝﹣6＜0，∴方程没有实数根．故选：A．【点评】本题考查了根的判别式：一元二次方程ax2+bx+c＝0（a≠0）的根与Δ＝b2﹣4ac 有如下关系，当Δ＞0时，方程有两个不相等的实数根；当Δ＝0时，方程有两个相等的实数根；当Δ＜0时，方程无实数根．上面的结论反过来也成立．16．已知一次函数y＝kx+b（k、b为常数）的图象如图所示，那么关于x的不等式kx+b＞0的解集是（）A．x＞0B．x＜0C．x＜2D．x＞2．【分析】从图象上得到函数的增减性及与x轴的交点的横坐标，即能求得不等式kx+b＞0的解集．【解答】解：函数y＝kx+b的图象经过点（2，0），并且函数值y随x的增大而减小，所以当x＜2时，函数值大于0，即关于x的不等式kx+b＞0的解集是x＜2．故选：C．【点评】此题主要考查了一次函数与一元一次不等式的关系：从函数的角度看，就是寻求使一次函数y＝kx+b的值大于（或小于）0的自变量x的取值范围；从函数图象的角度看，就是确定直线y＝kx+b在x轴上（或下）方部分所有的点的横坐标所构成的集合．17．下列说法正确的是（）A．一个人的体重与他的年龄成正比例关系B．圆的周长与直径成正比例关系C．周长一定时，长方形的长与宽成反比例关系D．车辆行驶的速度v一定时，行驶的路程s与时间t成反比例关系【分析】根据正比例函数的定义和反比例函数的定义，可以判断各个选项中的说法是否正确，从而可以解答本题．【解答】解：一个人的体重与他的年龄不成正比例关系，故选项A不符合题意；圆的周长与直径成正比例关系，故选项B符合题意；周长一定时，长方形的长与宽不成反比例关系，故选项C不符合题意；车辆行驶的速度v一定时，行驶的路程s与时间t成正比例关系，故选项D不符合题意；故选：B．【点评】此题主要考查了反比例函数和正比例函数的定义，正确得出函数关系是解题关键．18．美国数学家伽菲尔德在1876年提出了证明勾股定理的一种巧妙方法，如图，在直角梯形ABCD中，AB∥CD，∠B＝90°，E是边BC上一点，且BE＝CD＝a，AB＝EC＝b．如果△ABE的面积为1，且a﹣b＝1，那么△ADE的面积为（）A．1B．2C．2.5D．5【分析】根据全等三角形的性质得到AE＝DE，∠AEB＝∠EDC，推出△AED是等腰直角三角形，求得△ADE的面积＝AE2，根据完全平方公式和勾股定理即可得到结论．【解答】解：∵AB∥CD，∠B＝90°，∴∠C＝∠B＝90°，∵BE＝CD＝a，AB＝EC＝b，∴△ABC≌△ECD（SAS），∴AE＝DE，∠AEB＝∠EDC，∵∠EDC+∠DEC＝∠AEB+∠DEC＝90°，∴∠AED＝90°，∴△AED是等腰直角三角形，∴△ADE的面积＝AE2，∵△ABE的面积为1，∴ab＝1，∴ab＝2，∵a﹣b＝1，∴（a﹣b）2＝a2+b2﹣2ab＝1，∴a2+b2＝5，∴△ADE的面积＝×5＝，故选：C．【点评】本题考查了勾股定理的证明，全等三角形的判定和性质，等腰直角三角形的判定和性质，三角形面积的计算，熟练掌握勾股定理是解题的关键．三、解答题：（本大题共有7题，第19、20题每题6分，第21、22、23题每题8分，第24、25题每题12分，满分60分）19．（6分）解方程：（x﹣1）2＝5﹣5x．【分析】原方程整理为（x﹣1）2+5（x﹣1）＝0，再利用提公因式法求解即可．【解答】解：（x﹣1）2＝5﹣5x，（x﹣1）2﹣5+5x＝0，（x﹣1）2+5（x﹣1）＝0，（x﹣1）（x﹣1+5）＝0，x﹣1＝0或x+4＝0，解得x1＝1，x2＝﹣4．【点评】本题考查了解一元二次方程，掌握提公因式法因式分解是解答本题的关键．20．（6分）用配方法解方程：x2﹣4x﹣2＝0．【分析】解题时要注意解题步骤的准确应用，把左边配成完全平方式，右边化为常数．【解答】解：x2﹣4x﹣2＝0，x2﹣4x＝2，x2﹣4x+8＝2+8，（x﹣2）2＝10，x﹣2＝±，解得x1＝2+，x2＝2﹣．【点评】本题考查了配方法解一元二次方程．配方法的一般步骤：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上一次项系数一半的平方．选择用配方法解一元二次方程时，最好使方程的二次项的系数为1，一次项的系数是2的倍数．21．（8分）A、B两地相距45千米，甲骑电瓶车从A地出发前往B地，乙同时骑自行车从距离A地20千米的C地出发前往B地．图中的线段OP和线段MN分别反映了两人与A 地的距离y（千米）和行驶时间x（小时）的函数关系．根据图象提供的信息回答下列问题：（1）两人谁先到达B地？甲．（填“甲”或“乙”）（2）甲到达B地用了小时．（3）两人在出发多少小时后相遇？【分析】（1）根据图象可知，甲先到达B地；（2）根据图象中的数据，可以先计算出甲的速度，然后即可计算出甲到达B地用的时间；（3）根据图象中的数据，先计算乙的速度，然后设两人在出发a小时后相遇，再根据甲行驶的路程＝乙行驶的路程+20，列出相应的方程，然后求解即可．【解答】解：（1）由图象可得，甲先到达B地，故答案为：甲；（2）由图象可得，甲的速度为：25÷1＝25（千米/小时），甲到达B地用了：45÷25＝（小时），故答案为：；（3）由图象可，乙的速度为：（30﹣20）÷1＝10（千米/小时），设两人在出发a小时后相遇，20+10a＝25a，解得a＝，即两人在出发小时后相遇．【点评】本题考查一次函数的应用，解答本题的关键是明确题意，利用数形结合的思想解答．22．（8分）已知：如图，在矩形ABCD中，AB＝4，BC＝2．对角线AC的垂直平分线分别交AB、CD于点E、F．求线段CF的长．【分析】联结AF，由矩形的性质得AD＝BC＝2，DC＝AB＝4，∠D＝90°，由线段的垂直平分线的性质得AF＝CF，根据勾股定理得AD2+DF2＝AF2，则22+（4﹣CF）2＝CF2，即可求得CF＝．【解答】解：连接AF，∵四边形ABCD是矩形，∴AD＝BC＝2，DC＝AB＝4，∠D＝90°，∵EF垂直平分AC，∴AF＝CF，∵AD2+DF2＝AF2，且DF＝4﹣CF，∴22+（4﹣CF）2＝CF2，解得CF＝，∴CF的长为．【点评】此题重点考查矩形的性质、线段的垂直平分线的性质、勾股定理的应用等知识，正确地作出所需要的辅助线是解题的关键．23．（8分）如图，已知△ABC中，∠C＝2∠B，AH⊥BC于点H，D是AC中点，DE∥AB，求证：EH＝AC．【分析】连接DH，由平行线的性质可得∠C＝2∠DEC，利用直角三角形斜边上中线的性质可得HD＝AC＝CD，结合等腰三角形的性质可得∠DHC＝2∠DEC，再根据三角形外角的性质可得∠DEC＝∠HDE，即可得DH＝EH，进而可证明结论．【解答】证明：连接DH，∵DE∥AB，∴∠B＝∠DEC，∵∠C＝2∠B，∴∠C＝2∠DEC，∵AH⊥BC于点H，D是AC中点，∴HD＝AC＝CD，∴∠C＝∠DHC，∴∠DHC＝2∠DEC，∵∠DHC＝∠DEC+∠HDE，∴∠DEC＝∠HDE，∴DH＝EH，∴EH＝AC．【点评】本题主要考查等腰三角形的性质，直角三角形的性质，三角形外角的性质，证明DH＝EH是解题的关键．24．（12分）已知：如图，反比例函数的图象与直线y＝kx相交于点A，直线AC与x 轴交于点C（2，0），与y轴交于点B，点C是AB的中点．（1）求直线y＝kx的函数解析式；（2）求点C到直线OA的距离；（3）若点D是直线OA上一点，且△ABD是直角三角形，求点D的坐标．【分析】（1）根据中点坐标公式求出点A的横坐标，进而求出点A坐标，即可求出答案；（2）先求出点B坐标，进而求出AB，最后用面积公式建立方程求解，即可求出答案；（3）设出点D的坐标，分三种情况利用勾股定理建立方程求解，即可求出答案．【解答】解：（1）设点A的坐标为（m，），∵点C（2，0）是AB的中点，∴2（m+0）＝2，∴m＝4，∴A（4，2），∵点A在直线y＝kx上，∴4k＝2，∴k＝，∴直线y＝kx的解析式为y＝x；（2）由（1）知，点A（4，2），∴OA＝2，∵点C（2，0），∴直线AC的解析式为y＝x﹣2，∴B（0，﹣2），设点C到直线OA的距离为h，则S△AOB＝OB•|x A|＝OA•h，∴h＝＝＝，即点C到直线OA的距离为；（3）由（1）知，直线OA的解析式为y＝x，设点D（n，n），∵A（4，2），B（0，﹣2），∴AB2＝32，BD2＝n2+（n+2）2，AD2＝（n﹣4）2+（n﹣2）2，∵△ABD是直角三角形，∴①当∠ABD＝90°时，BD2+AB2＝AD2，∴n2+（n+2）2+32＝（n﹣4）2+（n﹣2）2，∴n＝﹣，∴D（﹣，﹣），②当∠BAD＝90°时，AD2+AB2＝BD2，∴（n﹣4）2+（n﹣2）2+32＝n2+（n+2）2，∴n＝4（不符合题意，舍去），③当∠ADB＝90°时，AD2+BD2＝AB2，∴（n﹣4）2+（n﹣2）2+n2+（n+2）2＝32，∴n＝4（不符合题意，舍去）或n＝﹣，∴D（﹣，﹣），即D（﹣，﹣）或（﹣，﹣）．【点评】此题是反比例函数综合题，主要考查了待定系数法，三角形的面积公式，勾股定理，用分类讨论的思想解决问题是解本题的关键．25．（12分）如图，在△ABC中，D是AB的中点，E是边AC上一动点，联结DE，过点D 作DF⊥DE交边BC于点F（点F与点B、C不重合），延长FD到点G，使DG＝DF，联结EF、AG，已知AB＝10，BC＝6，AC＝8．（1）求证：AC⊥AG；（2）设AE＝x，CF＝y，求y与x的函数解析式，并写出自变量x的取值范围；（3）当△BDF是以BF为腰的等腰三角形时，求AE的长．【分析】（1）根据勾股定理的逆定理得到△ABC是直角三角形，由D是AB的中点，得到AD＝BD，根据全等三角形的性质得到∠GAB＝∠B，推出∠EAG＝90°，于是得到结论；（2）连接EG，根据勾股定理得到EF2＝（8﹣x）2+y2，根据全等三角形的性质得到AG ＝BF，由勾股定理得到EG2＝x2+（6﹣y）2，于是得到方程（8﹣x）2+y2＝x2+（6﹣y）2，即可得到结论（3）①当BF＝DB时，6﹣y＝5，列方程得到AE＝；②当DF＝FB时，连接DC，过点D作DH⊥FB，垂足为点H，可得DF＝FB＝6﹣y，根据勾股定理得方程（6﹣y）2＝42+（3﹣y）2，求得y＝，于是得到＝求得AE＝．【解答】（1）证明：∵BC＝6，AC＝8，∴BC2+AC2＝36+64＝100，∵AB2＝100，∴BC2+AC2＝AB2，∴△ABC是直角三角形，且∠ACB＝90°，∵D是AB的中点，∴AD＝BD，在△ADG和△BDF中，∴△ADG≌△BDF，∴∠GAB＝∠B，∵∠ACB＝90°，∴∠CAB+∠B＝90°，∴∠CAB+∠GAB＝90°，∴∠EAG＝90°，即：AC⊥AG；（2）连接EG，∵AE＝x，AC＝8，∴EC＝8﹣x，∵∠ACB＝90°，由勾股定理，得EF2＝（8﹣x）2+y2，∵△ADG≌△BDF，∴AG＝BF，∵CF＝y，BC＝6，∴AG＝BF＝6﹣y，∵∠EAG＝90°，由勾股定理，得EG2＝x2+（6﹣y）2，∵DG＝DF，DF⊥DE，∴EF＝EG，∴（8﹣x）2+y2＝x2+（6﹣y）2，∴y＝，自变量x的取值范围：＜x＜；（3）①当BF＝DB时，6﹣y＝5，∴y＝1，∴1＝，∴x＝，即AE＝；②当DF＝FB时，连接DC，过点D作DH⊥FB，垂足为点H，可得DF＝FB＝6﹣y，∵∠ACB＝90°，D是AB的中点，∴DC＝DB＝5，∵DH⊥FB，BC＝6，∴CH＝HB＝3，∴FH＝3﹣y，∵DH⊥FB，由勾股定理，得DH＝4，在Rt△DHF中，可得（6﹣y）2＝42+（3﹣y）2，解得：y＝，∴＝解得x＝，即AE＝，综上所述，AE的长度是，．【点评】本题考查了全等三角形的判定和性质，等腰三角形的性质，勾股定理，勾股定理的逆定理，正确的作出辅助线构造直角三角形是解题的关键．。

2022上海市初三数学一模(25题)压轴题精解精析(二)解析版

例 2022年上海市宝山区第25题如图1，已知正方形ABCD，将边AD绕点A逆时针旋转n°（0＜n＜90）到AP的位置，分别过点C、D作CE⊥BP，DF⊥BP，垂足分别为E、F．（1）求证：CE＝EF；（2）联结CF，如果13DPCF=，求∠ABP的正切值；（3）联结AF，如果22AF AB=，求n的值．图1满分解答（1）如图2，过点F作DC的平行线交EC于点M，所以∠FME＝∠DCE．已知CE⊥BP，DF⊥BP，所以CE//DF．所以四边形CDFM是平行四边形．所以FM＝DC＝CB．根据同角的余角相等，得∠DCE＝∠CBE．所以∠FME＝∠CBE．于是根据“AAS”，可证得△FME≌△CBE．所以EF＝EC．图2 图3 图4 （2）如图3，设BP与AD交于点G．设∠ABP＝α．在等腰三角形ABP中，AB＝AP，所以∠APB＝α．在Rt△ABG和Rt△DFG中，根据内角和相等，得∠ADF＝α．在等腰三角形ADP中，∠ADP＝∠APD．所以∠ADP－α＝∠APD－α．所以∠FDP＝∠FPD．所以FD＝FP．所以△FDP和△ECF都是等腰直角三角形，DP//CE（如图4所示）．如图4，延长CD交BP的延长线于点N．那么∠N＝α．如果13DPCF=，那么1236PF mFE m==，13NPNF=．所以122NP mPF m==．在Rt△NEC中，tan∠N＝62623CE mNE m m m==++．所以tan∠ABP＝23．（3）第一步，点F是一个关键点．如图5，根据“边边边”，可以证得△AFD≌△AFP．所以AF平分∠DAP，∠AFD＝∠AFP＝135°．所以∠AFB＝45°．所以∠AFC＝90°，△AFC始终是直角三角形（如图6所示）．第二步，计算说理．如图6，因为22AB AC=，如果22AF AB=，那么12AF AC=．所以∠ACF＝30°，∠F AC＝60°．所以∠F AD＝60°－45°＝15°．所以n°＝2∠F AD＝30°，n＝30．图5 图6例 2022年上海市崇明区第25题如图1，正方形ABCD 的边长为1，在射线AB 上取一点E ，联结DE ，将△ADE 绕点D 逆时针旋转90°，点E 落在点F 处，联结EF ，直线EF 与对角线BD 所在直线交于点M ，与射线DC 交于点N ．（1）当13AE =时，求tan ∠EDB 的值；（2）当点E 在线段AB 上，如果AE ＝x ，FM ＝y ，求y 关于x 的函数解析式，并写出定义域；（3）联结AM ，直线AM 与直线BC 交于点G ，当13BG =时，求AE 的值．图1满分解答（1）如图2，作EH ⊥BD 于H ．在Rt △ABD 中，AB ＝AD ＝1，所以BD ＝2，∠ABD ＝45°．在等腰直角三角形△BEH 中，BE ＝AB －AE ＝23，所以BH ＝EH ＝23．在Rt △DEH 中，DH ＝BD －BH ＝223-＝223，所以tan ∠EDB ＝EH DH ＝12．图2 图3 （2）如图3，在Rt △BEF 中，BE ＝1－x ，BF ＝1＋x ，由勾股定理，得222EF x =+ 过点F 作BF 的垂线交BD 的延长线于点Q ，那么△BFQ 是等腰直角三角形．由QF //BE ，得11FM QF x EM BE x+==-．所以11(1)(1)2FM x x EF x x ++==++-． 21222x x +=+．所以2(1)22x x y ++．定义域是0≤x ≤1．（3）按照点G 的位置，分两种情况讨论：①如图4，点G 在BC 上．由13BM BG DM AD ==，得43BD DM =．所以33244DM BD =如图5，由∠DEF＝∠DBA＝45°，∠BDE是公共角，得△DEM∽△DBE．所以DE DBDM DE=．所以2332242DE DB DM=⋅=⨯=．在Rt△AED中，AE2＝DE2－AD2＝31122-=．所以AE＝22．图4 图5 ②如图6，点G在CB的延长线上．由13BM BGDM AD==，得23BDDM=．所以33222DM BD==．如图7，由∠DEF＝∠DBA＝45°，根据等角的补角相等，得∠DEM＝∠DBE．又因为∠BDE是公共角，得△DEM∽△DBE．所以DE DBDM DE=．所以232232DE DB DM=⋅=⨯=．在Rt△AED中，AE2＝DE2－AD2＝3－1＝2．所以AE＝2．图6 图7例 2022年上海市奉贤区第25题如图1，已知锐角△ABC 的高AD 、BE 相交于点F ，延长AD 至G ，使DG ＝FD ，联结BG 、CG ．（1）求证：BD ∙AC ＝AD ∙BG ；（2）如果BC ＝10，设tan ∠ABC ＝m ．①如图2，当∠ABG ＝90°时，用含m 的代数式表示△BFG 的面积；②当AB ＝8，且四边形BGCE 是梯形时，求m 的值．图1 图2满分解答（1）如图3，在Rt △ADC 和Rt △BEC 中，根据同角的余角相等，得∠1＝∠2．因为BD 垂直平分FG ，所以BF ＝BG ．根据等腰三角形的“三线合一”，得∠2＝∠3．所以∠1＝∠3．由cos ∠1＝cos ∠3，得AD BD AC BG=．所以BD ∙AC ＝AD ∙BG ．图3 图4（2）①如图4，如果∠ABG ＝90°，那么∠3＝∠4．所以∠1＝∠2＝∠3＝∠4．．根据“ASA ”，可证△ADB ≌△ADC ．所以BD ＝CD ＝5．由△ABC ∽△BFG ，根据相似三角形的面积比等于对应高的比的平方，得()222tan ABC BFG S AD ABC m S BD ⎛⎫==∠= ⎪⎝⎭△△．所以S △BFG ＝21m S △ABC ．而S △ABC ＝225AD BC AD BC m BC⋅=⋅=，所以S △BFG ＝21m S △ABC ＝25m ． ②分两种情况讨论梯形BGCE ．情况一：如图5，当CG ∥BE 时，∠2＝∠5．又因为∠2＝∠3，所以∠3＝∠5．所以GB ＝GC ．根据等腰三角形的“三线合一”，可知GD 垂直平分BC ．所以BD ＝CD ＝5．在Rt△ABD中，AB＝8，BD＝5，所以AD＝39，m＝tan∠ABC＝395ADBD=．情况二：如图6，当BG∥CE时，∠3＝∠6．又因为∠1＝∠3，所以∠1＝∠6，△ADC是等腰直角三角形．设BD＝x，那么AD＝DC＝10－x．由BD2＋AD2＝AB2，得(10－x)2＋x2＝82．解得x1＝57-，x2＝57+（此时△ABC是钝角三角形，舍去）．当x＝57-，m＝tan∠ABC＝10571657957AD xBD x-++===-．图5 图6例 2022年上海市虹口区第25题如图1，在△ABC 中，∠ACB ＝90°，AB ＝10，tan B ＝34，点D 是边BC 延长线上的一点，在射线AB 上取一点E ，使得∠ADE ＝∠ABC ．过点A 作AF ⊥DE 于点F ．（1）当点E 在线段AB 上时，求证：AF DE AC BD=；（2）在（1）题的条件下，设CD ＝x ，DE ＝y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）记DE 交射线AC 于点G ，当△AEF 与△AGF 相似时，求CD 的长．图1满分解答（1）如图2，已知∠ADE ＝∠ABC ，∠BAD 是公共角，所以△ADE ∽△ABD ．如图3，根据相似三角形对应高的比等于对应边的比，得AF DE AC BD=．图2 图3 图4（2）在Rt △ABC 中，由AB ＝10，tan B ＝34，可得AC ＝6，BC ＝8．如图4，在Rt △ACD 中，CD ＝x ，AC ＝6，所以AD ＝236x +．在Rt △ADF 中，sin ∠ADF ＝sin ∠B ＝35，所以AF ＝35AD ＝23365x +．由（1），得AF DE AC BD=．所以2336568x y x +=+．整理，得21(8)3610y x x =++．x 的取值范围是0＜x ≤8．当x ＝8时，E 、B 两点重合．（3）△AEF 和△AGF 有公共的直角边AF ，分两种情况讨论相似．①如图5，AE 和AG 在AF 的两侧．此时AF 垂直平分EG ，∠GDC ＝∠GAF ＝∠EAF ＝α．设AF 的延长线与BC 交于点M ，那么点M 到∠BAC 两边的距离相等，等于MC ．由S △ABC ＝12BC AC ⋅＝1()2MC AB AC ⋅+，得863106BC AC MC AB AC ⋅⨯===++．图5 再由∠AMD ＝∠ABC ＋α，∠ADM ＝∠ADE ＋α，∠ABC ＝∠ADE ，得∠AMD ＝∠ADM ．所以AM ＝AD ．根据等腰三角形的“三线合一”，得CD ＝MC ＝3．②如图6，AE 和AG 在AF 的同侧．此时∠GDC ＝∠GAF ＝∠E ＝α．所以BE ＝BD ＝8＋x ．如图7，由△ABD ∽△ADE ，得AB AD AD AE=．所以AD 2＝AB ·AE ．所以x 2＋36＝10×(10＋8＋x )．整理，得x 2－10x －144＝0．解得x ＝18，或x ＝－8（舍去）．图6 图7例 2022年上海市黄浦区第25题如图1，在Rt △ABC 和Rt △ABD 中，∠ACB ＝∠DAB ＝90°，AB 2＝BC ∙BD ，AB ＝3，过点A 作AE ⊥BD ，垂足为点E ，延长AE 、CB 交于点F ，联结DF ．（1）求证：AE ＝AC ；（2）设BC ＝x ，=AE y EF，求y 关于x 的函数关系式及定义域；（3）当△ABC 和△DEF 相似时，求边BC 的长．图1满分解答（1）如图2，因为AB 2＝BC ∙BD ，所以=AB BD BC AB．所以Rt △ACB ∽Rt △DAB ．所以∠4＝∠2．因为AE ⊥BD ，所以∠4＋∠3＝90°．又因为∠1＋∠3＝90°，所以∠4＝∠1．所以∠1＝∠2．根据“AAS ”，可证得△AEB ≌△ACB ．所以AE ＝AC ．图2 图3（2）已知AB 2＝BC ∙BD ，AB ＝3，BC ＝BE ＝x ，所以9BD x=．设M 为Rt △ABD 的斜边BD 的中点，那么MB ＝MA ＝MD ．所以∠MAB ＝∠MBA ．又因为∠MBA ＝∠CBA ，所以∠MAB ＝∠CBA ．所以MA //FC ．所以229192222x BD BE AE ME x x y EF BE BE x x ---=====．定义域是0＜x 32 （3）如图4，因为△ABC ∽△ABE ≌△DAE ，若△ABC 与△DEF 相似，我们灵活运用相似三角形的传递性，分两种情况讨论．①如图4，当∠1＝∠5时，AB //DF ．所以BE AEyED EF==．所以229292x xxxx-=-．整理，得x2＝3．解得x＝±3．所以BC＝3．②如图5，当∠1＝∠6时，等量代换，得∠4＝∠6．此时AE＝EF．所以229212-==xyx．整理，得x2＝94．解得x＝±32．所以BC＝32．图4 图5例 2022年上海市嘉定区第25题在平行四边形ABCD中，对角线AC与边CD 垂直，34ABAC=，四边形ABCD的周长是16，点E是AD延长线上的一点，点F是射线AB上的一点，∠CED＝∠CDF．（1）如图1，如果点F与点B重合，求∠AFD的余切值；（2）如图2，点F是在边AB上一点，设AE＝x，BF＝y，求y关于x的函数关系式，并写出它的定义域；（3）如果BF∶FA＝1∶2，求△CDE的面积．图1 图2 备用图满分解答（1）如图3，过点D向直线AB作垂线，垂足为H，那么四边形ACDH是矩形．由AB＝DC，DC＝HA，得HA＝AB．所以BH＝2AB．在Rt△DBH中，cot∠AFD＝233242 BH ABDH AC==⨯=．图3 图4（2）如图3，在Rt△ABC中，34ABAC=，设AB＝3m，AC＝4m，那么BC＝5m．已知平行四边形ABCD的周长为16，所以2(3m＋5m)＝16．解得m＝1．所以AB＝3，AC＝4，BC＝5．如图4，由DC//AB，得∠EDC＝∠F AD，∠CDF＝∠DF A＝α．又已知∠CDF＝∠CED＝α，所以∠CED＝∠DF A＝α．所以△EDC∽△F AD．所以35 DE DCAF AD==．所以5335xy-=-．整理，得53433y x=-+．定义域是5＜x≤345．当E、D两点重合时，x＝5．当F、B两点重合时，53435y x=-+=，解得x＝345．（3）如图5，由△CDE∽△DAF，得2239525 CDEDAFS CDS DA⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭△△．而S△DAF＝12AF DH⋅＝142AF⨯＝2AF，所以S△CDE＝925S△DAF＝9225AF⨯＝1825AF．分两种情况讨论BF∶FA＝1∶2．①如图5，当点F在AB上时，AF＝23AB＝2．此时S△CDE＝1825AF＝18225⨯＝3625．②如图6，当点F在AB的延长线上时，AF＝2AB＝6．此时S△CDE＝1825AF＝18625⨯＝10825．图5 图6例 2022年上海市金山区第25题如图1，AD ⊥直线MN ，垂足为D ，AD ＝8，点B 是射线DM 上的一个动点，∠BAC ＝90°，边AC 交射线DN 于点C ，∠ABC 的平分线分别与AD 、AC 相交于点E 、F ．（1）求证：△ABE ∽△CBF ；（2）如果AE ＝x ，FC ＝y ，求y 关于x 的函数解析式；（3）联结DF ，如果以点D 、E 、F 为顶点的三角形与△BCF 相似，求AE 的长．图1满分解答（1）如图2，∠ACD 和∠BAD 都是∠ABC 的余角，所以∠ACD ＝∠BAD ．又因为BF 平分∠ABC ，所以∠1＝∠2．所以△ABE ∽△CBF ．（2）如图3，由∠1＝∠2，∠BAF ＝∠BDE ，得△BAF ∽△BDE ．所以=AF BF DE BE ．所以∠AFB ＝∠BED ＝∠AEF ．所以AF ＝AE ．已知AE ＝x ，所以AF ＝x ，ED ＝AD －AE ＝8－x ．由（1），得△ABE ∽△CBF ．所以=CF BF AE BE．等量代换，得=CF AF AE DE ．所以8=-y x x x．整理，得28=-x y x ．图2 图3 （3）如图4，因为△ABE ∽△CBF ，如果△DEF 与△BCF 相似，那么△DEF 与 △ABE 也相似．因为∠AEB ＝∠DEF ，分两种情况讨论．①如图4，如果∠3＝∠4，那么△AEB ∽△FED ．所以EA EB EF ED=．又因为∠AEF ＝∠BED ，所以△AEF ∽△AED ．所以∠AFE ＝∠BDE ＝90°，不符合题意，舍去．②如图5，若∠3＝∠1，那么DF //AB ．所以=FD DE AB AE ，=FD CF AB CA ．等量代换，得=CF DE CA AE．所以8-=+y x y x x ．代入28=-x y x，整理，得x 2＋8x －64＝0．解得x 1＝445-+x 2＝445--．所以AE ＝445-+图4 图5例 2022年上海市静安区第25题如图1，四边形ABCD 中，∠BAD 的平分线AE 交边BC 于点E ，已知AB ＝9，AE ＝6，AE 2＝AB ∙AD ，且DC //AE ．（1）求证：DE 2＝AE ∙DC ；（2）如果BE ＝9，求四边形ABCD 的面积；（3）如图2，延长AD 、BC 交于点F ，设BE ＝x ，EF ＝y ，求y 关于x 的函数解析式，并写出定义域．图1 图2满分解答（1）如图3，如图4，因为AE 平分∠BAD ，所以∠1＝∠2＝α．因为AE 2＝AB ∙AD ，所以=AB AE AE AB．所以△ABE ∽△AED ．所以∠3＝∠4＝β，∠5＝∠6＝θ．因为DC //AE ，所以∠4＝∠7＝β，∠9＝∠5＝θ．所以∠9＝∠6＝θ．所以△AED ∽△EDC ．所以=AE DE DE DC．所以DE 2＝AE ∙DC ．图3 图4（2）如图5所示，如果BE ＝BA ＝9，那么α＝θ．此时△ABE 、△AED 、△DEC 是两两相似的等腰三角形．所以AE ＝ED ＝DC ＝6．因为AD //BC ，所以四边形ABCD 是梯形，四边形AECD 是平行四边形．由966AD=，得EC ＝AD ＝4．如图6，作DH ⊥EC 于H ，那么EH ＝HC ＝2．在Rt △DHC 中，DC ＝6，HC ＝2，由勾股定理，得364DH -42所以S 梯形ABCD ＝1()2+⋅AD BC DH ＝1(494)422++⋅＝342图5 图6（3）如图，由△ADE ∽△AEB ，得AE DE AB BE =．所以69DE x =．解得DE ＝23x ．由△EDC ∽△ABE ，得DE DC EC AB BE AE==．所以2396x DC EC x ==．解得DC ＝2227x ，EC ＝49x ，则CF ＝49y x -．由DC //AE ，得DC CF AE EF=．所以2242796x y x y -=．整理，得23681x y x=-．定义域为0＜x ＜9．。

三角比勾股定理压轴题(含答案)

AB DP10月6日、7日月考模拟卷班级学号姓名1、Rt △ABC 中，CD 是斜边AB 上的高，则下列正确的是( ) A 、B CDAD sin = B 、B CDAD cos = C 、B CDAD tan = D 、B CDAD cot =2、在△ABC 中，点D 、E 分别在边AB 、AC 上，DE //BC ，AD ∶BD = 1:3，那么S △DBE :S △CBE 等于( ) A 、1:4； B 、1:3； C 、1:2； D 、1:6．3、下列命题中，说法正确的个数为( )(1)两个等边三角形一定相似； (2)有一个角相等的菱形一定相似； (3)腰上的高和腰对应成比例的两个等腰三角形一定相似； (4)两边及第三边上的中线对应成比例的两个三角形相似； (5)三条垂线对应成比例的两个三角形相似. A 、2个 B 、3个 C 、4个 D 、5个4、如图，P 、D 分别在等边△ABC 的边BC 、AC 上，∠APD =60°，BP =1，CD =32，则△ABC 的边长为( )A 、3B 、4C 、5D 、65、如图，E 、F 、H 、G 分别为为正方形ABCD 的边上，且AE =BF =CH =DG =31AB ，则图中阴影部分的面积与正方形ABCD 的面积之比为( ) A 、53 B 、94 C 、21 D 、526、在△ABC 中，已知tan A =45，cos B =109，那么△ABC 的形状为( )A 、锐角三角形；B 、直角三角形；C 、钝角三角形；D 、无法判定.7、图纸上某个零件的长是 320mm ，如果比例尺是 1:20，这个零件的实际长米. 8、计算：2sin 230°－cos 260°+tan30°·cot30°=9、如图，DE 是△ABC 的中位线，F 是DE 的中点，BF 的延长线交AC 于H ，则AH :HE 等于 10、在△ABC 中，D 为AB 边上一点，∠ACD =∠B ，AC =6，BD =2.5，则AD 的长为11、在梯形ABCD 中，AD ∥BC ，O 为对角线AC 、BD 的交点，若S △ACD =10，S △BOC =9，那么S 梯形ABCD =12、正方形ABCD 中，E 在边BC 所在的直线上，BE :EC =2:1，AE 交BD 于F ，则△AFD 与由D 、F 、E 、C 为顶点的四边形的面积之比为18题图A B C MN EA13、在△ABC 中，AB =15，AC =20，D 为AB 上一点，BDAB =3，在AC 边上取点E ，得到△ADE ，若图中的两个三角形相似，则AE =14、如图，□ABCD 的面积为10，P 是AB 上一点，PQ //AD 交BD 于Q ，当AP :BP =1:4时，则四边形PBCQ 的面积为 15、已知D 为等边△ABC 的边BC 上一点，向下折叠△ABC ，折痕为MN ，M 、N 分别在AB 、AC 边上，点A 落在点D 处，若BD :DC =2:3，则AM :AN =16 一张等腰三角形纸片，底边长15cm ，底边上的高长22.5cm.现沿底边依次从下向上裁剪宽度均为3cm 的矩形纸条，如图所示.已知剪得的纸条中有一张是正方形，则这张正方形纸条是第张．17、已知点A (－1，0)、B (0，2)，O 为原点，将△AOB 绕点B 逆时针旋转90°得到△BCD ，其中点C 与点O 对应，点D 与点A 对应，点P 是y 轴上一个动点，当△BCD 与△BDP 相似时，点P 的坐标为18、如图，在△ABC 中，MN //AC ，直线MN 将△ABC 分割成面积相等的两部分.将△BMN 沿直线MN 翻折，点B 恰好落在点E 处，联结AE ，若AE //CN ，则AE :NC 的值为19、Rt △ABC 中，∠C =90°，∠A =α，AB 边上高为h ，那么AB 的长等于20、如图，△ABC 中，点D 是AC 边上一点，且AD :DC =2:1．设a BA =，b BC =. (1)用b y a x +(x 、y 为实数)的形式表示BD ．(2)在图中画出BD 在a 、b 方向上的分向量.A N DC B A C A21、如图，为测量河宽，在河北岸东西方向设置了两个标志物A 、B ，它们相距100米. 在河南岸设置了一个观察点P . 标志物A 在点P 北偏东30°，标志物B 在点P 北偏西45°.求河宽(精确到1米).(≈1.41≈1.73)22、如图，AD 是△ABC 的角平分线，过点B 、C 分别作AD 的垂线，垂足分别为F 、E ，CF 和EB 相交于点P ，联结AP ． (1)求证：△ABF ∽△ACE ；(2)求证：EC //AP ． 23、、如图，已知CA ⊥AB ，BD ⊥AB ，点M 是AB 上一点，∠AMC =∠BMD ，AD 与BC 交于N 点. 求证：MN ∥AC24、等腰Rt △ABC 中，∠ACB =90°，AC =BC ，∠DCB 的正切值为21.过点D 作DE 交等腰Rt △ABC 的腰于点E ，且∠CDE =∠DCB ，DE =2，求AB 的长. 30°45°PA BFE D CA BCDFA25、△ABC 中，AC =BC ，∠ACB =90°，E 是BC 的中点，D 在边AC 上，BD 和AE 交于点F . (1)如图1，当AD =CD 时，求AFAE 的值；(2)如图2，当41 AC AD 时，求∠BFE 的正切值.26、如图，四边形ABCD 中，∠ACB =90°，DF ⊥AC 于E ，AB =15，DE =744，tan B =43，且S △AEF :S四边形EFBC=1:8. 求：(1)EF的长；(2)∠DAB 的度数.27、如图，Rt △ABC 中，∠B =90°，BC =4cm ，AB =8cm ，D 、E 、F 分别为AB 、AC 、BC 边上中点，若P 为AB 边上有个动点，PQ //BC 且交AC 于点Q ，以PQ 为边，在点A 的异侧作正方形PQMN ，记正方形PQMN 与矩形EDBF 的公共部分面积为y . (1)当AP =3cm 时，求y 的值；(2)设AP =x ，求y 与x 的函数关系式；(3)当y =2cm 2时，确定点P 的位置.F EDBCAAF D CBB AD ME CB A DC 备用FE DBA28、如图，△ABC 中，∠ACB =90°，CD ⊥AB 于D ，E 为AC 的中点，DE 的延长线交BC 的延长线于F ，BC =8，tan B =21. 求EF 的长.29、如图，点A 是∠MON 的边ON 上一点，且OA =10，cos O =53，P 是OA 上的一个动点(与O 、A 不重合)，过P 作PD ⊥OM于D ，以P A 为边作正方形P ABC (在∠MON 内部)，设OD =x ，P A =y .(1)求y 关于x 的函数解析式并写出函数的定义域；(2)当x 为何值时，△PCD 为等腰三角形？30、已知AB =2，AD =4，∠DAB =90°，AD //BC (如图)．E 是射线BC 上的动点(点E 与点B 不重合)，M 是线段DE 的中点． (1)设BE =x ，△ABM 的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域；(2)联结BD ，交线段AM 于点N ，如果△AND 与△BME 相似，求线段BE 的长．M D B CNP A O31、在Rt △ABC 中，∠ACB =90°，BC =30，AB ＝50．点P 是AB 边上任意一点，直线PE ⊥AB ，与边AC 或BC 相交于E ．点M 在线段AP 上，点N 在线段BP 上，EM =EN ，sin ∠EMP =1312．(1)如图1，当点E 与点C 重合时，求CM 的长；(2)如图2，当点E 在边AC 上时，点E 不与点A 、C 重合，设AP =x ，BN =y ，求y 关于x 的函数关系式，并写出函数的定义域；(3)若△AME ∽△ENB （△AME 的顶点A 、M 、E 分别与△ENB 的顶点E 、N 、B 对应），求AP 的长．32、如图，在△ABC 中，∠C =90°，AC =4，BC =3，O 是AB 上一点，且AO :OB =2:5．P 是边AC 上的一个动点，作PQ ⊥OP 交线段BC 于Q (不与B 、C 重合). 当△OPQ 与△CPQ 相似时，求AP 的长.图1 图2 备用图 QP O C B33、已知△ABC ，D 、 E 是射线BC 上的两点，且BD =AB ，CE =AC 。

初三数学压轴题练习3

初三压轴题复习(一)1. 如图,点F在正方形ABCD的边AB上，AE =1 ，BE = 2，点F 在边BC的延长线上，且CF = BC ，P 是边BC上的动点（与点B 不重合）P Q⊥EF，垂足为O，并交边AD 与点Q ，Q H⊥BC，垂足为H 。

（1）求证：△QP H∽△FEB。

（2）设BP = x ，EQ = y，求y关于x 的函数解析式，并写出它的定义域。

（3）试探索△PEQ 是否可能为等腰三角形？如果可能，请求出x 的值；如果不可能请说明理由。

2。

如图,已知在直角梯形中，A D∥BC , D C⊥BC，P是边AB上一动点，P E⊥CD ,垂足为点F , P M⊥AB，交边CD 与点M ，AD =1, AB = 5 ，CD = 4（1）求证：∠PME = ∠B（2）设A P 两点的距离为x ，EM = y ，求y关于x 的函数解析式，并写出它的定义域。

（3）连接PD ，当△PDM是以PM 为腰的等腰三角形，求AP 的长。

3. 已知一次函数y=2x+1的图像过点A(a, -3)，二次函数y=x²-(m+1)x+m 的图像顶点为 D ，（1）求证：此二次函数的图像与X 轴一定有交点。

（2）当二次函数的图像过点A 时，求此二次函数的解析式。

（3）在（2）的条件下, 设二次函数图像与x轴的交点为M , 试判断直线DM 与直线y=2x+1 是否平行，请证明，若不平行，请说明理由。

4. 已知二次函数y = ½X²-(m + 3)x+ m²-12的图像与x轴相交与A (X1 ,0 ),B (X2 ,0 )两点，且X1 <0 ，X2 >0，图像与y轴交与点C, OB=2OA ,(1) 求二次函数的解析式(2) 在x 轴上，点A 的左侧，求一点E ，使△ECO与△CAO 相似，并说明直线EC 经过（1）中二次函数图像的顶点D（3）过（2）中的点E 的直线y= ¼x+b与（1）中的抛物线相交与M ,N 两点，分别过M ,N 作X 轴的垂线，垂足为M′,N′，点P 为线段MN上的一点，点P 的横坐标为t ，过点p 作平行于y 轴的直线交（1）中所求抛物线于点Q是否存在t的值，使S梯形MM′N′N：S△QMN =35：12，若存在求出满足条件的t 的值,若不存在,请说明理由。

上海十年中考数学压轴题与答案解析

XX 十年中考数学压轴题解析2001年XX 市数学中考27．已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2．（1）如图8，P 为AD 上的一点，满足∠BPC ＝∠A ．图8①求证；△ABP ∽△DPC ②求AP 的长．（2）如果点P 在AD 边上移动（点P 与点A 、D 不重合），且满足∠BPE ＝∠A ，PE 交直线BC 于点E ，同时交直线DC 于点Q ，那么①当点Q 在线段DC 的延长线上时，设AP ＝x ，CQ ＝y ，求y 关于x 的函数解析式，并写出函数的定义域； ②当CE ＝1时，写出AP 的长（不必写出解题过程）．27．（1）①证明：∵∠ABP ＝180°－∠A －∠APB ，∠DPC ＝180°－∠BPC －∠APB ，∠BPC ＝∠A ，∴∠ABP ＝∠DPC ．∵在梯形ABCD 中，AD ∥BC ，AB ＝CD ，∴∠A ＝∠D ．∴△ABP ∽△DPC ．②解：设AP ＝x ，则DP ＝5－x ，由△ABP ∽△DPC ，得DCPD AP AB =，即252xx -=，解得x 1＝1，x 2＝4，则AP 的长为1或4．（2）①解：类似（1）①，易得△ABP ∽△DPQ ，∴DQ AP PD AB =．即y xx +=-252，得225212-+-=x x y ，1＜x ＜4． ②AP ＝2或AP ＝3－5．（题27是一道涉与动量与变量的考题，其中（1）可看作（2）的特例，故（2）的推断与证明均可借鉴（1）的思路．这是一种从模仿到创造的过程，模仿即借鉴、套用，创造即灵活变化，这是中学生学数学应具备的一种基本素质，世上的万事万物总有着千丝万缕的联系，也有着质的区别，模仿的关键是发现联系，创造的关键是发现区别，并找到应付新问题的途径．）XX市2002年中等学校高中阶段招生文化考试27．操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q．图1 图2 图3探究：设A、P两点间的距离为x．（1）当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到结论；（2）当点Q在边CD上时，设四边形PBCQ的面积为y，求y与x之间的函数解析式，并写出函数的定义域；（3）当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由．五、（本大题只有1题，满分12分，（1）、（2）、（3）题均为4分）27．图1 图2 图3（1）解：PQ＝PB……………………（1分）证明如下：过点P作MN∥BC，分别交AB于点M，交CD于点N，那么四边形AMND和四边形BCNM都是矩形，△AMP 和△CNP都是等腰直角三角形（如图1）．∴NP＝NC＝MB．……………………（1分）∵∠BPQ＝90°，∴∠QPN＋∠BPM＝90°．而∠BPM＋∠PBM＝90°，∴∠QPN＝∠PBM．……………………（1分）又∵∠QNP＝∠PMB＝90°，∴△QNP≌△PMB．……………………（1分）∴PQ ＝PB ．（2）解法一由（1）△QNP ≌△PMB ．得NQ ＝MP ． ∵AP ＝x ，∴AM ＝MP ＝NQ ＝DN ＝x 22，BM ＝PN ＝CN ＝1－x 22， ∴CQ ＝CD －DQ ＝1－2·x 22＝1－x 2．得S △PBC ＝21BC ·BM ＝21×1×（1－x 22）＝21－42x ． ………………（1分） S △PCQ ＝21CQ ·PN ＝21×（1－x 2）（1－x 22）＝21－x 423＋21x 2 （1分） S 四边形PBCQ ＝S △PBC ＋S △PCQ ＝21x 2－x 2＋1．即 y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分，1分）解法二作PT ⊥BC ，T 为垂足（如图2），那么四边形PTCN 为正方形． ∴PT ＝CB ＝PN ．又∠PNQ ＝∠PTB ＝90°，PB ＝PQ ，∴△PBT ≌△PQN ．S 四边形PBCQ ＝S △四边形PBT ＋S 四边形PTCQ ＝S 四边形PTCQ ＋S △PQN ＝S 正方形PTCN…（2分）＝CN 2＝（1－x22）2＝21x 2－x 2＋1 ∴y ＝21x 2－x 2＋1（0≤x ＜22）． ……………………（1分）（3）△PCQ 可能成为等腰三角形①当点P 与点A 重合，点Q 与点D 重合，这时PQ ＝QC ，△PCQ 是等腰三角形，此时x ＝0 ……………………（1分） ②当点Q 在边DC 的延长线上，且CP ＝CQ 时，△PCQ 是等腰三角形（如图3） ……………………（1分）解法一此时，QN ＝PM ＝x 22，CP ＝2－x ，CN ＝22CP ＝1－x 22．∴CQ ＝QN －CN ＝x 22－（1－x 22）＝x 2－1．当2－x ＝x 2－1时，得x ＝1． ……………………（1分）解法二此时∠CPQ ＝21∠PCN ＝22.5°，∠APB ＝90°－22.5°＝67.5°， ∠ABP ＝180°－（45°＋67.5°）＝67.5°，得∠APB ＝∠ABP ，∴AP ＝AB ＝1，∴x ＝1． ……………………（1分）XX 市2003年初中毕业高中招生统一考试27.如图，在正方形ABCD 中，AB ＝1，弧AC 是点B 为圆心，AB 长为半径的圆的一段弧。

2019-2020年上海市中考数学各地区模拟试题分类：圆压轴题专项(含解析)

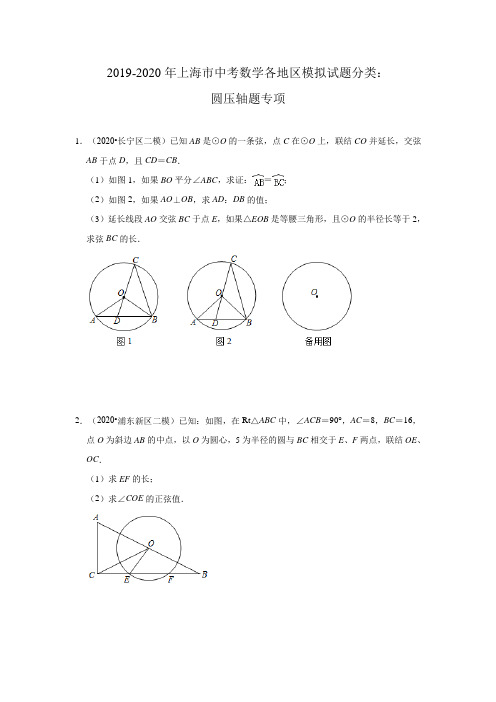
2019-2020年上海市中考数学各地区模拟试题分类：圆压轴题专项1．（2020•长宁区二模）已知AB是⊙O的一条弦，点C在⊙O上，联结CO并延长，交弦AB于点D，且CD＝CB．（1）如图1，如果BO平分∠ABC，求证：＝；（2）如图2，如果AO⊥OB，求AD：DB的值；（3）延长线段AO交弦BC于点E，如果△EOB是等腰三角形，且⊙O的半径长等于2，求弦BC的长．2．（2020•浦东新区二模）已知：如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝16，点O为斜边AB的中点，以O为圆心，5为半径的圆与BC相交于E、F两点，联结OE、OC．（1）求EF的长；（2）求∠COE的正弦值．3．（2020•崇明区二模）如图已知⊙O经过A、B两点，AB＝6，C是的中点，联结OC 交弦AB与点D，CD＝1．（1）求圆⊙O的半径；（2）过点B、点O分别作点AO、AB的平行线，交于点G，E是⊙O上一点，联结EG 交⊙O于点F，当EF＝AB，求sin∠OGE的值．4．（2020•宝山区二模）已知：如图，⊙O与⊙P相切于点A，如果过点A的直线BC交⊙O 于点B，交⊙P于点C，OD⊥AB于点D，PE⊥AC于点E．求：（1）求的值；（2）如果⊙O和⊙P的半径比为3：5，求的值．5．（2020•闵行区一模）在圆O中，弦AB与CD相交于点E，且弧AC与弧BD相等．点D 在劣弧AB上，联结CO并延长交线段AB于点F，联结OA、OB．当OA＝，且tan∠OAB ＝．（1）求弦CD的长；（2）如果△AOF是直角三角形，求线段EF的长；（3）如果S△CEF ＝4S△BOF，求线段AF的长．6．（2020•宝山区一模）如图，直线l：y＝x，点A1坐标为（1，0），过点A1作x轴的垂线交直线l于点B1，以原点O为圆心，OB1为半径画弧交x轴于点A2；再过点A2作x 的垂线交直线l于点B2，以原点O为圆心，OB2长为半径画弧交x轴于点A3，…，按此做法进行下去．求：（1）点B1的坐标和∠A1OB1的度数；（2）弦A4B3的弦心距的长度．7．（2020•闵行区一模）如图，梯形ABCD中，AD∥BC，∠ADC＝90°，AD＝2，BC＝4，tan B＝3．以AB为直径作⊙O，交边DC于E、F两点．（1）求证：DE＝CF；（2）求：直径AB的长．8．（2020•都江堰市模拟）如图，已知Rt△ABC中，∠ACB＝90°，AC＝，BC＝16．点O在边BC上，以O为圆心，OB为半径的弧经过点A．P是弧AB上的一个动点．（1）求半径OB的长；（2）如果点P是弧AB的中点，联结PC，求∠PCB的正切值；（3）如果BA平分∠PBC，延长BP、CA交于点D，求线段DP的长．9．（2020•亳州模拟）如图，⊙O1和⊙O2相交于A、B两点，O1O2与AB交于点C，O2A 的延长线交⊙O1于点D，点E为AD的中点，AE＝AC，联结OE．（1）求证：O1E＝O1C；（2）如果O1O2＝10，O1E＝6，求⊙O2的半径长．10．（2019•杨浦区三模）△ABC中，∠ACB＝90°，tan B＝，AB＝5，点O为边AB上一动点，以O为圆心，OB为半径的圆交射线BC于点E，以A为圆心，OB为半径的圆交射线AC于点G．（1）如图1，当点E、G分别在边BC、AC上，且CE＝CG时，请判断圆A与圆O的位置关系，并证明你的结论；（2）当圆O与圆A存在公共弦MN时（如图2），设OB＝x，MN＝y，求y关于x的函数解析式，并写出定义域；（3）设圆A与边AB的交点为F，联结OE、EF，当△OEF为以OE为腰的等腰三角形时，求圆O的半径长．11．（2019•青浦区二模）已知：在Rt△ABC中，∠ACB＝90°，AC＝1，D是AB的中点，以CD为直径的⊙Q分别交BC、BA于点F、E，点E位于点D下方，连接EF交CD于点G．（1）如图1，如果BC＝2，求DE的长；（2）如图2，设BC＝x，＝y，求y关于x的函数关系式及其定义域；（3）如图3，连接CE，如果CG＝CE，求BC的长．12．（2019•浦东新区二模）已知AB是圆O的一条弦，P是圆O上一点，过点O作MN⊥AP，垂足为点M，并交射线AB于点N，圆O的半径为5，AB＝8．（1）当P是优弧的中点时（如图），求弦AP的长；（2）当点N与点B重合时，试判断：以圆O为圆心，为半径的圆与直线AP的位置关系，并说明理由；（3）当∠BNO＝∠BON，且圆N与圆O相切时，求圆N半径的长．13．（2019•静安区二模）已知：如图8，梯形ABCD中，AD∥BC，AD＝2，AB＝BC＝CD ＝6．动点P在射线BA上，以BP为半径的⊙P交边BC于点E（点E与点C不重合），联结PE、PC．设BP＝x，PC＝y．（1）求证：PE∥DC；（2）求y关于x的函数解析式，并写出定义域；（3）联结PD，当∠PDC＝∠B时，以D为圆心半径为R的⊙D与⊙P相交，求R的取值范围．14．（2019•普陀区二模）如图1，在Rt△ABC中，∠ACB＝90°，AB＝5，cos∠BAC＝，点O是边AC上一个动点（不与A、C重合），以点O为圆心，AO为半径作⊙O，⊙O 与射线AB交于点D，以点C为圆心，CD为半径作⊙C，设OA＝x．（1）如图2，当点D与点B重合时，求x的值；（2）当点D在线段AB上，如果⊙C与AB的另一个交点E在线段AD上时，设AE＝y，试求y与x之间的函数解析式，并写出x的取值范围；（3）在点O的运动过程中，如果⊙C与线段AB只有一个公共点，请直接写出x的取值范围．15．（2019•嘉定区二模）在圆O中，AB是圆O的直径，AB＝10，点C是圆O上一点（与点A、B不重合），点M是弦BC的中点．（1）如图1，如果AM交OC于点E，求OE：CE的值；（2）如图2，如果AM⊥OC于点E，求sin∠ABC的值；（3）如图3，如果AB：BC＝5：4，点D为弦BC上一动点，过点D作DF⊥OC，交半径OC于点H，与射线BO交于圆内点F．探究一：如果设BD＝x，FO＝y，求y关于x 的函数解析式及其定义域；探究二：如果以点O为圆心，OF为半径的圆经过点D，直接写出此时BD的长度；请你完成上述两个探究．16．（2019•虹口区二模）如图，AD∥BC，∠ABC＝90°，AD＝3，AB＝4，点P为射线BC 上一动点，以P为圆心，BP长为半径作⊙P，交射线BC于点Q，联结BD、AQ相交于点G，⊙P与线段BD、AQ分别相交于点E、F．（1）如果BE＝FQ，求⊙P的半径；（2）设BP＝x，FQ＝y，求y关于x的函数关系式，并写出x的取值范围；（3）联结PE、PF，如果四边形EGFP是梯形，求BE的长．17．（2019•长宁区二模）如图，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，点P在边AC上（点P与点A不重合），以点P为圆心，PA为半径作⊙P交边AB于另一点D，ED⊥DP，交边BC于点E．（1）求证：BE＝DE；（2）若BE＝x，AD＝y，求y关于x的函数关系式并写出定义域；（3）延长ED交CA的延长线于点F，联结BP，若△BDP与△DAF相似，求线段AD的长．18．（2019•宝山区二模）如图已知：AB是圆O的直径，AB＝10，点C为圆O上异于点A、B的一点，点M为弦BC的中点．（1）如果AM交OC于点E，求OE：CE的值；（2）如果AM⊥OC于点E，求∠ABC的正弦值；（3）如果AB：BC＝5：4，D为BC上一动点，过D作DF⊥OC，交OC于点H，与射线BO交于圆内点F，请完成下列探究．探究一：设BD＝x，FO＝y，求y关于x的函数解析式及其定义域．探究二：如果点D在以O为圆心，OF为半径的圆上，写出此时BD的长度．19．（2019•徐汇区二模）如图，△ABC中，AC＝BC＝10，cos C＝，点P是AC边上一动点（不与点A、C重合），以PA长为半径的⊙P与边AB的另一个交点为D，过点D作DE⊥CB于点E．（1）当⊙P与边BC相切时，求⊙P的半径．（2）连接BP交DE于点F，设AP的长为x，PF的长为y，求y关于x的函数解析式，并直接写出x的取值范围．（3）在（2）的条件下，当以PE长为直径的⊙Q与⊙P相交于AC边上的点G时，求相交所得的公共弦的长20．（2019•金山区二模）如图，在Rt△ABC中，∠C＝90°，AC＝16cm，AB＝20cm，动点D由点C向点A以每秒1cm速度在边AC上运动，动点E由点C向点B以每秒cm速度在边BC上运动，若点D，点E从点C同时出发，运动t秒（t＞0），联结DE．（1）求证：△DCE∽△BCA．（2）设经过点D、C、E三点的圆为⊙P．①当⊙P与边AB相切时，求t的值．②在点D、点E运动过程中，若⊙P与边AB交于点F、G（点F在点G左侧），联结CP并延长CP交边AB于点M，当△PFM与△CDE相似时，求t的值．参考答案一．解答1．（1）证明：如图1中，∵BO平分∠ABC，∴∠ABO＝∠CBO，∵OB＝OA＝OC，∴∠A＝∠ABO，∠C＝∠OBC，∴∠A＝∠C，∵OB＝OB，∴△OBA≌△OBC（AAS），∴AB＝BC，∴＝．（2）解：如图2中，作DM⊥OB于M，DN⊥OA于N，设OM＝a．∵OA⊥OB，∴∠MON＝∠DMO＝∠DNO＝90°，∴四边形DMON是矩形，∴DN＝OM＝a，∵OA＝OB，∠AOB＝90°，∴∠A＝∠ABO＝45°，∵OC＝OB，CD＝CB，∴∠C＝∠OBC，∠CDB＝∠CBD，∵∠C+∠CDB+∠CBD＝180°，∴3∠C+90°＝180°，∴∠C＝30°，∴∠CDB＝∠CBD＝75°，∵∠DMB＝90°，∴∠MDB＝∠DBM＝45°，∴DM＝BM，∠ODM＝30°，∴DM＝OM＝a，DN＝DM＝a，AD＝DN＝a，∴＝＝．（3）解：如图3﹣1中，当BO＝BE时，∵CD＝CB，∴∠CDB＝∠CBD，∴∠A+∠AOD＝∠OBA+∠OBC，∵∠A＝∠ABO，∴∠AOD＝∠OBC＝∠C，∵AOD＝∠COE，∴∠C＝∠COE＝∠CBO，∵∠C＝∠C，∴△OCE∽△BCO，∴＝，∴＝，∴EC2+2EC﹣4＝0，解得EC＝﹣1+或﹣1﹣（舍弃），∴BC＝+1．如图3﹣2中，当EO＝EB时，同法可证△OEB是等腰直角三角形，∴EO＝EB＝EC＝OB＝，∴BC＝2，∵∠OEB＝∠C+∠COE＞∠OBE，∴OE≠OB，综上所述，BC的值为+1或2．2．解：（1）作OM⊥EF于M，如图，则EM＝FM，∵∠ACB＝90°，∴OM⊥BC，∴OM＝AC＝×8＝4，在Rt△OEM中，EM＝＝3，∴EF＝2EM＝6；（2）CM＝BC＝8，∴CE＝8﹣3＝5，∴CE＝OE，∴∠OEC＝∠OCE，在Rt△OCM中，OC＝＝4，∴sin∠OCM＝＝＝，∴∠COE的正弦值为．3．解：（1）∵AB＝6，C是的中点，CD＝1，∴OC⊥AB且OC平分AB，∴AD＝3，∠ODA＝90°，设OA＝r，则OD＝r﹣1，∴r2＝32+（r﹣1）2，解得，r＝5，即圆⊙O的半径为5；（2）作OH⊥EF于点H，∵AB＝EF，OD＝r﹣1＝4，∴OH＝OD＝4，∠OHG＝90°，∵OA∥BG，OG∥AB，∴四边形OABG是平行四边形，∴OG＝AB，∵AB＝6，∴OG＝6，∴sin∠OGH＝＝＝，即sin∠OGE＝．4．解：（1）∵OD⊥AB，PE⊥AC，OD过O，PE过P，∴AD＝AB，AE＝AC，∴；（2）连接OP，OP必过切点A，连接OB、CP，∵OB＝OA，PA＝PC，∴∠OBA＝∠OAB＝∠PAC＝∠PCA，即∠OBA＝∠PCA，∠BAO＝∠PAC，∴△OOA∽△CPA，∴＝，∵⊙O和⊙P的半径比为3：5，即＝，∴＝．5．解：（1）如图，过点O作OH⊥AB于点H，∵tan∠OAB＝＝，∴设OH＝a，AH＝2a，∵AO2＝OH2+AH2＝5，∴a＝1，∴OH＝1，AH＝2，∵OH⊥AB，∴AB＝2AH＝4，∵弧AC＝弧BD∴＝，∴AB＝CD＝4；（2）∵OA＝OB，∴∠OAF＝∠OBA，∴∠OAF＝∠ECF，①当∠AFO＝90°时，∵OA＝，tan∠OBA＝，∴OC＝OA＝，OF＝1，AB＝4，∴EF＝CF•tan∠ECF＝CF•tan∠OBA＝；②当∠AOF＝90°时，∵OA＝OB，∴∠OAF＝∠OBA，∴tan∠OAF＝tan∠OBA＝，∵OA＝，∴OF＝OA•tan∠OAF＝，∴AF＝，∵∠OAF＝∠OBA＝∠ECF，∠OFA＝∠EFC，∴△OFA∽△EFC，∴＝＝，∴EF＝OF＝，即：EF＝或；（3）如图，连接OE ，∵∠ECB ＝∠EBC ，∴CE ＝EB ，∵OE ＝OE ，OB ＝OC ，∴△OEC ≌△OEB ，∴S △OEC ＝S △OEB ，∵S △CEF ＝4S △BOF ，∴S △CEO +S △EOF ＝4（S △BOE ﹣S △EOF ）， ∴＝， ∴＝，∴FO ＝CO ＝，∴OH ＝＝1，∴HF ＝＝，∴AF ＝AH +HF ＝2+．6．解：（1）∵直线的解析式y ＝x ，∴tan ∠A 1OB 1＝＝， ∴∠A 1OB 1＝60°，OA 1＝1，∴A 1B 1＝，OA 2＝OB 1＝2， ∴B 1（1，）．（2）连接A 4B 3，作OH ⊥A 4B 3于H ．由题意OA1＝1，OA2＝2，OA3＝4，OA4＝8，∵OA4＝OB3，OH⊥A4B3，∴∠A4OH＝∠A4OB3＝30°，∴OH＝OA4•cos30°＝8×＝4．7．（1）证明：过点O作OH⊥DC，垂足为H．∵AD∥BC，∠ADC＝90°，OH⊥DC，∴∠BCN＝∠OHC＝∠ADC＝90°．∴AD∥OH∥BC．又∵OA＝OB．∴DH＝HC．∵OH⊥DC，OH过圆心，∴EH＝HF，∴DH﹣EH＝HC﹣HF．即：DE＝CF．（2）解：过点A作AG⊥BC，垂足为点G，∠AGB＝90°，∵∠AGB＝∠BCN＝90°，∴AG∥DC．∵AD∥BC，∴AD＝CG．∵AD＝2，BC＝4，∴BG＝BC﹣CG＝2．在Rt△AGB中，∵tan B＝3，∴AG＝BG•tan B＝2×3＝6．在Rt△AGB中，AB2＝AG2+BG2∴AB＝．8．解：（1）∵Rt△ABC中，∠ACB＝90°，AC＝，BC＝16，∴AB＝＝12，如图1，过O作OH⊥AB于H，则BH＝AB＝6，∵∠BHO＝∠ACB＝90°，∠B＝∠B，∴△BHO∽△BCA，∴，∴＝，∴OB＝9；（2）如图2，连接OP交AB于H，过P作PE⊥BC于E，∵点P是弧AB的中点，∴OP⊥AB，AH＝BH＝AB＝6，在Rt△BHO中，OH＝＝＝3，在△POE与△BOH中，，∴△POE≌△BOH（AAS），∴PE＝HB＝6，OE＝OH＝3，∴CE＝BC﹣OB+OE＝10，∴∠PCB的正切值＝＝；（3）如图3，过A作AE⊥BD于E，连接CP，∵BA平分∠PBC，AC⊥BC，∴AE＝AC＝4，∵∠AED＝∠ACB＝90°，∠D＝∠D，∴△ADE∽△BDC，∴＝，设DE＝x，∴＝，∴AD＝，在Rt△ACB与Rt△AEB中，，∴Rt△ACB≌Rt△AEB（HL），∴BE＝BC＝16，∵CD2+BC2＝BD2，∴（4+）2+162＝（16+x）2，解得：x＝，∴AD＝，BD＝16+＝，∴CD＝，∴OB＝9，过O作OF⊥PB交PB于F，则△OBF∽△DBC，∴，∴＝，∴BF＝7，∴PB＝2BF＝14，∴PD＝BD﹣BP＝．9．（1）证明：连接O1A，∵点E为AD的中点，∴O1E⊥AD，∵⊙O1和⊙O2相交于A、B两点，O1O2与AB交于点C，∴O1C⊥AB，在Rt△O1EA和Rt△O1CA中，，∴Rt△O1EA≌Rt△O1CA（HL）∴O1E＝O1C；（2）解：设⊙O2的半径长为r，∵O1E＝O1C＝6，∴O2C＝10﹣6＝4，在Rt△O1EO2中，O2E＝＝8，则AC＝AE＝8﹣r，在Rt△ACO2中，O2A2＝AC2+O2C2，即r2＝（8﹣r）2+42，解得，r＝5，即⊙O2的半径长为5．10．解：（1）圆A与圆O外切，理由如下：∵∠ACB＝90°，tan B＝，AB＝5，∴AC＝3，BC＝4，作OP⊥BE于P，如图1所示：则PB＝PE，OP∥AC，∴＝，设PB＝PE＝x，则CG＝CE＝4﹣2x，∴OB＝＝x，AG＝AC﹣CG＝2x﹣1，∵AG＝OB，∴2x﹣1＝x，解得：x＝，∴OB═，∴OA＝AB﹣OB＝5﹣＝＝2OB，∴圆A与圆O外切；（2）连接OM，如图2所示：∵圆O与圆A存在公共弦MN，∴OA与MN垂直平分，∴∠ODM＝90°，DM＝MN＝y，AD＝OD＝（5﹣x），由勾股定理得：DM2＝OM2﹣OD2，即（y）2＝x2﹣（）2，整理得：y2＝3x2+10x﹣25，∴y＝（＜x＜5）；（3）分三种情况：①当圆O与圆A外切，OE＝OF时，圆O与圆A外切，圆O的半径长OB＝；②当OE＝FE时，圆O与圆A相交，如图3所示：作EH⊥OF于H，则OF＝OH＝﹣OB，∵∠B＝∠B，∠EHB＝90°＝∠C，∴△BEH∽△BAC，∴＝，∴EH＝＝，在Rt△OEH中，由勾股定理得：（）2+（﹣OB）2＝OE2＝OB2，解得：OB＝；③当O与A重合时，OE＝OF，F与B重合，OE＝AB＝5；综上所述，当△OEF为以OE为腰的等腰三角形时，圆O的半径长为或或5．11．解：（1）如图1中，连接CE．在Rt△ACB中，∵∠ACB＝90°，AC＝1，BC＝2，∴AB＝＝，∵CD是⊙Q的直径，∴∠CED＝90°，∴CE⊥AB，∵BD＝AD，∴CD＝AB＝，∵•AB•CE＝•BC•AC，∴CE＝，在Rt△CDE中，DE＝＝＝．（2）如图2中，连接CE，设AC交⊙Q于K，连接FK，DF，DK．∵∠FCK＝90°，∴FK是⊙Q的直径，∴直线FK经过点Q，∵CD是⊙Q的直径，∴∠CFD＝∠CKD＝90°，∴DF⊥BC，DK⊥AC，∵DC＝DB＝DA，∴BF＝CF，CK＝AK，∴FK∥AB，∴＝，∵BC＝x，AC＝1，∴AB＝，∴DC＝DB＝DA＝，∵△ACE∽△ABC，∴可得AE＝，∴DE＝AD﹣AE＝﹣，∴＝，∴＝，∴y＝（x＞1）．（3）如图3中，连接FK．∵CE＝CG，∴∠CEG＝∠CGE，∵∠FKC＝∠CEG，∵FK∥AB，∴∠FKC＝∠A，∵DC＝DA，∴∠A＝∠DCA，∴∠A＝∠DCA＝∠CEG＝∠CGE，∴∠CDA＝∠ECG，∴EC＝DE，由（2）可知：＝﹣，整理得：x2﹣2x﹣1＝0，∴x＝1+或1﹣（舍弃），∴BC＝1+．12．解：（1）连接PO并延长交弦AB于点H，如图1所示：∵P是优弧的中点，PH经过圆心O，∴PH⊥AB，AH＝BH，在△AOH中，∠AHO＝90°，AH＝AB＝4，AO＝5，∴OH＝＝＝3，在△APH中，∠AHP＝90°，PH＝OP+OH＝5+3＝8，∴AP＝＝＝4；（2）当点N与点B重合时，以点O为圆心，为半径的圆与直线AP相交；理由如下：作OG⊥AB于G，如图2所示：∵∠OBG＝∠ABM，∠OGB＝∠AMB，∴△OBG∽△ABM，∴＝，即＝，解得：BM＝，∴OM＝﹣5＝，∵＜，∴当点N与点B重合时，以点O为圆心，为半径的圆与直线AP相交；（3）①当点N在线段AB延长线上时，当圆N与圆O相外切时，作OD⊥AB于D，如图3所示：∵OA＝OB＝5，∴AD＝DB＝AB＝4，∴OD＝＝＝3，∵∠BNO＝∠BON，∴BN＝OB＝5，∴DN＝DB+BN＝9，在Rt△ODN中，由勾股定理得：ON＝＝＝3，∵圆N与圆O相切，∴圆N半径＝ON﹣5＝3﹣5；当圆N与圆O相内切时，圆N半径＝ON+5＝3+5；②当点N在线段AB上时，此时点P在弦AB的下方，点N在圆O内部，如图4所示：作OE⊥AB于E，则AE＝BE＝4，OE＝＝3，∵∠BNO＝∠BON，∴BN＝OB＝5，∴EN＝BN＝BE＝1，在Rt△OEN中，由勾股定理得：ON＝＝＝，∴圆N半径为5﹣或5+；综上所述，当∠BNO＝∠BON，且圆N与圆O相切时，圆N半径的长为3﹣5或3+5或5﹣或5+．13．（1）∵证明：梯形ABCD，AB＝CD，∴∠B＝∠DCB，∵PB＝PE，∴∠B＝∠PEB，∴∠DCB＝∠PEB，∴PE∥CD；（2）解：分别过P、A、D作BC的垂线，垂足分别为点H、F、G．∵梯形ABCD中，AD∥BC，AF⊥BC，DG⊥BC，PH⊥BC，∴四边形ADGF是矩形，PH∥AF，∵AD＝2，BC＝DC＝6，∴BF＝FG＝GC＝2，在Rt△ABF中，AF＝＝＝4，∵PH∥AF，∴＝＝，即＝＝，∴PH＝x，BH＝x，∴CH＝6﹣x，在Rt△PHC中，PC＝，∴y＝，即y＝（0＜x＜9）；（3）解：作EM∥PD交DC于M．∵PE∥DC，∴四边形PDME是平行四边形．∴PE＝DM＝x，即MC＝6﹣x，∴PD＝ME，∠PDC＝∠EMC，又∵∠PDC＝∠B，∠B＝∠DCB，∴∠DCB＝∠EMC＝∠PBE＝∠PEB．∴△PBE∽△ECM，∴＝，即＝，解得：x＝，即BE＝，∴PD＝EC＝6﹣＝，当两圆外切时，PD＝r P+R，即R＝0（舍去）；当两圆内切时，PD＝r P﹣R，即R1＝0（舍去），R2＝；即两圆相交时，0＜R＜．14．解：（1）如图1中，在Rt△ABC中，∵∠ACB＝90°，AB＝5，cos∠BAC＝，∴AC＝4，BC＝＝＝3，∵OA＝OB＝x，∴OC＝4﹣x，在Rt△BOC中，∵OB2＝BC2+OC2，∴x2＝32+（4﹣x）2，∴x＝（2）如图2中，作CH⊥AB于H，OG⊥AB于G，EK⊥AC于K，连接CE．∵•AB•CH＝•BC•AC，∴CH＝，AH＝，∵OD＝OA＝x，OG⊥AD，∴AG＝DG＝OA•cos A＝x，∴AD＝x，DH＝x﹣，∴CD2＝（）2+（x﹣）2，∵AK＝AE•cos A＝y，EK＝y，∴CE2＝（4﹣y）2+（y）2，∵CD＝CE，∴（）2+（x﹣）2＝（4﹣y）2+（y）2，∴x2﹣x＝y2﹣y，∴（y﹣）2＝（x﹣2）2，∵y＜，x＞2，∴﹣y＝x﹣，∴y＝﹣x+（2＜x≤）．（3）①如图3﹣1中，当⊙C经过点B时，易知：BH＝DH＝，∴BD＝，∴AD＝5﹣＝，∴x＝，∴x＝，观察图象可知：当0＜x＜时，⊙C与线段AB只有一个公共点．②如图3﹣2中，当⊙C与AB相切时，CD⊥AB，易知OA＝2，此时x＝2，③如图3﹣3中，当＜x＜4时，⊙C与线段AB只有一个公共点．综上所述，当0＜x＜或x＝2或＜x＜4时，⊙C与线段AB只有一个公共点．15．解：（1）过点O作ON∥BC交AM于点N，如图1∴，，∵∴∵点M是弦BC的中点∴BM＝MC∴，∴OE：CE＝1：2；（2）联结OM，如图2∵点M是弦BC的中点，OM经过圆心O ∴OM⊥BC，∠OMC＝90°，∵AM⊥OC，∴∠MEO＝90°∴∠OMC＝∠MEO＝90°，又∵∠MOC＝∠EOM∴△MOC∽△EOM；∴，∵OE：CE＝1：2∴，∵OB＝OC∴∠ABC＝∠OCM在直角△MOC中，∴；（3）探究一：如图3，过点D作DL⊥DF交BO于点L，取BC中点M，连接OM∵DF⊥OC，∴DL∥OC，∴∠LDB＝∠C＝∠B∴BL＝DL，∵AB＝10，AB：BC＝5：4，∴BC＝8，OC＝5，∵BM＝CM＝4，∴cos∠OCM＝∵DL∥OC，∴设BD＝x，则CD＝8﹣x，∴BL＝DL＝x，CH＝（8﹣x），OH＝OC﹣CH＝5﹣（8﹣x），∵OH∥DL，∴，∴＝；∴y关于x的函数解析式是定义域是，探究二：∵以O为圆心，OF为半径的圆经过D，∴OF＝OD，∵DF⊥OC，∴OC垂直平分DF，FO＝OL，∴y＝5﹣x，∴，解得：x＝，∴BD＝．16．解：（1）∵BE＝FQ，∴∠BPE＝∠FPQ，∵PE＝PB，∴∠EBP＝（180°﹣∠EPB），同理∠FQP＝（180°﹣∠FPQ），∴∠EBP＝∠FQP，∵AD∥BC，∴∠ADB＝∠EBP，∴∠FQP＝∠ADB，∴tan∠FQP＝tan∠ADB＝，设⊙P的半径为r，则tan∠FQP＝＝，∴＝，解得：r＝，∴⊙P的半径为；（2）过点P作PM⊥FQ，垂足为点M，如图1所示：在Rt△ABQ中，cos∠AQB＝＝＝＝，在Rt△PQM中，QM＝PQ cos∠AQB＝，∵PM⊥FQ，PF＝PQ，∴FQ＝2QM＝，∴，当圆与D点相交时，x最大，作DH⊥BC于H，如图2所示：则PD＝PB＝x，DH＝AB＝4，BH＝AD＝3，则PH＝BP﹣BH＝x﹣3，在Rt△PDH中，由勾股定理得：42+（x﹣3）2＝x2，解得：x＝，∴x的取值范围为：；（3）设BP＝x，分两种情况：①EP∥AQ时，∴∠BEP＝∠BGQ，∵PB＝PE，∴∠PBE＝∠BEP，∴∠BGQ＝∠PBE，∴QG＝QB＝2x，同理：AG＝AD＝3，在Rt△ABQ中，由勾股定理得：42+（2x）2＝（3+2x）2，解得：x＝，∴QG＝QB＝2x＝，∵EP∥AQ，PB＝PQ，∴BE＝EG，∵AD∥BC，∴＝，即＝，解得：BG＝，∴BE＝BG＝；②PF∥BD时，同①得：BG＝BQ＝2x，DG＝AD＝3，在Rt△ABD中，由勾股定理得：42+32＝（3+2x）2，解得：x＝1或x＝﹣4（舍去），∴BQ＝2，∴BP＝1，作PN⊥BG于N，则BE＝2BN，如图3所示：∵AD∥BC，∴∠PBN＝∠ADB，∴cos∠PBN＝cos∠ADB＝，即＝，∴BN＝，∴BE＝2BN＝；综上所述，或．17．（1）证明：∵ED⊥DP，∴∠EDP＝90°．∴∠BDE+∠PDA＝90°．又∵∠ACB＝90°，∴∠B+∠PAD＝90°．∵PD＝PA，∴∠PDA＝∠PAD．∴∠BDE＝∠B．∴BE＝DE．（2）∵AD＝y，BD＝BA﹣AD＝5﹣y．过点E作EH⊥BD垂足为点H，由（1）知BE＝DE，∴．在Rt△EHB中，∠EHB＝90°，∴．在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4．∴AB＝5．∴．∴，∴．（3）设PD＝a，则，在等腰△PDA中，，易得在Rt△PDF中，∠PDF＝90°，．∴，．若△BDP∽△DAF又∠BDP＝∠DAF①当∠DBP＝∠ADF时，即，解得a＝3，此时．②当∠DBP＝∠F时，即，解得，此时．综上所述，若△BDP与△DAF相似，线段AD的长为或．18．解：（1）如图1，过点O作ON∥BC交AM于点N，∵点O是AB的中点，∴点N是AM的中点，∴ON＝BM，∵点M为弦BC的中点，∴BM＝CM，∴ON＝CM，∵ON∥BC，∴＝；（2）如图1，连接OM，∵点M为弦BC的中点，∴OM⊥BC，∵AM⊥OC于点E，∴∴∠OME+∠CME＝∠CME+∠C＝90°，∴∠OME＝∠MCE，∴△OME∽△MCE，∴ME2＝OE•CE，设OE＝x，则CE＝2x，ME＝x，在Rt△MCE中，CM＝＝x，∴sin∠ECM＝＝＝∴sin∠ABC＝；（3）探究一：如图2，过点D作DL⊥DF交BO于点L，∵DF⊥OC，∴DL∥OC，∴∠LDB＝∠C＝∠B，∴BL＝DL，∵AB＝10，AB：BC＝5：4，设BD＝x，则CD＝8﹣x，BL＝DL＝x，CH＝，OH＝OC﹣CH＝5﹣（8﹣x），∵OH∥DL，∴＝，∴，∴y＝（其中）；探究二：∵以O为圆心，OF为半径的圆经过D，∴OF＝OD，∵DF⊥OC，∴OC垂直平分DF，FO＝OL，∴y＝5﹣x，∴，解得：x＝，∴BD＝．19．解：（1）设⊙P与边BC相切的切点为H，圆的半径为R，连接HP，则HP⊥BC，cos C＝，则sin C＝，sin C＝＝＝，解得：R＝；（2）在△ABC中，AC＝BC＝10，cos C＝，设AP＝PD＝x，∠A＝∠ABC＝β，过点B作BH⊥AC，则BH＝BC sin C＝8，同理可得：CH＝6，HA＝4，AB＝4，则：tan∠CAB＝2BP＝＝，DA＝x，则BD＝4﹣x，如下图所示，PA＝PD，∴∠PAD＝∠CAB＝∠CBA＝β，PD∥BE，tanβ＝2，则cosβ＝，sinβ＝，EB＝BD cosβ＝（4﹣x）×＝4﹣x，∴PD∥BE，∴，即：＝，整理得：y＝（0＜x＜10）；（3）以EP为直径作圆Q如下图所示，点D在圆P上，EP是圆Q的直径，则点D也在圆Q上，故GD为相交所得的公共弦，设∠DCP＝∠PDC＝∠α，GD是公共弦，则GD⊥PE，则∠PED＝∠BDE，∵∠EDP＝90°，∴∠PDE+∠EPD＝90°＝∠EPD+∠GDP，故∠PED＝∠EDP＝∠α，由（2）知tan∠BAC＝tanβ＝2，故tan，则cosα＝，则AD＝AG＝x，在Rt△EPD中，ED＝2PD＝2x，在Rt△BED中，ED＝2x，则EB＝ED＝x，则EC＝CB﹣BE＝10﹣x，在Rt△CGE中，CG＝AC﹣AG＝10﹣2x，cos∠C＝＝＝，解得：x＝；GD＝2PD cosα＝2x cosα＝2××＝．20．（1）证明：由题意得：CD＝t，CE＝t，由勾股定理得，BC＝＝12，＝，＝＝，∴＝，又∠C＝∠C，∴△DCE∽△BCA；（2）①连结CP并延长CP交AB于点H，∵∠ACB＝90°，∴DE是⊙P的直径，即P为DE中点，∴CP＝DP＝PE＝DE，∴∠PCE＝∠PEC，∵△DCE∽△BCA，∴∠CDE＝∠B，∵∠CDE+∠CED＝90°，∴∠B+∠HCB＝90°，即CH⊥AB，∵⊙P与边AB相切，∴点H为切点，CH为⊙P的直径，∵sin A＝＝，∴＝，解得，CH＝，∴DE＝，sin A＝sin∠CED＝＝，即＝，解得，CD＝，∴t＝；②由题意得，0＜t≤12，即0＜t≤9，∵CD＝t，CE＝t，∴DE＝＝t，由①得，CM＝，CP＝DE＝t，CM⊥AB，∴PM＝﹣t，PF＝CP＝t，∠PMF＝90°，当△FMP∽△DCE时，＝，即＝，解得，t＝；当△PMF∽△DCE时，＝，即＝，解得，t＝；∴综上所述：当△PFM与△CDE相似时．t＝或t＝．。

初三数学冲刺复习题

初三冲刺复习题1．等腰三角形的两条边分别为5、6，则此三角形底角的余弦值为． 2．点P 的坐标为)5,2( ，以点P 为圆心，半径为r 的圆与x 轴相离，与y 轴相交，则r 的取值范围为． 3．已知：如图，将△ABC 绕点B 逆时针旋转30那么△BC 1C 的面积是．4．将一副直角三角尺如图摆放在一起，连接的余切值为． 5．如图，在平面直角坐标系中，△ABC 的顶点A 在原点，边AC 在x 轴的正半轴，AC ＝16，∠BAC ＝60°，AB ＝10，⊙P 分别与边AB 、AC 相切于D 、E(切点D 、E 不在边AB 、AC 的端点)，ED 的延长线与CB 的延长线相交于点F. （1）求BC 边的长和△ABC 的面积；（2）设AE ＝x ，DF ＝y ，写出y 与x 的函数解析式，并写出自变量x 的取值范围；（3）探索△ADC 与△DBF 能否相似？若能相似，请求出x 的值，同时判断此时⊙P 与边BC 的位置关系，并证明之；若不能相似，请说明理由。

（4）当⊙P 与△ABC 内切时，⊙P 与边BC 相切于G 点，请写出切点D 、E 、G 的坐标(不必写出计算过程).A6．已知，如图△ABC 为直角三角形，AD ⊥BC ，tgB ＝，BC ＝5，用一直角三角板的直角顶点放在点D 上转动，交AB 于E ，交AC 于F 。

（1）证明：（2）设AF ＝x ，，求y 关于x 的函数解析式并求出x 的取值范围。

（3）△AED 能否为等腰三角形，若能则求出AF 的长，若不能，请说明理由。

7．如图,已知⊙O 1和⊙O 2的半径分别为R 、r ，连结O 1O 2交⊙O 1于点M 、交⊙O 2•于点N ．将一个直角三角尺的直角顶点C 放在直线O 1O 2的上方,•让两个直角边所在的直线分别经过点M 、N ，CM 交⊙O 1于点A ，CN 交⊙O 2于点B ． (1) 求证：O 1A ∥O 2B ；（2）直线AB 和直线O 1O 2能否平行？若能够，试指出什么条件下，AB ∥O 1O 2；若不能，试说明理由．(3) 是否存在一点C ，使CB CN CA CM ⋅=⋅？若存在,请说明如何确定点C 的位置, 并证明你的结论；如果不存在,请说明理由．43ABACBE AF =y S ADE=△DBCA8．已知，二次函数y =12)3(2122-++--m x m x 的图象与x 轴相交于A )0,(1x 、B(x 2,0)两点，且x 1<0，x 2>0，图象与y 轴交于点C ，OB =2OA ；(1) 求二次函数的解析式；(2) 在x 轴上，点A 的左侧，求一点E ，使△ECO 与△CAO 相似，并说明直线EC 经过(1)中二次函数图象的顶点D ；(3) 过(2)中的点E 的直线y =b x +41与(1)中的抛物线相交于M 、N 两点，分别过M 、N 作x 轴的垂线，垂足为M ΄、N ΄，点P 为线段MN 上一点，点P 的横坐标为t ，过点P 作平行于y 轴的直线交(1)中所求抛物线于点Q ，是否存在t 值，使S N N MM ''梯形:S QMN ∆=35:12. 若存在，求出满足条件的t 值；若不存在，请说明理由.9．已知：如图，点A 在∠MON 的边OM 上，以点A 为顶点的∠BAC 与∠MON 的边ON 分别相交于点B 和点C （点B 在点C 的左边），OA =2，∠BAC =∠MON =30°，设点O 与点B 的距离为x ，OC =y ．（1）求证：线段AC 是线段OC 与BC 的比例中项；（2）求y 关于x 的函数解析式，并写出它的定义域；（3）如果以线段BC 为直径的圆P 与直线OM 相切，求线段OB 的长．A MBC N。

中考数学压轴题二

1．如图，点P是反比例函数y＝－2x（x＜0）图象上一动点，点A、B分别在x轴，y轴上，且OA＝OB＝2，PM⊥x轴于M，交AB于E，PN⊥y轴于N，交AB于F．（1）当动点P的纵坐标为53时，连接OE（2）设动点P的坐标为P（a，b）（－2＜探索：以AE、EF、BF2、如图，在△OAB中，OA＝OB，点A坐标为（－33，3），点B在x轴负半轴上．（1）将△OAB沿x轴向右平移a个单位后，点A恰好落在反比例函数y＝63x的图象上，求a的值；（2）将△OAB绕点O按逆时针方向旋转α角（0°＜α＜90°）．①当α＝30°时，点B恰好落在反比例函数y＝k的图象上，求k的值；②点A、B请说明理由．3．如图1，在Rt△ABC中，∠C＝90°，AC＝BC，D是AB边上一点，E是AC边上的一个动点（与点A、C不重合），DF⊥DE，DF与射线BC相交于点F．（1）如图2，若点D是边AB的中点，求证：DE＝DF；（2）若AD:DB＝m，求DE:DF的值；（3）若AC＝BC＝6，AD:DB＝1:2，设AE＝x，BF＝y．①求y关于x的函数关系式，并写出自变量x的取值范围；②以CE为直径的圆与直线AB是否可相切，若可能，求出此时x的值，若不可能，请说明理由．B图1B图2B 备用图B 备用图4．Rt △ABC 的直角顶点B 在Rt △DEF 的斜边DF 上，已知AB ＝DF ，DE ＝EF ，∠A ＝30°．固定△DEF 不动，将△ABC 绕点B 旋转，并使边AB 与边DE 交于点P ，边BC 与边EF 于点Q ．（1）如图1，若FBBD ＝m ，求BPBQ的值，并确定m 的取值范围；（2）若DF ＝30， FBBD＝2，连接PQ ，设△BPQ 的面积为S ，在旋转过程中：①如图2，当点E 恰好落在边AC 上时，求AE 的长；②S 是否存在最大值或最小值？若存在，求出最大值或最小值，若不存在，请说明理由； ③随着S 取不同的值，对应△BPQ 的个数有哪些变化？求相应S 值的取值范围．Q E D F B A PC 图1 Q ED FBA PC图2 H5．如图，已知抛物线y＝(3－m)x2＋2(m－3)x＋4m－m2的顶点A在双曲线y＝3x上，直线y＝mx＋b经过点A，与y轴交于点B，与x轴交于点C．（1）求直线AB的解析式；（2）将直线AB绕点O顺时针旋转90°，与x轴交于点D，与y轴交与点E，求sin∠BDE 的值；（3）过点B作x轴的平行线与双曲线交于点F，点M在直线BF上，且到抛物线的对称轴的距离为6．若点N在直线BF上，直接写出使得∠AMB＋∠ANB＝45°的点N的坐标．6．如图，在平面直角坐标系中，直线y＝mx（m＞0）与双曲线y＝kx交于A、B两点，过点A作AC∥x轴，过点B作BC∥y轴，AC与BC交于点C，AC与y轴交于点M，BC与x 轴交于点N，若∠BAC＝60°，AB＝4．（1）求m、k的值；（2）将一把三角尺的直角顶点放在原点O处，绕着点O旋转三角尺，三角尺的两直角边分别交射线CA、射线BC于点P、Q，设点P的横坐标为x，PQ的长为L，当点P在边AC上运动时，求L与x的函数关系式；（3）当△PQC的面积为32时，求点P的坐标．7．如图，矩形ABCD的顶点A在坐标原点，顶点B坐标为（－2，1），顶点C在y轴上．（1）求顶点D的坐标；（2）将矩形ABCD绕点O顺时针旋转，使点D落在x轴的点G处，得到矩形AEFG，EF 与AD交于点M，过点M的反比例函数图象交FG于点N（3）求证：△AMN是直角三角形．8．在平面直角坐标系中，点A （3，0），B （0，4）．以点A 为旋转中心，把△ABO 顺时针旋转，得△ACD ．记旋转转角为α，∠ABO 为β．（1）如图①，当旋转后点D 恰好落在AB 边上时，求点D 的坐标；（2）如图②，当旋转后满足BC ∥x 轴时，求α与β之间的数量关系；（3）当旋转后满足∠AOD ＝β时，求直线CD 的解析式．图①图②9．已知∠MON ＝60°，射线OT 是∠MON 的平分线，点P 是射线OT 上的一个动点，射线PB 交射线ON 于点B ．（1）如图，若射线PB 绕点P 顺时针旋转120°后与射线OM 交于点A ，求证：P A ＝PB ；（2）在（1）的条件下，若点C 是AB 与OP 的交点，且满足PC ＝32PB ，求△POB 与△PBC 的面积之比；（3）当OB ＝2时，射线PB 绕点P 顺时针旋转120°后与直线OM 交于点A （点A 不与点O 重合），直线P A 交射线ON 于点D ，且满足∠PBD ＝∠ABO ，求OP 的长．B C M A N PT M N T 备用图MNT 备用图10．已知一次函数y＝－12x＋b的图象与反比例函数y＝6x（x＞0）的图象交于A、B两点，与x轴、y轴分别交于C、D两点．（1）如图1，若AB＝2AC，求b的值；（2）在（1）的条件下，将一块直角三角板的直角顶点P放在反比例函数y＝6x（x＞0）图象的AB段上滑动，两直角边始终与坐标轴平行，且与线段AB分别交于Q、R两点．设点P 的横坐标为x，QR的长为L，求L关于x的函数关系式，并求L的最大值；（3）如图2，过点A作直线AE∥x轴，交轴于点E；过点B作直线BF∥轴交x轴于点F，交直线AE于点并说明理由．11．如图，在直角梯形ABCD 中，AD ∥BC ，AB ⊥BC ，AD ＝AB ＝1，BC ＝2．将点A 折叠到CD 边上，记折叠后A 点对应的点为P （P 与D 点不重合），折痕EF 只与边AD 、BC 相交，交点分别为E 、F ．过点P 作PN ∥BC 交AB 于N ，交EF 于M ，连结P A 、PE 、AM ，EF 与P A 相交于O ．（1）指出四边形PEAM 的形状（不需证明）；（2）记∠EPM ＝α，△AOM 、△AMN 的面积分别为S 1、S 2．①求证：S 1tanα2＝18P A 2；②设AN ＝x ，y ＝S 1－S 2tanα2，试求出以x 为自变量的函数y 的解析式，并确定y 的取值范围．OABCDPE FMN12．已知：在△ABC 中，BC ＝2AC ，∠DBC ＝∠ACB ，BD ＝BC ，CD 交线段AB 于点E ．（1）如图l ，当∠ACB ＝90°时，则线段DE 、CE 之间的数量关系为____________________；（2）如图2，当∠ACB ＝120°时，求证：DE ＝3CE ；（3）如图3，在（2）的条件下，点F 是BC 边的中点，连接DF ，DF 与AB 交于点G ，△DKG 和△DBG 关于直线DG 对称（点B 的对称点是点K ），延长DK 交AB 于点H ．若BH ＝10，求CE 的长．C A B DE 图1C A BDE 图2C AB D E 图3K HG F13．如图，在平面直角坐标系中，已知点A（－1，0），点B（9，0），以AB为直径作⊙M，交y轴的负半轴于点C，连接AC、BC，抛物线经过A、B、C三点．（2）点E是AC延长线上一点，∠BCE的平分线CD交⊙M于点D，连接BD，求直线BD的解析式；（3）在（2）的条件下，抛物线上是否存在点P，使得∠PDB＝∠CBD？若存在，求出P点坐标；若不存在，请说明理由．14．如图，二次函数y＝ax2＋bx（a＞0）的图象与反比例函数y＝kx的图象相交于A，B两点，且点A的坐标为（1，4），点B在第三象限．（1）求该二次函数的表达式；（2）设二次函数图象与x轴的另一个交点为D，E点为线段OD上的动点（与O，D不重合），过E点作EF∥OB，交BD于F，连接BE①设OE的长为m，△BEF的面积为S，求S②当△BEF为等腰三角形时，求点E15．如图，在Rt△ABC中，∠C＝90°，AC＝BC＝6，点D为AC中点，点E为边AB上一动点，点F为射线BC上一动点，且∠FDE＝90°．（1）当DF∥AB时，连接EF，求cos∠DEF的值；（2）当点F在线段BC上时，设AE＝x，BF＝y，求y关于x的函数关系式，并写出自变量x的取值范围；（3）连接CE，若△CDE为等腰三角形，求BF的长．ACB DEF16．如图，Rt△ABC中，∠ACB＝90°，AC＝3cm，CB＝4cm．点P、Q分别是AB、CB上动点，它们分别从A、C同时出发向B点匀速移动，移动速度为1cm/秒，设P、Q移动时间为t秒（0≤t≤4）．（1）当∠CPQ＝90°时，求t的值；（2）是否存在t，使△CPQ成为等边三角形？若存在，求出t的值；若不存在，能否改变Q 的运动速度（P的速度不变），使△CPQ成为等边三角形？如何改变？并求出相应的t值．17．如图，抛物线y＝－14x2＋4交x轴于A、B两点（A在B的左侧），交y轴于点C，连接AC、BC，D是线段OB上一动点，以CD为一边向右侧作正方形CDEF，连接BF，交DE于点P．（1）试判断△ABC的形状，并说明理由；（2）求证：BF⊥AB；（3）连接CP，记△CPF的面积为S1，△CPB的面积为S2，若S＝S1－S2，试探究S的最小值．18．如图，Rt△ABC中，∠A＝30°，BC＝10cm，点Q在线段BC上从B向C运动，点P在线段BA上从B向A运动．Q、P两点同时出发，运动的速度相同，当点Q到达点C时，两点都停止运动．作PM⊥PQ交CA于点M，过点P分别作BC、CA的垂线，垂足分别为E、F．（1）求证：△PQE∽△PMF；（2）当点P、Q运动时，请猜想线段PM与MA的大小有怎样的关系？并证明你的猜想；（3）设BP＝x，△PEM的面积为y，求y关于x的函数关系式，当x为何值时，y有最大值，并将这个值求出来．EQAC19．在△ABC中，AB＝AC，∠BAC＝α，点D是BC上一动点（不与B、C重合），将线段AD绕点A逆时针旋转α后到达AE位置，连接DE、CE，设∠BCE＝β．（1）如图1，若α＝90°，求β的大小；（2）如图2，当点D在线段BC上运动时，试探究α与β之间的数量关系，并证明你的结论；（3）当点D在线段BC的反向延长线上运动时，（2）中的结论是否仍然成立？若成立，请证明，若不成立，请写出α与β之间的数量关系，并说明理由．EA图1E A图220．如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M是BC的中点，P（0，m）是线段OC上一动点（C点除外），直线PM交AB的延长线于点D．（1）求点D的坐标（用含m的代数式表示）；（2）当△APD是等腰三角形时，求m的值；（3）设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2）．当点P从点O向点C运动时，点H也随之运动，请直接写出点H所经过的路径长．（不必写解答过程）图121．在四边形ABCD 中，对角线AC 、BD 相交于点O ，设锐角∠DOC ＝α，将△DOC 绕点O 按逆时针方向旋转得到△D ′OC ′（0°＜旋转角＜90°），连接AC ′、BD ′，AC ′ 与BD ′ 相交于点M ．（1）当四边形ABCD 是矩形时，如图1，请猜想AC ′ 与BD ′ 的数量关系以及∠AMB 与α的大小关系，并证明你的猜想；（2）当四边形ABCD 是平行四边形时，如图2，已知AC ＝kBD ，请猜想此时AC ′ 与BD ′ 的数量关系以及∠AMB 与α的大小关系，并证明你的猜想；（3）当四边形ABCD 是等腰梯形时，如图3，AD ∥BC ，此时（1）AC ′ 与BD ′ 的数量关系是否成立？∠AMB 与α的大小关系是否成立？不必证明，直接写出结论．M B C A O D C ′ D ′ 图1MB C A O D C ′D ′ 图2MB C A O D C ′ D ′图322．在矩形ABCD中，点E是AD边上一点，∠ABE＝30°，BE＝DE，连接BD．动点M从点E出发沿射线ED运动，过点M作MN∥BD交直线BE于点N．（1）如图1，当点M在线段ED上时，求证：BE＝PD＋33MN；（2）若BC＝6，设MN长为x，以M、N、D为顶点的三角形面积为y，求y关于x的函数关系式；（3）在（2）的条件下，当点M运动到线段ED的中点时，连接NC，过点M作MF⊥NC 于F，MF交对角线BD于点G（如图2），求线段MG的长．A E M DNC图1 A E DC备用图A E M DN图2GF23．如图1，边长为2的正方形ABCD 中，E 是BA 延长线上一点，且AE ＝AB ，点P 从点D 出发，以每秒1个单位长度的速度沿D →C →B 向终点B 运动，直线EP 交AD 于F ，过点F 作直线FG ⊥DE 于G ，交AB 于Q ．设点P 运动时间为t （秒）．（1）求证：AF ＝AQ ；（2）当t 为何值时，四边形PQBC 是矩形？（3）如图2，连接PB ，当t 为何值时，△PQB 是等腰三角形？A B C E D F G Q P 图1 A B C E D FG Q P 图224．如图，已知抛物线y＝ax2＋bx＋8（a≠0）与x轴交于点A（－2，0）、B，与y轴交于点C，tan∠ABC＝2．（1）求抛物线的解析式及其顶点D的坐标；（2）设直线CD交x轴于点E．在线段OB的垂直平分线上是否存在点P，使得经过点P 的直线PM垂直于直线CD，且与直线OP的夹角为75°？若存在，求出点P的坐标；若不存在，请说明理由；（3）过点B作x轴的垂线，交直线CD于点F，将抛物线沿其对称轴向上平移，使抛物线与线段EF25．已知正方形ABCD，点P是对角线AC所在直线上的动点，点E在DC边所在直线上，且始终保持PE＝PD．（1）如图1，当点P在对角线AC上时，请你通过测量、观察，猜想PE与PB有怎样的关系？（直接写出结论不必证明）；（2）如图2，当点P运动到CA的延长线上时，（1）中猜想的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由；（3）如图3，当点P运动到CA的反向延长线上时，请你利用图3画出满足条件的图形，并判断此时PE与PB有怎样的关系？（直接写出结论不必证明）B 图1B 图226．如图，在直角梯形ABCD 中，AD ∥BC ，∠A ＝90°，AB ＝6，BC ＝8，AD ＝14，点E 、F 、G 分别在BC 、AB 、AD 上，且BE ＝3，BF ＝2，以EF 、FG 为邻边作□EFGH ，连接CH 、DH ．（1）直接写出点H 到AD 的距离；（2）若点H 落在梯形ABCD 内或其边上，求△HGD 面积的最大值与最小值；（3）当△EHC 为等腰三角形时，求AG 的长．A D C GB F E H27．如图，四边形OABC的四个顶点坐标分别为O（0，0），A（8，0），B（4，4），C（0，4），直线l：y＝kx＋b保持与四边形OABC的边交于点M、N（M在折线AOC上，N在折线ABC上）设四边形OABC在l右下方部分的面积为S1，在l左上方部分的面积为S2，记S＝|S1－S2|．（1）求∠OAB的大小；（2）当M、N重合时，求l的解析式；（3）当b≤0时，问线段AB上是否存在点N使得S＝0？若存在，求b的值；若不存在，请说明理由；（4）求S与b的函数关系式。

2022年上海市崇明区中考数学二模试卷

2022年上海市崇明区中考数学二模试卷试题数：25，总分：1501.（单选题，4分）下列各数中，无理数是（）A. 65B. 0.3C. √73D. √272.（单选题，4分）如果最简二次根式√3x−5与√x+3是同类二次根式，那么x的值是（）A.1B.2C.3D.43.（单选题，4分）将抛物线y=2x2向右平移1个单位，再向上平移2个单位后，所得新抛物线和原抛物线相比，不变的是（）A.对称轴B.开口方向C.和y轴的交点D.顶点4.（单选题，4分）为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间频数分布直方图如图所示，那么所调查学生睡眠时间的众数，中位数分别为（）A.7小时，7小时B.8小时，7.5小时C.7小时，7.5小时D.8小时，8小时5.（单选题，4分）下列命题是真命题的是（）A.对角线相等的四边形是平行四边形B.对角线互相平分且相等的四边形是矩形C.对角线互相垂直的四边形是菱形D.对角线互相垂直平分的四边形是正方形6.（单选题，4分）Rt△ABC中，已知∠C=90°，BC=3，AC=4，以点A、B、C为圆心的圆分别记作圆A、圆B、圆C，这三个圆的半径长都是2，那么下列结论中，正确的是（）A.圆A与圆C相交B.圆B与圆C外切C.圆A与圆B外切D.圆A与圆B外离7.（填空题，4分）计算：（-2mn3）2=___ ．8.（填空题，4分）分解因式：xy3-9xy=___ ．9.（填空题，4分）方程√3x−1 =2的根是___ ．10.（填空题，4分）已知关于x的一元二次方程x2-mx-m+3=0有两个相等的实数根，那么m的值为 ___ ．x的取值范围是 ___ ．11.（填空题，4分）函数y=√3x+112.（填空题，4分）当0＜k＜1时，一次函数y=（k-1）x+k的图象不经过第 ___ 象限．13.（填空题，4分）一个不透明的袋子里装有3个红球和5个黑球，它们除颜色外其余都相同．从袋中任意摸出一个球是红球的概率为 ___ ．14.（填空题，4分）《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相同，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各重多少两？设黄金每枚重x两，白银每枚重y两，根据题意可列方程组___15.（填空题，4分）一个正多边形，它的一个内角等于一个外角的2倍，那么这个正多边形的边数是 ___ ．16.（填空题，4分）如图，在平行四边形ABCD 中，点E 是边CD 中点，联结AE 交对角线BD 于F ，设 AB ⃗⃗⃗⃗⃗ = a ， BC ⃗⃗⃗⃗⃗ = b ⃗ ，那么 BF ⃗⃗⃗⃗⃗ 可用 a 、 b⃗ 表示为 ___ ． 17.（填空题，4分）如图，⊙O 是Rt△ABC 的外接圆，OE⊥AB 交⊙O 于点E ，垂足为点D ，AE ，CB 的延长线交于点F ．如果OD=3，AB=8，那么FC 的长是 ___ ．18.（填空题，4分）如果三角形一条边上的中线恰好等于这条边的长，那么我们称这个三角形为“匀称三角形”．在Rt△ABC 中，∠C=90°，AC ＞BC ，若Rt△ABC 是“匀称三角形”，那么BC ：AC ：AB=___ ．19.（问答题，10分）计算：2-1+sin30°-√3+1 -（ √3 -1）0．20.（问答题，10分）解方程组： {x +2y =2①x 2−5xy +4y 2=0② ．21.（问答题，10分）已知在平面直角坐标系xOy 中，正比例函数与反比例函数的图象交于点P （1，2），直线AB 垂直于x 轴，垂足为点C （点C 在原点的右侧），并分别与正比例函数和反比例函数的图象相交于点A 、B ，且AC+BC=5．（1）求正比例函数和反比例函数的解析式；（2）求△AOB 的面积．22.（问答题，10分）为解决群众“健身去哪儿”问题，某区2021年新建、改建90个市民益智健身苑点，图1是某益智健身苑点中的“侧摆器”．锻炼方法：面对器械，双手紧握扶手，双脚站立于踏板上，腰部发力带动下肢做左右摆式运动．（1）如图2是侧摆器的抽象图，已知摆臂OA的长度为80厘米，在侧摆运动过程中，点A 为踏板中心在侧摆运动过程中的最低点位置，点B为踏板中心在侧摆运动过程中的最高点位置，∠BOA=25°，求踏板中心点在最高位置与最低位置时的高度差．（精确到0.1厘米）（sin25°≈0.423，cos25°≈0.906，tan25°≈0.466）（2）小杰在侧摆器上进行锻炼，原计划消耗400大卡的能量，由于小杰加快了运动频率，每小时能量消耗比原计划增加了100大卡，结果比原计划提早12分钟完成任务，求小杰原计划完成锻炼需多少小时？23.（问答题，12分）已知：如图，在四边形ABCD中，∠ABC=∠BCD，点E在边BC上，且AE || CD，DE || AB，作CF || AD交线段AE于点F，连接BF．（1）求证：△ABF≌△EAD；（2）如果BE2=AB⋅EF，求证：∠ECF=∠BAE．24.（问答题，12分）如图．在平面直角坐标系中，抛物线y=ax2+2x+c（a≠0）与x轴交于点A、B，与y轴交于点C，点A的坐标为（-1，0），对称轴为直线x=1．点M为线段OB上的一个动点，过点M作直线l平行于y轴交直线BC于点F，交抛物线y=ax2+2x+c（a≠0）于点E．（1）求抛物线的解析式；（2）当以C、E、F为顶点的三角形与△ABC相似时，求线段EF的长度；（3）如果将△ECF沿直线CE翻折，点F恰好落在y轴上点N处，求点N的坐标．25.（问答题，14分）如图，在Rt△ABC中，∠C=90°，∠CAB=30°，AB=10．点E是线段AB上一动点，点G在BC的延长线上，且CG=AE，联结EG，以线段EG为对角线作正方形EDGF，边ED交AC边于点M，线段EG交AC边于点N，边EF交BC边于点P．（1）求证：NG=2EN；（2）设AE=x，△AEN的面积为y，求y关于x的函数解析式，并写出x的定义域；（3）联结NP，当△EPN是直角三角形时，求AE的值．2022年上海市崇明区中考数学二模试卷参考答案与试题解析试题数：25，总分：1501.（单选题，4分）下列各数中，无理数是（）A. 65B. 0.3C. √73D. √27【正确答案】：C【解析】：根据无理数的定义进行判断即可．是分数，属于有理数，不是无理数，故此选项不符合题意；【解答】：解：A、65B、0.3是有限小数，属于有理数，不是无理数，故此选项不符合题意；C、√7是无理数，故此选项符合题意；3 =3，3是整数，属于有理数，不是无理数，故此选项不符合题意．D、√27故选：C．【点评】：此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，√6，0.8080080008…（每两个8之间依次多1个0）等形式．2.（单选题，4分）如果最简二次根式√3x−5与√x+3是同类二次根式，那么x的值是（）A.1B.2C.3D.4【正确答案】：D【解析】：根据同类项二次根式的定义可得3x-5=x+3，然后进行计算即可解答．【解答】：解：由题意得：3x-5=x+3，解得：x=4，故选：D．【点评】：本题考查了最简二次根式，同类项二次根式，熟练掌握同类项二次根式的定义是解题的关键．3.（单选题，4分）将抛物线y=2x2向右平移1个单位，再向上平移2个单位后，所得新抛物线和原抛物线相比，不变的是（）A.对称轴B.开口方向C.和y轴的交点D.顶点【正确答案】：B【解析】：抛物线平移后的形状不变，故a不变．【解答】：解：将抛物线y=2x2向右平移1个单位，再向上平移2个单位后，所得新抛物线和原抛物线相比，形状不变，故开口方向不变．故选：B．【点评】：本题考查的是二次函数的图象与几何变换，由于抛物线平移后的形状不变，故a不变．4.（单选题，4分）为了落实“作业、睡眠、手机、读物、体质”等五项管理要求，了解学生的睡眠状况，调查了一个班50名学生每天的睡眠时间，绘成睡眠时间频数分布直方图如图所示，那么所调查学生睡眠时间的众数，中位数分别为（）A.7小时，7小时B.8小时，7.5小时C.7小时，7.5小时D.8小时，8小时【正确答案】：C【解析】：根据直方图中的数据，可以直接写出众数，然后再观察直方图，可知第25个数据是7，第26个数据是8，从而可以计算出中位数．【解答】：解：由直方图可得，所调查学生睡眠时间的众数是7小时，中位数是（7+8）÷2=7.5（小时），故选：C．【点评】：本题考查频数分布直方图、中位数、众数，解答本题的关键是明确题意，利用数形结合的思想解答．5.（单选题，4分）下列命题是真命题的是（）A.对角线相等的四边形是平行四边形B.对角线互相平分且相等的四边形是矩形C.对角线互相垂直的四边形是菱形D.对角线互相垂直平分的四边形是正方形【正确答案】：B【解析】：根据平行四边形及特殊平行四边形的判定，逐个判断即可．【解答】：解：A、对角线互相平分的四边形是平行四边形，对角线相等的四边形也可能是等腰梯形等四边形，故A不符合题意；B、对角线互相平分的四边形是平行四边形，若对角线再相等，则四边形是矩形，故B符合题意；C、对角线互相垂直的四边形不能判定是平行四边形，也就不能判定是菱形，故C不符合题意；D、对角线互相垂直平分的四边形是菱形，不能判断它的内角有直角，故D不符合题意；故选：B．【点评】：本题考查平行四边形、特殊平行四边形的判定，解题的关键是掌握平行四边形、矩形、菱形、正方形的判定定理．6.（单选题，4分）Rt△ABC中，已知∠C=90°，BC=3，AC=4，以点A、B、C为圆心的圆分别记作圆A、圆B、圆C，这三个圆的半径长都是2，那么下列结论中，正确的是（）A.圆A与圆C相交B.圆B与圆C外切C.圆A与圆B外切D.圆A与圆B外离【正确答案】：D【解析】：根据已知条件画出图形即可得出三个圆的位置关系．【解答】：解：根据题意作图如下：∴圆A与圆C外切，圆A与圆C外离，圆B与圆C相交，故选：D．【点评】：本题主要考查圆与圆的位置关系，根据题意画出图象是解题的关键．7.（填空题，4分）计算：（-2mn3）2=___ ．【正确答案】：[1]4m2n6【解析】：根据幂的乘方与积的乘方法则，进行计算即可解答．【解答】：解：（-2mn3）2=4m2n6，故答案为：4m2n6．【点评】：本题考查了幂的乘方与积的乘方，熟练掌握幂的乘方与积的乘方运算法则是解题的关键．8.（填空题，4分）分解因式：xy3-9xy=___ ．【正确答案】：[1]xy（y+3）（y-3）【解析】：原式提取公因式，再利用平方差公式分解即可．【解答】：解：原式=xy（y2-9）=xy（y+3）（y-3），故答案为：xy（y+3）（y-3）【点评】：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．9.（填空题，4分）方程√3x−1 =2的根是___ ．【正确答案】：[1]x= 53【解析】：两边平方得出3x-1=4，求出即可．【解答】：解：∵ √3x−1 =2，∴3x-1=4，，∴x= 53是原方程组的解，经检验x= 53．故答案为：x=53【点评】：本题考查了解无理方程，能把无理方程转化成有理方程是解此题的关键．10.（填空题，4分）已知关于x的一元二次方程x2-mx-m+3=0有两个相等的实数根，那么m的值为 ___ ．【正确答案】：[1]2或-6【解析】：根据方程的系数结合根的判别式Δ=b2-4ac=0，即可得出关于m的一元二次方程，解之即可得出m的值．【解答】：解：∵关于x的一元二次方程x2-mx-m+3=0有两个相等的实数根，∴Δ=b2-4ac=（-m）2-4×1×（-m+3）=0，解得：m1=2，m2=-6，∴m的值为2或-6．故答案为：2或-6．【点评】：本题考查了根的判别式，牢记“当Δ=0时，方程有两个相等的实数根”是解题的关键．11.（填空题，4分）函数y=x的取值范围是 ___ ．√3x+1【正确答案】：[1]x＞- 13【解析】：根据二次根式的被开方数是非负数、分母不为0列出不等式，解不等式，得到答案．【解答】：解：由题意得：3x+1＞0，，解得：x＞- 13．故答案为：x＞- 13【点评】：本题考查的是函数自变量的取值范围的确定，掌握二次根式的被开方数是非负数、分母不为0是解题的关键．12.（填空题，4分）当0＜k＜1时，一次函数y=（k-1）x+k的图象不经过第 ___ 象限．【正确答案】：[1]三【解析】：根据一次函数的性质即可得到结论．【解答】：解：∵0＜k＜1，∴k-1＜0，∴一次函数y=（k-1）x+k的图象不经过第三象限．故答案为：三．【点评】：本题考查了一次函数y=kx+b（k≠0，k，b为常数）的性质．它的图象为一条直线，当k＞0，图象经过第一，三象限，y随x的增大而增大；当k＜0，图象经过第二，四象限，y 随x的增大而减小；当b＞0，图象与y轴的交点在x轴的上方；当b=0，图象过坐标原点；当b＜0，图象与y轴的交点在x轴的下方．13.（填空题，4分）一个不透明的袋子里装有3个红球和5个黑球，它们除颜色外其余都相同．从袋中任意摸出一个球是红球的概率为 ___ ．【正确答案】：[1] 38【解析】：先求出球的总个数，再根据概率公式即可得出摸出一个球是红球的概率．【解答】：解：∵一个不透明的袋子里装有3个红球和5个黑球，∴共有8个球，．∴从袋中任意摸出一个球是红球的概率为38．故答案为：38【点评】：本题考查了概率公式，用到的知识点为：概率=所求情况数与总情况数之比．14.（填空题，4分）《九章算术》是我国古代数学的经典著作，书中有一个问题：“今有黄金九枚，白银一十一枚，称之重适等，交易其一，金轻十三两，问金、银一枚各重几何？”意思是：甲袋中装有黄金9枚（每枚黄金重量相同），乙袋中装有白银11枚（每枚白银重量相同），称重两袋相同，两袋互相交换1枚后，甲袋比乙袋轻了13两（袋子重量忽略不计），问黄金、白银每枚各重多少两？设黄金每枚重x 两，白银每枚重y 两，根据题意可列方程组 ___【正确答案】：[1] {9x =11y (10y +x )−(8x +y )=13【解析】：根据题意可得等量关系： ① 9枚黄金的重量=11枚白银的重量； ② （10枚白银的重量+1枚黄金的重量）-（1枚白银的重量+8枚黄金的重量）=13两，根据等量关系列出方程即可．【解答】：解：设每枚黄金重x 两，每枚白银重y 两，由题意得： {9x =11y (10y +x )−(8x +y )=13，故答案为： {9x =11y (10y +x )−(8x +y )=13．【点评】：此题主要考查了由实际问题抽象从二元一次方程组的知识，关键是正确理解题意，找出题目中的等量关系．15.（填空题，4分）一个正多边形，它的一个内角等于一个外角的2倍，那么这个正多边形的边数是 ___ ．【正确答案】：[1]6【解析】：设正多边形的一个外角的度数为x°，根据正多边形的一个内角等于一个外角的2倍列方程可求解一个外角的度数，再利用多边形外角和为360°可求解．【解答】：解：设正多边形的一个外角的度数为x°，由题意得2x+x=180°，解得x=60，360°÷60°=6，所以这个正多边形的边数是6．故答案为6．【点评】：本题主要考查正多边形的性质，多边形的内角与外角，求解正多边形一个外角的度数是解题的关键．16.（填空题，4分）如图，在平行四边形ABCD 中，点E 是边CD 中点，联结AE 交对角线BD 于F ，设 AB ⃗⃗⃗⃗⃗ = a ， BC ⃗⃗⃗⃗⃗ = b ⃗ ，那么 BF ⃗⃗⃗⃗⃗ 可用 a 、 b⃗ 表示为 ___ ．【正确答案】：[1]- 23 a + 23 b ⃗ 【解析】：根据三角形法则求得 BD⃗⃗⃗⃗⃗⃗ ；利用平行四边形的性质和平行线分线段成比例求得BF= 23BD ，继而求得答案．【解答】：解：∵四边形ABCD 是平行四边形，∴AD=BC ，AD || BC ，∴ BC ⃗⃗⃗⃗⃗ = AD ⃗⃗⃗⃗⃗ = b⃗ ， ∴ BD ⃗⃗⃗⃗⃗⃗ = BA ⃗⃗⃗⃗⃗ + AD ⃗⃗⃗⃗⃗ =- a + b⃗ ， ∵在平行四边形ABCD 中，AB=CD ，AB || CD ，∴ DE AB = DF BF． ∵点E 是边CD 中点，∴ DE AB = DF BF = 12 ．∴ BF ⃗⃗⃗⃗⃗ = 23 BD ⃗⃗⃗⃗⃗⃗ =- 23 a + 23 b ⃗ ．故答案是：- 23 a + 23 b⃗ ．【点评】：本题考查平面向量，平行四边形的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．17.（填空题，4分）如图，⊙O 是Rt△ABC 的外接圆，OE⊥AB 交⊙O 于点E ，垂足为点D ，AE ，CB 的延长线交于点F ．如果OD=3，AB=8，那么FC 的长是 ___ ．【正确答案】：[1]10AB=4，【解析】：根据垂直定义可得∠ADO=90°，从而可得OD || BC，进而可得AD=DB= 12AE=EF，然后利用三角形的中位线定理可得CF=2OE，最后在Rt△ADO中，利用勾股定理求出OA的长，进行计算即可解答．【解答】：解：∵OE⊥AB，∴∠ADO=90°，∵∠ABC=90°，∴∠ABC=∠ADO=90°，∴OD || BC，∵OA=OC，AB=4，AE=EF，∴AD=DB= 12∴OE是△AFC的中位线，∴CF=2OE，在Rt△ADO中，AO= √AD2+OD2 = √42+32 =5，∴CF=2OE=10，故答案为：10．【点评】：本题考查了垂径定理，三角形的中位线定理，勾股定理，三角形的外接圆与外心，熟练掌握垂径定理，以及三角形的中位线定理是解题的关键．18.（填空题，4分）如果三角形一条边上的中线恰好等于这条边的长，那么我们称这个三角形为“匀称三角形”．在Rt△ABC中，∠C=90°，AC＞BC，若Rt△ABC是“匀称三角形”，那么BC：AC：AB=___ ．【正确答案】：[1] √3：2：√7【解析】：根据题意做出图形，设CD为x，根据“匀称三角形”的定义求出三角形的各边长即可得出结论．【解答】：解：根据题意作图如下：∵BD=AC=2CD，∴∠CBD=90°，设CD=x，则AC=2x，BC= √3 x，∴AB= √BC2+AC2 = √7 x，∴BC：AC：AB= √3：2：√7，故答案为：√3：2：√7．【点评】：本题主要考查勾股定理，三角形中线，特殊角三角函数等知识，正确理解“匀称三角形”的定义是解题的关键．19.（问答题，10分）计算：2-1+sin30°-√3+1-（√3 -1）0．【正确答案】：【解析】：根据负整数指数幂、特殊角的三角函数值、分母有理化和零指数幂可以解答本题．【解答】：解：2-1+sin30°-√3+1-（√3 -1）0= 12+12- √3−12-1= 1−√32．【点评】：本题考查二次根式的混合运算，熟练掌握运算法则是解答本题的关键．20.（问答题，10分）解方程组：{x+2y=2①x2−5xy+4y2=0②．【解析】：分解因式，将二元二次方程组化为二元一次方程组即可求解．【解答】：解：由 ② 得：（x-y ）（x-4y ）=0，∴x -4y=0或x-y=0，∴原方程组可以化为两个二元一次方程组： {x +2y =2x −4y =0 或 {x +2y =2x −y =0，解 {x +2y =2x −4y =0 ，得 {x =43y =13，解 {x +2y =2x −y =0 ，得 {x =23y =23 ， ∴原方程组的解是 {x =43y =13 或 {x =23y =23．【点评】：本题考查解二元二次方程组，解题的关键是将二元二次方程组降次，化为二元一次方程组．21.（问答题，10分）已知在平面直角坐标系xOy 中，正比例函数与反比例函数的图象交于点P （1，2），直线AB 垂直于x 轴，垂足为点C （点C 在原点的右侧），并分别与正比例函数和反比例函数的图象相交于点A 、B ，且AC+BC=5．（1）求正比例函数和反比例函数的解析式；（2）求△AOB 的面积．【解析】：（1）将点P坐标代入可确定正比例函数，反比例函数的关系式；（2）设点C的坐标，进而表示出AC、BC的长，根据AC+BC=5，求出点C的坐标，进而确定点A、B的坐标，由三角形的面积公式进行计算即可．【解答】：解：（1）设正比例函数解析式为y=k1x，反比例函数解析式为y= k2x，∵函数y=k1x和y= k2x的图象经过点P（1，2），解得k1=2，k2=2，∴正比例函数的表达式为y=2x，反比例函数的表达式为y=2x；（2）设点C（m，0），则A（m，2m），B（m，2m），∵AC+BC=5，∴ 2m+2m=5，解得m=2或m= 12，当m=2时，A（2，4），B（2，1），∴△AOB的面积为：12AB•OC= 12×3×2=3，当m= 12时，A（12，1），B（12，4），∴△AOB的面积为：12AB•OC= 12×3× 12= 34，∴△AOB的面积为：34或3．【点评】：本题考查反比例函数与一次函数的交点坐标，确定函数关系式，求出相应点的坐标以及三角形面积的计算方法是正确解答的前提．22.（问答题，10分）为解决群众“健身去哪儿”问题，某区2021年新建、改建90个市民益智健身苑点，图1是某益智健身苑点中的“侧摆器”．锻炼方法：面对器械，双手紧握扶手，双脚站立于踏板上，腰部发力带动下肢做左右摆式运动．（1）如图2是侧摆器的抽象图，已知摆臂OA的长度为80厘米，在侧摆运动过程中，点A为踏板中心在侧摆运动过程中的最低点位置，点B为踏板中心在侧摆运动过程中的最高点位置，∠BOA=25°，求踏板中心点在最高位置与最低位置时的高度差．（精确到0.1厘米）（sin25°≈0.423，cos25°≈0.906，tan25°≈0.466）（2）小杰在侧摆器上进行锻炼，原计划消耗400大卡的能量，由于小杰加快了运动频率，每小时能量消耗比原计划增加了100大卡，结果比原计划提早12分钟完成任务，求小杰原计划完成锻炼需多少小时？【正确答案】：【解析】：（1）过点B作BD⊥OA垂足为D，由题意得：OB=OA=80cm，然后在Rt△BOD中，利用锐角三角函数的定义求出OD的长，进行计算即可解答；（2）先设小杰原计划x小时完成锻炼，然后根据实际每小时的能量消耗-原计划每小时的能量消耗=100，列出方程进行计算即可解答．【解答】：解：（1）过点B作BD⊥OA垂足为D，由题意得：OB=OA=80cm，在Rt△BOD中，∠BOA=25°，∴OD=BO•cos25°≈80×0.906=72.48（cm），∴AD=OA-OD=80-72.48≈7.5（cm），∴踏板中心点在最高位置与最低位置时的高度差约为7.5厘米；（2）设小杰原计划x小时完成锻炼，由题意得：400x−15−400x=100，解得：x1=1，x2=−45，经检验：x1=1，x2=−45都是原方程的根，但x=−45不符合题意，舍去，答：小杰原计划锻炼1小时完成．【点评】：本题考查了解直角三角形的应用，分式方程的应用，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．23.（问答题，12分）已知：如图，在四边形ABCD中，∠ABC=∠BCD，点E在边BC上，且AE || CD，DE || AB，作CF || AD交线段AE于点F，连接BF．（1）求证：△ABF≌△EAD；（2）如果BE2=AB⋅EF，求证：∠ECF=∠BAE．【正确答案】：【解析】：（1）根据平行线的性质易证四边形AFCD是平行四边形，进一步根据SAS即可得证；（2）根据已知条件可证△EBF∽△EAB，可得∠FBE=∠BAE，根据平行四边形的性质以及全等三角形的性质可得∠FBE=∠ECF，即可得证．【解答】：证明：（1）∵AE || CD，∴∠AEB=∠DCE，∵DE || AB，∴∠ABE=∠DEC，∠BAF=∠AED，∵∠ABC=∠BCD，∴∠ABE=∠AEB，∠DCE=∠DEC，∴AB=AE，DE=DC，∵AF || CD，AD || CF，∴四边形AFCD是平行四边形，∴AF=CD，∴AF=DE，在△ABF和△EAD中，{AB=AE∠BAF=∠AED AF=DE，∴△ABF≌△EAD（SAS）；（2）∵BE2=AB⋅EF，AB=AE，∴ BE AE =EFBE，又∵∠AEB=∠BEF，∴△EBF∽△EAB，∴∠FBE=∠BAE，由（1）得△ABF≌△EAD，∴BF=AD，在平行四边形AFCD中，AD=CF，∴BF=CF，∴∠FBE=∠ECF，∴∠ECF=∠BAE．【点评】：本题考查了全等三角形的判定和性质，平行四边形的判定和性质，相似三角形的判定和性质，平行线的性质，本题综合性较强，属于中考常考题型．24.（问答题，12分）如图．在平面直角坐标系中，抛物线y=ax2+2x+c（a≠0）与x轴交于点A、B，与y轴交于点C，点A的坐标为（-1，0），对称轴为直线x=1．点M为线段OB上的一个动点，过点M作直线l平行于y轴交直线BC于点F，交抛物线y=ax2+2x+c（a≠0）于点E ．（1）求抛物线的解析式；（2）当以C 、E 、F 为顶点的三角形与△ABC 相似时，求线段EF 的长度；（3）如果将△ECF 沿直线CE 翻折，点F 恰好落在y 轴上点N 处，求点N 的坐标．【正确答案】：【解析】：（1）根据点A 的坐标和对称轴可得关于a 、c 的方程组，解方程组可得答案；（2）首先利用点B 、C 的坐标可得直线BC 的解析式为：y=-x+3，则∠MBF=∠FBM=∠CFE=45°，设F （m ，-m+3），则E （m ，-m 2+2m+3），表示出EF 和CF 的长度，再根据相似三角形的判定与性质，从而解决问题；（3）根据平行线的性质和翻折的性质可得CF=EF ，从而得出m 的方程，即可解决问题．【解答】：解：（1）由题意得： {0=a −2+c −22a=1 ，解得： {a =−1c =3，所以，所求的抛物线的解析式是：y=-x 2+2x+3；（2）由题意得：B （3，0），C （0，3），∴直线BC 的解析式为：y=-x+3，∴∠MBF=∠FBM=∠CFE=45°，设F （m ，-m+3），则E （m ，-m 2+2m+3），∴ EF =−m 2+2m +3−(−m +3)=−m 2+3m ，CF =√(0−m )2+(3+m −3)2=√2m ，当以C 、E 、F 为顶点的三角形与△ABC 相似时，① 若EFAB =CFCB，则−m2+3m4=√2m3√2，∴ m=53或m=0（舍去），∴ EF=−m2+3m=209，② 若CFAB =EFCB，则√2m4=23√2，∴ m=32或m=0（舍去），∴ EF=−m2+3m=94，∴EF= 209或94；（3）∵△CEN是由△CEF沿直线CE翻折而得，∴CN=CF，∠NCE=∠ECF，∵NC || EF，∴∠NCE=∠CEF，∴∠ECF=∠CEF，∴CF=EF，∵ −m2+3m=√2m，解得：m=3−√2，m=0（舍去），∴ ON=OC+CN=OC+CF=3+√2(3−√2)=3√2+1，所以，N的的坐标是(0，3√2+1)．【点评】：本题是二次函数综合题，主要考查了待定系数法求函数解析式，相似三角形的判定与性质，平行线的性质，翻折的性质，一元二次方程等知识，熟练掌握平行线与角平分线得出等腰三角形是解决问题（3）的关键．25.（问答题，14分）如图，在Rt△ABC中，∠C=90°，∠CAB=30°，AB=10．点E是线段AB 上一动点，点G在BC的延长线上，且CG=AE，联结EG，以线段EG为对角线作正方形EDGF，边ED交AC边于点M，线段EG交AC边于点N，边EF交BC边于点P．（1）求证：NG=2EN；（2）设AE=x，△AEN的面积为y，求y关于x的函数解析式，并写出x的定义域；（3）联结NP，当△EPN是直角三角形时，求AE的值．【正确答案】：【解析】：（1）过点E作EH || BC交AC于H，由直角三角形的性质证出EH=12CG，由相似三角形的性质得出ENNG =EHCG，则可得出结论；（2）由直角三角形的性质求出CH，NH，AN，由三角形面积公式可得出答案；（3）分两种情况：① 当∠PNE=90°时，② 当∠EPN=90°时，过E点作EQ⊥BC交BC边于Q 点，由全等三角形的性质及直角三角形的性质可得出答案．【解答】：（1）证明：过点E作EH || BC交AC于H，∴∠ACB=∠AHE，∵∠ACB=90°，∠CAB=30°，∴ EH=12AE，∵CG=AE，∴ EH=12CG，∵EH || BC，∴ EN NG =EHCG，∴NG=2EN；（2）由题意得：BC=5，AC=5√3，EH=12x，AH=√32x．∴CH=5 √3 - √32x，∴NH= 13 CH= 5√33−√36x，∴ AN=AH+HN=√32x+(5√33−√36x)=53√3+√33x，∴y= 12AN•EH= 12× 12x（53√3+√33x）= 512√3x+√312x2，定义域为：5√3−5≤x≤10；（3）① 当∠PNE=90°时，∵∠FEG=45°，∠ENP=90°，∴∠EPN=45°，∴EN=PN，∵∠EHN=∠PCN=90°，∴∠PNC+∠ENH=90°，∠ENH+∠NEH=90°，∴∠PNC=∠NEH，∴△PNC≌△NEH（AAS），∴EH=CN，即EH=23CH，∴ 1 2x=23(5√3−√32x)，解得x=40−20√3，∴AE=40-20 √3；② 当∠EPN=90°时，过E点作EQ⊥BC交BC边于Q点，∵AE=x，∠B=60°，∴BE=10-x，∴EQ=5 √3 - √32x，同① 可得△EQP≌△PCN（AAS），∴ EQ=CP=5√3−√32x，PQ=CN，∵EQ || CN，∴ CN EQ =NGEG=23，∴CN= 23EQ，∴ PQ=CN=23(5√3−√32x)，∵ BQ=5−13x，BC= 12AB=5，∴ 5√3−√32x+23(5√3−√32x)+5−12x=5，解得x=125−25√311．∴AE= 125−25√311，综上所述，AE的长为40-20 √3或125−25√311．【点评】：本题属于四边形综合题，考查了正方形的性质，相似三角形的判定和性质，解直角三角形等知识，解题的关键是学会用分类讨论的思想思考问题．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

设DQ＝a
则有：
但是
从数学老师的眼光看上述几种做法的弊端是为了做题而做题
没有教给学生进入的方法
让学生听完以后又一次陷入题海战术中
能不能找到一种学生在学习完这种题的解法后能在以后学习中举一反三
使得学生在能力上有所提高的办法呢？
初三的很多老师都知道一句话："在做后一小题感到困难的时候
应该去看看前一小题
以前都是看别个上传的文档，这次上传点文档与大家一起分享！
黄浦区2007年初三数学模拟考压轴题的分析
黄浦区光明初级中学刘颖颋
如图
在平面直角坐标系中
△ABC的顶点A在原点
边AC在x轴的正半轴
AC＝16
∠BAC＝
AB＝10
⊙P分别与边AB、AC相切与D、E（切点D、E不在边AB、AC的端点）
ED的延长线与CB的延长线相交于点F
（i）求BC的边长和△ABC的面积；
（ii）设AE＝x
DF＝y
写出y关于x的函数关系式
并写出自变量x的取值范围；
（iii）探索△ADC与△DBF能否相似？若能相似
请求出x的值
同时判断此时⊙P与边BC的位置关系
并证明之
若不能相似
请说明理由；
（iv）当⊙P与△ABC内切时
⊙P与边BC相切于G点
请写出切点D、E、G的坐标（不必写出计算过程）
空壳准备：
过B作AC边上的高BH
易知
求y关于x的函数关系式的解法1：
过C作CQ∥AB交FE的延长线于Q
所以可以推出点F的坐标为
把点F的坐标代入BC的解析式也可得出
求y关于x的函数关系式的解法3：（其实这个图形若能静下心来仔细观察
会发现它的背景是初三上学期我们特别强调的三角形中有两条交叉线的问题
当时我们是作平行线－在两个三角形中处理"横档"问题－等量代换）
过D作OC的平行线（其实过E作AB的平行线也是一样的）交FC于Q
因为它又可能是后一小题的铺垫"
但这里第一小题只是求三角形的面积
它会对我们起到什么帮助吗？
求y关于x的函数关系式的解法4：从
可知：
推导出：
求y关于x的函数关系式的解法5：其实做综合题还应该老老实实地在做完空壳准备后
画出所有的运动状态
观察其中极限状态下x的取值
考虑y是否存在
求出x的取值范围
∵△ADE是正三角形
∴△EQC也是பைடு நூலகம்三角形
即CQ＝EQ＝CE＝16－x
而DB＝10－x
故有：
（但是这种解法学生是不太会想到的）
求y关于x的函数关系式的解法2：（对初二一次函数比较熟悉的同学说不定会有这样的进入方法）
先根据B（5
）
C（16
0）计算出直线BC的解析式为：
而∠FEA＝
在第一种极限状态下求一下y的值
目的是为了给后面寻找解题方法的提示
在动圆还没有开始"动"的时候
我们求BF的方法是：
那么在求y关于x的函数关系式的时候我们也可以用这个办法：
在这里我只想抛砖引玉
我的一些方法有可能很不成熟
还望同行批评指正！
1