第三章投影变换——换面法
第3章变换投影面法
第3章 变换投影面法 我们知道，当空间的直线和平面对投影面处于一般位置时，它们的投影都不能直接反映真实大小、度量和定位关系，也不具有积聚性；但当它们和投影面处于特殊位置时，则它们的投影有的可直接真实地反映度量关系和定位关系或具有积聚性，如图３－１所示。
由此可知，若能把几何元素由一般位置改变成特殊位置，有些问题就容易解决，而变换投影面法就是解决这一问题常用的一种图解方法。
图３－１ 特殊位置几何元素的投影图直接反映真实大小和度量示例图３－２ V H 体系变换为V １H体系§３－１ 变换投影面法的基本概念 在两投影面体系中，空间几何元素的位置保持不动，用新的投影面来代替某一旧的投影面，保留原有的另一投影面，新投影面垂直于保留的投影面，使空间几何元素对新投影面的相对位置变成有利于解题的特殊位置，然后作出几何元素在新投影面上的投影。
在新投影面与保留的原有投影面组成的新的两投影面体系中解题，必要时还可将解题结果返回到原有的两投影面体系中去。
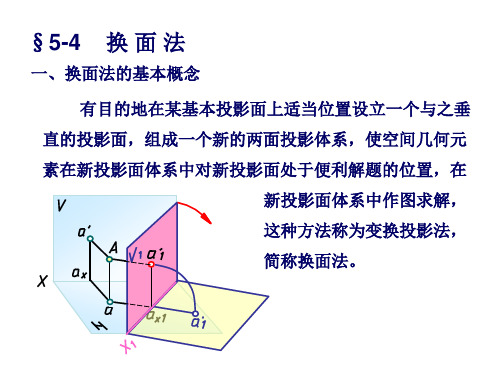
这种方法称为变换投影面法，简称换面法。
如图３－２所示，△ABC 平面为一铅垂面，该面在V 、H 两投影面体系即V H体系中的两个投影都不反映真形。
取一个平行于△ABC 且垂直于H 面的V １面来代替V 面，则新的V １面和保留的H 面相交成新的投影轴X １，构成一个新的两投影面体系即V １H 。
△ABC 平面在V １H 体系中V １面上的投影△a ′１b ′１c ′１就反映了△ABC 平面的真形。
再将V １面绕新投影轴X １旋转展开到与H 面成一个平面，从而得出V １H体系的投影图。
显然新投影面V １是不能任意选择的，首先要使空间几何元素在新的投影面上的投影能够有利于解题，并且新投影面V １和保留的H 面仍要构成一个由两个互相垂直的投影面组成的两投影面体系，这样才能应用前面所讲述的正投影原理作图。
因此，用换面法时，新投影面的选择必须符合下面两个基本条件： （１）新投影面必须垂直于保留的投影面，以构成新的两投影面体系。
第3章 变换投影面法
将一般位置平面变换为投影面垂直面的作图 步骤如下： 1.在空间平面内作一投影面平行线（下图 中作了一条水平线） 2.设置与投影面平行线成垂直的新投影 面（如下图中设置的V1面）
要注意理解新投影面垂直于空 间平面内的一条线，也就垂直于 空间平面。
例：将△ABC平面变换为投 影面垂直面。 作图步 骤如图 示：
点的二次变换的分析： 图中先变换的是V1面，接着作第二次变换。 此时的H1面与V1面垂直，被替换是H面，而 V1面为不变投影面。
O2X2为新的投影轴，O1X1则成了旧投影轴。
（点击图形演示动画）
例：作出A点的二次变换投影图。
作图分析：两次变换的规律是一样的， 要注意的是在作第二次变换时定准点的 新投影的位置。
求一般位置直线 的实长和一般位 置平面的实形的 方法有多种，这 一节介绍的是用 变换投影面的方 法求得实长和实 形。
3.1
变换投影面法的基本概念
正投影的“真实性”表明，当空间的 直线或平面与投影面成平行时，其投影能 够反映直线的实长和平面的实形。变换投 影面的基本方法是，设置新的投影面来代 替原来的某一投影面，并使新投影面与空 间几何元素处于有利于解题的特殊位置。 变换投影面法的应用1： 在V、H两投影面体系中，AB为一 般位置直线，其两面投影均不能反映实 长。
从下图可以看到，所设置的新投影面应符 合以下两点原则： 1.新投影面必须垂直于原投影面体系中的一 个投影面，并与它组成新的投影面体系。必 要时可作连续变换。 2.新投影面应处于有利于解题的位置。 关于换面法的术语解释： 1.旧投影面—指图中的V、H面 2.旧投影—指几何元素在V、H面上的投影
3.被替换的投影面—图中的新面V1与H面垂 直，替换了旧投影面V，因此V面为被替换 的投影面,V面上的投影称为被替换的投影 4.不变的投影面及不变投影—指图中的H面 以及几何要素在H面上的投影
换面法
解题步骤： 1.将两已知平行 直线构成的平面 经两次变换，变 变换，变成投影 面平行面 2.求作EF 的实长
实长
例: 平行四边形ABCD 给定一平面，试求点S 至该平面的距离 空间分析：
. 距离
解题步骤：
1.将平面ABCD 变换为新投 影面的垂直面 2.点S 随之变换 3.过S 作ABCD 的垂线,s1’k1’ 即为所求
解题步骤：
1.将直线EF 变换 为新投影面的 平行线 2.点A 随之变换 3.过a1’作e1’f1’的 垂线,得k1’ 4.将k1’a1’返回原 体系
例：试求某炼油厂的球罐A到输油管BC的最短净距离（5-9）
a2
b’
b’ c’
L
c2 (b2)
a’
X
b a
V O H
a’ c’ a1’ b a
b1 ’
保留投影面
保留投影
.
v1
新投影
作图步骤： 1)画X1 轴； 2)过a’ 作X1 轴的垂线； 3)在垂线上截取 新投影面
a1aX1 = aaX 。
2）点在V/H1体系中的投影 （用Ｈ1面代替Ｈ面，求点的新投影）
H1ห้องสมุดไป่ตู้
保留投影 新投影
旧投影
新投影面的设立原则：
１．新投影面必须设立在使空间元素处在有利于解题的位置 ． ２．新投影面必须垂直于原有投影面体系中的一个投影面．
∥
∥
∧
二、例题
例：求图中所示下料漏斗两相邻斗壁的夹角θ（例5-8）
(a’) f’ (d’)
(b’) (c’) e’
a b e f d
d1 a1 f1 c1 e1 b1 d’2 (c’2 ) θ a’2
换面法
换面法一、 换面法概述当直线或平面相对于投影面处于特殊位置（平行、垂直）时，它们的投影反映线段的实长、平面的实形及其与头面的倾角。
当直线或平面和投影面处于一般位置时，则它们的投影不具备上述特性。
换面法的目的，就在于将直线或平面从一般位置变换为和投影面平行或垂直的位置，以便于解决它们的度量和定位问题。
1．换面法的基本概念换面法就是保持空间几何元素不动，用一个新的投影面替换其中一个原来的投影面，使新投影面对于空间几何元素处于有利于解题的位置。
然后找出其在新投影面上的投影。
2．新投影面的选择原则（1）新投影面必须和空间的几何元素处于有利于解题的位置；（2）新投影面必须垂直于一个原有的投影面；（3）在新建立的投影体系中仍然采用正投影法。
二、 点的换面点是一切几何元素的基本元素。
因此在研究换面时，首先从点的投影变换来研究换面法的投影规律。
1．点的一次换面（1）换V 面图2-25（a ）表示点A 在原投影体系V/H 中，其投影为a 和a '现令H 面不动，用新投影面V 1来代替V 面，V 1面必须垂直于不动的H 面，这样便形成新的投影体系V 1/H ，O 1X 1是新投影轴。
过点A 向V 1面作垂线，得到V 1面上的新投影1a '，点1a '是新投影，点a '是旧投影，点a 是新、旧投影体系中的共有的不变投影。
a 和1a '是新的投影体系中的两个投影，将V 1面绕O 1X 1轴旋转到与H 面重合的位置时，就得到图2-25（b ）所示的投影图。
由于在（a）（b）（c）图2-25点的一次变换（换V面）新投影体系中，仍采用正投影方法，又在V/H投影体系和V1/H体系中，具有公共的H面，所以点a到H面的距离（Z坐标）在两个题词体系中是相等的。
所以有如下关系：1a'a⊥O1X1轴；1a'1xa=a'xa=A a，即：换V面时Z坐标不变。
由此得出点的投影变换规律是：①点的新投影和不便投影的连线，必垂直于新投影轴；②点的新投影到新投影轴（O1X1）的距离等于被替换的点的旧投影到旧投影轴（OX）的距离，也即换V面时高度坐标不变。
第三章投影变换换面法
c'
b'
XV
Hc a
a' e
a1'
b
e1´
b1'
c1'
3. 把一般位置平面变换成投影面垂直面
功用：可求解平面与投影面的倾角， 点与平面的距离， 两平行面间的距离等。
问题的关键：在平面上作一条投影面平行线，新 轴必须垂直与该平行线反映实长的那个投影。
3. 把一般位置平面变换成投影面垂直面
空间分析：
空间及投影分析：
作图:
求C点到直线AB的距离， c
b
就是求垂线CD的实长。
如下图：当直线AB 垂直于投影面时，CD平
XV H
行于投影面，其投影反映 c
a d
b
距离
实长。
AD
C
B
abd
P
c
ad
.
H X1 P1
a1 d. 1
b 1. a2b2d2
c 1
P1 P2
c 2
X2
过c1作线平行于x2轴。
m1n1⊥c1d1。
A
M CN
d1 ●
D B a1m1b1
a1≡b●1≡m1
.
●n1 c● 1
c1
P1
n1
d1
圆半径=MN
例6：求平面ABC和ABD的夹角。
空间及投影分析：
垂所时直求所在于。由得投该几两影投何交图影定线中面理之,，知间两它：的平们两夹面的面角的投角。交影为线积两垂聚平直成面于直同投线时影，与面直第时线三，间平则的面两夹垂平角直面为相交
四、解题时一般要注意下面几个问题：
⒈ 分析已给条件的空间情况，弄清原始条件中物体 与原投影面的相对位置，并把这些条件抽象成几 何元素（点、线、面等）。
第3章 投影变换---换面法
广东技术师范学院天河学院教案2012 年月日第周单元教案首页第三章投影变换——换面法第一节换面法的基本概念一、换面法的基本概念空间几何元素的位置保持不变，用新的投影面来代替旧的投影面，使空间几何元素对新的投影面的相对位置变成有利于解题的位置，然后找出其在新投影面上的投影。
这种方法称为换面法。
用换面解题时应遵循下列两原则:⒈选择新投影面时,应使几何元素处于有利于解题的位置；⒉新投影面必须垂直于原投影面体系中不被变换的投影面，并与它组成新投影面体系，必要时可连续变换。
(a) (b)图3.1 将一般位置直线变换成投影面平行线如图3.1,新投影面必须垂直于不变换的投影面，即V1⊥H，X1为新投影轴。
这时，不变换投影面上的投影a、b与V1面上的新投影a1＇、b1＇的投影连线a a1＇⊥X1、b b1＇⊥X1。
并且a1＇、b1＇到X1的距离等于被代替的投影a＇、b＇到被代替的投影轴的距离，即a1＇a X1＝a＇a X＝A a＝Z A, b1＇b X1＝b＇b X＝B b＝Z B。
第二节点的换面二、点的投影变换规律（一）点的一次变换点是一切几何形体的基本元素。
因此，必须首先掌握点的投影变换规律。
现在来研究更换正立投影面时，点的投影变换规律。
图3表示点A在V/H 体系中，正面投影为a′，水平投影为a。
现在令H面不变，取一铅垂面V1（V1⊥H）来代替正立投影面V，形成新投影面体系V1/H。
将点A向V1投影面投射，得到新投影面上的投影a′1。
这样，点A在新、旧两体系中的投影（a，a′1）和(a，a′)都为已知。
其中a′1为新投影，a′为旧投影，而a为新、旧体系中共有的不变投影。
它们之间有下列关系：1. 由于这两个体系具有公共的水平面H，因此点A到H面的距离（即z坐标），在新旧体系中都是相同的，即a′ax=Aa=a′1ax1。
2. 当V1面绕X1轴重合到H面时，根据点的投影规律可知aa′1必定垂直于X1轴。
这和aa′⊥X轴的性质是一样的。
第三章投影变换----换面法
b a
H X1 V1 a1′
b1′ a2 (b2)
V1 H2 X2
X1 // ab
X2 a b1
1
[例题]
求两直线AB与CD的公垂线 。
b 1 2
1 2 22 d2 c'1 2'1 1'1 d'1 c2
12 a 2b2
例
k'
求点K到直线AB之距。
b' l'
在什么情况下所 求其实长 如何确定 求线段的投影直 接反映其实长? 新投影轴的位置 AB P KL// P A 将AB//线 K L 将AB线 B 过点K作直线与 空间分析 投影分析 AB垂直相交并
V H
当两平面的 X a 交线AB垂直 d 于新投影面 d1′ c 1′ 时它们在该 投影面上的 a ′ 1 投影反映其 夹角 b1′
a2 (b2)
例 试完成矩形ABCD的两面投影，已知AB平行于 △EFG, B、C分别属于MN、AS。
a′
X V
d′ a
m
n′ b′ s′ c′ e′ m′ b e n
二、将一般位置线变换成投影面垂直线
X2 (a2)b2 V a' H2 A b' X a B a1 V1 b1
两次换面
Hb
将一般位置线 投影面平行线
X1 将投影面平行线 投影面垂直线
将一般位置线变换成投影面垂直线
作图
V X H a'
b'
将一般位置线 投影面平行线
将投影面平行线 投影面垂直线
解决此类问题，较简单的方法通常是 换面法
解决此类问题的方法通常是：分析、 确定解题方案及投影图上实现。 分析是十分重要的，首先根据给 出已知条件和求解要求，想出已知空 间几何模型，然后进行空间思维，想 象出最终结果的空间几何模型，再分 析确定从已知几何模型到最终结果几 何模型的空间解题步骤。
机械制图 第2版 第3章 换面法
第三章 换面法
一、点的一次换面 1.更换V面
V a'
V1 A a1'
a'
X
a
X
a
X1
H
H
换面规律:
X1 V1
a1'
1) 新投影和不变投影的连线垂直于新轴;
2)新投影到新轴的距离等于旧投影到旧轴的距离
2.更换H面
第三章 换面法
X1
V a'
A
a1 H1
X1 H1
a1
V
a'
X
a H
X
a
第三章 换面法
b'
c'
a' X
b
d'
O d
a
c
d'1
H V1 a'1
X1
b'1(c’1)
所求夹角
B
C b(c)
D
d A a
P
分析:
△ABC与△ABD的交线 AB→垂直线
第三章 换面法
本次作业共1页
第三章 换面法
本章学习目标：
熟悉换面法的基本原理，掌握用一次换面法求一般位置直线实长、 投影面垂直面实形&倾角的方法 。
主要内容：
支撑知识点
换面法的基本知识 点的一次换面 直线的一次换面 平面的一次换面
扩展知识点
1.换面法概念 2.换面原则 1.更换V面 2.更换H面 1.一般直线→新投影面平行线 2.投影面平行线→新投影面垂直线
投影面垂直面→新投影面平行面
第三章 换面法 换面法的基本知识
V b'
X
a'
A
a1' V1
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
以自学。
看书：P41~P47 作业：3－4、8、9、10、11、12
旋转法
3.3.1 问题的提 出 3.3.2 旋转法 的概念
3.3.3
绕垂直轴 旋转 3.3.4
3.3 旋转法
3.3.1 问题的提出
a’ o’
实形
O A
b’ c’
铅垂面ABC在V/H 投影面上均不反映 实形，如何求ABC 实形？
绕垂直轴 一次旋转 可解决四 种作图问 题
3.3.5
绕垂直轴 二次旋转
c1’
o’ C1
c1
B C
O
a
(b)
c
使ABC绕轴旋转 到与V面平行的位 置，则ABC1在V 面的投影反映实
形。
结束 返回
旋转法
3.3.1 问题的提 出 3.3.2 旋转法 的概念
3.3.3
绕垂直轴 旋转
3.3.4
绕垂直轴 一次旋转 可解决四 种作图问 题
四、解题时一般要注意下面几个问题：
⒈ 分析已给条件的空间情况，弄清原始条件中物体 与原投影面的相对位置，并把这些条件抽象成几 何元素（点、线、面等）。
⒉ 根据要求得到的结果，确定出有关几何元素对新 投影面应处于什么样的特殊位置（垂直或平行）， 据此选择正确的解题思路与方法。
⒊ 在具体作图过程中，要注意新投影与原投影在变 换前后的关系， 既要在新投影体系中正确无误地 求得结果，又能将结果返回到原投影体系中去。
d
b
a
a1 ●
●d1
X
V H
c a
●c1
●b1
θ
.
dc
.
b
a2≡ b2 ● θ ●d2
c2●
例7:求两交叉直线的公垂线.
四、换面法的应用
例1：求点C到直线AB的距离，并求垂足D。
空间及投影分析：
作图:
求C点到直线AB的距离， c
b
就是求垂线CD的实长。
如下图：当直线AB 垂直于投影面时，CD平
例：求直线AB的实长及与H面的夹角。
空间分析：用P1面代替V面，在P1/H投影体系中，AB//P1。
a
V
b
P1a1
A
b1
B
作图：
a
XV H
b b
a
Hb
换H面行吗？ 不行！
a
.
H
X1 P1
a●1
b●1
新投影轴的位置？
与ab平行。
2. 把一般位置直线变换成投影面垂直线
空间分析： 一次换面把直线变成投影面平行线；
返回
第一节 概述
特殊位置的直线：可直接反映实长、倾角问题
a
b
a(b)
X
OX
O
a
b 实长
实长
b
a
特殊位置的平面：可直接反映实形、倾角问题
c 实形
a
b
X
O
a
cb
正平面
c b
X
O
b
a
c 正垂面
特殊位置的几何元素：可直接反映度量、定位问题
a
c
b m c
e
f
b d
当一直线绕正垂轴旋转时， 其正面投影长度保持不变。直线 对V面的倾角不变。
旋转法
3.3.1 问题的提 出 3.3.2 旋转法 的概念
3.3.3
绕垂直轴 旋转
3.3.4
绕垂直轴 一次旋转 可解决四 种作图问 题
3.3.5 绕垂直轴 二次旋转
结束 返回
3、平面的旋转规律：
当一平面图形 绕铅垂轴旋转时， 其水平投影的大小 和形状保持不变， 该平面对H面的倾角 的大小不变。
二次换面把投影面平行线变成投影面垂直线。
V X
X2
a2b2 b P2
ax2
P1
a
b1
B A
a1
作图：
b
a
XV
H
b
a
b
H1
a
X1 P1a1●
●.
b1
a2b2
H
X1 X2轴的位置？
与a1 b1 垂直
例1 已知等腰三角
形ABC的底边 为AB，试用 换面法求出等 腰三角形ABC 的正面投影。
e
a(b)
f
c(d)
m b
a c
距离
a
点到直线的距离
一、基本概念
改变空间几何元素与投影面的相对位 置，使它们相互之间处于某一特殊位置的 情况，从而使问题简化、得到解决——投 影变换。
二、投影变换的方法 1. 辅助投影面法（换面法） 2. 旋转法
一. 换面法的基本概念
旧面
新面 c1'
V1
c1 ' b1'
作图分析：由于△ABC平面为一 铅垂面 ，则O1X1轴应平行于平面的 积聚性投影。
作 图 过 程 如 图 所 示：
例 3 已知直线AB与CDE平面平行，且相距20mm，
求直线AB的 水平投影。
b1 a1
c1
c'
e1 d1
a'
e' XHV d' c
b'
e
da b
例4：求点C到直线AB的距离，并求垂足D。
新轴 a1'
b1'
旧轴a1'
不变面
X1
X1
V/H 体系变为V1/H 体系
换面法—空间几何元素的位置保持不动，用新的投影面 来代替旧的投影面，使对新投影面的相对位置变成有利 解题的位置，然后找出其在新投影面上的投影。
返回
二、点的换面及规律
1. 点的一次变换
V1
a1 '
X1
返回
2. 点的两次变换
a2
3.3.4
绕垂直轴 一次旋转 可解决四 种作图问 题
3.3.5 绕垂直轴 二次旋转
结束 返回
2、直线的旋转规律：
R
0
0
R
直线绕某轴旋转一角度时， 只要使该直线上的两个点绕同一 轴，沿相同方向，旋转同一角度， 然后把旋转后的两个点连接起来， 即为该直线的新投影。
当一直线绕铅垂轴旋转时， 其水平投影长度保持不变。直线 对H面的倾角不变。
c'
b'
XV
Hc a
a' e
a1'
b
e1´b1'c Nhomakorabea'
3. 把一般位置平面变换成投影面垂直面
功用：可求解平面与投影面的倾角， 点与平面的距离， 两平行面间的距离等。
问题的关键：在平面上作一条投影面平行线，新 轴必须垂直与该平行线反映实长的那个投影。
3. 把一般位置平面变换成投影面垂直面
空间分析：
第三章 投影变换——换面法
一、投影变换及换面法的基本概念 二、点的换面作图规则 三、换面法的四个基本作图 四、应用及举例
返回
求解距离、夹角、实形、交点的最佳投影分析
b’ a’
a
b
两点之间距离
c’ b’
a’
a
c
b
三角形实形
c’ a’
d’ dc a
两平面夹角
c’
d’ b’ a’
b’
a
cd
b
b
直线 与平面的交点
m1n1⊥c1d1。
A
M CN
d1 ●
D B a1m1b1
a1≡b●1≡m1
.
●n1 c● 1
c1
P1
n1
d1
圆半径=MN
例6：求平面ABC和ABD的夹角。
空间及投影分析：
垂所时直求所在于。由得投该几两影投何交图影定线中面理之,，知间两它：的平们两夹面的面角的投角。交影为线积两垂聚平直成面于直同投线时影，与面直第时线三，间平则的面两夹垂平角直面为相交
V1 H2 c2
22
12
d2
a2b2
21' d1'
11'
返回
例3: 过C点作直线CD与AB相交成60º角。
空间及投影分析：AB与CD都平行于投影面时，其投影
的夹角才反映实大（60°），因此需将AB与C点所确定的 平面变换成投影面平行面。
作 图： c●
几个解？
a
d b
两个解！
●a2
X
V H
a
3.3.3
绕垂直轴 旋转
3.3.4
绕垂直轴 一次旋转 可解决四 种作图问 题
3.3.5 绕垂直轴 二次旋转
结束 返回
3.3.3 绕垂直轴旋转
1、点的旋转规律：点A绕铅垂轴旋转；
a’
a1’ a o a1
o’
a’
a1’
a
o
a1
旋转法
3.3.1 问题的提 出 3.3.2 旋转法 的概念
3.3.3
绕垂直轴 旋转
XV H
行于投影面，其投影反映 c
a d
b
距离
实长。
AD
C
B
abd
P
c
ad
.
H X1 V1
a1' d. 1'
b1'. a2b2d2
如何确定d1 点的位置？
c1'
V1 H2
c 2
X2
过c1作线平行于x2轴。
例2. 求两直线AB与CD的公垂线 。
b' 1'
2'
1 2 c1'
X2
1、将一般位置直线旋转成投影面平行线；
(a)旋转成正平线 选铅垂线为旋转轴