中考数学难点探究专题复习抛物线与几何图形的综合(选做)
2024年中考数学一轮复习考点精析及真题精讲—抛物线与几何综合

2024年中考数学一轮复习考点精析及真题精讲—抛物线与几何综合二次函数是非常重要的函数,年年都会考查,总分值为18~20分,预计2024年各地中考还会考,它经常以一个压轴题独立出现,有的地区也会考察二次函数的应用题,小题的考察主要是二次函数的图象和性质及或与几何图形结合来考查.→➊考点精析←1、函数存在性问题解决二次函数存在点问题,一般先假设该点存在,根据该点所在的直线或抛物线的表达式,设出该点的坐标;然后用该点的坐标表示出与该点有关的线段长或其他点的坐标等;最后结合题干中其他条件列出等式,求出该点的坐标,然后判别该点坐标是否符合题意,若符合题意,则该点存在,否则该点不存在.2、函数动点问题(1)函数压轴题主要分为两大类:一是动点函数图象问题;二是与动点、存在点、相似等有关的二次函数综合题.(2)解答动点函数图象问题,要把问题拆分,分清动点在不同位置运动或不同时间段运动时对应的函数表达式,进而确定函数图象;解答二次函数综合题,要把大题拆分,做到大题小做,逐步分析求解,最后汇总成最终答案.(3)解决二次函数动点问题,首先要明确动点在哪条直线或抛物线上运动,运动速度是多少,结合直线或抛物线的表达式设出动点的坐标或表示出与动点有关的线段长度,最后结合题干中与动点有关的条件进行计算.→➋真题精讲←考向一抛物线与三角形有关问题1.(2023·浙江金华·统考中考真题)如图,直线y x =x 轴,y 轴分别交于点,A B ,抛物线的顶点P 在直线AB 上,与x 轴的交点为,C D ,其中点C 的坐标为()2,0.直线BC 与直线PD 相交于点E .(1)如图2,若抛物线经过原点O .①求该抛物线的函数表达式;②求BE EC的值.(2)连接,PC CPE ∠与BAO ∠能否相等?若能,求符合条件的点P 的横坐标;若不能,试说明理由.【答案】(1)①2y x =+;②13;(2)能,6或23或67-或143-.【分析】(1)①先求顶点的坐标,然后待定系数法求解析式即可求解;②过点E 作EH OC ⊥于点H .设直线BC 为y kx =+()2,0C 代入,得02k =+解得2k =-,直线BC 为y x =+OP 为2y x =.联立两直线解析式得出12E ⎛ ⎝⎭,根据EH BO ∥,由平行线分线段成比例即可求解;(2)设点P 的坐标为2t t ⎛ ⎝,则点D 的坐标为()22,0t -.①如图2-1,当2t >时,存在CPE BAO ∠=∠.记,CPE BAO APC αβ∠=∠=∠=,则APD αβ∠=+.过点P 作PF x⊥轴于点F ,则2AF t =+.在Rt APF 中,2cos 3AF BAO AP ∠==,进而得出点P 的横坐标为6.②如图2-2,当02t <≤时,存在CPE BAO ∠=∠.记,CPE BAD APD αβ∠=∠=∠=.过点P 作PF x ⊥轴于点F ,则2AF t =+.在Rt APF 中,2cos 3AF BAO AP ∠==,得出点P 的横坐标为23.③如图23-,当20t -<≤时,存在CPE BAO ∠=∠.记BAO α∠=.过点P 作PF x ⊥轴于点F ,则2AF t =+.在Rt APF 中,2cos 3AF BAO AP =∠=,得出点P 的横坐标为67-.④如图2-4,当2t ≤-时,存在CPE BAO ∠=∠.记BAO α∠=.过点P 作PF x ⊥轴于点F ,则2AF t =--.在Rt APF 中,2cos 3AF PAF AP =∠=,得出点P 的横坐标为143-.【详解】(1)解:①∵2OC =,∴顶点P 的横坐标为1.∴当1x =时,y =+=∴点P 的坐标是1,2⎛ ⎝⎭.设抛物线的函数表达式为2(1)y a x =-+,把()0,0代入,得0a =解得2a =-.∴该抛物线的函数表达式为21)y x =-,即2y x =+.②如图1,过点E 作EH OC ⊥于点H .设直线BC 为y kx =,把()2,0C 代入,得02k =+,解得2k =-,∴直线BC为y =同理,直线OP为y x =.由2.y x y x ⎧=⎪⎪⎨⎪=⎪⎩解得1,2x y ⎧=⎪⎪⎨⎪=⎪⎩∴12E ⎛ ⎝⎭.∴113,2222OH HC ==-=.∵EH BO ∥,∴13BE OH EC HC ==.(2)设点P的坐标为2t t ⎛ ⎝,则点D 的坐标为()22,0t -.①如图21-,当2t >时,存在CPE BAO ∠=∠.记,CPE BAO APC αβ∠=∠=∠=,则APD αβ∠=+.∵PCD ∠为PAC △的外角,∴PCD αβ∠=+.∵PC PD =.∴PDC PCD αβ∠=∠=+.∴APD ADP ∠=∠.∴2AP AD t ==.过点P 作PF x ⊥轴于点F ,则2AF t =+.在Rt APF 中,2cos 3AF BAO AP ∠==,∴2223t t +=,解得6t =.∴点P 的横坐标为6.②如图2-2,当02t <≤时,存在CPE BAO ∠=∠.记,CPE BAD APD αβ∠=∠=∠=.∵PDC ∠为PAD 的外角,∴PDC αβ∠=+.∴PCD PDC αβ∠=∠=+∴APC ACP ∠=∠.∴4AP AC ==.过点P 作PF x ⊥轴于点F ,则2AF t =+.在Rt APF 中,2cos 3AF BAO AP ∠==,∴2243t +=,解得23t =.∴点P 的横坐标为23.③如图2-3,当20t -<≤时,存在CPE BAO ∠=∠.记BAO α∠=.∵PC PD =,∴1122PDC PCD CPE α∠=∠=∠=.∴1122APD BAO PDC αα∠=∠-∠=-=.∴APD PDA ∠=∠.∴2AD AP t ==-.过点P 作PF x ⊥轴于点F ,则2AF t =+.在Rt APF 中,2cos 3AF BAO AP =∠=,∴2223t t +=-,解得67t =-.∴点P 的横坐标为67-.④如图2-4,当2t ≤-时,存在CPE BAO ∠=∠.记BAO α∠=.∵PC PD =,∴1122PCD PDC CPE α∠=∠=∠=.∴1122APC BAO PCD ααα∠=∠-∠=-=.∴4PA CA ==.过点P 作PF x ⊥轴于点F ,则2AF t =--.在Rt APF 中,2cos 3AF PAF AP =∠=,∴2243t --=,解得143t =-.∴点P 的横坐标为143-.综上,点P 的横坐标为26146,,,373--.【点睛】本题考查了二次函数综合运用,解直角三角形,平行线分线段成比例,熟练掌握以上知识,分类讨论是解题的关键.2.(2023·内蒙古通辽·统考中考真题)在平面直角坐标系中,已知抛物线()2803y ax x c a =++≠与x 轴交于点()1,0A 和点B ,与y 轴交于点()0,4C -.(1)求这条抛物线的函数解析式;(2)P 是抛物线上一动点(不与点A ,B ,C 重合),作PD x ⊥轴,垂足为D ,连接PC .①如图,若点P 在第三象限,且tan 2CPD ∠=,求点P 的坐标;②直线PD 交直线BC 于点E ,当点E 关于直线PC 的对称点E '落在y 轴上时,请直接写出四边形PECE '的周长.【答案】(1)248433y x x =+-;(2)①1377,816P ⎛⎫-- ⎪⎝⎭②354或854【分析】(1)将A ,C 两点坐标代入抛物线的解析式,从而求得a ,c ,进而求得结果;(2)①设248,433P x x x ⎛⎫+- ⎪⎝⎭,过点C 作CE PD ⊥于点E ,求出,PE CE ,根据tan 2CE CPD PE∠==列出方程求出x 的值即可;②可推出四边形'PECE 是菱形,从而得出PE CE =,分别表示出PE 和CE ,从而列出方程,进一步求得结果.【详解】(1)∵抛物线()2803y ax x c a =++≠与x 轴交于点()1,0A ,与y 轴交于点()0,4C -,∴把()1,0A ,()0,4C -代入()2803y ax x c a =++≠得,8034a c c ⎧++=⎪⎨⎪=-⎩,解得,434a c ⎧=⎪⎨⎪=-⎩,∴抛物线的函数解析式为248433y x x =+-;(2)①设248,433P x x x ⎛⎫+- ⎪⎝⎭,过点C 作CE PD ⊥于点E,如图,∴90,PEC CED ∠=∠=︒∵()0,4,C -∴4,OC =∵PD x ⊥轴,∴90,PDO ∠=︒又90,DOC ∠=︒∴四边形DOCE 是矩形,∴4,DE OC DO CE x ====-,∴22484844,3333PE PD DE x x x x ⎛⎫=-=-+--=-- ⎪⎝⎭∵tan 2,CE CPD PE∠==∴22,4833x x x -=--∴1213,08x x =-=(不合题意,舍去)∴248774,3316x x +-=-∴1377,816P ⎛⎫-- ⎪⎝⎭;②设248,433P m m m ⎛⎫+- ⎪⎝⎭,对于248433y x x =+-,当0y =时,2484=033x x +-,解得,121,3,x x ==-∴()3,0,B -∵4,OC =由勾股定理得,5;BC =当点P 在第三象限时,如图,过点E 作EF y ⊥轴于点F ,则四边形DEFO 是矩形,EF DO m ∴==-,∵点E 与点E '关于PC 对称,∴,,ECP E CP CE CE ''∠=∠=∵PE y ∥轴,∴,EPC PCE '∠=∠∴,EPC ECP ∠=∠∴,PE CE =∴,PE CE '=∴四边形PECE '是平行四边形,∴四边形PECE '是菱形,∵,EF OA ∥∴,CEF CBO ∴,CE EF BC BO =∴,53CE m -=∴5,3CE m =-设直线BC 的解析式为y kx b =+,把()()3,0,0,4B C --代入得,304k b b -+=⎧⎨=-⎩,解得,434k b ⎧=-⎪⎨⎪=-⎩,∴直线BC 的解析式为443y x =--,∴4,43E m m ⎛⎫-- ⎪⎝⎭,∴224844124433333PE m m m m ⎛⎫⎛⎫=-+-+--=-- ⎪ ⎪⎝⎭⎝⎭,又5,3CE m =-且,PE CE =∴24125,333m m m --=-解得,127,04m m =-=(舍去)∴5735,4416CE ⎛⎫=-⨯-= ⎪⎝⎭∴四边形PECE '的周长353544164C CE ==⨯=;当点P 在第二象限时,如图,同理可得:24125+,333m m m =-解得,1217,04m m =-=(舍去)∴51785,4416CE ⎛⎫=-⨯-= ⎪⎝⎭∴四边形PECE '的周长858544164C CE ==⨯=;综上,四边形PECE '的周长为354或854.【点睛】本题考查了求一次函数和二次函数的解析式,等腰三角形的判定和性质,相似三角形的判定和性质,菱形的判定和性质,轴对称性质等知识,解决问题的关键是正确分类,作辅助线,表示出线段的数量.3.(2023·重庆·统考中考真题)如图,在平面直角坐标系中,抛物线214y x bx c =++与x 轴交于点A ,B ,与y 轴交于点C ,其中()3,0B ,()0,3C -.(1)求该抛物线的表达式;(2)点P 是直线AC 下方抛物线上一动点,过点P 作PD AC ⊥于点D ,求PD 的最大值及此时点P 的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点E 为点P 的对应点,平移后的抛物线与y 轴交于点F ,Q 为平移后的抛物线的对称轴上任意一点.写出所有使得以QF 为腰的QEF △是等腰三角形的点Q 的坐标,并把求其中一个点Q 的坐标的过程写出来.【答案】(1)211344y x x =+-;(2)PD 取得最大值为45,52,2P ⎛⎫-- ⎪⎝⎭;(3)Q 点的坐标为9,12⎛⎫- ⎪⎝⎭或9,52⎛⎫ ⎪⎝⎭或97,24⎛⎫ ⎪⎝⎭【分析】(1)待定系数法求二次函数解析式即可求解;(2)直线AC 的解析式为334y x =--,过点P 作PE x ⊥轴于点E ,交AC 于点Q ,设211,344P t t t ⎛⎫+- ⎪⎝⎭,则3,34Q t t ⎛⎫-- ⎪⎝⎭,则45PD PQ =,进而根据二次函数的性质即可求解;(3)根据平移的性质得出219494216y x ⎛⎫=-- ⎪⎝⎭,对称轴为直线92x =,点52,2P ⎛⎫-- ⎪⎝⎭向右平移5个单位得到53,2E ⎛⎫- ⎪⎝⎭,()0,2F ,勾股定理分别表示出222,,EF QE QF ,进而分类讨论即可求解.【详解】(1)解:将点()3,0B ,()0,3C -.代入214y x bx c =++得,2133043b c c ⎧⨯++=⎪⎨⎪=-⎩解得:143b c ⎧=⎪⎨⎪=-⎩,∴抛物线解析式为:211344y x x =+-,(2)∵211344y x x =+-与x 轴交于点A ,B ,当0y =时,2113044x x +-=解得:124,3x x =-=,∴()4,0A -,∵()0,3C -.设直线AC 的解析式为3y kx =-,∴430k --=解得:34k =-∴直线AC 的解析式为334y x =--,如图所示,过点P 作PE x ⊥轴于点E ,交AC 于点Q ,设211,344P t t t ⎛⎫+- ⎪⎝⎭,则3,34Q t t ⎛⎫-- ⎪⎝⎭,∴223111334444PQ t t t t t ⎛⎫=---+-=-- ⎪⎝⎭,∵AQE PQD ∠=∠,90AEQ QDP ∠=∠=︒,∴OAC QPD ∠=∠,∵4,3OA OC ==,∴5AC =,∴4cos cos =5PD AO QPD OAC PQ AC ∠==∠=,∴()222441141425545555PD PQ t t t t t ⎛⎫==--=--=-++ ⎪⎝⎭,∴当2t =-时,PD 取得最大值为45,()()2211115322344442t t +-=⨯-+⨯--=-,∴52,2P ⎛⎫-- ⎪⎝⎭;(3)∵抛物线211344y x x =+-211494216x ⎛⎫=+- ⎪⎝⎭将该抛物线向右平移5个单位,得到219494216y x ⎛⎫=-- ⎪⎝⎭,对称轴为直线92x =,点52,2P ⎛⎫-- ⎪⎝⎭向右平移5个单位得到53,2E ⎛⎫- ⎪⎝⎭∵平移后的抛物线与y 轴交于点F ,令0x =,则2194924216y ⎛⎫=⨯-= ⎪⎝⎭,∴()0,2F ,∴22251173224EF ⎛⎫=++= ⎪⎝⎭∵Q 为平移后的抛物线的对称轴上任意一点.则Q 点的横坐标为92,设9,2Q m ⎛⎫ ⎪⎝⎭,∴22295322QE m ⎛⎫⎛⎫=-++ ⎪ ⎪⎝⎭⎝⎭,()222922QF m ⎛⎫=+- ⎪⎝⎭,当QF EF =时,()22922m ⎛⎫+- ⎪⎝⎭=1174,解得:1m =-或5m =,当QE QF =时,2295322m ⎛⎫⎛⎫-++ ⎪ ⎝⎭⎝⎭=()22922m ⎛⎫+- ⎪⎝⎭,解得:74m =综上所述,Q 点的坐标为9,12⎛⎫- ⎪⎝⎭或9,52⎛⎫ ⎪⎝⎭或97,24⎛⎫ ⎪⎝⎭.【点睛】本题考查了二次函数综合问题,解直角三角形,待定系数法求解析式,二次函数的平移,线段周长问题,特殊三角形问题,熟练掌握二次函数的性质是解题的关键.4.(2023·湖北随州·统考中考真题)如图1,平面直角坐标系xOy 中,抛物线2y ax bx c =++过点(1,0)A -,(2,0)B 和(0,2)C ,连接BC ,点(,)P m n (0)m >为抛物线上一动点,过点P 作PN x ⊥轴交直线BC 于点M ,交x 轴于点N .(1)直接写出....抛物线和直线BC 的解析式;(2)如图2,连接OM ,当OCM 为等腰三角形时,求m 的值;(3)当P 点在运动过程中,在y 轴上是否存在点Q ,使得以O ,P ,Q 为顶点的三角形与以B ,C ,N 为顶点的三角形相似(其中点P 与点C 相对应),若存在,直接写出....点P 和点Q 的坐标;若不存在,请说明理由.【答案】(1)抛物线:22y x x =-++;直线BC :2y x =-+;(2)1m =或m =2m =;(3)P ,1)Q -或(11P --,(0,1)Q 或(13P +--,(0,2)Q -【分析】(1)由题得抛物线的解析式为(1)(2)y a x x =+-,将点(0,2)C 代入求a ,进而得抛物线的解析式;设直线BC 的解析式为y kx t =+,将点B ,C 的坐标代入求k ,t ,进而得直线BC 的解析式.(2)由题得(,2)M m m -+,分别求出OC ,OM ,CM ,对等腰OCM 中相等的边进行分类讨论,进而列方程求解;(3)对点P 在点B 左侧或右侧进行分类讨论,设法表示出各线段的长度,利用相似三角形的相似比求解m ,进而可得P ,Q 的坐标.【详解】(1)解: 抛物线过点(1,0)A -,(2,0)B ,∴抛物线的表达式为(1)(2)y a x x =+-,将点(0,2)C 代入上式,得22a =-,∴1a =-.∴抛物线的表达式为(1)(2)y x x =-+-,即22y x x =-++.设直线BC 的表达式为y kx t =+,将点(2,0)B ,(0,2)C 代入上式,得022k t t =+⎧⎨=⎩,解得12k t =-⎧⎨=⎩.∴直线BC 的表达式为2y x =-+.(2)解: 点M 在直线BC 上,且(,)P m n ,∴点M 的坐标为(,2)m m -+.∴2OC =,2222(0)(22)2CM m m m =-+-+-=,()22222244OM m m m m =+-+=-+.当OCM 为等腰三角形时,①若CM OM =,则22CM OM =,即222244m m m =-+,解得1m =.②若CM OC =,则22CM OC =,即224m =,解得m =m =(舍去).③若OM OC =,则22OM OC =,即22444m m -+=,解得0m =(舍去)或2m =.综上,1m =或m 2m =.(3)解: 点P 与点C 相对应,∴POQ CBN ∽或POQ CNB ∽.①若点P 在点B 左侧,则45CBN ∠=︒,2BN m =-,CB =当POQ CBN ∽,即45POQ ∠=︒时,直线OP 的表达式为y x =,∴22m m m -++=,解得m m =.∴2224OP =+=,即2OP =.∴OP OQBC BN ==解得1OQ =-.∴P ,1)Q .当POQ CNB ∽,即45PQO ∠=︒时,PQ =,22222OQ m m m m m =-+++=-++,∴PQ OQCB NB =2222m m m -++=-,解得1m =1m =-.②若点P 在点B 右侧,则135CBN ∠=︒,2BN m =-.当POQ CBN ∽,即135POQ ∠=︒时,直线OP 的表达式为y x =-,∴22m m m -++=-,解得1m =1m =,∴OP∴OP OQBC BN ==,解得1OQ =.∴(11P --,(0,1)Q.当POQ CNB ∽,即135PQO ∠=︒时,PQ =,22222OQ m m m m m =-+++=--.∴PQ OQCB NB =2222m m m --=-,解得1m =1m =-.∴(13P --,(0,2)Q -.综上,P ,1)Q 或(11P +--,(0,1)Q 或(13P --,(0,2)Q -.【点睛】本题是二次函数的综合应用,考查了待定系数法求函数解析式,等腰三角形的性质与判定,平面直角坐标系中两点距离的算法,相似三角形的性质与判定等,熟练掌握相关知识是解题的关键.考向二抛物线与线段有关问题5.(2023·甘肃武威·统考中考真题)如图1,抛物线2y x bx =-+与x 轴交于点A ,与直线y x =-交于点()4,4B -,点()0,4C -在y 轴上.点P 从点B 出发,沿线段BO 方向匀速运动,运动到点O 时停止.(1)求抛物线2y x bx =-+的表达式;(2)当22BP =时,请在图1中过点P 作PD OA ⊥交抛物线于点D ,连接PC ,OD ,判断四边形OCPD 的形状,并说明理由.(3)如图2,点P 从点B 开始运动时,点Q 从点O 同时出发,以与点P 相同的速度沿x 轴正方向匀速运动,点P 停止运动时点Q 也停止运动.连接BQ ,PC ,求CP BQ +的最小值.【答案】(1)23y x x =-+;(2)四边形OCPD 是平行四边形,理由见解析;(3)3【分析】(1)用待定系数法求二次函数解析式即可;(2)作PD OA ⊥交抛物线于点D ,垂足为H ,连接PC ,OD ,由点P 在y x =-上,可知OH PH =,45POH ∠=︒,连接BC ,得出42OB =则2222222OH PH ===⨯,当2D x =时,4322D DH y ==-+⨯=,进而得出PD OC =,然后证明PD OC ∥,即可得出结论;(3)由题意得,BP OQ =,连接BC .在OA 上方作OMQ ,使得45MOQ ∠=︒,OM BC =,证明()SAS CBP MOQ △≌△,根据CP BQ MQ BQ MB +=+≥得出CP BQ +的最小值为MB ,利用勾股定理求得MB ,即可得解.【详解】(1)解:∵抛物线2y x bx =-+过点()4,4B -,∴1644b -+=-,∴3b =,∴23y x x =-+;(2)四边形OCPD 是平行四边形.理由:如图1,作PD OA ⊥交抛物线于点D ,垂足为H ,连接PC ,OD .∵点P 在y x =-上,∴OH PH =,45POH ∠=︒,连接BC ,∵4OC BC ==,∴OB =∵BP =,∴OP OB BP =-=∴222OH PH ===⨯,当2D x =时,4322D DH y ==-+⨯=,∴224PD DH PH =+=+=,∵()0,4C -,∴4OC =,∴PD OC =,∵OC x ⊥轴,PD x ⊥轴,∴PD OC ∥,∴四边形OCPD 是平行四边形;(3)如图2,由题意得,BP OQ =,连接BC .在OA 上方作OMQ ,使得45MOQ ∠=︒,OM BC =,∵4OC BC ==,BC OC ⊥,∴45CBP ∠=︒,∴CBP MOQ ∠=∠,∵BP OQ =,CBP MOQ ∠=∠,BC OM =,∴()SAS CBP MOQ △≌△,∴CP MQ =,∴CP BQ MQ BQ MB +=+≥(当M ,Q ,B 三点共线时最短),∴CP BQ +的最小值为MB ,∵454590MOB MOQ BOQ ∠=∠+∠=︒+︒=︒,∴MB =即CP BQ +的最小值为【点睛】本题考查了二次函数的综合应用,待定系数法,平行四边形的性质与判定,勾股定理,全等三角形的判定和性质等知识,熟练掌握二次函数的图象和性质是解题的关键.6.(2023·四川乐山·统考中考真题)已知()()1122,,,x y x y 是抛物211:4C y x bx =-+(b 为常数)上的两点,当120x x +=时,总有12y y =(1)求b 的值;(2)将抛物线1C 平移后得到抛物线221:()1(0)4C y x m m =--+>.探究下列问题:①若抛物线1C 与抛物线2C 有一个交点,求m 的取值范围;②设抛物线2C 与x 轴交于A ,B 两点,与y 轴交于点C ,抛物线2C 的顶点为点E ,ABC 外接圆的圆心为点F,如果对抛物线1C 上的任意一点P ,在抛物线2C 上总存在一点Q ,使得点P 、Q 的纵坐标相等.求EF 长的取值范围.【答案】(1)0;(2)①22m ≤≤+②7922EF ≤≤【分析】(1)根据2211122211,44y x bx y x bx =-+=-+,且120x x +=时,总有12y y =,变形后即可得到结论;(2)按照临界情形,画出图象分情况讨论求解即可.【详解】(1)解:由题可知:2211122211,44y x bx y bx =-+=-+120x x += 时,总有12y y =,2211221144x bx x bx ∴-+=-+.则()()()212121104x x x x b x x -+--=,∴()()2121104x x x x b ⎡⎤-+⎢-=⎥⎣⎦,∴()210b x x --=总成立,且210x x -≠,0b ∴=;(2)①注意到抛物线2C 最大值和开口大小不变,m 只影响图象左右平移下面考虑满足题意的两种临界情形:(i )当抛物线2C 过点(0,0)时,如图所示,此时,210,104x y m ==-+=,解得2m =或2-(舍).(ii )当抛物线2C 过点(2,1)-时,如图所示,此时,212,(2)114x y m ==--+=-,解得222m =+222-,综上,2222m ≤≤+②同①考虑满足题意的两种临界情形:(i )当抛物线2C 过点(0,1)-时,如图所示,此时,210,114x y m ==-+=-,解得2m =或22-(舍).(ii )当抛物线2C 过点(2,0)时,如图所示,此时,212,(2)104x y m ==--+=,解得4m =或0(舍).综上24m ≤≤,如图,由圆的性质可知,点E 、F 在线段AB 的垂直平分线上.令21()104y x m =--+=,解得2,2A B x m x m =-=+,22HB m m ∴=+-=,FB FC = ,2222FH HB FG GC ∴+=+,设FH t =,22222214m t t m ⎛⎫∴+=--+ ⎪⎝⎭,22221214044m m t m ⎛⎫⎛⎫∴---+-= ⎪ ⎪⎝⎭⎝⎭,22123044m m t ⎛⎫⎛⎫∴--+= ⎪⎪⎝⎭⎝⎭,22,m ≥ 2104m ∴-≠,22304m t ∴-+=,即2382m t =+,224m ≤≤ .5722t ∴≤≤,即5722FH ≤≤,1EF FH =+ ,7922EF ∴≤≤【点睛】此题考查了二次函数的图象和性质、垂径定理、解一元二次方程等知识,数形结合和分类讨论是解题的关键.考向三抛物线与角度有关问题7.(2023·湖南岳阳·统考中考真题)已知抛物线21:Q y x bx c =-++与x 轴交于()3,0,A B-两点,交y 轴于点()0,3C .(1)请求出抛物线1Q 的表达式.(2)如图1,在y 轴上有一点()0,1D -,点E 在抛物线1Q 上,点F 为坐标平面内一点,是否存在点,E F 使得四边形DAEF 为正方形?若存在,请求出点,E F 的坐标;若不存在,请说明理由.(3)如图2,将抛物线1Q 向右平移2个单位,得到抛物线2Q ,抛物线2Q 的顶点为K ,与x 轴正半轴交于点H ,抛物线1Q 上是否存在点P ,使得CPK CHK ∠=∠?若存在,请求出点P 的坐标;若不存在,请说明理由.【答案】(1)223y x x =--+;(2)()2,3E -;()1,2F ;(3)点P 的坐标为(1,0)或(2,3)-【分析】(1)把()()300,3A C -,,代入21:Q y x bx c =-++,求出2,3b c =-=即可;(2)假设存在这样的正方形,过点E 作ER x ⊥于点R ,过点F 作FI y ⊥轴于点I ,证明,EAR AOD FID DOA ≅≅ ,可得3,1,1,2,ER AR FI IO ====故可得()2,3E -,()1,2F ;(3)先求得抛物线2Q 的解析式为22(12)4(1)4y x x =-+-+=--+,得出(1,4)K ,()3,0H ,运用待定系数法可得直线BC 的解析式为3y x =-+,过点K 作KT y ⊥轴于点T ,连接BC ,设KP 交直线BC 于M 或N ,如图2,过点C 作PS y ⊥轴交BK 于点S ,交抛物线1Q 于点P ,连接PK ,利用等腰直角三角形性质和三角函数定义可得1tan3CK CHK CH ∠==,进而可求得点P 的坐标.【详解】(1)∵抛物线21:Q y x bx c =-++与x 轴交于()3,0,A -两点,交y 轴于点()0,3C ,∴把()()300,3A C -,,代入21:Q y x bx c =-++,得,930,3b c c --+=⎧⎨=⎩解得,2,3b c =-⎧⎨=⎩∴解析式为:223y x x =--+;(2)假设存在这样的正方形DAEF ,如图,过点E 作ER x ⊥于点R ,过点F 作FI y ⊥轴于点I ,∴90,AER EAR ∠+∠=︒∵四边形DAEF 是正方形,∴,90,AE AD EAD =∠=︒∴90,EAR DAR ∠+∠=︒∴,AER DAO ∠=∠又90,ERA AOD ∠=∠=︒∴AER DAO ≅ ,∴,,AR DO ER AO ==∵()()3,0,0,1,A D --∴3,1,OA OD ==1,3,AR ER ∴==∴312,OR OA AR =-=-=∴()2,3E -;同理可证明:FID DOA ≅ ,∴1,3,FI DO DI AO ====∴312,IO DI DO =-=-=∴()1,2F ;(3)解:抛物线1Q 上存在点P ,使得CPK CHK ∠=∠.2223(1)4y x x x =--+=-++ ,∴抛物线1Q 的顶点坐标为(1,4)-, 将抛物线1Q 向右平移2个单位,得到抛物线2Q ,∴抛物线2Q 的解析式为22(12)4(1)4y x x =-+-+=--+, 抛物线2Q 的顶点为K ,与x 轴正半轴交于点H ,(1,4)K ∴,()3,0H ,设直线BC 的解析式为y kx n =+,把(0,3)C ,()3,0H 代入得330n k n =⎧⎨+=⎩,解得:13k n =-⎧⎨=⎩,∴直线BC 的解析式为3y x =-+,过点K 作KT y ⊥轴于点T ,连接BC ,设KP 交直线BC 于M 或N ,如图2,过点C 作PS y ⊥轴交BK 于点S ,交抛物线1Q 于点P ,连接PK ,则(0,4)T ,(,3)M m m -+,(,3)N t t -+,1KT TC ∴==,90KTC ∠=︒,CKT ∴△是等腰直角三角形,45KCT ∴∠=︒,CK ==3OH OC == ,90COH ∠=︒,COH ∴△是等腰直角三角形,45HCO ∴∠=︒,CH ==,18090KCH KCT HCO ∴∠=︒-∠-∠=︒,1tan 3CK CHK CH ∴∠==,CPK CHK ∠=∠ ,1tan tan 3CPK CHK ∴∠=∠=,1tan 3OB BCO OC ∠== ,BCO CHK ∴∠=∠,∵BK OC ∥,CBK BCO ∴∠=∠,CBK CHK ∴∠=∠,即点P 与点B 重合时,CPK CHK ∠=∠,1)0(1,P ∴;1SK = ,3PS =,1tan 3SK CPK PS ∴∠==,CPK CHK ∴∠=∠,点P 与点C 关于直线=1x -对称,(2,3)P ∴-;综上所述,抛物线1Q 上存在点P ,使得CPK CHK ∠=∠,点P 的坐标为(1,0)或(2,3)-.【点睛】本题是二次函数综合题,考查了待定系数法求解析式,二次函数的性质,全等三角形的判定与性质,正方形的性质等知识,运用数形结合思想解决问题是解题的关键.考向四抛物线与四边形有关问题8.(2023·四川达州·统考中考真题)如图,抛物线2y ax bx c =++过点()()()1,0,3,,00,3A B C -.(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出PBC 的最大面积及此时点P 的坐标;(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以BC 为边,点B C M N 、、、为顶点的四边形是菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.【答案】(1)223y x x =-++;(2)PBC 的最大面积为278,315,24P ⎛⎫ ⎪⎝⎭;(3)存在,(17或(4,17或()143-,()2,143--,见解析【分析】(1)利用待定系数法代入求解即可;(2)利用待定系数法先确定直线BC 的解析式为3y x =-+,设点()2,23(03)P x x x x -++<<,过点P 作PD x ⊥轴于点D ,交BC 于点E ,得出23PE x x =-+,然后得出三角形面积的函数即可得出结果;(3)分两种情况进行分析:若BC 为菱形的边长,利用菱形的性质求解即可.【详解】(1)解:将点()()()1,0,3,,00,3A B C -代入解析式得:09303a b c a b c c -+=⎧⎪++=⎨⎪=⎩,解得:123a b c =-⎧⎪=⎨⎪=⎩,∴抛物线的解析式为223y x x =-++;(2)设直线BC 的解析式为y kx b =+,将点B 、C 代入得:303k b b +=⎧⎨=⎩,解得:13k b =-⎧⎨=⎩,∴直线BC 的解析式为3y x =-+,∵()3,0B ,∴3OB =,设点()2,23(03)P x x x x -++<<,过点P 作PD x ⊥轴于点D ,交BC 于点E ,如图所示:∴(),3E x x -+,∴()222333PE x x x x x =-++--+=-+,∴()22211393327332222228PBCS PE OB x x x x x ∆⎛⎫=⨯⨯=⨯-+⨯=-+=--+ ⎪⎝⎭,∴当32x =时,PBC 的最大面积为278,2915233344x x -++=-++=,∴315,24P ⎛⎫ ⎪⎝⎭(3)存在,()2,2N 或(或(4,或()3-,()2,3-,证明如下:∵()()3,0,0,3B C ,∵抛物线的解析式为223y x x =-++,∴对称轴为:1x =,设点()()1,,M t N x y ,,若BC 为菱形的边长,菱形BCMN ,则22BC CM =,即()221813t =+-,解得:13t =,23t =,∵31003x t y +=+⎧⎨+=+⎩,∴4,3x y t ==-,∴(1N ,(24,N ;若BC 为菱形的边长,菱形BCNM ,则22BC BM =,即()221831t =-+,解得:1t =2t =,∵30103x y t +=+⎧⎨+=+⎩,∴2,3x y t =-=+,∴()33N -+,()42,3N -;综上可得:(或(4,或()3-,()2,3-.【点睛】题目主要考查二次函数的综合应用,包括待定系数法确定函数解析式,三角形面积问题及特殊四边形问题,全等三角形的判定和性质等,理解题意,综合运用这些知识点是解题关键.9.(2023·山东·统考中考真题)如图,直线4y x =-+交x 轴于点B ,交y 轴于点C ,对称轴为32x =的抛物线经过B C ,两点,交x 轴负半轴于点A .P 为抛物线上一动点,点P 的横坐标为m ,过点P 作x 轴的平行线交抛物线于另一点M ,作x 轴的垂线PN ,垂足为N ,直线MN 交y 轴于点D.(1)求抛物线的解析式;(2)若302m <<,当m 为何值时,四边形CDNP 是平行四边形?(3)若32m <,设直线MN 交直线BC 于点E ,是否存在这样的m 值,使2MN ME =?若存在,求出此时m 的值;若不存在,请说明理由.【答案】(1)234y x x =-++;(2)63m =;(3)存在,12m =【分析】(1)利用待定系数法求函数解析式;(2)结合平行四边形的性质,通过求直线MN 的函数解析式,列方程求解;(3)根据2MN ME =,确定E 点坐标,从而利用一次函数图象上点的特征计算求解.【详解】(1)解:在直线4y x =-+中,当0x =时,4y =,当0y =时,4x =,∴点()4,0B ,点()0,4C ,设抛物线的解析式为232y a x k ⎛⎫=-+ ⎪⎝⎭,把点()4,0B ,点()0,4C 代入可得2234023042a k a k ⎧⎛⎫-+=⎪ ⎪⎪⎝⎭⎨⎛⎫⎪-+= ⎪⎪⎝⎭⎩,解得1254a k =-⎧⎪⎨=⎪⎩,∴抛物线的解析式为223253424y x x x ⎛⎫=--+=-++ ⎪⎝⎭;(2)解:由题意,()2,34P m m m -++,∴234PN m m =-++,当四边形CDNP 是平行四边形时,PN CD =,∴223443OD m m m m =-++-=-+,∴()20,3D m m -,(),0N m ,设直线MN 的解析式为213y k x m m =+-,把(),0N m 代入可得2130k m m m +-=,解得13k m =-,∴直线MN 的解析式为()233y m x m m =-+-,又∵过点P 作x 轴的平行线交抛物线于另一点M ,且抛物线对称轴为32x =,∴()23,34M m m m --++∴()2223334m m m m m -+-=-++,解得1m =,2m =(3)解:存在,理由如下:∵2MN ME =,∴点E 为线段MN 的中点,∴点E 的横坐标为3322m m -+=,∵点E 在直线4y x =-+上,∴35,22E ⎛⎫ ⎪⎝⎭,把35,22E ⎛⎫ ⎪⎝⎭代入()233y m x m m =-+-中,可得()2353322m m m -+-=,解得14m =(不合题意,舍去),212m =.【点睛】本题考查一次函数和二次函数的综合应用,掌握待定系数法求函数解析式,利用数形结合思想和方程思想解题是关键.10.(2023·四川南充·统考中考真题)如图1,抛物线23y ax bx =++(0a ≠)与x 轴交于()1,0A -,()3,0B 两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 在抛物线上,点Q 在x 轴上,以B ,C ,P ,Q 为顶点的四边形为平行四边形,求点P 的坐标;(3)如图2,抛物线顶点为D ,对称轴与x 轴交于点E ,过点()1,3K 的直线(直线KD 除外)与抛物线交于G,H 两点,直线DG ,DH 分别交x 轴于点M ,N .试探究EM EN ⋅是否为定值,若是,求出该定值;若不是,说明理由.【答案】(1)223y x x =-++;(2)()2,3或()13-或()13-;(3)定值,理由见详解【分析】(1)将()()1,03,0A B -,两点代入抛物线的解析式即可求解;(2)根据P ,Q 的不确定性,进行分类讨论:①过C 作CP x ∥轴,交抛物线于1P ,过1P 作11PQ BC ∥,交x 轴于1Q ,可得13Py =,由2233x x -++=,可求解;②在x 轴的负半轴上取点2Q ,过2Q 作22Q P BC ∥,交抛物线于2P ,同时使22Q P BC =,连接2CQ 、2BP ,过2P 作2P D x⊥轴,交x 轴于D ,23P y =-,即可求解;③当BC 为平行四边形的对角线时,在①中,只要点Q 在点B 的左边,且满足1BQ BQ =,也满足条件,只是点P 的坐标仍是①中的坐标;(3)可设直线GH 的解析式为()13y k x =-+,()2,23G m m m -++,()2,23H n n n -++,可求2m n k mn k +=-⎧⎨=-⎩,再求直线DG 的解析式为()13y m x m =--++,从而可求311m EM m +=--,同理可求EN ,即可求解.【详解】(1)解: 抛物线2()30y ax bx a =++≠与x 轴交于()()1,03,0A B -,两点,309330a b a b -+=⎧∴⎨++=⎩,解得12a b =-⎧⎨=⎩,故抛物线的解析式为223y x x =-++.(2)解:①如图,过C 作CP x ∥轴,交抛物线于1P ,过1P 作11PQ BC ∥,交x 轴于1Q ,∴四边形11BCPQ 是平行四边形,13P y ∴=,2233x x ∴-++=,解得:12x =,20x =,()12,3P ;②如图,在x 轴的负半轴上取点2Q ,过2Q 作22Q P BC ∥,交抛物线于2P ,同时使22Q P BC =,连接2CQ 、2BP ,过2P 作2P D x ⊥轴,交x 轴于D,∴四边形22BCQ P 是平行四边形,222CBQ P Q B ∴∠=∠,在2CBQ 和22P Q B 中,2222222BQ Q B CBQ P Q B CB P Q =⎧⎪∠=∠⎨⎪=⎩,∴222CBQ P Q B ≌(SAS ),23P D CO ∴==,23P y ∴=-,2233x x ∴-++=-,解得:11x =-21x =+()213P ∴-;如上图,根据对称性:()317,3P -,③当BC 为平行四边形的对角线时,由①知,点Q 在点B 的左边,且12BQ BQ ==时,也满足条件,此时点P 的坐标仍为()2,3;综上所述:P 的坐标为()2,3或()17,3-或()17,3-.(3)解:是定值,理由:如图, 直线GH 经过()1,3K ,∴可设直线GH 的解析式为()13y k x =-+,G 、H 在抛物线上,∴可设()2,23G m m m -++,()2,23H n n n -++,()21323k x x x ∴-+=-++,整理得:()220x k x k +--=,∴1x m =,2x n =,2m n k mn k+=-⎧∴⎨=-⎩,当1x =时,212134y =-+⨯+=,()14D ∴,,设直线DG 的解析式为11y k x b =+,则有21111234mk b m m k b ⎧+=-++⎨+=⎩,解得()1113k m b m ⎧=--⎨=+⎩,∴直线DG 的解析式为()13y m x m =--++,当0y =时,()130m x m --++=,解得:31m x m +=-,3,01m M m +⎛⎫∴ ⎪-⎝⎭,311m EM m +∴=--41m =--,同理可求:41EN n =-,4411EM EN m n ∴⋅=-⋅--()161mn m n =--++()1621k k =----+()1621k k =----+16=;当G 与H 对调位置后,同理可求16EM EN ⋅=;故EM EN ⋅的定值为16.【点睛】本题考查了二次函数与一次函数的综合问题,待定系数法求函数解析式,求函数图象与坐标轴交点坐标,动点产生的平行四边形判定,一元二次方程根与系数的关系,理解一次函数与二次函数图象的交点,与对应一元二次方程根的关系,掌握具体的解法,并会根据题意设合适的辅助未知数是解题的关键.考向五抛物线与圆有关问题11.(2023·江苏苏州·统考中考真题)如图,二次函数268y x x =-+的图像与x 轴分别交于点,A B (点A 在点B 的左侧),直线l 是对称轴.点P 在函数图像上,其横坐标大于4,连接,PA PB ,过点P 作PM l ⊥,垂足为M ,以点M 为圆心,作半径为r 的圆,PT 与M 相切,切点为T .(1)求点,A B 的坐标;(2)若以M 的切线长PT 为边长的正方形的面积与PAB 的面积相等,且M 不经过点()3,2,求PM 长的取值范围.【答案】(1)()()2,0,4,0A B ;(2)1PM <<2PM <<或2PM >【分析】(1)令0y =求得点,A B 的横坐标即可解答;(2)由题意可得抛物线的对称轴为3x =,设()2,68P m m m -+,则()23,68M m m -+;如图连接MT ,则MT PT ⊥,进而可得切线长PT 为边长的正方形的面积为()223m r --;过点P 作PH x ⊥轴,垂足为H ,可得21682PAB S AB PH m m =⋅=-+ ;由题意可得()222368m r m m --=-+,解得1r =;然后再分当点M 在点N 的上方和下方两种情况解答即可.【详解】(1)解:令0y =,则有:2680x x -+=,解得:2x =或4x =,∴()()2,0,4,0A B .(2)解:∵抛物线过()()2,0,4,0A B ∴抛物线的对称轴为3x =,设()2,68P m m m -+,∵PM l ⊥,∴()23,68M m m -+,如图:连接MT ,则MT PT ⊥,∴()222223PT PM MT m r =-=--,∴切线PT 为边长的正方形的面积为()223m r --,过点P 作PH x ⊥轴,垂足为H ,则:21682PAB S AB PH m m =⋅=-+ ,∴()222368m r m m --=-+∵0r >,∴1r =,假设M 过点()3,2N ,则有以下两种情况:①如图1:当点M 在点N 的上方,即()3,3M ∴2683m m -+=,解得:5m =或1m =,∵4m >∴5m =;②如图2:当点M 在点N 的上方,即()3,1M ∴2681m m -+=,解得:32m =∵4m >∴32m =综上,32PM m =-=2∴当M 不经过点()3,2时,1PM <<2PM <<或2PM >.【点睛】本题主要考查了二次函数的性质、切线的性质、勾股定理等知识点,掌握分类讨论思想是解答本题的关键.12.(2023·山东烟台·统考中考真题)如图,抛物线25y ax bx =++与x 轴交于,A B 两点,与y 轴交于点,4C AB =.抛物线的对称轴3x =与经过点A 的直线1y kx =-交于点D ,与x 轴交于点E .(1)求直线AD 及抛物线的表达式;(2)在抛物线上是否存在点M ,使得ADM △是以AD 为直角边的直角三角形?若存在,求出所有点M 的坐标;若不存在,请说明理由;(3)以点B 为圆心,画半径为2的圆,点P 为B 上一个动点,请求出12+PC PA 的最小值.【答案】(1)直线AD 的解析式为1y x =-;抛物线解析式为265y x x =-+;(2)存在,点M的坐标为()4,3-或()0,5或()5,0【分析】(1)根据对称轴3x =,4AB =,得到点A 及B 的坐标,再利用待定系数法求解析式即可;(2)先求出点D 的坐标,再分两种情况:①当90DAM ∠=︒时,求出直线AM 的解析式为1y x =-+,解方程组2165y x y x x =-+⎧⎨=-+⎩,即可得到点M 的坐标;②当90ADM ∠=︒时,求出直线DM 的解析式为5y x =-+,解方程组2565y x y x x =-+⎧⎨=-+⎩,即可得到点M 的坐标;(3)在AB 上取点F ,使1BF =,连接CF ,证得BF PB PB AB=,又PBF ABP ∠=∠,得到PBF ABP ∽,推出12PF PA =,进而得到当点C 、P 、F 三点共线时,12+PC PA 的值最小,即为线段CF 的长,利用勾股定理求出CF 即可.【详解】(1)解:∵抛物线的对称轴3x =,4AB =,∴()()1,0,5,0A B ,将()1,0A 代入直线1y kx =-,得10k -=,解得1k =,∴直线AD 的解析式为1y x =-;将()()1,0,5,0A B 代入25y ax bx =++,得5025550a b a b ++=⎧⎨++=⎩,解得16a b =⎧⎨=-⎩,∴抛物线的解析式为265y x x =-+;(2)存在点M ,∵直线AD 的解析式为1y x =-,抛物线对称轴3x =与x 轴交于点E .∴当3x =时,12y x =-=,∴()3,2D ,①当90DAM ∠=︒时,设直线AM 的解析式为y x c =-+,将点A 坐标代入,得10c -+=,解得1c =,∴直线AM 的解析式为1y x =-+,解方程组2165y x y x x =-+⎧⎨=-+⎩,得10x y =⎧⎨=⎩或43x y =⎧⎨=-⎩,∴点M 的坐标为()4,3-;②当90ADM ∠=︒时,设直线DM 的解析式为y x d =-+,将()3,2D 代入,得32d -+=,解得5d =,∴直线DM 的解析式为5y x =-+,解方程组2565y x y x x =-+⎧⎨=-+⎩,解得05x y =⎧⎨=⎩或50x y =⎧⎨=⎩,∴点M 的坐标为()0,5或()5,0综上,点M 的坐标为()4,3-或()0,5或()5,0;(3)如图,在AB 上取点F ,使1BF =,连接CF ,∵2PB =,∴12BF PB =,∵2142PB AB ==,、∴BF PB PB AB=,又∵PBF ABP ∠=∠,∴PBF ABP ∽,∴12PF BF PA PB ==,即12PF PA =,∴12PC PA PC PF CF +=+≥,∴当点C 、P 、F 三点共线时,12+PC PA 的值最小,即为线段CF 的长,∵5,1514OC OF OB ==-=-=,∴CF =∴12+PC PA【点睛】此题是一次函数,二次函数及圆的综合题,掌握待定系数法求函数解析式,直角三角形的性质,勾股定理,相似三角形的判定和性质,求两图象的交点坐标,正确掌握各知识点是解题的关键.考向六抛物线与面积有关问题13.(2023·湖南常德·统考中考真题)如图,二次函数的图象与x 轴交于()1,0A -,()5,0B 两点,与y 轴交于点C ,顶点为D .O 为坐标原点,1tan 5ACO ∠=.(1)求二次函数的表达式;(2)求四边形ACDB 的面积;(3)P 是抛物线上的一点,且在第一象限内,若ACO PBC ∠=∠,求P 点的坐标.【答案】(1)()()15y x x =-+-;(2)30;(3)127,24P ⎛⎫ ⎪⎝⎭【分析】(1)用两点式设出二次函数的解析式,然后求得C 点的坐标,并将其代入二次函数的解析式,求得a 的值,再将a 代入解析式中即可.(2)先将二次函数变形为顶点式,求得顶点坐标,然后利用矩形、三角形的面积公式即可求得答案.(3)根据各点的坐标的关系及同角三角函数相等的结论可以求得相关联的函数解析式,最后联立一次函数与二次函数的解析式,求得点P 的坐标.【详解】(1)∵二次函数的图象与x 轴交于()()1,0,5,0A B -两点.∴设二次函数的表达式为()()15y a x x =+-∵11,tan 5AO ACO =∠=,∴5OC =,即C 的坐标为()0,5则()()50105a =+-,得1a =-∴二次函数的表达式为()()15y x x =-+-;(2)()()215(2)9y x x x =-+-=--+∴顶点的坐标为()2,9过D 作DN AB ⊥于N ,作DM OC ⊥于M ,四边形ACDB 的面积AOC CDM DNBOMDN S S S S =+-+△△△矩形()()111152929552930222=⨯⨯+⨯-⨯-+⨯-⨯=;。
中考压轴题专项训练1——抛物线专题(带答案解析)

中考压轴题专项训练1——抛物线专题考点分析:命题预测:函数是数形结合的重要体现,是每年中考的必考内容,函数的概念主要用选择、填空的形式考查自变量的取值范围,及自变量与因变量的变化图像、平面直角坐标系等,一般占2%左右.一次函数与一次方程有紧密地联系,是中考必考内容,一般以填空、选择、解答题及综合题的形式考查,占5%左右.反比例函数的图像和性质的考查常以客观题形式出现,要关注反比例函数与实际问题的联系,突出应用价值,3—6分;二次函数是初中数学的一个十分重要的内容,是中考的热点,多以压轴题出现在试卷中.要求:能通过对实际问题情景分析确定二次函数的表达式,并体会二次函数的意义;会用描点法画二次函数图像,能丛图像上分析二次函数的性质;会根据公式确定图像的顶点、开口方向和对称轴,并能解决复杂的图形综合问题。
二次函数常考点汇总:1. 两点间的距离公式:22)()(AB B A B A x x y y -+-=2. 中点坐标公式:已知A ),(A A y x ,B ),(B B y x ,则线段AB 的中点C 的坐标为⎪⎭⎫⎝⎛++2,2B A B A y y x x 。
3. 在平面直角坐标系中求面积的方法:公式法、割补法(做铅垂高或水平宽) 4. 几何分析法:特别是构造“平行四边形”、“梯形”、“相似三角形”、“直角三角形”、“等腰三角形”等图形时,利用几何分析法能给解题带来方便。
例题精讲:1.如图,直线y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,抛物线y=﹣x2+bx+c 经过点A,B.(1)求点B的坐标和抛物线的解析式;(2)M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N.①点M在线段OA上运动,若以B,P,N为顶点的三角形与△APM相似,求点M的坐标;②点M在x轴上自由运动,若三个点M,P,N中恰有一点是其它两点所连线段的中点(三点重合除外),则称M,P,N三点为“共谐点”.请直接写出使得M,P,N三点成为“共谐点”的m的值.2.如图①,抛物线y=﹣x2+(a+1)x﹣a与x轴交于A,B两点(点A位于点B的左侧),与y轴交于点C.已知△ABC的面积是6.(1)求a的值;(2)求△ABC外接圆圆心的坐标;(3)如图②,P是抛物线上一点,Q为射线CA上一点,且P、Q两点均在第三象限内,Q、A是位于直线BP同侧的不同两点,若点P到x轴的距离为d,△QPB的面积为2d,且∠P AQ=∠AQB,求点Q的坐标.3.已知,在平面直角坐标系xoy 中,点A 的坐标为(0,2),点P (m ,n )是抛物线2114y x =+上的一个动点.(1)①如图1,过动点P 作PB ⊥x 轴,垂足为B ,连接PA ,求证:PA=PB ; ②如图2,设C 的坐标为(2,5),连接PC ,AP+PC 是否存在最小值?如果存在,求点P 的坐标;如果不存在,请说明理由;(2)如图3,过动点P 和原点O 作直线交抛物线于另一点D ,若AP=2AD ,求直线OP 的解析式.4.【变式】在平面直角坐标系xOy 中,抛物线21124y x =+的顶点为M ,直线2y x =,点()0P n ,为x 轴上的一个动点,过点P 作x 轴的垂线分别交抛物线21124y x =+和直线2y x =于点A ,点B.(1)直接写出A ,B 两点的坐标(用含n 的代数式表示);⑵设线段AB 的长为d ,求d 关于n 的函数关系式及d 的最小值,并直接写出此时线段OB 与线段PM 的位置关系和数量关系;(3) 已知二次函数2y ax bx c =++(a ,b ,c 为整数且0a ≠),对一切实数x 恒有x ≤y ≤2124x +,求a ,b ,c 的值.5.如图,已知二次函数()21y x m x m =+--(其中0<m <1)的图像与x 轴交于A 、B 两点(点A在点B 的左侧),与y 轴交于点C ,对称轴为直线l .设P 为对称轴l 上的点,连接P A 、PC ,P A =PC . (1)∠ABC 的度数为 °;(2)求P 点坐标(用含m 的代数式表示);(3)在坐标轴上是否存在点Q (与原点O 不重合),使得以Q 、B 、C 为顶点的三角形与△P AC 相似,且线段PQ 的长度最小?如果存在,求出所有满足条件的点Q 的坐标;如果不存在,请说明理由.6.(本题满分10分)如图,二次函数2y x bx c =++的图像与x 轴交于A 、B 两点,与y 轴交于点C ,C OB =O .点D 在函数图像上,CD//x 轴,且CD 2=,直线l 是抛物线的对称轴,E 是抛物线的顶点.(1)求b 、c 的值;(2)如图①,连接BE ,线段C O 上的点F 关于直线l 的对称点F '恰好在线段BE 上,求点F 的坐标; (3)如图②,动点P 在线段OB 上,过点P 作x 轴的垂线分别与C B 交于点M ,与抛物线交于点N .试问:抛物线上是否存在点Q ,使得Q ∆P N 与∆APM 的面积相等,且线段Q N 的长度最小?如果存在,求出点Q 的坐标;如果不存在,说明理由.7.(8分)如图,已知抛物线y=x2﹣4与x轴交于点A,B(点A位于点B的左侧),C 为顶点,直线y=x+m经过点A,与y轴交于点D.(1)求线段AD的长;(2)平移该抛物线得到一条新拋物线,设新抛物线的顶点为C′.若新抛物线经过点D,并且新抛物线的顶点和原抛物线的顶点的连线CC′平行于直线AD,求新抛物线对应的函数表达式.答案解析1.【解答】解:(1)∵y=﹣x+c与x轴交于点A(3,0),与y轴交于点B,∴0=﹣2+c,解得c=2,∴B(0,2),∵抛物线y=﹣x2+bx+c经过点A,B,∴,解得,∴抛物线解析式为y=﹣x2+x+2;(2)①由(1)可知直线解析式为y=﹣x+2,∵M(m,0)为x轴上一动点,过点M且垂直于x轴的直线与直线AB及抛物线分别交于点P,N,∴P(m,﹣m+2),N(m,﹣m2+m+2),∴PM=﹣m+2,AM=3﹣m,PN=﹣m2+m+2﹣(﹣m+2)=﹣m2+4m,∵△BPN和△APM相似,且∠BPN=∠APM,∴∠BNP=∠AMP=90°或∠NBP=∠AMP=90°,当∠BNP=90°时,则有BN⊥MN,∴N点的纵坐标为2,∴﹣m2+m+2=2,解得m=0(舍去)或m=2.5,∴M(2.5,0);当∠NBP=90°时,过点N作NC⊥y轴于点C,则∠NBC+∠BNC=90°,NC=m,BC=﹣m2+m+2﹣2=﹣m2+m,∵∠NBP=90°,∴∠NBC+∠ABO=90°,∴∠ABO=∠BNC,∴Rt△NCB∽Rt△BOA,∴=,∴=,解得m=0(舍去)或m=,∴M(,0);综上可知当以B,P,N为顶点的三角形与△APM相似时,点M的坐标为(2.5,0)或(,0);②由①可知M(m,0),P(m,﹣m+2),N(m,﹣m2+m+2),∵M,P,N三点为“共谐点”,∴有P为线段MN的中点、M为线段PN的中点或N为线段PM的中点,当P为线段MN的中点时,则有2(﹣m+2)=﹣m2+m+2,解得m=3(三点重合,舍去)或m=;当M为线段PN的中点时,则有﹣m+2+(﹣m2+m+2)=0,解得m=3(舍去)或m=﹣1;当N为线段PM的中点时,则有﹣m+2=2(﹣m2+m+2),解得m=3(舍去)或m=﹣;综上可知当M,P,N三点成为“共谐点”时m的值为或﹣1或﹣.2.【解答】解:(1)∵y=﹣x2+(a+1)x﹣a令y=0,即﹣x2+(a+1)x﹣a=0解得x1=a,x2=1由图象知:a<0∴A(a,0),B(1,0)∵s△ABC=6∴解得:a=﹣3,(a=4舍去)(2)设直线AC:y=kx+b,由A(﹣3,0),C(0,3),可得﹣3k+b=0,且b=3∴k=1即直线AC:y=x+3,A、C的中点D坐标为(﹣,)∴线段AC的垂直平分线解析式为:y=﹣x,线段AB的垂直平分线为x=﹣1代入y=﹣x,解得:y=1∴△ABC外接圆圆心的坐标(﹣1,1)(3)作PM⊥x轴,则=∵∴A、Q到PB的距离相等,∴AQ∥PB设直线PB解析式为:y=x+b∵直线经过点B(1,0)所以:直线PB的解析式为y=x﹣1联立解得:∴点P坐标为(﹣4,﹣5)又∵∠P AQ=∠AQB可得:△PBQ≌△ABP(AAS)∴PQ=AB=4设Q(m,m+3)由PQ=4得:解得:m=﹣4,m=﹣8(当m=﹣8时,∠P AQ≠∠AQB,故应舍去)∴Q坐标为(﹣4,﹣1)3.【解答】解:(1)①设P(m,n)∴n=m2+1,∵PB⊥x 轴,∴PB=m2+1,∵A(0,2)∴AP==m2+1,∴PB=PA;②过点P作PB⊥x轴于B,由(1)得PA=PB,所以要使AP+CP最小,只需当BP+CP最小,因此当C,P,B共线时取得,此时点P的横坐标等于点C(2,5)的横坐标,所以点P的坐标为(2,2),(2)如图,作DE⊥x轴于E,作PF⊥x轴于F,由(1)得:DA=DE,PA=PF∵PA=2DA,∴PF=2DE,∵△ODE∽△OPF,∴==,设P(m,m2+1),则D(m,m2+)∵点D在抛物线y=x2+1上,∴m2+=(m)2+1,解得m=±2,∴P 1(,3),直线OP 的解析式为y=x , P 2(﹣,3)直线OP 的解析式为y=﹣x , 综上所求,所求直线OP 的解析式为y=x 或y=﹣x .4.【解答】解:(1)21(2)4A n n +,,()B n n ,. (2) d =AB=A B y y -=2124n n -+.∴ d =2112()48n -+=2112()48n -+.∴ 当14n =时,d 取得最小值18. 当d 取最小值时,线段OB 与线段PM 的位置 关系和数量关系是OB ⊥PM 且OB=PM. (如图)(3) ∵对一切实数x 恒有 x ≤y ≤2124x +, ∴对一切实数x ,x ≤2ax bx c ++≤2124x +都成立. (0a ≠) ①当0x =时,①式化为 0≤c ≤14.xy111APBMO∴整数c 的值为0.此时,对一切实数x ,x ≤2ax bx +≤2124x +都成立.(0a ≠) 即 222,12.4x ax bx ax bx x ⎧≤+⎪⎨+≤+⎪⎩ 对一切实数x 均成立. 由②得 ()21ax b x +-≥0 (0a ≠) 对一切实数x 均成立.∴()210,10.a b >⎧⎪⎨∆=-≤⎪⎩ 由⑤得整数b 的值为1.此时由③式得,2ax x +≤2124x +对一切实数x 均成立. (0a ≠) 即21(2)4a x x --+≥0对一切实数x 均成立. (0a ≠) 当a=2时,此不等式化为14x -+≥0,不满足对一切实数x 均成立.当a≠2时,∵ 21(2)4a x x --+≥0对一切实数x 均成立,(0a ≠)∴2220,1(1)4(2)0.4a a ->⎧⎪⎨∆=--⨯-⨯≤⎪⎩∴由④,⑥,⑦得 0 <a ≤1.∴整数a 的值为1.∴整数a ,b ,c 的值分别为1a =,1b =,0c =.5.【解答】解:(1)45.理由如下:令x =0,则y =-m ,C 点坐标为(0,-m ).令y =0,则()210x m x m +--=,解得11x =-,2x m =. ∵0<m <1,点A 在点B 的左侧,∴B 点坐标为(m ,0).∴OB =OC =m .∵∠BOC =90°,∴△BOC 是等腰直角三角形,∠OBC =45°. (2)如图①,作PD ⊥y 轴,垂足为D ,设l 与x 轴交于点E ,由题意得,抛物线的对称轴为12mx -+=. 设点P 坐标为(12m-+,n ). ∵P A = PC , ∴P A 2= PC 2,即AE 2+ PE 2=CD 2+ PD 2.∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭.解得12m n -=.∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭. ④⑤② ③ ⑥ ⑦图①图②(3)存在点Q 满足题意.∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭, ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ∵AC 2=21m +,∴P A 2+ PC 2=AC 2.∴∠APC =90°. ∴△P AC 是等腰直角三角形.∵以Q 、B 、C 为顶点的三角形与△P AC 相似, ∴△QBC 是等腰直角三角形.∴由题意知满足条件的点Q 的坐标为(-m ,0)或(0,m ). ①如图①,当Q 点的坐标为(-m ,0)时,若PQ 与x 轴垂直,则12m m -+=-,解得13m =,PQ =13. 若PQ 与x 轴不垂直, 则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. ∵0<m <1,∴当25m =时,2PQ 取得最小值110,PQ .<13, ∴当25m =,即Q 点的坐标为(25-,0)时, PQ 的长度最小.②如图②,当Q 点的坐标为(0,m )时,若PQ 与y 轴垂直,则12m m -=,解得13m =,PQ =13. 若PQ 与y 轴不垂直, 则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. ∵0<m <1,∴当25m =时,2PQ 取得最小值110,PQ .<13, ∴当25m =,即Q 点的坐标为(0,25)时, PQ 的长度最小.综上:当Q 点坐标为(25-,0)或(0,25)时,PQ 的长度最小.6. 【解答】解:(1).3)(03,20.0,c -),,0(,.2,12.1x 2CD x //2-=∴=-=++=∴∴=-==-∴=∴=c c c c c c B c C OC OB b bl CD ,舍去或解得)点坐标为(:抛物线对称轴为直线,轴,(2)设点F 坐标为(0,m ).∵对称轴是直线,1:=x l ∴点F 关于直线l 的对称点’F 的坐标为(2,m ). ∵直线BE 经过点B (3,0),E (1,-4),∴利用待定系数法可得直线BE 的表达式为y=2x-6. ∵点’F 在BE 上,∴m=2⨯2-6=-2,即点F 的坐标为(0,-2). (3)存在点Q 满足题意。
2024陕西数学中考备考重难专题:抛物线与几何综合题三角形全等、相似问题含位似(课件)

6
6
3
练习题图
练习 (2022西安铁一中模拟)如图,Rt△ABC中,∠ACB=90°,AB=8,AC
=4,以AB所在直线为x轴,建立平面直角坐标系,若C(0, (3)l为抛物线对称轴,P是直线l右侧抛物线上的点,过点P作l的垂线,垂足为
D,E是l上的点.要使以P、D、E为顶点的三角形与△ABC全等,求满足条
解图
∵点A(-3,0),点C(0,3),∴OA=OC=3,
∵∠DQP=∠AOC=90°,
∴当PQ=DQ时,△DQP与△AOC相似,
设点P的坐标为(m,m2-2m-3),则点Q的坐标为(m,0),
∴PQ=|m2-2m-3|,DQ=|m+1|,
当m2-2m-3=m+1时,解得m=-1(舍去)或m=4,
解
三角
答
直角三角
式
(2)得到△PDE和
形全 2023 24 题 10
形
/ (2)求满足 △PDE是直角三角形,
等
两个三角 需分两种情况讨论计算
形全等时 (等角的三角函数值相
的点坐标 等/对应边相等)
典例精讲
例 (2022陕西黑白卷)在平面直角坐标系中,已知抛物线L:y=-x2-x+2与
x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,L关于y轴对称的抛物
形
两个三角 线上,得∠C′CO=
形相似时 ∠BOP,需分两种情况
的点坐标 讨论计算(对应边成比
例)
类型 年份 题号 题型 分值 图形形状 结合变化 设问形式
考查内容
(1)待定系数法求表达
式
(1)求抛物 (2)根据抛物线关于原
线的表达 点对称特点确定求表达
解
人教版九年级数学上知识点巩固与综合运用 专题8 抛物线与特殊图形存在性问题【跨单元整合】

③列方程求参数的值.
(2)2023内江中考T28(3)考法点 Q 为抛物线对称轴
上一点,是否存在点 Q ,使以点 A , B , Q 为顶点的三
角形是直角三角形?若存在,请求出点 Q 的坐标;若
不存在,请说明理由.
解:存在点 Q ,使以点 A , B , Q 为顶点
的三角形是直角三角形.由题知抛物线的对
即18=12+( t -3)2,
解得 t1= +3, t2=- +3.
+ = + ,
∵ቊ
∴ m =4, n =t -3.
+ = + ,
∴ N1(4, ), N2(4,- ).
若 BC 为菱形 BCNM 的边长,则 BC2= BM2,
即18=(3-1)2+ t2,
平面内一点,是否存在以 BC 为边,以 B , C , M ,
N 为顶点的四边形是菱形?若存在,请求出点 N 的坐
标;若不存在,请说明理由.
解:(2)存在.
∵ B (3,0), A (-1,0),
∴抛物线的对称轴为直线 x =1.
设点 M (1, t ), N ( m , n ),
若 BC 为菱形 BCMN 的边长,则 BC2= CM2,
是以 AB 为底边的等腰三角形?若不存
在,请说明理由;若存在,请求出点 F
的坐标.
解:存在点 F ,使△ ABF 是以 AB 为底边的等腰
三角形.由点 F 在抛物线上,可设 F ( t ,- t 2 +2
t +3).
∵△ ABF 是以 AB 为底边的等腰三角形,
∴ AF = BF .
∴ AF 2 = BF 2 .
称轴为直线 x =1.
2024年中考数学一轮复习题型突破与专题精练—抛物线与几何综合题

2024年中考数学一轮复习题型突破与专题精练—抛物线与几何综合题题型一抛物线与三角形有关问题1.如图,抛物线2()30y ax bx a =++≠与x 轴交于点()1,0A 和点()3,0B -,与y 轴交于点C,连接BC ,与抛物线的对称轴交于点E,顶点为点D.(1)求抛物线的解析式;(2)点P 是对称轴左侧抛物线上的一个动点,点Q 在射线ED 上,若以点P、Q、E 为顶点的三角形与BOC 相似,请直接写出点P 的坐标.【答案】(1)223y x x =--+;(2)12(1(2,3)P P --【分析】(1)根据抛物线y=ax 2+bx+3(a≠0)与x 轴交于点A(1,0)和点B(﹣3,0),即可得到关于a、b 的方程,从而可以求得a、b 的值,然后即可写出抛物线的解析式;(2)根据(1)中抛物线的解析式,设点P 的坐标,然后再根据BOC 是等腰直角三角形,得出PQE V 是等腰直角三角形,再分类讨论,列出方程,即可求解.【详解】解:(1)∵抛物线y=ax 2+bx+3(a≠0)与x 轴交于点A(1,0)和点B(﹣3,0),∴309330a b a b ++=⎧⎨-+=⎩解得12a b =-⎧⎨=-⎩∴此抛物线的解析式为:223y x x =--+(2)当0x =时,3y =,所以,OB=OC=3,∴BOC 是等腰直角三角形,以点P、Q、E 为顶点的三角形与BOC 相似,∴PQE V 是等腰直角三角形,设点P 的坐标为2(23)m m m --+,,抛物线的对称轴为直线21221b x a -=-=-=--⨯,设BC 的解析式为y kx n =+,将B(﹣3,0),C(0,3)代入得,303k n n -+=⎧⎨=⎩,解得,13k n =⎧⎨=⎩,故BC 的解析式为3y x =+,把1x =-代入得,2y =,则E 点坐标为(12)-,,如图,当E 为直角顶点时,2232m m --+=,解得,11m =-,21m =-把11m =-代入得,2232m m --+=,则P 点坐标为(12)-,当Q 为直角顶点时,PQ=QE,即22321m m m --+-=--,解得12m =-,20m =(舍去),把12m =-代入得,2233m m --+=,则P 点坐标为(2,3)-;当P 为直角顶点时,作PM⊥EQ 于M,PM=ME,即22321m m m --+-=--,解得12m =-,20m =(舍去),则P 点坐标为(2,3)-;综上,P 点坐标为(12)--或(2,3)-.【点睛】本题考查了待定系数法求二次函数解析式和相似三角形与等腰直角三角形的性质,解题关键是熟练运用待定系数法和设出点的坐标,根据题意列出方程.2.如图,在平面直角坐标系中,抛物线223y x x =--与x 轴相交于点A、B(点A 在点B 的左侧),与y 轴相交于点C,连接,AC BC .(1)求线段AC 的长;(2)若点Р为该抛物线对称轴上的一个动点,当PA PC =时,求点P 的坐标;(3)若点M 为该抛物线上的一个动点,当BCM 为直角三角形时,求点M 的坐标.(2)()11,-(3)()14-,或()25-,或⎝⎭或⎝⎭【分析】(1)根据解析式求出A,B,C 的坐标,然后用勾股定理求得AC 的长;(2)求出对称轴为x=1,设P(1,t),用t 表示出PA 2和PC 2的长度,列出等式求解即可;(3)设点M (m,m 2-2m-3),分情况讨论,当222CM BC BM +=,222BM BC CM +=,222BM CM BC +=分别列出等式求解即可.(1)223y x x =--与x 轴交点:令y=0,解得121,3x x =-=,即A(-1,0),B(3,0),223y x x =--与y 轴交点:令x=0,解得y=-3,即C(0,-3),∴AO=1,CO=3,∴AC ==;(2)抛物线223y x x =--的对称轴为:x=1,设P(1,t),∴()()22221104PA t t =++-=+,()()()222210313PC t t =-++=++,∴24t +()213t =++∴t=-1,∴P(1,-1);(3)设点M(m,m 2-2m-3),()()()()22222223230323BM m m m m m m =-+---=-+--,()()()222222202332CM m m m m m m =-+--+=+-,()()222300318BC =-++=,①当222CM BC BM +=时,()()()222222218323m m m m m m +-+=-+--,解得,10m =(舍),21m =,∴M(1,-4);②当222BM BC CM +=时,()()()222222323182m m m m m m -+--+=+-,解得,12m =-,23m =(舍),∴M(-2,5);③当222BM CM BC +=时,()()()222222323218m m m m m m -+--++-=,解得,m =∴M 1522⎛ ⎝⎭或1522⎛⎫ ⎪ ⎪⎝⎭;综上所述:满足条件的M 为()14-,或()25-,或1522⎛⎫ ⎪ ⎪⎝⎭或1522⎛ ⎝⎭.【点睛】本题是二次函数综合题,考查了与坐标轴交点、线段求值、存在直角三角形等知识,解题的关键是学会分类讨论的思想,属于中考压轴题.3.如图1,已知二次函数()20y ax bx c a =++>的图象与x 轴交于点()1,0A -、()2,0B ,与y轴交于点C,且tan 2OAC ∠=.(1)求二次函数的解析式;(2)如图2,过点C 作CD x ∥轴交二次函数图象于点D,P 是二次函数图象上异于点D 的一个动点,连接PB、PC,若PBC BCD S S =△△,求点P 的坐标;(3)如图3,若点P 是二次函数图象上位于BC 下方的一个动点,连接OP 交BC 于点Q.设点P 的横坐标为t,试用含t 的代数式表示PQ OQ 的值,并求PQ OQ的最大值.【答案】(1)22y x x =--;;(3)12【分析】(1)在Rt△AOC 中求出OC 的长,从而确定点C 的坐标,将二次函数设为交点式,将点C 的坐标代入,进一步求得结果;(2)可分为点P 在第三象限和第一象限两种情况:当点P 在第三象限时,设点P (a,22a a --),可表示出△BCD 的面积,作PE∥AB 交BC 于E,先求出直线BC,从而得到E 点坐标,从而表示出△PBC 的面积,根据S △PBC=S △BCD,列出方程,进一步求得结果,当P 在第一象限,同样的方法求得结果;(3)作PN⊥AB 于N,交BC 于M,根据P(t,22t t --),M(t,2t -),表示出PM 的长,根据PN∥OC,得出△PQM∽△OQC,从而得出PQ PM OQ OC=,从而得出PQ OQ 的函数表达式,进一步求得结果.(1)∵A(-1,0),∴OA=1,又∵∠AOC=90°,tan∠OAC=2OC OA =,∴OC=2OA=2即点C 的坐标为(0,-2),设二次函数的解析式为y=a(x+1)(x-2),将C 点坐标代入得:a=1,∴y=(x+1)(x-2)=22x x --;(2)设点P(a,22a a --),如图所示,当点P 在第三象限时,作PE∥AB 交BC 于E,∵B(2,0),C(0,-2),∴直线BC 的解析式为:y=x-2,∴当22y a a =--时,x=y+2=2a a -,∴PE=2a a a --=22a a -,∴S △PBC=12PE·OC,∵抛物线的对称轴为y=12,CD∥x 轴,C(0,-2),∴点D(1,-2),∴CD=1,∴S △BCD=12CD·OC,∴12PE·OC=12CD·OC,∴a 2-2a=1,解得a 1(舍去),a 2当时,y=22a a --),如图,当点P 在第一象限时,作PE⊥x 轴于点E,交直线BC 于F,∴F(a,a-2),∴PF=(22a a --)-(a-2)=22a a -,∴S △PBC=12PF·OB=12CD·OC,∴22a a -=1,解得a 1,a 2(舍去);当时,y=22a a --,),综上所述,P ;(3)如图,作PN⊥AB 于N,交BC 于M,由题意可知,P(t,22t t --),M(t,t-2),∴PM=(t-2)-(22t t --)=-22t t +,又∵PN∥OC,∴△PQM∽△OQC,∴2221(1)22PQ PM t t t OQ OC -+===--+12,∴当t=1时,(PQ OQ )最大=12.【点睛】本题考查二次函数的综合应用,三角函数的应用、二次函数的解析式、相似三角形的综合和配方法求最值等,熟练掌握二次函数的图象与性质是解决此类问题的关键.4.如图,抛物线21262y x x =+-与x 轴交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C ,连接AC ,BC .(1)求A ,B ,C 三点的坐标并直接写出直线AC ,BC 的函数表达式;(2)点P 是直线AC 下方抛物线上的一个动点,过点P 作BC 的平行线l ,交线段AC 于点D .①试探究:在直线l 上是否存在点E ,使得以点D ,C ,B ,E 为顶点的四边形为菱形,若存在,求出点E 的坐标;若不存在,请说明理由;②设抛物线的对称轴与直线l 交于点M ,与直线AC 交于点N .当DMN AOC S S =△△时,请直接写出DM 的长.【答案】(1)点A 的坐标为()6,0-,点B 的坐标为()2,0,点C 的坐标为()0,6-,直线AC 的函数表达式为:6y x =--;直线BC 的函数表达式为:36y x =-;(2)①存在,点E 的坐标为()6,8--或(2-;②【分析】(1)分别令0y =和0x =时即可求解A ,B ,C 三点的坐标,然后再进行求解直线AC ,BC 的函数表达式即可;(2)①设点D 的坐标为(),6m m --,其中60m -<<,由题意易得222(2)(6)BD m m =-++,2222640BC =+=,22222DC m m m =+=,当DE BC =时,以D ,C ,B ,E 为顶点的四边形是平行四边形,进而可根据菱形的性质分当BD BC =时,BDEC 是菱形,当CD CB =时,CBED 是菱形,然后分别求解即可;②由题意可作图,则由题意可得抛物线的对称轴为直线2x =-,由(1)可得直线AC 的函数表达式为:6y x =--;直线BC 的函数表达式为:36y x =-,点A 的坐标为()6,0-,点C 的坐标为()0,6-,进而可得166182AOC S =⨯⨯= ,设点()2,M m -,然后可求得直线l 的解析式为36y x m =++,则可求得点1212,44m m D +-⎛⎫- ⎪⎝⎭,所以就有4MN m =+,最后根据面积公式及两点距离公式可进行求解.【详解】解:(1)当0y =时,212602x x +-=,解得16x =-,22x =,∵点A 在点B 的左侧,∴点A 的坐标为()6,0-,点B 的坐标为()2,0,当0x =时,6y =-,∴点C 的坐标为()0,6-,设直线AC 的函数表达式为y kx b =+,代入点A、C 的坐标得:606k b b -+=⎧⎨=-⎩,解得:16k b =-⎧⎨=-⎩,∴直线AC 的函数表达式为:6y x =--.同理可得直线BC 的函数表达式为:36y x =-;(2)①存在.设点D 的坐标为(),6m m --,其中60m -<<,∵点B ,点C 的坐标分别为()2,0,()0,6-,∴222(2)(6)BD m m =-++,2222640BC =+=,22222DC m m m =+=,∵//DE BC ,∴当DE BC =时,以D ,C ,B ,E 为顶点的四边形是平行四边形,当BD BC =时,BDEC 是菱形,如图所示:∴()()222640m m -++=,解得14m =-,20m =(舍去),∴点D 的坐标为()4,2--,∴点E 的坐标为()6,8--;当CD CB =时,CBED 是菱形,如图所示:∴2240m =,解,得125m =-225m =(舍去),∴点D 的坐标为()25,256-,∴点E 的坐标为(25,5-;综上所述,存在点E ,使得以D ,B ,C ,E 为顶点的四边形为菱形,且点E 的坐标为()6,8--或(225,25-;②由题意可得如图所示:由题意可得抛物线的对称轴为直线2x =-,由(1)可得直线AC 的函数表达式为:6y x =--;直线BC 的函数表达式为:36y x =-,点A 的坐标为()6,0-,点C 的坐标为()0,6-,∴点()2,4N --,6OA OC ==,∴166182AOC S =⨯⨯= ,设点()2,M m -,∵//l BC ,∴设直线l 的解析式为3y x b =+,把点M 的坐标代入得:6b m -+=,解得:6b m =+,∴直线l 的解析式为36y x m =++,∴联立直线l 与直线AC 的解析式得:636x x m --=++,解得:124m x +=-,∴12123644m m y m +-⎛⎫=⨯-++= ⎪⎝⎭,∴点1212,44m m D +-⎛⎫- ⎪⎝⎭,∵点P 是直线AC 下方抛物线上的一个动点,且18DMN AOC S S ==△△,∴点M 在点N 的上方才有可能,∴4MN m =+,∴()()241124218248DMNm m S m ++⎛⎫=⨯+⨯-+== ⎪⎝⎭ ,解得:128,16m m ==-(不符合题意,舍去),∴()()2,8,5,1M D ---,∴由两点距离公式可得DM ==.【点睛】本题主要考查二次函数的综合及菱形的性质,熟练掌握二次函数的综合及菱形的性质是解题的关键.5.如图所示,抛物线与x 轴交于A、B 两点,与y 轴交于点C,且2OA =,4OB =,8OC =,抛物线的对称轴与直线BC 交于点M,与x 轴交于点N.(1)求抛物线的解析式;(2)若点P 是对称轴上的一个动点,是否存在以P、C、M 为顶点的三角形与MNB 相似?若存在,求出点P 的坐标,若不存在,请说明理由.(3)D 为CO 的中点,一个动点G 从D 点出发,先到达x 轴上的点E,再走到抛物线对称轴上的点F,最后返回到点C.要使动点G 走过的路程最短,请找出点E、F 的位置,写出坐标,并求出最短路程.(4)点Q 是抛物线上位于x 轴上方的一点,点R 在x 轴上,是否存在以点Q 为直角顶点的等腰Rt CQR △?若存在,求出点Q 的坐标,若不存在,请说明理由.【答案】(1)228y x x =-++;(2)存在,()1,2P 或171,2P ⎛⎫ ⎪⎝⎭;(3)点()2,0,1,23E F ⎛⎫ ⎪⎝⎭,最短路程为Q 为直角顶点的等腰Rt CQR △时,点Q ⎝⎭或3322Q ⎛⎫ ⎪ ⎪⎝⎭,理由见详解.【分析】(1)由题意易得()()()2,0,4,0,0,8A B C -,然后设二次函数的解析式为()()24y a x x =+-,进而代入求解即可;(2)由题意易得BMN CMP ∠=∠,要使以点P、C、M 为顶点的三角形与△MNB 相似,则可分①当90CPM MNB ∠=∠=︒时,②当90PCM MNB ∠=∠=︒时,进而分类求解即可;(3)由题意可得作点D 关于x 轴的对称点H,作点C 关于抛物线的对称轴的对称点I,然后连接HI,分别与x 轴、抛物线的对称轴交于点E、F,此时的点E、F 即为所求,HI 即为动点G 所走过的最短路程,最后求解即可;(4)由题意可分①当点Q 在第二象限时,存在等腰Rt CQR △,②当点Q 在第一象限时,存在等腰Rt CQR △,然后利用“k 型”进行求解即可.【详解】解:(1)∵2OA =,4OB =,8OC =,∴()()()2,0,4,0,0,8A B C -,设二次函数的解析式为()()24y a x x =+-,代入点C 的坐标可得:88a -=,解得:1a =-,∴二次函数的解析式为()()24y x x =-+-,即为228y x x =-++;(2)存在以点P、C、M 为顶点的三角形与△MNB 相似,理由如下:由(1)可得抛物线的解析式为228y x x =-++,则有对称轴为直线1x =,设直线BC 的解析式为y kx b =+,代入点B、C 坐标可得:408k b b +=⎧⎨=⎩,解得:28a b =-⎧⎨=⎩,∴直线BC 的解析式为28y x =-+,∴点()1,6M ,()1,0N ,∴由两点距离公式可得3,6,BN MN BM CM ===若使以点P、C、M 为顶点的三角形与△MNB 相似,则有BMN CMP ∠=∠,①当90CPM MNB ∠=∠=︒时,则有//CP x 轴,如图所示:∴点()1,8P ,②当90PCM MNB ∠=∠=︒时,如图所示:∴35562 PM BMCM MN===,∴52 PM=,∴点17 1,2P⎛⎫ ⎪⎝⎭;(3)由题意得:动点G从点D出发,先到达x轴上的点E,再走到抛物线对称轴上的点F,最后返回到点C.根据轴对称的性质及两点之间线段最短可知要使点G走过的路程最短则有作点D关于x轴的对称点H,作点C关于抛物线的对称轴的对称点I,然后连接HI,分别与x轴、抛物线的对称轴交于点E、F,此时的点E、F即为所求,HI即为动点G所走过的最短路程,如图所示:∵OC=8,点D 为CO 的中点,∴OD=4,∴()0,4D ,∵抛物线的对称轴为直线1x =,∴()()2,8,0,4I H -,设直线HI 的解析式为y kx b =+,则把点H、I 坐标代入得:284k b b +=⎧⎨=-⎩,解得:64k b =⎧⎨=-⎩,∴直线HI 的解析式为64y x =-,当y=0时,则有064x =-,解得:23x =,当x=1时,则有6142y =⨯-=,∴点()2,0,1,23E F ⎛⎫ ⎪⎝⎭,∴点G 走过的最短路程为()()222084237HI -++=(4)存在以点Q 为直角顶点的等腰Rt CQR △,理由如下:设点()2,28Q a a a -++,则有:①当点Q 在第二象限时,存在等腰Rt CQR △时,如图所示:过点Q 作QL⊥x 轴于点L,过点C 作CK⊥QL,交其延长线于点K,如图所示,∴90CKQ QLR LOC ∠=∠=∠=︒,∴四边形COLK 是矩形,∴CK=OL,∵等腰Rt CQR △,∴,90CQ QR CQR =∠=︒,∴90CQK KCQ CQK LQR ∠+∠=∠+∠=︒,∴KCQ LQR ∠=∠,∴()KCQ LQR AAS ≌,∴QL CK =,∴QL CK OL ==,∵点()2,28Q a a a -++,∴228a a a -=-++,解得:12a a ==∴Q ⎝⎭;②当点Q 在第一象限时,存在等腰Rt CQR △时,如图所示:同理①可得228a a a =-++,解得:12a a =(不符合题意,舍去),∴Q ⎝⎭;综上所述:当以点Q 为直角顶点的等腰Rt CQR △时,点Q ⎝⎭或3322Q ⎛⎫ ⎪ ⎪⎝⎭.【点睛】本题主要考查二次函数的综合、相似三角形的性质与判定、轴对称的性质及等腰直角三角形的性质,熟练掌握二次函数的综合、相似三角形的性质与判定、轴对称的性质及等腰直角三角形的性质是解题的关键.6.如图,已知抛物线2y x x 2=--交x 轴于A 、B 两点,将该抛物线位于x 轴下方的部分沿x 轴翻折,其余部分不变,得到的新图象记为“图象W ”,图象W 交y 轴于点C .(1)写出图象W 位于线段AB 上方部分对应的函数关系式;(2)若直线y x b =-+与图象W 有三个交点,请结合图象,直接写出b 的值;(3)P 为x 轴正半轴上一动点,过点P 作PM y ∥轴交直线BC 于点M ,交图象W 于点N ,是否存在这样的点P ,使CMN △与OBC 相似?若存在,求出所有符合条件的点P 的坐标;若不存在,请说明理由.【答案】(1)()2212y x x x =-++-≤≤(2)2b =或3b =(3)存在,()1,0或117,02⎛⎫ ⎪ ⎪⎝⎭或()15,0+【分析】(1)先求出点A、B、C 坐标,再利用待定系数法求解函数关系式即可;(2)联立方程组,由判别式△=0求得b 值,结合图象即可求解;(3)根据相似三角形的性质分∠CNM=90°和∠NCM=90°讨论求解即可.(1)解:由翻折可知:()0,2C .令220x x --=,解得:11x =-,22x =,∴()1,0A -,()2,0B ,设图象W 的解析式为()()12y a x x =+-,代入()0,2C ,解得1a =-,∴对应函数关系式为()()12y x x =-+-=22x x -++()12x -≤≤.(2)解:联立方程组22y x b y x x =-+⎧⎨=-++⎩,整理,得:2220x x b -+-=,由△=4-4(b-2)=0得:b=3,此时方程有两个相等的实数根,由图象可知,当b=2或b=3时,直线y x b =-+与图象W 有三个交点;(3)解:存在.如图1,当CN OB ∥时,OBC NMC △∽△,此时,N 与C 关于直线x=12对称,∴点N 的横坐标为1,∴()1,0P ;如图2,当CN OB ∥时,OBC NMC △∽△,此时,N 点纵坐标为2,由222x x --=,解得1x =212x =(舍),∴N 的横坐标为12+,所以12P ⎛⎫+ ⎪ ⎪⎝⎭;如图3,当90NCM ∠=︒时,OBC CMN △∽△,此时,直线CN 的解析式为2y x =+,联立方程组:222y x y x x =+⎧⎨=--⎩,解得11x =+21x =,∴N 的横坐标为1所以()1P +,因此,综上所述:P 点坐标为()1,0或1,02⎛⎫ ⎪ ⎪⎝⎭或()1.【点睛】本题考查二次函数的综合,涉及翻折性质、待定系数法求二次函数解析式、二次函数与一次函数的图象交点问题、相似三角形的性质、解一元二次方程等知识,综合体现数形结合思想和分类讨论思想的运用,属于综合题型,有点难度.题型二抛物线与线段有关问题7.在平面直角坐标系xoy 中,已知抛物线y=-x 2+bx+c 经过点A (-1,0)和点B (0,3),顶点为C,点D 在其对称轴上,且位于点C 下方,将线段DC 绕点D 按顺时针方向旋转90°,点C 落在抛物线上的点P 处.(1)求抛物线的解析式;(2)求点P 的坐标;(3)将抛物线平移,使其顶点落在原点O,这时点P 落在点E 的位置,在y 轴上是否存在点M,使得MP+ME 的值最小,若存在,求出点M 的坐标;若不存在,请说明理由.【答案】(1)2y x 2x 3=-++(2)(2,3)P (3)存在,1(0,)3M 【分析】(1)根据点,A B 的坐标,利用待定系数法即可得;(2)先求出抛物线的对称轴,再设点D 的坐标为(1,)(4)D a a <,则4CD a =-,根据旋转的性质可得90,4CDP PD CD a ∠=︒==-,从而可得(5,)P a a -,将点P 代入抛物线的解析式求出a 的值,由此即可得;(3)先根据点坐标的平移规律求出点(1,1)E -,作点E 关于y 轴的对称点E ',连接PE ',从而可得PE '与y 轴的交点即为所求的点M ,再利用待定系数法求出直线PE '的解析式,由此即可得出答案.(1)解:将点(1,0),(0,3)A B -代入2y x bx c =-++得:103b c c --+=⎧⎨=⎩,解得23b c =⎧⎨=⎩,则抛物线的解析式为2y x 2x 3=-++.(2)解:抛物线2223(1)4y x x x =-++=--+的对称轴为直线1x =,其顶点C 的坐标为(1,4)C ,设点D 的坐标为(1,)(4)D a a <,则4CD a =-,由旋转的性质得:90,4CDP PD CD a ∠=︒==-,(14,)P a a ∴+-,即(5,)P a a -,将点(5,)P a a -代入2(1)4y x =--+得:2(51)4a a ---+=,解得3a =或4a =(舍去),当3a =时,5532a -=-=,所以点P 的坐标为(2,3)P .(3)解:抛物线2y x 2x 3=-++的顶点C 的坐标为(1,4)C ,则将其先向左平移1个单位长度,再向下平移4个单位长度恰好落在原点O ,这时点P 落在点E 的位置,且(2,3)P ,(21,34)E ∴--,即(1,1)E -,恰好在对称轴直线1x =上,如图,作点E 关于y 轴的对称点E ',连接PE ',则MP ME MP ME '+=+,由两点之间线段最短可知,PE '与y 轴的交点即为所求的点M ,此时MP ME '+的值最小,即MP ME +的值最小,由轴对称的性质得:(1,1)E '--,设直线PE '的解析式为y kx m =+,将点(2,3)1,(,1)E P '--代入得:231k m k m +=⎧⎨-+=-⎩,解得4313k m ⎧=⎪⎪⎨⎪=⎪⎩,则直线PE '的解析式为4133y x =+,当0x =时,13y =,故在y 轴上存在点M ,使得MP ME +的值最小,此时点M 的坐标为1(0,)3M .【点睛】本题考查了求二次函数的解析式、二次函数的图象与性质、旋转的性质、点坐标的平移规律等知识点,熟练掌握待定系数法和二次函数的图象与性质是解题关键.8.抛物线21y x =-交x 轴于A ,B 两点(A 在B的左边).(1)ACDE 的顶点C 在y 轴的正半轴上,顶点E 在y 轴右侧的抛物线上.①如图(1),若点C 的坐标是()0,3,点E 的横坐标是32,直接写出点A ,D 的坐标;②如图(2),若点D 在抛物线上,且ACDE 的面积是12,求点E 的坐标;(2)如图(3),F 是原点O 关于抛物线顶点的对称点,不平行y 轴的直线l 分别交线段AF ,BF (不含端点)于G ,H 两点,若直线l 与抛物线只有一个公共点,求证FG FH +的值是定值.【答案】(1)①()1,0A -,517,24D ⎛⎫ ⎪⎝⎭;②点E 的坐标是()2,3.(2)见解析【分析】(1)①根据函数图象与x 轴的交点,令y=0,求出()1,0A -,点E 在抛物线上,求出纵坐标为54,再根据平行四边形的性质,求出517,24D ⎛⎫ ⎪⎝⎭;②连CE ,过点E 作x 轴垂线,垂足为M ,过点C 作CN EM ⊥,垂足为N ,设点C 坐标为()0,n ,点E 坐标为()2,1m m -,根据平行四边形的性质,与点在抛物线上,得到221(1)1m n m -+=+-,再由则AMNC ACE AME CNE S S S S =--△△△梯形,列出方程求解;(2)方法一:先求出G、H 两点的横坐标,再利用()1sin sin sin G H H G x x FG FH x x AFO BFO AFO -+==-∠∠∠求解即可;方法二:先用待定系数法求出直线BF 与直线l 的表达式,根据直线l 与抛物线有唯一的交点,求出点H 坐标为1,12m m +⎛⎫- ⎪⎝⎭,点G 坐标为1,12m m -⎛⎫-- ⎪⎝⎭,再求出结果.【详解】(1)解:①∵抛物线21y x =-交x 轴于A ,B 两点(A 在B 的左边),∴令21y x =-=0,解得:121,1x x =-=,AF BF =∴()1,0A -,∵点E 在抛物线上,点E 的横坐标是32,∴235()124y =-=,∵四边形ACDE 是平行四边形,∴35+1,+324D 骣琪琪桫∴517,24D ⎛⎫ ⎪⎝⎭;②设点C 坐标为()0,n ,点E 坐标为()2,1m m -.∵四边形ACDE 是平行四边形,∴将AC 沿AE 平移可与ED 重合,点D 坐标为()21,1m m n +-+.∵点D 在抛物线上,∴221(1)1m n m -+=+-.解得,21n m =+,所以()0,21C m +.连CE ,过点E 作x 轴垂线,垂足为M ,过点C 作CN EM ⊥,垂足为N .则AMNC ACE AME CNE S S S S =--△△△梯形,∵12ACDE S = ,()1,0A -,∴()()221116(1)(21)(1)1211222m m m m m m m m ⎡⎤=+++-+--+--⎣⎦.∴23100m m +-=,解得12m =,25m =-(不合题意,舍去).∴点E 的坐标是()2,3.(2)方法一:证明:依题意,得()10B ,,()0,2F -,∴设直线BF 解析式为y kx b =+,则02k b b +=⎧⎨=-⎩,解得22k b =⎧⎨=-⎩.∴直线BF 的解析式为22y x =-.同理,直线AF 的解析式为22y x =--.设直线l 的解析式为y tx n =+.联立21y tx n y x =+⎧⎨=-⎩,消去y 得210x tx n ---=.∵直线l 与抛物线只有一个公共点,∴2()4(1)0t n =----= ,214t n =--.联立22214y x t y tx =-⎧⎪⎨=--⎪⎩,且2t ≠,解得,24H t x +=,同理,得24G t x -=.∵A ,B 两点关于y 轴对称,∴AFO BFO ∠=∠.∴()1sin sin sin G H H G x x FG FH x x AFO BFO AFO-+=+=-=∠∠∠∴FG FH +方法二:证明:同方法一得直线BF 的解析式为22y x =-.设直线l 的解析式为y px q =+,l 与抛物线唯一公共点为()2,1m m -.联立21y px q y x =+⎧⎨=-⎩,消去y 得210x px q ---=,∴1m m p mm q +=⎧⎨=--⎩.解得221p m q m =⎧⎨=--⎩.∴直线l 的解析式为221y mx m =--.联立22122y mx m y x ⎧=--⎨=-⎩,且1m ≠,解得121m x y m +⎧=⎪⎨⎪=-⎩.∴点H 坐标为1,12m m +⎛⎫- ⎪⎝⎭.同理,点G 坐标为1,12m m -⎛⎫-- ⎪⎝⎭.∵11m -<<,∴(1)(1)22FG FH m m +=-++=∴FG FH +【点睛】本题是二次函数综合题,主要考查二次函数、一次函数、三角形面积、方程组等知识点,解题的关键是学会利用参数,学会用方程组求两个函数图象的交点坐标,学会把问题转化为方程解决,属于压轴题.9.在平面直角坐标系中,O 为坐标原点,直线3y x =-+与x 轴交于点B,与y 轴交于点C,二次函数2y ax 2x c =++的图象过B、C 两点,且与x 轴交于另一点A,点M 为线段OB 上的一个动点,过点M 作直线l 平行于y 轴交BC 于点F,交二次函数2y ax 2x c =++的图象于点E.(1)求二次函数的表达式;(2)当以C、E、F 为顶点的三角形与ABC 相似时,求线段EF 的长度;(3)已知点N 是y 轴上的点,若点N、F 关于直线EC 对称,求点N 的坐标.【答案】(1)2y x 2x 3=-++;(2)209或94;(3)N(0,1)【分析】(1)先求出B(3,0),C(0,3),再利用待定系数法即可求解;(2)先推出∠MBF=∠FBM=∠CFE=45°,可得以C、E、F 为顶点的三角形与ABC 相似时,EF CF AB CB =或CF CF AB EB =,设F(m,-m+3),则E(m,223m m -++),根据比例式列出方程,即可求解;(3)先推出四边形NCFE 是平行四边形,再推出FE=FC,列出关于m 的方程,求出m 的值,从而得CN=EF=2,进而即可得到答案.【详解】解:(1)∵直线3y x =-+与x 轴交于点B,与y 轴交于点C,∴B(3,0),C(0,3),∵二次函数2y ax 2x c =++的图象过B、C 两点,∴3096c a c =⎧⎨=++⎩,解得:31c a =⎧⎨=-⎩,∴二次函数解析式为:2y x 2x 3=-++;(2)∵B(3,0),C(0,3),l∥y 轴,∴OB=OC,∴∠MBF=∠FBM=∠CFE=45°,∴以C、E、F 为顶点的三角形与ABC 相似时,EF CF AB CB =或CF EF AB CB =,设F(m,-m+3),则E(m,223m m -++),∴EF=223m m -++-(-m+3)=23m m -+=,∴234m m -+=24=∴53m =或0m =(舍去)或32m =或0m =(舍去),∴EF=23m m -+=209或94;(3)∵l∥y 轴,点N 是y 轴上的点,∴∠EFC=∠NCG,∵点N、F 关于直线EC 对称,∴∠CNE=∠EFC,∴∠CNE=∠NCG,∴NE∥FC,∴四边形NCFE 是平行四边形,∵点N、F 关于直线EC 对称,∴∠NCE=∠FCE,∵l∥y 轴,∴∠NCE=∠FEC,∴∠FCE=∠FEC,∴FE=FC,∴23m m -+,解得:3m =0m =(舍去),∴CN=EF=2,∴ON=2+3=1+,∴N(0,1).【点睛】本题主要考查二次函数与几何的综合,相似三角形的判定,掌握函数图像上点的坐标特征,用点的横坐标表示出相关线段的长,是解题的关键.题型三抛物线与角度有关问题10.如图,在平面直角坐标系中,已知抛物线()240y ax bx a =++≠经过点()2,0A -和点()4,0B .(1)求这条抛物线所对应的函数表达式;(2)点P 为该抛物线上一点(不与点C 重合),直线CP 将ABC 的面积分成2:1两部分,求点P 的坐标;(3)点M 从点C 出发,以每秒1个单位的速度沿y 轴移动,运动时间为t 秒,当OCA OCB OMA ∠=∠-∠时,求t 的值.【答案】(1)2142y x x =-++;(2)点P (6,-8);(3)当点M 从点C 出发,以每秒1个单位的速度沿y 轴正方向移动时,=2t 秒;沿CO 方向在y 轴移动时,=10t 秒.【分析】(1)根据待定系数法将AB 两点坐标代入函数解析式求解即可;(2)在ABC 的AB 边上找到将AB 分成2:1两部分的点Q,此时CQ 将ABC 的面积分成2:1两部分,求出直线CQ 与抛物线交点坐标即是点P 坐标;(3)先利用图形在OCB ∠内构造A CB OCB OCA '∠=∠-∠,求出tan A CB '∠,在Rt OAM 中由tan =tan OMA A CB '∠∠,2OA =,求出OM 长即可解答,【详解】解:(1)由抛物线()240y ax bx a =++≠经过点()2,0A -和点()4,0B ,得:424=016440a b a b -+⎧⎨++=⎩,解得:1=21a b ⎧-⎪⎨⎪=⎩即:条抛物线所对应的函数表达式为:2142y x x =-++;(2)由(1)可知点C 坐标为(0,4)∵点()2,0A -和点()4,0B .∴6AB =,∴将AB 分成2:1两部分的点有原点和Q(2,0),此时CQ 将ABC 的面积分成2:1两部分,如解(2)图,∵点P 为该抛物线上一点(不与点C 重合),∴直线CP 经过Q 点,设直线CP 解析式为:y kx b =+,经过C(0,4),Q(2,0)两点,得:=42=0b k b ⎧⎨+⎩,∴=4=2b k ⎧⎨-⎩,即可设直线CP 解析式为:24y x =-+,联立函数解析式为:214224y x x y x ⎧=-++⎪⎨⎪=-+⎩,解得:1104x y =⎧⎨=⎩,2268x y =⎧⎨=-⎩,故P 点坐标为(6,-8),(3)如解(3)图取点A 关于y 轴对称点A ',连接CA ',过点A '作A H BC '⊥,垂足为H,由轴对称性质可知:2OA OA '==,A CO ACO '∠=∠,∴A CB BCO A CO BCO ACO ''∠=∠-∠=∠-∠,∵OCA OCB OMA ∠=∠-∠,即OMA OCB OCA ∠=∠-∠,∴OMA A CB'∠=∠∵4OB OC ==,90BOC ∠=°,∴45OCB OBC ∠=∠=︒,2BA '=,BC =∴HB HA '==∴HC BC BH =-=,∴1tan tan 3A H OMA A CB CH ''∠=∠==,∴126tan 3OA OM OMA ==÷=∠,点M 从点C 出发,以每秒1个单位的速度远动:当沿y 轴正方向移动时,=642MC OM OC =--=,则=2t 秒,当沿y 轴CO 方向移动时,64=10MC OM OC =+=+,则=10t 秒,综上所述:当点M 从点C 出发,以每秒1个单位的速度沿y 轴正方向移动时,=2t 秒;沿CO 方向在y 轴移动时,=10t 秒.【点睛】本题主要考查了二次函数与几何综合,问题(1)关键是在三角形边上找到将ABC 的面积分成2:1两部分直线CP 经过的点,问题(3)关键是通过对称构造A CB OMA '∠=∠,再通过解三角形求解OM 长.11.如图,在平面直角坐标系中,抛物线24y x x =-+经过坐标原点,与x 轴正半轴交于点A,点(,)M m n 是抛物线上一动点.(1)如图1,当0m >,0n >,且3n m =时,①求点M 的坐标:②若点15,4B y ⎛⎫ ⎪⎝⎭在该抛物线上,连接OM,BM,C 是线段BM 上一动点(点C 与点M,B 不重合),过点C 作//CD MO ,交x 轴于点D,线段OD 与MC 是否相等?请说明理由;(2)如图2,该抛物线的对称轴交x 轴于点K,点7,3E x ⎛⎫ ⎪⎝⎭在对称轴上,当2m >,0n >,且直线EM 交x 轴的负半轴于点F 时,过点A 作x 轴的垂线,交直线EM 于点N,G 为y 轴上一点,点G 的坐标为180,5⎛⎫ ⎪⎝⎭,连接GF.若2EF NF MF +=,求证:射线FE 平分AFG ∠.【答案】(1)①(1,3)M ;②OD MC =,见解析;(2)见解析【分析】(1)①直接将点(,)M m n 代入解析式,又有3n m =,即可解出坐标;②相等,先求出点B ,由两点求出直线的方程,添加辅助线构建直角三角形,利用勾股定理求出边长,证明三角形是等腰三角形即可;(2)根据已知条件求出点,E M 的坐标,再求出所在直线的解析式,求出直线与y 轴的交点,添加辅助线,利用三角形相似对应边成比例,找到边与边之间的关系,在直角三角形中利用勾股定理建立等式求出边长,再根据角平分线上的点到两条线之间的距离相等,即可判断出为角平分线.【详解】解:(1)如答案图6.① 点(,)M m n 在抛物线上,且3n m =,243m m m ∴-+=,解得10m =,(舍去)21m =,3n ∴=,(1,3)M ∴.②OD MC =,点15(,)4B y 在该抛物线上,1516y ∴=,1515(,416B ∴.设直线MB 交x 轴于点H,解析式为11y k x b =+,11113,1515.416k b k b +=⎧⎪∴⎨+=⎪⎩解得113,415.4k b ⎧=-⎪⎪⎨⎪=⎪⎩31544y x ∴=-+当0y =时,5x =,(5,0)H ∴,5OH ∴=.过点M 作MR x ⊥轴,垂足为R,1OR ∴=,3MR =,4RH ∴=,∴根据勾股定理得5MH =,OH MH ∴=,HOM HMO ∴∠=∠.CD MO ∥,HOM HDC ∴∠=∠,HMO HCD ∠=∠,HDC HCD ∴∠=∠,HD HC ∴=,OD MC ∴=.(2)如答案图7.证明:对称轴422(1)x =-=⨯-,72,3E ⎛⎫∴ ⎪⎝⎭,2EF NF MF += ,NF MF MF EF ∴-=-,MN ME ∴=.过点M 作MQ x ⊥轴,垂足为Q,EK MQ NA ∴∥∥,QK ME QA MN∴=,QK QA ∴=.当240-+=x x 时,解得10x =,24x =,(4,0)A ∴.(2,0)K ,(,0)Q m ,24m m ∴-=-,3m ∴=.23433n ∴=-+⨯=,(3,3)M ∴.设直线EM 的解析式为22y k x b =+,22227233 3.k b k b ⎧+=⎪∴⎨⎪+=⎩解得222,31.k b ⎧=⎪⎨⎪=⎩213y x ∴=+.设直线EM 交y 轴于点S,过点S 作SP GF ⊥,垂足为P .当0x =时,1y =.(0, 1)S ∴.当0y =时,32x =-,3(,0)2F ∴-,32∴=OF ,1OS =.180,5G ⎛⎫ ⎪⎝⎭,185OG ∴=,135GS ∴=.90GPS GOF ∠=∠=︒ ,PGS OGF ∠=∠,GPS GOF ∴△∽△,GP PS GO OF ∴=,125GP PS ∴=.设12GP a =,则5PS a =.在Rt GPS △中,222GP PS GS += ,22213(12)(5)()5a a ∴+=.15a ∴=±(负值舍去),15a ∴=,1PS ∴=,PS OS ∴=.SP GF ⊥ ,SO AF ⊥,∴射线FE 平分AFG ∠.【点睛】本题考查了一次函数和二次函数的综合运用,还涉及等腰三角形的性质、直角三角形、相似三角形的判定与性质、角平分线的判定,题目综合性强,涉及知识点多、难度较大,解题的关键是:掌握以上相关知识点后,需要做到灵活运用,同时考查了添加辅助线的能力.题型四抛物线与四边形有关问题12.已知抛物线2y x bx c =++.(1)如图①,若抛物线图象与x 轴交于点()3,0A ,与y 轴交点()0,3B -.连接AB .①求该抛物线所表示的二次函数表达式;②若点P 是抛物线上一动点(与点A 不重合),过点P 作PH x ⊥轴于点H ,与线段AB 交于点M .是否存在点P 使得点M 是线段PH 的三等分点?若存在,请求出点P 的坐标;若不存在,请说明理由.(2)如图②,直线43y x n =+与y 轴交于点C ,同时与抛物线2y x bx c =++交于点()3,0D -,以线段CD 为边作菱形CDFE ,使点F 落在x 轴的正半轴上,若该抛物线与线段CE 没有交点,求b 的取值范围.【答案】(1)①223y x x =--,②存在,点P 坐标为(2,-3)或(12,-154),理由见解析(2)b<32-或b>133【分析】(1)①直接用待定系数法求解;②先求出直线AB 的解析式,设点M(m,m-3)点P (m,m 2-2m-3)若点M 是线段PH 的三等分点,则13HM HP =或23HM HP =,代入求解即可;(2)先用待定系数法求出n 的值,再利用勾股定理求出CD 的长为5,因为四边形CDFE 是菱形,由此得出点E 的坐标.再根据该抛物线与线段CE 没有交点,分两种情况(CE 在抛物线内和CE 在抛物线右侧)进行讨论,求出b 的取值范围.(1)①解:把()3,0A ,()0,3B -代入2y x bx c =++,得20333b cc ⎧=++⎨-=⎩,解得:23b c =-⎧⎨=-⎩,∴223y x x =--②解:存在,理由如下,设直线AB 的解析式为y=kx+b,把()3,0A ,()0,3B -代入,得303k b b +=⎧⎨=-⎩,解得13k b =⎧⎨=-⎩,∴直线AB 的解析式为y=x-3,设点M(m,m-3)、点P(m,m 2-2m-3)若点M 是线段PH 的三等分点,则13HMHP =或23HM HP =,即232331m m m -=--或232332m m m -=--,解得:m=2或m=12或m=3,经检验,m=3是原方程的增根,故舍去,∴m=2或m=12∴点P 坐标为(2,-3)或(12,-154)(2)解:把点D(-3,0)代入直线43y x n =+,解得n=4,∴直线443y x =+,当x=0时,y=4,即点C(0,4)∵四边形CDFE 是菱形,∴CE=EF=DF=CD=5,∴点E(5,4)∵点()3,0D -在抛物线2y x bx c =++上,∴(-3)2-3b+c=0,∴c=3b-9,∴239y b x bx =++-,∵该抛物线与线段CE 没有交点,分情况讨论当CE 在抛物线内时52+5b+3b-9<4解得:b<32-当CE 在抛物线右侧时,3b-9>4解得:b>133综上所述,b<32-或b>133【点睛】此题考查了二次函数和一次函数以及图形的综合,解题的关键是数形结合和分情况讨论.13.如图,在平面直角坐标系中,抛物线2y x bx c =-++交x 轴于点A 和()1,0C ,交y 轴于点()0,3B ,抛物线的对称轴交x 轴于点E ,交抛物线于点F .(1)求抛物线的解析式;(2)将线段OE 绕着点О沿顺时针方向旋转得到线段'OE ,旋转角为()090αα︒<<︒,连接'AE ,'BE ,求13''BE AE +的最小值.(3)M 为平面直角坐标系中一点,在抛物线上是否存在一点N ,使得以A ,B ,M ,N 为顶点的四边形为矩形?若存在,请直接写出点N 的横坐标;若不存在,请说明理由;【答案】(1)223y x x =--+;(3)存在,N 点的横坐标分别为:2,1-【分析】(1)待定系数法求二次函数解析式,设解析式为2y x bx c =-++将()1,0C ,()0,3B 两点代入求得b ,c 的值即可;(2)胡不归问题,要求13''BE AE +的值,将折线化为直线,构造相似三角形将13'AE 转化为13'DE ,再利用三角形两边之和大于第三边求得13''BE AE +最值;。
中考数学难点探究专题复习抛物线与几何图形的综合(选做)

难点探究专题:抛物线与几何图形的综合(选做) ——代几结合,突破面积及点的存在性问题◆类型一二次函数与三角形的综合一、全等三角形的存在性问题1.如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:(1)求抛物线的解析式;(2)若抛物线与x轴的两个交点为A,B,与y轴交于点C.在该抛物线上是否存在点D,使得△ABC与△ABD全等?若存在,求出D点的坐标;若不存在,请说明理由.二、线段(或周长)的最值问题及等腰三角形的存在性问题2.(凉山州中考)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.◆类型二二次函数与平行四边形的综合3.如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B 两点,A点在B点左侧.若点E在x轴上,点P在抛物线上,且以A,C,E,P 为顶点的四边形是平行四边形,则符合条件的点P有()A.1个B.2个C.3个D.4个4.如图,抛物线y=12x2+x-32与x轴相交于A,B两点,顶点为P.(1)求点A,B的坐标;(2)在抛物线上是否存在点E,使△ABP的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由;(3)坐标平面内是否存在点F,使得以A,B,P,F为顶点的四边形为平行四边形?直接写出所有符合条件的点F的坐标.◆类型三 二次函数与矩形、菱形、正方形的综合5.如图,在平面直角坐标系中,点A 在抛物线y =x 2-2x +2上运动.过点A 作AC ⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,连接BD ,则对角线BD 的最小值为________.第5题图 第6题图6.如图,抛物线y =ax 2-x -32与x 轴正半轴交于点A(3,0).以OA 为边在x 轴上方作正方形OABC ,延长CB 交抛物线于点D ,再以BD 为边向上作正方形BDEF.则a =,点E 的坐标是_________________.7. (新疆中考)如图,对称轴为直线x =72的抛物线经过点A(6,0)和B(0,-4).(1)求抛物线的解析式及顶点坐标;(2)设点E(x ,y)是抛物线上一动点,且位于第一象限,四边形OEAF 是以OA 为对角线的平行四边形,求平行四边形OEAF 的面积S 与x 之间的函数关系式;(3)当(2)中的平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形.8.(百色中考)正方形OABC的边长为4,对角线相交于点P,抛物线l经过O,P,A三点,点E是正方形内的抛物线l上的动点.(1)建立适当的平面直角坐标系,①直接写出O,P,A三点的坐标;②求抛物线l的解析式;(2)求△OAE与△OCE面积之和的最大值.答案:。
初中数学抛物线与几何专题训练及答案

b , OC t t
b , t
6
∴ | OB | | OC | | (t 即t2
b t
b )( t t
b b 2 )| | t | t 2 OA 2 , t t
t 2 , 所以当 b 2 t 3 时, 存在抛物线 F 使得 | OA | 2 | OB | | OC | .-- 2 分
2
3、(青海西宁)如图,已知半径为 1 的 O1 与 x 轴交于 A,B 两点, OM 为 O1 的 y M
点. (1)求二次函数的解析式; (2)求切线 OM 的函数解析式;
4
O
A
O1
B x
( 3)线段 OM 上是否存在一点 P ,使得以 P,O,A 为顶点的三角形与 △OO1M 相 似.若存在,请求出所有符合条件的点 P 的坐标; 若不存在,请说明理由. 4、(辽宁 12 市)如图,在平面直角坐标b 的方程;(2)讨论
t 的取值范围,来求抛物线 F 对应的二次函数的解析式。
【例 2】(江苏常州)如图,抛物线 y x 4 x 与 x 轴分别相交于点 B、 O,它的顶点为 A,连
2
接 AB,把 AB 所的直线沿 y 轴向上平移,使它经过原点 O,得到直线 l,设 P 是直线 l 上一动点.
5
(2)求抛物线的函数表达式; (3)在 x 轴的上方是否存在点 P ,点 Q ,使以点 O,B,P,Q 为顶点的平行四边形的 面积是矩形 ABOC 面积的 2 倍,且点 P 在抛物线上,若存在,请求出点 P ,点 Q 的坐标; 若不存在,请说明理由.
7、(苏州市)如图,抛物线 y=a(x+1)(x-5)与 x 轴的交点为 M、N.直线 y=kx+b 与 x 轴 交 于 P(- 2, 0), 与 y 轴 交 于 C. 若 A、 B 两 点 在 直 线 y= kx+ b 上 , 且
中考总复习(抛物线载体下的几何图形)

【解题思路】延长EA,交y轴于点F,构造出 △AFC与△AED全等,从而得到AF=AE,根据B、 A点坐标特征分别用含m的代数式表示出线段AF、 AE、BF的长度,借助相似可求得DE的长度;
(3)①设点D的坐标为(x,y),求y关于x的函数解析式;
【解题思路】关键是能发现A、D两点的坐标特征,根据A点的坐 标写出D点的坐标,通过等量代换,寻求出y关于x的函数解析式.
(2)过点B作线段AB的垂线交抛物线于点 D,如果以点C为圆心 的圆与直线BD相切,请判断抛物线的对称轴l与OC的位置关系,并 给出证明; 【解题思路】分别求出圆的半径及圆心到直 线的距离即可判别直线与圆的位置关系
( 3 )在抛物线上是否存在一点 P ,使△ACP 是以 AC 为直角边的 三角形,若存在,求出点P的坐标;若不存在,请说明理由.
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点 P、A、N为顶点的三角形与△MAO相似?若存在,求点P的坐标; 若不存在,请说明理由. 【解题思路】在各个象限内,分类讨论 以点P、 A、 N为顶点的三角形与△MAO 相 似.因为没有相似的对应点,所以需要点在 不同象限内时,△PAN 的形状,确定出对 应边,然后利用相似三角形的性质得到对 应边相等.然后将对应边的长度转化为点的 坐标,从而确定点的坐标.
纵观近几年的中考试卷,在压轴题里面,以函数(特别是二次 函数)为载体,综合几何图形的题型是中考的热点和难点,这 类试题常常需要用到数形结合思想,转化思想,分类讨论思想 等,这类试题具有拉大考生分数差距的作用.它既突出考查了 初中数学的主干知识,又突出了与高中衔接的重要内容. 本课时主要研究抛物线与等腰三角形、直角三角形、相似三角 形、平行四边形的综合问题,解决这类试题的关键是弄清函数 与几何图形之间的联系,在解题的过程中,将函数问题几何化 .同时能够学会将大题分解为小题,逐个击破.
人教版九年级数学上册中考专题复习题含答案全套

人教版九年级数学上册中考专题复习题1.类比归纳专题:配方法的应用2.类比归纳专题:一元二次方程的解法3.易错易混专题:一元二次方程中的易错问题4.考点综合专题:一元二次方程与其他知识的综合5.解题技巧专题:抛物线中与系数a,b,c有关的问题6.易错易混专题:二次函数的最值或函数值的范围7.难点探究专题:抛物线与几何图形的综合(选做)8.抛物线中的压轴题9.易错专题:抛物线的变换10.解题技巧专题:巧用旋转进行计算11.旋转变化中的压轴题12.类比归纳专题:圆中利用转化思想求角度13.类比归纳专题:切线证明的常用方法14.解题技巧专题:圆中辅助线的作法15.解题技巧专题:圆中求阴影部分的面积16.考点综合专题:圆与其他知识的综合17.圆中的最值问题18.抛物线与圆的综合19.易错专题:概率与放回、不放回问题类比归纳专题:配方法的应用——体会利用配方法解决特定问题◆类型一 配方法解方程1.一元二次方程x 2-2x -1=0的解是( )A .x 1=x 2=1B .x 1=1+2,x 2=-1- 2C .x 1=1+2,x 2=1- 2D .x 1=-1+2,x 2=-1- 22.用配方法解下列方程时,配方有错误的是( )A .x 2-2x -99=0化为(x -1)2=100B .x 2+8x +9=0化为(x +4)2=25C .2t 2-7t -4=0化为⎝⎛⎭⎫t -742=8116 D .3x 2-4x -2=0化为⎝⎛⎭⎫x -232=1093.利用配方法解下列方程:(1)(2016·淄博中考)x 2+4x -1=0;(2)(x +4)(x +2)=2;(3)4x 2-8x -1=0;(4)3x 2+4x -1=0.◆类型二 配方法求最值或证明 4.代数式x 2-4x +5的最小值是( ) A .-1 B .1 C .2 D .55.下列关于多项式-2x 2+8x +5的说法正确的是( )A .有最大值13B .有最小值-3C .有最大值37D .有最小值1 6.(2016-2017·夏津县月考)求证:代数式3x 2-6x +9的值恒为正数.7.若M =10a 2+2b 2-7a +6,N =a 2+2b 2+5a +1,试说明无论a ,b 为何值,总有M >N .◆类型三 完全平方式中的配方 8.如果多项式x 2-2mx +1是完全平方式,则m 的值为( )A .-1B .1C .±1D .±29.若方程25x 2-(k -1)x +1=0的左边可以写成一个完全平方式,则k 的值为( )A .-9或11B .-7或8C .-8或9D .-6或7◆类型四 利用配方构成非负数求值 10.已知m 2+n 2+2m -6n +10=0,则m +n 的值为( )A .3B .-1C .2D .-211.已知x 2+y 2-4x +6y +13=0,求(x +y )2016的值.答案:类比归纳专题:一元二次方程的解法——学会选择最优的解法◆类型一 一元二次方程的一般解法方法点拨: 形如(x +m )2=n (n ≥0)的方程可用直接开平方法;当方程二次项系数为1,且一次项系数为偶数时,可用配方法;若方程移项后一边为0,另一边能分解成两个一次因式的积,可用因式分解法;如果方程不能用直接开平方法和因式分解法求解,则用公式法.1.用合适的方法解下列方程:(1)⎝⎛⎭⎫x -522-14=0;(2)x 2-6x +7=0;(3)x 2-22x +18=0;(4)3x (2x +1)=4x +2.◆*类型二 一元二次方程的特殊解法 一、十字相乘法方法点拨:例如:解方程:x 2+3x -4=0.第1种拆法:4x -x =3x (正确), 第2种拆法:2x -2x =0(错误), 所以x 2+3x -4=(x +4)(x -1)=0,即x +4=0或x -1=0,所以x 1=-4,x 2=1. 2.解一元二次方程x 2+2x -3=0时,可转化为解两个一元一次方程,请写出其中的一个一元一次方程____________.3.用十字相乘法解下列一元二次方程: (1)x 2-5x -6=0; (2)x 2+9x -36=0.二、换元法方法点拨:在已知或者未知条件中,某个代数式几次出现,可用一个字母来代替它从而简化问题,这就是换元法,当然有时候要通过变形才能换元.把一些形式复杂的方程通过换元的方法变成一元二次方程,从而达到降次的目的.4.若实数a ,b 满足(4a +4b )(4a +4b -2)-8=0,则a +b =_______.5.解方程:(x 2+5x +1)(x 2+5x +7)=7.1.解:(1)移项,得⎝⎛⎭⎫x -522=14, 两边开平方,得x -52=±14, 即x -52=12或x -52=-12,∴x 1=3,x 2=2;(2)移项,得x 2-6x =-7,配方,得x 2-6x +9=-7+9,即(x -3)2=2, 两边开平方,得x -3=±2, ∴x 1=3+2,x 2=3-2;(3)原方程可化为8x 2-42x +1=0. ∵a =8,b =-42,c =1,∴b 2-4ac =(-42)2-4×8×1=0, ∴x =-(-42)±02×8=24,∴x 1=x 2=24; |(4)原方程可变形为(2x +1)(3x -2) =0,∴2x +1=0或3x -2=0, ∴x 1=-12,x 2=23.2. x -1=0或x +3=0.3.解:(1)原方程可变形为(x -6)(x +1) =0,∴x -6=0或x +1=0, ∴x 1=6,x 2=-1;(2)原方程可变形为(x +12)(x -3) =0,∴x +12=0或x -3=0, ∴x 1=-12,x 2=3. 4.-12或15.解:设x 2+5x +1=t ,则原方程化为t (t +6)=7,∴t 2+6t -7=0,解得t =1或-7.当t =1时,x 2+5x +1=1,x 2+5x =0, x (x +5)=0,∴x =0或x +5=0,∴x 1=0,x 2=-5; 当t =-7时,x 2+5x +1=-7,x 2+5x +8=0,∴b 2-4ac =52-4×1×8<0,此时方程 无实数根.∴原方程的解为x 1=0,x 2=-5.易错易混专题:一元二次方程中的易错问题◆类型一 利用方程或其解的定义求待定系数时,忽略“a ≠0”1.(2016-2017·江都区期中)若关于x的方程(a +3)x |a |-1-3x +2=0是一元二次方程,则a 的值为______.【易错1】2.关于x 的一元二次方程(a -1)x 2+x +a 2-1=0的一个根是0,则a 的值是( )A .-1B .1C .1或-1D .-1或0 3.已知关于x 的一元二次方程(m -1)x 2+5x +m 2-3m +2=0的常数项为0.(1)求m 的值; (2)求方程的解.◆类型二 利用判别式求字母取值范围时,忽略“a ≠0”及“a 中的a ≥0”4.(2016-2017·抚州期中)若关于x 的一元二次方程(m -2)2x 2+(2m +1)x +1=0有解,那么m 的取值范围是( )A .m >34B .m ≥34C .m >34且m ≠2D .m ≥34且m ≠25.已知关于x 的一元二次方程x 2+k -1x -1=0有两个不相等的实数根,则k的取值范围是________.6.若m 是非负整数,且关于x 的方程(m -1)x 2-2x +1=0有两个实数根,求m 的值及其对应方程的根.◆类型三 利用根与系数关系求值时,忽略“Δ≥0”7.(2016·朝阳中考)关于x 的一元二次方程x 2+kx +k +1=0的两根分别为x 1,x 2,且x 21+x 22=1,则k 的值为_______.【易错2】 8.已知关于x 的方程x 2+2(m -2)x +m 2+4=0有两个实数根,且这两根的平方和比两根的积大21,求m 的值.【易错2】◆类型四 与三角形结合时忘记取舍 9.已知三角形两边长分别为2和9,第三边的长为一元二次方程x 2-14x +48=0的根,则这个三角形的周长为( )A .11B .17C .17或19D .1910.在等腰△ABC 中,三边分别为a ,b ,c ,其中a =5,若关于x 的方程x 2+(b +2)x +6-b =0有两个相等的实数根,求△ABC 的周长.考点综合专题:一元二次方程与其他知识的综合◆类型一一元二次方程与三角形、四边形的综合1.(雅安中考)已知等腰三角形的腰和底的长分别是一元二次方程x2-4x+3=0的根,则该三角形的周长可以是()A.5 B.7 C.5或7 D.102.(广安中考)一个等腰三角形的两条边长分别是方程x2-7x+10=0的根,则该等腰三角形的周长是()A.12 B.9C.13 D.12或93.(罗田县期中)菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为()A.16 B.12 C.16或12 D.244.(烟台中考)等腰三角形边长分别为a,b,2,且a,b是关于x的一元二次方程x2-6x+n-1=0的两根,则n的值为()A.9 B.10C.9或10 D.8或105.(齐齐哈尔中考)△ABC的两边长分别为2和3,第三边的长是方程x2-8x+15=0的根,则△ABC的周长是________.6.(西宁中考)若矩形的长和宽是方程2x2-16x+m=0(0<m≤32)的两根,则矩形的周长为_________.【方法8】7.已知一直角三角形的两条直角边是关于x的一元二次方程x2+(2k-1)x+k2+3=0的两个不相等的实数根,如果此直角三角形的斜边是5,求它的两条直角边分别是多少.【易错4】◆类型二一元二次方程与一次函数的综合8.(泸州中考)若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是()9.(安顺中考)若一元二次方程x2-2x -m=0无实数根,则一次函数y=(m+1)x +m-1的图象不经过()A.第四象限B.第三象限C.第二象限D.第一象限10.(葫芦岛中考)已知k、b是一元二次方程(2x+1)(3x-1)=0的两个根,且k>b,则函数y=kx+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限11.(广元中考)从3,0,-1,-2,-3这五个数中抽取一个数,作为函数y=(5-m2)x和关于x的一元二次方程(m+1)x2+mx+1=0中m的值.若恰好使函数的图象经过第一、三象限,且使方程有实数根,则满足条件的m的值是______.◆类型三一元二次方程与二次根式的综合12.(达州中考)方程(m-2)x2-3-mx +14=0有两个实数根,则m的取值范围为()A.m>52B.m≤52且m≠2C.m≥3 D.m≤3且m≠213.(包头中考)已知关于x的一元二次方程x2+k-1x-1=0有两个不相等的实数根,则k的取值范围是______.答案:12.B 13.解题技巧专题:抛物线中与系数a,b,c有关的问题◆类型一由某一函数的图象确定其他函数图象的位置1.二次函数y=-x2+ax-b的图象如图所示,则一次函数y=ax+b的图象不经过()A.第一象限B.第二象限C.第三象限D.第四象限第1题图第2题图2.已知一次函数y=-kx+k的图象如图所示,则二次函数y=-kx2-2x+k的图象大致是()3.已知函数y=(x-a)(x-b)(其中a>b)的图象如图所示,则函数y=ax+b的图象可能正确的是()第3题图第4题图4.如图,一次函数y1=x与二次函数y2=ax2+bx+c的图象相交于P,Q两点,则函数y=ax2+(b-1)x+c的图象可能是()◆类型二由抛物线的位置确定代数式的符号或未知数的值5.(2016·新疆中考)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是【方法10】()A.a>0B.c<0C.3是方程ax2+bx+c=0的一个根D.当x<1时,y随x的增大而减小第5题图第7题图6.(2016·黄石中考)以x为自变量的二次函数y=x2-2(b-2)x+b2-1的图象不经过第三象限,则实数b的取值范围是【方法10】()A.b≥54B.b≥1或b≤-1C.b≥2 D.1≤b≤27.(2016·孝感中考)如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数是()A.1个B.2个C.3个D.4个8.(2016·天水中考)如图,二次函数y =ax2+bx+c(a≠0)的图象与x轴交于A,B 两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②b2-4ac4a>0;③ac-b+1=0;④OA·OB =-ca .其中正确结论的序号是____________.答案:易错易混专题:二次函数的最值或函数值的范围——类比各形式,突破给定范围求最值◆类型一 没有限定自变量的范围求最值 1.函数y =-(x +1)2+5的最大值为_______. 2.已知二次函数y =3x 2-12x +13,则函数值y 的最小值是【方法11】( )A .3B .2C .1D .-13.已知函数y =x(2-3x),当x 为何值时,函数有最大值还是最小值?并求出最值.◆类型二 限定自变量的取值范围求最值4.(2016-2017·双台子区校级月考)函数y =x 2+2x -3(-2≤x ≤2)的最大值和最小值分别是( )A .4和-3B .-3和-4C .5和-4D .-1和-45.二次函数y =-12x 2+32x +2的图象如图所示,当-1≤x ≤0时,该函数的最大值是【方法11】( )A .3.125B .4C .2D .06.已知0≤x ≤32,则函数y =x 2+x +1( ) A .有最小值34,但无最大值B .有最小值34,有最大值1C .有最小值1,有最大值194D .无最小值,也无最大值◆类型三 限定自变量的取值范围求函数值的范围7.从y =2x 2-3的图象上可以看出,当-1≤x ≤2时,y 的取值范围是( )A .-1≤y ≤5B .-5≤y ≤5C .-3≤y ≤5D .-2≤y ≤18.已知二次函数y =-x 2+2x +3,当x ≥2时,y 的取值范围是( )A .y ≥3B .y ≤3C .y >3D .y <39.二次函数y =x 2-x +m(m 为常数)的图象如图所示,当x =a 时,y <0;那么当x =a -1时,函数值CA .y <0B .0<y <mC .y >mD .y =m◆类型四 已知函数的最值,求自变量的取值范围或待定系数的值10.当二次函数y =x 2+4x +9取最小值时,x 的值为( )A .-2B .1C .2D .911.已知二次函数y =ax 2+4x +a -1的最小值为2,则a 的值为( )A.3 B.-1C.4 D.4或-112.已知y=-x(x+3-a)+1是关于x 的二次函数,当x的取值范围在1≤x≤5时,y在x=1时取得最大值,则实数a的取值范围是()A.a=9 B.a=5 C.a≤9 D.a≤513.在△ABC中,∠A,∠B所对的边分别为a,b,∠C=70°.若二次函数y=(a+b)x2+(a+b)x-(a-b)的最小值为-a2,则∠A=_______度.14.★已知函数y=-4x2+4ax-4a-a2,若函数在0≤x≤1上的最大值是-5,求a的值.答案:难点探究专题:抛物线与几何图形的综合(选做)——代几结合,突破面积及点的存在性问题◆类型一二次函数与三角形的综合一、全等三角形的存在性问题1.如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:(1)求抛物线的解析式;(2)若抛物线与x轴的两个交点为A,B,与y轴交于点C.在该抛物线上是否存在点D,使得△ABC与△ABD全等?若存在,求出D点的坐标;若不存在,请说明理由.二、线段(或周长)的最值问题及等腰三角形的存在性问题2.(2016·凉山州中考)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P 的坐标;(3)点M也是直线l上的动点,且△MAC 为等腰三角形,请直接写出所有符合条件的点M的坐标.◆类型二二次函数与平行四边形的综合3.如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,A点在B点左侧.若点E在x轴上,点P 在抛物线上,且以A,C,E,P为顶点的四边形是平行四边形,则符合条件的点P有()A.1个B.2个C.3个D.4个4.如图,抛物线y=12x2+x-32与x轴相交于A,B两点,顶点为P.(1)求点A,B的坐标;(2)在抛物线上是否存在点E,使△ABP 的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由;(3)坐标平面内是否存在点F,使得以A,B,P,F为顶点的四边形为平行四边形?直接写出所有符合条件的点F的坐标.◆类型三 二次函数与矩形、菱形、正方形的综合5.如图,在平面直角坐标系中,点A 在抛物线y =x 2-2x +2上运动.过点A 作AC ⊥x 轴于点C ,以AC 为对角线作矩形ABCD ,连接BD ,则对角线BD 的最小值为________.第5题图 第6题图6.如图,抛物线y =ax 2-x -32与x 轴正半轴交于点A(3,0).以OA 为边在x 轴上方作正方形OABC ,延长CB 交抛物线于点D ,再以BD 为边向上作正方形BDEF.则a =,点E 的坐标是_________________.7. (2016·新疆中考)如图,对称轴为直线x =72的抛物线经过点A(6,0)和B(0,-4). (1)求抛物线的解析式及顶点坐标; (2)设点E(x ,y)是抛物线上一动点,且位于第一象限,四边形OEAF 是以OA 为对角线的平行四边形,求平行四边形OEAF 的面积S 与x 之间的函数关系式;(3)当(2)中的平行四边形OEAF 的面积为24时,请判断平行四边形OEAF 是否为菱形.8.(2016·百色中考)正方形OABC 的边长为4,对角线相交于点P ,抛物线l 经过O ,P ,A 三点,点E 是正方形内的抛物线l 上的动点.(1)建立适当的平面直角坐标系,①直接写出O ,P ,A 三点的坐标; ②求抛物线l 的解析式;(2)求△OAE 与△OCE 面积之和的最大值.答案:拔高专题抛物线中的压轴题一、基本模型构建常见模型思考在边长为1的正方形网格中有A, B, C三点,画出以A,B,C为其三个顶点的平行四边形ABCD。
中考复习专题之抛物线与图形结合专题(参数计算)
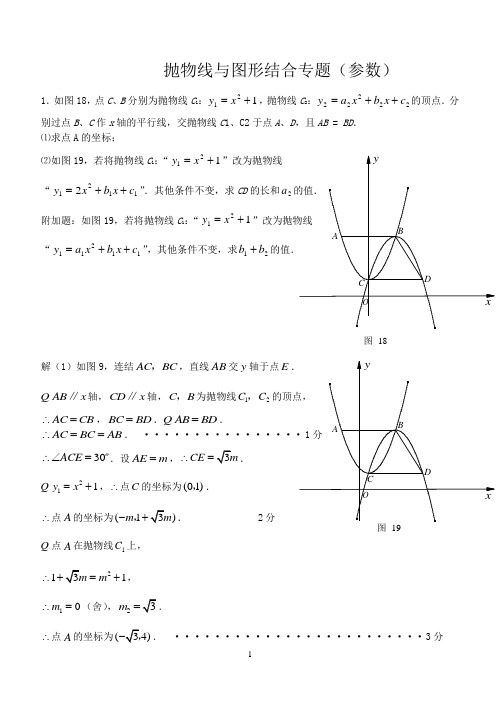
抛物线与图形结合专题(参数)1.如图18,点C 、B 分别为抛物线C 1:121+=x y ,抛物线C 2:22222c x b x a y ++=的顶点.分别过点B 、C 作x 轴的平行线,交抛物线C 1、C2于点A 、D ,且AB = BD . ⑴求点A 的坐标;⑵如图19,若将抛物线C 1:“121+=x y ”改为抛物线 “11212c x b x y ++=”.其他条件不变,求CD 的长和2a附加题:如图19,若将抛物线C 1:“121+=x y “11211c x b x a y++=”,其他条件不变,求21b b +解(1)如图9,连结AC BC ,,直线AB 交y 轴于点E AB x ∥轴,CD x ∥轴,C B ,为抛物线12C C ,AC CB ∴=,BC BD =.AB BD = .AC BC AB ∴==. 30ACE ∴∠= .设AE m =,CE ∴=.211y x =+ ,∴点C 的坐标为(01),. ∴点A 的坐标为(1)m -,. 2分 点A 在抛物线1C 上, 211m ∴=+,10m ∴=(舍),2m = ∴点A 的坐标为(. ·························3分 图 18(2)如图10,过点C 作CE AB ⊥于E . 设抛物线221111122()y x b x c x h k =++=-+,∴点C 的坐标为11()h k ,.设AE m =,CE ∴=.∴点A 的坐标为11()h m k -,.···················· 4分 点A 在抛物线21112()y x h k =-+上,211112()k h m h k ∴=--+.解得10m =(舍),22m =. ························ 5分 由(1)同理可得,CD BD BC AB ===. ·················· 6分2AB AE ==CD ∴CD ······················· 7分由题意得,点B 的坐标为11322h k ⎛⎫++ ⎪⎪⎝⎭.又 点B 是抛物线2C 的顶点,2221132y a x h k ⎛∴=--++ ⎝⎭. ······················ 8分 抛物线2C 经过点11()C h k ,,21211132k a h h k ⎛∴=--++ ⎝⎭. ······················ 9分 22a ∴=-,即2a 的值为2-. ······················· 10分附加解:如图10,设221111111()y a x b x c a x h k =++=-+,∴点C 的坐标为11()h k ,.过点C 作CE AB ⊥于E ,设AE m =,则CE =.∴点B的坐标为11()h m k +,.点B 在抛物线1C上,211111()k a h m h k ∴=+-+.0m ≠,1m ∴=∴点B的坐标为11113h k a ⎛⎫+ ⎪ ⎪⎝⎭. ···················· 1分 点B 为抛物线2C的顶点,22211113y a x h k a ⎛∴=-++ ⎝⎭. 抛物线2C 经过点11()C h k ,,212111113k a h h k a ⎛∴=-++ ⎝⎭. 21a a ∴=-.································ 2分22111113y a x h k a ⎛∴=--++ ⎝⎭22111111132a x h x h k a a a ⎡⎤⎛⎫⎛⎢⎥=--+++++ ⎪ ⎪ ⎢⎥⎝⎭⎝⎭⎣⎦.··············· 3分21112b a h ⎛∴= ⎝⎭. ···························4分1211122b b a a a ⎛∴=-+ ⎝⎭.21b b ∴=-+.12b b ∴+=12b b +的值为 ··················· 5分2.如图,抛物线F :y =ax2+bx +c 的顶点为P ,抛物线F 与y 轴交于点A ,与直线OP 交于点B .过点P 作PD ⊥x 轴于点D ,平移抛物线F 使其经过点A 、D 得到抛物线F ′:y =a ′x2+b ′x +c ′,抛物线F ′与x 轴的另一个交点为C .图10(1)当a =1,b =-2,c =3时,求点C 的坐标(直接写出答案);(2)若a 、b 、c 满足b2=2ac ,①求b :'b 的值;②探究四边形OABC 的形状,并说明理由.解:(1) C (3,0);…………………………………………………3分 (2)①抛物线c bx ax y ++=2,令x =0,则y =c , ∴A 点坐标(0,c ).∵ac b 22=,∴242424442ca ac a ac ac ab ac ==-=-, ∴点P 的坐标为(2,2ca b -). ……………………………………………………4分 ∵PD ⊥x 轴于D ,∴点D 的坐标为(0,2ab-). ……………………………………5分 根据题意,得a=a ′,c= c ′,∴抛物线F ′的解析式为c x b ax y ++='2.又∵抛物线F ′经过点D (0,2a b-),∴c a b b ab a +-+⨯=)2('4022.……………6分 ∴ac bb b 4'202+-=.又∵ac b 22=,∴'2302bb b -=.∴b :b ′=32.…………………………………………………………………………………7分②由①得,抛物线F ′为c bx ax y ++=232.令y=0,则0232=++c bx ax .………………………………………………………………8分∴abx a b x -=-=21,2.∵点D 的横坐标为,2a b -∴点C 的坐标为(0,ab-). ……………………………………9分 设直线OP 的解析式为kx y =.∵点P 的坐标为(2,2ca b -), ∴k a b c 22-=,∴22222b b b b ac b ac k -=-=-=-=,∴x by 2-=.………………………10分 ∵点B 是抛物线F 与直线OP 的交点,∴x bc bx ax 22-=++.∴abx a b x -=-=21,2.∵点P 的横坐标为a b 2-,∴点B 的横坐标为ab-.把a b x -=代入x by 2-=,得c a ac a b a b b y ===--=222)(22. ∴点B 的坐标为),(c ab-.…………………………………………………………………11分∴BC ∥OA ,AB ∥OC .(或BC ∥OA ,BC =OA ), ∴四边形OABC 是平行四边形.又∵∠AOC =90°,∴四边形OABC 是矩形. ………………………………………………12分3.如图17,抛物线F :2(0)y ax bx c a =++>与y 轴相交于点C ,直线1L 经过点C 且平行于x 轴,将1L 向上平移t 个单位得到直线2L ,设1L 与抛物线F 的交点为C 、D ,2L 与抛物线F 的交点为A 、B ,连接AC 、BC (1)当12a =,32b =-,1c =,2t =时,探究△ABC 的形状,并说明理由; (2)若△ABC 为直角三角形,求t 的值(用含a 的式子表示);(3)在(2)的条件下,若点A 关于y 轴的对称点A ’恰好在抛物线F 的对称轴上,连接A ’C ,BD ,求四边形A ’CDB 的面积(用含a 的式子表示)(1)213122y x x =-+ ,∴C 的坐标为(0,1),当t=2时,y=3,所以有2133122x x =-+,解得121; 4.x x =-= (1,3),(4,3)A B ∴-,5,CA CB AB ∴===222AB CB AC ∴=+,则△ABC 是直角三角形。
2024年中考数学复习(全国版)第8讲 抛物线与几何综合题(考点精析)(原卷版)

第8讲抛物线与几何综合→➊考点精析←→➋真题精讲←考向一抛物线与三角形有关问题考向二抛物线与线段有关问题考向三抛物线与角度有关问题考向四抛物线与四边形有关问题考向五抛物线与圆有关问题考向六抛物线与面积有关问题第9讲抛物线与几何综合二次函数是非常重要的函数,年年都会考查,总分值为18~20分,预计2024年各地中考还会考,它经常以一个压轴题独立出现,有的地区也会考察二次函数的应用题,小题的考察主要是二次函数的图象和性质及或与几何图形结合来考查.→➊考点精析←1、函数存在性问题解决二次函数存在点问题,一般先假设该点存在,根据该点所在的直线或抛物线的表达式,设出该点的坐标;然后用该点的坐标表示出与该点有关的线段长或其他点的坐标等;最后结合题干中其他条件列出等式,求出该点的坐标,然后判别该点坐标是否符合题意,若符合题意,则该点存在,否则该点不存在.2、函数动点问题(1)函数压轴题主要分为两大类:一是动点函数图象问题;二是与动点、存在点、相似等有关的二次函数综合题.(2)解答动点函数图象问题,要把问题拆分,分清动点在不同位置运动或不同时间段运动时对应的函数表达式,进而确定函数图象;解答二次函数综合题,要把大题拆分,做到大题小做,逐步分析求解,最后汇总成最终答案.(3)解决二次函数动点问题,首先要明确动点在哪条直线或抛物线上运动,运动速度是多少,结合直线或抛物线的表达式设出动点的坐标或表示出与动点有关的线段长度,最后结合题干中与动点有关的条件进行计算.→➋真题精讲←考向一抛物线与三角形有关问题(1)如图2,若抛物线经过原点O .①求该抛物线的函数表达式;②求BE EC的值.(2)连接,PC CPE 与BAO 能否相等?若能,求符合条件的点P 的横坐标;若不能,试说明理由.(1)求这条抛物线的函数解析式;(2)P 是抛物线上一动点(不与点A ,B ,C 重合),作PD ①如图,若点P 在第三象限,且tan 2CPD ,求点P 的坐标;②直线PD 交直线BC 于点E ,当点E 关于直线PC 的对称点四边形PECE 的周长.(1)求该抛物线的表达式;(2)点P是直线AC下方抛物线上一动点,过点P作PD 点P的坐标;(3)在(2)的条件下,将该抛物线向右平移5个单位,点yC,N为顶点的三角形相似(其中点P与点C相对应),若存在,直接写出....点P和点Q的坐标;若不存在,请说明理由.考向二抛物线与线段有关问题考向三抛物线与角度有关问题7.(2023·湖南岳阳·统考中考真题)已知抛物线21:Q y x bx c 与x 轴交于 3,0,A B 两点,交y 轴于点 0,3C .(1)请求出抛物线1Q 的表达式.(2)如图1,在y 轴上有一点 0,1D ,点E 在抛物线1Q 上,点F 为坐标平面内一点,是否存在点,E F 使得四边形DAEF 为正方形?若存在,请求出点,E F 的坐标;若不存在,请说明理由.(3)如图2,将抛物线1Q 向右平移2个单位,得到抛物线2Q ,抛物线2Q 的顶点为K ,与x 轴正半轴交于点H ,抛物线1Q 上是否存在点P ,使得CPK CHK ?若存在,请求出点P 的坐标;若不存在,请说明理由.考向四抛物线与四边形有关问题(1)求抛物线的解析式;(2)设点P 是直线BC 上方抛物线上一点,求出PBC 的最大面积及此时点(3)若点M 是抛物线对称轴上一动点,点N 为坐标平面内一点,是否存在以B C M N 、、、为顶点的四边形是菱形,若存在,请直接写出点明理由.9.(2023·山东·统考中考真题)如图,直线4y x 交x 轴于点为32x 的抛物线经过B C ,两点,交x 轴负半轴于点A .P 标为m ,过点P 作x 轴的平行线交抛物线于另一点M ,作x(1)求抛物线的解析式;(2)若32m,当m为何值时,四边形CDNP是平行四边形?(3)若32m ,设直线MN交直线BC于点E,是否存在这样的m值,使求出此时m的值;若不存在,请说明理由.(1)求抛物线的解析式;(2)点P 在抛物线上,点Q 在x 轴上,以B ,C ,P ,Q 为顶点的四边形为平行四边形,求点P 的坐标;(3)如图2,抛物线顶点为D ,对称轴与x 轴交于点E ,过点 1,3K 的直线(直线KD 除外)与抛物线交于G ,H 两点,直线DG ,DH 分别交x 轴于点M ,N .试探究EM EN 是否为定值,若是,求出该定值;若不是,说明理由.考向五抛物线与圆有关问题11.(2023·江苏苏州·统考中考真题)如图,二次函数268y x x 的图像与x 轴分别交于点,A B (点A 在点B 的左侧),直线l 是对称轴.点P 在函数图像上,其横坐标大于4,连接,PA PB ,过点P 作PM l ,垂足为M ,以点M 为圆心,作半径为r 的圆,PT 与M 相切,切点为T .(1)求点,A B 的坐标;(2)若以M 的切线长PT 为边长的正方形的面积与PAB 的面积相等,且M 不经过点 3,2,求PM 长的取值范围.12.(2023·山东烟台·统考中考真题)如图,抛物线25y ax bx 与x 轴交于,A B 两点,与y 轴交于点,4C AB .抛物线的对称轴3x 与经过点A 的直线1y kx 交于点D ,与x 轴交于点E .(1)求直线AD及抛物线的表达式;(2)在抛物线上是否存在点M,使得ADM△是以所有点M的坐标;若不存在,请说明理由;(3)以点B为圆心,画半径为2的圆,点P为考向六抛物线与面积有关问题(1)求二次函数的表达式;(2)求四边形ACDB 的面积;(3)P 是抛物线上的一点,且在第一象限内,若ACO PBC ,求P 点的坐标.14.(2023·安徽·统考中考真题)在平面直角坐标系中,点O 是坐标原点,抛物线 20y ax bx a 经过点 3,3A ,对称轴为直线2x .(1)求,a b 的值;(2)已知点,B C 在抛物线上,点B 的横坐标为t ,点C 的横坐标为1t .过点B 作x 轴的垂线(1)若函数的图象与坐标轴...有两个公共点,且(2)如图,若函数的图象为抛物线,与交于点P,连接l x m m:(04)△的面积为1S,点E.设PBE①当点P为抛物线顶点时,求②探究直线l在运动过程中,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
难点探究专题:抛物线与几何图形的综合(选做)——代几结合,突破面积及点的存在性问题
◆类型一二次函数与三角形的综合
一、全等三角形的存在性问题
1.如图,抛物线y=x2+bx+c经过点(1,-4)和(-2,5),请解答下列问题:
(1)求抛物线的解析式;
(2)若抛物线与x轴的两个交点为A,B,与y轴交于点C.在该抛物线上是否存在点△D,使得ABC与△ABD全等?若存在,求出D点的坐标;若不存在,请说明理由.
二、线段(或周长)的最值问题及等腰三角形的存在性问题
2.(凉山州中考)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,-3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
4.如图,抛物线y=x2+x-与x轴相交于A,B两点,顶点为P.
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
◆类型二二次函数与平行四边形的综合
3.如图,抛物线y=ax2+2ax+c(a>0)与y轴交于点C,与x轴交于A,B 两点,A点在B点左侧.若点E在x轴上,点P在抛物线上,且以A,C,E,P 为顶点的四边形是平行四边形,则符合条件的点P有()
A.1个B.2个C.3个D.4个
13
22
(1)求点A,B的坐标;
(2)在抛物线上是否存在点△E,使ABP的面积等于△ABE的面积?若存在,求出符合条件的点E的坐标;若不存在,请说明理由;
(3)坐标平面内是否存在点F,使得以A,B,P,F为顶点的四边形为平行四边形?直接写出所有符合条件的点F的坐标.
2 2
◆类型三 二次函数与矩形、菱形、正方形的综合
5.如图,在平面直角坐标系中,点 A 在抛物线 y =x 2-2x +2 上运动.过点
A 作 AC⊥x 轴于点 C ,以 AC 为对角线作矩形 ABCD ,连接 BD ,则对角线 BD 的最小
值为________.
第 5 题图
第 6 题图
3 6.如图,抛物线 y =ax 2-x - 与 x 轴正半轴交于点 A(3,0).以 OA 为边在 x 轴
上方作正方形 OABC ,延长 CB 交抛物线于点 D ,再以 BD 为边向上作正方形 BDEF.
则 a =,点 E 的坐标是_________________.
7 7. (新疆中考)如图,对称轴为直线 x = 的抛物线经过点 A(6,0)和 B(0,
-4).
(1)求抛物线的解析式及顶点坐标;
(2)设点 E(x ,y)是抛物线上一动点,且位于第一象限,四边形 OEAF 是以 OA
为对角线的平行四边形,求平行四边形 OEAF 的面积 S 与 x 之间的函数关系式;
(3)当(2)中的平行四边形 OEAF 的面积为 24 时,请判断平行四边形 OEAF 是
否为菱形.
8.(百色中考)正方形OABC的边长为4,对角线相交于点P,抛物线l经过O,P,A三点,点E是正方形内的抛物线l上的动点.
(1)建立适当的平面直角坐标系,
①直接写出O,P,A三点的坐标;
②求抛物线l的解析式;
(2)求△OAE与△OCE面积之和的最大值.
答案:。
