线性代数练习册习题及答案本
线性代数练习题(有答案)

《线性代数》 练习题一、选择题1、 设A ,B 是n 阶方阵,则必有 ……………………………………………( A )A 、|AB |=|BA | B 、2222)(B AB A B A ++=+C 、22))((B A B A B A -=-+D 、BA AB = 2、设A 是奇数阶反对称矩阵,则必有( B ) (A)、1=A (B)、0=A (C)、0≠A (D)、A 的值不确定3、向量组)0,1,1(,)9,0,3(-,)3,2,1(,)6,1,1(--的秩为____2 ________4、向量组)1,3,1,2(-,)4,5,2,4(-,)1,4,1,2(--的秩为______2__ ___.5、设A 是n m ⨯阶矩阵,r A r =)(,则齐次线性方程组O AX =的基础解系中包含解向量的个数为( C )(A)、r (B)、n (C)、r n - (D)、r m - 二、计算与证明题6、设⎪⎪⎪⎭⎫ ⎝⎛----=020212022A , ⎪⎪⎪⎭⎫⎝⎛---=221021132B 求(1)32AB A -,(2).T B A6、解(1). A AB 23-2202313212120020122--⎛⎫⎛⎫ ⎪⎪=-- ⎪⎪ ⎪⎪---⎝⎭⎝⎭2202212020-⎛⎫⎪--- ⎪ ⎪-⎝⎭2223186240-⎛⎫ ⎪=-- ⎪ ⎪--⎝⎭2202212020-⎛⎫ ⎪--- ⎪ ⎪-⎝⎭210612622680-⎛⎫ ⎪=- ⎪ ⎪--⎝⎭(2). 220231231212120120020122122T A B ---⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪=--= ⎪⎪ ⎪ ⎪⎪ ⎪-----⎝⎭⎝⎭⎝⎭222186240-⎛⎫⎪=-- ⎪ ⎪--⎝⎭7、设A ,B 是n 阶方阵满足AB B A =+,证明:E A -可逆. 7、解、1()A E B E --=-8、设方阵A 满足0332=--E A A ,证明:A 可逆,并求1-A .8、解、由2330A A E --=有A (3A E -)=3E ,于是,A [21(3A E -)]=E ,所以A 可逆,且11(3)3A A E -=-.9、计算行列式:1014300211321221---=D9、69D =-.10、计算行列式D =4232002005250230---- 10、解:D =423200200525230----0205252304--=55208---=80-=11、计算n 阶行列式abbb b a bb b a D =11、1[(1)]()n D a n b a b -=+--。
线性代数 课后作业及参考答案

《线性代数》作业及参考答案一.单项选择题1.设行列式a aa a11122122=m,a aa a13112321=n,则行列式a a aa a a111213212223++等于()A. m+nB. -(m+n)C. n-mD. m-n2.设矩阵A=100020003⎛⎝⎫⎭⎪⎪⎪,则A-1等于()A.130012001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪B.100120013⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪C.13000100012⎛⎝⎫⎭⎪⎪⎪⎪⎪D.120013001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪3.设矩阵A=312101214---⎛⎝⎫⎭⎪⎪⎪,A*是A的伴随矩阵,则A *中位于(1,2)的元素是()A. –6B. 6C. 2D. –24.设A是方阵,如有矩阵关系式AB=AC,则必有()A. A =0B. B≠C时A=0C. A≠0时B=CD. |A|≠0时B=C5.已知3×4矩阵A的行向量组线性无关,则秩(A T)等于()A. 1B. 2C. 3D. 46.设两个向量组α1,α2,…,αs和β1,β2,…,βs均线性相关,则()A.有不全为0的数λ1,λ2,…,λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λs βs=0B.有不全为0的数λ1,λ2,…,λs使λ1(α1+β1)+λ2(α2+β2)+…+λs(αs+βs)=0C.有不全为0的数λ1,λ2,…,λs使λ1(α1-β1)+λ2(α2-β2)+…+λs(αs-βs)=0D.有不全为0的数λ1,λ2,…,λs和不全为0的数μ1,μ2,…,μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r,则A中()A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是()A.η1+η2是Ax=0的一个解B.12η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆,则必有()A.秩(A)<nB.秩(A)=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n(≥3)阶方阵,下列陈述中正确的是()A.如存在数λ和向量α使Aα=λα,则α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α,使(λE-A)α=0,则λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1,λ2,λ3是A的3个互不相同的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,则α1,α2,α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有()A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵,则下列结论错误的是()A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行(列)向量组是正交单位向量组13.设A是实对称矩阵,C是实可逆矩阵,B=C T AC.则()A.A与B相似B. A与B不等价C. A与B有相同的特征值D. A与B合同15.设有矩阵Am×n,Bm×s,Cs×m,则下列运算有意义的是()。
(完整版)线性代数试题及答案

线性代数习题和答案第一部分 选择题 (共 28 分)、单项选择题(本大题共 14 小题,每小题 2 分,共 28 分)在每小题列出的四个选项中只有一个是符合题目要求的,请将其代码填在题后的括号内。
错选或未选均无分。
C. 3D. 46.设两个向量组 α1,α2,⋯, αs 和β 1,β2,⋯, βs 均线性相关,则()A. 有不全为 0 的数λ 1,λ2,⋯,λs 使λ1α1+λ2α2+⋯+λs αs =0 和λ 1β 1+λ 2β 2+⋯λ s βs =0B. 有不全为 0 的数λ 1,λ 2,⋯,λ s 使λ 1(α1+β1)+λ2(α2+β2)+⋯+λs ( α s + β s )=0C. 有不全为 0 的数λ 1,λ 2,⋯,λ s 使λ1(α 1- β1)+λ2(α2- β2)+⋯+λs (αs - βs )=0D.有不全为 0的数λ 1,λ 2,⋯,λ s 和不全为 0的数μ 1,μ 2,⋯,μ s 使λ1α1+λ2α2+⋯+ λ s α s =0 和μ 1β1+μ2β2+⋯+μ s βs =07.设矩阵 A 的秩为 r ,则 A 中( )A. 所有 r- 1阶子式都不为 0B.所有 r- 1阶子式全为 0C.至少有一个 r 阶子式不等于 0D.所有 r 阶子式都不为 08. 设 Ax=b 是一非齐次线性方程组, η1,η2是其任意 2 个解,则下列结论错误的是( )A. m+n C. n- m a 11a 12a 13 a 11=m ,a 21a 22a 23 a 21a 11 a 12 a 13等于(2.设矩阵 A=0 ,则 A - 1 等于( 3A. 0 1 3C. 03.设矩阵 A=a 21 a 22 a 23B. - (m+n) D. m- nB.D.21 ,A *是 A 的伴随矩阵,则 A *中位于 41,2)的元素是(A. –6 C. 2 4.设 A 是方阵,如有矩阵关系式 AB=AC ,则必有( A. A =0 C. A 0 时 B=C 5.已知 3×4 矩阵 A 的行向量组线性无关,则秩( A. 1B. 6 D. –2 ) B. B D. |A| 0 时 B=C C 时 A=0 A T )等于( )B. 21.设行列式 =n ,则行列式10.设 A 是一个 n (≥3)阶方阵,下列陈述中正确的是( )A. 如存在数λ和向量 α使 A α=λα,则α是 A 的属于特征值λ的特征向量B. 如存在数λ和非零向量 α,使(λE- A )α=0,则λ是 A 的特征值C. A 的 2 个不同的特征值可以有同一个特征向量D. 如λ 1,λ 2,λ 3是A 的 3个互不相同的特征值, α1,α2,α3依次是 A 的属于λ 1,λ2, λ3的特征向量,则 α 1,α 2, α 3有可能线性相关 11. 设λ 0是矩阵 A 的特征方程的 3重根, A 的属于λ 0的线性无关的特征向量的个数为 k ,则必有( )222(a 11A 21+a 12A 22+a 13A 23) +(a 21A 21+a 22A 22+a 23A 23) +(a 31A 21+a 32A 22+a 33A 23) =.18. 设向量( 2, -3, 5)与向量( -4, 6, a )线性相关,则 a= .19. 设A 是 3×4矩阵,其秩为 3,若η1,η2为非齐次线性方程组 Ax=b 的 2个不同的解,则它 的通解为 .20. 设 A 是 m ×n 矩阵, A 的秩为 r (<n ) ,则齐次线性方程组 Ax=0 的一个基础解系中含有解的个A. η1+η2 是 Ax=0 的一个解 C. η 1-η 2是 Ax=0 的一个解 9. 设 n 阶方阵 A 不可逆,则必有(A. 秩 (A )<n C.A=0 11B.η1+ η2是 Ax=b 的一个解22D. 2 η 1-η 2 是 Ax=b 的一个解 ) B. 秩 (A)=n- 1D. 方程组 Ax=0 只有零解A. k ≤ 3C. k=312. 设 A 是正交矩阵,则下列结论错误的是(A.| A| 2必为 1 C. A - 1=A T 13. 设 A 是实对称矩阵, C 是实可逆矩阵,A.A 与 B 相似B. A 与 B 不等价C. A 与 B 有相同的特征值D. A 与 B 合同 14.下列矩阵中是正定矩阵的为()23 A.34 1 0 0C. 0 2 30 3 5第二部分B. k<3 D. k>3 )B.|A|必为 1D.A 的行(列)向量组是正交单位向量组 B=C T AC .则( ) 34 B. 26 1 1 1 D. 1 2 0102 非选择题(共 72 分)2 分,共 20 分)不写解答过程,将正确的答案写在每1 1 115. 3 569 25 361 111 2 316.设 A=B=.则 A+2B=1 111 2 417. 设 A =(a ij )3 × 3 , |A|=2 , A ij 表示 |A|中 元 素a ij 的 代 数 余 子 式 ( i,j=1,2,3 ) , 则数为.21. 设向量α、β的长度依次为2和3,则向量α+β与α-β的内积(α+β,α- β)=22.设 3阶矩阵 A 的行列式 |A |=8,已知 A 有 2个特征值 -1和 4,则另一特征值为 .0 10 6223.设矩阵 A=1 3 3 ,已知 α = 1 是它的一个特征向量,则α 所对应的特征值2 10 82为24.设实二次型 f (x 1,x 2,x 3,x 4,x 5)的秩为 4,正惯性指数为 3,则其规范形为 三、计算题(本大题共 7 小题,每小题 6分,共 42分)26.试计算行列式4 2 327.设矩阵 A= 110, 求矩阵 B 使其满足矩阵方程AB=A+2B.12321 3 028.给定向量组α 1=1,3 α2=, α=, α10 2 2 =4.3419试判断 α 4 是否为 α 1, α2,α3 的线性组合;若是, 则求出组合系数。
线性代数习题集(带答案)

. .. . ..第一部分 专项同步练习第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26.在函数1323211112)(x x xxx f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)011. 若2235001011110403--=D ,则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题. .. . ..1. n 2阶排列)12(13)2(24-n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是.4.若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=100111010100111.6.行列式=-000100002000010n n .7.行列式=--001)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式=--+---+---1111111111111111x x x x .11.n 阶行列式=+++λλλ111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321=D ,j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式,则=+++44434241234A A A A .14.已知db c a cc a b b a b c a cb a D =, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321-==D ,j A 4为)4,3,2,1(4=j a j 的代数余子式,则=+4241A A ,=+4443A A .. .. . ..16.已知行列式nn D001030102112531-=,D 中第一行元的代数余子式的和为.17.齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.18.若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1.cb a d b a dc ad c b dcbad c b a d c b a++++++++33332222; 2.yxyx x y x y y x y x +++;3.解方程0011011101110=x x xx ; 4.111111321321221221221----n n n n a a a a x a a a a x a a a a xa a a a x;5. na a a a 111111111111210(n j a j ,,1,0,1 =≠); 6. bn b b ----)1(1111211111311117. n a b b b a a b b a a a b 321222111111111; 8.xa a a a x a a a a x a a a a x n nn321212121;9.2212221212121111nn n nnx x x x x x x x x x x x x x x +++; 10. 21000120000021001210001211.aa a aa a a a aD ---------=1101100011000110001.. .. . ..四、证明题1.设1=abcd ,证明:011111111111122222222=++++dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a xb a -=++++++.3.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a d c b a d c b a +++------=.4.∏∑≤<≤=----=nj i i jni innn nn nn n nna aa a a a a a a a a a a a a 1121222212222121)(111.5.设c b a ,,两两不等,证明0111333=c b a c ba 的充要条件是0=++cb a .参考答案一.单项选择题A D A C C D ABCD B B 二.填空题1.n ;2.”“-;3.43312214a a a a ;4.0;5.0;6.!)1(1n n --;7.1)1(212)1()1(n n n n n a a a ---; 8.M 3-; 9.160-; 10.4x ; 11.1)(-+n n λλ; 12.2-;13.0; 14.0; 15.9,12-; 16.)11(!1∑=-nk k n ; 17.3,2-≠k ; 18.7=k三.计算题1.))()()()()()((c d b d b c a d a c a b d c b a ------+++-; 2. )(233y x +-; 3. 1,0,2-=x ; 4.∏-=-11)(n k kax5.)111()1(00∑∏==-+-nk k nk k a a ; 6. ))2(()1)(2(b n b b ---+- ;7. ∏=--nk k kna b1)()1(; 8. ∏∑==-+nk k nk k a x a x 11)()(;9. ∑=+nk k x 11; 10. 1+n ;11. )1)(1(42a a a ++-. 四. 证明题 (略). .. . ..第二章 矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是( )。
线性代数习题集及其答案

第一章行列式一.填空题1.四阶行列式中带有负号且包含a 12和a 21的项为______.解.a 12a 21a 33a 44中行标的排列为1234,逆序为0;列标排列为2134,逆序为1.该项符号为“-”,所以答案为a 12a 21a 33a 44.2.排列i 1i 2…i n 可经______次对换后变为排列i n i n -1…i 2i 1.解.排列i 1i 2…i n 可经过1+2+…+(n -1)=n(n -1)/2次对换后变成排列i n i n -1…i 2i 1.3.在五阶行列式中3524415312)23145()15423()1(a a a a a ττ+-=______3524415312a a a a a .解.15423的逆序为5,23145的逆序为2,所以该项的符号为“-”.4.在函数xx x x x x f 21112)(---=中,x 3的系数是______.解.x 3的系数只要考察234222x x xxx x +-=--.所以x 3前的系数为2.5.设a ,b 为实数,则当a =______,且b =______时,010100=---a b b a .解.0)(11010022=+-=--=---b a ab ba ab b a .所以a =b =0.6.在n 阶行列式D =|a ij |中,当i <j 时a ij =0(i ,j =1,2,…,n ),则D =______.解.nnn n a a a a a a a a 221121222111000=7.设A 为3×3矩阵,|A |=-2,把A 按行分块为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=321A A A A ,其中A j (j =1,2,3)是A 的第j 行,则行列式=-121332A A A A ______.解.=-121332A A A A 6||33233211213=-=-=-A A A A A A A A .二.计算证明题1.设4322321143113151||-=A 计算A 41+A 42+A 43+A 44=?,其中A 4j (j=1,2,3,4)是|A |中元素a 4j 的代数余子式.解.A 41+A 42+A 43+A 441111321143113151-=210320206)1(000121013201206114--=-=+=62103202061=--2.计算元素为a ij =|i -j |的n 阶行列式.解.111111110021201110||--------=n n n n n A 每行减前一行由最后一行起,)1(2)1(1000201201121--=--------n n n n n n n列每列加第3.计算n 阶行列式nx x x nx x x nx x x D n n n n +++++++++=212121222111(n ≥2).解.当2>n n x x x n x x x n x x x D n n n n ++++++=222222111+n x x n x x n x x n n ++++++ 2121212211=n x x x x n x x x x n x x x x n n nn++++++ 33322221111+nx x x n x x x n x x x n n n++++++ 323232222111+nx x x n x x x n x x x n n n ++++++ 313131222111+nx x n x x n x x n n ++++++ 32132********=-n x x x n x x x n x x x n n n++++++ 313131222111=-n x x x n x x x n x x x n n n+++ 111222111-nx x nx x n x x n n+++ 3131312211=0当2=n 2122112121x x x x x x -=++++4.证明:奇数阶反对称矩阵的行列式为零.证明:||||)1(||||||,A A A A A A A nTT-=-=-==-=(n 为奇数).所以|A |=0.5.试证:如果n 次多项式nn x C x C C x f ++=10)(对n +1个不同的x 值都是零,则此多项式恒等于零.(提示:用范德蒙行列式证明)证明:假设多项式的n +1个不同的零点为x 0,x 1,…,x n .将它们代入多项式,得关于C i 方程组0010=++nn x C x C C 01110=++n n x C x C C …………10=++n n n n x C x C C 系数行列式为x 0,x 1,…,x n 的范德蒙行列式,不为0.所以010====n C C C 6.设).(',620321)(232x F xx x x x xx F 求=解.x x x x x x x F 620321)(232==x x x x x x 3103211222=x x x x x x 310201222=xxx x x 3102101222=32220021012xxx x x x =26)('x x F =第二章矩阵一.填空题1.设α1,α2,α3,α,β均为4维向量,A =[α1,α2,α3,α],B =[α1,α2,α3,β],且|A |=2,|B |=3,则|A -3B |=______.解.βαααα3222|3|321----=-B A =βαααα38321-⨯-=αααα321(8⨯-56|)|3|(|8)3321=--=-B A βααα2.若对任意n ×1矩阵X ,均有AX =0,则A =______.解.假设[]m A αα 1=,αi 是A 的列向量.对于j =1,2,…,m ,令⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡=010 j X ,第j 个元素不为0.所以[]m αα 10010==⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡j α (j =1,2,…,m ).所以A =0.3.设A 为m 阶方阵,存在非零的m ×n 矩阵B ,使AB =0的充分必要条件是______.解.由AB =0,而且B 为非零矩阵,所以存在B 的某个列向量b j 为非零列向量,满足Ab j =0.即方程组AX =0有非零解.所以|A |=0;反之:若|A |=0,则AX =0有非零解.则存在非零矩阵B ,满足AB =0.所以,AB =0的充分必要条件是|A |=0.4.设A 为n 阶矩阵,存在两个不相等的n 阶矩阵B ,C ,使AB =AC 的充分条件是______.解.0||0)(=⇔-=-⇔=≠A C B C B A AC AB C B 非零且且5.[]42121b b b a a a n ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=______.解.[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡n n n n n n n b a b a b a b a b a b a b a b a b a b b b a a a 212221212111421216.设矩阵12,23,3211-+-=⎥⎦⎤⎢⎣⎡-=B E A A B A 则=______.解.=2A ⎥⎦⎤⎢⎣⎡-3211⎥⎦⎤⎢⎣⎡-3211=⎥⎦⎤⎢⎣⎡--7841E A A B 232+-==⎥⎦⎤⎢⎣⎡--7841-⎥⎦⎤⎢⎣⎡-9633+⎥⎦⎤⎢⎣⎡2002=⎥⎦⎤⎢⎣⎡--021221||*1==-B B B ⎥⎦⎤⎢⎣⎡--2210=⎥⎥⎦⎤⎢⎢⎣⎡--112107.设n 阶矩阵A 满足12,032-=++A E A A 则=______.解.由,0322=++E A A 得E E A A 3)2(-=+.所以0|3||2|||≠-=+E E A A ,于是A 可逆.由,0322=++E A A 得)2(31,03211E A A AE A +-==++--8.设)9()3(,10002010121E A E A A -+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-则=______.解.=2A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100020101⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100020101=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100040201=-E A 92⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---800050208,=+E A 3⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡400050104→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100010001400050104 →⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡4100010001100050104 →⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-41000104101100050004 ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-41000510161041100010001 ,⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=+-4100051161041)3(1E A )9()3(21E A E A -+-=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-4100051161041⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---800050208=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---2000101029.设.______])2[(______,)(_______,,3342122111*1*1=-==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=---A A A A 则解.|A|=-3-12+8+8+6-6=1→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----100010001334212211 →⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----104012001570230211 →⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------104031320015703210211 →⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----137320313203131310032103401 →⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----137322524933100010001 →⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------372252493100010001 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=-3722524931A ====---||)(,||,||1*1**1A AA A A A A AA ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----3342122111131*4)2(||)2()2(|2|)2(---=--=--=-A A A A A A 414)4(])2[(111*===----A A A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----33421221110.设矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=3111522100110012A ,则A 的逆矩阵1-A =______.解.⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-211111121,⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡-215331521使用分块求逆公式⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡-----1111100B CAB A BC A -⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡--11212153⎥⎦⎤⎢⎣⎡--2111=⎥⎦⎤⎢⎣⎡--1173019所以⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=-21117533019002100111A 二.单项选择题1.设A 、B 为同阶可逆矩阵,则(A)AB =BA(B)存在可逆矩阵P ,使B AP P =-1(C)存在可逆矩阵C ,使BAC C T=(D)存在可逆矩阵P 和Q ,使BPAQ =解.因为A 可逆,存在可逆E AQ P Q P A A A A =使,.因为B 可逆,存在可逆E BQ P Q P B B B B =使,.所以A A AQ P =B B BQ P .于是BQ AQ P P B A A B =--11令A B P P P 1-=,1-=BA Q Q Q .(D)是答案.2.设A 、B 都是n 阶可逆矩阵,则⎥⎦⎤⎢⎣⎡--1002B A T等于(A)12||||)2(--B A n(B)1||||)2(--B A n(C)||||2B A T-(D)1||||2--B A 解.121||||)2(002---=⎥⎦⎤⎢⎣⎡-B A B A n T.(A)是答案.3.设A 、B 都是n 阶方阵,下面结论正确的是(A)若A 、B 均可逆,则A +B 可逆.(B)若A 、B 均可逆,则AB 可逆.(C)若A +B 可逆,则A -B 可逆.(D)若A +B 可逆,则A ,B 均可逆.解.若A 、B 均可逆,则111)(---=A B AB .(B)是答案.4.设n 维向量)21,0,,0,21( =α,矩阵ααTE A -=,ααT E B 2+=其中E 为n 阶单位矩阵,则AB =(A)0(B)-E(C)E(D)ααTE +解.AB =)(ααTE -)2(ααT E +=ααT E -+2ααT -2ααT ααT =E .)21(=ααT (C)是答案.5.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=233322322131131211232221a a a a a a a a a a a a B ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1000010101P ,设有P 2P 1A =B ,则P 2=(A)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101010001(B)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-101010001(C)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100010101(D)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-100010101解.P 1A 表示互换A 的第一、二行.B 表示A 先互换第一、二行,然后将互换后的矩阵的第一行乘以(-1)加到第三行.所以P 2=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-101010001.(B)是答案.6.设A 为n 阶可逆矩阵,则(-A )*等于(A)-A *(B)A *(C)(-1)n A *(D)(-1)n -1A *解.(-A )*=*111)1()1(1||)1()(||A A A A A n n ----=--=--.(D)是答案.7.设n 阶矩阵A 非奇异(n ≥2),A *是A 的伴随矩阵,则(A)A A A n 1**||)(-=(B)A A A n 1**||)(+=(C)AA A n 2**||)(-=(D)AA A n 2**||)(+=解.1*||-=AA A AA A A A A A A A A A A A n n 211111*1**||||||||)|(|||||)|(|)(-------====(C)是答案.8.设A 为m ×n 矩阵,C 是n 阶可逆矩阵,矩阵A 的秩为r 1,矩阵B =AC 的秩为r,则(A)r >r 1(B)r <r 1(C)r =r 1(D)r 与r 1的关系依C 而定解.n C r C A B n n n m ==⨯⨯)(,,所以1)()()(r n C r A r AC r r =-+≥=又因为1-=BC A ,于是rn C r B r BC r r =-+≥=--)()()(111所以r r =1.(C)是答案.9.设A 、B 都是n 阶非零矩阵,且AB =0,则A 和B 的秩(A)必有一个等于零(B)都小于n (C)一个小于n ,一个等于n(D)都等于n解.若0,0.,)(1===-B AB A n A r 得由存在则,矛盾.所以n A r <)(.同理n B r <)(.(B)是答案.三.计算证明题1.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=243121013A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=143522011B .求:i.AB -BA ii.A 2-B 2iii.B T A T解.=-BA AB ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----1618931717641,=-22B A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----1326391515649=T T A B ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--2211531517652.求下列矩阵的逆矩阵i.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------111111*********1ii.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-1000cos sin 0sin cos ααααiii.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0001001001001000iv.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-110210000120025解.i.→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------10000100001000011111111111111111 →⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---------1010101001100010220202022001111 →⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------1001001102102100010220220010101111 →⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------110000110210210210212200220010100101 →⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡----1100002121021021021021220011010100101 →⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-----11110021210210210212104000110010101001→⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-----414141410021210210210212101000110010101001 ⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------414141414141414141414141414141411000010000100001 ,⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡------=-414141414141414141414141414141411A ii.⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡--ααααααααcos sin sin cos cos sin sin cos 1.由矩阵分块求逆公式:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡---1110000B A B A 得到:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-100cos sin 0sin cos 1ααααA iii.⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-011001101.由矩阵分块求逆公式:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡---0000111A B B A 所以⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=-00010010010010001A iv.由矩阵分块求逆公式:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡---111000B A B A 得到:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡---=-313100323100005200211A 3.已知三阶矩阵A 满足)3,2,1(==i i A i i αα.其中T)2,2,1(1=α,T )1,2,2(2-=α,T )2,1,2(3--=α.试求矩阵A .解.由本题的条件知:=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---212122221A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---622342641→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---100010001212122221 →⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----102012001630360221 →⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----0313231032001120210221 →⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----3231323103232031300210201 →⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----9291923103232031100210201 →⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---929192919292929291100010001 ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=232323235032037929192919292929291622342641A 4.k 取什么值时,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=11100001k A 可逆,并求其逆.解.01110001||≠=-=k k A →⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-10011101000001001 k ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--101110010010001001 k →⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-111100010010001001k k 所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-1110100011k k A 5.设A 是n 阶方阵,且有自然数m ,使(E +A )m =0,则A 可逆.解.因为)(1=+==+∑∑==mi i i m mi iimmA c E A c A E所以∑=-=-mi i im E A c A 11)(.所以A 可逆.6.设B 为可逆矩阵,A 是与B 同阶方阵,且满足A 2+AB +B 2=0,证明A 和A +B 都是可逆矩阵.解.因为022=++B AB A ,所以2)(B B A A -=+.因为B 可逆,所以0||)1(||22≠-=-B B n所以0|||)(|2≠-=+B B A A .所以B A A +,都可逆.7.若A ,B 都是n 阶方阵,且E +AB 可逆,则E +BA 也可逆,且AAB E B E BA E 11)()(--+-=+解.AAB E B BA E BA E A AB E B E BA E 11)()())()((--++-+=+-+=AAB E AB E B BA E A AB E BAB B BA E 11))(())((--++-+=++-+=E BA BA E =-+所以A AB E B E BA E 11)()(--+-=+.8.设A ,B 都是n 阶方阵,已知|B |≠0,A -E 可逆,且(A -E )-1=(B -E )T ,求证A 可逆.解.因为(A -E )-1=(B -E )T ,所以(A -E )(B -E )T =E 所以E E B E B A T T =+--)(,TT B E B A =-)(由|B |≠0知11)(--TB B ,存在.所以E B E B A T T =--1))((.所以A 可逆.9.设A ,B ,A +B 为n 阶正交矩阵,试证:(A +B )-1=A-1+B -1.解.因为A ,B ,A +B 为正交矩阵,所以111,,)()(---==+=+B B A A B A B A TTT所以111)()(---+=+=+=+B A B A B A B A T T T 10.设A ,B 都是n 阶方阵,试证明:||E AB BE EA -=.解.因为⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡AB E B E B E E A E A E E E 0000所以ABE BEB E E A E A E E E -=-0000||)1(01)1(2E AB AB E BEB E E A n n --=-=⋅⋅-因为n n )1()1(2-=-,所以||E AB BE EA -=11.设A 为主对角线元素均为零的四阶实对称可逆矩阵,E 为四阶单位矩阵)0,0(00000000000000>>⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=l k l k B i.试计算|E +AB |,并指出A 中元素满足什么条件时,E +AB 可逆;ii.当E +AB 可逆时,试证明(E +AB )-1A 为对称矩阵.解.i.⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=44342414342313242312141312000a a a a a a a a a a a a a A ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=l k a a a a a a a a a a a a a AB 000000000000000044342414342313242312141312⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0000000000343424231413ka la la ka la ka AB E +⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1001001001343424231413ka la la ka la ka ,2341||kla AB E -=+所以当2341a kl≠时,E +AB 可逆.ii.11111)()]([)(-----+=+=+B A AB E A A AB E 因为A ,B 为实对称矩阵,所以B A +-1为实对称矩阵,所以(E +AB )-1A 为对称矩阵.12.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=λλλ100100A ,求A n .解.使用数学归纳法.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2222210200100100100100λλλλλλλλλλλA =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=λλλλλλλλ1001002102002223A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+323233)21(0300λλλλλλ假设k A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++---k k k k k kk k k λλλλλλ121)11(000则1+k A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++---k k k k k k k k k λλλλλλ121)11(000⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡λλλ100100=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+++++-++1111)1()1(0)1(00k k k k k k k k k λλλλλλ 所以n A =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++---nn n n n n n n n λλλλλλ121)11(000=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----n n n n n nn n n n λλλλλλ1212)1(00013.A 是n 阶方阵,满足A m =E ,其中m 是正整数,E 为n 阶单位矩阵.今将A 中n 2个元素a ij 用其代数余子式A ij 代替,得到的矩阵记为A 0.证明E A m=0.解.因为A m =E ,所以1||=m A ,所以A 可逆.11*0)(||]|[|)(--===T T T A A A A A A 所以EE A A A A A A m T m m m T m ====---1110||])[(||])(|[|14.设矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=010101001A i.证明:n ≥3时,E A A A n n-+=-22(E 为三阶单位矩阵)ii.求A 100.解.i.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=010*******A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010101001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=101011001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1010110013A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010101001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=011102001+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=-+010*******E A A -⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡101011001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100010001⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=0111020013A =所以E A A A -+=-2233假设EA A A k k -+=-22则=-+=-+A A A A k k 311A E A A A k --++-21=EA A k -+-+221)(所以EA A A n n -+=-22ii.=-+=E A A A298100E A E A A 4950222296-==-+ -⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=50050050500050⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡490004900049⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=1050015000115.当⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=21232321A 时,A 6=E .求A 11.解.121232321||=-=A ,所以==-||*1A A A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-21232321因为1112116--===EA A A A E A ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=2123232116.已知A ,B 是n 阶方阵,且满足A 2=A ,B 2=B ,与(A -B )2=A +B ,试证:AB =BA =0.解.因为(A -B )2=A +B ,所以))(())(()(3B A B A B A B A B A -+=+-=-于是2222B AB BA A B AB BA A --+=-+-,所以BAAB =BA B BA AB A B A B A +=+--+=-222,)(因为A 2=A ,B 2=B ,所以2AB =0,所以0==BA AB .第三章向量一.填空题1.设)1,2,0,1(),,1,0,1(),0,3,2,4(),5,0,1,2(4321-=-=--=-=ααααk ,则k =______时,α1,α2,α3,α4线性相关.解.考察行列式1102131181105213000011182105213000211142k k k -----=-----=-----316102038++-+--=k k =13k +5=0.135-=k 2.设)0,,3,1(),4,3,5,0(),2,0,2,1(),0,3,1,2(4321t -=-=-=-=αααα,则t =______时,α1,α2,α3,α4线性相关.解.考察行列式4243355504243335551000042030335211012---=----=----t tt t 0603020306020=--+++-=t t .所以对任何t ,α1,α2,α3,α4线性相关.3.当k =______时,向量β=(1,k ,5)能由向量),1,1,2(),2,3,2(21-=-=αα线性表示.解.考察行列式,012513211=--k 得k =-8.当k =-8时,三个向量的行列式为0,于是21,,ααβ线性相关.显然21,αα线性无关,所以β可用21,αα线性表示.4.已知)1,4,0,1,1(),3,1,3,0,2(),10,5,1,2,0(),1,2,2,1,1(4321-=-=-==αααα,则秩(α1,α2,α3,α4)=______.解.将α1,α2,α3,α4表示成矩阵→⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---131********210211201→⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------21102550211002201201⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------211052110211001101201⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---→20052000200001101201.所以r (α1,α2,α3,α4)=35.设⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----=3224211631092114047116A ,则秩(A)=______.解.→⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----=3224211631092114047116A →⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-----3224211631711614040921⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------3408012550755110140800921⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡---------→8351051510117510815100921⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡------→410004030008845000815100921所以r (A )=3.6.已知),2,0,1,0(,)2,1,0,1(=-=βαT矩阵A =α·β,则秩(A )=______.解.A =α·β=()→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-402020100000201020102101⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡0020000000002010所以r (A )=1.7.已知向量),6,5,4(),6,5,4,3(),5,4,3,2(),4,3,2,1(4321t ====αααα,且秩(α1,α2,α3,α4)=2,则t =______.解.A =(α1,α2,α3,α4)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=t 654654354324321⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------=16630642032104321t ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=700000032104321t 所以当t =7时,r (A )=2.二.单项选择题1.设向量组α1,α2,α3线性无关,则下列向量组线性相关的是(A)α1+α2,α2+α3,α3+α1(B)α1,α1+α2,α1+α2+α3(C)α1-α2,α2-α3,α3-α1(D)α1+α2,2α2+α3,3α3+α1解.由0)()()(133322211=-+-+-ααααααk k k 得)()()(323212131=-+-+-αααk k k k k k 因为向量组α1,α2,α3线性无关,所以得关于321,,k k k 的方程组⎪⎩⎪⎨⎧=+-=+-=-000322131k k k k k k 321,,k k k 的系数行列式为011110011101=-=---.所以321,,k k k 有非零解,所以α1-α2,α2-α3,α3-α1线性相关.(C)是答案.2.设矩阵A m ×n 的秩为R (A )=m <n ,E m 为m 阶单位矩阵,下列结论正确的是(A)A 的任意m 个列向量必线性无关(B)A 的任意一个m 阶子式不等于零(C)若矩阵B 满足BA =0,则B =0(D)A 通过行初等变换,必可以化为(E m ,0)的形式解.(A),(B)都错在“任意”;(D)不正确是因为只通过行初等变换不一定能将A 变成(E m ,0)的形式;(C)是正确答案.理由如下:因为BA =0,所以0)()()()()(B r m m B r m A r B r BA r =-+=-+≥=.所以)(B r =0.于是B =0.3.设向量组(I):T T T a a a a a a a a a ),,(,),,(,),,(332313332221223121111===ααα;设向量组(II):T T T a a a a a a a a a a a a ),,,(,),,,(,),,,(433323133423222122413121111===βββ,则(A)(I)相关⇒(II)相关(B)(I)无关⇒(II)无关(C)(II)无关⇒(I)无关(B)(I)无关⇔(II)无关解.由定理:若原向量组线性无关,则由原向量组加长后的向量组也线性无关.所以(B)是答案.4.设β,α1,α2线性相关,β,α2,α3线性无关,则(A)α1,α2,α3线性相关(B)α1,α2,α3线性无关(C)α1可用β,α2,α3线性表示(D)β可用α1,α2线性表示解.因为β,α1,α2线性相关,所以β,α1,α2,α3线性相关.又因为β,α2,α3线性无关,所以α1可用β,α2,α3线性表示.(C)是答案.5.设A ,B 是n 阶方阵,且秩(A )=秩(B ),则(A)秩(A -B )=0(B)秩(A +B )=2秩(A)(C)秩(A -B )=2秩(A)(D)秩(A +B )≤秩(A )+秩(B )解.(A)取B A ≠且|A |≠0,|B |≠0则A -B ≠0,则r (A -B )≠0.排除(A);(B)取A =-B ≠0,则秩(A +B )≠2秩(A);(C)取A =B ≠0,则秩(A -B )≠2秩(A).有如下定理:秩(A +B )≤秩(A )+秩(B ).所以(D)是答案.三.计算证明题1.设有三维向量⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111k α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=112k α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=2113α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=21k k β问k 取何值时i.β可由α1,α2,α3线性表示,且表达式唯一;ii.β可由α1,α2,α3线性表示,但表达式不唯一;iii.β不能由α1,α2,α3线性表示.解.)1(22221111112-=-=k k k k k k i.10≠≠k k 且时,α1,α2,α3线性无关,四个三维向量一定线性相关,所以β可由α1,α2,α3线性表示,由克莱姆法则知表达式唯一;ii.当k =1时→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡121111111111 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡010********* .系数矩阵的秩等于增广矩阵的秩为2.所以所以β可由α1,α2,α3线性表示,但表示不惟一;iii.当0=k 时→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡021********* ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡021********* ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→011011100101 ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-→100011100101 .系数矩阵的秩等于2,增广矩阵的秩为3,所以所以β不能由α1,α2,α3线性表示.2.设向量组α1,α2,α3线性相关,向量组α2,α3,α4线性无关,问i.α1能否由α2,α3线性表出?证明你的结论;ii.α4能否由α1,α2,α3线性表出?证明你的结论解.i.α1不一定能由α2,α3线性表出.反例:T )1,1(1=α,T )0,1(2=α,T )0,2(3=α.向量组α1,α2,α3线性相关,但α1不能由α2,α3线性表出;ii.α4不一定能由α1,α2,α3线性表出.反例:T )0,0,2(1=α,T )0,0,1(2=α,T )0,1,0(3=α,T )1,0,0(4=α.α1,α2,α3线性相关,α2,α3,α4线性无关,α4不能由α1,α2,α3线性表出.3.已知m 个向量α1,α2,…αm 线性相关,但其中任意m -1个都线性无关,证明:i.如果存在等式k 1α1+k 2α2+…+k m αm =0则这些系数k 1,k 2,…k m 或者全为零,或者全不为零;ii.如果存在两个等式k 1α1+k 2α2+…+k m αm =0l 1α1+l 2α2+…+l m αm =0其中l 1≠0,则mm l k l k l k === 2211.解.i.假设k 1α1+k 2α2+…+k m αm =0,如果某个k i =0.则k 1α1+…+k i -1αi -1+k i+1αi+1…+k m αm =0因为任意m -1个都线性无关,所以k 1,k 2,…k i -1,k i+1,…,k m 都等于0,即这些系数k 1,k 2,…k m 或者全为零,或者全不为零;ii.因为l 1≠0,所以l 1,l 2,…l m 全不为零.所以m m l l l l ααα12121---= .代入第一式得:0)(2212121=+++---m m m m k k l l l l k αααα 即0)()(1122112=+-+++-m m m k k l l k k l l αα 所以02112=+-k k l l ,…,011=+-m m k k l l 即mm l k l k l k === 22114.设向量组α1,α2,α3线性无关,问常数a ,b ,c 满足什么条件a α1-α2,b α2-α3,c α3-α1线性相关.解.假设0)()()(133322211=-+-+-ααααααc k b k a k 得)()()(323212131=-+-+-αααk c k k b k k a k 因为α1,α2,α3线性无关,得方程组⎪⎩⎪⎨⎧=+-=+-=-000322131ck k bk k k ak当行列式0100110=---cba 时,321,k k k 有非零解.所以1=abc 时,a α1-α2,b α2-α3,c α3-α1线性相关.5.设A 是n 阶矩阵,若存在正整数k ,使线性方程组A k x =0有解向量α,且A k -1α≠0,证明:向量组α,A α,⋯,A k -1α是线性无关的.解.假设01110=+++--αααk k A a A a a .二边乘以1-k A 得010=-αk A a ,0=a 由0111=++--ααk k A a A a .二边乘以1-k A 得011=-αk A a ,1=a ………………………………最后可得011=--αk k A a ,1=-k a 所以向量组α,A α,⋯,A k -1α是线性无关.6.求下列向量组的一个极大线性无关组,并把其余向量用极大线性无关组线性表示.i.)3,2,1,2(),7,4,3,1(),6,5,1,4(),3,1,2,1(4321=----=---==αααα.ii.).10,5,1,2(),0,2,2,1(),14,7,0,3(),2,1,3,0(),4,2,1,1(54321=-===-=ααααα解.解.i.→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------3763245113122141→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---------34180039031902141⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---3200320031902141⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--→0000320031902141所以321,,ααα是极大线性无关组.由3322114ααααk k k ++=得方程组⎪⎩⎪⎨⎧-==+=-+323924332321k k k k k k 解得2331-==k k ,212=k 所以3214232123αααα-+-=ii.→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--1001424527121203121301→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--24220101103133021301⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--24220313301011021301⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--→04000010001011021301所以421,,ααα是极大线性无关组.由4322115ααααk k k ++=得方程组⎪⎪⎩⎪⎪⎨⎧=-=-==+0401233231k k k k k 解得21=k ,12=k ,03=k 所以421502αααα++=由4322113ααααk k k ++=得方程组⎪⎪⎩⎪⎪⎨⎧=-=-==+0401333231k k k k k 解得31=k ,12=k ,03=k 所以421303αααα++=7.已知三阶矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=x yyy x y y yxA ,讨论秩(A)的情形.解.i.0==y x ,)(=A r ii.0,00,0=≠≠=y x y x 或,3)(=A r iii.0≠=y x ,1)(=A r iv.0≠-=y x ,3)(=A r iv.yx y x ±≠≠≠,0,0⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=x y y y x yy yxA ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡→2222x xyxy xy x xy y y xy ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----→2222222200y x y xy y xy y x y y xy ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++→y x yy y x y yx00⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++→)2(00y x x yy x y y x 所以,当y x 2-=时,2)(=A r ;当y x 2-≠时,3)(=A r 8.设三阶矩阵A 满足A 2=E(E 为单位矩阵),但A ≠±E ,试证明:(秩(A -E )-1)(秩(A +E )-1)=0解.由第十一题知3)()(=-++E A r E A r 又因为A ≠±E ,所以0)(≠+E A r ,0)(≠-E A r 所以)(E A r +,)(E A r -中有一个为1所以(秩(A -E )-1)(秩(A +E )-1)=09.设A 为n 阶方阵,且A 2=A ,证明:若A 的秩为r ,则A -E 的秩为n -r ,其中E 是n 阶单位矩阵.解.因为A 2=A ,所以)(=-E A A 所以n E A r A r E A A r --+≥-=)()())((0所以nE A r A r ≤-+)()(又因为n E r A E A r A E r A r E A r A r ==-+≥-+=-+)()()()()()(所以n E A r A r =-+)()(.所以rn E A r -=-)(10.设A 为n 阶方阵,证明:如果A 2=E ,则秩(A +E )+秩(A -E )=n.解.因为A 2=E ,所以))((0E A E A +-=所以n E A r E A r E A E A r --++≥-+=)()()))(((0所以nE A r E A r ≤-++)()(又因为n E r A E E A r A E r E A r E A r E A r ==-++≥-++=-++)2()()()()()(所以n E A r E A r =-++)()(.第四章线性方程组一.填空题1.在齐次线性方程组A m ×n x =0中,若秩(A)=k 且η1,η2,…,ηr 是它的一个基础解系,则r =_____;当k =______时,此方程组只有零解.解.k n r -=,当n k =时,方程组只有零解.2.若n 元线性方程组有解,且其系数矩阵的秩为r,则当______时,方程组有唯一解;当______时,方程组有无穷多解.解.假设该方程组为A m ×n x =b,矩阵的秩r A r =)(.当n r =,方程组有惟一解;当n r <,方程组有无穷多解.3.齐次线性方程组⎪⎩⎪⎨⎧=+=++=++0302032321321x kx x x x x kx x 只有零解,则k 应满足的条件是______.解.03011211≠kk ,53,0623≠≠--+k k k k 时,方程组只有零解.4.设A 为四阶方阵,且秩(A)=2,则齐次线性方程组A *x =0(A *是A 的伴随矩阵)的基础解系所包含的解向量的个数为______.解.因为矩阵A 的秩31412)(=-=-<=n A r ,所以0)(*=A r ,A *x =0的基础解系所含解向量的个数为4-0=4.5.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=112011121A ,则A x =0的通解为______.解.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=000110101110110121112011121A 2)(=A r ,基础解系所含解向量个数为3-2=1.⎩⎨⎧=-=-003231x x x x ,取1,1123===x x x 则.基础解系为(1,1,1)T.A x =0的通解为k (1,1,1)T,k 为任意常数.6.设α1,α2,…αs 是非齐次线性方程组A x =b 的解,若C 1α1+C 2α2+…+C s αs 也是A x =b 的一个解,则C 1+C 2+…+C s =______.解.因为A b A i 且,=α(C 1α1+C 2α2+…+C s αs )=b,所以b b C C s =++)(1 ,11=++s C C .7.方程组A x =0以TT)1,1,0(,)2,0,1(21-==ηη为其基础解系,则该方程的系数矩阵为___.解.方程组A x =0的基础解系为TT)1,1,0(,)2,0,1(21-==ηη,所以2)(=-A r n ,即2)(3=-A r ,)(A r =1.所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=22111αααk k A ,假设),,(1312111a a a =α.由01=ηA ,得02201),,(1311131211=+=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡a a a a a 由02=ηA ,得0110),,(1312131211=-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-a a a a a 取2,1,0111213-===a a a 得.所以)1,1,2(1-=α,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=22111αααk k A (其中2,1k k 为任意常数).8.设A x =b,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=112210321A ,则使方程组有解的所有b 是______.解.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=112210321A ,05112210321||≠=-=A ,所以)(A r =3.因为A x =b 有解,所以⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-b r r 112210321112210321所以⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=123112201321k k k b ,其中321,,k k k 为任意常数.9.设A,B 为三阶方阵,其中⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=110121211A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=11202314k B ,且已知存在三阶方阵X ,使得B AX =,则k =___________.解.由题设B X A =⨯⨯3333,又因为0110121211||=-=A ,所以0||||||==X A B ,即0266411202314=+--=--k k k ,2-=k .二.单项选择题1.要使ξ1=(1,0,1)T ,ξ2=(-2,0,1)T 都是线性方程组0=Ax 的解,只要系数矩阵A 为(A)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡112213321(B)⎥⎦⎤⎢⎣⎡-211121(C)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡123020010(D)⎥⎦⎤⎢⎣⎡-020010解.因为21,ξξ的对应分量不成比例,所以21,ξξ线性无关.所以方程组0=Ax 的基础解系所含解向量个数大于2.(A)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=112213321A ,3)(,0112213321||=≠=A r A .因为A 是三阶矩阵,所以0=Ax 只有零解,排除(A);(B)2)(,211121=⎥⎦⎤⎢⎣⎡-=A r A .所以方程组0=Ax 的基础解系所含解向量个数:3-1)(=A r .排除(B);(C)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=123020010A ,2)(=A r .所以方程组0=Ax 的基础解系所含解向量个数:3-1)(=A r .排除(C);(D)⎥⎦⎤⎢⎣⎡-=020010A ,1)(=A r .所以方程组0=Ax 的基础解系所含解向量个数:3-2)(=A r ,(D)是答案.2.设0,,321=Ax 是ξξξ的基础解系,则该方程组的基础解系还可以表成(A)321,,ξξξ的一个等阶向量组(B)321,,ξξξ的一个等秩向量组(C)321211,,ξξξξξξ+++(C)133221,,ξξξξξξ---解.由0)()(321321211=+++++ξξξξξξk k k ,得0)()(332321321=+++++k k k k k k ξξξ.因为0,,321=Ax 是ξξξ的基础解系,所以321,,ξξξ线性无关.于是⎪⎩⎪⎨⎧==+=++000332321k k k k k k ,所以0321===k k k ,则321211,,ξξξξξξ+++线性无关.它也可以是方程组的基础解系.(C)是答案.(A)不是答案.例如321,,ξξξ和21321,,,ξξξξξ+等价,但21321,,,ξξξξξ+不是基础解系.3.n 阶矩阵A 可逆的充分必要条件是(A)任一行向量都是非零向量(B)任一列向量都是非零向量(C)b Ax =有解(D)当0≠x 时,0≠Ax ,其中Tn x x x ),,(1 =解.对(A),(B):反例⎥⎦⎤⎢⎣⎡=2121A ,不可逆;对于(C)假设A 为n×n 矩阵,A 为A 的增广矩阵.当n A r A r <=)()(时,b Ax =有无穷多解,但A 不可逆;(D)是答案,证明如下:当0≠x 时,0≠Ax ,说明0=Ax 只有零解.所以1,0||-≠A A 存在.4.设n 元齐次线性方程组0=Ax 的系数矩阵A 的秩为r,则0=Ax 有非零解的充分必要条件是(A )n r =(B )n r ≥(C )n r <(D )n r >解.(C )为答案.5.设n m A ⨯为矩阵,m n B ⨯为矩阵,则线性方程组0)(=x AB (A )当m n >时仅有零解.(B )当m n >时必有非零解.(C )当n m >时仅有零解.(D )当n m >时必有非零解.解.因为AB 矩阵为m m ⨯方阵,所以未知数个数为m 个.又因为n A r AB r ≤≤)()(,所以,当n m >时,m n A r AB r <≤≤)()(,即系数矩阵的秩小于未知数个数,所以方程组有非零解.(D )为答案.6.设n 阶矩阵A 的伴随矩阵0*≠A ,若4321,,,ξξξξ是非齐次线性方程组b Ax =的互不相等的解,则对应的齐次线性方程组0=Ax 的基础解系(A )不存在(B )仅含一个非零解向量(C )含有二个线性无关解向量(D )含有三个线性无关解向量解.因为⎪⎩⎪⎨⎧-<-===1)(,01)(,1)(,*)(n A r n A r n A r n A r 因为0*≠A ,所以1)(-≥n A r ;又因为4321,,,ξξξξ是非齐次线性方程组b Ax =的互不相等的解,所以b Ax =的解不唯一,所以1)(-≤n A r ,所以1)(-=n A r .于是:基础解系所含解向量个数1)1()(=--=-=n n A r n (B )为答案.三.计算证明题1.求方程组⎪⎩⎪⎨⎧=----=+-+-=-+-174952431132542143214321x x x x x x x x x x x 的通解,并求满足方程组及条件16354321-=-++x x x x 的全部解.解.将条件方程与原方程组构成矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-------→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----------56144280287214028721401132511163517409152413113251⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---→⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----→0000000000287214017409100000000002872140113251 i.条件方程与原方程组兼容,即加上条件后的方程组与原方程组有相同的通解;ii.2)()(==A r A r ,方程组有解.齐次方程组的基础解系含解向量的个数为2)(4=-A r ;iii.齐次方程的基础解系:⎩⎨⎧=-+-=++07214049432421x x x x x x 令27,41,03142=-===x x x x 得令7,90,13142=-===x x x x 得基础解系为:T T)0,7,1,9(,)1,27,0,4(--iv.非齐次方程的通解:⎩⎨⎧=-+--=++2872141749432421x x x x x x 令2,10,02143-====x x x x 得所以全部解为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-127040719002121k k 2.设有线性方程组⎪⎩⎪⎨⎧=++--=++=++kmx x x x x x x x x 3213213214132303,问m,k 为何值时,方程组有惟一解?有无穷多组解?有无穷多组解时,求出一般解.解.⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--→⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--110010700131170107001314113230131k m k m k m i.当3)()(,1==-≠A r A r m 时,方程组有惟一解;ii.当)()(,1,1A r A r k m ≠≠-=时,方程组无解;iii.当32)()(,1,1<===-=A r A r k m 时,方程组有无穷多解.此时基础解系含解向量个数为1)(3=-A r 齐次方程组:⎩⎨⎧==++07032321x x x x ,所以02=x .令1,113-==x x 得.基础解系解向量为:T)1,0,1(-.非齐次方程组:⎩⎨⎧==++17032321x x x x ,所以712=x .令73,013-==x x 得.非齐次方程特解为:T)0,71,73(-.通解为:⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=10107173k x 3.问λ为何值时,线性方程组⎪⎩⎪⎨⎧+=+++=++=+324622432132131λλλx x x x x x x x 有解,并求出解的一般形式.。
线性代数练习册第一章部分答案(本)

1 .AAT E; 3 . A2 E 2. AT A
AAT E A1 AT ; A2 E A1 A AT A1 A
或 或
AAT E AAAT AE AT A
AAT E, A2 E A( AT A) 0, A可逆 A1 A( AT A) A1 0 AT A
2 −3 1 r2 − 2 r1 0 0 1 3 0 2r2 0 −1 −3 r − 2r 0 4 1
2 0 0
−3 1 10
2 −3 1 r1 + 3r2 0 1 0 1 3 0 r1 0 0 0 0 2 −4 −4 −2 −2 3 5 3 4 3 1 0 −1 −4 3 −4 1 −2 0 −2 −1
而 B11 所以,
(1)11 0 1 0 1 0 , 11 211 0 2 0 2 0
11
1 4 1 0 1 1 4 A11 PB11 P 1 11 1 1 0 2 3 1 1 4 213 1 1 213 1 4 1 1 213 3 1 211 1 1 3 1 211 4 211 2731 2732 683 684
1 0 0
0 5 1 3 0 0
1 (2)B = 3 2 3 解:
−1 −3 −2 −3
3 5 3 4 −1 −3 −2 −3
1 B= 3 2 3 r2 − 3r1 r3 − 2r1 r4 − 3r1
1 0 0 0
3 −1 3 − 4 −8 0 −4 8 0 −3 6 −6 0 −5 10 −10 3 1 0 0 0 1 0 0 −4 −2 0 0 2 −2 0 0 3 2 0 0 −3 2 0 0
线性代数练习题及答案10套

1 0 1 14.设矩阵 A= 0 2 0 ,矩阵 B A E ,则矩阵 B 的秩 r(B)= __2__. 0 0 1 0 0 1 B A E = 0 1 0 ,r(B)=2. 0 0 0
15.向量空间 V={x=(x1,x2,0)|x1,x2 为实数}的维数为__2__. 16.设向量 (1,2,3) , (3,2,1) ,则向量 , 的内积 ( , ) =__10__. 17.设 A 是 4×3 矩阵,若齐次线性方程组 Ax=0 只有零解,则矩阵 A 的秩 r(A)= __3__. 18 . 已 知 某 个 3 元 非 齐 次 线 性 方 程 组 Ax=b 的 增 广 矩 阵 A 经 初 等 行 变 换 化 为 :
三、计算题(本大题共 6 小题,每小题 9 分,共 54 分)
Ibugua
交大打造不挂女神的领跑者
123 23 3 21.计算 3 阶行列式 249 49 9 . 367 67 7 123 23 3 100 20 3 解: 249 49 9 200 40 9 0 . 367 67 7 300 60 7
线代练习题及答案(一)
一、单项选择题(本大题共 10 小题,每小题 2 分,共 20 分)
1.设 A 为 3 阶方阵,且 | A | 2 ,则 | 2 A 1 | ( D A.-4 B.-1 C. 1 ) D.4
| 2 A 1 | 2 3 | A | 1 8
1 4. 2
)
1 2 3 1 2 2. 设矩阵 A= (1, 2) , B= C= 则下列矩阵运算中有意义的是 ( B 4 5 6 , 3 4 ,
行成比例值为零.
a1b2 a 2 b2 a 3 b2
线性代数习题集带答案

线性代数习题集带答案第一部分专项同步练习第一章行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)243512.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26.在函数1323211112)(x x xxx f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9.已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若573411111326478----=D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3-(D)011. 若2235001011110403--=D ,则D 中第四行元的余子式的和为( ). (A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时,齐次线性方程组=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是.4.若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式100111010100111.6.行列式=-000100002000010n n .7.行列式=--001)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式=--+---+---111111111111111x x x x .11.n 阶行列式=+++λλλ111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321=D ,j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式,则=+++44434241234A A A A .14.已知db c a cc a b b a b c a cb a D =, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321-==D ,j A 4为)4,3,2,1(4=j a j 的代数余子式,则=+4241A A ,=+4443A A .16.已知行列式nn D001030102112531-=,D 中第一行元的代数余子式的和为.17.齐次线性方程组=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是. 18.若齐次线性方程组??=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1.cb a db a dc a dc bd c b a d c ba d cb a++++++++3333222; 2.yxyx x y x y y x y x +++;3.解方程0011011101110=x x xx ; 4.111111321321221221221----n n n n a a a a x a a a a x a a a a xa a a a x ;5. na a a a 111111111111210(n j a j ,,1,0,1 =≠); 6. bn b b----)1(111121111311117. n a b b b a a b b a a a b 321222 111111111; 8.xa a a a x a a a a x a a a a x n nn 321212121;9.2212221212121111nn n nnx x x x x x x x x x x x x x x +++; 10. 21000120000021001210001211.aa a a a a aa a D ---------= 110001100011000110001.四、证明题1.设1=abcd ,证明:011111111111122222222=++++dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a x b a -=++++++.3.))()()()()()((111144442222d c b a c d b d b c a d a c a b d c b a d c b adc b a +++------=.4.∏∑≤<≤=----=nj i i jni innn nn nn n nna aa a a a a a a a a a a a a 1121222212222121)(111.5.设c b a ,,两两不等,证明01 11333=c b a c ba 的充要条件是0=++cb a .参考答案一.单项选择题A D A C C D ABCD B B 二.填空题1.n ;2.”“-;3.43312214a a a a ;4.0;5.0;6.!)1(1n n --;7.1)1(212)1()1(n n n n n a a a ---; 8.M 3-; 9.160-; 10.4x ; 11.1)(-+n n λλ;12.2-;13.0; 14.0; 15.9,12-; 16.)11(!1∑=-nk k n ; 17.3,2-≠k ; 18.7=k三.计算题1.))()()()()()((c d b d b c a d a c a b d c b a ------+++-;2. )(233y x +-;3. 1,0,2-=x ;4.∏-=-11)(n k kax5.)111()1(00∑∏==-+-nk k nk k a a ; 6. ))2(()1)(2(b n b b ---+- ;7. ∏=--nk k kna b1)()1(; 8. ∏∑==-+nk k nk k a x a x 11)()(;9. ∑=+nk k x 11; 10. 1+n ;11. )1)(1(42a a a ++-. 四. 证明题 (略)第二章矩阵一、单项选择题1. A 、B 为n 阶方阵,则下列各式中成立的是( )。
线性代数习题及解答完整版

线性代数习题及解答 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】线性代数习题一说明:本卷中,A -1表示方阵A 的逆矩阵,r (A )表示矩阵A 的秩,||α||表示向量α的长度,αT表示向量α的转置,E 表示单位矩阵,|A |表示方阵A 的行列式. 一、单项选择题(本大题共10小题,每小题2分,共20分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.设行列式111213212223313233a a a a a a a a a =2,则111213313233213122322333333a a a a a a a a a a a a ------=( ) A .-6 B .-3 C .3D .62.设矩阵A ,X 为同阶方阵,且A 可逆,若A (X -E )=E ,则矩阵X =( ) A .E +A -1B .E -AC .E +AD .E -A -13.设矩阵A ,B 均为可逆方阵,则以下结论正确的是( )A .⎛⎫⎪⎝⎭A B 可逆,且其逆为-1-1⎛⎫⎪⎝⎭A B B .⎛⎫⎪⎝⎭A B 不可逆 C .⎛⎫⎪⎝⎭A B 可逆,且其逆为-1-1⎛⎫ ⎪⎝⎭B AD .⎛⎫⎪⎝⎭A B 可逆,且其逆为-1-1⎛⎫⎪⎝⎭A B 4.设α1,α2,…,αk 是n 维列向量,则α1,α2,…,αk 线性无关的充分必要条件是( )A .向量组α1,α2,…,αk 中任意两个向量线性无关B .存在一组不全为0的数l 1,l 2,…,l k ,使得l 1α1+l 2α2+…+l k αk ≠0C .向量组α1,α2,…,αk 中存在一个向量不能由其余向量线性表示D .向量组α1,α2,…,αk 中任意一个向量都不能由其余向量线性表示5.已知向量2(1,2,2,1),32(1,4,3,0),T T+=---+=--αβαβ则+αβ=( ) A .(0,-2,-1,1)TB .(-2,0,-1,1)TC .(1,-1,-2,0)TD .(2,-6,-5,-1)T6.实数向量空间V ={(x , y , z )|3x +2y +5z =0}的维数是( ) A .1B .2C .3D .47.设α是非齐次线性方程组Ax =b 的解,β是其导出组Ax =0的解,则以下结论正确的是( )A .α+β是Ax =0的解B .α+β是Ax =b 的解C .β-α是Ax =b 的解D .α-β是Ax =0的解8.设三阶方阵A 的特征值分别为11,,324,则A -1的特征值为( ) A .12,4,3 B .111,,243C .11,,324D .2,4,39.设矩阵A =121-,则与矩阵A 相似的矩阵是( )A .11123--B .01102C .211- D .121-10.以下关于正定矩阵叙述正确的是( ) A .正定矩阵的乘积一定是正定矩阵 B .正定矩阵的行列式一定小于零 C .正定矩阵的行列式一定大于零D .正定矩阵的差一定是正定矩阵二、填空题(本大题共10小题,每空2分,共20分)请在每小题的空格中填上正确答案,错填、不填均无分。
线性代数 课后作业及参考答案

《线性代数》作业及参考答案一.单项选择题1.设行列式a aa a11122122=m,a aa a13112321=n,则行列式a a aa a a111213212223++等于()A. m+nB. -(m+n)C. n-mD. m-n2.设矩阵A=100020003⎛⎝⎫⎭⎪⎪⎪,则A-1等于()A.130012001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪B.100120013⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪C.13000100012⎛⎝⎫⎭⎪⎪⎪⎪⎪D.120013001⎛⎝⎫⎭⎪⎪⎪⎪⎪⎪3.设矩阵A=312101214---⎛⎝⎫⎭⎪⎪⎪,A*是A的伴随矩阵,则A *中位于(1,2)的元素是()A. –6B. 6C. 2D. –24.设A是方阵,如有矩阵关系式AB=AC,则必有()A. A =0B. B≠C时A=0C. A≠0时B=CD. |A|≠0时B=C5.已知3×4矩阵A的行向量组线性无关,则秩(A T)等于()A. 1B. 2C. 3D. 46.设两个向量组α1,α2,…,αs和β1,β2,…,βs均线性相关,则()A.有不全为0的数λ1,λ2,…,λs使λ1α1+λ2α2+…+λsαs=0和λ1β1+λ2β2+…λs βs=0B.有不全为0的数λ1,λ2,…,λs使λ1(α1+β1)+λ2(α2+β2)+…+λs(αs+βs)=0C.有不全为0的数λ1,λ2,…,λs使λ1(α1-β1)+λ2(α2-β2)+…+λs(αs-βs)=0D.有不全为0的数λ1,λ2,…,λs和不全为0的数μ1,μ2,…,μs使λ1α1+λ2α2+…+λsαs=0和μ1β1+μ2β2+…+μsβs=07.设矩阵A的秩为r,则A中()A.所有r-1阶子式都不为0B.所有r-1阶子式全为0C.至少有一个r阶子式不等于0D.所有r阶子式都不为08.设Ax=b是一非齐次线性方程组,η1,η2是其任意2个解,则下列结论错误的是()A.η1+η2是Ax=0的一个解B.12η1+12η2是Ax=b的一个解C.η1-η2是Ax=0的一个解D.2η1-η2是Ax=b的一个解9.设n阶方阵A不可逆,则必有()A.秩(A)<nB.秩(A)=n-1C.A=0D.方程组Ax=0只有零解10.设A是一个n(≥3)阶方阵,下列陈述中正确的是()A.如存在数λ和向量α使Aα=λα,则α是A的属于特征值λ的特征向量B.如存在数λ和非零向量α,使(λE-A)α=0,则λ是A的特征值C.A的2个不同的特征值可以有同一个特征向量D.如λ1,λ2,λ3是A的3个互不相同的特征值,α1,α2,α3依次是A的属于λ1,λ2,λ3的特征向量,则α1,α2,α3有可能线性相关11.设λ0是矩阵A的特征方程的3重根,A的属于λ0的线性无关的特征向量的个数为k,则必有()A. k≤3B. k<3C. k=3D. k>312.设A是正交矩阵,则下列结论错误的是()A.|A|2必为1B.|A|必为1C.A-1=A TD.A的行(列)向量组是正交单位向量组13.设A是实对称矩阵,C是实可逆矩阵,B=C T AC.则()A.A与B相似B. A与B不等价C. A与B有相同的特征值D. A与B合同15.设有矩阵Am×n,Bm×s,Cs×m,则下列运算有意义的是()。
线性代数习题册参考解答.docx

第一章行列式1、 求下列排列的逆序数,并确定它们的奇偶性。
(1) 1347265; (2) 〃(〃 —1)・・・321。
【解(1) r(1347265)=0 + 0 + 0 + 0 + 3 + l + 2 = 6,偶排列;(2) "〃(〃_1)...321] = 0 + ] + 2 + ... + (〃_1) = 〃(;1)。
当〃=4奴4女+ 1时,〃(〃;1)=2机4*—1),2机4* + 1)为偶数,即为偶排列;当〃 = 412,413时,丝* = (2*+1)(4*+ 1),(2*+1)(4*+ 3)为奇数,即为奇 排列。
■2、 用行列式定义计算2x x 1 21x1-1 f (X )=-- [3 2x1111%中『和r 的系数,并说明理由。
【解】由行列式定义可知:含b 有的项只能是主对角线元素乘积,故的系数为2; 含有尸的项只能是(1, 2), (2, 1), (3, 3), (4, 4)的元素乘积项,而7(2134) = 0 + 1 + 0 + 0 = 1,故/的系数为一1. ■2-512 --37-14 3、 求 =o45 -9 2 7 4-612【解】三角化法:2-5121-522 1-522 尸2+八1-12 0 6C[0 2-160 113D 4 =- _八3-211 1 0 3 0 113 0 2-16 r 4+r 211 0 60 1160 1161 -52 2 r3~2r 2 0 11 3r4~r 2 00 -3 00 0 31111 rk~r l0 10 0=120= 120o )l=2,3,40 0 100 0 0 1【解】箭形行列式(爪形行列式):利用对角线上元素将第一行(或列)中元素1化为零。
1 x 2q+C2 +•••+&n D"=(,-就1 x 2-mi=l1x21 0 0C k -X L C I 凡 q (»i) k=2,3,---,n1 —m ••- 01 0…-m【解】观察特点: 行和相等。
线代练习册参考答案

第一章 行列式练习一一、填空题 1.()1!n - 2.()()12121n n n λλλ-- 3. 26,2x -4. (8,3)5.12213344a a a a -6. 2- 二、选择题1.(D)2.(B)3.(C)更正:1112n nq p q p p qa a a 改为1122n n q p q p q p a a a三、解答题1.1x =2.4-3. x a x b ==或4. 2014!5.112ln 3sin 4cos 2525C θθθ+++ 练习二一、填空题1.16-2.()()33x a x a +- 3. 1204. 27 二、选择题 1.(B)2.(D) 三、解答题1.(1)500-(2)160(3)02. (1)9-(2)3-(3)1练习三一、填空题1.62.0,0a b ==3. 124. 2 二、选择题1.(D)2. (D)更正: (D)222--改为3.(B)4. (A)5. (D) 三、解答题1.270-2.1n +3. 64. 12341,2,3,1x x x x ====-第一章复习自测题一、选择题1.(C)2. (D)3.(C)4. (B) (D)5. (A)6. (D)7.(B) 二、填空题1.122460002.53. 1a =更正:去掉b =4. 245. 2014-! 三、解答题1.(1)7-(2)()()()()a b c b a c a c b ++---2.()221n a a --3.略第二章 矩阵及其运算练习一一、填空题1.24210;121363-⎛⎫ ⎪- ⎪ ⎪-⎝⎭2.8212⎛⎫⎪⎪ ⎪⎝⎭3.112233122221321231212333222x x x x x a a a a x x x a a x +++++4. 72- 二、选择题1.(B)2.(D)3.(A)4.(C)5.(A)三、解答题1.1602.86,1441810310⎛⎫⎪- ⎪ ⎪⎝⎭3. 146561717173,5139181651122-⎛⎫⎛⎫ ⎪ ⎪---- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭ 4. 112125224336-⎛⎫⎪- ⎪ ⎪-⎝⎭5.略 练习二一、填空题1.8,6a b ==2.33140416513-⎛⎫⎪- ⎪ ⎪--⎝⎭,更正:222()4AB A B A ==改为 3. 04. 1 5. cos sin sin cos θθθθ⎛⎫⎪-⎝⎭6. 100122010345⎛⎫⎪⎪ ⎪⎝⎭二、选择题1.(D)更正:最后一选项改为(D)2.(A)3.(B)4.(C) 三、解答题1.3476814234-⎛⎫⎪-- ⎪ ⎪-⎝⎭2. 1122212221n n n n ++⎛⎫-- ⎪--⎝⎭ 3.102427-4.略5.()()1111;(2)324A A E A E A E --=-+=-- 练习三一、填空题1.4更正:*A A B =+=改为2.03. 64.100-5.(1)3mn mab - 6. 100010003100051007⎛⎫ ⎪ ⎪⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭ ,10007100051003100⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭二、计算题1.020024001320013320057-⎛⎫ ⎪-- ⎪⎪-- ⎪--⎝⎭,,2.4411644643400252550430005252510,120000222001122O A A A O -⎛⎫- ⎪⎪⎛⎫ ⎪⎪--⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎪ ⎪-⎝⎭, 第二章复习自测题一、填空题1.36924612310,⎛⎫⎪ ⎪ ⎪⎝⎭2.3412⎛⎫⎪⎝⎭3. 1005011023A ⎛⎫ ⎪ ⎪=- ⎪ ⎪- ⎪⎝⎭4. 10010110553211052⎛⎫ ⎪ ⎪⎪ ⎪⎪ ⎪ ⎪⎝⎭5.26. 22350035a a b b ⎛⎫-+ ⎪-+⎝⎭7. 68.21(3)2A A E -+ 二、选择题1.(C)2. (D)3.(A)4. (C)5. (B)6. (B)7.(C)8.(B) 三、解答题1.1123212331236312491016x z z z x z z z x z z z =-++⎧⎪=-+⎨⎪=--+⎩2.123503x x x =⎧⎪=⎨⎪=⎩ 3.321⎛⎫⎪ ⎪ ⎪⎝⎭4.27312732683684⎛⎫ ⎪--⎝⎭5.201030102⎛⎫ ⎪ ⎪ ⎪⎝⎭6.100020011223400252543002525⎛⎫⎪ ⎪⎪-⎪ ⎪ ⎪⎪⎪⎪-⎝⎭第三章矩阵的初等变换与线性方程组练习一 一、填空题1.123123123c c c b b b a a a ⎛⎫ ⎪ ⎪ ⎪⎝⎭2.212322111312313332b b b b b b b b b ⎛⎫⎪ ⎪ ⎪⎝⎭二、选择题1.(B)2.(A)3.(B)4.(D)1.(1)100001000012⎛⎫ ⎪ ⎪ ⎪-⎝⎭(2)10202011030001400000-⎛⎫⎪- ⎪⎪ ⎪⎝⎭2.当||0A k =≠时,A 可逆且1100010111A k k -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦3. 11111444411111444411114444411114444A A -⎡⎤⎢⎥⎢⎥--⎢⎥==⎢⎥--⎢⎥⎢⎥--⎢⎥⎣⎦4. 033123110⎛⎫ ⎪- ⎪ ⎪⎝⎭5.001010100-⎛⎫⎪-⎪ ⎪-⎝⎭ 练习二 一、填空题1.02.33. 14. 25. 3二、选择题1.(D)2.(B)3.(A)4.(B)三、解答题1.秩是2,32721=--是一个最高阶非零子式2. (1)当1k =时,()1R A =;(2)当2k =-且1k ≠时,()2R A =; (3)当1k ≠且2k ≠-时,()3R A =.练习三1.(B)2.(C)3.(D)4.(B)二、填空题1.1-2.n3. 1238315x x x =-⎧⎪=-⎨⎪=⎩三、计算题1.12123421100001x x k k x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(k 1,k 2为任意常数).2.211210x y k z --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(k 为任意常数). 3.提示:在第二个方程组中求一组特解. 令34211,1,1,0x x x x ==-==解得. 将该组特解代入第一个方程组中得: 1,4,4a b c ===.更正:第一个方程组中12342x ax x x +++=改为12341x ax x x +++=4.(1)当1m ≠-时, 方程组有惟一解; (2)当1,1,m k =-≠时方程组无解; (3)当1,1,m k =-=时方程组有无穷多解.通解为: 37110710x k ⎛⎫- ⎪-⎛⎫ ⎪⎪ ⎪=+ ⎪ ⎪⎪ ⎪⎝⎭⎪ ⎪⎝⎭第三章复习自测题一、填空题1.32.3-3. 2314113-⎛⎫⎪-⎝⎭4. 11n -- 5.1 二、选择题1.(D)2. (D)3.(B)4. (C)5. (B)三、解答题1.3862962129--⎛⎫⎪-- ⎪ ⎪-⎝⎭2.秩为3,0755********-=≠是一个最高阶非零子式.3.720335203322233⎛⎫- ⎪ ⎪ ⎪- ⎪ ⎪ ⎪-- ⎪⎝⎭4.2t ≠-无解2t =-且8p =-时, 121234411221100010x x c c x x --⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪=++ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭ (12,c c 为常数)2t =-且8p ≠-时,123411210010x x c x x --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪=+ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(c 为常数)5.(1)方程组()I 通解为: 21415201x k -⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪=+ ⎪ ⎪- ⎪ ⎪⎝⎭⎝⎭(2)将2450-⎛⎫⎪- ⎪ ⎪- ⎪⎝⎭代入方程组()II 得2,4,6m n t ===第四章 向量组的线性相关性练 习 一一、C D A B A二、1、3≠t 2、无关 三、线性相关 练 习 二一、D A D C B 二、1、 3 ,531,,ααα2、 6=k , 21,αα3、21r r = 三、12,a a 四、123,,ααα 422αα=练 习 三 一、C C B二、1、)(,)0,0,1()1,1,1(31R k k TT ∈+2、13、(2,1,0,1)Tk -- 4、n r -三、 基础解系 133(,,1,0)22T ξ=,237(,,0,1)44T ξ-= 四、 基础解系 ξ1=(-9, 1, 7, 0)T , ξ2=(1, -1, 0, 2)T特解 η=(1, -2, 0, 0)T复 习 自 测 题一、B B D D D 二、1、22、 相关3、(1111)T4、1三、1012101212100111210013a b a b ⎛⎫⎛⎫ ⎪ ⎪-→-- ⎪ ⎪ ⎪ ⎪----⎝⎭⎝⎭当1-=a 且3≠b 时,方程组无解 当1-≠a 时,方程组有唯一解当1-=a 且3=b 时,方程组有无穷多解.四、向量组的秩为3,124,,ααα是一个最大线性无关组,并且312ααα=-+,51242αααα=-++. 五、基础解系为: 4534,121001ξξ--==⎛⎫⎛⎫⎪ ⎪ ⎪⎪⎝⎭⎝⎭,六、方程组的通解为: 2111011191212011311040150--=++⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭x x c c x x (12,c c 为任意常数) 七、略第五章相似矩阵及二次型练 习 一 一、D C C二、1、 1或-12、12n λλλ ,12n λλλ+++3、 -15 ,94、()T1,0,12-=α,T⎪⎭⎫ ⎝⎛--=21,1,213α5、 -1 三、⎪⎪⎭⎫ ⎝⎛==11111a b ,⎪⎪⎭⎫ ⎝⎛-=-=101],[],[1112122b b b a b a b , ⎪⎪⎭⎫ ⎝⎛-=--=12131],[],[],[],[222321113133b b b a b b b b a b a b . 四、25五、(1)10λ=,22λ=,33λ=,112121p -⎛⎫⎪⎪-⎪= ⎪ ⎪⎪ ⎪⎝⎭,2110p -⎛⎫ ⎪= ⎪⎪⎝⎭,3111p ⎛⎫ ⎪= ⎪ ⎪⎝⎭ (2)1232λλλ===,1120p ⎛⎫ ⎪= ⎪ ⎪⎝⎭,2001p ⎛⎫ ⎪= ⎪ ⎪⎝⎭六、02321a ,b ,c ,λ==-== 练 习 二 一、A AB二、555555156656650112001102212111102011122121110001011222A P P -⎛⎫⎛⎫--+--⎛⎫⎛⎫⎪ ⎪⎪ ⎪=Λ=--=-+-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭⎝⎭三、01000P ⎛⎫⎪⎪⎪=⎪⎪,且1100010005P AP --⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦四、11/1/,1/p ⎛ = ⎝211,0p ⎛⎫ =- ⎪⎝⎭311,2p ⎛⎫ ⎪= ⎪ -⎝ 令123(,,)P p p p =,则1800020002P AP -⎛⎫⎪= ⎪ ⎪⎝⎭五、1(2)01(2)102021(2)01(2)nn n n ⎛⎫+--- ⎪ ⎪⎪--+-⎝⎭练 习 三一、 C C C C D 二、1、可逆2、大于零3、 1,0三、1232/32/31/32/3,1/3,2/31/32/32/3p p p -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪===- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,令123(,,)P p p p =,则所用线性变换的矩阵为P ,且令x Py =,则22212325f y y y =-++。
线性代数习题册(答案)

线性代数习题册答案第一章 行列式练习 一班级 学号 姓名1.按自然数从小到大为标准次序,求下列各排列的逆序数: (1)τ(3421)= 5 ; (2)τ(135642)= 6 ;(3)τ(13…(2n-1)(2n)…42) = 2+4+6+…+(2 n-2)= n (n-1).2.由数字1到9组成的排列1274i56j9为偶排列,则i= 8 、j= 3 .3.在四阶行列式中,项12233441a a a a 的符号为 负 .4.00342215= -24 .5.计算下列行列式:(1)122212221-----= -1+(-8)+(-8)-(-4)-(-4)―(-4)= -5或(2)111111λλλ---= -3λ+1+1-(-λ)-(-λ)―(-λ) = -3λ+3λ+2=2(2)(1)λλ-+练习 二班级 学号 姓名 1.已知3阶行列式det()ij a =1,则行列式det()ij a -= -1 . 3(1)11-⋅=-2. 1112344916= 2 .3.已知D=1012110311101254--,则41424344A A A A +++= —1 .用1,1,1,1替换第4行4. 计算下列行列式: (1)111ab c a b c abc +++= 13233110110011,0110111111r r r r c c a b c bcabcabc-----+-==++++++(2) xy x y y x y x x yxy+++(3)130602121476----(4)1214012110130131-5.计算下列n 阶行列式:(1)n xa a a x a D aax=(每行都加到第一行,并提公因式。
)(2)131111n +(3) 123123123n n n a ba a a a ab a a a a a a b+++练习 三班级 学号 姓名 1.设线性方程组123123123111x x x x x x x x x λλλ--=⎧⎪++=⎨⎪-++=⎩有惟一解,则λ满足的条件是什么?1,0,1λλλ≠-≠≠2. 求解线性方程组12341234123412345242235232110x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩3.已知齐次线性方程组123123123000x x x x x x x x x λλλ--=⎧⎪-++=⎨⎪--+=⎩有非零解,求λ的值。
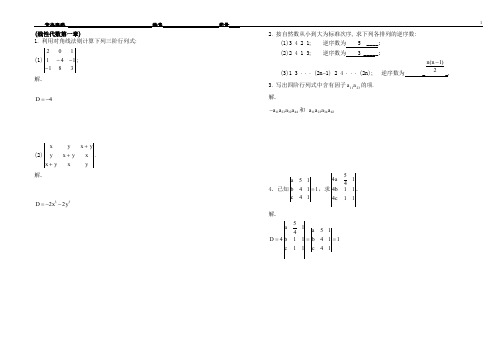
线性代数练习册习题及答案本

1252,yD第四章线性方程组§ 4-1克拉默法则一、选择题 1.下列说法正确的是( C )A. n 元齐次线性方程组必有 n 组解;B. n 元齐次线性方程组必有 n 1组解;C. n 元齐次线性方程组至少有一组解,即零解;D. n 元齐次线性方程组除了零解外,再也没有其他解 2.下列说法错误的是( B )A. 当D 0时,非齐次线性方程组只有唯一解;B. 当D 0时,非齐次线性方程组有无穷多解;C. 若非齐次线性方程组至少有两个不同的解,则 D 0 ;二、填空题1. 已知齐次线性方程组2. X iX i X1X 3X 2 2 x 2X 3 X30有非零解,由克拉默法则可知,如果非齐次线性方程组的系数行列式 0,则方程组有唯一解x i D i D、用克拉默法则求解下列方程组 8x 1. 6x 3y 2y 解: D 1 D 2所以,D.若非齐次线性方程组有无解,则0.D 1 1,y1DX 1 2X 2X 322. 2X !X 23X 31X 1 X 2 X 3 0解:1 2 1r2 r 12 1D 213 r2 2r1 0 3 55 0r 3 r 11 1 1—1 022 151 1 3A 2D 1 1350 1 10 111215D 2 2 1 3 r 1 2D 21 0 11 12 2 5 D3 2 1 1 r 1 2D 2 1 1 01 所以, X 1 D 1,X 2 D 2 D 2X z 13. 2X 4y z 1X 8y 3z 2D i51 3 100 1 0 0 1 1 51 0D 3 2,X 3 D 3 1210 0 2 41 G 2C 3 0 4 1 8 35 8 D 解:11 20 0 3 0 1 01|I 1 1 4 1C 3 G 1 2 8 322 1 1I 2 11 cC 2 1 2314 8 22 1 2 0 1 D 1D 20 205 , 1 01 0 02 5 , D 30 1 0 4 8 25 0 1 4 1 20 8 2所以,D 2 0,z42628 C35C1 211解:2313 8 5 1411 102 5 183 5 281 0 0 0 32 142 22x 2 x 3 5x2x 2 X 3 4x 42 2x 1 3x 2X 3 5x 423% X 2 2x 311x 4 04.1 1 1 1 「2 A 1 1 1 1 1 2 1 4 「3 Or 0 1 2 3 2 3 15 2r 13A 0 5 3 7 r 4 312 112 18DD a 25 11 D 21 123 1 1 2 3 7 12 15 1 2 3 152 25 2 2 02 31 1 1 I |1 5 111 4P2 r10 7 2 3 1 5「3 " 0 12 3 7 211r L=3r ^|0 15 1831 I 230 13/ 2r333 0 31 15 1 8 5 12 4 c3C 225 C 4 11Q 01110 2182C2 旳152 15 211 3 0 1 0 29 515 220 0 7 2728410 18 28 0D 1142 5 5 2 22 2 0 0 1 13 5 55§ 4-2齐次线性方程组、选择题的两个不同的解,k 为任意常数,则方程组 AX 0的通解为(D )A. k 1 ;B.k 2 ; C. k( i 2) ;D.k( 12).解:因为m n 矩阵A 的秩为n 1,所以方程组 AX 0的基础解系 含1个向量。
同济大学-线性代数-习题册+答案
所以 B A E
1
0 0 1 1 0 2 2 0 1 A E 0 1 0 0 3 0 0 3 0 1 0 0 2 0 1 1 0 2
2
13 设方阵 A 满足 A A 2E O 证明 A 及 A 2E 都可逆 并求 A 及 ( A 2 E )
解.
0 0 ; 1 d
a
1 4 D 10 0 2 1 5 1 0 2 2 1 2 1 2 4 0 7 0 0 15 7 0 1 0 2 1 2 2 4 0 1 2 20 0 15 1 7 0 7 0 2 1 2 0 2 1 7 0 1 1 7 0 2 20 0 0 17 85 2 4 0 0 9 45
D 2 x3 2 y3
解.
a D4b c
5 1 a 5 1 4 1 1 b 4 1 1 1 1 c 4 1
专业班级
姓名
学号
2
5 计算下列各行列式
4 1 (1) 10 0
解.
1 2 5 1
2 0 2 1
4 2 ; 0 7
a 1 0 1 b 1 (3) 0 1 c 0 0 1
所以 B AB 也是对称矩阵。
T
10.设 A 为 n 阶方阵,且 A
专业班级
姓名
学号
6
1 4 2 0 3 1 12 解矩阵方程 X . 1 2 1 1 0 1
解.
1 4 2 0
1 0 1 14 设 A 0 2 0 且 AB E A2 B 求 B 1 0 1
1 | B | _______ 9 ______.
* 1 ,则 2A* 2 A 2 11.设矩阵 A 、 B 、C 满足 AB AC ,则 B C 成立的一个充分条件是____C_____. (A) A 为方阵 (B) A 为非零矩阵 (C) A 为可逆方阵 (D) A 为对角阵
线性代数练习册(第1章)

第一章习题一(行列式的基本概念)一、填空题1. 按自然数从小到大为标准次序,排列2413的逆序数是 .2. 按自然数从小到大为标准次序,排列4637251的逆序数是 .3. 按自然数从小到大为标准次序,排列()n n 2241213 -的逆序数是 .4.若排列4153972j i 为偶排列,则=i ,=j . 5. 四阶行列式中含有因子2311a a 的项是 . 6. 在5级行列式中,项4524513213a a a a a 前带的符号是 . 二、解答题 1. 求行列式的值.(1) 200146213-;(2) 987654321.2. 证明(1)))()((111222a c c b b a c b a c b a---=.(2)()32211122b a b b a a b aba -=+.(3)()()4242313144312211000000y y x x y y x x x y x y y x y x --=.第一章习题二(行列式的性质)一、填空题1.行列式403212101的值是 .2. 行列式211312707458-的值是 .3. 行列式322000000111d d c dc b a = .;=dcb a .二、解答题1. 计算下列各行列式:(1)71100251020214214.(2)2605232112131412-.(3)efcfbf de cd bdae ac ab ---. 2. 证明(1)2222222224c b a b a bccabc a c ab ca ab c b =+++.(2)()()()()()()()()()()()()03213213213212222222222222222=++++++++++++d d d d c c c c b b b b a a a a .(3)()()()()()()()d c b a d c d b c b d a c a b a d c b a d c b a dc b a+++------=444422221111.第一章习题三(行列式按行或列展开)一、填空题1.设4阶行列式1221304312107301----=D ,则(1)D 的代数余子式14A = ; (2) 1413121122A A A A -+-= ;2.行列式12334152--=aD 的代数余512=A ,则a = .3.行列式xd d d x c c c x b b b x a a a D 3213213213214=,则=+++41312111A A A A .二、解答题1.设1121013=z y x ,求111314111zy x ---.2. 计算n 阶行列式n222232222222221.3.证明1221100001001n nn n x xD x a a a a a x----=-+12121,(2)n n n n n x a x a x a x a n ---=+++++≥.4.计算行列式00100200100000n D n n =-.5.计算n 阶行列式0001000000000001000n a a a D a a=.第一章习题四(克拉默法则)一、填空题1.如果线性方程组的系数行列式D ,则线性方程组一定有解且解是 .2.如果齐次线性方程组的系数行列式0≠D ,则齐次线性方程组没有 解.3.当=λ 时,齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=+=+=-=+02,0,02,043214131x x x x x x x x λλ有非零解.二、解答题1.用克拉默法则解线性方程组.⎪⎪⎩⎪⎪⎨⎧=-+=-+-=+--=+-.5534,12523,432,543321421431432x x x x x x x x x x x x2.已知齐次线性方程组()()()⎪⎩⎪⎨⎧=-+-=--=++-0124,02,0332132321x x x x x x x x λλλ有非零解,求λ的值.3.问μλ,取何值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++02,0,0321321321x x x x x x x x x μμλ有非零解?4.问λ取何值时,齐次线性方程组()()()⎪⎩⎪⎨⎧=-++=+-+=+--01,032,0421321321321x x x x x x x x x λλλ有非零解?5(思考题). 计算行列式βααββαβααββααββα+++++=10000010001000n D .。
线性代数习题(带答案解析)

第一部分 专项同步练习第一章 行列式一、单项选择题1.下列排列是5阶偶排列的是 ( ).(A) 24315 (B) 14325 (C) 41523 (D)24351 2.如果n 阶排列n j j j 21的逆序数是k , 则排列12j j j n 的逆序数是( ). (A)k (B)k n - (C)k n -2! (D)k n n --2)1(3. n 阶行列式的展开式中含1211a a 的项共有( )项.(A) 0 (B)2-n (C) )!2(-n (D) )!1(-n4.=0001001001001000( ).(A) 0 (B)1- (C) 1 (D) 25.=0001100000100100( ).(A) 0 (B)1- (C) 1 (D) 26.在函数1323211112)(x x x x x f ----=中3x 项的系数是( ).(A) 0 (B)1- (C) 1 (D) 27. 若21333231232221131211==a a a a a a a a a D ,则=---=323133312221232112111311122222 2a a a a a a a a a a a a D ( ). (A) 4 (B) 4- (C) 2 (D) 2- 8.若a a a a a =22211211,则=21112212ka a ka a ( ).(A)ka (B)ka - (C)a k 2 (D)a k 2-9. 已知4阶行列式中第1行元依次是3,1,0,4-, 第3行元的余子式依次为x ,1,5,2-, 则=x ( ).(A) 0 (B)3- (C) 3 (D) 210. 若5734111113263478----=D ,则D 中第一行元的代数余子式的和为( ). (A)1- (B)2- (C)3- (D)011. 若22351011110403--=D ,则D 中第四行元的余子式的和为( ).(A)1- (B)2- (C)3- (D)012. k 等于下列选项中哪个值时,齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x kx x kx x kx x x 有非零解.( )(A)1- (B)2- (C)3- (D)0二、填空题1. n 2阶排列)12(13)2(24-n n 的逆序数是.2.在六阶行列式中项261365415432a a a a a a 所带的符号是.3.四阶行列式中包含4322a a 且带正号的项是. 4.若一个n 阶行列式中至少有12+-n n 个元素等于0, 则这个行列式的值等于.5. 行列式=100111010100111.6.行列式=-000100002000010n n .7.行列式=--001)1(2211)1(111n n n n a a a a a a .8.如果M a a a a a a a a a D ==333231232221131211,则=---=323233312222232112121311133333 3a a a a a a a a a a a a D .9.已知某5阶行列式的值为5,将其第一行与第5行交换并转置,再用2乘所有元素,则所得的新行列式的值为.10.行列式=--+---+---1111111111111111x x x x .11.n 阶行列式=+++λλλ111111111.12.已知三阶行列式中第二列元素依次为1,2,3, 其对应的余子式依次为3,2,1,则该行列式的值为.13.设行列式5678123487654321=D ,j A 4)4,3,2,1(=j 为D 中第四行元的代数余子式,则=+++44434241234A A A A .14.已知db c a cc a b b a b c a c b a D =, D 中第四列元的代数余子式的和为.15.设行列式62211765144334321-==D ,j A 4为)4,3,2,1(4=j a j 的代数余子式,则=+4241A A ,=+4443A A .16.已知行列式nn D001030102112531-=,D 中第一行元的代数余子式的和为.17.齐次线性方程组⎪⎩⎪⎨⎧=+-=+=++0020232121321x x x kx x x x kx 仅有零解的充要条件是.18.若齐次线性方程组⎪⎩⎪⎨⎧=+--=+=++0230520232132321kx x x x x x x x 有非零解,则k =.三、计算题1. cb a db a dc a dc bd c b a d c b a d c b a++++++++33332222; 2.yxyx x y x y y x y x +++;3.解方程0011011101110=x x xx ; 4.111111321321221221221----n n n n a a a a x a a a a x a a a a xa a a a x ;5. na a a a 111111111111210(n j a j ,,1,0,1 =≠);6. bn b b ----)1(1111211111311117. n a b b b a a b b a a a b 321222111111111; 8.xa a a a x a a a a x a a a a x n nn 321212121;9.2212221212121111nn n nnx x x x x x x x x x x x x x x +++; 10. 21000120000021001210001211.aa a a a a aa a D ---------=110001100011000110001.四、证明题1.设1=abcd ,证明:011111111111122222222=++++dddd c c c c b b b b a a a a .2.3332221112333332222211111)1(c b a c b a c b a x c b x a x b a c b x a x b a c b x a xb a -=++++++.。
《线性代数》习题集(含答案)

《线性代数》习题集(含答案)第一章【1】填空题 (1) 二阶行列式2a ab bb=___________。
(2) 二阶行列式cos sin sin cos αααα-=___________。
(3) 二阶行列式2a bi b aa bi+-=___________。
(4) 三阶行列式xy zzx y yzx =___________。
(5) 三阶行列式a bc c a b c a bbc a+++=___________。
答案:1.ab(a-b);2.1;3.()2a b -;4.3333x y z xyz ++-;5.4abc 。
【2】选择题(1)若行列式12513225x-=0,则x=()。
A -3;B -2;C 2;D 3。
(2)若行列式1111011x x x=,则x=()。
A -1, B 0, C 1, D 2,(3)三阶行列式231503201298523-=()。
A -70;B -63;C 70;D 82。
(4)行列式00000000a ba b b a ba=()。
A 44a b -;B ()222a b-;C 44b a -;D 44a b 。
(5)n 阶行列式0100002000100n n -=()。
A 0;B n !;C (-1)·n !;D ()11!n n +-•。
答案:1.D ;2.C ;3.A ;4.B ;5.D 。
【3】证明33()by az bz ax bx ay x y z bx ay by az bz ax a b zx y bz ax bx ay by azyzx++++++=++++ 答案:提示利用行列式性质将左边行列式“拆项”成八个三阶行列式之和,即得结果。
【4】计算下列9级排列的逆序数,从而确定他们的奇偶性: (1)134782695;(2)217986354;(3)987654321。
答案:(1)τ(134782695)=10,此排列为偶排列。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 线性方程组§4-1 克拉默法则一、选择题1.下列说法正确的是( C )A.n 元齐次线性方程组必有n 组解;B.n 元齐次线性方程组必有1n -组解;C.n 元齐次线性方程组至少有一组解,即零解;D.n 元齐次线性方程组除了零解外,再也没有其他解. 2.下列说法错误的是( B )A.当0D ≠时,非齐次线性方程组只有唯一解;B.当0D ≠时,非齐次线性方程组有无穷多解;C.若非齐次线性方程组至少有两个不同的解,则0D =;D.若非齐次线性方程组有无解,则0D =. 二、填空题1.已知齐次线性方程组1231231230020x x x x x x x x x λμμ++=⎧⎪++=⎨⎪++=⎩有非零解,则λ= 1 ,μ= 0 .2.由克拉默法则可知,如果非齐次线性方程组的系数行列式0D ≠, 则方程组有唯一解i x =iD D. 三、用克拉默法则求解下列方程组1.832623x y x y +=⎧⎨+=⎩解:832062D ==-≠123532D ==-,2821263D ==-所以,125,62D Dx y D D====-2.123123123222310x x x x x x x x x -+=-⎧⎪+-=⎨⎪-+-=⎩解:213112112122130355011101r r D r r ---=--=-≠+---11222100511321135011011D r r ---=-+-=---,212121505213221310101101D r r --=-+-=-----, 3121225002112211511110D r r --=+=---所以, 3121231,2,1D D Dx x x D D D ======3.21241832x z x y z x y z -=⎧⎪+-=⎨⎪-++=⎩解:132010012412041200183583D c c --=-+-=≠-13110110014114020283285D c c -=-+=,2322112102112100123125D c c -=-+=--, 31320101241204120182582D c c =-=--所以, 3121,0,1D D Dx y z D D D======4.12341234123412345242235232110x x x x x x x x x x x x x x x x +++=⎧⎪+-+=-⎪⎨---=-⎪⎪+++=⎩解:2131412131111111111214012322315053733121102181231235537013814222180514r r D r r r r r r r r ---=------------+=----=-+---3214212325111511102221422518231523528110121101005110010525182733214210252823522c c D c c c c c c --------=----------+=-----=----212314113231511151112140723222150123733021101518723230132123733031284315181518r r D r r r r r r r r -----=--------------=----=------12342213111512151031224522182325111132283101101002510200251521852974265211228115127c c D c c c c c c -------=---------+=-----=----12432322111152115312125252223121135231200100215215552502714251152604c c D c c r r r r --------=----------+=----=---所以, 312412341,2,3,1D D D Dx x x x D D D D========-§4-2 齐次线性方程组一、选择题1.已知m n ⨯矩阵A 的秩为1n -,12,αα是齐次线性方程组0AX = 的两个不同的解,k 为任意常数,则方程组0AX =的通解为( D ). A.1k α; B.2k α; C.12()k αα+; D.12()k αα-.解:因为m n ⨯矩阵A 的秩为1n -,所以方程组0AX =的基础解系 含1个向量。
而12,αα是齐次线性方程组0AX =的两个不同的解, 所以120αα-≠为0AX =的解,则方程组0AX =的通解为12()k αα-。
2.设线性方程组1231231230020kx x x x kx x x x x ++=⎧⎪++=⎨⎪-+=⎩ 有非零解,则正确的是( C )A.k 必定为0;B. k 必定为1;C. k 为0或1;D.这样的k 值不存在.3.111212122212n n n n n n a b a b a b a b a b a b A a b a b a b ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,且0i a ≠(1,2,,)i n =,0(1,2,,)j j n b ≠=, 则0Ax =的基础解系中含有( A )个向量.A.1n -;B.n ;C.1;D.不确定. 解:因为()1112112122221212n n n n n n n n a b a b a b a a b a b a b a A b b b a b a b a b a ⎛⎫⎛⎫⎪ ⎪⎪ ⎪== ⎪ ⎪⎪ ⎪⎝⎭⎝⎭所以,11()10()1R A a b R A ≤≠⇒≥;又,所以,()1R A =。
4.设A 为n 阶方阵,()3r A n =- ,且123,,a a a 是0Ax =的三个 线性无关的解向量,则0Ax =的基础解系为( A ).A .122331,,a a a a a a +++;B .213213,,a a a a a a ---;C .21321312,,2a a a a a a ---; D .1233213,,2a a a a a a a ++---. 二、填空题1.n 元齐次线性方程组0m n A X ⨯=有非零解的充分必要条件是 ()R A n < .2.当 023λλλ===或或 时,齐次线性方程组123123123(1)2402(3)0(1)0x x x x x x x x x λλλ--+=⎧⎪+-+=⎨⎪++-=⎩有非零解.3.写出一个基础解系由[]12,1,0T η=-,[]23,0,1Tη=组成的齐次线性方程组___ __123230x x x +-= .解:方程组可为123223323x x x x x x x =-+⎧⎪=⎨⎪=⎩即123230x x x +-=三、求解齐次线性方程组1234512345134512345233703230226054330x x x x x x x x x x x x x x x x x x x ++++=⎧⎪+++-=⎪⎨+++=⎪⎪+++-=⎩解:213141323223421231233712337332113048824A 1022602111554331061212361233710004/3(1/3)(1/4)0122601004/3220033110011623000000r r r r r r r r r r r r r r r r r ⎛⎫⎛⎫- ⎪ ⎪-----⎪⎪-= ⎪⎪----- ⎪⎪-----⎝⎭⎝⎭-⎛⎫⨯⨯- ⎪- ⎪+- ⎪+-- ⎪⎝⎭11/30000⎛⎫⎪⎪ ⎪⎪⎝⎭所以,同解方程组为152534544554/34/311/3x x x x x x x x xx x =⎧⎪=⎪⎪=--⎨⎪=⎪⎪=⎩,则1204/304/3,111/31001ξξ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎪ ⎪==-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭为一组基础解系,所以,通解为1122x k k ξξ=+。
四、已知3阶非零矩阵B 的每一列都是方程组1231231232202030x x x x x x x x x λ+-=⎧⎪-+=⎨⎪+-=⎩ 的解.①求λ的值;②证明0B =.① 解:因为3阶非零矩阵B 的每一列都是方程组的解,所以方程组有非零解。
系数行列式A =122210311λ--=⇒-1λ=。
② 证明:依题意,AB O =。
假设0B ≠,则B 可逆,11AB O ABB OB A O --=⇒=⇒=,矛盾。
所以,0B =。
补充:求证:,m n n p A B ⨯⨯,0()()AB R A R B n =⇒+≤. 证明:依题意,矩阵B 的所有列向量1,,p ββ都是齐次线性方程组0Ax =的解,而0Ax =解空间的维数是()n R A -,所以,1()(,,)()p R B R n R A ββ=≤-,即()()R A R B n +≤。
§4-3 非齐次线性方程组一、选择题1.若()R A r n =<,则n 元线性方程组m n A X b ⨯= D .A.有无穷多个解;B.有唯一解;C.无解;D.不一定有解.2.线性方程组⎩⎨⎧=+=+012121x x x x ( A ).A. 无解;B. 只有0解;C. 有唯一解;D. 有无穷多解.3.方程組 12312321231x x x x x x x x x λλλλλ⎧++=⎪++=⎨⎪++=⎩ 有唯一解,则λ应满足( A ).A.2,1-≠≠λλ;B.2,1==λλ;C.2,1≠≠λλ;D.2,1≠-≠λλ.4.设A =1100011000111001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦,1234a a b a a ⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦,Ax b =有解的充分必要条件为( D ). A .1234a a a a ===; B .12341a a a a ====; C .12340a a a a +++=; D .12340a a a a -+-= .二、填空题1.n 元非齐次线性方程组m n A X b ⨯=有解的充分必要条件是 ()(,)R A R A b =.2.若5元线性方程组AX b =的基础解系中含有2个线性无关的解向量,则()r A =3 .3.设有一个四元非齐次线性方程组AX b =,()3R A =,又123,,ααα是它的三个解向量,其中12(1,1,0,2)T αα+=,23(1,0,1,3)Tαα+=,则非齐次线性方程组的通解为 (0,1,1,1)(1,1,0,2)T Tk --+ .解:因为123,,ααα是AX b =三个解向量,则1223()()(1,1,0,2)(1,0,1,3)(0,1,1,1)0T T T αααα+-+=-=--≠是0AX =的解,而()3R A =,所以(0,1,1,1)T--是0AX =的一组基础解系, 又1211()(1,1,0,2)22T αα+=是AX b =的解, 所以,AX b =的通解为(0,1,1,1)(1,1,0,2)T T k --+三、求解非齐次线性方程组23424538213496x y z x y z x y z x y z ++=⎧⎪-+=-⎪⎨+-=⎪⎪-+=-⎩解:231410211245011238213~000041960000r A -⎛⎫⎛⎫⎪ ⎪--- ⎪ ⎪ ⎪ ⎪- ⎪ ⎪--⎝⎭⎝⎭=同解方程组为212x z y z z z =--⎧⎪=+⎨⎪=⎩令211ξ-⎛⎫ ⎪= ⎪ ⎪⎝⎭为一组基础解系则通解为2112,()10x y c c R z --⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪=+∈ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭四、,a b 取何值时,线性方程组1231231233244x ax x x ax x x x bx ++=⎧⎪++=⎨⎪++=⎩(1)有唯一解;(2)无解;(3)有无穷多解?说明: 对于方程个数与未知量个数相等的含参数的线性方程组,判别其由唯一解, 有无穷解或无解时最好用:方程组有唯一解⇔系数行列式||0A ≠, 此种方法简单 又不容易出错.解: 方程组有唯一解⇔系数行列式||0A ≠2131111111||121001101101(1)(1)011a a r rA a a r r b a b aa b a b +-=---⨯-=-≠--而按第一列展开21233123(1)101310131013,101400010111~11401110001~()2(,)3,. (3)113,12141114r r r r A b r r b b b R A R A b a r r A b a ∴≠≠-⎛⎫⎛⎫⎛⎫↔ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭=≠=∴⎛⎫↔ ⎪ ⎪ ⎪⎝⎭当a 0且b 1时,方程组有唯一解 (2)当a=0时,增广矩阵()=则此时方程组无解当b=1时,()=21312311141114121402100~11130101~ 11141114,~000001/201~01/2010000()2(,)3, 111,~r r a r r a a r r A b R A R A b A b -⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎛⎫⎛⎫↔ ⎪ ⎪-- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭==<∴≠当a=1/2时,()则此时方程组有无穷多解.当a 1/2时,()4021000001()2(,)3,a R A R A b ⎛⎫ ⎪- ⎪⎪-⎝⎭=≠=∴则此时方程组无解.。
