2011年清华自主招生数学试题和答案解析
清华、北大2011-2015年自主招生面试真题汇总

清华、北大2011-2015年自主招生面试真题汇总2016年自主招生即将来临,考生和家长需要着手准备了。
除了报名申请材料之外,自主招生最重要的环节就是笔试和面试部分。
下面中国自主招生网小编汇总了清华大学、北京大学2011-2015年部分面试题,供报考2016自主招生的考生们参考。
清华大学清华大学2015年自主招生面试部分真题1.假设给你一次穿越的机会,你最希望穿越到什么时候?做什么人?干什么?2.清华大学的校训是什么?你是如何理解的?如果你被清华大学录取,你如何去践行这一校训?自强不息,厚德载物自强不息厚德载物——清华大学校训解释:来源于《周易》的两句话:一句是“天行健,君子以自强不息”(乾卦);一句是“地势坤,君子以厚德载物”(坤卦)。
民国时期,梁启超在清华大学任教时,曾给当时的清华学子作了《论君子》的演讲,他在演讲中希望清华学子们都能继承中华传统美德,并引用了《易经》上的“自强不息”“厚德载物”等话语来激励清华学子。
此后,清华人便把“自强不息,厚德载物”8个字写进了清华校规,后来又逐渐演变成为清华校训。
“天行健,君子以自强不息”“地势坤,君子以厚德载物”两句意谓:天(即自然)的运动刚强劲健,相应于此,君子处世,应像天一样,自我力求进步,刚毅坚卓,发愤图强,永不停息;大地的气势厚实和顺,君子应增厚美德,容载万物。
译为:君子应该像天宇一样运行不息,即使颠沛流离,也不屈不挠;如果你是君子,接物度量要像大地一样,没有任何东西不能承载。
3.如果你是班长,如何组织一次关于雷锋精神的班级活动?活动内容,请向班里同学发表一段两分钟的“学雷锋”活动动员演讲。
4.“是休学创业,还是毕业后创业。
”老师同学们:上午好!51年前的今天,毛主席亲笔题词,号召全国人民“向雷锋同志学习”。
从此,“学习雷锋好榜样”的歌曲响彻中国大地,雷锋的精神影响了一代又一代中国人,并且也影响到全世界。
因此,每年的3月5日,就被确定为学习雷锋纪念日。
2011华约试题

2011年清华等高校联合自主招生试题一、选择题(本题共10小题,每小题3分,共30分.在每小题给出的四个选项中,有一个或多个选项符合题目要求,把符合题目要求的选项前的字母填在题后括号内)1.根据玻尔原子理论,当一个氢原子吸收一个光子后 ( B )A .氢原子所处的能级下降B .氢原子的电势能增大C .电子绕核运动的轨道半径减小D .电子绕核运动的动能增加2.如图所示,AB 杆以恒定角速度ω绕A 点转动,并带动套在水平杆OC 上小环M 运动.运动开始时,AB 杆在竖直位置,则运动中小环M 的加速度将(A ) A .逐渐增大 B .先减小后增大 C .先增加后减小D .逐渐减小3.在杨氏双缝干涉实验中,如果单色光源S 从图所示的中轴位置沿垂直SO 的方向向上移动一段微小的距离,则中心干涉条纹向何方向移动?相邻明条纹间的间距如何变化? ( C )A .相邻明条纹间的间距不变中心干涉明条纹向上移动B .相邻明条纹间的间距变大中心干涉明条纹向下移动C .相邻明条纹间的间距不变中心干涉明条纹向下移动D.相邻明条纹间的间距变小中心干涉明条纹向上移动上移动4.一质点沿直线做简谐运动,相继通过距离为16cm 的两点A和B ,历时ls ,并且在A 、B两点处具有相同的速率;再经过ls ,质点第二次通过B 点,该质点运动的周期和振幅分别为( D)A .3s ,83cmB .3s ,82cmC .4 s ,83cmD .4s ,82cm5.水流以与水平方向成角度θ的速度冲入到水平放置的水槽中,则从左面流出水量的和从右面流出的水量的比值可能为 (D )A .l 十2sin 2θB .l 十2cos 2θC .l+2tan 2θD .l 十2cot 2θ6.如图所示,带电质点P 1固定在光滑的水平绝缘桌面上,在桌面上距P 1一定距离处有另一个带电质点P 2,P 2在桌面上运动,某一时刻质点P 2的速度沿垂直于P 1P 2的连线方向,则 ( ACD) A .若P 1、P 2为同种电荷,以后P 2一定做速度变大的曲线运动B .若P 1、P 2为同种电荷,以后P 2一定做加速度变大的曲线运动2 PC .若P 1、P 2为异种电荷,以后P 2的速度大小和加速度大小可能都不变D .若P 1、P 2为异种电荷,以后P 2可能做加速度、速度都变小的曲线运动7.空间某区域内存在匀强磁场,磁场的上下边界水平,方向向和竖直平面(纸面)垂直,两个由完全相同的导线制成的刚性线框a 和b ,其形状分别是周长为4l 的正方形和周长为6l 的矩形,线框a 和b 在竖直平面内从图示位置开始自由下落,若从开始下落到线框完全离开磁场的过程中安培力对两线框的冲量分别为I a 、I b ,则I a ∶I b为 ( A ) A .3:8 B .1:2 C .1:1 D .3:2二、实验题(共12分,根据题目要求作答)11.当压强不变且温度变化量T 不太大时,液体或固体在某一温度下的体膨胀系数α可以表示为T V V ∆∆=α,式中为该温度时的体积,△V 为体积的变化量.一般来说,在常温下液体的体膨胀系数分别在10-3/K 量级和10-6~10-5/K 量级.如图所示的装置,可以用来测量控温箱中圆筒形玻璃控温箱容器内液体的体膨胀系数,实验步骤如下:①拿掉浮标,将液体的温度调为接近室温的某一温度T 0,测量液柱的高度化h .②放入浮标,保持压强不变,将液体的温度升高一个不太大的量△T ,用精密的位置传感器确定指针高度的变化量△h .③利用步骤①和②中测得的数据,计算液体在T 0时的体膨胀系数α.回答下列问题:(1)不考虑温度变化导致的液体密度变化,写出用测量量表示的α的表达式;(2)步骤②在温度升高过程中,液体密度变化会对用上面的表达式计算出的结果有什么影响?为什么?(3)当所用的浮标为直立圆柱体时,某同学对如何减少这一影响提出以下条几建议,其中有效的是 .(填大入正确选项前的字母)A .选用轻质材料制成的浮标B .选用底面积较大的浮标C .选用高度较小的浮标D .尽量增大液柱的高度hE .尽量选用底面积大的玻璃容器解析 (1)不考虑温度变化导致的液体密度变化,由于液体质量不变,则液体的体积V 不变.设圆筒形玻璃容器内液体的底面积为S ,则Th h T Sh h S T V V ∆∆=∆∆=∆∆=α (2) α会偏大.因为温度升高,导致液体体积变大,故液体密度ρ液会变小,根据阿基米德定× × × × × × B a b l 2l律可得ρ液V 排g=ρ物V 物g ,则V 物变大,即浮标进入液体的深度会更深,测得的△h 会偏大,α会偏大.(3)由ρ液V 排g=mg 可知,浮标质量越小,对V 物的影响就越小,即对△h 的影响减少,故A 选项正确.从ρ液V 排g=ρ物V 物g 可知,浮标底面积的大小及浮标的高度都不影响V 物,即△h 不变,则B 、C 选项错误;增大液柱的高度h 、选用底面积较大的玻璃容器,浮标进入液体的深度变化对液柱高度的变化量△h 影响减小,则D 、E 选项正确三、推理、论证题(共32分.解答时应写出必要的文字说明和推理过程)14.我们知道,在压强不太大、温度不太低的情况下,气体分子本身的大小比分子间的距离要小很多,因而,在理想气体模型中通常会忽略分子的大小.己知液氮的密度ρ=810kg/m 3,氮气的摩尔质量M mol =28×10-3kg/mol .假设液氮可看作是由立方体分子堆积而成的,根据所给数据对标准状态下的氮气做出估算,说明上述结论的合理性.解析 1个氮分子自身的体积为3293232mol 0m 108.5m 1002.68101028--⨯=⨯⨯⨯==A N M V ρ 1个氮分子的边长为m 104m 108.51032930--⨯≈⨯==V l1个氮气分子占据的体积为 AN V V m ol =氮气分子间的距离为 m 193m 1002.6104.22932333mol 3--⨯≈⨯⨯===A N V V d 比较可知,气体分子本身的大小比分子间的距离要小很多,因此可以忽略分子的大小.四、计算题(共26分·解答时应写出必要的文字说明、方程式和主要演算步骤,只写出最后结果不能得分)15.(12分)竖直墙面和水平地面均光滑,质量分别为m A =m ,m B =3m 的A 、B 两物体如图所示放置,其中物体A 紧靠墙壁,A 、B 之间由质量不计的轻弹簧相连,现对物体B 缓慢施加一个向左的力,该力做功为W ,使A 、B 之间轻弹簧被压缩且保持系统静止,然后突然撤去向左的推力解除压缩,求: (1)从撤去外到物块A 开始运动,墙对A 冲量多大?(2)A 、B 都运动后,A 、B 两物体的最小速度各为多少?解析 (1)压缩弹簧时,外力做的功全部转化为弹性势能;撤去外力后,物体B 在弹力作用下做加速运动;在弹簧恢复原长的过程中,系统的机械能守恒.设弹簧恢复原长时,物体B 的速度为v B0.,则有 20321B mv W ⋅= 得 mW v B 320= 此过程中墙壁对A 的冲量大小等于弹簧对A 的冲量大小,也等于弹簧对B 的冲量大小,则有mW mv I B 630==(2)当弹簧恢复原长后,A 离开墙壁开始运动,因开始时B 的速度比A 的速度大,弹簧伸长,A 在弹簧弹力作用下做加速运动,B 做减速运动,弹簧伸长量增大,当A 、B 速度相等时弹簧伸长到最长,之后A 的速度比B 的速度大,弹簧的形变量减小,过程中A 仍做加速运动,B 仍做减速运动当弹簧恢复到原长时,物体A 的速度为最大,B 的速度最小,此时A 的速度比B 的速度大,弹簧开始压缩,A 做减速运动,B 做加速运动,当弹簧再次恢复到原长时A 的速度最小,B 的速度为最大.设弹簧恢复到原长时A 的速度为为v A ,B 的速度为v B ,在此过程中系统的动量守恒、机械能守恒.则有3mv B0=mv A +3mv B222032121321B A B mv mv mv ⋅+=⋅ 联立解得v A1=0, v B1=v B00223B A v v =,0221B B v v = 所以,物体A 的最小速度为0,B 的最小速度为m W v v B B 62102==. 16.(14分)在xOy 平面内,x >0,y >0的空间区域内存在匀强电场,场强大小为100V/m ;x >0,y <3m 的区域内存在垂直于xOy 平面的磁场.现有一带负电的粒子,电量为q =2×10-7C ,质量为m =1×10-6 k g ,从坐标原点O 以一定的初动能射出,经过点P (4,3)时,其动能变为初动能的0.2倍,速度方向平行于y 轴正方向.最后,粒子从y 轴上点M (0,5)射出电场,此时动能变为过O 点时初动能的0.52倍.粒子重力不计.(1)写出在线段OP 上与M 点等电势点Q 的坐标;(2)求粒子由P 点运动到M 点所需的时间.解析 (1)设粒子在O 点时的动能为E k0,则在M 点的动能为0.52E k0,由于洛伦兹力不做功,粒子从O 点到P 点和从P 点到M 点的过程中,电场力做的功分别为―0.8 E k0、―0.48 E k0,O 、P 及O 、M 间的电势差分别为q E U k OP 08.0=、q E U k OM 048.0= 点及M 点的电势差分别为 如图所示,由几何关系知OP 的长度为5m ,沿OP 方向电势均匀降落,电势每米下降qE k 016.0,则OQ =3m . 设OP 与x 轴的夹角为α,则sin α=3/5,cos α=4/5,Q 点的坐标为x Q =OQ cos α=3×0.8m=2.4my Q =OQ sin α=3×0.6m=1.8m(2)M 、Q 是等势点,MQ 是电场的一条等势线,等势线与电场垂直,可知电场方向沿OP 方向.电场强度的x 分量为E x =E cos α=100×0.8V/m=80 V/m粒子由P 点运动到M 点,在x 方向上作初速度为0的匀加速直线运动,则221t mqE x x P = s 22s 8010241012276=⨯⨯⨯⨯⨯==--x P qE mx t。
清华北大自主招生模拟试题(数学)

自主招生模拟试题--04说明:第1--4题每题15分,第5--6题每题20分,试卷总分为100分. 1.求最小的正实数k ,使得111()9ab bc ca k a b c+++++≥对所有的正实数,,a b c 都成立.2.如图,已知O 分别与等边三角形ABC 的三边,,AB BC CA 相切于点,,D E F ,设劣弧DF 上的点P 到三边,,AB BC CA 的距离依次为123,,d d d ,求证:132d d d +=.3.设定义在[1,1]-上的函数221()||33f x x bx c =-++的最大值为M ,求M 的最小值.4.如图,O 是边长为1的正六边形ABCDEF 的中心,一条路径是指从点O 出发,沿着线段又回到点O ,求长度为2013的路径条数.5.已知非直角三角形ABC 的最小边长为5,且tan tan tan [tan ][tan ][tan ]A B C A B C ++≤++,其中符号[]x 表示不超过实数x 的最大整数,求ABC ∆的面积?6.已知函数()bf x ax c x=++(0)a >的图像在点(1,(1))f 处的切线方程为1y x =-. (1)将,b c 用a 表示出来;(2)若()ln f x x ≥在[1,)+∞上恒成立,求a 的取值范围; (3)求证:对所有正整数n ,都有1111ln(1)232(1)n n n n ++++>+++ .OFABCEDd 1d 3d 2F DOE ABCP自主招生模拟试题答题纸1. 2.d 1d 3d 2FDOEABCP4.OFA B CE D参考答案1.求最小的正实数k ,使得111()9ab bc ca k a b c+++++≥对所有的正实数,,a b c 都成立. 解:首先令1a b c ===,则有2k ≥. 其次,证明:1112()9ab bc ca a b c+++++≥对所有的正实数,,a b c 都成立. 由于3111133ab ab a b a b++≥⋅⋅⋅=,同理可得:113bc b c ++≥,113ca c a ++≥.以上三式相加即得:1112()9ab bc ca a b c+++++≥. 综上可知,所求k 的最小值为2.2.如图,已知O 分别与等边三角形ABC 的三边,,AB BC CA 相切于点,,D E F ,设劣弧DF 上的点P 到三边,,AB BC CA 的距离依次为123,,d d d ,求证:132d d d +=.证明:如图,以O 为原点,OA 所在直线为y 轴建立坐标系,不妨设O 的半径为1,则点P 坐标为(cos ,sin )θθ(30150)θ︒≤≤︒,则由题意可得:直线AC 的方程为:cos30cos3010x y ︒+︒-=; 直线AB 的方程为:cos150cos15010x y ︒+︒-=; 直线BC 的方程为:01=+y .由点到直线的距离公式可得:13|cos cos30sin cos301||cos cos150sin cos1501|d d θθθθ+=︒+︒-+︒+︒-222sin (15)2sin (75)2[sin(15)sin(75)]2222θθθθ=-︒+-︒=-︒--︒2sin 12cos 2sin )2cos 2)(sin15sin 15(cos 2d =+=+=+︒-︒=θθθθθ.故,132d d d +=成立.3.设定义在[1,1]-上的函数221()||33f x x bx c =-++的最大值为M ,求M 的最小值. 解:由题意可知对任意的[1,1]x ∈-都有()f x M ≤,则: 21(1)|1|f b c M -=--+≤,1(0)||f c M =≤,21(1)|1|f b c M -=-++≤.y xd 1d 3d 2F DOEABCP故4(1)2(0)(1)M f f f ≥-++21121|1|2|||1|33333b c c b c =--+++-++21121|121|233333b c c b c ≥--+-⋅-++=. 即,12M ≥.事实上,当30,2b c ==时,21()||2f x x =-+在[1,1]-上的最大值为12.所以,实数M 的最小值为12. 4.如图,O 是边长为1的正六边形ABCDEF 的中心,一条路径是指从点O 出发,沿着线段又回到点O ,求长度为2013的路径条数. 解:由题意设从点O 出发沿着线段又回到点O ,且长度为n 的路径条数为n a ,从点A 出发沿着线段到点O ,且长度为n 的路径条数为n b ,则有11162n n n n n a b b a b ---=⎧⎨=+⎩1226n n n a a a --⇒=+.又由于6,021==a a ,故可求得1((77)(17)(77)(17))14n n n a =-⋅+++⋅-. 从而可得长度为2013的路径条数2013201320131((77)(17)(77)(17))14a =-⋅+++⋅-. 5.已知非直角三角形ABC 的最小边长为5,且tan tan tan [tan ][tan ][tan ]A B C A B C ++≤++,其中符号[]x 表示不超过实数x 的最大整数,求ABC ∆的面积?解:由题意知对所有实数x ,都有[]x x ≤,故tan tan tan [tan ][tan ][tan ]A B C A B C ++≥++.结合题目条件可知tan tan tan [tan ][tan ][tan ]A B C A B C ++=++,其中tan ,tan ,tan A B C 均为整数.不妨设tan ,tan ,tan A x B y C z ===(,,x y z 均为非零整数,且x y z ≤≤),则由tan tan()C A B =-+可得xyz x y z =++,而,,A B C 中最多一个钝角,即,y z 必为正整数,03xyz x y z z <=++≤,故3xy ≤,从而1,1x y ==,或1,2x y ==,或1,3x y ==.当1,1x y ==时,由xyz x y z =++知无解; 当1,2x y ==时,由xyz x y z =++知3z =;当1,3x y ==时,由xyz x y z =++知2z =,这与x y z ≤≤不符.故,在ABC ∆中,tan 1,tan 2,tan 3A B C ===,且5BC =.过点B 作高BD ,则在Rt BCD ∆中可求得DBACOFA BCE D1021,1023==CD BD ,在Rt ABD ∆中可求得3102AD =,故210AC =,故ABC ∆的面积为15. 6.已知函数()bf x ax c x=++(0)a >的图像在点(1,(1))f 处的切线方程为1y x =-.(1)将,b c 用a 表示出来;(2)若()ln f x x ≥在[1,)+∞上恒成立,求a 的取值范围; (3)求证:对所有正整数n ,都有1111ln(1)232(1)nn n n ++++>+++ . 解:(1)求导得2'()bf x a x =-,再由题意得'(1)1(1)0f a b f a b c =-=⎧⎨=++=⎩,解得112b a c a=-⎧⎨=-⎩(0)a >. (2)由(1)可知1()12a f x ax a x-=++-(0)a >. 令1()()ln 12ln a g x f x x ax a x x -=-=++--,[1,)x ∈+∞,则21(1)()'()aa x x a g x x ---=.当102a <<时,11a a ->,若1(1,)a x a-∈,则'()0g x <,故()g x 在区间1(1,)aa -上单调递减.所以,当1(1,)ax a -∈时,()(1)0g x g <=,即()ln f x x <,不合题意. 当12a ≥时,11aa-≤,若1x ≥,则'()0g x ≥,故()g x 在区间(1,)+∞上单调递增.所以,当[1,)x ∈+∞时,()(1)0g x g ≥=,即()ln f x x ≥,符合题意.综上可知,实数a 的取值范围为1[,)2+∞.(3)由(2)的结论知:当12a ≥时,()ln f x x ≥在[1,)+∞上恒成立. 取12a =时有11()()ln 2f x x x x =-≥在[1,)+∞上恒成立,当1x >时,11()()ln 2f x x x x=->.依次令2341,,,,123n x n += 可得:212111ln ln 20()(1)121222=-<-=+;3132111ln ln 3ln 2()()2223223=-<-=+;4143111ln ln 4ln 3()()3234234=-<-=+;……111111lnln(1)ln ()()2121n n n n n n n n n n ++=+-<-=+++.将以上n 个等式相加,整理可得:1111ln(1)232(1)nn n n ++++>+++ .。
2011年北大、清华等十所名校自主招生面试题集锦

2011年北大、清华等十所名校自主招生面试题集锦作者:千叶草草2011年北大自主招生的30道面试真题1.马克思在《资本论》中论述机器夺走了工人的饭碗时写道:"蒸汽机一开始就是人力的对头"。
请谈谈你的看法。
2.近期房产税、车船税、"馒头税"等均引发社会热议,请谈谈你对纳税与公民权利关系的理解。
3.哈佛大学图书馆墙上写有这样一句话:"请享受无法回避的痛苦",谈谈你的理解。
4.假如用一种植物比喻中国人的国民性,你会选择什么?为什么?5.有人说:"智慧比体力更重要,成功的关键在于如何使用智慧",请谈谈你的看法。
6.现在很多家长在高中阶段就把孩子送到国外学习,谈谈你的看法。
7.国家最近规定,中央和省级机构录用公务员,一般情况下都须具有两年以上基层工作经历,不再招收应届毕业生,你对此有何评论。
8."穷则独善其身, 达则兼济天下",在今天是否还适用?9.目前一些人富裕了但并没感到幸福,谈谈你的看法。
10.有人认为"三纲"(君臣、父子、夫妻)无益,"五常"(仁义礼智信)可取。
试述你的观点。
11.近来续写《红楼梦》又成为社会热点话题。
你认为后人可以续写、仿写、改写经典名著吗?12.古人云"诗画同源","诗是无形画,画是有形诗"。
请谈谈你的见解。
13.请从世界历史和国际政治的角度,分析"只有永远的利益,没有永远的朋友"这句话的含义。
14.今年是辛亥革命100周年,海峡两岸将共同举行隆重庆典。
你认为大陆和台湾看待辛亥革命的角度和意义会有什么不同?15.网络带来丰富的信息,但也存在着许多虚假报道和伪装成民意的倾向性意见,你认为政府如何才能从网络上获取真实的社情民意?16.日本政府最近称,由于中国的GDP已经超过日本,所以要大幅削减对华援助,你如何看待此事?17.在鲁迅的小说《祝福》中,"我"作为一个现代知识分子,为什么不告诉祥林嫂"人死后是没有灵魂的"?18.牛顿第一定律可以被实验验证吗?19."火"被古人当成一种物质元素,今天我们如何认识"火&quo20.诗曰:"我看青山多妩媚,料青山看我应如是",说说你的理解。
2011年清华自主招生联盟笔试试题、

1、2011年清华自主招生联盟模拟试题(语文)声明:内容由上海交通大学出版社提供,选自《全国重点大学自主招生试题与模拟预测试卷丛书》A 0.90B 0.95C 0.95D 0.94E 0.942、清华大学保送生暨自主招生北京冬令营数学笔试试题(2006年12月30日)1.求()xe f x x=的单调区间及极值.2.设正三角形1T 边长为a ,1n T +是n T 的中点三角形,n A 为n T 除去1n T +后剩下三个三角形内切圆面积之和.求1limnkn k A→∞=∑.3.已知某音响设备由五个部件组成,A 电视机,B 影碟机,C 线路,D 左声道和E 右声道,其中每个部件工作的概率如下图所示.能听到声音,当且仅当A 与B 中有一工作,C 工作,D 与E 中有一工作;且若D 和E 同时工作则有立体声效果.求:(1)能听到立体声效果的概率; (2)听不到声音的概率.4.(1)求三直线60x y +=,12y x =,0y =所围成三角形上的整点个数; (2)求方程组21260y x y x x y <⎧⎪⎪>⎨⎪+=⎪⎩的整数解个数.5.已知(1,1)A --,△ABC 是正三角形,且B 、C 在双曲线1(0)xy x =>一支上. (1)求证B 、C 关于直线y x =对称; (2)求△ABC 的周长.6.对于集合2M R ⊆,称M 为开集,当且仅当0P M ∀∈,0r ∃>,使得 20{}P R PP r M ∈<⊆.判断集合{(,)4250}x y x y +->与{(,)0,0}x y x y ≥>是否为开集,并证明你的结论.3、五校合作自主选拔通用基础测试说明一、考试科目文科:语文、数学、英语、人文与社会(含历史,政治,地理)理科:语文、数学、英语、自然科学(含物理,化学)二、考试形式与试卷结构每科考试时间90分钟,分值100分。
考试采用闭卷、笔试形式。
《北大清华自主招生数学试题的分析与解》试读本

兰琦 毕业于清华大学计算机系 " # # . 年高考数学满分 邮箱 6 9 K 6 6 9 A @ @ $$ / -! 6 7 8 L 博客地址 9 : : H G M K ! 7 @ ; 5 N
" #
三测 高考难度 $ " # $ % 年清华大学 OPQ ( ( R O 测试文科数学 三测 高考难度 $ " # $ % 年清华大学 OPQ ( ( R O 测试理科数学 # 二测 高考难度 " " # $ + 年清华大学 OPQ ( ( R O 测试理科数学 " 一测 高考难度 " # $ + 年清华大学 OPQ ( ( R O 测试理科数学 " 二测 . " # $ + 年清华大学 OPQ ( ( R O 附加科目测试数学部分 " # $ + 年清华大学自主招生暨领军计划试题 / " " # $ + 年清华大学 . " & 学术能力测试数学试题 + 4 " # $ + 年清华大学暑期学校测试 % + " # $ + 年北京大学自主招生数学试题 & 数学测试试题 $ " # $ + 年北京大学优特 Q , O A B : # # " # $ + 年北京大学优秀中学生夏令营数学试题 $ # & " # $ + 年北京大学博雅计划数学试题 $ $ " # $ / 年清华大学自主招生暨领军计划试题 $ " " # $ / 年清华大学夏令营数学试题 $ & " # $ / 年北京大学自主招生数学试题 $ . . " # $ / 年北京大学数学学科夏令营初赛试题 $ 4 # " # $ / 年北京大学生命科学冬令营试卷数学部分试题 $ 4 " # $ / 年北京大学全国优秀中学生暑期夏令营试题 $ / # " # $ / 年北京大学博雅计划试题 $ / " " # $ 4 年清华大学自主招生暨领军计划试题 $ / + " # $ 4 年清华大学金秋营基础部分试题 $ + % " # $ 4 年北京大学博雅计划数学试卷 $ % " " # $ 4 年北京大学化学体验营数学试题 $ % . " # $ 4 年北京大学生命科学冬令营试卷数学部分试题 $ % / " # $ 4 年北京大学优秀中学生体验营综合测试数学科目试题 $ % & " # $ 4 年北京大学自主选拔录取考试试题 $ & $ " # $ . 年清华大学等五校联考自主招生试题 $ & . " # $ . 年北京大学全国优秀中学生体验营数学试卷 $ & %
清华、北大2011-2015年自主招生面试真题汇总

清华、北大2011-2015年自主招生面试真题汇总清华.北大2011-2015年自主招生面试真题汇总2016年自主招生即将来临,考生和家长需要着手准备了。
除了报名申请材料之外,自主招生最重要的环节就是笔试和面试部分。
下面中国自主招生网小编汇总了清华大学、北京大学2011-2015年部分面试题,供报考2016自主招生的考生们参考。
清华大学清华大学2015年自主招生面试部分真题1.假设给你一次穿越的机会,你最希望穿越到什么时候?做什么人?干什么?2.清华大学的校训是什么?你是如何理解的? 如果你被清华大学录取,你如何去践行这一校训?自强不息,厚德载物自强不息厚建载物一清华大学校训解释:来源于《周易》的两句话:一句是"天行健,君子以自强不息"(乾卦);一句是"地势坤,君子以厚德载物"(坤卦)。
民国时期,梁启超在清华大学任教时,曾给当时的清华学子作了《论君子》的演讲,他在演讲中希望清华学子1i]都能继承中华传统美德,并引用了《易务》上的"自强不息""厚德载物" 等话语来激励清华学子。
此后,清华人便把"自强不息,厚德载物” 8个字写进了清华校规,后来又逐渐趣成为清华校训。
"天行健,君子以自强不息""地势坤,君子以厚德载物"两句意谓:天(即自然)的运动刚强劲健,相应于此,君子处世,应像天一样,自我力求逬步,刚毅坚卓,发愤图强,永不停息;大地的气势厚实和顺,君子应增厚美德,容载万物。
译为:君子应该像天宇一样运行不息,即使颠沛流离,也不屈不挠;如果你是君子,接物度虽要像大地一样,没有任何东西不能承载。
3.如果你是班长,如何组织一次关于雷锋精神的班级活动?活动内容,请向班里同学发表一段两分钟的“学雷锋”活动动员演讲。
4.“是休学创业,还是毕业后创业老师同学们:上午好!51年前的今天,毛主席亲笔题词,号召全国人民“向雷锋同志学习”。
清华大学自主招生试题 数学 Word版含解析

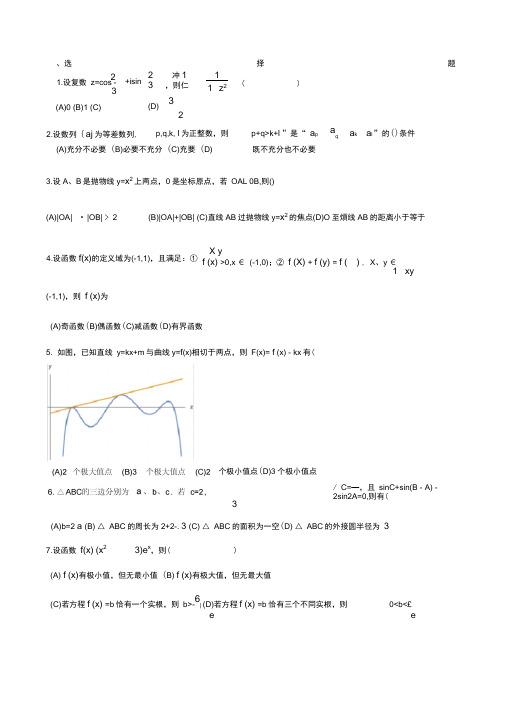
一、选择题1.设复数z=cos 23π+isin 23π,则2111-1z z +-=( ) (A)0 (B)1 (C)12 (D)322.设数列{}n a 为等差数列,p,q,k,l 为正整数,则“p+q>k+l ”是“p q k l a a a a +>+”的( )条件(A)充分不必要 (B)必要不充分 (C)充要 (D)既不充分也不必要 3.设A 、B 是抛物线y=2x 上两点,O 是坐标原点,若OA ⊥OB,则( )(A)|OA|·|OB|≥2 (B)|OA|+|OB|≥22(C)直线AB 过抛物线y=2x 的焦点 (D)O 到直线AB 的距离小于等于14.设函数()f x 的定义域为(-1,1),且满足:①()f x >0,x ∈(-1,0);②()f x +()f y =()1x yf xy++,x 、y ∈(-1,1),则()f x 为 (A)奇函数 (B)偶函数 (C)减函数 (D)有界函数5.如图,已知直线y=kx+m 与曲线y=f (x)相切于两点,则F(x)=f (x)−kx 有( )(A)2个极大值点 (B)3个极大值点 (C)2个极小值点 (D)3个极小值点 6.△ABC 的三边分别为a 、b 、c .若c=2,∠C=3π,且sinC+sin(B −A)−2sin2A=0,则有( ) (A)b=2a (B)△ABC 的周长为3 (C)△ABC 的面积为33(D)△ABC 的外接圆半径为337.设函数2()(3)xf x x e =-,则( )(A)()f x 有极小值,但无最小值 (B) ()f x 有极大值,但无最大值 (C)若方程()f x =b 恰有一个实根,则b>36e(D)若方程()f x =b 恰有三个不同实根,则0<b<36e 8.已知A={(x,y)∣222x y r +=},B={(x,y)∣222()()x a y b r -+-=,已知A∩B={(11,x y ),(22,x y )},则( )(A)0<22a b +<22r (B)1212()(y )0a x x b y -+-= (C)12x x +=a ,12y y +=b (D)22a b +=1122ax by +9.已知非负实数x,y,z 满足22244x y z +++2z=3,则5x+4y+3z 的最小值为( ) (A)1 (B)2 (C)3 (D)410.设数列{n a }的前n 项和为n S ,若对任意正整数n ,总存在正整数m ,使得n S =m a ,则( )(A ){n a }可能为等差数列 (B ){n a }可能为等比数列(C ){n a }的任意一项均可写成{n a }的两项之差(D)对任意正整数n ,总存在正整数m ,使得n a =m S11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测:3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名.比赛后发现没有并列名次,且甲、乙、丙、丁中只有1人猜对比赛结果,此人是( ) (A)甲 (B)乙 (C)丙 (D)丁12.长方体ABCD −1111A B C D 中,AB=2,AD=A 1A =1,则A 到平面1A BD 的距离为( )(A)13 (B)23(C)22 (D)6313.设不等式组||||22(1)x y y k x +≤⎧⎨+≤+⎩所表示的区域为D ,其面积为S ,则( )(A)若S=4,则k 的值唯一 (B)若S=12,则k 的值有2个(C)若D 为三角形,则0<k ≤23(D)若D 为五边形,则k>4 14.△ABC 的三边长是2,3,4,其外心为O ,则OA AB OB BC OC CA ⋅+⋅+⋅=( ) (A)0 (B)−15 (C)−212(D)−29215.设随机事件A 与B 互相独立,且P(B)=0.5,P(A −B)=0.2,则( )(A)P(A)=0.4 (B)P(B −A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916.过△ABC 的重心作直线将△ABC 分成两部分,则这两部分的面积之比的( ) (A)最小值为34 (B)最小值为45 (C)最大值为43 (D 最大值为5417.从正15边形的顶点中选出3个构成钝角三角形,则不同的选法有( )(A)105种 (B)225种 (C)315种 (D)420种18.已知存在实数r ,使得圆周222x y r +=上恰好有n 个整点,则n 可以等于( ) (A)4 (B)6 (C)8 (D)12 19.设复数z 满足2|z|≤|z −1|,则( ) (A)|z|的最大值为1 (B)|z|的最小值为13 (C)z 的虚部的最大值为23(D)z 的实部的最大值为1320.设m,n 是大于零的实数,a =(mcosα,msinα),b =(ncosβ,nsinβ),其中α,β∈[0,2π)α,β∈[0,2π).定义向量12a =(2m α2m α),12b =(2n β2n β),记θ=α−β,则( )(A)12a ·12a =a (B)1122a b ⋅=2mn θ(C)112222||44a b mn θ-≥(D)112222||44a b mn θ+≥21.设数列{n a }满足:1a =6,13n n n a a n++=,则( ) (A)∀n ∈N ∗,n a <3(1)n + (B)∀n ∈N ∗,n a ≠2015 (C)∃n ∈N ∗,n a 为完全平方数 (D)∃n ∈N ∗, n a 为完全立方数 22.在极坐标系中,下列方程表示的图形是椭圆的有( ) (A )ρ=1cos sin θθ+ (B )ρ=12sin θ+ (C )ρ=12cos θ- (D )ρ=112sin θ+23.设函数2sin ()1xf x x x π=-+,则( )(A )()f x ≤43(B)|()f x |≤5|x| (C)曲线y=()f x 存在对称轴 (D)曲线y=()f x 存在对称中心24.△ABC 的三边分别为a ,b,c ,若△ABC 为锐角三角形,则( ) (A)sinA>cosB (B)tanA>cotB (C)222a b c +> (D)333a b c +>25.设函数()f x 的定义域是(−1,1),若(0)f =(0)f '=1,则存在实数δ∈(0,1),使得( ) (A)()f x >0,x ∈(−δ,δ) (B)()f x 在(−δ,δ)上单调递增 (C)()f x >1,x ∈(0,δ) (D)()f x >1,x ∈(−δ,0)26.在直角坐标系中,已知A(−1,0),B(1,0).若对于y 轴上的任意n 个不同的点k P (k=1,2,…,n),总存在两个不同的点i P ,j P ,使得|sin ∠A i P B −sin ∠A j P B|≤13,则n 的最小值为( )(A)3 (B)4 (C)5 (D)627.设非负实数x,y 满足2x+y=1,则22x y + )(A)最小值为45 (B)最小值为25(C)最大值为1 (D)最大值为12328.对于50个黑球和49个白球的任意排列(从左到右排成一行),则( )(A)存在一个黑球,它右侧的白球和黑球一样多 (B)存在一个白球,它右侧的白球和黑球一样多(C)存在一个黑球,它右侧的白球比黑球少一个 (D)存在一个白球,它右侧的白球比黑球少一个29.从1,2,3,4,5中挑出三个不同数字组成五位数,其中有两个数字各用两次,例如12231,则能得到的不同的五位数有( ) (A)300个 (B)450个 (C)900个 (D)1800个30.设曲线L 的方程为42242(22)(2)y x y x x +++-=0,则( ) (A)L 是轴对称图形 (B)L 是中心对称图形 (C)L ⊂{(x,y)∣22x y +≤1} (D)L ⊂{(x,y)∣−12≤y ≤12} ##Answer## 1.【解析】2111-1z z +-=211-zz z zz z +-=11-z z z z +-=22cos sin 1332221-cos sin 2sin 333i i i πππππ-+--=212sin 2sincos333i πππ-⋅-22cos()sin()333(cossin )22i i ππππ-+-+ =cos 0sin 02sin [cos()sin()]366i i πππ+-+-77)sin()]663i ππ-+- 31sin )6623i i ππ+=1,选B2.【简解】 ()p q k l a a a a +-+=[(p+q)-(k+l)]d ,与公差d 的符号有关,选D3.【解析】设A(211,x x ),B(222,x x ),OA OB ⋅=1212(1)x x x x +=0⇒211x x =-答案(A),||||OA OB ⋅2211221111(1)(1)x x x x ++2121111x x +++11122||||x x +⋅=2,正确;答案(B),|OA|+|OB|≥2||||OA OB ⋅22,正确;答案(C),直线AB 的斜率为222121x x x x --=21x x +=111x x - 方程为y-21x =(111x x -)(x-1x ),焦点(0,14)不满足方程,错误;答案(D),原点到直线AB :(111x x -)x-y+1=0的距离2111()1x x -+1,正确。
2011年清华等五校联考(华约)自主招生数学试卷1

8. 某生产队想筑一面积为 144 m2 的长方形围栏, 围栏一边靠墙 . 现有铁丝网 50 m ,筑成这样 的围栏最少要多少铁丝网?已有的墙最多利用多长?最少利用多长?
9. 在正方形 ABCD 中,过一个顶点 D 作对角线 CA 的平行线 DE ,若 CE CA ,且 CE 交边 DA 于点 F . 求证: AE AF .
12. 以 A 为圆心, 以 2cos (0
) 为半径的圆外有一点 B . 已知 AB 2sin ,设过 B 且与 2
圆 A 外切于点 C 的圆的圆心为 M .
(1)当 取某个值时,说明点 M 的轨迹 P 是什么曲线?
( 2)点 M 是轨迹 P 上的动点,点 N 是圆 A 上的动点,记 MN 的最小值为 f . 求 f 的
2011 年清华等五校联考(华约)自主招生数学试卷
1. 设 n N * , n 15 . 集合 A 、 B 都是 I 1,2, , n 的真子集, A B 集合 A 或 B 中,必有两个不同的数,它们的和为完全平方数 .
, A B I . 证明:
2. 设 f x ax2 bx x(a 0) ,方程 f x 0 t x1 . 试比较 f t 与 x1 的大小 .
x 的两个根是 x1 和 x2 ,且 x1 0 , x2 x1 1 ,又 a
3. 求函数 f x max x 1 , x2 5 的最小值,并求出相应的 x 的值 .
4. 已 知 f x 是 定 义 在 R 上 的 不 恒 为 0 的 函 数 , 且 对 于 任 意 的 a, b R , 有
f a b a f b b f. a
取值范围 .
13. 设数列 an 的前 n 项和为 Sn ,点 (n, Sn )( n N * ) 均在函数 y 3x 2 的图像上 . n
2011年---2013“北约”、“华约”自主招生数学试题

2011年“北约”13校联考自主招生数学试题2012年北约自主招生数学试题1、求x 的取值范围使得12)(-+++=x x x x f 是增函数;2、求1210272611=+-+++-+x x x x 的实数根的个数;3、已知0)2)(2(22=+-+-n x x m x x 的4个根组成首项为41的等差数列,求n m -;4、如果锐角ABC ∆的外接圆的圆心为O ,求O 到三角形三边的距离之比;5、已知点)0,2(),0,2(B A -,若点C 是圆0222=+-y x x 上的动点,求ABC ∆面积的最小值。
6、在2012,,2,1Λ中取一组数,使得任意两数之和不能被其差整除,最多能取多少个数?7、求使得a x x x x =-3sin sin 2sin 4sin 在),0[π有唯一解的a ; 8、求证:若圆内接五边形的每个角都相等,则它为正五边形;9、求证:对于任意的正整数n ,n )21(+必可表示成1-+s s 的形式,其中+∈N s2012年自主招生北约联考数学试题解答2013年北约自主招生数学试题解析12312为两根的有理系数多项式的次数最小是多少?解析:显然,多项式23()(2)(1)2f x x x ⎡⎤=---⎣⎦2和312-于是知,2和312为两根的有理系数多项式的次数的最小可能值不大于5. 若存在一个次数不超过4的有理系数多项式432()g x ax bx cx dx e =++++,其两根分别为和1,,,,a b c d e不全为0,则:420(42)(2020a c eg a c e b db d++=⎧=++++=⇒⎨+=⎩(1(7)(232(630g a b c d e a b c d a b c=-+----+++++702320a b c d ea b c d+---=⎧⇒⎨+++=⎩即方程组:420(1)20(2)70(3)2320(4)630(5)a c eb da b c d ea b c da b c++=⎧⎪+=⎪⎪+---=⎨⎪+++=⎪++=⎪⎩,有非0有理数解.由(1)+(3)得:110a b c d++-=(6)由(6)+(2)得:1130a b c++=(7)由(6)+(4)得:13430a b c++=(8)由(7)-(5)得:0a=,代入(7)、(8)得:0b c==,代入(1)、(2)知:0d e==.于是知0a b c d e=====,与,,,,a b c d e不全为0矛盾.所以不存在一个次数不超过4的有理系数多项式()g x和1-和1为两根的有理系数多项式的次数最小为5.2.在66⨯的表中停放3辆完全相同的红色车和3辆完全相同的黑色车,每一行每一列只有一辆车,每辆车占一格,共有几种停放方法?解析:先从6行中选取3行停放红色车,有36C种选择.最上面一行的红色车位置有6种选择;最上面一行的红色车位置选定后,中间一行的红色车位置有5种选择;上面两行的红色车位置选定后,最下面一行的红色车位置有4种选择。
高考自主招生2011年清华大学自主招生真题解析

2011年清华大学自主招生真题详解1.(2011,认识事物类)为什么要把清华大学作为第一志愿填报?【考点提示】本题题干中的关键词为“为什么”,主要考查学生对自己的决定的认知和把握能力。
在答题时,考生需要将中心落在原因分析上。
【思路点拨】解答本题需要考生从自身的感受出发。
像清华一样的一流高等学府,有很多自身的特点存在,考生可以从清华的优势、清华的风格、自己的清华梦、自己崇拜的清华人、自己崇尚的清华精神等方面出发来分析为什么第一志愿填报。
【答题要点】每个人在自己成长的过程中都会有无数个怦然心动的时刻,这一刻你就像是被人施了魔法一样,深深被吸引却浑然不觉。
清华对于我一直都是神秘的代名词。
爸爸妈妈从小就在嘴里念叨清华这清华那,并且总是寄予我将来能进入清华这样的高等学府的期望。
刚开始我很自然的对清华产生排斥感,恐怕是因为它来自父母口中。
心里一直想着,哪时候我一定要去清华看看,它究竟哪里那么大的魅力。
终于,在我高二这一年我来到了闻名已久的清华。
第一眼觉得没太大的特别之处。
从进到校园看到开阔的视野,道路两旁的银杏树,或现代或古典的建筑,匆忙或悠闲的人流及他们脸上洋溢的喜怒哀乐…那一刻,我确实怦然了,并且被深深吸引了。
我在思索,是什么样的力量在牵引着我向清华靠近呢?其实一直都说不太清楚。
后来还去了北京大学、中国人民大学等高等学府。
它们的校园也很有魅力,但不知为何,我的心就像已经被清华俘虏一样,对清华念念不忘。
尤其是,即便那时我没有仔细研究过清华的历史、清华的精神,但初次所见时它那大气、硬朗的风格已让我深深折服,让我身处清华的时候感到无比向往,无比自豪。
从那一刻起,我就想要成为一名清华人。
清华的竞争非常激烈,我深深清楚这一点,但我仍然选择将清华作为第一志愿填报。
因为清华对于我来说,更像是一个激励我永远前进的梦想。
也许我会与自己理想中的殿堂失之交臂,但这并不会让我一蹶不振。
我会用自己的行动来证明,无论是在清华内还是在清华外,清华都将是指引我的明灯。
清华、北大2011-2015年自主招生面试真题汇总【KS5U 高考】

清华、北大2011-2015年自主招生面试真题汇总2016年自主招生即将来临,考生和家长需要着手准备了。
除了报名申请材料之外,自主招生最重要的环节就是笔试和面试部分。
下面中国自主招生网小编汇总了清华大学、北京大学2011-2015年部分面试题,供报考2016自主招生的考生们参考。
清华大学清华大学2015年自主招生面试部分真题1.假设给你一次穿越的机会,你最希望穿越到什么时候?做什么人?干什么?2.清华大学的校训是什么?你是如何理解的?如果你被清华大学录取,你如何去践行这一校训?3.如果你是班长,如何组织一次关于雷锋精神的班级活动?活动内容,请向班里同学发表一段两分钟的“学雷锋”活动动员演讲。
4.“是休学创业,还是毕业后创业。
”5.要不要休学当老板?清华大学2014年自主招生面试部分真题一、领军计划:1、怎么看待单独二孩政策?2、谈谈对节假日安排的看法,有什么建议?3、怎么看待社会公平?二、自强计划:1、请讲一个你的经历中体现你“自强”的故事。
2、你对自己的大学生活有何规划?将来想从事何种职业?3、你认为自己的家乡至今仍然贫困的原因有哪些?应该如何解决?4、你曾经遇到过的最大困难是什么?你是如何面对和解决的?5、谈谈“如何看待春运一票难求的现象,怎么解决这个问题?6、如何看待社会公平?7、结合考生的申请材料,提出一些与考生自身经历有关的问题,如问考生家乡的特产是什么。
清华大学2013年自主招生面试部分真题【综合面试】分上午与下午两场进行:每场考生都有三道相同的必答题目,面试时间为10分钟左右,三位考官对一位考生。
另根据面试时间的剩余情况,考官也会根据考生的特点增加其他题目。
据考生回忆,必答题有:1.“人类一思考,上帝就发笑。
请在90秒内作答?基于你的评价,你打算在当下、在未来做些什么?”2.请以“我和诺贝尔奖的距离”为题发表一段2 分钟的演讲,可准备1 分钟。
3.近期上海、南京、杭州等地接连出现H7N9型禽流感的感染病例,并且造成数名感染者死亡,世界卫生组织和中国政府都高度关注这一病情,并且采取了积极的救治措施,但是公众依然非常想要知道和这个事件相关的各种信息。
[转载]2011年高校自主招生考试试题评析
![[转载]2011年高校自主招生考试试题评析](https://img.taocdn.com/s3/m/16848eebc9d376eeaeaad1f34693daef5ef71396.png)
[转载]2011年⾼校⾃主招⽣考试试题评析原⽂地址:2011年⾼校⾃主招⽣考试试题评析作者:家长平台2011年⾼校⾃主招⽣考试试题评析2011年“北约”“华约”⾃主招⽣考试简单试题分析在去年和今年的AAA测试中,都出现了⼀道和其他学科联系的题⽬,2010年五校联考出了⼀个⽣物背景的题⽬,2011年的七校联考则出了⼀个不折不扣的物理问题:⼀个均匀的质量为a的杯⼦,⾥⾯装满⽔,⽔的质量为b,问⾥⾯装多少⽔的时候重⼼最低?从物理意义上来分析,这个题⽬很显然,当重⼼落在⽔⾯上的时候是重⼼最低的时候,数学强调的是推导意义,因此只要抽象出基本的数学模型,⽤最简单的函数知识就可以解决。
类似于这样的问题,其实母体仍然出现在⾼考当中,只是较之⾼考,更加强调⼀般性问题的解决,更加强调在数学层⾯上的分析和推导,这和北约⽅数学试题的第6个题思路不谋⽽合。
平⾯上给定两个定圆,⼀个动圆和两个定圆相切,求动圆圆⼼的轨迹,并证明。
这个题⽬笔者在今年学⽽思秋季的数学课程上详细讲解过,这个题⽬有两个关键点,⼀个是处理相切时的状态,得到点之间的距离关系;⼀个是注意在定圆的不同位置关系下和动圆的不同相切(内切和外切)状态下有不同的结论。
本题可以分很多种情况,不妨解释其中的⼀种:这个问题其实在⾼考复习阶段,很多练习中会有⼀个到两个的具体例⼦,但是很多同学对这个问题并没有重视,这个题⽬就是从特殊情况(练习中的例⼦)到⼀般情况的⼀个拓展,学⽣如果平时不注重分析,这个题⽬往往会⽆法下⼿或者考虑情况不全,从这个意义上来说,⾃主招⽣并不是要⼀味求难求偏,⽽更强调在平时学习中能够“多想⼀点,多⾛⼀步”,这样的积极主动学习会给⾃主招⽣这类考试带来极⼤的益处。
2011年“北约”“华约”⾃主招⽣语⽂试题评析简单地说,2011⾃主招⽣语⽂试题其之所以发⽣变化,全在于联考阵营的扩⼤。
因此,在先前⼏年⾃主招⽣语⽂试题逐渐摸索到⾃⾝成熟的命制形式后,今年的试题变化主要体现在难度降低。
清华北大自主招生模拟试题(数学)

自主招生模拟试题--02说明:第1--5题每题14分,第6--7题每题15分,试卷总分为100分. 1.求所有的实数[0,]2x π∈,使得(2sin 2)sin()14x x π-+=.2.已知实数,,a x y 满足5533x y x y x y a +=+=+=,求实数a 的所有可能值.3.如图,在四边形ABCD 中,20BAC ∠=︒,30BDC ∠=︒,40ACD ∠=︒,且BAD ADC ∠=∠,求ACB ∠的大小.4.设二次函数2()f x x bx c =++,若当2x ≥时,()0f x ≥,且()f x 在区间(2,3]上的最大值为1,求22b c +的最大值和最小值.5.已知集合{1,2,3,,100} 的子集,A B 满足:①集合A 与B 的元素个数相同;②A B 为空集;③当n A ∈时总有22n B +∈,求集合A B 的元素个数的最大值?6.已知点P 在直线2y x =-上运动,过P 点作抛物线22x y =的切线,切点分别为,A B . (1)求证:直线AB 过定点;(2)求PAB ∆面积S 的最小值,以及相应的P 点坐标.7.称直角坐标系中纵横坐标均为整数的点为“格点”,称一格点沿坐标线到原点的最短路程为该点到原点的“格点距离”(是一个正整数),格点距离为定值(正整数)的点的轨迹称为“格点圆”,该定值称为格点圆的半径,而每一条最短路程称为一条半径,原点称为格点圆的圆心. (1)写出半径为正整数n 的格点圆方程;(2)求出半径为正整数n 的格点圆上的格点数n N ; (3)求出半径为正整数n 的格点圆半径的条数.CBDA自主招生模拟试题答题纸1.2.4. CBDA6.参考答案1.求所有的实数[0,]2x π∈,使得(2sin 2)sin()14x x π-+=. 解:设t x =+)4sin(π,则t x x 2cos sin =+,122sin 2-=t x ,从而有1)23(2=-t t ,即01323=+-t t ,解得1=t ,或1231>+=t (舍),或0231<-=t (舍).于是,有唯一的实数4π=x 符合题意.2.已知实数,,a x y 满足5533x y x y x y a +=+=+=,求实数a 的所有可能值.解:设b xy a y x ==+,,则由题意有b a y x 2222-=+,ab a y x xy y x y x 3)(3)(3333-=+-+=+,从而可得:2352322233225555)3)(2()())((ab b a a ab ab a b a y x y x y x y x y x +-=---=+-++=+.又由已知a y x y x =+=+3355可得a ab a =-33,且a ab b a a =+-23555. 显然,0=a 符合题意;当0≠a 时,则有132=-b a ,且155224=+-b b a a .消去b ,整理得04524=+-a a ,解得1±=a ,2±=a .综上可知,实数a 的所有可能值有:2,1,0,1,2--.3.如图,已知在四边形ABCD 中,20BAC ∠=︒,30BDC ∠=︒,40ACD ∠=︒,且BAD ADC ∠=∠,求ACB ∠的大小.解:在AC 上取一点E ,使得AE AD =,连接DE 并延长交AB 的延长线于点F ,连接CF .因18040(20)ACD CAD ADC BAD BAD ︒=∠+∠+∠=︒+∠-︒+∠,故80BAD ADC ∠=∠=︒.从而60CAD ∠=︒,50ADB ∠=︒,于是50ABD ADB ∠=︒=∠,AB AD =.由于AE AD =,60CAD ∠=︒,因此ADE ∆为等边三角形.于是60CAD ADF AED ∠=∠=∠=︒,且AE DE AD AB ===.又由20BAC ∠=︒可得80ABE AEB ∠=∠=︒,从而可得40BEF BFE ∠=∠=︒,得BE BF =.由FAD CDA ∠=∠,AD DA =,AFD DAC ∠=∠可得F A D C D∆≅∆,从而可得F D C A =,于是有E F E C =,而60FEC AED ∠==︒,故FEC ∆为等边三角形,故CE CF =,且60ECF ∠=︒.由BE BF =,CE CF =,BC BC =得BCE BCF ∆≅∆,故30BCE BCF ∠=∠=︒.CBD AFECBDA4.设二次函数2()f x x bx c =++,若当2x ≥时,()0f x ≥,且()f x 在区间(2,3]上的最大值为1,求22b c +的最大值和最小值.解:由题意函数图象为开口向上的抛物线,且()f x 在区间(]2,3上的最大值只能在闭端点取得,故有(2)(3)1f f =≤,从而5b -≥且38c b =--. 若()0f x =有实根,则240b c ∆=-≥,在区间[]2,2-有(2)0,(2)0,22,2f f b ⎧⎪-⎪⎨⎪⎪-⎩≥≥≤≤ 即420,420,44,b c b c b -+⎧⎪++⎨⎪-⎩≥≥≤≤ 消去c ,解出4,54,44,b b b ⎧-⎪⎪-⎨⎪-⎪⎩≤≤≤≤即4b =-,这时4c =,且0∆=.若()0f x =无实根,则240b c ∆=-<,将38c b =--代入解得84b -<<-. 综上54b --≤≤.所以22222(38)104864b c b b b b +=+--=++,单调递减. 故2222min max ()32,()74b c b c +=+=.5.已知集合{1,2,3,,100} 的子集,A B 满足:①集合A 与B 的元素个数相同;②A B 为空集;③当n A ∈时总有22n B +∈,求集合A B 的元素个数的最大值?解:首先证明|A ∪B |≤66,只需证明|A |≤33,由分析知需要证明:若A 是{1,2,3,…,49}的任何一个34元子集,则必存在n ∈A,使得2n+2∈A.证明如下:将{1,2,3,…,49}分成如下33个集合:{1,4},{3,8},{5,12},…,{23,48},共12个;{2,6},{10,22},{14,30},{18,38},共4个;{25},{27},{29},…,{49},共13个;{26},{34},{42},{46},共4个.若A 是{1,2,3,…,49}的任何一个34元的子集,则由抽屉原理可知上述33个集合中至少有一个2元集合中的两个数均属于A ,即存在n ∈A ,2n +2∈A .所以|A |≤33.事实上,如取A ={1,3,5,…,23,2,10,14,18,25,27,29,…,49,26,34,42,46},B ={2n +2|n ∈A },则A ,B 满足题中要求,且|A ∪B |=66.所以集合A ∪B 的元素个数最多为66.6.已知点P 在直线2y x =-上运动,过P 点作抛物线22x y =的切线,切点分别为,A B . (1)求证:直线AB 过定点;(2)求PAB ∆面积S 的最小值,以及相应的P 点坐标.解:由题意可设点P 的坐标为(,2)m m -,点,A B 的坐标分别为2111(,)2x x ,2221(,)2x x ,其中12x x ≠.因此以A 为切点的切线PA 的方程为21112x x y x ⋅=+,以B 为切点的切线PB 的方程为22212x x y x ⋅=+,于是有:211222122122x m m x x m m x ⎧⋅=-+⎪⎪⎨⎪⋅=-+⎪⎩.将两式作差,化简得122x x m +=,将两式相加,化简得1224x x m ⋅=-.(1)由题意可知直线AB 的斜率k 一定存在,且有2212121211222x x x x k m x x -+===-,因此直线AB 的方程为 22111111()()2(1)222y m x x x mx mx x mx m m x =-+=--=-+=-+.故直线AB 过定点(1,2)C .(2)由点(,2)P m m -到直线AB :2y mx m =-+的距离为2222|24|2411m m m m d m m -+-+==++;边AB 的长度为22222121212||1||1()42124AB m x x m x x x x m m m =+⋅-=+⋅+-=+⋅-+.于是PAB ∆的面积221||(24)242S AB d m m m m =⋅=-+⋅-+.因2243m m -+≥,其中当1m =时,“=”成立,故 当1m =,即点P 的坐标为(1,1)P -时,PAB ∆的面积S 取得最小值33.7.称直角坐标系中纵横坐标均为整数的点为“格点”,称一格点沿坐标线到原点的最短路程为该点到原点的“格点距离”(是一个正整数),格点距离为定值(正整数)的点的轨迹称为“格点圆”,该定值称为格点圆的半径,而每一条最短路程称为一条半径,原点称为格点圆的圆心. (1)写出半径为正整数n 的格点圆方程;(2)求出半径为正整数n 的格点圆上的格点数n N ; (3)求出半径为正整数n 的格点圆半径的条数.解 (1)设格点圆上任一点的坐标为(),P x y (,x y 为整数),由定义,不管按什么路线走,其水平方向的最短路程均为x 个单位(相当于投影到x 轴没有出现重叠,否则不是最短路线),其竖直方向的最短路程均为y个单位.故可得格点圆方程为x y n +=(,x y 为整数). (2)解法1:由格点圆方程可列举如下表x 01± 2±…… ()1n ±-n ±yn ±()1n ±-()2n ±-…… 1±0 格点数244442共计4n N n =.解法2:由格点圆方程可得1n =时有4个格点()()()()0,1,01,1,0,1,0--,14N =.当n 由k 到1k +时,第一象限及x 轴正半轴由x 可取1,2,,k 变为可取1,2,,,1k k + 增加了1个整点,由对称性,共增加了4个整点,有14k k N N +-=,由等差数列的通项公式得()1414n N N n n =+-=. (3)由格点圆方程可知x 有1n +个可取值0,1,2,,1,n n - .当0x =时,格点在y 轴上时,有2条半径,记为02n C ;当x n =时,格点在x 轴上时,有2条半径,记为2nn C .当x k =(0k n <<)时,考虑第一象限,每一个格点(),A k n k -(0k n <<)对应着一个以O 、A 为对角顶点的()k n k ⨯-矩形,从A 到O 的每一条最短路程都是从()k n k ⨯-矩形中取出n 条单位线段,其中k 条为水平单位线段,其余n k -条为竖直单位线段,所以,每一条半径对应着从n 条单位线段中取出k 条水单位线段,有kn C 条半径.再由对称性,得4个象限共有4kn C 条半径.求和,得格点圆半径的总条数为()0121012124442441n n n n n n n n n n n n n n C C C C C C C C C C --+++++⎡⎤=+++++-⎣⎦ .()421n =-.。
2011年清华大学等七校联考试题

难度超高考一天内完成初试3门科目清华七校联考难度高于一般的高考试题;考试结束后,考生拿到的“考生评价报告”可通过对答题情况的分析,对考生学习情况进行诊断……昨日起,清华大学“七校联盟”自主招生选拔工作全面启动,报名申请从即日至12月30日。
文理科生不限制专业选择考生在申请清华大学自主招生的同时,可以申请XX交通大学、中国人民大学、中国科学技术大学、XX交通大学、XX大学和XX大学中的一所。
考生应当将两个选择分别填入A志愿高校和B志愿高校之中。
A、B志愿不分先后。
“也就是说,无论考生将学校作为A志愿高校还是B志愿高校,其申请材料专家评审的标准、初试的成绩要求、复试的安排都没有任何差别。
”清华大学招办表示,报名时没有申请清华的考生,如果获得了其A志愿和B志愿高校的同意,可以在规定时间内向清华提出自主招生的申请,如果达到了要求,可以进入复试。
考生必须通过“2011高水平大学自主选拔学业能力测试报名”(211.151.240.112/Student2011/)进行报名。
初试(即AAA测试)在2011年2月19日进行,复试在初试成绩公布后择日举行。
除个别专业对考生外语语种有要求外,申请清华大学自主招生和保送生的考生可以在学校所公布的全部专业X围内进行申请。
也就是说,清华没有因为文理科而限制考生的专业选择X围。
理科生可以选择社会科学实验班、新闻学等一般意义上的文科专业,建筑学、工业工程等传统意义上的理工科专业也欢迎文科生报考。
中英文阅读写作各占100分清华大学“七校联盟”测试分成通用基础测试、高校特色测试和面试三个模块。
通用基础测试是初试,考生应当参加阅读与写作、数学的考试,并在自然科学、人文与社会中选择参加其一。
阅读与写作测试时间3小时,满分为200分,考察重点为考生运用中英文进行阅读与写作的能力,其中中文阅读与写作占100分,英文阅读与写作与中英文综合应用占100分。
数学测试时间1.5小时,满分为100分,测试内容会适当考虑高中文科数学教学内容,考查重点为逻辑思维能力、运算变形能力、空间想象能力、综合创新能力。
清华大学自主招生试题含答案
、选择题2( )(A)充分不必要(B)必要不充分(C)充要(D)3.设A、B是抛物线y=x2上两点,0是坐标原点,若OAL 0B,则()(A)|OA| •|OB| > 2 (B)|OA|+|OB| (C)直线AB过抛物线y=x2的焦点(D)O至煩线AB的距离小于等于X yf (x) >0,x € (-1,0);② f (X) + f (y) = f ( ) , X、y €1 xy(-1,1),则f (x)为(A)奇函数(B)偶函数(C)减函数(D)有界函数5. 如图,已知直线y=kx+m与曲线y=f(x)相切于两点,则F(x)= f (x) - kx有(/ C=—,且sinC+sin(B - A) -2sin2A=0,则有(3(A)b=2 a (B) △ ABC的周长为2+2-. 3 (C) △ ABC的面积为一空(D) △ ABC的外接圆半径为37.设函数f(x) (x23)e x,则( )(A) f (x)有极小值,但无最小值(B) f (x)有极大值,但无最大值(C)若方程f (x) =b恰有一个实根,则b>-6| (D)若方程f (x) =b恰有三个不同实根,则0<b<£e e1.设复数z=cos -3+isin (A)0 (B)1 (C) 2 冲13 ,则仁(D)3211 z22.设数列{aj为等差数列, p,q,k, l为正整数,则p+q>k+l ”是“ a p aqa k a l ”的()条件既不充分也不必要4.设函数f(x)的定义域为(-1,1),且满足:①个极小值点(D)3个极小值点8.已知 A={(x,y) 1 x 22 2y r },B={(x,y)1 (x2 2 2a) (y b) r ,已知 A n B={(x 1,yJ ,( X 2,y 2)},则()(A)0< a 2 b 2 <2r 2(B)aXX 2) b(y1 y 2) 0(C)X 1 X 2 = a , y 1y 2=b (D)2a b 2 = 2ax 1 2by 19.已知非负实数x,y,z满足4x 24y 22z +2z=3, 则5x+4y+3z 的最小值为()(A)1 (B)2 (C)3 (D)410.设数列{ a n }的前n 项和为S n ,若对任意正整数n ,总存在正整数 m,使得S n =a m ,则( )(A ){ a n }可能为等差数列(B ){ a n }可能为等比数列(c ){a n }的任意一项均可写成{a n }的两项之差(D)对任意正整数n ,总存在正整数 m 使得a n = S m 11.运动会上,有6名选手参加100米比赛,观众甲猜测:4道或5道的选手得第一名;观众乙猜测: 3道的选手不可能得第一名;观众丙猜测:1,2,6道选手中的一位获得第一名;观众丁猜测:4,5,6道的选手都不可能获得第一名•比赛后发现没有并列名次,且甲、乙、丙、丁中只有 1人猜对比赛结果,此人是( )(A)甲(B)乙(C)丙(D) 丁1(A)若S=4,则k 的值唯一(B) 若S=^,贝U k 的值有2个22(C)若D 为三角形,则0<k <(D)若D 为五边形,则312.长方体 ABCDAEGD 中,AB=2, AD=A A 1=1,贝U A 到平面 A BD 的距离为((A) - (B)3(D)13.设不等式组|x| |y| 2 y 2 k(x 1)所表示的区域为 D,其面积为S,U(k>414. △ ABC 勺三边长是 2,3,4,其外心为 0,则 uuu uuu OA AB uuu uuu uuur uuu OB BC 0C CA =((A)0 (B)-15 (C) -21(D)229 215. 设随机事件 A 与B 互相独立,且 P(B)=0.5(A)P(A)=0.4 (B)P(B -A)=0.3 (C)P(AB)=0.2 (D)P(A+B)=0.916. 过厶ABC 的重心作直线将厶 3(A)最小值为一(B)最小值为417. 从正15边形的顶点中选出,P(A- B)=0.2,则(ABC 分成两部分,则这两部分的面积之比的(4 4(C)最大值为一533个构成钝角三角形,5(D 最大值为一4则不同的选法有((A)105 种(B)225 种(C)315 种(D)420 种18. 已知存在实数r,使得圆周x2y2 r2上恰好有n个整点,则n可以等于(22.在极坐标系中,下列方程表示的图形是椭圆的有(4 2 1 V2(A)最小值为一(B)最小值为一 (C)最大值为1 (D)最大值为--------------------5 5 3(A)4 (B)6 (C)8 (D)1219. 设复数z 满足2|z| w |z-1|,则(1(A)|z|的最大值为1 (B)|z| 的最小值为—(C)z321的虚部的最大值为2(D)z 的实部的最大值为13320.设 m,n 是大于零的实数, a =(mcos a ,msin a ),b =(ncos 3 ,nsin 3 ),其中 a , B€ [0,2 n ) a , B€r 1, _[0,2 n ) •定义向量 a 2 =( 、、. m cos — ,、. m sin 一 ), b 2=(、. n 2cos — 2 ,、齐 sin —),记 9 = a - 3,贝U2r [ r 1 r r 1 r 1 ___ (A) a 2 • a 2 = a (B) a 2 b 2=、.mn cos — (C) 2r] r] … |a 2 b 2|4、一 mn sin 2 —4r 1 r] 2 _ 2 (D) |a 2 b 2 |24, mncos 2 —421.设数列{ a n }满足:a 1=6, an 1,则((A) ? n € N?, a n <(n 1)3 (B) ? n € N?, a n 丰 2015 (C) ? n € N?, a n 为完全平方数(D)? n € N?, a n 为完全立方数1 (A )p=cos sin23. 设函数 f(x)s in x,则( x x 14(A ) f(x) w (B)| f (x) | w 5|x| (C)曲线 y= f (x)存在对称轴324. △ ABC 的三边分别为a ,b,c ,若△ ABC 为锐角三角形,则((B )p=—1(C ) 2 sin1p= —2 cos(D )(D) 1 1 2si n曲线y= f (x)存在对称中心(A)si nA>cosB (B)ta nA>cotB (C) a 2 b 2 c 2 (D) a 3 b 3 c 325.设函数f (x)的定义域是(-1,1), 若f(0) = f (0) =1,则存在实数 s€ (0,1),使得()(A) f (x) >0, x € (- S , S) (B)f (x)在(-S , S )上单调递增 (C) f (x) >1, x € (0, S) (D)f (x)>1 , x € (- S ,0)26.在直角坐标系中,已知A(-1,0),B(1,0) •若对于y 轴上的任意n 个不同的点 P k (k=1,2,…,n),总存在两个不同的点R ,P j ,1使得 |sin / A P j B-sin / A P j B| w —,贝V n 的最小值为( 3(A)3 (B)4(C)5 (D)627.设非负实数x,y 满足2x+y=1,则 x+ x 2 y 2 的()128.对于50个黑球和49个白球的任意排列(从左到右排成一行),则((A)存在一个黑球,它右侧的白球和黑球一样多(B)存在一个白球,它右侧的白球和黑球一样多(C)存在一个黑球,它右侧的白球比黑球少一个 (D)存在一个白球,它右侧的白球比黑球少一个 29.从1,2,3,4,5 中挑出三个不同数字组成五位数, 同的五位数有( (A)300 个(B)450其中有两个数字各用两次,例如 12231,则能得到的不 30.设曲线L 的方程为 (A)L 是轴对称图形 (C)L ? {(x,y) I ##A nswer##1.【解析】 丄1-z) 个(C)900 y 4 (2x 2(B)L 个(D)1800 个 2 4 2 2)y (x 2x ) =0,则(是中心对称图形 1 (D)L ? {(x,y)zz 1 zz_______ 1 - 2. 21-cos i sin332 cos 3..2 i sin ___ 3 2 2i sin32sin 2 i 2sin cos —3 3 3 cos0 isinO 2sin — [cos( —) i sin(-)i sin(3、、3(cos —2-洽 2os(cos( i sin ) 27) i sin(67)]丄(cos — isi n —.3 6 6△ )=1,选 B22.【简解】 a p (a k Q )=[(p+q)-(k+l)]d ,与公差 d 的符号有关,选 3.【解析】设A( 2X 1,X 1 ),B( 2 uuu uuu X 2,X 2 ), OA OB =X 1X 2(1 X 1X 2) =0 X 2 X1 答案(A), |0A| l OBI ^x^(1 好)4(1 —1^) = j1 X2 1 2 X 11 > /2 2|X 1 | 丄=2,正确; |X 1 | 答案(B),|OA|+|OB| > 2..|OA 「|OB| > 2 .2,正确;答案(C),直线 AB 的斜率为 2 22^=X 2 x 2 x 1X1程为 y- xj =( x 1 1)(x-x 1),焦点(0, 1)不满足方程,错误;答案(D),原点到直线AB :(4X11)x-y+ 仁X 1的距离d=w 1,正确。
清华大学自主招生考试数学试题研究

B.有 2析:设直线 l1 , l2 , l3 分别与直线 y kx m 平行且与 函数 y f ( x) 相切,则三条直线 y kx m , l1 , l2 , l3 和函数 y f ( x) 的切点设为
A( x A , f ( x A )), B ( xB , f ( xB )), C ( xC , f ( xC )), D( xD , f ( xD )), E ( xE , f ( xE ))
2
3.2 试题考点分布统计 2006 年-2016 年自主招生数学试题主要考点分布统计表 2006 三角函数 复数 函数与方程 概率与统计 数列、不等式 向量 平面几何 立体几何 解析几何 排列与组合 数论与推理 1 1 0 1 0 0 0 1 1 0 1 2007 0 0 1 1 1 0 0 0 1 0 0 2008 1 0 1 1 1 0 0 1 1 0 2 2009 0 2 1 2 1 0 0 1 2 7 2 2010 2 1 1 1 1 1 1 3 2 1 0 2011 2 1 2 1 2 1 2 2 2 1 0 2012 2 1 1 1 1 1 1 1 2 2 1 2013 1 0 1 1 1 0 0 0 1 2 1 2014 1 0 1 1 1 0 0 0 1 0 1 2015 3 2 5 1 6 2 1 1 4 2 3 合计 13 8 14 11 15 5 5 10 17 14 11
1 1 , cos x cos y ,求 sin( x y ), cos( x y ) 的值. 2 5
分析: 解决数学问题就是要建立已知与未知之间的联系, 本题的已知条件与问题之间很容易 发现下面的这个关系:
x y x y x , 2 2 y x y x y . 2 2
2011年华约自招——数学

13.已知函数 f x 2x 、、 f 1 1
ax b
f
1 2
2 3
.令
x1
1、 2
xn1 f xn .
1 数列xn的通项公式;
2
证明
x1 x2
xn1
1 2e
.
14.已知双曲线 C :
x2 a2
y2 b2
1a
0、、、b
0
F1
F2 分别为 C 的左右焦点. P 为 C 右
支上一点,且使 F1PF2
1 p1 、、、 p2 p3 p4 ;
2 探究数列pn的递推公式,并给出证明;
讨论数列 pn 的单调性及其极限,并阐述该极限的概率意义.
D.任何一种分法所分出的三角形都恰有 1 个锐角三角形
二、解答题
11.已知 △ABC 不是直角三角形. 1 证明: tan A tan B tan C tan A tan B tan C ;
2 若 3 tan C 1 tan B tan C 、 且 sin 2A、、、sin 2B tan A
b
3 2
x2 y2 z2 的最小值为(
A.1
B. 4 3
1 2
c
3 2
)
C. 3 2
1 2
xa yb zc 1
1则
D. 2
8. AB 为过抛物线 y2 4x 焦点 F 的弦, O 为坐标原点,且 OFA 135、
物线准线与 x 轴的交点,则 ACB 的正切值为(
)
A. 2 2
角的正切为 2 .则异面直线 DM 与 AN 所成角的余弦为( )
A. 1 3
B. 1 6
C. 1 8
D. 1 12
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年高水平大学自主招生选拔学业能力测试数学注意事项:1. 答卷前,考试务必将自己的姓名、准考证号填写在答题卡上。
2. 将答案写在答题卡上,写在本试卷上无效。
3. 考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题3分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设复数z 满足|z|<1且15|z+|2z=,则|z |=( ) A 45 B 34 C 23 D 12解析:设|z |a bi =+代入15|z+|2z =整理得22221174a b a b ++=+,又|z |<1,所以2214a b +=,|z |=12=(2)在正四棱锥P-ABCD 中,M 、N 分别为PA 、PB 的中点,且侧面与底面所成二面角的正切.则异面直线DM 与AN 所成角的余弦值为( ) A13 B 16 C 18 D 112解析:设2AB =,容易算出2PB =,以底面中心为原点建立空间坐标系,1111(1,1,0),(1,1,0),(,,(,,222222D A M N ------,由1cos 6|DM AN ||DM ||AN |θ⋅==⋅uuu u r uuu ruuuu r uuu r (3)过点(1,1)-的直线l 与曲线3221y x x x =--+相切,且(1,1)-不是切点,则直线l 的斜率是( )A 2B 1C 1-D 2-解析:32221(),()322y x x x f x f x x x '=--+==--,设切点(),()t f t ,()()()y f t f t x t '-=-,把(1,1)-代入且1t ≠-得到1t =,所以2k =-(4)若23A B π+=,则22cos cos A B +的最小值和最大值分别为( )A.312-, B.1322,C.11D.112, 解析:2222211cos cos cos cos ()1cos(2)323A B A A A ππ+=+-=++,选B (5)如图,1O e 和2O e 外切于点C ,1O e ,2O e 又都和O e 内切,切点分别为,A B . 设AOB ACB αβ∠=∠=,,则( ) A cos sin02αβ+= B sin cos02αβ-=C sin 2sin 0βα+=D sin 2sin 0βα-= 解析:连接12O O 过点C ,设12CAO CBO ∠=∠∠=∠,,12O C O C 、,则+1+2=+21+22=βαπ∠∠∠∠,即2=βαπ-,只有D 是错的。
(6)已知异面直线,a b 成060角,A 为空间中一点,则过A 与,a b 都成045角的平面( ) A 有且只有一个 B 有且只有两个 C 有且只有三个 D 有且只有四个解析:060,范围是00,60⎡⎤⎣⎦,有两个;0120,范围是00,30⎡⎤⎣⎦,没有。
选B(7)已知向量11(0,1)()(),(1,1)2222a b c xa yb zc ==--=-++=r r r r r r ,,.则 222x y z ++的最小值为( )A 1 B43 C 32D 2 解析:由11(0,1)()),(1,1)22a b c xa yb zc ==-=-++=r r r r r r ,,消去,x z 整理得到 222243(3x y z y ++=++,选B (8)AB 为过抛物线24y x =焦点F 的弦,O 为坐标原点,且0135OFA ∠=,C 为抛物线准线与x 轴的交点,则ACB ∠的正切值为( ) A 5 C 3 D 3解析:直线AB 方程是1y x =-,联立抛物线24y x =解得ECBFDA(32(32A B ++--,容易算出直线AC,BC 的斜率,由tan()αβ+得到ACB ∠的正切值为(9)如图,已知ABC ∆的面积为2,D ,E 分别为边AB ,边AC 上的点,F 为线段DE 上一点,设AD AE DFx y z AB AC DE===,,,且1y z x +-=,则BDF ∆面积的最大值为( ) A8B 1027C 1427D 1627 ,1,BDE ABE ABEABCS S S S z x y ∆∆∆∆==-=,于是(1)2BDF ABCS S z x y∆∆-=联立1y z x +-= 得到[]2()(2(122BDF ABCS S zy zyy zzy ∆∆=-+≤-=- 3(14822432727BDF S ∆⎡⎤-++⎢⎥≤=∴≤⎢⎥⎢⎥⎣⎦(10)将一个正11边形用对角线划分为9个三角形,这些对角线在正11边形内两两不相交,则( )A 存在某种分法,所分出的三角形都不是锐角三角形B 存在某种分法,所分出的三角形恰有两个锐角三角形C 存在某种分法,所分出的三角形至少有3个锐角三角形D 任何一种分法所分出的三角形都恰有1个锐角三角形 解析:思路暂缺。
二、解答题:解答应写出文字说明,证明过程或演算步骤。
(11)(本小题满分14分)已知BC A ∆不是直角三角形.(I )证明:tan tan tan tan tan tan A BC A B C ++=; (II tan tan 1tan B CC A+-=,且sin 2sin 2sin 2A B C ,,的倒数成等差数列. 求cos2A C-的值.(12)(本小题满分14分)已知圆柱形水杯质量为a 克,其重心在圆柱轴的中点处(杯底厚度及重量忽略不计,且水杯直立放置).质量为b 克的水恰好装满水杯,装满水后的水杯的重心还在圆柱轴的中点处。
(I )若3b a =,求装入半杯水后的水杯的重心到水杯底面的距离与水杯高的比值; (II )水杯内装多少克水可以使装入水后的水杯的重心最低?为什么?(13)(本小题满分14分)已知函数212()(1)1().23x f x f f ax b ===+,, 令111()2n n x x f x +==,(I )求数列{}n x 的通项公式; (II )证明121>2n x x x e⋅⋅⋅.(14)(本小题满分14分)已知双曲线2222:1(0,0)x y C a b a b -=>>,12,F F 分别为C 的左,右焦点。
P 为C 右支上一点,且使123F PF ∠=π,又12F PF ∆的面积为2.(Ⅰ)求C 的离心率e ;(Ⅱ)设A 为C 的左顶点,Q 为第一象限内C 上的任意一点,问是否存在常数(0)λλ>,使得22QF A QAF λ∠=∠恒成立。
若存在,求出λ的值;若不存在,请说明理由.(15)将一枚均匀的硬币连续抛掷n 次,以n p 表示未出现连续3次正面的概率.(Ⅰ)求1234,,p p p p 和;(Ⅱ)探究数列{}n p 的递推公式,并给出证明;(Ⅲ)讨论数列{}n p 的单调性及其极限,并阐述该极限的概率意义.2011年高水平大学自主选拔学业能力测试数学解答题试题、参考答案、评分标准(11)已知△ABC不是直角三角形.(Ⅰ)证明:tan tan tan tan tan tanA B C A B C++=;tan tan1tanB CCA+-=,且sin2A,sin2B,sin2C的倒数成等差数列,求cos2A C-的值.评分标准:(Ⅰ)证法1:由A B Cπ++=,得A B Cπ+=-,由△ABC不是直角三角形,上式两端同时取正切,得()tan tanA B C+=-,展开,得tan tantan1tan tanA BCA B+=--⋅,去分母,整理得tan tan tan tan tan tanA B C A B C++=. ……………5分证法2:()tan tan tan tan tan tanA B C A B A B++=+-+tan tantan tan1tan tanA BA BA B+=+--⋅()()()tan tan1tan tan tan tan1tan tanA B A B A BA B+-⋅-+=-⋅()tan tan tan tantan tan tan1tan tanA B A BA B CA B-+⋅==-⋅. ……………5分证法3:由()tan0A B C++=,得()()tan tan1tan tanA B CA B C++=-+,分子()tan tantan tan tan01tan tanB CA B C AB C+++=+=-,整理即得结论. ……………5分证法4:sin sin sintan tan tancos cos cosA B CA B CA B C++=++sin cos cos sin cos cos sin cos coscos cos cosA B C B A C C A BA B C++=()sin cos cos coscos sin sin cos coscos cos cos cos cos cosC C A BC C C A BA B C A B C++==sin sin sintan tan tancos cos cosC A BA B CA B C==. ……………5分tan tan1tanB CCA+-=及(Ⅰ),得tan tan tan tan tan tan tanA C ABC A B C⋅=++=⋅⋅,因为(),0,A Cπ∈,所以tan B=,得3Bπ=,……………7分由sin2A,sin2B,sin2C的倒数成等差数列,得211sin2sin2sin2B A C=+,)sin2sin24sin2sin2A C A C+=⋅,由积化和差及和差化积公式,得()()()()cos2cos2cos2A C A C A C A C+-=-+--⎡⎤⎣⎦,将23A Cπ+=代入上式,整理得()()2cos23cos10A C A C---+=,所以()()24cos3cos10A C A C----=,解得()cos1A C-=或()1cos4A C-=-,……………12分由cos2A C-=得cos12A C-=或cos2A C-=……………14分阅卷说明:1、第(Ⅰ)问5分或0分,通常只要有()tan tantan tan1tan tanA BC A BA B+=-+=--⋅,后面作差或通分通常会对.2、第(Ⅰ)问凡是用余弦定理的学生,只要有主要推导步骤,没有核心步骤就得出证明的等式不能给分.3、第(Ⅰ)、(Ⅱ)两问独立给分.4、第(Ⅱ)问有3个得分点:得出tan B=或3Bπ=给2分;然后直接找()cos1A C-=或()1cos4A C-=-,全对给5分,否则不给分;最后看cos12A C-=或cos2A C-=2分,否则不给分.多解、少解、错解均不给分!(12)已知圆柱形水杯质量为a 克,其重心在圆柱轴的中点处(杯底厚度及重量忽略不计,且水杯直立平放),质量为b 克的水恰好装满水杯,装满水后的水杯重心还在圆柱轴的中点处.(Ⅰ)若b =3a ,求装入半杯水后的水杯的重心与水杯高的比值; (Ⅱ)水杯内装多少克水可以使装入水后的水杯的重心最低?为什么? 评分标准:(Ⅰ)解:设杯高为l ,设装水后水杯的重心与水杯底面的距离为h ,半杯水质量为322b a=, 水的重心与水杯底面的距离为14,所以131()()422a h a h -=-, ……………4分 解得720h =, 所以水杯的重心与水杯高的比值是720. ……………6分 (Ⅱ)解:设装入水的质量为xb 克时水杯重心最低,则水的重心与水杯底面的距离为2x , 设装水后水杯的重心与水杯底面的距离为y ,所以122x xb y a y ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭,解得()22bx a y a bx +=+, ……………9分由()22222b x abx ab y a bx +-'=+,令0y '=,解得x =(负值舍去),a 克水时,重心最低. ……………14分阅卷说明: 第(Ⅰ)问: 1、先看结果720对,即得6分; 2、结果不是720,再往上看131()()422a h a h -=-对得4分,否则得0分.第(Ⅱ)问:1a 克对,第2问得满分(8分),第1问亦对时,即得14分;2a ,再往上看()22bx ay a bx +=+是否对,对得小分(3分),第1问亦对时,即得9分.否则第2问得0分.注意除标准解答中解析式外,以下解析式也正确:①设装入水的质量为x 克时,()()22x abf x h b a x +=⋅+(h 为杯高); ②设装水后,水面距杯底高度为x ,则()2222ah bx f x ah bx +=+(h 为杯高);③设装水后,水面距杯底高度为xh ,则()()22bx af x h a bx +=⋅+(h 为杯高).(13)已知函数()2x f x ax b =+,()11f =,12()23f =,令112x =,()1n n x f x +=. (Ⅰ)求数列{}n x 的通项公式; (Ⅱ)证明:12312n x x x x e⋅⋅⋅>. 评分标准:(Ⅰ)解法一:由()11f =,12()23f =,解得1a =,1b =,所以()21xf x x =+, ……………5分 则121n n n x x x +=+,即1111122n n x x +=⋅+,则1111112n n x x +⎛⎫-=- ⎪⎝⎭, 令1n n y x =,从而有()11112n n y y +-=-, 又111y -=,可知12n n y -+=,故11221n n n x --=+. ……………10分解法二:同解法一求出()21xf x x =+, ……………5分 由112x =,求出223x =,345x =,489x =,猜想出11221n n n x --=+. ………7分证明:1)当n =1时,112x =满足11221n n n x --=+;2)假设当n =k 时成立,即11221k k k x --=+,则当1n k =+时,()122121kk k k k k x x f x x +===++, 所以当1n k =+时结论成立.由1)2)知,11221n n n x --=+. ……………10分解法三:同解法一求出()21xf x x =+, ……………5分则121n n n x x x +=+,即1111122n n x x +=⋅+,令1n n y x =,则11122n n y y +-=, 11122n n y y --=, 121122n n y y ---=, ………321122y y -=, 211122y y -=, 以上式子分别乘以012⎛⎫ ⎪⎝⎭,112⎛⎫ ⎪⎝⎭,212⎛⎫ ⎪⎝⎭,……,212n -⎛⎫⎪⎝⎭,112n -⎛⎫⎪⎝⎭,相加1211111()1()()2222n n n y -+-=+++⋅⋅⋅+, ……………………7分所以1212n n n y ++=,则11221n n n x --=+………………………10分注:若将11122n n y y +-=变形为11222n n n n n x x ++=-,得用累加或其他方法等同于此法 (Ⅱ)令()ln(1),(0)0,g x x x g =-+=,当0x >时,可知1()101g x x'=->+, 可知0ln(1)x x <+<,2311111111ln()[ln(1)ln(1)ln(1)]()1242242n n n x x x --⋅⋅⋅=-++++⋅⋅⋅++>-++⋅⋅⋅+>-12312n x x x x e ⋅⋅⋅>…………………………12分评卷说明:第(Ⅰ)问满分10分,分两个得分点计算: 1. 求出,a b 或求出()f x 得5分,否则得0分。
