选 择 排 序 算 法 原 理
排列组合解题方法

排列组合解题方法
排列组合是一个数学问题,也是一个常见的解题方法。
在解决排列组合问题时,可以
按照以下步骤进行操作:
1. 确定问题中的元素个数和要求的组合方式。
例如,给定一组数字,要求按照一定的
规则进行排列或组合。
2. 确定排列或组合的顺序。
排列是指考虑元素的顺序,组合是指不考虑元素的顺序。
3. 根据题目要求确定进行排列或组合的元素个数。
例如,给定一组数字,要求从中选
取特定个数的数字进行排列或组合。
4. 根据排列或组合的特性,确定计算排列或组合的公式。
例如,排列可以使用阶乘来
计算,组合可以使用组合公式来计算。
5. 根据公式计算排列或组合的结果。
6. 根据题目要求,处理计算结果。
例如,将排列或组合的结果进行排序、筛选或统计。
在实际解题时,可以参考以上步骤进行操作。
根据具体的问题,选择合适的方法和公
式进行计算,最终得出满足题目要求的排列组合结果。
第十章排序(可编辑修改word版)

作业布置
10-4(2),(4),(5),10-6,
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
重点难点
希尔的思想,实现,算法分析
要求掌握知识点和
分析方法
1.概念:排序,主(次)关键字,内部(外部)排序,比较排序算法的技术指标2。插入排序的基本思想;3。直接直接插入排序和希尔的思想,实现,算法分析。
教授思路,采 用 的 教学方法和辅助手段,板书设计,重 点 如 何突出,难点如何解决,师 生 互 动等
难点:堆的调整辅助手段:多媒体
作业布置
10-7,10-8
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
章节
10.5归并排序10.6基数排序
讲授主要内容
归并排序 ,基数排序
重点难点
归并排序 ,基数排序的基本思想与算法实现
本章思考题和习题
主 要 参考资料
1.《数据结构》,严蔚敏 吴伟民,清华大学出版社;2.数据结构题集(C语言版),
严蔚敏 吴伟民,清华大学出版社;
备注
章节
10.1概念10.2插入排序
讲授主要内容
1.概念:排序,主(次)关键字,内部(外部)排序,比较排序算法的技术指标2.
插入排序的基本思想;3。直接直接插入排序和希尔的思想,实现,算法分析。
教授思路,采 用 的 教学方法和辅助手段, 板书设计,重 点 如 何突出,难点如何解决,师 生 互 动等
教学思路:
排列组合的基本原理

排列组合的基本原理尊敬的读者:在数学中,排列组合是一种重要的概念,它用于计算可能性和确定事件发生的方式。
本文将介绍排列组合的基本原理,包括排列和组合的定义、计算方法以及应用。
希望通过本文的阐述,您能够更好地理解和运用排列组合的基本原理。
1. 排列的定义和计算方法在数学中,排列指的是从一个集合中选取若干个元素,按照一定顺序排列的方式。
排列通常用P(n,m)表示,其中n为集合的元素个数,m 为选取的元素个数。
排列的计算方法可分为两种情况:1.1 当选取的元素个数m小于或等于集合的元素个数n时,排列的计算公式为:P(n,m) = n! / (n-m)!1.2 当选取的元素个数m大于集合的元素个数n时,排列的计算公式为0,即不存在这种情况。
2. 组合的定义和计算方法组合指的是从一个集合中选取若干个元素,不考虑顺序的方式。
组合通常用C(n,m)表示,其计算方法可分为两种情况:2.1 当选取的元素个数m小于或等于集合的元素个数n时,组合的计算公式为:C(n,m) = n! / (m! * (n-m)!)2.2 当选取的元素个数m大于集合的元素个数n时,组合的计算公式为0,即不存在这种情况。
3. 排列组合的应用排列组合在实际问题中的应用非常广泛,下面举几个例子来说明:3.1 生日排列问题:假设有5个人,每个人的生日在一年中任意选择。
我们可以用排列来计算不考虑年份的情况下,5个人生日的所有可能排列数量。
根据排列的计算公式,可知P(365,5)即为所求。
3.2 钥匙排列问题:某人有5把钥匙,但只有其中一把能打开家门。
每次进门都尝试一把钥匙,直到能够打开为止。
这个过程中,我们可以用排列来计算需要尝试的所有可能方式的数量。
根据排列的计算公式,可知P(5,5)即为所求。
3.3 选课组合问题:某学校的学生需要选择4门选修课,而学校提供了8门选修课供选择。
我们可以用组合来计算学生选择的所有可能组合的数量。
根据组合的计算公式,可知C(8,4)即为所求。
排列的方法

排列的方法排列是数学中的一个重要概念,它在各个领域都有着广泛的应用。
在数学中,排列是指从给定的元素中按照一定的顺序取出一部分或全部元素,形成一个有序的序列。
在实际生活中,排列也是我们经常会用到的方法之一,比如整理书籍、安排座位等。
本文将介绍排列的方法,以及在实际中如何应用排列。
首先,我们来看一下排列的基本概念。
排列是指从n个不同元素中取出m(m≤n)个元素,按照一定的顺序排成一列。
这个过程可以用数学符号表示为P(n,m),其中n表示总的元素个数,m表示取出的元素个数。
排列的计算公式为P(n,m) = n! / (n-m)!,其中n!表示n的阶乘,即n×(n-1)×(n-2)×…×2×1。
这个公式告诉我们,当我们从n个元素中取出m个元素进行排列时,一共有n! / (n-m)!种不同的排列方法。
接下来,我们来看一下排列的应用。
在实际生活中,排列经常用于解决各种问题。
比如,我们要从8本书中挑选3本书排在书架上,问有多少种不同的排列方法?这个问题就可以用排列的方法来解决。
根据排列的计算公式,我们可以得到答案,P(8,3) = 8! / (8-3)! = 8×7×6 = 336。
所以,从8本书中挑选3本书排列的方法有336种。
除了在实际问题中的应用,排列还在数学领域有着重要的地位。
在组合数学中,排列是一个重要的概念,它与组合、排列组合等概念密切相关。
排列的概念也是许多数学问题的基础,比如排列组合、概率论等。
因此,了解排列的方法对于理解数学问题、解决实际问题都有着重要的意义。
在计算机科学领域,排列也有着广泛的应用。
比如,在算法设计中,排列是一个常见的问题,如全排列、字典序排列等。
排列的方法也经常用于解决搜索、排序等问题。
因此,了解排列的方法对于计算机科学领域的学习和工作也是非常重要的。
总之,排列是数学中的一个重要概念,它在各个领域都有着广泛的应用。
排序算法实验报告
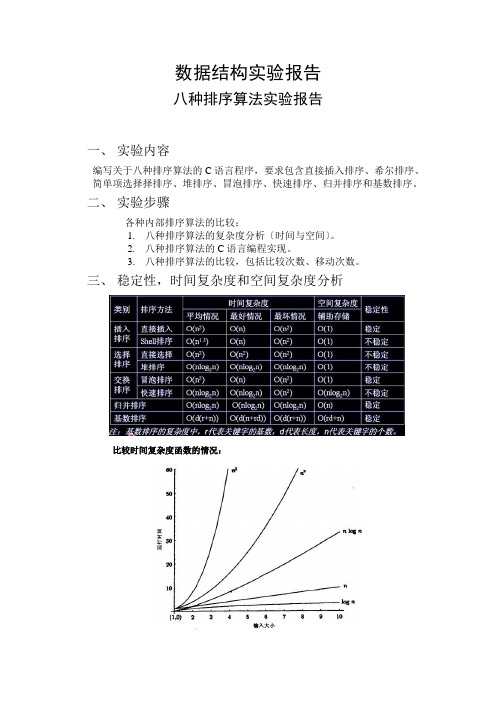
数据结构实验报告八种排序算法实验报告一、实验内容编写关于八种排序算法的C语言程序,要求包含直接插入排序、希尔排序、简单项选择择排序、堆排序、冒泡排序、快速排序、归并排序和基数排序。
二、实验步骤各种内部排序算法的比较:1.八种排序算法的复杂度分析〔时间与空间〕。
2.八种排序算法的C语言编程实现。
3.八种排序算法的比较,包括比较次数、移动次数。
三、稳定性,时间复杂度和空间复杂度分析比较时间复杂度函数的情况:时间复杂度函数O(n)的增长情况所以对n较大的排序记录。
一般的选择都是时间复杂度为O(nlog2n)的排序方法。
时间复杂度来说:(1)平方阶(O(n2))排序各类简单排序:直接插入、直接选择和冒泡排序;(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序;(3)O(n1+§))排序,§是介于0和1之间的常数。
希尔排序(4)线性阶(O(n))排序基数排序,此外还有桶、箱排序。
说明:当原表有序或基本有序时,直接插入排序和冒泡排序将大大减少比较次数和移动记录的次数,时间复杂度可降至O〔n〕;而快速排序则相反,当原表基本有序时,将蜕化为冒泡排序,时间复杂度提高为O〔n2〕;原表是否有序,对简单项选择择排序、堆排序、归并排序和基数排序的时间复杂度影响不大。
稳定性:排序算法的稳定性:假设待排序的序列中,存在多个具有相同关键字的记录,经过排序,这些记录的相对次序保持不变,则称该算法是稳定的;假设经排序后,记录的相对次序发生了改变,则称该算法是不稳定的。
稳定性的好处:排序算法如果是稳定的,那么从一个键上排序,然后再从另一个键上排序,第一个键排序的结果可以为第二个键排序所用。
基数排序就是这样,先按低位排序,逐次按高位排序,低位相同的元素其顺序再高位也相同时是不会改变的。
另外,如果排序算法稳定,可以防止多余的比较;稳定的排序算法:冒泡排序、插入排序、归并排序和基数排序不是稳定的排序算法:选择排序、快速排序、希尔排序、堆排序四、设计细节排序有内部排序和外部排序,内部排序是数据记录在内存中进行排序,而外部排序是因排序的数据很大,一次不能容纳全部的排序记录,在排序过程中需要访问外存。
选择法排序

a[0]
9 6 17 2 12
9
9
9 6 17
9 6
k
a[1]
2
k
a[2]
j k
6 17 2 12
k 6
j k
17 2 12
第一轮,i=0; k=i; for(j=i+1;j<5;j++) if(a[k]>a[j]) k=j; if(k!=j) {t=a[k];a[k]=a[i];a[i]=t;}
17 9 12
ቤተ መጻሕፍቲ ባይዱ
17 9
17 9 12
a[3]
{t=a[k];a[k]=a[i];a[i]=t;} 第四轮 I=3;k=I;
j
12 12
for(j=i+1;j<5;j++) if(a[k]>a[j])k=j;
a[4]
j
if(k!=i)
{t=a[k];a[k]=a[i];a[i]=t;}
i从0变到3 for(i=0;i<4;i++) 第i轮 k=I;认为第I个数最小, 从下一个数到最后一个数与 a[k]比较, If(a[k]>a[j]) k=j;k就赋值小数 的下标 If(k!=i) {t=a[k];a[k]=a[i];a[i]=t;}既a[k] 与第I个位置上的数交换位 置。
选择法排序(以5个数为例) 基本思路:
第一轮i=0:认为第一个数a[0]最小,把它的下标赋值给k,k=i;(k=0;) 从下一个数(a[1])到最后一个数a[4]与a[k]比较,如果a[k]大于哪个 数,k就赋值哪个数的下标,一轮结束后,k放最小数的下标,则a[k]与 a[0]交换位置。 第二轮i=1;k=i;认为a[1]最小,下标赋给k,将a[k]从下一个数(a[2]) 开始到最后一个数(a[4])比较,找到最小数,把它的下标赋给k,然后 a[k]与a[1]交换位置。 ……5个数比4轮,第i轮认为第i个位置上的数最小(k=i),将a[k]从 下一个数a[i+1]开始到最后一个数一一比较。找出最小数,把下标赋给 k,将a[k]与第i个位置上的数a[i]交换。
2021-CSP-S(提高组)认证第一轮试题详细解析

iiff tt==11 rreettuurrnn11
eellssee rreettuurrnn 55** ssoollvvee(ቤተ መጻሕፍቲ ባይዱtt--1l,,nn))mmoodd nn 则则 ssoolvlev(e(2233,,2233)) 的的结结果果为为(( ))。。
比比如如 initn t数数组组【[11,,11,,11,6,,64,]中4】a中[0 ]a,【a[01】],,a[a2【]的1】值,相a【等2】,的在值排相序等,时在不排改序变时不其改序变列其,序则列,称则所称用所用的的方方法法
是是稳稳定定的的..((插插入入排排序序、、冒冒泡泡排排序序、、二二叉叉树树排排序序、二路归并排序及其他线形排序是稳定的的;;选 择择排排序序、、希希尔尔排排序序、、快快速速排排序序、、堆堆排排序序是是不不稳稳定定的的))..
BB..系系统统分分配配的的队队列列空空间间溢出
CC.系. 系统统分分配配的的链链表表空空间间溢出
DD.系. 系统统分分配配的的堆堆空空间间溢溢出
【解析】递归需要使使用用到到系系统统堆堆栈栈空空间间,,如如果果递递归归层层数数过过多多,,导导致致系系统统堆堆栈栈空空间间不不足足。。
44.以.以下下排排序序方方法法中中,,(())是是不不稳稳定定的的。。
AA1. 1 B.B.77C.C1. 212 D.D.2222
【解析】程程序序的的运运行行结结果果为为552222mmoodd 2233,,根据费马小定理:∶如如果果是是素素数数,,aa是是一一
个个整整数数,,那那么么 aaPp-11≡=11 mmoodd pp,,可可以以得得 552222mmoodd 2233=≡11mmodo d2233,,结结果果为为11
2.聚合物合成工艺学课后习题全解

。展发有亦 聚缩相固来 年近�聚缩面界和、聚缩液溶、聚缩融熔是要主法方施实的聚缩型 线�中业工成合子分高在 。应反衡平逆可步逐的物聚高型线 成生时同的子分 小去缩在�应反生发间之团能官在�物合化子分低的团能官个两有含是�答 �种几哪有法方施实的合聚型线�合聚型线谓何 .91 。质性的端末链长增响影显明会 同不的类种其在存常 程过合聚子离单 �响影无应反长增链对类种剂发引中程过合聚基由自在 。合聚锁连的子离为心中性活长增�合聚子离 法方续连和法方歇间有法方作操 。制控格严应量水含中料原 他其和体单且并 �合聚液溶和合聚体本 用采能只合聚子离 �合聚液乳和合聚浮悬用采能不即 �质介为作水用能不中 法方施实的合聚子离 �此因 �感敏为极水对剂发引的用所合聚子离 �答 。因原 明说并�同不何有合聚基由自与法方作操和法方合聚中合聚子离在论讨 .81 剂发引元三— iN 是 剂 发 引 的 用 常 合 聚 — a 是 成 组 的 本 基 最 剂 发 引 attaN — relgeiZ 的 烯丙 聚 规 有 产 生于 用 剂 发 引的 合 聚 为 配 烯 丙 ② 法孚美为称常�上铝化氧性活于载钼化氧三。上体载铝化氧三 —硅化氧二于载 铬化氧三 �种两有的用常 。物化氧属金的上体载于载是剂发引的用常法压中 lC2)5H2C(lA+4lCiT 是剂发引的用常法压低 剂发引的合聚为配烯乙①�答 。剂发引的合聚为配的烃烯二和烯丙、烯乙出写 .71 点衡平相三③ �BLH� 值衡平油亲—水亲② �CMC� 度浓束胶界临① �征表来标指个三有 �能性 5.5 于低好最,用使下件条的 7<hP 在是常 通�剂性活面表子离阴 。用使下件条的 7>hP 在是常通�的广最用应中业工合 聚液乳是剂性活面表子离阳�用使 。种四型子离非和性两、型子离阴、型子离 阳�类种的剂化乳 。溶增体单是�束胶成形③ 定稳液乳是�聚凝止防�层护 保成形面表滴液在② 滴液小细成散分体单使�力张面表低降①�用作 。用作化乳为称用 作种这 �液乳的层分以难的定稳 为成系体散分的成组水和体单使能 �用作护保有滴液体单对 �用作溶增有体 单对�力张面界的水低降能质物些某。剂化乳为称质物的用作化乳有具�答 �能性的剂化乳征表来标指些哪有 � 同不 何 有 用 使� 种 几 哪 有 剂 化乳� 么 什 是 用作 剂 化 乳 �剂 化 乳 谓 何 .61 。产生的物 合聚用作合聚用胶橡用以可且而 �产生的物合聚用脂树 成合于用以可仅不合聚液乳⑤ 。高很也量质子分对相的物 合聚 �高很以可料 塑合聚的合聚液乳 �象现速加动自了除消上本基中系体合聚液乳④ 杂复较程 过序工�序工等燥干和洗水、乳破质解电加要需�是物合聚体固用③ 。用利接 直等剂理处面 表或料涂、剂黏胶为作以可胶乳物合聚�作操续连行进以可�良 优性定稳系体散分② 利有分十热传对且�全安廉价�质介为水以①�点特 。易较热散�热比的高 较有�质介散分为作�水质介② 。用作化 乳为称用作种这 �液乳的层分以难 的定稳为成系体散分的成组水和体单使能 �用作护保有滴 液体单对�用作溶 增有体单对�力张面界的水低降能质物些某�用作化乳的剂化乳①�用作 。水质介和剂化乳性溶水、剂发引性溶水、体单性溶油�分组
排序算法

{for (i=1; i<n; i++) /* 对无序记录序列进行n−1趟扫描 */
{ flag = 0; /* 这一趟是否发生交换的标志 */ for (j=1; j<=n-i; j++) /* 这趟扫描的范围是从1到n−i
*/
} if (r[j].key>r[j+1].key) /* 通过temp进行交换 */ { temp = r[j]; r[j] = r[j+1]; r[j+1] = temp; flag = 1;} if (flag == 0) break; /* 若没发生交换,就结束算法 */
11
直接插入排序算法
用一维数组 r 做存储结构, n 表示记录个
数,MAXSIZE是常量并且 MAXSIZE>n。约定n
个记录分别存放在 r[1],r[2],…,r[n] 之中。
直接插入排序算法如下:
2016/6/17
12
void stinsort ( node r[MAXSIZE], int n) {for (i=2; i<=n; i++) /*共进行n-1趟插入*/ {r[0]=r[i];/* r[0]为监视哨*/ j=i-1; while (r[j].key> r[0].key) {r[j+1]=r[j];j--;} r[j+1]=r[0]; /*将r[0]即原r[i]记录内容,插到r[j]后一位置*/ } }/*sinsort*/
2016/6/17
24
算法思路:
1.先取一个正整数d1(d1 <n),把全 部记录分成d1 个组,所有距离为d1 的倍数的 记录看成一组,假设d1=4,那么记录共分4组: 第1组:r[1],r[5],r[9],…; 第2组:r[2],r[6],r[10]…; 第3组:r[3],r[7],…; 第4组:r[4],r[8],…;
排列组合专题二 筛选法

排列组合专题二筛选法引言排列组合是数学中常见的概念,可以用于解决诸如选择、排列问题等。
而在排列组合中,筛选法是一种常用的方法,能够帮助我们有效地进行选取和筛选。
本文将介绍排列组合专题二中的筛选法。
筛选法的基本原理筛选法是一种基于逻辑筛选的方法,通过设定条件来选取符合要求的对象。
在排列组合中,筛选法常用于从一个较大的集合中选择出满足特定条件的子集合。
筛选法的步骤1. 确定筛选条件:首先,需要明确所需的筛选条件。
这可以是某些元素的特定属性,或者是满足一定关系的组合。
2. 构建筛选算法:根据筛选条件,构建一个合适的筛选算法。
这可以是一系列的判断语句或循环控制语句,用于按照条件筛选出符合要求的对象。
3. 应用筛选算法:将筛选算法应用到待筛选的集合中。
可以逐个对象进行判断,或者通过循环依次检查每个对象。
4. 输出筛选结果:将符合筛选条件的对象输出为最终的筛选结果。
这可以是一个单一的对象,或者是一个满足条件的子集合。
示例以下是一个简单的排列组合示例,展示了筛选法的应用:给定一个集合 {A, B, C, D, E},现要从中选取含有两个元素的子集合,且子集合中的元素必须按字母表顺序排列。
1. 确定筛选条件:满足条件的子集合必须含有两个元素,并且元素按字母表顺序排列。
2. 构建筛选算法:构建一个循环控制语句,遍历集合中的每个元素对,并判断是否满足条件。
3. 应用筛选算法:依次检查每个元素对,如果满足条件,则将其加入符合条件的子集合中。
4. 输出筛选结果:最终的筛选结果为 {AB, AC, AD, AE, BC, BD, BE, CD, CE, DE}。
结论筛选法是一种有效的排列组合方法,能够帮助我们按需筛选出满足条件的对象。
通过明确筛选条件、构建筛选算法、应用算法和输出结果,我们可以灵活运用筛选法解决各种排列组合问题。
南阳理工学院OJ第1版解题报告V1 0

首�想思心贪用采。围范]w,0[盖覆段线的少最用为换转题问�段线盖覆的囿个每算计�路思题解
。出输接直�路思题解 离分数偶奇 .11
。划规态劢典经�路思题解
乘阶数大 .82 。SFD�路思题解 目数池水 .72
。了功成就本基表数素出打�路思题解 题问数素生孪 .62
。索搜分二后然�表数素打�2 法方�历遍右向左向别分 M 从�1 法方�路思题解 。题问离距数素 .42 .31.1-11.1》美乊
。数函 rahcteg 和 steg 的快更用使者戒�fnacs 用要得记候时个这�时超会往往 nic 用使�时
�呢数个4么那�次3是数次较比的要需少最序排行迚法算的较比亍基用使数个三�考思散发
泡冒�序排llehS�序排入插表链�序排入插半折�序排入插接直括包�的以可是也法方序排 �c和a断判再�b和a断判先以可�较比次三行迚是法方的单简最�序排母字个三�法方题解 的用使想你种一何任用使然弼。可即置位b在放的小次将�c和b较比后然�数的小最是a得使
。标坐心重解求式公学理物
� �标坐心重
列序号括建构要需丌�拟模律规找以可�版强加的 4 题问展扩 配匹号括�5 题问展扩 做法方性线以可�拟模 算计列序 P 的号括�4 题问展扩 本版号括个三的题原 弟弟的她和佳佳�2 题问展扩 律规找 式达表号括�3 题问展扩
划规态劢的乘连阵矩似类 tekcarB�6 题问展扩
。置位置放尿邮
。 器水喷 的大径半用使量尽�法算心贪�路思题解 �一� 置装水喷 .6
、praK-nibbaR、PMK 虑考以可�大变模规串本文是其尤�大变模规量据数果如�考思散发 。做力暴可�小较模规亍由�配匹串符字�路思题解 gnihctaM gnirtS yraniB .5
二项式拓展之:解排列组合问题的五大原则

二项式拓展之:解排列组合问题的五大原则排列、组合是高中数学的重要内容,新教材中概率与统计的增加更突出了排列、组合的重要性.高考对排列组合的考查以两个基本原理——分类加法计数原理和分步乘法计数原理为出发点,侧重检测解题思想和解题技巧,因而对解题策略和思维模式的培养和提炼是平时训练的核心.下面通过具体的例题来解析排列组合问题的解题策略之“五大原则”.一、 分类讨论原则:例1.(2012德州二模)2012年伦敦奥运会某项目参赛领导小组要从甲、乙、丙、丁、戊五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同工作,若其中甲、乙只能从事前三项工作,其余三人均能从事这四项工作,则不同的选派方案共有A .18种B .36种C .48种D .72种二、 特殊优先原则该原则是指在有限制的排列组合问题中优先考虑特殊元素或特殊位置.例2.(2012烟台二模)甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门相同的选法种数为(用数字作答)___答案:30解析:可先求出所有两人各选修2门的种数2424C C =36,再求出两人所选两门都都不同的种数均为2242C C =6,故只至少有1门相同的选法有36-6=30种。
评注:特殊优先原则是解有限制的排列组合问题的总原则,对有限制的元素和有限制的位置一定要优先考虑.三、先取后排原则该原则充分体现了m m m n m n C A A =·的精神实质,先组合后排列,从而避免了不必要的重复与遗漏.例3.(2009重庆卷理)将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有 种(用数字作答).答案:36解析分两步完成:第一步将4名大学生按,2,1,1分成三组,其分法有21142122C C C A ⋅⋅;第二步将分好的三组分配到3个乡镇,其分法有33A 所以满足条件得分配的方案有211342132236C C C A A ⋅⋅⋅= 评注:先取后排原则也是解排列组合问题的总原则,尤其是排列与组合的综合问题.若本例简单分步:先从4名教师中取3名教师分给3所学校有34A 种方法,再将剩下的1名教师分给3所学校有3种选择,则共有34372A =·种分配方案,则有明显重复(如:甲、乙、丙、丁和甲、乙、丁、丙).因此,处理多元素少位置问题时一般采用先取后排原则.四、正难则反原则若从正面直接解决问题有困难时,则考虑事件的对立事件,从不合题意要求的情况入手,再整体排除.例4.【2012高考真题四川理11】方程22ay b x c =+中的,,{3,2,0,1,2,3}a b c ∈--,且,,a b c 互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )A 、60条B 、62条C 、71条D 、80条答案:B解析:本题可用排除法,,,{3,2,0,1,2,3}a b c ∈--,6选3全排列为120,这些方程所表示的曲线要是抛物线,则0a ≠且0b ≠,,要减去40225=A ,又22或-=b 和33或-=b 时,方程出现重复,用分步计数原理可计算重复次数为18233=⨯⨯,所以不同的抛物线共有120-40-18=62条.故选B.评注:正难则反原则也是解决排列组合问题的总原则,如果从正面考虑不易突破,一般寻找反面途径.利用正难则反原则的语境有其规律,如当问题中含有“至少”,“最多”等词语时,易用此原则.五、策略针对原则不同类型的排列、组合问题有着不同的应对策略,不同的限制条件要采用不同的解题方法.1.相邻问题捆绑法(整体法),相隔问题插空法例5. 某校高三年级举行一次演讲比赛,共有10位同学参赛,其中一班有3位,二班有2位,其他班有5位.若采用抽签的方式确定他们的演讲顺序,则一班的3位同学恰好被安排到一起(演讲序号相连),而2班的2位同学没有被排在一起的概率为( ) A.110 B.120 C.140 D.1120解析:10人的全排列数是1010A ,即所有的演讲顺序有1010A 种.符合要求的演讲顺序有两个限制:一班的3位同学相邻,而2班的2位同学不相邻,因此分步完成:①把一班的3位同学看成一个整体,他们自身全排列有33A 种安排;②把这个整体当成1个元素与其他班5个元素一起排列有66A 种安排;③把这6个元素排定后有7个空位(包含两端),从这7个空位中任取2个空位安排2班的2位同学有27A 种排法(这样确保2位同学不相邻).满足条件的排列共有362367A A A ··种,即所求概率是3623671010120A A A A =··,故选B. 评注:处理相邻问题和不相邻问题时易采用整体法(确保相邻)和插空法(确保相隔),只是要注意是先整体后插空(相邻与不邻的综合问题)或先排后插(单纯的相隔问题),再就是要注意整体元素的排列顺序问题.2.合理分类直接分步法例6.【2012高考真题陕西理8】两人进行乒乓球比赛,先赢三局着获胜,决出胜负为止,则所有可能出现的情形(各人输赢局次的不同视为不同情形)共有( )A. 10种B.15种C. 20种D. 30种答案:C.解析:首先分类计算假如甲赢,比分3:0是1种情况;比分3:1共有3种情况,分别是前3局中(因为第四局肯定要赢),第一或第二或第三局输,其余局数获胜;比分是3:2共有6种情况,就是说前4局2:2,最后一局获胜,前4局中,用排列方法,从4局中选2局获胜,有6种情况.甲一共就1+3+6=10种情况获胜.所以加上乙获胜情况,共有10+10=20种情况.故选C.评注:合理分类与直接分步是两个基本原理———分类加法计数原理和分步乘法计数原理最直接的体现,是解排列组合问题的最原始的方法.诸多排列组合问题总是从合理分类,直接分步得到解决的.3.顺序一定消序法(用除法)例7. 某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这两个节目插入原节目中,那么不同插法的种数为( ).A.42 B.30 C.20 D.12解析:新插入两个节目,而原来的5个节目顺序不变,从结果考虑,7个节目的全排列是77A ,而顺序不变的5个节目的全排列是55A ,不变的顺序是总体的551A ,则一共有775542A A =种不同的插入种数,故选A .评注:某些元素顺序不变的排列用除法解决,即若共有n 个元素,其中m 个元素顺序不变,则其不同的排列数为.当然本题可以这样考虑:最终有7个节目位置,从7个位置中任选2个位置安排新增节目有27A 种方法,其他5个位置按原5个节目的固定顺序排列,因此共有2742A =种不同的插入方法.4.对象相同隔板法例8. (1)高二年级要从3个班级抽取10人参加数学竞赛,每班至少1人,一共有______种不同的安排方法.(2)(2003年荆州市质检卷Ⅱ)10个相同的小球放到3个不同的盒中,每个盒不空,一共有______种不同的放法.解析:两例的实质一样,属于同一模型———对象相同,这类问题处理方式较多,但隔板法简单易操作:10个相同的小球有9个空档(确保盒子不空).从9个空档中选2个空档放入两块隔板,将小球分成三部分(每一种放档板的放法对应着10个小球分成3部分的分法),每部分一一对应着一个不同的小盒.因此一共有29C 种不同的放法,即2936C =种.而把10个竞赛名额分配给3个班,每班至少1个名额的方法与此一模一样.评注:研究的对象是不加区别的元素时,一般考虑隔板法.这是一个基本的数学模型,由此变形的问题是:10x y z ++=有多少组正整数解?而解法不变.。
高三数学选修2-3_解排列组合问题的四大原则

解排列组合问题的四大原则排列、组合是高中数学的重要内容,新教材中概率与统计的增加更突出了排列、组合的重要性.高考对排列组合的考查以两个基本原理——分类加法计数原理和分步乘法计数原理为出发点,侧重检测解题思想和解题技巧,因而对解题策略和思维模式的培养和提炼是平时训练的核心.下面通过具体的例题来解析排列组合问题的解题策略之“四大原则”.一、特殊优先原则该原则是指在有限制的排列组合问题中优先考虑特殊元素或特殊位置. 例1 (2003年北京市西城区一模题(文))甲、乙、丙三个同学在课余时间负责一个计算机房的周一至周六的值班工作,每天1人值班,每人值班2天,如果甲同学不值周一的班,则可以排出不同的值班表有( )A .90种B .89种C .60种D .59种解析:特殊元素优先考虑,甲同学不值周一的班,则先考虑甲,分步完成:①从除周一的5天中任取2天安排甲有25C 种;②从剩下的4天中选2天安排乙有24C 种;③仅剩2天安排丙有22C 种.由分步乘法计数原理可得一共有22254260C C C =··种,即选C .评注:特殊优先原则是解有限制的排列组合问题的总原则,对有限制的元素和有限制的位置一定要优先考虑.二、先取后排原则该原则充分体现了m m m n m n C A A =·的精神实质,先组合后排列,从而避免了不必要的重复与遗漏.例2 (2004年高考全国卷Ⅲ)将4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有( ).A .12种B .24种C .36种D .48种解析:先分组再排列:将4名教师分成3组有24C 种分法,再将这三组分配到三所学校有33A 种分法,由分步乘法计数原理知一共有234336C A =·种不同分配方案.评注:先取后排原则也是解排列组合问题的总原则,尤其是排列与组合的综合问题.若本例简单分步:先从4名教师中取3名教师分给3所学校有34A 种方法,再将剩下的1名教师分给3所学校有3种选择,则共有34372A =·种分配方案,则有明显重复(如:甲、乙、丙、丁和甲、乙、丁、丙).因此,处理多元素少位置问题时一般采用先取后排原则.三、正难则反原则若从正面直接解决问题有困难时,则考虑事件的对立事件,从不合题意要求的情况入手,再整体排除.例3 (2004年北京市春招卷)在100件产品中有6件次品,现从中任取3件产品,至少取到1件次品的不同取法的种数是( )A .12694C CB .12699C C C .3310094C C -D .3310094A C -解析:从100件次品中取3件产品,至少有1件次品的对立事件是取到3件全部是正品,即从94件正品中取3件正品有394C 种取法,所以满足条件的不同取法是3310094C C -,故选C .如果从正面考虑,则必须分取到1,2,3件次品这三类,没有应用排除法来得简单.而本例最易迷惑人的是B :12699C C ,即从6件次品中取1件确保了至少有1件次品,再从剩下的99件产品中任取2件即可.事实上这样分步并不相互独立,第一步对第二步有明显影响,设次品为ABCDEF ,正品为甲乙丙丁戊…则12699C C 可以是AB甲,也可能是BA甲,因而重复. 评注:正难则反原则也是解决排列组合问题的总原则,如果从正面考虑不易突破,一般寻找反面途径.利用正难则反原则的语境有其规律,如当问题中含有“至少”,“最多”等词语时,易用此原则.四、策略针对原则不同类型的排列、组合问题有着不同的应对策略,不同的限制条件要采用不同的解题方法.1.相邻问题捆绑法(整体法),相隔问题插空法例4 (2004年高考重庆卷(理))某校高三年级举行一次演讲比赛,共有10位同学参赛,其中一班有3位,二班有2位,其他班有5位.若采用抽签的方式确定他们的演讲顺序,则一班的3位同学恰好被安排到一起(演讲序号相连),而2班的2位同学没有被排在一起的概率为( )A .110B .120C .140D .1120解析:10人的全排列数是1010A ,即所有的演讲顺序有1010A 种.符合要求的演讲顺序有两个限制:一班的3位同学相邻,而2班的2位同学不相邻,因此分步完成:①把一班的3位同学看成一个整体,他们自身全排列有33A 种安排;②把这个整体当成1个元素与其他班5个元素一起排列有66A 种安排;③把这6个元素排定后有7个空位(包含两端),从这7个空位中任取2个空位安排2班的2位同学有27A 种排法(这样确保2位同学不相邻).满足条件的排列共有362367A A A ··种,即所求概率是3623671010120A A A A ··,故选B . 评注:处理相邻问题和不相邻问题时易采用整体法(确保相邻)和插空法(确保相隔),只是要注意是先整体后插空(相邻与不邻的综合问题)或先排后插(单纯的相隔问题),再就是要注意整体元素的排列顺序问题.2.合理分类直接分步法例5 (2004年高考全国卷Ⅱ)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有( )个. ( )A .56B .57C .58D .60解析:所有大于23145且小于43521的数由以下几类构成:由分类加法计数原理可得,一共有234322343212222158A A A A A ++++++=个,故选C .评注:合理分类与直接分步是两个基本原理———分类加法计数原理和分步乘法计数原理最直接的体现,是解排列组合问题的最原始的方法.诸多排列组合问题总是从合理分类,直接分步得到解决的.3.顺序一定消序法(用除法)例6 (2003年北京市春招卷)某班新年联欢会原定的5个节目已排成节目单,开演前又增加了两个新节目,如果将这两个节目插入原节目中,那么不同插法的种数为( ).A .42B .30C .20D .12解析:新插入两个节目,而原来的5个节目顺序不变,从结果考虑,7个节目的全排列是77A ,而顺序不变的5个节目的全排列是55A ,不变的顺序是总体的551A ,则一共有775542A A =种不同的插入种数,故选A . 评注:某些元素顺序不变的排列用除法解决,即若共有n 个元素,其中m 个元素顺序不变,则其不同的排列数为.当然本题可以这样考虑:最终有7个节目位置,从7个位置中任选2个位置安排新增节目有27A 种方法,其他5个位置按原5个节目的固定顺序排列,因此共有2742A =种不同的插入方法.4.对象相同隔板法例7 (1)(2004年湖北省四校联考卷)高二年级要从3个班级抽取10人参加数学竞赛,每班至少1人,一共有______种不同的安排方法.(2)(2003年荆州市质检卷Ⅱ)10个相同的小球放到3个不同的盒中,每个盒不空,一共有______种不同的放法.解析:两例的实质一样,属于同一模型———对象相同,这类问题处理方式较多,但隔板法简单易操作:10个相同的小球有9个空档(确保盒子不空).从9个空档中选2个空档放入两块隔板,将小球分成三部分(每一种放档板的放法对应着10个小球分成3部分的分法),每部分一一对应着一个不同的小盒.因此一共有29C 种不同的放法,即2936C =种.而把10个竞赛名额分配给3个班,每班至少1个名额的方法与此一模一样.评注:研究的对象是不加区别的元素时,一般考虑隔板法.这是一个基本的数学模型,由此变形的问题是:10++=有多少组正整数解?而解法不变.x y z。
排列组合定位问题优先法

排列组合定位问题优先法排列组合定位问题是一个在数学和计算领域中经常遇到的问题。
它涉及到排列和组合的概念,并在实际应用中具有广泛的应用场景。
排列是指从给定的元素集合中选择若干元素并按照一定的顺序进行排列,而组合是指从给定的元素集合中选择若干元素,不考虑顺序的方式进行组合。
排列组合定位问题是在一定条件下,通过对元素集合进行不同的排列和组合,确定某个特定元素的位置。
这种问题在信息定位、搜索算法和排列组合分析等领域中具有重要应用价值。
了解排列和组合的定义以及排列组合定位问题的背景,有助于读者对本问题的基本概念有所了解,并为后续的内容理解和应用提供基础。
2.基本原理这一部分将详细解释排列组合定位问题的基本原理和解决方法。
我们将讲解排列的计算公式和组合的计算公式,以及如何应用这些公式来解决定位问题。
同时,我们还将提供一些具体的例子和计算步骤,以帮助读者理解和应用这些原理。
3.算法应用在解决排列组合定位问题时,可以使用各种算法。
其中,常用的算法包括回溯算法和动态规划算法等。
这些算法在定位问题中发挥着重要的作用。
回溯算法是一种逐步搜索可能解的算法。
它通过不断尝试各种可能的组合,找到满足条件的解。
在解决排列组合定位问题时,回溯算法可以用于遍历所有可能的位置排列组合,从而找到最优解。
动态规划算法是一种将大问题划分为小问题并逐步解决的算法。
它通过对子问题的解进行保存和重复利用,提高了算法的效率。
在解决排列组合定位问题时,动态规划算法可以用于计算每个位置对应的最优解,并逐步递推得到整个问题的最优解。
通过编程实现这些算法可以更有效地解决排列组合定位问题。
可以使用编程语言编写相应的代码,并提供一些示例来说明算法的具体实现。
在讨论算法的同时,还需要考虑算法的时间复杂度和空间复杂度。
时间复杂度可以用来评估算法的执行时间,而空间复杂度可以用来评估算法所需的额外空间。
通过对算法的复杂度进行分析,可以选择合适的算法来解决定位问题,并进行进一步的优化。
人教版高中数学选修(2-3)-1.3解排列组合问题的四大原则

解排列组合问题的四大原则排列、组合是高中数学的重要内容,新教材中概率与统计的增加更突出了排列、组合的重要性.高考对排列组合的考查以两个基本原理——分类加法计数原理和分步乘法计数原理为出发点,侧重检测解题思想和解题技巧,因而对解题策略和思维模式的培养和提炼是平时训练的核心.下面通过具体的例题来解析排列组合问题的解题策略之“四大原则”. 一、特殊优先原则该原则是指在有限制的排列组合问题中优先考虑特殊元素或特殊位置. 例1 (2003年北京市西城区一模题(文))甲、乙、丙三个同学在课余时间负责一个计算机房的周一至周六的值班工作,每天1人值班,每人值班2天,如果甲同学不值周一的班,则可以排出不同的值班表有( ) A .90种 B .89种 C .60种 D .59种解析:特殊元素优先考虑,甲同学不值周一的班,则先考虑甲,分步完成:①从除周一的5天中任取2天安排甲有25C 种;②从剩下的4天中选2天安排乙有24C 种;③仅剩2天安排丙有22C 种.由分步乘法计数原理可得一共有22254260C C C =··种,即选C .评注:特殊优先原则是解有限制的排列组合问题的总原则,对有限制的元素和有限制的位置一定要优先考虑. 二、先取后排原则该原则充分体现了m m mn m n C A A =·的精神实质,先组合后排列,从而避免了不必要的重复与遗漏.例2 (2004年高考全国卷Ⅲ)将4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有( ). A .12种 B .24种 C .36种 D .48种解析:先分组再排列:将4名教师分成3组有24C 种分法,再将这三组分配到三所学校有33A 种分法,由分步乘法计数原理知一共有234336C A =·种不同分配方案.评注:先取后排原则也是解排列组合问题的总原则,尤其是排列与组合的综合问题.若本例简单分步:先从4名教师中取3名教师分给3所学校有34A 种方法,再将剩下的1名教师分给3所学校有3种选择,则共有34372A =·种分配方案,则有明显重复(如:甲、乙、丙、丁和甲、乙、丁、丙).因此,处理多元素少位置问题时一般采用先取后排原则. 三、正难则反原则若从正面直接解决问题有困难时,则考虑事件的对立事件,从不合题意要求的情况入手,再整体排除.例3 (2004年北京市春招卷)在100件产品中有6件次品,现从中任取3件产品,至少取到1件次品的不同取法的种数是( )A .12694C C B .12699C CC .3310094C C - D .3310094A C -解析:从100件次品中取3件产品,至少有1件次品的对立事件是取到3件全部是正品,即从94件正品中取3件正品有394C 种取法,所以满足条件的不同取法是3310094C C -,故选C .如果从正面考虑,则必须分取到1,2,3件次品这三类,没有应用排除法来得简单.而本例最易迷惑人的是B :12699C C ,即从6件次品中取1件确保了至少有1件次品,再从剩下的99件产品中任取2件即可.事实上这样分步并不相互独立,第一步对第二步有明显影响,设次品为ABCDEF ,正品为甲乙丙丁戊…则12699C C 可以是AB甲,也可能是BA甲,因而重复. 评注:正难则反原则也是解决排列组合问题的总原则,如果从正面考虑不易突破,一般寻找反面途径.利用正难则反原则的语境有其规律,如当问题中含有“至少”,“最多”等词语时,易用此原则. 四、策略针对原则不同类型的排列、组合问题有着不同的应对策略,不同的限制条件要采用不同的解题方法.1.相邻问题捆绑法(整体法),相隔问题插空法例4 (2004年高考重庆卷(理))某校高三年级举行一次演讲比赛,共有。
选择排序解题思路

选择排序解题思路
选择排序是一种简单直观的排序算法,其基本思想是每次从待排序的数据中选择最小(或最大)的元素,放到已排序序列的末尾,直到全部待排序的数据元素排完为止。
具体的解题步骤如下:
1. 设立一个标志位,标记当前要排序的元素的位置;
2. 从当前标志位开始,通过遍历待排序序列,找到最小(或最大)的元素;
3. 将找到的最小(或最大)元素与当前标志位的元素进行交换;
4. 更新标志位,将其后移一位;
5. 重复2-4步骤,直到标志位为最后一个元素。
通过不断选择最小(或最大)元素并交换的方式,将待排序序列分为已排序和未排序的部分,最终实现整个序列的有序。
选择排序的时间复杂度为O(n^2),其中n为待排序序列的长度。
有序和无序排列组合公式

有序和无序排列组合公式好的,以下是为您生成的关于“有序和无序排列组合公式”的文章:咱先来说说啥是有序和无序排列组合公式哈。
打个比方,你去超市买水果,苹果、香蕉、橙子摆在那,你要是规定了先拿苹果再拿香蕉最后拿橙子,这就是有序;要是不管顺序,随便拿,这就是无序。
咱先瞅瞅有序排列,也就是排列公式。
比如说从 5 个不同的东西里选 3 个,按照一定顺序排好,这就可以用排列公式 A(5, 3) 来算。
就像学校组织活动,选 3 个同学分别当主持人、表演节目和后勤服务,这就得考虑顺序,谁先谁后作用可不一样。
再讲讲无序组合,也就是组合公式。
还是那 5 个东西,这次不考虑顺序,只要选出 3 个就行,那就用组合公式 C(5, 3) 。
比如说选 3 个人参加知识竞赛,不管谁在前谁在后,只要选出来就行。
我记得之前给学生讲这个的时候,有个小同学特别可爱。
他瞪着大眼睛问我:“老师,这和我搭积木有啥关系?”我笑着跟他说:“你搭积木的时候,要是规定了先放红色的再放蓝色的,这就是有序;要是随便拿随便放,不讲究顺序,那就是无序呀。
”这小家伙一听,好像恍然大悟了。
在生活中,有序和无序排列组合公式的应用可多了去了。
比如你安排假期出去玩,有 5 个景点,你计划 3 天逛完,每天去一个,这就得用有序排列来算算有多少种安排方法。
要是你只是想挑 3 个景点去,不管先后顺序,那就是无序组合的问题啦。
还有啊,咱过年包饺子,准备了 3 种馅,韭菜鸡蛋、猪肉大葱和虾仁三鲜。
要是规定了第一顿吃韭菜鸡蛋的,第二顿吃猪肉大葱的,第三顿吃虾仁三鲜的,这就是有序;要是不管顺序,反正这三顿就吃这三种馅,这就是无序组合。
再比如说抽奖,从 10 个号码里抽 3 个中奖号码,这就不管顺序,是无序组合。
但要是颁奖,先颁三等奖,再颁二等奖,最后颁一等奖,这就得考虑顺序,是有序排列。
所以说,这有序和无序排列组合公式啊,就藏在咱们生活的角角落落里,等着咱们去发现,去用它们解决问题。
位序计分法公式

位序计分法公式位序计分法的基本原理是将问题或选项按照重要程度进行排序,然后为每个选项分配一个权重,最后根据权重的加权和来评估每个选项的得分。
具体的计算公式如下所示:得分= Σ(权重× 位序)其中,Σ表示对所有选项进行求和,权重表示每个选项的重要程度,位序表示每个选项的排列顺序。
通过这个公式,我们可以将不同的选项按照其重要程度进行评估,并得到一个客观的得分。
位序计分法的应用非常广泛。
在教育领域,老师可以利用该方法对学生的作业或考试成绩进行评估。
通过设定权重,老师可以更加客观地评判每个学生的表现。
在体育比赛中,裁判员可以根据选手的表现以及对比选手的重要程度,给予不同的评分,从而产生公正的比赛结果。
在市场调研中,位序计分法也被广泛使用。
调研人员可以将不同的产品或服务按照其重要程度排序,并为每个选项赋予相应的权重。
通过对受访者进行问卷调查或实地观察,可以得到不同选项的位序,最终得出每个选项的得分。
这样一来,市场调研人员可以更加客观地评估不同产品或服务的市场潜力。
除了上述领域,位序计分法还可以应用于各种决策问题。
例如,在招聘过程中,雇主可以根据求职者的不同技能和经验,为每个求职者的技能和经验分配不同的权重,并根据位序计分法得到最终的评分。
这样一来,雇主可以更加客观地评估每个求职者的能力和适应性。
在使用位序计分法时,我们需要注意一些问题。
首先,我们需要明确每个选项的位序,确保在计算时不会出现混淆或错误。
其次,我们需要合理地设定权重,确保每个选项的重要程度得到准确的体现。
最后,我们需要对得分结果进行合理解读,不仅仅看得分的大小,还要考虑不同选项之间的差异以及权重的设置是否合理。
位序计分法是一种常用的评估方法,它通过给不同的选项赋予不同的权重,并根据位序计算得分,从而评估每个选项的重要程度。
该方法在教育、体育、市场调研等领域得到广泛应用,并可以帮助我们做出更加客观和准确的决策。
在使用该方法时,我们需要注意位序的设置、权重的设定以及得分结果的合理解读。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选择排序原理证明及Java实现
简单介绍
选择排序是较为简单的排序算法之一,它的原理就是每次把剩余元素中最小的那个挑选出来放在这些剩余元素的首位置,举个栗子:
长度为5的一个数组:3,0,-5,1,8
第一次选择后: -5,0,3,1,8
第二次选择后: -5,0,3,1,8
第三次选择后: -5,0,1,3,8
第四次选择后: -5,0,1,3,8
最后一次选择: -5,0,1,3,8
注:标记红色字体的为发生交换的元素,下划线标记的为剩余元素
简单证明
设数组a共有N个元素,对其进行选择排序:
第一次选择将最小元素放在的位置,即此刻最小
第二次选择将上一步操作后的剩余元素中的最小元素放在?的位置,因此必然小于等于,由于此刻的是从上一步操作后的剩余元素中选出的,必然也大于等于
同理,共经过N次选择后:
Java代码实现
public class SelectionSort {
public static void sort(Comparable[] a){ --排序操作
int min,i,j;
for (i=0;i=a.length-1;i++){ --从头到尾选择length次
for (j=i+1;j=a.length-1;j++){
if (isLess(a[j],a[min]))
} --采用打擂原理获取最小值的索引
exchange(a,i,min);
public static boolean isLess(Comparable x,Comparable y){ return pareTo(y)0;
} --判断x是否小于y
public static void exchange(Comparable[] a,int i,int j){ --交换数组a中索引i和j所指的元素的值
Comparable t=a[i];
a[i]=a[j];
public static boolean isOrdered(Comparable[] a){ --判断数组是否有序
for (int i=0;i=a.length-2;i++){
if (a[i].compareTo(a[i+1])=0)
continue;
return false;
return true;
public static void show(Comparable[] a){ --打印数组
for (int i=0;i=a.length-2;i++){
System.out.print(a[i]+" ");
System.out.println(a[a.length-1]);
import java.util.Scanner;
import java.util.Random;
public class SelectionSortTest {
public static void main(String[] args){
Scanner sb=new Scanner(System.in);
int length;
int choice;
System.out.println("请输入数组元素的个数:");
length=sb.nextInt();
Integer[] a=new Integer[length]; --任意实现Comparable接口的数组皆可为参数,这里以Integer型数组为例
System.out.println("请选择创建数组的方式:1.手动 2.自动");
choice=sb.nextInt();
if (choice==1)
for (int i=0;i=a.length-1;i++){
a[i]=new Integer(sb.nextInt());
Random r=new Random();
for (int i=0;i=a.length-1;i++){
a[i]=new Integer(r.nextInt(length*length)); --随机生成[0,length*length)范围内一个整数
} --并初始化一个Integer对象
SelectionSort.sort(a);
System.out.println("数组是否有序:"+SelectionSort.isOrdered(a));
System.out.println("是否打印数组:1.是 2.否");
choice=sb.nextInt();
if (choice==1)
SelectionSort.show(a);
sb.close();
请输入数组元素的个数:
请选择创建数组的方式:1.手动 2.自动
数组是否有序:true
是否打印数组:1.是 2.否
19 23 47 68 72 99 130 206 248 326 326 338 338 365 403 417 461 466 517 541 555 593 625 626 704 806 833 849 871 873 Process finished with exit code 0
效率分析
通过查看代码我们可以精确地得到,0到N-1(length-1)的任意i都会进行一次交换和N-1-i次比较,因此共有N次交换以及
(N-1)+(N-2)+.+2+1=N(N-1)-2次比较。
算法的时间复杂度为。
用的IDE是IntelliJ IDEA
2? for i ------ length[A] - 1 downto 1
int *parent = new int[size];--父结点子针?
public static void main(String[] args) {
[2] Thomas H.Cormnen ,Charles E.Lesersion et.al .Introduction to Algorithms second Edition.
Scanner sb=new Scanner(System.in);
print(bubbleSort([1, 3, 1, 4, 5, 2, 0]))
for(int i=n-2;i=0;--i){--从第[n-2]个记录开始进行筛选建堆
for (int i = 0; i a.length-1; i++)
swap(array[minpos], array[left]);
实际上当没有数据交换的时候,序列就是完全有序的了,此时我们也可以认为排序已经完成,不用在继续执行后面的冒泡操作了。
