用样本估计总体练习题
高一数学用样本估计总体试题

高一数学用样本估计总体试题1.一个样本的方差是.【答案】5【解析】由样本可得,所以平均数为4;所以样本的方差为.【考点】样本数值特征.2.在一次选拔运动员中,测得7名选手的身高(单位:cm)的茎叶图为:,记录的平均身高为177 cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为.【答案】8【解析】由茎叶图可知:7名选手的身高分别为170、173、170+x、178、179、180、181,所以由此可得,所以x=8.【考点】茎叶图.3.在一次选拔运动员中,测得7名选手的身高(单位:cm)的茎叶图为:,记录的平均身高为177 cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为.【答案】8【解析】由茎叶图可知:7名选手的身高分别为170、173、170+x、178、179、180、181,所以由此可得,所以x=8.【考点】茎叶图.4.设的平均数是,标准差是,则另一组数的平均数和标准差分别是_________.【答案】,.【解析】另一组数的平均数为:,标准差为:,所以则另一组数的平均数和标准差分别是,.【考点】统计中的期望与方差.5.为了了解某校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,第1小组的频数为6,则报考飞行员的学生人数是()A.36B.40C.48D.50【答案】C【解析】设报考飞行员的人数为,根据前3个小组的频率之比为,可设前三小组的频率分别为;由题意可知所求频率和为1,即,解得,则,解得.故选C.【考点】频率分布直方图.6.200辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,则时速在[60,70)的汽车大约()A.30辆B.40辆C.60辆D.80辆【答案】D【解析】时速在[60,70)的频率为,故汽车大约有辆.【考点】频率分布直方图的应用.7.某同学使用计算器求30个数据的平均数时,错将其中一个数据105输人为15,那么由此求出的平均数与实际平均数的差是( ).A.3.5B.-3C.3D.-0.5【答案】B【解析】数据相差了,平均数相差,故求出的平均数与实际平均数相差.【考点】平均数.8.某教师出了一份三道题的测试卷,每道题1分,全班得3分、2分、1分和0分的学生所占比例分别为30%、50%、10%和10%,则全班学生的平均分为分.【答案】2【解析】设班级总人数为n人,得3分的是人,得2分的是人,得1分的是人,得0分的是人,故班级平均分.【考点】数据的平均数公式及数据的基本处理能力.9.若样本的频率分布直方图中一共有个小矩形,中间一个小矩形的面积等于其余个小矩形面积和的,且样本容量为160,则中间一组的频数是()A.32B.20C.40D.25【答案】A【解析】设中间一个小矩形的面积为,其余个小矩形的面积之和为,依题意有,求解得到,所以中间一组的频率为,中间一组的频数为,故选A.【考点】频率分布直方图.10.200辆汽车通过某一段公路时,时速的频率分布直方图如右图所示,则时速在[50,70)的汽车大约有().A.60辆 B.80辆C.70辆D.140辆【答案】D【解析】需根据直方图中求出各个矩形的面积,即为各组频率,再由总数乘以频率即得各组频数.解:由直方图可知,时速在[50,60]的频率为0.03×10=0.3 时速在[60,70]的频率为0.04×10=0.4 所以时速在[50,70]的汽车大约有200×(0.3+0.4)=140辆.故答案为D.【考点】直方图点评:本题考查频率分布直方图的相关知识.直方图中的各个矩形的面积代表了频率,所以各个矩形面积之和为1.11.某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:,,,,.(1)求图中的值;(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;(3)若这100名学生语文成绩某些分数段的人数()与数学成绩相应分数段的人数()之比如下表所示,求数学成绩在之外的人数.分数段【答案】(1).(2)73.(3)10【解析】(1)依题意得,,解得.(2)这100名学生语文成绩的平均分为:(分).(3)数学成绩在的人数为:,数学成绩在的人数为:,数学成绩在的人数为:,数学成绩在的人数为:.所以数学成绩在之外的人数为:.【考点】本题考查了频率分布直方图的运用点评:注意频率分布直方图中用小长方形面积的大小来表示在各个区间内取值的频率,所以在求频率时,通过已知求出所要区间的面积即可12.为了让学生了解更多“社会法律”知识,某中学举行了一次“社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为000,001,002,…,799,试写出第二组第一位学生的编号;(2)填充频率分布表的空格①②③④并作出频率分布直方图;(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?【答案】(1)016 ;(2) 1 8 2 0.28 3 14 4 0.20;(3)256.【解析】(1)编号为016- -2分(2) 1 8 2 0.28 3 14 4 0.20- 每空1分2分在被抽到的学生中获二奖的人数是9+7=16人, 1分占样本的比例是, 1分所以获二等奖的人数估计为800×32%=256人. 1分答:获二等奖的大约有256人. 1分【考点】系统抽样;频率分布表;频率分布直方图。
用样本估计总体(平均数、中位数、众数)练习

用样本估计总体(平均数、中位数、众数)练习1、某厂10名工人在一个小时内生产零件的个数分别是15,17,14,10,15,17,17,16,14,12,设该组数据的平均数为a,中位数为b,众数为c,则有( )A.a>b>c B.b>c>a C.c>a>b D.c>b>a2、如图所示的茎叶图记录了一组数据,关于这组数据,其中说法正确的序号是________.①众数是9;②平均数是10;③中位数是9或10;④标准差是3.4.3、某次测量中A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A 样本数据每个都加2后所得数据,则A,B两样本的下列数字特征对应相同的是( ) A.众数 B.平均数 C.中位数 D.标准差4、已知一组数据的频率分布直方图如图所示.求众数、中位数、平均数.5、如图所示是一样本的频率分布直方图,则由图形中的数据,可以估计众数与中位数)分别是( )A.12.5、12.5 B.12.5 、13C.13、12.5 D.13、136、从下列频率分布直方图中估计所有中位数与众数之和为元。
7.一个样本a,3,5,7的平均数是b,且a、b是方程x2-5x+4=0的两根,则这个样本的方差是( )A.3 B.4 C.5 D.68.关于统计数据的分析,有以下几个结论:①一组数不可能有两个众数;②将一组数据中的每个数据都减去同一个数后,方差没有变化;③调查剧院中观众观看感受时,从50排(每排人数相同)中任意抽取一排的人进行调查,属于分层抽样;④一组数据的方差一定是正数;⑤如右图是随机抽取的200辆汽车通过某一段公路时的时速分布直方图,根据这个直方图,可以得到时速在[50,60)的汽车大约是60辆.则这5种说法中错误的个数是( )A.2 B.3 C.4 D.59、某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成、绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100].(1)求图中a的值;(2)根据频率分布直方图,估计这100名学生语文成绩的平均分及众数.(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示,求数学成绩在[50,90)之外的人数.10、如图是某市有关部门根据该市干部的月收入情况,画出的样本频率分布直方图,已知图中第一组的频数为4 000,请根据该图提供的信息解答下列问题.(1)求样本中月收入在[2 500,3 500)的人数;(2)为了分析干部的收入与年龄、职业等方面的关系,必须从样本中按月收入用分层抽样方法抽出100人作进一步分析,则月收入在[1 500,2 000)的这组中应抽多少人?(3)试估计样本数据的中位数.答案:1、D 2、①② 3、D 4、众数:65,中位数:65,平均数:67 5、B 6、7400 7、C 8、B 9、(1)0.005(2)73(3)10人 10、(1)2000(2)20人(3)1750元。
28.2《用样本估计总体》综合练习

《用样本估计总体》综合练习◆随堂检测1、某“中学生暑假环保小组”的同学,随机调查了“幸福小区”10户家庭一周内使用环保方便袋的数量,数据如下:(单位:只):6,5,7,8,7,5,8,10,5,9,利用上述数据估计该小区2000户家庭一周内需要环保方便袋约()A.2000只B.14000只C.21000只D.98000只2、在2008年的世界无烟日(5月31日),小华学习小组为了解本地区大约有多少成年人吸烟,随机调查了100个成年人,结果其中有15个成年人吸烟.对于这个数据收集与处理的问题,下列说法正确的是()A.调查的方式是普查B.本地区只有85个成年人不吸烟C.样本是15个吸烟的成年人D.本地区约有15℅的成年人吸烟3、为了解一批节能灯的使用寿命,宜采用的方式进行调查.(填:“全面调查”或“抽样调查”)4、为了了解某所初级中学学生对2008年6月1日起实施的“限塑令”是否知道,从该校全体学生1200名中,随机抽查了80名学生,结果显示有2名学生“不知道”.由此,估计该校全体学生中对“限塑令”约有名学生“不知道”.5、为了了解某市老人的身体健康状况,在以下抽样调查中,你认为样本选择较好的是____________(填序号)①100位女性老人②公园内100位老人③在城市和乡镇选10个点,每个点任选10位老人.◆典例分析为了解某地区30万电视观众对新闻、动画、娱乐三类节目的喜爱情况,根据老年人、成年人、青少年各年龄段实际人口的比例3︰5︰2,随机抽取一定数量的观众进行调查,得到如下统计图.(1)上面所用的调查方法是(填“全面调查”或“抽样调查”);(2)写出折线统计图中A、B所代表的值;A:;B:;(3)求该地区喜爱娱乐类节目的成年人的人数.分析:通过利用扇形统计图计算出各个部分的数量,必须要弄清楚各个部分的百分比即可.解:由题意得:(1)抽样调查(2)A=20, B=40(3)5 300000150000352⨯=++10830%360=15000030%45⨯=◆课下作业●拓展提高1、苏州阳澄湖是全国著名的大闸蟹产地,某养蟹专业户为了估计他承包的蟹塘里有多少只蟹,先捕上100只蟹做上标记,然后放回塘里,过了一段时间,待带标记的蟹和塘里的蟹混合后,再捕上100条,发现其中带标记的蟹有10条,则塘里大约有蟹()A.10B.1000C.100D.100002、在元旦晚会上,班长准备了若干张相同的卡片,上面写的是晚会上同学们要回答的问题.晚会开始后,班长问小明:你能设计一个方案,估计晚会共准备了多少张卡片?小明用20张空白卡片(与写有问题的卡片相同),和全部写有问题的卡片洗匀,从中随机抽取10张,发现有2张空白卡片,马上正确估计出了写。
用样本的数字特征估计总体的数字特征练习

在关于居民月均用水量的例子中,平均数
x 1.973
标准差s=0.868
所以
x s 2.841, x 2s 3.709
x s 1.105, x 2s 0.237.
这 100个 数据 中, 在区 间x
2 s ,x
2 s
0 . 2 3 7 , 3 . 790
外 的 只 有 4 个也。就是说, x
7.如果一组数中每个数减去同一个非零
常数,则这一组数的( D).
A.平均数不变,方差不变 B.平均数改变,方差改变 C.平均数不变,方差改变 D.平均数改变,方差不变
6
频率
频率分布直方图
组距
0.6 前四个小矩形的 面积和=0.49
0.5
0.4
0.25
后四个小矩形的 面积和=0.26
0.3 0.22
均单位面积产量如下(单位:t/hm2),试
根据这组数据估计哪一种水稻品种的产量
比较稳定。
品种 第1年 第2年 第3年 第4年 第5年
甲
9.8
9.9 10.1 10 10.2
乙
9.4 10.3 10.8 9.7
9.8
解:甲品种的样本平均数为10,样本方差 为 [(9.8-10)2 +(9.9-10)2+(10.1-10)2+ (10-10)2+(10.2-10)2]÷5=0.02.
一个社会调查机构就某地居民的月收入调 查了10000人,并根据所得数据画了样本的 频率分布直方图如图所示,根据样本估计 月收入的平均数为 2400 ,众数为2500 中位数为 2400
练习:”八.一”前夕,某中学举行国防知识竞赛:满分为 100分,80分以上为优秀,现将高一的两个班参赛学生的 成绩进行整理后分成五组绘制成如图所示的频率分布直 方图,已知图中从左到右的第一、第二、第三、第四、 第五小组的频率分别是0.3,0.4,0.15,0.1,0.05
高一数学用样本估计总体试题答案及解析

高一数学用样本估计总体试题答案及解析1.从某小学随机抽取100名学生,将他们的身高(单位:厘米)数据绘制成频率分布直方图(如图).若要从身高在[120,130),[130,140),[140,150]三组内的学生中,用分层抽样的方法选取20人参加一项活动,则从身高在[120,130内的学生中选取的人数应为.【答案】10【解析】由频率分布直方图可得:;则[120,130),[130,140),[140,150]三组人数所占的比例为,则在[120,130内选取的人数应为.【考点】频率分布直方图.2.设的平均数是,标准差是,则另一组数的平均数和标准差分别是_________.【答案】,.【解析】另一组数的平均数为:,标准差为:,所以则另一组数的平均数和标准差分别是,.【考点】统计中的期望与方差.3.200辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,则时速在[60,70)的汽车大约( )A.30辆B.40辆C.60辆D.80辆【答案】D【解析】时速在[60,70)的频率为,故汽车大约有辆.【考点】频率分布直方图的应用.4.某校五四演讲比赛中,七位评委为一选手打出的分数如下:90 86 90 97 93 94 93去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为()A.B.C.D.【答案】B【解析】由题意知,去掉一个最高分和一个最低分后,所剩数据的平均数为;方差为故选B.【考点】样本平均数和方差的计算.5.统计某校800名学生的数学期末成绩,得到频率分布直方图如图所示,若考试采用100分制,并规定不低于60分为及格,则及格率为.【答案】0.8【解析】由图形可知及格率为,答案为0.8.【考点】频率分布直方图6.甲、乙、丙、丁四人参加某运动会射击项目选拔赛,四人的平均成绩和方差如下表所示:甲乙丙丁从这四个人中选择一人参加该运动会射击项目比赛,最佳人选是( ).A.甲B.乙C.丙D.丁【答案】C.【解析】分析表格可知,乙与丙的平均环数最多,又丙的方差比乙小说明丙成绩发挥的较为稳定,所以最佳人选为丙.【考点】数据的平均数与方差的意义.7.一次选拔运动中,测得7名选手的身高(单位:cm)分布茎叶图如图,记录的平均身高为177cm,有一名候选人的身高记录不清楚,其末位数记为x,那么x的值为( )A.5B.6C.7D.8【答案】D【解析】由图可知7名同学的身高分别为180、181、170、173、,178、179而7名同学的平均身高为177,所以有得=178,所以【考点】茎叶图8.由正整数组成的一组数据,其平均数和中位数都是,且标准差等于,则这组数据为 .(从小到大排列)【答案】【解析】由已知不妨假设,则,又因为标准差等于,所以,且都是正整数,观察分析可知这组数据只可为:1,1,3,3.【考点】1.平均数与中位数;2.标准差;3.方程组思想.9.某路段属于限速路段,规定通过该路段的汽车时速不得超过70km/h,否则视为违规扣分,某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车运行时速的频率分布直方图,如下图所示,则违规扣分的汽车大约为辆.【答案】120.【解析】易求得70-80这组的频率为1-0.05-0.18-0.38-0.27=0.12,则违规扣分的汽车大约为辆.【考点】频率分布直方图中每组对应的长方形面积为,总面积为1,频数=频率样本容量.10.对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:(1)[25,30)年龄组对应小矩形的高度为________;(2)据此估计该市“四城同创”活动中志愿者年龄在[25,35)的人数为________.【答案】0.04;440【解析】由频率分布直方图得:,解得;志愿者年龄在[25,35)的人数为.【考点】概率与统计.11.将某选手的7个得分去掉1个最高分,去掉1个最低分,剩余5个得分的平均分为91,现场做的7个得分的茎叶图(如图)后来有一个数据模糊,无法辨认,在图中用表示,则x的值为( )A.0B.4C.5D.7【答案】A【解析】如果是最高得分的话,,所以是最大值,那么,解得,故选A.【考点】茎叶图12.某老师从星期一到星期五收到的信件数分别为10,6,8,5,6,则该组数据的方差______.【答案】3.2【解析】由平均数及方差的定义可得;.【考点】样本数据的数字特征:平均值与方差.13.在育民中学举行的电脑知识竞赛中,将九年级两个班参赛的学生成绩(得分均为整数)进行整理后分成五组,绘制如图所示的频率分布直方图.已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.30,0.15,0.10,0.05,第二小组的频数是40.(1)求第二小组的频率,并补全这个频率分布直方图;(2)求这两个班参赛的学生人数是多少;(3)这两个班参赛学生的成绩的中位数应落在第几小组内.【答案】(1)第二小组的频率为,补全的频率分布直方图详见解析;(2)100人;(3)九年级两个班参赛学生的成绩的中位数应落在第二小组内.【解析】(1)先从所给的直方图中得出第一、三、四、五小组的频率,然后用1减去第一、三、四、五小组的频率和得到第二小组的频率,接着由确定第二小组的小长方形的高,从而可补全频率分布直方图;(2)用第二小组的频数除以该组的频率,即可计算出九年两个班参赛学生的总人数;(3)要确定中位数所在的小组,只需先确定各小组的频数,从第一小组开始累加,当和达到总人数的一半时的组就是中位数所在的小组.试题解析:(1)∵各小组的频率之和为1.00,第一、三、四、五小组的频率分别是0.30,0.15,0.10,0.05∴第二小组的频率为:∴落在59.5~69.5的第二小组的小长方形的高,则补全的频率分布直方图如图所示(2)设九年级两个班参赛的学生人数为人∵第二小组的频数为40人,频率为0.40∴,解得所以这两个班参赛的学生人数为100人(3)因为0.3×100=30,0.4×100=40,0.15×100=15,0.10×100=10,0.05×100=5即第一、第二、第三、第四、第五小组的频数分别为30,40,15,10,5所以九年级两个班参赛学生的成绩的中位数应落在第二小组内【考点】1.频率分布直方图;2.转化与运算能力.14.在样本的频率分布直方图中, 共有9个小长方形, 若第一个长方形的面积为0.02, 前五个与后五个长方形的面积分别成等差数列且公差互为相反数,若样本容量为160, 则中间一组(即第五组)的频数为()A.12B.24C.36D.48【答案】C【解析】设公差为d,那么9个小长方形的面积分别为0.02,0.02+d,0.02+2d,0.02+3d,0.02+4d,0.02+3d,0.02+2d,0.02+d,0.02,而9个小长方形的面积和为 1,可得0.18+16d=1 可以求得d=∴中间一组的频数为:160×(0.02+4d)=36.故答案为:36.故选C。
5_1_4_用样本估计总体练习(原卷版)

5.1.4用样本估计总体【基础练习】一、单选题1.从某小区抽取100户居民进行月用电量调查,发现其月用电量都在50至350度之间,频率分布直方图如图所示,则这100户居民月用电量的中位数大约为()A.150B.177.8C.183.3D.2002.如图,这是某校高三年级甲、乙两班在上学期的5次数学测试的班级平均分的茎叶图,则下列说法不正确的是()A.甲班的数学成绩平均分的平均水平高于乙班B.甲班的数学成绩的平均分比乙班稳定C.甲班的数学成绩平均分的中位数高于乙班D.甲、乙两班这5次数学测试的总平均分是1033.有4万个不小于70的两位数,从中随机抽取了3000个数据,统计如下:请根据表格中的信息,估计这4万个数据的平均数为()A.92.16B.85.23C.84.73D.77.974.如图是某学校的教研处根据调查结果绘制的本校学生每天放学后的自学时间情况的频率分布直方图:根据频率分布直方图,求出自学时间的中位数和众数的估计值(精确到0.01)分别是()A .2.20,2.25B .2.29,2.20C .2.29,2.25D .2.25,2.255.某歌手大赛进行电视直播,比赛现场有6名特约嘉宾给每位参赛选手评分,场内外的观众可以通过网络平台给每位参赛选手评分.某选手参加比赛后,现场嘉宾的评分情况如下表,场内外共有数万名观众参与了评分,组织方将观众评分按照[)70,80,[)80,90,[]90,100分组,绘成频率分布直方图如下:嘉宾评分的平均数为1x ,场内外的观众评分的平均数为2x ,所有嘉宾与场内外的观众评分的平均数为x ,则下列选项正确的是( ) A .122x x x +=B .122x x x +>C .122x x x +<D .12122x x x x x +>>>二、填空题6.解放战争中,国民党军队拥有过多辆各型坦克,编成了1个装甲兵团(师级编制).我军为了知道这个装甲兵团的各型坦克的数量,釆用了两种方法:一种是传统的情报窃取,一种是用统计学的方法进行估计.统计学的方法最后被证实比传统的情报收集更精确.这个装甲兵团对各型坦克从1开始进行了连续编号,在解放战争期间我军把缴获的这些坦克的编号进行记录并计算出这些编号的平均值为112.5,假设缴获的坦克代表了所有坦克的一个随机样本,则利用你所学过的统计知识估计这个装甲兵团的各型坦克的数量大约有_______.7.为了解某市居民用水情况,通过抽样,获得了100位居民某年的月均用水量(单位:吨),将该数据按照[0,0.5),[0.5,1),…[4.4.5]分成9组,绘制了如图所示的频率分布直方图,政府要试行居民用水定额管理,制定了一个用水量标准a,使85%的居民用水量不超过a(假设a为整数),按平价收水费,超出a的部分按议价收费,则a的最小值为_____.8.我国高铁发展迅速,技术先进,经统计在经停某站的高铁列车,有10个车次的正点率为0.97,有20个车次的正点率为0.99,有10个车次的正点率为0.98,则经停该站高铁列车的所有车次的平均正点率估计值为______.三、解答题9.某工厂为生产一种标准长度为40cm的精密器件,研发了一台生产该精密器件的车床,该精密器件的实际长度为acm,“长度误差”为40a cm,只要“长度误差”不超过0.03cm就认为合格.已知这台车床分昼、夜两个独立批次生产,每天每批次各生产1000件.已知每件产品的成本为5元,每件合格品的利润为10元.在昼、夜两个批次生产的产品中分别随机抽取20件,检测其长度并绘制了如下茎叶图:(1)分别估计在昼、夜两个批次的产品中随机抽取一件产品为合格品的概率;(2)以上述样本的频率作为概率,求这台车床一天的总利润的平均值.10.《中华人民共和国个人所得税法》规定,公民月收入总额(工资、薪金等)不超过免征额的部分不必纳税,超过免征额的部分为全月应纳税所得额,个人所得税税款按税率表分段累计计算.为了给公民合理减负,稳步提升公民的收入水平,自2018年10月1日起,个人所得税免征额和税率进行了调整,调整前后的个人所得税税率表如下:(1)已知小李2018年9月份上交的税费是295元,10月份工资、薪金等税前收入与9月份相同,请帮小李计算一下税率调整后小李10月份的税后实际收入是多少?(2)某税务部门在小李所在公司利用分层抽样方法抽取某月100位不同层次员工的税前收入,并制成下面的频率分布直方图.(i)请根据频率分布直方图估计该公司员工税前收入的中位数;(ii)同一组中的数据以这组数据所在区间中点的值作代表,按调整后税率表,试估计小李所在的公司员工该月平均纳税多少元?【提升练习】1.某校为了解高二年级学生某次数学考试成绩的分布情况,从该年级的1120名学生中随机抽取了100 名学生的数学成绩,发现都在[80,150]内现将这100名学生的成绩按照 [80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组后,得到的频率 分布直方图如图所示则下列说法正确的是( )A .频率分布直方图中a 的值为 0.040B .样本数据低于130分的频率为 0.3C .总体的中位数(保留1位小数)估计为123.3分D .总体分布在[90,100)的频数一定不总体分布在[100,110)的频数相等2.学校为了解新课程标准提升阅读要求对学生阅读兴趣的影响情况,随机抽取了100名学生进行调查.根据调查结果绘制学生周末阅读时间的频率分布直方图如图所示:将阅读时间不低于30分钟的观众称为“阅读霸”,则下列命题正确的是( ) A .抽样表明,该校有一半学生为阅读霸 B .该校只有50名学生不喜欢阅读 C .该校只有50名学生喜欢阅读 D .抽样表明,该校有50名学生为阅读霸3.某次测试成绩满分是为150分,设n 名学生的得分分别为()12,,,1n i a a a a N i n ∈≤≤,()1150k b k ≤≤为n名学生中得分至少为k 分的人数.记M 为n 名学生的平均成绩,则( )A .12150b b b M n ++= B .12150150b b b M ++=C .12150b b b M n++>D .12150150b b b M ++>4.某赛季甲、乙两名篮球运动员每场比赛得分用茎叶图表示,茎叶图中甲得分的部分数据被墨迹污损不清(如图1),但甲得分的折线图完好(如图2),则下列结论错误的是( )A .乙运动员得分的中位数是17,甲运动员得分的极差是19B .甲运动员发挥的稳定性比乙运动员发挥的稳定性差C .甲运动员得分有12的叶集中在茎1上 D .甲运动员得分的平均值一定比乙运动员得分的平均值低5.学校随机抽查了本校20个学生,调查他们平均每天进行体育锻炼的时间(单位:min ),根据所得数据的茎叶图,以5为组距将数据分为8组,分别是[0,5),[5,10),…,[35,40],作出频率分布直方图如图所示,则原始的茎叶图可能是( )A .B .C .D .6.在一次体育水平测试中,甲、乙两校均有100名学生参加,其中:甲校男生成绩的优秀率为70%,女生成绩的优秀率为50%;乙校男生成绩的优秀率为60%,女生成绩的优秀率为40%.对于此次测试,给出下列三个结论:①甲校学生成绩的优秀率大于乙校学生成绩的优秀率;②甲、乙两校所有男生成绩的优秀率大于甲、乙两校所有女生成绩的优秀率;③甲校学生成绩的优秀率与甲、乙两校所有学生成绩的优秀率的大小关系不确定.其中,所有正确结论的序号是____________.7.为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s 1、s 2、s 3,则它们的大小关系为 .(用“>”连接)8.2020年年初,新冠肺炎疫情袭击全国.口罩成为重要的抗疫物资,为了确保口罩供应,某工厂口罩生产线高速运转,工人加班加点生产.设该工厂连续5天生产的口罩数依次为1x ,2x ,3x ,4x ,5x (单位:十万只),若这组数据1x ,2x ,3x ,4x ,5x 的方差为1.44,且21x ,22x ,23x ,24x ,25x 的平均数为4,则该工厂这5天平均每天生产口罩__________十万只.9.某市约有20万住户,为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值a ,若某住户某月用电量不超过a 度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过a 度,则超出部分按议价b (单位:元/度)计费,未超出部分按平价计费.为确定a 的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).(1)若该市计划让全市70%的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值a;(2)在(1)的条件下,假定出台“阶梯电价”之后,月用电量未达a度的住户用电量保持不变;月用电量超过a度的住户节省“超出部分”的60%,试估计全市每月节约的电量.10.某校的3000名高三学生参加了天一大联考,为了分析此次联考数学学科的情况,现随机从中抽取15名学生的数学成绩(满分:150分),并绘制成如图所示的茎叶图.将成绩低于90分的称为“不及格”,不低于120分的称为“优秀”,其余的称为“良好”.根据样本的数字特征估计总体的情况.(1)估算此次联考该校高三学生的数学学科的平均成绩.(2)估算此次联考该校高三学生数学成绩“不及格”和“优秀”的人数各是多少.(3)在国家扶贫政策的倡导下,该地教育部门提出了教育扶贫活动,要求对此次数学成绩“不及格”的学生分两期进行学业辅导:一期由优秀学生进行一对一帮扶辅导,二期由老师进行集中辅导.根据实践总结,优秀学生进行一对一辅导的转化率为20%;老师集中辅导的转化率为30%,试估算经过两期辅导后,该校高三学生中数学成绩仍然不及格的人数.注:转化率=-辅导前不及格人数辅导后不及格人数辅导前不及格人数100%⨯。
高中数学必修第二册用样本估计总体练习题(平均数、方差、众数、百分位数等)
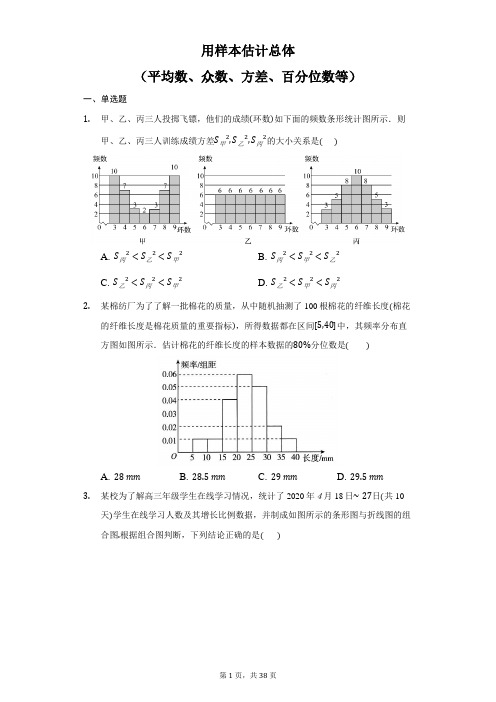
用样本估计总体(平均数、众数、方差、百分位数等)一、单选题1.甲、乙、丙三人投掷飞镖,他们的成绩(环数)如下面的频数条形统计图所示.则甲、乙、丙三人训练成绩方差S甲2,S乙2,S丙2的大小关系是()A. S丙2<S乙2<S甲2B. S丙2<S甲2<S乙2C. S乙2<S丙2<S甲2D. S乙2<S甲2<S丙22.某棉纺厂为了了解一批棉花的质量,从中随机抽测了100根棉花的纤维长度(棉花的纤维长度是棉花质量的重要指标),所得数据都在区间[5,40]中,其频率分布直方图如图所示.估计棉花的纤维长度的样本数据的80%分位数是()A. 28mmB. 28.5mmC. 29mmD. 29.5mm3.某校为了解高三年级学生在线学习情况,统计了2020年4月18日∼27日(共10天)学生在线学习人数及其增长比例数据,并制成如图所示的条形图与折线图的组合图.根据组合图判断,下列结论正确的是()A. 这10天学生在线学习人数的增长比例在逐日减小B. 前5天在线学习人数的方差大于后5天在线学习人数的方差C. 这10天学生在线学习人数在逐日增加D. 前5天在线学习人数增长比例的极差大于后5天在线学习人数增长比例的极差4.下列说法中,正确的是()A. 数据5,4,4,3,5,2的众数是4B. 一组数据的标准差的平方是这组数据的方差C. 数据2,3,4,5的方差是数据4,6,8,10的方差的一半D. 频率分布直方图中各小矩形的面积等于相应各组的频数5.为促进精准扶贫,某县计划引进一批果树树苗免费提供给贫困户种植.为了解果树树苗的生长情况,现从甲、乙两个品种中各随机抽取了100株,进行高度测量,并将高度数据制作成了如图所示的频率分布直方图.由频率分布直方图求得甲、乙两个品种高度的平均值都是66.5,用样本估计总体,则下列描述正确的是()A. 甲品种的平均高度高于乙品种,且乙品种比甲品种长的整齐B. 乙品种的平均高度高于甲品种,且甲品种比乙品种长的整齐C. 甲、乙品种的平均高度差不多,且甲品种比乙品种长的整齐D. 甲、乙品种的平均高度差不多,且乙品种比甲品种长的整齐6.从某中学抽取10名同学,他们的数学成绩如下:82,85,88,90,92,92,92,96,96,98(单位:分),则这10名同学数学成绩的众数、第25百分位数分别为()A. 92,85B. 92,88C. 95,88D. 96,857.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是13,那么另一组数3x1−2,3x2−2,3x3−2,3x4−2,3x5−2的平均数,方差分别是()A. 2,13B. 2,1 C. 4,3 D. 4,238.甲、乙、丙、丁四人参加奥运会射击项目选拔赛,四人的平均成绩和方差如下表所示:甲乙丙丁平均环数x8.68.98.98.2方差s2 3.5 3.5 2.1 5.6从这四人中选择一人参加奥运会射击项目比赛,最佳人选是()A. 甲B. 乙C. 丙D. 丁9.如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为x A和x B,样本标准差分别为s A和s B,则()A. x A>x B,s A>s BB. x A<x B,s A<s BC. x A>x B,s A<s BD. x A<x B,s A>s B10.某工厂的机器上有一种易损元件,这种元件发生损坏时,需要及时维修.现有甲、乙两名工人同时从事这项工作,下表记录了某月1日到10日甲、乙两名工人分别维修这种元件的件数.日期1日2日3日4日5日6日7日8日9日10日甲3546463784乙4745545547由于甲、乙的任务量大,拟增加工人,为使增加工人后平均每人每天维修的元件不超过3件,请利用上表数据估计最少需要增加工人的人数为()A. 2B. 3C. 4D. 5二、多选题(本大题共2小题,共10.0分)11.某赛季甲乙两名篮球运动员各6场比赛得分情况如表:场次123456甲得分31162434189乙得分232132113510则下列说法正确的是()A. 甲运动员得分的极差小于乙运动员得分的极差B. 甲运动员得分的中位数小于乙运动员得分的中位数C. 甲运动员得分的平均值大于乙运动员得分的平均值D. 甲运动员的成绩比乙运动员的成绩稳定12.一组样本数据的频率分布直方图如图所示,每组数据取中间值为代表,则下列说法正确的是()A. 此样本数据的中位数估计值为12B. 此样本数据的众数估计值为12C. 此样本数据的均值估计值为11.52D. 若将样本数据中每个数扩大1倍,则数据的方差也扩大1倍第II卷(非选择题)三、单空题13.200辆汽车通过某一段公路时的时速的频率分布直方图如图所示,则时速的众数、中位数的估计值分别为.14.某学校组织学生参加数学测试,成绩的频率分布直方图如图,数据的分组依次为[20,40),[40,60),[60,80),[80,100],则60分为成绩的第百分位数.15.为了解中学生课外阅读情况,现从某中学随机抽取200名学生,收集了他们一年内的课外阅读量(单位:本)等数据,图是根据数据绘制的统计图表的一部分.下面有四个推断:①这200名学生阅读量的平均数可能是26本;②这200名学生阅读量的75%分位数在区间[30,40)内;③这200名学生中的初中生阅读量的中位数一定在区间[20,30)内;④这200名学生中的初中生阅读量的25%分位数可能在区间[20,30)内.所有合理推断的序号是.四、多空题16.对某市“四城同创”活动中800名志愿者的年龄抽样调查统计后得到频率分布直方图(如图),但是年龄组为[25,30)的数据不慎丢失,则依据此图可得:(1)年龄组[25,30)对应小长方形的高度为;(2)由频率分布直方图估计这800名志愿者年龄的85%分位数为岁.(精确到0.01)五、解答题17.某市为了了解人们对“中国梦”的伟大构想的认知程度,对不同年龄和不同职业的人举办了一次“一带一路”知识竞赛,满分100分(90分及以上为认知程度高),现从参赛者中抽取了x人,按年龄分成5组(第一组:[20,25),第二组:[25,30),第三组:[30,35),第四组:[35,40),第五组:[40,45]),得到如图所示的频率分布直方图,已知第一组有5人.(1)求x;(2)求抽取的x人的年龄的50%分位数(结果保留整数);(3)以下是参赛的10人的成绩:90,96,97,95,92,92,98,88,96,99,求这10人成绩的20%分位数和平均数,以这两个数据为依据,评价参赛人员对“一带一路”的认知程度,并谈谈你的感想.18.某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200千瓦时的部分按0.5元/千瓦时收费,超过200千瓦时但不超过400千瓦时的部分按0.8元/千瓦时收费,超过400千瓦时的部分按1.0元/千瓦时收费.(1)求某户居民用电费用y(单位:元)关于月用电量x(单位:千瓦时)的函数解析式.(2)为了了解居民的用电情况,通过抽样获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图.若这100户居民中,今年1月份用电费用不超过260元的占80%,求a,b的值.(3)根据(2)中求得的数据计算用电量的75%分位数.19.某校研究性学习课题小组为了了解某市工薪阶层的工资水平,从该市工薪阶层中随机调查了50位市民,调查结果如下表.(1)完成下图的月收入频率分布直方图(注意填写纵坐标);(2)估计该市市民月收入的第25和70百分位数.20.起源于汉代的“踢键子”运动,虽有两千多年历史,但由于简便易行,至今仍很流行.某校为丰富课外活动、增强学生体质,在高一年级进行了“踢键子”比赛,以学生每分钟踢毯子的个数记录分值,一个记一分.参赛学生踢键子的分值均在40∼100分之间,从中随机抽取了100个样本学生踢键子的成绩进行统计分析,绘制了如图所示的频率分布直方图,并称得分在80∼90之间为“踢毽健将”,90分以上为“踢建达人”.(1)求样本的平均值x(同一组数据用该区间的中点值代替);(2)求下列数据的四分位数.13,15,12,27,22,24,28,30,31,18,19,20.(3)求上述数据的40百分位数。
23.4 用样本估计总体(习题)

6.(青岛中考)某茶厂用甲、乙两台分装机分装某种茶
叶(每袋茶叶的标准质量为200 g). 为了监控分装质
量,该厂从它们各自分装的茶叶中随机抽取了50袋,
测得它们的实际质量分析如下表:
甲分装机 乙分装机
平均数(g) 200 200
方差 16.23 5.84
则这两台分装机中,分装的茶叶质量更稳定的是 ____乙_____(填“甲”或“乙”).
B.170千克
C.180千克
D.200千克
3.某商场4月份随机抽查了6天的营业额,并由此估算 出该商场4月份的总营业额大约是96万元.已知这6天 的统计数据(单位:万元)前五天的分别是:2.8,3.2, 3.4,3.7,3.0,则第6天的数据是万元__3_.__1__. 4.某地举行了一次数学竞赛,为了估计平均成绩,在 抽取的部分试卷中,有1人得10分,3人得9分,8人得8 分,12人得7分,9人得6分,7人得5分,则样本容量是 40,样本平均数是__6_._8_5_分___.由此估计这次数学竞赛 的平均成绩是_6_._8_5_分__.
14.为了解某一路口某一时段的汽车流量,小明同学 10天中在同一时段统计通过该路口的汽车数量(单位: 辆),将统计结果绘制成如下折线统计图:
由此估计一个月(30天)该时段通过该路口的汽车数量 超过200辆的天数为___1_2___天.
知识点2 用样本方差估计总体方差 5. (东营中考)市运会举行射击比赛,某校射击队从甲 、乙、丙、丁四人中选拔一人参赛,在选拔赛中,每 人射击10次,计算他们10次成绩的平均数(环)及方差 如下表,请你根据表中数据选一人参加比赛,最合适 的人选是____丙_____.
平均数 方差
甲
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23.4 用样本估计总体习题课
1、随机抽样的三种方法是、、
2、在简单随机抽样中,常用的两种办法是、
3、画频率分布直方图的步骤是:
4、茎叶图的两个优点是:
(1)
(2)
课内探究一:用样本的平均数估计总体的平均数
【例1】从一种棉花中各抽测了25根棉花的纤维长度(单位:mm),结果如下:271 273 280 285 285 287 292 294 295 301 303 303 307 308 310 314 319 323 325 325 328 331 334 337 352
计算这25根棉花的纤维的平均长度,并估计这种棉花的纤维的平均长度?
问题一:计算数据的平均数有没有较为简便的方法?
跟踪训练:上图是CBA篮球联赛中,甲乙两名运动员某赛季一些场次得分的茎叶图,则平均得分高的运动员是________.
课内探究二:用样本的标准差估计总体的标准差
【例2】在一次跳远选拔比赛中,甲、乙两名运动员各进行了10次测试,成绩如下:
甲运动员﹕5.85 5.93 6.07 5.91 5.99 6.13 5.89 6.05 6.00 6.19;
乙运动员﹕6.11 6.08 5.83 5.92 5.84 5.81 6.18 6.17 5.85 6.21;
观察上述样本数据,如果你是教练,选哪位选手去参加正式比赛?为什么?
跟踪训练:
1、甲、乙两台机床同时加工直径为100mm的零件,为了检验产品的质量,从产品中各随机抽取6件进行测量,测得数据如下(单位:mm):
甲:99,100,98,100,100,103
乙:99,100,102,99,100,100
(1)分别计算上述两组数据的平均数和方差;
(2)根据(1)的计算结果,说明哪一台机床加工的这种零件更符合要求.
2、某校开展“爱我海西、爱我家乡”摄
影比赛,9位评委为参赛作品A给出的
分数如茎叶图所示.记分员在去掉一个
最高分和一个最低分后,算得平均分为
91.复核员在复核时,发现有一个数字(茎叶图中的x)无法看清.若记分员计算无误,则数字x应该是________.。
