04-4.2 薄壁圆筒的扭转
第四章 扭转(张新占主编 材料力学)

2M A M e M B 0 (2)
联立式(1)与式(2),得
Me MB 3
MA MB Me 3
26
4.6 等直圆轴扭转时的应变能
圆轴在外力偶作用下发生扭转变形,轴内将积蓄应变能。这种 应变能在数值上等于外力所做的功。
T1 在位移 d1上所做的功为 dW T1d1
PB M eB M eC 9549 n 796(N m) PA M eA 9549 1910(N m) n PD M eD 9549 318(N m) n
5
(2)求扭矩(扭矩按正方向假设) 1-1 截面
M M M
x
0
T1 M eB 0
T1 M eB 796N m
d1 85.3 mm
取 d1 85.3 mm。 BC段:同理,由扭转强度条件得 d2 67.4 mm ,由扭转刚度条件得
d 2 74.4 mm
取 d 2 74.4 mm。
23
(2)将轴改为空心圆轴后,根据强度条件和刚度条件确定轴的 外径D。 由强度条件得 D 96.3 mm 由刚度条件得 D 97.3 mm 取 D 97.3 mm ,则内径为
T Me
M e RdA RRd 2R 2
A 0
2
Me 2 2R
8
二、切应力互等定理
M
z
0
(dy)dx ( dx)dy
得到
切应力互等定理:在单元体在相互垂直的一对平面上,切应力 同时存在,数值相等,且都垂直于两个平面的交线,方向共同 指向或共同背离这一交线。 纯剪应力状态:单元体上四个侧面上只有切应力,而无正应力 作用
薄壁圆筒扭转

谢谢观看
对薄壁圆筒施加扭矩,并 记录扭矩值。
将扭矩测量仪连接到薄壁 圆筒上,并调整测量仪的 零点。
在施加扭矩的过程中,观 察薄壁圆筒的变形情况, 并记录下来。
实验结果与数据分析
实验结果
在扭转过程中,薄壁圆筒的扭矩随角度增加而增加,同时薄壁圆筒发生变形。
数据分析
通过对实验数据的分析,可以得出薄壁圆筒的扭矩与角度之间的关系,以及薄 壁圆筒的变形情况。这些数据可以帮助我们了解薄壁圆筒在扭转过程中的力学 性能和行为。
加强筋设计
在圆筒的关键部位增加加强筋,以提高圆筒的刚度和 稳定性。
开孔优化
合理布置圆筒上的开孔,以减小开孔对圆筒强度和稳 定性的影响。
工艺参数优化
热处理工艺
通过优化热处理工艺,改善材料的力学性能和 耐腐蚀性能。
加工工艺
优化圆筒的加工工艺,如焊接、切割、磨削等, 以提高圆筒的精度和表面质量。
装配工艺
薄壁圆筒的稳定性分析
01
薄壁圆筒在受到过大的扭转力矩时,可能会发生失稳现象,如 扭曲变形或破裂。
02
稳定性分析的目的是确定薄壁圆筒在给定的扭转力矩下的临界
失稳应力,以及失稳形态和失稳模态。
稳定性分析的方法包括有限元法、能量法、摄动法等。通过分
03
析,可以确定薄壁圆筒的安全工作范围和设计准则。
03
薄壁圆筒扭转
目录
• 薄壁圆筒扭转的基本概念 • 薄壁圆筒扭转的力学分析 • 薄壁圆筒扭转的实验研究 • 薄壁圆筒扭转的数值模拟 • 薄壁圆筒扭转的优化设计
01
薄壁圆筒扭转的基本概 念
定义与特性
定义
薄壁圆筒扭转是指一个薄壁圆筒受到 扭矩作用而产生的旋转运动。
薄壁圆筒的扭转薄壁圆筒

6.3、等直圆杆在扭转时的应力
实验观察现象 圆周线绕杆轴线相对旋 转了一个角度,大小和 形状均未改变; 圆周线间的距离未变; 纵向线倾斜了一个角度。 满足平面假设 横截面上只有剪应力
剪应力计算
G1G d tg dx dx
此式表达了横截面上任 一处的剪应变随该点在横 截面上的位置而变化的规律。
2 D 2 d 2
(
d ) D
d O
d
D
32 D 4 (1 4 ) 0.1D 4 (1 4 ) 32
(D4 d 4 )
应力分布情况?
确定最大剪应力:
T 知:当 Ip d R , max 2 d T T T 2 max d Wt I I 2
解:①设计杆的外径
Tmax Wt [ ]
D Wt ( 1 4)
3
16
16Tmax D 4 1 ) [ ] (
代入数值得:
1 3
D 0.0226m。
② 由扭转刚度条件校核刚度
Tmax 180 32 40 180 max 1 . 89 9 2 4 4 GIP 80 10 D ( 1 )
③右端面转角为:
T 10 2 40 20x dx 0 dx ( 4 x x2 ) GIP GIP GIP
L 0
2 0
0.033 (弧度)
圆柱形密圈螺旋弹簧的应力计算 T Q
=
Q
+
T
T
P
近似值:
PD P d 8DP 2 3 2 1 3 d d 2D d 16 4
04.圆轴的扭转

一、圆周扭转时的变形分析(续1)
2. 变形分析: 假想沿n-n和m-m两个相距dx的横截面将轴切取一薄
四指沿扭矩的方向屈起, 拇指的方向离开截面,扭 矩为正,反之为负。
三、横截面的内力矩——扭矩(续2)
3.扭矩正负号的规定:
(1)右手螺旋法则:
四个手指沿扭矩转动的方向,大拇指即为扭矩的方向。
(2)扭矩正负号:
离开截面为正,指向截面为负。 (3)外力偶矩正负号的规定:
指向截面
与坐标轴同向为正,反向为负
' 量显然可以用弧线 :c c 表示,其值为:
(书P54)
cc' Rd
n-n截面在b点处的 角应变:
g=cc' R d (5-5)
dx dx
一、圆周扭转时的变形分析(续3)
观察截面n-n上距圆心为ρ处的bρ 点, 如左图,bρ点处的角应变:
g
=
c c' dx
d
dx
(5-6)
d 表示扭转角沿轴线x的变化率,为两个截面相隔单
g
Mn
B
x
j
B'
1.受力特点:构件两端受到两个在垂直于轴线平面内的 力偶作用,两力偶大小等,转向相反。
2.变形特点:各横截面绕轴线发生相对转动。 3.扭转角:任意两截面间有相对的角位移,这种角位移
称为扭转角。
轴的概念
工程上,将以扭转变形为主要变形的构件通 称为轴。(对比:以弯曲为主要变形的构件在工 程上通称为梁)同时,多数轴是等截面直轴。
第7讲 扭转时的内力、薄壁圆筒的扭转-6页精选文档

第7讲教学方案——扭转时的内力、薄壁圆筒的扭转第 1 页第三章 扭转§3-1 概述工程上的轴是承受扭转变形的典型构件,如图4-1所示的攻丝丝锥,图4-2所示的桥式起重机的传动轴以及齿轮轴等。
扭转有如下特点:1.受力特点:在杆件两端垂直于杆轴线的平面内作用一对大小相等,方向相反的外力偶——扭转力偶。
其相应内力分量称为扭矩。
2.变形特点:横截面绕轴线发生相对转动,出现扭转变形。
若杆件横截面上只存在扭矩一个内力分量,则这种受力形式称为纯扭转。
§3-2 外力偶矩与扭矩的计算 扭矩图1.外力偶矩m如图4-3所示的传动机构,通常外力偶矩m 不是直接给出的,而是通过轴所传递的功率N 和转速n 由下列关系计算得到的。
nN m 9550= (4-1a) 如轴在m 作用下匀速转动φ角,则力偶做功为φm A =,由功率定义ωφm dtd m dt dA N =⋅==。
角速度ω与转速n (单位为转/分,即r/min )。
关系为60/2n πω=(单位为弧度/秒,rad/s )。
由于1kW=1000N ·m/s ,N 千瓦的功率相当于每秒钟作功N W ⨯=1000,单位为N ·m ;而外力偶在1秒钟内所作的功为m n 2m W ⋅=⋅=πω/60 (N ·m )第 3 页由于二者作的功应该相等,则有m n N ⋅=⨯π21000/60由此便得(4-1)式。
式中:N —传递功率(千瓦,kW ) n —转速(r/min )如果传递功率单位是马力(PS),由于1PS=735.5 N ·m/s ,则有nN m 7024=(N ·m ) (4-1b) 式中:N —传递功率(马力,PS )n —转速(r/min )2.扭矩T求出外力偶矩m 后,可进而用截面法求扭转内力——扭矩。
如图4-4所示圆轴,由0=∑x m ,从而可得A —A截面上扭矩TT 称为截面A —A 上的扭矩;扭矩的正负号规定为:按右手螺旋法则,T 矢量离开截面为正,指向截面为负。
材料力学—薄壁圆筒扭转时的切应力

2
内力
3
应力
4
变形
外力偶矩Me
扭矩T
切应力
……
T 2πr02
向相反的一对力偶矩。
实验现象:
Me
Me
dx
( 1 )圆周线:圆筒表面各圆周线的大小、形状不变,各 圆周线间距离保持不变,只是作了相对转动;
( 2 )纵向线:纵向平行线仍然保持为直线且相互平行, 只是倾斜了一个角度。
推论:横截面上没有正应力,只有切应力。
采用截面法将薄壁圆筒沿 m-m 截面截开,横截面上分布 有与截面平行的切应力。 由于筒壁很薄,可以假设 切应力沿壁厚均匀分布。数值 可由静力学关系求得。
扭转变形:杆件受到大小相等,方向相反且作用平面垂直于杆件 轴线的力偶作用, 使得杆件的横截面绕轴线产生相对转动。
(2)扭矩:
用截面法研究受扭圆 轴横截面上的内力:
T = Me
扭矩方向规定:
右手螺旋法则
扭矩矢量的指向与截面外法线的指向一致, 为正;反之为负。
T1
n (+) (-)
T4
n
n
n
T2
T3
(3)扭矩图:扭矩随构件横截面的位置变化的图线。
MA
1
2
MC
1
MB
T1 M A
2
T
(+)
X
(-)
T2 M C
§3.3.1
薄壁圆筒扭转时的切应力
r0
好处:( 1)应力分布均匀,变形情况易预测; ( 2)应力状态简单—纯剪切。
实验方法:
将一薄壁圆筒表面用纵向平行线和圆周线划分成方
《材料力学》 — 薄壁圆筒扭转时的切应力
薄壁圆筒的扭转

实验步骤
将薄壁圆筒固定在实验台上,确保其稳定不动 。
01
使用扭矩测量装置测量施加的扭矩大小, 并记录数据。
03
02
在薄壁圆筒的一端施加扭矩,使其发生扭转 。
04
使用位移传感器测量薄壁圆筒在扭转过程 中的位移,并记录数据。
使用应力应变测量仪测量薄壁圆筒在扭转 过程中的应力应变分布,并记录数据。
工程实例一
总结词:桥梁结构
详细描述:薄壁圆筒的扭转在桥梁结构设计中有着广泛应用。例如,桥梁的桥墩和桥台通常采用薄壁圆筒结构,这些结构在 承受扭转力时表现出良好的稳定性。
工程实例二
总结词:建筑结构
详细描述:在高层建筑或大型工业建筑中,薄壁圆筒的扭转被广泛应用于建筑结构的支撑和抗扭设计 中。这些薄壁圆筒可以增强建筑的稳定性和抗风能力。
薄壁圆筒的扭转
• 引言 • 薄壁圆筒扭转的基本概念 • 薄壁圆筒的力学性能 • 薄壁圆筒的扭转实验 • 薄壁圆筒的扭转模拟 • 薄壁圆筒的扭转在实际中的转是一个涉及材料力学 、流体力学和工程设计等多个领域的 主题。它主要研究薄壁圆筒在扭矩作 用下的应力、应变和稳定性等特性。
在薄壁圆筒的扭转过程中,圆筒的一端固定,另一端施加扭矩,使圆筒产生旋转 运动。
薄壁圆筒扭转的原理
01
当对薄壁圆筒施加扭矩时,圆筒的横截面将受到剪切应力和弯 曲应力的作用。
02
由于薄壁圆筒的壁厚很薄,剪切应力和弯曲应力会在横截面上
产生很大的应力集中,可能导致圆筒破裂或变形。
因此,在薄壁圆筒的扭转过程中,需要合理选择材料、壁厚和
模拟结果分析
应力和应变分布
通过模拟结果分析薄壁圆筒在不 同扭转状态下的应力和应变分布 情况,验证是否满足强度要求。
薄壁圆筒在弯曲和扭转组合变形下的主应力测试实验

薄壁圆筒在弯曲和扭转组合变形下的主应力测试实验
实验目的: (1)了解在弯曲和扭转组合变形情况下的测试方法
(2)测定薄壁圆筒试件在弯曲和扭转组合受力情况下,试件表面某
点的正应力,并与理论值比较。
实验仪器: XL3418材料力学多功能试验台;测力仪;静力电阻应变仪。
实验原理: 薄壁圆筒受弯曲和扭转组合作用,使圆筒的m 点处于平面应力状态如图1所示。
在m 点单元体上有弯矩引起来的正应力x σ,和由扭矩引起来的剪应力n τ。
主应力是一对拉应力1σ和一对压应力3σ。
理论值计算:
132x σσσ= 022n
x
tg τασ-=
x z M W σ= 4
3132z D d W D π⎡⎤
⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ M P L =∆⋅
n T T W τ= 43116T D d W D π⎡⎤
⎛⎫=-⎢⎥ ⎪⎝⎭⎢⎥⎣⎦
T P a =∆⋅
实验值计算:
°
°
145453()2(1)E εεσσμ-+=±- °°°°°45-450045-45()2(2)
tg εεαεεε-=
--
图1 圆筒m 点的应力状况。
薄壁圆筒的扭转熟悉扭矩

BC
D
A
BC
D
A
351Nm 351Nm
1170Nm 468Nm 468Nm
351Nm
702Nm (a)
351Nm 351Nm 468Nm
351Nm 702Nm (b)
1170Nm 1170Nm
3、增大极惯性矩和抗扭截面模量。
G
d
dx
τmax
max
Tn
O
Tn
O
3、静力学方面
圆轴扭转变形的基本公式
Tn I
I 2dA,称为截面的极惯性矩。
圆轴的极惯性矩 I
d 4
32
最大扭转剪应力
max
Tn R I
Tn I R
W
I 为抗扭截面模量, max
R
Tn W
0 GI
GI
薄壁圆管
Tnl 2GR03t
二、圆轴扭转刚度条件
单位长度内的扭转角 d Tn
dx GI
刚度条件
T GI
p
max
或max
Tn max GI
180
许用扭转角查设计标准或规范。
单位换算:rad
教学要求
了解扭转的概念,薄壁圆筒的扭转 熟悉扭矩、扭矩图,圆轴扭转时的应力, 圆轴扭转时的强度计算掌握圆轴扭转时的 变形和刚度计算,提高圆轴扭转强度和刚 度的措施。
教学重点与难点
重点:扭矩图的绘制,圆轴扭转时的 应力,圆轴扭转时的强度计算
难点:圆轴扭转时的变形和刚度计算
§8、2-1 扭转的概念 §8.2-2 圆轴扭转时的应力 §8.2-3 薄壁圆筒的扭转 §8.2-4 圆轴扭转时的应力分析 §8.2-5 圆轴扭转时的强度计算 §8.2-6 圆轴扭转时的变形与刚度计算
薄壁圆筒的弯扭组合变形实验

1薄壁圆筒的弯扭组合变形实验一、试验目的1.测定薄壁圆筒弯扭组合变形时指定点的主应力和主方向,并与理论计算值进行比较。
2.测定薄壁圆筒弯扭组合变形时指定截面上的弯矩、扭矩和剪力引起的应力,并与理论值比较。
3. 学习布片原则、应变成份分析和各种组桥方法。
二、设备和仪器1. 力学试验台。
2. 静态应变仪。
3. 辅助工具和量具。
三、试样与试验装置薄壁圆筒试样(见图5.1a )左端固定,籍固定在圆筒右端的水平杆加载。
圆筒用不锈钢1C r 18N i 9T i 或其它钢材制成,材料弹性模量E 和泊松比µ为己知,或由试验者自行测定,圆筒外径D ,内径d 。
四、试验原理1. 指定点的主应力和主方向测定弯扭组合变形任一截面(如I-I 截面)上b 点的应力状态如图5.1(b)所示,相应其它各测点的应力状态见图 5.1(d)。
根据理论分析可知:弯曲正应力WM M =σ,式中:M=Fl I-I,()143απ−=D W ,D d /=α;薄壁圆筒扭转切应力PT W T=τ,式中:T=Fh ,()16143p απ−=D W ;弯曲切应力Q QF 0 F R tτπ=,()40d D R +=,()2d D t −=;由此可求得相应点的主应力1`2`3σσσ及主方向0α的理论值如何由实验来测定任一截面的主应力和主方向呢?据平面应变分析理论知,若某点任意三个方向的线应变已知,就能计算出该点的主应变和主方向,从而计算出该点的主应力和主方向。
因此测量某点的主应力和主方向时,必须在测点布置三枚应变片,工程中常用应变花 测定。
常见的应变花有45o 应变花和等角应变花等。
在图5.1a 中的I-I 截面的b 、d (或a 、c ),即采用了45o 应变花进行测量,其展示图如图5.61(c)所示。
2采用单臂(多点)半桥公共温度补偿测量法,等量逐级加载。
在每一载荷作用下,分别测得b 、d (或a 、c )两点沿-45o 、0o 、和45o 方向的应变值o o o ``45045εεε−和后,将测量结果记录在实验报告中。
薄壁圆筒的扭转

B
Me
D C dx δ
2
4.推导公式 (Derivation of formula)
A dA r r A dA r(2π r ) T
T 2πr 2
此式为薄壁圆筒扭转时横截面上切应力的计算公式.
薄壁筒扭转时横截面上的切应力均匀分布, 与半径垂直,
指向与扭矩的转向一致.
τ T
τ
二、切应力互等定理 (Shearing Stress Theorem)
§3-3 薄壁圆筒的扭转
(Torsion of thin-walled cylindrical Vessels)
薄壁圆筒:壁厚
1 10
r0(r0—圆筒的平均半径)
一、应力分析 (Analysis of stress)
1.实验前
(1)画纵向线,圆周线;
(2)施加一对外力偶.
2.实验后 (1)圆筒表面的各圆周线的形状、大小和 Me 间距均未改变,只是绕轴线作了相对转动;
r
l
T
从 T 与 之间的线性关系,可推出 与 间
的线性关系 . G
O
该式称为材料的剪切胡克定律
(Hooke’s law for shear)
G –剪切弹性模量
三个弹性常数的关系 G E
2(1 )
O
知识回顾 Knowledge Review
(2)各纵向线均倾斜了同一微小角度 ; (3)所有矩形网格均歪斜成同样大小的平行四边形.
3.推论(Inference)
Me
(1)横截面上无正应力,只
有切应力;
(2)切应力方向垂直半径或 与圆周相切.
圆周各点处切应力的方向于圆周相切, A
且数值相等, 近似的认为沿壁厚方向各点处
薄壁圆筒扭转试验

薄壁圆筒扭转试验薄壁圆筒扭转试验如所示纤维复合材料薄壁圆筒纤维与轴线平行,薄壁圆筒平均半径为,壁厚为在簿壁圆筒两端施加对轴线的力偶矩扭矩。
在纤维复合材料薄壁圆筒的扭转试验中假定:当时,可以认为横截面团环上各点切应力沿半径在厚度上均匀分布。
由动员矩守恒原理,对于静力学的纤维复合材料薄壁圆筒问题,各点的切应力满足切应力互等定律。
即:对于内外表面均处于自由状态的纤维复合材料薄壁圆筒,横截面内外因周线上各点切应力均沿团周切线方向铂向。
且由假定可知,同一半径上内外因周线上两点切应力相等。
通过观察可以看出,对于端部受一对外力偶矩,且处在平衡状态的纤维复合材料薄壁圆筒,其外表面上各点处的切应变相同。
该假定给出纤维复合材料薄壁圆筒处于均匀纯剪切应力状态,即对于纤维复合材料薄壁圆筒,由截面法可确定其任意横截面上的扭矩均为。
纤维复合材料湾壁圆筒任意横截面上的扭矩是横截面上分布切应力向轴线简化的主矢量在纤维复合材料荫壁圆筒外表面上任取一点,如图ABC电子所示。
点在弹性主向面内的应力状态如图所示。
对于点弹性主向面内的纯剪切应力状态,当切应力?达到极限应力。
时通过与对应的极限扭矩严可以确定剪切权限应力对于纤维复合材料薄壁圆筒扭转试验,其结果表明,应力—应变之间为非线性关系,如图复合材料单层板沿纤维方向单向拉伸试验确定了复合材料单层板与纤维正交方向单向拉伸试验确定了复合材料单层板与纤维成。
角方向单向拉伸试验确定了纤维复合材料薄壁圆筒纤维与轴线平行的扭转试验确定对于拉伸与压缩强度不相同的复合材料单层扳正交各向异性线弹性体平面应力问题,只须IC现货商将复合材料单层板沿纤维方向单向拉伸试验、复合材料单层板与纤维正交方向单向拉伸试验中的拉仲裁荷换成压缩载荷即可确定。
表给出了种纤维增强复合材料的相关刚度参数及强度指标。
在应用平面应力状态二向最大应力理论的强度条件是应该特别注意,式、式中的应力是正交各向异性线弹性体弹性主向的应力这里下标是弹性主向,并不是应力状态分析中的应力主方向。
材料力学
G :材料的切变模量,量纲与 相同
弹性模量E、泊松比 和切变模量G 关系: G E
2(1 )
本节放映完毕。请返回上级菜单
第三节 薄壁圆筒扭转
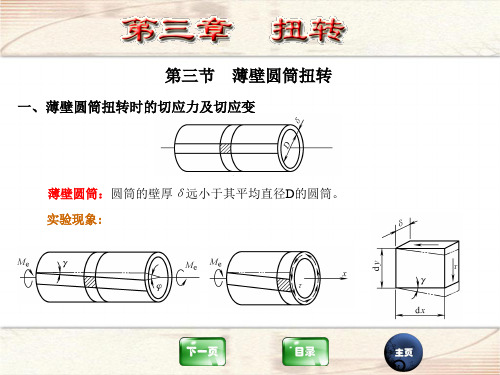
一、薄壁圆筒扭转时的切应力及切应变
薄壁圆筒:圆筒的壁厚δ远小于其平均直径D的圆筒。 实验现象:
1、横截面上没有正应力;
2、横截面上有切应力 ,且切应力的方向与径向垂直。
由于筒壁厚度 很小,可以认为沿筒壁厚度切应力不变。
Me 2πr r
M组成力偶相平衡:
MZ 0
(dy)dx ( dx)dy
所以
切应力互等定理:在相互垂直的两个平面上,切应力必然成对存在,且数值 相等,两者都垂直于两个平面的交线,方向则共同指向或共同背离这一交线。
三、剪切胡克定律
剪切胡克定律:当切应力不超过材料的剪切比例极限 P时,切应变 与切 应力 成正比。
《材料力学》课件3-2薄壁圆筒的扭转

切应力计算
根据材料力学的基本原理,切应力的大小可以通过扭矩和横截面 面积的比值计算得到。
变形量计算
通过测量薄壁圆筒在扭转变形前后的长度变化,可以计算出其变 形量。
弹性模量
在一定条件下,切应力和变形量之间的关系可以用弹性模量来描 述。
薄壁圆筒的变形特性
变形方向
薄壁圆筒的扭转变形是沿着圆筒轴线的方向进行的。
04
根据实验结果,讨论薄壁圆筒在纯扭状态 下横截面上的应力分布规律。
实验结论与讨论
01
实验结果表明,薄壁圆筒在纯扭 状态下横截面上的应力分布符合 剪切应力与剪切应变线性关系;
02
与理论公式对比,实验结果与理 论公式基本一致,验证了理论公
式的正确性;
在实验过程中,应采取措施减小 误差,提高实验精度;
薄壁圆筒的扭转原理
当薄壁圆筒受到一对大小相等、 方向相反的力偶作用时,圆筒
就会发生扭转。
薄壁圆筒的剪切模量是衡量 其抗扭能力的物理量,剪切 模量越大,抗扭能力越强。
薄壁圆筒的弯曲应力与轴向应 力在剪切模量中得到体现,弯 曲应力与轴向应力的比值决定
了圆筒的形状变化。
薄壁圆筒的扭转应用
薄壁圆筒广泛应用于机械、化工、建筑等工程领域,如管道、压力容器、塔器等。
计算时应根据实际情况选择合适的 公式进行计算。
薄壁圆筒的应力特性
01
薄壁圆筒的应力特性主要表现为剪切应力和弯曲应力的共同作 用。
02
在扭转载荷作用下,圆筒的外侧受到较大的剪切应力和弯曲应
力,而内侧受到较小的剪切应力和弯曲应力。
圆筒的应力特性与圆筒的材料属性、几何形状以及扭转载荷的
03
大小有关。
03
《材料力学》课件3-2薄壁圆 筒的扭转
材料力学—薄壁圆筒扭转时的切应力

(2)扭矩:
用截面法研究受扭圆 轴横截面上的内力:
T = Me
扭矩方向规定:
右手螺旋法则
扭矩矢量的指向与截面外法线的指向一致, 为正;反之为负。
T1
n (+) (-)
T4
n
n
n
T2
T3
2
内力
3
应力
4
变形
外力偶矩Me
扭矩T
切应力
……
T 2πr02
(2)研究思路:
Me
m r0
dA
x
m
d A r 0 T 根据应力分布可知: 由 A
r0 d A T
A
T T 2 r0 d A r0 (2πr0 ) 2πr0
A
T
薄壁圆筒扭转时横截面上的切应力均匀分布,与半径
垂直,指向与扭矩的转向一致。
小结:
(1)研究内容:
1
外力
(3)扭矩图:扭矩随构件横截面的位置变化的图线。
MA
1
2
MC
1
MBT1 M A2T(+)
X
(-)
T2 M C
§3.3.1
薄壁圆筒扭转时的切应力
r0
好处:( 1)应力分布均匀,变形情况易预测; ( 2)应力状态简单—纯剪切。
实验方法:
将一薄壁圆筒表面用纵向平行线和圆周线划分成方
《材料力学》 — 薄壁圆筒扭转时的切应力
徐州工程学院 机电工程学院
王晓溪 2015年4月
知识回顾:
1 扭转变形
薄壁圆筒扭转时的切应力补充.pdf
[ ] τ max
=
Tmax WP
≤
τ
2、截面设计——已知载荷及[σ],根据强度条件设计
截面尺寸;
WP
≥
Tmax
[τ ]
3、许可载荷——已知A及[σ],根据强度条件确定许
可载荷;
Tmax ≤ [τ ]WP
例1 一轴AB传递的功率为PK=7.5kW , 转 速 n=360r/min 。 轴 AC 段 为 实 心 圆 截 面 , CB 段 为 空 心 圆 截 面 , 如 图 所 示 。 已 知 D=3cm,d=2cm。试计算AC段横截面边缘处 的切应力以及CB段横截面内外边缘处的切
所以传动轴满足强度条件
(2)若把该传动轴改为实心轴,其最大切应力应为51MPa。
设实心轴的直径为D2 ,则有
τ max
=
T WP
=
1500
π
16
D23
= 51×106 Pa
D2
=
3
1500 ×16 3.14× 51×106
= 0.0531m
在两轴长度和材料相同时,两轴重量之比等于横截面面积之比。
设空心轴和实心轴的横截面面积分别为A1、A2,则
应解力:。(1)计算扭矩,轴所受的外力偶矩为
Me
=
9549
P n
= 199 N⋅ m
由截面法,各横截面上的扭矩均为
T = Me = 199 N⋅ m
(2)计算极惯性矩,AC段和CB段轴横截面的极 惯性矩分别为
( ) I P1
=
πD 4 32
=
7 .95 cm
4
IP2
=
π 32
D4 − d4
= 6 .38 cm 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
材料力学大连理工大学王博
纯剪切
切应力互等定理剪切胡克定律
t r
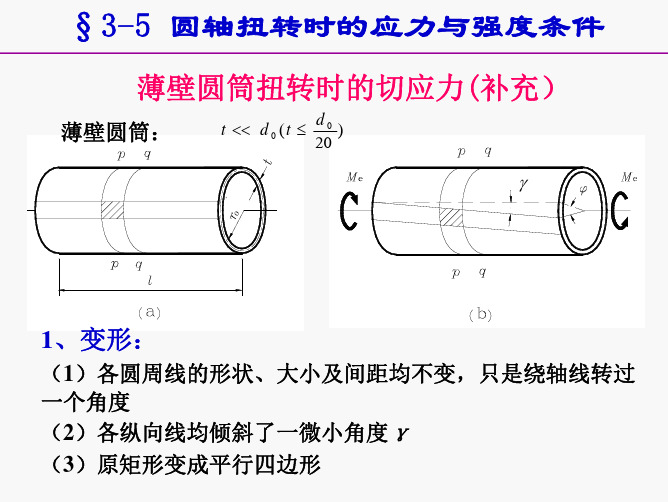
1. 变形特点
圆周线 形状、大小、间距未变
绕轴线旋转不同角度
纵向线 间距未变,倾斜角度相同
一、横截面上的切应力(目的:由内力表征出应力)
薄壁圆筒扭转 纯剪切
什么是薄壁圆筒? ——壁厚 t 远小于平均半径 r
圆周线 纵向线
2. 横截面上的应力
猜测(特点)切应力τ
σ = 0 ;
(2)大小 沿壁厚均匀分布、
数值由静力学关系求得
(1)方向 垂直于所在半径、 对轴线的矩与扭矩一致
Q :从合力的作用效果分析,切应力与之前所学的连接件切应力有何不同? F τ τ
τ ≠ 0 推断(有无) M e T
得 t T
r
或 其中A 0为壁厚中线所围的面积
由静力等效 ⎰=⋅⋅=⋅A
T
r t r A r τπτ2d 22πT r t τ=02T A t τ=t
T r 2
0πA r =d A τd A
x y
z 二、切应力互等定理
Theorem of Conjugate Shearing Stress 应力单元体特点 1.各边长无穷小 2.各面应力均匀分布 3.平行两面对应应力数值相等 d y d x d z y z x d x
d y d z
τ'
∑M x =0, ∴ 定理 在互相垂直的两个截面上
1.垂直于截面交线的切应力数值相等
2.方向同时指向截面交线,
或同时背离截面交线 τ()()d d d d d d 0x y z x z y ττ'-==ττ'
圆筒扭转横截面边缘各点切应力τ的方向
为什么一定与边线相切(垂直于半径)?
切应力互等定理——小试牛刀!!
τM e
τ
τ
τ
T
τ τ
三、剪切胡克定律 Hooke ’s Law in Shear τ
τ γ γ 回忆 材料的拉压胡克定律 当 σ ε
σp P =E σσσε≤,
弹性常数之关系 当 τ ≤ τp
τ = Gγ
式中 τp — 剪切比例极限
G — 切变模量 Shear Modulus 单位 GPa τ © 变形后 线性
剪切胡克定律 τ τ γ τp ()ν+=12E G。
