独立增量过程
第三章泊松(Poisson)过程.

4. 齐次泊松过程的两个相关随机变量
设{N (t), t 0}是强度为的泊松过程,Wn(n 1)
表示事件第n次出现的等待时间.
W0 0
记 Ti Wi Wi1, i 1,2, 则Ti 表示第n-1次
事件发生到第n次事件发生的时间间隔.
(每小时)的泊松过程 {N(t), t 0}, 若每个人消费 的金额(元)为独立同分布的随机变量 Yn:
f ( y) 0.05e0.05 y ( y 0)
设 X(t) 表示 [0,t) 时间内该超市的总营业额,求3 小时内总营业额的期望和方差.
基础部张守成 2020年2月28日星期五
令 s 0, 根据假设 N (0) 0 可得
均值函数: E[N (t)] t,
方差函数: DN (t) Var[N (t )] t
E[ N (t)].
t
泊松过程的强度等于单位长时间间隔内发生的事件 数目的均值.
基础部张守成 2020年2月28日星期五
(2) 协方差函数:
设{N(t), t0}是强度的泊松过程,{Yk,k=1,2,}是
独立同分布随机变量序列,且与{N(t), t0}独立,令
N (t)
X (t) Yk , t 0 k 1
则称为复合泊松过程. 例 设N(t)是在(0, t]内来到某商店的顾客数,Yk是
N (t)
第k个顾客的花费,则 X (t) 是Yk (0, t]内的营业额. k 1
如果对任意的实数h 和 0 s h t h,
X (t h) X (s h) 和 X (t) X (s) 具有相同的分布, 则称增量具有平稳性.
2.独立增量过程

相关函数
R X ( s , t ) = C X ( s , t ) = σ 2 min( s , t ) .
s, t ≥ 0
四、正态过程 定义:如果随机过程 X (t ) 的任何 有限维分布都是正态分布,则称 X (t ) 为正态过程,或称高斯(Gauss)过程。
注:维纳过程是正态过程.
正态过程的全部统计特性完全由其 均值函数和协方差函数(相关函数)所 确定。
例3: 设 X ( t ) = A cos ω t + B sin ω t , t ∈ T = ( −∞ , ∞ ) 其中 A,B 是相互独立,且都服从正态分布 N ( 0, σ 2 ) 的随机变量,ω 是常数。试证明 X (t ) 是正态过程,并且求它的均值函数和相关 函数. 解: A,B 是相互独立的正态变量, 变量。对 ∀ n ∈ N , t1 , t2 ,L, tn ∈ T ,
S(t2 ) − S(t1 ) ~ π ((λ + μ)(t2 − t1 ))
∴ S(t2 ) − S(t1 ) = Z1 + Z2 ~ π ((λ + μ)(t2 − t1 ))
∴ S ( t ) = X ( t ) + Y ( t ) 是具有强度 λ + μ 的泊松过程 .
例 2:设{ X ( t ), t ≥ 0}是泊松过程,且对任意 的t 2 > t1 > 0 E[ X ( t 2 ) − X ( t1 )] = 2( t 2 − t1 )}
③对充分小的 Δt 有
∑ Pj (t , t + Δt ) = ∑ P{ X (t , t + Δt ) = j} = ο (Δt )
j =2 j =2
ห้องสมุดไป่ตู้
3.2-纯粹随机过程、Markov过程、独立增量过程

6ቤተ መጻሕፍቲ ባይዱ
5
独立增量过程
独立增量过程是指对任意n和任意0≤t1<t2<…<tn , 随机过程{ξt }t≥0的增量∆ 1ξt (t),∆ 2ξt(t),…, ∆nξt(t)相互独立,其中∆nξ(t)= ξ(tn)- ξ(tn-1)。 独立增量过程是指随机过程的变化量是独立的, 是Markov过程的一种类型。
4
马尔可夫性(无后效性 马尔可夫性 无后效性) 无后效性
过程或(系统)在时刻t0所处的状态为已知的
条件下,过程在时刻t > t0所处状态的条件分布与
与过程在时刻t0之前所处的状态无关的特性称为
马尔可夫性或无后效性 马尔可夫性或无后效性. 过程“将来”的情况与“过去” 即: 过程“将来”的情况与“过去”的情况是无 关的. 关的
3
Markov过程 过程
Markov过程是指对每个 和任意0≤t1<t2<…<tn, 过程是指对每个n和任意 ≤ 过程是指对每个 和任意 随机过程{ξ 随机过程 ξt }t≥0的条件分布函数满足 的条件分布函数满足 Fn(xn+1,tn+1 / x1,t1; x2,t2; …; xn,tn) = Fn(xn+1,tn+1 / xn,tn)。 。 Markov过程的记忆性比纯粹随机过程要好点,但 过程的记忆性比纯粹随机过程要好点, 过程的记忆性比纯粹随机过程要好点 变量未来的变化也只与现在有关, 变量未来的变化也只与现在有关,与该变量的历史 及其到现在以前的演变形式无关, 及其到现在以前的演变形式无关,这种性质成为马 尔科夫性。 尔科夫性。
纯粹随机过程、Markov过程 过程、 纯粹随机过程、Markov过程、独 立增量过程
【国家自然科学基金】_独立增量过程_基金支持热词逐年推荐_【万方软件创新助手】_20140729
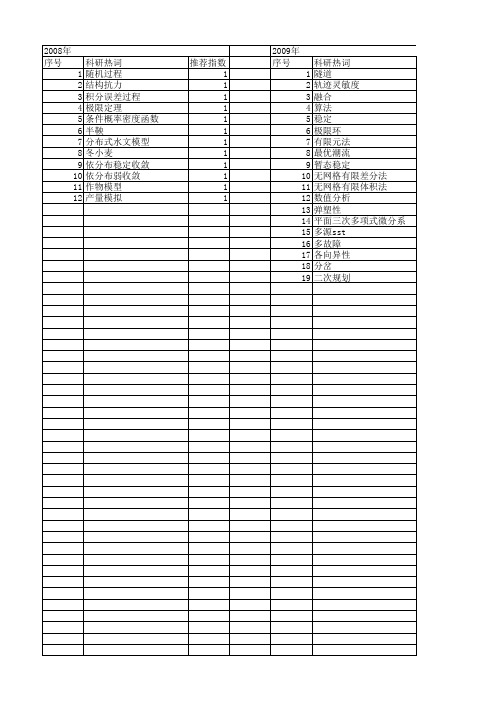
科研热词 隧道 轨迹灵敏度 融合 算法 稳定 极限环 有限元法 最优潮流 暂态稳定 无网格有限差分法 无网格有限体积法 数值分析 弹塑性 平面三次多项式微分系统 多源sst 多故障 各向异性 分岔 二次规划
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9
科研热词 随机过程 退化结构 空间金字塔匹配 独立子空间分析 特征基元 概率模型 时变可靠度 增量学习 场景分类
推荐指数 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
科研热词 随机过程 过程回归分析 性能退化 可靠性 障碍规避 软着陆 规则子集 裂纹扩展 脆弱性曲线 置信限曲线 线性过程 混合trie结构 桥梁工程 机动能力 并行查找 增量更新 增量动力分析 基于概率 地震危害性 包分类 制导律 两脉冲机动
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 随机过程 结构抗力 积分误差过程 极限定理 条件概率密度函数 半鞅 分布式水文模型 冬小麦 依分布稳定收敛 依分布弱收敛 作物模型 产量模拟
推荐指数 1 1 1 1 1 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2014年 序号 1 2 3 4 5 6 7 8 9
2014年 科研热词 紧耦合结构 精密定位 社区检测 社会网络 直线超声电机 模块性 复合控制 压电 fn算法 推荐指数 1 1 1 1 1 1 1 1 1
21独立增量过程

f n x n x n 1 ; t n , t n 1 f X x n ; t n |x n 1 , t n 1 无后效性
数学期望: E X t 1 P X t 1 ( 1 ) P X t 1
e tc h (t) s h (t) e 2 t
自相关函数:R X t1 ,t2 e 2 t1 t2 e 2 R X
功率谱密度:G X e 2 ej d 4 2 4 2
举例〔随机电报信号〕
随 机 变 量 A 与 半 随 机 电 报 信 号 X ( t ) 独 立 , 其 中 A 的 分 布 律 : A 1 1 P 0 .5 0 .5
定 义 随 机 电 报 信 号 为 Y (t) A X (t)
数学期望: E Yt E A X (t)0
自相关函数:R Y t 1 ,t2 e 2 t 1 t2 e 2 R Y R X
此外,维纳过程是一个非平稳的高斯过程。
苏格兰植物学家罗伯特•布朗1827年夏天对各种植物的花粉颗粒浸在水中 时的运动做了研究。这种浸泡在水中花粉粒子的奇异的、不规那么的运 动后来被称为“布朗运动〞。
维纳过程
定义1:假设独立增量过程X(t),其增量的概率分布服从高 斯分布,那么称X (t) 为维纳过程。 定义2:对所有样本函数几乎处处连续的齐次独立增量过程 称为维纳过程。〔两种定义等价,证明见书P266)
增量的概率分布唯一确定。
证 明 : 令 增 量 X t i X t i 1 Y t i Y t 1 ,Y t2 , ,Y tn 相 互 独 立
独立增量过程

CY (s, t) Cov(Y (s),Y (t)) Cov( X (s L) X (s), X (t L) X (t))
Cov( X (s L), X (t L)) Cov( X (s), X (t L)) Cov( X (s L), X (t)) Cov( X (s), X (t))
域内它又就是构造一类重要噪声(散粒噪声)得基础。
例、设{X(t)}就是强度为得泊松过程,定义Y(t)=X(t+L)-
X(t),其中L>0为常数,求Y(t),RY(s,t)、
解: Y(t)=E[Y(t)]=E[X(t+L)-X(t)]=(t+L)-t=L;
RY(s,t)=CY(s,t)+Y(s)Y(t),
所以
RX
(
s,
t
)
2
L2
2
L
L2
|
s
t
|
| s t | L | s t | L
三、维纳过程 又称布朗运动
引言 维纳过程就是布朗运动得数学模型、 英国植
物学家布朗在显微镜下, 观察漂浮在平静得液面 上得微小粒子, 发现它们不断地进行着杂乱无章 得运动, 这种现象后来称为布朗运动、
以W(t)表示运动中一微粒从时刻t=0到时刻t>0
2、泊松过程数字特征
3、泊松过程得一些定理
设{N(t),t≥0}为泊松过程,N(t)表示到t时刻时质点出 现得个数,W1,W2,、、、分别表示第一个,第二个,…质点出 现得时间,Tn(n≥1)表示从第n-1个质点出现到第n个质点 出现得时间间隔、
T1
T2
Tk
0 W1
W2
Wk-1 Wk
2独立增量过程解析

生的次数。
例如:若用N1(t)表某电话交换台在[0,t]内接到的电话呼 唤次数;
若用N2(t)表示[0,t]这段时间内到达某商场的顾客数; 若用N3(t)表示时间[0,t]内某放射性物质放射出的粒子数; 若用N4(t)表示在时间[0,t]内某地段出现的交通事故次数等, 这些Ni(t)均为计数过程。 为了建模方便,我们把“事件A”发生一次说成质点出现 一个,于是计数过程N(t)看作在时间轴上区间[0,t]内质点 出现的个数。
DX ( s)
同理,当0t<s时,有 C X ( s, t ) DX (t )
于是可知对于任意的s,t≧0,协方差函数可表示为: C X ( s, t ) DX (min( s, t )).
二、泊松过程
1.定义
定义1. 称随机过程{N(t),t≧0}为计数过程,若N(t)表示 [0,t]时段内“事件A”发生的次数,且N(t)满足下列条件 (1) N(t)≧0; (2) N(t)取整数; (3) 若0≤s<t,则 N(s)≤N(t); (4) 当s<t 时, N(t)-N(s)等于在间隔(s,t)上“事件A”发
DY(t)= E[Y2(t )].所以,当0s<t 时,有
C X ( s, t ) E[Y ( s)Y (t )] E [Y ( s) Y (0)][(Y (t ) Y ( s)) Y ( s)]
E[Y ( s) Y (0)]E[Y (t ) Y ( s)] E[Y 2 ( s)]
所以, T1具有参数为的指数分布。 (2)为求T2的分布,先求T1的条件下T2的条件分布,由独立增量
性有 P T2 t 0 T1 s P 在s, s t 内无质点出现 T1 s
P 在s, s t 内无质点出现
2014第七章 马尔可夫过程

若 ta tc tb td,则时间间隔 (ta tb ) 和 (tc td ) 相重叠(图2b)),因此, 上式不再成立。
td td tc tb (b) tb (a) tc ta ta
PX n X 1 ,, X n1 xn ; t n x1 , , xn 1 ; t1 , , t n 1
Pn xn xn1; tn1 , tn
PX n X n1 xn ; t n xn 1 ; t n 1
PX n X n1 xn , xn 1 ; t n 1 , t n PX n1 xn 1 ; t n 1
k
e
(k 1)!
k 1
k 1
= e e (ta tb ) ②. 均方值与方差 令 (ta tb ) ,故均方值为
k k k E[( X (ta ) X (tb )) ] k e k (k 1) e k e k! k! k! k 0 k 0 k 0 k 2 2 2 2 (ta tb )2 (ta tb ) = e k 2 (k 2)!
a b
先来讨论服从泊松分布的随机变量[ X (ta ) X (tb )] 及 [ X (tc ) X (td )] 的数学期望,方差和相关函数等统计量。
(ta tb ) ,因此,均值为 ①.数学期望 令
E[ X (ta ) X (tb )] k e k! k 0
2 2
而方差为
两参数齐次独立增量过程在原点的局部性质

i) lim sup Υ(us, v t) Υ(s, t) - 1 = 0; u↓1, v↓1 s, t
ii) 对任意 Ε> 0, 存在 Α(Ε) > 0, 使 P [X (z ) < - ΕΥ(z ) ] ≤ 1 - Α(Ε) ;
∫∫1 1
1) 如果 {P [X (s, t) > Υ(s, t) ] st}d sd t < ∞, 则 P [ lim X (s, t) Υ(s, t) ≤ 1} = 1;
P [A (m , n) ]= 1- exp {- M [ d (m , n) ] 2m + n+ 2}.
由于事件 A (m , n) 相互独立, 且由 (3)
∞∞
∞∞
∑∑ ∑∑ [A (m , n) ] =
{1 - exp {- M [ d (m , n) ] 2m + n+ 2} = ∞.
m = 1 n= 1
关键词 独立增量过程, 累积量, 局部增长. 分类号 AM S (1991) 60J 30 CCL O 211. 62
1 引 言
设R
2 +
=
{ (s, t) : s≥0, t≥0}, 对任意 z i=
(si,
ti)
∈R
2 +
,
z
1 ≤z
2和
z 1<
z 2均表示 z 1, z 2的分量有
相应的关系.
如 z 1<
P [ sup X (s, t) > (1 + 2Ε) Υ(am , an) ] ≤ P [X (u , v ) > (1 + Ε) Υ(am , an) ] Α(Ε) , 0≤s≤am , 0≤t≤an
独立增量过程为马氏过程

Ç Ä ð øÄ .
Ý Ð Ç Ä ½Ý :
.
Ç Ǒ èÑ ðÐ ,
0
S
Ý ∀ 0 ≤ t1 < t2 < · · · < tn, ∀ i1, . . . , in ∈ S, n ≥ 3,
á Ä X = {Xt : t ≥ 0}
Ý Ǒ øÄ .
X
,
P{Xtn = in|Xtn−1 = in−1, . . . , Xt1 = i1} = P{Xtn = in|Xtn−1 = in−1}.
111
Stat/219 Math 136 - Stochastic Processes Notes on Markov Processes
1 Notes on Markov processes
The following notes expand on Proposition 6.1.17.
1.1 Stochastic processes with independent increments
The idea of the proof is similar to the proof of Lemma 1.1 above. One further result is: Lemma 1.2 If {Xt, t ≥ 0} is a stationary process and a Markov process then it is homogeneous.
Î ùþ
P{Xtn = in|Xtn−1 = in−1, . . . , Xt1 = i1}
=
P{Xtn = in, Xtn−1 = in−1, . . . , Xt1 = i1} P{Xtn−1 = in−1, . . . , Xt1 = i1}
泊松分布 ppt课件

1.计数过程:设
为一随机过程,
如果N(t)是取非负整数值的随机变量,且满足s<t时,
N(s) ≤N(t),则称 XT {N(t),t T [0,)} 为计数过程(counting process).
若用N(t)表示电话交换台在时间[0,t]中接到
电话呼叫的累计次数,则{N(t) ,t≥0}就是一计数过程.
定义1 称随机过程{N(t),t0}为计数过程,若N(t)表示到 时刻t为止已发生的“事件A”的总数,且N(t)满足下列条件: (1) N(t)0 (2)N(t)取正整数; (3)若s<t,则N(s)<N(t); (4)当s<t,N(t)-N(s)等于区间(s,t]中发生的“事件A”的次数.
若t1<t2t3<t4,则在(t1,t2]内事件A发生的次数N(t2)-N(t1) 与在(t3,t4]内时间A发生的次数N(t4)-N(t3)相互独立,此时 计数过程N(t)是独立增量过程.
P{N(t) - N(s) k} [(t s)]k e(ts) , k 0,1, 2,
k!
则称{N(t),t0}为参数(或平均率、强度)为的(齐次) 泊松过程。[泊松过程的第二种定义方式]
注:由条件(3)知,泊松过程是平稳增量过程且E[X(t)]= t. 由于, =E[X(t)]/t表示单位时间内事件A发生的平均个数, 故称为此过程的速率或强度
X(t)-X(s),0≤s<t 为随机过程在 (s , t] 的增量.如果对 任意选定的正整数n和任意选定的0≤t0<t1<t2<…<tn, n个增量X(t1)-X(t0),X(t2)-X(t1), …,X(tn)-X(tn-1)相互 独立,则称 {X(t),t≥0}为独立增量过程.
泊松分布

2.泊松计数过程过程 : {N(t) ,t≥0} 称为强度为 λ 的 泊松过程,如果满足条件: (1)在不相重叠的区间上的增量具有独立性;
在X(0)=0和方差函数为已知的条件下, 独立增量过程协方差函数可用方差函数表示为:
CX(s,t)X 2(min(s,t))
1、 泊松过程举例 (Poisson process )
现实世界许多偶然现象可用泊松分布来描述, 大量自然界中的物理过程可以用泊松过程来刻画. 泊松过程是随机建模的重要基石,也是学习随机过程 理论的重要直观背景.著名的例子包括盖格计数器上 的粒子流,二次大战时伦敦空袭的弹着点,电话总机所 接到的呼唤次数,交通流中的事故数,某地区地震发生 的次数,细胞中染色体的交换等等.这类变化过程可粗 略地假定为有相同的变化类型.我们所关心的是随机 事件的数目,而每一变化可用时间或空间上的一个点 来表示.这类过程有如下两个特性:一是时间和空间 上的均匀性,二是未来的变化与过去的变化没有关系. 我们将基于这些性质来建立泊松过程的模型.
若t1<t2t3<t4,则在(t1,t2]内事件A发生的次数N(t2)-N(t1) 与在(t3,t4]内时间A发生的次数N(t4)-N(t3)相互独立,此时 计数过程N(t)是独立增量过程.
若计数过程N(t)在(t,t+s]内(s>0),事件A发生的次数N(t+s)N(t)仅与时间差s有关,而与t无关,则计数过程N(t)是平稳独 立增量过程.
注:由条件(3)知,泊松过程是平稳增量过程且E[X(t)]= t. 由于, =E[X(t)]/t表示单位时间内事件A发生的平均个数, 故称为此过程的速率或强度
独立增量过程

四 高斯过程(正态过程)
一、定义:
设{X(t)}为随机过程,如果对任意的正整数n及任意 t1,t2,…,tnT,n 维随机变量(X(t1),X(t2),…,X(tn))服 从n维正态分布,则称{X(t)}为正态过程。
正态过程是二阶矩过程。 记其均值函数为μX(t),协方差函数为CX(s,t)。
二、正态过程的性质:
(2)独立增量过程{X(t),t≧0}在X(0)=0的条件下,{X(t)}的协
方差函数为 C X (s, t) DX (min( s, t)).
证明: 记Y(t )=X(t)-X(t),当X(t)具有独立增量时, Y(t )也具有独立增量;且Y(0)=0,E[Y(t )]=0, DY(t)= E[Y2(t )]=DX(t) .所以,当0s<t 时,有
生的次数。
例如:若用N1(t)表某电话交换台在[0,t]内接到的电话呼 唤次数;
若用N2(t)表示[0,t]这段时间内到达某商场的顾客数;
若用N3(t)表示时间[0,t]内某放射性物质放射出的粒子数;
若用N4(t)表示在时间[0,t]内某地段出现的交通事故次数等, 这些Ni(t)均为计数过程。
为了建模方便,我们把“事件A”发生一次说成质点出现 一个,于是计数过程N(t)看作在时间轴上区间[0,t]内质点 出现的个数。
例.设{X(t)}是强度为的泊松过程,定义Y(t)=X(t+L)-
X(t),其中L>0为常数,求Y(t),RY(s,t).
解: Y(t)=E[Y(t)]=E[X(t+L)-X(t)]=(t+L)-t=L;
RY(s,t)=CY(s,t)+Y(s)Y(t),
对任意0≤s<t,有
CY (s, t) Cov(Y (s),Y (t)) Cov( X(s L) X(s), X(t L) X(t)) Cov( X (s L), X (t L)) Cov( X (s), X (t L)) Cov( X (s L), X (t)) Cov( X (s), X (t))
几种常用的随机过程

第十讲 几种常用的随机过程10.1 马尔可夫过程 10.1.1马尔可夫序列马尔可夫序列是指时间参数离散,状态连续的马尔可夫过程。
一个随机变量序列x n (n=1,2,…),若对于任意的n 有)|(),...,,|(1121x x F x xx x F n n X n n nX---= (10.1)或)|(),...,,|(1121xx f x xx x f n nXn n nX---=(10.2)则称x n 为马尔可夫序列。
x n 的联合概率密度为)()|( )|()|(),...,,(11221121x f x x f xx f x x f x x x f XXn n Xn nXnX⋅⋅---=(10.3)马尔可夫序列有如下性质:(1) 一个马尔可夫序列的子序列仍为马尔可夫序列。
(2) )|(),...,,|(121xx f x x x x f n nXk n n n n X -+++=(10.4)(3) )|(),...,|(111x X x x X n n n n E E --=(10.5)(4) 在一个马尔可夫序列中,若已知现在,则未来与过去相互独立。
即)|()|()|,(1x x f xx f x x x f rsXn nXrsnX-=,n>r>s (10.6)(5) 若条件概率密度)|(1x x f n nX-与n 无关,则称马尔可夫序列是齐次的。
(6) 若一个马尔可夫序列是齐次的,且所有的随机变量X n 具有同样的概率密度,则称该马尔可夫序列为平稳的。
(7) 马尔可夫序列的转移概率满足切普曼—柯尔莫哥洛夫方程,即)|()|()|(x x fx x fx x fsr Xrn Xsn X⎰∞∞-=,n>r>s (10.7)10.1.2马尔可夫链马尔可夫链是指时间参数,状态方程皆为离散的马尔可夫过程。
1 马尔可夫链的定义 设),2,1( =n X n 为离散时间随机过程,其状态空间},,,{21a a a N I =。
10—3

[N(t) N(s)]与[N(t 相 互t)独N(立s , t)] 则称 [N(t)为,独t>立0]增量计数过程。
(2)在计数随机过程中,如果 [t,t 内t] 出现事件A 的次数 [N(t 仅t)与 N时(t)]间差 有关,而t 与起 始时刻t无关,则称该随机过程为平稳增量计数 过程。
待时间是连续随机变量。
从图中可看出,计数 函数的值和相应的等待时 间序列之间存在一个明显
的关系。 FW(k t) P{Wk t}
计数函数曲线
注意到事件{Wk t }和{N(t)>k-1}是等价的。
Wn的分布函数FWn (t ) P{Wn t} 因为{Wn t} {N (t ) n}, 所以FWn (t) P{Wn t} 1 P{Wn t}
et
0
fti1 (ti1 )dti1
et
0 fti1 (ti1 )dti1
et , t 0,
fTi (t) 0, t 0.
et , t 0,
fTi (t ) 0,
t 0.
i 2, 3,.
结论
点间间距序列{Ti } 服从相同的指数分布. 理论上, T1, T2,,Ti ,是相互独立的随机变量.
记 Y(t) X(t) X (t).
当 X (t) 具有独立增量时 , Y (t) 也具有独立增量; Y (0) 0, E[Y (t)] 0, DY (t) E[Y 2 (t)] DX (t).
因此, 当 0 s t 时, 有
CY (s,t) E[Y (s)Y (t)]
E{[Y (s) Y (0)][(Y (t) Y (s)) Y (s)]}
独立过程与独立增量过程

X t h X s h与X t X s 有相同的概率分布。 则称随机过程 {X(t) ,t T} 为平稳独立增量过程。
二项计数过程
几 种 重 要 的 随 机 过 程
性质1: 随机过程 { X( t ) ,t T }为平稳独立增量过程 X(0)=0 ,则 1)均值函数 mt m t m为常数
若X t , t T 为独立随机过程,有 Fn t1 , t 2 ,..., t n ; x1 , x2 ,..., xn F1 t k , xk
k 1 n
即:独立随机过程的任 意有限维分布簇由其一 维分布簇确定。
白 噪 声
几 种 重 要 的 随 机 过 程
二.独立增量过程 定义: 随机过程 { X( t ) ,t T }T=[0,+∞),如果对任意的正 整数n≥2及任意的t1 < t2 < …<tn T 随机过程的增 量 X(t2)-X(t1) , X(t3)-X(t2),…, X(tn)-X(tn-1)相 互独立,则称随机过程 {X(t) ,t T} 为独立增量 过程。 定义:随机过程 { X( t ) ,t T } ,T=[0,+∞) 若对所有的s , t T及h 0 , s h , t h T
2)方差函数 3)协方差函数 Dt 2t C s, t 2 min s, t
为常数
性质2: 随机过程 { X( t ) ,t T }为独立增量过程 则其有限维分布由一维分布 T }为平稳独立增量过程
则其有限维分布由一维分布确定。
几 种 重 要 的 随 机 过 程
独立过程和独立增量过程 一.独立过程 定义:如果对任意的正整数n及任意 n 个不相同的t1 , t2 , …,tn T, 随机变量X(t1) , X(t2) ,…, X(tn)相互 独立,则称随机过程 {X(t) ,t T} 为独立过程。
平稳独立增量过程中几种条件分布的研究

平稳独立增量过程中几种条件分布的研究作者:杨元启来源:《科技风》2017年第24期摘要:本文研究和讨论了平稳独立增量过程中的几个条件分布,特别是泊松过程、伯努利过程中的几个时间变量的条件分布。
关键词:计数过程;独立增量;平稳增量;泊松过程;伯努利过程;条件分布以Nt表示到时刻t为止已发生的“某事件”的次数,若满足Nt≥0; Nt是整数值;s另外,若对一切t10,在时间段t1+s,t2+s中事件的个数与时间段t1,t2中事件的个数有相同的分布,则称计数过程{Nt}有平稳增量。
记Xi为事件第i1次与第i次发生的时间间隔,Si为事件第i次发生的时刻,i=1,2,…,约定X0=0,N(0)=0。
以下着重研究几个平稳的独立增量过程中的条件分布。
先讨论泊松过程中的几个条件分布。
设{Nt}为平稳的独立增量过程,在任一长度为t的区间中事件的个数服从均值为λt的泊松分布,即对一切s,t≥0,P(Nt+s-Ns=n)=e-λt(λt)nn!,n=0,1,…,则称{Nt}是强度为λ的泊松过程。
易知(1)ENt-Ns=DNt-Ns=λt-s;(2) CovN(s),N(t)=λmins,t ;(3)Xi,i=1,2,…,相互独立,均服从参数为λ的指数分布;(4)Si,i=1,2,…,服从参数为λ,i的Γ-分布。
(1)设{Nt}是强度为λ的泊松过程,则Nt=1条件下,S1服从0,t上的均匀分布。
亦即,如果已知时间段0,t内发生了一个事件,则此事件发生的时刻等可能取值于0,t。
证明:对s≤t有PS1≤s|Nt=1=PS1≤s,Nt=1PNt=1=P在(0,s]内有1个事件,在(s,t]内没有事件PNt=1=P(N(s)=1)P(Nt-N(s)=0)PNt=1=λse-λse-λt-sλte-λt=st(2)设0,t内发生的事件数为n,即{N(t)=n},则这n个事件发生的时刻,在不考虑发生的先后次序时,是独立同分布于0,t上的均与分布的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
令N(s,t)=N(t)-N(s),0≤s<t,给出泊松过程的另一定义:
定义3. 称计数过程{N(t),t≥0}为具有参数>0的泊松过程,
若它满足下列条件 (1) N(0)=0;零初值性 (2) N(t)是独立增量过程; (3) N(t)满足: PN (t , t t ) 1 t t
X(tn) =Y1+ Y2 + …+ Yn,即X(tn) 是Y1 ,…Yn的线性函数,
推广结果: Y1,Y2, …,Yn的联合分布确定了{X(t)}的有限维分布函数。
(2)独立增量过程{X(t),t≧0}在X(0)=0的条件下,{X(t)}的协
方差函数为
C X ( s, t ) DX (min(s, t )).
例如:若用N1(t)表示某电话交换台在[0,t]内接到的电话
呼唤次数;
若用N2(t)表示[0,t]这段时间内到达某商场的顾客数; 若用N3(t)表示时间[0,t]内某放射性物质放射出的粒子数;
若用N4(t)表示在时间[0,t]内某地段出现的交通事故次数等,这些 Ni(t)均为计数过程。
为了建模方便,我们把“事件A”发生一次说成质点出现 一个,于是计数过程N(t)看作在时间轴上区间[0,t]内质点 出现的个数。
E[Y ( s) Y (0)]E[Y (t ) Y ( s)] E[Y 2 ( s)]
DX ( s)
同理,当0t<s时,有 C X ( s, t ) DX (t )
于是可知对于任意的s,t≧0,协方差函数可表示为: C X ( s, t ) DX (min( s, t )).
二、泊松类重要的随机过程。
在通信工程、服务行业、生物学、物理学、公
用事业等领域的许多问题都可以用泊松过程来
描述。如:商店接待的顾客流,数字通信中已
编码信号的误码流等
随机质点流:质点(或事件)陆续地随机到达(或随
机发生),则形成一个随机质点流. 例如:商店接待的顾客流、 等车的乘客流、 数字通信中已编码信号的误码流、
Cov( X ( s L) X ( s ), X (t L) X (t ))
Cov( X ( s L), X ( t L)) Cov( X ( s ), X ( t L)) Cov( X ( s L), X ( t )) Cov( X ( s ), X ( t ))
(1)独立增量过程{X(t),t≧0}在X(0)=0的条件下,{X(t)}的有限维分 布函数可以由增量X(t)-X(s), 0s<t 的分布确定.
证:令Yk= X(tk )- X(tk-1 ), k=1,2, …,n. t0=0. 由条件,增量的分布已知,且具有独立增量,则
Y1,Y2, …,Yn的联合分布即可确定, 而 X(t1)=Y1, X(t2) =Y1+ Y2, ……
证明: 记Y(t )=X(t)-X(t),当X(t)具有独立增量时, Y(t )也具有独立增量;且Y(0)=0,E[Y(t )]=0,
DY(t)= E[Y2(t )]=DX(t) .所以,当0s<t 时,有
C X ( s, t ) E[Y ( s)Y (t )] E [Y ( s) Y (0)][(Y (t ) Y ( s)) Y ( s)]
P Wn t PN (t ) n e t
j n
( t ) j j!
上式对t求导,得Wn的概率密度是
t t n1 e f Wn ( t ) n 1! 0 t0 t0
定理2.设{Wn , n=1,2,…}是与泊松过程{N(t),t≥0}
s L, t L mins, t L mins L, t mins, t min
| s L t | | s t L | | s t | 2
s t 2L | s t | s t L | s t L | s t L | s L t | 2 2 2 s t | s t | 2
随机事件的来到数都可以得到一个计数过程,而同一 时刻只能至多发生一个来到的就是简单计数过程.
计数过程的一个典型的样本函数如图 N(t)
t
计数过程N(t)是独立增量过程 如果计数过程在不相重叠的时间间隔内,事件A发生的次 数是相互独立的。
计数过程N(t)是平稳增量过程 若计数过程N(t)在(t,t+s]内(S>0),事件A发生的次 数N(t+s)-N(t)仅与时间差s有关,而与t无关。
三、维纳过程 又称布朗运动
引言 维纳过程是布朗运动的数学模型. 英国植物 学家布朗在显微镜下, 观察漂浮在平静的液面上 的微小粒子, 发现它们不断地进行着杂乱无章的 运动, 这种现象后来称为布朗运动. 以W(t)表示运动中一微粒从时刻t=0到时刻t>0 的位移的横坐标(同样也可以讨论纵坐标), 且设 W(0)=0, 根据爱因斯坦1905年提出的理论, 微粒 的这种运动是由于受到大量随机的相互独立的分 子的碰撞的结果. 于是, 粒子在时段(s,t]上的位 移可以看作是许多微小位移的代数和. 则W(t)W(s)服从正态分布.
T1
T2
Tk
0
W1
W2
Wk-1 Wk
t
通常称 Wn为第n个质点出现的等待时间,Tn为第n个时 间间隔,它们都是随机变量。
定理1. 设{N(t),t≥0}是具有参数的泊松过程,
{Tn,n≥1,2,...}是对应的时间间隔序列,则随机变量序列
Tn,n=1,2,...为独立的且均服从参数为的指数分布。
若对于任意的实数s, t 和0s+h<t+h, X(t+h)-X(s+h)与X(t)-X(s)
具有相同的分布,则称增量具有平稳性,并称相应的独立增量过程为齐 次的或时齐的。
即:增量X(t)-X(s)的分布函数实际上只依赖于时间差ts,而不依赖于t与s本身,即与观察的起始时刻无关。
2.独立增量过程的性质
第十章 随机过程及统计描述
一、独立增量过程
二、泊松过程
三、维纳过程
四、高斯过程(正态过程)
一、独立增量过程
1.定义
设{X(t),t0}为一随机过程,对于0s<t,称随机变量
X(t)-X(s)为随机过程在区间[s,t]上的增量.
若对于任意的正整数n及任意的0t0<t1<t2<…<tn,n个增 量 X(t1)-X(t0),X(t2)-X(t1),…,X(tn)-X(tn-1) 相互独立,称{X(t),t0}为独立增量过程。
实际上假设了在足够小的时间间隔内出现一个质点的 概率与时间间隔成正比,而出现质点数不少于2的概率是关 于时间间隔的高阶无穷小——这一般是与实际情况相吻合 的。
2.泊松过程数字特征
3.泊松过程的一些定理
设{N(t),t≥0}为泊松过程,N(t)表示到t时刻时质点出
现的个数,W1,W2,...分别表示第一个,第二个,…质点 出现的时间,Tn(n≥1)表示从第n-1个质点出现到第n个质 点出现的时间间隔.
例.设{X(t)}是强度为的泊松过程,定义Y(t)=X(t+L)X(t),其中L>0为常数,求Y(t),RY(s,t).
解: Y(t)=E[Y(t)]=E[X(t+L)-X(t)]=(t+L)-t=L;
RY(s,t)=CY(s,t)+Y(s)Y(t), 对任意0≤s<t,有
CY ( s, t ) Cov(Y ( s),Y (t ))
对应的一等待时间序列,则Wn服从参数为n与的
分布,其概率密度为
t t n1 e t0 f Wn ( t ) n 1! 0 t0
定理3. 如果相继出现的两个质点的时间间隔是相互独
立,且服从同一指数分布,则质点流构成了强度为的
泊松过程。
该定理告诉我们确定一个过程是不是泊松过程只要用 统计方法检验点间间距是否独立且服从同一指数分布。 注:泊松过程或泊松流是研究排队理论的工具,在技术领 域内它又是构造一类重要噪声(散粒噪声)的基础。
| L | s t || | L | s t || | s t | 2
( L | s t |) 0 | s t | L | s t | L
2 L2 L | s t | | s t | L 所 以 R X ( s, t ) 2 2 | s t | L L
定义2: 称计数过程{N(t),t≧0}为具有参数>0的泊松过程, 若它满足下列条件 (1) N(0)=0;零初值性 (2) N(t)是(平稳)独立增量过程; (3) 对于任意的s,t≥0, N(t+s)-N(s)服从参数为t的泊松 k 分布 t e t PN ( t s ) N ( s ) k , k 1,2, , k! 从条件(3):泊松过程的均值函数为 N (t ) t E[ N (t )] ,表示单位时间内质点出现的平均个数,故称 t 为此过程的强度。
PN (t , t t ) 2 t
定理: 定义2与定义3是等价的。
例:设为N(t)为[0,t)时段内某电话交换台收到的呼
叫次数,t>=0, N(t)的状态空间为{0,1,2,…}, 具有如下性质: (4)在足够小的时间间隔△t内
Pt时间间隔内无呼叫 P{N (t )=0}=1- t t Pt时间间隔内有一次呼叫 P{N (t )=1}= t t Pt时间间隔内有两次以上呼叫 P{N (t )>1}= t
经过中国上空的流星流、
放射性物质所放射出的粒子流、 要求在机场降落的飞机流,等等。
随机质点流的强度:通常称单位时间内平均出现的
