求数组中最长递增子序列

合集下载

C程序经典算法50例

C程序经典算法50例1.二分查找算法：在有序数组中查找指定元素。

2.冒泡排序算法：通过不断比较相邻元素并交换位置，将较大的元素向后冒泡。

3.快速排序算法：通过选择一个基准元素，将数组分割为左右两部分，并递归地对两部分进行快速排序。

4.插入排序算法：将数组划分为已排序和未排序两部分，每次从未排序中选择一个元素插入到已排序的合适位置。

5.选择排序算法：遍历数组，每次选择最小元素并放置在已排序部分的末尾。

6.希尔排序算法：将数组按照一定间隔进行分组并分别进行插入排序，然后逐步减小间隔并重复这个过程。

7.归并排序算法：将数组递归地划分为两部分，然后将两个有序的部分进行合并。

8.桶排序算法：将元素根据特定的映射函数映射到不同的桶中，然后对每个桶分别进行排序。

9.计数排序算法：统计每个元素的出现次数，然后根据计数进行排序。

10.基数排序算法：从低位到高位依次对元素进行排序。

11.斐波那契数列算法：计算斐波那契数列的第n项。

12.阶乘算法：计算给定数字的阶乘。

13.排列问题算法：生成给定数组的全排列。

14.组合问题算法：生成给定数组的所有组合。

15.最大连续子序列和算法：找出给定数组中和最大的连续子序列。

16.最长递增子序列算法：找出给定数组中的最长递增子序列。

17.最长公共子序列算法：找出两个给定字符串的最长公共子序列。

18.最短路径算法：计算给定有向图的最短路径。

19.最小生成树算法：构建给定连通图的最小生成树。

20.汉诺塔算法：将n个圆盘从一个柱子移动到另一个柱子的问题。

21.BFS算法：广度优先算法，用于图的遍历和查找最短路径。

22.DFS算法：深度优先算法，用于图的遍历和查找连通分量。

23.KMP算法：字符串匹配算法，用于查找一个字符串是否在另一个字符串中出现。

24.贪心算法：每次都选择当前情况下最优的方案，适用于求解一些最优化问题。

25.动态规划算法：将一个大问题划分为多个子问题，并通过子问题的解求解整个问题，适用于求解一些最优化问题。

C语言实现最长递增子序列问题的解决方法

C语⾔实现最长递增⼦序列问题的解决⽅法本⽂实例展⽰了C语⾔实现最长递增⼦序列问题的解决⽅法。

分享给⼤家供⼤家参考。

具体⽅法如下：问题描述：给定⼀个序列，找出其最长递增⼦序列长度。

⽐如输⼊ 1 3 7 5输出 3算法解决思路：利⽤动态规划的思想，以序列的每个点最为最右端，找出每个点作为最右端时的⼦序列长度的最⼤值，即问题的求解。

因此，在计算前⾯的每个点的时候，将其结果保存下来，后⾯的点与前⾯的点的数值进⾏⽐较，如果⼤，则在其长度基础上加1，并且找出所有可能情况下最长的保存为当前点的长度。

形成递归。

具体实现代码如下：#include "stdio.h"#include "stdlib.h"#define MAXDATA 10000int main(){int data[MAXDATA]; /*数据序列*/int lgs[MAXDATA]; /*最长⼦序列长度*/int n,temp,k; /*n 序列长度 temp ⼦序列长度中间变量 */scanf("%d",&n);if(n>10000){return 0;}for(int i=0;i<n;i++){scanf("%d",&data[i]);}for(int i=0;i<MAXDATA;i++){lgs[i]=1; /*给每⼀个序列点作为右端时的最⼤序列长度为1*/}for(int i=1;i<n;i++){temp=1;for(int j=0;j<i;j++){ /*与其前⾯的每⼀个进⾏⽐较*/if(data[i]>data[j]){ /*如果数据⽐前⾯的某⼀个的值⼤*/if(lgs[i]+lgs[j]>temp){ /*找出该点的最⼤⼦序列长度*/temp=lgs[i]+lgs[j];}}}lgs[i]=temp;}temp=lgs[0];for(int i=1;i<n;i++){if(lgs[i]>temp){temp=lgs[i];}}printf("%d",temp);system("pause");}希望本⽂所述对⼤家C程序算法设计的学习有所帮助。

二维数组最长递增子序列

二维数组最长递增子序列在计算机科学和算法设计中，最长递增子序列（Longest Increasing Subsequence，简称LIS）是一个经典的问题，它在很多实际应用中都有重要的作用。

而二维数组最长递增子序列则是在这个问题的基础上进行了扩展，考虑了二维数组的特殊性。

我们来定义什么是二维数组的最长递增子序列。

给定一个二维数组，我们要找到其中一个最长的递增子序列，使得子序列中的元素按照从左上到右下的顺序排列。

换句话说，我们要找到一个路径，使得路径上的元素逐个递增。

这个问题可以用动态规划的方法来解决。

假设二维数组为matrix，其中matrix[i][j]表示第i行第j列的元素。

我们可以定义一个二维数组dp，其中dp[i][j]表示以matrix[i][j]为结尾的最长递增子序列的长度。

初始时，dp的所有元素都初始化为1，因为任意一个元素本身就可以作为一个递增子序列。

然后，我们从左上角开始遍历二维数组，对于每个元素matrix[i][j]，我们需要考虑它的上方、左方和左上方的元素。

如果matrix[i][j]大于这些元素，那么我们可以将它加入到以它们为结尾的递增子序列中，从而得到以matrix[i][j]为结尾的更长的递增子序列。

我们可以通过比较这些递增子序列的长度来更新dp[i][j]的值。

具体而言，我们有以下的状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1 if matrix[i][j] > matrix[i-1][j] and matrix[i][j] > matrix[i][j-1] and matrix[i][j] > matrix[i-1][j-1]dp[i][j] = 1 otherwise通过这样的动态规划过程，我们可以得到整个二维数组dp。

最终，dp中的最大值就是二维数组的最长递增子序列的长度。

动态规划-最长单调递增子序列（dp）

动态规划-最长单调递增⼦序列（dp）解题思想：动态规划1.解法1(n2)　状态：d[i] = 长度为i+1的递增⼦序列的长度　状态转移⽅程：dp[i] = max(dp[j]+1, dp[i]);分析：最开始把dp数组初始化为1，然后从前往后考虑数列的元素，对于每个aj，如果a[i] > a[j]，就⽤dp[i] = max(dp[i], dp[j] + 1)进⾏更新，再从dp数组中找出最⼤值即为结果举例：abklmncdefg dp[0] = 1; dp[1] = 2; dp[2] = 3; dp[3] = 4; dp[4] = 5; dp[5] = 6; dp[7] = 3; dp[8] = 4; dp[9] = 5; dp[10] = 6; dp[11] = 7; 最⼤值为7　代码：1 #include<iostream>2 #include<cstdio>3 #include<cstring>4using namespace std;5const int MAX_N = 10005;6int n;7char a[MAX_N];8int dp[MAX_N];9int main() {10int n;11 cin >> n;12while(n--) {13int ans = 0;14 fill(dp, dp+MAX_N, 1);15 cin >> a;16int len = strlen(a);17for(int i = 0; i < len; i++) {18for(int j = 0; j < i; j++) {19if(a[j] < a[i]) dp[i] = max(dp[i], dp[j] + 1);20 }21 ans = max(ans, dp[i]);22 }23 cout << ans << endl;24 }25return0;26 }View Code2.解法2(n2)　状态：d[i] = 长度为i+1的递增⼦序列中末尾的最⼩值(不存在就是INF)　分析：最开始⽤INF初始化dp数组的值，然后从前往后考虑数列的元素，对于每个aj，如果i = 0或者a[j] >= a[i]，使得a[j] = a[i]并且break出来，最后第⼀个dp数组中值为INF的下标即为结果　举例：abklmncdefg a; ab; abk; abkl; abklm; abklmn; abclmn; abcdmn; abcden; abcdef; abcdefg; 第⼀个INF的下标为7　　代码：1 #include<iostream>2 #include<cstdio>3 #include<cstring>4using namespace std;5const int MAX_N = 10005;6const int INF = 127;7int n;8char a[MAX_N];9char dp[MAX_N];10int main() {11int n;12 cin >> n;13while(n--) {14 fill(dp, dp+MAX_N, INF);15 cin >> a;16int len = strlen(a);17for(int i = 0; i < len; i++) {18for(int j = 0; j < len; j++) {19if(!i || dp[j] >= a[i]) {20 dp[j] = a[i]; break;21 }22 }23 }24int ans = 0;25while(dp[ans] != INF) ans++;26 cout << ans << endl;27 }28return0;29 }View Code3.解法3(nlogn)　分析：思路与解法2⼀样，但是解法2可以进⼀步优化，在解法2中dp数组是单调递增的，每次要从头到尾找到第⼀个⼤于等于a[i]的值，这是o(n2)的，既然是顺序的可以使⽤⼆分查找进⾏改进，这样可以在o(nlogn)时间内求出结果，这⾥利⽤到了STL中的lower_bound(dp, dp + n, a[i])，找出dp数组中⼤于等于a[i]的最⼩的指针，upper_boundlower_bound(dp, dp + n, a[i])，找出dp数组中⼤于a[i]的最⼤的指针代码：1 #include<iostream>2 #include<cstdio>3 #include<cstring>4 #include<algorithm>5using namespace std;6const int MAX_N = 10005;7const int INF = 127;8int n;9char a[MAX_N];10char dp[MAX_N];11int main() {12int n;13 cin >> n;14while(n--) {15 fill(dp, dp+MAX_N, INF);16 cin >> a;17int len = strlen(a);18for(int i = 0; i < len; i++) {19 *lower_bound(dp, dp+len, a[i]) = a[i];20 }21 cout << lower_bound(dp, dp+len, INF) - dp << endl;22 }23return0;24 }View Code。

软件设计师2014年11月下午题(附答案)

[需求分析结果]
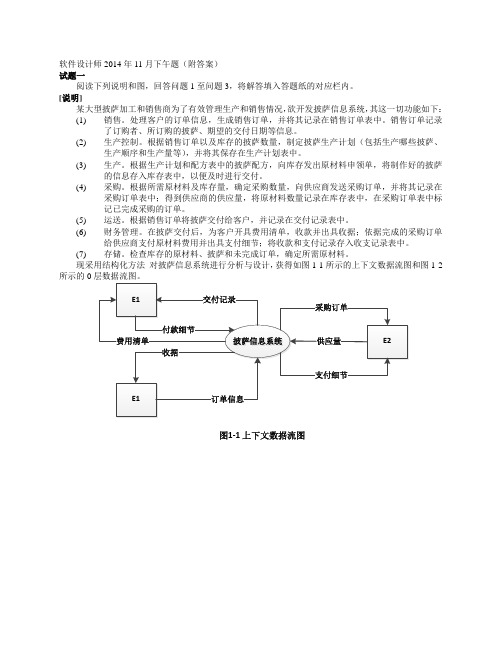
(1)超市信息包括：超市名称、地址、经理和电话，其中超市名称唯一确定超市关系的每一个元组。每个超市只有一名经理。
(2)超市设有计划部、账务部、销售部等多个部门，每个部门只有一名部门经理，有多名员工，每个员工只属于一个部门。部门信息包括：超市名称、部门名称、部门经理和联系电话。超市名称、部门名称唯一确定部门关系的每一个元组。
Light* light;
Public:
LightOffCommand(Light* light){this->light = light;}
Void execute(){(3);}
};
Class RemoteControl(//遥控器
Priavte:
Command* onCommands[7];
Command* offCommands[7];
(2)假设超市需要增设一个经理的职位，那么超市与经理之间的联系类型应修改为(d)，超市关系应修改为(e)。
试题三
阅读下列说明和图，回答问题1至问题3，将解答填入答题纸的对应栏内。
[说明]
某公司欲开发一个管理选民信息的软件系统。系统的基本需求描述如下;
(1)每个人（Person）可以是一个合法选民（Eligible）或者无效的选民（Ineligible）。
}
(1);
For(I= 1;I< n; i++){
For(j = 0; len = 0;(2); j++){
If((3)&& len < b[j])
Len = b[j];
}
(4);
}
Printf(“len: %d\n”, maxL(b,n) );

动态规划之最长递增子序列（LIS）

动态规划之最长递增⼦序列（LIS）在⼀个已知的序列{ a1,a2,……am}中，取出若⼲数组成新的序列{ ai1, ai2,…… aim},其中下标 i1,i2, ……im保持递增，即新数列中的各个数之间依旧保持原数列中的先后顺序，那么称{ ai1, ai2,……aim}为原序列的⼀个⼦序列。

若在⼦序列中，当下标 ix > iy时，aix > aiy，那么称其为原序列的⼀个递增⼦序列。

最长递增⼦序列问题就是在⼀个给定的原序列中，求得其最长递增⼦序列的长度。

求最长递增⼦序列的递推公式为：F(1) = 1;F(i) = max{ 1, F[j]+1 | aj<ai && j<i}拦截导弹题⽬描述某国为了防御敌国的导弹袭击，开发出⼀种导弹拦截系统。

但是这种导弹拦截系统有⼀个缺陷：虽然它的第⼀发炮弹能够到达任意的⾼度，但是以后每⼀发炮弹都不能⾼于前⼀发的⾼度。

某天，雷达捕捉到敌国的导弹来袭，并观测到导弹依次飞来的⾼度，请计算这套系统最多能拦截多少导弹。

拦截来袭导弹时，必须按来袭导弹袭击的时间顺序，不允许先拦截后⾯的导弹，再拦截前⾯的导弹。

输⼊描述:每组输⼊有两⾏，第⼀⾏，输⼊雷达捕捉到的敌国导弹的数量k（k<=25），第⼆⾏，输⼊k个正整数，表⽰k枚导弹的⾼度，按来袭导弹的袭击时间顺序给出，以空格分隔。

输出描述:每组输出只有⼀⾏，包含⼀个整数，表⽰最多能拦截多少枚导弹。

⽰例1输⼊8300 207 155 300 299 170 158 65输出6解题思路：要求最多能拦截多少枚导弹，即在按照袭击顺序排列的导弹⾼度中求其最长不增⼦序列。

其中F(1) = 1;F(i) = max{ 1, F[j]+1 | aj>=ai && j<i}1 #include<stdio.h>2 #include<stdlib.h>34int list[26]; //按顺序保存导弹⾼度5int dp[26]; //保存以第i个导弹结尾的最长不增长序列长度6int max( int a,int b)7 {8//选取最⼤值9return a>b? a:b;10 }11int main()12 {13int n;14int tmax,ans;15int i,j;16while( scanf("%d",&n)!=EOF)17 {18for( i=1; i<=n; i++)19 {20 scanf("%d",&list[i]);21 dp[i] = 0;22 }23for( i=1; i<=n; i++)24 {25 tmax = 1; //最长不增长⼦序列长度⾄少为126for( j=1; j<i; j++) //遍历其前所有导弹⾼度27 {28if( list[j]>=list[i]) //若j号导弹不⽐当前导弹低29 {30 tmax = max( tmax,dp[j]+1);31 }32 }33 dp[i] = tmax;34 }35 ans = 1;36for( i=1; i<=n; i++)37 ans = max( ans, dp[i]);38 printf("%d\n",ans);39 }4041return0;42 }。

java算法最长连续递增子序列

java算法最长连续递增⼦序列给定⼀个顺序存储的线性表，请设计⼀个算法查找该线性表中最长的连续递增⼦序列。

例如，(1,9,2,5,7,3,4,6,8,0)中最长的递增⼦序列为(3,4,6,8)。

输⼊格式:输⼊第1⾏给出正整数n（≤105）；第2⾏给出n个整数，其间以空格分隔。

输出格式:在⼀⾏中输出第⼀次出现的最长连续递增⼦序列，数字之间⽤空格分隔，序列结尾不能有多余空格。

输⼊样例：1. 152. 1 9 2 5 7 3 4 6 8 0 11 15 17 17 10输出样例：3 4 6 8import java.io.BufferedReader;import java.io.IOException;import java.io.InputStreamReader;public class Main {public static void main(String[] args) throws IOException {BufferedReader sr = new BufferedReader(new InputStreamReader(System.in));int n=Integer.parseInt(sr.readLine());int[] res=new int[n];String s[] = sr.readLine().split(" ");for(int i=0;i<n;i++)res[i]=Integer.parseInt(s[i]);int max=0,count=0,ss=0,x=0,y=0;for(int i=0;i<n-1;i++) {y=i+1;//判断是否递增，是的话count++;if(res[i+1]>res[i]) {count++;if(count>max) {max=count;ss=x;}}else {count=0;x=y;//不连续递增，则索引改变为下⼀个⽬标}}for(int i=ss;i<=ss+max;i++) {if(i==(ss+max)) {System.out.print(res[i]);}else {System.out.print(res[i]+" ");}}}}实现⼆：public class Sample {public static void main(String[] args) {int []nums = {1,3,4,5,6,7,2,8,9,10};for (int[] lu : findAllLowUpIndex(nums)) {System.out.printf("下标:%d, 上标:%d, 长度%d\n", lu[0], lu[1], lu[1]-lu[0]);}}public static List<int[]> findAllLowUpIndex(int[] nums) {Map<Integer, int[]> map = new HashMap<>(); //map的key是长度，value是数组的上下标for (int i=0, j=0; i<nums.length-1; i++) {for (j=i+1; j<nums.length && nums[j-1]<nums[j]; j++) {map.put(j-i, new int[] {i, j}); //j-i就是长度，i是下标，j是上标，相同长度的返回较⼤的index，所以后来的index直接覆盖之前的信息}}return map.entrySet().stream().sorted((e1,e2)->e1.getKey().compareTo(e2.getKey())) //这⾥是为了按长度排序.map(e->e.getValue()).collect(Collectors.toList()); //这⾥是去掉长度信息只保留上下标信息 }}实现三：public class Test3 {public static void main(String[] args) {int[] nums = new int[]{5, 6, 7, 0,1, 2, 3, 8, 4, 5, 7, 9, 21};calc(nums);}public static void calc(int[] nums) {int[] max = null;int start = 0;int end = 0;for (int i = 1; i < nums.length; i++) {int pre = nums[i - 1];int cur = nums[i];if (cur > pre) {end = i;}if (cur <= pre || i == nums.length - 1) {if (max == null || max[1] - max[0] <= end - start) {max = new int[]{start, end};}start = i;}}System.out.println(String.format("[%s,%s]", max[0], max[1]));}}实现四：public class Sample {public static void main(String[] args) {int []nums = {1,3,4,5,6,7,2,8,9,10,3,4,5,6,7,1,8,6,5};for (int[] lu : findAllLowUpIndex(nums)) {System.out.printf("y:%d=>%d\n", lu[0], lu[1]);}}public static List<int[]> findAllLowUpIndex(int[] nums) {List<int[]> result = new ArrayList<>();for (int i=0, j=0; i<nums.length-1; i=j) {for (j=i+1; j<nums.length && nums[j-1]<nums[j]; j++);if (j-1>i) { //长度为2以上则保存结果result.add(new int[] {i, j-1});}}return result;}}。

华为最新算法面试题目(3篇)

第1篇一、题目背景随着信息技术的飞速发展，华为作为全球领先的通信设备供应商，对于算法工程师的要求越来越高。

为了选拔出优秀的人才，华为在面试过程中设置了多轮技术面试，其中算法面试是考察应聘者逻辑思维能力、编程能力和问题解决能力的重要环节。

以下将详细介绍华为最新算法面试题目，帮助广大求职者更好地准备面试。

一、题目一：最大数组和【题目描述】给定一个整数数组，找出一个连续子数组，使其和最大。

返回这个最大和。

【输入】输入为一个整数数组，例如：[-2,1,-3,4,-1,2,1,-5,4]【输出】输出最大连续子数组的和，例如：6【思路】1. 贪心算法：从左到右遍历数组，维护一个变量currentSum，用于记录当前子数组的和。

如果currentSum小于0，则丢弃之前的元素，重新开始计算。

最大和maxSum用于记录遍历过程中遇到的最大和。

2. 动态规划：定义一个数组dp[i]，表示以第i个元素结尾的连续子数组的最大和。

dp[i]的值可以通过dp[i-1]与当前元素x的较大值来确定，即dp[i] =max(dp[i-1]+x, x)。

【示例代码】```pythondef maxSubArray(nums):if not nums:return 0currentSum, maxSum = nums[0], nums[0]for x in nums[1:]:currentSum = max(currentSum + x, x)maxSum = max(maxSum, currentSum)return maxSum```二、题目二：换零钱【题目描述】给定一个整数数组arr和一个整数aim，其中arr中的元素表示可用的零钱面额，aim表示需要凑齐的金额。

请找出最少数量的零钱，使得可以凑齐aim元。

【输入】输入为两个整数数组，例如：arr = [1, 2, 5]，aim = 11【输出】输出最少数量的零钱，例如：3【思路】1. 动态规划：定义一个数组dp[i]，表示凑齐i元需要的最少硬币数。

分组分解法的10道例题

分组分解法的10道例题分组分解法是一种常用的求解问题的方法，它通过将问题分解为若干子问题来进行求解。

这种方法在算法设计和求解复杂问题时特别有用。

接下来，我们将给出十道使用分组分解法解决的例题，并详细介绍每个例题的思路和解决方法。

1. 斐波那契数列题目描述：求取斐波那契数列第n个数的值。

思路：斐波那契数列是一个非常经典的递归问题，我们可以通过分组分解的方法来求解。

将问题分解为求取第n-1个数和第n-2个数的和，然后再依次往前递归求解，直到求取第1个数和第0个数。

然后通过逐层返回的方式求得最终结果。

2. 整数拆分题目描述：将一个正整数n分解为多个正整数的和，求分解方式的总数。

思路：通过分组分解的方法，我们可以将整数拆分问题分解为计算n减去一个正整数后的拆分方式的总数。

将问题分解为求取n-1, n-2, n-3, ..., 1的拆分方式的总数，然后相加即可得到最终结果。

3. 装箱问题题目描述：有n个物品和一些容量为C的箱子，每个物品都有一个重量和一个价值，希望找到一种装箱方式，使得装入箱子的物品总重量不超过C，同时总价值最大。

思路：装箱问题可以通过分组分解法转化为一个递归问题。

我们可以将问题分解为是否将第n个物品放入箱子中的两种情况，然后再依次递归到前面的物品。

对于每个物品，可以选择放入或不放入箱子中，然后根据递归结果，选择价值最大的情况。

4. 图的连通性题目描述：给定一个无向图，判断其中两个节点是否连通。

思路：通过分组分解的方法，可以将连通性问题分解为判断两个节点是否直接相连或者通过其他中间节点连通。

我们可以通过递归的方式，从一个节点出发，遍历所有和它直接相连的节点，然后再递归遍历这些节点，直到找到目标节点或者遍历结束。

5. 最长递增子序列题目描述：给定一个序列，找到其中最长的递增子序列的长度。

思路：最长递增子序列问题可以通过分组分解法转化为一个递归问题。

我们可以将问题分解为是否将第n个元素放入递增子序列中的两种情况，然后再依次递归到前面的元素。

lis算法详解

介绍一：LIS（Longest Increasing Subsequence）最长上升（不下降）子序列，有两种算法复杂度为O(n*logn)和O(n^2)。

在上述算法中，若使用朴素的顺序查找在D1..Dlen查找，由于共有O(n)个元素需要计算，每次计算时的复杂度是O(n)，则整个算法的时间复杂度为O(n^2)，与原来算法相比没有任何进步。

但是由于D的特点(2)，在D中查找时，可以使用二分查找高效地完成，则整个算法时间复杂度下降为O(nlogn)，有了非常显著的提高。

需要注意的是，D 在算法结束后记录的并不是一个符合题意的最长上升子序列！算法还可以扩展到整个最长子序列系列问题。

有两种算法复杂度为O(n*logn)和O(n^2)O(n^2)算法分析如下（a[1]...a[n] 存的都是输入的数）1、对于a[n]来说，由于它是最后一个数，所以当从a[n]开始查找时，只存在长度为1的不下降子序列；2、若从a[n-1]开始查找，则存在下面的两种可能性：（1）若a[n-1] < a[n] 则存在长度为2的不下降子序列a[n-1],a[n].（2）若a[n-1] > a[n] 则存在长度为1的不下降子序列a[n-1]或者a[n]。

3、一般若从a[t]开始，此时最长不下降子序列应该是按下列方法求出的：在a[t+1],a[t+2],...a[n]中，找出一个比a[t]大的且最长的不下降子序列，作为它的后继。

4、为算法上的需要，定义一个数组：d:array [1..n,1..3] of integer;d[t,1]表示a[t]d[t,2]表示从i位置到达n的最长不下降子序列的长度d[t,3]表示从i位置开始最长不下降子序列的下一个位置最长不下降子序列的O(n*logn)算法先回顾经典的O(n^2)的动态规划算法，设A[t]表示序列中的第t个数，F[t]表示从1到t 这一段中以t结尾的最长上升子序列的长度，初始时设F[t] = 0(t = 1, 2, ..., len(A))。

python经典算法100例

python经典算法100例Python是一种简单易学的编程语言，它具有丰富的库和模块，可以实现各种算法。

下面将介绍100个经典的Python算法例子，帮助读者更好地理解和掌握Python编程。

1. 二分查找算法：在有序数组中查找指定元素的位置。

2. 冒泡排序算法：对数组进行排序，每次比较相邻的两个元素并交换位置。

3. 快速排序算法：通过选择一个基准元素，将数组分为两部分，递归地对两部分进行排序。

4. 插入排序算法：将数组分为已排序和未排序两部分，每次从未排序部分选择一个元素插入到已排序部分的正确位置。

5. 选择排序算法：每次从未排序部分选择最小的元素放到已排序部分的末尾。

6. 归并排序算法：将数组分为两部分，递归地对两部分进行排序，然后将两部分合并。

7. 堆排序算法：通过构建最大堆或最小堆，将数组进行排序。

8. 计数排序算法：统计数组中每个元素的出现次数，然后按照次数进行排序。

9. 桶排序算法：将数组分为多个桶，每个桶内部进行排序，然后将桶中的元素按照顺序合并。

10. 基数排序算法：按照元素的位数进行排序，从低位到高位依次进行。

11. 斐波那契数列算法：计算斐波那契数列的第n个数。

12. 阶乘算法：计算一个数的阶乘。

13. 最大公约数算法：计算两个数的最大公约数。

14. 最小公倍数算法：计算两个数的最小公倍数。

15. 素数判断算法：判断一个数是否为素数。

16. 矩阵相加算法：计算两个矩阵的和。

17. 矩阵相乘算法：计算两个矩阵的乘积。

18. 斐波那契堆算法：实现斐波那契堆的插入、删除和合并操作。

19. 最短路径算法：计算图中两个节点之间的最短路径。

20. 最小生成树算法：计算图中的最小生成树。

21. 拓扑排序算法：对有向无环图进行拓扑排序。

22. 最大流算法：计算网络中的最大流。

23. 最小费用流算法：计算网络中的最小费用流。

24. 最大子序列和算法：计算数组中连续子序列的最大和。

25. 最长递增子序列算法：计算数组中最长递增子序列的长度。

最长单调递增子序列问题

最长单调递增子序列问题最长单调递增子序列问题是一个经典的动态规划问题，它需要找出给定序列中最长的单调递增子序列的长度。

在解决这个问题之前，我们首先来了解一下什么是单调递增子序列。

单调递增子序列是指在给定序列中，选取若干元素组成新的序列，使得新序列中的元素逐个递增。

例如，对于序列[1, 3, 2, 5, 4, 6]，其最长的单调递增子序列为[1, 2, 4, 6]，长度为4。

解决最长单调递增子序列问题的一个常用方法是动态规划。

我们可以定义一个长度与给定序列相同的数组dp，其中dp[i]表示以第i 个元素结尾的最长单调递增子序列的长度。

初始时，所有元素的最长单调递增子序列长度都为1，即dp[i]=1。

然后，我们可以通过遍历给定序列的每个元素，计算dp[i]的值。

具体的计算方法是，对于给定序列中的第i个元素，我们可以从第1个元素到第i-1个元素中选择一个小于第i个元素的元素，将其加入到以第i个元素结尾的最长单调递增子序列中，从而得到一个长度加1的递增子序列。

我们选择其中长度最长的递增子序列，将其长度加1作为dp[i]的值。

通过这种方法，我们可以依次计算出dp[1]、dp[2]、...、dp[n]的值，其中n为给定序列的长度。

最终，最长单调递增子序列的长度即为dp数组中的最大值。

下面，我们以一个具体的例子来说明这个算法的过程。

假设给定序列为[1, 3, 2, 5, 4, 6]。

初始化dp数组为[1, 1, 1, 1, 1, 1]，因为每个元素本身就构成一个长度为1的递增子序列。

然后，从第2个元素开始遍历给定序列。

对于第2个元素3，我们可以选择第1个元素1作为它的前一个元素，得到长度为2的递增子序列[1, 3]。

因此，更新dp[2]的值为2。

接下来，对于第3个元素2，我们可以选择第1个元素1作为它的前一个元素，得到长度为2的递增子序列[1, 2]。

因此，更新dp[3]的值为2。

对于第4个元素5，我们可以选择第1个元素1或者第3个元素2作为它的前一个元素，得到长度为2的递增子序列[1, 5]或者[2, 5]。

最长严格递增子序列长度

最长严格递增子序列最长严格递增子序列（Longest Increasing Subsequence，简称LIS）是序列的一个重要特性，它在算法和数据结构中都有广泛的应用。

在给出最长严格递增子序列的长度时，我们首先需要了解这个序列的特性。

定义：设A 是一个有限序列，如果存在一个索引集合I，使得对于所有的i∈I，都有A[i]>A[j]，其中j∈I 且j<i，那么我们称A[I] 是A 的一个最长严格递增子序列。

为了求解最长严格递增子序列的长度，我们可以使用动态规划的方法。

假设A 是一个长度为n 的序列，我们定义一个数组dp，其中dp[i] 表示以A[i] 结尾的最长严格递增子序列的长度。

显然，如果A[i] 是序列中的最小值，那么以A[i] 结尾的最长严格递增子序列的长度就是1。

否则，我们可以考虑在A[i] 之前的所有元素中，哪些元素的严格递增子序列可以以A[i] 结尾。

对于每一个这样的元素A[j]，如果dp[j]+1>dp[i]，那么我们就更新dp[i] 为dp[j]+1。

最终，最长严格递增子序列的长度就是所有dp[i] 中的最大值。

下面是一个简单的Python 实现：pythondef length_of_LIS(A):n = len(A)if n == 0:return 0dp = [1] * nfor i in range(1, n):for j in range(i):if A[j] < A[i] and dp[j] + 1 > dp[i]:dp[i] = dp[j] + 1return max(dp)在最坏情况下，这个算法的时间复杂度是O(n2)。

然而，如果序列是有序的，那么最长严格递增子序列的长度就是序列的长度，而我们可以通过线性扫描来求解。

因此，在最好情况下，时间复杂度是O(n)。

动态规划应用案例

动态规划应用案例动态规划是一种解决复杂问题的优化算法。

它通过将问题拆分成多个子问题，并记录每个子问题的解，以避免重复计算，从而提高算法的效率。

在实际应用中，动态规划被广泛用于解决各种问题，包括最优化问题、路径搜索问题、序列问题等。

本文将介绍几个动态规划的应用案例，以展示其在实际问题中的强大能力。

案例一：背包问题背包问题是动态规划中经典的一个例子。

假设有一个背包，容量为V，现有n个物品，每个物品的重量为wi，价值为vi。

要求在不超过背包容量的前提下，选取一些物品放入背包，使得背包中的物品总价值最大。

这个问题可以用动态规划来解决。

首先定义一个二维数组dp，其中dp[i][j]表示在前i个物品中选择一些物品，使得它们的总重量不超过j时的最大总价值。

然后，可以得到如下的状态转移方程：dp[i][j] = max(dp[i-1][j], dp[i-1][j-wi] + vi)最后，根据状态转移方程，可以循环计算出dp[n][V]的值，即背包中物品总价值的最大值，从而解决了背包问题。

案例二：最长递增子序列最长递增子序列是指在一个序列中，选取一些数字，使得这些数字按照顺序排列，且长度最长。

动态规划也可以应用于解决最长递增子序列问题。

假设有一个序列nums，长度为n。

定义一个一维数组dp，其中dp[i]表示以nums[i]为结尾的最长递增子序列的长度。

然后，可以得到如下的状态转移方程：dp[i] = max(dp[j] + 1)，其中j < i且nums[j] < nums[i]最后，循环计算出dp数组中的最大值，即为最长递增子序列的长度。

案例三：最大子数组和最大子数组和问题是指在一个数组中，选取一段连续的子数组，使得子数组的和最大。

动态规划也可以用于解决最大子数组和问题。

假设有一个数组nums，长度为n。

定义一个一维数组dp，其中dp[i]表示以nums[i]为结尾的连续子数组的最大和。

然后，可以得到如下的状态转移方程：dp[i] = max(dp[i-1] + nums[i], nums[i])最后，循环计算出dp数组中的最大值，即为最大子数组的和。

亮点给力大试卷年级【含答案】

亮点给力大试卷年级【含答案】专业课原理概述部分一、选择题（每题1分，共5分）1. 下列哪个概念是“专业课原理概述部分”中的核心概念？A. 数据结构B. 算法分析C. 编程语言D. 计算机组成原理2. 在“专业课原理概述部分”中，下列哪种方法是常用于解决复杂问题的？A. 逐步求精B. 模块化设计C. 递归算法D. 整体优化3. 下列哪个是“专业课原理概述部分”中讨论的主要问题？A. 程序设计B. 数据库管理C. 计算机网络D. 操作系统4. 在“专业课原理概述部分”中，下列哪种技术是用于提高算法效率的？A. 贪心算法B. 动态规划C. 分治算法D. 回溯算法5. 下列哪个是“专业课原理概述部分”中讨论的主要应用领域？A.B. 计算机图形学C. 网络安全D. 数据挖掘二、判断题（每题1分，共5分）1. “专业课原理概述部分”主要讨论的是计算机科学的基本原理。

（）2. 在“专业课原理概述部分”中，算法的效率通常是通过时间复杂度和空间复杂度来衡量的。

（）3. “专业课原理概述部分”中，数据结构是解决问题的关键。

（）4. 在“专业课原理概述部分”中，编程语言的选择对算法的实现没有影响。

（）5. “专业课原理概述部分”主要讨论的是计算机硬件的基本原理。

（）三、填空题（每题1分，共5分）1. “专业课原理概述部分”中，算法的时间复杂度通常用来衡量算法的______。

2. 在“专业课原理概述部分”中，______是一种常见的数据结构，用于存储具有相同数据类型的元素。

3. “专业课原理概述部分”中，______是一种常见的算法设计技术，用于将复杂问题分解为更小的子问题。

4. 在“专业课原理概述部分”中，______是一种常见的编程范式，用于描述程序的执行流程。

5. “专业课原理概述部分”中，______是一种常见的算法分析技术，用于比较不同算法的效率。

四、简答题（每题2分，共10分）1. 简述“专业课原理概述部分”中算法的时间复杂度和空间复杂度的概念。

高中信息奥赛试题及答案

高中信息奥赛试题及答案试题一：算法设计题目：给定一个整数数组，找出其中最长的连续递增子序列的长度。

要求：1. 编写一个函数，输入为整数数组，输出为最长连续递增子序列的长度。

2. 考虑时间复杂度和空间复杂度。

答案：```pythondef find_longest_increasing_subsequence(arr):if not arr:return 0n = len(arr)dp = [1] * n # dp[i] 表示以 arr[i] 结尾的最长递增子序列长度max_length = 1 # 至少包含一个元素for i in range(1, n):for j in range(i):if arr[j] < arr[i]:dp[i] = max(dp[i], dp[j] + 1)max_length = max(max_length, dp[i])return max_length```试题二：数据结构题目：设计一个队列，支持以下操作：1. 入队（enqueue）2. 出队（dequeue）3. 获取队列大小（size）4. 判断队列是否为空（is_empty）要求：1. 使用链表实现队列。

2. 确保所有操作的时间复杂度为 O(1)。

答案：```pythonclass Node:def __init__(self, value):self.value = valueself.next = Noneclass Queue:def __init__(self):self.head = Noneself.tail = Noneself.size = 0def enqueue(self, value):new_node = Node(value)if self.is_empty():self.head = new_nodeelse:self.tail.next = new_node self.tail = new_nodeself.size += 1def dequeue(self):if self.is_empty():raise Exception("Queue is empty")value = self.head.valueself.head = self.head.nextif self.head is None:self.tail = Noneself.size -= 1return valuedef size(self):return self.sizedef is_empty(self):return self.size == 0```试题三：编程语言特性题目：请解释以下C++代码片段的功能，并指出可能的问题。

计算机面试题目(3篇)

第1篇一、基础知识1. 请解释一下什么是位运算，并举例说明其应用场景。

位运算是指对二进制位进行操作的运算，主要包括按位与（&）、按位或（|）、按位异或（^）、按位取反（~）、左移（<<）和右移（>>）等。

以下是一些应用场景：（1）按位与：用于判断两个整数的某一位是否同时为1。

（2）按位或：用于将两个整数的对应位进行或运算，得到结果。

（3）按位异或：用于将两个整数的对应位进行异或运算，如果两个位相同，则结果为0；如果两个位不同，则结果为1。

（4）按位取反：用于将整数的每一位取反，即将0变为1，将1变为0。

（5）左移：用于将整数的二进制表示向左移动指定的位数，右边的位被丢弃，左边补0。

（6）右移：用于将整数的二进制表示向右移动指定的位数，左边的位被丢弃，右边补0。

2. 请解释一下什么是数据类型，并列举常见的几种数据类型。

数据类型是指用于定义变量存储的数据种类的类型。

以下是一些常见的几种数据类型：（1）整型（int）：用于存储整数，如int a = 10；（2）浮点型（float、double）：用于存储实数，如float b = 3.14；（3）字符型（char）：用于存储单个字符，如char c = 'A'；（4）布尔型（bool）：用于存储布尔值，如bool d = true；（5）数组：用于存储一系列相同类型的数据，如int arr[10]；（6）结构体（struct）：用于存储不同类型的数据，如struct Person {int age; char name[20];}；（7）指针：用于存储变量的地址，如int ptr = &a。

3. 请解释一下什么是面向对象编程，并举例说明其应用场景。

面向对象编程（OOP）是一种编程范式，它将数据和行为封装在对象中，强调继承、封装和多态。

以下是一些应用场景：（1）设计大型软件系统，如操作系统、数据库等；（2）开发图形用户界面（GUI）应用程序；（3）开发网络应用程序，如Web应用、移动应用等；（4）开发游戏和模拟软件。

双端diff算法和最长递增子序列-概述说明以及解释

双端diff算法和最长递增子序列-概述说明以及解释1.引言文章1.1 概述：双端diff算法和最长递增子序列是两种常用的算法，在软件开发和数据处理领域有着广泛的应用。

双端diff算法用于比较两个文本之间的差异，可以用于版本控制系统、代码审查工具等场景。

最长递增子序列是一个经典的动态规划问题，用于求解给定序列中最长的递增子序列，可以应用于任务调度、DNA序列分析等领域。

本文首先介绍了双端diff算法的原理和实现步骤。

双端diff算法通过将两个文本同时从头和尾部进行比较，以便更准确地找到差异部分。

该算法分为两个主要步骤：首先，通过计算输入文本的行号和内容的哈希值，构建两个文本的哈希字典。

然后，通过比较哈希字典的方式，快速找到两个文本之间的差异部分。

通过引入双端比较的思想，双端diff算法在效率和准确性方面都有着良好的表现。

接下来，本文介绍了最长递增子序列的定义与性质以及求解方法。

最长递增子序列是指在给定序列中找到最长的递增数字序列，该子序列中的元素保持原序列中的相对顺序。

本文介绍了通过动态规划算法来解决最长递增子序列问题的基本思想和步骤。

该算法通过定义状态和状态转移方程，可以高效地求解给定序列的最长递增子序列。

最后，本文总结了双端diff算法和最长递增子序列的主要内容，并展望了它们在未来的应用前景。

双端diff算法可以进一步改进以提高比较效率和准确性，为软件开发和数据处理提供更好的支持。

最长递增子序列算法可以应用于更多领域，如机器学习、自然语言处理等，为解决实际问题提供更多可能性。

通过本文的介绍，读者将对双端diff算法和最长递增子序列有更全面的了解，并能够在实际应用中灵活运用它们来解决相应的问题。

对于软件开发人员和数据处理工程师来说，掌握这两种算法将有助于提高工作效率和质量。

文章结构部分的内容可以描述整篇文章的组织和内容安排。

以下是文章结构部分的可能内容：1.2 文章结构本文将会介绍双端diff算法和最长递增子序列两个重要的算法。

软件设计师算法题

软件设计师算法题一、简介本题库是为了帮助软件设计师更好地掌握算法和数据结构相关知识而设计的。

通过解答这些题目，软件设计师可以更好地理解算法的原理、设计和实现方法，提高解决实际问题的能力。

二、题目列表1.合并两个有序链表给定两个单链表l1和l2，合并后得到的链表l并返回。

假设链表已经有序，不进行交换和重构。

2.找到最大的子数组和给定一个整数数组nums和一个整数target，返回以nums[i]为右边的最大子数组和。

假设nums数组中存在重复元素，但只考虑不重复的元素。

3.数组中出现次数超过一半的数字给定一个整数数组nums，找到出现次数超过数组长度一半的数字，并返回其索引位置。

4.最长回文子串给定一个字符串s，找到最长的回文子串，并返回其长度。

可以使用动态规划或双指针等方法解决。

5.数组中出现次数超过n/3的数字给定一个整数数组nums，找到出现次数超过n/3的数字，并返回其索引位置。

6.斐波那契数列给定两个整数p1和p2，返回从p1开始到p2之间的斐波那契数列（包括p1和p2）。

可以使用动态规划或递归等方法解决。

7.字符串匹配算法实现给定一个主字符串text和一个模式字符串pattern，在主字符串中查找模式字符串的出现位置，并返回第一个出现的位置。

可以使用KMP算法、BM算法或朴素算法等方法实现。

8.最长递增子序列给定一个整数数组nums，找到最长递增子序列的长度，并返回该长度。

可以使用动态规划或双指针等方法解决。

三、答案解析1.合并两个有序链表答案：首先定义两个链表的头结点head1和head2，分别表示两个链表的起始位置。

然后使用双指针法将两个链表合并成一个有序链表l，其中一个指针从head1开始遍历l1，另一个指针从head2开始遍历l2。

当其中一个链表遍历完之后，将另一个链表剩余的部分依次加入到l中即可得到最终结果。

最后返回链表l的头结点即可。

解析：本题主要考察链表的合并操作和有序链表的实现方法。