小数乘法单元知识结构
小数乘法知识点总结六年级

小数乘法知识点总结六年级小数乘法知识点总结小数乘法是数学中的一种基本运算,它在六年级的学习中是非常重要的一部分。
掌握了小数乘法的知识点,可以帮助我们更好地解决实际问题。
本文将对小数乘法的知识点进行总结,并阐述其应用。
一、小数的基本概念小数是指整数与分数之间的数,用小数点表示。
在小数中,小数点的位置可以是任意的,位于小数点左边的数是整数,位于小数点右边的数是小数部分。
二、小数的乘法运算法则小数的乘法运算与整数的乘法运算类似,只要注意小数点的位置即可。
具体运算步骤如下:1. 把两个小数的小数点对齐,使得它们的小数点在同一列;2. 从右到左,按位相乘,进行乘法运算;3. 将所得的乘积进行进位操作,使得小数点在正确的位置;4. 若有多个小数相乘,重复以上步骤。
三、小数乘以整数小数乘以整数的运算方法较为简单,将整数乘以小数的整数部分,然后将小数点移到正确的位置即可。
例如:0.2 × 6 = 1.2四、小数乘以小数小数乘以小数需要注意小数点的位置,并进行适当的进位操作。
具体操作如下:1. 将小数转化为分数,使得计算更加简便;2. 按照小数的乘法运算规则计算;3. 乘法运算完成后,将所得的分数化简为最简形式;4. 若需要,将分数转化为小数形式。
五、小数乘法的应用小数乘法在实际生活中有着广泛的应用。
下面以几个例子来说明:1. 钱的计算:小数乘法在计算打折、找零等场景中发挥着重要作用。
通过小数乘法,我们可以快速计算出折扣后的价格,或者计算出找零的金额。
2. 长度的计算:当我们需要计算长度的时候,有时会遇到小数乘法的情况。
比如,当我们需要计算长方形的面积时,需要将两个小数相乘。
3. 科学实验:在科学实验中,小数乘法也经常被使用。
比如,在计算浓度、体积、密度等方面,都需要进行小数乘法运算来获得准确的结果。
六、小数乘法的拓展除了基础的小数乘法运算,六年级的学习还会拓展到更加复杂的小数乘法知识。
例如,带有括号的小数乘法、小数与整数的混合运算等等。
小数乘法知识点总结

小数乘法知识点总结小数乘法是数学中的一项基本运算,它涉及到小数的计算和推导,是我们在日常生活和学习中经常会遇到的问题。
下面将对小数乘法的一些基本知识点进行总结和梳理,希望对大家理解和掌握小数乘法有所帮助。
一、小数的乘法原理小数的乘法可以通过对小数点的位置进行对齐,然后按照整数的乘法法则进行运算。
具体来说,就是先不考虑小数点,将两个数按照整数的乘法进行计算,然后再根据小数位数确定小数点的位置。
例如,计算0.5乘以0.2,可以先将小数点移动两位,变为整数相乘,得到结果10,再根据原来小数点的位置,将结果右移两位,得到最终结果0.1。
二、小数的位数运算在小数乘法中,我们需要注意处理小数位数的运算。
当两个小数相乘时,小数位数的和就是最终结果的小数位数。
因此,在进行计算时,我们要注意保持小数位数的一致性。
例如,计算0.25乘以0.3,首先对齐小数点,然后按照整数的乘法进行计算,得到结果075。
最后,根据原来小数点的位置,将结果右移两位,得到最终结果0.075。
三、小数与整数的乘法在小数乘法中,我们还经常会遇到小数与整数相乘的情况。
这时,我们可以将整数看作小数的特殊形式,即整数后有一个小数点。
例如,计算2.5乘以6,可以先将6看作6.0,然后进行小数乘法的运算。
对齐小数点,得到结果150.0,再去掉末尾多余的0,得到最终结果150.四、小数乘以小数的运算顺序在多个小数相乘的运算中,我们可以改变运算的顺序,但结果不会受到影响。
这是因为小数的乘法满足交换律。
例如,计算0.2乘以0.3乘以0.4,可以先计算两个小数的乘积,再与第三个小数相乘;也可以先计算第二个小数与第三个小数的乘积,再与第一个小数相乘。
两种方式得到的结果都是0.024。
五、应用实例:计算总价小数乘法在日常生活中有着广泛的应用,例如计算购物时的总价。
假设购买了一台价格为1299.99元的电视机,折扣为0.75,需要计算打折后的价格。
我们可以先计算折扣后的价格,再用原价减去折扣后的价格,得到优惠的金额。
小数乘法知识点总结

小数乘法知识点总结
意义:小数乘法的意义在于求几个相同加数的和的简便运算,或者是求一个数的几分之几是多少。
例如,3.2+3.2+3.2+3.2+3.2可以表示为3.2×5,意义是5个3.2的和;而1.5×0.8则是求1.5的十分之八是多少。
计算方法:首先,将小数扩大成整数,然后按照整数乘法的法则进行计算。
接着,看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
最后,如果计算结果中小数部分末尾有0,则可以去掉,将小数化简。
积的扩大缩小规律:在乘法中,如果一个因数不变,另一个因数扩大或缩小a倍,那么积也会扩大或缩小a倍。
同时,如果两个因数都扩大或缩小,那么积会扩大或缩小相应的倍数。
估算:小数乘法估算的方法通常是将两个因数四舍五入保留整数,然后再进行相乘。
此外,还可以使用其他估算方法,如根据积与因数的关系来估算。
运算顺序:小数四则混合运算的顺序与整数四则混合运算的顺序相同。
同级运算,从左往右;两级运算,先二后一;有括号的,先里后外。
此外,乘法的交换律、结合律、分配律同样适用于小数乘法。
求近似数的方法:求小数乘法的近似数通常使用四舍五入法。
根据要精确的位数下一位的值,如果大于等于5则入1到前一位,如果小于等于4则舍去。
以上是小数乘法的知识点总结,包括了小数乘法的意义、计算方法、积的扩大缩小规律、估算、运算顺序以及求近似数的方法等内容。
小数乘法知识点总结简单

小数乘法知识点总结简单一、小数乘法的基本规则1. 小数相乘的运算法则是先忽略小数点,将小数转换为整数相乘,然后再进行小数点的位置确定。
在进行小数乘法的运算时,先将小数乘法转化为整数乘法,然后再确定小数点的位置。
2. 小数与整数相乘:小数与整数相乘时,可以将小数点去掉,将小数转换为整数,然后进行整数相乘的运算,最后再根据小数点的位置确定结果的小数点位置。
3. 两个小数相乘:两个小数相乘时,先将小数转为整数,然后进行整数相乘的运算,最后根据小数位数确定结果的小数点位置。
4. 整数乘以小数:整数乘以小数时,可以将小数点去掉,将小数转换为整数,然后进行整数相乘的运算,最后根据小数点的位置确定结果的小数点位置。
5. 正负数相乘:正数与正数相乘,结果为正数;负数与负数相乘,结果为正数;正数与负数相乘,结果为负数。
二、小数乘法的计算方法小数乘法的计算方法主要有以下几种:1. 规范乘法:两个小数相乘时,先将小数转为整数,然后进行整数相乘的运算,最后根据小数位数确定结果的小数点位置。
例如:计算0.5×0.3将小数转为整数,即50×3=150,然后根据小数点位置确定结果的小数点位置,0.5对应一位小数,0.3对应一位小数,共两位小数,所以结果为0.15。
2. 分步乘法:两个小数相乘时,可以先将小数表示为分数,然后进行分数相乘,最后将结果化为小数形式。
例如:计算0.6×0.7将小数表示为分数,即0.6=6/10,0.7=7/10,然后进行分数相乘,得42/100,最后将结果化为小数形式,即0.42。
3. 计算法则:小数乘法遵循整数乘法的计算法则,注意保留正确的小数位数,避免出现计算错误。
例如:计算0.25×0.4先将小数转为整数,即25×4=100,然后根据小数点位置确定结果的小数点位置,0.25对应两位小数,0.4对应一位小数,共三位小数,所以结果为0.1。
三、小数乘法的应用技巧1. 对于小数乘法的计算,可以将小数转为整数进行计算,然后再确定小数点的位置,避免出现计算错误。
《小数乘法》知识结构图

基本信息
姓名:杨会春性别:女年龄:37
学历:本科职称:小学高级教龄:18
职务:教师所任学科:数学
教材版本:人教版单元名称:五年级上册第一单元(专题)第课
《小数乘法》
知识结构分析
第一单元小数乘法
1、小数乘整数小数乘整数与整数乘法的联系;小数乘整数的计算方法
2、小数乘小数小数乘小数的计算方法;积与因数的关系
3、倍数是小数的实际问题和乘法验算一个数的小数倍数是多少的问题的解题方法;
小数乘法的验算方法
4、积的近似数用“四舍五入”法求出积的近似数
5、整数乘法运算定律推广到小数运用运算定律进行简便计算
6、解决问题用小数的估算解决购物问题;用小数乘加、乘减解决问题。
小数乘法与小数除法平移旋转知识结构

小数乘法知识结构1、积的扩大缩小规律:1)在乘法里,一个因数不变,另外一个因数扩大(或缩小)a倍,积也扩大(或缩小)a倍。
2)在乘法里,一个因数扩大a 倍,另外一个因数扩大(或缩小)b倍,积就扩大(或缩小)a×b倍。
3)在乘法里,一个因数缩小a 倍,另外一个因数缩小b倍,积就缩小a×b倍。
4)在乘法里,如果一个因数扩大10倍、100倍、1000倍…,另外一个因数缩小10倍、100倍、1000倍…,那么积的扩大或缩小就看a和b的大小,哪个大就顺从哪个。
2、积不变规律:在乘法里,一个因数扩大a 倍,另外一个因数缩小a倍,积不变。
3、小数乘整数计算方法:1)先把小数扩大成整数2)按整数乘法乘法法则计算出积3)看被乘数有几位小数点,就从积的右边起数出几位点上小数点。
若积的末尾有0可以去掉4、小数乘小数的计算方法:1)先把小数扩大成整数2)按整数乘法乘法法则计算出积3)看积中有几位小数就从积的右边起数出几位,点上小数点。
如果乘得的积的位数不够,要在前面用0补足。
5、计算结果发现小数末尾有0的,要先点小数点,再把0去掉。
顺序不可调换。
6、积的小数位数等于两个因数的小数位数之和。
7、小数点的位移规律:把一个小数扩大10倍、100倍、1000倍、……只要把小数点向右移动一位、两位、三位……位数不够时,要用“0”补足。
把一个小数缩小10倍、100倍、1000倍、……只要把小数点向左移动一位、两位、三位……位数不够时,要用“0”补足。
数小数点的方法:1、数数字2、数间隔8、一个数(0除外)乘大于1的数,积比原来的数大。
一个数(0除外)乘小于1的数,积比原来的数小。
9、小数的四则混合运算和整数相同,都是先算乘法和除法,再算加法和减法,有小括号的要先算小括号里的。
10、乘法的交换律、结合律、分配律同样适用于小数乘法,应用这些运算定律,可以使计算简便。
乘法交换律 a×b=b×a乘法结合律 a×(b×c)=(a×b)×c乘法分配律 a×(b+c)=a×b+a×c a×(b—c)=a×b — a×c11、积的近似数:保留a位小数,就看第a+1位,再用四舍五入的方法取值。
《小数乘法》知识点

《小数乘法》知识点小数乘法是数学中一个重要的计算内容,它在日常生活和学习中都有广泛的应用。
下面我们就来详细了解一下小数乘法的相关知识。
一、小数乘法的意义小数乘法的意义与整数乘法的意义相同,都是求几个相同加数的和的简便运算。
例如,05×3 表示 3 个 05 相加的和是多少。
但在实际应用中,小数乘法还有另外的意义。
比如,05×12 可以表示 05 的 12 倍是多少。
二、小数乘法的计算方法1、先按照整数乘法的计算方法算出积。
2、看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
3、如果积的小数位数不够,就在前面用 0 补足,再点上小数点。
4、如果积的末尾有 0,要先点小数点,再根据小数的性质去掉积末尾的 0。
例如:计算 25×04先计算 25×4 = 100因为 25 有一位小数,04 有一位小数,一共有两位小数,所以从积的右边起数出两位,点上小数点,得到 100,化简为 1。
三、积的变化规律1、一个因数不变,另一个因数扩大(或缩小)几倍,积也扩大(或缩小)相同的倍数。
例如:25×4 = 10,如果 25 不变,4 扩大 2 倍变成 8,那么积就扩大 2 倍,变成 20。
2、一个因数扩大(或缩小)a 倍,另一个因数扩大(或缩小)b 倍,积就扩大(或缩小)a×b 倍。
比如:12×2 = 24,如果 12 扩大 3 倍变成 36,2 扩大 2 倍变成 4,那么积就扩大 3×2 = 6 倍,变成 144。
3、一个因数扩大 a 倍,另一个因数缩小 b 倍,如果 a>b,积就扩大(a÷b)倍;如果 a<b,积就缩小(b÷a)倍。
例如:3×4 = 12,3 扩大 5 倍变成 15,4 缩小 2 倍变成 2,因为 5>2,所以积扩大 5÷2 = 25 倍,变成 30。
四、小数乘法的运算定律小数乘法同样适用整数乘法的运算定律,包括乘法交换律、乘法结合律和乘法分配律。
小数乘法单元知识图(陈莉)
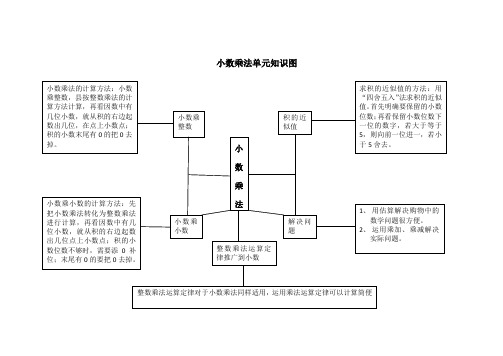
小数乘 整数
积的近 似值
小 数 乘
小数乘小数的计算方法:先 把小数乘法转化为整数乘法 进行计算,再看因数中有几 位小数,就从积的右边起数 出几位点上小数点;积的小 数位数不够时,需要添 0 补 位;末尾有 0 的要把 0 去掉。
法
小数乘 小数 整数乘法运算定 律推广到小数 解决问 题
1、 用估算解决购物中的 数学问题很方便。 2、 运用乘加、乘减解决 实际问题。
整数乘法运算定律对于小数乘法同样适用,运用乘法运算定律可以计算简便
小数乘法单元知识图
小数乘法的计算方法:小数 乘整数,县按整数乘法的计 算方法计算,再看因数中有 几位小数,就从积的右边起 数出几位,在点上小数点; 积的小数末尾有 0 的把 0 去 掉。 求积的近似值的方法:用 “四舍五入” 法求积的近似 值。 首先明确要保留的小数 位数; 再看保留小数位数下 一位的数字,若大于等于 5,则向前一位进一,若小 于 5 舍去。
小数乘法知识点汇总

小数乘法知识点汇总在数学学习中,小数乘法是一个重要的知识点,掌握小数乘法的方法和技巧对于解决实际问题具有重要意义。
本文将对小数乘法的相关知识进行汇总,包括小数相乘的基本原理、运算规则与技巧、实际应用等。
通过对这些知识点的综合了解,相信读者能够更好地掌握小数乘法的要点,并在实际应用中灵活运用。
一、小数相乘的基本原理小数相乘的基本原理是将小数转化为分数,然后按照分数乘法的规则进行计算。
具体来说,我们可以将小数表示为分子除以分母的形式,然后将两个小数相乘时,将其转化为两个分数的乘法,最后将结果转化为小数形式。
举例说明:0.5 × 0.3 = (5/10) × (3/10) = 5 × 3 / 10 × 10 = 15 / 100 = 0.15二、小数相乘的运算规则与技巧1. 小数点的位置:两个小数相乘时,先按照整数相乘的方法计算出结果,然后将小数点的位置确定在计算结果的右侧。
具体方法是,将两个小数的小数位数相加,然后将小数点向左移动相应的位数。
举例说明:0.6 × 0.8 = 48, 小数位数之和为2位,所以结果应该保留2位小数,即0.48。
2. 乘法运算顺序:当需要计算多个小数相乘时,可以按照任意顺序进行运算,结果都是相同的。
举例说明:0.4 × 0.2 × 0.1 = (0.4 × 0.2) × 0.1 = 0.08 × 0.1 = 0.0083. 近似计算:当进行小数相乘时,可以先进行粗略的估算,然后根据需要确定结果的有效位数。
举例说明:0.02 × 0.03 ≈ 0.02 × 0.03 = 0.0006 (估算)三、小数相乘的实际应用小数相乘在日常生活和学习中有着广泛的应用,特别是在测量、货币计算和比例问题中。
1. 测量:在测量长度、重量和时间等物理量时,常常需要进行小数相乘来计算。
五年级上册数学全册知识结构图+知识要点.重点.难点梳理期末复习必备

五年级上册数学全册知识结构图+知识要点.重点.难点梳理!期末复习必备!第一单元小数乘法1.小数乘整数:意义——求几个相同加数的和的简便运算。
如:1.5×3表示1.5的3倍是多少或3个1.5是多少。
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
2.小数乘小数:意义——就是求这个数的几分之几是多少。
如:1.5×0.8(整数部分是0)就是求1.5的十分之八是多少。
1.5×1.8(整数部分不是0)就是求1.5的1.8倍是多少。
计算方法:先把小数扩大成整数;按整数乘法的法则算出积;再看因数中一共有几位小数,就从积的右边起数出几位点上小数点。
注意:计算结果中,小数部分末尾的0要去掉,把小数化简;小数部分位数不够时,要用0占位。
3.规律:一个数(0除外)乘大于1的数,积比原来的数大;一个数(0除外)乘小于1的数,积比原来的数小。
4.求近似数的方法一般有三种:⑴四舍五入法;⑵进一法;⑶去尾法5.计算钱数,保留两位小数,表示计算到分。
保留一位小数,表示计算到角。
6.小数四则运算顺序跟整数是一样的。
7.运算定律和性质:加法:加法交换律:a+b=b+a加法结合律:(a+b)+c=a+(b+c)乘法:乘法交换律:a×b=b×a乘法结合律:(a×b)×c=a×(b×c)乘法分配律:(a+b)×c=a×c+b×c或a×c+b×c=(a+b)×c(b=1时,省略b)变式:(a-b)×c=a×c-b×c或a×c-b×c=(a-b)×c减法:减法性质:a-b-c=a-(b+c)除法:除法性质:a÷b÷c=a÷(b×c)第二单元位置8.确定物体的位置,要用到数对(先列:即竖,后行即横排)。
小数乘法知识点公式总结

小数乘法知识点公式总结一、小数乘法的基本概念1. 小数的定义:小数是指整数和分数之间的数,其数值介于两个整数之间。
2. 小数点的作用:小数点用于将整数部分和小数部分分开,小数点的位置决定了小数的大小。
3. 小数乘法的含义:小数乘法是指两个小数相乘的运算,其规则与整数乘法相同。
二、小数乘法的运算规则1. 保留小数点的位置:小数乘法中,我们需要注意小数点的位置,乘法运算后,小数点的位置为两个小数点的位数之和。
2. 0的处理:当小数乘法中出现0时,我们需要注意0的位置和作用,0与其他数相乘的结果都为0。
3. 进位和舍位:小数乘法中,我们需要注意进位和舍位的规则,乘法运算结果需要进行进一步的取舍。
三、小数乘法的公式1. 十进制乘法的公式:a) 小数乘法的公式:a.b x c.d = (a x c) + (a x d/10) + (b x c/10) + (b x d/100)b) 例如:2.3 x 4.5 = 10.352. 百分数乘法的公式:a) 百分数乘法的公式:a% x b% = (a x b)/10000b) 例如:25% x 40% = (25 x 40)/10000 = 1000/10000 = 0.13. 小数点乘法的公式:a) 小数点乘法的公式:0.a x 0.b = a x b/100b) 例如:0.25 x 0.4 = 25/100 = 0.1四、小数乘法的解题技巧1. 理解小数乘法的含义:在解题时,我们需要理解小数乘法的含义,明确小数点的位置和数字的含义。
2. 善于简化计算:在解题时,我们可以对小数进行简化,减少计算复杂性。
3. 灵活处理0的情况:在解题时,我们需要灵活处理0的情况,理解0与其他数相乘的结果。
五、小数乘法的应用领域小数乘法是数学中常见的运算方法,其应用领域非常广泛。
在现实生活中,小数乘法常常应用于货币计算、测量单位、百分比计算等方面。
在科学研究、经济学、工程技术、财务管理等领域,小数乘法也有着广泛的应用。
小数乘法知识点总结

小数乘法知识点总结小数乘法是数学学习中的一个重要内容,它在日常生活和实际应用中都有着广泛的用途。
下面我们来详细总结一下小数乘法的相关知识点。
一、小数乘法的意义小数乘法的意义与整数乘法的意义相同,都是求几个相同加数的和的简便运算。
但在实际应用中,小数乘法还有一些特殊的意义,比如表示一个数的几分之几是多少。
例如,05×3 可以表示 3 个 05 相加的和是多少,也可以表示 05 的 3 倍是多少;而 05×03 则表示 05 的十分之三是多少。
二、小数乘法的计算方法1、先按照整数乘法的计算方法算出积。
2、看因数中一共有几位小数,就从积的右边起数出几位,点上小数点。
3、如果积的小数位数不够,要在前面用 0 补足,再点小数点。
4、如果积的末尾有 0,要先点小数点,再把小数末尾的 0 去掉。
例如:计算 25×04先计算 25×4 = 100因为 25 有一位小数,04 有一位小数,所以因数一共有两位小数,从积的右边起数出两位,点上小数点,得到 100,化简为 1 。
再比如:计算 025×004先计算 25×4 = 100因为025 有两位小数,004 有两位小数,所以因数一共有四位小数,而积 100 只有三位数字,所以要在前面用 0 补足,得到 00100 ,然后化简为 001 。
三、积的变化规律1、一个因数不变,另一个因数扩大(或缩小)几倍,积也扩大(或缩小)相同的倍数。
例如:如果一个因数是 25 不变,另一个因数从 04 扩大到 08 ,扩大了 2 倍,那么积也从 25×04 = 1 扩大到 25×08 = 2 ,扩大了 2 倍。
2、一个因数扩大(或缩小) a 倍,另一个因数扩大(或缩小) b 倍,积就扩大(或缩小) a×b 倍。
比如:一个因数从 2 扩大到 6 ,扩大了 3 倍,另一个因数从 05 扩大到 15 ,扩大了 3 倍,那么积就从 2×05 = 1 扩大到 6×15 = 9 ,扩大了 3×3 = 9 倍。
五年级上册小数乘法单元知识结构图

五年级上册小数乘法单元知识结构图(一)教学内容本单元的主要内容包括:单元主题图、小数乘整数、小数乘小数、积的近似值、解决问题、整理与复习。
(二)教学目标1、知识与技能(1)掌握小数乘法的笔算方法,能正确计算较简单的小数乘法,能在解决具体问题的过程中,选择合适的方法(口算、估算或笔算)进行计算。
鼓励学生独立探索,提倡策略多样化。
(2)掌握小数乘法的估算方法,进一步强化估算意识。
培养估算能力。
(3)能借助计算器进行较复杂的小数乘法计算,解决简单的实际问题。
体会小数乘法在现实生活中的广泛应用。
(4)掌握保留积的近似值的方法,会根据具体情况保留积的近似值。
2、过程与方法通过创设情境,探究现实生活中小数乘法的问题;在合作交流、探索与思考中,感受新旧知识的联系与区别,有效地运用原有知识推动新知识的学习;在解决问题的过程中,深化对所学知识理解,增强学生的应用意识。
3、情感、态度与价值观感受小数乘法在实际生活中的应用,体验小数乘法的应用价值,通过课本知识与实际问题的联系,增强学生自主探究的欲望,获得成功的体验,坚定学生学好数学的信心。
(三)教学重难点、关键1、重点::理解小数乘法的意义,掌握小数乘法的计算方法;强化估算意识,培养估算能力;会求积的近似值,并能根据具体情况保留积的近似值。
2、难点:积的小数点位置的确定;根据具体情况保留积的近似值。
3、关键:让学生通过现实情境理解小数乘法的意义;启动学生原有的认知经验,让学生在整数比较和辨析中抓住新知识的关键所在-----积的小数点位置的确定;思考如何在原有知识的基础上找到解决新问题的办法的途径,从而主动地掌握新知识;其间,突出对算理的探究,引导学生切实掌握小数乘法的计算方法。
(四)教学思路本单元主题图呈现生活中应用小数计算的数学情境,激发学生的学习兴趣和动力;小数乘整数是学生借助整数乘法的有关知识探究小数计算方法的开始,学生通过探究,初步感知小数乘法的计算方法;然后通过小数乘小数的教学,深化学生对小数乘法计算方法的理解,归纳出小数乘法的计算方法,并要求学生将掌握的计算方法灵活应用于解题实际,提高学生对小数乘法计算方法的掌握水平;在此基础上,再通过积的近似值的学习,巩固小数乘法的计算方法,同时让学生理解生活中为什么需要积的近似值以及如何处理积的近似值;解决问题是学生体验小数乘法的应用价值的重要途径,在解决问题的过程中,学生可以掌握一些新的解决问题的策略,提高解决问题的能力;最后通过整理和复习,沟通本单元知识与知识之间的联系,提高学生对本单元知识的掌握质量。
小数乘法单元知识结构图

小数乘法单元知识结构图
一、积的扩大缩小规律:
二、积不变规律:
三、1、小数乘整数计算方法:
2、小数乘小数的计算方法:
3、计算结果发现小数末尾有0的,要先点小数点,再把0去掉。
顺序不可调换。
4、积的小数位数等于两个因数的小数位数之和。
5、小数点的位移规律:
6、一个数(0除外)乘大于1的数,积比原来的数大。
7、小数的四则混合运算和整数相同,都是先算乘法和除法,再算加法和减法,
有小括号的要先算小括号里的。
四、乘法的交换律、结合律、分配律同样适用于小数乘法,应用这些运算定律,可以使计算简便。
五、积的近似数:保留a位小数,就看第a+1位,再用四舍五入的方法取值。
