模糊集合及其运算
模糊集合及其运算

40
31 0.78 110 85 0.75
50
39 0.78 120 95 0.79
60
47 0.78 129 101 0.78
70
53 0.76
由表 1可见,隶属频率随试验次数 n 的增加而呈现
稳定性,稳定值为 0.78,故有 [青年人] (27) = 0.78。
模糊统计与概率统计的区别: 模糊统计:变动的圆盖住不动的点 概率统计:变动的点落在不动的圆内
(2)随着n的增大,频率呈现稳定,此稳定值即为
u 0 对A的隶属度:
* u A 的次数 0 A ( u )lim 0 n n
例 取年龄作论域 X,通过模糊试验确定 x0= 27(岁)
对模糊集“青年人” A 的隶属度。
张南伦曾对 129 名学生进行了调查试验,要求
每个被调查者按自己的理解确定“年青人” (即 A)
0.1 0.2 0.2 B A 0.3 0.3 0.3 0.4 0.5 0.5
(3)模糊矩阵的转置
T ( a ) , 定义:设 A 称 A (aji )nm为A的 ij m n
转置矩阵。 (4)模糊矩阵的 截矩阵 定义:设 A 对任意的 称 [ 0 , 1 ], ( a ) , ij m n
1 0 0 0 0 0 0 1 0 0 0 1 1 0 1 1
A0 .5
0 0 0 0 0 1 1 0 1 1
A0 .8
三、隶属函数的确定 1、模糊统计法
模糊统计试验的四个要素:
(1)论域U; (2)U中的一个固定元素 u 0 ;
* A (3)U中的一个随机运动集合 ;
~
A 称为 A 隶属函 确定了一个U上的模糊子集 A 。映射 ~ ~ ~
二、模糊计算

§2.3 模糊集合的运算 2.3.1 模糊集合的基本运算 一、模糊集合并、交、补运算定义2.3.1 模糊集合的包含、相等设A ~、B ~为论域X 上的两个模糊集合,对于X 中每一个元素x ,都有)()(~~x x BAμμ≥,则称A ~包含B ~,记作B A ~~⊇。
如果B A ~~⊇,且A B ~~⊇,则说A ~与B ~相等,记作B A ~~=。
由于模糊集合是通过隶属函数来表征的,模糊集合相等也可用隶属函数来定义。
若对于X 上的所有元素x ,都有)()(~~x x BAμμ=,模糊集合A ~与B ~相等。
定义2.3.2 模糊空集设A ~为论域X 上的模糊集合,对于X 中每一个元素x ,都有0)(~=x Aμ,则称A ~为模糊空集,记作φ=A ~。
定义2.3.3 模糊集合并、交、补基本运算设A ~、B ~为论域X 上的两个模糊集合,令B A ~~ 、B A ~~ 、C A ~分别表示模糊集合A ~与B ~的并集、交集、补集,对应的隶属函数分别为B A~~ μ、B A ~~ μ、C A~μ,对于X 的任一元素x ,定义: )(V )()(B ~A ~B ~A~x x x μμμ∆ (2.3.1) )()()(B ~A~B ~A~x x x μμμΛ∆ (2.3.2)补算子 (2.3.3) 式中“V ”表示取大运算,“Λ”表示取小运算,称其为Zadeh 算子。
在此定义下,两个模糊集合的并、交实质是在做下面的运算①)](,)(max[B ~A ~B ~A~x x μμμ= 并算子 (2.3.4) )](,)(min[B ~A~B ~A~x x μμμ= 交算子 (2.3.5) 为了加深对模糊集合并、交、补基本运算的理解,现在给出模糊集合A ~和B ~,见图2.3.1(a)。
其中A ~为高斯分布,B ~为三角分布,二者的并、交运算结果如图2.3.1(b)的图2.3.1(c)所示,当然模糊集合的并、交运算可以推广到任意个模糊集合。
模糊集合及其运算(教材)
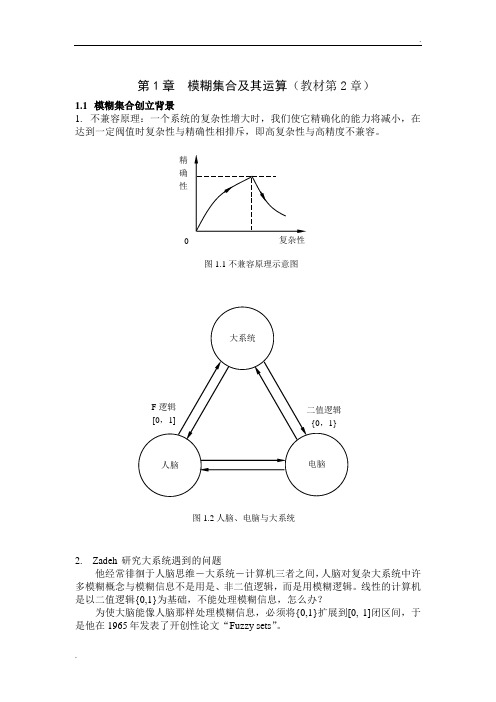
第1章 模糊集合及其运算(教材第2章)1.1 模糊集合创立背景1. 不兼容原理:一个系统的复杂性增大时,我们使它精确化的能力将减小,在达到一定阀值时复杂性与精确性相排斥,即高复杂性与高精度不兼容。
2. Zadeh 研究大系统遇到的问题他经常徘徊于人脑思维-大系统-计算机三者之间,人脑对复杂大系统中许多模糊概念与模糊信息不是用是、非二值逻辑,而是用模糊逻辑。
线性的计算机是以二值逻辑{0,1}为基础,不能处理模糊信息,怎么办?为使大脑能像人脑那样处理模糊信息,必须将{0,1}扩展到[0, 1]闭区间,于是他在1965年发表了开创性论文“Fuzzy sets ”。
0 复杂性 精 确 性图1.1不兼容原理示意图图1.2人脑、电脑与大系统举例解释模糊性与随机性两个概念的差异。
1.2 经典集合及其运算 1. 复习经典集合理论定义: 基于某种属性的、确定的、彼此可区别的事物全体。
论域: 研究对象的全体称为论域(全域、全集、空间、话题) 元素与集合之间的关系: 属于与不属于 集合之间关系: 包含与相等集合的基本运算: 并、交、补运算 集合的三种基本形式如下:定义式:A B {x |x A x B }∈∈U @或(只用符合字母)描述式:(只用文字)由属于一个集合或另一个集合的元素构成的集合称为这两个集合的并文氏图:(只用图)集合的直积(叉积,笛卡尔积):两个集合A,B 的直积:A B {(x,)|x A y B }y ∆⨯=∈∈且注意几点:(1) 序偶不能颠倒顺序(x, y )≠ (y, x), 因此A ×B ≠ B ×A ; (2) 直积可推广到n 个集合; (3) 当R 为实数集,即R={x|-∞<x < +∞},R×R={(x, y)| -∞<x<+∞,-∞<y<+∞}称R×R=R 2为二维欧氏空间。
2. 映射与关系(1) 映射f :x→y ; (2) 关系:集合X×Y 直积的一个子集R 称为X 到Y 的二元关系,简称关系; (3) 映射是关系的特例,因为f :x→y 显然{(x, y)|y=f(x)}⊂X×Y 。
模糊集合论及其应用

模糊集合论及其应用模糊集合论是一种重要的数学工具,它能够处理现实世界中的模糊、不确定和不精确的信息,具有广泛的应用前景。
本文首先介绍模糊集合论的基本概念和运算,然后探讨其在决策分析、控制理论、人工智能等领域的应用,并最后展望其未来发展方向。
一、模糊集合论的基本概念和运算1.1 模糊集合的定义在传统的集合论中,一个元素只能属于集合或不属于集合,不存在中间状态。
而在模糊集合论中,一个元素可以同时属于多个集合,并且对于不同的元素,其属于集合的程度也不同。
因此,模糊集合论将集合的概念进行了扩展,使其能够更好地描述现实世界中的不确定性和模糊性。
设X为一个非空的集合,称为全集,一个模糊集A是一个从X到[0,1]的函数,即:$$A(x):Xrightarrow[0,1]$$其中,A(x)表示元素x属于模糊集A的隶属度,取值范围为[0,1]。
当A(x)=1时,表示x完全属于A;当A(x)=0时,表示x完全不属于A;当0<A(x)<1时,表示x部分属于A。
1.2 模糊集合的运算模糊集合的运算包括模糊集合的交、并、补和乘积等。
模糊集合的交:对于两个模糊集合A和B,其交集为:$$(Acap B)(x)=min{A(x),B(x)}$$模糊集合的并:对于两个模糊集合A和B,其并集为:$$(Acup B)(x)=max{A(x),B(x)}$$模糊集合的补:对于一个模糊集合A,其补集为:$$(eg A)(x)=1-A(x)$$模糊集合的乘积:对于两个模糊集合A和B,其乘积为:$$(Atimes B)(x,y)=min{A(x),B(y)}$$其中,(A×B)(x,y)表示元素(x,y)属于模糊集合A×B的隶属度。
1.3 模糊关系和模糊逻辑在模糊集合论中,还有两个重要的概念,即模糊关系和模糊逻辑。
模糊关系是指一个元素对另一个元素的隶属度,可以用矩阵表示。
例如,设A和B是两个模糊集合,它们之间的模糊关系R可以表示为: $$R=begin{bmatrix} R_{11} & R_{12} R_{21} & R_{22}end{bmatrix}$$其中,Rij表示元素i与元素j之间的隶属度。
模糊集合的运算以及合成

模糊集合的运算以及合成标题:模糊集合的运算与合成概述:模糊集合是一种用于处理不确定性和模糊性问题的数学工具。
它能够更好地描述现实世界中的不确定性和模糊性情况。
本文将讨论模糊集合的运算及其合成方法,并通过人类视角的叙述,使读者更好地理解和感受这一概念。
引言:在现实生活中,我们常常遇到一些模糊的问题,比如说“这个人高吗?”、“这个饭菜辣吗?”等等。
这些问题往往没有一个确定的答案,而是具有一定的不确定性。
为了更好地处理这种不确定性,人们提出了模糊集合的概念。
1. 模糊集合的运算模糊集合的运算包括交集、并集和补集。
通过这些运算,我们可以对模糊集合进行综合和分析。
1.1 交集运算交集运算是指将两个模糊集合的元素逐个比较,取其中相对较小的隶属度作为交集结果的隶属度。
例如,对于模糊集合A和B,其交集记为A∩B,其隶属度的计算公式为:μ(A∩B) = min{μA(x), μB(x)}1.2 并集运算并集运算是指将两个模糊集合的元素逐个比较,取其中相对较大的隶属度作为并集结果的隶属度。
例如,对于模糊集合A和B,其并集记为A∪B,其隶属度的计算公式为:μ(A∪B) = max{μA(x), μB(x)}1.3 补集运算补集运算是指将一个模糊集合的元素的隶属度取反,得到其补集。
例如,对于模糊集合A,其补集记为A',其隶属度的计算公式为:μ(A') = 1 - μA(x)2. 模糊集合的合成模糊集合的合成是指将多个模糊集合综合起来,得到一个新的模糊集合。
合成方法包括合取、析取和修正。
2.1 合取合成合取合成是指将多个模糊集合的隶属度进行逐个相乘,得到新的模糊集合。
例如,对于模糊集合A和B,其合取合成记为A⊗B,其隶属度的计算公式为:μ(A⊗B) = μA(x)* μB(x)2.2 析取合成析取合成是指将多个模糊集合的隶属度进行逐个相加,得到新的模糊集合。
例如,对于模糊集合A和B,其析取合成记为A⊕B,其隶属度的计算公式为:μ(A⊕B) = μA(x) + μB(x) - μA(x) * μB(x)2.3 修正合成修正合成是指将一个模糊集合的隶属度与另一个模糊集合的隶属度进行修正,得到新的模糊集合。
模糊数学第二讲 模糊集合及其运算

实际生活中有些概念并非清晰概念, 例如鲜美的食品、美丽 的景色、魁梧的身材、漂亮的服装、高个子…等等.对于这些 概念,普通集合就无能为力.
7
2014-8-15
定义1 :设U为论域,U在闭区间[0,1]上的任一映射A[0,1]称 为U上的隶属函数。 对于任意的xU,隶属函数值A(x)称为x对A的隶属度。A为论 域U上的模糊集合。
( A B) C ( A C ) ( B C )
论域:被讨论对象的全体组成的集合称为论域。
包含: AB :对于任意xA ,必有yB. 空集:若对于任意集合A,都有A,则称是任意集合A的空集.
幂集:设U是论域,U的所有子集所组成的集合称为U的幂集, 记为P(U). 例如,U={a,b,c},则
P(U)={,{a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}}
2014-8-15
两个模糊子集的交并运算还可以推广到任意多个 模糊集合的情形。
定义3 设At F (U ), t T , T 是指标集.u U , 规定 ( ( 称
tT tT tT
At )(u ) At (u ) sup At (u );
tT tT tT
At )(u ) At (u ) inf At (u ).
A U U , A U A,
A AC A B) c Ac B c ,
2014-8-15
( A B) c Ac B c
5
特征函数
特征函数CA(u) 表示论域U中的元素u是否属于U的子集A. 若uA, 则CA(u) =1;若 uA ,则CA(u) =0. 显然,特征函数是论域U到{0,1}的一 个映射. 例如,设U自然数组成的集合,A={1,2,3},则A的特征函数为
模糊控制02-模糊集合及其基本运算

中心 如果一个模糊集的隶属度函数达到最大值的 有点的均值是一个有限值,则该均值就是模 有点的均值是一个有限值 集的中心; µ(x) 1 如果均值是正(负) 穷大,则将中心定义 所有最大隶属度值的 中最小(最大)点。
模糊集合的一些基本概念
交叉点 论域U中模糊集A的隶属度值等于0.5 论域U中模糊集A的隶属度值等于0.5的点。 0.5的点。 模糊集的高度 µ(x) 指模糊集内任意点所达到的 1 大隶属度值。 a 模糊集高度为1 模糊集高度为1时,该模糊 该模糊 称为标准模糊集。
1
supp( A) = {x ∈ U | µ A ( x) > 0}
0
模糊集合的一些基本概念
空模糊集 如果一个模糊集的支撑集为空集,则该模糊 如果一个模糊集的支撑集为空集 为空模糊集。 模糊单值 µ(x) 1 如果模糊集的支撑集仅包 则该模糊集 U中的一个点,则该模糊集 模糊单值。
模糊集合的一些基本概念
x
z
模糊集合的运算
模糊集合A 模糊集合A 和B等价 对于任意 x∈U,当且仅当µA(x)=µB(x), 当且仅当µ 当且仅当 (x), 称A和B是等价的。 模糊集合A 模糊集合A被B包含 对于任意 x∈U,当且仅当 µA(x)≤µB(x) , 当且仅当 称B包含A。 包含A
模糊集合的运算
糊集合A 糊集合A 的补集 模糊集合A 模糊集合A的补集记作 ,A ,隶属度函数为 µ A (x) = 1 − µ A (x) 糊集合A 糊集合A和B的并集 AU B 模糊集合A 模糊集合A和B的并集记作 ,隶属度函数为 µ A∪ B (x) = max[µ A ( x), µ B ( x)] 糊集合A 糊集合A和B的交集 AI B 模糊集合A 模糊集合A和B的交集记作 ,隶属度函数为
CH1-1~2模糊集的概念及其运算

超越它,精确性和有意义性就变成两个相互排斥的特性。” 扎德
11
例如,要你某时到某地去迎接一个“大胡子高个子长
头发戴宽边黑色眼镜的中年男人”. 尽管这里只提供了一个精确信息------男人,而其他
信息------大胡子、高个子、长头发、宽边黑色眼镜、
中年等都是模糊概念,但是你只要将这些模糊概念
经过头脑的综合分析判断,就可以接到这个人.
12
三、研究方向及应用
理论上的研究方向
1、发展模糊集的理论和方法,建立 自身的理论体系; 2、将各个经典数学分支进行模糊化; 3、应用上将fuzzy集方法打入各个 学科专业领域。
模糊数学在实际中的应用几乎涉及到国民经济的 各个领域及部门,农业、林业、气象、环境、地质 勘探、医学、经济管理等方面都有模糊数学的广泛 而又成功的应用.
22
到了20世纪90年代初, 市场上已经出现了大量 的模糊消费产品。在日本出现了“模糊”热, 家电产品中, 不带Fuzzy的产品几乎无人购买。 空调器、电冰箱、洗衣机、洗碗机等家用电器 中已广泛采用了模糊控制技术。我国也于20世 纪90年代初在杭州生产了第一台模糊洗衣机。 模糊数学于1976年传入我国后, 得到迅速发展。 1980年成立了模糊数学与模糊系统学会, 1981 年创办《模糊数学》(华中工学院)杂志, 1987 年创办《模糊系统学会》(国防科技大学)。中 国被公认为模糊数学研究的四大中心 (美国、 欧洲、日本、中国) 之一。
13
四、模糊数学发展历程
1. 模糊理论的萌芽(20世纪60年代) 对模糊性的讨论, 可以追溯得很早。20世纪的 大 哲 学 家 罗 素 (B.Russel) 在 1923 年 一 篇 题 为 《含糊性》(Vagueness) 的论文里专门论述过 我们今天称之为“模糊性”的问题(严格地说, 两者稍有区别), 并且明确指出: “认为模糊知 识必定是靠不住的, 这种看法是大错特错的。” 尽管罗素声名显赫, 但这篇发表在南半球哲学 杂志的文章并未引起当时学术界对模糊性或含 糊性的很大兴趣。这并非是问题不重要, 也不 是因为文章写得不深刻, 而是“时候未到”。
2.3模糊集合及其运算

2.3 模糊集合及其运算2.3.1 模糊子集的定义及表示模糊子集的定义:设给定论域U ,U 到[0,1]闭区间的任一映射A μ→U A :μ[0,1])(u u A μ→ (2-3-1)都确定U 的一个模糊子集A ,A μ称为模糊子集的隶属函数,)(u A μ称为u 对于A 的隶属度。
隶属度也可记为)(u A 。
在不混淆的情况下,模糊子集也称模糊集合。
上述定义表明,论域U 上的模糊子集A 由隶属函数A μ来表征。
)(u A μ取值范围为闭区间[0,1],)(u A μ的大小反映了u 对于模糊子集的从属程度。
)(u A μ的值接近于l ,表示u 从属于A 的程度很高; )(u A μ的值接近于O ,表示u 从属A 的程度很低。
可见,模糊子集完全由隶属函数所描述。
当)(u A μ的值域={0,1}时,)(u A μ蜕化成一个经典子集的特征函数,模糊子集A 便蜕化成一个经典子集。
由此不难看出,经典集合是模糊集合的特殊形态,模糊集合是经典集合概念的推广。
模糊集合的表达方式有以下几种:1.当U 为有限集{}n u u u ,,21 时,通常有如下三种方式。
(1)Zadeh 表示法nn A A A u u u u u u A )()()(2211μμμ+++=其中ii A u u )(μ并不表示“分数”,而是表示论域中的元素i u 与其隶属度)(i A u μ之间的对应关系。
“+”也不表示“求和”,而是表示模糊集合在论域U 上的整体。
在论域U 中,)(u A μ的元素集称为A 的台,又称为模糊集合A 的支集。
实际上若某元素的隶属函数值为零。
即它不属于这个集合,则用台来表示一个模糊集合,可使表达式简单明了。
以下采用台的方式给出模糊集合,例如模糊集合“几个”可表示为83.077.0615147.033.0+++++=A 若对于模糊集合A 有一个有限的台,{}n u u u ,,21,则可表示为如下一般形式 nn A A A u u u u u u A )()()(2211μμμ+++=∑==ni ii A u u 1)(μ (2-3-3)(2)序偶表示法将论域中的元素i u 与其隶属度)(i A u μ构成序偶来表示A ,则))}(,(,)),(,()),(,{(2211n A n A A u u u u u u A μμμ⋅⋅⋅= (2-3-4)采用序偶表示法,例1中的A 可写为(){})3.0,8(),7.0,7)(1,6(),1,5(),7.0,4(,3.0,3=A此种方法隶属度为0的项可不写入。
第七章 模糊控制技术第三节模糊集合中的基本定义和运算

2.模糊集合的基本运算
• 设A和B是U中的模糊子集,隶属函数分别为μA和μB,则模 糊集合中的并、交、补等运算可以定义如下: 并运算:并(A∪B)的隶属函数μA∪B,对所有μ∈U被逐 点定义为取极大值运算即:(式中“∨”为取极大值运算 )
交运算:交பைடு நூலகம்A∩B)的隶属函数μA∩B,对所有μ∈U被逐点 定义为取极小值运算即:(式中“∧”为取极小值运算)
第七章 模糊控制技术
主要内容
一、模糊集合 二、隶属函数及其确定 三、模糊集合中的基本定义和运算 四、模糊关系 五、模糊推理 六、模糊控制器的设计 七、模糊控制器设计实例
三、模糊集合中的基本定义和运算
1.基本定义
• 与经典集合论一样,模糊集合也定义了基本运算如并、交、 补等。以下定义模糊集合的幂集、空集、全集、集合的包含 和相等。 论域U中模糊集合的全体称为U中的模糊幂集,记做F(U):
补运算:模糊集合A的补隶属函数μA ,对所有被逐点定义 为
三、模糊集合中的基本定义和运算
3.模糊集合运算的基本定律
模糊集合的运算满足以下的基本定律:
设U为论域。A、B、C为U中的任意模糊子集,则下列等式成立:
幂等律:
结合律: 交换律:
分配律:
同一律:
零一律:
吸收律:
双重否认律:
德·摩根律:
➢ 可以看出,模糊集与经典集的集合运算的基本性质完全相同,但是 模糊集运算不满足互补律,即:
对于任一u∈U,若μG(x)=0,称A为空集φ;若μG(x)=1,则 称为全集,A=U。
设A和B是U的模糊集,即A、B∈F(U),若对任一u∈U都有 B(U)≤B(U),则称B包含于A,或称B是A的子集,记做 。若对于任一u∈U都有B(U)=A(U),则称B等于A,记做B=A 。
第二章:二、模糊集合的运算

µ
模糊集的代数运算仍然满足结合律、交换律、德•摩根律、同一律和零一律。 但不满足幂等律、分配律和吸收律。当然也不满足互补律。 ⊕ 定义2-9 称 aΘ、 为有界算子,对 ∀a , b ∈ [ 0 , 1 ] ,有
A+ B
∧
( u ) = µ A ( u ) + µ B ( u ) − µ A ( u ) µ B (u )
g v 2 (v1 ) (2 − 27) max( g v 2 (v1 ) , g v1 (v 2 ) ) 这里, v1 、v 2 ∈ U 。 若以 g (vi / v j )(i , j = 1, 2) 为元素,且定义 时,则可构造出矩阵G,并称G为相及矩阵。 g (v i / v j ) = 1 , 当 i = j
重叠鲁棒性=10 / 20 = 0.5
µ
A1
A2
重叠率=5 / 35 = 0.143
0.25
0 20
重叠鲁棒性=2.5 / 10 = 0.25
35
5
35
40
55
速度 /( km ⋅ h −1 )
图2-6 隶属度函数重叠的范例 隶属度函数是模糊控制的应用基础,正确构造隶属度函数是能 否用好模糊控制的关键之一。 1)模糊统计法
计算相及矩阵G。因为 g (vi / v j ) = g v j (vi ) / max( g v j (vi ) , g v i (v j ) ) ,所以,相及矩 阵为
模糊控制03-模糊集合的其他运算

模糊并——s-范数
4、直和 5、爱因斯坦和 6、代数和 7、最大
模糊并——s-范数
例3.1,通过图形的方式,表现出Yager的s-范 数和代数和s-范数大于最大算子。 定理3.1 对任意一个s-范数(即满足公理s1~s4 的函数s:[0,1]×[0,1]→[0,1]),当a,b∈[0,1]时, 下面不等式成立: max(a,b)≤s(a,b)≤sds(a,b)
模糊并——s-范数
对前式进行等式变换,可得:
1 1 1 1 [( 1) /( 1)] ln( 1) ln( 1) a b a b lim ln z lim 1 1 [( 1) /( 1)] 1 a b 1 ln( 1) b
模糊并——s-范数
先证明 max(a,b)≤s(a,b) 因a=a且b≥0,由公理s3,则s(a,b)≥s(a,0), 由公理s1,有s(a,0)=a,所以s(a,b)≥a; 由公理s2,有s(a,b)=s(b,a) ≥s(b,0) ≥b; 所以,s(a,b) ≥max(a,b)
模糊并——s-范数
公理s3:a≤a’且b≤b’,则s(a,b)≤s(a’,b’)
模糊并——s-范数
μ(x)
a b c x a
μ(x)
b c x
公理s4:s(s(a,b),c)=s(a,s(b,c));
模糊并——s-范数
定义3.2 任意一个满足公理s1~s4的函数 s:[0,1]×[0,1]→[0,1]都叫s-范数 常见的范数主要有7种: 1、Dombi的s-范数 2、Dubois-Prade的s-范数 3、Yager的s-范数
c[ A ( x)] A ( x)
按前述的模糊补集定义,映射c可以表示为: c[ A ( x)] 1 A ( x)
模糊集合

设A、B为论域U上的模糊集 A=φ 对任何 u∈U,μA(u) = 0
A = B 对任何 u∈U,μA(u) =μB(u)
A ∪ B 对任何 u∈U,μA(u) ∨μB(u) A ∩ B 对任何 u∈U,μA(u) ∧μB(u) Ac 对任何 u∈U,1-μA(u)
1 Y x x[25,100] x[0,25]
[1 (
x 25 2 1 ) ] 5 x
x 50 2 1 [1 ( ) ] 0 5 O x x[50,100] x x[0,50]
二、模糊子集的运算
1、定义
定义模糊集合的运算方法,与定义普通集合的 运算方法一样,是利用参与模糊集合的隶属函 数来定义运算结果所得新模糊集合的隶属函 数。 两模糊集合的具体运算,实际上就是逐点地对 隶属度作相应的运算。包括: 交 并 补
2 1 0 x 25 c B 1 1 x 5 0 x 25 x 25 x 100
3、模糊集合运算性质
(1)幂等律:A∪A=A , A∩A=A; (2)交换律:A∪B=B∪A, A∩B=B∩A; (3)结合律:(A∪B)∪C=A∪(B ∪C), (A∩B)∩C=A∩(B∩C); (4)吸收律:A∩(A∪B)= A, A∪(A∩B)=A; (5)分配律: (A∪B)∩C=( A∩C)∪(B∩C), (A∩B)∪C= ( A∪C)∩(B∪C);
6、模糊集合的表示-无限集
当论域U为无限集时,A = ∫x∈U μA(x) / x
注意:这里的积分号不表示积分,也不表示求
和,而是表示各个元素与隶属度对应关系的一个 总括。
这种表示法可以推广到有限、无限、离散、连续等 各种情况。
模糊数学第二讲--模糊集合及其运算

A(u)
[1
(
u
50 5
)2
]1
, 50 u 100
1
0 u 25
B(u)
[1
(
u
25 5
)2
]1
25 u 100
A
B A(u) B(u)
1
[1 (u 25)2 ]1
5
[1 (u 50)2 ]1 5
uU
u
u 0u25
25u u*
u
u* u100
u
A
B A(u) B(u)
2024/7/20
20
五、模糊截集
1. -截集(-cut)
引例:
奴隶社会 1/ 夏 1/ 商 0.9 / 西周 0.7 / 春秋 0.5/战国 0.4 / 秦 0.3/ 西汉 0.1/东汉
若要求至少应达到0.5 水平,则有夏、商、西 周、春秋、战国
若要求至少应达到0.7 水平,则有夏、商、西周、 春秋
(A B) C (A C) (B C)
5、吸收律: (A B) A A, (A B) A A 6、复原律: (Ac )c A 7、对偶律: ( A B)c Ac Bc , ( A B)c Ac Bc 8、0 –1律: A U U , A A
AU A, A
k 1
uk
k 1
uk
u k 1
k
(2) 设论域U为无限集且A A(u), B B(u),
uU u
uU u
则A B A(u) B(u),A B A(u) B(u),AC 1 A(u)
uU
u
uU
u
uU
u
2024/7/20
16
例2 设模糊集A和B的隶属函数为
模糊集合的运算以及合成

模糊集合的运算以及合成模糊集合是一种数学工具,用于处理不确定性和模糊性的问题。
它可以将不同程度的隶属度分配给各个元素,以表示它们与某个概念的相似程度。
模糊集合的运算和合成可以帮助我们更好地理解和处理这些模糊性问题。
模糊集合的运算包括交集、并集和补集。
交集运算将两个模糊集合的隶属度相对较小的元素作为结果集合的元素,表示它们在两个概念中的相似程度。
并集运算将两个模糊集合的隶属度相对较大的元素作为结果集合的元素,表示它们在两个概念中的共同部分。
补集运算将一个模糊集合中的元素的隶属度取反,表示它们不属于某个概念。
模糊集合的合成是将多个模糊集合按照一定的规则组合成一个新的模糊集合。
常见的合成方法包括最小值合成和最大值合成。
最小值合成将多个模糊集合的隶属度取最小值,表示它们的相似程度取决于其中最不相似的部分。
最大值合成将多个模糊集合的隶属度取最大值,表示它们的相似程度取决于其中最相似的部分。
以一个具体的例子来说明模糊集合的运算和合成。
假设我们要描述一个人的身高,我们可以定义一个模糊集合“高”,其中元素的隶属度表示身高与高的相似程度。
同样地,我们可以定义一个模糊集合“矮”,其中元素的隶属度表示身高与矮的相似程度。
如果我们要计算一个人同时属于“高”和“矮”,可以使用交集运算。
将“高”和“矮”两个模糊集合取交集,得到一个新的模糊集合,表示同时具备高和矮的特征。
这个新的模糊集合的元素的隶属度取决于身高与高和矮的相似程度。
如果我们要计算一个人属于“高”或“矮”,可以使用并集运算。
将“高”和“矮”两个模糊集合取并集,得到一个新的模糊集合,表示具备高或矮的特征。
这个新的模糊集合的元素的隶属度取决于身高与高或矮的相似程度。
如果我们要将一个人的身高与“高”和“矮”两个模糊集合合成,可以使用最大值合成。
将身高与“高”和“矮”两个模糊集合的隶属度取最大值,得到一个新的模糊集合,表示身高在高和矮中的相似程度。
模糊集合的运算和合成可以帮助我们处理不确定性和模糊性的问题,以更好地理解和描述现实世界中的现象和概念。
模糊集的基本运算

A ={(x1, 0.4), (x2, 0.5), (x3, 0), (x4, 0.6)}.
四.模糊集的运算性质
1. 经典集合的运算性质 经典集合关于并、交、补运算具有以下性质: 设X为论域, A, B, C为X上的经典集合, 则
A=(0.55, 0.78, 0.91, 0.56). X上的模糊集B为:
帅哥
B=(0.35, 0.52, 0.65, 0.37). 则根据定义有BA.
超男
定义 论域X上的模糊集A与B称为是相等的, 如果AB 且BA, 即对任意xX有A(x)= B(x).
3. 模糊集的并 设X为非空论域, A, B为X上的两个经典集合。 A∪B={xX| xA或xB}.
第二章 模糊集的基本运算
一. 模糊集的表示方法
模糊集合是论域X 到[0,1]的映射, 因此用隶属函 数来表示模糊集合是最基本的方法。除此以外, 还有 以下的表示方法: 1)序偶表示法
A={(x, A(x)|xX}. 例如: 用集合X={x1, x2, x3, x4}表示某学生宿舍中的四 位男同学, “帅哥”是一个模糊的概念。经某种方法 对这四位学生属于帅哥的程度(“帅度”)做的评价依 次为: 0.55, 0.78, 0.91, 0.56, 则以此评价构成的模糊集 合A记为:
A(x)
1 0
xa xa
1
xa
A(x) ek(xa) x a, k 0
A(x)
1 ek
( xa )2
xa x a, k 01A( x)源自11 b(x a)c
xa x a (b, c 0)
模糊集合的运算以及合成

模糊集合的运算以及合成
模糊集合是指其元素的隶属度不是二元的,而是在0到1之间的一个连续的实数。
模糊集合的运算包括交集、并集、补集和差集等。
交集运算是指对应元素的隶属度取较小值,即取最小规则。
并集运算是指对应元素的隶属度取较大值,即取最大规则。
补集运算是指对应元素的隶属度取1减去原隶属度的值。
差集运算是指对应元素的隶属度取最大值减去最小值。
这些运算可以帮助我们对模糊集合进行逻辑运算和推理。
另外,模糊集合的合成是指将两个或多个模糊集合通过某种规则进行合并得到一个新的模糊集合。
常见的合成方法包括最小-最大合成法、最大-最大合成法、乘积合成法等。
最小-最大合成法是指首先对两个模糊集合进行最小化合成,然后再对结果进行最大化合成。
最大-最大合成法是指对两个模糊集合进行最大化合成。
乘积合成法是指对应元素的隶属度进行乘积运算。
这些合成方法可以根据具体的应用场景选择合适的方法进行合成,以得到符合实际情况的模糊集合。
总之,模糊集合的运算和合成是模糊逻辑理论中的重要内容,通过这些运算和合成方法,我们可以更好地处理模糊信息,进行模
糊推理和决策,应用于控制系统、人工智能等领域。
希望我对模糊集合的运算和合成能够给你提供一些帮助。
模糊集合及其运算
模糊集合的基本运算
1、模糊集合相等 若两个模糊集合A和B,对于所有的 ,均有 则称模糊集合A与B相等,记作 。 2、模糊集合的包含关系 若两个模糊集合A和B,对于所有的 ,均有 则称模糊集合A包含于B,记作 。
模糊集合的基本运算
3、模糊空集
若对所有 ,均有 ,则称A为模糊空集,记
作。
4、模糊集合的并集
B 1 0.9 1 0.4 1 0 1 0.7 0.1 0.6 1 0.3
x1
x2
x3
x4
x1 x2 x3 x4
模糊集合运算的基本性质B C) (A B) (A C)
2、结合律 (A B) C A (B C) (A B) C A (B C)
8、双重否定律
A A
模糊集合运算的基本性质
提问: 为什么在模糊集合里排中律不成立?
9、其它运算类型 见板书
模糊关系
定义:n元模糊关系R是定义在直积X1×X2×... ×Xn上的模糊集合,它可以表示为
R X1X2 Xn
R (x1, x2 , , xn ) /(x1, x2 , , xn )
X1X 2 X n
6,1)
,(7,0.7),(8,0.3),(9,0),(10,0)}
或者A=
=
模糊集合的其它表示方式
例2.2 若以年龄为论域,并设X=[0,200]。设O表 示模糊集合“年老”,Y表示模糊集合“年轻”。 已知“年老”和“年轻”的隶属度函数分别表示 为
模糊集合的其它表示方式
O
(x,0)
0
x
50
x,
模糊集合的定义及表示方法
概念:如果将篮子里的所有“大苹果”看作是一个集合,那么 “大苹果”就是一个模糊集合,因为我们没有确切的定义什 么样的苹果叫做大苹果。另一方面,如果我们认为3两以上 的苹果算是绝对的大苹果,也就是说3两以上的苹果属于 “大苹果”的程度为1,那么2.9两的苹果属于“大苹果”的 程度大概就可以是0.9左右,2.8两的苹果大概就是0.8。这种 属于程度就称为隶属度函数,其值在0~1之间连续变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相等: A B A( x) B( x),x U
包含: A B A( x) B( x),x U
并: ( A B)(x) A( x) B( x),x U 交: ( A B)(x) A( x) B( x),x U
表示取大; 表示取小。
余: Ac ( x) 1 A( x),x U
取小运算
例:设A 1 0.1, B 0.4 0 ,则 0.2 0.3 0.3 0.2
A B 1 0.1 A B 0.4 0
0.3 0.3
0.2 0.2
Ac 0 0.9 0.8 0.7
Bc 0.6 1 0.7 0.8
(2)模糊矩阵的合成 定义:设 A (aij )ms , B (bij )sn , 称模糊矩阵 A B (cij )mn
1
1/2
0
a1 a1 a 2 a2
x
2
(3) 中间型( 型):这种类型的隶属函数在 ( -,
a) 上为偏大型,在 (a, +) 为偏小型,所以称为中间 型.
描述“中”,“暖和”、“中年”等处于中间的模 糊现象。
越居中越好(人的体重)
A(x)
1)矩形分布
0 , x a b ,
1
Ax 1, a b x a b ,
Ac= (0.2, 0.45, 1, 0.7, 0). Bc= (0.9, 0.79, 0.14, 0.4, 1). 可见Ac B, Bc A. 商品质量不好商品质量坏 又 A∪Ac = (0.8, 0.55, 1, 0.7, 1) U,
A∩Ac = (0.2, 0.45, 0, 0.3, 0) .
越大越好(食品中营养物质的含量)
1)升半矩形0分, 布x a, A(x)
A(x) 1, x a.
1
0
a
x
2)升半 分布
0,
x a,
A(x) 1 ek(xa) , x a.
A(x)
1
0
a a+1/k x
图 3.8
3)升半正态分布
0,
x a,
A(x) 1 ek(xa)2 , x a. k 0
模糊集合的截集
定义:设 AF ( X ) , [0,1],记 (A) ={ xX | A(x) },
称 (A) 为 A 的 截集,简记为 A 。
例取 则有
A 1 0.8 0.6 0.5 0.2 0
x1 x2
x3
x4
x5 x6
A1 {x1}, A0.8 {x1, x2}, A0.7 {x1, x2}, A0.6 {x1, x2 , x3}, A0.4 {x1, x2 , x3 , x4}, A0.2 {x1, x2 , x3 , x4 , x5} A0 X。
(5)有界和、乘积算子 (,)
a b 1 (a b),a b ab
(6)Einstain算子 ( , )
a b
ab
,a b
ab
1 ab
1 (1 a)(1 b)
3、模糊矩阵 定义:设 R (rij )mn ,0 rij 1,称R为模糊矩阵。
当 rij 只取0或1时,称R为布尔(Boole)矩阵。 当模糊方阵 R (rij )nn的对角线上的元素 rii 都为1时, 称R为模糊自反矩阵。
2、指派方法 这是一种主观的方法,但也是用得最普遍的一种
方法。它是根据问题的性质套用现成的某些形式的模 糊分布,然后根据测量数据确定分布中所含的参数。
(1) 偏大型(S 型):这种类型的隶属函数随 x 的 增大而增大,随所选函数的形式不同又分为:
描述“大”,“热”、“老年”等偏向大的一方的 模糊现象。
例 设论域U = {x1, x2, x3, x4, x5}(商品集),在U 上定义两个模糊集: A =“商品质量好” B =“商 品质量坏”,并设
A = (0.8, 0.55, 0, 0.3, 1). B = (0.1, 0.21, 0.86, 0.6, 0). 则Ac=“商品质量不好”, Bc=“商品质量不坏”.
A(x) 1
0
a
x
5)降半梯形分布
1 ,
Ax
a2 a2
x a1
,
0 ,
x a1 , a1 x a2 , a2 x .
A(x)
1
0
a1
a2 x
6)降岭形分布
Ax
1 , 1 2
1 2
sin
x
a2
a1 a1
, (x
a2
2
a1
)
,
0 ,
a2 x .
A(x)
a1 x a2 ,
(2)序偶表示法 A {( x1, A( x1)),( x2, A( x2 )), ,( xn , A( xn ))}
(3)向量表示法 A ( A( x1), A( x2 ), , A( xn ))
若论域U为无限集,其上的模糊集表示为:
A A( x) xU x
2、模糊集的运算
定义:设A,B是论域U的两个模糊子集,定义
(4)U中的一个以 A* 作为弹性边界的模糊子集A,
制约着 A* 的运动。A* 可以覆盖 u0 ,也可以不覆盖 u0 , 致使 u0对A的隶属关系是不确定的。
特点:在各次试验中,u0是固定的,而 A* 在随机变动。 模糊统计试验过程:
(1)做n次试验,计算出
u0对A的隶属频率
u0
A*的次数 n
(2)随着n的增大,频率呈现稳定,此稳定值即为
A : U {0,1} u A(u),
其中
A (u)
1, 0,
u A u A
函数 A 称为集合A的特征函数。
二、模糊集合及其运算
美国控制论专家Zadeh教授正视了经典集合描述的 “非此即彼”的清晰现象,提示了现实生活中的绝大多数 概念并非都是“非此即彼”那么简单,而概念的差异常以 中介过渡的形式出现,表现为“亦此亦彼”的模糊现象。 基于此,1965年, Zadeh教授在《Information and Control》杂志上发表了一篇开创性论文“Fuzzy Sets”, 标志着模糊数学的诞生。
A
~
和A
~
。
“高个子”——1.80高个子,1.79可以略低于1 (99%)的程度属于高个.
模糊子集通常简称模糊集,其表示方法有: (1)Zadeh表示法
A A( x1) A( x2 ) A( xn )
x1
x2
xn
这里
A( xi xi
)
表示
xi
对模糊集A的隶属度是
A( xi
)。
如
A 1 0.8 0.2 0 12 34
0 , a b x .
0 a-b a a+b x
2)尖分布
A x
ek xa ek xa
, ,
几个常用的算子:
(1)Zadeh算子 (,) a b max{a,b},a b min{a,b}
(2)取大、乘积算子 (,) a b max{a,b},a b ab
(3)环和、乘积算子 (ˆ ,) a ˆ b a b ab,a b ab
(4)有界和、取小算子 (,)
a b 1 (a b),a b min{a,b}
(1)模糊矩阵间的关系及运算 定义:设 A (aij )mn , B (bij )mn 都是模糊矩阵,定义 相等:A B aij bij 包含:A B aij bij
并: A B (aij bij )mn
取大运算
交: A B (aij bij )mn 余: Ac (1 aij )mn1)降半矩形分布 NhomakorabeaAx
1 , 0 ,
xa, x a.
1
0
a
x
2)降半分布
Ax
1 , ek
xa
,
xa, xa,
其中
k 0.
A(x)
1
0
a a+1/k
x
3)降半正态分布
Ax
1 ,
e
k
x
a
2
,
xa, xa,
其中
k 0.
A(x) 1
0
a
x
4)降半柯西分布
Ax
1 , 1
x
a
1
,
xa,
x a ,其中 0, 0 .
为A与B的合成,其中 cij {(aik bkj ) 1 k s} 。
模糊矩阵的幂 A2 Ao A
例:
设A 0.4 0.1
0.5 0.2
0.6 , B 0.3
0.1 0.3 0.5
0.2 0.4
,
则
0.6
A B 0.5 0.6 0.3 0.3
0.1 0.2 0.2 B A 0.3 0.3 0.3
A(x)
1
0
a
x
图 3.9
4)升半柯西分布
0,
A(x) [1 (x a) ]1,
x a, x a.
0, 0
A(x)
1
0
a
x
5)升半梯形分布
0,
A(
x)
x a2
a1 a1
,
1
x a, a1 x a2
a2 x.
A(x)
1
0
a1 a2
x
6)升岭形分布
0,
A(
x)
62 68 76 85 95 101 0.78 0.76 0.76 0.75 0.79 0.78
由表 1可见,隶属频率随试验次数 n 的增加而呈现
稳定性,稳定值为 0.78,故有 [青年人] (27) = 0.78。
模糊统计与概率统计的区别:
模糊统计:变动的圆盖住不动的点 概率统计:变动的点落在不动的圆内
