数学(七下)2.3平行线的性质(二)

合集下载

七年级数学下册课件(北师大版)平行线的性质

A．35° B．40° C．45° D．50°
3 如图，在平行线a，b 之间放置一块直角三角板，三角板的顶点A，B 分别在直线a，b上，则∠1＋∠2的值为（ A ）
A．90° B．85° C．80° D．60°
4 如图，AB∥CD，点E 在线段BC 上，若∠1＝40°，
∠2＝30°，则∠3的度数是( A ) A．70° B．60° C．55° D．50°
2.3平行线的性质
第1课时
复
习
回
顾
平
条件
行
线同位角相等
的内错角相等判定同旁内角互补
结论两直线平行
猜想：交换它们的条件与结论，是否成立？
两直线平行
同位角相等内错角相等同旁内角互补
知识点 1 “同位角”的性质
探究如图，利用坐标纸上的直线，或者用直尺和三
角尺画两条平行线a∥b，然后，画一条截线c 与这两条平行线
1 如图所示，AB∥CD，AC∥BD. 分别找出与∠1相等或互补的角.
解：如图，与∠1相等的角有∠3， ∠5，∠7，∠9，∠11，∠13，∠15；与∠1互补的角有∠2，∠4，∠6，∠8，∠10，∠12， ∠14，∠16.
2 如图所示，要在一条公路的两侧铺设平行管道，已知一侧铺设的角度为120°，为使管道对接，另一侧铺设的角度大小应为( D ) A．120° B．100° C．80° D．60°
总结
解决学具操作题，关键是要掌握学具作为几何图形具有的性质特征，以及学具作为特殊图形中特殊内角的度数．
例2 如图，将一张长方形的纸片沿EF 折叠后，点D，C 分别落在D′，C ′位置上，ED ′与BC 的交点为点G，若 ∠EFG＝50°，求∠EGB 的度数．

苏教版七下7.2 探索平行线的性质(2)

数学教学设计教材：义务教育教科书·数学（七年级下册）作者：王灿龙（泰州市靖江外国语学校）7.1 探索平行线的性质（2）几何画板”制作的课件的动画演示两直线平行，同位角相等”“两同旁内角互补”.教师用《几何画板》课件验证，让学生直观感受猜想.在学生操作感知的基础上，画板”演示，从而让学生在观察悟“两直线平行，同位角相等”行，同旁内角互补”这一性质．据“两直线平行，同位角相等”说平行，内错角相等”.学生尝试着用演绎推理的方法说明两直线平行，内错角相等.参考答案：因为a∥b，所以∠1＝∠2．又因为∠1与∠3是对顶角，所以∠1＝∠3．所以∠2＝∠3．让学生经历观察、实验、猜数学活动过程，发展合情推理能演绎推理能力．通过师生互动，口头表达能力，树立学生勇于发的信心．流：据“两直线平行，同位角相等”说平行，同旁内角互补”.学生动手解题，然后由学生发表意见，表达观点，相互补充．参考答案：因为a∥b，所以∠1＝∠2.又因为∠1＋∠3＝180º，所以∠2＋∠3＝180º.引导学生从“说点儿理”向过渡，由模仿到独立操作逐步培理能力. 教师关注学生推理过程知识的合理迁移、书写是否正确生生互动，既是学生与学生交换思想的过程，又是拓展他们培养思维能力的过程，同时也是作精神、交往能力得到培养和提°，∠D＝又因为∠C＝40°，所以∠CED＝180º－40º＝140º．，AB、CD被所截，AB∥CD.＝°（已知AB∥CD，AD∥BC．AB∥CD＝∠（用三种语言表示平行线的性质与角相等的方法有哪些？性质的方法，提升学生的认识.条件：角的关系→平行关系特征：平行关系→角的关系。

(新人教版)数学七年级下册：5.3.1《平行线的性质(第2课时)》教学设计(两套)

5.3.2平行线的性质(第2课时)平行线的性质(二)教学目标1.经历观察、操作、推理、交流等活动,进一步发展空间观念,推理能力和有条理表达能力.2.理解两条平行线的距离的含义,了解命题的含义,会区分命题的题设和结论.3.能够综合运用平行线性质和判定解题. 重点、难点重点:平行线性质和判定综合应用,两条平行的距离,命题等概念. 难点:平行线性质和判定灵活运用. 教学过程一、复习引入1.平行线的判定方法有哪些?(注意:平行线的判定方法三种,另外还有平行公理的推论)2.平行线的性质有哪些.3.完成下面填空.已知:如图,BE 是AB 的延长线,AD ∥BC,AB ∥CD,若∠D=100°,则∠C=_____, ∠A=______,∠CBE=________.4.a ⊥b,c ⊥b,那么a 与c 的位置关系如何?为什么?cb二、进行新课1.例1 已知:如上图,a ∥c,a ⊥b,直线b 与c 垂直吗?为什么?学生容易判断出直线b 与c 垂直.鉴于这一点,教师应引导学生思考:(1)要说明b ⊥c,根据两条直线互相垂直的意义, 需要从它们所成的角中说明某个角是90°,是哪一个角?通过什么途径得来?(2)已知a ⊥b,这个“形”通过哪个“数”来说理,即哪个角是90°.(3)上述两角应该有某种直接关系,如同位角关系、内错角关系、同旁内角关系,你能确定它们吗?让学生写出说理过程,师生共同评价三种不同的说理. 2.实践与探究(1)下列各图中,已知AB ∥EF,点C 任意选取(在AB 、EF 之间,又在BF 的左侧).请测量各图中∠B 、∠C 、∠F通过上述实践,试猜想∠B 、∠F 、∠C 之间的关系,写出这种关系,试加以说明.E D C B AFECBAFECBA(1) (2) 教师投影题目:学生依据题意,画出类似图(1)、图(2)的图形,测量并填表,并猜想:∠B+∠F=∠C.在进行说理前,教师让学生思考:平行线的性质对解题有什么帮助? 教师视学生情况进一步引导:①虽然AB ∥EF,但是∠B 与∠F 不是同位角,也不是内错角或同旁内角. 不能确定它们之间关系.②∠B 与∠C 是直线AB 、CF 被直线BC 所截而成的内错角,但是AB 与CF 不平行.能不能创造条件,应用平行线性质,学生自然想到过点C 作CD ∥AB,这样就能用上平行线的性质,得到∠B=∠BCD.③如果要说明∠F=∠FCD,只要说明CD 与EF 平行,你能做到这一点吗?以上分析后,学生先推理说明, 师生交流,教师给出说理过程.FEDCB A作CD ∥AB,因为AB ∥EF,CD ∥AB,所以CD ∥EF(两条直线都与第三条直线平行, 这两条直线也互相平行).所以∠F=∠FCD(两直线平行,内错角相等).因为CD ∥AB.所以∠B=∠BCD(两直线平行,内错角相等).所以∠B+∠F=∠BCF. (2)教师投影课本P23探究的图(图5.3-4)及文字.①学生读题思考:线段B 1C 1,B 2C 2……B 5C 5都与两条平行线的横线A 1B 5和A 2C 5垂直吗?它们的长度相等吗?②学生实践操作,得出结论:线段B 1C 1,B 2C 2……,B 5C 5同时垂直于两条平行直线A1B5和A 2C 5,并且它们的长度相等.③师生给两条平行线的距离下定义.学生分清线段B 1C 1的特征:第一点线段B 1C 1两端点分别在两条平行线上,即它是夹在这两条平行线间的线段,第二点线段B 1C 1同时垂直这两条平行线. 教师板书定义:(像线段B 1C 1)同时垂直于两条平行线, 并且夹在这两条平行线间的线段的长度,叫做这两条平行线的距离.④利用点到直线的距离来定义两条平行线的距离.F EDCBA教师画AB ∥CD,在CD 上任取一点E,作EF ⊥AB,垂足为F.学生思考:EF 是否垂直直线CD?垂线段EF 的长度d 是平行线AB 、CD 的距离吗? 这两个问题学生不难回答,教师归纳:两条平行线间的距离可以理解为:两条平行线中,一条直线上任意一点到另一条直线的距离.教师强调:两条平行线的距离处处相等,而不随垂线段的位置改变而改变. 3.了解命题和它的构成.(1)教师给出下列语句,学生分析语句的特点.①如果两条直线都与第三条直线平行,那么这条直线也互相平行; ②等式两边都加同一个数,结果仍是等式; ③对顶角相等;④如果两条直线不平行,那么同位角不相等.这些语句都是对某一件事情作出“是”或“不是”的判断. (2)给出命题的定义.判断一件事情的语句,叫做命题.教师指出上述四个语句都是命题,而语句“画AB ∥CD”没有判断成分,不是命题.教师让学生举例说明是命题和不是命题的语句. (3)命题的组成.①命题由题设和结论两部分组成.题设是已知事项,结论是由已知事项推出的事项. ②命题的形成.命题通常写成“如果……，那么……”的形式，“如果”后接的部分是题设，“那么”后接的部分是结论.有的命题没有写成“如果……，那么……”的形式，题设与结论不明显，这时要分清命题判断了什么事情，有什么已知事项，再改写成“如果……，那么……”形式. 师生共同分析上述四个命题的题设和结论,重点分析第②、③语句. 第②命题中,“存在一个等式”而且“这等式两边加同一个数”是题设， “结果仍是等式”是结论。

平行线的性质教学设计]

七年级数学（下）第二章平行线与相交线2.3《平行线的性质》教案临渭区三马路中学张伟莉一、教学目标：知识与能力：1、经历观察、操作、推理、交流等活动，进一步发展空间观念、推理能力和有条理地表达的能力；2、经历探索平行线特征的过程，掌握平行线的特征，并能解决一些实际问题。

过程与方法：通过测量、剪纸、推理等方法来探索平行线的特征，并能解决实际问题。

体会平行线的特征广泛性、应用性，培养学生感受生活——认知规律——运用规律的思维方法，促进分析、归纳、概括等一般能力。

情感、态度、价值观：使学生在观察、操作、推理、交流的基础上，培养学生积极探索和合作交流意识，体会学数学的快乐和用数学的意识；体会平行线的特征在现实生活中广泛的应用性和丰富的文化价值，产生对数学的亲切感，激发学生学好数学的欲望。

二、教学重点：经历探索平行线特征的过程，由两直线平行得到同位角相等、内错角相等、同旁内角互补。

三、教学难点：平行线特征与直线平行的条件的综合应用。

四、教法：引导探究、合作学习法。

五、学法：根据本节的教学内容，教学目标及学生已有的知识实际，在教学时，我主要采用观察、操作、推理，归纳，合作交流等方法进行教学，指导学生学会观察，善于思考，积极探索，学会与他人合作。

为了突出重点，分散难点，在教学过程中，我借助多媒体进行直观形象的演示，通过不断的提出问题，分析问题，解决问题的过程，使学生的思维沿着“问题情景——数学模型——方法归纳”的模式，从具体的问题情景中抽象出数学问题，概括平行线的特征，使学生循序渐进的获得知识和提高能力。

六、教具准备：学生准备：画好的一组平行线、剪刀、量角器等。

教师准备：制作多媒体教学课件投影片20张。

七、教学过程设计：本节课设计了五个教学环节：（一）、目标预习、自主探究（二）、合作交流、课堂展示（三）、目标检测、拓展升华（四）、颗粒归仓、感悟收获（五）、分层作业、巩固新知。

第一环节：目标预习、自主探究1、活动内容：通过有趣的实际问题，设置悬念，激发学生的求知欲和好奇心，如图，是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片，工作人员从玉片上已经量得∠A=115°，∠D=110°。

2022七年级数学第二讲平行线的性质与判定(提升版)

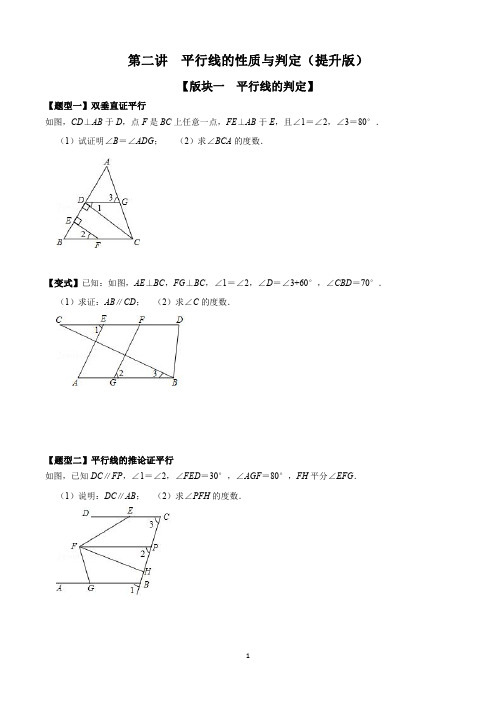
第二讲平行线的性质与判定（提升版）【版块一平行线的判定】【题型一】双垂直证平行如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1＝∠2，∠3＝80°．（1）试证明∠B＝∠ADG；（2）求∠BCA的度数．【变式】已知：如图，AE⊥BC，FG⊥BC，∠1＝∠2，∠D＝∠3+60°，∠CBD＝70°．（1）求证：AB∥CD；（2）求∠C的度数．【题型二】平行线的推论证平行如图，已知DC∥FP，∠1＝∠2，∠FED＝30°，∠AGF＝80°，FH平分∠EFG．（1）说明：DC∥AB；（2）求∠PFH的度数．【变式】如图，已知：点A在射线BG上，∠1＝∠2，∠1+∠3＝180°，∠EAB＝∠BCD．求证：EF∥CD．【题型三】平行线的判定（同位角、内错角、同旁内角）如图，AC∥FE，∠1+∠3＝180°．（1）判定∠FAB与∠4的大小关系，并说明理由；（2）若AC平分∠FAB，EF⊥BE于点E，∠4＝78°，求∠BCD的度数．【变式1】如图，已知点E、F在直线AB上，点G在线段CD上，ED与FG交于点H，∠C＝∠EFG，∠CED＝∠GHD．（1）试判断∠AED与∠D之间的数量关系，并说明理由；（2）若∠EHF＝80°，∠D＝30°，求∠AEM的度数．【变式2】如图1，在四边形ABCD中，∠ABC+∠ADC＝180°，BE、DF分别是∠ABC与∠ADC的平分线，∠ADF与∠AFD互余．（1）试判断直线BE与DF的位置关系，并说明理由；（2）如图2，延长CB、DF相交于点G，过点B作BH⊥FG，垂足为点H，试判断∠FBH与∠GBH的大小关系，并说明理由．【题型四】隐含的条件（对顶角相等、邻补角互补）如图，已知∠1+∠2＝180°，∠3＝∠B．（1）试判断DE与BC的位置关系，并说明理由．（2）若DE平分∠ADC，∠2＝3∠B，求∠1的度数．【变式1】如图，已知∠1＝∠2，∠3＝∠4，∠5＝∠6，试判断ED与FB的位置关系，并说明为什么．【变式2】如图，∠ADE+∠BCF＝180°，BE平分∠ABC，∠ABC＝2∠E．（1）AD与BC平行吗？请说明理由；（2）AB与EF的位置关系如何？为什么？（3）若AF平分∠BAD，试说明：∠E+∠F＝90°．【题型五】推导角（综合）如图，AD交BC于点D，点F在BA的延长线上，点E在线段CD上，EF与AC相交于点G，∠BDA+∠CEG＝180°．（1）证明AD∥EF；（2）若点H在FE的延长线上，且∠EDH＝∠C，∠F＝∠H，则∠BAD和∠CAD相等吗？请说明理由；（3）在（2）的条件下，若FH⊥BC，∠C＝30°，求∠F的度数．【版块二平行线的性质】【题型一】平行线+角平分线，等腰现【例题】如图，已知AB∥CD，CE平分∠ACD，且∠A＝120°，则∠1＝（）A．45°B．60°C．40°D．30°【变式】如图，AF是∠BAC的平分线，EF∥AC交AB于点E．若∠1＝50°，则∠2的度数为（）A．12.5°B．25°C．30°D．40°例题图变式图【题型二】折叠问题【例题】如图，ABCD为一长条形纸带，AB∥CD，将ABCD沿EF折叠，A、D两点分别与A′、D′对应，若∠1＝2∠2，则∠AEF的度数为（）A．60°B．65°C．72°D．75°【变式1】如图，已知长方形纸片ABCD，点E，H在AD边上，点F，G在BC边上，分别沿EF，GH折叠，使点B和点C都落在点P处，若∠FEH+∠EHG＝118°，则∠FPG的度数为（）A．54°B．55°C．56°D．57°【变式2】如图，将长方形纸片沿EB，CF折叠成图1，使AB，CD在同一直线上，再沿BF折叠成图2，使点D落在点D'处，BD'交CF于点P，若∠CEB＝37°，则∠CPB的度数为（）A．110°B．111°C．112°D．113°例题图变式1图变式2图【变式3】如图（1）所示为长方形纸带，将纸带沿EF折叠成图；（2）再沿BF折叠成图；（3）继续沿EF折叠成图（4）按此操作，最后一次折叠后恰好完全盖住∠EFG，整个过程共折叠了9次，则图（1）中∠DEF的度数为【题型三】平移如图，平移△ABC得到△DEF，其中点A的对应点是点D，则下列结论中不成立的是（）A．AD∥BE B．∠BAC＝∠DFE C．AC＝DF D．∠ABC＝∠DEF【变式1】如图，两个直角三角形重叠在一起，将其中一个沿点B到点C的方向平移到△DEF的位置，AB ＝10，DH＝4，BC＝15，平移距离为6，则阴影部分的面积（）A．40B．42C．45D．48【变式2】如图，面积为6cm2的△ABC纸片沿BC方向平移至△DEF的位置，平移的距离是BC长的2倍，则△ABC纸片扫过的面积为（）A．18cm2B．21cm2C．27cm2D．30cm2【变式3】已知，大正方形的边长为5厘米，小正方形的边长为2厘米，起始状态如图所示．大正方形固定不动，把小正方形以1厘米/秒的速度向右沿直线平移，设平移的时间为t秒，两个正方形重叠部分的面积为S平方厘米．当S＝2时，小正方形平移的时间为秒．变式1图变式2图变式3图【变式4】如图，直线AB∥CD，∠B＝∠D＝120°，E，F在AB上，且∠1＝∠2，∠3＝∠4（1）求证：AD∥BC；（2）求∠ACE的度数；（3）若平行移动AD，那么∠CAF：∠CFE的值是否发生变化？若变化，找出变化规律或求出其变化范围；若不变，求出这个比值．【巩固训练】1．如图，把一张上下两边平行的纸条沿EF折叠，若∠2＝132°，则∠1的度数为（）A．48°B．84°C．24°D．96°2．如图，∠1＝70°，直线a平移后得到直线b，则∠2﹣∠3＝（）A．70°B．180°C．110°D．80°3．如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为cm2．4．如图，长方形ABCD中，AB＝3，BC＝4，则图中四个小长方形的周长之和为．第1题图第2题图第3题图第4题图5．如图1的长方形纸带中∠DEF＝25°，将纸带沿EF折叠成图2，再沿BF折叠成图3，则图3中∠CFE 度数是（）A．105°B．120°C．130°D．145°6．如图，CD∥AB，∠DCB＝70°，∠CBF＝20°，∠EFB＝130°，问直线EF与CD有怎样的位置关系？为什么？7．如图，已知CF⊥AB于F，ED⊥AB于D，∠1＝∠2，求证：FG∥BC．。

专题平行线的判定与性质(解析版)--七年级数学下册

专题02平行线的判定与性质1．（2022秋•项城市期末）如图，已知∠B＝∠ADE，∠EDC＝∠GFB，GF⊥AB，求证：CD⊥AB．把以下证明过程补充完整，并在括号内填写理由或数学式．证明：∵∠B＝∠ADE（已知）∴DE∥BC（同位角相等，两直线平行）∴∠EDC＝∠DCB（两直线平行，内错角相等）又∠EDC＝∠GFB（已知）∴∠DCB＝∠GFB（等量代换）∴GF∥CD（同位角相等，两直线平行）【分析】根据平行线的判定与性质即可证得．【解答】证明：∵∠B＝∠ADE（已知），∴DE∥BC（同位角相等；两直线平行），∴∠EDC＝∠DCB（两直线平行，内错角相等），又∠EDC＝∠GFB（已知），∴∠DCB＝∠DFG（等量代换），∴GF∥CD（同位角相等，两直线平行），故答案为：DE，BC，同位角相等，两直线平行，两直线平行，内错角相等，∠GFB，GF，CD，同位角相等，两直线平行．2．（2023秋•道里区校级期中）将下面的解答过程补充完整：如图，已知DE∥BC，EF平分∠CED，∠A＝∠CFE，那么EF与AB平行吗？为什么？解：因为DE∥BC（已知），所以∠DEF＝∠CFE（两直线平行，内错角相等①），因为EF平分∠CED（已知），所以∠DEF＝∠CFE②（角平分线的定义），所以∠CFE＝∠CEF（等量代换③），因为∠A＝∠CFE（已知），所以∠A＝∠CEF④（等量代换），所以EF∥AB（同位角相等，两直线平行⑤）．【分析】先根据两直线平行，内错角相等，得到∠DEF＝∠CFE，再根据角平分线得出∠DEF＝∠CEF，进而得到∠CFE＝∠CEF，再根据∠A＝∠CFE，即可得出∠A＝∠CEF，进而根据同位角相等，两直线平行，判定EF∥BC．【解答】解：因为DE∥BC（已知），所以∠DEF＝∠CFE（两直线平行，内错角相等①），因为EF平分∠CED（已知），所以∠DEF＝∠CFE②（角平分线的定义），所以∠CFE＝∠CEF（等量代换③），因为∠A＝∠CFE（已知），所以∠A＝∠CEF④（等量代换），所以EF∥AB（同位角相等，两直线平行⑤）故答案为：两直线平行，内错角相等，∠CFE．等量代换，∠CEF，同位角相等，两直线平行．3．（2022秋•尤溪县期末）如图，∠1+∠2＝180°，∠B＝∠3．（1）求证：DE∥BC；（2）若∠C＝76°，∠AED＝2∠3，求∠CEF的度数．【分析】（1）由已知条件可证得AB∥EF，从而有∠B＝∠EFC，则得∠3＝∠EFC，得证DE∥BC；（2）由（1）得DE∥BC，利用两直线平行，同旁内角互补可求解．【解答】（1）证明：∵∠1+∠2＝180°，∠2＝∠4，∴AB∥EF，∴∠B＝∠EFC，∵∠B＝∠3，∴∠3＝∠EFC，∴DE∥BC；（2）解：∵DE∥BC，∠C＝76°，∴∠C+∠DEC＝180°，∠AED＝∠C＝76°，∵∠AED＝2∠3，∴∠3＝38°∵∠DEC＝180°﹣∠C＝104°，∴∠CEF＝∠DEC﹣∠3＝104°﹣38°＝66°．4．（2023秋•怀宁县期中）如图，已知EF∥CD，数学课上，老师请同学们根据图形特征添加一个关于角的条件，使得∠BEF＝∠CDG，并给出证明过程．小明添加的条件：∠B＝∠ADG．请你帮小明将下面的证明过程补充完整．证明：∵EF∥CD（已知）∴∠BEF＝∠BCD（两直线平行，同位角相等）∵∠B＝∠ADG（添加条件）∴BC∥DG（同位角互补，两直线平行）∴∠CDG＝∠BCD（两直线平行，内错角相等）∴∠BEF＝∠CDG（等量代换）．【分析】证明BC∥DG即可解答．【解答】证明：∵EF∥CD（已知），∴∠BEF＝∠BCD（两直线平行，同位角相等），∵∠B＝∠ADG，∴BC∥DG（同位角相等，两直线平行），∴∠CDG＝∠BCD（两直线平行，内错角相等），∴∠BEF＝∠CDG（等量代换）；故答案为：∠BCD，两直线平行，同位角相等；DG，同位角互补，两直线平行；∠BCD，两直线平行，内错角相等，等量代换．5．（2022秋•长春期末）请把以下证明过程补充完整，并在下面的括号内填上推理理由：已知：如图，∠1＝∠2，∠A＝∠D．求证：∠B＝∠C证明：∵∠1＝∠2，（已知）又：∵∠1＝∠3，对顶角相等∴∠2＝∠3，（等量代换）∴AE∥FD同位角相等，两直线平行∴∠A＝∠BFD两直线平行，同位角相等∵∠A＝∠D（已知）∴∠D＝∠BFD（等量代换）∴AB∥CD内错角相等，两直线平行∴∠B＝∠C两直线平行，内错角相等．【分析】先根据题意得出∠2＝∠3，故可得出AE∥FD，故∠A＝∠BFD，再由∠A＝∠D可得出∠D＝∠BFD，故可得出AB∥CD，进而可得出结论．【解答】证明：∵∠1＝∠2（已知），又∵∠1＝∠3对顶角相等，∴∠2＝∠3（等量代换），∴AE∥FD（同位角相等，两直线平行），∴∠A＝∠BFD（两直线平行，同位角相等）．∵∠A＝∠D（已知），∴∠D＝∠BFD（等量代换），∴AB∥CD（内错角相等，两直线平行）．∴∠B＝∠C（两直线平行，内错角相等）．故答案为：对顶角相等；∠3；同位角相等，两直线平行；两直线平行，同位角相等；∠BFD；AB，内错角相等，两直线平行；两直线平行，内错角相等．6．（2022秋•闽清县期末）如图，AB∥CD，E是BC的延长线上的一点，AE交CD于点F，∠1＝∠2，∠3＝∠4．求证：（1）∠B＝∠D；（2）AD∥BE．【分析】（1）根据∠3＝∠4，可得∠AFD＝∠3，再由三角形内角和定理，即可求证；（2）根据平行线的性质可得∠B+∠BCD＝180°，从而得到∠BCD+∠D＝180°，即可求证．【解答】证明：（1）∵∠AFD＝∠4，∠3＝∠4，∴∠AFD＝∠3，∵∠B＝180°﹣∠1﹣∠3，∠D＝180°﹣∠2﹣∠AFD，又∠1＝∠2，∴∠B＝∠D；（2）∵AB∥CD，∴∠B+∠BCD＝180°，∵∠B＝∠D．∴∠BCD+∠D＝180°，∴AD∥BE．7．（2023春•石城县期末）如图，已知∠ABC＝180°﹣∠A，BD⊥CD于D，EF⊥CD于E．（1）求证：AD∥BC；（2）若∠ADB＝36°，求∠EFC的度数．【分析】（1）求出∠ABC+∠A＝180°，根据平行线的判定推出即可；（2）根据平行线的性质求出∠DBC，根据垂直推出BD∥EF，根据平行线的性质即可求出∠EFC．【解答】（1）证明：∵∠ABC＝180°﹣∠A，∴∠ABC+∠A＝180°，∴AD∥BC；（2）∵AD∥BC，∠ADB＝36°，∴∠DBC＝∠ADB＝36°，∵BD⊥CD，EF⊥CD，∴BD∥EF，∴∠DBC＝∠EFC＝36°8．（2022秋•淇县期末）如图，已知AD∥FE，∠1＝∠2．（1）试说明DG∥AC；（2）若∠BAC＝70°，求∠AGD的度数．【分析】（1）只要证明∠2＝∠DAC即可．（2）利用平行线的性质解决问题即可．【解答】解：（1）∵AD∥EF，∴∠1＝∠DAC，∵∠1＝∠2，∴∠2＝∠DAC，∴DG∥AC．（2）∵DG∥AC，∴∠AGD+∠BAC＝180°，∵∠BAC＝70°，∴∠AGD＝110°9．（2022秋•禅城区期末）已知：如图，点D，E，F分别是三角形ABC的边BC，CA，AB上的点，DF∥CA，∠FDE＝∠A；（1）求证：DE∥BA．（2）若∠BFD＝∠BDF＝2∠EDC，求∠B的度数．【分析】（1）根据平行线的性质与判定方法证明即可；（2）设∠EDC＝x°，由∠BFD＝∠BDF＝2∠EDC可得∠BFD＝∠BDF＝2x°，根据平行线的性质可得∠DFB＝∠FDE＝2x°，再根据平角的定义列方程可得x的值，进而得出∠B的度数．【解答】解：（1）证明：∵DF∥CA，∴∠DFB＝∠A，又∵∠FDE＝∠A，∴∠DFB＝∠FDE，（2）设∠EDC＝x°，∵∠BFD＝∠BDF＝2∠EDC，∴∠BFD＝∠BDF＝2x°，由（1）可知DE∥BA，∴∠DFB＝∠FDE＝2x°，∴∠BDF+∠EDF+∠EDC＝2x°+2x°+x°＝180°，∴x＝36，又∵DE∥AB，∴∠B＝∠EDC＝36°．30．（2023春•驿城区校级期末）如图，AB∥DG，∠1+∠2＝180°．（1）试说明：AD∥EF；（2）若DG是∠ADC的平分线，∠2＝142°，求∠B的度数．【分析】（1）由平行线的性质可得∠BAD＝∠1，从而可求得∠BAD+∠2＝180°，即可判断；（2）由题意可求得∠1＝38°，再由角平分线的定义可得∠CDG＝∠1＝38°，再利用平行线的性质即可求解．【解答】（1）证明：∵AB∥DG，∴∠BAD＝∠1，∵∠1+∠2＝180°，∴∠BAD+∠2＝180°，（2）解：∵∠1+∠2＝180°，∠2＝142°，∴∠1＝38°，∵DG是∠ADC的平分线，∴∠CDG＝∠1＝38°，∵AB∥DG，∴∠B＝∠CDG＝38°．11．（2023秋•香坊区校级期中）完成下面推理过程，并在括号里填写推理依据：如图，已知：AB∥EF，EP⊥EQ，∠EQC+∠APE＝90°，求证：AB∥CD．证明：∵AB∥EF（已知），∴∠APE＝∠PEF，∵EP⊥EQ（已知），∴∠PEQ＝90°），即∠QEF+∠PEF＝90°，∴∠QEF+∠APE＝90°，∵∠EQC+∠APE＝90°（已知），∴∠EQC＝∠QEF（同角的余角相等），∴EF∥CD（内错角相等，两直线平行），又∵AB∥EF，∴AB∥CD（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．【分析】根据平行线的性质、判定填空即可．【解答】解：∵AB∥EF，∴∠APE＝∠PEF．∵EP⊥EQ，∴∠PEQ＝90°（垂直的定义）．即∠QEF+∠PEF＝90°．∴∠APE+∠QEF＝90°．∵∠EQC+∠APE＝90°，∴∠EQC＝∠QEF（同角的余角相等）．∴EF∥CD（内错角相等，两直线平行）．∴AB∥CD（如果两条直线都与第三条直线平行，那么这两条直线也互相平行）．故答案为：PEF；∠QEF；同角的余角相等；CD，内错角相等，两直线平行；如果两条直线都与第三条直线平行，那么这两条直线也互相平行．12．（2022秋•邓州市期末）如图，点M在CD上，已知∠BAM+∠AMD＝180°，AE平分∠BAM，MF平分∠AMC，请说明AE∥MF的理由．解：因为∠BAM+∠AMD＝180°（已知），∠AMC+∠AMD＝180°（平角的定义），所以∠BAM＝∠AMC（等量代换）．因为AE平分∠BAM，所以∠BAM（角平分线的定义）．因为MF平分∠AMC，所以∠AMC，得∠1＝∠2（等量代换），所以AE∥MF（内错角相等，两直线平行）．【分析】根据角平分线的定义，平行线的判定定理完成填空即可求解．【解答】解：因为∠BAM+∠AMD＝180°（已知），∠AMC+∠AMD＝180°（平角的定义），所以∠BAM＝∠AMC（等量代换）．因为AE平分∠BAM，所以∠BAM（角平分线的定义）．因为MF平分∠AMC，所以∠AMC，得∠1＝∠2（等量代换），所以AE∥MF（内错角相等，两直线平行）故答案为：已知；平角的定义；等量代换；∠BAM；角平分线的定义；∠AMC；∠1＝∠2；等量代换；AE∥MF；内错角相等，两直线平行．13．（2022秋•桐柏县期末）完成下面推理过程．如图：已知，∠A＝112°，∠ABC＝68°，BD⊥DC于点D，EF⊥DC于点F，求证：∠1＝∠2．证明：∵∠A＝112°，∠ABC＝68°（已知）∴∠A+∠ABC＝180°∴AD∥BC（同旁内角互补，两直线平行）∴∠1＝∠3（两直线平行，内错角相等）∵BD⊥DC，EF⊥DC（已知）∴∠BDF＝90°，∠EFC＝90°（垂直的定义）∴∠BDF＝∠EFC＝90°∴BD∥EF（同位角相等，两直线平行）∴∠2＝∠3（两直线平行，同位角相等）∴∠1＝∠2（等量代换）【分析】根据推理过程，填上依据即平行线的性质或者判定．【解答】证明：∵∠A＝112°，∠ABC＝68°（已知），∴∠A+∠ABC＝180°．∴AD∥BC（同旁内角互补，两直线平行）．∴∠1＝∠3（两直线平行，内错角相等）．∵BD⊥DC，EF⊥DC（已知），∴∠BDF＝90°，∠EFC＝90°（垂直的定义）．∴∠BDF＝∠EFC＝90°．∴BD∥EF（同位角相等，两直线平行）．∴∠2＝∠3（两直线平行，同位角相等）．∴∠1＝∠2（等量代换）．故答案为：同旁内角互补，两直线平行；∠3；两直线平行，内错角相等；垂直的定义；同位角相等，两直线平行；∠3；两直线平行，同位角相等；等量代换．14．（2023秋•天山区校级期中）已知，GP平分∠BGH，HP平分∠GHD，∠GPH＝90°．（1）求证：AB∥CD；（2）若∠AGE＝60°，求∠4的度数．【分析】（1）依据三角形内角和定理，即可得到∠1+∠3＝90°，再根据角平分线的定义，即可得到∠BGH+∠DHG＝2（∠1+∠3）＝180°，进而得出AB∥CD；（2）依据对顶角相等以及平行线的性质，即可得到∠DHG＝180°﹣60°＝120°，再根据HP平分∠GHD，即可得到结论．【解答】解：（1）∵∠GPH＝90°，∴△GHP中，∠1+∠3＝90°，又∵GP平分∠BGH，HP平分∠GHD，∴∠BGH＝2∠1，∠DHG＝2∠3，∴∠BGH+∠DHG＝2（∠1+∠3）＝180°，∴AB∥CD；（2）∵∠BGH＝∠AGE＝60°，∴∠DHG＝180°﹣60°＝120°，又∵HP平分∠GHD，∴∠4＝∠DHG＝×120°＝60°．15．（2023春•覃塘区期末）如图：已知，∠HCO＝∠EBC，∠BHC+∠BEF＝180°．（1）求证：EF∥BH；（2）若BH平分∠EBO，EF⊥AO于F，∠HCO＝64°，求∠CHO的度数．【分析】（1）要证明EF∥BH，可通过∠E与∠EBH互补求得，利用平行线的性质说明∠EBH＝∠CHB 可得结论．（2）要求∠CHO的度数，可通过平角和∠FHC求得，利用（1）的结论及角平分线的性质求出∠FHB 及∠BHC的度数即可．【解答】证明：（1）∵∠HCO＝∠EBC，∴EB∥HC．∴∠EBH＝∠CHB．∵∠BHC+∠BEF＝180°，∴∠EBH+∠BEF＝180°．∴EF∥BH．（2）解：∵∠HCO＝∠EBC，∴∠HCO＝∠EBC＝64°，∵BH平分∠EBO，∴∠EBH＝∠CHB＝∠EBC＝32°．∵EF⊥AO于F，EF∥BH，∴∠BHA＝90°．∴∠FHC＝∠BHA+∠CHB＝122°．∵∠CHO＝180°﹣∠FHC＝180°﹣122°＝58°．16．（2023春•新化县期末）如图，点E，F分别在AB，CD上，AF⊥CE，垂足为点O．已知∠1＝∠B，∠A+∠2＝90°．（1）求证：AB∥CD；（2）若AF＝12，BF＝5，AB＝13，求点F到直线AB的距离．【分析】（1）应用平行线的判定与性质进行求解即可得出答案；（2）设点F到直线AB的距离为h，根据等面积法可得SAFB＝，代入计算即可得出h△的值，即可得出答案．【解答】（1）证明：因为∠l＝∠B（已知），所以CE∥BF（同位角相等，两直线平行），因为AF⊥CE（已知），所以AF⊥BF（垂直的性质），所以∠AFB＝90°（垂直的定义），又因为∠AFC+∠AFB+∠2＝180°（平角的定义）．即∠AFC+∠2＝90°，又因为∠A+∠2＝90，所以∠AFC＝∠A（同角的余角相等），所以AB∥CD（内错角相等，两直线平行）；（2）解：因为AF⊥BF（已证），且AF＝12，BF＝5，AB＝13．设点F到直线AB的距离为h．所以SAFB＝，△所以，即h＝，所以点F到直线AB的距离为．17．（2023春•温州月考）如图，已知∠1＝∠3，∠2＝∠B．（1）试判断DE与BC的位置关系，并说明理由；（2）若DE平分∠ADC，∠1＝3∠B，求∠EFC的度数．【分析】（1）根据已知条件判定AB∥EF，再结合平行线的性质可得∠ADE＝∠B，从而判定出最终结论．（2）设∠B＝x，结合已知条件，分别把∠1，∠ADE，∠ADC表示出来，根据∠ADB是平角列出方程，求出x的值，进而求出∠EFC的度数．【解答】解：（1）DE∥BC，理由如下：∵∠1＝∠3，∴AB∥EF，∴∠2＝∠ADE，∵∠2＝∠B，∴∠ADE＝∠B，∴DE∥BC（2）设∠B＝x，则∠1＝3∠B＝3x，∵DE∥BC，∴∠ADE＝∠B＝x，∵DE平分∠ADC，∴∠ADC＝2∠ADE＝2x，∴x＝36°，∴∠ADC＝2x＝72°，∵AB∥EF，∴∠EFC＝∠ADC＝72°18．（2023春•仙居县期末）如图是一个汉字“互”字，其中，AB∥CD，HF∥GE，∠HGE＝∠HFE，M、H、G三点在同一直线上，N、E、F三点在同一直线上．求证：（1）GH∥EF；（2）∠CMH＝∠BNE．【分析】（1）根据“两直线平行，同旁内角互补”和“同旁内角互补，两直线平行”证明即可；（2）延长EF，与CD交于点I．根据“两直线平行，内错角相等”和角的等量代换证明即可．【解答】证明：（1）∵HF∥GE，∴∠HFE+∠GEF＝180°（两直线平行，同旁内角互补）．又∵∠HGE＝∠HFE，∴∠HGE+∠GEF＝180°，∴GH∥EF（同旁内角互补，两直线平行）．（2）延长EF，与CD交于点I．∵GH∥EF，∴∠CMH＝∠MIF．又∵AB∥CD，∴∠MIF＝∠BNE．∴∠CMH＝∠BNE．19．（2022秋•东阳市期末）如图，长方形纸片ABCD中，G、H分别是AB、CD边上的动点，连GH，将长方形纸片ABCD沿着GH翻折，使得点B，C分别落在点E，F位置．（1）若∠BGH＝110°，求∠AGE的度数．（2）若∠FHD＝20°，求∠CHG的度数．（3）已知∠BGH和∠CHG始终互补，若∠BGH＝α，请直接写出∠FHC的度数（含α的代数式）．【分析】（1）根据折叠得到∠BGH＝∠EGH＝110°，再根据平角的定义，利用∠AGE＝∠BGH+∠EGH ﹣180°计算可得；（2）根据折叠得到∠CHG＝∠FHG，再根据平角的定义计算即可；（3）根据互补得到∠BGH+∠CHG＝180°，从而求出∠CHG＝∠FHG＝180°﹣α，继而可得结果．【解答】解：（1）由折叠可得：∠BGH＝∠EGH＝110°，∵∠BGH+∠AGH＝180°，∴∠AGE＝∠BGH+∠EGH﹣180°＝40°；（2）由折叠可得：∠CHG＝∠FHG，∴；（3）∵∠BGH和∠CHG始终互补，∴∠BGH+∠CHG＝180°，∵∠BGH＝α，∴∠CHG＝180°﹣α，∴∠FHG＝180°﹣α，∴∠FHC＝∠FHG+∠CHG＝360°﹣2α．20．（2023春•金牛区校级期中）如图1，直线GH与直线l1，l2分别交于B，A两点，点C在直线l2上，射线AD平分∠BAC交直线l1于点E，∠GBE＝2∠BAE．（1）求证：直线l1∥l2；（2）如图2，点Q在直线l1上（B点左侧），AM平分∠BAQ交l1于点M，过点M作MN⊥AD交AD于点N，请猜想∠BQA与∠AMN的关系；并证明你的结论；（3）若点P是线段AB上一点，射线EP交直线l2于点F，∠GBE＝130°．点N在射线AD上，且满足∠EBN＝∠EFC连接BN，请补全图形，探究∠BNA与∠FEA满足的等量关系，并证明．【分析】（1）根据角平分线的定义可得∠BAC＝2∠BAE，等量代换可得∠GBE＝∠BAC，根据平行线的判定定理，即可得证；（2）设∠DAB＝∠DAC＝α，∠BAM＝∠QAM＝β，根据三角形的内角和定理以及平行线的性质得出∠BQA，∠AMN，即可求解；（3）根据题意补充图形，分两种情况讨论，①当N在AE上时，设∠EBN＝∠EFC＝θ，根据平行线的性质以及三角形的外角的性质，分别表示出∠BNA，∠FEA，可的结论；②当点N在AE的延长线上时，根据平行线的性质，即可求解．【解答】（1）证明：∵射线AD平分∠BAC交直线l1于点E，∠GBE＝2∠BAE，∴∠BAC＝2∠BAE，∴∠GBE＝∠BAC，∴l1∥l2；（2）解：∠BQA＝2∠AMN；理由如下，∵AD平分∠BAC，AM平分∠BAQ，∴，设∠DAB＝∠DAC＝α，∠BAM＝∠QAM＝β，∵MN⊥AD，∴∠MNA＝90°，则∠AMN＝90°﹣∠MAD＝90°﹣（∠MAB+∠DAB）＝90°﹣（α+β），∵l1∥l2，∴∠BQA＝180°﹣∠QAC＝180°﹣2（α+β），∴∠BQA＝2∠AMN；（3）解：∠BNA+∠FEA＝130°，理由如下，补全图形，如图所示，①当N在AE上时，∵∠EBN＝∠EFC，设∠EBN＝∠EFC＝θ，∵l1∥l2，∠GBE＝130°，∴∠BEF＝∠EFC＝θ，∠BAC＝∠GBE＝130°，∵AD平分∠BAC，，∵l1∥l2，∴∠BEA＝∠EAC＝65°，∴∠BNA＝∠NBE+∠BEN＝65°+θ，∠FEA＝∠NEB﹣∠BEF＝65°﹣θ，∴∠BNA+∠FEA＝130°，②如图，当点N在AE的延长线上时，∠BNA＝∠FEA，∵l1∥l2，∴∠BEF＝∠EFC，∵∠EBN＝∠EFC，∴∠BEF＝∠EBN，∴BN∥EF，∴∠BNA＝∠FEA．21．（2023春•义乌市校级期中）今年除夕夜长江两岸的灯光秀璀璨夺目，照亮山城的山水桥梁城市楼阁，人民欢欣鼓舞．观看表演的小语同学发现两岸的灯光运动是有规律的，如图1所示，灯A射出的光线从AQ开始顺时针旋转至AP便立即回转，灯B射出的光线从BM开始顺时针旋转至BN便立即回转，两灯不停旋转．假设长江两岸是平行的，即PQ∥MN，点A在PQ上，B、C、D在MN上，连接AB、AC、AD，已知AC平分∠BAP，AD平分∠CAP．（1）如图1，若∠ABD＝40°，则∠CAQ＝110°；（2）如图2，在PQ上另有一点E，连接CE交AD于点F，点G在MN上，连接AG，若∠CAG＝∠CAE，∠EFD+∠DAG＝180°，试证明：EC∥AB．（3）如图3，已知灯A射出的光线旋转的速度是每秒10°，灯B射出的光线旋转的速度是每秒30°，若灯B射出的光线从BM出发先转动2秒，灯A射出的光线才从AQ出发开始转动，设灯A转动的时间为t秒，在转动过程中，当0≤t≤12时，请直接写出灯A射出的光线与灯B射出的光线相交且互相垂直时的时间t的值．【分析】（1）根据两直线平行内错角相等，得出∠QAB＝∠ABD＝40°，再根据平角的定义，得出∠BAP ＝140°，再根据角平分线的定义，得出∠BAC＝70°，再根据角之间的数量关系，计算即可得出答案；（2）根据角平分线的定义，得出∠CAE＝2∠CAF，进而得出，再根据对顶角相等和三角形的内角和定理，得出∠EFD＝∠AFC，∠AFC+∠ACE+∠CAF＝180°，进而得出，再根据等量代换，得出∠ACE＝∠CAE，即∠ACE＝∠CAP，再根据角平分线的定义，得出∠CAP＝∠CAB，再根据等量代换，得出∠ACE＝∠CAB，再根据内错角相等两直线平行，即可得出结论；（3）根据题意，分三种情况：当0≤t≤4时、当4＜t≤10时、当10＜t≤12时，分别画出图形，根据角之间的数量关系，列出方程进行计算即可．【解答】解：（1）∵PQ∥MN，∠ABD＝40°，∴∠QAB＝∠ABD＝40°，∴∠BAP＝180°﹣∠QAB＝180°﹣40°＝140°，∵AC平分∠BAP，∴，∴∠CAQ＝∠BAC+∠QAB＝70°+40°＝110°；故答案为：110°；（2）∵AD平分∠CAP，∴∠CAE＝2∠CAF，∵，∴，∵∠EFD＝∠AFC，∠AFC+∠ACE+∠CAF＝180°，又∵，∴，∴，∴，∴，∴3∠CAF＝∠ACE+∠CAF，即∠ACE＝2∠CAF，∴∠ACE＝∠CAE，即∠ACE＝∠CAP，∵AC平分∠BAP，∴∠CAP＝∠CAB，∴∠ACE＝∠CAB，∴EC∥AB；（3）当0≤t≤4时，如图，∵∠M'AC＝10°t，∠MBM'＝30°（2+t），∵AQ'⊥BM'，∴∠BM'A＝90°﹣10°t，∵PQ∥MN，∴∠MBM'+∠AM'B＝180°，即30°（2+t）+（90°﹣10°t）＝180°，解得：；当4＜t≤10时，如图，∵∠N'AC＝10°t，∵AQ'⊥BN'，∴∠BN'A＝90°﹣10°t，∵∠NBN'＝30°（t﹣4），∴90°﹣10°t＝30°（t﹣4），解得：；当10＜t≤12时，如图，∵∠MBM'＝30（t﹣10），AQ'⊥BM'，∴∠AQ'M＝90+30（t﹣10），∵∠QAQ'＝10t，PQ∥MN，∴90+30（t﹣10）＝10t，解得：，在图形的左边垂直，10t+20t﹣120+30（t﹣10）＝90，综上所述，t的值秒或秒或或9.75秒．22．（2022秋•萍乡期末）已知点A在射线CE上，∠C＝∠ADB．（1）如图1，若AD∥BC，求证：AC∥BD；（2）如图2，若BD⊥BC，垂足为B，BD交CE于点G，请探究∠DAE与∠C的数量关系，写出你的探究结论，并说明理由；（3）如图3，在（2）的条件下，过点D作DF∥BC交射线CE于点F，当∠BAC＝∠BAD，∠DFE＝8∠DAE时，求∠BAD的度数．【分析】（1）根据AD∥BC，可得∠DAE＝∠C，再根据∠C＝∠ADB，即可得到∠DAE＝∠ADB，即可得证；（2）∠DAE+2∠C＝90°．根据三角形外角的性质，可得到∠CGB＝∠ADB+∠DAE，根据直角三角形两锐角互余，有∠CGB+∠C＝90°，再根据∠C＝∠ADB即可得到∠DAE与∠C的数量关系；（3）设∠DAE＝α，则∠DFE＝8α，∠AFD＝180°﹣8α，根据DF∥BC，即可得到∠C＝∠AFD＝180°﹣8α，再根据∠DAE+2∠C＝90°，即可得到α+2（180°﹣8α）＝90°，求得α的值，即可运用三角形内角和定理得到∠BAD的度数．【解答】（1）证明：∵AD∥BC，∴∠DAE＝∠C，又∵∠C＝∠ADB，∴∠DAE＝∠ADB，∴AC∥BD；（2）解：∠DAE+2∠C＝90°理由如下：∵∠CGB是△ADG的外角，∴∠CGB＝∠ADB+∠DAE，∵BD⊥BC，∴∠CBD＝90°，∴在△BCG中，∠CGB+∠C＝90°，∴∠ADB+∠DAE+∠C＝90°，又∵∠C＝∠ADB，∴∠DAE+2∠C＝90°；（3）解：设∠DAE＝α，则∠DFE＝8α，∴∠AFD＝180°﹣8α，∵DF∥BC，∴∠C＝∠AFD＝180°﹣8α，又∵∠DAE+2∠C＝90°，∴2（180°﹣8α）+α＝90°，∴α＝18°，∴∠C＝180°﹣8×18°＝36°，∴∠ADB＝∠C＝36°，又∵∠BAC＝∠BAD，∴∠ABC＝180°﹣∠C﹣∠BAC＝180°﹣∠ADB﹣∠BAD＝∠ABD，∵∠CBD＝90°，∴，∴在△ABD中，∠BAD＝180°﹣45°﹣36°＝99°，∴∠BAD的度数为99°．23．（2022秋•鲤城区校级期末）如图①，已知AB∥CD，一条直线分别交AB、CD于点E、F，∠EFB＝∠B，FH⊥FB，点Q在BF上，连接QH．（1）已知∠EFD＝70°，求∠B的度数；（2）求证：FH平分∠GFD．（3）在（1）的条件下，若∠FQH＝30°，将△FHQ绕着点F顺时针旋转，如图②，若当边FH转至线段EF上时停止转动，记旋转角为α，请求出当α为多少度时，QH与△EBF某一边平行？（4）在（3）的条件下，直接写出∠DFQ与∠GFH之间的关系．【分析】（1）由AB∥CD，得∠B＝∠BFD，又∠B＝∠EFB，得证；（2）由（1）∠EFB＝∠BFD，由FH⊥FB，得∠BFD+∠DFH＝90°，∠EFB+∠GFH＝90°，由等角的余角相等，得∠DFH＝∠GFH，命题得证；（3）由QH分别与△EBF的三边分别平行，分情况讨论处理；（4）在（3）的各种情况下，分别计算∠DFQ与∠GFH的度数，可得结论∠DFQ与∠GFH相差20°．【解答】解：（1）∵AB∥CD，∴∠B＝∠BFD，又∠B＝∠EFB，∴，∴∠B＝35°；（2）∵FH⊥FB，∴∠BFD+∠DFH＝90°，∠EFB+∠GFH＝90°，∴∠DFH＝∠GFH，∴FH平分∠GFD．（3）①QH与△EFB的边BF平行时，如下图1及图4，如图1，∵BF∥HQ，∴∠H+∠BFH＝180°，又∠H＝60°，∴∠BFH＝120°，α＝∠BFQ＝120°﹣∠HFQ＝120°﹣90°＝30°；如图4，∠HFB＝∠H＝60°，α＝∠1+∠2+∠3＝360°﹣（∠HFB+∠HFQ）＝360°﹣（60°+90°）＝210°；②QH与△EFB的边BE平行时，如下图2，∠1＝∠3＝35°，∠2＝∠4＝30°，∴α＝∠BFQ＝∠1+∠2＝35°+30°＝65°；③QH与△EFB的边EF平行时，如下图3，∠3＝∠Q＝30°，∴α＝∠BFQ＝∠1+∠2+∠3＝35°+110°+30°＝175°，综上，旋转角为α＝30°或65°或175°或210°．（4）α＝30°时，∠DFQ＝∠DFB﹣∠BFQ＝35°﹣30°＝5°，∠GFH＝90°﹣∠EFB﹣∠BFQ＝90°﹣35°﹣30°＝25°；α＝65°时，∠DFQ＝65°﹣35°＝30°，∠GFH＝90°﹣∠GFQ＝90°﹣（180°﹣35°﹣65°）＝10°；α＝175°时，∠DFQ＝175°﹣35°＝140°，∠GFH＝180°﹣60°＝120°；α＝210°时，∠DFQ＝210﹣35°＝175°，∠GFH＝360°﹣110°﹣35°﹣60°＝155°；综上，∠DFQ与∠GFH相差20°．24．（2023秋•香坊区校级期中）如图1，直线MN与直线AB、CD分别交于点E、F，∠1+∠2＝180°．（1）求证：AB∥CD；（2）如图2，∠BEF与∠EFD的角平分线交于点P，延长EP交CD于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；（3）如图3，在（2）的条件下，连接PH，∠HPQ＝45°，K是GH上一点，连接PK，作PQ平分∠EPK，若∠PHG＝15°，求∠QPK的度数．【分析】（1）根据同旁内角互补，两条直线平行即可判断直线AB与直线CD平行；（2）先根据两条直线平行，同旁内角互补，再根据∠BEF与∠EFD的角平分线交于点P，可得∠EPF ＝90°，进而证明PF∥GH；（3）根据直角三角形的性质求出∠HPG＝75°，根据角的和差及邻补角定义求出∠EPQ＝60°，根据角平分线定义求解即可．【解答】（1）证明：∵∠1+∠2＝180°，又∵∠1＝∠AEF，∠2＝∠CFE，∴∠AEF+∠CFE＝180°，∴AB∥CD；（2）证明：由（1）知，AB∥CD，∴∠BEF+∠EFD＝180°，又∵∠BEF与∠EFD的角平分线交于点P，∴∠FEP+∠EFP＝（∠BEF+∠EFD）＝90°，∴∠EPF＝90°，即EG⊥PF，∵GH⊥EG，∴PF∥GH；（3）解：∵∠PHG＝15°，GH⊥EG，∴∠HPG＝90°﹣15°＝75°，∵∠HPQ＝45°，∴∠QPG＝∠HPQ+∠HPG＝120°，∵∠QPG+∠EPQ＝180°，∴∠EPQ＝60°，∵PQ平分∠EPK，∴∠QPK＝∠EPQ＝60°．25．（2023秋•吉林期中）如图①，直角三角形DEF与直角三角形ABC的斜边在同一直线上，∠ACB＝∠E ＝90°，∠EDF＝36°，∠ABC＝40°，CD平分∠ACB，将△DEF绕点D按逆时针方向旋转，如图②，记∠ADF为α（0°＜α＜180°），在旋转的过程中：（1）当∠α＝4°时，DE∥BC，当∠α＝94°时，DE⊥BC；（2）如图③，当顶点C在△DEF的内部时，边DF、DE分别交BC、AC的延长线于点M、N．①求出此时∠α的度数范围；②∠1与∠2的度数和是否变化？若不变，请直接写出∠1与∠2的度数和；若变化，请说明理由．【分析】（1）由DE∥BC得∠EDA＝∠ABC＝40°，再根据α＝∠EDA﹣∠EDF可得出答案；先求出∠A ＝50°，由DE⊥BC得DE∥AC，进而得∠EDA+∠A＝180°，由此得∠EDA＝＝130°，然后根据α＝∠FDA＝∠EDA﹣∠EDF可得出答案；（2）①先求出∠BCD＝∠ACD＝45°，∠CDA＝85°，求出当DE和CD重合时α＝∠CDA﹣∠EDF＝49°，当EF与CD重合时，α＝∠CDA＝85°，据此可求出∠α的度数范围；②连接MN，在△CMN中得∠CNM+∠CMN+∠MCN＝180°，则∠CNM+∠CMN＝90°，在△MND中得∠DNM+∠DMN+∠MDN＝180°，即∠2+∠CNM+∠1+∠CMN+∠MDN＝180°，据此可得∠1+∠2的度数【解答】解：（1）∵∠ABC＝40°，∴当DE∥BC时，∠EDA＝∠ABC＝40°，如图①所示：又∵∠EDF＝36°，∴α＝∠EDA﹣∠EDF＝40°﹣36°＝4°，故当∠α＝4°时，DE∥BC；在△ABC中，∠ACB＝90°，∠ABC＝40°，∴∠A＝180°﹣（∠ACB+∠ABC）＝50°，当DE⊥BC时，则DE∥AC，如图②所示：∴∠EDA+∠A＝180°，∴∠EDA＝180°﹣∠A＝130°，又∠EDF＝36°，∴α＝∠FDA＝∠EDA﹣∠EDF＝130°﹣36°＝94°，故当α＝94°时，DE⊥BC．故答案为：4，94．（2）①∵∠ACB＝90°，CD平分∠ACB，∴∠BCD＝∠ACD＝45°，∴∠CDA＝180°﹣（∠ACD+∠A）＝180°﹣（45°+50°）＝85°，当DE和CD重合时，α＝∠CDA﹣∠EDF＝85°﹣36°＝49°，当EF与CD重合时，α＝∠CDA＝85°，∴当顶点C在△DEF的内部时，∠α的度数范围是：49°＜α＜85°．②∠1与∠2的度数和不发生变化，∠1+∠2＝54°，理由如下：连接MN，如图③所示：在△CMN中，∠CNM+∠CMN+∠MCN＝180°，∵∠MCN＝∠ACB＝90°，∴∠CNM+∠CMN＝90°，在△MND中，∠DNM+∠DMN+∠MDN＝180°，即∠2+∠CNM+∠1+∠CMN+∠MDN＝180°，∵∠CNM+∠CMN＝90°，∠MDN＝∠EDF＝36°，∴∠1+∠2+90°+36°＝180°，∴∠1+∠2＝180°﹣90°﹣36°＝54°．。

北师大版七年级下数学第二章《相交线与平行线》全套教案

1北师大版七年级下数学第二章《相交线与平行线》教案《2.1两条直线的位置关系》教案一：教学目标1、掌握两条直线平行与垂直的条件；2、会运用条件判断两直线是否平行或垂直；3、能运用条件确定两平行或垂直直线的方程系数.二：教学重点、难点两条直线平行与垂直的条件，两条直线平行与垂直的条件的应用.三：教学设计（一）情景引入A ：两条直线位置关系当中平行为简单；现在我们来研究平面内两条直线平行的关系. ①先入为主的思想；在研究直线问题时首先考虑特殊情况：α=90°时，画图.这个情况很简单：当α=90°时只要x 1≠x 2，则两条直线平行.②一般情况：α≠90°时，则k 存在，∴y 1=kx +b 1 y 2=kx +b 2已知直线l 1，l 2的斜截式方程为：l 1：y =k 1x +b 1 l 2：y =k 2x +b 2，若l 1//l 2，则有α1=α2且b 1≠b 2，∴tan α=tan α [α1∈[0，180°），α2∈[0，180°）]∴k 1=k 2反之，是否成立？若k 1=k 2且b 1≠b 2则有tan α=tan α，∵0≤α1，α2＜π，∴α1=α2且b 1≠b 2，∴l 1//l 2结论一：①特殊情况：若两条直线l 1，l 2斜率都不存在也不重合，则两直线l 1，l 2平行； ②有斜率的两条直线l 1//l 2 <=> k 1=k 2且b 1≠b 2∴判断不重合的两条直线平行的程序：两条直线方程——两条直线斜率都不存在且不重合→平行.两条直线方程——化为斜截式方程→求两条直线斜率.若k 1=k 2且b 1≠b 2→平行若k 1≠k 2→相交或者若A 1B 2≠B 1A 2且B 1C 2≠B 2C 1或A 1B 2=A 2B 1且A 1C 2≠A 2C 1 则两条直线平行.例1：已知两条直线l 1:4x +2y -7=0，l 2:2x -y -5=0求证l 1∥l 212122∵l 1的斜率为，l 2的斜率为 ∴k 1=k 2∴l 1∥l 2 例2：求过点A （1，-4）且与直线2x +3y +5=0平行的直线的方程？解：已知直线的斜率为-，因为所求直线与已知直线平行，因此它的斜率也是-. 根据点斜式，得到所求直线的方程是：y +4=-（x -1）即2x +3y +10=0 例3：如果直线ax +2y +2=0与3x -y -2=0平行，那么系数a =（）A .3B .-6C .-D . 例4：求与直线3x +4y +1=0平行，且在两坐标轴上截距之和为的直线l 的方程？法一：设直线方程为3x +4y +m =0，交x 轴于点（-，0）交y 轴于点（0，-），由题意可得（-）+（-）=即m =-4， ∴所求直线l 的方程为3x +4y -4=0，法二：设直线方程为+=1， ∴a +b =，-=-，可得a =，b =1， ∴所求直线l 的方程为3x +4y -4=0B ：平时我们已经理解了；接下来我们来研究两直线相互垂直的关系.①同样的先考虑特殊情况：若已知一条直线的倾斜角为90°，x =x 1，则求其另一条与它垂直的直线方程.②一般情况：若已知两条直线l 1:y =k 1x +b 1，l 2:y =k 2 x +b 2，相互垂直则k 1与k 2有何关系？ α+（π-β）= ∴α-β=- ∴β=α+ 21213232322332373m 4m 3m 4m 37a x b y 37a b 43342π2π2π3tan β=tan （α+）=-cot α ∴tan α·tan β=tan α·（-cot α）=-1∴最后我们得证:若两条直线垂直则k 1k 2=-1.③α=90°时=>β=0°（特殊情况）k 1=0，k 2不存在.或者k 1不存在，k 2=0.例4:已知直线l 1：ax -y +2a =0与l 2：（2a -1）x +ay +a =0互相垂直，求a 的值一、①当α=90°即a =0时，l 2：x =0 ∴l 1：y =0 ∴l 1⊥l 2②当α≠90°则k 1·k 2=a ·（-）=-1 ∴a =1 二、A 1A 2+B 1B 2=0 =>a （2a -1）-a =0 2a ²-2a =0 =>a =1或a =0例5：求与3x +4y +1=0平行，且在两坐标轴上截距之和为7/3的直线l 的方程.（一）设直线方程为3x +4y +m =0，交x 轴于点（-，0）交y 轴于点（0，-） ∴（-）+（-）= ∴m =-4∴所求直线l 的方程为3x +4y -4=0（二）设直线方程为+=1 =>a +b =；-=-=>a =，b =1 ∴l ：3x +4y -4=0例6：已知三角形两条高线为x +y =0和2x -3y +1=0且一个顶点C （1，2），求三角形AC ，BC 边所在直线的方程.∵AC ，BC 与两条高线垂直∴AC ，BC 的斜率为1和- ∴边AC ，BC 所在直线的方程为y -2=1（x -1），y -2=-（x -1）即x -y +1=0，3x +2y -7=0《2.2探索直线平行的条件》教案一、导学目标1.使学生能够熟练识别同位角；2πaa )12(-3m 4m 3m 4m 37a xb y 37a b 433423232.使学生会用同位角相等判定二条直线平行.二、重点难点1.重点（1）识别同位角.（2）用同位角相等判定二条直线平行.2.难点用同位角相等判定二条直线平行.三、导学过程一、自主学习：操作---观察---探索如图：3根木条（或硬纸条）相交成∠1、∠2，固定木条b、c，转动木条a.问：1.在木条a的转动过程中，木条a、b的位置关系发生了什么变化？∠2与∠1的大小关系发生了什么变化？2.改变图中∠1的大小，按照上面的方式再试一试，当∠2与∠1的大小满足什么关系时，木条a与木条b平行？二、合作探究：活动一：利用平移三角尺的方法画平行线，探索直线平行的条件.当∠1与∠2相等，直线a、b就；当∠1与∠2不相等时，直线a、b平行吗？活动二：通过观察、比较，认识“同位角”，探索直线平行的条件.直线a、b被第三条直线c所截而成的8个角中，像∠1与∠2这样的一对角称为.请问图中还有没有其他的同位角？4归纳：相等，两直线.活动三：例题讲解.例：如图，∠1=∠C，∠2=∠C，请找出图中互相平行的直线，并说明理由.三、拓展提高：1.∠1与∠C、∠2与∠B、∠ 3与∠ C分别是哪两条直线被哪一条直线截成的同位角？2.如图，直线a、b被直线c所截，∠1=35°，∠2=145°，问：直线a与b平行吗？四、达标检测：1.如图，∠1与∠B是直线和被直线所截构成的同位角；∠2与∠A直线和被直线所截构成的同位角.2.如图，∠1、∠2、∠3中，和是同位角.3.如图，如果∠B=∠1，根据，那么可得DE//BC；如果∠B=∠2，根据同位角相等，两直线平行，那么可得// .4.如图，已知直线AB、CD被直线EF所截，如果∠BMN＝∠DNF，∠1＝∠2，那么MQ∥NP，为什么？AB CD EF13256《2.3平行线的性质》教案教学目标：理解平行线的性质的推导，掌握平行线的性质.教学重点：平行线的性质以及应用.教学难点：平行线的性质公理与判定公理的区别.教学过程：一、梳理旧知，引出新课平行线的判定：判定方法1、同位角相等，两直线平行.判定方法2、内错角相等，两直线平行.判定方法3、同旁内角互补，两直线平行.问题：反过来也成立吗？过去我们学过：如果两个数的和为0，这两个数互为相反数.反过来，如果两个数互为相反数，那么这两个数的和为0.这两个句子都是正确的.现在换一个例子：如果两个角是对顶角，那么这两个角相等.它是对的.反过来，如果两个角相等，这两个角是对顶角.对吗？再看下面的例子：“如果一个整数个位上的数字是5，那么它一定能够被5整除.”对吗？这句话反过来怎么说？对不对？【结论】如果一个句子是正确的，反过来说（因果对调），就未必正确.二、动手操作，归纳性质上一节课，我们学过：同位角相等，两直线平行.反过来怎么说？它还是对的吗？（板书）性质1、两直线平行，同位角相等.P Q M N21F ED C B A7如果把平行线性质1：“两直线平行，同位角相等”看作是基本事实（公理），我们可以利用这个公理证明平行线性质2：“两直线平行，内错角相等”.【例】如图，已知：直线a 、b 被直线c 所截，且a ∥b ，求证：∠1=∠2.证明：∵a ∥b ，∴∠1=∠3（__________________）.∵∠3=∠2（对顶角相等），∴∠1=∠2（等量代换）.（板书）性质2、两直线平行，内错角相等【变式】下面我们来证明平行线的性质3：两直线平行，同旁内角互补.请模仿范例写出证明.如图，已知：直线a 、b 被直线c 所截，且a ∥b ，求证：∠1+∠2=180º.证明：（略）（板书）性质：两直线平行，同旁内角互补三、巩固新知，深化理解例1、如图，平行线AB ，CD 被直线AE 所截.（1）从∠1=110º．可以知道∠2是多少度吗？为什么？（2）从∠1=110º可以知道∠3是多少度吗？为什么？（3）从∠1=110º可以知道∠4是多少度吗？为什么？例2、如图，已知AB ∥CD ，AE ∥CF ，∠A = 39°，∠C 是多少度？为什么？ab1 2 3 c ab 1 23c ED CB A12348方法一解：∵AB ∥CD ， ∴ ∠C=∠1．∵ AE ∥CF ，∴ ∠A=∠1．∴ ∠C=∠A ．∵∠A = 39º，∴∠C = 39º．方法二解：∵AB ∥CD ，∴ ∠C=∠2.∵ AE ∥CF ，∴ ∠A=∠2.∴ ∠C=∠A .∵∠A = 39º，∴∠C = 39º．练习1：如图，已知直线a 、b 被直线c 所截，在括号内为下面各小题的推理填上适当的根据：（1）∵a ∥b ，∴∠1=∠3（___________________）；（2）∵∠1=∠3，∴a ∥b （_________________）.（3）∵a ∥b ，∴∠1=∠2（__________________）；（4）∴a ∥b ，∴∠1+∠4=180º（_____________________________________）（5）∵∠1=∠2，∴a ∥b （___________________）；（6）∵∠1+∠4=180º，∴a ∥b （_______________）.练习2：教材第51页随堂练习四、盘点收获，布置作业1、（1）平行线的性质是什么？（2）你能用自己的语言叙述研究平行线性质的过程吗？（3）性质2和性质3是通过简单推理得到的，在推理论证中需要注意哪些问题？2、作业G FED C B Aa b12 3 c 49《2.4用尺规作角》教案教学目的：1、经历尺规作角的过程，进一步培养学生的动手操作能力，增强学生的数学应用和研究意识.2、能按作图语言来完成作图动作，能用尺规作一个角等于已知角.教学重点：能按作图语言来完成作图动作，能用尺规作一个角等于已知角.教学难点：作图步骤和作图语言的叙述，及作角的综合应用.教学过程：一、问题的提出如图，要在长方形木板上截一个平行四边形，使它的一组对边在长方形木板的边缘上，另一组对边中的一条边为AB .（1）请过点C 画出与AB 平行的另一条边.（2）如果你只有一个圆规和一把没有刻度的直尺，你能解决这个问题吗？二、新课内容一：（请按作图步骤和要求操作，别忘了留下作图痕迹）（一）用尺规作一个角等于已知角.（1）已知：∠AOB求作：∠A′O′B′，使∠A′O′B′=∠AOB（2）已知：∠10求作：∠AOB ，使∠AOB=∠（二）用尺规作一个角等于已知角的倍数：（3）已知：∠1求作：∠MON ，使∠MON=2∠1∠COD ，使∠COD=3∠1（三）用尺规作一个角等于已知角的和：（4）已知：∠1、∠2、∠3求作：①∠AOB ，使∠AOB=∠1+∠2②∠POQ ，使∠POQ=∠1+∠2+∠3③∠MON ，使∠MON=2∠1+∠2（四）用尺规作一个角等于已知角的差：已知：∠、∠、∠求作：①∠AOB ，使∠AOB=∠－∠②∠POQ ，使∠POQ=∠－∠－∠③求作一个角，使它等于2∠－∠（五）综合练习：（通过以下练习，意味着你掌握了作角的真本领，多动一下脑筋，你一定会完成得很出色的）1、已知：线段AB 、 ∠、∠αα1αβγαβγαβαβγβγαβ13211求作：分别过点A 、点B 作∠CAB=∠、∠CBA=∠2、如图，点P 为∠ABC 的边AB 上的一点，过点P 作直线EF//BC .3、已知：直线L 和L 外一点P ，求作：一条直线，使它经过点P ，并与已知直线L 平行.4、已知：△ABC ，求作：直线MN ，使MN 经过点A ，且MN//BC .5、如图，以点B 为顶点，射线BA 为一边，在∠ABC 外再作一个角，使其等于∠ABC .（六）小结（七）作业αβLA αβ。

北师大版初中数学七年级下册《第2章相交线与平行线：2.3 平行线的性质》同步练习卷2020.2

北师大新版七年级下学期《2.3 平行线的性质》2020年同步练习卷一．解答题（共60小题）1．已知AB∥CD，点M、N分别是AB、CD上两点，点G在AB、CD之间，连接MG、NG．（1）如图1，若GM⊥GN，求∠AMG+∠CNG的度数；（2）如图2，若点P是CD下方一点，MG平分∠BMP，ND平分∠GNP，已知∠BMG ＝30°，求∠MGN+∠MPN的度数；（3）如图3，若点E是AB上方一点，连接EM、EN，且GM的延长线MF平分∠AME，NE平分∠CNG，2∠MEN+∠MGN＝105°，求∠AME的度数．2．如图1，MN∥EF，C为两直线之间一点．（1）如图1，若∠MAC与∠EBC的平分线相交于点D，若∠ACB＝100°，求∠ADB的度数．（2）如图2，若∠CAM与∠CBE的平分线相交于点D，∠ACB与∠ADB有何数量关系？并证明你的结论．（3）如图3，若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D，请直接写出∠ACB与∠ADB之间的数量关系：．3．如图1，直线AB∥CD，直线EF交AB于点E，交CD于点F，点G和点H分别是直线AB和CD上的动点，作直线GH，EI平分∠AEF，HI平分∠CHG，EI与HI交于点I．（1）如图1，点G在点E的左侧，点H在点F的右侧，若∠AEF＝70°，∠CHG＝60°，求∠EIH的度数．（2）如图2，点G在点E的右侧，点H也在点F的右侧，若∠AEF＝α，∠CHG＝β，其他条件不变，求∠EIH的度数．（3）如图3，点G在点E的右侧，点H也在点F的右侧，∠GHC的平分线HJ交∠KEG 的平分线EJ于点J．其他条件不变，若∠AEF＝α，∠CHG＝β，求∠EJH的度数．4．如图，已知直线AB∥射线CD，∠CEB＝100°．P是射线EB上一动点，过点P作PQ ∥EC交射线CD于点Q，连结CP．作∠PCF＝∠PCQ，交直线AB于点F，CG平分∠ECF．（1）若点P，F，G都在点E的右侧．①求∠PCG的度数；②若∠EGC﹣∠ECG＝40°，求∠CPQ的度数．（2）在点P的运动过程中，是否存在这样的情形，使？若存在，求出∠CPQ 的度数；若不存在，请说明理由．5．已知点D，E，F分别是△ABC的边AB，AC，BC上的点，DE∥BC，DF∥AC．（1）如图1，点G是线段FD延长线上一点，连接EG，∠CEG的平分线EM交AB于点M，交FD于点N．则∠A，∠AME，∠CEG之间存在怎样的数量关系？请写出证明过程；（2）如图2，在（1）的条件下，若EG平分∠AED，∠AME＝35°，且∠EDF﹣∠A＝30°，求∠C的度数．6．如图1，已知直线EF分别与直线AB，CD相交于点E，F，AB∥CD，EM平分∠BEF，FM平分∠EFD（1）求证：∠EMF＝90°．（2）如图2，若FN平分∠MFD交EM的延长线于点N，且∠BEN与∠EFN的比为4：3，求∠N的度数．（3）如图3，若点H是射线EA之间一动点，FG平分∠HFE，过点G作GQ⊥FM于点Q，请猜想∠EHF与∠FGQ的关系，并证明你的结论．7．已知直线AB∥CD，直线EF分别交AB、CD于A、C，CM是∠ACD的平分线，CM交AB于H，过A作AG⊥AC交CM于G．（1）如图1，点G在CH的延长线上时，①若∠GAB＝36°，则∠MCD＝．②猜想：∠GAB与∠MCD之间的数量关系是．（2）如图2，点G在CH上时，（1）②猜想的∠GAB与∠MCD之间的数量关系还成立吗？如果成立，请给出证明；如果不成立，请写出∠GAB与∠MCD之间的数量关系，并说明理由．8．如图1，AB∥CD，P为AB、CD之间一点（1）若AP平分∠CAB，CP平分∠ACD．求证：AP⊥CP；（2）如图（2），若∠BAP＝∠BAC，∠DCP＝∠ACD，且AE平分∠BAP，CF平分∠DCP，猜想∠E+∠F的结果并且证明你的结论；（3）在（1）的条件下，当∠BAQ＝∠BAP，∠DCQ＝∠DCP，H为AB上一动点，连HQ并延长至K，使∠QKA＝∠QAK，再过点Q作∠CQH的平分线交直线AK于M，问当点H在射线AB上移动时，∠QMK的大小是否变化？若不变，求其值；若变化，求其取值范围．9．如图，已知直线AB∥CD．（1）在图1中，点E在直线AB上，点F在直线CD上，点G在AB、CD之间，若∠1＝30°，∠3＝75°，则∠2＝；（2）如图2，若FN平分∠CFG，延长GE交FN于点M，EM平分∠AEN，当∠N+∠FGE＝54°时，求∠AEN的度数；（3）如图3，直线MF平分∠CFG，直线NE平分∠AEG相交于点H，试猜想∠G与∠H的数量关系，并说明理由．10．已知：如图，点A、B、C、D在同一直线上，BE∥CG，CG平分∠DCF，若∠1＝50°，求∠ABE的度数．11．如图1，AM∥CN，点B为平面内一点，AB⊥BC于B，过B作BD⊥AM．（1）求证：∠ABD＝∠C；（2）如图2，在（1）问的条件下，分别作∠ABD、∠DBC的平分线交DM于E、F，若∠BFC＝1.5∠ABF，∠FCB＝2.5∠BCN，①求证：∠ABF＝∠AFB；②求∠CBE的度数．12．问题情境在综合与实践课上，老师让同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG（∠EFG＝90°，∠EGF＝60°）”为主题开展数学活动．操作发现（1）如图（1），小明把三角尺的60°角的顶点G放在CD上，若∠2＝2∠1，求∠1的度数；（2）如图（2），小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明∠AEF与∠FGC之间的数量关系；结论应用（3）如图（3），小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若∠AEG＝α，则∠CFG等于（用含α的式子表示）．13．如图，AB∥CD，∠1＝∠B，∠2＝∠D，试说明BE⊥DE．14．已知直线AB∥CD．（1）如图1，直接写出∠BME、∠E、∠END的数量关系为；（2）如图2，∠BME与∠CNE的角平分线所在的直线相交于点P，试探究∠P与∠E之间的数量关系，并证明你的结论；（3）如图3，∠ABM＝∠MBE，∠CDN＝∠NDE，直线MB、ND交于点F，则＝．15．已知：AB∥CD，点E在直线AB上，点F在直线CD上．（1）如图（1），∠1＝∠2，∠3＝∠4．①若∠4＝36°，求∠2的度数；②试判断EM与FN的位置关系，并说明理由；（2）如图（2），EG平分∠MEF，EH平分∠AEM，试探究∠GEH与∠EFD的数量关系，并说明理由．16．已知：∠MON＝48°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O重合），连接AC交射线OE于点D．设∠OAC＝x°（1）如图1，若AB∥ON，则：①∠ABO的度数是°；②当∠BAD＝∠ABD时，x＝°；③当∠BAD＝∠BDA时，x＝°．（2）如图2，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．17．如图，两条射线AM∥BN，线段CD的两个端点C、D分别在射线BN、AM上，且∠A ＝∠BCD＝108°．E是线段AD上一点（不与点A、D重合），且BD平分∠EBC．（1）求∠ABC的度数．（2）请在图中找出与∠ABC相等的角，并说明理由．（3）若平行移动CD，且AD＞CD，则∠ADB与∠AEB的度数之比是否随着CD位置的变化而发生变化？若变化，找出变化规律；若不变，求出这个比值．18．如图，已知AM∥BN，∠A＝60°，点P是射线AM上一动点（与点A不重合），BC，BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．（1）求∠CBD的度数；（2）当点P运动时，∠APB：∠ADB的比值是否随之变化？若不变，请求出这个比值；若变化，请找出变化规律；（3）当点P运动到某处时，∠ACB＝∠ABD，求此时∠ABC的度数．19．如图，点C在∠AOB的边OA上，过点C的直线DE∥OB，CF平分∠ACD，CG⊥CF 于C．（1）若∠O＝40°，求∠ECF的度数；（2）试说明CG平分∠OCD；（3）当∠O为多少度时，CD平分∠OCF？并说明理由．20．如图，已知CD∥AB，OE平分∠BOD，OE⊥OF，∠CDO＝62°，分别求出∠BOE，∠DOF的度数．21．生活中处处有数字，只要同学们学会数学的眼光观察生活，就会有许多意想不到的收获，如图两幅图都是由同一副三角板拼凑得到的．（1）图1中的∠ABC的度数是多少？（2）图2中已知AE∥BC，则∠AFD的度数是多少？22．P是三角形ABC内一点，射线PD∥AC，射线PE∥AB．（1）当点D，E分别在AB，BC上时，①补全图1；②猜想∠DPE与∠A的数量关系，并证明；（2）当点D，E都在线段BC上时，你在（1）中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由．23．已知：如图，直线a∥b，直线c与直线a、b分别相交于C、D两点，直线d与直线a、b分别相交于A、B两点，点P在直线AB上运动（不与A、B两点重合）．（1）如图1，当点P在线段AB上运动时，总有：∠CPD＝∠PCA+∠PDB，请说明理由；（2）如图2，当点P在线段AB的延长线上运动时，∠CPD、∠PCA、∠PDB之间有怎样的数量关系，并说明理由；（3）如图3，当点P在线段BA的延长线上运动时，∠CPD、∠PCA、∠PDB之间又有怎样的数量关系（只需直接给出结论）？24．如图，已知BC∥AD，BE∥AF．（1）请说明∠A＝∠B．（2）若∠DOB＝135°，求∠A的度数．25．已知：如图，AD∥BC，∠B＝∠D，求证：∠E＝∠F．26．如图，AB∥CD，直线PQ分别交AB、CD于E、F，FG⊥PQ，若∠PEB＝130°，求∠CFG的度数．27．如图，∠ACD是△ABC的外角，∠ABC与∠ACD的角平分线交于点O．（1）若∠ABC＝66°，∠ACB＝34°，则∠A＝°，∠O＝°；（2）探索∠A与∠O的数量关系，并说明理由；（3）若AB∥CO，AC⊥BO，求∠ACB的度数．28．如图，已知平面内有两条直线AB、CD，且AB∥CD，P为一动点．（1）当点P移动到AB、CD之间时，如图（1），这时∠P与∠A、∠C有怎样的关系？证明你的结论．（2）当点P移动到如图（2）的位置时，∠P与∠A、∠C又有怎样的关系？请证明你的结论．29．已知△ABC中，∠A＝60°，∠ACB＝40°，D为BC边延长线上一点，BM平分∠ABC，E为射线BM上一点．（1）如图1，连接CE，①若CE∥AB，求∠BEC的度数；②若CE平分∠ACD，求∠BEC的度数．（2）若直线CE垂直于△ABC的一边，请直接写出∠BEC的度数．30．如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC＝116°，∠ACF＝25°，求∠FEC 的度数．31．如图，已知AB∥CD，∠B＝96°，EF平分∠BEC，EG⊥EF，求∠BEG和∠DEG的度数．32．如图，已知直线a∥b，∠3＝131°，求∠1、∠2的度数（填理由或数学式）解：∵∠3＝131°（）又∵∠3＝∠1 （）∴∠1＝（）∵a∥b（）∴∠1+∠2＝180°（）∴∠2＝（）．33．如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB 于点E，PN交CD于点F（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为；（2）当△PMN所放位置如图②所示时，求证：∠PFD﹣∠AEM＝90°；（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝30°，∠PEB＝15°，求∠N的度数．34．如图，已知AB∥CD，∠1：∠2：∠3＝1：2：3，那么BA是否平分∠EBF，试说明理由．35．已知AD∥BC，AB∥CD，E为射线BC上一点，AE平分∠BAD．（1）如图1，当点E在线段BC上时，求证：∠BAE＝∠BEA．（2）如图2，当点E在线段BC延长线上时，连接DE，若∠ADE＝3∠CDE，∠AED＝60°．①求证：∠ABC＝∠ADC；②求∠CED的度数．36．如图，某工程队从A点出发，沿北偏西67度方向修一条公路AD，在BD路段出现塌陷区，就改变方向，由B点沿北偏东23度的方向继续修建BC段，到达C点又改变方向，使所修路段CE∥AB，此时∠ECB有多少度？试说明理由．37．（1）①如图1，已知AB∥CD，∠ABC＝60°，根据可得∠BCD＝°；②如图2，在①的条件下，如果CM平分∠BCD，则∠BCM＝°；③如图3，在①、②的条件下，如果CN⊥CM，则∠BCN＝°．（2）尝试解决下面问题：已知如图4，AB∥CD，∠B＝40°，CN是∠BCE的平分线，CN⊥CM，求∠BCM的度数．38．阅读理解如图1，已知点A是BC外一点，连接AB，AC，求∠BAC+∠B+∠C的度数．（1）阅读并补充下面推理过程解：过点A作ED∥BC∴∠B＝∠，∠C＝∠．又∵∠EAB+∠BAC+∠DAC＝180°（平角定义）∴∠B+∠BAC+∠C＝180°从上面的推理过程中，我们发现平行线具有“等角转化”的功能，将∠BAC，∠B，∠C “凑”在一起，得出角之间的关系，使问题得以解决（2）如图2，已知AB∥ED，求∠B+∠BCD+∠D的度数．小明受到启发，过点C作CF∥AB如图所示，请你帮助小明完成解答：（3）已知AB∥CD，点C在点D的右侧，∠ADC＝70°．BE平分∠ABC，DE平分∠ADC，BE，DE所在的直线交于点E，点E在AB与CD两条平行线之间．①如图3，点B在点A的左侧，若∠ABC＝60°，则∠BED的度数为°．②如图4，点B在点A的右侧，且AB＜CD，AD＜BC．若∠ABC＝n°，则∠BED的度数为°（用含n的代数式表示）39．如图，已知AB∥CD，C在D的右侧，BE平分∠ABC，DE平分∠ADC，BE、DE所在直线交于点E．∠ADC＝70°．（1）求∠EDC的度数；（2）若∠ABC＝n°，求∠BED的度数（用含n的式子表示）；（3）将线段BC沿DC方向平移，使得点B在点A的右侧，其他条件不变，画出图形并判断∠BED的度数是否改变，若改变，求出它的度数（用含n的式子表示），不改变，请说明理由．40．如图，已知AD∥BC，∠1＝∠2，求证：∠3+∠4＝180°．41．如图所示，把三角板的直角顶点放在直尺的一边上，若∠1＝30°，求∠2的度数．42．如图，已知DE∥BC，BE平分∠ABC，∠C＝65°，∠ABC＝50°．（1）求∠BED的度数；（2）判断BE与AC的位置关系，并说明理由．43．如图，是我们生活中经常接触的小刀，由刀片和刀柄组成，在刀柄ABCD中，∠A和∠B都是直角，在刀片EFGH中，EF∥GH．转动刀片时会形成∠1、∠2，试判断∠1与∠2的度数和是一个定值吗？若是，请求出∠1与∠2的度数和；若不是，请说明理由44．如图1，对于直线MN同侧的两个点A，B，若直线MN上的点P满足∠APM＝∠BPN，则称点P为A，B在直线MN上的反射点．已知如图2，MN∥HG，AP∥BQ，点P为A，B在直线MN上的反射点，判断点B是否为P，Q在直线HG上的反射点，如果是请证明，如果不是，请说明理由．45．如图，MN∥OP，点A为直线MN上一定点，B为直线OP上的动点，在直线MN与OP之间且在线段AB的右方作点D，使得AD⊥BD．设∠DAB＝α（α为锐角）．（1）求∠NAD与∠PBD的和；（提示过点D作EF∥MN）（2）当点B在直线OP上运动时，试说明∠OBD﹣∠NAD＝90°；（3）当点B在直线OP上运动的过程中，若AD平分∠NAB，AB也恰好平分∠OBD，请求出此时α的值46．（1）如图1，AB∥CD，点E是在AB、CD之间，且在BD的左侧平面区域内一点，连结BE、DE．求证：∠E＝∠ABE+∠CDE．（2）如图2，在（1）的条件下，作出∠EBD和∠EDB的平分线，两线交于点F，猜想∠F、∠ABE、∠CDE之间的关系，并证明你的猜想．（3）如图3，在（1）的条件下，作出∠EBD的平分线和△EDB的外角平分线，两线交于点G，猜想∠G、∠ABE、∠CDE之间的关系，并证明你的猜想．47．如图，直线AB∥CD，直线EF分别交直线AB、CD于点E、F，FH平分∠EFD，若∠FEH＝110°，求∠EHF的度数．48．如图，已知AB∥CD∥EF，∠CMA＝30°，∠CNE＝80°，CO平分∠MCN．求∠MCN，∠DCO的度数（要求有简要的推理说明）．49．如图，∠AOB＝40°，OC平分∠AOB，点D，E在射线OA，OC上，点P是射线OB 上的一个动点，连接DP交射线OC于点F，设∠ODP＝x°．（1）如图1，若DE∥OB．①∠DEO的度数是°，当DP⊥OE时，x＝；②若∠EDF＝∠EFD，求x的值；（2）如图2，若DE⊥OA，是否存在这样的x的值，使得∠EFD＝4∠EDF？若存在，求出x的值；若不存在，说明理由．50．如图，已知AB∥DE，∠ABC、∠CED的平分线交于点F．探究∠BFE与∠BCE之间的数量关系，并证明你的结论．51．如图，点C在∠AOB的一边OA上，过点C的直线DE平行直线OB，CF平分∠ACD，CG⊥CF于点C．（Ⅰ）若∠O＝50°，求∠ACE的度数；（Ⅱ）求证：CG平分∠OCD；（Ⅲ）当∠O为多少度时，CD平分∠OCF，并说明理由．52．已知AB∥CD，解决下列问题：（1）如图①，BP、DP分别平分∠ABE、∠CDE，若∠E＝100°，求∠P的度数．（2）如图②，若∠ABP＝∠ABE，∠CDP＝∠CDE，试写出∠P与∠E的数量关系并说明理由．（3）如图③，若∠ABP＝∠ABE，∠CDP＝∠CDE，设∠E＝m°，求∠P的度数（直接用含n、m的代数式表示，不需说明理由）．53．如图，AB∥CD，∠B＝120°，EF是∠CEB的平分线，FG∥HD，求∠EDH的度数．54．如图，已知直线11∥12，且13和11、12分别交于A、B两点，点P在直线AB上．（1）试说明∠1，∠2，∠3之间的关系式；（要求写出推理过程）（2）如果点P在A、B两点之间（点P和A、B不重合）运动时，试探究∠1，∠2，∠3之间的关系是否发生变化？（只回答）（3）如果点P在A、B两点外侧（点P和A、B不重合）运动时，试探究∠1，∠2，∠3之间的关系．（要求写出推理过程）55．已知，两直线AB，CD，且AB∥CD，点M，N分别在直线AB，CD上，放置一个足够大的直角三角尺，使得三角尺的两边EP，EQ分别经过点M，N，过点N作射线NF，使得∠ENF＝∠ENC．（1）转动三角尺，如图①所示，当射线NF与NM重合，∠FND＝45°时，求∠AME 的度数；（2）转动三角尺，如图②所示，当射线NF与NM不重合，∠FND＝60°时，求∠AME 的度数．（3）转动直角三角尺的过程中，请直接写出∠FND与∠AME之间的数量关系．56．问题情境：如图1，AB∥CD，∠P AB＝130°，∠PCD＝120°，求∠APC的度数．小明的思路是过点P作PE∥AB，通过平行线的性质来求∠APC．（1）按照小明的思路，求∠APC的度数；（2）问题迁移：如图2，AB∥CD，点P在射线ON上运动，记∠P AB＝α，∠PCD＝β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；（3）在（2）的条件下，如果点P不在B、D两点之间运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．57．如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线l3上有点P（点P 与点C、D不重合），点A在直线l1上，点B在直线l2上．（1）如果点P在C、D之间运动时，试说明∠1+∠3＝∠2；（2）如果点P在直线l1的上方运动时，试探索∠1，∠2，∠3之间的关系又是如何？（3）如果点P在直线l2的下方运动时，试探索∠P AC，∠PBD，∠APB之间的关系又是如何？（直接写出结论）58．模型与应用．【模型】（1）如图①，已知AB∥CD，求证∠1+∠MEN+∠2＝360°．【应用】（2）如图②，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6的度数为．如图③，已知AB∥CD，则∠1+∠2+∠3+∠4+∠5+∠6+…+∠n的度数为．（3）如图④，已知AB∥CD，∠AM1M2的角平分线M1O与∠CM n M n﹣1的角平分线M n O 交于点O，若∠M1OM n＝m°．在（2）的基础上，求∠2+∠3+∠4+∠5+∠6+……+∠n ﹣1的度数．（用含m、n的代数式表示）59．如图，已知BC∥GE，AF∥DE，点D、F分别在直线BC、GE上，∠1＝50°．（1）求∠AFG的度数；（2）若AQ平分∠F AC，交BC于点Q，且∠Q＝15°，求∠ACB的度数．60．①如图1，O是直线AB上一点，OE平分∠AOC，OF平分∠BOC，求证：OE⊥OF．②如图2，AB∥CD，∠1＝∠B，∠2＝∠D．求证：BE⊥DE北师大新版七年级下学期《2.3 平行线的性质》2020年同步练习卷参考答案与试题解析一．解答题（共60小题）1．已知AB∥CD，点M、N分别是AB、CD上两点，点G在AB、CD之间，连接MG、NG．（1）如图1，若GM⊥GN，求∠AMG+∠CNG的度数；（2）如图2，若点P是CD下方一点，MG平分∠BMP，ND平分∠GNP，已知∠BMG ＝30°，求∠MGN+∠MPN的度数；（3）如图3，若点E是AB上方一点，连接EM、EN，且GM的延长线MF平分∠AME，NE平分∠CNG，2∠MEN+∠MGN＝105°，求∠AME的度数．【分析】（1）过G作GH∥AB，依据两直线平行，内错角相等，即可得到∠AMG+∠CNG 的度数；（2）过G作GK∥AB，过点P作PQ∥AB，设∠GND＝α，利用平行线的性质以及角平分线的定义，求得∠MGN＝30°+α，∠MPN＝60°﹣α，即可得到∠MGN+∠MPN＝30°+α+60°﹣α＝90°；（3）过G作GK∥AB，过E作ET∥AB，设∠AMF＝x，∠GND＝y，利用平行线的性质以及角平分线的定义，可得∠MEN＝∠TEN﹣∠TEM＝90°﹣y﹣2x，∠MGN＝x+y，再根据2∠MEN+∠G＝105°，即可得到2（90°﹣y﹣2x）+x+y＝105°，求得x＝25°，即可得出∠AME＝2x＝50°．【解答】解：（1）如图1，过G作GH∥AB，∵AB∥CD，∴GH∥AB∥CD，∴∠AMG＝∠HGM，∠CNG＝∠HGN，∵MG⊥NG，∴∠MGN＝∠MGH+∠NGH＝∠AMG+∠CNG＝90°；（2）如图2，过G作GK∥AB，过点P作PQ∥AB，设∠GND＝α，∵GK∥AB，AB∥CD，∴GK∥CD，∴∠KGN＝∠GND＝α，∵GK∥AB，∠BMG＝30°，∴∠MGK＝∠BMG＝30°，∵MG平分∠BMP，ND平分∠GNP，∴∠GMP＝∠BMG＝30°，∴∠BMP＝60°，∵PQ∥AB，∴∠MPQ＝∠BMP＝60°，∵ND平分∠GNP，∴∠DNP＝∠GND＝α，∵AB∥CD，∴PQ∥CD，∴∠QPN＝∠DNP＝α，∴∠MGN＝30°+α，∠MPN＝60°﹣α，∴∠MGN+∠MPN＝30°+α+60°﹣α＝90°；（3）如图3，过G作GK∥AB，过E作ET∥AB，设∠AMF＝x，∠GND＝y，∵AB，FG交于M，MF平分∠AME，∴∠FME＝∠FMA＝∠BMG＝x，∴∠AME＝2x，∵GK∥AB，∴∠MGK＝∠BMG＝x，∵ET∥AB，∴∠TEM＝∠EMA＝2x，∵CD∥AB∥KG，∴GK∥CD，∴∠KGN＝∠GND＝y，∴∠MGN＝x+y，∵∠CND＝180°，NE平分∠CNG，∴∠CNG＝180°﹣y，∠CNE＝∠CNG＝90°﹣y，∵ET∥AB∥CD，∴ET∥CD，∴∠TEN＝∠CNE＝90°﹣y，∴∠MEN＝∠TEN﹣∠TEM＝90°﹣y﹣2x，∠MGN＝x+y，∵2∠MEN+∠G＝105°，∴2（90°﹣y﹣2x）+x+y＝105°，∴x＝25°，∴∠AME＝2x＝50°．【点评】本题主要考查了平行线的性质与判定的综合运用，解决问题的关键是作辅助线构造内错角，利用平行线的性质以及角的和差关系进行推算．2．如图1，MN∥EF，C为两直线之间一点．（1）如图1，若∠MAC与∠EBC的平分线相交于点D，若∠ACB＝100°，求∠ADB的度数．（2）如图2，若∠CAM与∠CBE的平分线相交于点D，∠ACB与∠ADB有何数量关系？并证明你的结论．（3）如图3，若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D，请直接写出∠ACB与∠ADB之间的数量关系：∠ADB＝90°﹣ACB．【分析】（1）如图1，根据平行线的性质得到∠1＝∠ADH，∠2＝∠BDH，∠MAC＝∠ACG，∠EBC＝∠BCG，根据角平分线的定义得到∠1＝ACG，∠2＝，即可得到结论；（2）根据平行线的性质得到∠1＝∠ADH，∠2＝∠BDH，∠NAC＝∠ACG，∠FBC＝∠BCG，根据角平分线的定义得到∠1＝ACG，∠2＝，根据平角的定义即可得到结论；（3）根据平行线的性质得到∠1＝∠ADH，∠2＝∠BDH，∠NAC＝∠ACG，∠FBC＝∠BCG，根据平行线的定义得到∠1＝MAC，∠2＝∠CBF，根据四边形的内角和和角的和差即可得到结论．【解答】解：（1）如图1，过C作CG∥MN，DH∥MN，∵MN∥EF，∴MN∥CG∥DH∥EF，∴∠1＝∠ADH，∠2＝∠BDH，∠MAC＝∠ACG，∠EBC＝∠BCG，∵∠MAC与∠EBC的平分线相交于点D，∴∠1＝ACG，∠2＝，∴∠ADB＝（∠ACG+∠BCG）＝∠ACB；∵∠ACB＝100°，∴∠ADB＝50°；（2）如图2，过C作CG∥MN，DH∥MN，∵MN∥EF，∴MN∥CG∥DH∥EF，∴∠1＝∠ADH，∠2＝∠BDH，∠NAC＝∠ACG，∠FBC＝∠BCG，∵∠MAC与∠EBC的平分线相交于点D，∴∠1＝ACG，∠2＝，∴∠ADB＝∠1+∠2＝（∠MAC+∠EBC）＝（180°﹣∠NAC+180°﹣∠FBC）＝（360°﹣∠ACB），∴∠ADB＝180°﹣∠ACB；（3）如图3，过C作CG∥MN，DH∥MN，∵MN∥EF，∴MN∥CG∥DH∥EF，∴∠1＝∠ADH，∠2＝∠BDH，∠NAC＝∠ACG，∠FBC＝∠BCG，∵∠MAC与∠FBC的平分线相交于点D，∴∠1＝MAC，∠2＝∠CBF，∵∠ADB＝360°﹣∠1﹣（180°﹣∠2）﹣∠ACB＝360°﹣∠MAC﹣（180°﹣∠CBF）﹣∠ACB＝360°﹣（180°﹣∠ACG）﹣（180°﹣∠BCG）＝90°﹣∠ACB．∴∠ADB＝90°﹣ACB．故答案为：∠ADB＝90°﹣ACB．【点评】本题考查了平行线的性质，角平分线的定义，正确的作出辅助线是解题的关键．3．如图1，直线AB∥CD，直线EF交AB于点E，交CD于点F，点G和点H分别是直线AB和CD上的动点，作直线GH，EI平分∠AEF，HI平分∠CHG，EI与HI交于点I．（1）如图1，点G在点E的左侧，点H在点F的右侧，若∠AEF＝70°，∠CHG＝60°，求∠EIH的度数．（2）如图2，点G在点E的右侧，点H也在点F的右侧，若∠AEF＝α，∠CHG＝β，其他条件不变，求∠EIH的度数．（3）如图3，点G在点E的右侧，点H也在点F的右侧，∠GHC的平分线HJ交∠KEG 的平分线EJ于点J．其他条件不变，若∠AEF＝α，∠CHG＝β，求∠EJH的度数．【分析】（1）过点I作IM∥AB，依据平行线的性质以及角平分线的定义，即可得到∠EIH 的度数．（2）过点I作IM∥AB，依据平行线的性质以及角平分线的定义，即可得到∠EIH的度数．（3）过点J作MN∥AB，依据平行线的性质、对顶角相等以及角平分线的定义，即可得到∠EJH的度数．【解答】（1）解：如图1，过点I作IM∥AB，∵EI平分∠AEF，HI平分∠CHG，∠AEF＝70°，∠CHG＝60°，∴∠AEI＝35°，∠CHI＝30°，∵IM∥AB，∴∠MIE＝∠AEI＝35°，∵AB∥CD，IM∥AB，∴IM∥CD，∴∠MIH＝∠CHI＝30°，∴∠EIH＝∠MIE+∠MIH＝35°+30°＝65°；（2）解：如图2，过点I作IM∥AB，∵EI平分∠AEF，HI平分∠CHG，∠AEF＝α，∠CHG＝β，∴∠AEI＝，∠CHI＝，∵IM∥AB，∴∠MIE＝∠AEI＝，∵AB∥CD，IM∥AB，∴IM∥CD，∴∠MIH＝∠CHI＝，∴∠EIH＝∠MIE+∠MIH＝+；（3）解：如图3，过点J作MN∥AB，∵∠AEF＝α，∴∠KEB＝α，∵EJ平分∠KEB，HJ平分∠CHG，∠KEB＝α，∠CHG＝β，∴∠JEG＝，∠JHF＝，∵MN∥AB，∴∠MJE＝∠JEG＝，∵AB∥CD，MN∥AB，∴MN∥CD，∴∠NJH＝∠CHJ＝，∴∠EJH＝180°﹣∠MJE﹣∠NJH＝180°﹣﹣．【点评】本题主要考查了平行线的判定与性质的综合运用，用到的知识点为：两直线平行，内错角相等．4．如图，已知直线AB∥射线CD，∠CEB＝100°．P是射线EB上一动点，过点P作PQ ∥EC交射线CD于点Q，连结CP．作∠PCF＝∠PCQ，交直线AB于点F，CG平分∠ECF．（1）若点P，F，G都在点E的右侧．①求∠PCG的度数；②若∠EGC﹣∠ECG＝40°，求∠CPQ的度数．（2）在点P的运动过程中，是否存在这样的情形，使？若存在，求出∠CPQ 的度数；若不存在，请说明理由．【分析】（1）①依据平行线的性质以及角平分线的定义，即可得到∠PCG的度数；②依据平行线的性质以及角平分线的定义，即可得到∠ECG＝∠GCF＝20°，再根据PQ∥CE，即可得出∠CPQ＝∠ECP＝60°；（2）设∠EGC＝3x，∠EFC＝2x，则∠GCF＝3x﹣2x＝x，分两种情况讨论：①当点G、F在点E的右侧时，②当点G、F在点E的左侧时，依据等量关系列方程求解即可．【解答】解：（1）①∵∠CEB＝100°，AB∥CD，∴∠ECQ＝80°，∵∠PCF＝∠PCQ，CG平分∠ECF，∴＝；②∵AB∥CD∴∠QCG＝∠EGC，∠QCG+∠ECG＝∠ECQ＝80°，∴∠EGC+∠ECG＝80°又∵∠EGC﹣∠ECG＝40°，∴∠EGC＝60°，∠ECG＝20°∴∠ECG＝∠GCF＝20°，，∵PQ∥CE，∴∠CPQ＝∠ECP＝60°；（2）设∠EGC＝3x，∠EFC＝2x，则∠GCF＝3x﹣2x＝x，①当点G、F在点E的右侧时，则∠ECG＝∠PCF＝∠PCD＝x，∵∠ECD＝80°，∴4x＝80°，解得x＝20°，∴∠CPQ＝3x＝60°；②当点G、F在点E的左侧时，则∠ECG＝∠GCF＝x，∵∠CGF＝180°﹣3x，∠GCQ＝80°+x，∴180°﹣3x＝80°+x，解得x＝25°，∴∠FCQ＝∠ECF+∠ECQ＝50°+80°＝130°，∴，∴∠CPQ＝∠ECP＝65°﹣50°＝15°．【点评】本题主要考查了平行线的性质，解题时注意：两直线平行，同旁内角互补；两直线平行，内错角相等．5．已知点D，E，F分别是△ABC的边AB，AC，BC上的点，DE∥BC，DF∥AC．（1）如图1，点G是线段FD延长线上一点，连接EG，∠CEG的平分线EM交AB于点M，交FD于点N．则∠A，∠AME，∠CEG之间存在怎样的数量关系？请写出证明过程；（2）如图2，在（1）的条件下，若EG平分∠AED，∠AME＝35°，且∠EDF﹣∠A＝30°，求∠C的度数．【分析】（1）利用外角定理即可求解；（2）由平角AEC得：∠CEM+∠MED+∠DEA＝180°，即：2α+γ+α+γ＝180°；利用∠EDF﹣∠A＝30°，得：2α﹣∠A＝30°；利用∠CEM＝∠AME＝∠A，即可求解．【解答】解：（1）∠CEM＝∠A+∠AME，而∠CEG＝2∠CEM＝2∠A+2∠AME；（2）EG平分∠AED，设：∠GEA＝∠GED＝α，DF∥AC，则∠EDF＝2α，由平角AEC得：∠CEM+∠MED+∠DEA＝180°，即：2α+γ+α+γ＝180°…①，∠EDF﹣∠A＝30°，则2α﹣∠A＝30°…②，∠CEM＝∠AME＝∠A，即：35°+∠A＝α+γ…③，联立①②③并解得：α＝34°，∠C＝2α＝68°．【点评】本题考查的是平行线的性质，涉及到三角形内角和定理、外角定理、角平分线的性质等，综合性较强，难度较大．6．如图1，已知直线EF分别与直线AB，CD相交于点E，F，AB∥CD，EM平分∠BEF，FM平分∠EFD（1）求证：∠EMF＝90°．（2）如图2，若FN平分∠MFD交EM的延长线于点N，且∠BEN与∠EFN的比为4：3，求∠N的度数．（3）如图3，若点H是射线EA之间一动点，FG平分∠HFE，过点G作GQ⊥FM于点Q，请猜想∠EHF与∠FGQ的关系，并证明你的结论．【分析】（1）根据两直线平行，同旁内角互补，以及角平分线定义进行判断即可；（2）如图2中，由题意可以假设：∠BEN＝4x，∠EFN＝3x，（3）先根据题意得到∠GFQ＝90°﹣∠FGQ，再根据FG平分∠HFE，FM平分∠EFD，即可得出∠HFD＝2∠GFQ，最后根据∠EHF+∠HFD＝180°，即可得出∠EHF＝2∠FGQ．【解答】解：（1）如图1中，∵AB∥CD，∴∠BEF+∠DFE＝180°，∵EM平分∠BEF，FM平分∠EFD，∴∠FEM＝∠BEF，∠EFM＝∠DFE，∴∠FEM+∠EFM＝×180°＝90°，∴∠EMF＝90°．（2）如图2中，由题意可以假设：∠BEN＝4x，∠EFN＝3x，∵∠EMF＝90°，∠FEM＝∠MEB＝4x，∴∠EFM＝90°﹣4x，∴NFM＝∠NFD＝3x﹣（90°﹣4x）＝7x﹣90°，∵∠MFE＝∠MFD，∴90°﹣4x＝2（7x﹣90°），∴x＝15°，∴∠MFN＝15°，∴∠N＝90°﹣15°＝75°（3）如图3，∵GQ⊥FM，∴∠GFQ+∠FGQ＝180°﹣90°＝90°（三角形的内角和等于180°）．∴∠GFQ＝90°﹣∠FGQ．∵FG平分∠HFE，FM平分∠EFD，又∵∠GFQ＝∠GFE+∠QFE＝（∠HFE+∠EFD）＝∠HFD，∴∠HFD＝2∠GFQ．又∵AB∥CD，∴∠EHF+∠HFD＝180°，∴∠EHF＝180°﹣∠HFD＝180°﹣2∠GFQ＝180°﹣2（90°﹣∠FGQ）＝2∠FGQ，即无论点H在何处都有∠EHF＝2∠FGQ．【点评】本题主要考查了平行线的性质与判定，角平分线的定义，三角形内角和定理等知识，解决问题的关键是掌握：两直线平行，内错角相等；两直线平行，同旁内角互补．7．已知直线AB∥CD，直线EF分别交AB、CD于A、C，CM是∠ACD的平分线，CM交AB于H，过A作AG⊥AC交CM于G．（1）如图1，点G在CH的延长线上时，①若∠GAB＝36°，则∠MCD＝63°．②猜想：∠GAB与∠MCD之间的数量关系是2∠MCD﹣∠GAB＝90°．（2）如图2，点G在CH上时，（1）②猜想的∠GAB与∠MCD之间的数量关系还成立吗？如果成立，请给出证明；如果不成立，请写出∠GAB与∠MCD之间的数量关系，并说明理由．【分析】（1）①依据AG⊥AC，∠GAB＝36°，可得∠CAH的度数，依据角平分线的定义以及平行线的性质，即可得到∠MCD的度数；②设∠ACH＝∠AHC＝∠MCD＝α，∠GAB＝β，则∠AGC＝∠AHC﹣∠GAB＝α﹣β，依据Rt△ACG中，∠ACH+∠AGC＝90°，即可得出∠GAB与∠MCD之间的数量关系；（2）设∠ACH＝∠AHC＝∠MCD＝α，∠GAB＝β，则∠AGC＝∠AHC+∠GAB＝α+β，依据Rt△ACG中，∠ACH+∠AGC＝90°，即可得出∠GAB与∠MCD之间的数量关系．【解答】解：（1）①∵AG⊥AC，∠GAB＝36°，∴∠CAH＝90°﹣36°＝54°，∵CM是∠ACD的平分线，∴∠ACH＝∠DCH，∵AB∥CD，∴∠AHC＝∠DCH，∴∠ACH＝∠AHC＝（180°﹣∠CAH）＝×126°＝63°，故答案为：63°；②∠GAB与∠MCD之间的数量关系是2∠MCD﹣∠GAB＝90°；理由：∵CM是∠ACD的平分线，∴∠ACH＝∠DCH，∵AB∥CD，∴∠AHC＝∠DCH，∴∠ACH＝∠AHC，设∠ACH＝∠AHC＝∠MCD＝α，∠GAB＝β，则∠AGC＝∠AHC﹣∠GAB＝α﹣β，∵GA⊥AC，∴Rt△ACG中，∠ACH+∠AGC＝90°，即α+α﹣β＝90°，∴2α﹣β＝90°，即2∠MCD﹣∠GAB＝90°；故答案为：2∠MCD﹣∠GAB＝90°；（2）上述∠GAB与∠MCD之间的数量关系不成立，应该为2∠MCD+∠GAB＝90°，理由：∵CM是∠ACD的平分线，∴∠ACH＝∠DCH，∵AB∥CD，∴∠AHC＝∠DCH，∴∠ACH＝∠AHC，设∠ACH＝∠AHC＝∠MCD＝α，∠GAB＝β，则∠AGC＝∠AHC+∠GAB＝α+β，∵GA⊥AC，∴Rt△ACG中，∠ACH+∠AGC＝90°，即α+α+β＝90°，∴2α+β＝90°，即2∠MCD+∠GAB＝90°．【点评】本题主要考查了平行线的性质以及三角形外角性质和三角形内角和定理的运用，利用直角三角形两个锐角互余是解决问题的关键．8．如图1，AB∥CD，P为AB、CD之间一点（1）若AP平分∠CAB，CP平分∠ACD．求证：AP⊥CP；（2）如图（2），若∠BAP＝∠BAC，∠DCP＝∠ACD，且AE平分∠BAP，CF平分∠DCP，猜想∠E+∠F的结果并且证明你的结论；（3）在（1）的条件下，当∠BAQ＝∠BAP，∠DCQ＝∠DCP，H为AB上一动点，连HQ并延长至K，使∠QKA＝∠QAK，再过点Q作∠CQH的平分线交直线AK于M，问当点H在射线AB上移动时，∠QMK的大小是否变化？若不变，求其值；若变化，求其取值范围．【分析】（1）依据平行线的性质，以及角平分线的定义，即可得到∠P＝180°﹣90°＝90°，进而得到AP⊥CP；（2）过E作EG∥AB，过F作FH∥CD，依据平行线的性质即可得到∠AEC＝∠BAE+∠DCE，∠AFC＝∠BAF+∠DCF，再根据∠BAP＝∠BAC，∠DCP＝∠ACD，AE平分∠BAP，CF平分∠DCP，即可得到∠E+∠F＝108°；（3）过Q作QE∥AB，依据平行线的性质可得∠AQC＝∠AQE+∠CQE＝∠BAQ+∠DCQ，依据∠BAQ＝∠BAP，∠DCQ＝∠DCP，即可得出∠AQC＝30°，再根据∠M＝∠MQH﹣∠K进行计算，即可得出∠QMK的大小不变，是定值15°．【解答】解：（1）∵AB∥CD，∴∠BAC+∠ACD＝180°，又∵AP平分∠CAB，CP平分∠ACD，∴∠CAP＝∠CAB，∠ACP＝∠ACD，∴∠CAP+∠ACP＝（∠BAC+∠ACD）＝×180°＝90°，∴△ACP中，∠P＝180°﹣90°＝90°，即AP⊥CP；（2）∠E+∠F＝108°．证明：如图2，过E作EG∥AB，过F作FH∥CD，∵AB∥CD，∴EG∥AB∥FH∥CD，∠BAC+∠DCA＝180°，∴∠BAE＝∠AEG，∠DCE＝∠CEG，∠BAF＝∠AFH，∠DCF＝∠CFH，∴∠AEC＝∠BAE+∠DCE，∠AFC＝∠BAF+∠DCF，∵∠BAP＝∠BAC，∠DCP＝∠ACD，AE平分∠BAP，CF平分∠DCP，∴∠BAE＝∠BAC，∠DCF＝∠DCA，∴∠AEC＝∠BAC+∠ACD，∠AFC＝∠BAC+∠DCA，∴∠AEC+∠AFC＝∠BAC+∠ACD+∠BAC+∠DCA＝∠ACD+∠BAC＝（∠BAC+∠DCA）＝×180°＝108°；（3）如图，过Q作QE∥AB，∵AB∥CD，QE∥CD，∴∠BAQ＝∠AQE，∠DCQ＝∠CQE，∴∠AQC＝∠AQE+∠CQE＝∠BAQ+∠DCQ，由（1）可得∠BAP+∠DCP＝180°﹣90°＝90°，又∵∠BAQ＝∠BAP，∠DCQ＝∠DCP，∴∠AQC＝∠BAQ+∠DCQ＝∠BAP+∠DCP＝（∠BAP+∠DCP）＝30°，∵∠AQH是△AQK的外角，QA＝QK，∴∠K＝∠AQH，∵QM是∠CQH的平分线，∴∠MQH＝∠CQH，∵∠MQH是△MQK的外角，∴∠M＝∠MQH﹣∠K＝∠CQH﹣∠AQH＝（∠CQH﹣∠AQH）＝∠AQC＝30°＝15°，即∠QMK的大小不变，是定值15°．【点评】本题主要考查了平行线的性质、三角形外角性质以及角平分线的定义的综合运用，解题时注意：两直线平行，同旁内角互补；两直线平行，内错角相等．解决问题的关键是过拐点作平行线．9．如图，已知直线AB∥CD．（1）在图1中，点E在直线AB上，点F在直线CD上，点G在AB、CD之间，若∠1＝30°，∠3＝75°，则∠2＝45°；（2）如图2，若FN平分∠CFG，延长GE交FN于点M，EM平分∠AEN，当∠N+∠FGE＝54°时，求∠AEN的度数；（3）如图3，直线MF平分∠CFG，直线NE平分∠AEG相交于点H，试猜想∠G与∠H的数量关系，并说明理由．【分析】（1）过G作GH∥AB，依据AB∥CD∥GH，即可得到∠1＝∠EGH，∠2＝∠FGH，进而得出∠2的度数；（2）过G作GP∥CD，过N作NQ∥AB，依据平行线的性质以及角的和差关系，即可得到∠AEN的度数；（3）过H作HP∥CD，过G作GQ∥AB，依据平行线的性质以及角的和差关系，即可得到∠G与∠H的数量关系．【解答】解：（1）如图1所示，过G作GH∥AB，∵AB∥CD，∴AB∥CD∥GH，∴∠1＝∠EGH，∠2＝∠FGH，∴∠1+∠2＝∠EGF，即30°+∠2＝75°，∴∠2＝45°，故答案为：45°；（2）∵FN平分∠CFG，EM平分∠AEN，∴可设∠AEM＝∠NEM＝α，∠CFN＝∠GFN＝β，如图2所示，过G作GP∥CD，过N作NQ∥AB，∵AB∥CD，∴NQ∥AB∥CD∥PG，∴∠QNF＝∠CFN＝β，∠QNE＝∠AEN＝2α，∠PGE＝∠AEM＝α，∠PGF＝∠DFG＝180°﹣2β，∴∠FNE＝∠QNF﹣∠QNE＝β﹣2α，∠FGE＝∠PGE+∠PGF＝α+180°﹣2β，又∵∠FNE+∠FGE＝54°，∴β﹣2α+（α+180°﹣2β）＝54°，∴α＝24°，∴∠AEN＝2α＝48°；（3）猜想：∠G＝2∠H．理由：∵MF平分∠CFG，NE平分∠AEG，∴可设∠AEN＝∠NEG＝α，∠CFM＝∠GFM＝β，如图3所示，过H作HP∥CD，过G作GQ∥AB，∵AB∥CD，∴GQ∥AB∥CD∥PH，∴∠QGE＝∠AEG＝2α，∠QGF＝∠CFG＝2β，∠PHM＝∠CFM＝β，∠PHN＝∠AEN ＝α，。

北师大版七下数学2.3.2平行线的性质教案

北师大版七下数学2.3.2平行线的性质教案一. 教材分析《北师大版七下数学》2.3.2平行线的性质是学生在学习了直线、射线、线段以及平行线的基本概念之后的一个单元。

本节课主要引导学生探究平行线的性质，让学生通过观察、猜想、验证、归纳等过程，理解和掌握平行线的性质，培养学生的逻辑思维能力和空间想象力。

教材中提供了丰富的素材，通过学生的自主探究和合作交流，使学生能够深刻理解并熟练运用平行线的性质。

二. 学情分析学生在进入七年级之前，已经初步学习了直线、射线、线段等基本概念，对图形有了一定的认识。

但是，对于平行线的性质，他们可能还停留在直观的感受上，缺乏系统的理论支持。

因此，在教学过程中，教师需要从学生的实际出发，通过引导、启发、激励，让学生主动参与学习，提高他们的自主学习能力。

三. 教学目标1.理解平行线的性质，并能够熟练运用。

2.培养学生的观察能力、猜想能力、验证能力和归纳能力。

3.培养学生的逻辑思维能力和空间想象力。

4.培养学生的合作意识和团队精神。

四. 教学重难点1.重点：平行线的性质。

2.难点：平行线性质的证明和运用。

五. 教学方法1.引导法：教师通过提出问题，引导学生思考，激发学生的学习兴趣。

2.探究法：学生通过观察、猜想、验证、归纳等过程，自主探究平行线的性质。

3.合作交流法：学生分组进行讨论，分享学习心得，互相学习，共同进步。

六. 教学准备1.准备相关的图形素材，如直线、射线、线段、平行线等。

2.准备黑板、粉笔等教学工具。

3.准备课件，用于辅助教学。

七. 教学过程1.导入（5分钟）教师通过提问方式引导学生回顾直线、射线、线段等基本概念，为新课的学习做好铺垫。

2.呈现（10分钟）教师展示直线、射线、线段和平行线的图形，让学生观察并猜想平行线的性质。

3.操练（10分钟）教师引导学生进行小组讨论，分享各自的猜想，并尝试用已知知识验证平行线的性质。

教师巡回指导，解答学生的疑问。

4.巩固（10分钟）教师挑选一些典型的题目让学生进行练习，巩固对平行线性质的理解和运用。

第二节平行线的性质和判定(含答案)...七年级数学学而思

第二节平行线的性质和判定1．平行线(1)定义：在同一平面内，不相交的两条直线叫做平行线，直线a 与直线b 互相平行，记作a∥b；注：必须强调在同一平面内，否则无法说明平行．(2)平行公理：经过直线外一点，有且只有一条直线与已知直线平行，注：点必须在直线外，而不能在直线上； (3)平行公理的推论：如果两条直线都与第三条直线平行，那么这两条直线也相互平行，即“平行于同一条直线的两直线平行”．2．两条直线的位置关系在同一平面内，两条直线的位置关系只有两种：(1)相交；(2)平行，注：判断同一平面内两条直线的位置关系时，可以根据它们的公共点的个数来确定：①有且只有一个公共点，两直线相交；②无公共点，两直线平行． 3．两直线平行的判定方法 (1)平行线的定义； (2)平行公理的推论；(3)同位角相等，两直线平行； (4)内错角相等，两直线平行； (5)同旁内角互补，两直线平行． 4．平行线的性质(1)两直线平行，同位角相等；(2)两直线平行，内错角相等；(3)两直线平行，同旁内角互补．1.平行的判定和证明：证明平行一般从寻找相等的同位角，内错角或互补的同旁内角出发，而这些角关系的获得条件一般有： ①已知平行条件； ②三角形内角和； ③角平分线； ④垂直；⑤互余互补关系．例1．如图5-2-1所示，如果,//,//CD EF EF AB 请写出一个关于3,2,1∠∠∠的等量关系125-- 225-- 325--检测1．如图5-2-2所示，已知a ‖b,0701=∠,,402ο=∠则=∠3 例2．如图5-2-3所示，已知,9021ο=∠+∠,,//AG CD FC DE ⊥求证：.//FH AG检测2．如图5-2-4所示，直线a ，b 被直线c 所截，下列条件能使b a //的是;61∠=∠①;62∠=∠②;31∠=∠③;75∠=∠④+∠2⑤;1807ο=∠.71∠=∠⑥例3．（江西兴国县期末）学习了平行线后，小龙同学想出了“过已知直线m 外一点P 画这条直线的平行线的新方法”，他是通过折一张半透明的正方形纸得到的．525--观察图5-2-5所示，经两次折叠展开后折痕CD 所在的直线即为过点P 的已知直线m 的平行线．从图中可知，小明画平行线的依据有( )①两直线平行，同位角相等； ②两直线平行，内错角相等； ③同位角相等，两直线平行； ④内错角相等，两直线平行． A.①② B．②③ C ．③④ D ．①④425--检测3．如图5-2-6所示，把一个长方形纸片沿EF 折叠后，点D ，C 分别落在C D ,的位置，若,60ο=∠EFB 则=∠AED例4．已知，,100,//ο=∠=∠A B OA BC 试回答下列问题：725-- 825-- 925--(1)如图5-2-7所示，求证：;//AC OB(2)如图5-2-8所示，若点E ，F 在线段BC 上，且满足，AOC FOC ∠=∠并且OE 平分.BOF ∠则EOC ∠的度数等于（在横线上填上答案即可）；(3)在(2)的条件下，若平行移动AC ，如图5-2-9，那么OFB OCB ∠∠:的值是否随之发生变化？若变化，试说明理由；若不变，求出这个比值； (4)在(3)的条件下，如果平行移动AC 的过程中，若使,OCA OEB ∠=∠此时OCA ∠度数等于（在横线上填上答案即可）．检测4．（广东澄海区期末）如图5 -2 -10所示，直线MN 与直线AB 、CD 分别交于点E 、F ，1∠与2∠互补．(1)试判断直线AB 与直线CD 的位置关系，并说明理由； (2)如图5-2 -11所示，BEF ∠与FFD ∠的角平分线交于点P ，EP 与CD 交于点G ．点H 是MN 上一点，且GHlEG ，求证：;//GH PF(3)如图5-2 -12所示，在(2)的条件下，连接PH ，K 是GH 上一点使=∠PHK ,HPK ∠作PQ 平分EPK ∠问HPQ ∠的大小是否发生变化？若不变，请求出其值；若变化，说明理由，625---122-5-5--1110225-第二节平行线的性质和判定（建议用时 35分钟）实战演练1．（浙江绍兴期末）如图5-2-1所示，,//,////DB EG DC EF AB 则图中与1∠相等的角(1∠除外）共有( )6.A 个 5.B 个 4.C 个 3.D 个2．（浙江金华中考）以下四种沿AB 折叠的方法中，不一定能判定纸带两条边线以，6互相平行的是( )125-- 225-- 325-- 425-- 525--A ．如图5-2-2所示，展开后测得21∠=∠B ．如图5-2-3所示，展开后测得4321∠=∠∠=∠且C ．如图5-2-4所示，测得21∠=∠D ．如图5-2-5所示，展开后再沿CD 折叠，两条折痕的交点为0，测得,OB OA =OD =OC3．如图5-2-6所示是五条胡同的路线图，),(F F D C B A →--→→→经过测量得到C B ∠=∠,70ο=,110ο=∠=∠E D 则图中互相平行的线有( )A ．1对B ．2对C ．3对D ．4对625-- 725-- 825-- 925--4．（山东聊城中考）如图5-2-7所示，,//CD AB ,68ο=∠B ,20ο=∠E 则D ∠的度数为（）ο28.A o B 38. ο48.C ο88.D5．如图5-2-8所示，HG EF BC AD ,,//交于点HI P ,平分,GHF ∠PM 平分EPH ∠HI 交PM 的反向延长线于Q ，//PN,HI 下列结论：,GEP EGP ∠=∠①若则;//AD PM 2=∠GEP ②;MPN ∠,2Q FPN ∠=∠③其中正确的是( )①②③.A ①③.B ②③.C ①②.D6，（山东聊城模拟）如图5-2-9所示，在四边形ABCD 中，=∠B ,120ο,50oD =∠将C ∠向内折出一个,PRC ∆恰好使,//AB CP //CR ,AD 则C ∠的度数是( )ο80.A ο85.B ο95.C o D 110.7．如图5 -2 - 10所示，已知,AB GF ⊥,21∠=∠,B AGH ∠=∠则下列结论：;//BC GH ①;HGM D ∠=∠②;//FG DE ③,AB HE ⊥④其中正确的是( )①②⋅A ③ ②③④⋅B ①③④⋅C ①②③④⋅D1125-- 1225--8．（广西玉州区期末）如图5 -2 - 11所示，已知BAD CD AB ∠,//和BCD ∠的平分线交于点E ．,1001ο=∠,m BAD =∠ο则EC A ∠的度数为9，如图5 -2 - 12所示，直线,//21l l 若,125ο=∠A ,85ο=∠B 则=∠+∠21 10．如图 5 -2 - 13所示，已知,180ο=∠+∠BCD B .D B ∠=∠求证：.DFE E ∠=∠证明：οΘ180=∠+∠BCD B （）CD AB //∴（）=∠∴B （两直线平行，同位角相等）， D B ∠=∠Θ（已知）， D DCE ∠=∠∴（等量代换）， BF AD //∴（）DFE E ∠=∠∴（）11．如图5 -2 - 14所示，直线AB ，CD 被EF 所截，,21∠=∠,BME CNF ∠=∠求证：AB ,//CD .//NQ MP12.（山东招远市期耒）如图5-2 -15所示，点D ，E 分别在ABC ∆的边AB ，AC 上，点F 在DC 上，且,18021ο=∠+∠.3B ∠=∠求证：.//BC DE1325--1425--1525--13.小明将一直角三角板(ο30=∠A )放在如图5 -2 - 16所示的位置，且.21C ∠=∠+∠ (1)证明：;//b a(2)经测量知,1A ∠=∠求;2∠(3)如图5-2 - 17所示，将三角板进行适当转动，直角顶点始终在两直线间，M 在线段CD 上，且CEH CEM ∠=∠给出下列结论：BDFMEG∠∠①的值不变：BDF MEG ∠-∠②的值不变，可以证明，其中只有一个是正确的，请你作出正确的选择并直接写出此值，1625-- 1725--14.如图5-2-18所示，.F D B E C A ∠+∠+∠=∠+∠+∠求证：.//CD AF15.问题情景：如图5-2 - 19所示，,//CD AB ,130oPAB =∠,120ο=∠PCD 求APC ∠的度数． (1)天天同学看过图形后立即口答出：,110oAPC =∠请你补全他的推理依据．如图5 -2 - 20所示，过点P 作,//AB PE,//CD AB ΘCD AB PE ////∴（ .180ο=∠+∠∴APE Aο180=∠+∠CPE C （）,120,130οΘ=∠=∠PCD PAB O.60.50ο=∠=∴⊥CPE APE o1825--ο110=∠+∠=∠∴CPE APE APC （）问题迁移：(2)如图5-2- 21所示，,//BC AD 当点P 在A ，B 两点之间运动时，,α∠=∠ADP ,β∠=∠BCP 求βα∠∠∠,与CPD 之间有何数量关系？请说明理由．(3)在(2)的条件下，如果点P 在A ，B 两点外侧运动时（点P 与点A ，B ，0三点不重合），请你直接写出CPD ∠与βα∠∠,之间的数量关系．1925-- 2025-- 2125--拓展创新16.（辽宁鞍山期末）实验证明，平面镜反射光线的规律是：射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等．(1)如图5 -2 - 22所示，一束光线m 射到平面镜a 上，被a 反射到平面镜b 上，又被b 反射．若被6反射出的光线n 与光线m 平行，且,381ο=∠则=∠2 ;=∠3(2)在(1)中，若ο551=∠则=∠3 ;若,401ο=∠则=∠3(3)由(1)．(2)猜想：当两平面镜a ，b 的夹角=∠3 时，可以使任何射到平面镜a 上的光线m ，经过平面镜a ，b 的两次反射后，入射光线m 与反射光线n 平行．你能说明理由吗？拓展1．有一款灯，内有两面镜子AB ，BC ，当光线经过镜子反射时，入射角等于反射角，即图5 -2 - 23、图5-2 -24中的.43,21∠=∠∠=∠2225--2325-- 2425--(1)如图5 -2 - 23所示，当BC AB ⊥时，说明为什么进入灯内的光线EF 与离开灯的光线GH 互相平行； (2)如图5-2 - 24所示，若两面镜子的夹角为)900(οο<<αα时，进入灯内的光线与离开灯的光线的夹角为),900(οο<<ββ试探索α与β的数量关系；(3)若两面镜子的夹角为),18090(οο<<αα进入灯内的光线与离开灯的光线所在直线的夹角为).900(οο<<ββ直接写出α与β的数量关系．拓展2．（湖北武昌区期末）一个长方形台球桌面ABCD )90,//,//(ο=∠A BC AD DC AB 如图5 -2 - 25所示，已知台球在与台球桌边沿碰撞的过程中，撞击线路与桌边的夹角等于反射线路与桌边的夹角，即.21∠=∠(1)台球经过如图5 -2 - 26所示的两次反弹后，撞击线路EF ，第二次反弹线路GH ，求证：;//GH EF(2)台球经过如图5 -2 - 27所示的两次反弹后，撞击线路EF 和第二次反弹线路GH 是否仍然平行，给出你的结论并说明理由．2525-- 2625-- 2725--极限挑战17．平面上有100条直线，其中有20条是互相平行的，问这100条直线最多能将平面分成部分，课堂答案培优答案。

人教版数学第5章平行线的性质与判定及辅助线模型

平行线判定和性质以及四大模型汇总第一部分平行线的判定判定方法l：两条直线被第三条直线所截，如果同位角相等，那么这两条直线平行．简称：同位角相等，两直线平行．判定方法2：两条直线被第三条直线所截，如果内错角相等，那么这两条直线平行．简称：内错角相等，两直线平行，判定方法3：两条直线被第三条直线所截，如果同旁内角互补，那么这两条直线平行．简称：同旁内角互补，两直线平行，如上图：若已知∠1=∠2，则AB∥CD（同位角相等，两直线平行）；若已知∠1=∠3，则AB∥CD（内错角相等，两直线平行）；若已知∠1+ ∠4= 180°，则AB∥CD（同旁内角互补，两直线平行）．另有平行公理推论也能证明两直线平行：平行公理推论：如果两条直线都与第三条直线平行，那么这两条直线也互相平行．第二部分平行线的性质性质1：两条平行线被第三条直线所截，同位角相等．简称：两直线平行，同位角相等性质2：两条平行线被第三条直线所截，内错角相等.简称：两直线平行，内错角相等性质3：两条平行线被第三条直线所截，同旁内角互补．简称：两直线平行，同旁内角互补第三部分平行线的四大模型模型一“铅笔”模型点P在EF右侧，在AB、CD内部“铅笔”模型结论1：若AB∥CD，则∠P+∠AEP+∠PFC=3 60°；结论2：若∠P+∠AEP+∠PFC= 360°，则AB∥CD.模型二“猪蹄”模型（M模型）点P在EF左侧，在AB、CD内部“猪蹄”模型结论1：若AB∥CD，则∠P=∠AEP+∠CFP；结论2：若∠P=∠AEP+∠CFP，则AB∥CD.模型三“臭脚”模型点P在EF右侧，在AB、CD外部“臭脚”模型结论1：若AB∥CD，则∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP；结论2：若∠P=∠AEP-∠CFP或∠P=∠CFP-∠AEP，则AB∥CD.模型四“骨折”模型点P在EF左侧，在AB、CD外部“骨折”模型结论1：若AB∥CD，则∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP；结论2：若∠P=∠CFP-∠AEP或∠P=∠AEP-∠CFP，则AB∥CD.第四部分平行线的四大模型证明（1）已知AE // CF ,求证∠P +∠AEP +∠PFC = 360°.（2）已知∠P=∠AEP+∠CFP，求证AE∥CF．（3）已知AE∥CF，求证∠P=∠AEP-∠CFP.（4）已知∠P= ∠CFP -∠AEP,求证AE //CF.第五部分平行线的四大模型的应用案例1如图，a∥b,M、N分别在a、b上，P为两平行线间一点，那么∠l+∠2+∠3= ．2如图，AB∥CD，且∠A=25°，∠C=45°，则∠E的度数是．3如图，已知AB∥DE，∠ABC=80°，∠CDE =140°，则∠BCD= .4如图，射线AC∥BD，∠A= 70°，∠B= 40°，则∠P= ．5如图所示，AB ∥CD ，∠E =37°，∠C = 20°，则∠EAB 的度数为．6 如图，AB ∥CD ，∠B =30°，∠O =∠C ．则∠C = .7如图，已知AB ∥DE ，BF 、 DF 分别平分∠ABC 、∠CDE ，求∠C 、 ∠F 的关系.8如图，已知AB ∥DE ，∠FBC =n 1∠ABF ，∠FDC =n1∠FDE . (1)若n =2,直接写出∠C 、∠F 的关系； (2)若n =3，试探宄∠C 、∠F 的关系；(3)直接写出∠C 、∠F 的关系（用含n 的等式表示）.9如图，已知AB ∥CD ，BE 平分∠ABC ，DE 平分∠ADC ．求证：∠E = 2 (∠A +∠C ) .10如图，己知AB∥DE，BF、DF分别平分∠ABC、∠CDE，求∠C、∠F的关系.11如图，∠3==∠1+∠2，求证：∠A+∠B+∠C+∠D= 180°．12如图，AB⊥BC，AE平分∠BAD交BC于E，AE⊥DE，∠l+∠2= 90°，M、N分别是BA、CD的延长线上的点，∠EAM和∠EDN的平分线相交于点F则∠F的度数为（）．A. 120°B. 135°C. 145°D. 150°133如图，直线AB∥CD，∠EF A= 30°，∠FGH= 90°，∠HMN=30°，∠CNP= 50°，则∠GHM= .14如图，直线AB∥CD，∠EFG =100°，∠FGH =140°，则∠AEF+ ∠CHG= .15 已知∠B =25°，∠BCD=45°，∠CDE =30°，∠E=l0°，求证：AB∥EF．16已知AB∥EF，求∠l-∠2+∠3+∠4的度数.17如图(l )，已知MA 1∥NA n ，探索∠A 1、∠A 2、…、∠A n ，∠B 1、∠B 2…∠B n -1之间的关系．(2)如图(2)，己知MA 1∥NA 4，探索∠A 1、∠A 2、∠A 3、∠A 4，∠B 1、∠B 2之间的关系． (3)如图(3)，已知MA 1∥NA n ，探索∠A 1、∠A 2、…、∠A n 之间的关系．如图所示，两直线AB ∥CD 平行，求∠1+∠2+∠3+∠4+∠5+∠6．18如图1，直线AB ∥CD ，P 是截线MN 上的一点，MN 与CD 、AB 分别交于E 、F ． (1) 若∠EFB =55°，∠EDP = 30°，求∠MPD 的度数；(2) 当点P 在线段EF 上运动时，∠CPD 与∠ABP 的平分线交于Q ,问：DPBQ∠∠是否为定值？若是定值，请求出定值；若不是，说明其范围；(3) 当点P 在线段EF 的延长线上运动时，∠CDP 与∠ABP 的平分线交于Q ，问DPBQ∠∠的值足否定值，请在图2中将图形补充完整并说明理由．第六部分平行线的四大模型实战演练1.如图，AB // CD // EF , EH ⊥CD 于H ,则∠BAC +∠ACE +∠CEH 等于( ).A . 180°B . 270°C . 360°D . 450° 2 若AB ∥CD ，∠CDF =32∠CDE ，∠ABF =32∠ABE ，则∠E ：∠F =( )．A ．2:1B ．3:1C ．4:3D ．3:23.如图3，己知AE ∥BD ，∠1=130°，∠2=30°，则∠C = .4.如图，已知直线AB ∥CD ，∠C =115°，∠A = 25°，则∠E = ．5． 6． 7．8．如阁所示，AB∥CD，∠l=l l0°，∠2=120°，则∠α= .9．如图所示，AB∥DF，∠D =116°，∠DCB=93°，则∠B= .10．如图，将三角尺的直角顶点放在直线a上，a∥b.∠1=50°，∠2 =60°，则∠3的度数为 .11．如图，AB∥CD，EP⊥FP, 已知∠1=30°，∠2=20°．则∠F的度数为．9.如图，若AB∥CD，∠BEF=70°，求∠B+∠F+∠C的度数.10．已知，直线AB∥CD．(1)如图l，∠A、∠C、∠AEC之间有什么关系？请说明理由；（2）如图2，∠AEF、∠EFC、∠FCD之间有什么关系？请说明理由；(3)如图3，∠A、∠E、∠F、∠G、∠H、∠O、∠C之间的关是.第七部分平行线的性质和判定综合应用1．如图，直线AB∥EF，点C是直线AB上一点，点D是直线AB外一点，若∠BCD ＝95°，∠CDE＝25°，则∠DEF的度数是（）A．110°B．115°C．120°D．125°2．如图，将一副直角三角板按图中所示位置摆放，保持两条斜边互相平行，则∠1＝（）A．30°B．25°C．20°D．15°3．如图，AE∥BF，∠1＝110°，∠2＝130°，求∠3的度数为（）4．如图，∠B+∠C＝180°，∠A＝50°，∠D＝40°，则∠AED＝．5．如图，如果∠C＝70°，∠B＝135°，∠D＝110°，那么∠1+∠2＝6．如图，AB∥CD，求∠1+∠2+∠3+∠4＝7．如图，AB∥CD，试找出∠B、∠C、∠BEC三者之间的数量关系．8．如图，三角形ABC中，点E为BC上一点（1）作图：过点E作EM∥AC交AB于M，过点E作EN∥AB交AC于N；（2）求∠A+∠B+∠C的度数，写出推理过程．9．如图，AB∥CD，BE平分∠ABF，DE平分∠CDF，∠BFD＝120°，求∠BED．10．如图，AC∥BD．（1）作图，过点B作BM∥AP交AC于M；（2）求证：∠PBD﹣∠P AC＝∠P．11．如图，AB∥CD，∠B＝∠C，求证：BE∥CF．12．如图①，木杆EB与FC平行，木杆的两端B，C用一橡皮筋连接，现将图①中的橡皮筋拉成下列各图②③的形状，请问∠A、∠B、∠C之间的数量关系?。

北师大版七年级下2.3.1平行线的性质(第2课时)课件(金榜学案配套)

【跟踪训练】 1.(2012·衡阳中考)如图，直线a⊥直线c，直线b⊥直线c，若∠1=70°，则∠2＝( (A)70° (C)110° (B)90° (D)80° )
【解析】选A.因为a⊥c，b⊥c，所以a∥b. 所以∠1=∠3. 因为∠2=∠3，∠1=70°. 所以∠2=∠1=70°.
2.如图, 已知直线AB∥CD,∠C=115°,
【预习思考】
如何区分平行线的判定和性质？
提示：由两直线的位置关系得角的关系为性质；由角的关系得
两直线的位置关系为判定，即得出结论为角的关系则为性质，否则为判定.
平行线性质和条件的综合应用【例】(9分)已知，如图，∠1=∠2，∠C=∠D，请说明∠A=∠F.
【规范解答】因为∠1=∠2(已知)，∠2=∠3(对顶角相等)，所以∠1=∠3(等量代换)……………………………………3分所以BD∥CE(同位角相等，两直线平行)，所以∠D=∠CEF(两直线平行，同位角相等)，……………5分又因为∠C=∠D(已知)，
1 ∠ACE(角平分线的性质). 2
又因为AC∥DE(已知), 所以∠ACD=∠D＝70°(两直线平行，内错角相等),
所以∠ACE=2∠ACD=140°(等式的性质).
又因为AC∥DE(已知),
所以∠E+∠ACE=18ቤተ መጻሕፍቲ ባይዱ°(两直线平行，同旁内角互补),
所以∠E=40°(等式的性质).
(C)∠4=125°
(D)∠5=55°
【解析】选C.因为AB∥CD,EF∥GH,∠1=55°,
所以∠5=55°,所以∠4=55°,∠3=55°，∠2=125°，故C项错误.
3.AC∥BD，∠A=60°,∠C=62°,则∠2= ______,∠3=______,∠1=______. 【解析】因为AC∥BD,∠A=60°,∠C=62°, 所以∠2=∠A=60°,∠3=∠C=62°, ∠1=180°-60°-62°=58°. 答案：60° 62° 58°

《平行线的性质》教学设计

《平行线的性质》教学设计【课题】北师大版数学七年级下册第二章第三节【必修课时】第1课时【课程标准要求】课标要求：掌握平行线的性质定理，了解平行线性质定理的证明课程标准分析：考虑到七年级学生的年龄状况和认知特点，本部分侧重于合理推理，即通过归纳和类比，结合经验和直觉，推断图形的某些属性，同时渗透演绎推理的相关思想。

【教材及学情分析】教材分析：本课程是《汉语图板必修2》第2章第2节的内容。

在系统研究了第一章人口和第二章第一节关于城市空间结构的内容后，本节主要从时间维度探讨了城市的发展过程和未来趋势。

为此，本文重点研究了城市化的内涵和标志、世界城市化进程以及城市化对地理环境的影响。

其中，城市化的内涵是基础，城市化的过程和特征是关键，城市化对地理环境的影响是关键。

根据教科书的内容，它需要分为两类：第一类：什么是城市化进程和世界城市化。

第2课：城市化对地理环境的影响。

学情分析：学生的知识技能基础：学生在小学就已经直观认识了角、平行与垂直，对其性质有了一定的了解。

在本章前面几节课中，在学习判定直线平行的条件的同时，自然引入了“三线八角”，认识了同位角、内错角和同旁内角。

这些知识储备为学生本节课的学习奠定了良好的知识技能基础。

学生活动体验的基础：7年级第一学期，学生在学习几何知识的过程中经历了一些探索和发现的数学活动，积累了一些直观的活动体验，具有一定的图形识别能力和借助图形分析和解决问题的能力，初步感受到解释论证的必要性；同时，经过一个学期的合作与交流，七年级学生初步形成了一定的合作学习经验，具备了一定的合作与交流能力。

ｃ层学生整体思维活跃，学习主动性较强，数学思维能力及学习习惯方面较ａ层，b 层学生好，在教学过程中更应当给予足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程，进而达到发展学生思维的目的。

[学习目标]1.知识与技能：经历探索平行线性质的过程,掌握平行线的三条性质,进一步发展空间观念，推理能力和有条理的表达能力。

人教版七年级下册数学第五章平行线的性质(二)课件

引例
例、如图， AB∥EF， CD∥EF ，试说明 ∠B、∠D、∠BED的大小关系。
A
B
E
C D
F
范例例2、如图，AB∥CD，试说明∠B、 ∠D 、∠BED之间的大小关系。 A B
E
C D 辅助线：为帮助解题而添加的线
F
辅助线一般画成虚线
巩固 3、如图，AB∥CD，试说明∠B、 ∠D 、∠BED之间的大小关系。 A B E C D
B
C
需要辅助线吗？怎样添加？
小结 1、本节课你学了什么新知识？
2、你还学了什么新的解题方法？为帮助解题而添加的辅助线
作业 1、如图，AB∥CD，试说明∠B、 ∠D 、∠BED之间的大小关系。 A B
C E
D
作业 2、如图，AB∥CD，试说明∠ABE、 ∠D 、∠E之间的大小关系。 E
A
B C
D
作业 3、如图，已知三角形ABC，试说明∠BAC+∠B +∠C=180°。 A
平行线的性质(二)
复习
1、如图，BE是AB的延长线， AD∥BC，AB∥CD，若∠ D=100°，则∠C= ， ∠ A= ，
E
范例例1、如图，a∥c， a⊥b，直线c与b 垂直吗？为什么？转化思想垂直 b 90° a
90°
垂直
c
巩固 2、 a 、b、 c 为同一平面内的三条直线，下列判断不正确的是( ) A 若a⊥c ， b⊥c ，则a∥b B 若a∥c ， b∥c ，则a∥b C 若a∥b ， b⊥c ，则a⊥c D 若a⊥b ， b⊥c ，则a⊥c

人教版七年级数学下册课件第五章相交线与平行线平行线的性质(第二课时)

形的另外两个角分别是多少度？
解：因为梯形上、下两底AB与DC互相平行，根据“两直线平行，同旁内角互补”，可得∠A与 ∠D互补， ∠B与∠C互.补
于是
∠D = 180°-∠A=180°-100°=80°， ∠C = 180°-∠B=180°-115°=65° .
所以梯形的另外两个角分别是80°，65°.
例6：如图，若AB//CD，你能确定∠B、∠D与 ∠BED 的大小关系吗？说说你的看法．
解：过点E 作EF//AB．
A
∴∠B=∠BEF．
∵AB//CD．
∴EF//CD．
C
∴∠D =∠DEF．
∴∠B＋∠D＝∠BEF＋∠DEF
＝∠DEB．
即∠B＋∠D＝∠DEB．
B
E
F
D
变式1：
如图，AB//CD，探索∠B、∠D与∠DEB的大小关系 .
能推出什么结论, 一直推导出要说明的结论为止; (如导引 2) 3. 两头凑：当遇到复杂问题的时候，我们常常将分析法和综
合法同时进行，即由两头向中间推，寻找到中间的结合点．
例4 光线从空气射入水中时，传播方向会发生改变，这种现象叫做光的折射现象．同样，光线从水中射入空气中时，也会发生折射现象，一束光线从空气射入水中再从水中射入空气中时，
如图④，∵AB∥DE，∴∠ABC＝∠EPC. ∵BC∥EF，∴∠EPC＋∠DEF＝180°. ∴∠ABC＋∠DEF＝180°. 综上可知，∠ABC与∠DEF相等或互补．
本题易错之处在于学生往往只考虑到其中两种情况，而漏掉另外两种情况．
易错点：画图考虑不周导致漏解.
【课后练习】
● 1．一辆汽车在笔直的公路上，两次拐弯后，仍在原来的方向上平行前进，则这两

平行线的性质(知识讲解)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)

专题5.12平行线的性质（知识讲解）【学习目标】1．掌握平行线的性质，并能依据平行线的性质进行简单的推理；2．了解平行线的判定与性质的区别和联系，理解两条平行线的距离的概念；【要点梳理】要点一、平行线的性质性质1：两直线平行，同位角相等；性质2：两直线平行，内错角相等；性质3：两直线平行，同旁内角互补.特别说明：（1）“同位角相等、内错角相等”、“同旁内角互补”都是平行线的性质的一部分内容，切不可忽视前提“两直线平行”．(2)从角的关系得到两直线平行，是平行线的判定；从平行线得到角相等或互补关系，是平行线的性质．要点二、两条平行线的距离同时垂直于两条平行线，并且夹在这两条平行线间的线段的长度，叫做这两条平行线的距离．特别说明：（1）求两条平行线的距离的方法是在一条直线上任找一点，向另一条直线作垂线，垂线段的长度就是两条平行线的距离．（2）两条平行线的位置确定后，它们的距离就是个定值，不随垂线段的位置的改变而改变，即平行线间的距离处处相等．【典型例题】类型一、平行线的性质➽➼同位（内错）相等✮✮同旁内角互补➻➸两直线平行1．阅读下列推理过程，在括号中填写理由．如图，已知AD BC ⊥，EF BC ⊥，12∠=∠，试证明：∥DG BA ．解：AD BC ⊥ ，EF BC ⊥（已知），90EFB ADB ∴∠=∠=︒（______）∴______∥______（______）1BAD ∴∠=∠（______）又12∠=∠ （已知），∴______（______）∴∥DG BA （______）【答案】垂直的定义；EF AD ；；同位角相等，两直线平行；两直线平行，同位角相等；2BAD ∠=∠；等量代换；内错角相等，两直线平行【分析】根据平行线的判定定理与性质定理求解即可．解：AD BC ⊥ ，EF BC ⊥（已知），∴90EFB ADB ∠=∠=︒（垂直的定义），∴EF AD ∥（同位角相等，两直线平行），∴1BAD ∠=∠（两直线平行，同位角相等），又12∠=∠ （已知），∴2BAD ∠=∠（等量代换），∴∥DG BA （内错角相等，两直线平行），故答案为：垂直的定义；EF ；AD ；同位角相等，两直线平行；两直线平行，同位角相等；2BAD ∠=∠；等量代换；内错角相等，两直线平行．【点拨】此题考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．举一反三：【变式1】将下列证明过程及依据补充完整．如图，在ABC 中，CD 平分ACB ∠交AB 于点D ，E ，F 分别为BC ，AB 上的点，且AC DE ∥，CD EF ∥，求证：EF 平分DEB∠证明：∵CD 平分ACB ∠（已知），∴DCA DCE ∠=∠（角平分线的定义）．∵AC DE ∥（已知），∴DCA CDE ∠=∠（）∴DCE CDE ∠=∠（等量代换），∵CD EF ∥（已知），∠=∠（）∴DEF CDE∠=∠（）DCE BEF∴_____=______（等量代换），∴EF平分DEB∠（）【答案】两直线平行，内错角相等；两直线平行，内错角相等；两直线平行，同位角相等；DEF∠；BEF∠；角平分线的定义．【分析】根据平行线的性质和角平分线的概念求解即可．∠（已知），证明：∵CD平分ACB∠=∠（角平分线的定义）．∴DCA DCE∥（已知），∵AC DE∴DCA CDE∠=∠（两直线平行，内错角相等）∠=∠（等量代换），∴DCE CDE∵CD EF∥（已知），∠=∠（两直线平行，内错角相等）∴DEF CDEDCE BEF∠=∠（两直线平行，同位角相等）∴DEF∠=BEF∠（等量代换），∴EF平分DEB∠（角平分线的定义）故答案为：两直线平行，内错角相等；两直线平行，内错角相等；两直线平行，同位角相等；DEF∠；BEF∠；角平分线的定义．【点拨】本题考查了平行线的性质和平行线的判定在几何证明中的应用，明确相关性质及定理是解题的关键．【变式2】填空，将本题补充完整．如图，已知EF AD，∠1＝∠2，∠BAC＝65°．将求∠AGD的过程填写完整．解：∵EF AD （已知）∴∠2＝（）又∵∠1＝∠2（已知）∴∠1＝（等量代换）∴AB GD （）∴∠BAC +＝180°（）∵∠BAC ＝65°（已知）∴∠AGD ＝°【答案】∠3；两直线平行，同位角相等；∠3；内错角相等，两直线平行；∠AGD ；两直线平行，同旁内角互补；115°【分析】由EF AD ，可得∠2＝∠3，由等量代换可得∠1＝∠3，从而得到DG BA ，根据平行线的性质可得∠BAC ＋∠AGD ＝180°，即可求解．解：∵EF AD （已知）∴∠2＝∠3（两直线平行，同位角相等）又∵∠1＝∠2（已知）∴∠1＝∠3（等量代换）∴AB GD （内错角相等，两直线平行）∴∠BAC ＋∠AGD ＝180°（两直线平行，同旁内角互补）∵∠BAC ＝65°（已知）∴∠AGD ＝115°．【点拨】本题考查了平行线的性质与判定，此题比较简单，解题的关键是注意掌握两直线平行，同位角相等；两直线平行，同旁内角互补定理；内错角相等，两直线平行的应用．2．如图，已知AD BC ⊥，EF BC ⊥，12∠=∠．(1)求证：EF AD ∥；(2)求证：180BAC AGD ∠+∠=︒．【分析】（1）根据垂直得出90EFB ADB ∠=∠=︒，根据平行线的判定得出EF AD ∥；（2）根据平行线的性质得出1BAD ∠=∠，由12∠=∠得出2BAD ∠=∠，根据平行线的判定得出DG BA ∥，再根据平行线的性质即可得解．（1）证明：∵AD BC ⊥，EF BC ⊥，∴90EFB ∠=︒，90ADB ∠=︒（垂直的定义），∴∠=∠EFB ADB （等量代换），∴EF AD ∥（同位角相等，两直线平行）；（2）证明：∵EF AD ∥，∴1BAD ∠=∠（两直线平行，同位角相等），又12∠=∠ （已知），∴2BAD ∠=∠（等量代换），∴DG BA ∥（内错角相等，两直线平行），∴180BAC AGD ∠+∠=︒（两直线平行，同旁内角互补）．【点拨】本题主要考查了平行线的判定与性质，熟记平行线的判定定理与性质定理是解题的关键．举一反三：【变式1】如图，已知AB ∥CD ，BC 平分∠ABD 交AD 于点E ．(1)证明：∠1=∠3；(2)若AD ⊥BD 于点D ，∠CDA =34°，求∠3的度数．【答案】(1)见解析；(2)∠3=28°．，根据等量代【变式2】P是∠BAC内一点，射线PD//AB，射线PE//AC，连接BC，当点D在线段BC上，点E在射线AB上时，(1)补全图形；(2)猜想∠DPE与∠A的数量关系，并证明．【答案】(1)补全图形见解析；(2)∠DPE +∠A =180°，证明见解析【分析】（1）根据题中的要求直接补全图形即可；（2）根据平行线的性质得到BEP A ∠=∠，180BEP DPE ∠+∠=︒，等量代换即可证得结论．（1）解：补全图形，如下图所示：（2）解：180DPE A ∠+∠=︒．理由如下：PE AC ∥ ，BEP A ∴∠=∠，PD AB ∥ ,180BEP DPE ∴∠+∠=︒，即180DPE A ∠+∠=︒．【点拨】本题主要考查了平行线的性质的运用，解题的关键是熟练掌握平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补．类型二、平行线的性质➽➼由平行线性质探索角的关系3．如图：(1)若AB EF ∥，猜想图①中，B ∠、BDF ∠与F ∠之间的数量关系并加以证明；(2)若AB EF ∥，如图②，直接写出B ∠、BDF ∠与F ∠之间的数量关系：．(3)学以致用：一个小区大门栏杆的平面示意图如图所示，BA 垂直地面AE 于A ，CD 平行于地面AE ，若150BCD ∠=︒，则ABC ∠=．【答案】(1)BDF B F ∠=∠+∠，证明见解析；(2)360B BDF F ∠+∠+∠=︒；(3)120︒【分析】（1）过点D 作CD AB ∥；通过平行线的性质倒角即可；（2）过点D 作CD AB ∥；根据两直线平行同旁内角互补列出等式求解；（3）由（2）中的结论计算即可；（1）解：BDF B F ∠=∠+∠；理由如下：如图，过点D 作CD AB ∥；∴B BDC∠=∠∵AB EF∥∴CD EF∥∴CDF F∠=∠∵BDF BDC CDF∠=∠+∠∴BDF B F∠=∠+∠（2）解：360B BDF F ∠+∠+∠=︒；理由如下：如图，过点D 作CD AB ∥；∵AB EF∥∴AB CD EF∥∥∴180B BDC =∠+∠︒，180CDF F ∠+∠=︒∴360B BDF F B BDC CDF F ∠+∠+∠=∠+∠+∠+∠=︒（3）解：由（2）可知：BCD ABC BAE ∠+∠+∠=︒360∴90BAE ∠=︒∴ABC BAE BCD ∠=︒-∠-∠=︒360120【点拨】本题考查了平行线的性质以及传递性；熟练运用平行线的性质转化角是解题的关键．举一反三：【变式1】如图，已知三角形EFG 的顶点E ，F 分别在直线AB 和CD 上，且AB CD ．若90EFG ∠=︒，30FEG ∠=︒．(1)当221∠=∠时，求1∠的度数．(2)设AEG α∠=，CFG β∠=，求α和β的数量关系（用含α，β的等式表示）．∴180AEG EGM ∠+∠=︒，∴∥GM CD ，∴180MGF CFG ∠+∠=︒，∴360AEG EGM MGF CFG ∠+∠+∠+∠=︒，即360AEG EGF CFG ∠+∠+∠=︒，∵在Rt EGF 中，90EFG ∠=︒，30FEG ∠=︒，∴60EGF ∠=︒，∴36036060300AEG CFG EGF ∠+∠=︒-∠=︒-︒=︒，∵AEG α∠=，CFG β∠=，∴300αβ+=︒．【点拨】本题主要考查平行线与三角形的综合运用，掌握平行线的性质，三角形内角和定理是解题的关键．【变式2】请阅读小明同学在学习平行线这章知识点时的一段笔记，然后解决问题．小明：老师说在解决有关平行线的问题时，如果无法直接得到角的关系，就需要借助辅助线来帮助解答，今天老师介绍了一个“美味”的模型一“猪蹄模型”．即已知：如图1，AB CD ∥，E 为AB 、CD 之间一点，连接AE ，CE 得到AEC ∠．求证：AEC A C ∠=∠+∠，小明笔记上写出的证明过程如下：证明：过点E 作EF AB ∥，∴1B ∠=∠，∵AB CD ∥，EF AB ∥，∴EF CD∥∴2C ∠=∠，∵12AEC ∠=∠+∠，∴AEC A C ∠=∠+∠，请你利用“猪蹄模型”得到的结论或解题方法，完成下面的两个问题．(1)如图2，若AB CD ∥，60E ∠=︒，求B C F ∠+∠+∠的度数；(2)灵活应用：如图3，一条河流的两岸AB CD ∥当小船行驶到河中E 点时，与两岸码头B 、D 所形成的夹角为64︒（即64BED ∠=︒），当小船行驶到河中点F 时，恰好满足ABF EBF =∠∠，EDF CDF ∠=∠，请你直接写出此时点F 与码头B 、D 所形成的夹角BFD ∠＝_________．∵EN AB ∥，FM AB ∥，DC ∥∴EN CD ∥，FM CD ∥，EN ∴∠B =∠BEN ，∠NEF =∠EFM ∵∠BEN +∠NEF =∠BEF ，∠EFM类型三、平行线的性质➽➼由平行线性质求角度4．（1）如图AD 平分CAB ∠，DE AC ∥，28CAD ∠=︒．求1∠的度数．（2）如图已知1180C ∠+∠=︒，CF BE ∥．求证：B C ∠=∠．【答案】（1）1∠的度数为56︒；（2）见解析【分析】（1）根据角平分线的定义得到256CAB CAD ∠=∠=︒，由平行线的性质即可得到结论．（2）先证明AB CD ∥，再利用平行线的性质证明B CHE ∠=∠，C CHE ∠=∠，即可证明B C ∠=∠．解：（1）∵AD 平分CAB ∠，28CAD ∠=︒，∴256CAB CAD ∠=∠=︒，∵DE AC ∥，∴156CAB ∠=∠=︒；（2）证明：∵1180C ∠+∠=︒，1180AGC ∠+∠=︒，∴AGC C ∠=∠，∴AB CD ∥，∴B CHE ∠=∠，∵CF BE ∥，∴C CHE ∠=∠，∴B C ∠=∠．【点拨】本题考查了平行线的判定与性质，熟练掌握“同旁内角互补，两直线平行”、“内错角相等，两直线平行”及“两直线平行，内错角相等”是解答此题的关键．举一反三：【变式1】如图，已知点B 、C 在线段AD 的异侧，连接、AB CD ，点E 、F 分别是线段、AB CD 上的点，连接CE BF 、，分别与AD 交于点G ，H ，且AEG AGE ∠=∠，C DGC ∠=∠．(1)求证：AB CD ∥；(2)若180AGE AHF ︒∠+∠=，求证：B C ∠=∠；(3)在（2）的条件下，若117BFC C ∠=∠，求AHB ∠的度数．【答案】(1)证明见解析；(2)证明见解析；(3)70︒【分析】（1）只需要证明AEG C ∠=∠即可证明AB CD ∥；（2）先证明HGE AHF =∠∠得到BF CE 则B AEG =∠∠，再由AEG C ∠=∠即可证明B C ∠=∠；（3）根据平行线的性质得到180BFC C ∠+∠=︒，AHB DGC ∠=∠，再结合已知条件求出C ∠的度数即可得到答案．（1）证明：∵AEG AGE ∠=∠，C DGC ∠=∠，AGE DGC ∠=∠，∴AEG C ∠=∠，【变式2】类型四、平行线的性质➽➼平行线性质的应用5．如图，一条公路修在湖边，需拐弯绕道而过，如果第一次向右拐75°，第二次拐弯形成的拐角∠B ＝135°，第三次拐弯后道路恰好和第一次拐弯前的道路平行，那么第三次是如何拐弯的？【答案】向左拐30°【分析】过点B 作BM OA ∥，延长BC 到点P ．可得BM CN ∥．从而得到∠ABM ＝∠A ＝105°．再由∠ABC ＝135°，可得∠MBC ＝30°即可求解．解：过点B 作BM OA ∥，延长BC 到点P ．∵BM OA ∥，OA CN ∥，∴BM CN ∥．∵第一次向右拐75°，即∠A ＝105°，∴∠ABM ＝∠A ＝105°．∵∠ABC ＝135°，∴∠MBC ＝30°又∵BM CN ∥，∴∠NCP ＝∠MBC ＝30°．答：第三次应向左拐30°．【点拨】本题主要考查了平行线的判定和性质，熟练掌握平行线的判定和性质是解题的关键．举一反三：【变式1】ABC ∠和BCD ∠，量得63ABC ∠=︒，要保持两次拐弯前后的路线平行，BCD ∠的度数应为多少？为什么？【答案】117°，理由：同旁内角互补，两直线平行【分析】根据两直线平行同旁内角互补即可得出∠BCD 的度数．【详解】解：根据题意得，AB ∥CD ，∠ABC =63°∴∠BCD =180°-∠ABC =117°，∴要保持两次拐弯前后的路线平行，∠BCD 为117°，理由是同旁内角互补，两直线平行．【点拨】题目主要考查平行线的性质，理解题意是解题的关键．【变式2】潜望镜中的两面镜子是互相平行放置的，如图1，光线经过镜子反射时，12∠=∠，3=4∠∠，那么2∠和3∠有什么关系？为什么进入潜望镜的光线和离开潜望镜的光线是平行的？先画几何图形，如图2，再写已知未知．如图，//,12,34AB CD ∠=∠∠=∠，（1）猜想2∠和3∠有什么关系，并进行证明；（2）求证：//PM NQ ．【答案】（1）23∠∠=，证明见解析；（2）见解析【分析】（1）根据两面镜子是互相平行放置的可知//AB CD ，再根据平行线的性质（两直线平行，内错角相等）即可直接证明23∠∠=．（2）结合题意可证明1234∠=∠=∠=∠，再由125180∠+∠+∠=︒，346180∠+∠+∠=︒，即可证明56∠=∠，最后由平行线的判定定理（内错角相等，两直线平行），即可证明//P M N Q ．解：（1）根据题意可知//AB CD ，∴23∠∠=（两直线平行，内错角相等）.（2）∵23∠∠=，∴1234∠=∠=∠=∠；∵125180∠+∠+∠=︒，346180∠+∠+∠=︒，∴56∠=∠，∴//P M N Q （内错角相等，两直线平行）．【点拨】本题考查平行线的判定与性质在生活中的应用．掌握平行线的性质与判定是解答本题的关键．类型五、平行线的性质➽➼平行线间的距离✮✮应用6．探究规律：我们有可以直接应用的结论：若两条直线平行，那么在一条直线上任取一点，无论这点在直线的什么位置，这点到另一条直线的距离均相等．例如：如图1，两直线//m n ，两点H 、T 在m 上，HE n ⊥于E ，TF n ⊥于F ，则HE TF =．如图2，已知直线//m n ，A 、B 为直线n 上的两点，C 、D 为直线m 上的两点．（1）请写出图中面积相等的各对三角形：__________．（2）如果A 、B 、C 为三个定点，点D 在m 上移动，那么无论D 点移动到任何位置总有：_______与ABC 的面积相等；理由是：___________．【答案】（1）ABC 和ABD △，DCA △和DCB △，ACO △和DBO ；（2）ABD △，同底等高的两个三角形的面积相等【分析】（1）写出面积相等的各对三角形，我们拿ABC 与ABD △为例：两个三角形用公共边AB 为底，再由图1的结论知道高相等，由三角形面积公式知两个三角形面积相等，其它对分析类似；（2）根据同底等高的两个三角形的面积相等，可以得出结论．解：（1）有三对分别是：ABC 和ABD △，DCA △和DCB △，ACO △和DBO ，分析如下：ABC 和ABD △，两个三角形用公共边AB 为底，再由图1的结论知道高相等，由三角形面积公式知两个三角形面积相等；DCA △和DCB △，两个三角形以CD 为底，高相等，即面积相等；ACO △和DBO ，根据DCA △和DCB △面积相等，两个三角形同时减去CDO ，得ACO △和DBO 面积相等．故答案为：ABC 和ABD △，DCA △和DCB △，ACO △和DBO ，（2）如果A 、B 、C 为三个定点，点D 在m 上移动，那么无论D 点移动到任何位置总有：ABD △与ABC 的面积相等，分析如下：ABD △与ABC 同底，点D 在m 上移动，那么无论D 点移动到任何位置，点D 到另一条直线的距离相等，使得这两个三角形是：同底等高的两个三角形，即面积相等．故答案为：同底等高的两个三角形的面积相等【点拨】本题考查了两条平行直线间的距离和两个三角形面积相等问题，解题的关键是：理解两直线平行距离为定值及同底等高的两个三角形面积相等．举一反三：【变式1】如图，已知直线m//n ，A ，B 为直线m 上的两点，C ，P 为直线n 上的两点．（1）请写出图中面积相等的各对三角形：；（2）如果A ，B ，C 为三个定点，点P 在直线n 上移动，那么，无论P 点移动到任何位置，总有．理由是：．【答案】（1）ACP △与BCP 、ABC 与ABP 、AOC 与BOP △；（2）题（1）中三对面积相等的三角形，理由见解析．【分析】（1）根据两平行线之间的距离处处相等、三角形的面积公式即可得；（2）根据两平行线之间的距离处处相等即可得．【详解】（1）设平行线m 与n 之间的距离为h则ACP △和BCP 的边CP 上高均为h ，ABC 和ABP 的边AB 上高均为h由同底等高得：ACP △与BCP 的面积相等，ABC 与ABP 的面积相等又AOC ACP COP S S S =- ，BOP BCP COPS S S =- AOC BOPS S ∴= 即AOC 与BOP △的面积相等故答案为：ACP △与BCP 、ABC 与ABP 、AOC 与BOP △；（2）总有题（1）中三对面积相等的三角形理由：两平行线之间的距离相等、同底等高的三角形的面积相等、面积相等两个三角形都减去公共部分得到的两个三角形的面积也相等．【点拨】本题考查了平行线之间的距离，掌握平行线之间的距离是解题关键．【变式2】作图并写出结论：如图，直线CD与直线AB相交于C，根据下列语句画图.(1)过点P作PR⊥CD，垂足为R.(2)过点P作PQ∥CD，交AB于点Q.(3)若∠DCB=135°，则∠PQC度．(4)点Q到直线PR的距离是线段的长度．）∵PQ∥CD（已作），）∴∠DCB+∠PQC=180°，∵∠DCB=135）因为PR⊥CD，所以点Q到直线【点拨】本题的关键是掌握基本作图，并能运用平行线的性质知识解决问题类型六、平行线的性质➽➼平行线性质与判定综合➽➼证明✮✮计算7．如图，点B，C在线段AD的异侧，点E，F分别是线段AB，CD上的点，∠=∠．已知12∠=∠，3C(1)求证：AB CD ∥；(2)若24180∠+∠=︒，求证：180BFC C ∠+∠=︒；(3)在（2）的条件下，若3021BFC ∠-︒=∠，求B ∠的度数．【答案】(1)见解析；(2)见解析；(3)50B ∠=︒【分析】（1）已知12∠=∠，所以32∠=∠，又因为3C ∠=∠，可以得出1C ∠=∠即可判定AB CD ∥；（2）已知23∠∠=，24180∠+∠=︒，可以得出//BF EC ，即可得出180BFC C ∠+∠=︒；（3）由（1）（2）可知AB CD ∥，//BF EC ，可以得出1C ∠=∠，180BFC C ∠+∠=︒；可以得出30212BFC C ∠-︒=∠=∠，可以得出C ∠，又因为1C B ∠=∠=∠，即可求出B ∠的度数．（1）证明：12∠=∠ ，3C ∠=∠，23∠∠=，1C ∴∠=∠，//AB CD ∴；（2）证明：24180∠+∠=︒ ，23∠∠=，34180∴∠+∠=︒，//BF EC ∴，180BFC C ∴∠+∠=︒；（3）180BFC C ∠+∠=︒ ，30212BFC C ∠-︒=∠=∠ ，230BFC C ∴∠=∠+︒，230180C C ∴∠+︒+∠=︒，50C ∴∠=︒，130BFC ∴∠=︒，//AB CD ，180B BFC ∴∠+∠=︒，50B ∴∠=︒．【点拨】本题考查了对顶角相等，平行线的性质与判定，掌握平行线的性质与判定是解题的关键．举一反三：【变式1】如图，已知点E ，F 在直线上AB 上，点G 在线段CD 上，ED 与FG 交于点H ，180C EFG CED GHE ︒∠=∠∠+∠=，．(1)试判断AED ∠与D ∠之间的数量关系，并说明理由．(2)若7030EHF D ∠︒=︒∠=，，求AEM ∠的度数．【答案】(1)180AED D ∠+∠=︒，理由见解析；(2)100︒．【分析】（1）根据同旁内角互补，两直线平行可得CE ∥GF ，根据平行线的性质等量代换可得∠FGD ＝∠EFG ，进而判定AB ∥CD ，即可得出∠AED ＋∠D ＝180°；（2）根据平行线的性质可得∠CED ＝70EHF ∠=︒，∠DEF ＝∠D ＝30°，求出∠CEF ，依据对顶角相等即可得到∠AEM 的度数．（1）解：∠AED ＋∠D ＝180°；理由：∵180CED GHE ∠+∠=︒，∴CE ∥GF ，∴∠C ＝∠FGD ，∵∠C ＝∠EFG ，∴∠FGD ＝∠EFG ，∴AB ∥CD ，∴∠AED ＋∠D ＝180°；（2）解：∵CE ∥GF ，70EHF ∠=︒，∴∠CED ＝70EHF ∠=︒，∵∠D ＝30°，AB ∥CD ，∴∠DEF ＝∠D ＝30°，∴∠CEF ＝∠CED ＋∠DEF ＝70°＋30°＝100°，∴∠AEM ＝∠CEF ＝100°．【点拨】本题主要考查了平行线的判定与性质，平行线的判定是由角的数量关系判断两直线的位置关系，平行线的性质是由平行关系来寻找角的数量关系．如图，1245EF BD BAC ∠=∠∠=︒，，∥．求ADG ∠的度数．【答案】135ADG ∠=︒【分析】根据两直线平行，同位角相等，得出23∠∠=，，再根据等量代换，得出13∠=∠，再根据内错角相等，两直线平行，得到DG AB ∥，最后再根据两直线平行，同旁内角互补，计算即可得出答案．解：∵EF BD ∥，∴23∠∠=，∵12∠=∠，∴13∠=∠，∴DG AB ∥，∴180ADG BAC ∠+∠=︒，∵45BAC ∠=︒，∴18045135AGD ∠=︒-︒=︒．【点拨】本题主要考查了平行线的判定与性质，掌握平行线的判定与性质是解本题的关键．【变式2】完成下面的证明：如图，点B 在AG 上，AG CD ∥，连接BC ，CF 平分BCD ∠，ABE FCB ∠=∠，BE AF ⊥于点E ．求证：90F ∠=︒．证明：∵AG CD ∥，∴ABC BCD ∠=∠（_____________________）．∵ABE FCB ∠=∠，∴ABC ABE BCD FCB ∠-∠=∠-∠，即EBC FCD ∠=∠．∵CF 平分BCD ∠，∴FCB ∠=______（__________________）．∴EBC FCB ∠=∠，∴BE CF ∥（________________________）∴__________________F =∠（________________________）．∵BE AF ⊥，∴BEF ∠=______︒（______________________）．∴90F ∠=︒．∴90BEF ∠=︒（垂直的定义）．∴90F ∠=︒．故答案为：两直线平行，内错角相等；FCD ∠；角平分线的定义；内错角相等，两直线平行；BEF ∠；两直线平行，内错角相等；90；垂直的定义．【点拨】本题主要考查了平行线的性质与判定，角平分线的定义，垂直的定义，熟知相关知识是解题的关键．中考真题专练一、单选题1．（2022·山东东营·中考真题）如图，直线a b ，一个三角板的直角顶点在直线a 上，两直角边均与直线b 相交，140∠=︒，则2∠=（）A ．40︒B ．50︒C ．60︒D ．65︒【点拨】本题主要考查了几何图形中角度的计算，平行线的性质，三角板中角度的计算，熟知平行线的性质是解题的关键．2．（2022·湖北襄阳·中考真题）已知直线m∥n，将一块含30°角的直角三角板ABC（∠ABC ＝30°，∠BAC＝60°）按如图方式放置，点A，B分别落在直线m，n上．若∠1＝70°．则∠2的度数为（）A．30°B．40°C．60°D．70°故选：B．【点拨】本题主要考查了平行线的性质，关键是熟练掌握平行线的性质．∥，将一个等腰直角三角板放置到如图所示位置．若3．（2022·贵州安顺·中考真题）如图，a b∠=︒，则2∠的大小是（）115A．20︒B．25︒C．30︒D．45︒【答案】C∥，根据平行线的性质，可得【分析】如图，过等腰直角三角板的一个顶点作直线c a23,14∠=∠∠=∠，根据三角板可知3445∠+∠=︒，进而等量代换结合已知条件即可求解．∥解：如图，过等腰直角三角板的一个顶点作直线c a∵a∥b，∴∥∥，a b c∴∠=∠∠=∠，23,14，∠+∠=︒3445\Ð+Ð=°，1245Q，Ð=°115∴∠=︒．230故选：C．【点拨】本题考查了平行线的性质与判定，掌握平行线的性质是解题的关键．二、填空题，则α∠的度数是______．4．（2022·辽宁阜新·中考真题）一副三角板如图摆放，直线AB CD【答案】15︒##15度【分析】根据题意可得：90EBD ∠=︒，45BDE ∠=︒，30EDC ∠=︒，然后利用平行线的性质可得180ABD BDC ∠∠+=︒，从而进行计算即可解答．解：如图：由题意得：90EBD ∠=︒，45BDE ∠=︒，30EDC ∠=︒，//AB CD ，180ABD BDC ∠∠∴+=︒，180EBD BDE EDC∠α∠∠∠∴=︒---180904530=︒-︒-︒-︒15=︒，故答案为：15︒．【点拨】本题考查了平行线的性质，熟练掌握平行线的性质是解题的关键．5．（2022·湖北宜昌·中考真题）如图，C 岛在A 岛的北偏东50︒方向，C 岛在B 岛的北偏西35︒方向，则ACB ∠的大小是_____．【答案】85︒##85度【分析】过C 作CF DA ∥交AB 于F ，根据方位角的定义，结合平行线性质即可求解．解： C 岛在A 岛的北偏东50︒方向，50DAC ∴∠=︒，C 岛在B 岛的北偏西35︒方向，35CBE ∴∠=︒，过C 作CF DA ∥交AB 于F ，如图所示：DA CF EB ∴∥∥，50,35FCA DAC FCB CBE ∴∠=∠=︒∠=∠=︒，85ACB FCA FCB ∴∠=∠+∠=︒，故答案为：85︒．【点拨】本题考查方位角的概念与平行线的性质求角度，理解方位角的定义，并熟练掌握平行线的性质是解决问题的关键．三、解答题6．（2022·湖北武汉·中考真题）如图，在四边形ABCD 中，AD BC ∥，80B ∠=︒．(1)求BAD ∠的度数；(2)AE 平分BAD ∠交BC 于点E ，50BCD ∠=︒．求证：AE DC ∥．【答案】(1)100BAD ∠=︒；(2)详见解析【分析】（1）根据两直线平行，同旁内角互补，即可求解；（2）根据AE 平分BAD ∠，可得50DAE ∠=︒．再由AD BC ∥，可得50AEB DAE ∠=∠=︒．即可求证．（1）解：∵AD BC ∥，∴180B BAD ∠+∠=°，∵80B ∠=︒，∴100BAD ∠=︒．（2）证明：∵AE 平分BAD ∠，∴50DAE ∠=︒．∵AD BC ∥，∴50AEB DAE ∠=∠=︒．∵50BCD ∠=︒，∴BCD AEB ∠=∠．∴AE DC ∥．【点拨】本题主要考查了平行线的判定和性质，熟练掌握平行线的判定和性质定理是解题的关键。

七年级数学平行线的判定和性质(二)(北师版)(含答案)

学生做题前请先回答以下问题问题1：在同一平面内，__________的两条直线叫做平行线．问题2：平行线的判定定理：①____________________，两直线平行；②____________________，两直线平行；③____________________，两直线平行．问题3：平行线的性质定理：①两直线平行，____________________；②两直线平行，____________________；③两直线平行，____________________．问题4：平行线的判定定理是用来判定两条直线平行的定理，即已知角的关系证明平行，用平行线的判定定理．平行线的性质定理是由直线平行，可以得到的结论，即已知平行求角的关系，用平行线的性质定理．请根据下面推理，填写推理的依据．①已知：如图，直线a和直线b被直线c所截，∠1=∠2．求证：a∥b．证明：∵∠1=∠2（已知）∴a∥b（_______________________________）①已知：如图，直线a和直线b被直线c所截，a∥b．求证：∠1=∠2．证明：∵a∥b（已知）∴∠1=∠2（_______________________________）平行线的判定和性质（二）（北师版）一、单选题(共10道，每道10分)1.如图，直线DE经过点A，若∠B=∠DAB，则DE∥BC，其依据是( )A.两直线平行，内错角相等B.内错角相等，两直线平行C.同旁内角互补，两直线平行D.内错角相等答案：B解题思路：条件是∠B=∠DAB，结论是DE∥BC，且∠B和∠DAB是直线DE和直线BC被直线AB所截得到的内错角，由内错角相等得到两直线平行，依据是内错角相等，两直线平行，故选B．试题难度：三颗星知识点：平行线的判定2.如图，已知D，E在△ABC的边上，DE∥BC，可得∠ADE=∠B，依据是( )A.两直线平行，同位角相等B.两直线平行，内错角相等C.同位角相等D.同位角相等，两直线平行答案：A解题思路：条件是DE∥BC，结论是∠ADE=∠B．∠ADE和∠B是直线DE和直线BC被直线AB所截得到的同位角，由两直线平行得到同位角相等，依据是两直线平行，同位角相等，故选A．试题难度：三颗星知识点：平行线的性质3.如图，直线，分别与直线，相交，若∥，则∠1=_________，依据是_____________．( )A.∠2；两直线平行，内错角相等B.∠3；两直线平行，内错角相等C.∠2；内错角相等，两直线平行D.∠3；内错角相等，两直线平行答案：B解题思路：由平行得角的关系，先找截线，观察图形，与∠1有关的截线是直线，∠1和∠3是由直线和直线被直线所截得到的内错角，由∥，可以得到∠1=∠3，依据是两直线平行，内错角相等，故选B．试题难度：三颗星知识点：平行线的性质4.如图，若AB∥EF，则∠ADE=_________，依据是_____________．( )A.∠B；两直线平行，同位角相等B.∠DEF；内错角相等，两直线平行C.∠DEF；两直线平行，内错角相等D.∠CEF；两直线平行，同位角相等答案：C解题思路：由平行得角的关系，先找截线，观察图形，与∠ADE有关的截线是直线DE，∠ADE和∠DEF是由直线AB和EF被直线DE所截得到的内错角，若AB∥EF，则∠ADE=∠DEF，理由是两直线平行，内错角相等，故选C．试题难度：三颗星知识点：平行线的性质5.如图，两直线a，b被直线c所截形成八个角，若a∥b，则下列结论错误的是( )A.∠1=∠2B.∠3+∠8=180°C.∠5=∠6D.∠7+∠8=180°答案：D解题思路：A选项：∵a∥b（已知）∴∠1=∠2（两直线平行，内错角相等）故A选项结论正确；B选项：∵a∥b（已知）∴∠3+∠2=180°（两直线平行，同旁内角互补）∵∠8=∠2（对顶角相等）∴∠3+∠8=180°（等量代换）故B选项结论正确；C选项：∵a∥b（已知）∴∠3=∠6（两直线平行，同位角相等）∵∠3=∠5（对顶角相等）∴∠5=∠6（等量代换）故C选项结论正确；D选项：∵a∥b（已知）∴∠1=∠8（两直线平行，同位角相等）∵∠1=∠7（对顶角相等）∴∠7=∠8（等量代换）故D选项结论错误．故选D．试题难度：三颗星知识点：平行线的性质6.如图，若AD∥BC，则一定正确的是( )A.∠1=∠2B.∠3=∠4C.∠1=∠2，∠3=∠4D.∠2=∠3答案：B解题思路：根据平行线的性质，由AD∥BC，要找角之间的关系，需要找两条平行直线AD和BC被第三条直线所截得到的角，四个选项中，只有∠3和∠4是两条平行直线AD和BC被直线BD所截得到的内错角，根据两直线平行，内错角相等，得∠3=∠4，故选B．试题难度：三颗星知识点：平行线的性质7.如图，能判定EB∥AC的条件是( )A.∠C=∠ABEB.∠A=∠EBDC.∠C=∠ABCD.∠A=∠ABE答案：D解题思路：要证平行，考虑找同位角，内错角，同旁内角，分析可得只有选项D中，∠A与∠ABE是直线EB和直线AC被直线AB所截的内错角，根据内错角相等，两直线平行，可以判定EB∥AC，故选D．试题难度：三颗星知识点：平行线的判定8.如图，若BE∥CF，则一定正确的是( )A.∠1=∠2B.∠3=∠4C.AB∥CDD.∠ABC=∠BCD答案：B解题思路：根据平行线的性质，由BE∥CF，可以得到角之间的关系，需要找两条平行直线BE和CF被第三条直线所截得到的角，只有∠3和∠4是两条平行直线BE和CF被直线BC所截得到的内错角，根据两直线平行，内错角相等，得∠3=∠4，故选B．试题难度：三颗星知识点：平行线的性质9.如图，DE∥BC，则下列结论正确的( )A.∠1=∠3B.∠2=∠3C.∠4=∠CD.∠2=∠C答案：B解题思路：根据平行线的性质，由DE∥BC，可以得到角之间的关系，需要找两条平行直线DE和BC被第三条直线所截得到的角，分析可得只有∠2和∠3是两条平行线DE和BC被直线BE所截得到的内错角，根据两直线平行，内错角相等，得∠2=∠3，故选B．试题难度：三颗星知识点：平行线的性质10.如图，AB∥CD，AD平分∠BAC，若∠BAD=70°，则∠1的度数为( )A.35°B.40°C.45°D.50°答案：B解题思路：解：如图，∵AD平分∠BAC（已知）∴∠BAC=2∠BAD（角平分线的定义）∵∠BAD=70°（已知）∴∠BAC=2×70°=140°（等量代换）∵AB∥CD（已知）∴∠1+∠BAC=180°（两直线平行，同旁内角互补）∴∠1=40°（等式的性质）故选B．试题难度：三颗星知识点：平行线的性质。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五环节：归纳小结，反思提高
1、本节课主要应用了哪些知识？ 2、在应用它们时，你认为应该注意哪些问题？ 3、在写几何推理的过程中，因为和所以分别表达的意义是什么？根据是什么？
布置作业：
课本习题2.6.
第二章
相交线与平行线
3 平行线的性质（第2课时）
第一环节：复习回顾，夯实基础
问题1: 平行线的性质有哪几条？问题2：判别直线平行的条件有哪几个？你现在一共有几个判定直线平行的方法？问题3：在应用二者时应注意什么问题？
第二环节：层层递进，推理论证
问题1：如图，直线a，b被直线c所截，（1）当∠1=∠2时,你能结合图形用推理的方式来说明 a∥b吗？（2）若∠2+∠3=180°呢？
问题2：如图，AE∥CD，若∠1 = 37°， ∠D =54°，求∠2 和∠BAE的度数.
第四环节：及时巩固，深化提高
问题1：如图,选择合适的内容填空。（1）因为AB//CD 所以∠1=∠2（）（2）因为∠3＝∠1 所以 //__（同位角相等，两直线平行）（3）因为∠1＋∠ ＝180 ，所以AB//CD（）
第二环节：层层递进，推理论证
问题2 如图：（1）若∠1=∠2，可以判定哪两条直线平行根据是什么？（2）若∠2=∠M，可以判定哪两条直线平行？根据是什么（3）若∠2 +∠3=180°，可以判定哪两条直线平行？根据是什么？
第二环节：层层递进，推理论证
问题3 如图， AB∥CD，如果∠1=∠2，那么 EF 与 AB 平行吗？说说你的理由．
第三环节：独立探究，步骤规范
解：因为a∥b，根据“两直线平行，内错角相等” ，所以 ∠2 = ∠1 = 107° . 因为 c∥d，根据“两直线平行，同旁内角互补” ，所以 ∠1 ＋ ∠3 = 180° ，所以 ∠3 = 180°- ∠1 = 180°-107° = 73° .
第三环节：独立探究，步骤规范
第四环节：及时巩固，深化提高
问题2：如图，∠1=∠3，那么，∠1和∠2的大小有何关系？∠1和∠4的大小有何关系？为什么？由此你得到什么结论？源自第四环节：及时巩固，深化提高
问题3：如图，平行直线AB,CD被直线EF所截，分别交直线AB,CD于点G,M。GH和MN分别是 ∠EGB和∠EMD的角平分线。问：GH和MN平行吗？请说明理由。
第二环节：层层递进，推理论证
解：因为 ∠1 = ∠2，根据“内错角相等，两直线平行” ，所以 EF∥CD. 又因为 AB∥CD，根据“平行于同一条直线的两条直线平行” ，所以 EF∥AB．
第三环节：独立探究，步骤规范
问题1：如图，已知直线a∥b，直线c∥d， ∠1=107°，求∠2，∠3 的度数.