人教版九年级上册数学切线长定理练习题与答案及解析
人教版九年级数学上切线长定理和三角形的内切圆含答案

切线长定理和三角形的内切圆知识点1切线长定理1.如图24-2-36,PA,PB分别切☉O于A,B两点,如果∠P=60°,PA=2,那么AB的长为()图24-2-36A.1B.2C.3D.42.如图24-2-37是用一把直尺、含60°角的三角尺和光盘摆放而成的,A为60°角与直尺的交点,B为光盘与直尺的唯一交点.若AB=3,则光盘的直径是()图24-2-37A.6√3B.3√3C.6D.33.如图24-2-38,PA,PB分别切☉O于点A,B,MN切☉O于点C,分别交PA,PB于点M,N.若PA=7.5 cm,则△PMN的周长是()图24-2-38A.7.5 cmB.10 cmC.12.5 cmD.15 cm4.如图24-2-39,PA,PB,CD分别切☉O于点A,B,E,CD分别交PA,PB于C,D两点.若∠P=40°,则∠PAE+∠PBE的度数为()A.50°B.62°C.66°D.70°图24-2-39图24-2-405.[2019·盐城阜宁期中]如图24-2-40,☉O为△ABC的内切圆,AC=10,AB=8,BC=9,D,E分别为BC,AC上的点,且DE为☉O的切线,则△CDE的周长为()A.9B.7C.11D.86.如图24-2-41,PA,PB分别切☉O于点A,B,连接PO与☉O相交于点C,连接AC,BC.求证:AC=BC.图24-2-417.如图24-2-42所示,P为☉O外一点,PA,PB为☉O的切线,A,B为切点,AC为☉O的直径,PO 交☉O于点E.(1)试判断∠APB与∠BAC的数量关系,并说明理由.(2)若☉O的半径为4,P是☉O外一动点,是否存在点P,使四边形PAOB为正方形?若存在,请求出PO的长,并判断点P的个数及其满足的条件;若不存在,请说明理由.图24-2-42知识点2三角形的内切圆与内心8.三角形的内心是 ()A.三边垂直平分线的交点B.三条角平分线的交点C.三条高所在直线的交点D.三条中线的交点9.[2020·随州]如图24-2-43,设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h,r,R,则下列结论不正确的是()图24-2-43A.h=R+rB.R=2rC.r=√34a D.R=√33a10.《九章算术》是我国古代内容极为丰富的数学名著.书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何.”其意思是:“如图24-2-44,今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少.”其结果为()图24-2-44A.3步B.5步C.6步D.8步11.如图24-2-45,☉I是△ABC的内切圆,与AB,BC,CA分别相切于点D,E,F,∠DEF=50°,求∠A 的度数.图24-2-4512.如图24-2-46,在△ABC中,边AC上有一点D满足CD=2AD,点O是△BDC的内心,E,F分别为☉O与边BD,CD的切点,已知BD=BC.(1)求证:①AE⊥EF;②AE∥DO.(2)若AC=6,☉O的半径为1,求AE的长.图24-2-46能力拓展提升13.联想三角形内心的概念,我们可引出如下概念.定义:到三角形的两边距离相等的点,叫做此三角形的准内心.举例:如图24-2-47①,若PD=PE,则点P为△ABC的准内心.应用:如图②,BF为等边三角形ABC的角平分线,准内心P在BF上,PD⊥AB于点D,PE⊥BC BP.求证:点P是△ABC的内心.于点E,且PF=12图24-2-4714.联想三角形外心的概念,我们可引出如下概念:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.例如:如图24-2-48①,若PA=PB,则点P为△ABC的准外心.AB,连接AP,BP,求∠APB (1)如图②,CD为等边三角形ABC的高,准外心P在高CD上,且PD=12的度数;(2)如图③,若△ABC为直角三角形,∠C=90°,AB=13,BC=5,准外心P在AC边上,试探究PA 的长.图24-2-48典题讲评与答案详析1.B2.A3.D4.D[解析] ∵∠P=40°,∴∠PCD+∠PDC=140°.∵PA,PB,CD分别切☉O于点A,B,E,∴AC=CE,DE=DB,∴∠CAE=∠CEA,∠DEB=∠DBE.∵∠PCD=∠CAE+∠CEA=2∠PAE,∠PDC=∠DEB+∠DBE=2∠PBE,∴∠PCD+∠PDC=2(∠PAE+∠PBE)=140°, ∴∠PAE+∠PBE=70°.5.C6.证明:∵PA,PB分别切☉O于点A,B,∴PA=PB,∠APO=∠BPO.又∵PC=PC,∴△APC≌△BPC,∴AC=BC. 7.解:(1)∠APB=2∠BAC.理由:∵PA,PB为☉O的切线,A,B为切点,∴PA=PB,∠APO=∠BPO,∴∠PAB=∠PBA.∵∠APO+∠BPO+∠PAB+∠PBA=180°,∴∠APO+∠PAB=90°.∵PA是☉O的切线,∴∠PAO=90°,即∠PAB+∠BAC=90°,∴∠APO=∠BAC,∴∠APB=2∠BAC.(2)存在.∵PA,PB为☉O的切线,∴OA⊥PA,OB⊥PB, ∴∠OAP=∠OBP=90°,∴当OA⊥OB时,四边形PAOB为矩形.又∵OA=OB,∴四边形PAOB为正方形,∴PO=√2OA=4√2.这样的点P 有无数个,当点P 在以点O 为圆心,4√2为半径的圆上时,四边形PAOB 为正方形. 8.B9.C [解析] 如图.∵△ABC 是等边三角形,∴△ABC 的内切圆和外接圆是同心圆,设圆心为O.过点A 作AD ⊥BC 于点D ,则AD 过点O ,且D 为△ABC 的内切圆与边BC 的切点,设△ABC 的内切圆与边AC 的切点为E ,连接OE ,则OE ⊥AC. 由题意,得OE=r ,AO=R ,AD=h ,∴h=R+r ,故A 正确; ∵AD ⊥BC ,∴∠DAC=12∠BAC=12×60°=30°.在Rt △AOE 中,AO=2OE ,∴R=2r ,故B 正确; ∵AB=AC=BC=a , ∴AE=12AC=12a.在Rt △AOE 中,由勾股定理,得AE 2+OE 2=AO 2, 即12a 2+r 2=(2r )2,12a 2+12R 2=R 2,∴r=√3a 6,R=√33a ,故C 错误,D 正确.故选C .10.C [解析] 如图,设BC=8,AC=15, 则AB=√82+152=17.∵S △ABC =12AC ·BC=12AB ·r+12AC ·r+12BC ·r=12r (AB+AC+BC ),∴r=AC ·BCAB+AC+BC =8×158+15+17=3.故该直角三角形能容纳的圆形的直径是6步. 11.解:连接ID ,IF ,如图.∵∠DEF=50°,∵∠DIF=2∠DEF=100°.∵☉I 是△ABC 的内切圆,与AB ,CA 分别相切于点D ,F ,∴ID ⊥AB ,IF ⊥AC ,∴∠ADI=∠AFI=90°,∴∠A+∠DIF=180°, ∴∠A=180°-100°=80°.12.解:(1)证明:①如图,连接OB ,OF.∵点O 是△BDC 的内心,∴BO 平分∠DBC. ∵BD=BC ,∴OB ⊥CD.∵CD 与☉O 相切于点F ,∴OF ⊥CD , ∴B ,O ,F 三点共线,∴DF=CF.又∵CD=2AD ,∴AD=DF.∵BD 与☉O 相切,∴由切线长定理可知DE=DF , ∴AD=DE=DF ,∴∠DAE=∠DEA ,∠DEF=∠DFE. ∵∠DAE+∠DEA+∠DEF+∠DFE=180°, ∴∠DEA+∠DEF=90°, ∴∠AEF=90°,∴AE ⊥EF.②∵点O 是△BDC 的内心,∴DO 平分∠BDC ,∴∠EDF=2∠EDO.由①知∠DAE=∠DEA. 又∵∠EDF=∠DAE+∠DEA ,∴2∠EDO=2∠DEA ,∴∠EDO=∠DEA , ∴AE ∥DO.(2)如图,设DO 与EF 相交于点G. 由(1)可知DE=DF ,DO 平分∠EDF ,∴DO ⊥EF ,∴EF=2FG. ∵AD=DF=CF ,AC=6,∴DF=2. ∵OF=1,∴由勾股定理可求得OD=√5. ∵12DF ·OF=12OD ·FG ,即12×2×1=12×√5FG ,∴FG=2√55,∴EF=2FG=4√55. ∵AF=2DF=4,∠AEF=90°, ∴由勾股定理可求得AE=√AF 2-EF 2=√42-(4√55)2=8√55.13.证明:∵△ABC 是等边三角形,∴∠ABC=60°.∵BF 为△ABC 的角平分线, ∴∠PBE=30°,∴PE=12BP.∵BF 是等边三角形ABC 的角平分线, ∴BF ⊥AC.∵点P 是△ABC 的准内心,PD ⊥AB ,PE ⊥BC ,PF=12BP , ∴PE=PD=PF ,∴点P 是△ABC 的内心.14.解:(1)①若PB=PC ,则∠PCB=∠PBC.∵CD 为等边三角形ABC 的高, ∴AD=BD ,∠PCB=30°, ∴∠PBD=∠PBC=∠PCB=30°,∴PD=√33BD=√36AB ,与已知PD=12AB 矛盾,∴PB ≠PC ;②若PA=PC ,同理可推出矛盾,∴PA ≠PC ; ③若PA=PB ,由PD=12AB ,得PD=BD=AD.∵∠ADP=∠BDP=90°,∴∠PAB=∠APD=∠PBA=∠BPD=45°, ∴∠APB=90°.综上可得,∠APB=90°. (2)①若PB=PA ,连接PB. 设PA=x ,则PB=x.∵∠C=90°,AB=13,BC=5, ∴AC=12,∴PC=12-x.在Rt △BCP 中,有x 2=(12-x )2+52,解得x=16924,即PA=16924.②若PA=PC,则PA=6.③若PC=PB,由图知,此种情况不存在.综上可得,PA的长为16924或6.。
人教版数学九年级上册 《切线长定理的相关计算》必考题型专项分类专题练习(专题分类练习 详细答案)

《切线长定理的相关计算》必考经典题型专项分类专题练习(专题分类练习+详细解析)题型一:切线长定理与三角形问题1. 如图所示,PA,PB是☉O的切线,且∠APB=40°,下列说法不正确的是( )A.PA=PBB.∠APO=20°C.∠OBP=70°D.∠AOP=70°2. 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC,BC相切于点D,E.则AD为( )A.2.5B.1.6C.1.5D.13. 如图,半圆O与等腰直角三角形两腰CA,CB分别切于D,E两点,直径FG在AB 上,若BG=√2-1,则△ABC的周长为 .4.如图,PA,PB分别切圆O于点A,B,并与圆O的切线CD,分别相交于点D,C,已知△PCD的周长等于10cm,求PA.1. 如图,一圆内切于四边形ABCD,且BC=10,AD=7,则四边形的周长为( )A.32B.34C.36D.382. 如图,四边形ABCD中,AD∥BC,DC⊥AD,DC⊥BC,以CD为直径的半圆O与AD,BC 以及AB均相切,切点分别是点D,C,E.若半圆O的半径为2,AB长为5,则该四边形的周长是( )A.9B.10C.12D.143. 如图,AB,BC,CD分别与☉O相切于E,F,G,且AB∥CD,BO=6cm,CO=8cm.(1)求证:BO⊥CO.(2)求BE和CG的长.1. 在直角坐标系中,☉O的半径为1,则直线y=-2x+√5与☉O的位置关系是( )A.相离B.相交C.相切D.无法确定2. 如图,在平面直角坐标系中,☉P与x轴分别交于A,B两点,点P的坐标为(3,-1),AB=2√3.若将☉P向左平移,则☉P与y轴相切时点P的坐标为 _.3. (1)已知,如图1,△ABC的周长为l,面积为S,其内切圆圆心为O,半径为r,求.证:r=2Sl(2)已知,如图2,△ABC中,A,B,C三点的坐标分别为A(-3,0),B(3,0),C(0,4).若△ABC内心为D.求点D的坐标.(3)与三角形的一边和其他两边的延长线相切的圆,叫旁切圆,圆心叫旁心.请求出条件(2)中的△ABC位于第一象限的旁心的坐标.1. 如图,一个钢管放在V 形架内,点O 为钢管的圆心.如果MP=10cm,∠MON=120°,则钢管的半径OM 的值为 ( )A.10√33cm B.10√3cm C.50√33cm D.5√3cm2. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?” ( )A.3步B.5步C.6步D.8步3.如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB 处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E 两点,经测量发现AD 和BE 的长恰是方程x 2-25x+150=0的两根(单位:cm),则该自来水管的半径为________cm.4. 等腰Rt△ABC和☉O如图放置,已知AB=BC=1,∠ABC=90°,☉O的半径为1,圆心O与直线AB的距离为5.(1)若△ABC以每秒2个单位的速度向右移动,☉O不动,则经过多长时间△ABC的边与圆第一次相切?(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,☉O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?《切线长定理的相关计算》必考经典题型专项分类专题练习(专题分类练习+详细解析)题型一:切线长定理与三角形问题1. 如图所示,PA,PB是☉O的切线,且∠APB=40°,下列说法不正确的是( )A.PA=PBB.∠APO=20°C.∠OBP=70°D.∠AOP=70°【解析】选C.∵PA,PB是☉O的切线,且∠APB=40°,∴PA=PB,∠APO=∠BPO=20°,∠PAO=∠PBO=90°, ∴∠BOP=∠AOP=70°,∴C 是错误的.2. 如图,Rt △ABC 中,∠ACB=90°,AC=4,BC=6,以斜边AB 上的一点O 为圆心所作的半圆分别与AC,BC 相切于点D,E.则AD 为 ( )A.2.5B.1.6C.1.5D.1【解析】选B.连接OD,OE,OC,设OD=r,∵AC,BC 切☉O 于D,E, ∴∠ODC=∠OEC=90°,OD=OE, ∵S △AOC +S △BOC =S △ABC ,即12OD ·AC+12OE ·BC=12BC ·AC,12r ·4+12r ·6=12×6×4, r=2.4,AD=AC-r=1.6.3. 如图,半圆O 与等腰直角三角形两腰CA,CB 分别切于D,E 两点,直径FG 在AB 上,若BG=√2-1,则△ABC 的周长为 .【解析】如图,连接OD,OE,∵半圆O 与等腰直角三角形两腰CA,CB 分别切于D,E 两点,∴∠C=∠OEB=∠OEC=∠ODC=90°,∴四边形ODCE是矩形.∵OD=OE,∴四边形ODCE是正方形,∴CD=CE=OE.∵∠A=∠B=45°,∴△OEB是等腰直角三角形.设OE=r,则BE=r,∴OB=OG+BG=√2-1+r,∵OB=√2OE=√2r,∴√2-1+r=√2r,解得r=1.∴AC=BC=2r=2,AB=2OB=2×(1+√2-1)=2√2.∴△ABC的周长为:AC+BC+AB=4+2√2.4.如图,PA,PB分别切圆O于点A,B,并与圆O的切线CD,分别相交于点D,C,已知△PCD的周长等于10cm,求PA.【解析】设DC与☉O的切点为E.∵PA,PB分别是☉O的切线,且切点为A,B,∴PA=PB.同理,可得:DE=DA,CE=CB,则△PCD的周长=PD+DE+CE+PC=PD+DA+PC+CB=PA+PB=10cm.∴PA=PB=5cm.题型二:切线长定理与多边形问题1. 如图,一圆内切于四边形ABCD,且BC=10,AD=7,则四边形的周长为( )A.32B.34C.36D.38【解析】选B.如图,根据切线长定理可知,AE=AH,BE=BF,CF=CG,DG=DH.所以AE+DG=AH+DH=AD,BE+CG=BF+CF=BC,所以AB+BC+CD+DA=AE+BE+BC+CG+DG+DA=2AD+2BC=2×7+2×10=34.2. 如图,四边形ABCD 中,AD ∥BC,DC ⊥AD,DC ⊥BC,以CD 为直径的半圆O 与AD,BC 以及AB 均相切,切点分别是点D,C,E.若半圆O 的半径为2,AB 长为5,则该四边形的周长是( )A.9B.10C.12D.14【解析】选D.根据切线长定理,得AD=AE,BC=BE,所以四边形ABCD 的周长是5×2+4=14.3. 如图,AB,BC,CD 分别与☉O 相切于E,F,G,且AB ∥CD,BO=6cm,CO=8cm. (1)求证:BO ⊥CO. (2)求BE 和CG 的长.【解析】(1)∵AB ∥CD, ∴∠ABC+∠BCD=180°.∵AB,BC,CD 分别与☉O 相切于点E,F,G, ∴BO 平分∠ABC,CO 平分∠DCB, ∴∠OBC=12∠ABC,∠OCB=12∠DCB,∴∠OBC+∠OCB=12(∠ABC+∠DCB)=12×180°=90°, ∴∠BOC=90°,∴BO ⊥CO. (2)连接OF,则OF ⊥BC, ∴Rt △BOF ∽Rt △BCO, ∴BF BO =BOBC . ∵在Rt △BOC 中, BO=6cm,CO=8cm, ∴BC=√62+82=10(cm), ∴BF 6=610, ∴BF=3.6cm,∵AB,BC,CD 分别与☉O 相切, ∴BE=BF=3.6cm,CG=CF, ∵CF=BC-BF=10-3.6=6.4(cm). ∴CG=CF=6.4cm.题型三:切线长定理与坐标问题1. 在直角坐标系中,☉O 的半径为1,则直线y=-2x+√5与☉O 的位置关系 是 ( ) A.相离B.相交C.相切D.无法确定【解析】选C.如图所示,过O 作OC ⊥直线AB,垂足为C, 直线AB 为y=-2x+√5. 令x=0,解得:y=√5; 令y=0,解得:x=√52, ∴A (√52,0),B(0,√5), 即OA=√52,OB=√5.在Rt △AOB 中,根据勾股定理得:AB=2+OB 2=52, 又S △AOB =12AB ·OC=12OA ·OB, ∴OC=OA·OB AB =√52×√552=1,又圆O 的半径为1,则直线y=-2x+√5与圆O 的位置关系是相切.2. 如图,在平面直角坐标系中,☉P 与x 轴分别交于A,B 两点,点P 的坐标为(3,-1),AB=2√3.若将☉P 向左平移,则☉P 与y 轴相切时点P 的坐标为 _.【解析】(2,-1)或(-2,-1)3. (1)已知,如图1,△ABC 的周长为l ,面积为S,其内切圆圆心为O,半径为r,求证:r=2Sl .(2)已知,如图2,△ABC 中,A,B,C 三点的坐标分别为A(-3,0),B(3,0),C(0,4).若△ABC 内心为D.求点D 的坐标.(3)与三角形的一边和其他两边的延长线相切的圆,叫旁切圆,圆心叫旁心.请求出条件(2)中的△ABC 位于第一象限的旁心的坐标.【解析】(1)连接OA,OB,OC,设△ABC 的三边分别为a,b,c 则: S=S △OAB +S △OBC +S △OAC =12(a+b+c)r=12l r. ∴r=(2)∵A(-3,0),B(3,0),C(0,4),∴AB=6,AC=BC=5.l =AB+AC+BC=16,S=12AB ·OC=12.由条件(1)得:r==2×1216=32,得D (0,32). (3)如图,设∠B 和∠C 的外角平分线交于点P,则点P 为旁心.∵∠MCB=2∠PCB=2∠CBA,∴∠PCB=∠CBA,∴CP ∥AB.过点P 分别作PE ⊥x 轴于E,PF ⊥CB 于F,则PF=PE=OC=4.在Rt △PFC 中,PC=PF sin∠PCF =PF sin∠CBO =445=5.∴P 点坐标为(5,4).即条件(2)中的△ABC 位于第一象限的旁心的坐标为(5,4).题型四:切线长定理与实际问题1. 如图,一个钢管放在V 形架内,点O 为钢管的圆心.如果MP=10cm,∠MON=120°,则钢管的半径OM 的值为 ( )A.10√33cmB.10√3cmC.50√33cmD.5√3cm【解析】选A.由题意可得OM ⊥MP,ON ⊥NP.∵∠MON=120°,∴∠MOP=60°,设OM=xcm,则OP=2xcm,在Rt △OPM 中,OM 2+MP 2=OP 2,即x 2+102=(2x)2,解得x=10√33,∴OM 的值为10√33cm. 2. 《九章算术》是我国古代内容极为丰富的数学名著,书中有下列问题“今有勾八步,股十五步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为8步,股(长直角边)长为15步,问该直角三角形能容纳的圆形(内切圆)直径是多少?” ( )A.3步B.5步C.6步D.8步【解析】选A.3.如图,小敏家厨房一墙角处有一自来水管,装修时为了美观,准备用木板从AB 处将水管密封起来,互相垂直的两墙面与水管分别相切于D,E 两点,经测量发现AD 和BE 的长恰是方程x 2-25x+150=0的两根(单位:cm),则该自来水管的半径为________cm.【解析】连接OD,OE.解方程x 2-25x+150=0,得x 1=10,x 2=15,∴设AD=10,BE=15,半径为r,∴AB=AD+BE=25,∴(AD+r)2+(BE+r)2=AB 2,即(10+r)2+(15+r)2=252,解得:r=5.答案:54. 等腰Rt △ABC 和☉O 如图放置,已知AB=BC=1,∠ABC=90°,☉O 的半径为1,圆心O 与直线AB 的距离为5.(1)若△ABC以每秒2个单位的速度向右移动,☉O不动,则经过多长时间△ABC的边与圆第一次相切?(2)若两个图形同时向右移动,△ABC的速度为每秒2个单位,☉O的速度为每秒1个单位,则经过多少时间△ABC的边与圆第一次相切?【解析】(1)假设第一次相切时,△ABC移至△A′B′C′处,A′C′与☉O切于点E,连OE并延长,交B′C′于F.设☉O与直线l切于点D,连OD,则OE⊥A′C′,OD⊥直线l.由切线长定理可知C′E=C′D;设C′D=x,则C′E=x,易知C′F=√2x,∴√2x+x=1,则x=√2-1,∴CC′=BD-BC-C′D=5-1-(√2-1)=5-√2;∴△ABC运动的时间为5−√2秒.2(2)设经过t秒△ABC的边与圆第一次相切,设经过t秒△ABC的边与☉O第一次相切时,△ABC移至△A″B″C″处,☉O与BC所在直线的切点D移至D′处,A″C″与☉O切于点E,连OE并延长,交B″C″于F.∵CC″=2t,DD′=t,∴C″D′=CD+DD′-CC″=4+t-2t=4-t.由切线长定理得C″E=C″D′=4-t;又∵FC″=√2C″E=√2C″D′,而FC″+C″D′=FD′=1,∴(√2+1)C″D′=(√2+1)(4-t)=1,解得:t=5-√2.答:经过5-√2秒△ABC的边与圆第一次相切.学海迷津:数学学习十大方法1、配方法所谓配方,就是把一个解析式利用恒等变形的方法,把其中的某些项配成一个或几个多项式正整数次幂的和形式。
3.7 切线长定理(练习)(解析版)

第三章 圆第七节 切线长定理精选练习一、单选题1.(2021·北京九年级专题练习)如图,PA ,PB 为⊙O 的两条切线,点A ,B 是切点,OP 交⊙O 于点C ,交弦AB 于点D .下列结论中错误的是( )A .PA =PBB .AD =BDC .OP ⊥ABD .∠PAB =∠APB【答案】D【分析】利用切线长定理、等腰三角形的性质即可得出答案.【详解】解:由切线长定理可得:∠APO =∠BPO ,PA =PB ,从而AB ⊥OP ,AD =BD .因此A .B .C 都正确.无法得出∠PAB =∠APB ,可知:D 是错误的.综上可知:只有D 是错误的.故选:D .【点睛】本题考查了切线长定理、等腰三角形的性质,关键是利用切线长定理、等腰三角形的性质解答.2.(2021·全国九年级课时练习)如图,AB 是⊙O 的直径,点P 在BA 的延长线上,PA =AO ,PD 与⊙O 相切于点D ,BC ⊥AB 交PD 的延长线于点C ,若⊙O 的半径为1,则BC的长是( )A .1.5B .2CD 【答案】D【分析】连接OD ,根据切线的性质求出∠ODP =90°,根据勾股定理求出PD ,证明BC 是⊙O 的切线,根据切线长定理得出C D =BC ,再根据勾股定理求出BC 即可.【详解】连接OD ,如图所示∵PC 切⊙O 于D ∴∠ODP =90°∵⊙O 的半径为1,PA =AO ,AB 是⊙O 的直径 ∴PO =1+1=2,PB =1+1+1=3,OD =1∴由勾股定理得:PD ==∵BC ⊥AB ,AB 过O ∴BC 切⊙O 于B ∵PC 切⊙O 于D ∴CD =BC设CD =CB =x 在Rt △PBC 中,由勾股定理得:PC 2=PB 2+BC 2即222)3x x +=+ 解得:x 即BC故选:D【点睛】本题考查了切线的性质和判定,及切线长定理,切线的性质定理为:圆的切线垂直于过切点的半径,切线长定理为:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.同时考查了利用勾股定理解直角三角形.3.(2021·湖北武汉市·九年级一模)如图,经过A 、C 两点的⊙O 与△ABC 的边BC 相切,与边AB 交于点D ,若∠AD C =105°,BC =CD =3,则AD 的值为( )A .B .CD 【答案】A【分析】连接OC 、OD ,作OE AB ^于点E .易求出75CBD CDB Ð=Ð=°,30BCD Ð=°.再由切线的性质,即可求出60OCD Ð=°,即三角形OCD 为等边三角形.得出结论60ODC Ð=°,3OC OD CD ===.从而即可求出45ADO Ð=°,即三角形OED 为等腰直角三角形,由此即可求出DE 的长,最后根据垂径定理即可求出AD 的长.【详解】如图,连接OC 、OD ,作OE AB ^于点E .∵BC CD =,∴CBD CDB Ð=Ð,∵105ADC Ð=°,∴75CBD CDB Ð=Ð=°,∴18027530BCD Ð=°-´°=°.由题意可知OC BC ^,即90OCB Ð=°,∴903060OCD OCB BCD Ð=Ð-Ð=°-°=°,∵OD =OC ,∴三角形OCD 为等边三角形.∴60ODC Ð=°,3OC OD CD ===.∴1056045ADO ADC ODC Ð=Ð-Ð=°-°=°,∴三角形OED 为等腰直角三角形,∴3DE ===∴22AD DE ===故选:A .本题考查切线的性质,等腰三角形的性质,三角形外角的性质,等腰直角三角形与等边三角形的判定和性质以及垂径定理,综合性强.正确的连接辅助线是解答本题的关键.4.如图,直线AB,BC,CD分别与⊙O相切于E,F,G,且AB//CD,若OB=3cm,OC=4cm,则四边形EBCG的周长等于( )A.5cm B.10cm C.745cm D.625cm【答案】C【分析】连接OF,利用切线性质和切线长定理可证明BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,再根据平行线的性质证得∠BOC=90°,进而由勾股定理求得BC长,根据三角形的面积公式求得OF,进而可求得四边形的周长.【详解】解:连接OF,∵直线AB,BC,CD分别与⊙O相切于E,F,G,∴BE=BF,CG=CF,∠OBE=∠OBF,∠OCG=∠OCF,OF⊥BC,∵AB∥CD,∴∠ABC+∠DCB=180°,∴∠OBF+∠OCF=90°,即∠BOC=90°,∴在Rt△BOC中,OB=3cm,OC=4cm,由勾股定理得:BC==,由1122OB OC BC OF××=××得:OF=341255´=cm,∴OE=OG=OF= 125cm,∴四边形EBCG的周长为BE+BC+CG+EG=2OE+2BC=2×125+2×5=745cm,【点睛】本题考查切线的性质、切线长定理、平行线的性质、勾股定理、三角形的面积公式,熟练掌握切线长定理的运用,证得∠BOC =90°和利用等面积法求出OF 是解答的关键.5.(2021·山西吕梁市·九年级月考)如图,四边形ABCD 内接于⊙O ,AB =BC .AT 是⊙O 的切线,∠BAT =55°,则∠D 等于( )A .110°B .115°C .120°D .125°【答案】A【分析】连接AC ,OA ,OB ,先结合切线的性质以及圆的性质求得ACB BAT Ð=Ð,再结合等腰三角形的性质以及圆的内接四边形的性质求得2D ACB Ð=Ð即可.【详解】如图所示,连接AC ,OA ,OB ,则()11802AOB OBA OAB =°-ÐÐÐ=,∵2AOB ACB Ð=Ð,∴90ACB OAB =°-ÐÐ,∴90ACB OAB Ð=°-Ð,∵AT 是⊙O 的切线,∴90BAT OAB Ð=°-Ð,∴55ACB BAT Ð=Ð=°,∵AB BC =,∴1802ABC ACB Ð=°-Ð,根据圆的内接四边形可得:180D ABC Ð=°-Ð,∴2110D ACB Ð=Ð=°,故选:A .【点睛】本题考查圆的综合问题,理解圆的切线的性质以及内接四边形的性质是解题关键.6.(2021·浙江九年级专题练习)如图,⊙O 的弦AB =8,M 是弦AB 上的动点,若OM 的最小值是3,则⊙O 的半径是( )A .4B .5C .6D .7【答案】B【分析】过O 点作OH ⊥AB 于H ,连接OA ,如图,根据垂径定理得到AH =BH =4,利用垂线段最短得到OH =3,然后利用勾股定理计算出OA 即可.【详解】解:过O 点作OH ⊥AB 于H ,连接OA ,如图,∵OH ⊥AB ,∴AH =BH =12AB =12×8=4,∵OM 的最小值是3,∴OH =3,在Rt △OAH 中,OA =5,即⊙O 的半径是5.故选:B .【点睛】本题考查了垂径定理:直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了勾股定理.7.(2020·聊城市茌平区实验中学九年级月考)如图,P 为O 外一点,PA 、PB 分别切O 于点A 、B ,CD 切O 于点E 且分别交PA 、PB 于点C ,D ,若PA =4,则△PCD 的周长为( )A .5B .7C .8D .10【答案】C【分析】根据切线长定理求解即可【详解】解:∵PA 、PB 分别切O 于点A 、B ,CD 切O 于点E ,PA=4,∴PA=PB=4,AC=CE ,BD=DE ,∴△PCD 的周长为PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=4+4=8,故选:C .【点睛】本题考查切线长定理,熟练掌握切线长定理及其应用是解答的关键.8.(2021·北京九年级专题练习)如图,ABC D 的内切圆O e 与A B ,BC ,CA 分别相切于点D ,E ,F ,且2AD =,ABC D 的周长为14,则BC 的长为( )A .3B .4C .5D .6【答案】C 【分析】根据切线长定理得到AF =AD =2,BD =BE ,CE =CF ,由△ABC 的周长为14,可求BC 的长.【详解】解:O Qe 与A B ,BC ,CA 分别相切于点D ,E ,F2AF AD \==,BD BE =,CE CF =,ABC D Q 的周长为14,14AD AF BE BD CE CF \+++++=2()10BE CE \+=5BC \=故选:C .【点睛】本题考查了三角形的内切圆与内心,切线长定理,熟练掌握切线长定理是解题的关键.二、填空题9.如图,PA 、PB 、CD 是⊙O 的切线,A 、B 、E 是切点,CD 分别交PA 、PB 于C 、D 两点,若∠COD =70°,则∠AP B =_______.【答案】40°【分析】先利用切线长定理,得出∠BDO =∠CDO ,∠ACO =∠DCO ,再利用三角形内角和求出∠CDO +∠DCO 后得到∠BDC+∠A CD 的值,最后利用三角形外角的性质得到关于∠P 的方程,解方程即可得出答案.【详解】解:∵PA 、PB 、CD 是⊙O 的切线,∴∠BDO =∠CDO ,∠ACO =∠DCO ,∵∠COD =70°,∴∠CDO +∠DCO =180°-70°=110°,∴∠BDC +∠ACD =2(∠CDO +∠DCO )=2 ×110°=220°,∵∠BDC =∠DCP +∠P ,∠ACD =∠CDP +∠P ,∴∠DCP +∠P +∠CDP +∠P =220°,即180°+∠P =220°,∴∠P =40°,即∠APB =40°,故答案为:40°.【点睛】本题综合考查了圆的切线长定理、三角形的内角和定理、三角形外角的性质等,解决本题的关键是要牢记各定理与性质的内容,能灵活运用它们进行不同的角之间的转化,考查了学生推理分析的能力.10.(2021·浙江九年级其他模拟)如图,已知AD 是BAC Ð的平分线,以线段AB 为直径作圆,交BAC Ð和角平分线于C ,D 两点.过D 向AC 作垂线DE 垂足为点E .若24DE CE ==,则直径AB =_______.【答案】10【分析】连接CD 、OD 、OC 、BD ,运用勾股定理求得CD 的长,再证明DE 是圆O 的切线,运用全等三角形的判定与性质以及余角的性质得出∠CDE =∠BAD ,易得BD =CD ,然后再根据正切函数求得AD ,最后根据勾股定理解答即可.【详解】解:如图:连接CD 、OD 、OC 、BD∵AE ⊥DE , 24DE CE ==∴CD =∵OA =OD∴∠OAD =∠ODA∴∠BOD =∠OAD +∠ODA = 2∠OAD∵∠ODA =∠OAD∴∠EAD =∠ODA∴OD //AE∴OD ⊥DE ,即DE 是圆O 的切线∴∠CDE +∠ODC =90°∵AB是直径∴∠BAD+∠B=90°在△BOD和△DOC中OC=OB,DO=DO,BD=CD ∴△BOD≌△DOC∴∠ODC=∠OBD∴∠CDE=∠BAD∵∠BAD=∠DAC∴∠COD=∠BOD∴BD=CD=∵tan∠BAD=BDAD= tan∠CDE=12CEDE=,∴AD=∴AB10=.故填10.【点睛】本题主要考查了三角形的性质、圆的切线的判定与性质、勾股定理、三角函数等知识点,灵活应用相关知识成为解答本题的关键.11.(2020·湖北孝感市·九年级月考)如图,PA、PB是⊙O的切线,A、B为切点,点C、D在⊙O上.若∠P=108°,则∠B+∠D=_____.【答案】216°【分析】连接AB,根据切线得出PA=PB,求出∠PBA=∠PAB=36°,根据圆内接四边形的对角互补得出∠D+∠CBA=180°,再求出答案即可.【详解】解:连接AB,∵PA、PB是⊙O的切线,A、B为切点,∴PA=PB,∴∠PAB=∠PBA,∵∠APB=108°,∴∠PBA=∠PAB=12×(180°﹣∠APB)=36°,∵A、D、C、B四点共圆,∴∠D+∠CBA=180°,∴∠PBC+∠D=∠PBA+∠CBA+∠D=36°+180°=216°,故答案为:216°.【点睛】本题考查了切线长定理,圆周角定理,等腰三角形的性质,三角形内角和定理,圆内接四边形等知识点,能综合运用知识点进行推理和计算是解此题的关键.12.(2021·河北石家庄市·石家庄外国语学校九年级月考)已知△ABC中,⊙I为△ABC的内切圆,切点为H,若B C=6,AC=8,AB=10,则点A到圆上的最近距离等于_____.-【答案】2【分析】连接IA,IA与⊙I半径的差即为点A到圆上的最近距离,只需求出IA和⊙I半径即可得答案.【详解】解:连接IA,设AC、BC分别切⊙I于E、D,连接IE、ID,如图:∵BC=6,AC=8,AB=10,∴BC2+AC2=AB2∴∠C=90°∵⊙I为△ABC的内切圆,∴∠IEC=∠IDC=90°,IE=ID,∴四边形IDCE是正方形,设它的边长是x,则IE=EC=CD=ID=IH=x,∴AE=8﹣x,BD=6﹣x,由切线长定理可得:AH=8﹣x,BH=6﹣x,而AH+BH=10,∴8﹣x+6﹣x=10,解得x=2,∴AH=6,IH=2,∴IA,∴点A到圆上的最近距离为﹣2,故答案为:﹣2.【点睛】本题考查勾股定理、切线长定理、三角形的内切圆等知识,是重要考点,难度较易,掌握相关知识是解题关键.三、解答题13.(2021·浙江温州市·九年级一模)如图,点C ,D 在以AB 为直径的半圆O 上, AD BC=,切线DE 交AC 的延长线于点E ,连接OC .(1)求证:∠ACO =∠ECD .(2)若∠CDE =45°,DE =4,求直径AB 的长.【答案】(1)证明见详解;(2)【分析】(1)由 AD BC=,可得∠A =∠B ,内接四边形可得出∠ECD=∠B ,进而得出∠ACO =∠ECD ;(2))连接OD ,由切线的性质可得出∠ODE =90°,进而得出∠CDO =∠DCO=45°,再根据已知条件计算出∠E=∠ECD ,得到CD=DE =4,再利用勾股定理求出半径,进而得出答案;【详解】(1)证明:∵ AD BC=,∴∠A =∠B ;∵ABDC 是内接四边形∴∠ECD=∠B∴∠ECD=∠A∵AO =CO ;∴∠ACO =∠A∴∠ACO =∠ECD(2)连接OD∵DE 是圆的切线∴∠ODE =90°,∵∠CDE =45°,OC=OD∴∠CDO =∠DCO =45°,∴∠COD =90°,∵ AD BC=,∴ AC DC=,∴∠AOC =∠DOB=45°,∴AO =OC ,∴∠ACO =∠A=1804567.52°-°=° ;∵∠DCO =45°,∴∠ECD =180°-45°-67.5°=67.5°,∵∠E=180°-∠CDE -∠ECD =180°-45°-67.5°=67.5°,∴∠E=∠ECD∴CD=DE =4,∵∠COD =90°,∴222CD OC OD =+∴2216OC OD +=,即28OC =∴OC= 故⊙O 的半径为∴直径AB 的长,【点睛】本题属于圆综合题,考查了圆周角定理,内接四边形,切线性质定理,等腰三角形的判定与性质,勾股定理等知识,熟练掌握性质及定理是解决本题的关键.14.(2021·江苏无锡市·九年级期中)如图,AB 为⊙O 的直径,PD 切⊙O 于点C ,与BA 的延长线交于点D ,DE ⊥P O 交PO 延长线于点E ,连接PB ,∠EDB =∠EPB .(1)求证:PB 是⊙O 的切线.(2)若PB =3,tan ∠PDB =34,求⊙O 的半径.【答案】(1)见解析;(2)32【分析】(1)根据三角形的内角和定理可证E PBO Ð=Ð,然后根据垂直定义可得90E Ð=°,从而得出半径CB PB ^,根据切线的判定定理即可证出结论;(2)连接OC ,根据题意求出45BD PD ==,,再结合切线长定理得到3PC =,2CD =,从而设O e 的半径是r ,利用勾股定理求解即可.【详解】(1),EDB EPB DOE POB Ð=ÐÐ=ÐQ ,E PBO \Ð=Ð,DE PO ^Q ,90E \Ð=°,90PBO \Ð=°,\半径CB PB ^,PB \是O e 的切线.(2)如图,连接OC ,33tan 904PB PDB PBD =Ð=Ð=°Q ,,tan 45BD PB PDB PD \=Ð===g ,.PB Q 和PC 是O e 的切线,3PC PB \==,2CD PD PC \=-=,设O e 的半径是r ,则4OD DB OB r =-=-,PD Q 切O e 于点C ,OC PD \^,222CD OC OD \+=,()22224r r \+=-,32r \=.【点睛】本题考查圆的综合问题,理解切线的判定与性质定理以及正切函数的定义是解题关键.15.(2021·天津九年级学业考试)已知AB 为O e 的直径,点C ,D 为O e 上的两点,AD 的延长线于BC 的延长线交于点P ,连接CD ,30CAB Ð=°.(Ⅰ)如图①,若 2=CBCD ,4AB =,求AD 的长;(Ⅱ)如图②,过点C 作O e 的切线交AP 于点M ,若6CD AD ==,求CM 的长.【答案】(1)AD =;(2)CM = .【分析】(1)根据弧、圆周角之间的关系可求得∠BAD =45°,连接BD ,可得△ABD 为等腰直角三角形,求解即可;(2)根据弦、圆心角之间关系、等边对等角以及三角形外角的性质可求得∠PDM =60°,OC //AP ,再根据切线的性质定理易得△CDM 为直角三角形,解直角三角形即可.【详解】解:(1)∵ 2=CBCD ,30CAB Ð=°,∴1152CAD CAB Ð=Ð=°,∴∠BAD =45°,连接BD ,∵AB 为直径,∴∠BDA =90°,∴cos45AD AB =×°=(2)连接OD 、OC ,∵30CAB Ð=°,∴∠COB =60°,∠AOC =120°,∵6CD AD ==,∴∠AOD =∠COD =60°,∴∠ACD =∠CAD =30°,∠BAP =∠CAD +∠CAB =60°=∠COB ,∴OC //AP ,∠CDP =∠ACD +∠CAD =60°,∵CM 为O e 的切线,∴∠OCM =90°,∴∠AMC =180°-∠OCM =90°,在Rt △CDM 中,sin 60CM CD =×°=.【点睛】本题考查切线的性质定理,等腰三角形等边对等角,弧、圆心角、圆周角、弦之间的关系,解直角三角形.正确作出辅助线是解题关键.。
九年级数学切线长定理同步练习含答案
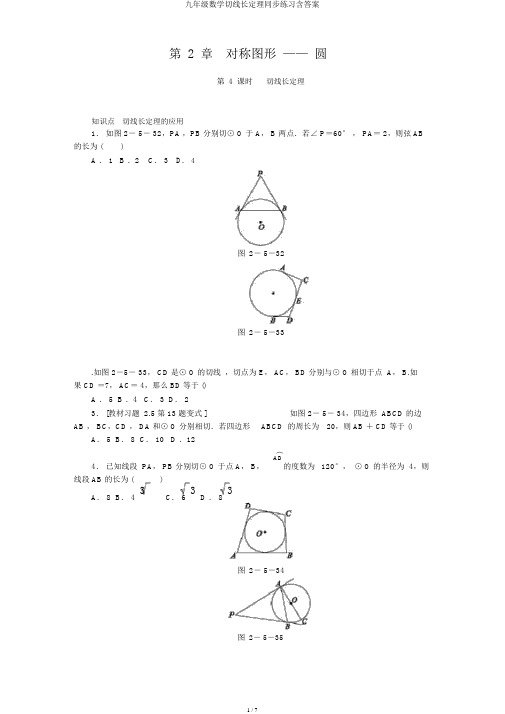
第 2 章 对称图形 —— 圆第 4 课时 切线长定理知识点 切线长定理的应用1. 如图 2- 5- 32,PA ,PB 分别切⊙ O 于 A , B 两点.若∠ P =60° , PA = 2,则弦 AB的长为 ()A . 1B .2C . 3D . 4图 2- 5-32图 2- 5-33.如图 2-5- 33, CD 是⊙ O 的切线 ,切点为 E , AC , BD 分别与⊙ O 相切于点 A , B.如果 CD =7, AC = 4,那么 BD 等于 ()A . 5B .4C . 3D . 23. [教材习题 2.5 第 13 题变式 ]如图 2- 5- 34,四边形 ABCD 的边AB , BC ,CD , DA 和⊙ O 分别相切.若四边形ABCD 的周长为 20,则 AB + CD 等于 ()A . 5B . 8C . 10D .12︵4. 已知线段 PA , PB 分别切⊙ O 于点 A , B ,AB120°, ⊙ O 的半径为 4,则的度数为 线段 AB 的长为 ()A . 8B . 43C . 6 3D . 83图 2- 5-34图 2- 5-35.如图 2-5- 35, PA, PB 是⊙ O 的切线,A , B 为切点, AC 是⊙ O 的直径,∠P= 40°,则∠ BAC 的度数为 ________.6.如图 2- 5- 36,PA , PB 分别切⊙ O 于点 A , B ,∠ AOP =50°,则∠PAB = ________°,∠ OPB= ________°.图2- 5-36图2- 5-377.如图 2- 5- 37,PA , PB, DE 分别切⊙ O 于点 A, B, C,若⊙ O 的半径为5, OP=13,则△ PDE 的周长为 ________.图2- 5-388.如图 2- 5- 38,P 是⊙ O 的直径 AB 的延长线上一点, PC, PD 分别切⊙ O 于点C,D. 若 PA = 6,⊙O 的半径为 2,则∠ CPD 的度数为 ________.9.如图 2- 5- 39,PA , PB 为⊙ O 的两条切线, A , B 为切点.若是⊙ O 的半径为5,∠OPA = 30°,求两条切线的夹角∠APB 的度数及切线PA 的长.图2- 5-39图 2- 5-40 10. [2016 ·梁溪区一模 ]AB = 4, AD = 5,AD , AB , BC 分别与⊙BC 于点 M ,切点为 N ,则 DM 的长为 (O 相切于点)如图2-5-40,在矩形ABCD 中,E,F, G,过点 D 作⊙ O 的切线交139 A. 34 13C. 39D. 2511.如图 2- 5- 41, PA, PB 是⊙ O 的切线, A , B 为切点, AC 是⊙ O 的直径,∠ ACB = 70°.求∠ P 的度数.图2- 5-4112.如图 2- 5- 42,△ ABC 的内切圆⊙ O 与 AC , AB , BC 分别相切于点D, E, F,且AB =5 cm, BC= 9 cm, AC = 6 cm,求 AE , BF 和 CD 的长.图2- 5-4213.如图 2- 5- 43, PA, PB 为⊙ O 的两条切线,切点分别为 A ,B ,直线 CD 切⊙ O 于点 E.(1)试试究△ PCD 的周长与线段 PA 的数量关系;(2)若∠ P=α,求∠ COD 的度数.图2- 5-4314.如图 2- 5- 44, AB 是⊙ O 的直径, AM , BN 分别切⊙ O 于点 A , B, CD 分别交AM , BN 于点 D ,C, DO 均分∠ ADC.(1)求证: CD 是⊙ O 的切线;(2)若 AD = 4, BC=9,求⊙ O 的半径 R.图2- 5-4415.如图 2- 5- 45, PA, PB 分别与⊙ O 相切于点 A , B,点 M 在 PB 上,且OM ∥ AP, MN ⊥ AP,垂足为 N.(1)求证: OM = AN ;(2)若⊙ O 的半径 R= 3, PB= 9,求 OM 的长.图2- 5- 45详解详析1. B2. C3. C4. B5. 20°[ 剖析 ]∵ PA,PB是⊙ O的切线,A,B为切点,1∴PA = PB,∴∠ BAP =∠ ABP =2×(180° - 40° )= 70° .由 PA 是⊙ O 的切线, A 为切点,AC 是⊙ O 的直径,得∠ PAC = 90°,∴∠ BAC =90° - 70°=20°. 6. 50 407. 24 [ 剖析 ]∵ PA,PB,DE分别切⊙ O于A,B,C三点,∴AD = CD , CE= BE , PA= PB,OA ⊥ PA.在Rt△ OAP 中,依照勾股定理,得 AP = 12,∴△ PDE 的周长为PD+ DE+ PE= PD+ AD + BE + PE= 2PA = 24.8. 60°[ 剖析 ] 连接 OC.∵ PA= 6,⊙O 的半径为2,∴OP= PA - OA =4.∵PC, PD 分别切⊙ O 于点 C,D ,∴∠ OPC=∠ OPD, OC⊥ PC.∵OP= 2OC,∴∠ OPC= 30°,∴∠ CPD=60° .9.解:连接 OA , OB,则 OA ⊥PA, OB ⊥ PB.∵OA = OB ,OP= OP,∴Rt△ OAP≌ Rt△ OBP ,∴∠ OPA=∠ OPB,∴∠ APB =2∠ OPA= 60° .在Rt△ AOP 中,可求得 OP= 2OA = 10,∴PA= OP2- OA 2=5 3.10. A [剖析 ] 如图,连接 OE, OF,ON , OG.在矩形 ABCD 中,∠ A =∠ B = 90°, CD = AB = 4.∵ AD , AB ,BC 分别与⊙ O 相切于点 E, F,G,∴∠ AEO =∠ AFO =∠ OFB=∠ BGO = 90°.又∵ OE= OF= OG,∴四边形AFOE ,四边形 FBGO 是正方形,∴AF = BF= AE = BG =2,∴DE = 3.∵ DM 是⊙ O 的切线,∴DN = DE =3, MN = MG ,∴CM =5- 2- MG = 3- MN.在Rt△ DMC 中, DM 2= CD2+ CM 2,∴ (3+ MN) 2= 42+ (3- MN) 2,4 4 13∴MN =3,∴ DM = 3+3=3.应选 A.11.解:连接 AB.∵AC 是⊙ O 的直径,∴∠ CBA = 90°,∴∠ BAC = 90° -∠ ACB = 20° .∵PA , PB 是⊙ O 的切线,∴PA = PB,∠ CAP= 90°,∴∠ PAB =90° - 20°= 70°.∵PA = PB,∴∠ PBA =∠ PAB = 70°,∴∠ P=180° -∠ PAB -∠ PBA = 40°.12.解:∵⊙ O 与△ ABC 的三边都相切,∴AE = AD ,BE = BF ,CD = CF.设AE = x cm, BF= y cm, CD=z cm,x+ y= 5,x=1,{y+z=9,) {y=4,)则 z+ x= 6,解得z= 5.即AE = 1 cm, BF= 4 cm, CD=5 cm.13.解: (1) △ PCD 的周长= 2PA. 原由以下:∵ PA , PB 分别切⊙ O 于点 A , B ,CD 切⊙ O 于点 E,∴PA = PB, AC = CE, BD = DE,∴△ PCD 的周长= PD+DE + PC+ CE= PB+ PA= 2PA ,即△ PCD 的周长= 2PA.(2)如图,连接 OA, OE, OB.由切线的性质,得OA⊥ PA,OB⊥PB,OE⊥ CD,BD=DE,AC=CE.∵OA = OE=OB ,易证△ AOC ≌△ EOC ,△EOD ≌△ BOD ,∴∠ AOC =∠ EOC,∠ EOD=∠ BOD ,11∴∠ COD =∠ EOC+∠ EOD= 2(∠ AOE +∠ BOE) = 2∠ AOB.∵∠ P=α,OA ⊥ PA, OB⊥PB ,∴∠ AOB = 180°-α,1∴∠ COD = 90°-2α.14 解: (1)证明:如图,过点 O 作 OE⊥ CD 于点 E.∵ AM 切⊙ O 于点 A,∴OA ⊥ AD.又∵ DO 均分∠ ADC ,∴OE= OA.∵ OA 为⊙ O 的半径,∴OE 是⊙ O 的半径,∴CD 是⊙ O 的切线.(2) 过点 D 作 DF⊥ BC 于点 F.∵ AM ,BN 分别切⊙ O 于点 A, B,∴AB ⊥ AD ,AB ⊥ BC,∴四边形 ABFD 是矩形,∴AD = BF , AB = DF.又∵ AD =4, BC = 9,∴ FC= 9- 4=5.∵AM ,BN , DC 分别切⊙ O 于点 A , B, E,∴ AD = DE ,BC= CE,∴CD = DE + CE=AD + BC = 4+9=13. 在 Rt△ DFC 中, CD2= DF2+ FC2,∴DF = CD2- FC2= 12,∴AB = 12,∴⊙ O 的半径 R 为 6.15.解: (1) 证明:如图,连接 OA ,则 OA ⊥PA.∵MN ⊥PA ,∴ MN ∥OA.∵OM ∥PA ,∴四边形ANMO 是平行四边形.又∵ MN ⊥ AP,∴?ANMO 是矩形,∴OM =AN.(2)如图,连接 OB,则 OB⊥ PB,∴∠ OBM =∠ MNP = 90° .∵四边形ANMO 是矩形,∴OA = MN.又∵ OA =OB ,∴OB = MN.∵OM ∥AP ,∴∠ OMB =∠ MPN ,∴△ OBM ≌△ MNP ,∴ OM = MP.设OM =x,则 MP= x, AN = x.∵PA = PB= 9,∴NP =9- x.在Rt△ MNP 中,有 x2= 32+ (9- x)2,解得 x= 5,即 OM = 5.。
2023学年九年级数学上册重要考点题(人教版)切线的判定与性质及切线长定理(10大题型(解析版)

切线的判定与性质及切线长定理(答案版)切线的判定定理经过半径的外端并且垂直于这条半径的直线是圆的切线.注意:切线的判定方法:(1)定义:直线和圆有唯一公共点时这条直线就是圆的切线;(2)定理:和圆心的距离等于半径的直线是圆的切线;(3)判定定理:经过半径外端并且垂直于这条半径的直线是圆的切线.(切线的判定定理中强调两点:一是直线与圆有一个交点二是直线与过交点的半径垂直缺一不可).题型1:切线的判定-连半径证垂直1.如图AB为⊙O的直径AC平分∠BAD交⊙O于点C CD⊥AD垂足为点D.求证:CD是⊙O 的切线.【答案】证明:连接OC∵AC平分∠DAB∴∠DAC=∠BAC∵OC=OA∴∠BAC=∠ACO∴∠DAC=∠ACO∴OC∠AD∵CD∠AD∴OC∠DC∵OC过圆心O∴CD是∠O的切线.【解析】【分析】连接OC 根据角平分线的定义和等腰三角形的性质得出∠DAC=∠BAC 根据平行线的判定得出OC∠AD 根据平行线的性质得出OC∠DC 再根据切线的判定得出结论。
【变式1-1】如图在∠O中AB为直径BP为∠O的弦AC与BP的延长线交于点C 且AB=AC PE⊥AC于点E 求证:PE是∠O的切线.【答案】解:连接AP OP∵AB为∠O直径∴∠APB=90°即AP⊥BC又∵AB=AC∴点P是BC的中点又∵O是AB的中点∴OP是△ABC的中位线∴OP∠AC∴∠OPE=∠PEC又∵PE⊥AC∴∠PEC=90°∴∠OPE=90°∴OP⊥PE.∴PE是∠O的切线.【解析】【分析】连接AP OP 由AB为直径可知AP⊥BC结合AB=AC可得点P为BC的中点而O是AB的中点可得OP是△ABC的中位线可知OP∠AC 进而∠OPE=∠PEC 然后结合PE⊥AC可得OP⊥PE即可得到结论。
【变式1-2】如图D为∠O上一点点C在直径BA的延长线上且∠CDA=∠CBD.求证:CD是∠O 的切线.【答案】证明:连接OD∵AB为直径∴∠ADO+∠BDO=90°又∵∠CDA=∠CBD∴∠CDA=∠BDO∴∠ADC+∠ADO=90°∴OD⊥CD∴CD是∠O的切线.【解析】【分析】连接OD 由圆周角定理可得∠ADO+∠BDO=90° 由已知条件以及等腰三角形的性质可得∠CDA=∠BDO 进而得到∠ADC+∠ADO=90° 据此证明.题型2:切线的判定-作垂直证半径2.ΔABC为等腰三角形O为底边BC的中点腰AB与⊙O相切于点D.求证:AC是⊙O的切线.【答案】证明:过点O作OE∠AC于点E 连结OD OA∵AB与O相切于点D∴AB∠OD∵∠ABC为等腰三角形O是底边BC的中点∴AO是∠BAC的平分线∴OE=OD 即OE是O的半径∵AC经过O的半径OE的外端点且垂直于OE∴AC是O的切线。
人教版九年级数学上册24.2.2 第3课时 切线长定理同步测试题及答案

第3课时切线长定理一、选择题1.下列说法中,不正确的是 ( )A.三角形的内心是三角形三条内角平分线的交点B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C.垂直于半径的直线是圆的切线D.三角形的内心到三角形的三边的距离相等2.给出下列说法:①任意一个三角形一定有一个外接圆,并且只有一个外接圆;②任意一个圆一定有一个内接三角形,并且只有一个内接三角形;③任意一个三角形一定有一个内切圆,并且只有一个内切圆;④任意一个圆一定有一个外切三角形,并且只有一个外切三角形.其中正确的有 ( )A.1个 B.2个 C.3个 D.4个3.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( ) A.21 B.20 C.19 D.184.如图,PA、PB分别切⊙O于点A、B,AC是⊙O的直径,连结AB、BC、OP,则与∠PAB相等的角(不包括∠PAB本身)有 ( )A.1个 B.2个 C.3个 D.4个4题图5题图6题图5.如图,已知△ABC的内切圆⊙O与各边相切于点D、E、F,则点O是△DEF的 ( ) A.三条中线的交点 B.三条高的交点C.三条角平分线的交点 D.三条边的垂直平分线的交点6.一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于 ( )A.21 B.20 C.19 D.18二、填空题6.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.P BAO6题图 7题图 8题图7.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.8.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.三、解答题9.如图,AE、AD、BC分别切⊙O于点E、D、F,若AD=20,求△ABC 的周长.10.如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60o,求弦AB的长.11.如图,PA、PB是⊙O的切线,A、B为切点,∠OAB=30°.(1)求∠APB的度数;(2)当OA=3时,求AP的长.12.已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.13.已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.14. 如图,在△ABC 中,已知∠ABC=90o,在AB 上取一点E ,以BE 为直径的⊙O 恰与AC 相切于点D ,若AE=2 cm ,AD=4 cm . (1)求⊙O 的直径BE 的长; (2)计算△ABC 的面积.15.已知:如图,⊙O 是Rt △ABC 的内切圆,∠C=90°. (1)若AC=12cm ,BC=9cm ,求⊙O 的半径r ; (2)若AC=b ,BC=a ,AB=c ,求⊙O 的半径r .四、体验中考16.(2011年安徽)△ABC 中,AB =AC ,∠A 为锐角,CD 为AB 边上的高,I 为△ACD 的内切圆圆心,则∠AIB 的度数是( )A .120°B .125°C .135°D .150°17.(2011年绵阳)一个钢管放在V 形架内,右图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN = 60︒,则OP =( ) A .50 cm B .253cm C .3350cm D .503cm 18. (2011年甘肃定西)如图,在△ABC 中,5cm AB AC ==,cos B 35=.如果⊙O 的半径为10cm ,且经过点B 、C ,那么线段AO = cm .17题图 18题图 19题图19. (2011年湖南怀化)如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且ο60=∠AEB ,则=∠P __ ___度.参考答案◆随堂检测 1. C2. B (提示:②④错误)3. 760 (提示:连接ID,IF ∵∠DEF=520 ∴∠DIF=1040 ∵D 、F 是切点 ∴DI ⊥AB,IF ⊥AC∴∠ADI=∠AFI=900 ∴∠A=1800-1040=760) 4. 52 (提示:AB+CD=AD+BC)5. 1150 (提示:∵∠A=500 ∴∠ABC+∠ACB=1300 ∵OB,OC 分别平分∠ABC,∠ACB ∴∠OBC+∠OCB=650∴∠BOC=1800-650=1150) ◆课下作业 ●拓展提高1. D (提示:AD=AF,BD=BE,CE=CF ∴周长=821218⨯+⨯=)2. C3. D4. 解:∵AD,AE 切于⊙O 于D,E ∴AD=AE=20 ∵AD,BF 切于⊙O 于D,F ∴BD=BF 同理:CF=CE∴C △ABC =AB+BC+AC=AB+BF+FC+AC=AB+BD+EC+AC=AD+AE=405. 解:连接BC ∵PA,PB 切⊙O 于A,B ∴PA=PB ∵∠P=600 ∴△ABC 是正三角形 ∵∠PAB=600∵PA 是⊙O 切线 ∴CA ⊥AP ∴∠CAP=900 ∴∠CAB=300 ∵直径AC ∴∠ABC=900∴cos300=ABAC∴AB=6. 解:(1)∵在△ABO 中,OA =OB ,∠OAB =30°∴∠AOB =180°-2×30°=120°∵PA 、PB 是⊙O 的切线∴OA ⊥PA ,OB ⊥PB .即∠OAP =∠OBP =90° ∴在四边形OAPB 中,∠APB =360°-120°-90°-90°=60°.(2)如图①,连结OP∵PA 、PB 是⊙O 的切线 ∴PO 平分∠APB ,即∠APO =12∠APB =30° 又∵在Rt △OAP 中,OA =3, ∠APO =30°∴AP =tan 30OA°=7. 解:(1)连接OD ∴OD ⊥AC ∴△ODA 是Rt △设半径为r ∴AO=r+2 ∴(r+2)2—r 2=16 解之得:r=3 ∴BE=6(2) ∵∠ABC=900 ∴OB ⊥BC ∴BC 是⊙O 的切线 ∵CD 切⊙O 于D ∴CB=CD 令CB=x∴AC=x+4,BC=4,AB=x ,AB=8 ∵2228(4)x x +=+ ∴6x = ∴S △ABC =186242⨯⨯= ●体验中考 1. C2. A (提示:∠MPN=600可得∠OPM=300 可得OP=2OM=50)3.(提示:连接OB ,易得:∠ABC=∠AOB ∴cos ∠AOB=cos ∠35=OBOA =)4. ∠P=600。
九年级数学 切线长定理 专题练习(含解析)

∴梯形对边和为:8+8=16, 则这个等腰梯形的上底与下底长的和为 16. 故选:D. 分析:直接利用圆外切四边形对边和相等,进而求出即可. 6.如图,⊙O 是△ABC 的内切圆,点 D、E 分别为边 AB、AC 上的点,且 DE 为⊙O 的切 线,若△ABC 的周长为 25,BC 的长是 9,则△ADE 的周长是( ) A.7 B.8 C.9 D.16
答案:C
解析:解答: ∵AB、AC 是⊙O 的两条切线,B、C 是切点, ∴∠B=∠C=90°,∠BOC=180°-∠A=110°. 故选 C. 分析:利用切线的性质可得,∠B=∠C=90°,再用四边形的内角和为 360 度可解. 10.如图,PA、PB 是⊙O 的两条切线,切点是 A、B.如果 OP=4,PA= 2 3 ,那么∠AOB 等于( ) A.90° B.100° C.110° D.120°
答案:B 解析:解答:∵PA、PB 都是⊙O 的切线, ∴PA=PB, 又∵∠P=60°, ∴△PAB 是等边三角形,即 AB=PA=8, 故选 B. 分析: 根据切线长定理知 PA=PB,而∠P=60°,所以△PAB 是等边三角形,由此求得弦 AB 的长. 8.如图,PA、PB 分别是⊙O 的切线,A、B 为切点,AC 是⊙O 的直径,已知∠BAC=35°, ∠P 的度数为( ) A.35° B.45° C.60° D.70°
答案:D 解析:解答: 根据切线的性质定理得∠PAC=90°, ∴∠PAB=90°-∠BAC=90°-35°=55°. 根据切线长定理得 PA=PB, 所以∠PBA=∠PAB=55°, 所以∠P=70°. 故选 D. 分析: 根据切线长定理得等腰△PAB,运用内角和定理求解. 9.如 图 , AB、 AC 是 ⊙O 的 两 条 切 线 , B、 C 是 切 点 , 若 ∠A=70°, 则 ∠BOC 的 度 数 为 ( ) A.130° B.120° C.110° D.100°
2021年人教版数学九年级上册《切线长定理》同步专项练习卷(含答案)

2021年人教版数学九年级上册《切线长定理》同步专项练习卷一、选择题1.如图,⊙O是△ABC的内切圆,则点O是△ABC的( )A.三条边的垂直平分线的交点B.三条角平分线的交点C.三条中线的交点D.三条高的交点2.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )A.4B.8C.4 3D.8 33.如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )A.15°B.30°C.60°D.75°4.把直尺和圆形螺母按如图所示放置在桌面上,∠CAB=60°,若量出AD=6 cm,则圆形螺母的外直径是( )A.12 cmB.24 cmC.6 3 cmD.12 3 cm5.如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于()A.50°B.60°C.70°D.70°6.如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为( )A.60° B.75° C.70° D.65°7.如图,已知⊙O上三点A,B,C,半径OC=1,∠ABC=30°,切线PA交OC延长线于点P,则PA 的长为( )A.2 B. C. D.8.如图,⊙O是△ABC的内切圆,切点分别是D、E、F,已知∠A=100°,∠C=30°,则∠DFE的度数是()A.55°B.60°C.65°D.70°9.如图,等边三角形ABC边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O半径为()A.2B.3C.4D.4﹣10.如图,△ABC是一张三角形纸片,⊙O是它的内切圆,点D、E是其中的两个切点,已知CD=6cm,小明准备用剪刀沿着与⊙O相切的一条直线MN剪下一块三角形(△CMN),则剪下的△CMN的周长是()A.9cmB.12cmC.15cmD.18cm11.如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F.给出下列说法:(1)AC与BD的交点是圆O的圆心;(2)AF与DE的交点是圆O的圆心;(3)BC与圆O相切,其中正确说法的个数是()A.0B.1C.2D.312.如图,等边△ABC的边长为2,⊙A的半径为1,D是BC上的动点,DE与⊙A相切于点E,DE 的最小值是()A.1B.C.D.2二、填空题13.把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为.14.已知三角形的三边分别是5、12、13,则其内切圆的直径与外接圆的直径之比是.15.如图,PA、PB是⊙0的切线,A、B为切点,AC是⊙O的直径,∠P=40°,则∠BAC= .16.如图,PA,PB切⊙O于点A,B,点C是⊙O上的一点,且∠ACB=65°,则∠P= .17.如图,PA,PB分别切⊙O于A,B,并与⊙O的切线,分别相交于C,D,已知△PCD的周长等于8cm,则PA= cm;已知⊙O的直径是6cm,PO= cm.18.如图,已知点O是△ABC的内切圆的圆心,若∠BOC=124°,则∠A= ______ .三、解答题19.如图所示,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.求:(1)PA的长;(2)∠COD的度数.20.如图所示,正方形ABCD的边长为4 cm,以正方形的一边BC为直径在正方形ABCD内作半圆,再过点A作半圆的切线,与半圆切于点F,与CD交于点E,求△ADE的面积.21.如图,已知直线PA交⊙O于A,B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.(1)求证:CD为⊙O的切线;(2)若DC+DA=6,⊙O的直径为10,求AB的长.22.如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连结BD.(1)求证:∠A=∠BDC;(2)若CM平分∠ACD,且分别交AD、BD于点M、N,当DM=1时,求MN的长.23.如图,在△ABC中,∠C=90°,∠ABC的平分线BE交AC于点E,过点E作直线BE的垂线交AB于点F,⊙O是△BEF的外接圆.(1)求证:AC是⊙O的切线;(2)过点E作EH⊥AB于点H,求证:EF平分∠AEH;(3)求证:CD=HF.参考答案1.答案为:B2.答案为:B.3.答案为:D.4.答案为:D.5.答案为:B6.答案为:D .7.答案为:B.8.答案为:C9.答案为:D.10.答案为:B11.答案为:C.12.答案为:B13.答案为:5.14.答案为:4:13.15.答案是:20°.16.答案为:50°.17.答案为:4,5.18.答案为:68°.19.解:(1)∵CA ,CE 都是⊙O 的切线,∴CA=CE.同理DE=DB ,PA=PB ,∴△PCD 的周长=PD +CD +PC=PD +BD +PC +CA=PB +PA=2PA=12,∴PA=6, 即PA 的长为6.(2)∵∠P=60°,∴∠PCE +∠PDE=120°,∴∠ACD +∠CDB=360°-120°=240°.∵CA ,CE ,DB ,DE 是⊙O 的切线,∴∠OCE=∠OCA=12∠ACD. ∠ODE=∠ODB=12∠CDB , ∴∠OCE +∠ODE=12(∠ACD +∠CDB)=120°,∴∠COD=180°-120°=60°.20.解:设DE=x cm ,则CE=(4-x)cm.∵CD ,AE ,AB 均为⊙O 的切线,∴EF=CE=(4-x)cm ,AF=AB=4 cm ,∴AE=AF +EF=(8-x)cm.在Rt △ADE 中,AE 2=AD 2+DE 2,即(8-x)2=42+x 2,解得x=3.∴S △ADE =12AD ·DE=12×4×3=6(cm 2). 21.解:(1)连接OC ,证∠DAC=∠CAO=∠ACO ,∴PA ∥CO ,又∵CD ⊥PA ,∴CO ⊥CD ,∴CD 为⊙O 的切线(2)过O 作OF ⊥AB ,垂足为F ,∴四边形OCDF 为矩形.∵DC +DA=6,设AD=x ,则OF=CD=6-x ,AF=5-x ,在Rt △AOF 中,有AF 2+OF 2=OA 2,即(5-x)2+(6-x)2=25, 解得x 1=2,x 2=9,由AD <DF 知0<x <5,故x=2,从而AD=2,AF=5-2=3,由垂径定理得AB=2AF=6.22.解:(1)如图,连接OD ,∵AB 为⊙O 的直径, ∴∠ADB=90°,即∠A+∠ABD=90°,又∵CD 与⊙O 相切于点D ,∴∠CDB+∠ODB=90°,∵OD=OB ,∴∠ABD=∠ODB ,∴∠A=∠BDC ;(2)∵CM 平分∠ACD ,∴∠DCM=∠ACM ,又∵∠A=∠BDC,∴∠A+∠ACM=∠BDC+∠DCM,即∠DMN=∠DNM,∵∠ADB=90°,DM=1,∴DN=DM=1,∴MN=.23.(1)证明:(1)如图,连接OE.∵BE⊥EF,∴∠BEF=90°,∴BF是圆O的直径,∴OB=OE,∴∠OBE=∠OEB,∵BE平分∠ABC,∴∠CBE=∠OBE,∴∠OEB=∠CBE,∴OE∥BC,∴∠AEO=∠C=90°,∴AC是⊙O的切线;(2)证明:∵∠C=∠BHE=90°,∠EBC=∠EBA,∴BEC=∠BEH,∵BF是⊙O是直径,∴∠BEF=90°,∴∠FEH+∠BEH=90°,∠AEF+∠BEC=90°,∴∠FEH=∠FEA,∴FE平分∠AEH.(3)证明:如图,连结DE.∵BE是∠ABC的平分线,EC⊥BC于C,EH⊥AB于H,∴EC=EH.∵∠CDE+∠BDE=180°,∠HFE+∠BDE=180°,∴∠CDE=∠HFE,∵∠C=∠EHF=90°,∴△CDE≌△HFE(AAS),∴CD=HF,。
部编数学九年级上册专题24.7切线长定理及三角形的内切圆【七大题型】(人教版)(解析版)含答案

专题24.7 切线长定理及三角形的内切圆【七大题型】【人教版】【题型1 利用切线长定理求周长】 (1)【题型2 三角形内切圆中求角度】 (5)【题型3 三角形内切圆中求面积】 (9)【题型4 三角形内切圆中求线段长度】 (13)【题型5 三角形内切圆中求半径】 (17)【题型6 三角形内切圆中求最值】 (20)【题型7 外接圆和内切圆的综合运用】 (25)【题型1 利用切线长定理求周长】【例1】(2022秋•宜兴市校级期中)如图,△ABC 是一张三角形的纸片,⊙O 是它的内切圆,点D 是其中的一个切点,已知AD =10cm ,小明准备用剪刀沿着与⊙O 相切的任意一条直线MN 剪下一块三角形(△AMN ),则剪下的△AMN 的周长为 20cm .【分析】利用切线长定理得出DM =MF ,FN =EN ,AD =AE ,进而得出答案.A B C I【解答】解:∵△ABC是一张三角形的纸片,⊙O是它的内切圆,点D是其中的一个切点,AD=10cm,∴设E、F分别是⊙O的切点,故DM=MF,FN=EN,AD=AE,∴AM+AN+MN=AD+AE=10+10=20(cm).故答案是:20cm.【变式1-1】(2022秋•莒南县期末)如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,分别交PA、PB于点C、D.若PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,求△PCD的周长.【分析】由PA、PB切⊙O于A、B两点,CD切⊙O于点E,根据切线长定理,可得PA=PB,又由PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,根据根与系数的关系,可求得PA与PB的长,又由CD切⊙O于点E,即可得△PCD的周长等于PA+PB.【解答】解:∵PA、PB的长是关于x的一元二次方程x2﹣mx+m﹣1=0的两个根,∴PA+PB=m,PA•PB=m﹣1,∵PA、PB切⊙O于A、B两点,∴PA=PB=m2,即m2•m2=m﹣1,即m2﹣4m+4=0,解得:m=2,∴PA=PB=1,∵PA、PB切⊙O于A、B两点,CD切⊙O于点E,∴AD=ED,BC=EC,∴△PCD的周长为:PD+CD+PC=PD+DE+EC+PC=PD+AD+BC+PC=PA+PB=2.【变式1-2】(2022•雨花区校级三模)如图,△ABC中,∠C=90°,BC=5,⊙O与△ABC的三边相切于点D、E、F,若⊙O的半径为2,则△ABC的周长为( )A.14B.20C.24D.30【分析】设AD=x,由切线长定理得AE=x,根据题意可得四边形OECF为正方形,则CE=CF=2,BD=BF=3,在直角三角形ABC中,利用勾股定理求出x,然后求其周长.【解答】解:连接OE、OF,设AD=x,由切线长定理得AE=x,∵⊙O与Rt△ABC的三边分别点D、E、F,∴OE⊥AC,OF⊥BC,∴四边形OECF为正方形,∵⊙O的半径为2,BC=5,∴CE=CF=2,BD=BF=3,∴在Rt△ABC中,∵AC2+BC2=AB2,即(x+2)2+52=(x+3)2,解得x=10,∴△ABC的周长为12+5+13=30.故选:D.【变式1-3】(2022秋•崇川区月考)如图,P是⊙O外一点,PA、PB分别和⊙O相切于点A、B,C是劣弧AB上任意一点,过C作⊙O切线DE,交PA、PB于点D、E,已知PA的长为5cm,∠DOE=65°,点M、N分别在PA、PB的延长线上,MN与⊙O相切于点F,已知DN、EM的长是方程x2﹣10x+k=0的两根.(1)求∠P的度数;(2)求△PDE的周长;(3)求四边形DEMN的周长.【分析】(1)只要证明∠AOB=130°,∠PAO=∠PBO=90°,再利用四边形内角和定理即可解决问题;(2)利用切线长定理即可解决问题;(3)因为DN、EM的长是方程x2﹣10x+k=0的两根.可得DN+EM=10,再利用切线长定理即可解决问题;【解答】解:(1)连接OA、OB、OC.∴PA、PB、DE是⊙O的切线,∴PA⊥OA,OB⊥PB,∠DOA=∠DOC,∠EOB=∠EOC,∵∠DOE=65°,∴∠AOB=130°,∠PAO=∠PBO=90°,∴∠P=360°﹣90°﹣90°﹣130°=50°.(2)∵PA、PB、DE是⊙O的切线,∴DA=DC,EC=EB,PA=PB=5,∴△PDE的周长=PD+DE+PE=PD+DA+PE+EB=PA+PB=10.(3)∵DN、EM的长是方程x2﹣10x+k=0的两根.∴DN+EM=10,∴PN,PM,MN是⊙O的切线,∴AN=NF,MF=MB,DA=DC,EC=EB,∴四边形EMND的周长=EM+MN+DN+DE=EM+BM+NA+DA+EB+DN=2(DN+EM)=20.【题型2 三角形内切圆中求角度】【例2】(2022•温州模拟)如图,在Rt△ABC中,∠A=90°,⊙O是它的内切圆,与AB,BC,CA分别切于点D,E,F,若∠ACB=40°,则∠DOE= 130° .【分析】利用直角三角形性质求出∠ABC=50°,再利用切线性质求出∠BDO=∠BEO=90°,再利用四边形内角和为360°,即可求得答案.【解答】解:在Rt△ABC中,∵∠A=90°,∠ACB=40°,∴∠ABC=90°﹣∠ACB=90°﹣40°=50°,∵⊙O是Rt△ABC的内切圆,与AB,BC,CA分别切于点D,E,F,∴AB、BC是⊙O的切线,∴∠BDO=∠BEO=90°,∴∠DOE=360°﹣∠BDO﹣∠BEO﹣∠ABC=130°,故答案为:130°.【变式2-1】(2022秋•昌平区期末)如图,⊙O是△ABC的内切圆,切点分别为D,E,F,已知∠A=40°,连接OB,OC,DE,EF,则∠BOC= 110 °,∠DEF= 70 °.【分析】连接OD和OF,根据内切圆的性质可得OB,OC平分∠ABC,∠ACB,再根据三角形内角和定理即可求出角BOC的度数;根据切线的性质可得∠DOF的度数,进而根据圆周角定理可得∠DEF的度数.【解答】解:如图,连接OD和OF,∵⊙O是△ABC的内切圆,切点分别为D,E,F,∠A=40°,∴OB,OC平分∠ABC,∠ACB,∴∠BOC=180°﹣∠OBC﹣∠OCB(∠ABC+∠ACB)=180°−12×140°=180°−12=110°,∵OD⊥AB,OF⊥AC,∴∠ADO=∠AFO=90°,∴∠DOF=360°﹣90°﹣90°﹣40°=140°,∠DOF=70°.∴∠DEF=12故答案为:110,70.【变式2-2】(2022•万年县校级模拟)如图,△ABC中,内切圆I与AB,BC,CA分别切于F,D,E,连接BI,CI,再连接FD,ED,(1)若∠A=40°,求∠BIC与∠FDE的度数.(2)若∠BIC=α;∠FDE=β,试猜想α,β的关系,并证明你的结论.(∠ABC+∠ACB),求出∠ABC+∠ACB 【分析】(1)根据圆I是△ABC的内切圆求出∠IBC+∠ICB=12的度数,求出∠IBC+∠ICB即可;连接IF、IE,求出∠FIE,即可求出∠FDE;(2)由(1)得出∠BIC=180°﹣(∠IBC+∠ICB),∠FDE=180°﹣2∠A,根据三角形的内角和定理求出∠BIC =90°+12∠A ,代入即可求出答案.【解答】解:(1)∵圆I 是△ABC 的内切圆,∴∠IBC =12∠ABC ,∠ICB =12∠ACB ,∴∠IBC +∠ICB =12(∠ABC +∠ACB ),∵∠ABC +∠ACB =180°﹣∠A =140°,∴∠IBC +∠ICB =70°,∴∠BIC =180°﹣(∠IBC +∠ICB )=110°,如图,连接IF 、IE ,∵圆I 是△ABC 的内切圆,∴∠IFA =∠IEA =90°,∵∠A =40°,∴∠FIE =360°﹣∠IFA ﹣∠IEA ﹣∠A =140°,∴∠EDF =12∠EIF =70°,答:∠BIC =110°,∠FDE =70°;(2)解:α=180°﹣β,证明:由圆周角定理得:∠FIE =2∠FDE ,由(1)知:2∠FDE =180°﹣∠A ,即∠A =180°﹣2∠FDE ,∴∠A =180°﹣∠EIF ,由(1)知:2∠FDE =180°﹣∠A ,∴∠A =180°﹣2∠FDE =180°﹣2β,∠BIC =180°﹣(∠IBC +∠ICB )=180°−12(∠ABC +∠ACB )=180°−1(180°﹣∠A)2∠A,=90°+12(180°﹣2β),∴∠BIC=α=90°+12即α=180°﹣β.【变式2-3】(2022秋•邗江区期中)如图,在△ABC中,AB=AC,AD⊥BC于点D,点M是△ABC内一点,连接BM交AD于点N,已知∠AMB=108°,若点M是△CAN的内心,则∠BAC的度数为( )A.36°B.48°C.60°D.72°【分析】过点M作ME⊥AD于点E,根据已知条件可得△ABC是等腰三角形,AD是BC边的中垂线,证明ME∥BC,可得∠NME=∠NBD,由点M是△CAN的内心,可得点M在∠NAC和∠ANC的角平分线上,设∠NAM=x,∠NBD=y,所以∠BAC=4x,∠NBD=∠NCD=∠NME=y,∠ENM=∠CNM=2y,然后利用∠AMB=108°,列出方程组y−x=18°2y+x=72°,求解即可得结论.【解答】解:如图,过点M作ME⊥AD于点E,∵AB=AC,AD⊥BC,∴△ABC是等腰三角形,AD是BC边的中垂线,∴NB=NC,∠BAD=∠CAD,∴∠NBD=∠NCD,∵ME⊥AD,AD⊥BC,∴ME∥BC,∴∠NME=∠NBD,∵点M是△CAN的内心,∴点M在∠NAC和∠ANC的角平分线上,∴∠NAM=∠CAM,∠ANM=∠CNM,设∠NAM=x,∠NBD=y,∴∠BAC=4x,∠NBD=∠NCD=∠NME=y,∴∠ENM=∠CNM=∠NBC+∠NCB=2y,∵∠AMB=108°,∴∠AME=∠AMB﹣∠EMN=108°﹣y,在△AEM中,∠EAM+∠AME=90°,∴x+108°﹣y=90°,∴y﹣x=18°,在△ANM中,∠NAM+∠ANM=180°﹣108°,∴x+2y=72°,y−x=18°2y+x=72°,解得x=12°y=30°,∴∠BAC=4x=48°.故选:B.【题型3 三角形内切圆中求面积】【例3】(2022秋•黄冈期中)如图,边长为1的正方形ABCD的边AB是⊙O的直径,CF是⊙O的切线,E 为切点,F点在AD上,BE是⊙O的弦,求△CDF的面积.【分析】设AF=x,由切线长定理可得EF=AF=x,则FD=1﹣x,CF=CE+EF=CB+EF=1+x,利用勾股定理建立方程求出x的值,再根据三角形的面积公式即可求出问题的答案.【解答】解:设AF=x,∵四边形ABCD是正方形,∴∠DAB=90°,∴DA⊥AB,∴AD是圆的切线,∵CF是⊙O的切线,E为切点,∴EF=AF=x,∴FD=1﹣x,∵CB⊥AB,∴CB为⊙O的切线,∴CB=CE,∴CF=CE+EF=CB+EF=1+x.∴在Rt△CDF中由勾股定理得到:CF2=CD2+DF2,即(1+x)2=1+(1﹣x)2,解得x=14,∴DF=1﹣x=34,∴S△CDF =12×1×34=38.【变式3-1】(2022•武汉模拟)如图,AB是⊙O的直径,C是⊙O上一点,E是△ABC的内心,OE⊥EB.若AE=ABE的面积为( )A .B .2CD .1【分析】延长BE 交⊙O 于点F ,连接AF ,OF ,根据AB 是⊙O 的直径,可得∠AFB =∠C =90°,证明△FEA 是等腰直角三角形,可得AF =EF =2,根据垂径定理可得EF =BE =2,进而可得△ABE 的面积.【解答】解:如图,延长BE 交⊙O 于点F ,连接AF ,OF ,∵AB 是⊙O 的直径,∴∠AFB =∠C =90°,∴∠CAB +∠CBA =90°,∵E 是△ABC 的内心,∴∠EAB =12∠CAB ,∠EBA =12∠CBA ,∴∠EAB +∠EBA =12(∠CAB +∠CBA )=45°,∴∠FEA =45°,∴△FEA 是等腰直角三角形,∴AE ==,∵AE =∴AF =EF =2,∵OE ⊥EB ,∴EF =BE =2,∴△ABE 的面积为:12BE •AF =12×2×2=2.故选:B .【变式3-2】(2022春•海曙区校级期中)如图,花边带上正三角形的内切圆半径为1cm .如果这条花边带有100个圆和100个正三角形,则这条花边的面积为( )A .150πB .C .D .200【分析】画出图形,连接AD ,OB ,则AD 过O ,求出∠OBD =30°,求出OB ,根据勾股定理求出BD ,同法求出CD ,求出BC 的长后求得一个三角形的面积即可求得花边的面积.【解答】解:从中选择一个等边三角形和其内接圆如图,⊙O 是△ABC 的内切圆,⊙O 切AB 于F ,切AC 于E ,切BC 于D ,连接AD ,OB ,则AD 过O (因为等边三角形的内切圆的圆心再角平分线上,也在底边的垂直平分线上),∵△ABC 是等边三角形,∴∠ABC =60°,∵⊙O 是△ABC 的内切圆,∴∠OBC =12∠ABC =30°,∵⊙O 切BC 于D ,∴∠ODB =90°,∵OD =1,∴OB =2,由勾股定理得:BD ==∴BC =∴S △ABC =12BC •AD =12××3=∴这条花边的面积=100S △ABC =故选:C .【变式3-3】(2022•齐齐哈尔一模)如图,正方形ABCD 边长为4cm ,以正方形的一边BC 为直径在正方形ABCD 内作半圆,过A 作半圆的切线,与半圆相切于F 点,与DC 相交于E 点,则△ADE 的面积( )cm2A.12B.24C.8D.6【分析】由于AE与圆O切于点F,根据切线长定理有AF=AB=4cm,EF=EC;设EF=EC=xcm.则DE=(4﹣x)cm,AE=(4+x)cm,然后在三角形BCE中由勾股定理可以列出关于x的方程,解方程即可求出,然后就可以求出△ADE的面积.【解答】解:∵AE与圆O切于点F,显然根据切线长定理有AF=AB=4cm,EF=EC,设EF=EC=xcm,则DE=(4﹣x)cm,AE=(4+x)cm,在三角形ADE中由勾股定理得:(4﹣x)2+42=(4+x)2,∴x=1cm,∴CE=1cm,∴DE=4﹣1=3cm,=AD•DE÷2=3×4÷2=6cm2.∴S△ADE故选:D.【题型4 三角形内切圆中求线段长度】【例4】(2022秋•乌兰察布期末)如图,⊙O分别切△ABC的三条边AB、BC、CA于点D、E、F、若AB =5,AC=6,BC=7,求AD、BE、CF的长.【分析】由切线长定理,可知:AF =AD ,CF =CE ,BE =BD ,用未知数设AD 的长,然后表示出BD 、CF 的长,即可表示出BE 、CE 的长,根据BE +CE =7,可求出AD 的长进而求出BE 、CF 的长.【解答】解:假设AD =x ,∵⊙O 分别切△ABC 的三条边AB 、BC 、CA 于点D 、E 、F ;∴根据切线长定理得出AD =AF ,BD =BE ,EC =FC ,∴AF =x ,∵AB =5,AC =6,BC =7,∴BE =BD =AB ﹣AD =5﹣x ,FC =EC =AC ﹣AF =6﹣x ,∴BC =BE +EC =5﹣x +6﹣x =7,解得:x =2,∴AD =2,BE =BD =5﹣2=3,CF =AC ﹣AF =6﹣2=4.【变式4-1】(2022秋•崇川区月考)如图,已知△ABC 的内切圆O 与三边分别切于D 、E 、F ,∠A =60°,CB =6cm ,△ABC 的周长为16cm ,则DF 的长等于( )A .2cmB .3cmC .4cmD .6cm【分析】利用三角形内切圆的性质以及切线长定理得出BD =BE ,CE =CF ,AD =AF ,进而得出△ADF 是等边三角形,即可得出答案.【解答】解:∵△ABC 的内切圆O 与三边分别切于D 、E 、F ,CB =6cm ,△ABC 的周长为16cm ,∴BD =BE ,CE =CF ,AD =AF ,∵BE +EC =BD +FC =6,∴AD =AF =12(AB +AC +BC ﹣BC ﹣BD ﹣CF )=12(16﹣6﹣6)=2,∵∠A =60°,∴△ADF 是等边三角形,∴DF =2.故选:A .【变式4-2】(2022秋•龙凤区期末)如图,在Rt △ABC 中,∠C =90°,AC =3,BC =4,⊙O 是△ABC的内切圆,点D是斜边AB的中点,则OD的长度是 .【分析】如图连接OE、OF、OQ,设⊙O的半径是r,由勾股定理求出AB=5,根据△ABC的内切圆,得到OE⊥AC,OF⊥BC,OE=OF,推出四边形CFOE是正方形,得到CE=CF=OF=OE,根据3﹣r+4﹣r=5求出r、AQ、OQ的长求出AD、DQ的长【解答】解:如图连接OE、OF、OQ,设⊙O的半径是r,由勾股定理得:AB=5,∵⊙O是三角形ABC的内切圆,∴OE⊥AC,OF⊥BC,OE=OF,AE=AQ,BF=BQ,∵∠C=90°,∴∠C=∠CFO=∠CEO=90°,∴四边形CFOE是正方形,∴CE=CF=OF=OE,∴3﹣r+4﹣r=5,r=1,AQ=AE=3﹣1=2,OQ=1,∵D是AB的中点,,∴AD=52,∴DQ=AD﹣AQ=12∴OD2=OQ2+DQ2,∴OD=【变式4-3】(2022•永定区模拟)如图,已知在矩形ABCD中,AB=12,BC=16,⊙O1和⊙O2分别是△ABC和△ADC的内切圆,点E、F为切点,则EF的长是 4 cm.【分析】根据矩形的性质得到AC=20,△ABC≌△CDA,则⊙O1和⊙O2的半径相等.如图,过O1作AB、BC的垂线分别交AB、BC于N、P,过O2作BC,CD、AD的垂线分别交BC,CD、AD于Q,G、H,由∠B=90°,推出四边形O1NBP是正方形,设圆的半径为r,根据切线长定理12﹣r+16﹣r=20,解得r=4,过O1作O1M⊥FO2于M,则O1M=PQ=8,QM=BN=4,同法可得DG=4,根据EF=AC﹣AE﹣CF计算即可.【解答】解:∵矩形ABCD中,AB=12,BC=16,∴AC=20,△ABC≌△CDA,则⊙O1和⊙O2的半径相等.如图,过O1作AB、BC的垂线分别交AB、BC于N、P,过O2作BC,CD、AD的垂线分别交BC,CD、AD于Q,G、H,∵∠B=90°,∴四边形O1NBP是正方形,设圆的半径为r,根据切线长定理12﹣r+16﹣r=20,解得r=4,∴BP=BN=4,同法可得DG=4,∴AN=AE=CG=CF=8,∴EF=AC﹣AE﹣CF=20﹣16=4故答案为:4.【题型5 三角形内切圆中求半径】【例5】(2022•定安县二模)如图,在矩形ABCD中,AD<AB,AD=9,AB=12,则△ACD内切圆的半径是( )A.1B.2C.3D.4【分析】根据矩形性质和勾股定理可得AC=15,设△ACD内切圆的圆心为O,△ACD内切圆的半径为r,连接OE,OF,OG,得四边形DFOG是正方形,然后根据切线长定理即可解决问题.【解答】解:在矩形ABCD中,∠B=90°,AD=BC=9,AB=12,根据勾股定理,得AC==15,设△ACD内切圆的圆心为O,△ACD内切圆的半径为r,如图,连接OE,OF,OG,得四边形DFOG是正方形,∴DF=DG=r,∴AG=AE=AD﹣DG=9﹣r,CF=CE=CD﹣DF=AB﹣DF=12﹣r,∵AE+CE=AC,∴9﹣r+12﹣r=15,解得r=3.∴△ACD内切圆的半径是3.故选:C.【变式5-1】(2022秋•张店区期末)如图,在Rt△ABC中,∠C=90°,BC=3,AB=5,⊙O是Rt△ABC 的内切圆,则⊙O的半径为( )A .1BC .2D .【分析】根据三角形内切圆与内心的性质和三角形面积公式解答即可.【解答】解:∵∠C =90°,BC =3,AB =5,∴AC ==4,如图,分别连接OA 、OB 、OC 、OD 、OE 、OF ,∵⊙O 是△ABC 内切圆,D 、E 、F 为切点,∴OD ⊥BC ,OE ⊥AC ,OF ⊥AB 于D 、E 、F ,OD =OE =OF ,∴S △ABC =S △BOC +S △AOC +S △AOB =12BC •DO +12AC •OE +12AB •FO =12(BC +AC +AB )•OD ,∵∠C =90°,∴12×AC •BC =12(BC +AC +AB )•OD ,∴OD =3×4345=1.故选:A .【变式5-2】(2022秋•虎丘区校级期中)若四边形ABCD 有内切圆(与四边形四边均相切),四边形面积为S ,各边长分别为a ,b ,c ,d ,则该圆的直径为( )A .a b c d SB .S a cC .c−d S(a b)D .2S a b c d【分析】连接OA 、OB 、OC 、OD .由S 四边形ABCD =S △OAB +S △OBC +S △OCD +S △AOD ,由S 四边形ABCD =12AB •r +12BC •r +12CD •r +12AD •r =12(a +b +c +d )•r =S ,即可推出r =2S a b c d .【解答】解:如图,连接OA 、OB 、OC 、OD .∵S 四边形ABCD =S △OAB +S △OBC +S △OCD +S △AOD又∵S △OAB =12AB •r ,S △OBC =12BC •r ,S △OCD =12CD •r ,S △AOD =12AD •r ,∴S 四边形ABCD =12AB •r +12BC •r +12CD •r +12AD •r =12(a +b +c +d )•r =S ,∴r =2S a b c d .故选:D .【变式5-3】(2022秋•南丹县期末)如图,△ABC 的内切圆⊙O 分别与AB ,AC ,BC 相切于点D ,E ,F .若∠C =90°,AC =6,BC =8,则⊙O 的半径等于 2 .【分析】连结OD ,OE ,OF ,设⊙O 半径为r ,根据勾股定理可得AB =10,证明四边形OECF 是正方形,可得CF =CE =OF =r ,然后根据切线长定理可得AE =AE =AC ﹣CE =6﹣r ,BF =BD =BC ﹣CF =8﹣r ,进而可以解决问题.【解答】解:如图,连结OD ,OE ,OF ,设⊙O 半径为r ,∵∠C =90°,AC =6,BC =8,∴AB ==10,∵△ABC 的内切圆⊙O 与AB ,BC ,AC 分别相切于点D ,F ,E ,∴AC ⊥OE ,AB ⊥OD ,BC ⊥OE ,且OF =OD =OE =r ,∴四边形OECF 是正方形,∴CF =CE =OF =r ,∴AE =AE =AC ﹣CE =6﹣r ,BF =BD =BC ﹣CF =8﹣r ,∵AD +BD =AB =10,∴6﹣r +8﹣r =10,∴r =2.∴⊙O 的半径等于2.故答案为:2.【题型6 三角形内切圆中求最值】【例6】(2022春•长兴县月考)如图,矩形ABCD ,AD =6,AB =8,点P 为BC 边上的中点,点Q 是△ACD 的内切圆圆O 上的一个动点,点M 是CQ 的中点,则PM +1 .【分析】由矩形性质和勾股定理可得AC =10,设△ADC 内切圆半径为r ,由面积法可得r =2,连接BQ ,易证PM 为△BCQ 的中位线,得出PM =12BQ ,当BQ 经过圆心O 时,BQ 最长,则此时PM 最大,作OE ⊥AD 与点E ,OF ⊥AB 与点F ,则BF =AB ﹣AF =8﹣2=6,OF =AE =AD ﹣DE =6﹣2=4,由勾股定理可得BO =BQ =BO +OQ =2,从而可得PM 的结果.【解答】解:∵四边形ABCD 为矩形,∴∠D =90°,CD =AB =8,∴AC ==10,设△ADC 的内切圆半径为r ,则有12r(AC +AD +DC)=12×6×8,即12r(10+6+8)=24,解得:r =2.连接BQ ,∵P为BC中点,M为CQ中点,∴PM为△BQC的中位线,BQ,∴PM=12当BQ经过圆心O时,BQ最长,则此时PM最大,作OE⊥AD与点E,OF⊥AB与点F,则BF=AB﹣AF=8﹣2=6,OF=AE=AD﹣DE=6﹣2=4,∴BO=∴BQ=BO+OQ=+2,BQ=1.∴PM=12+1.【变式6-1】(2022秋•扬州月考)如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是 4πcm2. .r 【分析】当该圆为三角形内切圆时面积最大,设内切圆半径为r,则该三角形面积可表示为:12•BC•AD,利用勾股定理可得AD,易得三角形(AB+AC+BC)=21r,利用三角形的面积公式可表示为12ABC的面积,可得r,求得圆的面积.【解答】解:如图1所示,S △ABC =12•r •(AB +BC +AC )=12r ×42=21r ,过点A 作AD ⊥BC 交BC 的延长线于点D ,如图2,设CD =x ,由勾股定理得:在Rt △ABD 中,AD 2=AB 2﹣BD 2=400﹣(7+x )2,在Rt △ACD 中,AD 2=AC 2﹣x 2=225﹣x 2,∴400﹣(7+x )2=225﹣x 2,解得:x =9,∴AD =12,∴S △ABC =12BC ×AD =12×7×12=42,∴21r =42,∴r =2,该圆的最大面积为:S =πr 2=π•22=4π(cm 2),故答案为:4πcm 2.【变式6-2】(2022•温州自主招生)设等边△ABC 的内切圆半径为2,圆心为I .若点P 满足PI =1,则△ABC 与△APC 的面积之比的最大值为 6 .【分析】P 满足PI =1,则P 在以I 为圆心,以1位半径的圆上,当P 是⊙O 和BE 的交点时,△ACP 的面积最小,即△ABC 与△APC 的面积之比最大.此时PE =2﹣1=1,则△ABC 与△APC 的面积的比值是BE 与PE 的比值,据此即可求解.【解答】解:点P 满足PI =1,则P 在以I 为圆心,以1位半径的圆上.作BE ⊥AC ,则BE 一定过点I ,连接AI .∵在直角△AIE 中,∠IAE =12∠BAC =12×60°=30°,IE =2,∴AI =2IE =4,∴BE =IE +BI =IE +AI =2+4=6.当P是⊙I和BE的交点时,△ACP的面积最小,即△ABC与△APC的面积之比最大.此时PE=2﹣1=1,则△ABC与△APC的面积的比值是BEPE =61=6.故答案是:6.【变式6-3】(2022秋•滨湖区期末)已知点C是⊙O上一动点,弦AB=6,∠ACB=120゜.(1)如图1,若CD平分∠ACB,求证:AC+BC=CD;(2)如图2,△ABC内切圆半径为r.①用含r的代数式表示AC+BC;②求r的最大值.【分析】(1)在CD上截取CE=BC,由∠ACD=∠BCD=60°得到△BCE为等边三角形,根据圆周角定理得∠ABD=∠ACD=60°,则BE=BC=CE,∠1+∠ABE=60°,∠ABE+∠2=60°,所以∠1=∠2,于是可根据“AAS”判断△ACB≌△DEB,得到AC=DE,由此得到CD=CE+DE=BC+AC;(2)①作弦CD平分∠ACB,设△ABC的内心为P点,作PQ⊥AB于Q,PH⊥BC于H,PF⊥AC于F,根据内心的性质得PF=PQ=PH=r,由∠ACD=∠BCD=60°得到∠CPF=∠CPH=30°,根据含30度的直角三角形三边的关系得到CF,CH==,然后根据切线长定理得到AF=AQ=AC﹣CF=AC,BH=BQ=BC﹣CH=BC,而AB=AQ+BQ,所以AC+BC=6,整理得AC+BC=6+;②由于AC+BC=CD得到CD=6,所以当CD为直径时,r最大;当CD为直径,根据垂径定理的推论得CD⊥AB,AM=BM=12AB=3,AC=BC,可计算出CD=AC=2CD=+=6+,可解得r=6﹣【解答】(1)证明:在CD上截取CE=BC,如图1,∵CD平分∠ACB,∠ACB=120゜,∴∠ACD=∠BCD=60°,∴△BCE为等边三角形,∠ABD=∠ACD=60°,∴BE=BC=CE,∠1+∠ABE=60°,∠ABE+∠2=60°,∴∠1=∠2,在△ACB和△DEB中∠A=∠D∠1=∠2,BC=BE∴△ACB≌△DEB,∴AC=DE,∴CD=CE+DE=BC+AC;(2)解:①作弦CD平分∠ACB,设△ABC的内心为P点,作PQ⊥AB于Q,PH⊥BC于H,PF⊥AC 于F,如图,则PF=PQ=PH=r,∵CD平分∠ACB,∠ACB=120゜,∴∠ACD=∠BCD=60°,∴∠CPF=∠CPH=30°,∴CF=,CH==,∴AF=AQ=AC﹣CF=AC,BH=BQ=BC﹣CH=BC,而AB=AQ+BQ,∴AC+BC=6,∴AC+BC=6+;②∵AC+BC=CD,∴CD=6+,∴当CD为直径时,r最大,如图3,当CD为直径,∴CD⊥AB,垂足为M,AB=3,AC=BC,∴AM=BM=12∵∠ACD=60°,∴∠CAM=30°,∴CD∴AC=2CD=∴+6,∴r=6﹣即r的最大值为6﹣【题型7 外接圆和内切圆的综合运用】【例7】(2022秋•滨湖区期末)设两直角边分别为3、4的直角三角形的外接圆和内切圆的半径长分别为R 和r,则R﹣r= 1.5 .【分析】利用三角形的外心与内心的性质即可进行计算.【解答】解:因为直角三角形的外接圆半径等于斜边长的一半,所以R==2.5;如图,若Rt △ABC 的边AC =3,BC =4,根据勾股定理,得AB =5,其内切圆⊙O 分别切AB 、BC 、AC 于D 、E 、F .设OE =OF =OD =r ,∴S △ABC =S △AOB +S △BOC +S △AOC ,即12AC •BC =12AB •OD +12BC •OE +12AC •OF ,12×3×4=12×5×r +12×4×r +12×3×r ,6=12r (5+4+3),6=6r ,∴r =1,则R ﹣r =2.5﹣1=1.5.故答案为:1.5.【变式7-1】(2022•鞍山模拟)如图,⊙O 内切于Rt △ABC ,切点分别为D 、E 、F ,∠C =90°.已知∠AOC =120°,则∠OAC = 15 °,∠B = 60 °.已知AC =4cm ,BC =3cm ,则△ABC 的外接圆的半径为 52 cm ,内切圆的半径为 1 cm .【分析】由三角形内心的性质得到OC 平分∠ACB ,求得∠ACO =12∠ACB =45°,根据三角形的内角和得到结论;根据勾股定理得到AB ==5,于是得到结论.【解答】解:∵⊙O 内切于Rt △ABC ,∠C =90°,∴OC 平分∠ACB ,∴∠ACO =12∠ACB =45°,∵∠AOC =120°,∴∠OAC =180°﹣45°﹣120°=15°,∵AO 平分∠BAC ,∴∠BAC =2∠OAC =30°,∴∠B =90°﹣30°=60°;∵AC =4cm ,BC =3cm ,∠C =90°,∴AB ==5,∴△ABC 的外接圆的半径为52;设内切圆的半径为r ,∴r =34−52=1,故答案为:15,60,52,1.【变式7-2】(2022•游仙区模拟)如图,在△ABC 中,∠BAC =60°,其周长为20,⊙I 是△ABC 的内切BIC 的外接圆直径为 .【分析】设△BIC 的外接圆圆心为O ,连接OB ,OC ,作CD ⊥AB 于点D ,在圆O 上取点F ,连接FB ,FC ,作OE ⊥BC 于点E ,设AB =c ,BC =a ,AC =b ,根据三角形内心定义可得S △ABC =12lr =12×20×=12AB •CD ,可得bc =40,根据勾股定理可得BC =a =7,再根据I 是△ABC 内心,可得IB 平分∠ABC ,IC 平分∠ACB ,根据圆内接四边形性质和圆周角定理可得∠BOC =120°,再根据垂径定理和勾股定理即可求出OB 的长.【解答】解:如图,设△BIC 的外接圆圆心为O ,连接OB ,OC ,作CD ⊥AB 于点D ,在圆O 上取点F ,连接FB ,FC ,作OE ⊥BC 于点E ,设AB =c ,BC =a ,AC =b ,∵∠BAC =60°,∴AD =12b ,CD ,∴BD =AB ﹣AD =c −12b ,∵△ABC 周长为l =20,△ABC 的内切圆半径为r∴S △ABC =12lr =12×20×12AB •CD ,∴=•c ,∴bc =40,在Rt △BDC 中,根据勾股定理,得BC 2=BD 2+CD 2,即a 2=(c −12b )2+)2,整理得:a 2=c 2+b 2﹣bc ,∵a +b +c =20,∴a 2=c 2+b 2﹣bc =(b +c )2﹣3bc =(20﹣a )2﹣3×40,解得a =7,∴BC =a =7,∵I 是△ABC 内心,∴IB 平分∠ABC ,IC 平分∠ACB ,∵∠BAC=60°,∴∠ABC+∠ACB=120°,∴∠IBC+∠ICB=60°,∴∠BIC=120°,∴∠BFC=180°﹣120°=60°,∴∠BOC=120°,∵OE⊥BC,,∠BOE=60°,∴BE=CE=72÷∴OB=72【变式7-3】(2022秋•鄞州区校级月考)如图,在Rt△ABC中,AC=8,BC=6,∠C=90°.⊙I分别切AC,BC,AB于点D,E,F,求Rt△ABC的内心I与外心O之间的距离.【分析】连接ID、IE、IF,如图,由AC=8,BC=6,∠C=90°,根据圆周角定理的推论和勾股定理AB=5,连接OI,设⊙I的得到AB为△ABC的外接圆的直径,AB=10,则外心O为AB的中点,BO=12半径为r,根据切线的性质和切线长定理得ID⊥AC,IE⊥BC,IF⊥AB,AD=AF,BE=BF,易得四边形IDCE为正方形,则DC=CE=r,所以AD=AC﹣DC=8﹣r,BE=BC﹣CE=6﹣r,即AF=8﹣r,BF=6﹣r,利用AF+BF=AB得8﹣r+6﹣r=10,解得r=2,所以BF=4,则OF=OB﹣BF=1,在Rt△IOF中,根据勾股定理得IO【解答】解:连接ID、IE、IF,如图,∵AC=8,BC=6,∠C=90°,∴AB为△ABC的外接圆的直径,AB=10,∴外心O为AB的中点,AB=5,∴BO=12连接OI,如图,设⊙I的半径为r,∵⊙I分别切AC,BC,AB于点D,E,F,∴ID⊥AC,IE⊥BC,IF⊥AB,AD=AF,BE=BF,而∠C=90°,∴四边形IDCE为正方形,∴DC=CE=r,∴AD=AC﹣DC=8﹣r,BE=BC﹣CE=6﹣r,∴AF=8﹣r,BF=6﹣r,而AF+BF=AB,∴8﹣r+6﹣r=10,解得r=2,∴BF=6﹣r=4,∴OF=OB﹣BF=5﹣4=1,在Rt△IOF中,IF=2,OF=1,∴IO=即Rt△ABC的内心I与外心O。
人教版九年级数学上册切线长定理习题.docx

初中数学试卷 马鸣风萧萧切线长定理习题 姓名1.如图,PA,PB,分别切⊙O 于点A,B,∠P=70°,∠C 等于 。
2.如图,在△ABC 中,AB=5cm BC=7cm AC=8cm, ⊙O 与BC 、AC 、 AB 分别相切于 D 、 E 、F ,则 AF=_____, BD=_______ 、CF=________3.如图,已知PA 、PB 切⊙O 于A 、B ,∠APB=60º,PA=4,则⊙O 的半径为 。
4.如图,PA 、PB 分别切圆O 于A 、B 两点,C 为劣弧AB 上一点,∠APB=30°,则∠ACB=( ).A .60°B .75°C .105°D .120°5.如图,PA 、PB 分别切圆O 于A 、B ,并与圆O 的切线,分别相交于C、D ,•已知PA=7cm,则△PCD 的周长等于_________.6.已知:如图,从两个同心圆O 的大圆上一点A ,作大圆的弦AB 切小圆于C 点,大圆的弦AD 切小圆于E 点.求证:(1)AB=AD ; (2)DE=BC .第1题 第2题 B A C PO 第4题 B A C D P O 第5题 第6题第3题第10题第9题 B A C E DO F8.如图,PA ,PB 为⊙O 的切线,A 、B 是切点,OP 与⊙O 交于C ,∠APB=60°,求证:OC=PC9.如图所示,EB 、EC 是⊙O 的两条切线,B 、C 是切点,A 、D 是⊙O 上两点,如果∠E=46°,∠DCF=32°,求∠A 的度数.10.已知:如图,在三角形ABC 中,内切圆O 与△ABC 的三边分别切于D ,E ,F 三点,∠DFE=56°,求∠A 得度数。
11.已知:如图,P 为⊙O 外一点,PA ,PB 为⊙O 的切线, A 和B 是切点,BC 是直径. 求证:AC ∥OP .12.如图,在△ABC 中,AB=5cm ,BC=7cm ,AC=8cm ,⊙O 与BC 、AC 、 AB 分别相切于 D 、 E 、F ,求 AF 、 BD 、CE 的长.P B C A O 第8题 第11题 第12题。
人教版九年级数学上册 24.2.2.3 _切线长定理 培优训练卷(含答案)

第二十四章圆24.2.2.3 切线长定理培优训练卷一、选择题(共10小题,3*10=30)1.如图,PA切⊙O于点A,PB切⊙O于点B,OP交⊙O于点C,下列结论中,错误的是( ) A.∠1=∠2 B.PA=PBC.AB⊥OP D.点C是OP的中点2.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )A.4 B.8C.4 3 D.8 33.如图,PA,PB分别与⊙O相切于A,B两点,若∠C=65°,则∠P的度数为( )A.50°B.65°C.100°D.130°4如图,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是( )A.15°B.30°C.60°D.75°5. 如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为( )A.(-2,3) B.(-3,2)C.(3,-2) D.(2,-3)6.如图,点O是△ABC的内切圆的圆心,若∠BAC=80°,则∠BOC=( )A.130°B.120°C.100°D.90°7.如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )A.56°B.62°C.68°D.78°8.如图,以正方形ABCD的边BC为直径作半圆O,过点D作直线切半圆于点F,交AB边于点E,则△ADE和四边形EBCD周长之比为( )A.3∶4 B.4∶5C.5∶6 D.6∶79.如图,四边形ABCD的各边分别与⊙O相切于点E,F,G,H,且AB=16,CD=10,则此四边形ABCD的周长为( )A.50 B.52C.54 D.5610.如图,O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则( ) A.EF>AE+BF B.EF<AE+BFC.EF=AE+BF D.EF≤AE+BF二.填空题(共8小题,3*8=24)11. 如图所示,AB是⊙O的直径,点C为⊙O外一点,CA,CD是⊙O的切线,A,D为切点,连接BD,AD.若∠ACD=30°,则∠DBA的大小是__________.12. 如图,在扇形CAB中,CD⊥AB,垂足为D,⊙E是△ACD的内切圆,连接AE,BE,则∠AEB 的度数为___________.13. 在Rt△ABC中,∠C=90°,CA=8,CB=6,则△ABC内切圆的周长为____________.14. 如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD 的度数是______.15.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,则△ABC的内切圆半径r=_______.16.如图,AB,AC,CE都是⊙O的切线,B,D,E为切点,P为劣弧上一点,若∠A+∠C=110°,则∠BPE=___________.如图,AB是⊙O的直径,直线DA与⊙O相切于点A,DO交⊙O于点C,连接BC,若∠ABC=21°,则∠ADC的度数为___________.18.如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线交BC于点M,切点为N,则DM的长为_______.三.解答题(共7小题,46分)19.(6分) 为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5 cm,求铁环的半径.20. (6分) 如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC =28 cm,CA=26 cm,求AF,BD,CE的长.21. (6分) 如图,AC⊥BC于点C,BC=4,AC=3,⊙O与直线AB,BC,CA均相切,求⊙O的半径.22. (6分) 如图,P是⊙O的直径AB的延长线上一点,PC、PD切⊙O于点C、D.若PA=6,⊙O的半径为2,求∠CPD.23.(6分) 如图,PA,PB是⊙O的切线,CD切⊙O于点E,△PCD的周长为12,∠APB=60°.(1)求PA的长;(2)求∠COD的度数.24.(8分) 如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D、E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN与AB,BC分别交于点M,N,若⊙O的半径为4cm,则Rt△MBN的周长是多少?25.(8分) 如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6 cm,CO=8 cm.(1)求证:BO⊥CO;(2)求BE和CG的长.参考答案1-5 DBADA 6-10 ACDBC11. 75°12. 135°13. 4π14. 70°15. 216. 55°17.48°18. 13 319. 解:设圆心为O,连接OA,OP.∵三角板有一个锐角为30°,∴∠PAO=60°.又∵PA与⊙O相切,∴∠OPA=90°,∴∠POA=30°,∵PA=5 cm,∴OA=10 cm,可求OP=5 3 cm,即铁环的半径为5 3 cm20. 解:根据切线长定理,得AE=AF,BF=BD,CE=CD.设AF=AE=x cm,则CE=CD=(26-x)cm,BF=BD=(18-x)cm.∵BC=28 cm,∴(18-x)+(26-x)=28,解得x=8,∴AF=8 cm,BD=10 cm,CE=18 cm21. 解:由切线长定理得BE=BF,CD=CF,AD=AE,连接OD,OF,则四边形DCFO为正方形,设OF=CD=x,则由BF=BE得BC+x=BA+AE=AB+3-x,∴4+x=5+3-x,∴x=2,∴⊙O的半径为222. 解:∵PA=6,⊙O的半径为2,∴PB=PA-AB=6-4=2,∴OP=4,∵PC、PD切⊙O于点C、D.∴∠OPC=∠OPD ,∴CO ⊥PC ,∴sin ∠OPC=2: 4 =0.5 ,∴∠OPC=30°,∴∠CPD=60°,23. 解:(1)由切线长定理可得CA =CE ,同理DE =DB ,PA =PB ,∴三角形PCD 的周长=PD +CD +PC =PD +PC +CA +BD =PA +PB =12,则PA 的长为6(2)连接OA ,OE ,OB ,∵∠P =60°,∴∠AOB =180°-∠P =120°,由切线长定理可得∠AOC =∠EOC =12∠AOE , ∠DOB =∠EOD =12∠EOB , ∴∠COD =∠EOC +∠EOD =12∠AOB =60° 24. 解:连接OD 、OE ,∵⊙O 是Rt △ABC 的内切圆,∴OD ⊥AB ,OE ⊥BC ,∵∠ABC=90°,∴∠ODB=∠DBE=∠OEB=90°,∴四边形ODBE 是矩形,∵OD=OE ,∴矩形ODBE 是正方形,∴BD=BE=OD=OE=4cm ,∵⊙O 切AB 于D ,切BC 于E ,切MN 于P ,NP 与NE 是从一点出发的圆的两条切线, ∴MP=DM ,NP=NE ,∴Rt △MBN 的周长为:MB+NB+MN=MB+BN+NE+DM=BD+BE=4cm+4cm=8cm ,25. 解:(1)连接OE ,OF ,∵BE 切⊙O 于点E ,BC 切⊙O 于点F ,∴BE =BF ,OE ⊥AB ,OF ⊥BC ,则△BOE ≌△BOF ,∴∠EBO=∠FBO,同理∠FCO=∠GCO,又∵AB∥CD,∴∠ABC+∠DCB=180°,∴∠OBC+∠OCB=90°,∴BO⊥CO(2)易得Rt△BOF∽Rt△BCO,∴BO2=BF·BC,∵BO=6 cm,OC=8 cm,∴BC=10 cm,∴BE=BF=BO2BC=3610=3.6(cm),∵AB,BC,CD分别与⊙O相切,∴BE=BF=3.6 cm,CG=CF,∵CF=BC-BF=10-3.6=6.4(cm),∴CG=CF=6.4 cm。
新人教版九年级数学上册24.2.2.3切线长定理习题

新人教版九年级数学上册24.2.2.3切线长定理习题要点感知1 经过圆外一点作圆的切线,这点和切点之间线段的长,叫做这点到圆的____.从圆外一点可以引圆的两条切线,它们的____相等,这一点和圆心的连线平分____.预习练习1-1 如图,PA,PB是⊙O的切线,切点分别是A,B,若PA=6 cm,则PB=____.1-2 如图,PA、PB是⊙O的切线,切点分别是A,B,若∠APB=60°,OA=2 cm,则OP=____.要点感知2 与三角形各边____的圆叫做三角形的内切圆,内切圆的圆心是____的交点,叫做三角形的____.三角形的内切圆只有____个,而圆的外切三角形有____个.预习练习2-1 如图,已知⊙O是△ABC的内切圆,且∠ABC=50°,∠ACB=80°,则∠BOC=____.知识点1 切线长定理1.如图,从⊙O外一点P引⊙O的两条切线PA,PB,切点分别为A,B.如果∠APB=60°,PA=8,那么弦AB的长是( )A.4B.8C.43D.832.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( )A.9B.10C.12D.143.(青海中考)如图,PA、PB切⊙O于点A、B,点C是⊙O上的一点,且∠ACB=65°,则∠P=____.4.为了测量一个圆形铁环的半径,某同学采用了如下办法:将铁环平放在水平桌面上,用一个锐角为30°的三角板和一个刻度尺,按如图所示的方法得到相关数据,进而可求得铁环的半径,若三角板与圆相切且测得PA=5 cm,求铁环的半径.知识点2 三角形的内切圆5.如图,点O 是△ABC 的内切圆的圆心,若∠BAC=80°,则∠BOC=( ) A.130° B.120° C.100° D.90°6.如图,在△ABC 中,点P 是△ABC 的内心,则∠PBC+∠PCA+∠PAB=____.7.已知在Rt △ABC 中,∠C=90°,AC=6,BC=8,则△ABC 的内切圆的半径为____.8.△ABC 的内切圆⊙O 与BC ,CA ,AB 分别相切于点D ,E ,F ,且AB=18 cm ,BC=28 cm ,CA=26 cm ,求AF ,BD ,CE 的长.9.一个钢管放在V 形架内,如图是其截面图,O 为钢管的圆心.如果钢管的半径为25 cm ,∠MPN=60°,则OP=( ) A.50 cmB.253cmC.3350cm D.503 cm10.如图,若AB 、AC 分别切⊙O 于B 、C ,延长OB 到D 使BD=OB ,连接AD ,∠DAC=78°,则∠ADO 的度数为( ) A.56° B.39° C.64° D.78°11.(青岛中考)如图,AB 是⊙O 的直径,BD ,CD 分别是过⊙O 上点B ,C 的切线,且∠BDC=110°.连接AC ,则∠A 的度数是____.12.如图,已知⊙O 是边长为2的等边△ABC 的内切圆,则⊙O 的半径为____.13.如图,PA,PB 分别与⊙O 相切于点A,B ,⊙O 的切线EF 分别交PA,PB 于点E,F ,切点C 在弧AB 上,若PA 长为2,则△PEF 的周长是____14.如图所示,点I 为△ABC 的内心,点O 为△ABC 的外心,若∠BOC=140°,求∠BIC 的度数.15.(河南中考)如图,CD 是⊙O 的直径,且CD=2 cm ,点P 为CD 的延长线上一点,过点P 作⊙O 的切线PA 、PB ,切点分别为点A、B.(1)若∠APO=90°证明:△ACP是等腰三角形(2)填空:①当DP=____cm时,四边形AOBD是菱形;②当DP=____cm时,四边形AOBP是正方形.挑战自我16.(曲靖中考)如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,AC、PB的延长线相交于点D.(1)若∠1=20°,求∠APB的度数;(2)当∠1为多少度时,OP=OD,并说明理由.参考答案要点感知1 切线长.切线长,两条切线的夹角.预习练习1-1 6 cm.1-2 4 cm.要点感知2 都相切,三角形三条角平分线,内心.一,无数.预习练习2-1 如115°.1.B2.D3.50°4.设圆心为O,连接OA,OP.∵三角板有一个锐角为30°,∴∠PAO=60°.又∵PA与⊙O相切,∴∠OPA=90°.∴∠POA=30°.∵PA=5 cm,OP=53cm.即铁环的半径为53 cm. 5.A 6.90度. 7.2.8.根据切线长定理得 AE=AF ,BF=BD ,CE=CD. 设AF=AE=x cm , 则CE=CD=(26-x)cm , BF=BD=(18-x)cm. ∵BC=28 cm ,∴(18-x)+(26-x)=28.解得x=8.∴AF=8 cm ,BD=10 cm ,CE=18 cm.9.A10.C11.35°.12.331. 13.4.14.∵点O 为△ABC 的外心,∠BOC=140°, ∴∠A=70°.又∵点I 为△ABC 的内心,∴∠BIC=125°.15.(1)连接OA.∵PA 为⊙O 的切线, ∴∠OAP=90°. 在Rt △AOP 中,∠AOP=90°-∠APO=90°-30°=60°. ∴∠ACP=21∠AOP=21×60°=30°. ∴∠ACP=∠APO.∴AC=AP .∴△ACP 是等腰三角形.(2)1,2-1(提示:①当四边形AOBD 是菱形时,AO=AD=OD ,∠AOP=60°,而∠OAP=90°,∴OP=2OA=2,∴DP=OP-OD=2-1=1;②当四边形AOBP 是正方形时,OP=2OA=2,∴DP=OP-OD=2-1.) 挑战自我16.(1)∵PA 是⊙O 的切线, ∴∠PAO=90°.∵∠1=20°,∴∠BAP=90°-∠1=70°. 又∵PA 、PB 是⊙O 的切线,∴PA=PB. ∴∠BAP=∠ABP=70°.∴∠APB=180°-70°×2=40°.(2)当∠1=30°时,OP=OD.理由如下: 当∠1=30°时,由(1)知∠BAP=∠ABP=60°, ∴∠APB=180°-60°×2=60°.∵PA、PB是⊙O的切线,∴∠OPB=12∠APB=30°.又∵∠D=∠ABP-∠1=60°-30°=30°,∴∠OPB=∠D.∴OP=OD.。
人教版初三数学:切线长定理—巩固练习(基础)(1)

切线长定理—巩固练习(基础)【巩固练习】 一、选择题1. 下列说法中,不正确的是 ( )A .三角形的内心是三角形三条内角平分线的交点B .锐角三角形、直角三角形、钝角三角形的内心都在三角形内部C .垂直于半径的直线是圆的切线D .三角形的内心到三角形的三边的距离相等2.△ABC 的三边长分别为a 、b 、c ,它的内切圆的半径为r ,则△ABC 的面积为( ) A.21(a +b +c )r B.2(a +b +c ) C.31(a +b +c )r D.(a +b +c )r3.(2015•黔西南州)如图,点P 在⊙O 外,PA 、PB 分别与⊙O 相切于A 、B 两点,∠P=50°,则∠AOB 等于( )A .150°B .130°C .155°D .135°4. 如图所示,⊙O 的外切梯形ABCD 中,如果AD ∥BC ,那么∠DOC 的度数为( )A.70°B.90°C.60°D.45°第4题图 第5题图5.如图,PA 是O ⊙的切线,切点为A ,PA =23,∠APO =30°,则O ⊙的半径为( )A.1B.3C.2D.46.已知如图所示,等边△ABC 的边长为2cm ,下列以A 为圆心的各圆中, 半径是3cm 的圆是( )二、填空题7.如图,⊙I 是△ABC 的内切圆,切点分别为点D 、E 、F ,若∠DEF=52o,则∠A 的度为________.第7题图 第8题图 第9题图8.如图,一圆内切于四边形ABCD ,且AB=16,CD=10,则四边形ABCD 的周长为________. 9.如图,已知⊙O 是△ABC 的内切圆,∠BAC=50o,则∠BOC 为____________度.10.如图,PA 、PB 分别切⊙O 于点A 、B ,点E 是⊙O 上一点,且 60=∠AEB ,则=∠P ____度.第10题图 第11题图11.如图,PA 与⊙O 相切,切点为A ,PO 交⊙O 于点C ,点B 是优弧CBA 上一点,若∠ABC=32°,则∠P 的度数为 .12.(2015•鄂州)已知点P 是半径为1的⊙O 外一点,PA 切⊙O 于点A ,且PA=1,AB 是⊙O 的弦,AB=,连接PB ,则PB= .三、解答题13. 已知:如图,AB 为⊙O 的直径,⊙O 过AC 的中点D ,DE ⊥BC 于点E .求证:DE 为⊙O 的切线.OEDCB A14.已知:如图,点D 是⊙O 的直径CA 延长线上一点,点B 在⊙O 上,且.OA AB AD == 求证:BD 是⊙O 的切线;FE D CBA O15.(2014秋•东城区月考)如图所示,PA、PB是⊙O的切线,切点分别是A、B,Q为⊙O上一点,过Q 点作⊙O的切线,交PA、PB于E、F点,已知PA=8cm,求:△PEF的周长.【答案与解析】一、选择题1.【答案】C.【解析】经过半径的外端,并且垂直于这条半径的直线是圆的切线. 2.【答案】A.【解析】连结内心与三个顶点,则△ABC 的面积等于三个三角形的面积之和,所以△ABC 的面积为21a ·r +21b ·r +21c ·r =21(a +b +c )r . 3.【答案】B ;【解析】∵PA、PB 是⊙O 的切线, ∴PA⊥OA,PB⊥OB, ∴∠PAO=∠PBO=90°, ∵∠P=50°, ∴∠AOB=130°. 故选B . 4.【答案】B ;【解析】由AD ∥BC ,得∠ADC+∠BCD=180°,又AD 、DC 、BC 与⊙O 相切,所以∠ODC=21∠ADC ,∠OCD=21∠BCD ,所以∠ODC+∠OCD=21×180°=90°,所以∠DOC=90°. 故选B.5.【答案】C ;【解析】连结OA ,则∠OAP=90°,设OA=x,则OP=2x,由勾股定理可求x=2,故选C. 6.【答案】C ;【解析】易求等边△ABC 的高为3cm 等于圆的半径,所以圆A 与BC 相切,故选C. 二、填空题 7.【答案】76°;【解析】连接ID,IF ∵∠DEF=52°, ∴∠DIF=104°,∵D 、F 是切点, ∴DI ⊥AB,IF ⊥AC , ∴∠ADI=∠AFI=90°, ∴∠A=1800-1040=76°.8.【答案】52;【解析】提示:AB+CD=AD+BC. 9.【答案】115°;【解析】∵∠A=500∴∠ABC+∠ACB=130°,∵OB,OC 分别平分∠ABC,∠ACB , ∴∠OBC+∠OCB=65°,∴∠BOC=1800-650=115°.10.【答案】60°;【解析】连结OA 、OB ,则∠AOB=120°,在四边形OAPB 中,∠P=360°-90°-90°-120°=60°. 11.【答案】26°;【解析】连结OA ,则∠AOC=64°,∠P=90°-64°=26°. 12.【答案】1或. 【解析】连接OA , (1)如图1,连接OA ,∵PA=AO=1,OA=OB ,PA 是⊙的切线, ∴∠AOP=45°∵OA=OB , ∴∠BOP=∠AOP=45°, 在△POA 与△POB 中,,∴△POA ≌△POB , ∴PB=PA=1;(2)如图2,连接OA ,与PB 交于C , ∵PA 是⊙O 的切线, ∴OA ⊥PA , 而PA=AO=,1 ∴OP=; ∵AB=, 而OA=OB=1, ∴AO ⊥BO ,∴四边形PABO 是平行四边形, ∴PB ,AO 互相平分; 设AO 交PB 与点C , 即OC=, ∴BC=,∴PB=.故答案为:1或. 三、解答题13.【答案与解析】如图,连接OD . ∵ D 为AC 中点, O 为AB 中点,∴ OD 为△ABC 的中位线. ∴OD∥BC. ∵ DE⊥BC, ∴∠DEC=90°.∴∠ODE=∠DEC=90°. ∴OD⊥DE 于点D. ∴ DE 为⊙O 的切线. 14.【答案与解析】 连接OB .∵,OA AB OA OB ==,∴OA AB OB ==.∴ABO ∆是等边三角形. ∴160BAO ∠=∠=︒.∵AB AD =,∴230D ∠=∠=︒. ∴1290∠+∠=︒. ∴DB BO ⊥ .又∵点B 在⊙O 上, ∴DB 是⊙O 的切线 . 15. 【答案与解析】解:∵PA 、PB 是⊙O 的切线,切点分别是A 、B ,Q 为⊙O 上一点,过Q 点作⊙O 的切线,交PA 、PB 于E 、F 点,231FE DCBA4O∴PA=PB,EA=EQ,FB=FQ,∵PA=8cm,∴△PEF的周长为:PE+EF+PF=PA+PB=8+8=16(cm).附录资料:《相似》全章复习与巩固--巩固练习(基础)【巩固练习】一、选择题1.(2015•乐山)如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F.已知,则的值为()A.B.C.D.2. (2016•奉贤区一模)用一个4倍放大镜照△ABC,下列说法错误的是()A.△ABC放大后,∠B是原来的4倍B.△ABC放大后,边AB是原来的4倍C.△ABC放大后,周长是原来的4倍D.△ABC放大后,面积是原来的16倍3.如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与相似的是( )4.如图,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0).以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是,则点B的横坐标是()A.B. C.D.5.下列说法:①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三角形斜边上的中线与斜边的比为1:2;④两个相似多边形的面积比为4:9,则周长的比为16:81中,正确的有( ) A.1个B.2个 C.3个 D.4个6. 如图,在正方形ABCD中,E是CD的中点,P是BC边上的点,下列条件中不能推出△ABP与以点E、C、P为顶点的三角形相似的是( )A.∠APB=∠EPC B.∠APE=90° C.P是BC的中点D.BP:BC=2:37. 如图,在△ABC中,EF∥BC,12AEEB,,S四边形BCFE=8,则S△ABC=()A.9 B.10 C.12 D.138.如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论正确的是()A.∠E=2∠K B.BC=2HIC.六边形ABCDEF的周长=六边形GHIJKL的周长D.S六边形ABCDEF=2S六边形GHIJKL二、填空题9. (2016•衡阳)若△ABC与△DEF相似且面积之比为25:16,则△ABC与△DEF的周长之比为.10. 如图,在△ABC中,D、E分别是AB和AC中点,F是BC延长线上一点,DF平分CE于点G,CF=1,则BC=_______,△ADE•与△ABC•的面积之比为_______,•△CFG与△BFD的面积之比为________.11. 如图,梯形ABCD中,AD∥BC,AC、BD交于O点,S△AOD:S△COB=1:9,则S△DOC:S△BOC=_______.12. 在相同时刻的物高与影长成比例.小明的身高为1.5米,在地面上的影长为2米,同时一古塔在面上的影长为40米,则古塔高为________.13. (2015•金华)如图,直线l1、l2、…l6是一组等距的平行线,过直线l1上的点A作两条射线,分别与直线l3、l6相交于点B、E、C、F.若BC=2,则EF的长是.14.如图,在△ABC中,MN∥BC,若∠C=68°,AM:MB=1:2,则∠MNA=_______度,AN:NC=_____________.15.如图,点D,E分别在AB、AC上,且∠ABC=∠AED。
人教版-数学-九年级上册-新版数学九上 切线长定理 配套练习

第5题切线长定理配套练习 姓名一、选择题:1.如图l ,已知PA ,PB 是⊙O 的切线,A 、B 为切点,AC 是 ⊙O 的直径,∠P=40°,则∠BAC 度数是( )A .70°B .40°C .50°D .20°2.已知圆的半径为6,圆心到圆外一点的距离为10,则该点到圆的切线长为( )A .7B . 8C .9D .103.下列命题中,是真命题的是( ) A .三角形的内心是三角形三条高的交点B .三角形的内心是三角形三条边垂直平分线的交点C .三角形的内心到三角形三边的距离相等D .三角形的内心是三角形各个顶点的距离相等4.如图,△ABC 的内切圆⊙O 与BC 、CA 、AB 分别 相切于点D 、E 、F ,且AB=3cm ,BC=4cm ,CA=5cm , 求AF 、BD 、CE 的长分别为( )A 、1,3,4B 、1,2,3C 、2,3,二、填空题:5.如图,PA 、PB 切⊙O 于A 、B ,∠P=60°,OP=4,则⊙O 的半径=_________.6.如图,已知圆外切等腰梯形ABCD 的中位线EF=15cm ,那么等腰梯形ABCD 的周长=___________.7.如图,PA 切⊙O 于A ,PB 切⊙O 于B ,∠APB=90°,OP=4,则⊙O 的半径=_________.8.如图,△ABC 中,∠ABC=50°,∠ACB=80°,点O 是 △ABC 的内心,则∠BOC 的度数为 。
A第1题APO .B第6题第7题FEDBC三、解答题:9.如图,⊙O是△ABC的内切圆,与AB、BC、CA分别切于点D、E、F,∠DOE=120°,∠EOF=150°,求△ABC的三个内角的度数.的度数.11.△ABC的内切圆⊙O与AC、AB、BC分别相切于点D、E、F,且AB=5厘米,BC=9厘米,AC=6厘米,求AE、BF和CD的长.12.如图,△ABC中,∠C =90º ,它的内切圆O分别与边AB、BC、CA相切于点D、E、F,且BD=12,AD=8,求⊙O的半径r.。
人教版九年级数学上册 24.2.2.3 切线长定理 同步练习题(含答案)

人教版九年级数学上册第24章24.2.2.3 切线长定理同步练习题一、选择题1.平面内,⊙O的半径为1,点P到圆心O的距离为2,过点P可作⊙O的切线条数为(C) A.0条 B.1条 C.2条 D.无数条2.如图,⊙O是△ABC的内切圆,则点O是△ABC的(B)A.三条边的垂直平分线的交点 B.三条角平分线的交点C.三条中线的交点 D.三条高的交点3.如图,P为⊙O外一点,PA,PB分别切⊙O于A,B两点.若PA=3,则PB=(B) A.2 B.3 C.4 D.54.如图,PA,PB为⊙O的切线,切点分别为A,B,PO交AB于点C,PO的延长线交⊙O于点D,下列结论不一定成立的是(D)A.PA=PB B.∠BPD=∠APD C.AB⊥PD D.AB平分PD5.将一把直尺,含60°角的直角三角板和光盘如图摆放,点A为60°角与直尺的交点,AB =3,则光盘的直径是(D)A.3 B.3 3 C.6 D.6 36.如图,边长为23的等边△ABC的内切圆的半径为(A)A.1 B. 3 C.2 D.2 37.如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD,下底BC以及腰AB 均相切,切点分别是D,C,E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是(D)A.9 B.10 C.12 D.148.如图,等边△ABC的边长为8,以BC上一点O为圆心的圆分别与边AB,AC相切,则⊙O 的半径为(A)A.2 3 B.3 C.4 D.4- 39.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=5,BC=13,CA =12,则阴影部分(即四边形AEOF)的面积是(A)A.4 B.6.25 C.7.5 D.910.如图,点O是△ABC的内心,过点O作EF∥AB,与AC,BC分别交于点E,F,则(C) A.EF>AE+BF B.EF<AE+BFC.EF=AE+BF D.EF≤AE+BF11.如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为(B)A.4.5 B.4 C.3 D.2二、填空题12.如图,PA,PB是⊙O的切线,A,B为切点,∠OAB=38°,则∠P=76°.13.如图,PA,PB是⊙O的切线,A,B为切点,点C,D在⊙O上.若∠P=102°,则∠A +∠C=219°.14.如图,已知△ABC的内切圆⊙O与BC边相切于点D,连接OB,OD.若∠ABC=40°,则∠BOD的度数是70°.15.如图,P是△ABC的内心,连接PA,PB,PC,△PAB,△PBC,△PAC的面积分别为S1,S2,S3,则S1<S2+S3.(填“<”“=”或“>”)三、解答题16.如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=18 cm,BC=28 cm,CA=26 cm,求AF,BD,CE的长.解:根据切线长定理,得AE=AF,BF=BD,CE=CD.设AF=AE=x cm,则CE=CD=(26-x)cm,BF=BD=(18-x)cm.∵BC=28 cm,∴(18-x)+(26-x)=28.解得x=8.∴AF=8 cm,BD=10 cm,CE=18 cm.17.如图,AB,BC,CD分别与⊙O相切于点E,F,G,若∠BOC=90°,求证:AB∥CD.证明:∵∠BOC=90°,∴∠OBC+∠OCB=90°.又∵BE与BF为⊙O的切线,∴BO为∠EBF的平分线.∴∠OBE=∠OBC.同理可得∠OCB=∠OCG.∴∠OBE+∠OCG=∠OBC+∠OCB=90°.∴∠OBC+∠OCB+∠OBE+∠OCG=180°,即∠ABF+∠DCF=180°.∴AB∥CD.18.如图,点I是△ABC的内心,BI的延长线与△ABC的外接圆⊙O交于点D,与AC交于点E,延长CD,BA相交于点F,∠ADF的平分线交AF于点G.求证:(1)DG∥CA;(2)AD=ID.证明:(1)∵点I 是△ABC 的内心,∴∠2=∠7=12∠ABC.∵DG 平分∠ADF , ∴∠1=12∠ADF.∵∠ADF =180°-∠ADC =∠ABC , ∴∠1=∠2.∵∠3=∠2,∴∠1=∠3.∴DG ∥AC. (2)∵点I 是△ABC 的内心,∴∠5=∠6. ∴∠4=∠7+∠5=∠3+∠6,即∠4=∠DAI. ∴DA =DI.。
