Gauss型求积公式
合集下载
Gauss型求积公式
Gauss型求积公式 一、Gauss型求积公式 定义： 个节点的具有2 定义 ： 把具有 n＋1 个节点的具有 2 n+1 次代 数精确度的插值型求积公式
∫
b
a
f (x)dx ≈ ∑A f (xk ) k
k=0
n
称为Gauss型求积公式， 称为Gauss型求积公式，其求积节点 xk k=0， Gauss型求积公式 （ =0， 称为高斯点 高斯点， 高斯系数。 1，……n）称为高斯点，系数 A 称为高斯系数 k称为高斯系数 Remark：构造Gauss Gauss型求积公式的关键在于确定高斯 Remark：构造Gauss型求积公式的关键在于确定高斯 个高斯点构造基函数， 点，再由n＋1个高斯点构造基函数，从而得到高斯 系数。 系数。
f (x) = P x) n+1(x) ( ω 的次数不超过2n+1。
故有
∫ω
a
b
n+1
( x )P( x )dx = ∑A ωn+1( xk )P( xk ) = 0 k
k=0
n
充分性 ： 设 ∫ ωn+1(x)P(x)dx = 0 对于任意次数不超过 a ω 2n+1的多项式 f (x),设 n+1(x)除f(x)的商为p(x),余 项为q(x)。
Ak 0.1713244924 0.3607615730 0.4679139346 0.1294849662 0.2797053915 0.3818300505 0.4179591837 0.1012285363 0.2223810345 0.3137066459 0.3626837834
6
7 4 0.3478548451 0.6521451549
Gauss型求积公式-第5章
5.2 Gauss型求积公式
形如
I n ( f ) Ak f ( xk )
k 0 n
插值型求积公式的代数精度至少为
n。
x0 x0
x1 x1
x0 x0
x1 x1
两点的求积公式为： 1 f ( x) dx A0 f ( x0 ) A1 f ( x1 ) 若限制等距节点，则 1、x0 , x1固定，A0 , A1 变量 2、确定 A0 , A1 需两个方程
x0 , x1 ,, xn 是Gauss点 x0 , x1 ,, xn 是Gauss点
n 1 ( x) 是正交多项式。
x , x ,, x
0 1
n
是正交多项式的根。
证明： 必要性
I ( f ) ( x) f ( x)dx
a
b
I n ( f ) Ak f ( xk )
n n 2
n 1 ( xk ) 1 ( x ) ( x xk ) f ( xk ) n 1 k
2
n 1 ( x) ( x xk ) f ( xk ) 1 ( xk )( x xk ) k 0 n
1
1
f ( x) dx
1 1 f f 3 3
对于任意区间 a, b 上权函数 x 1 的Gauss型求积公式，只需 作变量替换：
x
则有
x a, b t 1, 1 ，这样
ab ba t 2 2
n 1 ( xk ) f ( xk ), k 0,1,..., n H 2 n 1 ( xk ) f ( xk ), H 2
的2n+1次Hermite插值多项式，即（P110 例5）
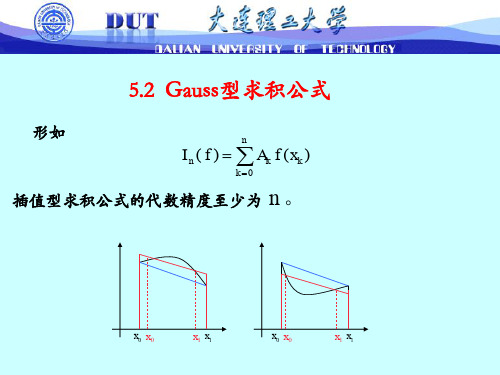
形如
I n ( f ) Ak f ( xk )
k 0 n
插值型求积公式的代数精度至少为
n。
x0 x0
x1 x1
x0 x0
x1 x1
两点的求积公式为： 1 f ( x) dx A0 f ( x0 ) A1 f ( x1 ) 若限制等距节点，则 1、x0 , x1固定，A0 , A1 变量 2、确定 A0 , A1 需两个方程
x0 , x1 ,, xn 是Gauss点 x0 , x1 ,, xn 是Gauss点
n 1 ( x) 是正交多项式。
x , x ,, x
0 1
n
是正交多项式的根。
证明： 必要性
I ( f ) ( x) f ( x)dx
a
b
I n ( f ) Ak f ( xk )
n n 2
n 1 ( xk ) 1 ( x ) ( x xk ) f ( xk ) n 1 k
2
n 1 ( x) ( x xk ) f ( xk ) 1 ( xk )( x xk ) k 0 n
1
1
f ( x) dx
1 1 f f 3 3
对于任意区间 a, b 上权函数 x 1 的Gauss型求积公式，只需 作变量替换：
x
则有
x a, b t 1, 1 ，这样
ab ba t 2 2
n 1 ( xk ) f ( xk ), k 0,1,..., n H 2 n 1 ( xk ) f ( xk ), H 2
的2n+1次Hermite插值多项式，即（P110 例5）
7-5Gauss型求积公式
参阅表 7-4.
其截断误差为
2 2n 1 (n! ) 4 ( 2n ) R( f ) f ( ) 3 (2n 1)(2n)!
(1,1)
任意区间上的Gauss-Legendre 公式
对积分
b
a
f ( x )dx
ba ba x t 做变换 利用 Gauss－Legendre 求积公式的求积节 2 2 ，
（7-51）
2．可以证明：若 f ( x) C a, b，Gauss 型求积公式当 n 时收敛于 定积分值。
3.Gauss型求积公式是数值稳定的。
3.Gauss 型求积公式是数值稳定的。
记 f * ( xk ) 为 f ( xk ) 的近似值，
∵
Ak ( x)lk ( x)dx 0 且 a
b
Gauss型求积公式的误差 设求积公式 ( x ) f ( x )dx A
b n a k 1
k
f ( x k ) 是 Gauss 型求
积公式，H ( x ) 为以
b n
n x Gauss 点 k k 1 为节点的 f ( x ) 的 2n 1 次
Hermite 插值多项式，则有
例
试确定求积公式： 1 f ( x)dx af 0.6 bf (0) cf 0.6 中 待定参数 a , b 和 c ，使其代数精确度尽量高，并指出公式具有 几次代数精确度,判断是否为 Gauss 型求积公式。
1
解：记 I ( f ) 1 f ( x )dx
1
f af 0.6 bf (0) cf I
n n ( x) Al l k ( xl ) Ak a ( x)lk ( x)dx a ( x) ( x xk ) n ( xk ) dx l 1 b b
数值分析(19)Gauss积分
数值分析
（2）利用正交多项式构造高斯求积公式
设Pn(x)，n=0,1,2,…,为正交多项式序列， Pn(x) 具有如下性质： 1）对每一个n ,Pn(x)是 n 次多项式。 n=0,1,… b 2） (正交性) ( x ) P ( x ) P ( x )dx 0,(i j )
a
i
j
3）对任意一个次数≤n-1的多项式P(x)，有
数值分析
数值分析
利用正交多项式构造高斯求积公式的基本步骤：
1. 以n 1次正交多项式的零点 x0 , x1 , xn作为积分点 (高斯点）， 2.用 高 斯 点 x0 , x1 , xn对f ( x )作Lagrange插 值 多 项 式
f ( x ) l i ( x ) f ( xi )
这样就可以用Gauss - Legendre求积公式计算一 般区间的积分.
数值分析
数值分析
例
对积分 f ( x )dx， 试利用n 1的两点Gauss Legendre
0
1
求积公式构造Gauss型求积公式。即确定x0 , x1和A0 , A1 使
1
0
f ( x )dx A0 f ( x0 ) A1 f ( x1 )
因为Guass求积公式也是插值型求积公式,故有 结论: n+1个节点的插值型求积公式的代数精度 d 满足： n d 2n+1。
数值分析
数值分析
(1) 用待定系数法构造高斯求积公式 例：选择系数与节点，使求积公式（1）
1
1
f ( x )dx c1 f ( x1 ) c2 f ( x2 )
数值分析
数值分析
数值分析课件_高斯求积公式
b
a
f ( x ) ( x )dx Ak f ( xk )
k 0
b b
n
2
a
f ( x ) ( x )dx p( x ) ( x )dx
a
b
a
p( x ) ( x )dx Ak p( xk )
k 0
n
n
0
2
m 2n 1
Ak p( xk ) Ak f ( xk )
证明：由Weierstrass定理知
f p max f p
a xb
则Gauss型求积公式（*）是收敛的。 对
0
b
存在m次多项式
下证
p( x ) 满足
fp
n
N ,
当n
N时
k 0
2 ( x )dx
a
b
a
f ( x ) ( x )dx Ak f ( xk )
的插值型求积公式的代数精度最高不超过2n+1次。 只需证明：对于上述插值型求积公式，存在一个 2n+2次多项式，使得求积公式不能精确成立。
2 n1
令 f ( x)
因为
b
( x)
b a
其中 n 1 ( x ) ( x xk )
k 0
n
f ( x)dx 而 A f (x ) 0
k 0
n
与任何不超过n次的多项式 p( x ) 带权正交:
b a
p( x )n1 ( x ) ( x )dx 0
证明： 必要性 设
p( x ) H n
高斯求积公式
(k = 0,1 ⋯ n), 使（5.1）具有 2n +1次代数精度. , ,
定义4 定义4
如果求积公式(5.1)具有 2n +1次代数精度，
则称其节点 xk (k = 0,1 ⋯, n) 为高斯点 高斯点，相应公式(5.1)称 高斯点 , 为高斯求积公式 高斯求积公式. 高斯求积公式
3
根据定义要使(5.1)具有 2n +1次代数精度，只要对
充分性. 对于 ∀f (x) ∈H2n+1, 用 ωn+1(x) 除 f (x) ， ， 记商为 P(x)，余式为 q(x) 即 f (x) = P(x)ωn+1(x) + q(x) , 其中 P(x),q(x)∈Hn. 由(5.5)可得
∫
b
a
f (x)ρ(x)dx = ∫ q(x)ρ(x)dx.
b a
18
令它对 f (x) =1, x 都准确成立，有
A + A = 2; 0 1 A − 1 + A 1 = 0. 1 0 3 3
由此解出 A = A =1, 从而得到两点高斯-勒让德求积公式 0 1
∫
1
1 −
f (x)dx ≈ f (−
1 1 ) + f (− ). 3 3
b n→ ∞ k =0 a n
16
4.5.2
高斯高斯-勒让德求积公式
在高斯求积公式(5.1)中，若取权函数 ρ(x) =1, 区间为
[−11 则得公式 , ],
n
∫
1
−1
f (x)dx ≈ ∑A f (xk ). k
k =0
（5.9）
由于勒让德多项式是区间 [−11]上的正交多项式，因此， , 勒让德多项式 P 1(x) 的零点就是求积公式(5.9)的高斯点. n+ 形如(5.9)的高斯公式称为高斯-勒让德求积公式. 高斯-勒让ρ(x) ≥ 0, 由积分中值定理得(5.1)的余项为
定义4 定义4
如果求积公式(5.1)具有 2n +1次代数精度，
则称其节点 xk (k = 0,1 ⋯, n) 为高斯点 高斯点，相应公式(5.1)称 高斯点 , 为高斯求积公式 高斯求积公式. 高斯求积公式
3
根据定义要使(5.1)具有 2n +1次代数精度，只要对
充分性. 对于 ∀f (x) ∈H2n+1, 用 ωn+1(x) 除 f (x) ， ， 记商为 P(x)，余式为 q(x) 即 f (x) = P(x)ωn+1(x) + q(x) , 其中 P(x),q(x)∈Hn. 由(5.5)可得
∫
b
a
f (x)ρ(x)dx = ∫ q(x)ρ(x)dx.
b a
18
令它对 f (x) =1, x 都准确成立，有
A + A = 2; 0 1 A − 1 + A 1 = 0. 1 0 3 3
由此解出 A = A =1, 从而得到两点高斯-勒让德求积公式 0 1
∫
1
1 −
f (x)dx ≈ f (−
1 1 ) + f (− ). 3 3
b n→ ∞ k =0 a n
16
4.5.2
高斯高斯-勒让德求积公式
在高斯求积公式(5.1)中，若取权函数 ρ(x) =1, 区间为
[−11 则得公式 , ],
n
∫
1
−1
f (x)dx ≈ ∑A f (xk ). k
k =0
（5.9）
由于勒让德多项式是区间 [−11]上的正交多项式，因此， , 勒让德多项式 P 1(x) 的零点就是求积公式(5.9)的高斯点. n+ 形如(5.9)的高斯公式称为高斯-勒让德求积公式. 高斯-勒让ρ(x) ≥ 0, 由积分中值定理得(5.1)的余项为
数值分析-高斯求积分
有（插值节点为x1
3 5 , x2 0, x3
3） 5
1
A1 A2 +A3
dx
1
A1 x1 A2 x2 +A3 x3
A1 x12 A2 x22 +A3 x32
2
1
xdx 0
1
x 2dx
2
1
3
解得 :
A1
5 9
,
A2
8 9
,
A3
3点Gauss型求积公式为：
1
f ( x)dx
1
5 f( 9
3 ) 8 f (0) 59
I sin tdt sin
dx
若用n=0 2的Gaus4s-L1egend4re公式，则
I
4
sin4
(1
0.5773503)
4
sin4
(1.5773503)
0.9984725
例题2
若用n=3的Gauss-Legendre公式，则
I 0.5555556 f (0.7745967) 0.8888889 f (0) 0.5555556 f (0.7745967)
5 9
5 f( 3) 95
例题1
1
例例11 用高斯—勒让德求积公式计算 cos xdx
使其具有五次代数精度。 1
解： 用三个节点的高斯—勒让德公式
1
51
8
51
f ( x)dx f ( 15) f (0) f ( 15),
1
95
9
95
5 0.5556, 8 0.8889,cos( 1 15) cos(1 15) 0.7147
多项式，即若p( x)为一个不超过n-1次得多项式，则
gauss型求积公式
gauss型求积公式一、Gauss型求积公式的基本概念。
1. 定义。
- 在数值积分中，Gauss型求积公式是一种高精度的求积公式。
对于积分∫_a^bf(x)ρ(x)dx（其中ρ(x)为权函数），Gauss型求积公式的形式为∫_a^bf(x)ρ(x)dx≈∑_i = 1^nA_if(x_i)。
这里x_i称为求积节点，A_i称为求积系数，n为求积公式的节点个数。
2. 特点。
- 高精度：Gauss型求积公式具有很高的代数精度。
对于n个节点的Gauss型求积公式，其代数精度为2n - 1。
这意味着对于次数不超过2n-1的多项式f(x)，该求积公式能精确成立，即∫_a^bP_m(x)ρ(x)dx=∑_i = 1^nA_iP_m(x_i)，其中m≤slant2n - 1，P_m(x)是m次多项式。
- 节点分布：Gauss型求积公式的节点x_i不是等距分布的。
这些节点是关于权函数ρ(x)正交的多项式的零点。
例如，当ρ(x) = 1，[a,b]=[- 1,1]时，对应的正交多项式是勒让德多项式P_n(x)，Gauss型求积公式的节点就是勒让德多项式的零点。
二、求积节点与求积系数。
1. 求积节点的确定。
- 以勒让德 - Gauss求积公式为例（ρ(x)=1，[a,b]=[-1,1]），求积节点x_i是勒让德多项式P_n(x)的零点。
勒让德多项式P_n(x)可以通过递推公式(n + 1)P_n +1(x)=(2n + 1)xP_n(x)-nP_n - 1(x)，P_0(x)=1，P_1(x)=x来计算。
通过求解P_n(x)=0得到求积节点x_i。
2. 求积系数的计算。
- 求积系数A_i可以通过多种方法计算。
一种常见的方法是利用正交性条件。
对于勒让德 - Gauss求积公式，求积系数A_i可以通过公式A_i=(2)/((1 -x_i)^2)[P_{n'(x_i)]^2}计算，其中P_n'(x)是勒让德多项式P_n(x)的导数。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
利用Schmidt正交化过程，
g ( x) f ( x) 0 0 n 1 ( f ( x), gi ( x)) g n ( x) f n ( x) n gi ( x) i 0 ( g i ( x ), g i ( x ))
n
就可以将多项式基函数
Ak 0.8535533905 0.1464466094 0.7110930099 0.2785177335 0.0103892565 0.6031541043 0.3574186924 0.0388879085 0.0005392947
n
5
3
xk 0.2635603197 1.4134030591 3.5964257710 7.0858100058 12.6408008442 0.2228466041 1.1889321016 2.9927363260 5.7751435691 9.8374674183 15.9828739806
三次Legendre多项式及其零点为：
1 P3 ( x ) (5 x 3 3x ), x0 0.6 , x1 0, x2 0.6 2
三、Gauss-Legendre求积公式
1 d n 1 2 n 1 xk (k 0,1,, n)为Pn 1 ( x ) ( x 1 ) n 1 n 1 ( n 1 )! 2 dx 的零点 。
Ak 2 1 0.5555555556 0.8888888889
n 6
xk ±0.9324695142 ±0.6612093865 ±0.2386191861 ±0.9491079123 ±0.7415311856 ±0.4058451514 0 ±0.9602898565 ±0.7966664774 ±0.5255324099 ±0.1834346425
问题： 若求积公式
I f ( x )dx Ak f ( xk )
b a k 0 n
中含有2n+2个待定参数 xk , Ak (k 0,1, 2,, n) 我们能否通过节点的选择将求积公式的 代数精度从n 或者n+1提高到2n+1？
一、Gauss型求积公式 定义：把具有 n＋1 个节点的具有 2 n+1 次代 数精确度的插值型求积公式
x x
n
所以,对[0, +)上权函数W(x)=1的积分,也可以构造类似的 Gauss-Laguerre求积公式:
0 f ( x)dx Ai e f ( xi )
xi i 1
n 2
xk 0.5858864376 3.4142135623 0.4157745567 2.2942803602 602899450829 0.3225476896 1.7457611011 4.5366202969 9.3950709123
b
即f ( x) P( x) n1 ( x) q( x)
其中P( x), q( x)的次数 n
b
a
f ( x )dx P ( x )n1 ( x )dx q( x )dx
a a
b
b
由条件 P( x )n1 ( x)dx 0，
a
b
所给的求积公式是插值型的，其代数精度至少为n。
证毕
两条结论：
①．高斯型求积公式一定是插值型求积公 式，其系数由高斯点唯一确定。 ②．高斯型求积公式是代数精度最高的求积 公式（2n＋1次）。
当高斯点确定以后，高斯系数 Ak (k 0,1,, n)
n b a dx Ak k 0 n b a xdx Ak x k k 0 n b n n a x dx Ak xk k 0
1, x,, x 变为正交基 p ( x), p ( x),, p ( x)
0 1 n
例： 解
求积分
2 x 1 f ( x)dx 的2点Gauss公式.
1
按 Schemite 正交化过程作出正交多项式:
p0 ( x) 1
( x, p 0 ( x)) p1 ( x) x p 0 ( x) ( p 0 ( x), p 0 ( x))
四、Gauss-Laguerre求积公式
区间[0,)上权函数W(x)=e-x的Gauss型求积公式,称为GaussLaguerre求积公式,其Gauss点为Laguerre多项式的零点.
公式的Gauss点和求积系数可在数学用表中查到 . 由
0 f ( x)dx 0 e e f ( x)dx
确定.
即可由线性方程组
也可以由插值型求积公式中的系数公式 Ak a lk ( x )dx 确定。
b
二、Legendre多项式
n＋1次Legendre多项式为：
1 d n 1 2 n 1 Pn 1 ( x ) ( x 1 ) ( x [1,1]; n 0,1,2,) n 1 n 1 (n 1)!2 dx
2 (1 xk ) Pn'1 ( xk ) 一点Gauss-Legendre求积公式为：
1
1
f ( x)dx Ak f ( xk )
k 0
n
Ak
2
2
(k 0,1,, n)
1
1
1
f ( x )dx 2 f (0)
两点Gauss-Legendre求积公式为：
3 3 1 f ( x)dx f ( 3 ) f ( 3 )
Gauss型求积公式
由前面的讨论已经知道，以a=x0<x1<…<xn=b为节点的N-C求积公式 的代数精度一般为n或n+1,这时节点简单地按照闭式等距的方式确定。 对一个求积公式而言，如果不固定节点的位置， 在节点数目不变的情况下，代数精度能否提高， 最多能达到多少?高斯型求积公式讨论的就是最高代数精度的求积公式.
ab ba x t 2 2
即可将区间[a,b]变换到[-1,1]上：
b
a
1 ba 1 ab ba f ( x )dx f( t )dt (t )dt 1 2 1 2 2
n 1 2 3
xk 0 ±0.5773502692 ±0.7745966692 0 ±0.8611363116 ±0.3399810436
其性质有 •1、n+1次Legendre多项式与任意不超过n次的多项 式在区间[-1,1]上正交。
•2、n+1次Legendre多项式的n+1个零点都在区间[1,1]内。
例： 一次Legendre多项式及其零点为：
P 1 ( x) x, x0 0
二次Legendre多项式及其零点为：
1 P2 ( x ) (3x 2 1), 2 3 3 x0 , x1 3 3
故 q( x )dx Ak q( xk )
b a n 0
n
所以求积公式至少具有2n＋1次代数精确度。对 于2n+2次多项式 有 f ( x ) 2 n1 ( x )
b
a
f ( x )dx 0
而
2 A k n1 ( x k ) 0 k 0
n
故求积公式的代数精确度是2n+1。
I
0
1
sin x dx x
1 sin(0.5773503 ) sin(0.5773503 ) 1 1 0.945363 . 2 0.5773503 0.5773503
高斯求积公式的截断误差为
22 n 3 (2 n 2) R[ f ] f ( ) 2 (2n 3)[(2n 2)!] 1 1
的n+1次多项式 n1 ( x) ( x x j ) 与任意次数不超
过n的多项式P(x)正交，即
b
a
n1 ( x )P ( x )dx 0
证明： 必要性 ： 设 xk (k 0,1,, n)是高斯点，于是对任意次数不超过n 的多项式P(x) ，
f ( x) P( x) n 1 ( x)的次数不超过2n+1。
2 2 ( x , p ( x )) ( x , p1 ( x)) 2 0 p 2 ( x) x p 0 ( x) p1 ( x) ( p 0 ( x), p 0 ( x)) ( p1 ( x), p1 ( x))
3 x 1 2 1 4 xx 5 1 x dx 1 x dx
3 5 3 5
x1
, x2
故两点Gauss公式为
2 1 x f ( x ) dx 1 3 [ f ( 1 3 5
) f(
3 5
)]
例 利用两点Gauss-Legendre求积公式计算 sin x 为偶函数 解:因为 x 1 1
sin x 1 sin x I dx dx x 2 1 x 0
1
1
f ( x)dx w0 f ( x0 ) w1 f ( x1 )
1 1 f ( x)dx f ( ) f ( ) 1 3 3
1
定理：插值型求积公式中的节点 x
n
斯点的充要条件是，在[a,b]上，以这些点为零点
j 0
是高 ( k 0 , 1 , , n ) k
b
a
f ( x )dx Ak f ( xk )
k 0
n
称为Gauss型求积公式，其求积节点 x k（k=0， 1，……n）称为高斯点，系数 Ak 称为高斯系数。 Remark：构造Gauss型求积公式的关键在于确定高斯 点，再由n＋1个高斯点构造基函数，从而得到高斯 系数。
节点 xi Ai ,(i 0,1,, n)，但是如何确定