四年级奥数-图形问题
四年级下册同步奥数图形运动植树问题

D
C
图形平移例题
用同样大小的瓷砖铺一个正方形的地面,两条对角线上铺 黑色的,其他地方铺白色的,如图所示。如果铺满这块地面共 用101块黑色瓷砖,那么白色瓷砖用了多少块?
2、如图所示,一个大长方形由7个完全相同的长方 形和3个小长方形(图中阴影部分)拼成,图中 白色部分的面积是多少平方厘米?
1、在一座长800米的大桥两边挂彩灯,起点和终点都挂, 一共挂了202盏,相邻两盏之间的距离都相等。求相邻 两盏彩灯之间的距离。
2、有一幢10层的大楼,由于停电,电梯停开,某人从1 层走到3楼需要30秒,照这样计算,他从3层走到10层需 要多少秒?
究极无敌抢答题三
阳光小学三年级有125人参加运动会入场式他们每5 人排一行,前后两行之间间隔2米。主席台长32米,他们 以每分40米的速度通过主席台,需要多长时间。
24cm
究极无敌抢答题二
在一个正方形中放入一个四个顶点与大正方形相接的一 个小正方形(如图),如果两个正方形的周长相差16厘米, 面积相差96平方厘米,小正方形的面积是多少平方厘米?
B
A
C
D
植树问题例题一
有一个圆形花坛,绕着它走一圈是120米。如果沿着这一 圈每隔6米栽一棵广玉兰,再在每相邻的两棵广玉兰之间等距 离的栽2株月季花,问可栽多少棵广玉兰,多少株月季花?
究极无敌抢答题四
正方形操场四周栽了一圈树,每两棵相隔5米。甲、乙从一个角上同 时出发,向不同的方向走去(如下图),甲的速度是乙的2倍,乙在拐了 一个弯之后的第5棵树与甲相遇。操场四周栽了多少棵树?
乙 甲
初中
初中
小学
初中
初中
初中
高中 高中
职专 技校
四年级奥数—几何中的计数问题
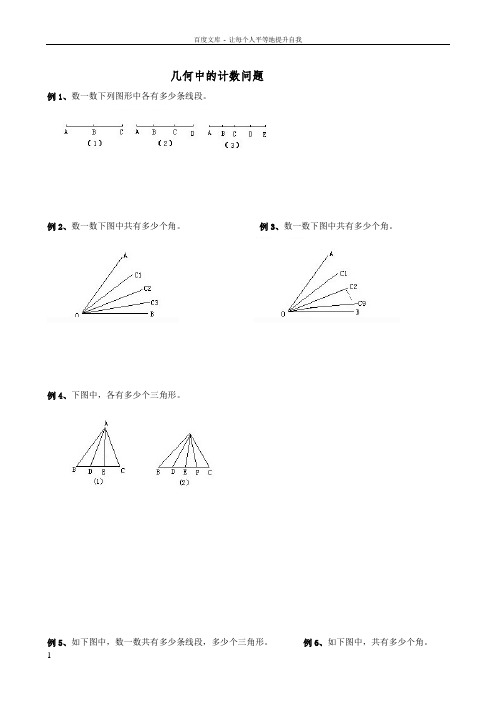
几何中的计数问题
例1、数一数下列图形中各有多少条线段。
例2、数一数下图中共有多少个角。
例3、数一数下图中共有多少个角。
例4、下图中,各有多少个三角形。
例5、如下图中,数一数共有多少条线段,多少个三角形。
例6、如下图中,共有多少个角。
例7、如下图,数一数共有多少个长方形。
例8、数一数下图中长方形的个数。
例9、数一数下面各图中所有正方形的个数。
例10、数一数下图中有多少个正方形。
例11、数一数下图三角形的个数。
例12、数一数下图中三角形的个数。
例13、数一数下图中三角形的个数。
例14、数一数下图中三角形的个数。
练:1、数一数下面各图中有多少条线段。
2、数一数下面各图中有多少个角。
3、数一数下面各图中,各有多少条线段。
4、数一数下面各图中,各有多少条线段,各有多少个三角形。
5、下面图中有多少个正方形。
6、下图中有多少个长方形。
7、下图中有多少个三角形。
8、下图中有多少个长方形。
9、下图中各有多少个三角形。
人教版四年级数学奥数 数数图形(课件)(共20张PPT)

【例题1】数一数下图中有多少个锐角。
【思路导航】 数角的方法和数线段的方法类似,图中的五条射线相当于线段上的五个点, 因此,要求图中有多少个锐角,可根据公式1+2+3……(总射线数-1)求得: 1+2+3+4=10(个).
【例题2】 数一数下图中有多少个长方形?
【思路导航】 图中的AB边上有线段1+2+3=6条,把AB边上的每一条线段作为长,AD边பைடு நூலகம்的
第12讲 数数图形
小学奥数 四年级
同学们对于图形肯定不陌生,但数学中经常会出现这样的题目: (1)下图中共有几条线段? (2)下图中共有几个长方形?
要正确解答这类问题,就要做到数图形时不重复、不遗漏。这就需要 我们按照一定的顺序去数,并找出它的规律,巧妙地数出图形的个数。数 图形的方法一般有两种:按顺序数和分类数。今天就让我们用数学的方法 巧妙地数图形吧!
实践与应用
【练习5】 P94 数一数,下图中共有多少个长方形?
同学们,图形世界是不是非赏精彩呢?数学的魅力就在于千变万化的图形和数字。通过 这一进,我们对图形有了更深的认识,遇到数图形的问题也能有序、严密地思索,关于数 图形,我们来总结一些最基本的方法吧。
(1)数线段。假设端点有n个(n是整数),那么线段的总条数就是从比n小1的数开始, 一直加到1。
每一条线段作为宽,每一个长配一个宽,就组成一个长方形,所以,图中共有 6×3=18个长方形。 数长方形可以用下面的公式:长边上的线段×短边上的线段=长方形的个数
【例题3】数一数下图中有多少个正方形?(其中每个小方格都是边长为1个 长度单位的正方形)
【思路导航】 边长是1个长度单位的正方形有3×2=6个,边长是2个长度单位的正方形有 2×1=2个。所以,图中正方形的总数为:6+2=8个。 经进一步分析可以发现,一般情况下,如果一个长方形的长被分成m等份, 宽被分成n等份(长和宽的每一份都是相等的)那么正方形的总数为: mn+(m-1)(n-1)+(m-2)(n-2)+…+(m-n+1)n.
四年级奥数-图形分割和拼接
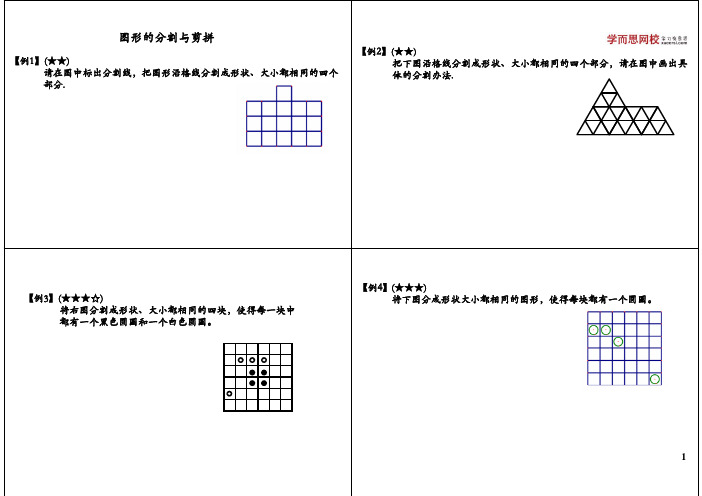
部分
部分.
图都图,得每都有个
将下图分成形状大小都相同的图形,使得每块都有一个圆圈。
用若干个边长为1,2,3,4的正方形纸片互不重叠地拼成一个边长为
个,,,拼个
5的大正方形,那么最少需要纸片____张。
图。
请你选取其中的一些或者全部,分别拼出一个五边形和一个七边
2cm2cm
下图是一个9×4的长方形,请把它分割成完全相等的两块,并拼成右图的方形请在左图中出分割线在右图中出拼接线
图的正方形,请在左图中画出分割线,在右图中画出拼接线。
如图,在5×8的长方形中,挖去了一个1×4的小长方形(阴影部分),图,中,个(影部),请你将它划分成两部分,使它们能拼成一个正方形。
小学四年级奥数第15讲 图形问题(含答案分析)

第15讲图形问题一、知识要点解答有关“图形面积”问题时,应注意以下几点:1.细心观察,把握图形特点,合理地进行切拼,从而使问题得以顺利地解决;2.从整体上观察图形特征,掌握图形本质,结合必要的分析推理和计算,使隐蔽的数量关系明朗化。
二、精讲精练【例题1】人民路小学操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方米?练习11、有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米、3分米,面积比原来减少多少平方分米?2、一块长方形铁板,长18分米,宽13分米。
如果长和宽各减少2分米,面积比原来减少多少平方分米?【例题2】一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
这个长方形原来的面积是多少平方米?练习21、一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?2、一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
这个长方形原来的面积是多少平方米?【例题3】下图是一个养禽专业户用一段16米的篱笆围成的一个长方形养鸡场,求它的占地面积。
练习31、下图是某个养禽专业户用一段长13米的篱笆围成的一个长方形养鸡场,求养鸡场的占地面积。
2、用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?【例题4】街心花园中一个正方形的花坛四周有1米宽的水泥路,如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?练习41、有一个正方形的水池,如下图的阴影部分,在它的周围修一个宽8米的花池,花池的面积是480平方米,求水池的边长。
2、已知大正方形比小正方形的边长多4厘米,大正方形的面积比小正方形面积大96平方厘米(如下图)。
四年级奥数专题第一讲 图形问题

四年级奥数专题第一讲图形问题【一】将一个长10厘米,宽5厘米的长方形纸片,剪成一个最大的正方形,这个正方形的面积是多少平方厘米?练习1、一个长方形,长24分米,如果长减少了4分米,就成了正方形,则原长方形的面积是多少?2、将一个长8厘米,宽5厘米的长方形纸片,剪成一个最大的正方形,要剪去多大面积的纸片?【二】有一块长方形土地,长6米,长是宽的2倍,这块长方形土地的面积是多少?练习1、有一块面积是18平方米的长方形草地,长是宽的2倍,长与宽各是多少?2、一块面积为25平方厘米的正方形手帕,它的边长是多少?【三】竹苑小学操场长60米,宽30米,改造后,长增加10米,宽增加10米。
现在操场面积比原来增加了多少平方米?练习1、有一块长方形的铁片,长16分米,宽9分米,如果长和宽分别减少6分米、5分米,面积比原来减少多少平方分米?2、一个长方形,长15分米,宽6分米,如果长和宽各减少3分米,面积比原来减少多少平方分米?【四】一个长方形,如果长增加3米,那么它的面积增加12平方米;如果宽减少2米,那么它的面积减少14平方米。
这个长方形原来的面积是多少平方米?练习1、一个长方形,如果宽不变,长减少2米,那么它的面积减少24平方米;如果长不变,宽增加3米,那么它的面积增加18平方米,这个长方形原来的面积是多少平方米?2、一个长方形,如果宽不变,长增加8米,那么它的面积增加32平方米,如果长不变,宽增加6米,那么它的面积增加36平方米,这个长方形原来的面积是多少平方米?【五】下图是一个果农在院子周围用一段长20米的篱笆围成的一个长方形围墙,求占地面积有多大?1、用1米长的铁丝围成一个长方形,要使它的宽为15厘米,则它的面积是多少平方厘米?2、一个正方形与一个长方形的周长相等,长方形的长与宽的和是14分米,则正方形的面积是多少?【六】中心小学一个正方形的花坛四周有1米宽的水泥路,如果水泥路的总面积是20平方米,这个花坛的面积是多少平方米?练习1、有一块长方形土地,长是宽的2倍,中间有一座雕塑,雕塑的地面是一个正方形,周围是草坪,那么草坪的面积是多少平方米?2、四个完全相同的长方形和一个小正方形拼成了一个大正方形(如图)。
四年级奥数图形的面积含答案

一、填空题①用一根长36厘米的铁丝围成一个正方形,它的面积是 平方厘米. ②一个长方形周长是68厘米,长比宽的3倍少2厘米,它的面积是 平方厘米.③一个长方形,长25厘米,如果长减少了5厘米,就变成了正方形.它的面积减少了 平方厘米.④如图的阴影部分是一个长方形的花坛,它的四周是用相同的正方形砌成的边框.已知边框的面积是60平方米,那么花坛不包括边框的面积是 平方1一个正方形的边长扩大到原来的2倍,它的面积扩大到原来的 倍.A 2 B4 C8 D 162边长为4厘米的正方形,它的面积和周长相比是 .A 面积大B 周长大C 一样大D 不可比三、简答题⑦如图,有一块长方形土地,长是宽的2倍,中间有一座雕塑,雕塑的底面是,草坪的面积是多少平方米8.如图,已知正方形ABCD 的边长为6分米,长方形BCEF 和长方形AGHD 的面积分别为24平方分米和20平方分米,求阴影部分的面积;2厘米,它的面积就增加16平方厘米,求原正方形面积;10.一个长方形的宽增加4厘米,就成了一个正方形,这样面积就增加了 48平方厘米,求原来长方形的面积.11.一条白色的正方形手帕,它的边长是18厘米,手帕上横、竖各有两道红条,即为如图所示的阴影部分,红条宽都是2厘米,问:这条手帕白色部分的12米,若正中一块正方形铺纯毛地毯,外围铺化纤地毯,共需费用22 455元.已知纯毛地毯每平方米250元,化纤地毯每平方米35,正方形的边长是15厘米,长方形的四个角的顶点,恰好分别把正方形四条迈都分成两段,其中长的一段是短的2倍.这个长答案1. 812.2253.1004.605.B6.D7.199平方米8.8平方分米9.9平方厘米10.96平方厘米11.196平方厘米13. 15平方分米14. 100平方厘米。
小学奥数图形找规律四年级

找规律是解决数学问题的一种重要的手段,而规律的找寻既需要敏锐的观察力,又需要严密的逻辑推理能力.一般地说,在观察图形变化规律时,应抓住一下几点来考虑问题: ⑴图形数量的变化;⑵图形形状的变化;⑶图形大小的变化; ⑷图形颜色的变化;⑸图形位置的变化;⑹图形繁简的变化.对于较复杂的图形,也可分为几部分来分别考虑,总而言之,只要全面观察,勤于思考就一定能抓住规律,解决问题.板块一 数量规律【例 1】 观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?【解析】 横着看,每行圆形的个数一次减少,而三角形的个数依次增加,但每行图形的总个数不变.因为圆形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个圆形。
【巩固】观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形??【解析】 (方法一)横着看,每行三角形的个数依次减少,而正方形的个数依次增加,但每行图形的总个数不变.因为三角形的个数是按4、3、?、1的顺序变化的,显然“?”处应填一个三角形△.(方法二)竖着看,三角形由左而右依次减少,而正方形由左而右依次增加,三角形按照4、?、2、1的顺序变化,也可以看出 “?”处应是三角形△.【例 2】 观察下面的图形,按规律在“?”处填上适当的图形.(5)(4)(3)(2)(1)?图形找规律【解析】本题中,几何图形的变化表现在数量关系上,图中黑三角形的个数从左到右依次增多,从(2)起,每一个格比前面一个格多两个黑三角形,所以,第(4)个方框中应填七个黑三角形.【例 3】观察图形变化规律,在右边补上一幅,使它成为一个完整系列。
【解析】观察发现,乌龟的顺序是:头、身→一只脚、背上一个点→两只脚、背上两个点→两只脚、一条尾、背上三个点→三只脚、一条尾、背上四个点,根据这个规律,最后一幅图应该是:→四只脚、一条尾、背上五个点.即:【例 4】观察图形变化规律,在右边再补上一幅,使它们成为一个完整的系列.【解析】第一格有8个圆圈,第二格有4个圆圈,第三格有2个圆圈,第四格有1个圆圈,第五格有半个圆圈.由此发现,前一格中的图减少一般,正好是后一格的图.所以第六格的图应该是第五格图的一半,即:板块二旋转、轮换型规律【例 5】相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?○□☆△○□☆△△○□☆△○□☆☆△○□☆△○□()()()()()()()()【解析】有几种方法可以找出密码:(方法一)后面一排和前面一排比,上排的第一个图形移到最后,其他每个图形都向前移动了一格,变成了下一排.(方法二)斜着看,每一斜列的图形是一样的.所以密码就是:□☆△○□☆△○【例 6】 观察下图的变化规律,画出丙图.DC BA丙乙甲DCB A【解析】ABCD【总结】旋转是数学中的重要概念,掌握好这个概念,可以提高观察能力,加快解题速度,对于许多问题的解决,也有事半而功倍的效果.【例 7】 下面各种各样的娃娃头好看吗?认真观察你能找到它们排列的规律吗?根据规律把最后一个画出来.【解析】【例 8】 观察图中所给出图形的变化规律,然后在空白处填画上所缺的图形.【解析】【例 9】 琪琪特别喜欢蝴蝶,她用直尺和圆规在纸上画了9幅蝴蝶图,并用剪刀将它们一一剪下来.她将这9只纸蝴蝶摆在桌上,见下图1,她发现这些纸蝴蝶排列挺有规律,突然一阵风来,吹走了3只纸蝴蝶,见下图2.你能找出蝴蝶的排列规律,将图2的3只蝴蝶放入图1的空缺处吗?图1987654321图2B CA【解析】 从已摆好的第一行和第一列来看,无论横看或竖看,同一行中3只蝴蝶的翅膀形状各不相同,翅膀上的斑点的形状也各不相同.根据这个规律,剩下的3只蝴蝶图案的排列应该是:6号位置放图案C ;8号位置放图案B ;9号位置放图案A.【例 10】 观察下列各组图的变化规律,并在“?”处画出相关的图形.(1)丁丙乙甲?【解析】 (1)这四个图形的变化规律是:每一个图形都是由其前一个图形顺时针旋转90°而得到的.见下面左图;(2)甲乙丙丁四个图形变化规律也类似,注意因为图形是由旋转而得到的,所以其中三角形、菱形的方向随旋转而变化,作图的时候要注意到这一点.丁图处的图形应是下面右图:丁【例 11】请你认真仔细观察,按照下面图形的变化规律,在“"”处画出合适的图形。
四年级奥数拼图形练习题及答案【三篇】

四年级奥数拼图形练习题及答案【三篇】
导读:本文四年级奥数拼图形练习题及答案【三篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【第一篇】用三块相同的正方形纸板只能拼成如图所示的两种不同的图形(拼时要求正方形的边要整边重合)。
现在给你四块相同的正方形纸板,最多可以拼成多少种不同的图形(通过翻转或旋转能相互得到的图形视为同一种图形)?
解答:最多可以拼成5种不同的图形通过画图我们可以得出下面的五个图形:
通过画图我们得到最多可以拼成5种不同的图形。
对于这类题目我们可以画图来获得正确的答案。
【第二篇】用三块相同的正方形纸板只能拼成如图所示的两种不同的图形(拼时要求正方形的边要整边重合)。
现在给你四块相同的正方形纸板,最多可以拼成多少种不同的图形(通过翻转或旋转能相互得到的图形视为同一种图形)?
解答:最多可以拼成5种不同的图形通过画图我们可以得出下面的五个图形:
【第三篇】1、数一数下图中有多少个三角形?
答案:6+6+3=15个
2、数一数下图*有多少个三角形?
答案:10+6+6+1+3+1=27。
四年级奥数专题图形周长与面积

• 题目:一个平行四边形的周长是20厘米,其中一条边长是a厘米,则其他三条边的长度是多少? 答案:其他三条边长度分别是:5 a厘米、5 - a厘米、a厘米 解析:根据平行四边形的周长公式,周长 = 2(a + b),其中a和b为平行四边形相邻的两边,可以求出其他 三条边的长度。
• 题目:一个长方形的周长是20厘米,长是a厘米,则宽是多少厘米? 答案:宽 = (20 - 2a) / 2 = 10 - a厘米 解析:根据长方形的周长 公式,周长 = 2(长 + 宽),可以求出宽的表达式。
• 答案:宽 = (20 - 2a) / 2 = 10 - a厘米 • 解析:根据长方形的周长公式,周长 = 2(长 + 宽),可以求出宽的表达式。
• 答案:其他三条边长度分别是:5 - a厘米、5 - a厘米、a厘米 • 解析:根据平行四边形的周长公式,周长 = 2(a + b),其中a和b为平行四边形相邻的两边,可以求出其他三条边的长度。
感谢观看
汇报人:XX
确性
圆形面积的计算
圆的面积公式: A = πr²,其 中r是圆的半径
推导过程:通 过将圆分割成 若干个小的扇 形,然后重新 排列组合成近 似长方形,利 用长方形面积 公式推导得出
计算方法:根 据给定的半径 值,代入公式
中进行计算
注意事项:计 算时要注意单 位的统一,以 及π取值的小
数位数
其他常见图形面积的计算
提高题目练习
四年级奥数思维第 15 周 图形问题

第15周图形问题一、教学内容及要求:1、细心观察,把握图形的特点,合理的进行切拼,从而使问题得以顺利的解答。
2、从整体上观察图形的特征,掌握图形的本质,结合必要的分析,推理和计算,使得隐藏的数量关系明朗化。
二、教学过程:例1:人民南路小学操场长90米,宽45米,改造后,长增加10米,宽增加5米。
现在操场的面积比原来增加了多少平方米?分析:疯狂操练1:1、有一块长方形木板,长22分米,宽8分米,如果长与宽分别减少10分米、3分米,面积比原来减少了多少平方分米?2、一块长方形木板,长18分米,宽13分米,如果长和宽都减少2分米,面积比原来减少了多少平方分米?3、一块长方形地,长是80米,宽是45米,如果把宽增加5米,要是面积不变,长应该减少多少米?例2:一个长方形,如果宽不变,长增加6米,那么面积增加54平方米,如果长不变,宽减少3米,那么它的面积减少36平方米,这个长方形的面积原来是多少平方米?分析:疯狂操练2:1、一个长方形,如果长不变,宽增加4米,那么面积就增加60平方米;如果宽不变,长减少3米,那么面积减少24平方米,这个长方形的面积原来是多少平方米?2、一个长方形,如果宽不变,长增加5米,那么面积就增加30平方米;如果长不变,宽增加3米,那么面积增加48平方米,这个长方形的面积原来是多少平方米?3、一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米,求这个长方形原来的面积。
4米墙墙例3:右图是一个养禽专业户用一段长16米的篱笆围成的一个长方形养鸡场,求占地面积有多大?分析:疯狂操练3:1、 右图是一个养禽专业户用一段长13米的篱笆围成的一个长方形养鸡场,求占地面积有多大?2、 用15长的栅栏沿着一面围墙围一个种植花草的长方形苗圃。
如果每边的长度都是整数,怎样才能使围成的面积最大?例4:街心花园中有一个正方形的花坛四周有1米宽的水泥路,如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?疯狂操练4:1、 有一个正方形水池,如下图的阴影部分,在它的四周修一个宽8米的花池,花池的面积是480平方米,求水池的边长。
奥数之图形问题及答案

奥数之图形问题及答案 Company Document number:WTUT-WT88Y-W8BBGB-BWYTT-19998图形问题(一)1.如图,在三角形ABC中,D是AB的中点,E是DB的中点,F是BC的中点,如果三角形ABC的面积是96cm2,那么三角形AEF的面积是多少平方厘米CFA D E B解:三角形ABF与三角形ABC有公用的顶点A,并且它们的底BC和BF在同一条直线上,所以它们的高相等,而三角形ABF的底BF只有三角形ABC的底BC的一半,所以三角形ABF的面积等于三角形ABC的一半,是96÷2=48(cm2)。
同理,三角形AFD的面积是48÷2=24(cm2),三角形DEF的面积是24÷2=12(cm2),因此,三角形AEF的面积是24+12=36(cm2)。
答:三角形AEF的面积是36 cm2。
2.如图所示,大正方形的边长为12 cm,小正方形的边长为10 cm,求阴影部分的面积。
解:阴影三角形的面积无法直接求出,可以用两个正方形面积的和,减去阴影部分周围三个三角形的面积。
所以,阴影部分的面积是122+102-12×(12+10)÷2-102÷2-12×(12-10)÷2=144+100-132-50-12=50(cm2)。
答:阴影部分的面积是50 cm2。
3.把三角形ABC的边AB三等分,AC四等分,如图。
已知三角形ADE的面积是1 cm2,求三角形ABC的面积是多少平方厘米AE DB C解:三角形AEC的面积是三角形AED的4倍,三角形ABC的面积是三角形AEC的3倍,所以三角形ABC的面积是三角形AED的4×3=12倍,是12(cm2)。
4.一个任意四边形ABCD,将各边延长一倍,得到四边形EFGH如图。
已知四边形ABCD的面积是5 cm2,那么四边形EFGH的面积是多少平方厘米HEA DB C GF解:连接BD、BE,三角形ABD、ABE、BEF的面积相等,所以三角形AEF的面积是三角形ABD的2倍,同理,三角形CHG的面积是三角形BCD的2倍,所以三角形AEF与CGH面积的和是四边形ABCD的2倍;同理,三角形EDH与BFG面积的和也是四边形ABCD的2倍。
四年级奥数-图形问题整理版

练 习 二 1、一个长方形,如果宽不变,长减少3米,那么它 的面积减少24平方米;如果长不变,宽增加4米,那 么它的面积增加60平方米。这个长方形原来的面积 是多少平方米?
2、一个长方形,如果它的长减少3米,或它的宽减 少2米,那么它的面积都减少36平方米。求这个长方 形原来的面积。
例3、下图是一个养禽专业户用一段16米的篱笆围 成的一个长方形养鸡场,求它的占地面积。
分析与解答:用操场现在的面积减去操场原来的面积, 就得到增加的面积。操场现在的面积是:
(90+10)×(45+5)=5000平方米,
操场原来的面积是: 90×45=4050平方米。 所以,现在的面积比原来增加; 5000-4050=950平方米。
练 习 一 1、有一块长方形的木板,长22分米,宽8分米。如 果长和宽分别减少10分米、3分米,面积比原来减少 多少平方分米?
2、一块长方形地,长是80米,宽是45米。如果把 宽增加5米,要使面积不变,长应减少多少米?
例2 、一个长方形,如果宽不变,长增加6米, 那么它的面积增加54平方米;如果长不变,宽 减少3米,那么它的面积减少36平方米。这个长 方形原来的面积是多少平方米?
分析 :由“宽不变,长增加6米,面积增加54平方米” 可知,它的宽为 54÷6=9米; 由“长不变,宽减少3米,面积减少36平方米”可知, 它的长为 36÷3=12米。 所以,这个长方形原来的面积是12×9=108平方米。
例5 、一块正方形的钢板,先截去宽5分米的长方形, 又截去宽8分米的长方形(如图),面积比原来的正方 形减少181平方分米。原正方形的边长是多少?
分析:把阴影部分剪下来,并把剪下的两个小长方形拼起来 (如图),再被上长、宽分别是8分米、5分米的小长方形, 这个拼合成的长方形的面积是: 181+8×5=221平方分米, 长是原来正方形的边长,宽是: 8+5=13分米。 所以,原来正方形的边长是: 221÷13=17分米。
四年级奥数巧解图形拼割问题

巧解图形拼割问题巧点晴——方法和技巧本讲主要讲述一些趣味性的拼图游戏以及图形面积的各种法,如平移、割补等。
要求同学们熟知一些特殊图形的面积计算公式,如三角形、长方形、梯形的面积公式;善于发现所求图形与基本图形之间的关系,熟练掌握图形的拼、割、补。
巧指导——例题精讲A级冲刺名校·基础点晴【例1】四边形ABCD是一个长方形,画一条直线把这个长方形分成两部分,并使这两部分能够拼成一个平行四边形、三角形或梯形。
问这条直线应该怎么画?做一做1 把下列各图分别剪成三块,各拼成正方形。
【例2】将一个长为9,宽为4的长方形(如下图①)分成两块,然后拼成一个正方形。
分析与解先算出所拼正方形的边长。
因为拼成的正方形的面积与原长方形的面积相等。
4×9=36=6×6,所以正方形的边长是6。
正方形的边长为6,将下图①分成两块,如下图②),然后拼成正方形,如下图③所示:③做一做2 将长为36,宽为25的长方形分成两块,然后拼成一个正方形。
【例3】如下图,用方格纸剪成面积是4平方厘米的图形,图形形状有7种。
其中有哪种图形可以拼成面积是16平方厘米的正方形?①②③④⑤⑥⑦做一做3 用方格剪成面积是4的图形,其形状只有以下7种。
如果用其中的四种图形拼成面积是16的正方形,那么这种图形的编号和的最小值是。
①②③④⑤⑥⑦B级培优竞赛·更上层楼【例4】怎样把两张正方纸拼成一个大正方形纸?分析与解1 把两张正方形纸都沿着其一条对角线剪开,然后拼成一张大正方形纸,如下图所示:分析与解2 把两张正方形纸中的一张正方形纸沿其两条对角线剪分析与解3 把两张正方形纸分别沿其两条对角线剪开,然后拼成一张大正方形纸,如下图所示:做一做4 你能想出例3的其他拼法吗?【例5】图钉钉画:把4张长方形画用图钉钉在墙上,要使每张画的4个角上都钉上图钉,一共需要几颗图钉?方法1 如下图所示,把4张画分开钉,每张需4个图钉,用16个图钉。
四年级奥数之数数图形一

数数图形
1 .数一数下图中有多少个长方形?
2 .数一数,下面各图中分别有几个长方形?
3 .数一数,下图中有多少个正方形?(每个小方格是边长为1的正方形)
4 .数一数下列各图中分别有多少个正方形?(每个小方格为边长是1的小正方形)
5 .数一数下图中有多少个正方形?(其中每个小方格都是边长为1个长度单位的正方形)
6.数一数下列各图中分别有多少个正方形。
7 .下图中有多少个长方形,其中有多少个是正方形?
8 .从广州到北京的某次快车中途要停靠8个大站,铁路局
要为这次快车准备多少种不同车的车票?这些车票中有多少种不同的票价?
9 .从上海到武汉的航运线上,有9个停靠码头,航运公司要为这段航运线准备多少种不同的船票?
10 .从上海至青岛的某次直快列车,中途要停靠6个大站,这次列车有几种不同票价?
11 .从成都到南京的快车,中途要停靠9个站,有几种不
同的票价?
12 .求下列图中线段长度的总和。
(单位:厘米)
13 .一条线段上有21个点(包括两个端点),相邻两点的距离都是4厘米,所有线段长度的总和是多少?
14 .求下图中所有线段的总和。
(单位:米)
15 .求下图中所有线段的总和。
(单位:厘米)。
四年级几何奥数题

四年级几何奥数题
一、题目示例
1. 一个等腰三角形的顶角是底角的4倍,求这个等腰三角形的底角和顶角各是多少度?
解析:
因为等腰三角形的两个底角相等,设底角的度数为公式,则顶角的度数为公式。
根据三角形内角和为公式,可列出方程公式。
合并同类项得公式。
解得公式。
那么顶角公式。
所以这个等腰三角形的底角是公式,顶角是公式。
2. 长方形的长是12厘米,宽是8厘米,求这个长方形的对角线长度。
解析:
根据长方形的性质,对角线与长和宽构成直角三角形,长和宽为直角边,对角线为斜边。
由勾股定理公式(其中公式、公式为直角边,公式
为斜边)。
这里公式厘米,公式厘米。
则对角线公式厘米。
3. 一个平行四边形的底是10厘米,高是8厘米,如果底减少3厘米,高不变,那么面积减少多少平方厘米?
解析:
原来平行四边形的面积公式平方厘米。
底减少3厘米后,新的底为公式厘米。
此时平行四边形的面积公式平方厘米。
面积减少的值为公式平方厘米。
(完整版)四年级奥数图形问题

图形问题:练习1:1.人民路小学操场长90米,宽45米,改造后,长和宽分别增加10米。
现在操场面积比原来增加了多少平方米?2.有一块长方形的木板,长22分米,宽8分米。
如果长和宽分别减少10分米和3分泌,面积比原来减少多少平方分米?3.一块长方形地,长是80米,宽是45米,如果把宽增加5米,要使面积不变,长应减少多少米?练习2:4.一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米;如果长不变,宽增加4米,那么它的面积增加60平方米。
这个长方形原来的面积是多少平方米?5.一个长方形,如果宽不变,长增加6米,那么它的面积增加54平方米;如果长不变,宽减少3米,那么它的面积减少36平方米。
问这个长方形的面积是多少平方米?6.一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米。
求这个长方形原来的面积。
练习3:7.右图是某个养禽专业户用一段长13米的篱笆围成一个长方形的养鸡场,求养鸡场的占地面积有多大?8.用56米长的木栏围成长或宽是20米的长方形,其中一边利用围墙,怎样才能使围成的面积最大?练习4:9.有一个正方形的水池,如右图的阴影部分,在它的周围修一个宽8米的花池,花池的面积是480平方米,求水池的边长。
11.四个完全相同的长方形和一个小正方形拼成一个大正方形(如右图)。
大正方形的面积是100平方分米,小正方形的面积是16平方分米,求每个小长方形的面积是多少平方分米?它的宽又是多少分米?巧妙求和(二)练习1:1.刘师傅做一批零件,第一天做了20个,以后每天都比前一天多做2个,第15天做了48个,正好做完。
这批零件共有多少个?2.胡倩读一本故事书,她第一天读了20页,从第二天起,每天读的页数都比前一天多5页,最后一天读了50页恰好读完。
这本书共有多少页?3.丽丽学英语单词,第一天学会了6个,以后每天都比前一天多学1个,最后一天学会了16个。
丽丽在这些天中学会了多少个单词?练习二:4.有80把锁的钥匙搞乱了,为了使每把锁都配上自己的钥匙,至多要试多少次?5.有一些锁的钥匙搞乱了,已知至多要试28次,就能使每把锁都配上自己的钥匙。
四年级奥数-巧数图形个数

姓名:巧数图形个数“数图形的个数”是趣味图形问题的一种,由于几何图形千变万化,错综复杂,要想准确地数出图形中所包含的某一个几何图形的个数,关键是要掌握有条理有次序地数图形的方法。
数图形的个数时,既不能同一图形数两次,又不能把有的图形漏掉不数,常用的计算方法有按顺序和分类数两种。
下面举例介绍两种方法的运用规律:例:数一数下面图中有多少条线段。
第一:按含基本线段的顺序去数。
上图一共有5条小线段,这每条小线段就是基本线段,有5条基本线段,包含有两条基本线段的有4条……第二:按端点进行分类去数。
以线段最左边的点为第一个端点,第二个点为第二个端点……为了方便同学们计数,向大家介绍数线段、三角形、角数量的公式:1+2+…+(n-2)+(n-1)=2)1(nn一、试一试,看谁数得又对又快。
一共有()个三角形。
一共有()个角。
二、填空。
1. 算式中有乘法和加、减法,应先算();算式中有除法和加、减法,应先算();算式中有括号的,应先算()。
2. 在计算25+13×2时,先算( )法,再算( )法。
3. 在计算78÷16×3时,先算()法,再算()法。
4. 在算式50-20÷5里,如果要先算减法,那么算式应该是:()。
里填上“<”“>”或“=”。
20×5+×(5+3)48÷6÷÷(6×8)280-37-280-(37+163)60-24÷60-24)÷12小故事明明和沉沉都十分喜欢数学。
一天明明问沉沉:“你最喜欢几?”“我最喜欢9。
”“那你说说从1数到100,要说几次‘9’?”“啊!……这”沉沉被难住了,“这要数一数才能知道,一分钟时间。
”同学们,请你在一分钟内说出从1到100有多少个9?。
小学四年级上册的奥数图形题

小学四年级上册的奥数图形题
一个正方形的边长是8厘米,它的面积是多少平方厘米?
一个长方形的长是12厘米,宽是8厘米,它的周长和面积分别是多少?
一个平行四边形的底是10厘米,高是6厘米,它的面积是多少平方厘米?
一个三角形的底是15厘米,高是8厘米,它的面积是多少平方厘米?一个梯形的上底是6厘米,下底是10厘米,高是8厘米,它的面积是多少平方厘米?
一个圆的半径是5厘米,它的周长和面积分别是多少?
一个圆环的内圆半径是4厘米,外圆半径是6厘米,它的面积是多少平方厘米?
一个长方形的周长是36厘米,长是宽的2倍,它的长和宽分别是多少厘米?
一个正方形的周长是40厘米,它的面积是多少平方厘米?
一个平行四边形的周长是52厘米,一条底边长是10厘米,它的高是多少厘米?
一个等腰三角形的周长是30厘米,一条腰长是10厘米,它的底边长是多少厘米?
一个等边三角形的边长是8厘米,它的周长和面积分别是多少?
一个直角三角形的两条直角边分别是6厘米和8厘米,它的斜边长是多少厘米?
一个长方体的长、宽、高分别是10厘米、8厘米、6厘米,它的表面积和体积分别是多少?
一个正方体的棱长是6厘米,它的表面积和体积分别是多少?
一个圆柱的底面半径是4厘米,高是10厘米,它的表面积和体积分别是多少?
一个圆锥的底面半径是3厘米,高是6厘米,它的体积是多少立方厘米?
一个长方体鱼缸的长是8分米,宽是4分米,高是6分米,它的容积是多少升?
一个正方体水池的棱长是2米,它最多能装多少立方米的水?
一块长方形菜地的长是20米,宽是15米,如果每平方米收菜5千克,这块菜地一共可以收菜多少千克?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
练 习 二 1、一个长方形,如果宽不变,长减少3米,那么它 的面积减少24平方米;如果长不变,宽增加4米,那 么它的面积增加60平方米。这个长方形原来的面积 是多少平方米?
2、一个长方形,如果它的长减少3米,或它的宽减 少2米,那么它的面积都减少36平方米。求这个长方 形原来的面积。
例3、下图是一个养禽专业户用一段16米的篱笆围 成的一个长方形养鸡场,求它的占地面积。
分析 :根据题意,因为一面利用着墙,所以两条长 加一条宽等于16米。而宽是4米,那么长是: (16-4)÷2=6米, 占地面积是: 6×4=24平方米。
练 习 三 1、右图是某个养禽专业户用一段长13米的篱笆围成 的一个长方形养鸡场,求养鸡场的占地面积。
2、用56米长的木栏围成长或宽是20米的长方形,其 中一边利用围墙,怎样才能使围成的面积最大?
练 习 三
3,用15米长的栅栏沿着围墙围一个种植花草 的长方形苗圃,其中一面利用着墙。如果每边 的长度都是整数,怎样才能使围成的面积最大?
例4 、街心花园中一个正方形的花坛四周有1米宽的 水泥路,如果水泥路的总面积是12平方米,中间花 坛的面积是多少平方米?
分析 :把水泥路分成四个同样大小的长方形(如上图)。因 此,一个长方形的面积是: 12÷4=3平方米。 因为水泥路宽1米,所以小长方形的长是:3÷1=3米。 从图中可以看出正方形花坛的边长是小长方形长与宽的差,所 以小正方形的边长是: 3-1=2米。 中间花坛的面积是 2×2=4平方米。
分析与解答:用操场现在的面积减去操场原来的面积, 就得到增加的面积。操场现在的面积是:
(90+10)×(45+5)=5000平方米,
操场原来的面积是: 90×45=4050平方米。 所以,现在的面积比原来增加; 5000-4050=950平方米。
练 习 一 1、有一块长方形的木板,长22分米,宽8分米。如 果长和宽分别减少10分米、3分米,面积比原来减少 多少平方分米?
练 习 五 1、一个正方形一条边减少6分米,另一条边减少10 分米后变为一个长方形,这个长方形的面积比正方 形的面积少260平方米,求原来正方形的边长。
2、一个长方形的木板,如果长减少5分米,宽减少2 分米,那么它的面积就减少66平方分米,这时剩下 的部分恰好是一个正方形。求原来长方形的面积。
练 习 四 1、有一个正方形的水池,如下图的阴影部分,在它 的周围修一个宽8米的花池,花池的面积是480平方 米,求水池的边长。
2、四个完全相同的长方形和一个小正方形拼成了一 个大正方形(如上图),大正方形的面积是64平方 米,小正方形的面积是4平方米,长方形的短边是多 少米?
练 习 四 3、已知大正方形比小正方形的边长多4厘米,大正 方形的面积比小正方形面积大96平方厘米(如下 图)。问大小正方形的面积各是多少?
专题简析: 1、细心观察,把握图形特点,合理地进行切拼,
解答有关“图形面积”问题时,应注意以下几点: 从而使问题得以顺利地解决;
2、从整体上观察图形特征,掌握图形本质,结
合必要的分析推理和计算,使隐蔽的数量关系明
朗化。
例1 、人民路小学操场长90米,宽45米。改造 后,长增加10米,宽增加5米。现在操场面积比 原来增加了多少平方米?
2、一块长方形地,长是80米,宽是45米。如果把 宽增加5米,要使面积不变,长应减少多少米?
例2 、一个长方形,如果宽不变,长增加6米, 那么它的面积增加54平方米;如果长不变,宽 减少3米,那么它的面积减少36平方米。这个长 方形原来的面积是多少平方米?
分析 :由“宽不变,长增加6米,面积增加54平方米” 可知,它的宽为 54÷6=9米; 由“长不变,宽减少3米,面积减少36平方米”可知, 它的长为 36÷3=12米。 所以,这个长方形原来的面积是12×9=108平方米。
例5 、一块正方形的钢板,先截去宽5分米的长方形, 又截去宽8分米的长方形(如图),面积比原来的正方 形减少181平方分米。原正方形的边长是多少?
分析:把阴影部分剪下来,并把剪下的两个小长方形拼起来 (如图),再被上长、宽分别是8分米、5分米的小长方形, 这个拼合成的长方形的面积是: 181+8×5=221平方分米, 长是原来正方形的边长,宽是: 8+5=13分米。 所以,原来正方形的边长是: 221÷13=17分米。
