建筑力学第三章 平面力系的平衡方程[精]
合集下载
建筑力学 第三章

[例] 已知:如图。求梁上分布荷载的合力。 解:荷载分布在一狭长 范围内,如沿构件的轴线分 布,则称为分布荷载。该问 题是一集度按线性变化的
线分布荷载求合力问题。
⒈求合力的大小
而在此微段上的荷载为:
x q 在坐标 x 处取长为 dx 的微段,其集度为: x q l
x dQ qx dx q dx l
x 1 因此,合力Q 的大小为: dQ q dx ql Q l 0 l 2
l
⒉ 求合力作用线的位置
由合力矩定理:M A (Q ) M A (dQ ) 则有:
x Q xc dQ x q dx l 0 l 1 1 2 即: ql xc ql 2 3 2 解得: xc l 3
雨搭 固定端(插入端)约束的构造
车刀
约束反力
①认为Fi这群力在同一
平面内;
② 将Fi向A点简化得一 力和一力偶; ③RA方向不定可用正交 分力YA, XA表示; ④ YA, XA, MA为固定端 约束反力; ⑤ YA, XA限制物体平动,
MA为限制转动。
§3-3-2
平面一般力系的简化结果 合力矩定理
第三章
平面力系的合成与平衡 引 言
力系分为:平面力系、空间力系 ①平面汇交力系 ②平面平行力系(平面力偶系是其中的特殊情况 ) ③平面一般力系(平面任意力系)
平面力系
平面汇交力系: 各力的作用线都在同一平面内且 汇交于一点的力系。
研究方法:图解法,数解法。
例:起重机的挂钩。
§3-1-1 平面汇交力系合成与平衡的图解法 P29
l
2
§3-4
由于
R
平面一般力系的平衡方程
一、平衡的必要与充分条件 =0 作用于简化中心的合力RO=0,则汇交力系平衡; 则力偶矩MO=0 ,因此附加力偶系也平衡。
建筑力学第三章 平面力系的平衡方程
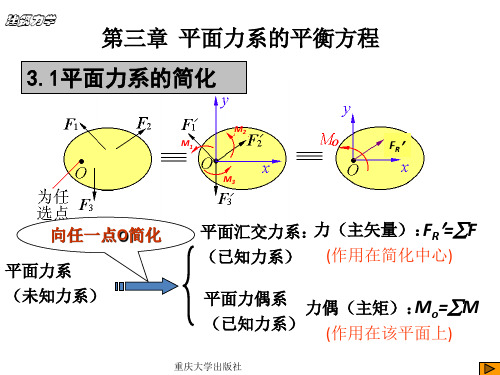
刚体等效于只有一个力偶的作用,(因为力偶可以在刚 体平面内任意移动,故这时,主矩与简化中心O无关。)
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时, 简化结果就是合力(这个力系的合力), FR FR'。(此时
与简化中心有关,换个简化中心,主矩不为零)
重庆大学出版社
建筑力学
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
重庆大学出版社
建筑力学
[例] 已知:Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求:
BC杆拉力和铰A处的支座反力?
解:(1)选AB梁为研究对象。
C
(2)画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
Байду номын сангаас
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
重庆大学出版社
建筑力学
物系平衡问题的特点: ①物体系统平衡,物系中每个单体也是平衡的。 ②每个单体可列3个(平面任意力系)平衡方程,整个系统
可列3n个方程(设物系中有n个物体)。
解物系问题的一般方法:
机构问题: 个体 个体
个体
“各个击破”
力系中各力对于同一点之矩的代数和。
重庆大学出版社
建筑力学
3.2平面力系的平衡方程及应用
FR=0, MO =0,力系平衡
FR =0 为力平衡
MO =0 为力偶也平衡 平面力系平衡的充要条件为:
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时, 简化结果就是合力(这个力系的合力), FR FR'。(此时
与简化中心有关,换个简化中心,主矩不为零)
重庆大学出版社
建筑力学
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
重庆大学出版社
建筑力学
[例] 已知:Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求:
BC杆拉力和铰A处的支座反力?
解:(1)选AB梁为研究对象。
C
(2)画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
Байду номын сангаас
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
重庆大学出版社
建筑力学
物系平衡问题的特点: ①物体系统平衡,物系中每个单体也是平衡的。 ②每个单体可列3个(平面任意力系)平衡方程,整个系统
可列3n个方程(设物系中有n个物体)。
解物系问题的一般方法:
机构问题: 个体 个体
个体
“各个击破”
力系中各力对于同一点之矩的代数和。
重庆大学出版社
建筑力学
3.2平面力系的平衡方程及应用
FR=0, MO =0,力系平衡
FR =0 为力平衡
MO =0 为力偶也平衡 平面力系平衡的充要条件为:
建筑力学平面一般力系的平衡方程及其应用

普通高等教育“十一五”国家级规划教材
满足平衡方程时,物体既不能移动,也不能 转动,物体就处于平衡状态。当物体在平面一般 力系的作用下平衡时,可用三个独立的平衡方程 求解三个未知量。 二、平衡方程的其它形式
1.二力矩形式的平衡方程 ∑FX= 0 ∑MA (F ) = 0 ∑MB (F ) = 0 式中x轴不可与A、B两点的连线垂直。
FAx
FNCD = 30kN (↗)
∑MD (F ) = 0
FNCD
- FAy×0.6 + 14 ×0.3 = 0
14kN 8kN
300
300 100
A 30° D B
FAy
C
FAy = 7kN (↑)
∑MC (F ) = 0
- FAx×0.6/ 3- 14 ×0.3
- 8 ×0.6 = 0 FAx = - 25.98kN (←)
5 + FAy= 0
普通高等教育“十一五”国家级规划教材
3kN·m 6kN
3m
6
A
B
5
5
3m
可取∑MB (F ) = 0这一未用过的方程进行校核: 3 + 5×3 - 6×3 = 0
说明计算无误。
普通高等教育“十一五”国家级规划教材
例4-4 梁AB一端是固定端支座,另一端无
约束,这样的梁称为悬臂梁。它承受荷载作用如
普通高等教育“十一五”国家级规划教材
在使用三力矩式计算出结果后,可用另外两 个投影方程之一进行校核。可知计算无误。
例4-6 外伸梁受荷载如图所示。已知均布荷载 集度q=20kN/m,力偶的力偶矩M=38kN·m,集中 力FP=10kN。试求支座A、B的反力。
10kN 20kN/m 38kN·m
建筑力学 平面一般力系的平衡
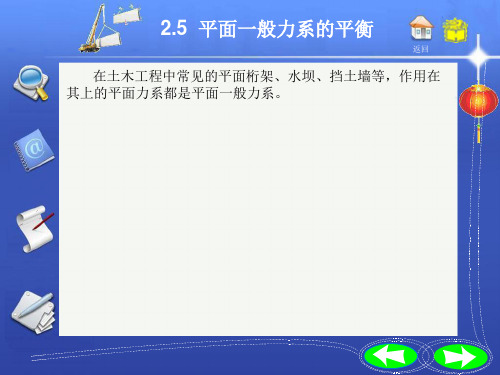
Fcy F 2 sin 60 F ND 20 0.866 8.66 8.66kN
(2) 取梁AC为研究对象,受力图如图(c)
M
A
(F
)
0,
F1
2
F
' Cy
6
F
NB
4
0
F
NB
F1 2
F
' Cy
4
6
10 2
8.66 6 4
17.99kN()
F
x
0,
F
Ax
F
' Cx
0
F
Ax
F
' Cx
10kN()
(1) 取梁CD 为研究对象,受力图如图(b)
M C (F ) 0, F 2 sin 60 2 F ND 4 0
F
ND
sin
60
2
8.66 k N()
F x 0, Fcx F 2 cos60 0
Fcx F 2 cos60 20 0.5 10kN
F y 0, F cy F ND F 2 sin 60 0
F
y
0,
F
Ay
F
NB
F1
F
' Cy
0
F
Ay
F
NB
F1
F
' Cy
17.99
10
8.66
0.67k
N()
求解物体系统平衡问题的要领如下: (1) “拆”:将物体系统从相互联系的地方拆开,在拆开的地方用 相应的约束力代替约束对物体的作用。这样,就把物体系统分解为若 干个单个物体,单个物体受力简单,便于分析。 (2)“ 比”:比较系统的独立平衡方程个数和未知量个数,若彼此 相等,则可根据平衡方程求解出全部未知量。一般来说,由n 个物体 组成的系统,可以建立3n 个独立的平衡方程。 (3) “取”:根据已知条件和所求的未知量,选取研究对象。通常 可先由整体系统的平衡,求出某些待求的未知量,然后再根据需要适 当选取系统中的某些部分为研究对象,求出其余的未知量。 (4) 在各单个物体的受力图上,物体间相互作用的力一定要符合作 用与反作用关系。物体拆开处的作用与反作用关系,是顺次继续求解 未知力的“桥”。在一个物体上,可能某拆开处的相互作用力是未知 的,但求解之后,对与它在该处联系的另一物体就成为已知的了。可 见,作用与反作用关系在这里起“桥”的作用。 (5) 注意选择平衡方程的适当形式和选取适当的坐标轴及矩心,尽 可能做到在一个平衡方程中只含有一个未知量,并尽可能使计算简化。
-平面力系及平衡方程

-平面力系及平衡方程
主矩:指原平面一般力系对简化中心之矩的代数和
mo (Fi ) 。
即 Mo mo (Fi )
MO mO (Fi )
主矩 MO正、负规定 : 转向 +
–
注意:因主矩等于各力对简化中心之矩的代数和, 所以它的大小和转向一般与简化中心有关。
-平面力系及平衡方程
平面力系简化结果的讨论
如果已知力F在直角坐标轴上的投影Fx和Fy, 则力F的大小和方向可由下式确定
F Fx2 Fy2
tan Fy
Fx
力F的指向和投影Fx和Fy的正负号判定: 如果把力F沿x、y轴分解为两个分力F1、F2, 投影的绝对值等于分力的大小,投影的正负号指明 了分力是沿该轴的正向还是负向。 (力的投影是代数量)。
图1-36平面汇交力系
(2)平面平行力系:力系中各力作用在同一个平面内,且各 个力的作用线都相互平行,如图1-37所示。
图1-37平面平行力系
(3)平面一般力系:力系中各力作用在同一个平面 内,且各个力的作用线在平面内任意分布,如图1-38 所示。
图1-38平面一般力系
二、平面汇交力系 1、力在坐标轴上的投影 设力F作用于物体的A点,如图所示。
(1)FR=0,而MO≠0,原力系合成为力偶。这时力系主矩MO 不随简化中心位置而变。
(2)MO=0,而FR≠0,原力系合成为一个力。作用于点O 的 力FR就是原力系的合力。
(3) FR≠ 0, MO≠0, 原力系简化成一个力偶和一个作用于 点O 的力。这时力系也可合成为一个力。
说明如下:
FR
MO
O
三、平面力偶系
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系 设有两个力偶
主矩:指原平面一般力系对简化中心之矩的代数和
mo (Fi ) 。
即 Mo mo (Fi )
MO mO (Fi )
主矩 MO正、负规定 : 转向 +
–
注意:因主矩等于各力对简化中心之矩的代数和, 所以它的大小和转向一般与简化中心有关。
-平面力系及平衡方程
平面力系简化结果的讨论
如果已知力F在直角坐标轴上的投影Fx和Fy, 则力F的大小和方向可由下式确定
F Fx2 Fy2
tan Fy
Fx
力F的指向和投影Fx和Fy的正负号判定: 如果把力F沿x、y轴分解为两个分力F1、F2, 投影的绝对值等于分力的大小,投影的正负号指明 了分力是沿该轴的正向还是负向。 (力的投影是代数量)。
图1-36平面汇交力系
(2)平面平行力系:力系中各力作用在同一个平面内,且各 个力的作用线都相互平行,如图1-37所示。
图1-37平面平行力系
(3)平面一般力系:力系中各力作用在同一个平面 内,且各个力的作用线在平面内任意分布,如图1-38 所示。
图1-38平面一般力系
二、平面汇交力系 1、力在坐标轴上的投影 设力F作用于物体的A点,如图所示。
(1)FR=0,而MO≠0,原力系合成为力偶。这时力系主矩MO 不随简化中心位置而变。
(2)MO=0,而FR≠0,原力系合成为一个力。作用于点O 的 力FR就是原力系的合力。
(3) FR≠ 0, MO≠0, 原力系简化成一个力偶和一个作用于 点O 的力。这时力系也可合成为一个力。
说明如下:
FR
MO
O
三、平面力偶系
平面力偶系:作用在物体同一平面的许多力偶叫平面力偶系 设有两个力偶
-建筑力学第三章平面力系的合成与平衡

平面汇交力系合成与平衡的几何法小 结
几何法解题步骤:1. 取研究对象;2. 画受力图; 3. 作力多边形;4. 选比例尺; 5. 解出未知数。
几何法解题不足: 1. 精度不够,误差大; 2. 作图要求精度高; 3. 不能表达各个量之间的函数关系。
平面汇交力系合成与平衡的另一种方法: 解析法(重点掌 握)。
R0
Rx2
R
2 y
0
或:力系中所有力在各个坐标轴上投影的代
数和分别等于零。
Rx Fx 0 Ry Fy 0
为平衡的充要条件, 也叫平衡方程
解析法求解汇交力系平衡问题的一般步骤:
1.选-对像;即依需选分离体,分离体选取应最好含题设
的已知条件; 2.画-分离体受力图,作到准确无误;
应用力线平移定理,可将刚体上平面任意力系中各个力
的作用线全部平行移到作用面内某一给定点O 。从而这
力系被分解为平面汇交力系和平面力偶系。这种变换的
方法称为力系向给定点O 的简化。点O 称为简化中心。 R0 -----主矢,与简化中心选取无关; M0 ---主矩,与简化中心有关。
2、主矢和主矩 (1)主矢R0
F3 F2
D
C
F2 F4 F3
R
F4
R
F4
E
E
3、汇交力系的合成结果
汇交力系可以合成为一个力,合力作用在力系
的公共作用点,它等于这些力的矢量和,并可由这
力系的力多边形的封闭边表示。
矢量的表达式:R F1 F 2
F1
A F2
F4 F3
F1
A
B F2
R
C
F3
D
F4
n
第3讲平面力系的平衡

M=MB(FP)=-FP×e=-100kN×0.4m=-40kN·m
负号表示该附加力偶的转向是顺时针转向的。
2.平面一般力系向作用平面内任一点的简化 平面一般力系向作用平面内任一点的简化
F'Rx = ∑Fx F'Ry = ∑Fy
y MO F'R α x
O·
FR' = Fx ' 2 + Fy ' 2
B
30° 60°
A
C W
[例1] 支架由直杆AB、AC构成,A、B、C三处都是铰链,在A点 例 悬挂重量为W=20kN的重物,如图所示,求杆AB、AC所受的力。杆 的自重不计。
B y FAB
30°
[解](1)选取研究对象 解 (2)画受力图 (3)建立坐标系 3 (4)列平衡方程并解之 ∑Fx=0, -FAC-Wcos60°=0 FAC =-Wcos60°=-10kN (压) ∑Fy=0, FAB-Wsin60°=0 FAB =Wsin60°=17.3 kN (拉)
第3讲 平面力系平衡
主讲教师:王艳 联系方式:wy_01021604@
预备知识
平面一般力系的合成
1.力的平移定理 力的平移定理
如果一个力大小、方向均不变,只是将力的作用线平行移 动到某一点,称为力向一点平移
F′ A· O F (a) A· O (b) A·
F′ M O (c)
1.力的平移定理 力的平移定理
F F′
O。 A。 O。 d
F
A。
F′
M A。 O。
F"
M=Fd=MO(F)
1.力的平移定理 力的平移定理
F F′
O。 A。 O。 d
F
平面力系的平衡方程及应用

研究方法:几何法,解析法。
各力的作用线都在同一平面内且 汇交于一点的力系。
正文
力在直角坐标轴上的投影
1
Fx=F·cosa ; Fy=F·sina = F ·cosb
说明: (1)力在坐标轴上的投影为代数量; (2)力的指向与坐标轴的正向一致时,力的投影为正值,否则为负。
正文
合力投影定理
推论1:力偶对刚体的作用与力偶在其作用面内的位置无关;
推论2:只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力的大小和力偶臂的长短,而不改变力偶对刚体的作用。
M
M
M
力偶表示方法
正文
思考:
力偶与力的异同
共同点:单位统一,符号规定统一。 差异点:1.力矩随矩心位置不同而变化;力 偶矩对物体作用效果与矩心选取无关。 2.力偶矩可以完全描述一个力偶;力对点之矩不能完全描述一个力。
′
F
M
单 手 攻 丝
正文
平面任意力系的简化
1
平面一般力系向平面内一点简化
F3
F1
F2
O
O
O
F
R′
MO
F
1′
M1
F1 =F1
′ M1=MO(F1)
F
2′
M2
F
3′
M3
F2 =F2
′ M2=MO(F2)
F3 =F3
′ M3=MO(F3)
简化中心
O
FR=F1+F2+F3= F1+F2+F3 MO=M1+M2+M3=MO(F1)+ MO(F2) + MO(F3)
正文
平面力偶系的合成与平衡
各力的作用线都在同一平面内且 汇交于一点的力系。
正文
力在直角坐标轴上的投影
1
Fx=F·cosa ; Fy=F·sina = F ·cosb
说明: (1)力在坐标轴上的投影为代数量; (2)力的指向与坐标轴的正向一致时,力的投影为正值,否则为负。
正文
合力投影定理
推论1:力偶对刚体的作用与力偶在其作用面内的位置无关;
推论2:只要保持力偶矩的大小和力偶的转向不变,可以同时改变力偶中力的大小和力偶臂的长短,而不改变力偶对刚体的作用。
M
M
M
力偶表示方法
正文
思考:
力偶与力的异同
共同点:单位统一,符号规定统一。 差异点:1.力矩随矩心位置不同而变化;力 偶矩对物体作用效果与矩心选取无关。 2.力偶矩可以完全描述一个力偶;力对点之矩不能完全描述一个力。
′
F
M
单 手 攻 丝
正文
平面任意力系的简化
1
平面一般力系向平面内一点简化
F3
F1
F2
O
O
O
F
R′
MO
F
1′
M1
F1 =F1
′ M1=MO(F1)
F
2′
M2
F
3′
M3
F2 =F2
′ M2=MO(F2)
F3 =F3
′ M3=MO(F3)
简化中心
O
FR=F1+F2+F3= F1+F2+F3 MO=M1+M2+M3=MO(F1)+ MO(F2) + MO(F3)
正文
平面力偶系的合成与平衡
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
建筑力学
第三章 平面力系的平衡方程
3.1平面力系的简化
M2
M1
FR
M3
向任一点O简化
平面力系 (未知力系)
平面汇交力系:力(主矢量):FR=F
(已知力系) (作用在简化中心)
平(面已力知偶力系系)力偶(作(用主在矩该)平:面M上o=)M
重庆大学出版社
建筑力学
一般情况:
主矢 : FR ' F1 F2 F3 Fi
FAy
FBC
A
FAx
l/2 a
P
B Q
l
MB (Fi ) 0 MC (Fi ) 0
l FAyl P 2 Q(l a) 0
FAx l
tg
P
l 2
Qa
0
FAy 2.1kN
FAx 11.4kN
重庆大学出版社
建筑力学
[例] 已知:P=20kN, M=16kN·m, q=20kN/m, a=0.8m
20 20 0.8 12
12(kN)
24(kN)
重庆大学出版社
建筑力学
FAy FAx
FB
静定(未知数三个)
FAy FAx
FBy FBx
静不定(未知数四个)
独立方程数目≥未知数数目时,是静定问题(可求解) 独立方程数目<未知数数目时,是静不定问题(超静定问题)
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
简化中心 (与简化中心位置无关) [因主矢等于各力的矢量和]
重庆大学出版社
建筑力学
主矩MO (转动效应)
大小:MO MO (Fi )
方向: 方向规定 + —
简化中心: (与简化中心有关) (因主矩等于各力对简化中心取矩的代数和)
重庆大学出版社
建筑力学
简化结果分析 合力矩定理
简化结果: 主矢FR',主矩 MO ,下面分别讨论。 ① FR' =0, MO =0,则力系平衡,下节专门讨论。 ② FR' =0, MO≠0,即简化结果为一合力偶, M=MO 此时
重庆大学出版社
建筑力学
[例] 已知:q, a , P=qa, M=Pa,求:A、B两点的支座反力?
解:① 选AB梁为研究对象。
② 画受力图
qP
FAy
qP
FB
A
B
M
2a
a
FAx
A
M
B
列平衡方程,求未知量。
Fx 0
Fy 0
FAx 0
FB FAy P 2qa 0,
M A(Fi ) 0
FAx
FBC
sin
l
P
l 2
Qa
0
FAy
FBC
A
l/2 P
B Q
a
l
FBC (Pl / 2 Qa) /(l sin ) 13.2kN
Fx 0
Fy 0
FAx FBC cos 0
FAx FBC cos 11.4kN
求:A、B的支反力。
q FA M FB
解:研究AB梁
P
MA(F ) 0;
A
B
a
a
a
FB
a
q
a
a 2
M
P
2a
0
Fy 0
FA FB qa P 0
FB
qa 2
M a
2P
20 0.8 16 2 20
2
0.8
FA P qa FB
a
l
MB (Fi ) 0
l FAyl P 2 Q(l a) 0
FAy 2.1kN
Fx 0
FAx FBC cos 0
FAx 11.4kN
重庆大学出版社
建筑力学
M A(Fi ) 0
FBC
sin
l
P
l 2
Qa
0
FBC 13.2KN
重庆大学出版社
建筑力学
[例] 已知:Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求:
BC杆拉力和铰A处的支座反力?
解:(1)选AB梁为研究对象。
C
(2)画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
4qa FAy 3
M A (Fi ) 0 P 2a q 2a a M FB 3a 0
5qa FB 3
重庆大学出版社
建筑力学
平面力系的平衡方程:
① 基本式(一矩式) ②二矩式
③三矩式
Fx 0
Fy 0
Fx 0 M A(Fi ) 0
主矩: MO M1 M2 M3
MO (F1) MO (F2) MO (Fi )
大小:FR ' F 'Rx2 F 'Ry2 ( Fx )2 ( Fy )2
主矢 FR'
(移动效应)
方向: tan1 FRy
FRx
tan1
Fy Fx
M A(Fi ) 0 MB (Fi ) 0
MO (Fi ) 0
MB (Fi ) 0
MC (Fi ) 0
条件:x 轴不垂直 于AB连线
条件:A,B,C不在 同一直线上
只有三个独立方程,只能求出三个未知数。
投影轴和矩心是任意选取的,一般先取矩。矩心选 择在多个未知力的交点上;投影轴尽量与未知力垂 直或平行。
重庆大学出版社
建筑力学
物系平衡问题的特点: ①物体系统平衡,物系中每个单体也是平衡的。 ②每个单体可列3个(平面任意力系)平衡方程,整个系统
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
简化为一个合力 FR。
FR FR FR
FR'
M0 FR d
FR'FR源自FRFR合力的大小等于原力系的主矢 FR FR' F
合力的作用线位置
d MO FR
结论:平面力系的简化结果 :①合力偶MO ; ②合力 FR
刚体等效于只有一个力偶的作用,(因为力偶可以在刚 体平面内任意移动,故这时,主矩与简化中心O无关。)
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时, 简化结果就是合力(这个力系的合力), FR FR'。(此时
与简化中心有关,换个简化中心,主矩不为零)
重庆大学出版社
建筑力学
FAy FBC sin P Q 0 FAy P Q FBC sin 2.1kN
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
M A(Fi ) 0
FAx
FBC
sin
l
P
l 2
Qa
0
FBC 13.2KN
FAy
FBC
A
l/2 P
B Q
第三章 平面力系的平衡方程
3.1平面力系的简化
M2
M1
FR
M3
向任一点O简化
平面力系 (未知力系)
平面汇交力系:力(主矢量):FR=F
(已知力系) (作用在简化中心)
平(面已力知偶力系系)力偶(作(用主在矩该)平:面M上o=)M
重庆大学出版社
建筑力学
一般情况:
主矢 : FR ' F1 F2 F3 Fi
FAy
FBC
A
FAx
l/2 a
P
B Q
l
MB (Fi ) 0 MC (Fi ) 0
l FAyl P 2 Q(l a) 0
FAx l
tg
P
l 2
Qa
0
FAy 2.1kN
FAx 11.4kN
重庆大学出版社
建筑力学
[例] 已知:P=20kN, M=16kN·m, q=20kN/m, a=0.8m
20 20 0.8 12
12(kN)
24(kN)
重庆大学出版社
建筑力学
FAy FAx
FB
静定(未知数三个)
FAy FAx
FBy FBx
静不定(未知数四个)
独立方程数目≥未知数数目时,是静定问题(可求解) 独立方程数目<未知数数目时,是静不定问题(超静定问题)
静不定问题在材料力学,结构力学,弹性力学中 用变形协调条件来求解。
简化中心 (与简化中心位置无关) [因主矢等于各力的矢量和]
重庆大学出版社
建筑力学
主矩MO (转动效应)
大小:MO MO (Fi )
方向: 方向规定 + —
简化中心: (与简化中心有关) (因主矩等于各力对简化中心取矩的代数和)
重庆大学出版社
建筑力学
简化结果分析 合力矩定理
简化结果: 主矢FR',主矩 MO ,下面分别讨论。 ① FR' =0, MO =0,则力系平衡,下节专门讨论。 ② FR' =0, MO≠0,即简化结果为一合力偶, M=MO 此时
重庆大学出版社
建筑力学
[例] 已知:q, a , P=qa, M=Pa,求:A、B两点的支座反力?
解:① 选AB梁为研究对象。
② 画受力图
qP
FAy
qP
FB
A
B
M
2a
a
FAx
A
M
B
列平衡方程,求未知量。
Fx 0
Fy 0
FAx 0
FB FAy P 2qa 0,
M A(Fi ) 0
FAx
FBC
sin
l
P
l 2
Qa
0
FAy
FBC
A
l/2 P
B Q
a
l
FBC (Pl / 2 Qa) /(l sin ) 13.2kN
Fx 0
Fy 0
FAx FBC cos 0
FAx FBC cos 11.4kN
求:A、B的支反力。
q FA M FB
解:研究AB梁
P
MA(F ) 0;
A
B
a
a
a
FB
a
q
a
a 2
M
P
2a
0
Fy 0
FA FB qa P 0
FB
qa 2
M a
2P
20 0.8 16 2 20
2
0.8
FA P qa FB
a
l
MB (Fi ) 0
l FAyl P 2 Q(l a) 0
FAy 2.1kN
Fx 0
FAx FBC cos 0
FAx 11.4kN
重庆大学出版社
建筑力学
M A(Fi ) 0
FBC
sin
l
P
l 2
Qa
0
FBC 13.2KN
重庆大学出版社
建筑力学
[例] 已知:Q=7.5kN, P=1.2kN , l=2.5m , a=2m , =30o , 求:
BC杆拉力和铰A处的支座反力?
解:(1)选AB梁为研究对象。
C
(2)画受力图
FAy
FBC
A
FAx
l/2 P
B Q
a
l
A
l/2 P
B Q
a
l
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
4qa FAy 3
M A (Fi ) 0 P 2a q 2a a M FB 3a 0
5qa FB 3
重庆大学出版社
建筑力学
平面力系的平衡方程:
① 基本式(一矩式) ②二矩式
③三矩式
Fx 0
Fy 0
Fx 0 M A(Fi ) 0
主矩: MO M1 M2 M3
MO (F1) MO (F2) MO (Fi )
大小:FR ' F 'Rx2 F 'Ry2 ( Fx )2 ( Fy )2
主矢 FR'
(移动效应)
方向: tan1 FRy
FRx
tan1
Fy Fx
M A(Fi ) 0 MB (Fi ) 0
MO (Fi ) 0
MB (Fi ) 0
MC (Fi ) 0
条件:x 轴不垂直 于AB连线
条件:A,B,C不在 同一直线上
只有三个独立方程,只能求出三个未知数。
投影轴和矩心是任意选取的,一般先取矩。矩心选 择在多个未知力的交点上;投影轴尽量与未知力垂 直或平行。
重庆大学出版社
建筑力学
物系平衡问题的特点: ①物体系统平衡,物系中每个单体也是平衡的。 ②每个单体可列3个(平面任意力系)平衡方程,整个系统
④ FR' ≠0,MO ≠0,为最任意的情况。此种情况还可以继续
简化为一个合力 FR。
FR FR FR
FR'
M0 FR d
FR'FR源自FRFR合力的大小等于原力系的主矢 FR FR' F
合力的作用线位置
d MO FR
结论:平面力系的简化结果 :①合力偶MO ; ②合力 FR
刚体等效于只有一个力偶的作用,(因为力偶可以在刚 体平面内任意移动,故这时,主矩与简化中心O无关。)
③ FR≠' 0,MO =0,即简化为一个作用于简化中心的合力。这时, 简化结果就是合力(这个力系的合力), FR FR'。(此时
与简化中心有关,换个简化中心,主矩不为零)
重庆大学出版社
建筑力学
FAy FBC sin P Q 0 FAy P Q FBC sin 2.1kN
重庆大学出版社
建筑力学
(3)列平衡方程,求未知量。
M A(Fi ) 0
FAx
FBC
sin
l
P
l 2
Qa
0
FBC 13.2KN
FAy
FBC
A
l/2 P
B Q
