2011年湖南高考数学试题(理科)
2011年高考试题——数学理(湖南卷)解析精校版

2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分。
参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
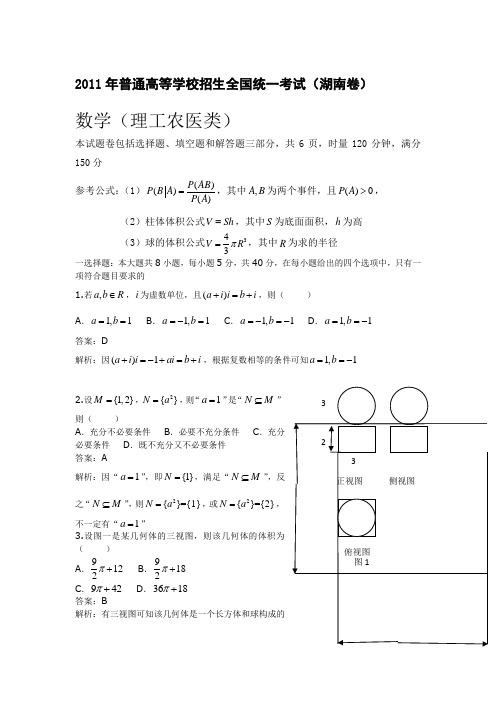
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==-2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 3.设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+C .942π+D .3618π+由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关”5.设双曲线221(0)x y a -=>的渐近线方程为320x y ±=,则a 的值为( )A .4B .3C .2D .1 6. 由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为( )A .12 B .1 C.2D7. 设1m >,在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为( )A.(1,1 B.(1)+∞ C .(1,3) D .(3,)+∞8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为( ) A .1 B .12 CD二填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
2011年湖南省高考数学试卷(理科)及答案

2011年湖南省高考数学试卷(理科)一、选择题(共8小题,每小题5分,满分40分)1.(5分)若a,b∈R,i为虚数单位,且(a+i)i=b+i则()A.a=1,b=1 B.a=﹣1,b=1 C.a=﹣1,b=﹣1 D.a=1,b=﹣12.(5分)设集合M={1,2},N={a2},则“a=1”是“N⊆M”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分又不必要条件3.(5分)设如图是某几何体的三视图,则该几何体的体积为()A.9π+42 B.36π+18 C. D.4.(5分)通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计6050110由算得,.P(K2≥k)0.0500.0100.001k 3.841 6.63510.828参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”5.(5分)设双曲线的渐近线方程为3x±2y=0,则a的值为()A.4 B.3 C.2 D.16.(5分)由直线x=﹣,x=,y=0与曲线y=cosx所围成的封闭图形的面积为()A.B.1 C.D.7.(5分)设m>1,在约束条件下,目标函数z=x+my的最大值小于2,则m的取值范围为()A.(1,)B.(,+∞)C.(1,3) D.(3,+∞)8.(5分)设直线x=t与函数f(x)=x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为()A.1 B.C.D.二、填空题(共8小题,每小题5分,满分35分)9.(5分)在直角坐标系xOy中,曲线C1的参数方程为(α为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x 轴正半轴为极轴)中,曲线C2的方程为p(cosθ﹣sinθ)+1=0,则C1与C2的交点个数为.10.(5分)设x,y∈R,且xy≠0,则的最小值为.11.如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为.12.(5分)设S n是等差数列{a n}(n∈N*)的前n项和,且a1=1,a4=7,则S9=.13.(5分)若执行如图所示的框图,输入x1=1,x2=2,x3=3,=2,则输出的数等于.14.(5分)在边长为1的正三角形ABC中,设,,则=.15.(5分)如图,EFGH 是以O为圆心,半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=;(2)P(B|A)=.16.(5分)对于n∈N+,将n 表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k﹣1×21+a k×20,当i=0时,a i=1,当1≤i≤k时,a1为0或1.记I(n)为上述表示中a i为0的个数(例如:1=1×20,4=1×22+0×21+0×20,故I(1)=0,I(4)=2),则(1)I(12)=;(2)=.三、解答题(共6小题,满分75分)17.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC 1)求角C大小;(2)求sinA﹣cos(B+)的最大值,并求取得最大值时角A,B的大小.18.(12分)某商店试销某种商品20天,获得如下数据:日销售量(件)0123频数1595试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.(Ⅰ)求当天商品不进货的概率;(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望.19.(12分)如图,在圆锥PO中,已知PO=,⊙O的直径AB=2,C是的中点,D为AC的中点.(Ⅰ)证明:平面POD⊥平面PAC;(Ⅱ)求二面角B﹣PA﹣C的余弦值.20.(13分)如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v﹣c|×S成正比,比例系数为;(2)其它面的淋雨量之和,其值为,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=时.(Ⅰ)写出y的表达式(Ⅱ)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.21.(13分)如图,椭圆C1:=1(a>b>0)的离心率为,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.(Ⅰ)求C1,C2的方程;(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.(i)证明:MD⊥ME;(ii)记△MAB,△MDE的面积分别是S1,S2.问:是否存在直线l,使得=?请说明理由.22.(13分)已知函数f(x)=x3,g (x)=x+.(Ⅰ)求函数h (x)=f(x)﹣g (x)的零点个数.并说明理由;(Ⅱ)设数列{a n}(n∈N*)满足a1=a(a>0),f(a n+1)=g(a n),证明:存在常数M,使得对于任意的n∈N*,都有a n≤M.2011年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011•湖南)若a,b∈R,i为虚数单位,且(a+i)i=b+i则()A.a=1,b=1 B.a=﹣1,b=1 C.a=﹣1,b=﹣1 D.a=1,b=﹣1【分析】利用复数的乘法运算将等式化简;利用复数相等实部、虚部分别相等;列出方程求出a,b的值.【解答】解:(a+i)i=b+i即﹣1+ai=b+i∴a=1,b=﹣1故选D2.(5分)(2011•湖南)设集合M={1,2},N={a2},则“a=1”是“N⊆M”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分又不必要条件【分析】先由a=1判断是否能推出“N⊆M”;再由“N⊆M”判断是否能推出“a=1”,利用充要条件的定义得到结论.【解答】解:当a=1时,M={1,2},N={1}有N⊆M当N⊆M时,a2=1或a2=2有所以“a=1”是“N⊆M”的充分不必要条件.故选A.3.(5分)(2011•湖南)设如图是某几何体的三视图,则该几何体的体积为()A.9π+42 B.36π+18 C. D.【分析】由三视图可知,下面是一个底面边长是3的正方形且高是2的一个四棱柱,上面是一个球,球的直径是3,该几何体的体积是两个体积之和,分别做出两个几何体的体积相加.【解答】解:由三视图可知,几何体是一个简单的组合体,下面是一个底面边长是3的正方形且高是2的一个四棱柱,上面是一个球,球的直径是3,该几何体的体积是两个体积之和,四棱柱的体积3×3×2=18,球的体积是,∴几何体的体积是18+,故选D.4.(5分)(2011•湖南)通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计6050110由算得,.P(K2≥k)0.0500.0100.001k 3.841 6.63510.828参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”【分析】题目的条件中已经给出这组数据的观测值,我们只要把所给的观测值同节选的观测值表进行比较,发现它大于6.635,得到有99%以上的把握认为“爱好这项运动与性别有关”.【解答】解:由题意算得,.∵7.8>6.635,∴有0.01=1%的机会错误,即有99%以上的把握认为“爱好这项运动与性别有关”故选:C.5.(5分)(2011•湖南)设双曲线的渐近线方程为3x±2y=0,则a的值为()A.4 B.3 C.2 D.1【分析】由题意,,即可求出a的值.【解答】解:由题意,,∴a=2,故选:C.6.(5分)(2011•湖南)由直线x=﹣,x=,y=0与曲线y=cosx所围成的封闭图形的面积为()A.B.1 C.D.【分析】为了求得与x轴所围成的不规则的封闭图形的面积,可利用定积分求解,积分的上下限分别为与,cosx即为被积函数.【解答】解:由定积分可求得阴影部分的面积S=cosxdx==﹣(﹣)=,所以围成的封闭图形的面积是.故选D.7.(5分)(2011•湖南)设m>1,在约束条件下,目标函数z=x+my的最大值小于2,则m的取值范围为()A.(1,)B.(,+∞)C.(1,3) D.(3,+∞)【分析】根据m>1,我们可以判断直线y=mx的倾斜角位于区间(,)上,由此我们不难判断出满足约束条件的平面区域的形状,再根据目标函数Z=X+my对应的直线与直线y=mx垂直,且在直线y=mx与直线x+y=1交点处取得最大值,由此构造出关于m的不等式组,解不等式组即可求出m 的取值范围.【解答】解:∵m>1故直线y=mx与直线x+y=1交于点,目标函数Z=X+my对应的直线与直线y=mx垂直,且在点,取得最大值其关系如下图所示:即,解得1﹣<m<又∵m>1解得m∈(1,)故选:A.8.(5分)(2011•湖南)设直线x=t与函数f(x)=x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为()A.1 B.C.D.【分析】将两个函数作差,得到函数y=f(x)﹣g(x),再求此函数的最小值对应的自变量x的值.【解答】解:设函数y=f(x)﹣g(x)=x2﹣lnx,求导数得=当时,y′<0,函数在上为单调减函数,当时,y′>0,函数在上为单调增函数所以当时,所设函数的最小值为所求t的值为故选D二、填空题(共8小题,每小题5分,满分35分)9.(5分)(2011•湖南)在直角坐标系xOy中,曲线C1的参数方程为(α为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为p(cosθ﹣sinθ)+1=0,则C1与C2的交点个数为2.【分析】先根据sin2α+cos2α=1,求出曲线C1的直角坐标方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,求出曲线C2的直角坐标方程,然后判定交点个数即可.【解答】解:∵曲线C1的参数方程为(α为参数),sin2α+cos2α=1∴曲线C1的直角坐标方程为x2+(y﹣1)2=1∵ρcosθ=x,ρsinθ=y,p(cosθ﹣sinθ)+1=0∴曲线C2的方程为x﹣y+1=0而圆心到直线的距离d=0<r,故C1与C2的交点个数为2故答案为:210.(5分)(2011•湖南)设x,y∈R,且xy≠0,则的最小值为9.【分析】对展开,利用基本不等式即可求得其最小值.【解答】解:∵x,y∈R,且xy≠0,∴=1+4+≥5+2=9当且仅当时等号成立,∴的最小值为9.故答案为9.11.(2011•湖南)如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为.【分析】根据半圆的三等分点,得到三个弧对应的角度是60°,根据直径所对的圆周角是直角得到直角三角形的有关长度,做出要求的线段的长度.【解答】解:∵A,E是半圆周上的两个三等分点∴弧EC是一个60°的弧,∴∠EBC=30°,则CE=2,连接BA,则BA=2,∴在含有30°角的直角三角形中,BD=1,DF=,AD=∴AF=,故答案为:12.(5分)(2011•湖南)设S n是等差数列{a n}(n∈N*)的前n项和,且a1=1,a4=7,则S9=81.【分析】先根据数列{a n}为等差数列,求出公差d,然后根据等差数列的前n项和公式求得S9.【解答】解:∵数列{a n}为等差数列,∴a n=a1+(n﹣1)d,S n=na1+∵a1=1,a4=7∴a4=1+(4﹣1)d=7∴d=2∴S9=9×1+×2=81故答案为:8113.(5分)(2011•湖南)若执行如图所示的框图,输入x1=1,x2=2,x3=3,=2,则输出的数等于.【分析】先弄清该算法功能,S=0+(1﹣2)2=1,i=1,满足条件i<3,执行循环体,依此类推,当i=3,不满足条件i<3,退出循环体,输出所求即可.【解答】解:S=0+(1﹣2)2=1,i=1,满足条件i<3,执行循环体,i=2S=1+(2﹣2)2=1,i=2,满足条件i<3,执行循环体,i=3S=1+(3﹣2)2=2,i=3,不满足条件i<3,退出循环体,则S=×2=故答案为:14.(5分)(2011•湖南)在边长为1的正三角形ABC中,设,,则=﹣.【分析】根据,,确定点D,E在正三角形ABC中的位置,根据向量加法满足三角形法则,把用表示出来,利用向量的数量积的运算法则和定义式即可求得的值.【解答】解:∵,∴D为BC的中点,∴,∵,∴,∴=)==﹣,故答案为:﹣.15.(5分)(2011•湖南)如图,EFGH 是以O为圆心,半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=;(2)P(B|A)=.【分析】此题是个几何概型.用面积法求出事件A“豆子落在正方形EFGH内”的概率p(A),同理求出P(AB),根据条件概率公式P(B|A)=即可求得结果.【解答】解:用A表示事件“豆子落在正方形EFGH内”,∴P(A)==,B表示事件“豆子落在扇形OHE(阴影部分)内”,P(AB)==,∴P(B|A)=.故答案为:.16.(5分)(2011•湖南)对于n∈N+,将n 表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k ×21+a k×20,当i=0时,a i=1,当1≤i≤k时,a1为0或1.记I(n)为上述表﹣1示中a i为0的个数(例如:1=1×20,4=1×22+0×21+0×20,故I(1)=0,I(4)=2),则(1)I(12)=2;(2)=1093.【分析】(1)根据题意,分析可得,将n 表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k×21+a k×20,实际是将十进制的数转化为二进制的数,易得12=1×23+1×22+0﹣1×21+0×20,由I(n)的意义,可得答案;(2)将n分为n=127,64≤n≤126,32≤n≤63,…n=1等7种情况,有组合数的性质,分析其中I(n)的取值情况,与二项式定理结合,可转化为等比数列的前7项和,计算可得答案.【解答】解:(1)根据题意,12=1×23+1×22+0×21+0×20,则I(12)=2;(2)127=1×26+1×25+1×24+1×23+1×22+1×21+1×20,设64≤n≤126,且n为整数;则n=1×26+a1×25+a2×24+a3×23+a4×22+a5×21+a6×20,a1,a2,a3,a4,a5,a6中6个数都为0或1,其中没有一个为1时,有C60种情况,即有C60个I(n)=6;其中有一个为1时,有C61种情况,即有C61个I(n)=5;其中有2个为1时,有C62种情况,即有C62个I(n)=4;…2I(n)=C6026+C61×25+C62×24+C63×23+C64×22+C65×2+1=(2+1)n=36,同理可得:=35,…=31,2I(1)=1;则=1+3+32+…+36==1093;故答案为:(1)2;(2)1093.三、解答题(共6小题,满分75分)17.(12分)(2011•湖南)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC1)求角C大小;(2)求sinA﹣cos(B+)的最大值,并求取得最大值时角A,B的大小.【分析】(1)利用正弦定理化简csinA=acosC.求出tanC=1,得到C=.(2)B=﹣A,化简sinA﹣cos(B+),通过0<A<,推出<A+<,求出2sin(A+)取得最大值2.得到A,B.【解答】解:(1)由正弦定理得sinCsinA=sinAcosC,因为0<A<π,所以sinA>0.从而sinC=cosC,又cosC≠0,所以tanC=1,C=.(2)有(1)知,B=﹣A,于是sinA﹣cos(B+)=sinA+cosA=2sin(A+).因为0<A<,所以<A+<,从而当A+=,即A=时2sin(A+)取得最大值2.综上所述sinA﹣cos(B+)的最大值为2,此时A=,B=.18.(12分)(2011•湖南)某商店试销某种商品20天,获得如下数据: 日销售量(件)0 1 2 3 频数1595试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率. (Ⅰ)求当天商品不进货的概率;(Ⅱ)记X 为第二天开始营业时该商品的件数,求X 的分布列和数学期望. 【分析】(I )“当天商品不进货”包含两个事件的和事件,利用古典概型概率公式求出两个事件的概率;再利用互斥事件的和事件概率公式求出当天商品不进货的概率.(II )求出x 可取的值,利用古典概型概率公式及互斥事件和事件的概率公式求出x 取每一个值的概率值;列出分布列;利用随机变量的期望公式求出x 的期望. 【解答】解:(I )P (“当天商店不进货”)=P (“当天商品销售量为0件”)+(“当天的商品销售量为1件”) =(II )由题意知,X 的可能取值为2,3 P (X=2)=P (“当天商品销售量为1件”)=P (X=3)=(“当天的销售量为0”)+P (“当天的销售量为2件”)+P (“当天的销售量为3件”)=故x 的分布列 x 2 3 pX 的数学期望为EX=19.(12分)(2011•湖南)如图,在圆锥PO中,已知PO=,⊙O的直径AB=2,C是的中点,D为AC的中点.(Ⅰ)证明:平面POD⊥平面PAC;(Ⅱ)求二面角B﹣PA﹣C的余弦值.【分析】(Ⅰ)连接OC,先根据△AOC是等腰直角三角形证出中线OD⊥AC,再结合PO⊥AC证出AC⊥POD,利用平面与平面垂直的判定定理,可证出平面POD ⊥平面PAC;(Ⅱ)过O分别作OH⊥PD于H,OG⊥PA于G,再连接GH,根据三垂线定理证明∠OGH为二面角B﹣PA﹣C的平面角,最后分别在Rt△ODA、Rt△ODP、Rt△OGH中计算出OH、OG和sin∠OGH,最后求出所求二面角的余弦值.【解答】解:(Ⅰ)连接OC,∵OA=OC,D是AC的中点∴AC⊥OD又∵PO⊥底面⊙O,AC⊂底面⊙O∴AC⊥PO∵OD、PO是平面POD内的两条相交直线∴AC⊥平面POD,而AC⊂平面PAC∴平面POD⊥平面PAC(Ⅱ)在平面POD中,过O作OH⊥PD于H,由(Ⅰ)知,平面POD⊥平面PAC 所以OH⊥平面PAC,又∵PA⊂平面PAC∴PA⊥HO在平面PAO中,过O作OG⊥PA于G,连接GH,则有PA⊥平面OGH,从而PA⊥HG.故∠OGH为二面角B﹣PA﹣C的平面角在Rt△ODA中,OD=OA•sin45°=在Rt△ODP中,OH=在Rt△OPA中,OG=在Rt△OGH中,sin∠OGH=所以cos∠OGH=故二面角B﹣PA﹣C的余弦值为20.(13分)(2011•湖南)如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E 移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v﹣c|×S成正比,比例系数为;(2)其它面的淋雨量之和,其值为,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=时.(Ⅰ)写出y的表达式(Ⅱ)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.【分析】(Ⅰ)E移动时的总淋雨量应该等于单位时间内的淋雨量乘以所用的时间,可先求出单位时间内的淋雨量的式子,再乘以时间即可;(Ⅱ)根据绝对值的性质,将(Ⅰ)中的函数分解为分段函数的形式,再由c的不同取值范围讨论函数的单调性,在不同的情况下,单调区间不同,总淋雨量最小值对应的v值也不同.【解答】解:(Ⅰ)由题意知,E移动时单位时间内的淋雨量为,故(Ⅱ)由(Ⅰ)知,当0<v≤c时,当c≤v≤10时,故(1)当0<c<时,y是关于v的减函数,故当v=10时,;(2)当时,在(0,c]上y是关于v的减函数,在(c,10]上,y是关于v的增函数,故当v=c时,答:(Ⅰ)函数y的表达式为(Ⅱ)(1)在0<c的情况下,当v=10时,总淋雨量y最少;(2)在的情况下,当v=c时,总淋雨量y最少.21.(13分)(2011•湖南)如图,椭圆C1:=1(a>b>0)的离心率为,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.(Ⅰ)求C1,C2的方程;(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.(i)证明:MD⊥ME;(ii)记△MAB,△MDE的面积分别是S1,S2.问:是否存在直线l,使得=?请说明理由.【分析】(Ⅰ)先利用离心率得到一个关于参数的方程,再利用x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长得另一个方程,两个方程联立即可求出参数进而求出C1,C2的方程;(Ⅱ)(i)把直线l的方程与抛物线方程联立可得关于点A、B坐标的等量关系,再代入求出k MA•k MB=﹣1,即可证明:MD⊥ME;(ii)先把直线MA的方程与抛物线方程联立可得点A的坐标,再利用弦长公式求出|MA|,同样的方法求出|MB|进而求出S1,同理可求S2.再代入已知就可知道是否存在直线l满足题中条件了.【解答】解:(Ⅰ)由题得e=,从而a=2b,又2=a,解得a=2,b=1,故C1,C2的方程分别为,y=x2﹣1.(Ⅱ)(i)由题得,直线l的斜率存在,设为k,则直线l的方程为y=kx,由得x2﹣kx﹣1=0.设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,于是x1+x2=k,x1x2=﹣1,又点M的坐标为(0,﹣1),所以k MA•k MB=====﹣1.故MA⊥MB,即MD⊥ME.(ii)设直线MA的斜率为k1,则直线MA的方程为y=k1x﹣1.由,解得或.则点A的坐标为(k1,k12﹣1).又直线MB的斜率为﹣,同理可得点B的坐标为(﹣,﹣1).于是s1=|MA|•|MB|=•|k1|••|﹣|=.由得(1+4k12)x2﹣8k1x=0.解得或,,则点D的坐标为(,).又直线ME的斜率为﹣.同理可得点E的坐标为(,).于是s2=|MD|•|ME|=.故=,解得k12=4或k12=.又由点A,B的坐标得,k==k1﹣.所以k=±.故满足条件的直线存在,且有两条,其方程为y=x和y=﹣x.22.(13分)(2011•湖南)已知函数f(x)=x3,g (x)=x+.(Ⅰ)求函数h (x)=f(x)﹣g (x)的零点个数.并说明理由;(Ⅱ)设数列{a n}(n∈N*)满足a1=a(a>0),f(a n+1)=g(a n),证明:存在常数M,使得对于任意的n∈N*,都有a n≤M.【分析】(Ⅰ)由h(x)=知,x∈[0,+∞),而h(0)=0,且h(1)=﹣1<0,h(2)=6﹣,再研究函数在(0,+∞)上的单调性,以确定零点个数即可(Ⅱ)记h(x)的正零点为x0,即,当a<x0时,由a1=a,即a1<x0,而,a2<x0.由此猜测a n<x0.当a≥x0时,由(Ⅰ)知,当x∈(x1,+∞)时,h(x)单调递增,h(a)>h(x0)=0,从而a2<a,由此猜测a n<a.然后用数学归纳法证明.【解答】解:(Ⅰ)由h(x)=知,x∈[0,+∞),而h(0)=0,且h (1)=﹣1<0,h(2)=6﹣,则x=0为h(x)的一个零点,且h(x)在(1,2)内有零点,∴h(x)至少有两个零点.由h(x)=,记,则,当x∈(0,+∞)时,g(x)单调递增,故可判断出h(x)在(0,+∞)仅有一个零点,综上所述,h(x)有且只有两个零点.(Ⅱ)记h(x)的正零点为x0,即,(1)当a<x0时,由a1=a,即a1<x0,而,∴a2<x0.由此猜测a n<x0.下面用数学归纳法证明:①当n=1时,a1<x0,成立.②假设当n=k时a k<x0成立,则当n=k+1时,由,知a k<x0.+1<x0成立.因此当n=k+1时,a k+1故对任意的n∈N*,a n≤x0成立.(2)当a≥x0时,由(Ⅰ)知,当x∈(x0,+∞)时,h(x)单调递增,∴h(a)>h(x0)=0,从而a2≤a,由此猜测a n≤a.下面用数学归纳法证明:①当n=1时,a1≤a,成立.②假设当n=k时a k<a成立,则当n=k+1时,由,知a k+1<a.<a成立.故对任意的n∈N*,a n≤a成立.因此当n=k+1时,a k+1综上所述,存在常数M,使得对于任意的n∈N*,都有a n≤M.。
2011年高考理科数学(湖南卷)

2011年普通高等学校招生全国统一考试(湖南卷)数 学(理工农医类)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分。
参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则 A .1,1a b == B .1,1a b =-= C .1,1a b =-=- D .1,1a b ==-2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 3.设图一是某几何体的三视图,则该几何体的体积为A .9122π+B .9182π+C .942π+D .3618π+由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯参照附表,得到的正确结论是A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关”5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为A .4B .3C .2D .1 6. 由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为A .12B .1 CD7. 设1m >,在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为A.(1,1+ B.(1)++∞ C .(1,3) D .(3,)+∞ 答案:A8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为A .1B .12C.2 D.2二填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
2011年湖南高考理科数学试题及标准答案

2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A.1,1a b == B .1,1a b =-= C.1,1a b =-=- D.1,1a b ==- 答案:D2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( ) A .充分不必要条件 B.必要不充分条件 C .充分必要条件 D.既不充分又不必要条件答案:A解析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”。
3.设图一是某几何体的三视图,则该几何体的体积为( ) A.9122π+ B.9182π+ C.942π+ D .3618π+ 答案:B解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
:由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别有关”答案:C解析:由27.8 6.635K ≈>,而2( 6.635)0.010P K ≥=,故由独立性检验的意义可知选C. 5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A .4 B.3 C.2 D .1答案:C解析:由双曲线方程可知渐近线方程为3y x a =±,故可知2a =。
2011年湖南高考理科数学试题详细解析

2011年湖南高考理科数学试题详细解析理科数学第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)复数212ii +-的共轭复数是 (A )35i - (B )35i (C )i - (D )i【解析】212i i+-=(2)(12),5i i i ++=共轭复数为i -,故选C (2)下列函数中,既是偶函数又在+∞(0,)单调递增的函数是(A )3y x = (B) 1y x =+ (C )21y x =-+ (D) 2xy -=【解析】由偶函数排除A,由在+∞(0,)单调递增,排除C ,D,故选B(3)执行右面的程序框图,如果输入的N 是6,那么输出的p 是(A )120 (B )720 (C )1440 (D )5040【解析】由程序框图知,k=1,p=1;k=2,p=2;k=3,p=6;k=4,p=24;k=5,p=120;k=6,p=720.故选B(4)有3个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为(A )13 (B )12 (C )23 (D )34【解析】每个同学参加的情形都有3种,故两个同学参加一组的情形有9种,而参加同一组的情形只有3种,所求的概率为p=3193=,故选A (5)已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos 2θ=(A )45- (B )35- (C )35 (D )45【解析】由已知tan 2θ=,222222cos sin 1tan 3cos2cos sin 1tan 5θθθθθθθ--===-++,选B(6)在一个几何体的三视图中,正视图和俯视图如右图所示, 则相应的侧视图可以为【解析】由题设知该几何体是由底面棱长为r 的正四棱锥沿底面对角线截出的部分与底面为半径为r 的圆锥沿对称轴截出的部分构成的。
普通高等学校招生全国统一考试数学理试题(湖南卷,解析

2011年普通高等学校招生全国统一考试数学理试题(湖南卷,解析版)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分。
参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==- 答案:D解析:因()1a i i ai b i +=-+=+,根据复数相等的条件可知1,1a b ==-。
2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 答案:A解析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”。
3.设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+ B .9182π+ C .942π+ D .3618π+答案:B解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:正视图侧视图俯视图 图1由22()()()()()n ad bcKa b c d a c b d-=++++算得22110(40302020)7.860506050K⨯⨯-⨯=≈⨯⨯⨯A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别有关”答案:C解析:由27.8 6.635K≈>,而2( 6.635)0.010P K≥=,故由独立性检验的意义可知选C.5.设双曲线2221(0)9x yaa-=>的渐近线方程为320x y±=,则a的值为()A.4 B.3 C.2 D.1答案:C解析:由双曲线方程可知渐近线方程为3y xa=±,故可知2a=。
2011年湖南高考数学理工试题 有详解 word

2011年湖南高考数学(理工农医类)试卷本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分.参考公式:(1)()()()P AB P B A P A =,其中A ,B 为两个事件,且P (A )>0.(2)柱体体积公式V=Sh ,其中S 为底面面积,h 为高.(3)球的体积公式343V R π=,其中R 为求的半径.一、选择题:本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若a ,b ∈R ,i 为虚数单位,且(a +i )i=b+i ,则( )A .a =1,b =1B .a =-1,b =1C .a =-1,b =-1D .a =1,b =-1 2.设M ={1,2},N ={a 2},则“a =1”是“N ⊆M ”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件3.某几何体的三视图如图所示,则该几何体的体积为( )A .9122π+B .9182π+ C .942π+ D .3618π+4.通过随机询问110名性别不同的大学生是否爱好某项运动,由2()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关”5.设双曲线2221(0)9x y a a -=>的渐近线方程为3x ±2y =0,则a 的值为( )A .4B .3C .2D .16.由直线,,033x x y ππ=-==与曲线y =cos x 所围成的封闭图形的面积为( )A .12B .1CD 正视图 侧视图7.设m>1,在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z=x+my 的最大值小于2,则m 的取值范围为( )A.(1,1 B.(1)+∞ C .(1,3) D .(3,+∞) 8.设直线x=t 与函数f (x )=x 2, g (x )=ln x 的图像分别交于点M ,N ,则当|MN |达到最小时t 的值为( )A .1B .12 C.2 D.2二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
2011年湖南高考理科数学精彩试题及问题详解

2011年普通高等学校招生全国统一考试(卷)数学(理工农医类)参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==- 答案:D2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 答案:A解析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”。
3.设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+ B .9182π+ C .942π+ D .3618π+答案:B解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+()。
由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关” 答案:C解析:由27.8 6.635K ≈>,而2( 6.635)0.010P K ≥=,故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A .4 B .3 C .2 D .1答案:C解析:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =。
2011年全国高考理科数学试题-湖南卷

2011年全国高考理科数学试题-湖南卷1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A. 1,1a b ==B. 1,1a b =-=C. 1,1a b =-=-D. 1,1a b ==- 答案:D分析:因()1a i i ai b i +=-+=+,根据复数相等的条件可知1,1a b ==-.2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( ) A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分又不必要条件 答案:A分析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”.3.设图1是某几何体的三视图,则该几何体的体积为( )A.9122π+ B. 9182π+C. 942π+D. 3618π+ 答案:B分析:由三视图可知该几何体是一个长方体和球构成的组合体,其体积3439()33218322V ππ=+⨯⨯=+.4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯. 附表:参照附表,得到的正确结论是( )A. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B. 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C. 有99%以上的把握认为“爱好该项运动与性别有关”D. 有99%以上的把握认为“爱好该项运动与性别无关” 答案:C分析:由3K 7.8 6.635≈>,而3(6.35)0.10P K ≥=,故由独立性检验的意义可知选C .5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A. 4 B. 3 C. 2 D. 1 答案:C分析:依题意知,双曲线的渐近线为,3y x a=±,故可知2a =.6.由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为( )A.12B. 1C.D. 答案:D分析:由定积分知识可得3333cos sin |(22S xdx x ππππ--===--=⎰D .7.设1m >,在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为( )A. (1,1B. (1)+∞C. (1,3)D. (3,)+∞ 答案:A分析:画出可行域如图所示,可知5z x y =+在点1(,)11mm m++取最大值,由21211m m m+<++,解得11m <<.8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为( ) A. 1B. 12C.D. 2答案:D分析:由题2||ln MN x x =-,(0)x >不妨令2()ln h x x x =-,则1()2h x x x'=-,令()0h x '=解得2x =,因(0,)2x ∈时,()0h x '<,当(,)2x ∈+∞时,()0h x '>,所以当x =时,||MN 达到最小,即t =9.在直角坐标系xOy 中,曲线1C 的参数方程为cos ,1sin x y αα=⎧⎨=+⎩(α为参数)在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为()cos sin 10ρθθ-+=,则1C 与2C 的交点个数为_____. 答案:2分析:曲线221:(1)1C x y +-=,2:10C x y -+=,由圆心到直线的距离01d ==<,故1C 与2C 的交点个数为2.10.设,x y R ∈,则222211()(4)x y y x++的最小值为_____. 答案:9分析:由柯西不等式可知2222211()(4)(12)9x y y x++≥+=.11.如图,,A E 是半圆周上的两个三等分点,直径4BC =,AD BC ⊥,垂足为D ,BE 与AD 相交与点F ,则AF 的长为_____.分析:由题可知,60AOB EOC ︒∠=∠=,2OA OB ==,得1OD B D ==,DF =,又23AD BD CD =⋅=,所以AF AD DF =-=12.设n S 是等差数列*{}()n a n N ∈的前n 项和,且141,7a a ==,则9S =_____. 答案:25分析:∵数列{}n a 为等差数列, ∴1(1)n a a n d =+-,1(1)2n n n S na d -=+, ∵141,7a a ==,∴41(41)7a d =+-=,∴2d =,99(91)912812S ⨯-∴=⨯+⨯=. 故答案为:81 .13.若执行如图所示的框图,输入1231,2,3,2x x x x ====,则输出的数等于_____.答案:23分析:由框图的算法功能可知,输出的数为三个数的方差,则222(12)(22)(32)233S -+-+-==.14.在边长为1的正三角形ABC 中,设2,3BC BD CA CE ==,则AD BE ⋅=_______ . 答案:14-分析:由题12AD CD CA CB CA =-=-,13BE CE CB CA CB =-=-, 所以111171()()232364AD BE CB CA CA CB CB CA ⋅=-⋅-=--+⋅=-.15.如图,EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则(1) ()P A =_____;(2) (|)=P B A _____.答案:见解析分析:(1)由几何概型概率计算公式可得;(2)由条件概率的计算公式可得21()14(|)===2()4P AB P B A P A ππ⨯.16.对于*n N ∈,将n 表示为1210012122222k k k k k n a a a a a ---=⨯+⨯+⨯++⨯+⨯,当0i =时,1i a =,当1i k ≤≤时,i a 为0或1,记()I n 为上述表示中i a 为0的个数,(例如0112=⨯,2104120202=⨯+⨯+⨯:故(1)0,(4)2I I ==)则 (1)(12)I =_____ ;(2)127()12I n n ==∑_____.答案:(1)2 ;(2)1093分析:(1)因32101212+120202=⨯⨯+⨯+⨯,故(12)2I =;(2)在2进制的(2)k k ≥位数中,没有0的有1个,有1个0的有11k C -个,有2个0的有21k C -个,……有m 个0的有1mk C -个,……有1k -个0的有111k k C --=个. 故对所有2进制为k 位数的数n ,在所求式中的()2I n 的和为:01122111111122223k k k k k k C C C ------⋅+⋅+⋅++⋅=. 又712721=-恰为2进制的最大7位数,所以1277()1122231093I n k n k -===+=∑∑.。
2011年湖南高考数学理科试卷(带详解)

2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的.1.若,a b ∈R ,i 为虚数单位,且(i)i i a b +=+,则 ( ) A .1,1a b == B .1,1a b =-= C .1,1a b =-=- D .1,1a b ==-【测量目标】复数的四则运算.【考查方式】利用复数相等的条件直接求值. 【难易程度】容易 【参考答案】D【试题解析】因(i)i 1i i a a b +=-+=+,根据复数相等的条件可知1,1a b ==-. 2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则 ( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分又不必要条件 【测量目标】集合间的关系,充分必要条件. 【考查方式】给出两个集合直接考查. 【难易程度】容易 【参考答案】A【试题解析】因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”.3.如图一是某几何体的三视图,则该几何体的体积为 ( )第3题图A .9π122+ B .9π182+ C .9π42+ D .36π18+【测量目标】由三视图求几何体的体积.【考查方式】给出三视图,通过判断直接求体积. 【难易程度】容易 【参考答案】B【试题解析】由三视图可知该几何体是一个长方体和球构成的组合体, 其体积3439π()332π+18322V =+⨯⨯=. 4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男 女 总计爱好40 20 60 不爱好20 30 50 总计60 50 110由22()()()()()n ad bc K a b c d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:2()P K k … 0.0500.010 0.001 k3.8416.63510.828参照附表,得到的正确结论是 ( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关” 【测量目标】独立性检验.【考查方式】给出统计图表直接考查. 【难易程度】容易 【参考答案】C【试题解析】由27.8 6.635,K ≈>而2( 6.635)0.010P K =…,故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为 ( )A .4B .3C .2D .1【测量目标】双曲线的简单几何性质.【考查方式】由双曲线方程直接求出渐近线方程,再结合给出的渐近线方程比较求解. 【难易程度】容易 【参考答案】C【试题解析】:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =. 6. 由直线ππ,,033x x y =-==与曲线cos y x =所围成的封闭图形的面积为( ) A .12 B .1 C.2D【测量目标】定积分的几何意义.【考查方式】直接给出曲线和直线方程求面积. 【难易程度】容易 【参考答案】D【试题解析】由定积分知识可得ππ33ππ33cosd sin |(22S x x --===-=⎰7. 设1m >,在约束条件1y xy mx x y ⎧⎪⎨⎪+⎩………下,目标函数z x my =+的最大值小于2,则m 的取值范围为 ( ) A.(1,1 B.(1)+∞ C .(1,3) D .(3,)+∞ 【测量目标】线性规划求最值.【考查方式】给出约束条件和目标函数的范围求目标函数y 轴系数的值. 【难易程度】容易 【参考答案】A【试题解析】可知z x my =+在点1(,)11m m m++取最大值,由 21211m m m+<++解得11m <<. 8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为 ( )A .1B .12C .2D .2【测量目标】利用导数判断单调性求最值.【考查方式】利用直线与曲线相交,求相交直线方程再运用导数性质求解. 【难易程度】容易 【参考答案】D【试题解析】由题2||ln MN x x =-,(0)x >不妨令2()ln h x x x =-,则1()2h x x x'=-,令()0h x '=解得2x =,因(0,)2x ∈时,()0h x '<,当()2x ∈+∞时,()0h x '>,所以当2x =时,||MN 达到最小,即2t =.二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上.一、选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题记分) 9.在直角坐标系xOy 中,曲线C 1的参数方程为cos ,1sin x y αα=⎧⎨=+⎩(α为参数)在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为()cos sin 10ρθθ-+=,则1C 与2C 的交点个数为 . 【测量目标】坐标系与参数方程.【考查方式】给出极坐标方程与参数方程,将其转化为普通方程后解不等式求解. 【难易程度】容易【参考答案】2【试题解析】曲线221:(1)1C x y +-=,2:10C x y -+=,由圆心到直线的距离01d ==<,故1C 与2C 的交点个数为2. 10.设,x y ∈R ,则222211()(4)x y y x++的最小值为 . 【测量目标】不等式选讲.【考查方式】给出两个乘式直接考查. 【难易程度】中等 【参考答案】9【试题解析】由柯西不等式可知2222211()(4)(12)9x y y x+++=…. 11.如图,,A E 是半圆周上的两个三等分点,直径4BC =,AD BC ⊥,垂足为D , BE 与AD 相交与点F ,则AF 的长为 .第11题图【测量目标】几何证明选讲.【考查方式】通过线段和圆的位置关系考查. 【难易程度】容易【参考答案】3【试题解析】由题可知,60AOB EOC ∠=∠=,2OA OB ==,得1OD BD ==,3DF =,又23AD BD CD ==,所以3AF AD DF =-=. 二、必做题(12~16题)12.设n S 是等差数列*{}()n a n ∈N 的前n 项和,且141,7a a ==,则5______S = 【测量目标】等差数列的前n 项和.【考查方式】给出等差数列某两项的值求出通项再求和. 【难易程度】容易 【参考答案】25【试题解析】由141,7a a ==可得11,2,21n a d a n ===-,所以5(19)5252S +⨯==. 13.若执行如图所示的框图,输入1231,2,3,2x x x x ====, 则输出的数等于 .第13 题图【测量目标】循环结构的程序框图. 【考查方式】直接给出程序框图考查. 【难易程度】中等 【参考答案】23【试题解析】由框图的算法功能可知,输出的数为三个数的方差,则222(12)(22)(32)233S -+-+-==. 14.在边长为1的正三角形ABC 中,设2,3BC BD CA CE == ,则________AD BE =.【测量目标】平面向量在平面几何中的运用. 【考查方式】给出向量间的关系求解. 【难易程度】容易 【参考答案】14-【试题解析】由题12AD CD CA CB CA =-=- ,13BE CE CB CA CB =-=-,所以111171()()232364AD BE CB CA CA CB CB CA =--=--+=-. 15.如图, EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则(1)=______P A ();(2)=______P B A (|)第15题图【测量目标】几何概型.【考查方式】利用两个图形面积的比值求解. 【难易程度】容易 【参考答案】(1)2π;(2)1=4PB A (|) 【试题解析】(1)由几何概型概率计算公式可得2==πS P A S 正圆(); (2)由条件概率的计算公式可得21×1π4===24πP AB P B A P A ()(|)().16.对于*n ∈N ,将n 表示为1210012122222k k k k k n a a a a a ---=⨯+⨯+⨯++⨯+⨯ ,当0i =时,1i a =,当1i k 剟时,i a 为0或1.记()I n 为上述表示中i a 为0的个数,(例如0112=⨯,2104120202=⨯+⨯+⨯:故(1)0,(4)2I I ==)则(1)(12)_____I = (2)127()12______I n n ==∑【测量目标】排列组合及其应用. 【考查方式】利用特定的条件求解. 【难易程度】较难 【参考答案】(1)2;(2)1093【试题解析】(1)因3211212+120202=⨯⨯+⨯+⨯,故(12)2I =;(2)在2进制的(2)k k …位数中,没有0的有1个,有1个0的有11C k -个,有2个0的有21C k -个,……有m 个0的有1C m k -个,……有1k -个0的有11C 1k k --=个.故对所有2进制为k 位数的数n ,在所求式中的()2I n 的和为:0112211111112C 2C 2C 23k k k k k k ------⨯++++=. 又712721=-恰为2进制的最大7位数,所以1277()1122231093I n k n k -===+=∑∑.三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)在ABC △中,角,,A B C 所对的边分别为,,a b c ,且满足sin cos c A a C =.(I )求角C 的大小;(II πcos()4A B -+的最大值,并求取得最大值时角,A B 的大小. 【测量目标】正弦定理,三角函数的最值. 【考查方式】给出边角之间的关系求解. 【难易程度】容易 【试题解析】(I )由正弦定理得sin sin sin cos .C A A C = 因为0π,A <<所以sin 0.A >πsin cos .cos 0,tan 1,4C C C C C =≠==从而又所以则.(步骤1) (II )由(I )知3π.4B A =-于是 πcos()cos(π)4A B A A -+=--πcos 2sin().6A A A =+=+3πππ11ππππ0,<+<,=,,46612623A A A A <<∴+= 从而当即时π2sin()6A +取最大值2.(步骤2)πcos()4A B -+的最大值为2,此时π5π,.312A B ==(步骤3) 18. 某商店试销某种商品20天,获得如下数据:当天营业结束后检查存货,若发现存货少于2件,则当天进货补充..至3件,否则不进货...,将频率视为概率.(Ⅰ)求当天商品不进货...的概率; (Ⅱ)记X 为第二天开始营业时该商品的件数,求X 的分布列和数学期望. 【测量目标】对立事件的概率,离散型随机变量的期望. 【考查方式】运用实际生活背景考查.【难易程度】容易 【试题解析】(I )P (“当天商店不进货”)=P (“当天商品销售量为0件”)+P (“当天商品销售量1件”)=153202010+=.(步骤1) (II )由题意知,X 的可能取值为2,3.51(2)()204P X P ====“当天商品销售量为1件”; (3)()+()+(1953)++32020204P X P P P ====“当天商品销售量为0件”“当天商品销售量为2件”“当天商品销售量为3件”(步骤)故X 的分布列为X2 3 P 14 34 X 的数学期望为13112+3=444EX =⨯⨯.(步骤4)19.(本题满分12分)如图,在圆锥PO 中,已知PO O = 的直径2,,A B C A B D A C=是的中点,为的中点. (I )证明:;POD PAC ⊥平面平面 (II )求二面角B PA C --的余弦值.第18题图【测量目标】面面垂直,二面角.【考查方式】在圆锥中考查. 【难易程度】容易 【试题解析】(I )连接OC , 因为OA OC =,D 为AC 中点,所以AC OD ⊥. 又,,.PO O AC O AC PO ⊥⊂⊥ 底面底面所以因为,OD PO 是平面POD 内的两条相交直线,所以AC POD ⊥平面而AC PAC ⊂平面,所以POD PAC ⊥平面平面.(步骤1)(II )在平面POD 中,过O 作OH PD ⊥于H ,由(I )知,POD PAC ⊥平面平面,所以,OH PAC ⊥平面又,PA PAC ⊂平面所以PA OH ⊥.在平面PAO 中,过O 作OG PA G ⊥于,连接HG ,则有PA OGH ⊥平面, 从而PA HG ⊥,所以OGH ∠是二面角B PA C --的平面角.(步骤2)在Rt ,sin 452ODA OD OA ==△中在Rt ,POD OH ===△中在Rt ,POA OG ===△中在Rt ,sin OH OHG OGH OG ∠===△中所以cos 5OGH ∠=. 故二面角B PA C --的余弦值为5.(步骤3)第19题图20. 如图,长方形物体E 在雨中沿面P (面积为S )的垂直方向作匀速移动,速度为(0)v v >,雨速沿E 移动方向的分速度为()c c ∈R .E 移动时单位时间....内的淋雨量包括两部分:(1)P 或P 的平行面(只有一个面淋雨)的淋雨量,假设其值与v c -×S 成正比,比例系数为110;(2)其它面的淋雨量之和,其值为12,记y 为E 移动过程中的总淋雨量,当移动距离d =100,面积S =32时. (Ⅰ)写出y 的表达式;(Ⅱ)设0<v …10,0<c …5,试根据c 的不同取值范围,确定移动速度v ,使总淋雨量y 最少.第19题图【测量目标】分段函数模型,利用函数单调性及最值. 【考查方式】利用将立体几何与函数综合考查. 【难易程度】中等【试题解析】(I )由题意知,E 移动时单位时间内的淋雨量为31||202v c -+, 故100315(||)(3||10)202y v c v c v v=-+=-+.(步骤1) (II )由(I)知,当0v c <…时,55(310)(3310)15c y c v v v+=-+=-; 当10c v <…时,55(103)(3310)15c y v c v v-=-+=+. 故5(310)15,05(103)15,10c v c vy c c v v +⎧-<⎪⎪=⎨-⎪+<⎪⎩…….(步骤2)(1)当1003c <…时,y 是关于v 的减函数.故当10v =时,min 3202cy =-.(步骤3) (2) 当1053c <…时,在(0,]c 上,y 是关于v 的减函数;在(,10]c 上,y 是关于v 的增函数;故当v c =时,min 50y c=.(步骤4) 21.(本小题满分13分) 如图,椭圆221221(0)x y C a b a b +=>>:,x轴被曲线22:C y x b =- 截得的线段长等于1C 的长半轴长.(Ⅰ)求1C ,2C 的方程;(Ⅱ)设2C 与y 轴的交点为M ,过坐标原点O 的直线l 与2C 相交于点A,B ,直线MA ,MB 分别与1C 相交于D ,E .(i )证明:MD ME ⊥;(ii)记△MAB ,△MDE 的面积分别是12,S S .问:是否存在直线l ,使得121732S S =? 请说明理由.第21题图【测量目标】椭圆的标准方程,直线与椭圆的位置关系. 【考查方式】利用直线与椭圆相交的位置关系和条件考查. 【难易程度】较难【试题解析】(I)由题意知c e a ==2a b =,又a =,解得2,1a b ==.故1C ,2C 的方程分别为2221,14x y y x +==-. (步骤1) (II )(i )由题意知,直线l 的斜率存在,设为k , 则直线l 的方程为y kx =.由21y kx y x =⎧⎨=-⎩得210x kx --=,(步骤2) 设1122(,),(,)A x y B x y ,则12,x x 是上述方程的两个实根,于是1212,1x x k x x +==-. 又点M 的坐标为(0,1)-,所以2221212121212121211(1)(1)()1111MA MBy y kx kx k x x k x x k k k k x x x x x x +++++++-++=====--故MA MB ⊥,即MD ME ⊥.(步骤3)(ii )设直线MA 的斜率为1k ,则直线MA 的方程为11y k x =-,由1211y kx y x =-⎧⎨=-⎩解得01x y =⎧⎨=-⎩或1211x k y k =⎧⎨=-⎩,则点A 的坐标为211(,1)k k -(步骤4) 又直线MB 的斜率为11k -,同理可得点B 的坐标为21111(,1)k k --.于是211111111||||||||.22||k S MA MB k k k +==-= (步骤5)由1221440y k x x y =-⎧⎨+-=⎩得2211(14)80k x k x +-=,解得01x y =⎧⎨=-⎩或12121218144114k x k k y k ⎧=⎪+⎪⎨-⎪=⎪+⎩,则点D 的坐标为2112211841(,)1414k k k k -++;(步骤6) 又直线ME 的斜率为11k -,同理可得点E 的坐标211221184(,)44k k k k --++ 于是2112221132(1)||1||||2(14)(4)k k S MD ME k k +==++ 因此21122111(417)64S k S k =++(步骤7) 由题意知,21211117(417)6432k k ++=,解得214k = 或2114k =. 又由点,A B 的坐标可知,21211111111k k k k k k k -==-+,所以3.2k =± 故满足条件的直线l 存在,且有两条,其方程分别为32y x =和32y x =-.(步骤8) 22.(本小题满分13分)已知函数f (x ) =3x ,g (x )=x(Ⅰ)求函数h (x )=f (x )-g (x )的零点个数,并说明理由;(Ⅱ)设数列*{}()n a n ∈N 满足1(0)a a a =>,1()()n n f a g a +=,证明:存在常数M ,使得对于任意的*n ∈N ,都有n a …M . 【测量目标】利用导数求单调性,不等式恒成立问题.【考查方式】给出两个函数式,利用导数及不等式求解.【难易程度】较难【试题解析】(I)由3()h x x x =-知,[0,)x ∈+∞,而(0)0h =,且(1)10,(2)60h h =-<=,则0x =为()h x 的一个零点,且()h x 在12(,)内有零点,因此()h x 至少有两个零点(步骤1) 122()(1)h x x x x -=--,记122()1x x x ϕ-=--,则321()22x x x ϕ-'=+. 当(0,)x ∈+∞时,()0x ϕ'>,因此()x ϕ在(0,)+∞上单调递增,则()x ϕ在(0,)+∞内至多只有一个零点.因此()h x 在(0,)+∞内也至多只有一个零点,综上所述,()h x 有且只有两个零点.(步骤2) (II )记()h x 的正零点为0x,即300x x =(1)当0a x <时,由1a a =,即10a x <.而332100a a x x ==,因此20a x <,由此猜测:0n a x <.下面用数学归纳法证明: ①当1n =时,10a x <显然成立;(步骤3) ②假设当(1)n k k =…时,有0k a x <成立,则当1n k =+时,由13300k k a a x x +=+<知,10k a x +<,因此,当1n k =+时,10k a x +<成立. 故对任意的*n ∈N ,0n a x <成立.(步骤4)(2)当0a x …时,由(1)知,()h x 在0(,)x +∞上单调递增.则0()()0h a h x =…,即3a a +….从而2331a a a a ==,即2a a …,由此猜测:n a a ….下面用数学归纳法证明:①当1n =时,1a a …显然成立;(步骤5) ②假设当(1)n k k =…时,有k a a …成立,则当1n k =+时,由133k k a a a a +=+知,1k a a +…,因此,当1n k =+时,1k a a +…成立.故对任意的*n ∈N ,n a a …成立. 综上所述,存在常数0max{,}M x a =,使得对于任意的*n ∈N ,都有n a M ….(步骤6)。
湖南高考数学卷理科

2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分。
参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高。
(3)球的体积公式343V R π=,其中R 为求的半径。
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+则A .1a =,1b = B. 1,1a b =-= C.1,1a b =-=- D. 1,1a b ==- 2.设集合{}{}21,2,,M N a ==则 “1a =”是“N M ⊆”的 A.充分不必要条件 B.必要不充分条件 C. 充分必要条件 D. 既不充分又不必要条件 3.设图1是某几何体的三视图,则该几何体的体积为A. 9122π+B. 9182π+C. 942π+D. 3618π+4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:由()()()()()22n ad bc k a b c d a c b d -=++++算得,()22110403020207.860506050k ⨯⨯-⨯=≈⨯⨯⨯.参照附表,得到的正确结论是A . 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B . 在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关” C.有99%以上的把握认为“爱好该项运动与性别有关” D.有99%以上的把握认为“爱好该项运动与性别无关”5.设双曲线()222109x y a a -=>的渐近线方程为320x y ±=,则a 的值为 A.4 B.3 C.2 D.1 6.由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为A.12B.1C. 27.设m >1,在约束条件1y xy mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数Z=x+my 的最大值小于2,则m 的取值范围为A.(1,1 B.(1++∞) C.(1,3 ) D.(3,+∞)8.设直线x=t 与函数2()f x x = ()ln g x x = 的图像分别交于点M,N,则当MN 达到最小时t 的值为A.1B. 122填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应号后的横线上。
2011年湖南高考数学试题(理科)

蟠叠翠”、“丰岭祥云”等景观,都在琅琊山区。可是,一州景观,分布广泛,不 都在琅琊山。浏览现存的几部旧志,从明万历《滁阳志》到民国《琅琊山志》,都 没有明确的记载。 早在盛唐时期,滁州已有记载琅琊史话的《图经》问世。二百 多年以后,北宋至道元年(995年),著名诗人王禹偁任滁州知州,查阅《图经》, 漫游琅琊,写了不少诗篇。 唐宋《图经》没有流传下来,琅琊寺里的《八绝诗》 碑也早已毁废,有赖于王禹偁《小畜集》中收入的《八绝诗》,琅琊八绝指的是庶 子泉、白龙泉、明月溪、清风亭、望日台、归云洞、阳冰篆和垂藤盖。双泉亭台、 碑篆岩洞、清溪古藤,有的至今尚存。 宋庆历五年(1045 年),欧阳修来到滁州, 对琅琊山上的佳丽景点,有了新的品评,写下了组诗《琅琊山六题》——题咏六处 胜景:归云洞、庶子泉、琅琊溪、石屏路、班春亭、惠觉方丈。前二景与“八绝” 相同,其余都有所改易。这“六题”,大概是欧阳修最欣赏的“琅琊六景”吧。他 的挚友、宣城诗人梅尧臣曾经和诗六首,题为《和永叔琅琊山六咏》,同欧阳修的 组诗一起流传至今,成为琅琊山史话中的又一美谈。 继“八绝”、“六题”之后, 由欧阳修命名的醉翁亭后来居上,著称于世,成为如今琅琊山上最为有名的胜迹。
2011年湖南省高考数学试卷(理科)及答案

2011年湖南省高考数学试卷(理科)一、选择题(共8小题,每小题5分,满分40分)1.(5分)若a,b∈R,i为虚数单位,且(a+i)i=b+i则()A.a=1,b=1 B.a=﹣1,b=1 C.a=﹣1,b=﹣1 D.a=1,b=﹣12.(5分)设集合M={1,2},N={a2},则“a=1”是“N⊆M”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分又不必要条件3.(5分)设如图是某几何体的三视图,则该几何体的体积为()A.9π+42 B.36π+18 C. D.4.(5分)通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计6050110由算得,.P(K2≥k)0.0500.0100.001k 3.841 6.63510.828参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”5.(5分)设双曲线的渐近线方程为3x±2y=0,则a的值为()A.4 B.3 C.2 D.16.(5分)由直线x=﹣,x=,y=0与曲线y=cosx所围成的封闭图形的面积为()A.B.1 C.D.7.(5分)设m>1,在约束条件下,目标函数z=x+my的最大值小于2,则m的取值范围为()A.(1,)B.(,+∞)C.(1,3) D.(3,+∞)8.(5分)设直线x=t与函数f(x)=x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为()A.1 B.C.D.二、填空题(共8小题,每小题5分,满分35分)9.(5分)在直角坐标系xOy中,曲线C1的参数方程为(α为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x 轴正半轴为极轴)中,曲线C2的方程为p(cosθ﹣sinθ)+1=0,则C1与C2的交点个数为.10.(5分)设x,y∈R,且xy≠0,则的最小值为.11.如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为.12.(5分)设S n是等差数列{a n}(n∈N*)的前n项和,且a1=1,a4=7,则S9=.13.(5分)若执行如图所示的框图,输入x1=1,x2=2,x3=3,=2,则输出的数等于.14.(5分)在边长为1的正三角形ABC中,设,,则=.15.(5分)如图,EFGH 是以O为圆心,半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=;(2)P(B|A)=.16.(5分)对于n∈N+,将n 表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k﹣1×21+a k×20,当i=0时,a i=1,当1≤i≤k时,a1为0或1.记I(n)为上述表示中a i为0的个数(例如:1=1×20,4=1×22+0×21+0×20,故I(1)=0,I(4)=2),则(1)I(12)=;(2)=.三、解答题(共6小题,满分75分)17.(12分)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC 1)求角C大小;(2)求sinA﹣cos(B+)的最大值,并求取得最大值时角A,B的大小.18.(12分)某商店试销某种商品20天,获得如下数据:日销售量(件)0123频数1595试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.(Ⅰ)求当天商品不进货的概率;(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望.19.(12分)如图,在圆锥PO中,已知PO=,⊙O的直径AB=2,C是的中点,D为AC的中点.(Ⅰ)证明:平面POD⊥平面PAC;(Ⅱ)求二面角B﹣PA﹣C的余弦值.20.(13分)如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v﹣c|×S成正比,比例系数为;(2)其它面的淋雨量之和,其值为,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=时.(Ⅰ)写出y的表达式(Ⅱ)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.21.(13分)如图,椭圆C1:=1(a>b>0)的离心率为,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.(Ⅰ)求C1,C2的方程;(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.(i)证明:MD⊥ME;(ii)记△MAB,△MDE的面积分别是S1,S2.问:是否存在直线l,使得=?请说明理由.22.(13分)已知函数f(x)=x3,g (x)=x+.(Ⅰ)求函数h (x)=f(x)﹣g (x)的零点个数.并说明理由;(Ⅱ)设数列{a n}(n∈N*)满足a1=a(a>0),f(a n+1)=g(a n),证明:存在常数M,使得对于任意的n∈N*,都有a n≤M.2011年湖南省高考数学试卷(理科)参考答案与试题解析一、选择题(共8小题,每小题5分,满分40分)1.(5分)(2011•湖南)若a,b∈R,i为虚数单位,且(a+i)i=b+i则()A.a=1,b=1 B.a=﹣1,b=1 C.a=﹣1,b=﹣1 D.a=1,b=﹣1【分析】利用复数的乘法运算将等式化简;利用复数相等实部、虚部分别相等;列出方程求出a,b的值.【解答】解:(a+i)i=b+i即﹣1+ai=b+i∴a=1,b=﹣1故选D2.(5分)(2011•湖南)设集合M={1,2},N={a2},则“a=1”是“N⊆M”的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分又不必要条件【分析】先由a=1判断是否能推出“N⊆M”;再由“N⊆M”判断是否能推出“a=1”,利用充要条件的定义得到结论.【解答】解:当a=1时,M={1,2},N={1}有N⊆M当N⊆M时,a2=1或a2=2有所以“a=1”是“N⊆M”的充分不必要条件.故选A.3.(5分)(2011•湖南)设如图是某几何体的三视图,则该几何体的体积为()A.9π+42 B.36π+18 C. D.【分析】由三视图可知,下面是一个底面边长是3的正方形且高是2的一个四棱柱,上面是一个球,球的直径是3,该几何体的体积是两个体积之和,分别做出两个几何体的体积相加.【解答】解:由三视图可知,几何体是一个简单的组合体,下面是一个底面边长是3的正方形且高是2的一个四棱柱,上面是一个球,球的直径是3,该几何体的体积是两个体积之和,四棱柱的体积3×3×2=18,球的体积是,∴几何体的体积是18+,故选D.4.(5分)(2011•湖南)通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男女总计爱好402060不爱好203050总计6050110由算得,.P(K2≥k)0.0500.0100.001k 3.841 6.63510.828参照附表,得到的正确结论是()A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”D.有99%以上的把握认为“爱好该项运动与性别无关”【分析】题目的条件中已经给出这组数据的观测值,我们只要把所给的观测值同节选的观测值表进行比较,发现它大于6.635,得到有99%以上的把握认为“爱好这项运动与性别有关”.【解答】解:由题意算得,.∵7.8>6.635,∴有0.01=1%的机会错误,即有99%以上的把握认为“爱好这项运动与性别有关”故选:C.5.(5分)(2011•湖南)设双曲线的渐近线方程为3x±2y=0,则a的值为()A.4 B.3 C.2 D.1【分析】由题意,,即可求出a的值.【解答】解:由题意,,∴a=2,故选:C.6.(5分)(2011•湖南)由直线x=﹣,x=,y=0与曲线y=cosx所围成的封闭图形的面积为()A.B.1 C.D.【分析】为了求得与x轴所围成的不规则的封闭图形的面积,可利用定积分求解,积分的上下限分别为与,cosx即为被积函数.【解答】解:由定积分可求得阴影部分的面积S=cosxdx==﹣(﹣)=,所以围成的封闭图形的面积是.故选D.7.(5分)(2011•湖南)设m>1,在约束条件下,目标函数z=x+my的最大值小于2,则m的取值范围为()A.(1,)B.(,+∞)C.(1,3) D.(3,+∞)【分析】根据m>1,我们可以判断直线y=mx的倾斜角位于区间(,)上,由此我们不难判断出满足约束条件的平面区域的形状,再根据目标函数Z=X+my对应的直线与直线y=mx垂直,且在直线y=mx与直线x+y=1交点处取得最大值,由此构造出关于m的不等式组,解不等式组即可求出m 的取值范围.【解答】解:∵m>1故直线y=mx与直线x+y=1交于点,目标函数Z=X+my对应的直线与直线y=mx垂直,且在点,取得最大值其关系如下图所示:即,解得1﹣<m<又∵m>1解得m∈(1,)故选:A.8.(5分)(2011•湖南)设直线x=t与函数f(x)=x2,g(x)=lnx的图象分别交于点M,N,则当|MN|达到最小时t的值为()A.1 B.C.D.【分析】将两个函数作差,得到函数y=f(x)﹣g(x),再求此函数的最小值对应的自变量x的值.【解答】解:设函数y=f(x)﹣g(x)=x2﹣lnx,求导数得=当时,y′<0,函数在上为单调减函数,当时,y′>0,函数在上为单调增函数所以当时,所设函数的最小值为所求t的值为故选D二、填空题(共8小题,每小题5分,满分35分)9.(5分)(2011•湖南)在直角坐标系xOy中,曲线C1的参数方程为(α为参数)在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为p(cosθ﹣sinθ)+1=0,则C1与C2的交点个数为2.【分析】先根据sin2α+cos2α=1,求出曲线C1的直角坐标方程,再利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,求出曲线C2的直角坐标方程,然后判定交点个数即可.【解答】解:∵曲线C1的参数方程为(α为参数),sin2α+cos2α=1∴曲线C1的直角坐标方程为x2+(y﹣1)2=1∵ρcosθ=x,ρsinθ=y,p(cosθ﹣sinθ)+1=0∴曲线C2的方程为x﹣y+1=0而圆心到直线的距离d=0<r,故C1与C2的交点个数为2故答案为:210.(5分)(2011•湖南)设x,y∈R,且xy≠0,则的最小值为9.【分析】对展开,利用基本不等式即可求得其最小值.【解答】解:∵x,y∈R,且xy≠0,∴=1+4+≥5+2=9当且仅当时等号成立,∴的最小值为9.故答案为9.11.(2011•湖南)如图,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为.【分析】根据半圆的三等分点,得到三个弧对应的角度是60°,根据直径所对的圆周角是直角得到直角三角形的有关长度,做出要求的线段的长度.【解答】解:∵A,E是半圆周上的两个三等分点∴弧EC是一个60°的弧,∴∠EBC=30°,则CE=2,连接BA,则BA=2,∴在含有30°角的直角三角形中,BD=1,DF=,AD=∴AF=,故答案为:12.(5分)(2011•湖南)设S n是等差数列{a n}(n∈N*)的前n项和,且a1=1,a4=7,则S9=81.【分析】先根据数列{a n}为等差数列,求出公差d,然后根据等差数列的前n项和公式求得S9.【解答】解:∵数列{a n}为等差数列,∴a n=a1+(n﹣1)d,S n=na1+∵a1=1,a4=7∴a4=1+(4﹣1)d=7∴d=2∴S9=9×1+×2=81故答案为:8113.(5分)(2011•湖南)若执行如图所示的框图,输入x1=1,x2=2,x3=3,=2,则输出的数等于.【分析】先弄清该算法功能,S=0+(1﹣2)2=1,i=1,满足条件i<3,执行循环体,依此类推,当i=3,不满足条件i<3,退出循环体,输出所求即可.【解答】解:S=0+(1﹣2)2=1,i=1,满足条件i<3,执行循环体,i=2S=1+(2﹣2)2=1,i=2,满足条件i<3,执行循环体,i=3S=1+(3﹣2)2=2,i=3,不满足条件i<3,退出循环体,则S=×2=故答案为:14.(5分)(2011•湖南)在边长为1的正三角形ABC中,设,,则=﹣.【分析】根据,,确定点D,E在正三角形ABC中的位置,根据向量加法满足三角形法则,把用表示出来,利用向量的数量积的运算法则和定义式即可求得的值.【解答】解:∵,∴D为BC的中点,∴,∵,∴,∴=)==﹣,故答案为:﹣.15.(5分)(2011•湖南)如图,EFGH 是以O为圆心,半径为1的圆的内接正方形.将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形EFGH内”,B表示事件“豆子落在扇形OHE(阴影部分)内”,则(1)P(A)=;(2)P(B|A)=.【分析】此题是个几何概型.用面积法求出事件A“豆子落在正方形EFGH内”的概率p(A),同理求出P(AB),根据条件概率公式P(B|A)=即可求得结果.【解答】解:用A表示事件“豆子落在正方形EFGH内”,∴P(A)==,B表示事件“豆子落在扇形OHE(阴影部分)内”,P(AB)==,∴P(B|A)=.故答案为:.16.(5分)(2011•湖南)对于n∈N+,将n 表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k ×21+a k×20,当i=0时,a i=1,当1≤i≤k时,a1为0或1.记I(n)为上述表﹣1示中a i为0的个数(例如:1=1×20,4=1×22+0×21+0×20,故I(1)=0,I(4)=2),则(1)I(12)=2;(2)=1093.【分析】(1)根据题意,分析可得,将n 表示n=a0×2k+a1×2k﹣1+a2×2k﹣2+…+a k×21+a k×20,实际是将十进制的数转化为二进制的数,易得12=1×23+1×22+0﹣1×21+0×20,由I(n)的意义,可得答案;(2)将n分为n=127,64≤n≤126,32≤n≤63,…n=1等7种情况,有组合数的性质,分析其中I(n)的取值情况,与二项式定理结合,可转化为等比数列的前7项和,计算可得答案.【解答】解:(1)根据题意,12=1×23+1×22+0×21+0×20,则I(12)=2;(2)127=1×26+1×25+1×24+1×23+1×22+1×21+1×20,设64≤n≤126,且n为整数;则n=1×26+a1×25+a2×24+a3×23+a4×22+a5×21+a6×20,a1,a2,a3,a4,a5,a6中6个数都为0或1,其中没有一个为1时,有C60种情况,即有C60个I(n)=6;其中有一个为1时,有C61种情况,即有C61个I(n)=5;其中有2个为1时,有C62种情况,即有C62个I(n)=4;…2I(n)=C6026+C61×25+C62×24+C63×23+C64×22+C65×2+1=(2+1)n=36,同理可得:=35,…=31,2I(1)=1;则=1+3+32+…+36==1093;故答案为:(1)2;(2)1093.三、解答题(共6小题,满分75分)17.(12分)(2011•湖南)在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC1)求角C大小;(2)求sinA﹣cos(B+)的最大值,并求取得最大值时角A,B的大小.【分析】(1)利用正弦定理化简csinA=acosC.求出tanC=1,得到C=.(2)B=﹣A,化简sinA﹣cos(B+),通过0<A<,推出<A+<,求出2sin(A+)取得最大值2.得到A,B.【解答】解:(1)由正弦定理得sinCsinA=sinAcosC,因为0<A<π,所以sinA>0.从而sinC=cosC,又cosC≠0,所以tanC=1,C=.(2)有(1)知,B=﹣A,于是sinA﹣cos(B+)=sinA+cosA=2sin(A+).因为0<A<,所以<A+<,从而当A+=,即A=时2sin(A+)取得最大值2.综上所述sinA﹣cos(B+)的最大值为2,此时A=,B=.18.(12分)(2011•湖南)某商店试销某种商品20天,获得如下数据: 日销售量(件)0 1 2 3 频数1595试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率. (Ⅰ)求当天商品不进货的概率;(Ⅱ)记X 为第二天开始营业时该商品的件数,求X 的分布列和数学期望. 【分析】(I )“当天商品不进货”包含两个事件的和事件,利用古典概型概率公式求出两个事件的概率;再利用互斥事件的和事件概率公式求出当天商品不进货的概率.(II )求出x 可取的值,利用古典概型概率公式及互斥事件和事件的概率公式求出x 取每一个值的概率值;列出分布列;利用随机变量的期望公式求出x 的期望. 【解答】解:(I )P (“当天商店不进货”)=P (“当天商品销售量为0件”)+(“当天的商品销售量为1件”) =(II )由题意知,X 的可能取值为2,3 P (X=2)=P (“当天商品销售量为1件”)=P (X=3)=(“当天的销售量为0”)+P (“当天的销售量为2件”)+P (“当天的销售量为3件”)=故x 的分布列 x 2 3 pX 的数学期望为EX=19.(12分)(2011•湖南)如图,在圆锥PO中,已知PO=,⊙O的直径AB=2,C是的中点,D为AC的中点.(Ⅰ)证明:平面POD⊥平面PAC;(Ⅱ)求二面角B﹣PA﹣C的余弦值.【分析】(Ⅰ)连接OC,先根据△AOC是等腰直角三角形证出中线OD⊥AC,再结合PO⊥AC证出AC⊥POD,利用平面与平面垂直的判定定理,可证出平面POD ⊥平面PAC;(Ⅱ)过O分别作OH⊥PD于H,OG⊥PA于G,再连接GH,根据三垂线定理证明∠OGH为二面角B﹣PA﹣C的平面角,最后分别在Rt△ODA、Rt△ODP、Rt△OGH中计算出OH、OG和sin∠OGH,最后求出所求二面角的余弦值.【解答】解:(Ⅰ)连接OC,∵OA=OC,D是AC的中点∴AC⊥OD又∵PO⊥底面⊙O,AC⊂底面⊙O∴AC⊥PO∵OD、PO是平面POD内的两条相交直线∴AC⊥平面POD,而AC⊂平面PAC∴平面POD⊥平面PAC(Ⅱ)在平面POD中,过O作OH⊥PD于H,由(Ⅰ)知,平面POD⊥平面PAC 所以OH⊥平面PAC,又∵PA⊂平面PAC∴PA⊥HO在平面PAO中,过O作OG⊥PA于G,连接GH,则有PA⊥平面OGH,从而PA⊥HG.故∠OGH为二面角B﹣PA﹣C的平面角在Rt△ODA中,OD=OA•sin45°=在Rt△ODP中,OH=在Rt△OPA中,OG=在Rt△OGH中,sin∠OGH=所以cos∠OGH=故二面角B﹣PA﹣C的余弦值为20.(13分)(2011•湖南)如图,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为v(v>0),雨速沿E移动方向的分速度为c(c∈R).E 移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与|v﹣c|×S成正比,比例系数为;(2)其它面的淋雨量之和,其值为,记y为E移动过程中的总淋雨量,当移动距离d=100,面积S=时.(Ⅰ)写出y的表达式(Ⅱ)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度v,使总淋雨量y最少.【分析】(Ⅰ)E移动时的总淋雨量应该等于单位时间内的淋雨量乘以所用的时间,可先求出单位时间内的淋雨量的式子,再乘以时间即可;(Ⅱ)根据绝对值的性质,将(Ⅰ)中的函数分解为分段函数的形式,再由c的不同取值范围讨论函数的单调性,在不同的情况下,单调区间不同,总淋雨量最小值对应的v值也不同.【解答】解:(Ⅰ)由题意知,E移动时单位时间内的淋雨量为,故(Ⅱ)由(Ⅰ)知,当0<v≤c时,当c≤v≤10时,故(1)当0<c<时,y是关于v的减函数,故当v=10时,;(2)当时,在(0,c]上y是关于v的减函数,在(c,10]上,y是关于v的增函数,故当v=c时,答:(Ⅰ)函数y的表达式为(Ⅱ)(1)在0<c的情况下,当v=10时,总淋雨量y最少;(2)在的情况下,当v=c时,总淋雨量y最少.21.(13分)(2011•湖南)如图,椭圆C1:=1(a>b>0)的离心率为,x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长.(Ⅰ)求C1,C2的方程;(Ⅱ)设C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于D,E.(i)证明:MD⊥ME;(ii)记△MAB,△MDE的面积分别是S1,S2.问:是否存在直线l,使得=?请说明理由.【分析】(Ⅰ)先利用离心率得到一个关于参数的方程,再利用x轴被曲线C2:y=x2﹣b截得的线段长等于C1的长半轴长得另一个方程,两个方程联立即可求出参数进而求出C1,C2的方程;(Ⅱ)(i)把直线l的方程与抛物线方程联立可得关于点A、B坐标的等量关系,再代入求出k MA•k MB=﹣1,即可证明:MD⊥ME;(ii)先把直线MA的方程与抛物线方程联立可得点A的坐标,再利用弦长公式求出|MA|,同样的方法求出|MB|进而求出S1,同理可求S2.再代入已知就可知道是否存在直线l满足题中条件了.【解答】解:(Ⅰ)由题得e=,从而a=2b,又2=a,解得a=2,b=1,故C1,C2的方程分别为,y=x2﹣1.(Ⅱ)(i)由题得,直线l的斜率存在,设为k,则直线l的方程为y=kx,由得x2﹣kx﹣1=0.设A(x1,y1),B(x2,y2),则x1,x2是上述方程的两个实根,于是x1+x2=k,x1x2=﹣1,又点M的坐标为(0,﹣1),所以k MA•k MB=====﹣1.故MA⊥MB,即MD⊥ME.(ii)设直线MA的斜率为k1,则直线MA的方程为y=k1x﹣1.由,解得或.则点A的坐标为(k1,k12﹣1).又直线MB的斜率为﹣,同理可得点B的坐标为(﹣,﹣1).于是s1=|MA|•|MB|=•|k1|••|﹣|=.由得(1+4k12)x2﹣8k1x=0.解得或,,则点D的坐标为(,).又直线ME的斜率为﹣.同理可得点E的坐标为(,).于是s2=|MD|•|ME|=.故=,解得k12=4或k12=.又由点A,B的坐标得,k==k1﹣.所以k=±.故满足条件的直线存在,且有两条,其方程为y=x和y=﹣x.22.(13分)(2011•湖南)已知函数f(x)=x3,g (x)=x+.(Ⅰ)求函数h (x)=f(x)﹣g (x)的零点个数.并说明理由;(Ⅱ)设数列{a n}(n∈N*)满足a1=a(a>0),f(a n+1)=g(a n),证明:存在常数M,使得对于任意的n∈N*,都有a n≤M.【分析】(Ⅰ)由h(x)=知,x∈[0,+∞),而h(0)=0,且h(1)=﹣1<0,h(2)=6﹣,再研究函数在(0,+∞)上的单调性,以确定零点个数即可(Ⅱ)记h(x)的正零点为x0,即,当a<x0时,由a1=a,即a1<x0,而,a2<x0.由此猜测a n<x0.当a≥x0时,由(Ⅰ)知,当x∈(x1,+∞)时,h(x)单调递增,h(a)>h(x0)=0,从而a2<a,由此猜测a n<a.然后用数学归纳法证明.【解答】解:(Ⅰ)由h(x)=知,x∈[0,+∞),而h(0)=0,且h (1)=﹣1<0,h(2)=6﹣,则x=0为h(x)的一个零点,且h(x)在(1,2)内有零点,∴h(x)至少有两个零点.由h(x)=,记,则,当x∈(0,+∞)时,g(x)单调递增,故可判断出h(x)在(0,+∞)仅有一个零点,综上所述,h(x)有且只有两个零点.(Ⅱ)记h(x)的正零点为x0,即,(1)当a<x0时,由a1=a,即a1<x0,而,∴a2<x0.由此猜测a n<x0.下面用数学归纳法证明:①当n=1时,a1<x0,成立.②假设当n=k时a k<x0成立,则当n=k+1时,由,知a k<x0.+1<x0成立.因此当n=k+1时,a k+1故对任意的n∈N*,a n≤x0成立.(2)当a≥x0时,由(Ⅰ)知,当x∈(x0,+∞)时,h(x)单调递增,∴h(a)>h(x0)=0,从而a2≤a,由此猜测a n≤a.下面用数学归纳法证明:①当n=1时,a1≤a,成立.②假设当n=k时a k<a成立,则当n=k+1时,由,知a k+1<a.<a成立.故对任意的n∈N*,a n≤a成立.因此当n=k+1时,a k+1综上所述,存在常数M,使得对于任意的n∈N*,都有a n≤M.。
2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)
2011年普通高等学校招生全国统一考试(湖南卷)数学(理工农医类)本试题卷包括选择题、填空题和解答题三部分,共6页,时量120分钟,满分150分参考公式:(1)()()()P AB P B A P A =,其中,A B 为两个事件,且()0P A >, (2)柱体体积公式V Sh =,其中S 为底面面积,h 为高(3)球的体积公式343V R π=,其中R 为求的半径一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的1.若,a b R ∈,i 为虚数单位,且()a i i b i +=+,则( )A .1,1a b ==B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==- 答案:D解析:因,根据复数相等的条件可知2.设{1,2}M =,2{}N a =,则“1a =”是“N M ⊆”则( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 答案:A解析:因“1a =”,即{1}N =,满足“N M ⊆”,反之“N M ⊆”,则2{}={1}N a =,或2{}={2}N a =,不一定有“1a =”3.设图一是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+C .942π+D .3618π+答案:B解析:有三视图可知该几何体是一个长方体和球构成的()1a i i ai b i +=-+=+1,1a b ==-3 32正视图侧视图俯视图 图1组合体,其体积由22()()()()()n ad bc K a bc d a c b d -=++++算得22110(40302020)7.860506050K ⨯⨯-⨯=≈⨯⨯⨯ 附表:参照附表,得到的正确结论是( )A .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别有关” 答案:C解析:由,而,故由独立性检验的意义可知选C.5.设双曲线2221(0)9x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A .4B .3C .2D .1答案:C解析:由双曲线方程可知渐近线方程为3yx a=±,故可知2a = 6.由直线,,033x x y ππ=-==与曲线cos y x =所围成的封闭图形的面积为( )A .12B .1CD 答案:D解析:由定积分知识可得3333cos sin |(22S xdx x ππππ--===--=⎰ D 3439+332=18322V ππ=⨯⨯+()27.8 6.635K ≈>2( 6.635)0.010P K ≥=7. 设1m >,在约束条件1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值小于2,则m 的取值范围为( )A.(1,1+ B.(1)++∞ C .(1,3) D .(3,)+∞ 答案:A解析:画出可行域,可知5z x y =+在点1(,)11mm m++取最大值,由21211m m m +<++解得11m <<8.设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于点,M N ,则当||MN 达到最小时t 的值为( ) A .1 B .12C.2 D.2答案:D解析:由题2||ln MN x x =-,(0)x >不妨令2()ln h x x x =-,则1'()2h x x x=-,令'()0h x =解得x =,因x ∈时,'()0h x <,当)x ∈+∞时,'()0h x >,所以当2x =时,||MN达到最小即2t =二填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上一、选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题记分)9.在直角坐标系xoy 中,曲线C 1的参数方程为cos ,1sin x y αα=⎧⎨=+⎩(α为参数)在极坐标系(与直角坐标系xoy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,曲线2C 的方程为()cos sin 10ρθθ-+=,则1C 与2C 的交点个数为 答案:2解析:曲线221:(1)1C x y +-=,2:10C x y -+=,由圆心到直线的距离|011|012d -+==<,故1C 与2C 的交点个数为2. 10.设,x y R ∈,则222211()(4)x y y x++的最小值为 答案:9解析:由柯西不等式可知2222211()(4)(12)9x y y x++≥+= 11.如图2,,A E 是半圆周上的两个三等分点,直径4BC =,AD BC ⊥,垂足为D,BE 与AD 相交与点F ,则AF 的长为答案:233解析:由题可知,60AOB EOC ∠=∠=︒,2OA OB ==,得1OD BD ==,33DF =, 又23AD BD CD =⋅=,所以233AF AD DF =-=.二、必做题(12~16题)12、设n S 是等差数列*{}()n a n N ∈的前n 项和,且141,7a a ==,则5______S =答案:25解析:由141,7a a ==可得11,2,21n a d a n ===-,所以5(19)5252S +⨯==13、若执行如图3所示的框图,输入1231,2,3,2x x x x ====,则输出的数等于 答案:23解析:由框图的算法功能可知,输出的数为三个数的方差,则222(12)(22)(32)233S -+-+-== 14、在边长为1的正三角形ABC 中,设2,3BC BD CA CE ==,则________AD BE ⋅=答案:14-解析:由题12AD CD CA CB CA =-=-,13BE CE CB CA CB =-=-, 所以111171()()232364AD BE CB CA CA CB CB CA ⋅=-⋅-=--+⋅=-15、如图4,EFGH 是以O 为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A 表示事件“豆子落在正方形EFGH 内”,B 表示事件“豆子落在扇形OHE (阴影部分)内”,则(1)=______P A ();(2)=______P A (B|) 答案:(1)2π;(2)1=4P A (B|)解析:(1)由几何概型概率计算公式可得2==S P A S π正圆(); (2)由条件概率的计算公式可得2114===24P AB P A P A ππ⨯()(B|)()16、对于*n N ∈,将n 表示为1210012122222k k k k k n a a a a a ---=⨯+⨯+⨯++⨯+⨯,当0i =时,1i a =,当1i k ≤≤时,i a 为0或1.记()I n 为上述表示中i a 为0的个数,(例如0112=⨯,2104120202=⨯+⨯+⨯:故(1)0,(4)2I I ==)则(1)(12)_____I = (2)127()12______I n n ==∑答案:(1)2;(2)1093解析:(1)因32101212+120202=⨯⨯+⨯+⨯,故(12)2I =;(2)在2进制的(2)k k ≥位数中,没有0的有1个,有1个0的有11k C -个,有2个0的有21k C -个,……有m 个0的有1m k C -个,……有1k -个0的有111k k C --=个故对所有2进制为k 位数的数n ,在所求式中的()2I n 的和为:01122111111122223k k k k k k C C C ------⋅+⋅+⋅++⋅= 又712721=-恰为2进制的最大7位数,所以1277()1122231093I n k n k -===+=∑∑三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤 17.(本小题满分12分)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足sin cos c A a C =. (I )求角C 的大小;(IIcos()4A B π-+的最大值,并求取得最大值时角,A B 的大小. 解析:(I )由正弦定理得sin sin sin cos .C A A C =因为0,A π<<所以sin 0.sin cos .cos 0,tan 1,4A C C C C C π>=≠==从而又所以则(II )由(I )知3.4B A π=-于是cos()cos()4cos 2sin().63110,,,,46612623A B A A A A A A A A A ππππππππππ-+=--=+=+<<∴<+<+==从而当即时2sin()6A π+取最大值2.cos()4A B π-+的最大值为2,此时5,.312A B ππ==18. 某商店试销某种商品20天,获得如下数据:试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充..至3件,否则不进货...,将频率视为概率 (Ⅰ)求当天商品不进货...的概率; (Ⅱ)记X 为第二天开始营业时该商品的件数,求X 的分布列和数学期望 解析:(I )P (“当天商店不进货”)=P (“当天商品销售量为0件”)+P (“当天商品销售量1件”)=153202010+= (II )由题意知,X 的可能取值为2,3.51(2)("")204P x P ====当天商品销售量为1件;(3)("")+("")+("1953")++2020204P x P P P ====当天商品销售量为0件当天商品销售量为2件当天商品销售量为3件故X 的分布列为X 2 3P14 34X 的数学期望为13112+3=444EX =⨯⨯19.(本题满分12分)如图5,在圆锥PO 中,已知2,PO O =的直径2,,AB C AB D AC =是的中点,为的中点.(I )证明:;POD PAC ⊥平面平面(II )求二面角B PA C --的余弦值. 解:(I )连接OC ,因为OA OC =,D 为的AC 中点,所以AC OD ⊥. 又,,.PO O AC O AC PO ⊥⊂⊥底面底面所以因为,OD PO 是平面POD 内的两条相交直线,所以AC POD ⊥平面。
2011年普通高等学校招生全国统一考试(湖南卷)数学试题 (理科)(解析版)

正视图 侧视图俯视图 图12011年普通高等学校招生全国统一考试(湖南卷)数学(理)试题解析本试题包括选择题、填空题和解答题三部分,共6页.时量120分钟,满分150分. 参考公式(1)柱体体积公式V Sh =,其中S 为底面面积,h 为高. (2)球的体积公式343V R π=,其中R 为球的半径.一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.)若,a b R ∈,i 为虚数单位,且()a i i b i +=+则 ( )A .1a =,1b =B .1,1a b =-=C .1,1a b =-=-D .1,1a b ==- 1. 解析:因()1a i i ai b i +=-+=+,根据复数相等的条件可知1,a =2.设集合{}{}21,2,,M N a ==则 “1a =”是“N M ⊆”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件3.设图1是某几何体的三视图,则该几何体的体积为( )A .9122π+B .9182π+C .942π+D .3618π+解析:有三视图可知该几何体是一个长方体和球构成的组合体,其体积3439+332=18322V ππ=⨯⨯+(。
4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男 女 总计爱好40 20 60 不爱好20 30 50 总计60 50 110 由()()()()()22n ad bc K a b c d a c b d -=++++算得,()22110403020207.860506050K ⨯⨯-⨯=≈⨯⨯⨯.2()P K k ≥0.050 0.010 0.001 k3.8416.63510.828参照附表,得到的正确结论是( )A .再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B .再犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C .有99%以上的把握认为“爱好该项运动与性别有关”D .有99%以上的把握认为“爱好该项运动与性别无关”解析:由27.8 6.635K ≈>,而2( 6.635)0.010P K ≥=,故由独立性检验的意义可知选C5.设双曲线()222109x y a a -=>的渐近线方程为320x y ±=,则a 的值为( ) A .4 B .3 C .2 D .1答案:C解析:由双曲线方程可知渐近线方程为3y x a=±,故可知2a =。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年湖南高考数学试题(理科)
参考公式:(1)
()
()
()
P AB
P B A
P A
,其中,A B为两个事件,且()0
P A,
(2)柱体体积公式V Sh,其中S为底面面积,h为高。
(3)球的体积公式3
4
3
V R,其中R为求的半径。
一选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若,a b R,i为虚数单位,且()
a i i
b i,则()
A.1,1
a b B.1,1
a b C.1,1
a b D.1,1
a b
2.设{1,2}
M,2
{}
N a,则“1
a”是“N M”则()
A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不
充分又不必要条件
3.设图一是某几何体的三视图,则该几何体的体积为()
A.9
12
2
B.
9
18
2
C.942D.3618
4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男女总计
爱好40 20 60
不爱好20 30 50
总计60 50 110
由
2
2
()
()()()()
n ad bc
K
a b c d a c b d
算得
2
2
110(4030202
7.8
60506050
K附表:
2
()
P K k
0.050 0.010 0.001
k 3.841 6.635 10.828
参照附表,得到的正确结论是()
A.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别有关”B.在犯错误的概率不超过0.1%的前提下,认为“爱好该项运动与性别无关”C.有99%以上的把握认为“爱好该项运动与性别有关”
D.有99%以上的把握认为“爱好该项运动与性别有关”
3
3
2
正视图侧视图
俯视图
图1。
