三角形的费马点
三角形 几何 费马点

三角形几何费马点
费马点,又称斯泰纳点,是指在三角形中,使得三角形内任意两点到该点的距离之和最短的点。
费马点是三角形的一个重要几何概念,具有广泛应用。
在三角形中,费马点也可以被定义为使得三角形内任意两点到该点的距离之和最大的点。
费马点的求解方法有多种,其中最常用的是通过构造等边三角形来确定费马点的位置。
具体来说,可以将三角形中的每个角度构造一个等边三角形,然后将这些等边三角形连接起来,得到一个正三角形。
该正三角形的中心即为费马点。
费马点有着许多有趣的性质,例如:
1.费马点和三角形的其他重要点(重心、垂心、外心、内心)构成的四边形是一个菱形。
2.费马点到三角形三边的距离相等。
3.在任意三角形中,费马点、重心、垂心、外心、内心都在一条直线上,这条直线称为欧拉线。
通过研究费马点及其相关性质,可以深入理解三角形的几何性质,为解决三角形相关问题提供帮助。
- 1 -。
三角形的费马点式方程

三角形的费马点式方程
费马点是指在三角形内部,到三个顶点的距离之和最小的点。
设三角
形的三个顶点分别为A、B、C,费马点为P,我们需要求解点P的坐标。
费马点的坐标可以通过费马原理求解。
费马原理是指在给定的两点A
和B之间找一个点P,使得PA+PB的长度最短。
我们可以利用费马原理求
解费马点的坐标。
假设三角形的边长分别为a、b、c,我们需要求解的点P的坐标为(x,y)。
设PA=d1、PB=d2和PC=d3、费马原理要求PA+PB+PC的长度最小,即d1+d2+d3的长度最小。
根据三角形的余弦定理,可以得到以下关系式:
- d1^2 = x^2 + y^2 - 2xy·cos(A)
- d2^2 = (a-x)^2 + y^2 - 2(a-x)y·cos(B)
- d3^2 = (b-x)^2 + (c-y)^2 - 2(b-x)(c-y)·cos(C)
其中,A、B、C分别为三角形的角度。
根据费马原理,d1+d2+d3最小,即要使得d1^2+d2^2+d3^2最小。
我们可以利用最小二乘法来求解上述方程。
将d1^2+d2^2+d3^2作为
目标函数,对x和y求导,并令导数为0,可以得到关于x和y的方程。
经过一系列的计算和化简,可以得到以下费马点的式方程:
x=(a^2+b^2-c^2)/(2a)
y=(b^2+c^2-a^2)/(2c)
其中,a、b、c分别为三角形的边长。
这就是三角形的费马点的式方程。
根据这个方程,我们可以计算出给定三角形的费马点的坐标。
费马点证明过程

费马点证明过程
费马点,也称为费马-托里拆利点,是在一个三角形内部的一个特殊点,从该点到三角形的三个顶点的距离之和最小。
这个点在三角形中的位置依赖于三角形的形状:在锐角三角形中,它位于三角形内部;在直角三角形中,它与直角顶点重合;在钝角三角形中,它位于三角形外部。
费马点的证明过程相对复杂,以下是其基本思路:
首先,考虑一个锐角三角形ABC。
假设P是三角形ABC内的任意一点。
不失一般性,我们可以假设角A是最小的角。
我们将三角形BPC绕点B旋转60度,使得BC与BA重合,得到新的点P'。
此时,点P'位于线段AP的延长线上。
然后,我们注意到三角形BPP'是一个等边三角形,所以BP=PP'。
因此,AP+BP+CP=AP+PP'+CP。
由于PP'+CP>PC',我们得到AP+BP+CP>AP+PC'。
这表明,点P到三角形三个顶点的距离之和大于点A到三角形三个顶点的距离之和。
同理,我们可以证明对于三角形内的任意点P,其到三角形三个顶点的距离之和都大于点A到三角形三个顶点的距离之和。
因此,点A就是使得距离和最小的点,也就是费马点。
对于直角三角形和钝角三角形,我们可以使用类似的方法进行证明,只是旋转的角度和点的位置会有所不同。
这个证明过程利用了三角形的性质和几何变换,展示了费马点的存在性和唯一性。
同时,它也展示了数学证明中的严谨性和创造性。
费马点问题

费马点问题若三角形内有一点,满足到三角形三顶点连线最短,则该点被称为“费马点”。
三角形中费马点分为两类:1、三角形三个顶角均小于120°,则费马点与各定点连线夹角均为120°;2、三角形有一角大于或等于120°,则费马点为这个角顶点。
一般情况下中学研究费马点情况属于第一种,证明方式如下:例:如图,△ABC中,∠BAC=30°,AB=3,AC=4,P为三角形内一点,求(P A+PB+PC)最小值。
证明方式如下:如图,将△APB绕A逆时针转60°至△AP’B’,则PB=P’B’,△APP’为等边三角形,AP=PP’,即AP+BP+CP=CP+PP’+P’B’,其中C和B’为定点,通过化折为直,最小值为线段CB’的长。
当取最小值时,∠APC=∠AP’B’=120°,可反推得∠APB=∠BPC=∠APC=120°。
最后∠CAB’=90°,利用勾股定理可解得CB’=5这就是费马点问题的一般解法,利用构造旋转全等将线段转移,且旋转角度一定是60°。
例1.如图,△ABC中,AB=AC,∠BAC=30°,P为△ABC内部一点,P A+PB+PC 最小值为24,求2BC。
例2.如图,△ABC中,AB=5,AC=3,∠BAC=60°,P为△ABC内一点,求(P A+PB+PC)最小值。
在上述问题中,P 与各点连线系数均为1,那如果系数不为1时,是否还能用同样方式求解呢。
如图,△ABC 中,AB =3,AC =2,∠BAC =30°,P 为平面内一点,求CP AP BP 23++最小值对于这题,一般解题思路可以为结合常见费马点解题方法,同时构造出AP 3和2CP ,由此可以考虑到结合含30°角直角三角形,因此有了如下辅助线构造:将△APC 绕A 逆时针旋转60°然后放大2倍,则可构造出2CP ,同时△APP ’为30°角直角三角形,有PP ’=AP 3,则CP AP BP 23++=BP +PP ’+P ’C ’,其中B 和C ’为定点,则四点共线时最短,接下来就是勾股运算了。
三角形费马点的证明

三角形费马点的证明费马点是指在一个三角形中,使得从该点到三角形的三个顶点的距离之和最小的点。
现在我们来证明费马点的存在性和唯一性。
我们先来看费马点的存在性。
设三角形的三个顶点分别为A、B、C,我们要证明存在一个点P,使得PA + PB + PC的和最小。
假设P点不在三角形内,而在三角形的外部某个位置。
我们可以通过以下步骤来构造一个在三角形内的点P',使得P'A + P'B + P'C 的和小于PA + PB + PC的和。
我们将三角形ABC的边AB和边AC的中垂线分别延长至点D和E。
然后,我们以D为圆心,AB的长度为半径作一个圆,以E为圆心,AC的长度为半径作一个圆。
这两个圆将会在点F相交。
现在,我们来比较两个三角形PAB和P'AF。
根据三角形的性质,我们知道P'AF的边长之和小于PAB的边长之和,即P'A + AF < PA + AB。
同理,我们可以比较三角形PAC和P'AE,以及三角形PBC和P'BF。
根据上述比较过程,我们可以得出以下结论:P'A + AF < PA + ABP'B + BF < PB + BCP'C + CE < PC + CA现在,我们将点F作为新的点P',根据上述不等式可以得出以下结论:P'A + P'B + P'C = P'A + AF + P'B + BF + P'C + CE < PA + AB + PB + BC + PC + CA = PA + PB + PC因此,P'点满足P'A + P'B + P'C的和小于PA + PB + PC的和,这与假设矛盾。
所以,我们可以得出结论:费马点一定存在于三角形的内部。
接下来,我们来证明费马点的唯一性。
假设存在两个费马点P和Q,我们要证明P和Q重合。
三角形的费马点

三角形的费马点有甲乙丙三个村庄,要在中间建一供水站向三地送水,现要确定供水站的位置以使所需管道总长最小,请同学们想一想,这个供水站应该建在哪里?事实上,这是法国著名数学家费马提出的一个关于三角形的有趣问题:在三角形所在平面上,求一点,使该点到三角形三个顶点距离之和最小,人们称这个点为“费马点”.当三角形有一个内角大于或等于120°的时候,费马点就是这个内角的顶点;当三角形三个内角都在120°以内,那么费马点就是三角形内与三角形三顶点的连线两两夹角为120°的点.显然在第一种情况下,费马点的位置就是那个大于或等于120°的内角的顶点.在第二种情况下,如图所示:我们只需要以△ABC三边AB、AC、BC为边在三角形外作三个等边△ABC1、△ACB1和△BCA1,连接AA1、BB1和CC1,三线交点P就是费马点.同学们肯定会想为什么?等同学们学习了三角形全等的知识后就可以去探索这其中的道理了.再看一个数学问题:将军从甲地出发到河边饮马,然后再到乙地军营视察,显然有许多走法,那走什么样的路线最短呢?这个问题被古希腊亚历山大里亚城的一位久负盛名的学者海伦解决了,后来被人们称作“将军饮马”问题.费马思考了这个问题,他觉得不仅是将军有这样的烦恼,运动着的车、船、飞机,包括人们每天走路都要遇到这样的问题.人们总希望寻求最佳的路线,尽量走近道,少走冤枉路.我们把这类求近道的问题统称最短路线问题.费马就把这样的问题联想到某一个图形中,他大胆提出在任意三角形中有且仅有一点到三个顶点的距离最短,并对此进行了充分的证明.现在研究表明不止是三角形,其它多边形也存在这样的点.平面四边形的费马点:在凸边形中,对角线交点即费马点;在凹四边形中,凹顶点即为费马点.那费马点在我们的生活中有没有应用价值呢?文章开头的供水站建在费马点肯定是最节约成本的;再譬如打篮球、踢足球时,你时刻注意的是怎样进攻,但要与自己的队友保持最好的距离和方位,前后左右都要顾及,这其实就是在找多边形中的“费马点”.数学为科学之母,现在已经有很多方面应用到费马点的性质,在医学上、建筑上、军事上……像类似费马点这样的问题还有很多,同学们只要你们积极思考,遇到问题多问几个为什么,多一些打破砂锅问到底的精神,你们也会像费马一样发现更多更有趣的数学问题.。
三角形费马点的证明及应用

三角形费马点的证明及应用费马点是指在平面上的任意三个不共线的点A、B、C中,使得∠ABC、∠ACB 和∠BAC的三个角的和最小的点。
费马点也称为斯纳尔·费马点,他是17世纪法国数学家斯纳尔·费马所研究的最小角三个角的位置问题。
为了证明费马点的存在,我们可以利用极限的思想进行推导。
首先假设在AB上存在一个点X使得∠CAX为等腰三角形CAX的顶角。
那么我们可以构造一个角为∠XAC的等腰三角形XAC。
显然,∠BAX=∠XAC,那么由三角形外角和定理可知∠ABC+∠AXC=180度。
由于AX是由三角形外一点引出的两条射线,所以AXC>180度,所以∠ABC<∠BAC。
同理,我们可以得到两个不等式:∠BAC<∠BCA,∠BCA<∠CAB。
将这三个不等式相加得到:∠ABC+∠BAC+∠BCA<∠ABC+∠BAC+∠CAB。
即∠ABC+∠BAC+∠BCA的和是最小的三个角的和。
我们可以进一步构造一个点P,在平面上使得∠BAP=∠BCP=∠CAP,即三角形ABP、BCP和CAP是等腰三角形。
由于三个等腰三角形所形成的角APB、BPC 和CPA的和一定是最小的,所以∠ABC+∠BAC+∠BCA的和一定是∠APB+∠BPC+∠CPA的和的一个下界。
我们可以发现,当P点与三角形ABC的内角A,B,C重合时,三角形ABP、BCP 和CAP都是等边三角形,此时∠APB+∠BPC+∠CPA=360度。
所以,∠ABC+∠BAC+∠BCA的和一定小于等于360度,在平面上一定存在一个点使得∠ABC+∠BAC+∠BCA的和为最小。
这个点就是费马点。
费马点的应用非常广泛,尤其是在物理学和工程学中。
例如,在导弹的航空导航中,费马点可以确定导弹的最短飞行路径,从而最大限度地节省燃料。
在通信网络中,费马点可以确定网络中的最佳传输路径,提高信息传输的效率。
此外,费马点还可以应用于地理学领域,确定地理坐标系统的最佳布局。
三角形的费马点问题
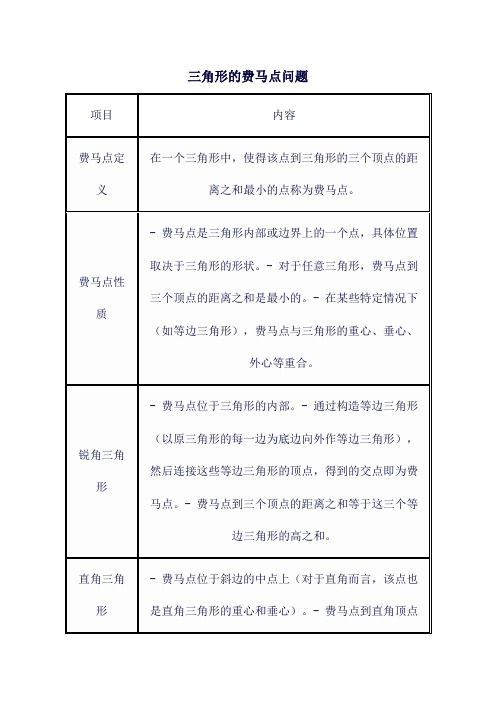
项目
内容费马Βιβλιοθήκη 定义在一个三角形中,使得该点到三角形的三个顶点的距离之和最小的点称为费马点。
费马点性质
- 费马点是三角形内部或边界上的一个点,具体位置取决于三角形的形状。- 对于任意三角形,费马点到三个顶点的距离之和是最小的。- 在某些特定情况下(如等边三角形),费马点与三角形的重心、垂心、外心等重合。
钝角三角形
- 费马点位于三角形的外部,且位于钝角的补角所对应的边的垂直平分线上。- 通过构造以钝角顶点为顶点的两个等腰三角形(腰长等于原三角形的钝角两边),然后连接这两个等腰三角形的底边中点,得到的交点(在三角形外部)即为费马点。- 费马点到三个顶点的距离之和等于这两个等腰三角形的腰长之和减去钝角两边之差(或加上它们的和,但通常我们关注的是减去的情况,因为费马点是使距离和最小的点)。
锐角三角形
- 费马点位于三角形的内部。- 通过构造等边三角形(以原三角形的每一边为底边向外作等边三角形),然后连接这些等边三角形的顶点,得到的交点即为费马点。- 费马点到三个顶点的距离之和等于这三个等边三角形的高之和。
直角三角形
- 费马点位于斜边的中点上(对于直角而言,该点也是直角三角形的重心和垂心)。- 费马点到直角顶点的距离等于斜边的一半,到另外两个顶点的距离之和等于斜边的另一半加上直角边之差(或和,取决于具体直角三角形的边长关系)。
特殊情况
- 对于等边三角形,费马点与重心、垂心、外心等重合,位于三角形的中心。- 对于等腰三角形,费马点位于底边的垂直平分线上,且到两个底边顶点的距离相等。
三角形费马点的证明

三角形费马点的证明费马点是指平面上的一个点,它到三角形的三个顶点的距离之和最小。
这个问题最早由法国数学家费马在17世纪提出,并且给出了一个简洁而美观的证明。
我们先来看一个特殊的情况,当三角形是等边三角形时,费马点就是三角形的重心。
重心是指三角形三条中线的交点,它到三个顶点的距离之和是最小的。
这个结论是很容易证明的,因为等边三角形的三个顶点到重心的距离都是相等的,所以它们的距离之和一定是最小的。
然而,当三角形不是等边三角形时,费马点的位置就不那么容易确定了。
我们可以通过以下步骤来证明费马点的存在,并且给出一个简单的构造方法。
我们将三角形的一条边延长,然后以这条边为直径画一个圆。
然后,我们再以另外两条边的延长线为切线,将圆与两条延长线相切于点A和点B。
接下来,我们连接点A和点B,并将这条线段的中点记为点C。
根据切线定理,我们知道切线与半径的垂线相互垂直。
所以,线段AC和线段BC与圆的切点A和B相互垂直。
而根据垂线定理,垂线的长度最短,所以线段AC和线段BC是与圆相切的两条线段中最短的。
现在我们来证明一下,点C就是三角形费马点的位置。
假设点C不是费马点,而是另外一个点D。
那么,三角形的三个顶点A、B和D 之间的距离之和一定小于三角形的三个顶点A、B和C之间的距离之和。
我们可以通过以下步骤来证明这一点。
首先,连接点A和点D,并延长线段AD,将圆与延长线段相交于点E。
然后,连接点B和点D,并延长线段BD,将圆与延长线段相交于点F。
现在我们来比较一下线段AE、线段CF和线段BC的长度。
根据切线定理,线段AE和线段BD是最短的。
而线段CF是线段AE和线段BD 的一条中线,根据中线定理,线段CF的长度一定小于等于线段AE 和线段BD的长度。
所以,线段CF的长度一定小于等于线段BC的长度。
同样的道理,我们可以比较一下线段BF、线段DE和线段AC的长度。
根据切线定理,线段BF和线段DE是最短的。
而线段AC是线段BF 和线段DE的一条中线,根据中线定理,线段AC的长度一定小于等于线段BF和线段DE的长度。
费马点证明

费马点定义在一个三角形中,到3个顶点距离之和最小的点叫做这个三角形的费马点。
(1)若三角形ABC的3个内角均小于120°,那么3条距离连线正好平分费马点所在的周角。
所以三角形的费马点也称为三角形的等角中心。
(2)若三角形有一内角不小于120度,则此钝角的顶点就是距离和最小的点。
费马点的判定(1)对于任意三角形△ABC,若三角形内或三角形上某一点E,若EA+EB+EC 有最小值,则E为费马点。
费马点的计算(2)如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
证明我们要如何证明费马点呢:费马点证明图形(1)费马点对边的张角为120度。
△CC1B和△AA1B中,BC=BA1,BA=BC1,∠CBC1=∠B+60度=∠ABA1,△CC1B和△AA1B是全等三角形,得到∠PCB=∠PA1B同理可得∠CBP=∠CA1P由∠PA1B+∠CA1P=60度,得∠PCB+∠CBP=60度,所以∠CPB=120度同理,∠APB=120度,∠APC=120度(2)PA+PB+PC=AA1将△BPC以点B为旋转中心旋转60度与△BDA1重合,连结PD,则△PDB为等边三角形,所以∠BPD=60度又∠BPA=120度,因此A、P、D三点在同一直线上,又∠CPB=∠A1DB=120度,∠PDB=60度,∠PDA1=180度,所以A、P、D、A1四点在同一直线上,故PA+PB+PC=AA1。
(3)PA+PB+PC最短在△ABC内任意取一点M(不与点P重合),连结AM、BM、CM,将△BMC 以点B为旋转中心旋转60度与△BGA1重合,连结AM、GM、A1G(同上),则AA1 <A1G+GM+MA=AM+BM+CM.所以费马点到三个顶点A、B、C的距离最短。
费马点性质:(1)平面内一点P到△ABC三顶点的之和为PA+PB+PC,当点P为费马点时,距离之和最小。
费马点

费马点一.费马点的发现者费马(Fermat,Pierre de Fermat) (1601~1665)法国数学家,被誉为“业余数学家之王。
”二.费马点的定义在一个三角形中,到3个顶点距离之和最小的点叫做这个三角形的费马点。
(1)若三角形ABC的3个内角均小于120°,那么3条距离连线正好平分费马点所在的周角。
所以三角形的费马点也称为三角形的等角中心。
(2)若三角形有一内角不小于120度,则此钝角的顶点就是距离和最小的点。
三.费马点的判定(1)对于任意三角形△ABC,若三角形内或三角形上某一点E,若EA+EB+EC有最小值,则E为费马点。
(2)如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
四.费马点的证明我们要如何证明费马点呢:费马点证明图形(1)费马点对边的张角为120度。
△CC1B和△AA1B中,BC=BA1,BA=BC1,∠CBC1=∠B+60度=∠ABA1,△CC1B和△AA1B是全等三角形,得到∠PCB=∠PA1B同理可得∠CBP=∠CA1P由∠PA1B+∠CA1P=60度,得∠PCB+∠CBP=60度,所以∠CPB=120度同理,∠APB=120度,∠APC=120度(2)PA+PB+PC=AA1将△BPC以点B为旋转中心旋转60度与△BDA1重合,连结PD,则△PDB为等边三角形,所以∠BPD=60度又∠BPA=120度,因此A、P、D三点在同一直线上,又∠CPB=∠A1DB=120度,∠PDB=60度,∠PDA1=180度,所以A、P、D、A1四点在同一直线上,故PA+PB+PC=AA1。
(3)PA+PB+PC最短在△ABC内任意取一点M(不与点P重合),连结AM、BM、CM,将△BMC 以点B为旋转中心旋转60度与△BGA1重合,连结AM、GM、A1G(同上),则AA1<A1G+GM+MA=AM+BM+CM.所以费马点到三个顶点A、B、C的距离最短。
费马点证明

费马点定义在一个三角形中,到3个顶点距离之和最小的点叫做这个三角形的费马点。
(1)若三角形ABC的3个内角均小于120°,那么3条距离连线正好平分费马点所在的周角。
所以三角形的费马点也称为三角形的等角中心。
(2)若三角形有一内角不小于120度,则此钝角的顶点就是距离和最小的点。
费马点的判定(1)对于任意三角形△ABC,若三角形内或三角形上某一点E,若EA+EB+EC 有最小值,则E为费马点。
费马点的计算(2)如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
证明我们要如何证明费马点呢:费马点证明图形(1)费马点对边的张角为120度。
△CC1B和△AA1B中,BC=BA1,BA=BC1,∠CBC1=∠B+60度=∠ABA1,△CC1B和△AA1B是全等三角形,得到∠PCB=∠PA1B同理可得∠CBP=∠CA1P由∠PA1B+∠CA1P=60度,得∠PCB+∠CBP=60度,所以∠CPB=120度同理,∠APB=120度,∠APC=120度(2)PA+PB+PC=AA1将△BPC以点B为旋转中心旋转60度与△BDA1重合,连结PD,则△PDB为等边三角形,所以∠BPD=60度又∠BPA=120度,因此A、P、D三点在同一直线上,又∠CPB=∠A1DB=120度,∠PDB=60度,∠PDA1=180度,所以A、P、D、A1四点在同一直线上,故PA+PB+PC=AA1。
(3)PA+PB+PC最短在△ABC内任意取一点M(不与点P重合),连结AM、BM、CM,将△BMC 以点B为旋转中心旋转60度与△BGA1重合,连结AM、GM、A1G(同上),则AA1 <A1G+GM+MA=AM+BM+CM.所以费马点到三个顶点A、B、C的距离最短。
费马点性质:(1)平面内一点P到△ABC三顶点的之和为PA+PB+PC,当点P为费马点时,距离之和最小。
费马点问题(含答案)

费马点的问题定义:数学上称,到三角形3个顶点距离之和最小的点为费马点。
它是这样确定的:1. 如果三角形有一个内角大于或等于120°,这个内角的顶点就是费马点;2。
如果3个内角均小于120°,则在三角形内部对3边张角均为120°的点,是三角形的费马点。
3。
费马点与3个顶点连成的线段是沟通3点的最短路线,容易理解,这个路线是唯一的.我们称这一结果为最短路线原理。
性质:费马点有如下主要性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
3.费马点为三角形中能量最低点。
4.三力平衡时三力夹角皆为120°,所以费马点是三力平衡的点。
例1:已知:△ABH是等边三角形.求证:GA+GB+GH最小证明:∵△ABH是等边三角形。
G是其重心.∴∠AGH=∠AGB=∠BGH=120°.以HB为边向右上方作等边三角形△DBH。
以HG为边向右上方作等边三角形△GHP.∵AH=BH=AB=12。
∴∠AGH=120°, ∠HGP=60°。
∴A、G、P三点一线.再连PD两点。
∵△ABH、△GHP和△BDH都是等边三角形,∠GHB=30°.∴∠PHD=30°,.在△HGB和△HPD中∵HG=HP∠GHB=∠PHD;HB=HD;∴△HGB≌△HPD;(SAS)∴∠HPD=∠HGB=120°;∵∠HPG=60°。
∴G、P、D三点一线。
∴AG=GP=PD,且同在一条直线上.∵GA+GH+GB=GA+GP+PD=AD。
∴G点是等边三角形内到三个顶点的距离之和最小的哪一点,费马点。
也就是重心.例2:已知:△ABC是等腰三角形,G是三角形内一点。
∠AGC=∠AGB=∠BGC=120°.求证:GA+GB+GC最小证明:将△BGC逆时针旋转60°,连GP,DB.则△HGB≌△HPD;∴∠CPD=∠CGB=120°,CG=CP,GB=PD,BC=DC,∠GCB=∠PCD.∵∠GCP=60°,∴∠BCD=60°,∴△GCP和△BCD都是等边三角形。
初中数学微专题——费马点

初中数学·几何综合几何模型·专题复习——费马点一、费马点及结论费马点:就是到三角形的三个顶点的距离之和最小的点。
费尔马的结论:对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点;对于有一个角超过120°的三角形,费马点就是这个内角的顶点。
二、费马点结论的证明例:P为△ABC内任一点,请找点P使它到ABC△三个顶点的距离之和PA+PB+PC最小?(1)当△ABC各角不超过120°时,如下图。
解析:如图,把△APC绕A点逆时针旋转60°得到△AP′C′,连接PP′.则△APP′为等边三角形,AP= PP′,P′C′=PC,所以PA+PB+PC= PP′+ PB+ P′C′.点C′可看成是线段AC绕A点逆时针旋转60°而得的定点,BC′为定长,所以当B、P、P′、C′四点在同一直线上时,PA+PB+PC最小.这时∠BPA=180°-∠APP′=180°-60°=120°,∠APC=∠A P′C′=180°-∠AP′P=180°-60°=120°,∠BPC=360°-∠BPA-∠APC=360°-120°-120°=120°因此,当ABC△的每一个内角都小于120°时,所求的点P对三角形每边的张角都是120°,可在AB、BC边上分别作120°的弓形弧,两弧在三角形内的交点就是P点。
(2)当△ABC有一个内角超过120°时,如下图。
解析:如图,延长BA至C'使得AC=AC',做∠C'AP'=∠CAP,并且使得AP'=AP, PC'=PC,(说了这么多,其实就是把三角形APC以A为中心做了个旋转)则△APC≌△AP'C'∵∠BAC≥120°∴∠PAP'=180°-∠BAP-∠C'AP'=180°-∠BAP-∠CAP=180°-∠BAC≤60°∴等腰三角形PAP'中,AP≥PP'∴PA+PB+PC≥PP'+PB+PC'>BC'=AB+AC所以A是费马点因此,当ABC△有一内角大于或等于120°时,所求的P点就是钝角的顶点.三、费马点的求法当△ABC是三个内角皆小于120°三角形时,分别以 AB、BC、CA为边,向三角形外侧做正三角形△ABD、△ACE,然后连接DC、BE,则二线交于一点,记作点P,则点P就是所求的费马点。
三角形的费马点

三角形的费马点
费马点是指在平面上给定一些点,费马点是这些点到达的其他点距离之和最短的点。
对于一个三角形来说,费马点就是使得三个顶点与费马点的距离之和最小的点。
在一个三角形中,费马点即为三条角平分线的交点,它也被称为费马点、斯坦纳点,或者直角三角形中的乌尔什拉斯点。
以一个三角形ABC为例,设费马点为P。
费马点满足三个角度相等的条件,即∠APB = ∠BPC = ∠CPA = θ。
在三角形ABC中,任意取一点P,可以得到AP、BP、CP与∠APB、∠BPC、∠CPA的关系:
1.根据三角形内角和定理,有∠APB + ∠BPC + ∠CPA = 180°。
2.根据正弦定理,有AP/sin(∠APB) = BP/sin(∠BPC) =
CP/sin(∠CPA)。
由于AP + BP + CP是常数,求解使得AB + BC + CA最小的点P,等价于求解使得AP + BP + CP最小的点P。
因此可以通过构造三个角等于θ的角平分线,找到这个最小值。
通过计算三个角度相等的角平分线的交点,即可确定费马点的位置。
这个点既可以在三角形内部,也可以在三角形外部,它到三角形的各个顶点的距离之和是最小的。
30度直角三角形的费马点

30度直角三角形的费马点
30度直角三角形的费马点指的是三角形的一个顶点,该顶点是三个顶点的等角中点。
在几何学上,30度直角三角形的费马点具有以下特征:
1、它是所有三角形中最接近90度的角。
所有三角形中,只有30度直角三角形的顶点有费马点。
2、它是两边的一半,它可以从比例的角度来描述。
因此,在30度直角三角形中,等腰三角形的两条线段,其一半分别等于另一半。
3、它是三个顶点的等角中点。
从几何学的角度看,费马点是三点之间的等角中点。
4、它是三角形的极轴。
三角形的极轴是指由两个顶点成角时所形成的线段,而这两个顶点必须相对靠近30度直角三角形的顶点。
5、它是一个三角形的夹角。
三角形的夹角是指费马点到另外两个顶点的夹角,这个夹角是60度。
6、它是三角形的垂面轴。
垂面轴就是从三角形的费马点出发,连线到另外两个顶点的线段,它的作用就是为了把另外两个顶点的垂线都连
接起来。
30度直角三角形的费马点不仅有着上述特征,而且,它对与三角形的展开,绘制和计算都有着重要的作用。
费马点的存在,让很多三角形的计算及应用变得更加简单容易,因此在几何学中被广泛应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的费马点
有甲乙丙三个村庄,要在中间建一供水站向三地送水,现要确定供水站的位置以使所需管道总长最小,请同学们想一想,这个供水站应该建在哪里?
事实上,这是法国著名数学家费马提出的一个关于三角形的有趣问题:在三角形所在平面上,求一点,使该点到三角形三个顶点距离之和最小,人们称这个点为“费马点”.
当三角形有一个内角大于或等于120°的时候,费马点就是这个内角的顶点;当三角形三个内角都在120°以内,那么费马点就是三角形内与三角形三顶点的连线两两夹角
为120°的点.显然在第一种情况下,费马点的位置就是那个大于或等于120°的内角的顶点.在第二种情况下,如图所示:我们只需要以△ABC三边AB、AC、BC为边在三角形外作三个等边△ABC1、△ACB1和△BCA1,连接AA1、BB1和CC1,三线交点P就是费马点.
同学们肯定会想为什么?等同学们学习了三角形全等
的知识后就可以去探索这其中的道理了.
再看一个数学问题:将军从甲地出发到河边饮马,然后再到乙地军营视察,显然有许多走法,那走什么样的路线最短呢?这个问题被古希腊亚历山大里亚城的一位久负盛名
的学者海伦解决了,后来被人们称作“将军饮马”问题.费马
思考了这个问题,他觉得不仅是将军有这样的烦恼,运动着的车、船、飞机,包括人们每天走路都要遇到这样的问题.人们总希望寻求最佳的路线,尽量走近道,少走冤枉路.我们把这类求近道的问题统称最短路线问题.费马就把这样的问题联想到某一个图形中,他大胆提出在任意三角形中有且仅有一点到三个顶点的距离最短,并对此进行了充分的证明.现在研究表明不止是三角形,其它多边形也存在这样的点.
平面四边形的费马点:在凸边形中,对角线交点即费马点;在凹四边形中,凹顶点即为费马点.
那费马点在我们的生活中有没有应用价值呢?文章开头的供水站建在费马点肯定是最节约成本的;再譬如打篮球、踢足球时,你时刻注意的是怎样进攻,但要与自己的队友保持最好的距离和方位,前后左右都要顾及,这其实就是在找多边形中的“费马点”.
数学为科学之母,现在已经有很多方面应用到费马点的性质,在医学上、建筑上、军事上……
像类似费马点这样的问题还有很多,同学们只要你们积极思考,遇到问题多问几个为什么,多一些打破砂锅问到底的精神,你们也会像费马一样发现更多更有趣的数学问题.。
