十二次费马点及拓展PPT课件

合集下载

2023-2024学年人教版初三下学期中考《旋转模型之费马点问题》知识点专题解析及练习PPT

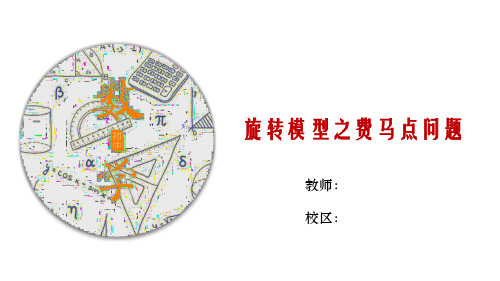
图1 图2
4 费马点的性质
1. 到三个顶点的距离之和最短：费马点是三角形内唯一一个使得从该点到三角形三个顶点的距离之和最短的点。 2. 等角性质：从费马点出发，向三角形的三个顶点引出的三条线段与对应的三角形边所成的角均相等，且均等于120 度。 3. 唯一性：在三角形内部，费马点是唯一的具有上述性质的点。
∵点A'可看成是线段CA绕C点顺时针旋转60°而得的定点，BA'为
定长，
∴当B、P、P'、A'四点在同一直线上时，PA+PB+PC 最小．最小
值为 BA' .
图2
【如图 1 和图 2，利用旋转、等边等条件转化相等线段.】
∴在图2中，∠APC=∠A′ P′C=180°-∠CP′P=180°-60°=120°， ∠BPC=180°-∠P′PC=180°-60°=120°， ∠APB=360°-∠BPC-∠APC=360°-120°-120°=120°.
情感、态度与价值观目标：
激发学生对于学习的热情，树立学生对于数学的追求。
五、教学过程
总结费马点的性质，构造
方法以及解题思路，最后
通过模型展示讲授费马点
布置作业。
的原理、证明过程以及如
何构建费马点。
讲解中考例题，引导学生
熟练运用费马点性质解题，
以介绍费马点
巩固加深学生的印象。
的来历和实践
开始课程。
中物理
（4）此时以BC为边作等边△BCF。连接AF必过点P。
这个图成立的一个必要条件是∠BAC<120°, 若∠BAC 120°, 这个图就会变成这
个样子：
D
E P
A
BHale Waihona Puke C此时CD与BE的交点P点还是我们的费马点吗？显然这时候就不是了，此时

费马点的应用举例课件

和通信。
05
CATALOGUE
费马点在经济学中的应用
金融市场中的费马点
投资组合优化
费马点理论可以应用于投资组合优化，通过计算不同资产之间的费马点，投资者可以确定最佳的资产配置策略，以实现风险和收
益的平衡。
股票价格预测
股票价格受到多种因素的影响，但费马点理论可以用于分析历史价格数据，预测未来的股票价格
财务资源配置
企业可以利用费马点理论来优化财务资源配置，确保资金流向最具有盈利潜力的项目或领域。
THANKS
感谢观看
航空航天中的费马点
飞行器设计
在飞行器设计中，费马点可以用于优化飞行器的结构和布局，提高飞行器的性能和稳定性。例如，在飞机设计中，利用费马点理论可以确定最佳的机翼位置和角度，以最大化飞机的升力和稳定性。
卫星轨道设计
在卫星轨道设计中，费马点可以用于优化卫星轨道的位置和高度，提高卫星观测和通信的效率和精度。例如，在地球同步卫星轨道设计中，利用费马点理论可以找到最佳的轨道位置和高度，以实现稳定的地球同步观测
通过分析供应链中的费马点，企业可以优化物流和运输策略，降低成本并提高效率。
资源分配中的费马点
人力资本管理
物资采购
在人力资源管理中，费马点理论可以用于分析员工的工作效率和绩效，以及制定最佳的人才招聘和培训计划。
在物资采购中，通过分析供应商之间的费马点，企业可以确定最佳的采购策略，以实现成本效益最大化。
费马点的性质
01
02
03
唯一性
对于任意三角形ABC，费马点是唯一的。
稳定性
费马点是相对稳定的，即使三角形ABC发生微小变化，费马点仍然会接近原来的位置。

费马点

费马点就是指在三角形所在的平面内,到三角形三个顶点的距离的和最小的点.回答者：幽幽￠晴空- 初入江湖二级7-12 20:59 浅谈三角形的费马点法国著名数学家费尔马曾提出关于三角形的一个有趣问题：在三角形所在平面上，求一点，使该点到三角形三个顶点距离之和最小．人们称这个点为“费马点”．这是一个历史名题，近几年仍有不少文献对此介绍．本文试以课本上的习题、例题为素材，根据初中学生的认知水平，针对这个问题拟定一则思维训练材料，引导学生通过自己的思维和学习，初步了解这个问题的产生、形成、推理和论证过程及应用．1．三角形的费马点已知：如图1，ΔABD、ΔAEC都是等边三角形．求证：BE=DC．这个题目证明比较容易，下面提几个问题供同学们思考．思考1 在ABC的BC边再作等边三角形BCF，并连接AF如图2，可得到什么结论？是否有(1)BE=CD=AF？(2)BE、CD、AF三线交于一点O？(3)∠AOB=∠BOC=∠COA=120°？思考2 如将原题的图1改成图3，并连接DE，还能得到什么结论？(1)原题的结论仍然成立：BE=CD．(2)若∠ADC=120°，则D点在等边ΔAEC的外接圆上．D、B、E共线，由BE=CD有：AD＋CD=DE；若∠ADC≠120°，易证AD ＋DC＞DE．得到下列命题．定理1 等边三角形外接圆上一点，到该三角形较近两顶点距离之和等于到另一顶点的距离；不在等边三角形外接圆上的点，到该三角形两顶点距离之和大于到另一点的距离．思考3 根据上述定理，在图2中还有(1)OA＋OB＋OC=AF．(2)在ΔABC内另取一点O，总有O′A＋O′B＋O′C＞AF，即OA＋OB＋OC＜O′A＋O′B＋O′C．(3)点O是ΔABC所在平面上到三个顶点距离之和为最小的点．定理2 三角形每一内角都小于120°时，在三角形内必存在一点，它对三条边所张的角都是120°，该点到三顶点距离和达到最小，称为“费马点”，当三角形有一内角不小于120°时，此角的顶点即为费马点．2．水管线路最短问题如图4，要在河边修建一个水泵站，分别向张村、李庄供水，修在河边什么地方，可使所用水管最短？这是一个很有意义的应用题，在公路，自来水或煤气管道线路设计等方面都有一定价值．假如不是由水泵站C直接向A、B两地供水，那么本例用“对称点”方法所确定的线路CA＋CB并不是最短线路．易知当A、B、C三点所确定的三角形各角都小于120°时，在该三角内必存在费马点O有OA＋OB＋OC＜CA＋CB，可见水管总长还可以更小一些．于是水管线路最短问题即为A、B两点在直线L同侧，点C为L上一个动点的费尔马问题，下面分两类情况讨论这个问题．(1)AB与L的夹角小于30”．如图5，以AB为一边作正三角形ABM，并作ΔABM的外接圆．当所作外接圆与直线L相离或相切时，从M点作直线L的垂线，交圆于O点，垂足为C．C即为水泵站位置，先把水引到O点，再从O点分别向A、B两地供水，此时点O 更短，即在L上另选一点都不会改进．优的了，因为∠ABC≥120°，费马点就是点C也就是在C建水泵站直接向A、B两地供水．如果水泵站C选在P点的左侧，如图7，此时△ABC的费马点O必在在点P上，故L上点P的左侧不会有更好的点可选，同理Q点的右边也找不出更好的点．(2)AB与L的夹角不小于30°．如图8，若A点离直线L较近，作AC⊥L交于C，点C为水泵站位置，因为∠CAB≥120°，点A即为ΔABC的费马点，此时水管总长为CA＋AB．在L上任意另取一点都不会再有改进．显然在点C的左侧取一点C′时，ΔABC′的费马点仍在A点，易知弧上(因为ΔABM的外接圆不会与L相交或相切)，故必有；O′A+O′B+O′C=O′M+O′C＞CA+AM=CA＋AB．综上所述水管的最短线路有三种分别为“Y”字型“V”字型及“厂”字型．3．两个应用题文(4)谈到95年全国高考命题组，对应用题选编时曾考虑过如下两个题目：(1)一条河宽1km，两岸各有一座城市A与B，A与B的直线距离是4km，今须铺设一条电缆连A与B，已知地下电缆修建费用为2万元/km，水下电缆为4万元/km，假定河两岸是直线，问应如何架设电缆方可使总施工费用达到最小？(2)有四个点位于一个正方形的四个顶点上，须用线将它们连成一个网络(即从任何一点出发，可沿此网络中的线达到别的点)，问此网络应以什么方式连接这四个点，方可使所用的线总长最小？汤建新，赵汉群曾在《中学数学》(湖北)1997．10月刊上发文(5)对(1)题作了详细讨论，并给出一个很巧妙的解答，使初中学生可以理解．用费马点也可这样去解，因为水底电缆每千米修建费为地下的两倍，如图9，实际上即为在河岸直线L上找一点C使AC ＋2BC最小，取B点关于L的对称点B′，因为BC=B′C故所求点C(电缆的下水点)即为ΔABB′的费马点，取∠BCA=120°即得．关于(2)题如图10，易知不论如何连接，所求的网络必通过正方形中心O点，问题转化为ΔABO与ΔDCO的费马问题，也可以转化为问题(1)，详细解答请同学们考虑费马点编辑本段费马点定义在一个多边形中，到每个顶点距离之和最小的点叫做这个多边形的费马点。

《尔马Fermat定理》课件

03
费马定理的推论
圆锥曲线上的费马定理
总结词
圆锥曲线上的费马定理指出，对于任何圆锥曲线，其上的任意一点到曲线的焦点的距离与该点到曲线的准线的距离之比等于该曲线的离心率。
详细描述
圆锥曲线包括椭圆、抛物线和双曲线。费马定理在圆锥曲线上同样适用，并且离心率是圆锥曲线的一个重要几何参数，它决定了曲线的形状和大小。
代数曲线上的费马定理
总结词
代数曲线上的费马定理指出，对于任何非退化的代数曲线，其上的任意一点到曲线的奇点的距离的平方等于该点所在直线的斜率的四次方。
详细描述
代数曲线是由多项式方程定义的平面曲线，奇点是曲线上使导数不存在的点。费马定理在代数曲线上同样成立，并且斜率是决定曲线形状的重要参数。
欧拉定理与费马定理的关系
定理证明
总结词
费马定理的证明需要用到代数和几何的知识，包括代数基本定理、无穷递降法和反证法等。
详细描述
费马定理的证明过程比较复杂，需要用到代数和几何的知识。其中，代数基本定理是证明过程中最关键的一步，它证明了任何n次多项式在模n意义下取值都是0，那么这个多项式必定等于0。无穷递降法和反证法也被应用到证明过程中，最终证明了费马定理的
正确性。
定理应用
总结词
费马定理在数论、代数和几何等领域有广泛的应用，例如在解方程、证明不等式和解决几何问题等方面都有重要的应用。
详细描述
费马定理的应用非常广泛，在数论中它可以用来证明一些数学猜想，如费马大定理和小定理等。在代数中它可以用来解方程和证明不等式，如在解一元二次方程和证明一些代数恒等式时可以用到费马定理。在几何中它可以用来解决一些几何问题，如证明一些几何命题和解决几何作图问题等。
THANKS

第十二次课费马点及拓展

特殊集散点-n个集散点构成正多边形
A
FP'BP NhomakorabeaE
C
D
E
A
D
s
s'
H
B
C
一般的费马点问题
平面上n个点Pi(xi,yi) 〔i=1,2,…,n〕，各点Pi的 “权重〞为Wi，试确定一点P(x,y)，使它到n个点的加权间隔最小？
数学模型
n
mC (ix ,n y ) miW n i (x i x )2 (y i y )2
BN
BN
代数函数模型
A
y210x 02(3 0x)
10
M
CX
D
ADC
u2100x2 x
BN
y 2 s1 i0 n (3 0 1t0 g ) [1(2 0 sc i o n )s ],
人有了知识，就会具备各种分析能力，明辨是非的能力。所以我们要勤恳读书，广泛阅读，古人说“书中自有黄金屋。 ”通过阅读科技书籍，我们能丰富知识，培养逻辑思维能力；通过阅读文学作品，我们能提高文学鉴赏水平，培养文学情趣；通过阅读报刊，我们能增长见识，扩大自己的知识面。有许多书籍还能培养我们的道德情操，给我们巨大的精神力量，鼓舞我们前进。
B
A B1
S1 S
B
A Q
P
费马点如何画？
C
A C'
间隔之和的最小值如何求？
H B
C
B' C
A'
一般费马点问题
F
A
E
有A,B,C三个村庄，各村庄的小学生人数分别为a,b,c，把学校建在什么地方，才能使所有学生所走的路程总和最短？

2011第十二次课费马点及拓展

最优化思想与数形结合
案例：费马点及拓展案例：
已知点在同一条直线上的“费马点” 已知点在同一条直线上的“费马点”
• 1、一条笔直的流水线上有5个机器人。现要在流水线上设置、一条笔直的流水线上有个机器人个机器人。一个零件供应站，使得各机器人到供应站的距离总和最短，一个零件供应站，使得各机器人到供应站的距离总和最短，问供应站应设在哪里？问供应站应设在哪里？ • 2、上题如果有n个机器人，供应站应设在哪里？、上题如果有个机器人供应站应设在哪里？个机器人， • 3、求函数y=|x-x1|+|x-x2|+…+|x-xn|的最小值。、求函数的最小值。的最小值 (x1<x2< …<xn,i=1,2,…,n) • 4、如果这条流水线上的五个点依次有机器人、3、2、5、2 、如果这条流水线上的五个点依次有机器人3、、、、个，供应站又应设在哪里呢？供应站又应设在哪里呢？ • 5、求函数y=k1|x-x1|+k2|x-x2|+…+kn|x-xn|最小值。、求函数最小值。最小值 (其中 1<x2< …<xn,ki为自然数其中x 为自然数,i=1,2,…,n) 其中 • 思考：6. （2011年北约校自主招生数学试题）思考：年北约13校自主招生数学试题年北约校自主招生数学试题） • 求f(x)=|x-1|+|2x-1|+……+|2011x-1| 的最小值。的最小值。 • 答案：f(1/1422)=832+491/711 答案：
B a100 l100 A j200 i150 0400 b100 C c200 D m400 k500 n300 p300 F E e100 d100

中考中的费马点详解加练习.pptx

P
A
APB源自CABC
P
B
C
9
书山有路
26、如图，四边形 ABCD 是正方形，△ABE 是等边三角形，M 为对角线 BD（不含 B 点）上任意一点，将 BM 绕点 B 逆时针旋转 60°得到 BN，连接EN、AM、CM． 1 求证：△AMB≌△ENB； 2 ①当 M 点在何处时，AM+CM 的值最小； ②当 M 点在何处时，AM+BM+CM 的值最小，并说明理由； 3 当 AM+BM+CM 的最小值为时，求正方形的边长．
6
1 求抛物线的解析式；
2 等边△OMN 的顶点M 、 N 在线段 AE 上，求 AE 及 AM 的长； 3 点 P 为△ ABO 内的一个动点，设 m PA PB PO ，请直接写出m
的最小值,以及m 取得最小值时，线段 AP 的长.
2013 房山一摸 24．（1）如图 1，△ABC 和△CDE 都是等边三角形，且 B、C、D 三点共线，联结 AD、BE 相交于点P，求证：BE=AD．（2）如图 2，在△BCD 中，∠BCD＜120°，分别以 BC、CD 和 BD 为边在△BCD 外部作等边三角形ABC、等边三角形 CDE 和等边三角形 BDF，联结AD、BE 和 CF 交于点P，下列结论中正确的是（只填序号即可） ①AD=BE=CF；②∠BEC=∠ADC；③∠DPE=∠EPC=∠CPA=60°；（3）如图 2，在（2）的条件下，求证：PB+PC+PD=BE．
② 请写出求 AP+BP+CP 的最小值的解题思路（结果可以不化简）.
A
2016 一月昌平
P
B
图3
C
6
书山有路

湘教版八年级数学上册《费马点的应用问题举例》课件

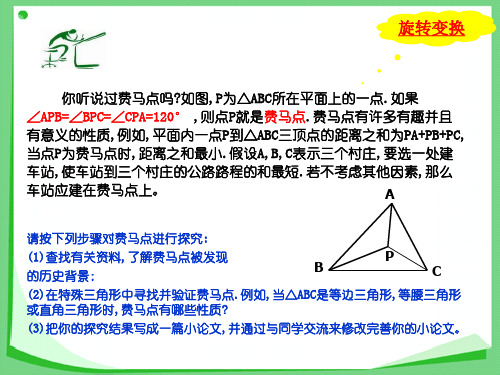
B A
C
D
平移变换
A 村和B 村在河的两侧，到河两岸的距离分别是6 千米和2 千米，河宽2 千米，两村的水平距离为6 千米。现欲在河上修建一座桥，使自A 村过桥到达B 村的距离最短（假设河的两岸平行，且桥要垂直于河岸修建）。请在图上标明桥址，并求出此最短距离。
A
河流
F C
D
E
B
“将军饮马”问题对称变换
Aቤተ መጻሕፍቲ ባይዱ
D
E
B
NC
问题9、如图，已知二次函数y=ax2+bx+c的图象交 x轴于A（1，0）和B（3，0），交y轴于C（0，3）， P是对称轴上的动点，求△PAC周长的最小值。
Y
X
问题10、在x轴上求一点P，使它到两个定点A(0， 2)，B(8，6)的距离之和最短。
(内江市06年中考题) 阅读并解答下面问题：（1）如图5所示，直线l的两侧有A、B两点，在l上求作一点P，使AP+BP的值最小（要求尺规作图，保留作图痕迹，不写画法和证明）
在人脑的记忆中，相关信息和技能越多，则迁移越可能发生
美国学者罗耶
问题1、如图，AB是⊙O的直径，AB=2，OC是⊙O 的半径，OC⊥AB，点D在弧AC上，弧AD=2弧CD， P是半径OC 上一个动点，求AP+PD的最小值。
问题2、如图，已知正方形ABCD的边长为8， M是DC上的一点，且DM=2，N是AC上的动点。求DN+MN的最小值。
白日登山望烽火，黄昏饮马傍交河。诗中隐含着一个有趣的数学问题：诗中将军在观望烽火之后从山脚上的A点出发，奔向交河旁边的C点饮马，饮马后再到B点宿营，试问怎样走，才能使总的路程最短？

(完整版)“费马点”说明及例举

费马点费马（Pierre de Fermat,1601--1665）法国业余数学家，拥有业余数学之王的称号,生于博蒙德罗曼。

其父曾任法国图卢兹地方法院的法律顾问。

本人身为律师，曾任图卢兹议会的顾问30多年。

他的一系列重要科学研究成果，都是利用业余时间完成的。

他是解析几何的发明者之一．在数学方面作出了卓越的贡献，早年主要研究概率论，对于数论和解析几何都有深入研究。

他对微分思想的运用比牛顿和莱布尼兹还要早，在他所著《求最大值和最小值的方法》一书中，已对微分理论进行了比较系统的探讨。

他把直线平面坐标应用于几何学也早于笛卡儿，在其所著〈平面及空间位置理论的导言〉中，最早提出了一次方程代表直线，二次方程代表截线，对一次与二次方程的一般形式，也进行了研究。

费马还研究了对方程221yax=+整数解的问题。

得出了求导数所有约数的系统方法。

所谓的“费马点”就是法国著名数学家费马在给数学朋友的一封信中提出关于三角形的一个有趣问题：“在三角形所在平面上，求一点，使该点到三角形三个顶点距离之和最小．”让人家想,并自称已经证明了。

这是费马通信的一贯作风。

当时欧洲所有数学家对他都十分头疼的。

人们称这个点为“费马点”。

还有象著名的费马大定理也是这样，给欧拉的信中提出的，自称已经“有了非常巧妙的证明”。

可到死也没告诉人家这个所谓证明。

结果困扰世界数学界一百多年。

直到去年才解决。

著名的费马大定理是费马提出的至今尚未解决的问题。

1637年费马提出：“不可能把一个整数的立方表示成两个立方的和，把一个四次方幂表示成两个四次方幂的和，一般地，不可能把任一个次数大于2的方幂表示成两个同方幂的和。

” 即：)3(,2≥=+nzyx nn无整数解。

1665年这一定理提出后，引起了许多著名数学家的关注，至今尚在研究如何证明它的成立，但始终毫无结果。

费马在光学方面，确立了几何光学的重要原理，命名为费马原理。

这一原理是几何光学的最重要基本理论之一，对于笛卡儿的“光在密媒质中比在疏媒质中传播要快”的观点给予了有力的反驳，把几何光学的发展推向了新的阶段。

费马小定理和欧拉定理PPT执教课件人教版1

若 p235 1 则 p是25 1 = 31或27 1 = 127的素因数或者 p 1 (mod 70)
由于 31和127是素数并且 235 1 = 31*127*8727391
所以，235 1的另外的素因数p只可能在数列
费马小定理和欧拉定理PP T执教课件人教版1（精品课件）
1 b ax = b db cy = b d(b c) y b d (mod m)。
若 x < 0，y > 0，由式(4)知
1 b cy = b db ax = b d(ba) x b d (mod m)。
费马小定理和欧拉定理PP T执教课件人教版1（精品课件）
费马小定理和欧拉定理PP T执教课件人教版1（精品课件）
针对性练习
一、设a，b，c，m是正整数，m > 1， (b, m)
= 1，并且b a 1 (mod m)，b c 1 (mod m)，记d = (a, c)，则bd 1 (mod m). 解利用辗转相除法可以求出整数x，y，使得ax cy = d，显然xy < 0. 若 x > 0，y < 0，由式(4)知
费马小定理和欧拉定理PP T执教课件人教版1（精品课件）
科普知识
费马生于法国南部，
贡献包括：与笛卡尔共同创立了解析几何；创造了作曲线切线的方法 . 最有名的是费马大定理，即不可能有满足 xn+yn=zn ，n>2的正整数 x，y，z，n存在.费马小定理是费马在1640年提出.
任意整数，且（ɑ， m ）=1，则
aφm 1modm,其中φm表示1，2，...，m

费马点及其在中考中的应用.pptx

(如图 5，G 点按照上述要求到达 A 点所用的时间为 t)
解法一设：GO=方x，程则解M法G=6 -x，AG=
，
则 t=
，
学海无涯
移项平方得：3x2+(12 -4t)x +36+24 t-4t2=0， ∵方程有解， Δ=(12 -4t)2-12(36+24 t-4t2)≥0 解得 t≥6 ，将 t=6 代回方程，求出 x=2 时，t 最小．
若 P 为△ABC 所在平面上一点，且∠APB=∠BPC=∠CPA=120°，则点 P 叫做△ ABC 的费马点． (1) 若点 P 为锐角△ABC 的费马点，且∠ABC=60°，PA=3，PC=4，
则 PB 的值为
；
(2) 如图 3，在锐角△ABC 外侧作等边△ACB，连结 BB′．求证：BB′过△ABC 的费马点 P，且 BB′=PA+PB+PC．
由于直线 y=kx+b 与 y 轴的交点坐标在第二问当中可求出 M(0，6 )，所以，本题第三问便可以转化为：AO⊥OM 于点 O，AO=6，MO=6 ，G 点从 M 出发，向 O 点运动到达 G 点后，再沿 GA 到达 A 点．若 G 点在 MO 上运动的速度是它在 GA 上运动速度的 2 倍，试确定 G 点的位置．
当 A′，P′，P 共线时，∵∠BP′P=60°，∴∠A′P′B=∠APB=120°．同理，若 P′，P，C 共线时，则∵∠BPP′=60°， ∴∠BPC=120°．所以点 P 为满足∠APB=∠BPC=∠CPA=120°的点．
三、费马点的简单应用近几年，在全国各地的中考中，时常可以看见费马点的影子．例 1(2009 浙江湖州--25)
解：(1)∵∠PBA+∠PBC=∠PBC+∠PCB=60°，∴∠PBA=∠PCB．又∠APB=∠BPC=120°， ∴△PBA∽△PCB，则 PB2=PA×PC=12，即 PB=2

中考数学几何模型专题12费马点问题(老师版) 知识点+例题

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题12费马点问题年8月17日﹣1665年1月12日），生于法国南部图卢兹（Toulouse ）附近的波蒙•德•罗曼，被誉为业余数学家之王．1643年，费马曾提出了一个著名的几何问题：给定不在一条直线上的三个点A ，B ，C ，求平面上到这三个点的距离之和最小的点的位置．另一位数学家托里拆利成功地解决了这个问题：如图1，△ABC （三个内角均小于120°）的三条边的张角都等于120°，即满足∠APB ＝∠BPC ＝∠APC ＝120°的点P ，就是到点A ，B ，C 的距离之和最小的点，后来人们把这个点P 称为“费马点”．下面是“费马点”的证明过程：如图2，将△APB 绕着点B 逆时针旋转60°得到△A ′P ′B ，使得A ′P ′落在△ABC 外，则△A ′AB 为等边三角形，∴P ′B ＝PB ＝PP ′，于是P A +PB +PC ＝P ′A ′+PP ′+PC ≥A ′C ，∴当A '，P '，P ，C 四点在同一直线上时P A +PB +PC 有最小值为A 'C 的长度， ∵P ′B ＝PB ，∠P 'BP ＝60°，∴△P 'BP 为等边三角形，则当A '，P '，P ，C 四点在同一直线上时，∠BPC ＝180°﹣∠P 'PB ＝180°﹣60°＝120°，∠APB ＝∠A 'PB ＝180°﹣∠BP 'P ＝180°﹣60°＝120°，∠APC ＝360°﹣∠BPC ﹣∠APC ＝360°﹣120°﹣120°＝120°，∴满足∠APB ＝∠BPC ＝∠APC ＝120°的点P ，就是到点A ，B ，C 的距离之和最小的点；为△ABC 所在平面上一点，且∠APB ＝∠BPC ＝∠CP A ＝120°，则点P 叫做△ABC 的费马点．（1）如点P为锐角△ABC的费马点．且∠ABC＝60°，P A＝3，PC＝4，求PB的长．（2）如图（2），在锐角△ABC外侧作等边△ACB′连接BB′．求证：BB′过△ABC的费马点P，且BB′＝P A+PB+PC．（3）已知锐角△ABC，∠ACB＝60°，分别以三边为边向形外作等边三角形ABD，BCE，ACF，请找出△ABC的费马点，并探究S△ABC与S△ABD的和，S△BCE与S△ACF的和是否相等．【分析】（1）由题意可得△ABP∽△BCP，所以PB2＝P A•PC，即PB＝2；（2）在BB'上取点P，使∠BPC＝120°，连接AP，再在PB'上截取PE＝PC，连接CE．由此可以证明△PCE为正三角形，再利用正三角形的性质得到PC＝CE，∠PCE＝60°，∠CEB'＝120°，而△ACB'为正三角形，由此也可以得到AC＝B'C，∠ACB'＝60°，现在根据已知的条件可以证明△ACP≌△B'CE，然后利用全等三角形的性质即可证明题目的结论；（3）作CP平分∠ACB，交BC的垂直平分线于点P，P点即费马点；要证明以上结论，需创造一些条件，首先可从△ABC中分出一部分使得与△ACF的面积相等，则过A作AM∥FC交BC于M，连接DM、EM，就可创造出这样的条件，然后再证其它的面积也相等即可．【解析】（1）∵∠P AB+∠PBA＝180°﹣∠APB＝60°，∠PBC+∠PBA＝∠ABC＝60°，∴∠P AB＝∠PBC，又∵∠APB＝∠BPC＝120°，∴△ABP∽△BCP，∴＝∴PB2＝P A•PC＝12，∴PB＝2；（2）证明：在BB'上取点P，使∠BPC＝120°．连接AP，再在PB'上截取PE＝PC，连接CE．∠BPC＝120°，∴∠EPC＝60°，∴△PCE为正三角形，∴PC＝CE，∠PCE＝60°，∠CEB'＝120°．∵△ACB'为正三角形，∴AC＝B′C，∠ACB'＝60°，∴∠PCA+∠ACE＝∠ACE+∠ECB′＝60°，∴∠PCA＝∠ECB′，∴△ACP≌△B′CE，∴∠APC＝∠B′EC＝120°，P A＝EB′，∴∠APB＝∠APC＝∠BPC＝120°，∴P为△ABC的费马点．∴BB'过△ABC的费马点P，且BB'＝EB'+PB+PE＝P A+PB+PC．（3）如下图，作CP平分∠ACB，交BC的垂直平分线于点P，P点就是费马点；证明：过A作AM∥FC交BC于M，连接DM、EM，∵∠ACB＝60°，∠CAF＝60°，∴∠ACB＝∠CAF，∴AF∥MC，∴四边形AMCF是平行四边形，又∵F A＝FC，∴四边形AMCF是菱形，∴AC＝CM＝AM，且∠MAC＝60°，∵在△BAC与△EMC中，CA＝CM，∠ACB＝∠MCE，CB＝CE，∴△BAC≌△EMC，∵∠DAM＝∠DAB+∠BAM＝60°+∠BAM∠BAC＝∠MAC+∠BAM＝60°+∠BAM∴∠BAC＝∠DAM在△ABC和△ADM中AB＝AD，∠BAC＝∠DAM，AC＝AM∴△ABC≌△ADM（SAS）故△ABC≌△MEC≌△ADM，在CB上截取CM，使CM＝CA，再连接AM、DM、EM（辅助线这样做△AMC就是等边三角形了，后边证明更简便）易证△AMC为等边三角形，在△ABC与△MEC中，CA＝CM，∠ACB＝∠MCE，CB＝CE，∴△ABC≌△MEC（SAS），∴AB＝ME，∠ABC＝∠MEC，又∵DB＝AB，∴DB＝ME，∵∠DBC＝∠DBA+∠ABC＝60°+∠ABC，∠BME＝∠BCE+∠MEC＝60°+∠MEC，∴∠DBC＝∠BME，∴DB∥ME，即得到DB与ME平行且相等，故四边形DBEM是平行四边形，∴四边形DBEM是平行四边形，∴S△BDM+S△DAM+S△MAC＝S△BEM+S△EMC+S△ACF，即S△ABC+S△ABD＝S△BCE+S△ACF．。

6最值系列之费马点

最值系列之费马点皮耶·德·费马，17世纪法国数学家，有“业余数学家之王”的美誉，之所以叫业余并非段位不够，而是因为其主职是律师，兼职搞搞数学．费马在解析几何、微积分等领域都有卓越的贡献，除此之外，费马广为人知的是以其名字命名的“费马小定理”、“费马大定理”等．据说费马在提出“费马大定理”时，在笔记本上写道：我已经想到了一个绝妙的证明方法，但是这个地方不够写，我就不写了吧。

看得出那个时候纸确实挺贵的，然后，直到1995年，才由英国数学家怀尔斯证明出，而距离费马逝世，已经过去了330年．果然，数学搞得好的都是装x的一把好手．言归正传，今天的问题不是费马提出来的，是他解决的，故而叫费马点．问题：在△ABC内找一点P，使得P A+PB+PC最小．APB C【分析】在之前的最值问题中，我们解决的依据有：两点之间线段最短、点到直线的连线中垂线段最短、作对称化折线段为直线段、确定动点轨迹求最值等．阿哈哈哈，此处一个也用不上！其实理论还是上面的理论，本题难点在于有3条线段，我们需要对这三条线段作一些位置上的变化，如果能变换成在一条直线上，问题就能解决了！算了算了，不墨迹了，直接报答案了：若点P满足∠P AB=∠BPC=∠CP A=120°，则P A+PB+PC值最小，P点称为该三角形的费马点．接下来讨论3个问题：（1）如何作三角形的费马点？（2）为什么是这个点？（3）费马点怎么考？一、如何作费马点问题要从初一学到的全等说起：（1）如图，分别以△ABC 中的AB 、AC 为边，作等边△ABD 、等边△ACE ．（2）连接CD 、BE ，即有一组手拉手全等：△ADC ≌△ABE ．（3）记CD 、BE 交点为P ，点P 即为费马点．（到这一步其实就可以了）（4）以BC 为边作等边△BCF ，连接AF ，必过点P ，有∠P AB =∠BPC =∠CP A =120°．EB ACAB CDE在图三的模型里有结论：（1）∠BPD =60°；（2）连接AP ，AP 平分∠DPE ．有这两个结论便足以说明∠P AB =∠BPC =∠CP A =120°．原来在“手拉手全等”就已经见过了呀，只是相逢何必曾相识！但是在这里有个小小的要求，细心的同学会发现，这个图成立的一个必要条件是 ∠BAC <120°，若120BAC ∠≥︒ ,这个图就不是这个图了，会长成这个样子：此时CD 与BE 交点P 点还是我们的费马点吗？显然这时候就不是了，显然P 点到A 、B 、C 距离之和大于A 点到A 、B 、C 距离之和．所以咧？是的，你想得没错，此时三角形的费马点就是A 点！当然这种情况不会考的，就不多说了．二、为什么是这个点为什么P点满足∠P AB=∠BPC=∠CP A=120°，P A+PB+PC值就会最小呢？归根结底，还是要重组这里3条线段：P A、PB、PC的位置，而重组的方法是构造旋转！在上图3中，如下有△ADC≌△ABE，可得：CD=BE．类似的手拉手，在图4中有3组，可得：AF=BE=CD．E巧的嘞，它们仨的长度居然一样长！更巧的是，其长度便是我们要求的P A+PB+PC的最小值，这一点是可以猜想得到的，毕竟最小值这个结果，应该也是个特别的值！接下来才是真正的证明：考虑到∠APB=120°，∴∠APE=60°，则可以AP为边，在PE边取点Q使得PQ=AP，则△APQ 是等边三角形．△APQ、△ACE均为等边三角形，且共顶点A，故△APC≌△AQE，PC=QE．以上两步分别转化P A=PQ，PC=QE，故P A+PB+PC=PB+PQ+QE=BE．没有对比就没有差别，我们换个P 点位置，如下右图，同样可以构造等边△APQ ，同样有△APC ≌△AQE ，转化P A =PQ ，PC =QE ，显然，P A +PB +PC =PB +PQ +QE >BE ．还剩下第3个问题！如果说费马点以前还算是课外的拓展内容，那现在，已经有人把它搬上了中考舞台！三、费马点怎么考？直接考，要不然还能怎么考？看看今年2019武汉中考填空最后一题：问题背景：如图1，将△ABC 绕点A 逆时针旋转60°得到△ADE ，DE 与BC 交于点P ，可推出结论：P A +PC =PE ．问题解决：如图2，在△MNG 中，MN =6，∠M =75°，MG=O 是△MNG 内一点，则点O 到△MNG 三个顶点的距离和的最小值是______．NG图2图1ABCD EP【分析】本题的问题背景实际上是提示了解题思路，构造60°的旋转，当然如果已经了解了费马点问题，直接来解决就好了！如图，以MG 为边作等边△MGH ，连接NH ，则NH 的值即为所求的点O 到△MNG 三个顶点的距离和的最小值．（此处不再证明）HGN M过点H作HQ⊥NM交NM延长线于Q点，根据∠NMG=75°，∠GMH=60°，可得∠HMQ=45°，∴△MHQ是等腰直角三角形，∴MQ=HQ=4，∴NH=．464QHGNM【练习】如图，在△ABC中，∠ACB=90°，AB=AC=1，P是△ABC内一点，求P A+PB+PC 的最小值．C 【分析】如图，以AD为边构造等边△ACD，连接BD，BD的长即为P A+PB+PC的最小值．至于点P的位置？这不重要！AB CD如何求BD？考虑到△ABC和△ACD都是特殊的三角形，过点D作DH⊥BA交BA的延长线于H点，根据勾股定理，222BD BH DH=+即可得出结果．HDCBA【练习】如图，已知矩形ABCD ，AB =4，BC =6，点M 为矩形内一点，点E 为BC 边上任意一点，则MA +MD +ME 的最小值为______．ABCDME【分析】依然构造60°旋转，将三条折线段转化为一条直线段．分别以AD 、AM 为边构造等边△ADF 、等边△AMG ，连接FG ，易证△AMD ≌△AGF ，∴MD =GF ∴ME +MA +MD =ME +EG +GF过F 作FH ⊥BC 交BC 于H 点，线段FH 的长即为所求的最小值．HFGE MDCBA。

费马点与加权费马点讲义及其旋转

费马点与加权费马点【例题1】．（1）知识储备①如图1，已知点P为等边△ABC外接圆的BC上任意一点．求证：PB+PC＝P A．②定义：在△ABC所在平面上存在一点P，使它到三角形三顶点的距离之和最小，则称点P为△ABC的费马点，此时P A+PB+PC的值为△ABC的费马距离．（2）知识迁移①我们有如下探寻△ABC（其中∠A，∠B，∠C均小于120°）的费马点和费马距离的方法：如图2，在△ABC的外部以BC为边长作等边△BCD及其外接圆，根据（1）的结论，易知线段的长度即为△ABC的费马距离．②在图3中，用不同于图2的方法作出△ABC的费马点P（要求尺规作图）．（3）知识应用①判断题（正确的打√，错误的打×）：ⅰ．任意三角形的费马点有且只有一个；ⅱ．任意三角形的费马点一定在三角形的内部．②已知正方形ABCD，P是正方形内部一点，且P A+PB+PC的最小值为，求正方形ABCD的边长．【练习1】．（1）阅读证明①如图1，在△ABC所在平面上存在一点P，使它到三角形三顶点的距离之和最小，则称点P为△ABC的费马点，此时P A+PB+PC的值为△ABC的费马距离．②如图2，已知点P为等边△ABC外接圆的上任意一点．求证：PB+PC＝P A．（2）知识迁移根据（1）的结论，我们有如下探寻△ABC（其中∠A，∠B，∠C均小于120°）的费马点和费马距离的方法：第一步：如图3，在△ABC的外部以BC为边长作等边△BCD及其外接圆；第二步：在上取一点P0，连接P0A，P0B，P0C，P0D．易知P0A+P0B+P0C＝P0A+（P0B+P0C）＝P0A+；第三步：根据（1）①中定义，在图3中找出△ABC的费马点P，线段的长度即为△ABC的费马距离．（3）知识应用已知三村庄A，B，C构成了如图4所示的△ABC（其中∠A，∠B，∠C均小于120°），现选取一点P打水井，使水井P到三村庄A，B，C所铺设的输水管总长度最小．求输水管总长度的最小值．【练习2】．问题探究将几何图形按照某种法则或规则变换成另一种几何图形的过程叫做几何变换．旋转变换是几何变换的一种基本模型．经过旋转，往往能使图形的几何性质明白显现．题设和结论中的元素由分散变为集中，相互之间的关系清楚明了，从而将求解问题灵活转化．问题提出：如图1，△ABC是边长为1的等边三角形，P为△ABC内部一点，连接P A、PB、PC，求P A+PB+PC的最小值．方法分析：通过转化，把由三角形内一点发出的三条线段（星型线）转化为两定点之间的折线（化星为折），再利用“两点之间线段最短”求最小值（化折为直）．问题解决：如图2，将△BP A绕点B逆时针旋转60°至△BP'A'，连接PP'、A'C，记A′C与AB交于点D，易知BA'＝BA＝BC＝1，∠A'BC＝∠A'BA+∠ABC＝120°．由BP'＝BP，∠P'BP＝60°，可知△P'BP为正三角形，有PB＝P'P．故．因此，当A'、P'、P、C共线时，P A+PB+PC 有最小值是．学以致用：（1）如图3，在△ABC中，∠BAC＝30°，AB＝4，CA＝3，P为△ABC内部一点，连接P A、PB、PC，则的最小值是．（2）如图4，在△ABC中，∠BAC＝45°，，P为△ABC内部一点，连接P A、PB、PC，求的最小值．（3）如图5，P是边长为2的正方形ABCD内一点，Q为边BC上一点，连接P A、PD、PQ，求P A+PD+PQ的最小值．【练习3】．如图，四边形ABCD是正方形，△ABE是等边三角形，M为对角线BD（不含B 点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM．（1）求证：△AMB≌△ENB；（2）①当M点在何处时，AM+CM的值最小；②当M点在何处时，AM+BM+CM的值最小，并说明理由；（3）当AM+BM+CM的最小值为时，求正方形的边长．【练习4】．在边长为2的正方形ABCD内求一点P，使得P A+PB+PC之和为最小，并求这个最小值及此时P A、PB、PC的大小．【练习5】．（1）阅读材料：如图（1），四边形ABCD是正方形，△ABE是等边三角形，M 为对角线BD（不含B点）上任意一点，将BM绕点B逆时针旋转60°得到BN，连接EN、AM、CM，①求证：△AMB≌△ENB；②当M点在何处时，AM+CM的值最小；③当M点在何处时，AM+BM+CM的值最小，并说明理由；（2）根据阅读材料所提供的数学思想和方法，完成下面的题目：如图（2），A、B、C、D四个城市恰好为一个正方形的四个顶点，要建立一个公路系统，使每两个城市之间都有公路相通，并使整个公路系统的总长为最短，应当如何修建？请画出你的设计图．【练习6】．如图，△ABC中，∠BAC＝30°且AB＝AC，P是底边上的高AH上一点．若AP+BP+CP的最小值为2，则BC＝．【练习8】．综合与实践：发现问题：如图①，已知：△OAB中，OB＝3，将△OAB绕点O逆时针旋转90°得△OA′B，连接BB′．则BB′＝．问题探究：如图②，已知△ABC是边长为4的等边三角形，以BC为边向外作等边△BCD，P为△ABC内一点，将线段CP绕点C逆时针旋转60°，P的对应点为Q．（1）求证：△DCQ≌△BCP（2）求P A+PB+PC的最小值．实际应用：如图③，某货运场为一个矩形场地ABCD，其中AB＝500米，AD＝800米，顶点A、D 为两个出口，现在想在货运广场内建一个货物堆放平台P，在BC边上（含B、C两点）开一个货物入口M，并修建三条专用车道P A、PD、PM．若修建每米专用车道的费用为10000元，当M，P建在何处时，修建专用车道的费用最少？最少费用为多少？【思考】专题—旋转在几何压轴题中的应用模型一共顶点等线段模型【例1】数学探究课上老师处这样一道题：“如图，等边△ABC中有一点P，且P A＝3，PB ＝4，PC＝5，试求∠APB的度数．”小明和小军探讨时发现了一种求∠APB度数的方法，下面是这种方法的一部分思路，请按照下列思路要求画图或判断（1）在图中画出△APC绕点A顺时针旋转60°后的△AP1B；（2）试判断△AP1P的形状，并说明理由；（3）试判断△BP1P的形状，并说明理由；（4）由（2）、（3）两问可知：∠APB＝．【例2】如图，在四边形ABCD中，∠ABC+∠ADC＝180°，AB＝AD，AE⊥BC于点E，若AE＝17，BC＝8，CD＝6，则四边形ABCD的面积为．【例3】问题：如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为BC边上一点（不与点B、C重合），将线段AD绕点A逆时针旋转90°得到AE，连接EC．求证：△ABD≌△ACE；探索：如图2，在Rt△ABC和Rt△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，将△ADE绕点A旋转，使点D落在BC边上，试探索线段AD2、BD2、CD2之间满足的数量关系，并证明你的结论；应用：如图3，在四边形ABCD中，∠ABC＝∠ACB＝∠ADC＝45°，若BD＝6，CD＝2，求AD的长．模型二费马点【例4】如图1，点P是等边△ABC内一点，已知P A＝3，PB＝4，PC＝5，求∠APB的度数．分析：要直接求∠A的度数显然很因难，注意到条件中的三边长恰好是一组勾股数，因此考虑借助旋转把这三边集中到一个三角形内．解：如图2，作∠P AD＝60°使AD＝AP，连接PD，CD，则△P AD是等边三角形．∴＝AD＝AP＝3，∠ADP＝∠P AD＝60°∵△ABC是等边三角形∴AC＝AB，∠BAC＝60°∴∠BAP＝∴△ABP≌△ACD∴BP＝CD＝4，＝∠ADC∵在△PCD中，PD＝3，PC＝5，CD＝4，PD2+CD2＝PC2∴∠PDC＝°∴∠APB＝∠ADC＝∠ADP+∠PDC＝60°+90°＝150°（2）如图3，在△ABC中，AB＝BC，∠ABC＝90°，点P是△ABC内一点，P A＝1，PB ＝2，PC＝3，求∠APB的度数．（3）拓展应用．如图（4），△ABC中，∠ABC＝30°，AB＝4，BC＝5，P是△ABC内部的任意一点，连接P A，PB，PC，则P A+PB+PC的最小值为．【例5】如图，P为正方形ABCD对角线BD上一动点，若AB＝2，AP+BP+CP的最小值是多少？【例6】问题提出（1）如图，点M、N是直线l外两点，在直线l上找一点K，使得MK+NK最小．问题探究（2）在等边三角形ABC内有一点P，且P A＝3，PB＝4，PC＝5，求∠APB度数的大小．问题解决（3）如图，矩形ABCD是某公园的平面图，AB＝30米，BC＝60米，现需要在对角线BD上修一凉亭E，使得到公园出口A、B，C的距离之和最小．问：是否存在这样的点E？若存在，请画出点E的位置，并求出EA+EB+EC的和的最小值；若不存在，请说明理由．模型三半角模型【例7】如图，在正方形ABCD中，E、F分别是边BC、CD上的点，∠EAF＝45°，△ECF的周长为8，则正方形ABCD的面积为（）A．9B．16C．20D．25【例8】如图，在△ABC中，∠BAC＝120°，AB＝AC，点M、N在边BC上，且∠MAN＝60°．若BM＝2，CN＝3，则MN的长为．。