实验三数字滤波实验

合集下载

大学数字实验报告

实验名称：数字信号处理实验实验日期：2023年3月15日实验地点：大学计算机实验室实验目的：1. 理解数字信号处理的基本概念和原理。

2. 掌握数字滤波器的设计和实现方法。

3. 学会使用数字信号处理软件进行实验和分析。

4. 培养实验操作能力和数据分析能力。

实验原理：数字信号处理（Digital Signal Processing，DSP）是利用计算机或专用处理硬件对数字信号进行操作的一门技术。

它包括信号的采样、量化、滤波、变换、压缩、解压缩等处理过程。

本实验主要涉及数字滤波器的设计和实现。

实验仪器：1. 实验计算机2. 数字信号处理软件（如MATLAB）3. 示波器4. 音频播放器实验内容：一、实验一：数字滤波器的基本概念1. 实验目的：理解数字滤波器的基本概念，掌握滤波器的类型和特点。

2. 实验步骤：a. 在MATLAB中创建一个简单的数字滤波器模型，例如低通滤波器。

b. 使用MATLAB的内置函数进行滤波器的设计，并观察滤波器的频率响应。

c. 分析滤波器的性能，包括通带、阻带、过渡带等。

3. 实验结果：a. 设计了一个低通滤波器，其截止频率为1000Hz。

b. 频率响应显示，在截止频率以下，滤波器对信号有较好的抑制效果；在截止频率以上，滤波器对信号有较好的通过效果。

c. 分析结果表明，该滤波器满足实验要求。

二、实验二：FIR滤波器的设计1. 实验目的：掌握FIR滤波器的设计方法，学会使用MATLAB进行FIR滤波器的设计和实现。

2. 实验步骤：a. 设计一个具有线性相位特性的FIR滤波器，例如汉明窗设计。

b. 使用MATLAB的内置函数进行滤波器的设计，并观察滤波器的频率响应。

c. 对滤波器进行时域和频域分析，评估滤波器的性能。

3. 实验结果：a. 设计了一个具有线性相位特性的低通FIR滤波器，其截止频率为1000Hz。

b. 频率响应显示，该滤波器具有较好的线性相位特性，且在截止频率以下对信号有较好的抑制效果。

IIR数字滤波器设计实验报告

实验三IIR数字滤波器设计实验报告一、实验目的：1.通过仿真冲激响应不变法和双线性变换法2.掌握滤波器性能分析的基本方法二、实验要求：1.设计带通IIR滤波器2.按照冲激响应不变法设计滤波器系数3. 按照双线性变换法设计滤波器系数4. 分析幅频特性和相频特性5. 生成一定信噪比的带噪信号，并对其滤波，对比滤波前后波形和频谱三、基本原理：㈠IIR模拟滤波器与数字滤波器IIR数字滤波器的设计以模拟滤波器设计为基础，常用的类型分为巴特沃斯（Butterworth）、切比雪夫（Chebyshev）Ⅰ型、切比雪夫Ⅱ型、贝塞尔（Bessel）、椭圆等多种。

在MATLAB信号处理工具箱里，提供了这些类型的IIR数字滤波器设计子函数。

（二）性能指标1.假设带通滤波器要求为保留6000hz~~7000hz频段，滤除小于2000hz和大宇9000hz频段2.通带衰减设为3Db,阻带衰减设为30dB，双线性变换法中T取1s.四、实验步骤：1.初始化指标参数2.计算模拟滤波器参数并调用巴特沃斯函数产生模拟滤波器3.利用冲激响应不变法和双线性变换法求数字IIR滤波器的系统函数Hd (z)4.分别画出两种方法的幅频特性和相频特性曲线5.生成一定信噪比的带噪信号6.画出带噪信号的时域图和频谱图6.对带噪信号进行滤波，并画出滤波前后波形图和频谱图五、实验结果模拟滤波器的幅频特性和相频特性：101010101Frequency (rad/s)P h a s e (d e g r e e s )1010101011010-5100Frequency (rad/s)M a g n i t u d e在本实验中，采用的带通滤波器为6000-7000Hz ，换算成角频率为4.47-0.55，在上图中可以清晰地看出到达了题目的要求。

冲击响应不变法后的幅频特性和相频特性：0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )双线性变换法的幅频特性和相频特性：0.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )00.10.20.30.40.50.60.70.80.91Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )通过上图比较脉冲响应不变法双线性变换法的幅频特性和相频特性，而在在幅频曲线上几乎没有差别，都能达到相同的结果。

华南理工大学数字信号处理实验三实验报告

% 默认采样率 4000Hz，通带波纹 1dB，最小阻带衰减 40dB
% 符号
符号说明
% fp
通带截止频率,单位:Hz
% fs
阻带截止频率,单位:Hz
% fsam
采样率,单位:Hz
% pr
通带波纹(passband ripple),单位:dB
% minsa
最小阻带衰减(minimum stopband attenuation),单位:dB
3.1 低通滤波器设计
3.1.1 实验题目
一、用双线性变换法设计如下 IIR 滤波器，（可以选择 butteworth or chebyshey）滤波器的性能指标：
低通滤波器：通带截止频率 1000Hz，阻带截止频率 1200Hz，采样率 4000Hz，通带波纹 1dB，最小阻带衰减 40dB；二、要画出滤波器的频率响应特性（用 freqz 函数）
2.2 低通滤波器
低通滤波器是容许低于截止频率的信号通过，但高于截止频率的信号不能通过的一种滤波器。其频谱响应形如图 1 所示。
图 1 低通滤波器频谱相应示例
2.3 高通滤波器
高通滤波器是一个使高频率比较容易通过而阻止低频率通过的系统。它去掉了信号中不必要的低频成分或者说去掉了低频干扰。其频谱相应如图 2。
数字 IIR 滤波器。掌握 MATLAB 函数书写，特别是用 MATLAB 函数封装自己设计的滤波器，
并实现参数可调。
2 实验原理
2.1 IIR 滤波器
按脉冲响应来分类，数字滤波器分为 IIR 和 FIR，即无限冲激响应滤波器和有限冲激响应滤波器；其中 IIR 网络中有反馈回路，FIR 网络中没有反馈回路。 IIR 滤波器是无限脉冲响应滤波器，又称递归型滤波器，即结构上带有反馈环路。特点：

滤波器实验

实验三滤波器实验一，实验目的1，通过实验了解滤波器的工作原理。

2，通过实验学习有源滤波器的特点。

3，学习滤波器在工程技术中的应用。

二，实验仪器及器材1，通用线路接插板2，电容、电阻、电位器、运算放大器等电子元器件3，晶体管毫伏表4，低频信号发生器5，直流稳压电源三，实验步骤及实验结果1，计算上截止频率为440Hz的RC低通滤波器的R、C数值。

实验电路如上图，其中电容，根据上截止频率点处解得：。

2，将选好的元件在线路插板上按上图接插成低通滤波器，测出其幅频特性。

采用两种方法测量，一种是通过示波器测量不同频率的响应幅值，从而得到幅频特性曲线。

另一种是直接测量幅频特性伯德图。

实验中直接测得幅频特性曲线：手动调整输入信号频率，测得输出放大倍率如下通过示波器测量频率为0~2k时的幅值响应数据如下:f/Hz 10 50 100 150 200 250 300幅值/mv 1.009 998.00 967.80 930.32 881.40 829.70 779.60350 400 450 500 600 800 1000 1500 2000 726.20 678.91 635.02 596.54 527.31 422.11 350.50 245.29 187.41得到的幅频特性曲线如下：可以看出通过测量各频率放大倍率绘制的幅频曲线图和实验中仪器绘制的波特图基本一致，截止频率440Hz左右。

3，在此低通滤波器的输出端并联一个1kΩ的负载电阻，再测其幅频特性，并与无负载情况下的幅频特性相比较。

分析可得上截止频率满足：实验中36kΩ，，代入上式求得：实验测出幅频特性曲线如下：分析数据：Freq (Hz) Gain (dB) Phase (deg)100.000 -30.235 -0.43814677.993 -33.457 -51.45117782.794 -34.382 -57.910从初始下降-3dB即为截止频率，可看出与理论计算基本相符。

数字信号处理Matlab实验三-IIR数字滤波器的设计

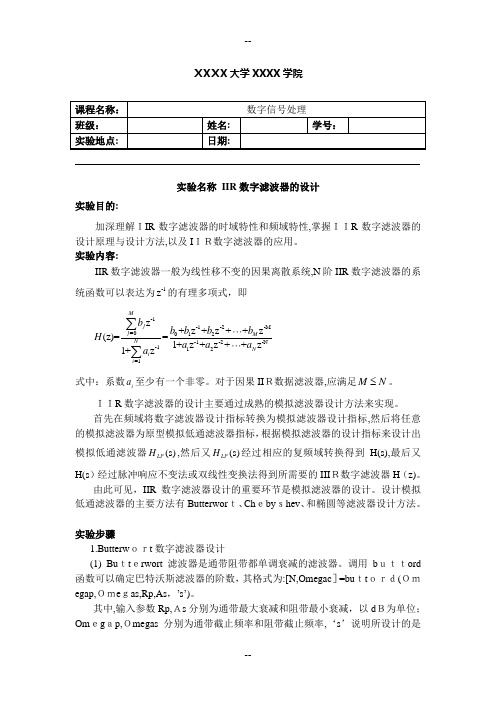
ＸX ＸX 大学XXXX 学院实验名称 IIR 数字滤波器的设计实验目的:加深理解ＩIR 数字滤波器的时域特性和频域特性,掌握ＩＩR 数字滤波器的设计原理与设计方法,以及I ＩＲ数字滤波器的应用。

实验内容:IIR 数字滤波器一般为线性移不变的因果离散系统,N 阶IIR 数字滤波器的系统函数可以表达为-1z 的有理多项式，即 -1-1-2-M =0012-1-2-N -112=1z +z +z ++z (z)==1+z +z ++z 1+zM j j M N Ni i b b b b b H a a a a ∑∑ 式中：系数i a 至少有一个非零。

对于因果II Ｒ数据滤波器,应满足M N ≤。

ＩＩR 数字滤波器的设计主要通过成熟的模拟滤波器设计方法来实现。

首先在频域将数字滤波器设计指标转换为模拟滤波器设计指标,然后将任意的模拟滤波器为原型模拟低通滤波器指标，根据模拟滤波器的设计指标来设计出模拟低通滤波器(s)LP H ,然后又(s)LP H 经过相应的复频域转换得到H(s),最后又H(s ）经过脉冲响应不变法或双线性变换法得到所需要的III Ｒ数字滤波器H （z)。

由此可见，IIR 数字滤波器设计的重要环节是模拟滤波器的设计。

设计模拟低通滤波器的主要方法有Butterwor ｔ、Ch ｅby ｓhev 、和椭圆等滤波器设计方法。

实验步骤1.Butterw ｏｒt 数字滤波器设计(1) Bu ｔt ｅrwort 滤波器是通带阻带都单调衰减的滤波器。

调用b ｕｔｔord 函数可以确定巴特沃斯滤波器的阶数，其格式为:[N,Omegac ］=bu ｔt ｏｒｄ(Ｏｍegap,Ｏｍe ｇas,Rp,As ，’s ’)。

其中,输入参数Rp,Ａs 分别为通带最大衰减和阻带最小衰减，以d Ｂ为单位；Om ｅg ａp,Ｏmegas 分别为通带截止频率和阻带截止频率,‘s ’说明所设计的是模拟滤波器。

输出参数为滤波器的阶数，Omeｇac为3ｄB截止频率。

数字滤波器设计实验报告

数字滤波器设计实验报告实验目的：1.掌握数字滤波器的基本理论知识。

2.学习数字滤波器设计方法。

3.实现数字滤波器的设计与模拟。

实验原理：FIR滤波器的特点是稳定性好、相位响应线性和易于设计。

FIR滤波器的设计方法主要有窗函数法、频率采样法和最小最大化法等。

IIR滤波器的特点是具有较窄的通频带宽率、相位响应非线性和较高的处理效率。

IIR滤波器的设计方法主要有双线性变换法、脉冲响应不变法和双正交变换法等。

实验步骤：1.根据实验要求和给定的参数，选择适合的滤波器类型（FIR或IIR）。

2.根据滤波器的设计方法，计算滤波器的系数。

3.使用MATLAB或其他工具进行滤波器的设计和仿真。

4.分析仿真结果，评估滤波器的性能。

5.根据实际需求，进行滤波器参数的优化和调整。

6.进行实验数据的滤波处理，并比较滤波前后的信号质量。

7.总结实验结果，写出实验报告。

实验结果：根据实验要求，我们选择了FIR滤波器进行设计。

通过使用窗函数法和最小最大化法，计算得到了滤波器的系数。

将滤波器的设计结果导入MATLAB进行仿真，得到了滤波器的频率响应和时域波形。

通过分析仿真结果，发现滤波器的设计基本满足了要求，但仍存在一些性能方面的改进空间。

根据实验需求和实际情况，我们对滤波器的参数进行了优化和调整。

经过多次迭代和调试，最终得到了满意的结果。

将优化后的滤波器应用于实验数据的滤波处理，可以看到滤波效果明显，信号质量得到了显著提升。

实验结论：通过本次实验，我们学习并掌握了数字滤波器的基本理论知识和设计方法。

通过实际操作和实验仿真，对数字滤波器的设计和应用有了更深入的了解。

实验结果表明，数字滤波器可以有效地对信号进行滤波处理，提高信号质量和准确度。

实验三FIR数字滤波器设计

实验三FIR数字滤波器的设计一、实验目的1.掌握用窗函数法，频率采样法及优化设计法设计FIR滤波器的原理及方法，熟悉响应的计算机编程；2.熟悉线性相位FIR滤波器的幅频特性和相频特性；3.了解各种不同窗函数对滤波器性能的影响。

二、实验原理与方法线性相位实系数FIR滤波器按其N值奇偶和h(n)的奇偶对称性分为四种：1、h(n)为偶对称，N为奇数H(e jω)的幅值关于ω=0，π，2π成偶对称。

2、h(n)为偶对称，N为偶数H(e jω)的幅值关于ω=π成奇对称，不适合作高通。

3、h(n)为奇对称，N为奇数H(e jω)的幅值关于ω=0，π，2π成奇对称，不适合作高通和低通。

4、h(n)为奇对称，N为偶数H(e jω)ω=0、2π＝0，不适合作低通。

(一)窗口法窗函数法设计线性相位FIR滤波器步骤∙确定数字滤波器的性能要求：临界频率{ωk}，滤波器单位脉冲响应长度N；∙根据性能要求，合理选择单位脉冲响应h(n)的奇偶对称性，从而确定理想频率响应H d(e jω)的幅频特性和相频特性；∙求理想单位脉冲响应h d(n)，在实际计算中，可对H d(e jω)按M(M远大于N)点等距离采样，并对其求IDFT得h M(n)，用h M(n)代替h d(n)；∙选择适当的窗函数w(n)，根据h(n)= h d(n)w(n)求所需设计的FIR滤波器单位脉冲响应；∙求H(e jω)，分析其幅频特性，若不满足要求，可适当改变窗函数形式或长度N，重复上述设计过程，以得到满意的结果。

窗函数的傅式变换W(e jω)的主瓣决定了H(e jω)过渡带宽。

W(e jω)的旁瓣大小和多少决定了H(e jω)在通带和阻带范围内波动幅度，常用的几种窗函数有：∙矩形窗 w(n)=R N(n)；∙Hanning窗；∙Hamming窗；∙Blackmen窗；∙Kaiser窗。

式中I o(x)为零阶贝塞尔函数。

（二）频率采样法频率采样法是从频域出发，将给定的理想频率响应Hd(e jω)加以等间隔采样然后以此Hd(k)作为实际FIR数字滤波器的频率特性的采样值H(k),即令由H(k)通过IDFT可得有限长序列h(n)将上式代入到Z变换中去可得其中Φ(ω)是内插函数（三）FIR滤波器的优化设计FIR滤波器的优化设计是按照最大误差最小化准则，使所设计的频响与理想频响之间的最大误差，在通带和阻带范围均为最小，而且是等波动逼近的。

数字滤波器的设计实验

实验二IIR数字滤波器的设计实验内容及步骤:数字滤波器的性能指标：通带临界频率fp、阻带临界频率fr；通带内的最大衰减Ap；阻带内的最小衰减Ar；采样周期T；(1)、fp=0.3KHz,Ap=0.8dB, fr=0.2KHz,Ar=20dB,T=1ms；设计一Chebyshev高通滤波器；观察其通带损耗和阻带衰减是否满足要求。

程序如下：fp=300; fr=200;Ap=0.8; Ar=20;T=0.001;fs=1/T;wp=2*pi*fp*T;wr=2*pi*fr*T;Wp=2/T*tan(wp/2);Wr=2/T*tan(wr/2);[N,Wn]=cheb1ord(Wp,Wr,Ap,Ar,'s');[B,A] = cheby1(N,Ap,Wn,'high','s');[num,den]=bilinear(B,A,1/T);[h,w]=freqz(num,den);plot(w*fs/(2*pi),20*log10(abs(h))); %衰减及频率都用归一化的1为单位显示axis([0,500,-30,0]);title('Chebyshev高通滤波器');xlabel('频率');ylabel('衰减');grid on;根据下图知道通带损耗与阻带衰减满足要求(2)、fp=0.2KHz,Ap=1dB, fr=0.3KHz,Ar=25dB,T=1ms；分别用脉冲响应不变法及双线性变换法设计一Butterworth数字低通滤波器，观察所设计数字滤波器的幅频特性曲线，记录带宽和衰减量，检查是否满足要求。

比较这两种方法的优缺点。

程序如下：fp=200; fr=300;Ap=1;Ar=25;T=0.001;fs=1/T;wp=2*pi*fp*T;wr=2*pi*fr*T;Wp=2/T*tan(wp/2);Wr=2/T*tan(wr/2);[N,Wn]=buttord(Wp,Wr,Ap,Ar,'s');[B,A] = butter(N,Wn,'s');[num1,den1]=impinvar(B,A,1/T); %脉冲响应不变法得出设计的传递函数[num2,den2]=bilinear(B,A,1/T); %双线性变换法得出设计的传递函数[h1,w]=freqz(num1,den1);plot(w*fs/(2*pi),20*log10(abs(h2)),w*fs/(2*pi),20*log10(abs(h1)), 'r.');grid on; %衰减及频率都用归一化的1为单位显示axis([0,500,-30,0]);title('Butterworth低通滤波器（红线—脉冲响应不变法蓝线—双线性变换法）');xlabel('ÆµÂÊ');ylabel('Ë¥¼õ');grid on;优缺点：采用脉冲响应不变法优点：1.h(n)完全模仿模拟滤波器的单位抽样响应时域逼近良好2线性相位模拟滤波器转变为线性相位数字滤波器缺点：1.对时域的采样会造成频域的“混叠效应”，故有可能使所设计数字滤波器的频率响应与原来模拟滤波器的频率响应相差很大2不能用来设计高通和带阻滤波器。

数字信号处理--实验三

一、实验目的1．了解工程上两种最常用的变换方法：脉冲响应不变法和双线性变换法。

2．掌握双线性变换法设计IIR 滤波器的原理及具体设计方法，熟悉用双线性设计法设计低通、带通和高通IIR 数字滤波器的计算机程序.3．观察用双线性变换法设计的滤波器的频域特性，并与脉冲响应不变法相比较,了解双线性变换法的特点。

4．熟悉用双线性变换法设计数字Butterworth 和Chebyshev 滤波器的全过程。

5．了解多项式乘积和多项式乘方运算的计算机编程方法。

二、实验原理与方法从模拟滤波器设计IIR 数字滤波器具有四种方法：微分－差分变换法、脉冲响应不变法、双线性变换法、z 平面变换法。

工程上常用的是其中的两种:脉冲响应不变法、双线性变换法。

脉冲响应不变法需要经历如下基本步骤：由已知系统传输函数H(S)计算系统冲激响应h(t)；对h(t)等间隔采样得到h （n ）=h （n T)；由h （n ）获得数字滤波器的系统响应H （Z)。

这种方法非常直观，其算法宗旨是保证所设计的IIR 滤波器的脉冲响应和模拟滤波器的脉冲响应在采样点上完全一致。

而双线性变换法的设计准则是使数字滤波器的频率响应与参考模拟滤波器的频率响应相似。

脉冲响应不变法一个重要的特点是频率坐标的变换是线性的（），其确定是有频谱的周期延拓效应，存在频谱混叠的现象。

为了克服脉冲响应不变法可能产生的频谱混叠，提出了双线性变换法，它依靠双线性变换式：，，其中 ,建立其S 平面和Z 平面的单值映射关系，数字域频率和模拟域频率的关系是： , （3－1）由上面的关系式可知,当时，终止在折叠频率处,整个轴单值的对应于单位圆的一周。

因此双线性变换法不同于脉冲响应不变法，不存在频谱混叠的问题。

从式（3－1）还可以看出，两者的频率不是线性关系。

这种非线性关系使得通带截至频率、过渡带的边缘频率的相对位置都发生了非线性畸变。

这种频率的畸变可以通过预畸变来校正。

用双线性变换法设计数字滤波器时，一般总是先将数字滤波器的个临界频率经过式（3－1）的频率预畸变,求得相应参考模拟滤波器的个临界频率，然后设计参考模拟滤波器的传递函数，最后通过双T Ω=ω1111--+-=z z s s s z -+=11Ω+=j s σωj re z =)2/(ωtg =Ω)(2Ω=arctg ω∞→Ωωπω=Ωj线性变换式求得数字滤波器的传递函数。

实验三：数字滤波器设计

二、用窗函数法设计FIR数字滤波器
• （一）实验目的
• 1 掌握用窗函数法设计FIR数字滤波器的原理和方法。 • 2 熟悉线性相位FIR数字滤波器特性。 • 3 了解各种窗函数对滤波特性的影响。
• （二）实验原理与方法
• 如果所希望的滤波器的理想频率响应函数为 Hd(e 的单位脉冲响应为 1 j j n hd ( n ) H d (e )e d 2
• 如果要求线性相位特性，则h(n)还必须满足：
h(n ) h( N 1 n )
• 根据上式中的正、负号和长度N的奇偶性又将线性相位FIR滤波器分成四类。要根据所设计的滤波特性正确选择其中一类。例如，要设计线性相位低通特性，可选择h(n)=h(N-1-n)一类，而
结束
图1 用窗函数法设计滤波器主程序框图
设
H ( k ) D F T [ h ( n )] H ( k ) H k ( k ) jH I ( k ) H (k ) H R (k ) H I (k )
2 2
• 3 上机实验内容。
e j a , c j H d (e ) c 0 a hd ( n ) N 1 2 1 2
实验三：数字滤波器设计
一、用双线性变换法设计IIR数字滤波器
•
（一）实验目的
• 1 熟悉用双线性变换法设计IIR数字滤波器的原理与方法。 • 2 掌握数字滤波器的计算机仿真方法。 • 3 通过观察对实际心电图信号的滤波作用，获得数字滤波的感性知识。
•
（二）实验内容
• 1 用双线性变换法设计一个巴特沃斯低通IIR数字滤波器。 • 2 以 0.02π为采样间隔，打印出数字滤波器在频率区间［0, π/2］上的幅频响应特性曲线。 • 3 用所设计的滤波器对实际心电图信号采样序列(在本实验后面给出)进行仿真滤波处理，并分别打印出滤波前后的心电图信号波形图，观察总结滤波作用与效果。

实验三IIR滤波器的设计与信号滤波

实验三 IIR 滤波器的设计与信号滤波１、实验目的（１）熟悉用双线性变换法设计IIR 数字滤波器的原理与方法。

（２）掌握数字滤波器的计算机仿真方法。

（３）通过观察对实际心电图信号的滤波作用，获得数字滤波的感性知识。

2、实验仪器：PC 机一台 MATLAB 软件3、实验原理利用双线性变换设计IIR 滤波器（只介绍巴特沃斯数字低通滤波器的设计），首先要设计出满足指标要求的模拟滤波器的传递函数)(s H a ，然后由)(s H a 通过双线性变换可得所要设计的IIR 滤波器的系统函数)(z H 。

如果给定的指标为数字滤波器的指标，则首先要转换成模拟滤波器的技术指标，这里主要是边界频率s p w w 和的转换，对s p αα和指标不作变化。

边界频率的转换关系为)21tan(2w T =Ω。

接着，按照模拟低通滤波器的技术指标根据相应设计公式求出滤波器的阶数N 和dB 3截止频率c Ω；根据阶数N 查巴特沃斯归一化低通滤波器参数表，得到归一化传输函数)(p H a ；最后，将c s p Ω=代入)(p H a 去归一，得到实际的模拟滤波器传输函数)(s H a 。

之后，通过双线性变换法转换公式11112--+-=zz T s ，得到所要设计的IIR 滤波器的系统函数)(z H 。

利用所设计的数字滤波器对实际的心电图采样信号进行数字滤波器。

4、实验步骤及内容（１）复习有关巴特沃斯模拟滤波器的设计和用双线性变换法设计IIR 数字滤波器的内容，用双线性变换法设计一个巴特沃斯IIR 低通数字滤波器。

设计指标参数为：在通带内频率低于π2.0时，最大衰减小于dB 1；在阻带内[]ππ,3.0频率区间上，最小衰减大于dB 15。

（２）绘制出数字滤波器的幅频响应特性曲线。

（３）用所设计的滤波器对实际心电图信号采样序列（实验数据在后面给出）进行仿真滤波处理，并分别绘制出滤波前后的心电图信号波形图，观察总结滤波作用与效果。

（４）输入为20Hz 正弦和200Hz 的正弦的叠加波形，要求用双线性变换法设计一巴特沃斯数字低通滤波器滤除200Hz 的正弦，使输出中只保留20Hz 的正弦波。

数字图像处理实验三中值滤波和均值滤波实验报告

数字图像处理实验三均值滤波、中值滤波的计算机实现12281166 崔雪莹计科1202 班一、实验目的：1）熟悉均值滤波、中值滤波处理的理论基础；2）掌握均值滤波、中值滤波的计算机实现方法；3）学习VC++ 6。

0 的编程方法；4）验证均值滤波、中值滤波处理理论；5）观察均值滤波、中值滤波处理的结果。

二、实验的软、硬件平台：硬件：微型图像处理系统，包括：主机，PC机；摄像机；软件：操作系统：WINDOWS2000或WINDOWSXP应用软件：VC++6.0三、实验内容：1）握高级语言编程技术；2）编制均值滤波、中值滤波处理程序的方法；3）编译并生成可执行文件；4）考察处理结果。

四、实验要求：1）学习VC+确6。

0编程的步骤及流程；2）编写均值滤波、中值滤波的程序；3）编译并改错；4）把该程序嵌入试验二给出的界面中（作适当修改）；5）提交程序及文档；6）写出本次实验的体会。

五、实验结果截图实验均值滤波采用的是3X3的方块，取周围的像素点取得其均值代替原像素点。

边缘像素的处理方法是复制边缘的像素点，增加一个边框，计算里面的像素值得均值滤波。

均值氓浜1W赵六、实验体会本次实验在前一次的实验基础上增加均值滤波和中值滤波，对于椒盐噪声的处理，发现中值滤波的效果更为好一点，而均值滤波是的整个图像变得模糊了一点，效果差异较大。

本次实验更加增加了对数字图像处理的了解与学习。

七、实验程序代码注释及分析// HistDemoADIg.h :头文件//#in elude "ImageWnd.h"#pragma once// CHistDemoADIg 对话框classCHistDemoADIg : public CDialogEx{//构造public:CHistDemoADlg(CWnd* pParent = NULL); // 标准构造函数intnWidth;intnHeight;intnLen;intnByteWidth;BYTE *lpBackup;BYTE *lpBitmap;BYTE *lpBits;CStringFileName;CImageWndsource,dest;// 对话框数据enum { IDD = IDD_HISTDEMOA_DIALOG };protected:virtual void DoDataExchange(CDataExchange* pDX); // DDX/DDV 支持// 实现protected:HICON m_hIcon;// 生成的消息映射函数virtual BOOL OnInitDialog();afx_msg void OnSysCommand(UINT nID, LPARAM lParam);afx_msg void OnPaint();afx_msg HCURSOR OnQueryDragIcon();DECLARE_MESSAGE_MAP()public:voidLoadBitmap(void);afx_msg void OnOpen();afx_msg void OnHist();voidHistogramEq(void);voidNoColor(void);void HistogramEq1(intnWidth,intnHeight,BYTE *lpInput,BYTE *lpOutput);voidMeanFilter(intnWidth,intnHeight,BYTE *lpInput,BYTE *lpOutput);voidMedianFilter(intnWidth,intnHeight,BYTE *lpInput,BYTE *lpOutput); afx_msgvoid OnBnClickedClose();afx_msg void OnBnClickedMeanfilter();afx_msg void OnBnClickedMedianfilter();};HistDemoADlg.cpp 对HistDemoADlg.h 进行具体的实现，OnOpen() 函数响应ID 为IDC_OPEN的按钮事件，而且会调取文件选择对话框，选取文件之后，会显示在原始图像区域显示对应的位图图像，OnHist()函数会响应ID为IDC_HIST的按钮事件，调用HistogramEq()进行直方图均衡化的处理，HistogramEq()会调用HistogramEq1()进行直方图均衡化的处理，并用dst.setlmage()显示处理之后的图像，以及NoColor()函数，对原始图像转化为灰度图像之后再显示。

实验三IIR数字滤波器设计及软件实现

实验三IIR数字滤波器设计及软件实现IIR数字滤波器是一种常见的数字滤波器类型，它可以实现对信号的频率响应进行调整和改变，常用于信号处理和通信系统中。

本实验将介绍IIR数字滤波器的设计方法和软件实现。

设计一个IIR数字滤波器的一般步骤如下：1.确定滤波器的类型：低通滤波器、高通滤波器、带通滤波器或带阻滤波器。

2.确定滤波器的阶数：阶数决定了滤波器的复杂程度和性能。

3.确定滤波器的截止频率：截止频率决定了滤波器对信号的频率响应的影响。

4.根据滤波器类型和截止频率的要求，选择适当的滤波器设计方法：脉冲响应不变法、双线性变换法等。

5.根据滤波器设计方法，计算出滤波器的系数：系数决定了滤波器的频率响应和性能。

6.实现滤波器的差分方程：将滤波器的系数代入差分方程中，得到滤波器的离散时间域表示。

7. 使用合适的软件工具进行滤波器的软件实现和仿真：可以使用MATLAB、Python等编程语言进行滤波器设计和实现。

在软件实现过程中，通常可以通过以下步骤来实现IIR数字滤波器：1.定义滤波器的参数和输入信号：定义滤波器的类型、阶数、截止频率等参数，并读取输入信号。

2.计算滤波器的系数：根据设计方法和参数，计算滤波器的系数。

3.实现滤波器的差分方程：根据滤波器的差分方程，使用循环结构来实现滤波器的运算。

4.输入信号进入滤波器：将输入信号输入滤波器，进行滤波处理。

5.输出滤波后的信号：获取滤波器的输出结果，并进行处理和显示。

需要注意的是，IIR数字滤波器的设计和实现需要对信号处理和数字滤波器的基本原理有一定的了解，并且需要根据实际需求选择合适的设计方法和参数。

参考资料：2. Zhu, Y., & Buck, J. (2024). VLSI signal processing. John Wiley & Sons.。

数字信号处理实验三 FIR数字滤波器的设计

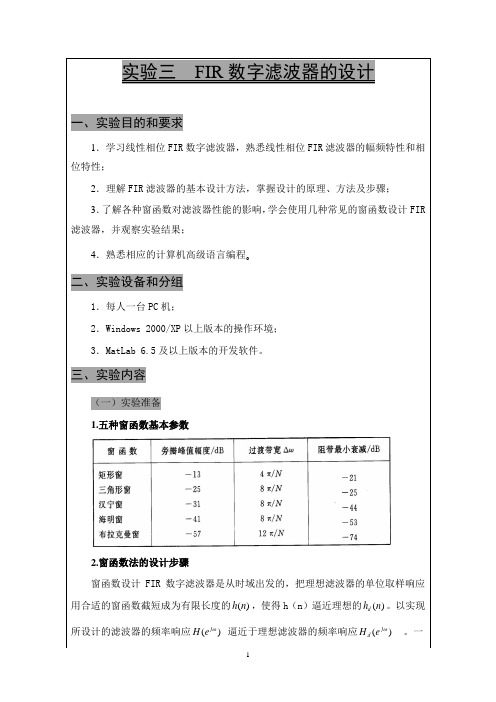
实验三 FIR 数字滤波器的设计一、实验目的和要求1．学习线性相位FIR 数字滤波器，熟悉线性相位FIR 滤波器的幅频特性和相位特性；2．理解FIR 滤波器的基本设计方法，掌握设计的原理、方法及步骤；3．了解各种窗函数对滤波器性能的影响，学会使用几种常见的窗函数设计FIR 滤波器，并观察实验结果；4．熟悉相应的计算机高级语言编程。

二、实验设备和分组1．每人一台PC 机；2．Windows 2000/XP 以上版本的操作环境；3．MatLab 6.5及以上版本的开发软件。

三、实验内容（一）实验准备1.五种窗函数基本参数2.窗函数法的设计步骤窗函数设计FIR 数字滤波器是从时域出发的，把理想滤波器的单位取样响应用合适的窗函数截短成为有限长度的()h n ，使得h （n ）逼近理想的()d h n 。

以实现所设计的滤波器的频率响应()j H e ω 逼近于理想滤波器的频率响应()j d H e ω 。

一个有限长的序列，如果满足频率采样定理的条件，可以通过频谱的有限个采样点的值准确地恢复。

频率抽样法正是采用这种思想来设计FIR 数字滤波器。

a ．给定希望逼近的频率响应函数H d (e jw )。

b ．求单位脉冲响应c ．由过渡带宽及阻带最小衰减的要求，可选定窗形状，并估计窗口长度N 。

原则是在保证阻带衰减满足要求的情况下，尽量选择主瓣窄的窗函数。

d. 计算所设计的FIR 滤波器的单位脉冲响应e ．由h (n )求FIR 滤波器的系统函数 3.MATLAB 提供了fir1函数，以实现线性相位FIR 滤波器。

调用格式如下：hn=fir1(N, wc, ‘ftype’, window)参数：N ：阶数wc ：归一化的数字频率，0≤wc ≤1。

ftype ：滤波器类型，如高通、带阻等。

当ftype=high 时，设计高通FIR 滤波器；当ftype=stop 时，设计带阻FIR 滤波器。

应当注意，在设计高通和带阻滤波器时，阶数N 只能取偶数(h(n)长度N+1为奇数)。

实验三数字滤波实验

实验三数字滤波实验1.实验原理与线路(1)原理①见图3-1图3-1 数字滤波原理图计算机对含有干扰的正弦信号R （约0.5～1HZ ）通过U20采样输入，然后进行数字滤波处理，以保留正弦信号，去除干扰，最后送至U21变成模拟量C 输出。

(2)摸拟带有尖脉冲干扰的正弦信号用RC 电路将U1单元的555输出方波（S 端）微分，将此微分信号视作干扰，再用U2 SIN 单元产生的正弦波，两信号迭加，如图3-2。

注意R 点波形不要超过±5V ，以免数字化溢出。

(3)滤波器的计算要求设计一个相当于的数字滤波器，由一阶差分法可得近似式（注1）1)()1(-+-=k k Y a X a Y其中，Xk ：输入，Yk 输出，τTa =-1。

上式中a 的取值范围：0.00～0.99。

1-a 、a 的值要分别保存在2F00H 和2F03H 地址中，存入方法：在调试窗口使用 E[地址] 命令可对指定地址中的内容进行修改，假设a=0.95，这个值要保存在2F03H 地址中。

> E 2F03↙> 0000:2F03 = CC_95↙启动相应程序后则会将BCD 码“95”转换成二进制小数，再按算式进行定点小数运算。

采样信号由8253得到，8253定时5ms ，采样周期T 为：5⨯=K T T msTk 需保存在2F60H 地址中，取值范围：01H ～FFH ，对应T 的范围：5ms ～1275ms 。

1－a ，a ，Tk 的存储区见表3-1。

注1：理论推导算式为11)1(Y --+-=k k k aY X a ，实验采用的算式作了近似处理。

(5)线路接线见图3-2，图中接入1点的信号为正弦波，2点为干扰信号。

图3-2 数字滤波线路图2.实验程序流程：见图3-3图3-3 一阶惯性数字滤波程序流程图3.实验内容及步骤⑴按图3-2接线，调节U1信号源单元中的W11，使S端的方波周期约为0.2s；调节U2单元电位器，使其输出周期为1s、幅值为3V的正弦信号；调节图3-2电路图中1、2端对应的电位器，使R端波形符合图3-1所示输入信号的要求。

数字滤波器实验报告

数字滤波器实验报告数字滤波器实验报告引言：数字滤波器是一种通过对数字信号进行处理来滤除噪声或者改变信号频率特性的工具。

在信号处理领域，数字滤波器被广泛应用于音频处理、图像处理、通信系统等方面。

本实验旨在通过设计和实现数字滤波器，探索其在信号处理中的应用，并验证其性能和效果。

一、实验目的本实验的主要目的是：1. 了解数字滤波器的原理和基本概念；2. 学习数字滤波器设计的方法和技巧；3. 实现数字滤波器，并进行性能测试和分析。

二、实验原理数字滤波器是一种通过对离散时间信号进行加权和求和的方式来改变信号频率特性的工具。

它可以分为两大类：有限长冲激响应（FIR）滤波器和无限长冲激响应（IIR）滤波器。

FIR滤波器的特点是稳定性好、易于设计，而IIR滤波器则具有更高的效率和更窄的通带。

在数字滤波器设计中，常用的方法有窗函数法、频率抽样法、脉冲响应法等。

窗函数法是一种常见的FIR滤波器设计方法，它通过在频域上对滤波器的频率响应进行加窗来实现滤波效果。

频率抽样法则是一种用于设计IIR滤波器的方法，它通过将模拟滤波器的频率响应进行抽样来得到数字滤波器。

三、实验步骤1. 确定滤波器类型和性能指标：根据实际需求，选择合适的滤波器类型（FIR或IIR）和性能指标（通带增益、截止频率等）。

2. 设计滤波器：根据选择的滤波器类型和性能指标，采用相应的设计方法进行滤波器设计。

3. 实现滤波器：根据设计结果，使用编程语言（如MATLAB或Python）编写代码实现滤波器。

4. 信号处理：将待处理的信号输入滤波器，进行滤波处理。

5. 性能测试与分析：对滤波后的信号进行性能测试和分析，评估滤波器的效果和性能。

四、实验结果与分析在本次实验中，我们选择了FIR滤波器，并采用窗函数法进行设计。

根据要求，我们设计了一个低通滤波器，截止频率为1kHz，通带增益为1，阻带增益为-60dB。

经过实验测试，我们得到了滤波后的信号，并进行了频谱分析。

实验三无限冲激响应滤波器(IIR)算法实验

实验三无限冲激响应滤波器(IIR)算法实验一．实验目的1．掌握设计IIR 数字滤波器的原理和方法。

2．熟悉IIR 数字滤波器特性。

3．了解IIR 数字滤波器的设计方法。

二．实验设备PC 兼容机一台操作系统为Windows2000(或Windows98，WindowsXP，以下默认为Windows2000)安装Code Composer Studio 3.1 软件三．实验原理1．无限冲激响应数字滤波器的基础理论。

2．模拟滤波器原理（巴特沃斯滤波器、切比雪夫滤波器、椭圆滤波器、贝塞尔滤波器）。

3．数字滤波器系数的确定方法。

4．根据要求设计低通IIR 滤波器：要求：低通巴特沃斯滤波器在其通带边缘1kHz 处的增益为-3dB，12kHz 处的阻带衰30dB，采样频率25kHz。

设计：- 确定待求通带边缘频率fp1Hz、待求阻带边缘频率fs1Hz 和待求阻带衰减-20logδsdB。

模拟边缘频率为：fp1=1000Hz，fs1=12000Hz阻带边缘衰减为：-20logδs=30dB-用Ω=2πf/fs 把由Hz 表示的待求边缘频率转换成弧度表示的数字频率，得到Ωp1 和Ωs1。

Ωp1=2πfp1/fs=2π1000/25000=0.08π弧度Ωs1=2πfs1/fs=2π12000/25000=0.96π弧度- 计算预扭曲模拟频率以避免双线性变换带来的失真。

由w=2fs tan(Ω/2)求得wp1 和ws1，单位为弧度/秒。

wp1=2fs tan(Ωp1/2)=6316.5 弧度/秒ws1=2fs tan(Ωs1/2)=794727.2 弧度/秒- 由已给定的阻带衰减-20logδs 确定阻带边缘增益δs。

因为-20logδs=30，所以logδs=-30/20，δs=0.03162- 计算所需滤波器的阶数：因此，一阶巴特沃斯滤波器就足以满足要求。

- 一阶模拟巴特沃斯滤波器的传输函数为：H(s)=wp1/(s+wp1)=6316.5/(s+6316.5) 由双线性变换定义s=2fs(z-1)/(z+1)得到数字滤波器的传输函数为：因此，差分方程为：y[n]=0.7757y[n-1]+0.1122x[n]+0.1122x[n-1]。

信号系统实验数字滤波器实验(有数据)

实验：数字滤波器一、实验目的1.了解数字滤波器的作用与原理；2.了解数字滤波器的设计实现过程。

二、实验原理说明当我们仅对信号的某些分量感兴趣时，可以利用选频滤波器，提取其中有用的部分，而将其它滤去，滤波器的一项基本任务即对信号进行分解与提取。

三、实验设备1.双踪示波器 1台2.信号系统实验箱 1台四、实验步骤1.连接P04 和P101；2.调节信号源，使P04输出f=4KHz的正弦波，调节W701使信号幅度为4V；3.按下SW101按钮，使程序指示灯D3D2DlD0=0010,指示灯对应数字滤波；4.观察TP801输出的信号；5.试着将P04输出信号频率调节到5K, 6K, 7K……观察TP801输出信号的变化；6.测量不同频率下信号输出幅度的变化，画出滤波器的相应曲线；7.将正弦波改变成方波信号，调节频率从1K-8K,观察TP801信号的变化。

五、数据处理与分析输出信号频率图像f=4kHzCH2：信号源CH1：滤波器输出f=5kHzCH2：信号源CH1：滤波器输出f=6kHzCH2：信号源CH1：滤波器输出f=7kHzCH2：信号源CH1：滤波器输出输出信号频率图像f=4kHzCH2：信号源CH1：滤波器输出f=5kHzCH2：信号源CH1：滤波器输出f=6kHzCH2：信号源CH1：滤波器输出f=7kHzCH2：信号源CH1：滤波器输出六、实验总结1.原始信号频率不同时，相应的输出信号频率和幅度发生改变。

2.对比原始信号，输出信号发生了相应的相移，且当增大原始信号的频率，相移变化更大。

3.有一定的滤波作用，但不是理想的。

实验三 数字滤波实验

大学数字实验报告

IIR数字滤波器设计实验报告

华南理工大学数字信号处理实验三实验报告

滤波器实验

数字信号处理Matlab实验三-IIR数字滤波器的设计

数字滤波器设计实验报告

实验三FIR数字滤波器设计

数字滤波器的设计实验

数字信号处理--实验三

实验三： 数字滤波器设计

实验三IIR滤波器的设计与信号滤波

数字图像处理实验三中值滤波和均值滤波实验报告

实验三IIR数字滤波器设计及软件实现

数字信号处理 实验三 FIR数字滤波器的设计

实验三 数字滤波实验

数字滤波器实验报告

实验三 无限冲激响应滤波器(IIR)算法实验

信号系统实验数字滤波器实验(有数据)

实验三数字滤波实验

实验三：数字滤波器设计

数字信号处理实验三 FIR数字滤波器的设计

实验三数字滤波实验

实验三无限冲激响应滤波器(IIR)算法实验