(通用版)201x年中考数学总复习 第一章 数与式 第1讲 实数及其运算(讲本)
(江西专用)201x中考数学总复习 第一部分 教材同步复习 第一章 数与式 第1讲 实数及其运算

3.141 5精确到0.01为3.14,精确到千分位为3.142.
6.用科学记数法表示下列各数. 384 000=_3_.8_4_×__1_0_5, 1 000 亿=_1_×__1_0_11__,0.001 293=__1_.2_9_3_× __结果为 2 090 万个,“2 090 万”这个数用科学记数法表示为__2_.0_9_×__1_0_7_________.
知识点四 实数的大小比较
直接比较法
数轴 比较法
正数>0>负数 (1)在数轴上,⑪___右____边的点所表示的数总比⑫__左_____ 边的点所表示的数大; (2)数轴上离原点越远的数绝对值⑬__越__大____; (3)数轴上字母比较大小时,可取特殊值判断其大小
绝对值
两个正数比较大小,绝对值大的数比较大;两个负数比较大小,
10.(2016·江西7题3分)计算:-3+2=___-__1___.
重难点 · 突破
重难点1 科学记数法 重点
例1 (2018·萍乡模拟)2018 年 1 月 4 日在萍乡市第十五届人民代表大会第三 次会议报告指出,去年我市城镇居民人均可支配收入 33 080 元,33 080 用科学记数 法可表示为___3_._3_0_8_×__1_0_4 ___.
(2)按性质分正 ④实 __0_数_ 负实数
2.正负数的意义:用来表示具有相反意义的量.如“比 0 高的得分与比 0 低的 得分”“零上温度与零下温度”“盈利额与亏损额”“收入与支出”都是具有相反 意义的量.
【注意】 0 既不是正数也不是负数.
1.实数 2,-3,12,-23,0.12,-0.2,0,+(-3.5),-π,-(-5),20%,(- 2)0,(13)-1,-|-4|中,正数有_2_,__12_,__0_._1_2_,__-__(_-__5_),_2_0_%__,__(_-__2_)_0 _,__(_13_)_-_1___,负数 有_-__3_,__-__23_,__-__0_._2_,__+__(-__3_._5_),__-__π__,__-__|-__4_|_________,既不是正数也不是负数的 是___0___.
中考数学通用版知识点梳理第一单元 数与式
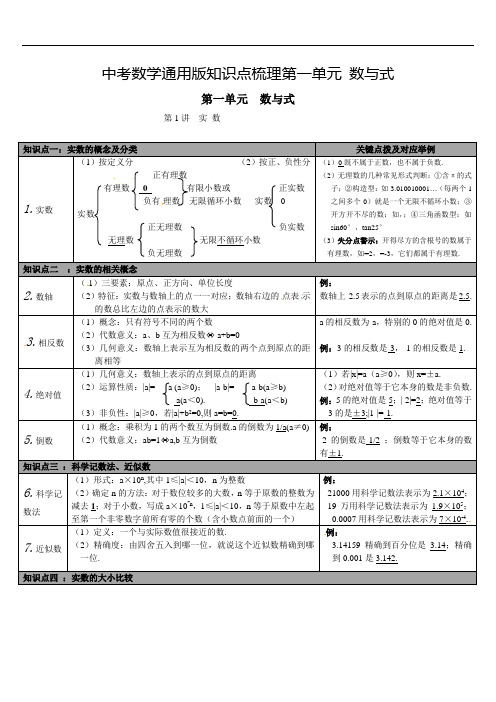
中考数学通用版知识点梳理第一单元数与式第一单元数与式第1讲实数(1)按定义分(2)按正、负性分正有理数有理数0 有限小数或正实数负有理数无限循环小数实数0实数正无理数负实数无理数无限不循环小数负无理数((((1)三要素:原点、正方向、单位长度(2)特征:实数与数轴上的点一一对应;数轴右边的点表示的数总比左边的点表示的数大例:数轴上3.相反数(((等于原数的整数为等于原数中左起例:21000用科学记数法表示为2.1³104;19万用科学记数法表示为1.9³105;0.0007用科学记数法表示为7³10-4.)精确度:由四舍五入到哪一位,就说这个近似数精确到哪例:3.14159精确到百分位是3.14;精确到0.001是3.142.第4讲二次根式知识点一:二次根式关键点拨及对应举例(1)二次根式的概念:形如a(a≥0)的式子.(2)二次根式有意义的条件:被开方数大于或等于0. (3)最简二次根式:①被开方数的因数是整数,因式是整式(分母中不含根号);②被开方数中不含能开得尽方的因数或因式失分点警示:当判断分式、二次根式组成的复合代数式有意义的条件时,注意确保各部分都有意义,即分母不为0,被开方数大于等于0等.例:若代数式11x-有意义,则x的取值范围是x>1.2.二次根式的性质(注意:初中阶段学过的非负数有:绝对值、偶幂、算式平利用二次根式的双重非负性解题:(1)值非负:当多个非负数的和为0时,可得各个非负数均为0.如1a++1b-=0,则a=-1,b=1.(2)被开方数非负:当互为相反数的两个数同时出现在二次根式的被开方数下时,可得这一对相反数的数均为0.如已知b= 1a-+1a-,则a=1,b=0.实数的(1)数轴比较法:数轴上的两个数,右边的数总比左边的数大.(2)性质比较法:正数>0>负数;两个负数比较大小,绝对值大的反而小.(3)作差比较法:a-b>0⇔a>b;a-b=0⇔a=b;a-b<0⇔a<b.(4)平方法:a>b≥0⇔a2>b2.例:例:(1)计算:1-2-6=_-7__;(-2)2=___4__;3-1=_1/3_;π0=__1__;(2)64的平方根是_±8__,算术平方根是__8_,立方根是__4__.失分点警示:类似“的算术平方根”计算错误. 例:相互对比填一填:16的算术平方根是4___,的算术平方根是___2__.算术平方根若x2=a(a≥0),则x=a±.其中a是算术平方根.先乘方、开方,再乘除,最后加减;同级运算,从左向右进行;如有括号,先做括号内的运算,按小括号、中括号、大括号一次进行.计算时,可以结合运算律,使问题简单化(2)两个重要性质:①(a)2=a(a≥0);②a2=|a|=()()a aa a⎧≥⎪⎨-<⎪⎩;(3)积的算术平方根:ab=a²b(a≥0,b≥0);(4)商的算术平方根:ab=ab(a≥0,b>0).例:计算:23.14=3.14;()22-=2;24=;=2 ;442939==注意:将运算结果化为最简二次根式.例:计算:3223⋅=1;323222==4.运算时,注意观察,有时运用乘法公式第2讲整式与因式分解二、知识清单梳理关键点拨及对应举例(1)代数式:用运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连接而成的式子,单独的一个数或一个字母也是代数式.(2)求代数式的值:用具体数值代替代数式中的字母,计算得出的结果,叫做求代数式的值.求代数式的值常运用整体代入法计算例:式单项式、项(1)单项式:表示数字与字母积的代数式,单独的一个数或一个字母也叫单项式.其中的数字因数叫做单项式的系数,所有字母的指数和叫做单项式的次数.(2)多项式:几个单项式的和.多项式中的每一项叫做多项式的项,次数最高的项的次数叫做多项式的次数.(3)整式:单项式和多项式统称为整式.(4)同类项:所含字母相同并且相同字母的指数也相同的项叫做同类项.所有的常数项都是同类项.例:(1)下列式子:①-2a2;②3a-5b;③x/2;④2/x;⑤7a2;⑥7x2+8x3y;⑦2017.其中属于单项式的是①③⑤⑦;多项式是②⑥;同类项是①和⑤.(2)多项式7m5n-11mn2+1是六次三项式,常数项是__1 .所得的结果作为系数,字母和字母的指“-”,失分警示:去括号时,如果括号外面是符号,一定要变号,且与括号内每一项相乘,不要有漏项.例:-2(3a-2b-1)=-6a+4b+2.(1)计算时,注意观察,善于运用它们的逆运算解决问题.例:已知2m+n=2,则3³2m³2n=6.(2)在解决幂的运算时,有时需要先化成同底数.例:2m²4m=23m.式乘运(1)单项式×单项式:①系数和同底数幂分别相乘;②只有一个字母的照抄.(2)单项式×多项式:m(a+b)=ma+mb.(3)多项式×多项式: (m+n)(a+b)=ma+mb+na+nb.(4)单项式÷单项式:将系数、同底数幂分别相除.(5)多项式÷单项式:①多项式的每一项除以单项式;②商相加.失分警示:意不能漏乘,不能丢项,不能出现变号错例:22注意乘法公式的逆向运用及其变形公式的运用注意计算顺序,应先算乘除,后算加减;若为化简求值,一般步骤为:化简、代入替换、计算.例:知识点五:因式分解7.因式分解(1)定义:把一个多项式化成几个整式的积的形式.(2)常用方法:①提公因式法:ma+mb+mc=m(a+b+c).②公式法:a2-b2=(a+b)(a-b);a2±2ab+b2=(a±b)2.(3)一般步骤:①若有公因式,必先提公因式;②提公因式后,看是否能用公式法分解;③检查各因式能否继续分解.(1)(2)第3讲分式三、知识清单梳理(2)最简分式:分子和分母没有公因式的分式.的(1)无意义的条件:当B=0时,分式BA无意义;(2)有意义的条件:当B≠0时,分式BA有意义;(3)值为零的条件:当A=0,B≠0时,分式BA=0.失分点警示:在解决分式的值为0,求值的问题时,一定要注意所求得的值满足分母不为0例:当211xx--的值为0时,则x=-1.A A C⋅A C÷的(1)同分母:分母不变,分子相加减.即ac±bc=a±bc;(2)异分母:先通分,变为同分母的分式,再加减.即ab±cd=ad±bcbd.例:6.分式的乘除法(1)a c ac a c ad(3)⎝⎭的混合运算(1)仅含有乘除运算:首先观察分子、分母能否分解因式,若能,就要先分解后约分.(2)含有括号的运算:注意运算顺序和运算律的合理应用.一般先算乘方,再算乘除,最后算加减,若有括号,先算括号里面的.失分点警示:分式化简求值问题,要先将分式化简到最简分式或整式的形式,再代入求值.代入数值时注意要使原分式有意义.有时也需运用到整体代入.。
中考数学第一轮章节复习课件01第一章 第一节实数及其运算

②减法:a-b=a+ _(_-__b_)_.
③乘法:a·b=ab;(-a)·(-b)=__a_b__;a·(-b)=-ab;0·a=
_0_. ④除法:a÷b=a· 1 (b≠0);0÷b=0(b≠0).
b (2)乘方运算
幂的符号的确定 正数的任何次幂都是正数;负数的奇次幂是负数,负数的偶次幂是正 数.
7.计算:23- 4 =_6_.
8.计算:(-1)2-2-1+ 9-( 解:原式=1- 1+3-1= 5.
)0. 3
2
2
(2)|a|=
即正数的绝对值是它本身,0的绝对值是
-a __0__,负数的绝对值是它的 _相__反__数__.
(3)一个数的绝对值是非负数,即|a|≥0.
(4)若|x|=a成立,则a≥0且x=±a.
❹倒数 (1)乘积为__1__的两个数互为倒数; (2)若a,b互为倒数,则ab=__1__; (3)非零实数a的倒数是 1,0没有倒数;1的倒数是1,-1的倒数是-1.
知识点六 平方根、算术平方根、立方根
知识点七 非负数
①常见的非负数有 a(a≥0),|a|,a2. ②几个非负数的和为0,则这几个非负数同时为0.例如:若|a|+b2+ c =0,则|a|=b2= c =0.
考点一 实数的有关概念
例1(2018·江西)-2的绝对值是( )
A.-2
B.2
C.- 1
相反数的确定方法 (1)定义法:判断两个数是否互为相反数,关键看这两个数除了符号外, 其余是否均相同; (2)运算法:若a,b互为相反数,则a+b=0; (3)性质法:非零实数a的相反数是-a.
❸绝对值 (1)在数轴上,一个数所对应的点与原点的 _距__离__叫做这个数的绝对值,
通用中考数学总复习第一章数与式第1节实数的有关概念及运算课件新人教版53

◆教材回顾 ◆Biblioteka 破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
中考数学总复习 第一部分 基础篇 第一章 数与式 考点1 实数的概念与运算数学课件

第一章 数 与 式
1 实数(shìshù)的概念与 运算
12/12/2021
第一页,共十二页。
目标(mùbiāo)方向
实数的有关概念与运算是中学数学重要的基础知识与
基本技能,大多以选择题、填空题的形式(xíngshì)直接考 查实数的概念(如相反数、倒数、绝对值、无理数等) 、科学记数法、对实数运算法则的理解与运用,有时 也以解答题的形式考查实数的混合运算.
12/12/2021
第二页,共十二页。
考点聚焦
考点(kǎo diǎn)一 实数的分类
12/12/2021
第三页,共十二页。
考点(kǎo diǎn)二 数轴、相反数、绝对值、倒数
12/12/2021
第四页,共十二页。
考点(kǎo diǎn)三 科学记数法与近似数
12/12/2021
第五页,共十二页。
解答题的形式考查实数的混合运算.。考点一 实数的分类。考点二 数轴、相反数、绝对值、倒 数。考点三 科学记数法与近似数。考点四 实数大小的比较
Image
12/12/2021
第十二页,共十二页。
考点四 实数(shìshù)大小的比较
12/12/2021
第六页,共十二页。
12/12/2021
第七页,共十二页。
考点五 实数(shìshù)的运算
12/12/2021
第八页,共十二页。
真题探源
12/12/2021
ห้องสมุดไป่ตู้
第九页,共十二页。
12/12/2021
第十页,共十二页。
12/12/2021
第十一页,共十二页。
内容(nèiróng)总结
中考数学总复习 第一章 数与式 第1节 实数的有关概念及运算课件

12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点Байду номын сангаас 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
12/9/2021 ◆教材回顾 ◆突破考点(考点一 考点二 考点三 考点四 考点五 考点六)
中考数学复习 第一章 数与式 第1课 实数课件

解:原式=2×9 -(-12) =18+12 =30.
9.计算: (2) 4-22×5-(-2.8)÷7;
解:原式= 4-4×5-(-0.4) = 4-20 + 0.4 =-16 + 0.4 =-15.6
(3)
2 2 2 2
0
5
1
16
解:原式=
2
1 2
2.实数的运算: (1)加法:同号两数取相相加同,的__符__号__,__并__把___________ __绝__对__值__相__加______,异号两数取相绝加对,值_较__大__的__符__号__,___ __并__把__较__大__的__绝__对__值__减__去__较__小__的__绝__对__值______________
3.三类非负数(请在下列横线上填“≥”“≤”“>”或“<”) (1) |a| __≥______0. (2) a2n ___≥_____0 (n是正整数). (3) a____≥____0 (a ≥ 0)
二、例题与变式
【考点1】实数的有关概念 例1.已知a,b是互为相反数,c,d互为倒数, 求 cd a b 1 的值
2
1
1 4
= 2 1 1 1
44
=1
(4)
1 3
1
3
64
3 2 1 12
解:原式= 3 4 2 3 (1 12)
= 1 3 2 1 2 3
= 23 3
2. 25的平方根是 ___5___;
4 9
2
的算术平方根是__3____;
27的立方根是___3___;-27的立方根是__-__3__.
中考数学复习 第一部分 中考基础复习 第一章 数与式 第1讲 实数课件

(1)几何意义:数轴上表示数的点与原点的距离.
绝对值 (2)|a|=a-aa≥a0<,0.
(3)|a|≥0
倒数
(1)a 与 1 (a≠0)互为倒数;0 没有倒数. a
(2)a,b 互为倒数⇔ab=1
(续表)
知识点
内容
比较实 数的 大小
(1)在数轴上,右边的数大于左边的数. (2)正数大于零,零大于负数.
第一部分 中考基础复习
第一章 数与式
第1讲 实数
1.理解实数的意义,能用数轴上的点表示实数,会比较实 数的大小.
2.借助数轴理解相反数和绝对值的意义,会求实数的相反 数与绝对值(绝对值符号内不含字母).
3.会用科学记数法表示数(包括在计算器上表示). 4.理解乘方的意义,掌握实数的加、减、乘、除、乘方及 简单的混合运算(以三步为主).
解:原式=-1+2 3× 23-4+1=-1+3-4+1=-1.
科学记数法
6.(2017 年天津)据《天津日报》报道,天津市社会保障制
度更加成熟完善,截至 2017 年 4 月末,累计发放社会保障卡
12 630 000 张.将 12 630 000 用科学记数法表示为( )
A.0.1263×108
(3)两个负数,绝对值大的反而小. (4)比较无理数的方法:①估算法;②平方法;③作差法等
(1)形式:a×10n ,其中 1≤|a|<10,n 是整数. (2)注意:若|a|≥1,则 n 是 a 整数位数减 1,也是小数点向
左移动的位数;
科学记 数法
若|a|<1,则 n 是 a 从左向右第一个不为 0 的数字前所有 0 的个数相反数,也是小数点向右移动的位数(n 是整数)
中考数学复习 第1章 数与式 第1讲 实数课件

2.平方根、算术(suànshù)平方根和立方根
2021/12/9
第四页,共二十六页。
考点3 实数的大小(dàxiǎo)比较 6年1考
常用方法
基本内容
注意事项
基本法则法
正实数都① 大于 0,负实数都 ② 小于 0;正实数③ 大于 一切负实数,两个负实数比较, 绝对值大的反而④ 小
除了基本法则、 数轴比较对于所 有实数都适用外, 其他几种方法在
2021/12/9
第二十一页,共二十六页。
10.[2016·潍坊,4,3分]近日,记者从潍坊市统计局获悉,2016年第一
季度潍坊全市实现生产总值1256.77亿元.将1256.77亿用科学记数法可表
示为(精确(jīngquè)到百亿位)( )
B
A.1.2×1011 B.1.3×1011
C.1.26×1011 D.0.13×1012
A.3.D1×104 B.0.31×105 C.3.06×104 D.3.07×104
得分要领(yàolǐng)►用科学记数法表示较小的数,一般形式为a×10-n ,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数 所决定.
2021/12/9
第二十五页,共二十六页。
内容 总结 (nèiróng)
【例1】[2017·菏泽(hé zé)中考]
的相反数是( B )
2021/12/9
第八页,共二十六页。
类型2 实数(shìshù)与数轴
【例2】[2017·北京中考]实数a,b,c,d在数轴上的对应点的位置(wèi
zhi)如图所示,则正确的结论是( )
C
A.a>-4 B.bd>0 C.|a|>|b| D.b+c>0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A. 5 B.2 C.0 D.-1
4.(2018·台州)比-1 小 2 的数是( D)
A.3 B.1 C.-2 D.-3
.
5.(2018·宁波)2018 中国(宁波)特色文化产业博览会于 4
月 16 日在宁波国际会展中心闭幕.本次博览会为期四天,参
观总人数超 55 万人次,其中 55 万用科学记数法表示为(B )
7 A.11
B.-171
11 C. 7
D.-171
.Leabharlann ..对应训练
6.(2018·嘉兴)2018 年 5 月 25 日,中国探月工程的“鹊桥
号”中继星成功运行于地月拉格朗日 L2 点,它距离地球约
1500000 km,数 1500000 用科学记数法表示为( B )
A.15×105
B.1.5×106
.
与数轴相关的问题 例 1.(2018·北京)实数 a,b,c 在数轴上的对应点的位置
如图所示,则正确的结论是( B )
A.|a|>4 C.ac>0
B.c-b>0 D.a+c>0
.
题组训练 1.(2018·贵阳)如图,数轴上有三个点 A,B,C,若点 A,
B 表示的数互为相反数,则图中点 C 对应的数是( C )
.
题组训练 2.(2018·黔南州)计算:|-2|-2cos60°+(16)-1- (2018- 3)0. 解:原式=2-2×12+6-1=2-1+6-1=6.
.
实数中的数字规律问题
例 3.(2018·咸宁)按一定顺序排列的一列数叫做数列,如
数列:12,16,112,210,…,则这个数列前 2018 个数的和
为
.
.
题组训练
3.(2018·黔南州)根据下列各式的规律,在横线处填空:
11+12-1=12,13+14-12=112,15+16-13=310,17+18-14=
516,…,20117+20118-
=2017×12018.
.
4.(2018·泰安)观察“田”字格中各数之间的关系:
则 c 的值为 270或28+14.
.
1.(2018·绍兴)如果向东走 2 m 记为+2 m,则向西走 3 m
可记为( C )
A.+3 m B.+2 m C.-3 m D.-2 m
2.(2018·哈尔滨)-57的绝对值是( A )
5 A.7
7 B.5
C.-57
D.-75
.
3.(2018·温州)给出四个实数 5,2,0,-1,其中负数
C.0.15×107
D.1.5×105
.
7.(2018·张家界)目前世界上能制造的芯片最小工艺水 平是 5 纳米,而我国能制造芯片的最小工艺水平是 16 纳 米,已知 1 纳米=10-9 米,用科学记数法将 16 纳米表示
为 1.6×10-8 米.
.
.
.
对应训练
8.(2018·金华)在 0,1,-12,-1 四个数中,最小的数是( D )
;(6)(-13)-2= 9
.
.
.
.
.
对应训练
1.下列说法错误的是( C )
A.0 不是正数也不是负数 B.3.14 是正有理数 C.-272是负无理数 D.有理数和无理数统称为实数
.
.
.
.
对应训练
2.(2018·乐山)如图,在数轴上,点 A 表示的数为-1,点
B 表示的数为 4,C 是点 B 关于点 A 的对称点,则点 C 表示
的数为 -6
.
.
3.(1)(2018·杭州)|-3|=( A )
A.3
B.-3
1 C.3
D.-13
(2)(2018·眉山)绝对值为 1 的实数共有( C )
A.0 个 B.1 个 C.2 个
D.4 个
.
4.如果 a 与-2 互为相反数,那么 a 等于( B )
A.-2
B.2
C.-12
1 D.2
5.(2018·陕西)-171的倒数是( D )
A.-2
B.0
C.1
D.4
.
实数的运算 例 2.(2018·齐齐哈尔)计算:(12)-2+( 3- 7)0-2cos60°- |3-π|.
【思路方法】直接利用负指数幂的性质以及零指数幂的性质和特 殊角的三角函数值以及绝对值的性质分别化简得出答案.
解:原式=4+1-2×12-(π-3)=5-1-π+3=7-π.
A.0 B.1 C.-12 D.-1
.
.
.
.
对应训练
9.(2018·铜仁)9 的平方根是( C )
A.3
B.-3
C.3 和-3
D.81
.
10.(2018·安顺)4 的算术平方根是( D )
A.± 2 B. 2 C.±2 D.2
11.(2018·上海)-8 的立方根是 -2
.
.
.
.
对应训练 12.(2018·绍兴)计算:2tan60°- 12-( 3-2)0+(13)-1. 解:原式=2 3-2 3-1+3=2
.
8.(2018·常德)已知实数 a,b 在数轴上的位置如图所示,
下列结论中正确的是( D )
A.a>b C.ab>0
B.|a|<|b| D.-a>b
.
中考失分点 1:负整数指数幂的运算
(1)2-2=
;(2)(-2)-2=
;
(3)(12)-2=
4 ;(4)(-12)-2= 4 ;
(5)(13)-2= 9
A.0.55×106
B.5.5×105
C.5.5×104
D.55×104
.
6.(2018·聊城)下列实数中的无理数是( C )
A. 1.21
3 B.
-8
3 -3 C. 2
22 D. 7
.
7.若方程(x-5)2=19 的两根为 a 和 b,且 a>b,则下列
结论中正确的是( C)
A.a 是 19 的算术平方根 B.b 是 19 的平方根 C.a-5 是 19 的算术平方根 D.b+5 是 19 的平方根
