高中数学直线与方程知识点归纳与常考题型专题练习(附解析)
高中直线与方程练习题及讲解

高中直线与方程练习题及讲解### 高中直线与方程练习题及讲解题目一:直线方程的求解题目描述:已知点A(2,3)和点B(-1,-2),求经过这两点的直线方程。
解题步骤:1. 首先,我们需要找到直线的斜率。
斜率公式为 \( k = \frac{y_2- y_1}{x_2 - x_1} \)。
2. 将点A和点B的坐标代入公式,得到 \( k = \frac{-2 - 3}{-1 - 2} = \frac{-5}{-3} = \frac{5}{3} \)。
3. 有了斜率,我们可以使用点斜式方程 \( y - y_1 = k(x - x_1) \) 来写出直线方程。
选择点A代入,得到 \( y - 3 = \frac{5}{3}(x - 2) \)。
4. 最后,将方程化为一般形式 \( Ax + By + C = 0 \),得到 \( 5x - 3y + 1 = 0 \)。
题目二:直线的平行与垂直题目描述:已知直线 \( l_1: 3x - 4y + 5 = 0 \),求与 \( l_1 \) 平行且与直线 \( 2x + y - 7 = 0 \) 垂直的直线方程。
解题步骤:1. 平行直线的斜率相同,所以 \( l_1 \) 的斜率为 \( k =\frac{3}{4} \)。
2. 垂直直线的斜率互为相反数的倒数,因此 \( l_1 \) 垂直的直线斜率为 \( -\frac{4}{3} \)。
3. 利用点斜式方程,我们可以选择直线 \( l_1 \) 上的一点,比如\( (0, 5/4) \),代入 \( y - y_1 = k(x - x_1) \),得到 \( y - \frac{5}{4} = -\frac{4}{3}(x - 0) \)。
4. 将方程化为一般形式,得到 \( 4x + 3y - 15 = 0 \)。
题目三:直线的交点题目描述:求直线 \( l_1: 2x + 3y - 6 = 0 \) 与直线 \( l_2: x - y + 1 = 0 \) 的交点坐标。
直线与方程知识点与练习试题
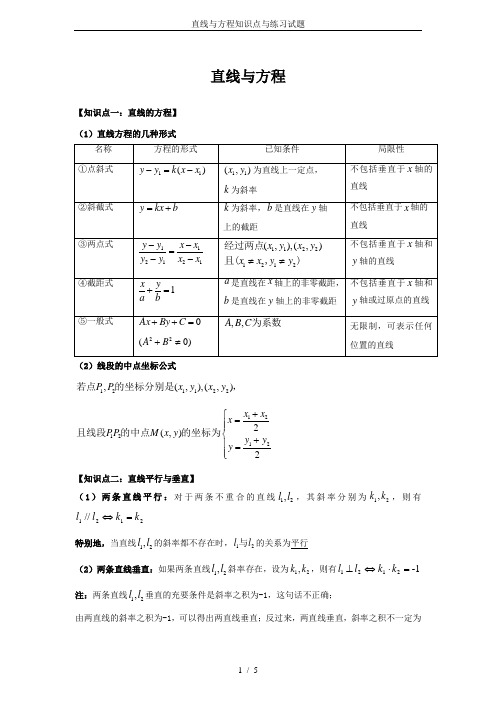
直线与方程【知识点一:直线的方程】 (1)直线方程的几种形式(2)线段的中点坐标公式121122,(,),(,)P P x y x y 若点的坐标分别是,1212122(,)2x x x PP M x y y y y +⎧=⎪⎪⎨+⎪=⎪⎩且线段的中点的坐标为 【知识点二:直线平行与垂直】(1)两条直线平行:对于两条不重合的直线12,l l ,其斜率分别为12,k k ,则有2121 // k k l l =⇔特别地,当直线12,l l 的斜率都不存在时,12l l 与的关系为平行(2)两条直线垂直:如果两条直线12,l l 斜率存在,设为12,k k ,则有1- 2121=⋅⇔⊥k k l l 注:两条直线12,l l 垂直的充要条件是斜率之积为-1,这句话不正确;由两直线的斜率之积为-1,可以得出两直线垂直;反过来,两直线垂直,斜率之积不一定为-1。
如果12,l l 中有一条直线的斜率不存在,另一条直线的斜率为0时,12l l 与互相垂直.【知识点三 直线的交点坐标与距离】 (1)两条直线的交点设两条直线的方程是1111:0l A x B y C ++=, 2222:0l A x B y C ++=两条直线的交点坐标就是方程组1112220A x B y C A x B y C ++=⎧⎨++=⎩的解。
①若方程组有唯一解,则这两条直线相交,此解就是交点的坐标; ②若方程组无解,则两条直线无公共点,此时两条直线平行. (2)几种距离两点间的距离:平面上的两点111222(,),(,)P x y P x y 间的距离公式12||PP =特别地,原点(0,0)O 与任一点(,)P x y的距离||OP =点到直线的距离:点00(,)o P x y 到直线0Ax By C ++=的距离d =两条平行线间的距离:两条平行线1200Ax By C Ax By C ++=++=与间的距离d =一、疑难辨析判断下列结论的正误.(正确的打“√”,错误的打“×”) 1.直线的倾斜角越大,其斜率越大.( )2.斜率公式k =y 2-y 1x 2-x 1,不适用于垂直于x 轴和平行于x 轴的直线.( )3.当直线的斜率不存在时,其倾斜角存在.( )4.过点P (x 1,y 1)的直线方程一定可设为y -y 1=k (x -x 1).( ) 5.直线方程的截距式x a +yb =1中,a ,b 均应大于0.( ) 二、选择题1.已知直线l 的斜率为-33,那么直线l 的倾斜角是( ) A .60° B .120° C .30° D .150°2直线l 经过原点O 和点P (-1,-1),则它的倾斜角是( )A .45°B .135°C .135°或225°D .0°3过点M (-2,m ),N(m ,4)的直线的斜率等于1,则m 的值为( )A .1B .4C .1或3D .1或44直线l 过点A (1,2)且不过第四象限,那么直线l 的斜率的取值范围为( )A .[0,2]B .(0,2)C .⎣⎡⎦⎤0,12D .⎝⎛⎭⎫0,12 5.中直线l 1、l 2、l 3的斜率分别为k 1、k 2、k 3,则 ( )A .k 1<k 2<k 3B .k 3<k 1<k 2C .k 3<k 2<k 1D .k 1<k 3<k 26经过点(1,3)且斜率不存在的直线方程为( )A .x =1B .x =3C .y =1D .y =3 7.已知点A (-3,4)和B (0,b ),且|AB |=5,则b 等于( )A .0或8B .0或-8C .0或6D .0或-6 8将方程3x -2y +1=0化成斜截式方程为( )A .y =23x +12B .y =32x +12C .y =32x +1D .y =23x +19直线l 过点(-1,2)且与直线2x -3y +4=0垂直,则l 的方程是( )A .3x +2y -1=0B .3x +2y +7=0C .2x -3y +5=0D .2x -3y +8=0直线l 过点(-1,2)且与直线2x -3y +4=0平行,则l 的方程是10直线l 1:ax -y +b =0,l 2:bx +y -a =0(ab ≠0)的图象只可能是( )11已知A (2,0),B (3,3),直线l ∥AB ,则直线l 的斜率k =( )A .-3B .3C .-13D .1312已知直线l 1的斜率为0,且l 1⊥l 2,则l 2的倾斜角为( ) A .0° B .135° C .90° D .180°13点P(2,5)关于直线x+y=0的对称点的坐标是()A.(5,2) B.(2,5)C.(-5,-2) D.(-2,5)14.经过直线2x-y+4=0与x-y+5=0的交点,且垂直于直线x-2y=0的直线方程是()A.2x+y-8=0 B.2x-y-8=0C.2x+y+8=0 D.2x-y+8=0三填空题15已知l1⊥l2,直线l1的倾斜角为60°,则直线l2的倾斜角为________.16直线l的方程为y-m=(m-1)(x+1),若l在y轴上的截距为7,则m=________.17倾斜角为30°,且过点(0,2)的直线的斜截式方程为________.18已知直线l1过点P(2,1)且与直线l2:y=x+1垂直,则l1的点斜式方程为________.19.直线y=kx+2(k∈R)不过第三象限,则斜率k的取值范围是________.20.直角坐标平面上连接点(-2,5)和点M的线段的中点是(1,0),那么点M到原点的距离为________.21.方程mx+(m2+m)y+4=0表示一条直线,则实数m≠________.22.已知直线l1过点A(-2,3),B(4,m),直线l2过点M(1,0),N(0,m-4),若l1⊥l2,则常数m的值是____________.四、解答题23经过两条直线2x-3y+10=0和3x+4y-2=0的交点,且垂直于直线3x-2y+4=0的直线的方程为________.24.已知A(1,-1),B(2,2),C(3,0)三点,求点D的坐标,使直线CD⊥AB,且CB∥A D.限时训练1.(2,1),B (3,-1)两点连线的斜率为( )A .-2B .-12C .12D .22.直线y =2x +10,y =x +1,y =ax -2交于一点,则a 的值为( )A .12B .-12C .23D .-233.直线y =-2x -1的斜率与纵截距分别为( )A .-2,-1B .2,-1C .-2,1D .2,14若过两点P (6,m )和Q(m ,3)的直线与斜率为12的直线M N 平行,则m 的值为( )A .5B .4C .9D .05经过两条直线2x -3y +10=0和3x +4y -2=0的交点,且垂直于直线3x -2y +4=0的直线的方程为________.。
(完整版)高一数学直线方程知识点归纳及典型例题

直线的一般式方程及综合【学习目标】1.掌握直线的一般式方程;2.能将直线的点斜式、两点式等方程化为直线的一般式方程,并理解这些直线的不同样形式的方程在表示直线时的异同之处;3.能利用直线的一般式方程解决有关问题. 【要点梳理】要点一:直线方程的一般式关于 x 和 y 的一次方程都表示一条直线.我们把方程写为 Ax+By+C=0 ,这个方程 (其中 A 、B 不全为零 )叫做直线方程的一般式.要点讲解:1.A 、 B 不全为零才能表示一条直线,若 A 、 B 全为零则不能够表示一条直线 .当 B ≠0时,方程可变形为 yA x C ,它表示过点 0,C,斜率为A的直线.B BBB当 B=0 , A ≠0时,方程可变形为Ax+C=0 ,即 xCx 轴垂直的直线.,它表示一条与A由上可知,关于 x 、 y 的二元一次方程,它都表示一条直线.2.在平面直角坐标系中,一个关于x 、y 的二元一次方程对应着唯一的一条直线,反过来,一条直线可以对应着无数个关于 x 、y 的一次方程 (如斜率为 2,在 y 轴上的截距为 1 的直线,其方程能够是 2x ―y+1=0 ,也能够是 x 1 y 1 0 ,还可以够是 4x ― 2y+2=0等.)2 2要点二:直线方程的不同样形式间的关系 直线方程的五种形式的比较以下表:名称方程的形式 常数的几何意义适用范围 点斜式y ―y( x 1, y 1)是直线上必然点, k 是斜率 不垂直于 x 轴1=k(x ―x 1)斜截式y=kx+bk 是斜率, b 是直线在 y 轴上的截距不垂直于 x 轴 两点式y y 1 x x 1 ( x 1, y 1 ),(x 2 ,y 2)是直线上两定点不垂直于 x 轴和 y 轴y 2 y 1x 2x 1截距式x y a 是直线在 x 轴上的非零截距,b 是直不垂直于 x 轴和 y 轴,a1线在 y 轴上的非零截距b且但是原点 一般式Ax+By+C=0 ( A 2+B 2≠0) A 、B 、 C 为系数任何地址的直线要点讲解:在直线方程的各种形式中,点斜式与斜截式是两种常用的直线方程形式,要注意在这两种形式中都要求 直 线 存 在 斜 率 , 两 点 式 是 点 斜 式 的 特 例 , 其 限 制 条 件 更 多 ( x 1≠x 2, y 1 ≠y 2), 应 用 时 若 采 用 (y 2―y 1)(x ―x 1) ― (x 2―x 1)(y ―y 1)=0 的形式,即可除掉限制性.截距式是两点式的特例,在使用截距式时,第一要判断可否满足 “直线在两坐标轴上的截距存在且不为零 ”这一条件.直线方程的一般式包含了平面上的所有直线形式.一般式常化为斜截式与截距式.若一般式化为点斜式,两点式,由于取点不同样,获取的 方程也不同样.要点三:直线方程的综合应用1.已知所求曲线是直线时,用待定系数法求.2.依照题目所给条件,选择合适的直线方程的形式,求出直线方程.关于两直线的平行与垂直,直线方程的形式不同样,考虑的方向也不同样.( 1)从斜截式考虑已知直线 l 1 : y k 1 x b 1 , l 2: y k 2 x b 2 ,l 1 // l 2 1 2k 1 k 2 (b 1 b 2 ) ;l 1 l 2tancot1 k 1k 211212k 12k 2于是与直线 y kx b 平行的直线能够设为 ykx b 1 ;垂直的直线能够设为y1 x b2 . ( 2)从一般式考虑:kl 1 : A 1x B 1 y C 1 0, l 2 : A 2 x B 2 y C 2l 1 l 2 A 1 A 2 B 1B 2l 1 // l 2A 1B 2 A 2B 1 0且 A 1C 2 A 2C 1 0 或 B 1C 2 B 2C 1 0 ,记忆式( A 1 B 1C1 )A 2B 2C 2l 1 与 l 2 重合, A 1B 2 A 2 B 1 0 , A 1C 2 A 2C 1 0 , B 1C 2 B 2C 1 0于 是 与 直 线 Ax By C 0 平 行 的 直 线 可 以 设 为 AxBy D 0 ; 垂 直 的 直 线 可 以 设 为Bx Ay D0 .【典型例题】种类一:直线的一般式方程例 1.依照以下条件分别写出直线的方程,并化为一般式方程.1 (1)斜率是,经过点 A ( 8, ―2);2(2)经过点 B ( 4, 2),平行于 x 轴;(3)在 x 轴和 y 轴上的截距分别是3,―3;2(4)经过两点 P 1( 3,―2), P 2( 5, ―4).【答案】( 1) x+2y ―4=0 ( 2) y ―2=0 ( 3) 2x ―y ―3=0 ( 4) x y 1 0【剖析】( 1)由点斜式方程得 y( 2)1( x 8) ,化成一般式得 x+2y ― 4=0.2(2)由斜截式得 y=2,化为一般式得 y ―2=0 .(3)由截距式得xy1 ,化成一般式得 2x ―y ―3=0 .3 32(4)由两点式得y 2x3,化成一般式方程为x y 1 0 .4 ( 2)5 3【总结升华】本题主若是让学生领悟直线方程的各种形式,以及各种形式向一般式的转变,关于直线方程的一般式,一般作以下约定: x 的系数为正, x ,y 的系数及常数项一般不出现分数,一般按含 x 项、 y 项、常数项序次排列.求直线方程的题目,无特别要求时,结果写成直线方程的一般式.贯穿交融:【变式 1】已知直线 l 经过点 B(3, 1) ,且倾斜角是 30 ,求直线的点斜式方程和一般式方程.【答案】 y 13(x3) 3x 3y3 3 3 03【剖析】由于直线倾斜角是30 ,所以直线的斜率 ktantan 303 ,所以直线的点斜式方程3为: y 13(x 3) ,化成一般式方程为:3x 3 y 3 3 30 .3例 2. ABC 的一个极点为 A( 1, 4) , B 、 C 的均分线在直线y 1 0和 x y 10 上,求直线 BC 的方程 .【答案】 x 2 y3 0【剖析】由角均分线的性质知,角均分线上的任意一点到角两边的距离相等,所以可得 A 点关于B 的均分线的对称点 A ' 在 BC 上, B 点关于C 的均分线的对称点 B ' 也在 BC 上.写出直线 A ' B ' 的方程,即为直线 BC 的方程 .例 3.求与直线 3x+4y+1=0 平行且过点( 1, 2)的直线 l 的方程.【答案】 3x+4y ―11=0 【剖析】解法一:设直线l 的斜率为 k ,∵ l 与直线 3x+4y+1=0 平行,∴ k3 .4又∵ l 经过点( 1, 2),可得所求直线方程为 y 23(x 1) ,即 3x+4y ― 11=0.4解法二:设与直线 3x+4y+1=0 平行的直线 l 的方程为 3x+4y+m=0 ,∵ l 经过点( 1, 2),∴ 3×1+4×2+m=0 ,解得 m=―11 .∴所求直线方程为 3x+4y ―11=0 .【总结升华】( 1)一般地, 直线 Ax+By+C=0 中系数 A 、B 确定直线的斜率, 所以,与直线 Ax+By+C=0平行的直线可设为 Ax+By+m=0 ,这是常采用的解题技巧.我们称 Ax+By+m=0 是与直线 Ax+By+C=0 平行的直线系方程.参数m 能够取 m ≠C 的任意实数,这样就获取无数条与直线Ax+By+C=0平行的直线.当m=C 时, Ax+By+m=0 与 Ax+By+C=0 重合.(2)一般地,经过点 A (x 0 ,y 0),且与直线 Ax+By+C=0 平行的直线方程为 A(x ―x )+B(y ―y )=0 .(3)近似地有:与直线 Ax+By+C=0 垂直的直线系方程为Bx ―Ay+m=0 ( A , B 不同样时为零) .贯穿交融:【变式 1】已知直线 l 1 : 3mx+8y+3m-10=0 和 l 2 :x+6my-4=0 . 问 m 为何值时 :(1) l 1 与 l 2 平行( 2) l 1 与 l 2 垂直 . 【答案】( 1) m2 ( 2) m3【剖析】当 m0 时, l 1 : 8y-10=0 ; l 2 : x-4=0 , l 1 l 2当 m 0 时, l 1 : y3m 10 3m: y 1x4x 8 ; l 2 6m86m由 3m1 ,得 m2 ,由 10 3m 4 得 m 2 或 886m38 6m 3 3 而 (3m ) ( 1 ) 1无解8 6m2综上所述( 1) m, l 1 与 l 2 平行.( 2) m 0 , l 1 与 l 2 垂直.3【变式 2】 求经过点 A ( 2, 1),且与直线 2x+y ―10=0 垂直的直线 l 的方程. 【答案】 x - 2y=0【剖析】由于直线 l 与直线 2x+y ―10=0 垂直,可设直线 l 的方程为 x 2y m 0 ,把点 A (2,1)代入直线 l 的方程得: m0 ,所以直线 l 的方程为: x -2y=0 .种类二:直线与坐标轴形成三角形问题例 4.已知直线 l 的倾斜角的正弦值为3,且它与坐标轴围成的三角形的面积为6,求直线 l 的方程.5【思路点拨】知道直线的倾斜角就能求出斜率,进而引进参数—— 直线在 y 轴上的截距 b ,再依照直线与坐标轴围成的三角形的面积为 6,即可求出 b .也能够依照直线与坐标轴围成的三角形的面积为6,设截距式直线方程,进而得出1| ab | 6 ,再依照它的斜率已知,进而获取关于a ,b 的方程组,解之即可.3 x23 x【答案】 y3 或 y 344【剖析】解法一:设 l 的倾斜角为,由 sin33,得 tan.3544设 l 的方程为yx b ,令 y=0,得 x4 b .3∴直线 l 与 x 轴、 y 轴的交点分别为 4 ,( 0,b ).b,03∴ S1 4b | b | 2b 2 6 ,即 b 2=9,∴ b=±3.23 3故所求的直线方程分别为y 3 x 3 或 y3 x 3 .44解法二:设直线l 的方程为xy 1,倾斜角为,由 sin3 ,得 tan3 .a b541| a | | b |6a 4∴2b3 ,解得.b 3a4故所求的直线方程为x y 1或 xy 1.4 3 4 3【总结升华】( 1)本例中,由于已知直线的倾斜角(与斜率有关)及直线与坐标轴围成的三角形的面积(与截距有关) ,所以可选择斜截式直线方程,也可采用截距式直线方程,故有“题目决定解法 ”之说.(2)在求直线方程时,要合适地选择方程的形式,每种形式都拥有特定的结论,所以依照已知条件恰 当地选择方程的种类经常有助于问题的解决.比方:已知一点的坐标,求过这点的直线方程,平时采用点 斜式,再由其他条件确定该直线在y 轴上的截距;已知截距或两点,选择截距式或两点式.在求直线方程的过程中,确定的种类后,一般采用待定系数法求解,但要注意对特别情况的谈论,省得遗漏.贯穿交融:【变式 1】( 2015 春 启东市期中)已知直线m : 2x ― y ―3=0 , n :x+y ―3=0 .( 1)求过两直线 m ,n 交点且与直线 l : x+2y ―1=0 平行的直线方程; (2)求过两直线 m , n 交点且与两坐标轴围成面积为4 的直线方程.【思路点拨】( 1)求过两直线 m , n 交点坐标,结合直线平行的斜率关系即可求与直线l : x+2y ―1=0平行的直线方程;( 2)设出直线方程,求出直线和坐标轴的交点坐标,结合三角形的面积公式进行求解即可.【答案】( 1) x+2y ―4=0 ;( 2)2x y 3 0 x 2 【剖析】( 1)由y3 ,解得y,x 01即两直线 m , n 交点坐标为( 2, 1),设与直线 l : x+2y ―1=0 平行的直线方程为 x+2y+c=0 ,则 2+2×1+c=0,解得 c=―4, 则对应的直线方程为 x+2y ―4=0 ;(2)设过( 2, 1)的直线斜率为 k ,( k ≠0),则对应的直线方程为 y ―1= k(x ―2) ,令 x=0, y=1―2k ,即与 y 轴的交点坐标为 A ( 0, 1―2k ) 令 y=0,则 x2 1 2k 1 ,即与 x 轴的交点坐标为 B(2k 1,0) ,k kk 则△AOB 的面积 S1 | 2k 1||1 2k | 4 ,2 k即 (2k 1)2 8 k ,即 4k 24k 8 k1 0 ,若 k > 0,则方程等价为 4k 212k1 0 ,解得 k3 2 2或 k 3 2 2 ,22若 k < 0,则方程等价为 4k 24k1 0 ,解得 k1 .2综上直线的方程为y 11( x 2) ,或 y 13 2 2 ( x 2) ,或 y 13 2 2( x 2)222即 y1 x2 ,或 y3 2 23 2 2x 2 2 22 x 2 2 2 ,或 y22种类三:直线方程的本质应用例 6.( 2015 春 湖北期末)光辉从点 A ( 2,3)射出,若镜面的地址在直线 l : x+y+1=0 上,反射光辉经过 B ( 1, 1),求入射光辉和反射光辉所在直线的方程,并求光辉从 A 到 B 所走过的路线长.【思路点拨】求出点 A 关于 l 的对称点,就可以求出反射光辉的方程,进一步求得入射点的坐标,从而可求入射光辉方程,可求光辉从A 到B 所走过的路线长.【答案】 41【剖析】设点 A 关于 l 的对称点 A '( x 0, y 0),x 0 2 y 0 3 1 0 x 04∵AA '被 l 垂直均分,∴2 2 ,解得y 0 3y 03x 0 12∵点 A '(―4, ―3), B (1, 1)在反射光辉所在直线上, ∴反射光辉的方程为y 3 x4,即 4x ―5y+1=0,1 3 1 44x 5y 1 0( 2 ,1) . 解方程组x y 10 得入射点的坐标为3 3y 1x 2由入射点及点 A 的坐标得入射光辉方程为3 3,即 5x ―4y+2=0 ,31 2 233光辉从 A 到 B 所走过的路线长为 | A' B |( 4 1)2 ( 3 1)241 .【总结升华】本题要点观察点关于直线的对称问题,观察入射光辉和反射光辉,解题的要点是利用对称点的连结被对称轴垂直均分.线 贯穿交融:【变式 1】( 2016 春 福建厦门期中)一条光辉从点 A (- 4,- 2)射出,到直线y=x 反射到 y 轴上的 C 点,又被 y 轴反射,这时反射光辉恰好过点 D (- 1,6).求 【答案】 10x - 3y+8=0【剖析】如图, A (- 4,- 2), D (- 1,6),y=x 上的 B 点后被直BC 所在直线的方程.由对称性求得 A (- 4,- 2)关于直线 y=x 的对称点 A '(- 2,- 4), D 关于 y 轴的对称点 D '( 1, 6),则由入射光辉和反射光辉的性质可得:过 A ' D '的直线方程即为 BC 所在直线的方程.由直线方程的两点式得: y 4 x 2 . 整理得: 10x - 3y+8=0 .64 1 2例 7.如图,某房地产公司要在荒地ABCDE 上划出一块长方形土地(不改变方向)建筑一幢8 层的公寓,如何设计才能使公寓占地面积最大?并求出最大面积.(精确到 1 m 2)【答案】 6017【剖析】建立坐标系,则 B ( 30, 0), A ( 0, 20).∴由直线的截距方程获取线段AB 的方程为x y 1 (0≤ x ≤ )30.30 202x . 设点 P 的坐标为( x , y ),则有 y203∴公寓的占地面积为S (100 x) (80y) (100 x) (80 20 2x)2 x 2 20 x 6000 (0≤ x ≤ )30.3 3 3 ∴当 x=5 , y50 时, S 取最大值,最大值为 S2 52 20 5 6000 6017(m 2 ) .333即当点 P 的坐标为 (5,50) 时,公寓占地面积最大,最大面积为6017 m 2.3P 的地址由两个条件确定,一是 A 、 P 、 B 三点共线,【总结升华】本题是用坐标法解决生活问题,点 二是矩形的面积最大.借三点共线追求x 与 y 的关系,利用二次函数知识研究最大值是办理这类问题常用的方法.。
必修二第三章直线与方程知识点总结及练习(答案)

必修二第三章直线与方程(1)直线的倾斜角定义: x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。
特别地,当直线与x 轴平行或重合时 , 我们规定它的倾斜角为0 度。
所以,倾斜角的取值范围是0°≤α< 180°(2)直线的斜率①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率常用 k 表示。
即k tan。
斜率反应直线与轴的倾斜程度。
当直线 l与 x 轴平行或重合时 ,α =0° , k = tan0° =0;当直线 l与 x 轴垂直时 ,α = 90 ° , k不存在 .当0,90 时,k 0;当90 ,180时, k 0 ;当90时, k 不存在。
②过两点的直线的斜率公式: k y2y1 (x1x2 )( P1(x1,y1),P2(x2,y2),x1≠ x2 )x2x1注意下边四点: (1)当 x1x2时,公式右侧无心义,直线的斜率不存在,倾斜角为90°;(2)k 与 P1、 P2的次序没关;(3)此后求斜率可不经过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率获得。
(3)直线方程①点斜式:y y1k( x x1 ) 直线斜率k,且过点x1, y1注意:当直线的斜率为= 0°时, k=0,直线的方程是y y1。
当直线的斜率为90°时,直线的斜率不存在,它的方程不可以用点斜式表示.但因l 上每一点的横坐标都等于x ,所以它的方程是x=x 。
11②斜截式:y kx b ,直线斜率为k,直线在 y 轴上的截距为b③两点式:y y1x x1( x1 x2 , y1y2)直线两点x1, y1,x2, y2y2y1x2x1④截矩式:xy 1 此中直线l与 x 轴交于点 (a,0) ,与y轴交于点 (0,b) ,即l与 x 轴、y轴a b的截距分别为 a,b 。
高中数学直线与方程知识点归纳与常考题型专题练习(附解析)

高中数学直线与方程知识点归纳与常考题型专题练习(附解析) 知识点:一、直线与方程(1)直线的倾斜角定义:x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。
特别地,当直线与x 轴平行或重合时,我们规定它的倾斜角为0度。
因此,倾斜角的取值范围是0°≤α<180°(2)直线的斜率①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率常用k 表示。
即。
斜率反映直线与轴的倾斜程度。
tan k α=当时,; 当时,; 当时,不存[) 90,0∈α0≥k () 180,90∈α0<k 90=αk 在。
②过两点的直线的斜率公式: )(211212x x x x y y k ≠--=注意下面四点:(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90°;21x x =(2)k 与P 1、P 2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。
(3)直线方程①点斜式:直线斜率k ,且过点)(11x x k y y -=-()11,y x 注意:当直线的斜率为0°时,k=0,直线的方程是y =y 1。
当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示.但因l 上每一点的横坐标都等于x 1,所以它的方程是x =x 1。
②斜截式:,直线斜率为k ,直线在y 轴上的截距为bb kx y +=③两点式:()直线两点,112121y y x x y y x x --=--1212,x x y y ≠≠()11,y x ()22,y x ④截矩式:1x y a b+=其中直线与轴交于点,与轴交于点,即与轴、轴的截距分别为。
l x (,0)a y (0,)b l x y ,a b ⑤一般式:(A ,B 不全为0)0=++C By Ax 注意:各式的适用范围 特殊的方程如:○1○2平行于x 轴的直线:(b 为常数); 平行于y 轴的直线:(a 为常数);b y =a x =(5)直线系方程:即具有某一共同性质的直线(一)平行直线系平行于已知直线(是不全为0的常数)的直线系:0000=++C y B x A 00,B A (C 为常数)000=++C y B x A (二)过定点的直线系(ⅰ)斜率为k 的直线系:,直线过定点;()00x x k y y -=-()00,y x (ⅱ)过两条直线,的交点的直线系方程0:1111=++C y B x A l 0:2222=++C y B x A l 为(为参数),其中直线不在直线系中。
高二数学直线的方程知识点及习题

直线的方程知识点及习题知识点一 直线的点斜式方程1.方程()00y y k x x -=-由直线上一定点及其斜率确定,我们把这个方程叫做直线的点斜式方程,简称点斜式.适用于斜率存在的直线.2.如果直线过点()000,P x y ,且与y 轴垂直,这时倾斜角为0︒,tan 00︒=,即0k =,由点斜式,得直线方程为0y y =,如图3.2-1.3.如果直线过点()000,P x y ,且与x 轴垂直,此时它的倾斜角为90︒(直线与y 轴平行或重合),斜率不存在,它的方程不能用点斜式表示,这时直线方程表示为0x x =,如图3.2-2.知识点二 直线的点斜式方程(1)我们把直线l 与y 轴交点()0,b 的纵坐标b 叫做直线l 在y 轴上的截距.若直线l 的斜率为k ,且在y 轴上的截距为b ,则直线l 的方程为()0y b k x -=-,即y kx b =+,这个方程叫做直线的斜截式方程,简称斜截式.(2)斜截式与一次函数的解析式相同,都是y kx b =+的形式,但有区别,当0k ≠时,y kx b =+即为一次函数;当0k =时,y b =不是一次函数,一次函数y kx b =+()0k ≠必是一条直线的斜截式方程. 例1.已知直线y kx b =+,当34x -≤≤时,813y -≤≤.求此直线方程.(3)截距①直线的斜截式方程是由点斜式推导而来的.直线与y 轴的交点()0,b 的纵坐标b 称为此直线的纵截距.值得强调的是,截距可能是正数,也可能是负数,还可能是0,不能将其理解为“距离”而恒为非负数.②直线与x 轴的交点(),0a 的横坐标a 称为此直线的横截距.并不是每条直线都有横截距和纵截距,如直线1x =没有纵截距,直线2y =没有横截距.练习(1)直线123y x =-+的斜率是_________,在y 轴上的截距是________,在x 轴上的截距是_________;(2)倾斜角为60︒,在y 轴上的截距为3的直线方程是_________.例2 已知直线1l 的方程为23y x =-+,2l 的方程为42y x =-,直线l 与1l 平行且与2l 在y 轴上的截距相同,求直线l 的斜截式方程.练习,.已知直线l 过点(1,2)和(,)a b ,求其方程.本题常见的错误是没有对a 进行分类讨论,而是直接利用斜率公式求斜率,然后套用点斜式写直线方程.在利用点斜式或斜截式求直线方程时,要注意直线方程的点斜式00()y y k x x -=-和斜截式y kx b =+都是斜率k 存在的前提下才能使用的,要认真分析,避免遗漏.1. 直线的两点式方程的定义212y y y y --=121x x x x --就是经过两点111222(,),(,)p x y p x y (其中1212,x x y y ≠≠)的直线方程,我们把它叫做直线的两点式方程,简称两点式.2.若点12,p p 的坐标分别为1122(,),(,)x y x y ,是线段12p p 的中点M 的坐标为(,),x y 则有中点坐标公式:121222x x x y y y +⎧=⎪⎪⎨+⎪=⎪⎩.例3:已知三角形的三个顶点分别为(6,7),(2,3),(2,1)A B C --,求AC 边上的中线所在的直线方程.3 直线的截距式方程直线与x 轴的交点(,0)a 的横坐标a 叫做直线在x 轴上的截距,若此时直线在y 轴上的截距为b ,则直线的方程为1(0),x yab a b+=≠此方程由直线在两个坐标轴上的截距a 与b 确定,所以叫做直线的截距式方程. 求截距的方法在直线l 的方程中,令0x =,解出y 的直线,即得直线l 在y 轴上的截距.令y 0=,解出x 的值,即得出直线l 在x 轴上的截距.例4:求过点A (1,1),且在两坐标轴上的截距相等的直线方程.4 直线的一般式方程1.定义在平面直角坐标系中,每一条直线都可以用一个关于,x y 的二元一次方程表示,每一个关于,x y 的二元一次方程都表示一条直线,我们把关于,x y 的二元一次方程Ax +0By C +=(其中A ,B 不同时为0)叫做直线的一般式方程,简称一般式. 2.适用范围在平面直角坐标系中,任何一条直线都可用一般式表示. 3.几何意义(1)当0B ≠时,A k B -=(斜率),C b B -=(y 轴上的截距); (2)当0A ≠时,Ca A-=(x 轴上的截距).例5.根据条件写出直线方程,并化成一般式. (1(5,3)A ; (2)在,x y 轴上的截距分别是3,1--.5直线过定点问题例5.已知直线:5530l ax y a --+=.(1)求证:不论a 为何值,直线l 总经过第一象限; (2)为使直线不经过第二象限,求a 的取值范围.6解决与面积、周长有关的问题例6.直线过点4(,2)3P ,且与x 轴的正半轴和y 轴的正半轴分别交与,A B 两点,O 为坐标原点,是否存在这样的直线能同时满足以下条件:①AOB ∆的周长为12;②AOB ∆的面积为6.若存在,求出直线的方程;若不存在,请说明理由.课堂练习1.已知直线方程34)y x -=-,则这条直线经过的定点和倾斜角分别 ( ) A.(4,3),60︒ B.(3,4),30--︒ C.(4,3),30︒ D.(4,3),60--︒2.若直线(32)6y t x =--不经过第一象限,则t 的取值范围为 .3.已知直线12y x k =+与两坐标轴围成的三角形的面积不小于1,则实数k 的取值范围是 . 4.若直线l 的倾斜角是直线1y x =+的倾斜角的2倍,且过定点(3,3)P ,则直线l 的方程为 . 5.若三条直线0,0,3x y x y x ay +=-=+=构成三角形,则a 的取值范围是( ) A.1a ≠± B.1,2a a ≠≠ C.2a ≠ D.1,2a a ≠±≠6.若直线350mx y +-=经过连接点(1,2),(3,4)A B --的线段的中点,则m = . 7.ABC ∆的三个顶点分别为(0,4),(2,6),(8,0)A B C --. 求:(1)边AC 所在直线的直线方程; (2)AC 边上的中线BD 所在直线方程.直线方程练习题一、选择题1.已知点)1,0(-M ,点N 在直线01=+-y x 上,若直线MN 垂直于直线032=-+y x , 则点N 的坐标是( )A .)1,2(--B .)3,2(C . )1,2(D .)1,2(- 2.点M ),(b a 与N )1,1(+-a b 关于下列哪种图形对称( ) A .直线01=+-y x B .直线01=--y xC .点(21,21-) D .直线0=--+b a y x3.若三条直线l 1:x -y =0;l 2:x +y -2=0; l 3:5x -ky -15=0围成一个三角形,则k 的取 值范围是( )A .k ∈R 且k ±≠5且k ≠1B .k ∈R 且k ±≠5且k ≠-10C .k ∈R 且k ±≠1且k ≠0D .k ∈R 且k ±≠ 54、如果直线(2a +5)x +(a -2)y +4=0与直线(2-a )x +(a +3)y -1=0互相垂直,则a 的值等于( ) A . 2 B .-2 C .2,-2 D .2,0,-25、两条直线mx+y -n =0和x+my +1=0互相平行的条件是( ) A m=1 B m=±1C ⎩⎨⎧-≠=11n m D ⎩⎨⎧≠-=⎩⎨⎧-≠=1111n m n m 或 6、下列说法正确的有( )①若两直线斜率相等,则两直线平行; ②若l 1∥l 2,则k 1=k 2;③若两直线中有一条直线的斜率不存在,另一条直线的斜率存在,则两直线相交; ④若两直线斜率都不存在,则两直线平行。
2025届高三数学专题复习:直线方程重难点专题(解析版)

直线的方程重难点专题常考结论及公式结论一:两直线平行与垂直的充要条件若l 1:y =k 1x +b 1,l 2:y =k 2x +b 2;①l 1∥l 2⇒k 1=k 2⇒≠b 2;②l 1⊥l 2⇔k 1k 2=-1.若l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,且A 1、A 2、B 1、B 2都不为零.①l 1∥l 2⇒A 1A 2=B 1B 2≠C 1C 2;l 1与l 2重合⇒A 1A 2=B 1B 2=C1C 2;②l 1⊥l 2⇔A 1A 2+B 1B 2=0.结论二:到角公式和夹角公式(1)l 1到l 2的角公式①tan α=k 2-k 11+k 2k 1.(l 1:y =k 1x +b 1,l 2:y =k 2x +b 2,k 1k 2≠-1);②tan α=A 1B 2-A 2B 1A 1A 2+B 1B 2(l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,A 1A 2+B 1B 2≠0)(2)夹角公式①tan α=k 2-k 11+k 1k 2.(l 1:y =k 1x +b 1,l 2:y =k 2x +b 2,k 1k 2≠-1);②tan α=A 1B 2-A 2B 1A 1A 2+B 1B 2.(l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0,A 1A 2+B 1B 2≠0)直线l 1⊥l 2时,直线l 1与l 2的夹角是π2.结论三:四种常用直线系方程(1)定点直线系方程:经过定点P 0(x 0,y 0)的直线系方程为y -y 0=k (x -x 0)(除直线x =x 0),其中k 是待定的系数;经过定点P 0(x 0,y 0)的直线系方程为A (x -x 0)+B (y -y 0)=0,其中A 、B 是待定的系数.(2)共点直线系方程:经过两直线l 1:A 1x +B 1y +C 1=0,l 2:A 2x +B 2y +C 2=0的交点的直线系方程为l 1:(A 1x +B 1y +C 1)+λ(A 2x +B 2y +C 2)=0(除l 2),其中λ是待定的系数.(3)平行直线系方程:直线y =kx +b 中当斜率k 一定而b 变动时,表示平行直线系方程.与直线Ax +By +C =0平行的直线系方程是Ax +By +λ=0(λ≠0),λ是参变量.(4)垂直直线系方程:与直线Ax +By +C =0(A ≠0,B ≠0)垂直的直线系方程是Bx -Ay +λ=0,λ是参变量.结论四:与对称有关的一些结论(1)点P (u ,v )关于点Q (s ,t )的对称点的坐标为:(2s -u ,2t -v ),特别地,点P (u ,v )关于原点的对称点的坐标为:(2×0-u ,2×0-v ),即(-u ,-v ).(2)直线Ax +By +C =0关于点P (-u ,-v )对称的直线的方程为:(2u -x )+B (2v -y )+C =0.(3)直线Ax +By +C =0关于原点、x 轴、y 轴对称的直线的方程分别为:A (-x )+B (-y )+C =0,Ax +B (-y )+C =0,A (-x )+By +C =0.(4)直线Ax +By +C =0关于直线x =u ,y =v 对称的直线的方程分为:A (2u -x )+By +C =0,Ax +B (2v -y )+C =0.(5)曲线f (x ,y )=0关于点P (u ,v )对称的直线的方程为:f (2u -x ,2v -y )=0.(6)点P (s ,t )关于直线Ax +By +C =0的对称点的坐标为:s -2A ∙As +Bt +C A 2+B 2,t -2B ∙As +Bt +CA 2+B2.特别地,当A =B ≠0时,点P (s ,t )关于直线Ax +By +C =0的对称点的坐标为:-Bt +C A,-As +CB .点P (s ,t )关于x 轴、y 轴,直线x =u ,直线y =v 的对称点的坐标分别为(s ,-t ),(-s ,t ),(2u -s ),(s ,2v -t ).题型一直线的倾斜角与斜率关系问题例1.直线x cos θ+y sin θ=0,θ∈0,5π6的斜率的取值范围为()A.-∞,3B.2,+∞C.-∞,0 ∪0,3D.-∞,2【答案】A【分析】求出直线的斜率的表达式,通过角的范围求解斜率的范围即可.【详解】由x cos θ+y sin θ=0,θ∈0,5π6 可得直线的斜率为:k =-cos θsin θ=-1tan θ.因为θ∈0,5π6 ,所以tan θ∈-∞,-33 ∪0,+∞ ,所以k =-1tan θ∈-∞,0 ∪0,3 当θ=π2时,易得k =0。
直线与方程题型总结答案

题型一:重点考查直线的倾斜角)2cos10,2sin10,)2cos130,2sin130,则直线.160【详解】方法一:由斜率和倾斜角关系,利用两点连线斜率公式可得tan 方法二:根据三角函数定义可知,P Q 在圆160QOM +,由此可得倾斜角.的倾斜角为)0180θ≤<,()()33cos10sin10sin 12010sin102sin1302sin10222cos1302cos10cos 12010cos1033cos10sin1022−+−−==−+−−−()()3sin10cos103sin 1030sin 20sin 202tan 20sin 70cos 2033sin 1060sin10cos102−−==−=−=−++tan160.PQ 的倾斜角为160;方法二:由三角函数的定义可知:点,P Q 在圆24x y +=上,如图所示,为直线PQ 与轴的交点,则10,130QOM ∠,120=,又OQ =,30OQM ∴∠,160QOM +∠,∴直线PQ 的倾斜角为160. 160.2023春·安徽合肥·高二统考开学考试)直线y ++ 34π⎤⎡⋃⎥⎢⎦⎣精练核心考点3,24ππ⎤⎡⎫⎪⎥⎢⎦⎣⎭3,24ππ⎤⎡⎫⎪⎥⎢⎦⎣⎭3,4ππ⎤⎡⎫⎪⎥⎢⎦⎣⎭【详解】解:直线l 的斜率为3≤,α∈3,4⎤⎡⎫⎪⎥⎢⎦⎣⎭ππ. .(2023·全国·高二专题练习)直线,135︒︒⎤⎦【详解】解:直线x y −,则3x =,直线的斜率不存在,倾斜角为90;1≤,可得为不等于90的倾斜角),90135θ︒<≤综合,倾斜角的取值范围是45︒≤.题型二:重点考查直线的斜率19,6⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭)因为点M 在函数)在线段AB ()19,6⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭,记点16,2P ⎛− ⎝16,2P ⎛⎫− ⎪⎝⎭,所以21y +精练核心考点30,则实数D .323303=两点的直线的方向向量为题型三:重点考查斜率与倾斜角的变化关系第一象限,则直线l 的倾斜角的取值范围是()30,60)30,90 )60,9060,90⎤⎦B【详解】因为直线:l ,直线23x y +()0,2B ;30; 90;)30,90.·全国·高二专题练习)经过点P10PA k −=且直线l 与连接点如下图所示,则tan PA k ≤α∴∈π[0,4故选:B例题3.(精练核心考点2.(2023·全国·高二专题练习)已知坐标平面内三点ABC 的边A .0,⎡⎢⎣C .3⎡⎢⎣【答案】D【详解】如图所示,1为ABC 的边BD 斜率k .(2023·全国·高二专题练习)若实数的取值范围为5,73⎡⎤⎢⎥⎣⎦题型四:重点考查斜率公式的应用精练核心考点题型五:重点考查由直线与线段相交求直线斜率(倾斜角)范围3,7⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭【详解】解:设过点P 且垂直于当直线l 由位置PA 绕点P 此时,11354725PA k k +≥==+当直线l 由位置PC 绕点P 此时,1254PB k k +≤==精练核心考点1,2⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭1,2⎤⎡⎫+∞⎪⎥⎢⎦⎣⎭题型六:重点考查两直线的平行或垂直关系;方法二:直线1l 的方向向量()6,3AB =−的方向向量(3,6CD =因为0AB CD ⋅=,所以AB CD ⊥,所以5.(2023·全国·高二专题练习)已知两条直线60my +=2)30m x y −+=,当m 为何值时,相交; 平行; 垂直.【答案】(1)m ≠−3;题型七:重点考查直线的方程.(2023·全国·高二专题练习)在ABC中,已知点轴上截距是y轴上截距的3⎫,即(−⎪⎭;题型八:重点考查两直线的交点坐标【详解】三条直线不能构成三角形三条直线相交于同一点S的最小值AOBS最小值为AOB题型九:重点考查两点间的距离公式故选:B.xA B'=所以函数的最小值为故答案为:42精练核心考点1.(2023·全国·高二专题练习)已知故选:B2.(2023·全国·高二课堂例题)【答案】32【详解】()2221x x x ++=+()(224824x x x −+=−+=如图,设点(),0A x ,()1,1B −,值.由于AB AC BC +≥,当A ,B 故答案为: 32.3.(2023·全国·高二专题练习)函数为 .【答案】41【详解】()()219f x x =−+1故答案为:41题型十:重点考查点到直线的距离公式例题2.(2023秋·高二课时练习)求垂直于直线3105的直线l 的方程. 【答案】390x y −+=或3x −【详解】设与直线35x y +−则由点到直线的距离公式知()()2310310⨯−−+−===mm d350y+=.春·上海·高二期中)已知ABC的三个顶点y+=,且60)2,3,所以因此有+24=723+6=0m n m n −−⎧⎨⎩或+24=723+6=0m n m n −−−⎧⎨⎩,解得:=3=4m n ⎧⎨⎩或=3=0m n −⎧⎨⎩, 所以点A 的坐标为:()3,4或()3,0−.题型十一:重点考查两条平行线间的距离公式精练核心考点。
高考数学专题《直线与直线方程》习题含答案解析

专题9.1 直线与直线方程1.(福建高考真题(文))“a=1”是“直线x+y =0和直线x-ay =0互相垂直”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充要条件 D .既不充分也不必要条件 【答案】C 【解析】直线x +y =0和直线x −ay =0互相垂直的充要条件是1×(−a)+1×1=0,即a =1,故选C2.(2020·肥东县综合高中月考(文))点(),P x y 在直线40x y +-=上,O 是坐标原点,则OP 的最小值是( ) A BC .D 【答案】C 【解析】原点到直线40x y +-===故选C. 3.【多选题】(2021·全国高二课时练习)(多选)已知直线:1l y =-,则直线l ( ). A .过点)2-B C .倾斜角为60° D .在y 轴上的截距为1【答案】BC 【分析】根据直线斜截式方程的定义,依次判断,即得解 【详解】 点)2-的坐标不满足方程1y =-,故A 错误;根据斜截式的定义,直线l 的斜率tan k θ=60°,故B ,C 正确; 由1y =-,知直线l 在y 轴上的截距为1-,故D 错误. 故选:BC4.【多选题】(2021·全国高二课时练习)(多选)已知直线:10l x my m -+-=,则下列说法正确的是( ). A .直线l 的斜率可以等于0练基础B .若直线l 与y 轴的夹角为30°,则m =或m =C .直线l 恒过点()2,1D .若直线l 在两坐标轴上的截距相等,则1m =或1m =- 【答案】BD 【分析】讨论0m =和0m ≠时直线的斜率和截距情况,判断AD 的正误;利用倾斜角和斜率的关系判断B 的正误;将方程化为()()110x m y ---=判断直线过定点,判断C 的正误. 【详解】当0m =时,直线:1l x =,斜率不存在, 当0m ≠时,直线l 的斜率为1m,不可能等于0,故A 选项错误; ∵直线l 与y 轴的夹角角为30°,∴直线l 的倾斜角为60°或120°,而直线l 的斜率为1m,∴1tan 60m =︒=1tan120m =︒=m 或m =B 选项正确; 直线l 的方程可化为()()110x m y ---=,所以直线l 过定点()1,1,故C 选项错误; 当0m =时,直线:1l x =,在y 轴上的截距不存在, 当0m ≠时,令0x =,得1m y m-=,令0y =,得1x m =-, 令11m m m-=-,得1m =±,故D 选项正确. 故选:BD .5.【多选题】(2021·全国高二课时练习)(多选)已知直线l 的方程为20ax by +-=,则下列判断正确的是( ).A .若0ab >,则直线l 的斜率小于0B .若0b =,0a ≠,则直线l 的倾斜角为90°C .直线l 可能经过坐标原点D .若0a =,0b ≠,则直线l 的倾斜角为0° 【答案】ABD 【分析】根据直线方程与斜率,倾斜角的关系,依次讨论各选项即可得答案. 【详解】对于A 选项,若0ab >,则直线l 的斜率0ab-<,A 正确; 对于B 选项,若0b =,0a ≠,则直线l 的方程为2x a=,其倾斜角为90°,B 正确; 对于C 选项,将()0,0代入20ax by +-=中,显然不成立,C 错误; 对于D 选项,若0a =,0b ≠,则直线l 的方程为2y b=,其倾斜角为0°,D 正确. 故选:ABD .6.(2021·全国高二课时练习)直线3240x y +-=的斜率为______,在x 轴上的截距为______. 【答案】32- 43【分析】将直线转化为斜截式即可得出斜率,令0y =可求出在x 轴上的截距. 【详解】由3240x y +-=,可得322y x =-+,故该直线的斜率32k =-.令0y =,得43x =,所以该直线在x 轴上的截距为43. 故答案为:32-;43.7.(2021·全国)已知直线1:1l y x =+,将直线1l 绕点()1,2按逆时针方向旋转45︒后,所得直线2l 的方程为_______,将直线1l 绕点()1,2按顺时针方向旋转45°后,所得直线3l 的方程为_______.【答案】1x = 2y = 【分析】根据斜率和倾斜角的关系得出直线2l 和直线3l 的斜率再求解其直线方程即可. 【详解】易知直线1l 的斜率为1,倾斜角为45︒,所以直线2l 的倾斜角为90︒,直线3l 的倾斜角为0︒, 又因为直线2l 和直线3l 都经过点()1,2, 所以直线2l 和直线3l 的方程分别为1x =,2y =. 故答案为:1x =;2y =8.(2021·浙江衢州·高二期末)已知直线1l :3480x y +-=和2l :320x ay -+=,且12l l //,则实数a =__________,两直线1l 与2l 之间的距离为__________. 【答案】-4; 2 【分析】根据两直线平行斜率相等求解参数即可;运用两平行线间的距离公式计算两直线之间的距离可得出答案. 【详解】解:直线1:3480l x y +-=和2:320l x ay -+=,12l l //, 334a -∴=,解得4a =-; ∴2:3420l x y ++= 两直线1l 与2l间的距离是:2d == .故答案为:4-;2.9.(2020·浙江开学考试)已知直线1l 的方程为3420x y --=,直线2l 的方程为6810x y --=,则直线1l 的斜率为___________,直线1l 与2l 的距离为___________. 【答案】34310【解析】直线1l 的方程为3420x y --=即为3142y x =-,斜率为34. 因为直线2l 的方程为6810x y --=即为13402x y --=, 所以直线1l 与2l 平行,则直线1l 与2l310=.故答案为:34;31010.(2021·抚松县第一中学高二月考)已知A (1,0),B (﹣1,2),直线l :2x ﹣ay ﹣a =0上存在点P ,满足|P A |+|PB |=a 的取值范围是 ___________. 【答案】2[,2]3-【分析】计算线段AB 的距离,得到点P 的轨迹,将点A ,B 分别代入2x ﹣ay ﹣a =0,得到a ,根据题意得到直线l 所过定点C,求出直线AC ,BC 的斜率,根结合直线l 与线段AB 始终有交点计算出a 的取值范围. 【详解】因为||AB ==||||PA PB += 由图可知,点P 的轨迹为线段AB ,将点A ,B 的坐标分别代入直线l 的方程,可得a =2,a =23-,由直线l 的方程可化为:2x ﹣a (y +1)=0,所以直线l 过定点C (0,﹣1), 画出图形,如图所示:因为直线AC 的斜率为k AC =1,直线BC 的斜率为k BC =2(1)10----=﹣3, 所以直线l 的斜率为k =2a ,令2123aa⎧≥⎪⎪⎨⎪≤-⎪⎩,解得23-≤a ≤2,所以a 的取值范围是[23-,2].故答案为:[23-,2].1.(2021·绥德中学高一月考)已知0a >,0b >,直线220ax by -+=恒过点(2-,1),则14a b+的最小值为( ) A .8 B .9 C .16 D .18【答案】B 【分析】利用给定条件可得1a b +=,再借助“1”的妙用即可计算得解. 【详解】因直线220ax by -+=恒过点(2-,1),则有2220a b --+=,即1a b +=, 又0a >,0b >,则14144()()559b a a b a b a b a b +=++=++≥+=,当且仅当4b a a b =,即2b a =时取“=”,练提升由21b a a b =⎧⎨+=⎩得12,33a b ==,所以当12,33a b ==时,14a b+取得最小值9.故选:B2.(2019·四川高考模拟(文))已知点(3,0)P -在动直线(1)(3)0m x n y -+-=上的投影为点M ,若点3(2,)2N ,那么||MN 的最小值为( ) A .2 B .32C .1D .12【答案】D 【解析】因为动直线()()130m x n y -+-=方程为,所以该直线过定点Q (1,3), 所以动点M 在以PQ5,2= 圆心的坐标为3(1,)2-,所以点N3=, 所以MN 的最小值为51322-=.故答案为:D 3.(2019·湖南衡阳市八中高三月考(文))已知直线的倾斜角为且过点,其中,则直线的方程为( )C.【答案】B 【解析】,, 则直线方程为:故选4.(四川高考真题(文))设m R ∈,过定点A 的动直线0x my +=和过定点B 的动直线l θ1sin()22l 20y --=40y +-=0x -=360y 122sin πθ⎛⎫-= ⎪⎝⎭1cos 2θ∴=-2 3πθ=tan θ=1y x -=40y +-=B30mx y m --+=交于点(,)P x y ,则PA PB +的取值范围是( )A. B. C. D.【答案】B 【解析】易得(0,0),(1,3)A B .设(,)P x y ,则消去m 得:2230x y x y +--=,所以点P 在以AB 为直径的圆上,PA PB ⊥,所以222||||10PA PB AB +==,令,PA PB θθ==,则)4PA PB πθθθ+=+=+.因为0,0PA PB ≥≥,所以02πθ≤≤.sin()14πθ≤+≤PA PB ≤+≤.选B. 法二、因为两直线的斜率互为负倒数,所以PA PB ⊥,点P 的轨迹是以AB 为直径的圆.以下同法一.5.(2020·浙江)已知点(2,1)M -,直线l 过点M 且与直线210x y -+=平行,则直线l 的方程为____________;点M 关于直线10x y -+=的对称点的坐标为_______________. 【答案】240x y -+= (0,1)- 【分析】根据所求直线与直线210x y -+=平行,设方程为()201x y n n -+=≠求解;设点M 关于直线10x y -+=的对称点的坐标为(),M x y ',由112211022y x x y -⎧=-⎪⎪+⎨-+⎪-+=⎪⎩求解.【详解】因为所求直线与直线210x y -+=平行, 所以设方程为()201x y n n -+=≠, 因为直线过点(2,1)M -, 代入直线方程解得4n =,所以所求直线方程为:240x y -+=;设点M 关于直线10x y -+=的对称点的坐标为(),M x y ', 则112211022y x x y -⎧=-⎪⎪+⎨-+⎪-+=⎪⎩,解得01x y =⎧⎨=-⎩,所以点M 关于直线10x y -+=的对称点的坐标为()0.1-故答案为:240x y -+=,(0,1)-6.(2019·黑龙江鹤岗·月考(文))已知直线l 经过点()4,3P ,且与x 轴正半轴交于点A ,与y 轴正半轴交于点B ,O 为坐标原点.(1)若点O 到直线l 的距离为4,求直线l 的方程; (2)求OAB ∆面积的最小值.【答案】(1)7241000x y +-=(2)24 【解析】(1)由题意可设直线l 的方程为()34y k x -=-,即430kx y k --+=,则4d ==,解得724k =-. 故直线l 的方程为774302424x y ⎛⎫---⨯-+= ⎪⎝⎭,即7241000x y +-=. (2)因为直线l 的方程为430kx y k --+=,所以34,0A k ⎛⎫-+ ⎪⎝⎭,()0,43B k -+, 则OAB ∆的面积为()113194431624222S OA OB k k k k ⎛⎫⎛⎫=⋅=-+⨯-+=--+ ⎪ ⎪⎝⎭⎝⎭. 由题意可知k 0<,则91624k k --≥=(当且仅当34k =-时,等号成立).故OAB ∆面积的最小值为()12424242⨯+=. 7.(2021·抚松县第一中学高二月考)已知直线l 1:2x +y +3=0,l 2:x ﹣2y =0.(1) 求直线l 1关于x 轴对称的直线l 3的方程,并求l 2与l 3的交点P ; (2)求过点P 且与原点O (0,0)距离等于2的直线m 的方程. 【答案】(1)2x ﹣y +3=0,P (﹣2,﹣1);(2) 3x +4y +10=0或x =﹣2. 【分析】(1)由对称关系求直线l 3的方程,联立l 2与l 3的方程,求点P 的坐标,(2)当直线m 的斜率存在时,设直线m 的点斜式方程,由点到直线距离公式列方程求斜率,由此可得直线m 的方程,再检验过点P 的斜率不存在的直线是否满足要求. 【详解】(1)由题意,直线l 3与直线l 1的倾斜角互补,从而它们的斜率互为相反数,且l 1与l 3必过x 轴上相同点3(,0)2-,∴直线l 3的方程为2x ﹣y +3=0,由230,20,x y x y -+=⎧⎨-=⎩解得2,1.x y =-⎧⎨=-⎩∴P (﹣2,﹣1).(2)当直线m 的斜率存在时,设直线m 的方程为y +1=k (x +2), 即kx ﹣y +2k ﹣1=0,∴原点O (0,0)到直线m2=,解得34k =-,∴直线m 方程为3x +4y +10=0,当直线m 的斜率不存在时,直线x =﹣2满足题意, 综上直线m 的方程为3x +4y +10=0或x =﹣2.8.(2021·宝山区·上海交大附中高一开学考试)如图,点(),4A m ,4,B n 在反比例函数()0ky k x=>的图象上,经过点A 、B 的直线与x 轴相交于点C ,与y 轴相交于点D .(1)若2m =,求n 的值; (2)求m n +的值;(3)连接OA 、OB ,若tan tan 1AOD BOC ∠+∠=,求直线AB 的函数关系式. 【答案】(1)2(2)0(3)2y x =+ 【分析】(1)先把A 点坐标代入()0k y k x =>求出k 的值得到反比例函数解析式为8y x=,然后把(4,)B n -代8y x=可求出n 的值; (2)利用反比例函数图象上点的坐标特征得到4m =k ,﹣4n =k ,然后把两式相减消去k 即可得到m +n 的值;(3)作AE ⊥y 轴于E ,BF ⊥x 轴于F ,如图,利用正切的定义得到tan ∠AOE 4AE mOE ==,tan 4BF n BOF OF -∠==,则144m n-+=,加上0m n +=,于是可解得2,2m n ==-,从而得到(2,4)A ,(4,2)B --,然后利用待定系数法求直线AB 的解析式.【详解】(1)当m =2,则A (2,4), 把A (2,4)代入ky x=得k =2×4=8, 所以反比例函数解析式为8y x=, 把(4,)B n -代入8y x=得﹣4n =8,解得n =﹣2; (2)因为点A (m ,4),B (﹣4,n )在反比例函数()0ky k x=>的图象上, 所以4m =k ,﹣4n =k , 所以4m +4n =0,即m +n =0;(3)作AE ⊥y 轴于E ,BF ⊥x 轴于F ,如图,在Rt △AOE 中,tan ∠AOE 4AE mOE ==, 在Rt △BOF 中,tan 4BF nBOF OF -∠==, 而tan ∠AOD +tan ∠BOC =1, 所以144m n-+=, 而m +n =0,解得m =2,n =﹣2, 则A (2,4),B (﹣4,﹣2), 设直线AB 的解析式为y =px +q ,把(2,4),(4,2)A B --代入得2442p q p q +=⎧⎨-+=-⎩,解得12p q =⎧⎨=⎩,所以直线AB 的解析式为y =x +2.9.(2021·全国高二课时练习)已知点()2,1P -. (1)求过点P 且与原点的距离为2的直线的方程.(2)是否存在过点P 且与原点的距离为6的直线?若存在,求出该直线的方程;若不存在,请说明理由.【答案】(1) 20x -=或34100x y --=;(2) 不存在这样的直线;理由见解析. 【分析】(1)分k 存在与不存在两种情况讨论,点斜式表示直线方程,利用点到直线距离公式即得解;(2)过点P 且与原点的距离最大的直线为过点P 且与OP 垂直的直线,分析即得解 【详解】(1)①当直线的斜率不存在时,直线方程为2x =,符合题意. ②当直线的斜率存在时,设斜率为k ,则直线方程为()12y k x +=-,即210kx y k ---=.2=,解得34k =,所以直线方程为34100x y --=.故所求直线方程为20x -=或34100x y --=. (2)不存在.理由如下:过点P 且与原点的距离最大的直线为过点P 且与OP 垂直的直线,OP =而6>10.(2021·全国高三专题练习)AOB 是等腰直角三角形,||AB =动直线l 过点(1,1)P 与AOB 的斜边、直角边分别交于不同的点M 、N (如图所示).(1)设直线l 的斜率为k ,求k 的取值范围,并用k 表示M 的坐标; (2)试写出表示AMN 的面积S 的函数解析式()S k ,并求()S k 的最大值.【答案】(1)0k >,1,11kM k k ⎛⎫ ⎪++⎝⎭;(2)112(1)()012(1)k k k S k kk k ⎧⎪+⎪=⎨-⎪<<⎪+⎩,max 1()4S k =.【分析】(1)根据题意,结合图象即可得到k 的取值范围,再联立直线方程即可得到M 的坐标; (2) 由于l 绕P 点转动,则N 点可落在OA 上,也可落在OB 上,AMNS的计算不一样,所以必须对l 的斜率不同的取值范围进行分类讨论,表示出()S k ,结合函数单调性即可求解. 【详解】(1)由已知条件得(1,0)A 、(0,1)B ,0k >,设直线l 的方程为1y kx k =+-.由11x y y kx k+=⎧⎨=+-⎩,得1,11kM k k ⎛⎫ ⎪++⎝⎭. (2)当1k 时,点N 在直角边OA 上,1,0k N k -⎛⎫⎪⎝⎭, 1111()1212(1)k S k k k k k -⎛⎫=-⋅= ⎪++⎝⎭. 当01k <<时,点k 在直角边OB 上,(0,1)N k -,111()11(1)122212(1)k k S k k k k k =⨯⨯--⨯-⨯=++.∴112(1)()012(1)k k k S k k k k ⎧⎪+⎪=⎨-⎪<<⎪+⎩,当1k 时,()S k 递减,∴max 1()(1)4S k S ==,当01k <<时,11111()22(1)244S k k =-<-=+. 综上所述,当1k =时,max 1()4S k =.1.(上海高考真题(文))已知直线1l :(3)(4)10k x k y -+-+=与2l :2(3)230k x y --+=平行,则k 的值是( ). A .1或3 B .1或5C .3或5D .1或2【答案】C 【解析】由两直线平行得,当k-3=0时,两直线的方程分别为1y =- 和32y =,显然两直线平行.当练真题k-3≠0时,由()k 34k1/32k 32--=≠--,可得 k=5.综上,k 的值是 3或5, 故选 C .2.(2020·山东高考真题)已知直线sin cos :y x l θθ=+的图像如图所示,则角θ是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角【答案】D 【分析】本题可根据直线的斜率和截距得出sin 0θ<、cos 0θ>,即可得出结果. 【详解】结合图像易知,sin 0θ<,cos 0θ>, 则角θ是第四象限角, 故选:D.3.(2021·山东高考真题)如下图,直线l 的方程是( )A 0y -=B 20y -=C 310y --=D .10x -=【答案】D 【分析】由图得到直线的倾斜角为30,进而得到斜率,然后由直线l 与x 轴交点为()1,0求解. 【详解】由图可得直线的倾斜角为30°,所以斜率tan 30k =︒=所以直线l 与x 轴的交点为()1,0,所以直线的点斜式方程可得l :)01y x -=-,即10x -=. 故选:D4.(2021·湖南高考真题)点(0,1)-到直线3410x y -+=的距离为( ) A .25B .35C .45D .1【答案】D 【分析】利用点到直线的距离公式即可求解. 【详解】点(0,1)-到直线3410x y -+=的距离为515d ==, 故选:D.5.(全国高考真题(理))已知点A (﹣1,0),B (1,0),C (0,1),直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( ) A.(0,1) B.112⎛⎫ ⎪ ⎪⎝⎭, C.113⎛⎤⎥ ⎝⎦, D.1132⎡⎫⎪⎢⎣⎭,【答案】B 【解析】由题意可得,三角形ABC 的面积为12AB OC ⋅⋅=1, 由于直线y =ax +b (a >0)与x 轴的交点为M (ba-,0), 由直线y =ax +b (a >0)将△ABC 分割为面积相等的两部分,可得b >0, 故ba-≤0,故点M 在射线OA 上. 设直线y =ax +b 和BC 的交点为N ,则由1y ax b x y =+⎧⎨+=⎩可得点N 的坐标为(11b a -+,1a ba ++).①若点M 和点A 重合,如图:则点N为线段BC的中点,故N(12,12),把A、N两点的坐标代入直线y=ax+b,求得a=b13 =.②若点M在点O和点A之间,如图:此时b13>,点N在点B和点C之间,由题意可得三角形NMB的面积等于12,即1122NMB y⋅⋅=,即111212b a ba a+⎛⎫⨯+⋅=⎪+⎝⎭,可得a212bb=->0,求得b12<,故有13<b12<.③若点M在点A的左侧,则b13<,由点M的横坐标ba--<1,求得b>a.设直线y =ax +b 和AC 的交点为P ,则由 1y ax b y x =+⎧⎨=+⎩求得点P 的坐标为(11b a --,1a ba --),此时,由题意可得,三角形CPN 的面积等于12,即 12•(1﹣b )•|x N ﹣x P |12=, 即12(1﹣b )•|1111b b a a ---+-|12=,化简可得2(1﹣b )2=|a 2﹣1|.由于此时 b >a >0,0<a <1,∴2(1﹣b )2=|a 2﹣1|=1﹣a 2 . 两边开方可得(1﹣b)=1,∴1﹣b ,化简可得 b >12-, 故有1b 13<. 综上可得b 的取值范围应是1122⎛⎫- ⎪ ⎪⎝⎭,, 故选:B .6.(2011·安徽高考真题(理))在平面直角坐标系中,如果与都是整数,就称点为整点,下列命题中正确的是_____________(写出所有正确命题的编号) ①存在这样的直线,既不与坐标轴平行又不经过任何整点 ②如果与都是无理数,则直线不经过任何整点 ③直线经过无穷多个整点,当且仅当经过两个不同的整点④直线经过无穷多个整点的充分必要条件是:与都是有理数 ⑤存在恰经过一个整点的直线 【答案】①③⑤ 【解析】①令直线为:,则其不与坐标轴平行且不经过任何整点,①正确; ②令直线为:,②错误;③令直线为:,过两个不同的整点,则,两式作差得: 即直线经过整点直线经过无穷多个整点,③正确;x y (,)x y k b y kx b =+l l y kx b =+k b l 12y x =+l y =-()2,0l y kx =()11,x y ()22,x y 112y kx y kx =⎧⎨=⎩()1212y y k x x -=-l ()1212,x x y y --∴l④令直线为:,则不过整点,④错误; ⑤令直线为:,则其只经过一个整点,⑤正确.本题正确结果:①③⑤l 1132y x =+ll y =()0,0。
直线与方程知识点归纳及对应习题

直线与方程一、直线倾斜角和斜率000180α≤<. k=tan α(α不为090)。
经过两点),(),,(222111y x P y x P (21x x ≠)的直线的斜率公式是1212x x y y k --=(21x x ≠) 练习:1、直线x +y -5=0的倾斜角为( )A. -30°B. 60°C. 120°D. 150°2、在下列四个命题中,正确的共有()①坐标平面内的任何一条直线均有倾斜角和斜率;②直线的倾斜角的取值范围是[0,π];③若一条直线的斜率为tanα,则此直线的倾斜角为α;④若一条直线的倾斜角为α,则此直线的斜率为tanα.A. 0个B. 1个C. 2个D. 3个二、直线的方程1、直线方程的几种形式点斜式:)(11x x k y y -=- (斜率存在) ; 两点式:121121x x x x y y y y --=--),(2121y y x x ≠≠其中 斜截式:b kx y += (斜率存在) ; 截距式:1=+by a x (0a ≠≠且b 0) 一般式:0=++C By Ax )不同时为其中0,(B A 练习:3、过点(-1,2)且在坐标轴上的截距相等的直线的一般式方程是______.4、 已知△ABC 的顶点A (5,1),AB 边上的中线CM 所在直线方程为2x-y-5=0,∠B 平分线BN 所在直线方程为x-2y-5=0.求:(1)顶点B 的坐标;(2)直线BC 的方程.5、已知△ABC 的顶点A (5,1),AB 边上的中线CM 所在的直线方程为2x-y-5=0,AC 边上的高BH 所在直线的方程为x-2y-5=0.(1)求直线BC 的方程;(2)求直线BC 关于CM 的对称直线方程.2、 两条直线位置关系的判定:已知 0:11=++C By Ax l , 0:22=++C By Ax l ,则:(1)0212121=+⇔⊥B B A A l l(2)1212211221//(1)-00(0);l l A B A B BC B C B ⇔=-≠≠且斜率存在,即1221(2)0(0).AC A C B -≠=斜率存在,即(3)1l 与2l 相交01221≠-⇔B A B A练习:6、若直线l1:(m-2)x-y-1=0与直线l2:3x-my=0互相平行,则m 的值为( )A. 0或或3B. 0或3C. 0或D. 或37、已知直线ax+3y-1=0与直线3x-y+2=0互相垂直,则a=( )A. -3B. -1C. 1D. 38、已知两条直线l1(3+m )x+4y=5-3m ,l2 2x+(5+m )y=8.当m 分别为何值时,l1与l2:(1)相交?(2)平行?(3)垂直?3、几种直线系方程(1)过两条直线0:1111=++C y B x A l , 0:2222=++C y B x A l 的交点的直线系方程为0)(222111=+++++C y B x A C y B x A λ(λ为参数),其中直线l 2不在直线系中. (2)平行于直线0n 0(n )Ax By C Ax By C ++=++=≠的直线可表示为(3)垂直于直线0m 0Ax By C Bx Ay ++=-+=的直线可表示为练习:9、过直线x+y-3=0和2x-y=0的交点,且与直线2x+y-5=0垂直的直线方程是()A. 4x+2y-3=0B. 4x-2y+3=0C. x+2y-3=0D. x-2y+3=010、已知直线l1:x-2y+3=0与直线l2:2x+3y-8=0的交点为M ,(1)求过点M 且到点P (0,4)的距离为2的直线l 的方程;(2)求过点M 且与直线l3:x+3y+1=0平行的直线l 的方程.三、直线的交点坐标与距离公式1.两条直线的交点2.几种距离平面上的两点),(),,(222111y x P y x P 间的距离公式21221221)()(y y x x P P-+-= 点),(00y x P 到直线0:=++C By Ax l 的距离2200B A CBy Ax d +++=(直线方程要化为一般式)两条平行线0:11=++C By Ax l , 0:22=++C By Ax l 间的距离2212B A C C d +-=(直线化为系数相同的一般式)练习:11、原点到直线y=-x+的距离为( ) A. 1 B. C. 2 D.12、直线3x+4y-12=0和6x+8y+6=0间的距离是______ .13、若直线l1:x-2y+1=0与l2:2x+ay-2=0平行,则l1与l2的距离为( ) A. B. C. D.3、 直线l 上一动点P 到两个定点A 、B 的距离“最值问题”:(1) 在直线l 上求一点P ,使PB PA +取得最小值:“同侧对称异侧连”(2)在直线l 上求一点P 使PB PA -取得最大值:“异侧对称同侧连” (3) 22PB PA +的最值:函数思想“转换成一元二次函数,找对称轴”。
直线与方程知识总结及典型 例题(高一人教版必修二)

)
(A)2x-3y=0;
(B)x+y+5=0;
(C)2x-3y=0或x+y+5=0
(D)x+y+5或x-y+5=0
4.直线x=3的倾斜角是( )
A.0 B. C. D.不存在
5.圆x2+y2+4x=0的圆心坐标和半径分别是( )
A.(-2,0),2 B.(-2,0),4 C.(2,0),2 D.(2,0),4
相交 平行 重合
交点 夹角 平行线间的距离
表示平面区域
直线 与方程
直线与直线位置关系 倾斜角 五种形式 直线方程
二元一次不等式
线性规划 斜率
与
与方程 点 关于直线的方程,直线的斜率、倾斜角,两点间距离公式,点到直
线的距离公式,夹角与到角公式,两直线的垂直、平行关系等知识的试 题,都属于基本要求,既有选择题、填空题,也有解答题,所占的分值 为5~10分,一般涉及到两个以上的知识点,这些仍将是今后高考考查 的热点。
(A)-
(B)-3;
(C) (D)3
12.直线当变动时,所有直线都通过定点( )
(A)(0,0)
(B)(0,1)
(C)(3,1)
(D)(2,1)
二、填空题(每题4分,共16分)
13.直线过原点且倾角的正弦值是,则直线方程为
14.直线mx+ny=1(mn≠0)与两坐标轴围成的三角形面积为
15.如果三条直线mx+y+3=0, xy2=0, 2xy+2=0不能成为一个三角形三边
7.点(2,1)到直线3x 4y + 2 = 0的距离是
(A) (B) (C) (D)
8.直线x y 3 = 0的倾斜角是( )
(A)30° (B)45° (C)60° (D)90°
高中数学必修第三章《直线与方程》知识点总结与练习

第八章平面解析几何第一节直线的倾斜角与斜率、直线的方程[知识能否忆起]一、直线的倾斜角与斜率1.直线的倾斜角(1)定义:x轴正向与直线向上方向之间所成的角叫做这条直线的倾斜角.当直线与x轴平行或重合时,规定它的倾斜角为0°.(2)倾斜角的范围为[0,π)_.2.直线的斜率(1)定义:一条直线的倾斜角α的正切值叫做这条直线的斜率,斜率常用小写字母k表示,即k=tan_α,倾斜角是90°的直线没有斜率.(2)过两点的直线的斜率公式:经过两点P1(x1,y1),P2(x2,y2)(x1≠x2)的直线的斜率公式为k==.二、直线方程的形式及适用条件1.(教材习题改编)直线x+y+m=0(m∈k)的倾斜角为()A.30°B.60°C.150°D.120°解析:选C由k=tanα=-,α∈[0,π)得α=150°.2.(教材习题改编)已知直线l过点P(-2,5),且斜率为-,则直线l的方程为() A.3x+4y-14=0 B.3x-4y+14=0C.4x+3y-14=0 D.4x-3y+14=0解析:选A由y-5=-(x+2),得3x+4y-14=0.3.过点M(-2,m),N(m,4)的直线的斜率等于1,则m的值为()A.1 B.4C.1或3 D.1或4解析:选A由1=,得m+2=4-m,m=1.4.(2012·长春模拟)若点A(4,3),B(5,a),C(6,5)三点共线,则a的值为________.解析:k AC==1,k AB==a-3.由于A,B,C三点共线,所以a-3=1,即a=4.答案:45.若直线l过点(-1,2)且与直线2x-3y+4=0垂直,则直线l的方程为________.解析:由已知得直线l的斜率为k=-.所以l的方程为y-2=-(x+1),即3x+2y-1=0.答案:3x+2y-1=01.求直线方程时要注意判断直线斜率是否存在,每条直线都有倾斜角,但不一定每条直线都存在斜率.2.由斜率求倾斜角,一是要注意倾斜角的范围;二是要考虑正切函数的单调性.3.用截距式写方程时,应先判断截距是否为0,若不确定,则需要分类讨论.典题导入[例1](1)(2012·岳阳模拟)经过两点A(4,2y+1),B(2,-3)的直线的倾斜角为,则y=()A.-1B.-3C.0 D.2(2)(2012·苏州模拟)直线x cosθ+y+2=0的倾斜角的范围是________.[自主解答](1)tan===y+2,因此y+2=-=-3.(2)由题知k=-cosθ,故k∈,结合正切函数的图象,当k∈时,直线倾斜角α∈,当k ∈时,直线倾斜角α∈,故直线的倾斜角的范围是∪.[答案](1)B(2)∪由题悟法1.求倾斜角的取值范围的一般步骤:(1)求出斜率k=tanα的取值范围;(2)利用三角函数的单调性,借助图象或单位圆数形结合,确定倾斜角α的取值范围.2.求倾斜角时要注意斜率是否存在.以题试法1.(2012·哈尔滨模拟)函数y=a sin x-b cos x的一条对称轴为x=,则直线l:ax-by+c =0的倾斜角为()A.45°B.60°C.120°D.135°解析:选D由函数y=f(x)=a sin x-b cos x的一条对称轴为x=知,f(0)=f,即-b=a,则直线l的斜率为-1,故倾斜角为135°.2.(2012·金华模拟)已知点A(1,3),B(-2,-1).若直线l:y=k(x-2)+1与线段AB相交,则k的取值范围是()B.(-∞,-2]C.(-∞,-2]∪解析:选D由题意知直线l恒过定点P(2,1),如右图.若l 与线段AB相交,则k PA≤k≤k PB.∵k PA=-2,k PB=,∴-2≤k≤.直线方程典题导入[例2](1)过点(1,0)且与直线x-2y-2=0平行的直线方程是________________.(2)(2012·东城模拟)若点P(1,1)为圆(x-3)2+y2=9的弦MN的中点,则弦MN所在直线的方程为______________.[自主解答](1)设所求直线方程为x-2y+m=0,由直线经过点(1,0),得1+m=0,m =-1.则所求直线方程为x-2y-1=0.(2)由题意得,×k MN=-1,所以k MN=2,故弦MN所在直线的方程为y-1=2(x-1),即2x-y-1=0.[答案](1)x-2y-1=0(2)2x-y-1=0由题悟法求直线方程的方法主要有以下两种:(1)直接法:根据已知条件,选择适当的直线方程形式,直接写出直线方程;(2)待定系数法:先设出直线方程,再根据已知条件求出待定系数,最后代入求出直线方程.以题试法3.(2012·龙岩调研)已知△ABC中,A(1,-4),B(6,6),C(-2,0).求:(1)△ABC中平行于BC边的中位线所在直线的一般式方程和截距式方程;(2)BC边的中线所在直线的一般式方程,并化为截距式方程.解:(1)平行于BC边的中位线就是AB,AC中点的连线.因为线段AB,AC中点坐标分别为,,所以这条直线的方程为=,整理一般式方程为得6x-8y-13=0,截距式方程为-=1.(2)因为BC边上的中点为(2,3),所以BC边上的中线所在直线的方程为=,即一般式方程为7x-y-11=0,截距式方程为-=1.典题导入[例3](2012·开封模拟)过点P(3,0)作一直线,使它夹在两直线l1:2x-y-2=0与l2:x +y+3=0之间的线段AB恰被点P平分,求此直线的方程.[自主解答]法一:设点A(x,y)在l1上,点B(x B,y B)在l2上.由题意知则点B(6-x,-y),解方程组得则k==8.故所求的直线方程为y=8(x-3),即8x-y-24=0.法二:设所求的直线方程为y=k(x-3),点A,B的坐标分别为(x A,y A),(x B,y B),由解得由解得∵P(3,0)是线段AB的中点,∴y A+y B=0,即+=0,∴k2-8k=0,解得k=0或k=8.若k=0,则x A=1,x B=-3,此时=≠3,∴k=0舍去,故所求的直线方程为y=8(x-3),即8x-y-24=0.由题悟法解决直线方程的综合问题时,除灵活选择方程的形式外,还要注意题目中的隐含条件,若与最值或范围相关的问题可考虑构建目标函数进行转化求最值.以题试法4.(2012·东北三校联考)已知直线l过点M(2,1),且分别与x轴,y轴的正半轴交于A,B两点,O为原点.(1)当△AOB面积最小时,求直线l的方程;(2)当|MA|·|MB|取得最小值时,求直线l的方程.解:(1)设直线l的方程为y-1=k(x-2)(k<0),A,B(0,1-2k),△AOB的面积S=(1-2k)=≥(4+4)=4.当且仅当-4k=-,即k=-时,等号成立.故直线l的方程为y-1=-(x-2),即x+2y-4=0.(2)∵|MA|=,|MB|=,∴|MA|·|MB|=·=2≥2×2=4,当且仅当k2=,即k=-1时取等号,故直线方程为x+y-3=0.[典例](2012·西安模拟)设直线l的方程为(a+1)x+y+2-a=0(a∈R).(1)若l在两坐标轴上的截距相等,求l的方程;(2)若l不经过第二象限,求实数a的取值范围.[尝试解题](1)当直线过原点时,该直线在x轴和y轴上的截距为零,此时截距相等.故a=2,方程即为3x+y=0.当直线不过原点时,由截距存在且均不为0,得=a-2,即a+1=1,故a=0,方程即为x+y+2=0.综上,l的方程为3x+y=0或x+y+2=0.(2)将l的方程化为y=-(a+1)x+a-2,则或∴a≤-1.综上可知,a的取值范围是(-∞,-1].——————[易错提醒]———————————————————————————1.与截距有关的直线方程求解时易忽视截距为零的情形.如本例中的截距相等,当直线在x轴与y轴上的截距为零时也满足.2.常见的与截距问题有关的易误点有:“截距互为相反数”;“一截距是另一截距的几倍”等,解决此类问题时,要先考虑零截距情形.注意分类讨论思想的运用.——————————————————————————————————————针对训练过点M(3,-4)且在两坐标轴上的截距互为相反数的直线方程为________________.解析:①当过原点时,直线方程为y=-x;②当不过原点时,设直线方程为+=1,即x-y=a.代入点(3,-4),得a=7.即直线方程为x-y-7=0.答案:y=-x或x-y-7=01.若k,-1,b三个数成等差数列,则直线y=kx+b必经过定点()A.(1,-2)B.(1,2)C.(-1,2) D.(-1,-2)解析:选A因为k,-1,b三个数成等差数列,所以k+b=-2,即b=-2-k,于是直线方程化为y=kx-k-2,即y+2=k(x-1),故直线必过定点(1,-2).2.直线2x+11y+16=0关于点P(0,1)对称的直线方程是()A.2x+11y+38=0 B.2x+11y-38=0C.2x-11y-38=0 D.2x-11y+16=0解析:选B因为中心对称的两直线互相平行,并且对称中心到两直线的距离相等,故可设所求直线的方程为2x+11y+C=0,由点到直线的距离公式可得=,解得C=16(舍去)或C=-38.3.(2012·衡水模拟)直线l1的斜率为2,l1∥l2,直线l2过点(-1,1)且与y轴交于点P,则P点坐标为()A.(3,0) B.(-3,0)C.(0,-3) D.(0,3)解析:选D∵l1∥l2,且l1斜率为2,∴l2的斜率为2.又l2过(-1,1),∴l2的方程为y-1=2(x+1),整理即得y=2x+3.令x=0,得P(0,3).4.(2013·佛山模拟)直线ax+by+c=0同时要经过第一、第二、第四象限,则a,b,c 应满足()A.ab>0,bc<0 B.ab>0,bc>0C.ab<0,bc>0 D.ab<0,bc<0解析:选A由于直线ax+by+c=0经过第一、二、四象限,所以直线存在斜率,将方程变形为y=-x-,易知-<0且->0,故ab>0,bc<0.5.将直线y=3x绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为() A.y=-x+B.y=-x+1C.y=3x-3 D.y=x+1解析:选A将直线y=3x绕原点逆时针旋转90°得到直线y=-x,再向右平移1个单位,所得直线的方程为y=-(x-1),即y=-x+.6.已知点A(1,-2),B(m,2),且线段AB的垂直平分线的方程是x+2y-2=0,则实数m的值是()A.-2 B.-7C.3 D.1解析:选C线段AB的中点代入直线x+2y-2=0中,得m=3.7.(2013·贵阳模拟)直线l经过点A(1,2),在x轴上的截距的取值范围是(-3,3),则其斜率的取值范围是________.解析:设直线l的斜率为k,则方程为y-2=k(x-1),在x轴上的截距为1-,令-3<1-<3,解得k<-1或k>.答案:(-∞,-1)∪8.(2012·常州模拟)过点P(-2,3)且在两坐标轴上的截距相等的直线l的方程为________.解析:直线l过原点时,l的斜率为-,直线方程为y=-x;l不过原点时,设方程为+=1,将点(-2,3)代入,得a=1,直线方程为x+y=1.综上,l的方程为x+y-1=0或2y+3x=0.答案:x+y-1=0或3x+2y=09.(2012·天津四校联考)不论m取何值,直线(m-1)x-y+2m+1=0恒过定点________.解析:把直线方程(m-1)x-y+2m+1=0整理得(x+2)m-(x+y-1)=0,则得答案:(-2,3)10.求经过点(-2,2),且与两坐标轴所围成的三角形面积为1的直线l的方程.解:设所求直线方程为+=1,由已知可得解得或故直线l的方程为2x+y+2=0或x+2y-2=0.11.(2012·莆田月考)已知两点A(-1,2),B(m,3).(1)求直线AB的方程;(2)已知实数m∈,求直线AB的倾斜角α的取值范围.解:(1)当m=-1时,直线AB的方程为x=-1;当m≠-1时,直线AB的方程为y-2=(x+1).(2)①当m=-1时,α=;②当m≠-1时,m+1∈∪(0,],∴k=∈(-∞,-]∪,∴α∈∪.综合①②知,直线AB的倾斜角α∈.12.如图,射线OA、OB分别与x轴正半轴成45°和30°角,过点P(1,0)作直线AB分别交OA、OB于A、B两点,当AB的中点C恰好落在直线y=x上时,求直线AB的方程.解:由题意可得k OA=tan45°=1,k OB=tan(180°-30°)=-,所以直线l OA:y=x,l OB:y=-x.设A(m,m),B(-n,n),所以AB的中点C,由点C在y=x上,且A、P、B三点共线得解得m=,所以A(,).又P(1,0),所以k AB=k AP==,所以l AB:y=(x-1),即直线AB的方程为(3+)x-2y-3-=0.1.若直线l:y=kx-与直线2x+3y-6=0的交点位于第一象限,则直线l的倾斜角的取值范围是()解析:选B由解得∵两直线交点在第一象限,∴解得k>.∴直线l的倾斜角的范围是.2.(2012·洛阳模拟)当过点P(1,2)的直线l被圆C:(x-2)2+(y-1)2=5截得的弦最短时,直线l的方程为________________.解析:易知圆心C的坐标为(2,1),由圆的几何性质可知,当圆心C与点P的连线与直线l垂直时,直线l被圆C截得的弦最短.由C(2,1),P(1,2)可知直线PC的斜率为=-1,设直线l的斜率为k,则k×(-1)=-1,得k=1,又直线l过点P,所以直线l的方程为x -y+1=0.答案:x-y+1=03.已知直线l:kx-y+1+2k=0(k∈R).(1)证明:直线l过定点;(2)若直线l不经过第四象限,求k的取值范围;(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.解:(1)证明:法一:直线l的方程可化为y=k(x+2)+1,故无论k取何值,直线l总过定点(-2,1).法二:设直线过定点(x0,y0),则kx0-y0+1+2k=0对任意k∈R恒成立,即(x0+2)k-y0+1=0恒成立,∴x0+2=0,-y0+1=0,解得x0=-2,y0=1,故直线l总过定点(-2,1).(2)直线l的方程为y=kx+2k+1,则直线l在y轴上的截距为2k+1,要使直线l不经过第四象限,则解得k的取值范围是[0,+∞).(3)依题意,直线l在x轴上的截距为-,在y轴上的截距为1+2k,∴A,B(0,1+2k).又-<0且1+2k>0,∴k>0.故S=|OA||OB|=×(1+2k)=≥(4+4)=4,当且仅当4k=,即k=时,取等号.故S的最小值为4,此时直线l的方程为x-2y+4=0.1.(2012·郑州模拟)已知直线l1的方向向量为a=(1,3),直线l2的方向向量为b=(-1,k).若直线l2经过点(0,5)且l1⊥l2,则直线l2的方程为()A.x+3y-5=0 B.x+3y-15=0C.x-3y+5=0 D.x-3y+15=0解析:选B∵kl1=3,kl2=-k,l1⊥l2,∴k=,l2的方程为y=-x+5,即x+3y-15=0.2.(2012·吴忠调研)若过点P(1-a,1+a)与Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是________.解析:k=tanα==.∵α为钝角,∴<0,即(a-1)(a+2)<0,故-2<a<1.答案:(-2,1)3.已知直线l过点P(3,2),且与x轴,y轴的正半轴分别交于A,B 两点如图,求△ABO的面积的最小值及此时直线l的方程.解:设A(a,0),B(0,b),(a>0,b>0),则直线l的方程为+=1,∵l过点P(3,2),∴+=1.∴1=+≥2,即ab≥24.∴S△ABO=ab≥12.当且仅当=,即a=6,b=4时,△ABO的面积最小,最小值为12.此时直线l的方程为+=1.即2x+3y-12=0.第二节两直线的位置关系[知识能否忆起]一、两条直线的位置关系设两条直线的方程是l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0,两条直线的交点坐标就是方程组的解,若方程组有唯一解,则两条直线相交,此解就是交点坐标;若方程组无解,则两条直线无公共点,此时两条直线平行;反之,亦成立.三、几种距离1.两点间的距离平面上的两点A(x1,y1),B(x2,y2)间的距离公式:d(A,B)=|AB|=.2.点到直线的距离点P(x1,y1)到直线l:Ax+By+C=0的距离d=.3.两条平行线间的距离两条平行线Ax+By+C1=0与Ax+By+C2=0间的距离d=.[小题能否全取]1.(教材习题改编)已知l1的倾斜角为45°,l2经过点P(-2,-1),Q(3,m).若l1⊥l2,则实数m为()A.6B.-6C.5 D.-5解析:选B由已知得k1=1,k2=.∵l1⊥l2,∴k1k2=-1,∴1×=-1,即m=-6.2.(教材习题改编)点(0,-1)到直线x+2y=3的距离为()C.5解析:选B d==.3.点(a,b)关于直线x+y+1=0的对称点是()A.(-a-1,-b-1) B.(-b-1,-a-1)C.(-a,-b) D.(-b,-a)解析:选B设对称点为(x′,y′),则解得x′=-b-1,y′=-a-1.4.l1:x-y=0与l2:2x-3y+1=0的交点在直线mx+3y+5=0上,则m的值为() A.3 B.5C.-5 D.-8解析:选D由得l1与l2的交点坐标为(1,1).所以m+3+5=0,m=-8.5.与直线4x+3y-5=0平行,并且到它的距离等于3的直线方程是______________________.解析:设所求直线方程为4x+3y+m=0,由3=,得m=10或-20.答案:4x+3y+10=0或4x+3y-20=01.在判断两条直线的位置关系时,首先应分析直线的斜率是否存在,两条直线都有斜率时,可根据斜率的关系作出判断,无斜率时,要单独考虑.2.在使用点到直线的距离公式或两平行线间的距离公式时,直线方程必须先化为Ax+By+C=0的形式,否则会出错.典题导入[例1](2012·浙江高考)设a∈R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x +(a+1)y+4=0平行”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件[自主解答]由a=1,可得l1∥l2;反之,由l1∥l2,可得a=1或a=-2.[答案] A在本例中若l1⊥l2,试求a.解:∵l1⊥l2,∴a×1+2×(a+1)=0,∴a=-.由题悟法1.充分掌握两直线平行与垂直的条件是解决本题的关键,对于斜率都存在且不重合的两条直线l1和l2,l1∥l2?k1=k2,l1⊥l2?k1·k2=-1.若有一条直线的斜率不存在,那么另一条直线的斜率是多少一定要特别注意.2.(1)若直线l1和l2有斜截式方程l1:y=k1x+b1,l2:y=k2x+b2,则直线l1⊥l2的充要条件是k1·k2=-1.(2)设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.则l1⊥l2?A1A2+B1B2=0.以题试法1.(2012·大同模拟)设a,b,c分别是△ABC中角A,B,C所对的边,则直线x sin A+ay+c=0与bx-y sin B+sin C=0的位置关系是()A.平行B.重合C.垂直D.相交但不垂直解析:选C由已知得a≠0,sin B≠0,所以两直线的斜率分别为k1=-,k2=,由正弦定理得k1·k2=-·=-1,所以两条直线垂直.典题导入[例2](2012·浙江高考)定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1:y=x2+a到直线l:y=x的距离等于曲线C2:x2+(y+4)2=2到直线l:y=x的距离,则实数a=________.[自主解答]因曲线C2:x2+(y+4)2=2到直线l:y=x的距离为-=2-=,所以曲线C1与直线l不能相交,故x2+a>x,即x2+a-x>0.设C1:y=x2+a上一点为(x0,y0),则点(x0,y0)到直线l的距离d===≥=,所以a =.[答案]由题悟法1.点到直线的距离问题可直接代入距离公式去求.注意直线方程为一般式.2.点到与坐标轴垂直的直线的距离,可用距离公式求解.也可用如下方法去求解:(1)点P(x0,y0)到与y轴垂直的直线y=a的距离d=|y0-a|.(2)点P(x0,y0)到与x轴垂直的直线x=b的距离d=|x0-b|.以题试法2.(2012·通化模拟)若两平行直线3x-2y-1=0,6x+ay+c=0之间的距离为,则c的值是________.解析:由题意得=≠,得a=-4,c≠-2,则6x+ay+c=0可化为3x-2y+=0,则=,解得c=2或-6.答案:2或-6典题导入[例3](2012·成都模拟)在直角坐标系中,A(4,0),B(0,4),从点P(2,0)射出的光线经直线AB反射后,再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是()A.2B.6C.3 D.2[自主解答]如图,设点P关于直线AB,y轴的对称点分别为D,C,易求得D(4,2),C(-2,0),由对称性知,D,M,N,C共线,则△PMN的周长=|PM|+|MN|+|PN|=|DM|+|MN|+|NC|=|CD|==2即为光线所经过的路程.[答案] A由题悟法对称问题主要包括中心对称和轴对称(1)中心对称①点P(x,y)关于O(a,b)的对称点P′(x′,y′)满足②直线关于点的对称可转化为点关于点的对称问题来解决.(2)轴对称①点A(a,b)关于直线Ax+By+C=0(B≠0)的对称点A′(m,n),则有②直线关于直线的对称可转化为点关于直线的对称问题来解决.以题试法3.(2012·南京调研)与直线3x-4y+5=0关于x轴对称的直线方程为()A.3x+4y+5=0B.3x+4y-5=0C.-3x+4y-5=0D.-3x+4y+5=0解析:选A与直线3x-4y+5=0关于x轴对称的直线方程是3x-4(-y)+5=0,即3x+4y+5=0.[典例](2012·银川一中月考)求经过直线l1:3x+2y-1=0和l2:5x+2y+1=0的交点,且垂直于直线l3:3x-5y+6=0的直线l的方程.[常规解法]解方程组得l1,l2的交点坐标为(-1,2).由l3的斜率得l的斜率为-.则由点斜式方程可得l的方程为y-2=-(x+1)即5x+3y-1=0.——————[高手支招]———————————————————————————运用直线系方程,有时会给解题带来方便,常见的直线系方程有:(1)与直线Ax+By+C=0平行的直线系方程是Ax+By+m=0(m∈R且m≠C);(2)与直线Ax+By+C=0垂直的直线系方程是Bx-Ay+m=0(m∈R);(3)过直线l1:A1x+B1y+C1=0与l2:A2x+B2y+C2=0的交点的直线系方程为A1x+B1y +C1+λ(A2x+B2y+C2)=0(λ∈R),但不包括l2.——————————————————————————————————————[巧思妙解]由于l过l1,l2的交点,故可设l的方程为3x+2y-1+λ(5x+2y+1)=0将其整理,得(3+5λ)x+(2+2λ)y+(-1+λ)=0,其斜率-=-,得λ=.代入直线系方程得l方程5x+3y-1=0.针对训练求与直线2x+6y-11=0平行,且与坐标轴围成的三角形面积为6的直线方程.解:由题意,设所求直线方程为2x+6y+b=0.令x=0,得y=-;令y=0,得x=-,则直线2x+6y+b=0与坐标轴的交点坐标分别为,.又所围成的三角形面积S=··=·=6,所以b2=144,所以b=±12.故所求直线方程为2x+6y+12=0或2x+6y-12=0.即为x+3y+6=0或x+3y-6=0.1.(2012·海淀区期末)已知直线l1:k1x+y+1=0与直线l2:k2x+y-1=0,那么“k1=k2”是“l1∥l2”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选C由k1=k2,1≠-1,得l1∥l2;由l1∥l2知k1×1-k2×1=0,所以k1=k2.故“k1=k2”是“l1∥l2”的充要条件.2.当0<k<时,直线l1:kx-y=k-1与直线l2:ky-x=2k的交点在()A.第一象限B.第二象限C.第三象限D.第四象限解析:选B解方程组得两直线的交点坐标为,因为0<k<,所以<0,>0,故交点在第二象限.3.(2012·长沙检测)已知直线l1的方程为3x+4y-7=0,直线l2的方程为6x+8y+1=0,则直线l1与l2的距离为()C.4 D.8解析:选B∵直线l1的方程为3x+4y-7=0,直线l2的方程为6x+8y+1=0,即为3x+4y+=0,∴直线l1与直线l2的距离为=.4.若直线l1:y=k(x-4)与直线l2关于点(2,1)对称,则直线l2恒过定点()A.(0,4) B.(0,2)C.(-2,4) D.(4,-2)解析:选B由于直线l1:y=k(x-4)恒过定点(4,0),其关于点(2,1)对称的点为(0,2).又由于直线l1:y=k(x-4)与直线l2关于点(2,1)对称,故直线l2恒过定点(0,2).5.已知直线l1:y=2x+3,若直线l2与l1关于直线x+y=0对称,又直线l3⊥l2,则l3的斜率为()A.-2 B.-D.2解析:选A依题意得,直线l2的方程是-x=2(-y)+3,即y=x+,其斜率是,由l3⊥l2,得l3的斜率等于-2.6.(2012·岳阳模拟)直线l经过两直线7x+5y-24=0和x-y=0的交点,且过点(5,1).则l的方程是()A.3x+y+4=0 B.3x-y+4=0C.x+3y-8=0 D.x-3y-4=0解析:选C设l的方程为7x+5y-24+λ(x-y)=0,即(7+λ)x+(5-λ)y-24=0,则(7+λ)×5+5-λ-24=0.解得λ=-的方程为x+3y-8=0.7.(2012·郑州模拟)若直线l1:ax+2y=0和直线l2:2x+(a+1)y+1=0垂直,则实数a 的值为________.解析:由2a+2(a+1)=0得a=-.答案:-8.已知平面上三条直线x+2y-1=0,x+1=0,x+ky=0,如果这三条直线将平面划分为六部分,则实数k的所有取值为________.解析:若三条直线有两条平行,另外一条与这两条直线相交,则符合要求,此时k=0或2;若三条直线交于一点,也符合要求,此时k=1,故实数k的所有取值为0,1,2.答案:0,1,29.(2013·临沂模拟)已知点P(4,a)到直线4x-3y-1=0的距离不大于3,则a的取值范围是________.解析:由题意得,点到直线的距离为=.又≤3,即|15-3a|≤15,解得,0≤a≤10,所以a∈[0,10].答案:[0,10]10.(2013·舟山模拟)已知+=1(a>0,b>0),求点(0,b)到直线x-2y-a=0的距离的最小值.解:点(0,b)到直线x-2y-a=0的距离为d==(a+2b)=≥(3+2)=,当且仅当a2=2b2,a+b=ab,即a=1+,b=时取等号.所以点(0,b)到直线x-2y-a=0的距离的最小值为.11.(2012·荆州二检)过点P(1,2)的直线l被两平行线l1:4x+3y+1=0与l2:4x+3y+6=0截得的线段长|AB|=,求直线l的方程.解:设直线l的方程为y-2=k(x-1),由解得A;由解得B.∵|AB|=,∴=,整理,得7k2-48k-7=0,解得k1=7或k2=-.因此,所求直线l的方程为x+7y-15=0或7x-y-5=0.12.已知直线l:3x-y+3=0,求:(1)点P(4,5)关于l的对称点;(2)直线x-y-2=0关于直线l对称的直线方程.解:设P(x,y)关于直线l:3x-y+3=0的对称点为P′(x′,y′).∵k PP′·k l=-1,即×3=-1.①又PP′的中点在直线3x-y+3=0上,∴3×-+3=0.②由①②得(1)把x=4,y=5代入③④得x′=-2,y′=7,∴P(4,5)关于直线l的对称点P′的坐标为(-2,7).(2)用③④分别代换x-y-2=0中的x,y,得关于l的对称直线方程为--2=0,化简得7x+y+22=0.1.点P到点A(1,0)和直线x=-1的距离相等,且点P到直线y=x的距离为,这样的点P的个数是()A.1 B.2C.3 D.4解析:选C∵点P到点A和定直线距离相等,∴P点轨迹为抛物线,方程为y2=4x.设P(t2,2t),则=,解得t1=1,t2=1+,t3=1-,故P点有三个.2.(2012·福建模拟)若点(m,n)在直线4x+3y-10=0上,则m2+n2的最小值是() A.2 B.2C.4 D.2解析:选C设原点到点(m,n)的距离为d,所以d2=m2+n2,又因为(m,n)在直线4x +3y-10=0上,所以原点到直线4x+3y-10=0的距离为d的最小值,此时d==2,所以m2+n2的最小值为4.3.在直线l:3x-y-1=0上求一点P,使得P到A(4,1)和B(0,4)的距离之差最大.解:如图所示,设点B关于l的对称点为B′,连接AB′并延长交l 于P,此时的P满足|PA|-|PB|的值最大.设B′的坐标为(a,b),则k BB′·k l=-1,即3·=-1.则a+3b-12=0.①又由于线段BB′的中点坐标为,且在直线l上,则3×--1=0,即3a-b-6=0.②解①②,得a=3,b=3,即B′(3,3).于是AB′的方程为=,即2x+y-9=0.解得即l与AB′的交点坐标为P(2,5).1.点(1,cosθ)(其中0≤θ≤π)到直线x sinθ+y cosθ-1=0的距离是,那么θ等于()或或解析:选B由已知得=,即|sinθ-sin2θ|=,∴4sin2θ-4sinθ-1=0或4sin2θ-4sinθ+1=0,∴sinθ=或sinθ=.∵0≤θ≤π,∴0≤sinθ≤1,∴sinθ=,即θ=或.2.已知直线l:x-y-1=0,l1:2x-y-2=0.若直线l2与l1关于l对称,则l2的方程是()A.x-2y+1=0 B.x-2y-1=0C.x+y-1=0 D.x+2y-1=0解析:选B l1与l2关于l对称,则l1上任一点关于l的对称点都在l2上,故l与l1的交点(1,0)在l2上.又易知(0,-2)为l1上一点,设其关于l的对称点(x,y),则得即(1,0),(-1,-1)为l2上两点,可得l2方程为x-2y-1=0.3.光线沿直线l1:x-2y+5=0射入,遇直线l:3x-2y+7=0后反射,求反射光线所在的直线方程.解:法一:由得即反射点M的坐标为(-1,2).又取直线x-2y+5=0上一点P(-5,0),设P关于直线l的对称点P′(x0,y0),由PP′⊥l可知,k PP′=-=.而PP′的中点Q的坐标为,Q点在l上,即3·-2·+7=0.由得根据直线的两点式方程可得所求反射光线所在直线的方程为29x-2y+33=0.法二:设直线x-2y+5=0上任意一点P(x0,y0)关于直线l的对称点为P′(x,y),则=-,又PP′的中点Q在l上,即3×-2×+7=0,由可得P点的坐标为x0=,y0=,代入方程x-2y+5=0中,化简得29x-2y+33=0,故所求反射光线所在的直线方程为29x-2y+33=0.。
必修2《直线与方程___知识点_总结》及习题

直线与方程 知识点 总结一、概念理解:1、倾斜角:①找α:直线向上方向、x 轴正方向; ②平行:α=0°;③范围:0°≤α<180° 。
2、斜率:①找k :k=tan α (α≠90°); ②与x 轴垂直:斜率k 不存在; ③范围: 斜率 k ∈ R 。
3、斜率与坐标:12122121tan x x y y x x y y k --=--==α ①构造直角三角形(数形结合); ②斜率k 值与两点先后顺序无关; ③注意下标的位置对应。
4、直线与直线的位置关系:222111:,:b x k y l b x k y l +=+= ①相交:斜率21k k ≠(前提是斜率都存在)特例----垂直时:<1> 0211=⊥k k x l 不存在,则轴,即; <2> 斜率都存在时:121-=∙k k 。
②平行:<1> 斜率都存在时:2121,b b k k ≠=; <2> 斜率都不存在时:两直线都与x 轴垂直。
③重合: 斜率都存在时:2121,b b k k ==; 二、方程与公式: 1、直线的五个方程:①点斜式:)(00x x k y y -=- 将已知点k y x 与斜率),(00直接带入即可;②斜截式:b kx y += 将已知截距 k b 与斜率 直接带入即可; ③两点式:),(2121121121y y x x x x x x y y y y ≠≠--=--其中, 将已知两点),(),,(2211y x y x 直接带入即可;④截距式:1=+bya x 将已知截距坐标),0(),0,(b a 直接带入即可;⑤一般式:0=++C By Ax ,其中A 、B 不同时为0 在距离公式当中会经常用到直线的“一般式方程”。
2、求两条直线的交点坐标:直接将两直线方程联立,解方程组即可(可简记为“方程组思想”)。
3、距离公式:①两点间距离:22122121)()(y y x x P P -+-=推导方法:构造直角三角形“勾股定理”; ②点到直线距离:2200B A C By Ax d +++=推导方法:构造直角三角形“面积相等”;③平行直线间距离:2221BA C C d +-=推导方法:在y 轴截距),0(1C 代入②式;4、中点坐标公式:已知两点),(),,(2211y x B y x A ①AB 中点),(00y x :)2,2(2121y y x x ++ 推导方法:构造直角“相似三角形”;一.选择题1.(安徽高考) 过点(1,0)且与直线x-2y=0平行的直线方程是( ) A.x-2y-1=0 B. x-2y+1=0 C. 2x+y-2=0 D. x+2y-1=02. 过点(1,3)P -且垂直于直线032=+-y x 的直线方程为( )A. 012=-+y xB. 052=-+y xC. 052=-+y xD. 072=+-y x 3. 已知过点(2,)A m -和(,4)B m 的直线与直线012=-+y x 平行,则m 的值为( ) A. 0 B. 8- C. 2 D. 104.(安徽高考)直线过点(-1,2),且与直线2x-3y+4=0垂直,则直线的方程是( ) A . 3x+2y-1=0 B. 3x+2y+7=0 C. 2x-3y+5=0 D. 2x-3y+8=05.设直线ax+by+c=0的倾斜角为θ,且sin cos 0θθ+=则a,b 满足 ( ) A. a+b=1 B. a-b=1 C. a+b=0 D. a-b=06. 如果直线ax+2y+2=0与直线3x-y-2=0平行,则系数a= A 、 -3 B 、-6 C 、23- D 、327.点P (-1,2)到直线8x-6y+15=0的距离为( ) A 2 B 21 C 1 D 278. 直线mx-y+2m+1=0经过一定点,则该点的坐标是 A (-2,1) B (2,1) C (1,-2) D (1,2)9. (上海文,15)已知直线12:(3)(4)10,:2(3)230,l k x k y l k x y -+-+=--+=与平行,则k 得值是( ) A. 1或3 B.1或5 C.3或5 D.1或210、若图中的直线L 1、L 2、L 3的斜率分别为K 1、K 2、K 3则( )A 、K 1﹤K 2﹤K 3B 、K 2﹤K 1﹤K 3C 、K 3﹤K 2﹤K 1D 、K 1﹤K 3﹤K 211.(北京卷)“m =21”是“直线(m +2)x +3my +1=0与直线(m -2)x +(m +2)y -3=0相互垂直”的( ) (A )充分必要条件 (B )充分而不必要条件(C )必要而不充分条件 (D )既不充分也不必要条件 12、与直线2x+3y-6=0关于点(1,-1)对称的直线是( )A.3x-2y-6=0B.2x+3y+7=0C. 3x-2y-12=0D. 2x+3y+8=0 13. 若直线ax + by + c = 0在第一、二、三象限,则( )A. ab >0,bc >0B. ab >0,bc <0C. ab <0,bc >0D. ab <0,bc <0 14.(北京文)“m=21”是“直线(m+2)x+3my+1=0与直线(m -2)x+(m+2)y -3=0相互垂直”的 ( )A.充分必要条件B.充分而不必要条件C.必要而不充分条件D.既不充分也不必要条件15. 如果直线 l 经过两直线2x - 3y + 1 = 0和3x - y - 2 = 0的交点,且与直线y = x 垂直,则原点到直线 l 的距离是( )A. 2B. 1C. 2 D 、22 16. 原点关于x - 2y + 1 = 0的对称点的坐标为( )A. ⎪⎭⎫ ⎝⎛52 ,54- B. ⎪⎭⎫ ⎝⎛54 ,52- C. ⎪⎭⎫ ⎝⎛52 ,54 D. ⎪⎭⎫ ⎝⎛54 ,52- 二、填空题1. 点(1,1)P -到直线10x y -+=的距离是________________.2.已知A(-4,-6),B(-3,-1),C(5,a)三点共线,则a 的值为( )3.经过两直线11x+3y -7=0和12x+y -19=0的交点,且与A (3,-2),B (-1,6)等距离的直线的方程是 。
必修二第三章直线与方程知识点总结及练习(答案)

必修二 第三章 直线与方程(1)直线的倾斜角定义:x轴正向与直线向上方向或重合时,我们规定它的倾斜角为0度。
因此,倾斜角的取值范围是(2)直线的斜率①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率常用 当直线l与x 轴平行或重合时, α=0°, k = tan0°=0; 当直线l 与x轴垂直时, α= 90°, k 不存在. 当[)90,0∈α时,0≥k ; 当()180,90∈α时,0<k ; 当90=α时,k 不存在。
②过两点的直线的斜率公式:)(211212x x x x y y k ≠--=( P1(x1,y1),P 2(x2,y2),x1≠x2)注意下面四点:(1)当21x x =时,公式右边无意义,直线的斜率不存在,倾斜角为90°;(2)k 与P 1、P 2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得; (4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。
注意:当直线的斜率为0°时,k=0,直线的方程是1。
当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示.但因l 上每一点的横坐标都等于x 1,所以它的方程是x=x1。
(7)两条直线的交点0:1111=++C y B x A l 0:2222=++C y B x A l 相交 交点坐标即方程组⎩⎨⎧=++=++00222111C y B x A C y B x A 的一组解。
方程组无解21//l l ⇔ ; 方程组有无数解⇔1l 与2l 重合 (8)两点间距离公式:设1122(,),A x y B x y ,()是平面直角坐标系中的两个点, 则222121||()()AB x x y y =-+-(9)点到直线距离公式:一点()00,y x P 到直线0:1=++C By Ax l 的距离2200BA C By Ax d +++=(10)两平行直线距离公式已知两条平行线直线1l 和2l 的一般式方程为1l :01=++C By Ax ,2l :02=++C By Ax ,则1l 与2l 的距离为2221BA C C d +-=直线的方程1.设a ,b ,c 是互不相等的三个实数,如果A (a,a 3)、B (b ,b3)、C (c ,c 3)在同一直线上,求证:a+b+c =0.证明 ∵A 、B 、C 三点共线,∴k AB =k AC ,∴ca c ab a b a --=--3333,化简得a2+ab +b 2=a 2+ac +c 2,∴b 2-c 2+ab -ac =0,(b -c )(a+b +c )=0, ∵a 、b 、c互不相等,∴b -c ≠0,∴a +b +c =0. 2.若实数x ,y 满足等式(x-2)2+y2=3,那么xy的最大值为ﻩ ﻩ( )A .21ﻩ B .33ﻩﻩ C.23ﻩ ﻩﻩ D .3答案D3.求经过点A(-5,2)且在x 轴上的截距等于在y 轴上的截距的2倍的直线方程; 解 ①当直线l 在x、y 轴上的截距都为零时,设所求的直线方程为y =kx, 将(-5,2)代入y =kx 中,得k =-52,此时,直线方程为y =-52x , 即2x +5y =0. ②当横截距、纵截距都不是零时,设所求直线方程为ay a x+2=1,将(-5,2)代入所设方程,解得a =-21, 此时,直线方程为x +2y+1=0.综上所述,所求直线方程为x +2y+1=0或2x +5y=0.4.直线l 经过点P (3,2)且与x ,y 轴的正半轴分别交于A、B 两点,△O AB的面积为12,求直线l 的方程.解 方法一 设直线l 的方程为1=+bya x (a >0,b >0), ∴A (a ,0),B(0,b ), ∴⎪⎩⎪⎨⎧=+=.123,24ba ab 解得⎩⎨⎧==.4,6b a∴所求的直线方程为46yx +=1,即2x +3y -12=0. 方法二 设直线l 的方程为y -2=k(x -3), 令y =0,得直线l 在x 轴上的截距a =3-k2,令x =0,得直线l 在y 轴上的截距b=2-3k. ∴⎪⎭⎫ ⎝⎛-k 23(2-3k )=24.解得k=-32.∴所求直线方程为y -2=-32(x -3).即2x +3y -12=0.9.已知线段PQ 两端点的坐标分别为(-1,1)、(2,2),若直线l :x +my +m =0与线段P Q有交点,求m的取值范围.解 方法一 直线x +my+m =0恒过A (0,-1)点. kAP =1011+--=-2,k AQ =2021---=23, 则-m 1≥23或-m 1≤-2, ∴-32≤m ≤21且m ≠0.又∵m =0时直线x +m y+m =0与线段PQ 有交点,∴所求m的取值范围是-32≤m≤21. 方法二 过P 、Q两点的直线方程为y -1=1212+-(x +1),即y =31x +34,代入x+my +m =0, 整理,得x=-37+m m . 由已知-1≤-37+m m ≤2, 解得-32≤m ≤21. 两直线方程例1 已知直线l 1:ax +2y+6=0和直线l 2:x+(a -1)y +a 2-1=0, (1)试判断l 1与l 2是否平行; (2)l 1⊥l 2时,求a的值.解 (1)方法一 当a=1时,l 1:x +2y +6=0,l 2:x =0,l1不平行于l2;当a=0时,l1:y =-3,l2:x -y -1=0,l 1不平行于l2; ﻩ ﻩ ﻩ当a≠1且a ≠0时,两直线可化为 l 1:y =-x a 2-3,l 2:y =x a-11-(a+1), l 1∥l2⇔⎪⎩⎪⎨⎧+-≠--=-)1(3112a a a ,解得a =-1, ﻩﻩﻩ综上可知,a=-1时,l1∥l 2,否则l 1与l2不平行.ﻩ ﻩ ﻩ ﻩ方法二 由A 1B 2-A 2B 1=0,得a(a -1)-1×2=0,由A1C 2-A2C 1≠0,得a(a2-1)-1×6≠0,ﻩ∴l 1∥l 2⇔⎪⎩⎪⎨⎧≠⨯--=⨯--061)1(021)1(2a a a a ﻩﻩ⇔⎪⎩⎪⎨⎧≠-=--6)1(0222a a a a ⇒a =-1,ﻩﻩﻩﻩ 故当a =-1时,l 1∥l 2,否则l1与l2不平行.ﻩ ﻩ ﻩﻩﻩﻩ(2)方法一 当a =1时,l 1:x +2y+6=0,l 2:x =0,l 1与l 2不垂直,故a =1不成立. ﻩﻩﻩﻩ当a ≠1时,l1:y =-2a x -3,l2:y=x a -11-(a+1),ﻩ由⎪⎭⎫⎝⎛-2a ·a-11=-1⇒a =32.ﻩ 方法二 由A1A 2+B 1B2=0,得a +2(a -1)=0⇒a =32.例3 已知直线l 过点P(3,1)且被两平行线l 1:x +y +1=0,l2:x +y+6=0截得的线段长为5,求直线l 的方程.解 方法一 若直线l 的斜率不存在,则直线l 的方程为x=3,此时与l1,l 2的交点分别是A (3,-4),B (3,-9), 截得的线段长|AB |=|-4+9|=5,符合题意.ﻩﻩﻩ若直线l的斜率存在时,则设直线l 的方程为y =k (x-3)+1,分别与直线l 1,l 2的方程联立,由⎩⎨⎧=+++-=011)3(y x x k y ,解得A⎪⎭⎫ ⎝⎛+-+-141,123k k k k .ﻩﻩﻩﻩ ﻩ ﻩ ﻩ 8分由⎩⎨⎧=+++-=061)3(y x x k y ,解得B ⎪⎭⎫ ⎝⎛+-+-191173k k ,k k ,由两点间的距离公式,得2173123⎪⎭⎫ ⎝⎛+--+-k k k k +2191141⎪⎭⎫⎝⎛+--+-k k k k =25, 解得k =0,即所求直线方程为y =1.ﻩﻩ ﻩ ﻩ ﻩﻩﻩ 综上可知,直线l 的方程为x =3或y =1. ﻩﻩ ﻩﻩﻩﻩ方法二 设直线l与l 1,l 2分别相交于A (x 1,y1),B (x 2,y 2),则x 1+y 1+1=0,x 2+y 2+6=0,两式相减,得(x 1-x2)+(y 1-y 2)=5 ﻩﻩ① ﻩﻩﻩﻩ6分又(x 1-x 2)2+(y 1-y 2)2=25ﻩﻩﻩ②联立①②可得⎩⎨⎧=-=-052121y y x x 或⎩⎨⎧=-=-502121y y x x ,ﻩﻩﻩﻩﻩ10分由上可知,直线l 的倾斜角分别为0°和90°, 故所求的直线方程为x=3或y =1.例4 求直线l 1:y=2x +3关于直线l :y=x +1对称的直线l2的方程.解 方法一 由⎩⎨⎧+=+=132x y x y 知直线l 1与l的交点坐标为(-2,-1),∴设直线l2的方程为y +1=k (x +2),即kx -y +2k -1=0.在直线l上任取一点(1,2),由题设知点(1,2)到直线l 1、l 2的距离相等, 由点到直线的距离公式得 221122kk k +-+-=22)1(2322-++-,解得k=21(k =2舍去),∴直线l2的方程为x -2y =0. 方法二 设所求直线上一点P (x ,y),则在直线l 1上必存在一点P 1(x 0,y 0)与点P 关于直线l对称. 由题设:直线P P1与直线l垂直,且线段PP 1的中点P 2⎪⎪⎭⎫ ⎝⎛++2,200y y x x 在直线l 上.∴⎪⎪⎩⎪⎪⎨⎧++=+-=•--122110000x x y y x x yy ,变形得⎩⎨⎧+=-=1100x y y x , 代入直线l 1:y=2x +3,得x +1=2×(y-1)+3,整理得x -2y =0.所以所求直线方程为x -2y =0.直线与方程1.设直线l 与x 轴的交点是P ,且倾斜角为α,若将此直线绕点P 按逆时针方向旋转45°,得到直线的倾斜角为α+45°,则ﻩﻩ ﻩ ﻩ ﻩ ﻩ ﻩ ( )A.0°≤α<180°ﻩ ﻩ ﻩﻩB.0°≤α<135°C . 0°<α≤135°ﻩﻩﻩﻩD. 0°<α<135°答案 D2.曲线y=x 3-2x +4在点(1,3)处的切线的倾斜角为ﻩﻩ( ) A .30°ﻩ ﻩB .45°ﻩﻩC .60° ﻩD .120°答案 B3.过点M (-2,m),N (m,4)的直线的斜率等于1,则m 的值为ﻩﻩ ﻩ( )A .1ﻩ ﻩﻩ ﻩB .4 ﻩﻩﻩC .1或3ﻩ ﻩD .1或4答案 A4.过点P(-1,2)且方向向量为a =(-1,2)的直线方程为ﻩﻩﻩﻩ( )A .2x+y=0B.x-2y +5=0 C .x -2y =0ﻩﻩﻩD .x +2y -5=0 答案 A5.一条直线经过点A (-2,2),并且与两坐标轴围成的三角形的面积为1,则此直线的方程为 . 答案 x +2y -2=0或2x+y +2=0例1 已知三点A (1,-1),B (3,3),C (4,5). 求证:A、B、C三点在同一条直线上.证明∵A (1,-1),B (3,3),C (4,5), ∴k A B=1313-+=2,k B C=3435--=2,∴k A B=kBC , ∴A 、B 、C三点共线.例2已知实数x ,y 满足y =x 2-2x +2 (-1≤x≤1). 试求:23++x y 的最大值与最小值. 解 由23++x y 的几何意义可知,它表示经过定点P(-2,-3)与曲线段AB 上任一点(x ,y )的直线的斜率k,如图可知:k P A≤k ≤k PB ,由已知可得:A (1,1),B (-1,5), ∴34≤k ≤8,故23++x y 的最大值为8,最小值为34.例3 求适合下列条件的直线方程:(1)经过点P (3,2),且在两坐标轴上的截距相等;(2)经过点A (-1,-3),倾斜角等于直线y =3x的倾斜角的2倍. 解 (1)方法一 设直线l 在x ,y 轴上的截距均为a ,若a=0,即l 过点(0,0)和(3,2),∴l 的方程为y=32x ,即2x -3y =0. 若a≠0,则设l 的方程为1=+b ya x ,∵l过点(3,2),∴123=+aa ,∴a =5,∴l的方程为x +y -5=0, 综上可知,直线l 的方程为2x -3y=0或x+y-5=0. 方法二 由题意知,所求直线的斜率k 存在且k ≠0,设直线方程为y-2=k(x-3),令y=0,得x=3-k2,令x =0,得y =2-3k, 由已知3-k 2=2-3k ,解得k =-1或k =32,∴直线l 的方程为:y -2=-(x -3)或y -2=32(x -3), 即x +y -5=0或2x -3y =0.(2)由已知:设直线y =3x 的倾斜角为α,则所求直线的倾斜角为2α. ∵tan α=3,∴t an2α=αα2tan 1tan 2-=-43.又直线经过点A (-1,-3),、 因此所求直线方程为y +3=-43(x +1),即3x +4y +15=0. 例4 (12分)过点P (2,1)的直线l 交x 轴、y 轴正半轴于A 、B两点,求使: (1)△AOB 面积最小时l的方程; (2)|P A|·|P B|最小时l的方程. 解 方法一 设直线的方程为1=+bya x (a >2,b >1), 由已知可得112=+b a (1)∵2ba 12•≤b a 12+=1,∴a b≥8.ﻩ∴S △A OB =21ab ≥4. ﻩﻩ当且仅当a 2=b 1=21,即a =4,b =2时,S △AOB 取最小值4,此时直线l 的方程为24yx +=1,即x+2y-4=0. 6分 (2)由a 2+b1=1,得ab -a-2b =0, 变形得(a -2)(b-1)=2,|PA |·|PB |=22)01()2(-+-a ·22)1()02(b -+-=]4)1[(]1)2[(22+-⋅+-b a ≥)1(4)2(2-⋅-b a .ﻩ当且仅当a -2=1,b -1=2,即a =3,b =3时,|PA |·|PB |取最小值4.此时直线l 的方程为x+y -3=0.ﻩ 方法二 设直线l 的方程为y-1=k(x-2) (k<0),则l 与x 轴、y 轴正半轴分别交于A ⎪⎭⎫ ⎝⎛-0,12k 、B (0,1-2k).(1)S △AOB =21⎪⎭⎫ ⎝⎛-k 12(1-2k )=21×⎥⎦⎤⎢⎣⎡-+-+)1()4(4k k ≥21(4+4)=4. 当且仅当-4k =-k 1,即k=-21时取最小值,此时直线l 的方程为y-1=-21(x-2),即x+2y-4=0.6分(2)|PA |·|PB |=22441)1(k k ++=84422++k k ≥4, 当且仅当24k=4k 2,即k =-1时取得最小值,此时直线l 的方程为y -1=-(x-2),即x +y -3=0.一、选择题1.过点(1,3)作直线l ,若经过点(a ,0)和(0,b),且a ∈N*,b ∈N *,则可作出的l 的条数为( )·A .1ﻩﻩ ﻩ B.2 ﻩﻩ C.3ﻩD .4答案B2.经过点P (1,4)的直线在两坐标轴上的截距都是正的,且截距之和最小,则直线的方程为( ) A .x +2y -6=0 ﻩﻩﻩ ﻩ ﻩ B .2x +y -6=0C .x -2y +7=0ﻩﻩﻩﻩD .x-2y -7=0答案B3.若点A (2,-3)是直线a 1x +b 1y +1=0和a2x +b 2y +1=0的公共点,则相异两点(a1,b1)和(a2,b 2)所确定的直线方程是 ﻩﻩﻩﻩﻩﻩ ﻩﻩﻩ ﻩ ( ) A .2x -3y+1=0ﻩﻩﻩﻩﻩB .3x -2y +1=0C .2x -3y -1=0 ﻩﻩﻩD.3x -2y -1=0答案A二、填空题4.已知a >0,若平面内三点A(1,-a),B (2,a 2),C (3,a 3)共线,则a = . 答案 1+25.已知两点A (-1,-5),B (3,-2),若直线l 的倾斜角是直线AB 倾斜角的一半,则l 的斜率是 . 答案31三、解答题6.已知线段P Q两端点的坐标分别为(-1,1)、(2,2),若直线l :x +my +m=0与线段PQ 有交点,求m 的取值范围.解 方法一 直线x +my +m =0恒过A (0,-1)点. k AP =1011+--=-2,kAQ =2021---=23,则-m 1≥23或-m 1≤-2,∴-32≤m≤21且m ≠0. 又∵m =0时直线x +my +m=0与线段PQ 有交点,∴所求m 的取值范围是-32≤m ≤21. 方法二 过P 、Q 两点的直线方程为 y-1=1212+-(x +1),即y =31x +34,代入x +my +m =0,整理,得x =-37+m m .由已知-1≤-37+m m ≤2, 解得-32≤m ≤21. 7.已知直线l 与两坐标轴围成的三角形的面积为3,分别求满足下列条件的直线l 的方程: (1)过定点A (-3,4);(2)斜率为61. 解 (1)设直线l的方程是y =k (x +3)+4,它在x 轴,y 轴上的截距分别是-k4-3,3k +4, 由已知,得(3k +4)(k4+3)=±6,解得k1=-32或k2=-38. 直线l 的方程为2x +3y -6=0或8x+3y +12=0. (2)设直线l在y 轴上的截距为b,则直线l 的方程是y =61x +b ,它在x 轴上的截距是-6b , 由已知,得|-6b ·b|=6,∴b =±1.∴直线l 的方程为x -6y +6=0或x -6y -6=0. 8.已知两点A (-1,2),B (m ,3). (1)求直线AB 的方程;(2)已知实数m ∈⎥⎥⎦⎤⎢⎢⎣⎡---13,133,求直线AB 的倾斜角α的取值范围. 解 (1)当m =-1时,直线AB的方程为x =-1,当m ≠-1时,直线AB 的方程为y -2=11+m (x +1). (2)①当m =-1时,α=090;②当m ≠-1时,m+1∈(]3,00,33 ⎪⎪⎭⎫⎢⎢⎣⎡-,∴k =11+m ∈(-∞,-3]∪⎪⎪⎭⎫⎢⎢⎣⎡+∞,33, ∴α∈[)(]0120,9090,30 .综合①②知,直线AB 的倾斜角α∈[]0120,30.9.过点P(3,0)作一直线,使它夹在两直线l 1:2x -y -2=0与l 2:x +y +3=0之间的线段AB 恰被点P 平分,求此直线的方程.解 方法一 设点A(x ,y )在l 1上,由题意知⎪⎪⎩⎪⎪⎨⎧=+=+0232B B y y x x ,∴点B (6-x ,-y ),解方程组⎩⎨⎧=+-+-=--03)()6(022y x y x ,得⎪⎪⎩⎪⎪⎨⎧==316311y x ,∴k =833110316=--. ∴所求的直线方程为y =8(x -3),即8x -y -24=0. 方法二 设所求的直线方程为y =k(x -3),则⎩⎨⎧=---=022)3(y x x k y ,解得⎪⎪⎩⎪⎪⎨⎧-=--=24223k ky k k x A A , 由⎩⎨⎧=++-=03)3(y x x k y ,解得⎪⎪⎩⎪⎪⎨⎧+-=+-=16133k ky k k x B B . ∵P (3,0)是线段AB的中点,∴y A +y B =0,即24-k k +16+-k k =0,∴k 2-8k=0,解得k=0或k =8. 又∵当k =0时,x A=1,xB =-3,此时32312≠-=+B A x x ,∴k =0舍去,∴所求的直线方程为y=8(x-3), 即8x-y-24=0.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学直线与方程知识点归纳与常考题型专题练习(附解析) 知识点:一、直线与方程(1)直线的倾斜角定义:x 轴正向与直线向上方向之间所成的角叫直线的倾斜角。
特别地,当直线与x 轴平行或重合时,我们规定它的倾斜角为0度。
因此,倾斜角的取值范围是0°≤α<180°(2)直线的斜率①定义:倾斜角不是90°的直线,它的倾斜角的正切叫做这条直线的斜率。
直线的斜率常用k 表示。
即。
斜率反映直线与轴的倾斜程度。
tan k α=当时,; 当时,; 当时,不存[) 90,0∈α0≥k () 180,90∈α0<k 90=αk 在。
②过两点的直线的斜率公式: )(211212x x x x y y k ≠--=注意下面四点:(1)当时,公式右边无意义,直线的斜率不存在,倾斜角为90°;21x x =(2)k 与P 1、P 2的顺序无关;(3)以后求斜率可不通过倾斜角而由直线上两点的坐标直接求得;(4)求直线的倾斜角可由直线上两点的坐标先求斜率得到。
(3)直线方程①点斜式:直线斜率k ,且过点)(11x x k y y -=-()11,y x 注意:当直线的斜率为0°时,k=0,直线的方程是y =y 1。
当直线的斜率为90°时,直线的斜率不存在,它的方程不能用点斜式表示.但因l 上每一点的横坐标都等于x 1,所以它的方程是x =x 1。
②斜截式:,直线斜率为k ,直线在y 轴上的截距为bb kx y +=③两点式:()直线两点,112121y y x x y y x x --=--1212,x x y y ≠≠()11,y x ()22,y x ④截矩式:1x y a b+=其中直线与轴交于点,与轴交于点,即与轴、轴的截距分别为。
l x (,0)a y (0,)b l x y ,a b ⑤一般式:(A ,B 不全为0)0=++C By Ax 注意:各式的适用范围 特殊的方程如:○1○2平行于x 轴的直线:(b 为常数); 平行于y 轴的直线:(a 为常数);b y =a x =(5)直线系方程:即具有某一共同性质的直线(一)平行直线系平行于已知直线(是不全为0的常数)的直线系:0000=++C y B x A 00,B A (C 为常数)000=++C y B x A (二)过定点的直线系(ⅰ)斜率为k 的直线系:,直线过定点;()00x x k y y -=-()00,y x (ⅱ)过两条直线,的交点的直线系方程0:1111=++C y B x A l 0:2222=++C y B x A l 为(为参数),其中直线不在直线系中。
()()0222111=+++++C y B x A C y B x A λλ2l (6)两直线平行与垂直当,时,111:b x k y l +=222:b x k y l +=;212121,//b b k k l l ≠=⇔12121-=⇔⊥k k l l注意:利用斜率判断直线的平行与垂直时,要注意斜率的存在与否。
(7)两条直线的交点相交0:1111=++C y B x A l 0:2222=++C y B x A l 交点坐标即方程组的一组解。
⎩⎨⎧=++=++00222111C y B x A C y B x A 方程组无解 ;方程组有无数解与重合21//l l ⇔⇔1l 2l (8)两点间距离公式:设是平面直角坐标系中的两个点,1122(,),A x y B x y ,()则 ||AB =(9)点到直线距离公式:一点到直线的距离()00,y x P 0:1=++C By Ax l 2200B A CBy Ax d +++=(10)两平行直线距离公式在任一直线上任取一点,再转化为点到直线的距离进行求解。
常考题:一.选择题(共20小题)1.直线L 1:ax+3y+1=0,L 2:2x+(a+1)y+1=0,若L 1∥L 2,则a 的值为( )A .﹣3B .2C .﹣3或2D .3或﹣22.直线xsinα+y+2=0的倾斜角的取值范围是( )A .[0,π)B .[0,]∪[,π)C .[0,]D .[0,]∪(,π)3.已知点A (﹣1,0),B (1,0),C (0,1),直线y=ax+b (a >0)将△ABC 分割为面积相等的两部分,则b 的取值范围是( )A .(0,1)B .C .D .4.直线3x+y﹣1=0的倾斜角是( )A .B .C .D .5.已知点(a ,2)(a >0)到直线l :x﹣y+3=0的距离为1,则a=( )A .B .C .D .6.已知点P 在直线x+3y﹣2=0上,点Q 在直线x+3y+6=0上,线段PQ 的中点为M (x 0,y 0),且y 0<x 0+2,则的取值范围是( )A .[﹣,0)B .(﹣,0)C .(﹣,+∞)D .(﹣∞,﹣)∪(0,+∞)7.设m ∈R ,过定点A 的动直线x+my=0和过定点B 的直线mx﹣y﹣m+3=0交于点P (x ,y ),则|PA|+|PB|的取值范围是( )A .[,2]B .[,2]C .[,4]D .[2,4]8.若直线l 1:mx+2y+1=0与直线l 2:x+y﹣2=0互相垂直,则实数m 的值为( )A.2B.﹣2C.D.﹣9.直线(2m+1)x+(m+1)y﹣7m﹣4=0过定点( )A.(1,﹣3)B.(4,3)C.(3,1)D.(2,3)10.直线(a2+1)x﹣2ay+1=0的倾斜角的取值范围是( )A.[0,]B.[,]C.[,]D.[0,]∪[,π)11.等腰三角形两腰所在直线的方程分别为x+y﹣2=0与x﹣7y﹣4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为( )A.3B.2C.D.12.若动点A,B分别在直线l1:x+y﹣7=0和l2:x+y﹣5=0上移动,则AB的中点M到原点的距离的最小值为( )A.3B.2C.3D.413.已知点(﹣1,2)和(,0)在直线l:ax﹣y+1=0(a≠0)的同侧,则直线l倾斜角的取值范围是( )A.(,)B.(0,)∪(,π)C.(,)D.(,)14.直线l过点P(﹣1,2)且与以点M(﹣3,﹣2)、N(4,0)为端点的线段恒相交,则l的斜率取值范围是( )A.[﹣,5]B.[﹣,0)∪(0,2]C.(﹣∞,﹣]∪[5,+∞)D.(﹣∞,﹣]∪[2,+∞)15.已知直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,垂足为P(1,p),则m﹣n+p的值是( )A.24B.20C.0D.﹣416.过点P(﹣2,2)作直线l,使直线l与两坐标轴在第二象限内围成的三角形面积为8,这样的直线l一共有( )A.3条B.2条C.1条D.0条17.已知直线l:3x﹣4y+m=0上存在不同的两点M与N,它们都满足与两点A (﹣1,0),B(1,0)连线的斜率k MA与k MB之积为﹣1,则实数m的取值范围是( )A.(﹣3,3)B.(﹣4,4)C.(﹣5,5)D.[﹣5,5]18.点P到点及到直线的距离都相等,如果这样的点恰好只有一个,那么a的值是( )A.B.C.D.19.已知直线l:x﹣my+m=0上存在点M满足与两点A(﹣1,0),B(1,0)连线的斜率k MA与k MB之积为3,则实数m的取值范围是( )A.B.∪C.∪D.以上都不对20.若两平行直线l1:x﹣2y+m=0(m>0)与l2:2x+ny﹣6=0之间的距离是,则m+n=( )A.0B.1C.﹣2D.﹣1二.填空题(共9小题)21.若直线l:+=1(a>0,b>0)经过点(1,2),则直线l在x轴和y轴的截距之和的最小值是 .22.在平面直角坐标系xOy中,设定点A(a,a),P是函数y=(x>0)图象上一动点,若点P,A之间的最短距离为2,则满足条件的实数a的所有值为 .23.已知两点A(﹣m,0),B(m,0)(m>0),如果在直线3x+4y+25=0上存在点P,使得∠APB=90°,则m的取值范围是 .24.已知直线(1﹣a)x+(a+1)y﹣4(a+1)=0(其中a为实数)过定点P,点Q在函数的图象上,则PQ连线的斜率的取值范围是 .25.直线l:xtan+y+1=0的倾斜角α= .26.已知动点P(x,y)满足|x﹣1|+|y﹣a|=1,O为坐标原点,若的最大值的取值范围为,则实数a的取值范围是 .27.过点P(3,﹣1)引直线,使点A(2,﹣3),B(4,5)到它的距离相等,则这条直线的方程为 .28.在平面直角坐标系xOy中,将点A(2,1)绕原点O逆时针旋转到点B,若直线OB的倾斜角为α,则cosα的值为 .29.在平面直角坐标系xOy中,直线l1:kx﹣y+2=0与直线l2:x+ky﹣2=0相交于点P,则当实数k变化时,点P到直线x﹣y﹣4=0的距离的最大值为 .三.解答题(共21小题)30.已知直线l1的方程为3x+4y﹣12=0.(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.31.已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.32.已知直线l:kx﹣y+1+2k=0(k∈R).(1)证明:直线l过定点;(2)若直线l不经过第四象限,求k的取值范围;(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.33.设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).(1)若l在两坐标轴上的截距相等,求l的方程;(2)若l不经过第二象限,求实数a的取值范围.34.已知直线l:y=(1﹣m)x+m(m∈R).(Ⅰ)若直线l的倾斜角,求实数m的取值范围;(Ⅱ)若直线l分别与x轴,y轴的正半轴交于A,B两点,O是坐标原点,求△AOB面积的最小值及此时直线l的方程.35.在直角坐标系中,已知射线OA:x﹣y=0(x≥0),OB:2x+y=0(x≥0).过点P(1,0)作直线分别交射线OA,OB于点A,B.(1)当AB的中点在直线x﹣2y=0上时,求直线AB的方程;(2)当△AOB的面积取最小值时,求直线AB的方程.(3)当PA•PB取最小值时,求直线AB的方程.36.在△ABC中,已知BC边上的高所在直线的方程为x﹣2y+1=0,∠A的平分线所在直线的方程为y=0.若点B的坐标为(1,2),求点C的坐标.37.已知x,y满足直线l:x+2y=6.(1)求原点O关于直线l的对称点P的坐标;(2)当x∈[1,3]时,求的取值范围.38.已知过原点O的一条直线与函数y=log8x的图象交于A、B两点,分别过点A、B作y轴的平行线与函数的y=log2x的图象交于C、D两点.(1)证明点C、D和原点O在同一条直线上;(2)当BC平行于x轴时,求点A的坐标.39.已知直线l:3x﹣y+3=0,求:(1)点P(4,5)关于l的对称点;(2)直线x﹣y﹣2=0关于直线l对称的直线方程.40.已知过点A(1,1)且斜率为﹣m(m>0)的直线l与x轴、y轴分别交于P、Q,过P、Q作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ面积的最小值.41.已知直线l=1.(1)若直线的斜率小于2,求实数m的取值范围;(2)若直线分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最小值及此时直线的方程.42.有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=13km,BC=10km.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)(Ⅰ)若希望点P到三镇距离的平方和为最小,点P应位于何处?(Ⅱ)若希望点P到三镇的最远距离为最小,点P应位于何处?43.已知直线l过点M(1,1),且与x轴,y轴的正半轴分别相交于A,B两点,O为坐标原点.求:(1)当|OA|十|OB|取得最小值时,直线l的方程;(2)当|MA|2+|MB|2取得最小值时,直线l的方程.44.光线从点A(2,3)射出,若镜面的位置在直线l:x+y+1=0上,反射光线经过B(1,1),求入射光线和反射光线所在直线的方程,并求光线从A到B 所走过的路线长.45.过点P(3,0)有一条直线l,它夹在两条直线l1:2x﹣y﹣2=0与l2:x+y+3=0之间的线段恰被点P平分,求直线l的方程.46.已知△ABC的两个顶点A(﹣10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.47.如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD 边所在直线的方程分别是x+4y﹣7=0,3x+2y﹣11=0,且对角线AC和BD的交点为M(2,0)(1)求点A的坐标(2)求CD边所在直线的方程.48.两条互相平行的直线分别过点A(6,2)和B(﹣3,﹣1),并且各自绕着A,B旋转,如果两条平行直线间的距离为d.求:(1)d的变化范围;(2)当d取最大值时两条直线的方程.49.已知三条直线l1:2x﹣y+a=0(a>0),l2:﹣4x+2y+1=0和l3:x+y﹣1=0,且l1与l2的距离是;(1)求a的值;(2)能否找到一点P同时满足下列三个条件:①P是第一象限的点;②点P到l1的距离是点P到l2的距离的;③点P到l1的距离与点P到l3的距离之比是:?若能,求点P的坐标;若不能,请说明理由.50.如图,矩形OABC的顶点O为原点,AB边所在直线的方程为3x+4y﹣25=0,顶点B的纵坐标为10.(Ⅰ)求OA,OC边所在直线的方程;(Ⅱ)求矩形OABC的面积.必修二第三章直线与方程知识点与常考题(附解析)参考答案与试题解析一.选择题(共20小题)1.直线L1:ax+3y+1=0,L2:2x+(a+1)y+1=0,若L1∥L2,则a的值为( )A.﹣3B.2C.﹣3或2D.3或﹣2【解答】解:直线L1:ax+3y+1=0的斜率为:,直线L1∥L2,所以L2:2x+(a+1)y+1=0的斜率为:所以=;解得a=﹣3,a=2(舍去)故选:A.2.直线xsinα+y+2=0的倾斜角的取值范围是( )A.[0,π)B.[0,]∪[,π)C.[0,]D.[0,]∪(,π)【解答】解:直线xsinα+y+2=0的斜率为k=﹣sinα,∵﹣1≤sinα≤1,∴﹣1≤k≤1∴倾斜角的取值范围是[0,]∪[π,π)故选:B.3.已知点A(﹣1,0),B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC 分割为面积相等的两部分,则b的取值范围是( )A.(0,1)B.C.D.【解答】解:解法一:由题意可得,三角形ABC的面积为=1,由于直线y=ax+b(a>0)与x轴的交点为M(﹣,0),由直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,可得b>0,故﹣≤0,故点M在射线OA上.设直线y=ax+b和BC的交点为N,则由可得点N的坐标为(,).①若点M和点A重合,则点N为线段BC的中点,故N(,),把A、N两点的坐标代入直线y=ax+b,求得a=b=.②若点M在点O和点A之间,此时b>,点N在点B和点C之间,由题意可得三角形NMB的面积等于,即=,即=,可得a=>0,求得b<,故有<b<.③若点M在点A的左侧,则b<,由点M的横坐标﹣<﹣1,求得b>a.设直线y=ax+b和AC的交点为P,则由求得点P的坐标为(,),此时,由题意可得,三角形CPN的面积等于,即•(1﹣b)•|x N﹣x P|=,即(1﹣b)•|﹣|=,化简可得2(1﹣b)2=|a2﹣1|.由于此时b>a>0,0<a<1,∴2(1﹣b)2=|a2﹣1|=1﹣a2 .两边开方可得(1﹣b)=<1,∴1﹣b<,化简可得b>1﹣,故有1﹣<b<.再把以上得到的三个b的范围取并集,可得b的取值范围应是,故选:B.解法二:当a=0时,直线y=ax+b(a>0)平行于AB边,由题意根据三角形相似且面积比等于相似比的平方可得=,b=1﹣,趋于最小.由于a>0,∴b>1﹣.当a逐渐变大时,b也逐渐变大,当b=时,直线经过点(0,),再根据直线平分△ABC的面积,故a不存在,故b<.综上可得,1﹣<b<,故选:B.4.直线3x+y﹣1=0的倾斜角是( )A.B.C.D.【解答】解:设直线3x+y﹣1=0的倾斜角是θ,θ∈[0,π).直线3x+y﹣1=0化为y=﹣x+,∴tanθ=﹣,∴.故选:C.5.已知点(a,2)(a>0)到直线l:x﹣y+3=0的距离为1,则a=( )A.B.C.D.【解答】解:由点到直线的距离公式得:=,∵a>0,∴a=.故选:C.6.已知点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ的中点为M(x0,y0),且y0<x0+2,则的取值范围是( )A.[﹣,0)B.(﹣,0)C.(﹣,+∞)D.(﹣∞,﹣)∪(0,+∞)【解答】解:∵点P在直线x+3y﹣2=0上,点Q在直线x+3y+6=0上,线段PQ 的中点为M(x0,y0),∴,化为x0+3y0+2=0.又y0<x0+2,设=k OM,当点位于线段AB(不包括端点)时,则k OM>0,当点位于射线BM(不包括端点B)时,k OM<﹣.∴的取值范围是(﹣∞,﹣)∪(0,+∞).故选:D.7.设m∈R,过定点A的动直线x+my=0和过定点B的直线mx﹣y﹣m+3=0交于点P(x,y),则|PA|+|PB|的取值范围是( )A.[,2]B.[,2]C.[,4]D.[2,4]【解答】解:由题意可知,动直线x+my=0经过定点A(0,0),动直线mx﹣y﹣m+3=0即m(x﹣1)﹣y+3=0,经过点定点B(1,3),∵动直线x+my=0和动直线mx﹣y﹣m+3=0的斜率之积为﹣1,始终垂直,P又是两条直线的交点,∴PA⊥PB,∴|PA|2+|PB|2=|AB|2=10.设∠ABP=θ,则|PA|=sinθ,|PB|=cosθ,由|PA|≥0且|PB|≥0,可得θ∈[0,]∴|PA|+|PB|=(sinθ+cosθ)=2sin(θ+),∵θ∈[0,],∴θ+∈[,],∴sin(θ+)∈[,1],∴2sin(θ+)∈[,2],故选:B.8.若直线l1:mx+2y+1=0与直线l2:x+y﹣2=0互相垂直,则实数m的值为( )A.2B.﹣2C.D.﹣【解答】解:∵直线l1:mx+2y+1=0与直线l2:x+y﹣2=0互相垂直,∴m×1+2×1=0,解得m=﹣2.故选:B.9.直线(2m+1)x+(m+1)y﹣7m﹣4=0过定点( )A.(1,﹣3)B.(4,3)C.(3,1)D.(2,3)【解答】解:直线方程整理得:2mx+x+my+y﹣7m﹣4=0,即(2x+y﹣7)m+(x+y﹣4)=0,∴,解得:,则直线过定点(3,1),故选:C.10.直线(a2+1)x﹣2ay+1=0的倾斜角的取值范围是( )A.[0,]B.[,]C.[,]D.[0,]∪[,π)【解答】解:①当a=0时,斜率不存在,即倾斜角为;②当a>0时,直线的斜率k=,∴k≥1,即直线的倾斜角的取值范围为[).③当a<0时,直线的斜率,∴k≤﹣1,即直线的倾斜角的取值范围为(].综上,直线的倾斜角的取值范围为,故选:C.11.等腰三角形两腰所在直线的方程分别为x+y﹣2=0与x﹣7y﹣4=0,原点在等腰三角形的底边上,则底边所在直线的斜率为( )A.3B.2C.D.【解答】解:l1:x+y﹣2=0,k1=﹣1,,设底边为l3:y=kx由题意,l3到l1所成的角等于l2到l3所成的角于是有,解得k=3或k=﹣,因为原点在等腰三角形的底边上,所以k=3.k=,原点不在等腰三角形的底边上(舍去),故选:A.12.若动点A,B分别在直线l1:x+y﹣7=0和l2:x+y﹣5=0上移动,则AB的中点M到原点的距离的最小值为( )A.3B.2C.3D.4【解答】解:∵l1:x+y﹣7=0和l2:x+y﹣5=0是平行直线,∴可判断:过原点且与直线垂直时,中的M到原点的距离的最小值∵直线l1:x+y﹣7=0和l2:x+y﹣5=0,∴两直线的距离为=,∴AB的中点M到原点的距离的最小值为+=3,故选:A.13.已知点(﹣1,2)和(,0)在直线l:ax﹣y+1=0(a≠0)的同侧,则直线l倾斜角的取值范围是( )A.(,)B.(0,)∪(,π)C.(,)D.(,)【解答】解:点(﹣1,2),(,0)在直线ax﹣y+1=0的同侧,(﹣a﹣2+1)(a+1)>0解不等式可得,﹣<a<﹣1∴,故选:D.14.直线l过点P(﹣1,2)且与以点M(﹣3,﹣2)、N(4,0)为端点的线段恒相交,则l的斜率取值范围是( )A.[﹣,5]B.[﹣,0)∪(0,2]C.(﹣∞,﹣]∪[5,+∞)D.(﹣∞,﹣]∪[2,+∞)【解答】解:如图,∵P(﹣1,2)、M(﹣3,﹣2)、N(4,0),∴,.由图可知,使直线l与线段MN相交的l的斜率取值范围是(﹣∞,﹣]∪[2,+∞).故选:D.15.已知直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,垂足为P(1,p),则m﹣n+p的值是( )A.24B.20C.0D.﹣4【解答】解:∵直线mx+4y﹣2=0与2x﹣5y+n=0互相垂直,∴×=﹣1,∴m=10,直线mx+4y﹣2=0即5x+2y﹣1=0,垂足(1,p)代入得,5+2p﹣1=0,∴p=﹣2.把P(1,﹣2)代入2x﹣5y+n=0,可得n=﹣12,∴m﹣n+p=20,故选:B.16.过点P(﹣2,2)作直线l,使直线l与两坐标轴在第二象限内围成的三角形面积为8,这样的直线l一共有( )A.3条B.2条C.1条D.0条【解答】解:假设存在过点P(﹣2,2)的直线l,使它与两坐标轴围成的三角形的面积为8,设直线l的方程为:,则.即2a﹣2b=ab直线l与两坐标轴在第二象限内围成的三角形面积S=﹣ab=8,即ab=﹣16,联立,解得:a=﹣4,b=4.∴直线l的方程为:,即x﹣y+4=0,即这样的直线有且只有一条,故选:C.17.已知直线l:3x﹣4y+m=0上存在不同的两点M与N,它们都满足与两点A (﹣1,0),B(1,0)连线的斜率k MA与k MB之积为﹣1,则实数m的取值范围是( )A.(﹣3,3)B.(﹣4,4)C.(﹣5,5)D.[﹣5,5]【解答】解:由题意可知,点M、N、A、B在以AB为直径的圆上,则该圆的方程为x2+y2=1.∵M、N是不同的两点,∴直线l与圆相交,且直线l与圆相切为临界条件,此时原点到直线l的距离等于圆的半径,即1=,∴m=±5.∴m的取值范围为(﹣5,5).故选:C.18.点P到点及到直线的距离都相等,如果这样的点恰好只有一个,那么a的值是( )A.B.C.D.【解答】解:法一由题意有点P在抛物线y2=2x上,设P(,y),则有(+)2=(﹣a)2+(y﹣2)2,化简得(﹣a)y2﹣4y+a2+=0,当a=时,符合题意;当a≠时,△=0,有a3﹣++=0,(a+)(a2﹣a+)=0,a=﹣.故选D.法二由题意有点P在抛物线y2=2x上,B在直线y=2上,当a=﹣时,B为直线y=2与准线的交点,符合题意;当a=时,B为直线y=2与抛物线通径的交点,也符合题意,故选D.故选:D.19.已知直线l:x﹣my+m=0上存在点M满足与两点A(﹣1,0),B(1,0)连线的斜率k MA与k MB之积为3,则实数m的取值范围是( )A.B.∪C.∪D.以上都不对【解答】解:设M(x,y),由k MA•k MB=3,得,即y2=3x2﹣3.联立,得.要使直线l:x﹣my+m=0上存在点M满足与两点A(﹣1,0),B(1,0)连线的斜率k MA与k MB之积为3,则△=,即.解得m∈∪.∴实数m的取值范围是∪.故选:C.20.若两平行直线l1:x﹣2y+m=0(m>0)与l2:2x+ny﹣6=0之间的距离是,则m+n=( )A.0B.1C.﹣2D.﹣1【解答】解:由题意,解得n=﹣4,即直线l2:x﹣2y﹣3=0,所以两直线之间的距离为d=,解得m=2,所以m+n=﹣2,故选:C.二.填空题(共9小题)21.若直线l:+=1(a>0,b>0)经过点(1,2),则直线l在x轴和y轴的截距之和的最小值是 3+2 .【解答】解:∵直线l:(a>0,b>0)经过点(1,2)∴=1,∴a+b=(a+b)()=3+≥3+2,当且仅当b=a时上式等号成立.∴直线在x轴,y轴上的截距之和的最小值为3+2.故答案为:3+2.22.在平面直角坐标系xOy中,设定点A(a,a),P是函数y=(x>0)图象上一动点,若点P,A之间的最短距离为2,则满足条件的实数a的所有值为 ﹣1或 .【解答】解:设点P,则|PA|===,令,∵x>0,∴t≥2,令g(t)=t2﹣2at+2a2﹣2=(t﹣a)2+a2﹣2,①当a≤2时,t=2时g(t)取得最小值g(2)=2﹣4a+2a2=,解得a=﹣1;②当a>2时,g(t)在区间[2,a)上单调递减,在(a,+∞)单调递增,∴t=a,g(t)取得最小值g(a)=a2﹣2,∴a2﹣2=,解得a=.综上可知:a=﹣1或.故答案为﹣1或.23.已知两点A(﹣m,0),B(m,0)(m>0),如果在直线3x+4y+25=0上存在点P,使得∠APB=90°,则m的取值范围是 [5,+∞) .【解答】解:∵P在直线3x+4y+25=0上,设点P(x,),∴=(x+m,),=(x﹣m,);又∠APB=90°,∴•=(x+m)(x﹣m)+=0,即25x2+150x+625﹣16m2=0;∴△≥0,即1502﹣4×25×(625﹣16m2)≥0,解得m≥5,或m≤﹣5,又m>0,∴m的取值范围是[5,+∞).故答案为:[5,+∞).24.已知直线(1﹣a)x+(a+1)y﹣4(a+1)=0(其中a为实数)过定点P,点Q在函数的图象上,则PQ连线的斜率的取值范围是 [﹣3,+∞) .【解答】解:已知直线(1﹣a)x+(a+1)y﹣4(a+1)=0即x+y﹣4+a (﹣x+y﹣4)=0,由,解得,故定点P的坐标为(0,4).设点Q(m,m+),m≠0,则PQ连线的斜率为=1+﹣=﹣3≥﹣3,故PQ连线的斜率的取值范围为[﹣3,+∞),故答案为[﹣3,+∞).25.直线l:xtan+y+1=0的倾斜角α= .【解答】解:根据题意,设直线的倾斜角为θ,有0≤θ<π,直线可化为y=﹣tan•x,由倾斜角与斜率的关系,可得tanθ=﹣tan,又有0≤θ<π,则θ=,故答案为:.26.已知动点P(x,y)满足|x﹣1|+|y﹣a|=1,O为坐标原点,若的最大值的取值范围为,则实数a的取值范围是 .【解答】解:考虑|x﹣1|+|y﹣a|=1的图象,如图,x必然是在0到2之间x取到0或2那么y只能取ax在两者之间y可以取两个值x取到1则y可以取a+1或a﹣1,图象是(0,a),(1,a﹣1),(1,a+1),(2,a)为端点的正方形,那么和O最远的应该是最远的两个端点之一,如果a>0就是(1,a+1)或(2,a)如果a<0就是(1,a﹣1)或(2,a)这样一来,||平方的最大值就是:当a>0,(a+1)2+1 或a2+4当a<0,(a﹣1)2+1 或a2+4比较它们的大小:当a≥1时,(a+1)2+1;﹣1<a<1时,a2+4;a≤﹣1时,(a﹣1)2+1.作以上函数图象,再读出y取值范围为[,17]时a取值范围是.故答案为:.27.过点P(3,﹣1)引直线,使点A(2,﹣3),B(4,5)到它的距离相等,则这条直线的方程为 4x﹣y﹣13=0或x=3 .【解答】解:由题意,所求直线有两条,其中一条是经过点P且与AB平行的直线;另一条是经过P与AB中点C的直线.∵A(2,﹣3),B(4,5),∴AB的斜率k==4,可得经过点P且与AB平行的直线方程为y+1=4(x﹣3),化简得4x﹣y﹣13=0,又∵AB中点为C(3,1)∴经过PC的直线方程为x=3,故答案为:4x﹣y﹣13=0或x=3.28.在平面直角坐标系xOy中,将点A(2,1)绕原点O逆时针旋转到点B,若直线OB的倾斜角为α,则cosα的值为 .【解答】解:设直线OA的倾斜角为θ,则tanθ=,则tanα====3,∴cosα===.故答案为:.29.在平面直角坐标系xOy中,直线l1:kx﹣y+2=0与直线l2:x+ky﹣2=0相交于点P,则当实数k变化时,点P到直线x﹣y﹣4=0的距离的最大值为 3 .【解答】解:∵直线l1:kx﹣y+2=0与直线l2:x+ky﹣2=0的斜率乘积=k×=﹣1,(k=0时,两条直线也相互垂直),并且两条直线分别经过定点:M(0,2),N(2,0).∴两条直线的交点在以MN为直径的圆上.并且k MN=﹣1,可得MN与直线x﹣y﹣4=0垂直.∴点M到直线x﹣y﹣4=0的距离d==3为最大值.故答案为:3.三.解答题(共21小题)30.已知直线l1的方程为3x+4y﹣12=0.(1)若直线l2与l1平行,且过点(﹣1,3),求直线l2的方程;(2)若直线l2与l1垂直,且l2与两坐标轴围成的三角形面积为4,求直线l2的方程.【解答】解:(1)由直线l2与l1平行,可设l2的方程为3x+4y+m=0,以x=﹣1,y=3代入,得﹣3+12+m=0,即得m=﹣9,∴直线l2的方程为3x+4y﹣9=0.(2)由直线l2与l1垂直,可设l2的方程为4x﹣3y+n=0,令y=0,得x=﹣,令x=0,得y=,故三角形面积S=•|﹣|•||=4∴得n2=96,即n=±4∴直线l2的方程是4x﹣3y+4=0或4x﹣3y﹣4=0.31.已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.【解答】解:(1)设C(m,n),∵AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.∴,解得.∴C(4,3).(2)设B(a,b),则,解得.∴B(﹣1,﹣3).∴k BC==∴直线BC的方程为y﹣3=(x﹣4),化为6x﹣5y﹣9=0.32.已知直线l:kx﹣y+1+2k=0(k∈R).(1)证明:直线l过定点;(2)若直线l不经过第四象限,求k的取值范围;(3)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.【解答】解:(1)直线l的方程可化为y=k(x+2)+1,故无论k取何值,直线l总过定点(﹣2,1).(2)直线l的方程可化为y=kx+2k+1,则直线l在y轴上的截距为2k+1,要使直线l不经过第四象限,则,解得k的取值范围是k≥0.(3)依题意,直线l在x轴上的截距为﹣,在y轴上的截距为1+2k,∴A(﹣,0),B(0,1+2k),又﹣<0且1+2k>0,∴k>0,故S=|OA||OB|=×(1+2k)=(4k++4)≥(4+4)=4,当且仅当4k=,即k=时,取等号,故S的最小值为4,此时直线l的方程为x﹣2y+4=0.33.设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).(1)若l在两坐标轴上的截距相等,求l的方程;(2)若l不经过第二象限,求实数a的取值范围.【解答】解:(1)令x=0,得y=a﹣2.令y=0,得(a≠﹣1).∵l在两坐标轴上的截距相等,∴,解之,得a=2或a=0.∴所求的直线l方程为3x+y=0或x+y+2=0.(2)直线l的方程可化为y=﹣(a+1)x+a﹣2.∵l不过第二象限,∴,∴a≤﹣1.∴a的取值范围为(﹣∞,﹣1].34.已知直线l:y=(1﹣m)x+m(m∈R).(Ⅰ)若直线l的倾斜角,求实数m的取值范围;(Ⅱ)若直线l分别与x轴,y轴的正半轴交于A,B两点,O是坐标原点,求△AOB面积的最小值及此时直线l的方程.【解答】解:(Ⅰ)由已知直线l斜率k=1﹣m,∵倾斜角,由k=tanα可得1≤k≤,∴1≤1﹣m≤,解得1﹣≤m≤0;(Ⅱ)在直线l:y=(1﹣m)x+m中,令x=0可得y=m,∴点B(0,m);令y=0可得x=,∴点A(,0),由题设可知m>1,∴△AOB面积S=|OA||OB|=•m•==[(m﹣1)++2]≥[2+2]=2,当且仅当(m﹣1)=即m=2时S取得最小值2,此时直线l的方程为:x+y﹣2=035.在直角坐标系中,已知射线OA:x﹣y=0(x≥0),OB:2x+y=0(x≥0).过点P(1,0)作直线分别交射线OA,OB于点A,B.(1)当AB的中点在直线x﹣2y=0上时,求直线AB的方程;(2)当△AOB的面积取最小值时,求直线AB的方程.(3)当PA•PB取最小值时,求直线AB的方程.【解答】解:(1)设A(a,a),B(b,﹣2b),则线段AB的中点为C.∴﹣2×=0,=,分别化为:a=5b,a+2b﹣3ab=0.解得:,∴直线AB的方程为:y﹣0=(x﹣1),化为:7x﹣4y﹣7=0.(2)设A(a,a),B(b,﹣2b),(a,b>0).a=b=1时,A(1,1),B(1,﹣2),S△OAB=×|OP|×|AB|==.a,b≠1时,S△OAB=×|OP|×(a+2b)=(a+2b),又,化为a+2b=3ab,∴a+2b=3ab=≤,解得:a+2b≥.∴S△OAB≥×=,当且仅当a=2b=时取等号.综上可得:当△AOB的面积取最小值时,直线AB的方程为:y=(x﹣1),化为:4x﹣y﹣4=0.(3)设直线AB的方程为:my=x﹣1..联立,解得A,可得|PA|==.联立,解得B,可得|PB|==.∴|PA|•|PB|====f(m),m=﹣3时,f(﹣3)=1;令m+3=k≠0,f(m)=g(k)==,k<0时,g(k)=≥=.k>0时,g(k)=≥=,而<,∴g(k)的最小值为:.当且仅当k=﹣时取等号.∴m=﹣﹣3.∴直线AB的方程为:(﹣﹣3)y=x﹣1.36.在△ABC中,已知BC边上的高所在直线的方程为x﹣2y+1=0,∠A的平分线所在直线的方程为y=0.若点B的坐标为(1,2),求点C的坐标.【解答】解:点A为y=0与x﹣2y+1=0两直线的交点,∴点A的坐标为(﹣1,0).∴k AB==1.又∵∠A的平分线所在直线的方程是y=0,∴k AC=﹣1.∴直线AC的方程是y=﹣x﹣1.而BC与x﹣2y+1=0垂直,∴k BC=﹣2.∴直线BC的方程是y﹣2=﹣2(x﹣1).由y=﹣x﹣1,y=﹣2x+4,解得C(5,﹣6).故点C的坐标(5,﹣6).37.已知x,y满足直线l:x+2y=6.(1)求原点O关于直线l的对称点P的坐标;(2)当x∈[1,3]时,求的取值范围.【解答】解:(1)设原点O关于直线l的对称点P的坐标为(a,b),则满足,解得a=,b=,故;(2)当x∈[1,3]时,的几何意义为到点C(2,1)的斜率的取值范围.当x=1时,y=,当x=3时,y=,由可得A(1,),B(3,),从而k BC==,k AC==﹣,∴k的范围为(﹣∞,﹣]∪[,+∞)38.已知过原点O的一条直线与函数y=log8x的图象交于A、B两点,分别过点A、B作y轴的平行线与函数的y=log2x的图象交于C、D两点.(1)证明点C、D和原点O在同一条直线上;(2)当BC平行于x轴时,求点A的坐标.【解答】解:(Ⅰ)设点A、B的横坐标分别为x1、x2由题设知,x1>1,x2>1.则点A、B纵坐标分别为log8x1、log8x2.因为A、B在过点O的直线上,所以,点C、D坐标分别为(x1,log2x1),(x2,log2x2).由于log2x1==3log8x1,log2x2==3log8x2OC的斜率,OD的斜率.由此可知,k1=k2,即O、C、D在同一条直线上.(Ⅱ)由于BC平行于x轴知log2x1=log8x2,即得log2x1=log2x2,∴x2=x13.代入x2log8x1=x1log8x2得x13log8x1=3x1log8x1.由于x1>1知log8x1≠0,∴x13=3x1.考虑x1>1解得x1=.于是点A的坐标为(,log8).39.已知直线l:3x﹣y+3=0,求:(1)点P(4,5)关于l的对称点;(2)直线x﹣y﹣2=0关于直线l对称的直线方程.【解答】解:(1)设P(x,y)关于直线l:3x﹣y+3=0的对称点为P′(x′,y′).∵k PP′•k1=﹣1,即×3=﹣1.①又PP′的中点在直线3x﹣y+3=0上,∴3×﹣+3=0.②由①②得把x=4,y=5代入③及④得x′=﹣2,y′=7,∴P(4,5)关于直线l的对称点P′的坐标为(﹣2,7).(2)用③④分别代换x﹣y﹣2=0中的x,y,得关于l的对称直线方程为﹣﹣2=0,化简得7x+y+22=0.40.已知过点A(1,1)且斜率为﹣m(m>0)的直线l与x轴、y轴分别交于P、Q,过P、Q作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ面积的最小值.【解答】解:设l的方程为y﹣1=﹣m(x﹣1),则P(1+,0),Q(0,1+m).从而可得直线PR和QS的方程分别为x﹣2y﹣=0和x﹣2y+2(m+1)=0.又PR∥QS,∴|RS|==.又|PR|=,|QS|=,四边形PRSQ为梯形,S四边形PRSQ =[+]•=(m++)2﹣≥(2+)2﹣=3.6.∴四边形PRSQ的面积的最小值为3.6.41.已知直线l=1.(1)若直线的斜率小于2,求实数m的取值范围;(2)若直线分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最小值及此时直线的方程.【解答】解:(1)直线l过点(m,0),(0,4﹣m),则2,解得m>0或m<﹣4且m≠4.∴实数m的取值范围是m>0或m<﹣4且m≠4;(2)由m>0,4﹣m>0得0<m<4,则,则m=2时,S有最大值,直线l的方程为x+y﹣2=0.42.有三个新兴城镇,分别位于A,B,C三点处,且AB=AC=13km,BC=10km.今计划合建一个中心医院,为同时方便三镇,准备建在BC的垂直平分线上的P点处,(建立坐标系如图)(Ⅰ)若希望点P到三镇距离的平方和为最小,点P应位于何处?(Ⅱ)若希望点P到三镇的最远距离为最小,点P应位于何处?【解答】解:(Ⅰ)设P的坐标为(0,y),则P至三镇距离的平方和为f(y)=2(25+y2)+(12﹣y)2=3(y﹣4)2+146.所以,当y=4时,函数f(y)取得最小值.答:点P的坐标是(0,4).(Ⅱ)解法一:P至三镇的最远距离为g(y)=由解得,记,因为在[y*,+∞)上是增函数,而|12﹣y|在(﹣∞,y*]上是减函数.所以y=y*时,函数g(y)取得最小值.答:点P的坐标是;解法二:P至三镇的最远距离为g(y)=由解得,记,函数x=g(y)的图象如图(a),因此,当y=y*时,函数g(y)取得最小值.答:点P的坐标是;解法三:因为在△ABC中,AB=AC=13,且,.所以△ABC的外心M在线段AO上,其坐标为,且AM=BM=CM.当P在射线MA上,记P为P1;当P在射线MA的反向延长线上,记P为P2,这时P到A、B、C三点的最远距离为P1C和P2A,且P1C≥MC,P2A≥MA,所以点P与外心M重合时,P到三镇的最远距离最小.答:点P的坐标是;43.已知直线l过点M(1,1),且与x轴,y轴的正半轴分别相交于A,B两点,O为坐标原点.求:(1)当|OA|十|OB|取得最小值时,直线l的方程;(2)当|MA|2+|MB|2取得最小值时,直线l的方程.【解答】解:(1)设点A(a,0),B(0,b),且a>0,b>0,直线l的方程为:+=1,且直线l过点M(1,1),∴+=1①;∴a+b=(a+b)•(+)=2++≥2+2=4,当且仅当=,即a=b时取“=”,将a=b代入①式得a=2,b=2;∴直线l的方程为x+y﹣2=0,即|OA|+|OB|取最小值4时,l的方程为x+y﹣2=0;(2)设直线方程为y﹣1=k(x﹣1)(k<0),则A(﹣+1,0),B(0,1﹣k),∴|MA|2+|MB|2=[(﹣)2+1]+[1+(﹣k)2]=2+k2+≥2+2•k2•=4,当且仅当k=﹣1时取“=”;∴当|MA|2+|MB|2取得最小值4时,直线l的方程为y﹣1=﹣(x﹣1),即x+y﹣2=0.44.光线从点A(2,3)射出,若镜面的位置在直线l:x+y+1=0上,反射光线经过B(1,1),求入射光线和反射光线所在直线的方程,并求光线从A到B 所走过的路线长.【解答】解:设点A关于l的对称点为A′(x0,y0),∵AA′被l垂直平分,∴,解得∵点A′(﹣4,﹣3),B(1,1)在反射光线所在直线上,∴反射光线的方程为=,即4x﹣5y+1=0,解方程组得入射点的坐标为(﹣,﹣).由入射点及点A的坐标得入射光线方程为,即5x﹣4y+2=0,光线从A到B所走过的路线长为|A′B|==.45.过点P(3,0)有一条直线l,它夹在两条直线l1:2x﹣y﹣2=0与l2:x+y+3=0之间的线段恰被点P平分,求直线l的方程.【解答】解:如图,设直线l夹在直线l1,l2之间的部分是AB,且AB被P (3,0)平分.设点A,B的坐标分别是(x1,y1),(x2,y2),则有,(4分)又A,B两点分别在直线l1,l2上,所以.(8分)由上述四个式子得,即A点坐标是,B(,﹣)(11分)所以由两点式的AB即l的方程为8x﹣y﹣24=0.(12分)46.已知△ABC的两个顶点A(﹣10,2),B(6,4),垂心是H(5,2),求顶点C的坐标.【解答】解:∴∴直线AC的方程为即x+2y+6=0(1)又∵k AH=0∴BC所直线与x轴垂直故直线BC的方程为x=6(2)解(1)(2)得点C的坐标为C(6,﹣6)47.如图,平行四边形ABCD(A,B,C,D按逆时针顺序排列),AB,AD 边所在直线的方程分别是x+4y﹣7=0,3x+2y﹣11=0,且对角线AC和BD的交点为M(2,0)(1)求点A的坐标(2)求CD边所在直线的方程.【解答】解:(1)由题意联立直线方程,解方程组可得,∴A(3,1)(2)解法一:A关于M的对称点为C,∴C(1,﹣1),又,∴CD边所在的直线方程为化为一般式可得:x+4y+3=0解法二:A关于M的对称点为C,∴C(1,﹣1),设CD边所在的直线方程为:x+4y+m=0,∴1+4×(﹣1)+m=0,解得m=3,∴CD边所在的直线方程为x+4y+3=0解法三:设P(x,y)为CD边所在的直线上的任一点,P关于点M的对称点为P′(x0,y0),。
