数学建模简单13个例子.共40页
数学建模简单13个例子全解

数学建模简单13个例子全解数学建模是一种将数学方法和技术应用于实际问题解决的过程。
它是数学领域的一个重要分支,具有广泛的应用和重要的研究价值。
数学建模能够帮助我们理解和解决许多复杂的现实问题,对于推动科学研究和技术开发具有重要作用。
在现代科学和工程领域,数学建模被广泛运用于各种领域,包括物理、生物、经济、环境、社会等。
通过数学建模,我们可以通过数学方法对问题进行抽象和化简,然后利用数学工具和技术进行分析和求解。
数学建模的过程通常包括问题定义、模型构建、模型分析和模型验证等步骤,其中数学模型的选择和建立是关键的一步。
数学建模的重要性在于它能够帮助我们更好地理解和解决复杂的现实问题。
通过数学建模,我们可以用精确的数学语言和方法描述问题,通过数学分析和计算实现对问题的量化和定量化,为问题的解决提供科学的依据和方法。
数学建模还能够帮助我们发现问题中的规律和关联,提供新的洞察和预测,促进科学的发展和技术的创新。
本文将介绍数学建模的概念和重要性,并给出简单13个例子的全解。
通过这些例子,我们可以更加深入地了解数学建模的基本方法和技巧,培养和提高自己的数学建模能力,为解决实际问题提供有益的借鉴和参考。
描述如何利用数学建模解决鱼群聚集问题,并阐述模型的步骤和应用在鱼群聚集模型中,我们希望通过数学建模来解释鱼群在水中聚集的现象,并找到一种合适的模型来描述鱼群的行为。
步骤:收集数据:首先,我们需要收集关于鱼群聚集的现实数据。
这些数据可以包括鱼群的数量、鱼群的密度、鱼群的移动速度等。
建立模型:基于收集到的数据,我们可以建立一个数学模型来描述鱼群的聚集行为。
常用的模型包括离散模型和连续模型。
离散模型:离散模型将鱼群视为一组个体,每个个体根据一定的规则进行移动和相互作用。
常见的离散模型包括离散元胞自动机模型和离散粒子模型等。
连续模型:连续模型将鱼群视为一个连续的流体,采用偏微分方程来描述鱼群密度的演化。
常见的连续模型包括Navier-Stokes方程和Birds模型等。
数学建模的简单实例ppt课件
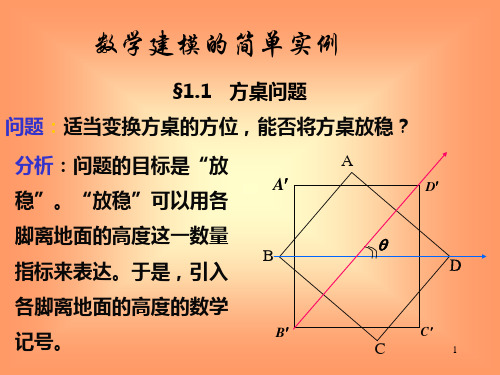
§1.1 方桌问题
问题:适当变换方桌的方位,能否将方桌放稳?
分析:问题的目标是“放
A
A
D
稳”。“放稳”可以用各
脚离地面的高度这一数量
B
指标来表达。于是,引入
各脚离地面的高度的数学
记号。
B
C
C
1
依次记 A、B、fc fD
A
D
fA( ) fB ( ) fC ( ) fD ( )
2
注意到,在任何情况下,总有三只脚能同时着地,且这三 只脚中总有两只脚处在对角位置上,于是我们记:
f ( ) fB( ) fD( ) g( ) fA( ) fC ( )
则 有 , f ( ) g( ) 0
仓库;可关闭2号或3号仓库。 公司不主张仓库的个数 超过4个。 由于向客户供货的运费和仓库改建的费用
均由公司负担, 故需建模为公司选择方案。
若有可能, 应将所建模型推广为适应于类似地更一般 情 形 下 的 方 案 选 择。
13
问题分析
公司的目标是费用尽可能小
费用是怎样构成的
工厂到仓库
运输费用
工厂到客户 问题分析
0
cij Ai到B j及Ck的单位运输费;
d jk B j到Ck的单位运输费;
e1 B1扩建的月增费; e5 B5的月增费; e2 , e3 B2 , B3变更时发生的费用;
保留B2 关闭B2
;
xij
Ai
到B
j
及C
的运
k
量;
新建B5 不建B5
;
y jk
B
j
到C
的运
最新数学建模小实例

精品文档1、司乘人员配备问题某昼夜服务的公交路线每天各时间区段内需司机和乘务人员如下:班次时间最少需要人数1 6:00—10:00 602 10:00—14:00 703 14:00—18:00 60418:022:050522:02:02062:06:030设司机和乘务人员分别在各时间区段一开始上班,并连续工作八小时,问该公交线路至少配备多少名司机和乘务人员?x i班应报到第的人员解: 设为i(i?1,2,?,6),建立线性模型如下:6?x min Z?i1i?精品文档.精品文档x?x?60?61?x?x?70?12?x?x?6032?s.t.x?x?50?43?x ?x?2045?x?x?30?65?x,x,...,x?0?162LINGO程序如下:MODEL:min=x1+x2+x3+x4+x5+x6;x1+x6>=60;x1+x2>=70;x2+x3>=60;x3+x4>=50;x4+x5>=20;x5+x6>=30;END得到的解为:x1=60,x2=10,x3=50,x4=0,x5= 30,x6=0;配备的司机和乘务人员最少为150人。
精品文档.精品文档2、铺瓷砖问题要用40块方形瓷砖铺下图所示形状的地面,但当时市场上只有长方形瓷砖,每块大小等于方形的两块。
一人买了20块长方形瓷砖,试着铺地面,结果无法铺好。
试问是这人的功夫不到家还是这个问题根本无解呢?解答:0 1 0 1 00 1 0 1 0 1 01 0 1 0 1 0 1精品文档.精品文档棋子颜色问题3、然随机排成一个圆圈。
n在任意拿出黑白两种颜色的棋子共个,在两颗颜色不同的棋后在两颗颜色相同的棋子中间放一颗黑色棋子,再重复以上的放完后撤掉原来所放的棋子,子中间放一颗白色棋子,问这样重复进行下去这样放下一圈后就拿走前次的一圈棋子,过程,各棋子的颜色会怎样变化呢?分析与求解:两颗不同色的棋子中间由于在两颗同色棋子中放一颗黑色棋子,这表示。
数学建模简单示例

否则一处的车辆将会越积越多。
例4 飞机失事时,黑匣子会自动打开,发射 出某种射线。为了搞清失事原因,人们必须 尽快找回匣子。确定黑匣子的位置,必须确 定其所在的方向和距离,试设计一些寻找黑 匣子的方法。由于要确定两个参数,至少要 用仪器检测两次,除非你事先知道黑匣子发 射射线的强度。
方法一
点光源发出的射线在各点处的照度与其到点光源的 2 的平方成反比,即
例2 某人第一天由 A地去B地,第二天由 B地沿原路返回 A 地。问:在什么条件下, 可以保证途中至少存在一地,此人在两天 中的同一时间到达该地。
分析 本题多少 有点象 数学中 解的存在 性条件 及证明,当 然 ,这里的情况要简单得多。 假如我们换一种想法,把第二天的返回改变成另一人在同 一天由B去A,问题就化为在什么条件下,两人至少在途中 相遇一次,这样结论就很容易得出了:只要任何一人的到 达时间晚于另一人的出发时间,两人必会在途中相遇。
初中数学建模的若干简要案例

初中数学建模的若干简要案例初中数学建模学习案例1 :----- 与自行车有关的问题(小组学习实践)课题:了解自行车中的数学问题,应用学过的数学知识,解决以下问题。
问题1 :用自己或同学的一辆自行车为观察对象,观察并解决下列问题:( 1 )我观察的这辆自行车是什么牌子的?( 2 )它的直径是_______cm ,轮子转动一周,在地面走过的距离是_______cm ,精确到1cm 。
( 3 )自行车中轴的大齿轮盘的齿数是_______齿,后轴的小齿轮(飞轮)的齿数是_______,中轴的大齿轮被踏动一周时,后轴的小齿轮在链条传动下,不计算惯性将转动_______周(保留2 位小数)。
问题2 :如果你有自行车,并骑车上学,你能借助于自行车,测量出从你的家到学校的路程吗?请你设计一个测量方案,并尽可能地通过实际操作测量出从你的家到学校的路程。
问题3 :如果你的(或你的朋友)自行车是可以变速的自行车(如山地车、多飞轮的自行车)、请你观察一下在这辆自行车上有几个(中轴上的)大轮盘,几个飞轮,它们都各有多少齿?记录这些数据。
如果你骑车时每一秒脚蹬一圈,请你根据上面测量的数据计算出这辆自行车运行时最大的速度和最小的速度各是每小时多少公里?:选做问题4 :你认为对问题 3 中的自行车的各个齿轮的齿数安排的合理吗?你能发现或提出什么样的问题?如果有可能请你做设计改进的话,你会做什么?求解工作的表格省略初中数学数学建模案例 2 :----- 线路设计问题(自学、探索、创新实践)课题:为所在小区设计一个最佳的邮政投递路线, 、一个合理的保安巡逻路线。
实施建议:1: 按居住地成立4-6 人的小组,对你们要研究的小区, 进行观察, 收集必要的数据和信息,( 如平面图, 楼的门洞的朝向, 道路情况, 小区的进出口位置等). 发挥各自的特长,分工合作完成测量方案的设计、实测、作图、计算、论证、比较、计算机文稿录入、结果介绍等。
数学建模简单13个例子_2022年学习资料

7、气象预报问题-在气象台A的正西方向300km处有一台风中心,它以-40km/h的速度向东北方向移动;根 台风的强度,在距-其中心250km以内的地方将受到影响,问多长时间后气象-台所在地区将遭受台风的影响?持续 间多长?-此问题是某气象台所遇到的实际问题,为了搞好气象-预报,现建立解析几何模型加以探-以气象台A为坐标 点建立-平而直角坐标系,设台风中心为B,-如图
某人第一天由A地去B地,第二天由B地沿原路-返回A地。问:在什么条件下,可以保证途中-至少存在一地,此人在 天中的同一时间到达该-假如我们换一种想法,把第二天的返回改变成另一-人在同一天由B去A,问题就化为在什么条 下,两-人至少在途中相遇一次,这样结论就很容易得出了:-只要任何一人的到达时间晚于另一人的出发时间,-两人 会在途中相遇。
1.皮的厚度一样2.汤圆(饺子)的形状-假设-R大皮的半径,r小皮的半-模型-S=ns-S=k R,V=k R3V=kS2-s=kr2,v=kr3 v=ks2-=n32v-应用-V=√nv≥vv是nv是√n倍-若1 0个汤圆(饺子包1公斤馅,-则50个汤圆(-问题杀羊方案-现有26只羊,要求7天杀完且每天必须杀奇数只,-问各天分别杀几只?-分析:-1 这是一个有限问题,解决此类问题的一-类方法是枚举,你可以试试。-建模:-2.依题意,设第i天杀2k,+1k 自然数只,-则所提问题变为在自然数集上求解方程-之2k,+10=26-i=1-于是,我们有了该问题的数学语 表达—数学模型-求解:-用反证法容易证明本问题的解不存在。-返回
x+y=l-y+z=m-x+7=n-由三元一次线性方程组解出x,y,z即得三根-电线的电阻。-说明:此问题 难,点也是可贵之处是用方程-“观点”、”立场”去分析,用活的数学思想使实-际问题转到新剑设的情景中去。-返
数学建模简单13个例子讲义.

支 球队中的胜者及轮空者进入下一轮,直至比赛结
束。问共需进行多少场比赛?
一般思维:
36 18 10 4 2 1 18 9 5 2 1 1 36 2 2 2 2 2
逆向思维:
每场比赛淘汰一名失败球队,只有一名冠军,即 就是淘汰了36名球队,因此比赛进行了36场。
4、爬山问题
某人早8时从山下旅店出发沿一条路径上山,下午5 时到达山顶并留宿,次日早8时沿同一路径下山,下午5 时回到旅店,则这人在两天中的同一时刻经过途中的 同—地点,为什么? 解法一: 将两天看作一天,一人两天的运动看作一天两 人同时分别从山下和山顶沿同一路径相反运功,因为 两人同时出发,同时到达目的地,又沿向一路径反向 运动,所以必在中间某一时刻t两人相遇,这说明某人 在两天中的同一时刻经过路途中的同一地点。
1、从包汤圆(饺子)
今天,1公斤面不变,馅比 1公斤多了,问应多包几 个(小一些),还是少包几个(大一些)?
通常,1公斤面, 1公斤馅,包100个汤圆(饺子)
问题
圆面积为S的一个皮,包成体积为V的汤圆。若 分成n个皮,每个圆面积为s,包成体积为v。
S V s v s v
…
s v
( 共 n个 )
定性分析
根据题意,A点的坐标为(-300,0), 单位为km.台风中心的运动轨迹为直 线BC,这里的∠CBA=450,当台风中 心在运动过程中处于以A为圆心、半径 为250 km的圆内(即MN上)时,气象台 A所在地区将遭受台风的影响。 因为圆的方程为: 直线BC的方程为: 当台风中心处于圆内时,有: 解得 其中参数t 为时间(单 位为h)。
马路的宽度D是容易测得的,问题的关键在于L的确定。 为确定L,还应当将L划分为两段:L1和L2。 其中 L1是司机在发现黄灯亮及判断应当刹车的反应 时间内驶过的路程,L2为刹车制动后车辆驶过的路程。 L1较容易计算,交通部门对司机的平均反应时间 t1早有测 算,反应时间过长将考不出驾照),而此街道的行驶速度 v 也是交管部门早已定好的,目的是使交通流量最大,可 另建模型研究,从而L1=v*t1。刹车距离 L2既可用曲线拟 合方法得出,也可利用牛顿第二定律计算出来 黄灯究竟应当亮多久现在已经变得清楚多了。 第一步,先计算出L应多大才能使看见黄灯的司机停 得住车。 第二步,黄灯亮的时间应当让已过线 D 的车顺利穿过马路, L 即T 至少应当达到 (L+D)/v。
最新数学建模简单13个例子讲义.教学内容精品课件

当台风中心处于圆内时,有:
其中参数t
为时间(单位 为h)。
解得
所以,大约在2h以后气象台A所在地区将会遭受台 风的影响,持续时间大约第为十四页,6共40.页。 6h。
8、黄灯应当(yīngdāng)亮多久
交通灯在绿灯转换成红灯时,有一个过渡状态— —亮一段时间的黄灯。请分析黄灯应当亮多久。
v 也是交管部门早已定好的,目的是使交通流量最大,可
另建模型(móxíng)研究,从而L1=v*t1。刹车距离 L2既可
用曲线拟合方法得出,也可利用牛顿第二定律计算出来
黄灯究竟应当亮多久现在已经变得清楚多了。
第一步,先计算出L应多大才能使看见黄灯的司机停
得住车。
第二步,黄灯亮的时间应当让已过线
的车顺利穿过马路,
x2 ( y - h)2 r2
汇合点即可p求必出位P于点此的圆坐标上和。θ2
的值。
y
(tan
1 ) x
b(护卫舰的路线本方模程型)虽简单,但分析极
清晰且易于(yìyú)实际应用
y (tan2 )x b(航母的路线方程 )
返回
第二十二页,共40页。
12、价格竞争
问题:两个加油站位于同一条公路旁,为在公路上行驶 的汽车提供同样的汽油,彼此竞争激烈.一天,甲加油站 推出“降价销售”吸引顾客.结果造成乙加油站的顾客被 拉走,影响了乙站的赢利.利润是受销价和销售量的影响 和控制.他们为了挽回损失采取对策,决定也降低销售价 以争取(zhēngqǔ)顾客.乙加油站如何决定汽油的价格, 既可以同甲站竞争,又可以获取尽可能高的利润.
在气象台A的正西方向300 km处有一台风(táifēng)中 心,它以40 km/h的速度向东北方向移动;根据台风 (táifēng)的强度,在距其中心250 km以内的地方将受到 影响,问多长时间后气象台所在地区将遭受台风 (táifēng)的影响?持续时间多长?
数学建模案例PPT课件

四、数学建模的特点
第25页/共41页
五、数学建模的分类
1)按变量的性质分:
离散模型
确定性模型
线性模型
连续模型
随机性模型
非线性模型
单变量模型 多变量模型
2)按时间变化对模型的影响分
静态模型 动态模型
参数定常模型 参数时变模型
第26页/共41页
3)按模型的应用领域(或所属学科)分 人口模型、交通模型、生态模型、城镇规划模型、 水资源模型、再生资源利用模型、污染模型、 生物数学模型、医学数学模型、地质数学模型、 数量经济学模型、数学社会学模型等。
经有限步使全体人员过河。
第1页/共41页
2、模型建立
xk --第k次渡河前此案的商人数 xk , yk 0,1,2,3
yk --第k次渡河前此案的随从数 k 1,2,
sk (xk , yk )过程的状态
S --允许状态集合
S {(x, y) | x 0, y 0,1, 2, 3; x 3, y 0,1, 2, 3; x y 1, 2}
1)模型准备: 了解问题的实际背景,明确建模目 的,掌握对象的各种信息如统计数据等,弄清实际 对象的特征。 有时需查资料或到有关单位了解情况等。
第21页/共41页
2)模型假设:根据实际对象的特征和建模目的,对问 题进行必要地合理地简化。不同的假设会得到不同的模型。如果假设过于简单可能会导 致模型的失败或部分失败,于是应该修改或补充假设,如“四足动物的体重问题”;如 果假设过于详细,试图把复杂的实际现象的各个因素都考虑进去,可能会陷入困境,无 法进行下一步工作。分清问题的主要方面和次要方面,抓主要因素,尽量将问题均匀化、 线性化。
➢ 1987年改为 Mathematical Contest in Modeling, 其缩写
数学建模简单个例子PPT课件

通常,1公斤面, 1公斤馅,包100个汤圆(饺子)
今天,1公斤面不变,馅比 1公斤多了,问应多包几 个(小一些),还是少包几个(大一些)?
问题
圆面积为S的一个皮,包成体积为V的汤圆。若 分成n个皮,每个圆面积为s,包成体积为v。
S
s s … s (共n个)
vv
v
V
V和 nv 哪个大? 定性分析
故Zn =1/(2n),从而上面 n块砖向右推出的
总距离为 n 1 ,
故有砖点n块出向人右意可料时 叠。k至1, 2knk任1 2意1k远,n这1 一21n结果多少返回
第17页/共38页
10、寻找黑匣子
飞机失事时,黑匣子会自动打开,发射出某种 射线。为了搞清失事原因,人们必须尽快找回匣子。 确定黑匣子的位置,必须确定其所在的方向和距离, 试设计一些寻找黑匣子的方法。由于要确定两个参 数,至少要用仪器检测两次,除非你事先知道黑匣 子发射射线的强度。
第4页/共38页
某人第一天由 A地去B地,第二天由 B地沿原路 返回 A 地。问:在什么条件下,可以保证途中至 少存在一地,此人在两天中的同一时间到达该地。
假如我们换一种想法,把第二天的返回改变成另一 人在同一天由B去A,问题就化为在什么条件下, 两人至少在途中相遇一次,这样结论就很容易得出 了:只要任何一人的到达时间晚于另一人的出发时 间,两人必会在途中相遇。
此问题是某气象台所遇到的实际问题,为了搞好气象 预报,现建立解析几何模型加以探讨。
以气象台A为坐标原点建立 平而直角坐标系,设台风中心为B, 如图
第13页/共38页
根据题意,A点的坐标为(-300,0), 单位为km.台风中心的运动轨迹为直 线BC,这里的∠CBA=450,当台风 中心在运动过程中处于以A为圆心、 半径为250 km的圆内(即MN上)时, 气象台A所在地区将遭受台风的影响。
简单数学建模应用例子

2024/1/713Fra bibliotek建模实例
这里是要用数学方法求解,一是为了给出建模 的示例,二是因为这类模型可以解决相当广泛 的一类问题,比逻辑思索的结果容易推广。
由于问题已经理想化了,所以不必再作假设。 安全渡河问题可以视为一个多步决策过程。每 一步即船由此岸驶向彼岸或从彼岸驶回此岸, 都要对船上的人员作出决策,在保证安全的前 题下,在有限步内使人员全部过河,
x(t t) x(t) rx(t)t
2024/1/7
24
建模实例
于是x(t)满足如下方程:
dx rx dt x(0) x0
易知其解为 x(t) x0ert
(2) (3)
2024/1/7
25
建模实例
上式表明了人口增长的指数规律,此时将t离 散化,并认为r较小,则可得(1)式,即(1) 为指数增长模型的一种离散形式的近似表示。 人们发现,在地广人稀的加拿大领土上,法国 移民后代的人口比较符合指数增长模型,而同 一血统的法国本土居民人口的增长却远低于这 个模型。
2024/1/7
7
建模实例
虽然椅子只有四个距离,但是由于正方形的中 心对称性,只要设两个距离函数就行了,记A, C两脚与地面的距离之和为f( ),B,D两脚与 地面的距离之和为g( ), f( ),g ( )≥0,由假设2, f与g均是连续函数。由假设3,椅子在任何位 置至少有三只脚着地,所以对于任意的 , f( ), g( )中至 少有一个为零,当 =0时 不妨设g( )=0, f( )>0。
数学建模
简单建模实例
1
建模实例
实例一:椅子能在不平的地面上放稳吗? 把椅子往不平的地面上放,通常只有三只脚着 地,放不稳,然而只需挪动几次,就可以使四 脚同时着地,放稳了。这看来似乎与数学无关 的现象能够用数学语言以表述,并用数学工具 来证实吗?
数学建模案例
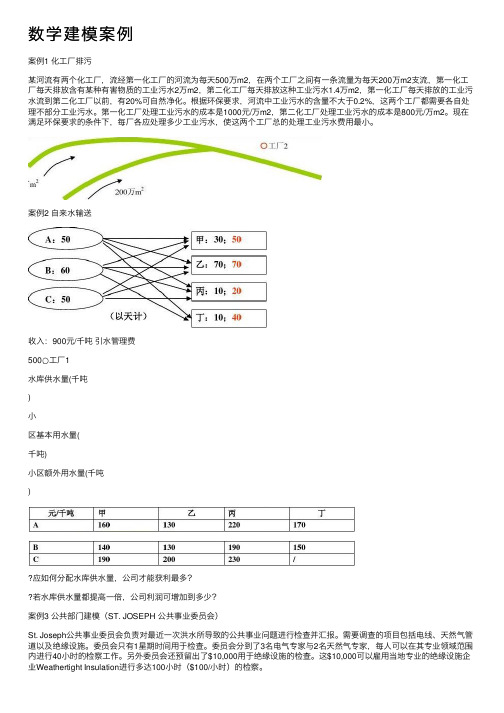
数学建模案例案例1 化⼯⼚排污某河流有两个化⼯⼚,流经第⼀化⼯⼚的河流为每天500万m2,在两个⼯⼚之间有⼀条流量为每天200万m2⽀流,第⼀化⼯⼚每天排放含有某种有害物质的⼯业污⽔2万m2,第⼆化⼯⼚每天排放这种⼯业污⽔1.4万m2,第⼀化⼯⼚每天排放的⼯业污⽔流到第⼆化⼯⼚以前,有20%可⾃然净化。
根据环保要求,河流中⼯业污⽔的含量不⼤于0.2%,这两个⼯⼚都需要各⾃处理不部分⼯业污⽔。
第⼀化⼯⼚处理⼯业污⽔的成本是1000元/万m2,第⼆化⼯⼚处理⼯业污⽔的成本是800元/万m2。
现在满⾜环保要求的条件下,每⼚各应处理多少⼯业污⽔,使这两个⼯⼚总的处理⼯业污⽔费⽤最⼩。
案例2 ⾃来⽔输送收⼊:900元/千吨引⽔管理费500○⼯⼚1⽔库供⽔量(千吨)⼩区基本⽤⽔量(千吨)⼩区额外⽤⽔量(千吨)应如何分配⽔库供⽔量,公司才能获利最多?若⽔库供⽔量都提⾼⼀倍,公司利润可增加到多少?案例3 公共部门建模(ST. JOSEPH 公共事业委员会)St. Joseph公共事业委员会负责对最近⼀次洪⽔所导致的公共事业问题进⾏检查并汇报。
需要调查的项⽬包括电线、天然⽓管道以及绝缘设施。
委员会只有1星期时间⽤于检查。
委员会分到了3名电⽓专家与2名天然⽓专家,每⼈可以在其专业领域范围内进⾏40⼩时的检察⼯作。
另外委员会还预留出了$10,000⽤于绝缘设施的检查。
这$10,000可以雇⽤当地专业的绝缘设施企业Weathertight Insulation进⾏多达100⼩时($100/⼩时)的检察。
这些专家需要对当地的民宅、写字楼以及⼯⼚进⾏检查。
⽬标是在指定时间内对尽可能多的建筑进⾏全⾯检查以收集所需信息。
但是检查的写字楼及⼯⼚数量均不能低于8处,且检查的民宅数量不能低于检查总数的60%。
⼀旦确定了需要检查的每种建筑的数量,接下来就将专家随机安排到各个建筑执⾏检查⼯作。
委员会指定了每种建筑及检查项⽬的⼤致检查时间:委员会雇⽤了⼀个管理咨询团队来确定需要检查的民宅、写字楼以及⼯⼚的数量。
数学建模小实例
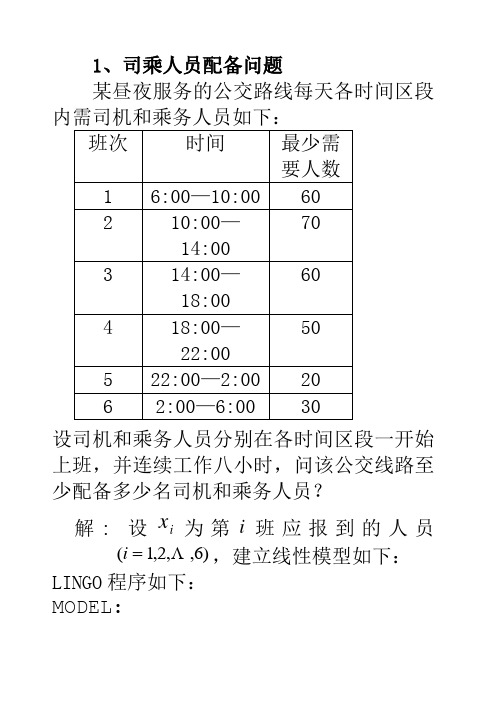
1、司乘人员配备问题某昼夜服务的公交路线每天各时间区段内需司机和乘务人员如下:设司机和乘务人员分别在各时间区段一开始上班,并连续工作八小时,问该公交线路至少配备多少名司机和乘务人员?解: 设i x为第i班应报到的人员i,建立线性模型如下:)6,(,2,1LINGO程序如下:MODEL:min=x1+x2+x3+x4+x5+x6;x1+x6>=60;x1+x2>=70;x2+x3>=60;x3+x4>=50;x4+x5>=20;x5+x6>=30;END得到的解为:x1=60,x2=10,x3=50,x4=0,x5=30,x6 =0;配备的司机和乘务人员最少为150人。
2、铺瓷砖问题要用40块方形瓷砖铺下图所示形状的地面,但当时市场上只有长方形瓷砖,每块大小等于方形的两块。
一人买了20块长方形瓷砖,试着铺地面,结果无法铺好。
试问是这人的功夫不到家还是这个问题根本无解呢?解答:3、 棋子颜色问题在任意拿出黑白两种颜色的棋子共n 个,随机排成一个圆圈。
然后在两颗颜色相同的棋子中间放一颗黑色棋子,在两颗颜色不同的棋子中间放一颗白色棋子,放完后撤掉原来所放的棋子,再重复以上的过程,这样放下一圈后就拿走前次的一圈棋子,问这样重复进行下去各棋子的颜色会怎样变化呢?分析与求解:由于在两颗同色棋子中放一颗黑色棋子,两颗不同色的棋子中间放一颗白色棋子,故可将黑色棋子用1表示,白色棋子用-1表示。
这是因为-1×(-1)=1,1×1=1,这代表两颗同色棋子中放一颗黑色棋子;1×(-1)= -1,这代表两颗不同色的棋子中间放一颗白色棋子。
设棋子数为n ,12,,,n a a a L 为初始状态。
当n=3时步数 状态(舍掉偶次项) 0 1a 2a 3a 1 21a a 32a a 13a a 2 31a a 21a a 32a a 3 32a a 31a a 21a a 4 12a a 23a a 31a a说明当n=3时,经过3步进入初始状态。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11、战争满足了,或曾经满足过人的 好斗的 本能, 但它同 时还满 足了人 对掠夺 ,破坏 以及残 酷的纪 律和专 制力的 欲望。 ——查·埃利奥 特 12、不应把纪律仅仅看成教育的手段 。纪律 是教育 过程的 结果, 首先是 学生集 体表现 在一切 生活领 域—— 生产、 日常生 活、学 校、文 化等领 域中努 力的结 果。— —马卡 连柯(名 言网)
13、遵守纪律的风气的培养,只有领 导者本 身在这 方面以 身作则 才能收 到成效 。—— 马卡连 柯 14、劳动者的组织性、纪律性、坚毅 精神以 及同全 世界劳 动者的 团结一 致,是 取得最 后胜利 的保证 。—— 列宁 摘自名言网
15、机会是不守纪律的。——雨果
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
