振动力学与结构动力学-(第一章)
结构动力学

§1.3 体系振动的自由度
象静力计算一样,在动力计算时,首先需要选取一个 合理的计算简图。但由于需要考虑惯性力,因此在动力计 算的简图中,多了一项关于质量分布的处理问题。当体系 振动时,它的惯性力与质量的运动情况有关,所以确定质 量在运动中的位置具有重要的意义。 振动的自由度:我们把确定体系上全部质量位置所需 的独立几何参变数的数目,称为该体系的振动自由度。 例1.1 如图(a)所示跨中置一质量为m电动机的简支梁,当 梁自身的质量远小于电动机的质量时,梁的质量可忽略不 计。其计算简图如图(b)所示。
Fp
如:具有偏心质量的回旋机器它所传递 给结构上的横向力就是时间 t 的函数。
t
这类荷载称为动力荷载
图(a)
显然,结构在动力荷载作用下的计 算与静力荷载作用下的计算将有很大的 的区别,而且要复杂的多。
Fpsin t
图(b)
这是因为,在进行动力计算时,除了需要考虑惯 性力外,还需取时间作为自变量。在动力问题中,内 力与荷载不能构成静力平衡,但根据达朗伯原理,可 以将动力问题转化为静力问题,方法是任一时刻在结 构上加入假想的惯性力作为外力。即结构在形式上处 于“平衡状态”,这样,就可以应用静力学的有关原 理和方法计算在给定时刻的内力和位移等。 在实际工程中,大多数荷载都是随时间的改变而 变化的,但有一些荷载使结构产生很小的振动,以至 于其上的惯性力可以忽略不计,此时为了简化计算, 可将其视为静力荷载。仅将那些随时间变化,且使结 构产生较大的振动的荷载才作为动力荷载来考虑。
dmy Fp t dt
1 2
t m y 1 3
当质量m不随时间变化时,有 Fp
0 即:Fp t m y
因此,如果把惯性力(-mÿ)加到原来受力的质量上,则动 力学问题就可以按静力平衡来处理,这种列运动方程的 方法常称为动静法。这种方法较为方便,因此得到广泛 应用。 (2)拉格朗日(Lagrange)方程 应用虚位移原理,作用在任意质量mi上的所有力 (包括惯性力),对任意的虚位移所作的虚功总和应 等于零,得
振动力学与结构动力学-(第一章).

摩擦力: Fd cdx2sgxn
c d :阻力系数
在运动方向不变的半个周期内计算耗散能量,再乘2:
Ecdx2sgxndx2
T/4
c T/4 d
x3dt
8 3
cd02
A2
等效粘性阻尼系数:
ce
8
3
cd0
A
24
四、结构阻尼
由于材料为非完全弹性,在变形过程中材料的内摩擦所引起 的阻尼称为结构阻尼
特征:应力-应变曲线存在滞回曲线
6
第一章 概 论
§1-1 动荷载及其分类 - 从广义上讲,如果表征一种运动的物理量作时而增大时而减
小的反复变化,就可以称这种运动为振动。 - 如果变化的物理量是一些机械量或力学量,例如物体的位移
、速度、加速度、应力及应变等,这种振动便称为机械振动 。 - 各种物理现象,诸如声、光、热等都包含振动
7
– 知识要点:结构被动控制、主动控制的基本概念。常用主动 控制方法的原理。结构主动控制在机械、土木结构工程中应 用简介。
– 重点难点:理解各种控制方法的原理及其具体实现。 – 教学方法:课堂讲授与引导讨论相结合。
主要参考书: • 刘延柱.振动力学.北京:高等教育出版社,1998 • 倪振华. 振动力学. 西安:西安交通大学出版社,1989 • 张准、汪凤泉. 振动分析.南京:东南大学出版社,1991 • 陈予恕.非线性振动. 天津:天津科技出版社,1983 • 龙驭球等编著.《结构力学》下册. 北京:高等教育出版 社,1994
– 教学方法:课堂讲授与引导讨论相结合
• 第六章 结构反应谱与地震荷载计算(8学 时)
– 知识要点:结构反应谱、单自由度和多自由度地震 荷载计算公式、规范中地震荷载计算公式。
动力学(第1章)
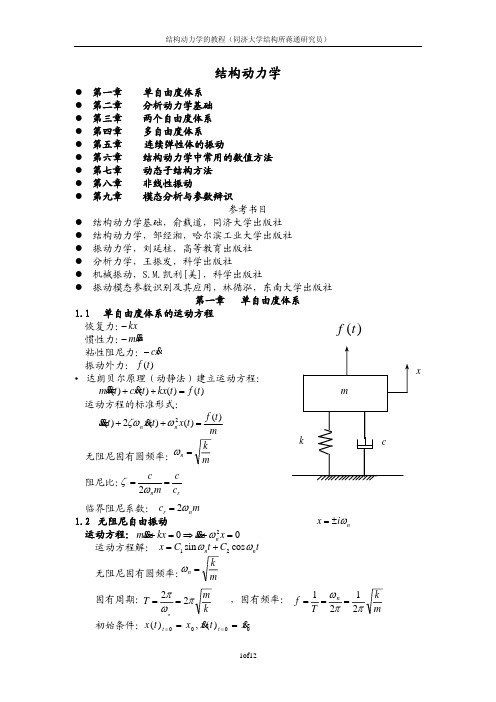
f
(t)
=
2P0
ωt π
∫ ∫ bi
=
2 T
T 0
f (t) sin(iωt)dt = 4ω π
π 2ω 0
f
(t) sin(iωt)dt
=
8P0 i2π 2
i −1
(−1) 2 (i
= 1,3,5,⋅⋅⋅)
6of12
结构动力学的教程(同济大学结构所蒋通研究员)
∑ 取
i=1~3
β1 算得:
=
1
−
1 ω2
= 1−ω
2ζω 3 2 + (2ζω )2
1+ 4ζ 2ω 2 (1− ω 2 )2 + (2ζω )2
5of12
结构动力学的教程(同济大学结构所蒋通研究员)
隔振要求: 频率比: ω
=
ω
>
2⇒
ωn
阻尼比小:ζ ↓⇒ A ↓
B
A <1 B
但过小通过共振区不利
主动隔振:将振源隔开,使振动传播不出去(隔振器)
+ϕ)
振幅与相位角: A=
x02
+
⎜⎜⎝⎛
x&0 ωn
⎟⎟⎠⎞2
,ϕ
=
arctg
ωn x0 x&0
x
A
x&0
x0
t ϕ /ωn
t t +T
例题 1-1 求图示体系的固有频率
悬臂梁刚度:k1
=
3EI l3
与 K2 并联后等效刚度:k = k1 + k2 固有频率:ωn = k / m (串联弹簧)
l m
• •
能量守衡:We +Wd + Wf = 0 → ω = ωn →
结构动力学课件PPT

my cy ky FP (t)
§2-5 广义单自由度体系:刚体集合
➢刚体的集合(弹性变形局限于局部弹性 元件中)
➢分布弹性(弹性变形在整个结构或某些 元件上连续形成)
➢只要可假定只有单一形式的位移,使得 结构按照单自由度体系运动,就可以按 照单自由度体系进行分析。
E2-1
x
p( x,t
)
=p
)
3
B'
M I1
E'
D'
F' G'
A
D
E
B
F
G
C
fD1
fI1
fS1
f D2
f I2
f S2
a
2a
a aa a
Z(t )
f S1
k1(EE')
3 4
k1Z (t )
f D1
d c1( dt
DD')
1 4
c1Z (t )
fS2
k1(GG')
1 3
k2
Z
(t
)
fD2 c2Z (t)
f
I1
m1
1 2
Z(t)
3. 有限单元法
—— 将有限元法的思想用于解决结构的动力计算问题。
要点:
▪ 先把结构划分成适当(任意)数量的单元;
▪ 对每个单元施行广义坐标法,通常取单元的节点位移作 为广义坐标;
▪ 对每个广义坐标取相应的位移函数 (插值函数);
▪ 由此提供了一种有效的、标准 化的、用一系列离散坐标 表示无限自由度的结构体系。
建立体系运动方程的方法
▪ 直接平衡法,又称动静法,将动力学问题转化为任一时刻 的静力学问题:根据达朗贝尔原理,把惯性力作为附加的 虚拟力,并考虑阻尼力、弹性力和作用在结构上的外荷载, 使体系处于动力平衡条件,按照静力学中建立平衡方程的 思路,直接写出运动方程。
第一章结构动力学概述1(长沙理工大学结构动力学)祥解PPT课件

1) 结构动力学的研究内容
当前结构动力学的研究内容可用下图表示
第一类问题:响应分析——正问题
输入 (动力荷载)
结构 (系统)
输出 (动力反应)
9
第二类问题:参数(或称系统)识别
输入 (动力荷载)
结构 (系统)
输出 (动力反应)
10
第三类问题:荷载识别。
结构动力学讲义
Tel.: Email:
1
教材 《结构动力学》
(杨茀康 人民交通出版社 张子明 清华大学出版社)
2
第一章、结构动力学概论
1.1 概述 1.2 基本概念 1.3 弹性系统的动力自由度 1.4 结构振动中的能量耗散-阻尼力 1.5结构运动方程的建立
3
1.1概述
首先请大家看中国唐山、日 本阪神地震及TOCOMA大桥 在风载下垮塌录像,希望能从 中体会到学习结构动力学的重 要性。更希望大家能学好结构 动力学!
m y(x)
广义坐标个数即 为自由度个数
m
结点位移个数即 为自由度个数
18
3. 自由度的确定
4)
1) 平面上的一个质点
• 理论计算法
对所设计的结构建立数学模型,通过计算机计算从理论 上验证设计是否满足动力性的要求。
• 试验量测法
用来检验数学模型的正确性,为理论计算提供确切数据。
• 试验与计算混合法
重要结构的动力研究常常需要将数值计算和试验结合起 来,一方面利用数值计算为结构试验提供依据,另一方 面,根据试验结果,不断修正模型以便数学模型能更好 地反映实际情况。
4
5
美国的TOCOMA大桥在风载下垮塌的案例
1940年7月1日,造型优美的塔科马钢铁大桥建成通车。大桥刚投入使用
结构动力学-课件(全10章+总结)(刘晶波,杜修力主编.机械工业出版社出版)

质量块mg 无质量弹簧k
(a) 弹簧-质点
2ust
动力反应
u
(b) 静力和动力反应
静力问题和动力问题位移反应的区别
1.4 结构离散化方法
离散化:把无限自由度问题转化为有限自由 度的过程
三种常用的离散化方法: 1、集中质量法、 2、广义坐标法、 3、有限元法。
F (t) = Asinωt F (t) = Acosωt F (t) = Asin(ωt − φ)
可以是机器转动引起的不平衡力等。
p(t)
t
(a) 简谐荷载
1.2 动力荷载的类型
(2)非简谐周期荷载
荷载随时间作周期性变化,是时间t的周期函数,但不
能简单地用简谐函数来表示。 例如:平稳情况下波浪对堤坝的动水压力;轮船螺旋 桨产生的推力等。
n =1
nπx
L
sin(.)— 形函数(形状函数),给定函数,满足边界条件;
bn(t)— 广义坐标,一组待定参数,对动力问题是作为时间的函数。
∑ u( x, t )
=
N n =1
bn
(t)
sin
nπx
L
2、广义坐标法
悬臂梁:
x
(b) 悬臂梁
用幂级数展开:
∞
∑ u(x) = b0 + b1x + b2 x2 + L = bn xn n=0
结构动力学和静力学的本质区别:考虑惯性力的影响
结构产生动力反应的内因(本质因素):惯性力
惯性力的产生是由结构的质量引起的,对结构中质量位 置及其运动的描述是结构动力分析中的关键,这导致 了结构动力学和结构静力学中对结构体系自由度定义 的不同。
结构动力学第一章概述

第1章概述研究结构在动荷载作用下的相应规律的学科称为结构动力学结构动力学着重研究结构关于动荷载的响应(如,位移、内力、速度、加速度等的时刻历程)以便确信结构的承载能力和动力学特性,或为改善结构的性能提供依据,结构动力学是抗震设计的基础,也是减震、隔震方法的理论依据。
§结构动力学研究对象与研究目的在动力作用下,结构产生振动,即结构在静平稳位置周围来回地运动(振动)。
振动的缘故,有的是结构本身固有的缘故引发的,如转动机械转子的偏心引发的振动;有的是外界干扰所引发的,如地震作用、风荷载作用,爆炸荷载的作用,和车辆行驶中由于路面不平顺引发的车辆及车辆引发的路面振动等。
因此结构动力学的研究对象正是工程结构的各类振动问题。
而结构动力学的研究目的确实是熟悉和了解工程结构的振动规律,并据此指导工程结构的设计实践及其他有关工作,有效地减轻以幸免有害的振动给工程结构造成破坏,从而为人类社会带来更多的福利,这确实是结构动力学研究的目的和意义。
1.1.1动荷载的概念作用在结构上的荷载是由三个因素确信的,即大小、方向和作用点。
若是这些因素不随时刻转变或随时刻缓慢转变,那么在求解结构的响应时可把其作为静荷载处置加以简化计算,如框架结构的衡宇在自身重力荷载作用下的内力和变形,水塔装满水后的内力和变形等都是结构静力学的范围。
若是作用在结构上的荷载的大小、方向和作用点随时刻转变,使得质量运动加速度所引发的惯性力与荷载相较大到不可轻忽时,那么把这种荷载称为动荷载。
如衡宇结构在风荷载作用下的内力和变形,桥梁结构在汽车荷载作用下的内力和变形,和轮船在海浪的冲击下的内力和变形等都是结构动力学的范围。
应当说明,静与动和加载慢与快是相对的,它与结构自振周期有紧密关系,假设荷载从零增至最大值的加载时刻远大于结构自振周期,例如前者为10s后者为1s,那么加载进程能够为是缓慢的,可作为静荷载对待。
可是假设荷载从零增至最大值的加载时刻接近或小于自振周期,那么加载进程应以为是快速的,这种荷载应作为动荷载来处置。
结构动力学习题解答(一二章)

第一章 单自由度系统1。
1 总结求单自由度系统固有频率的方法和步骤。
单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。
1、 牛顿第二定律法适用范围:所有的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析,得到系统所受的合力;(2) 利用牛顿第二定律∑=F x m,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率.2、 动量距定理法适用范围:绕定轴转动的单自由度系统的振动。
解题步骤:(1) 对系统进行受力分析和动量距分析;(2) 利用动量距定理J ∑=M θ,得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
3、 拉格朗日方程法:适用范围:所有的单自由度系统的振动.解题步骤:(1)设系统的广义坐标为θ,写出系统对于坐标θ的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式:L=T —U ; (2)由格朗日方程θθ∂∂-∂∂∂LL dt )( =0,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
4、 能量守恒定理法适用范围:所有无阻尼的单自由度保守系统的振动。
解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即0)(=+dtU T d ,进一步得到系统的运动微分方程;(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。
1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤.用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。
方法一:衰减曲线法.求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷的幅值i A 、1+i A .(2)由对数衰减率定义 )ln(1+=i iA A δ, 进一步推导有 212ζπζδ-=,因为ζ较小, 所以有πδζ2=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
y1 W=3
12)
9)弹性地面上的平面刚体
W=3
10)
W=13
m
EI
自由度为1的体系称作单自由度体系; 自由度大于1的体系称作多(有限)自由度体系; 自由度无限多的体系为无限自由度体系。 W=2
§1-3结构振动中的能量耗散-阻尼力 材料内部的分子运动
结构与支座或基础的相对运动
产生阻尼力的原因
目的是为了采用该式计算等效粘性阻尼系数
x ( t ) A sin( 0 t )
二、摩擦阻尼
阻尼力与摩擦接触面间的正压力成正比,方向相反。
F fd (t ) fFN
又称为库仑阻尼
x fFN sgn( x ) x
符号函数
f:摩擦系数
FN :正压力
0 x 1, 0, 0 sgn x x 1, x 0
- 振动也有它积极的一方面,是可以利用的
例如: 振动是通信、广播、电视、雷达等工作的基础
工业用的振动筛、振动沉桩、振动输送、地震仪等 。。。。。请同学举例
四、振动力学与结构动力学的研究内容和任务
1.振动力学与结构动力学的研究内容 当前的研究内容为: 第一类问题:响应分析(体系动力计算) 输入 (动力荷载) 结构 (系统) -----正问题 输出 (动力响应) -----反问题
Hale Waihona Puke - 通常假设在简谐激振力作用下非粘性阻尼系统的稳态响应仍 然为简谐振动
- 该假设只有在非粘性阻尼比较小时才是合理的
- 粘性阻尼在一个周期内消耗的能量 E 可近似地利用无阻尼 振动规律计算出:
dx cx dt c A E cx
2 0
T
2 0
2
T 0
cos2 (0t )dt c0 A2
• 第六章 结构反应谱与地震荷载计算(8学 时)
– 知识要点:结构反应谱、单自由度和多自由度地震 荷载计算公式、规范中地震荷载计算公式。 – 重点难点:理解地震荷载计算公式原理及其在工程 抗震中的具体应用。 – 教学方法:课堂讲授与引导讨论相结合。
• 第七章 结构振动控制的基本概念(8学时)
– 知识要点:结构被动控制、主动控制的基本概念。常用主动 控制方法的原理。结构主动控制在机械、土木结构工程中应 用简介。 – 重点难点:理解各种控制方法的原理及其具体实现。 – 教学方法:课堂讲授与引导讨论相结合。
二.动荷载的分类
动荷载
简谐荷载 周期 非简谐荷载 确定 冲击荷载 非周期 突加荷载 其他确定规律的动荷载 风荷载 地震荷载 不确定 其他无法确定变化规律的荷载
另一种分类
按激励的有无和性质,振动可以分为: 固有振动 无激励时系统所有可能的运动集合(不是现实的振动,仅反
映系统关于振动的固有属性)
自由振动 激励消失后系统所做的振动(现实的振动) 强迫振动 系统在外部激励作用下所做的振动 随机振动 系统在非确定性的随机激励下所做的振动,例如行驶在公路 上的汽车的振动 自激振动 系统在自身控制的激励作用下的振动 参数振动 激励以系统本身的参数随时间变化的形式出现的振动,例如
m
二. 自由度的确定 1) 平面上的一个质点
4)
y1
W=1
y2
2)
y1
W=2
5) W=2
W=2 弹性支座不减少动力自由度 3) 计轴变时 W=2 不计轴变时 W=1 7)
EI
6)
y2
y1
W=2
自由度数与质点个数无关,但 不大于质点个数的2倍。
为减少动力自由度,梁与刚架不 计轴向变形。
W=1
应力 加载
内摩擦所耗散的能量等于滞回环 所围的面积(实验得到):
E A2
:比例系数
等效粘性阻尼系数:
0
应变
ce 0
卸载
五、滞变阻尼
阻尼力与位移成正比,但其相位与速度相同,即朝前 位移90度。
Fhd (t ) kx(t T / 4)
自己推导等效粘性阻尼系数。
1) 集中质量法 将实际结构的质量看成(按一定规则) 集中在某些几何点上,除这些点之外物体是 无质量的。这样就将无限自由度系统变成一 有限自由度系统。
m
2) 广义坐标法
y ( x) ai i ( x) y ( x) ai i ( x)
i 1 i 1 n
a i ---广义坐标 i ( x) ---基函数 i (0) i (l ) 0
二. 自由度的确定 8) 平面上的一个刚体
4)
y1
W=1
y2
y1 W=3
5) W=2
9)弹性地面上的平面刚体
W=3
10)
6)
y2
y1
W=2
m
EI
自由度数与质点个数无关,但 不大于质点个数的2倍。 W=2 7)
EI
W=1
二. 自由度的确定 8) 平面上的一个刚体
11) W=1
y2
自激振动:激励是受系统振动本身控制的,在适当的反馈作用下,系统将自动 的激起定幅的振动。
秋千被越荡越高。秋千受到的激励以摆长随时间变化的形式 出现,而摆长的变化由人体的下蹲及站立造成
振动力学-借助数学、物理、实验和计算技 术,探讨各种振动现象,阐明振动的基本规 律,以便克服振动的消极因素,利用其积极 因素,为合理解决各种振动问题提供理论依 据的一门学科。 对象-刚体系统 结构动力学是研究动荷作用下结构动力响 应规律的学科。 对象-变形体系统
运动方向不变时摩擦力为常值,所作的功等于摩擦力与运
动距离的乘积。 摩擦力一个周期内所消耗的能量: 等效粘性阻尼系数:
E 4 fFN A
4 fFN ce πω0 A
三、 平方阻尼 工程背景:低粘度流体中以较大速度运动的物体 阻尼力与相对速度的平方成正比,方向相反 摩擦力:
2 sgn x Fd cd x
§1-4 运动方程式的建立
要了解和掌握系统动力响应的规律,必须首先建立描述系统运动的 (微分)方程。建立运动方程的方法很多,常用的有虚功法、变分法等。 下面介绍建立在达朗贝尔原理基础上的“动静法”。
施 力 物 体
m
P(t ) P(t ) (t ) y
(t ) P(t ) m y (t ) P(t ) m y
三、学习目的
- 许多情况下,振动是有害的 - 它常常是造成机械和结构破坏和失效的直接原因 例如:1940年美国的Tacoma Narrows吊桥可看视频。
1972年日本海南电厂的一台66万千瓦的气轮发电机组 美国第一颗人造卫星“探险者I号” ,“国际通讯卫星V号 ” 振动会影响精密仪器的功能,降低加工精度,加剧构件疲劳和磨损 桥梁因振动而倒塌,飞机机翼的颤振、机轮的抖振而造成事故 强烈的振动噪声而形成严重公害………请同学举例
周围介质对结构运动阻止作用
地基介质的耗散能量
一、粘性阻尼
阻尼力大小与速度成正比,方向相反。
(t ) Fvd cy
实际系统中存在各种其他类型的阻尼,其性质比粘性阻尼 复杂得多。一般通过能量等效的方法给出等效粘性阻尼。
原则:
等效粘性阻尼在一个周期内消耗的能量等于要简化的 非粘性阻尼在同一周期内消耗的能量
第二类问题:参数(或称系统)识别
输入 (动力荷载)
结构 (系统)
输出 (动力响应)
第三类问题:荷载识别。 输入 (动力荷载) 第四类问题:控制问题 输入 (动力荷载) 结构 (系统) 结构 (系统)
-----反问题 输出 (动力响应) -----控制问题 输出 (动力响应)
控制系统 (装置、能量)
11
(t )] 11[ P(t ) m y
P(t )
(t )] y (t ) 11[ P (t ) m y
(1)心脏的搏动、耳膜和声带的振动,(2)桥梁和建筑物在风和 地震作用下的振动,(3)飞机和轮船航行中的振动,(4)机床和 刀具在加工时的振动 一.动荷载的定义 大小、方向和作用点随时间变化;在其作用下,体系上的惯性力 与外荷比不可忽视的荷载。
自重、缓慢变化的荷载,其惯性力与外荷比很小,分析时仍视作 静荷载。 静荷只与作用位置有关,而动荷是坐标和时间的函数。
• 第四章 连续体系统振动(10学时)
–知识要点:杆的纵向振动、杆的扭转振动及梁的横 向振动。
–重点难点:重点包括杆的纵向振动、杆的扭转振动 及梁的横向振动。难点是分析连续系统振动的方法, 包括解析方法和几种重要的近似方法如集中质量法, 模态叠加法及有限单元法等。 –教学方法:课堂讲授与引导讨论相结合
T /4
cd :阻力系数
在运动方向不变的半个周期内计算耗散能量,再乘2:
8 3 2 2 cd x dt cd 0 A T / 4 3 8 cd 0 A 等效粘性阻尼系数: ce 3
sgn x dx 2 E cd x
2
四、结构阻尼 由于材料为非完全弹性,在变形过程中材料的内摩擦所引起 的阻尼称为结构阻尼 特征:应力-应变曲线存在滞回曲线 加载和卸载沿不同曲线
m y ( x)
广义坐标个数即 为自由度个数
3) 有限元法 和静力问题一样,可通过将实际结构 离散化为有限个单元的集合,将无限自由 度问题化为有限自由度来解决。 二. 自由度的确定
m
结点位移个数即 为自由度个数
1) 集中质量法 将实际结构的质量看成(按一定规则) 集中在某些几何点上,除这些点之外物体是 无质量的。这样就将无限自由度系统变成一 有限自由度系统。
运动方程 惯性力
m
P(t )
一、柔度法
(t ) m y
=1
1.在质量上沿位移正向加惯性力; 2.求外力和惯性力引起的位移; 形式上的平衡方程,实质上的运动方程 3.令该位移等于体系位移。
