正余弦的诱导公式经典练习题
02三角函数诱导公式(含经典例题+答案)
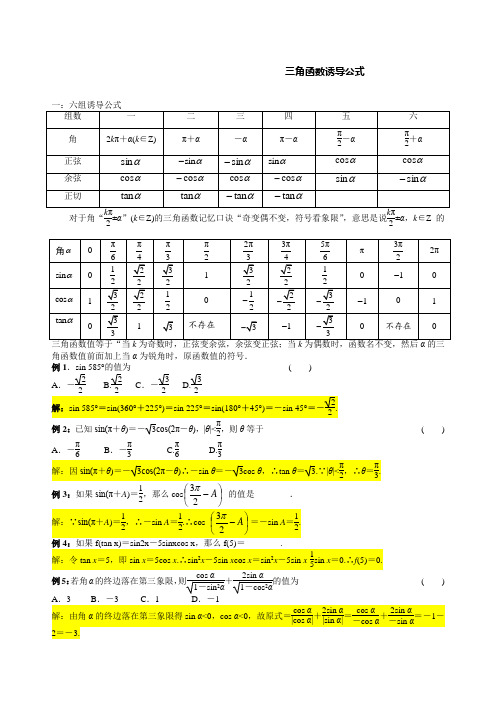
三角函数诱导公式对于角“k π2±α”(k ∈Z)的三角函数记忆口诀“奇变偶不变,符号看象限”,意思是说k π2±α,k ∈Z 的角函数值前面加上当α为锐角时,原函数值的符号.例1.sin 585°的值为 ( )A .-2 B.2 C .-3 D.3例2:已知sin(π+θ)=-3cos(2π-θ),|θ|<π2,则θ等于 ( )A .-πB .-π C.π D.π例3:如果sin(π+A )=12,那么cos ⎪⎫⎛-A 3 的值是________. 例5:若角α的终边落在第三象限,则cos α1-sin 2α+2sin α1-cos 2α的值为 ( )例6:已知α∈(-π,0),tan(3π+α)=31,则cos ⎪⎭⎫⎝⎛+απ23的值为 ( ) A.1010 B .-1010 C.31010 D .-31010解:tan α=13,cos ⎪⎭⎫⎝⎛+απ23=sin α.∵α∈(-π,0),∴sin α=-1010. A .-32 B.32 C.3-12 D.3+12解:sin 600°+tan 240°=sin(720°-120°)+tan(180°+60°)=-sin 120°+tan 60°=-32+3=32. ( ) A .3 B .5 C .1 D .不能确定解:f(2 011)=asin(2 011π+α)+bcos(2 011π+β)+4=asin(π+α)+bcos(π+β)+4=-asin α-bcos β+4 =5.∴asin α+bcos β=-1.∴f(2 012)=asin(2 012π+α)+bcos(2 012π+β)+4=asin α+bcos β+4 =-1+4=3.1.诱导公式在三角形中经常应用,常用的变形结论有:A +B =π-C ; 2A +2B +2C =2π;A 2+B 2+C 2=π2.2.求角时,一般先求出该角的某一三角函数值,再确定该角的范围,最后求角.例9:△ABC 中,cos A =13,则sin(B +C )=________.解:∵△ABC 中,A +B +C =π,∴sin(B +C )=sin(π-A )=sin A =1-cos 2A =223.例10:在△ABC 中,若sin(2π-A )=-2sin(π-B ),3cos A =-2cos(π-B ),求△ABC 的三个内角. 解:由已知得⎩⎨⎧sin A =2sin B ①3cos A =2cos B ②①2+②2得2cos 2A =1,即cos A =22或cos A =-22.(1)当cos A =22时,cos B =32,又A 、B 是三角形的内角,∴A =π4,B =π6,∴C =π-(A +B )=712π. A .B .C .D .2.cos (﹣30°)的值是( ) A .B .C .D .3.下列能与sin20°的值相等的是( ) A .cos20° B .sin (﹣20°) C .sin70° D .sin160°4.已知,则下列各式中值为的是( )A .B .sin (π+α)C .D .sin (2π﹣α)换元法与诱导公式例11:已知41)3sin(=+απ,则=-)6cos(απ 。
正弦余弦的诱导公式典例剖析(任意角的三角函数习题课)

[例1]已知cos α=m(|m |≤1),求sin α、tan α的值.选题意图:考查已知一个角的一个三角函数值,求这个角的其他三角函数值的方法和分类讨论的思想.解:当m =0时,α角的终边落在y 轴上若α的终边在y 轴的非负半轴上,则sin α=1,tan α不存在若α的终边在y 轴的非正半轴上,则sin α=-1,tan α不存在当m =±1时,α角的终边落在x 轴上,则sin α=0,tan α=0当|m |<1且m ≠0时若α在第一或第二象限时mm m 2221cos sin tan 1cos 1sin -==-=-=ααααα若α在第三或第四象限时 m m m 2221cos sin tan 1cos 1sin --==--=--=ααααα说明:确定角α的范围,以便确定三角函数值的符号,要对角的范围进行讨 论,不要遗漏终边在坐标轴上的情况.[例2]已知tan α=2,求下列各式的值.(1)sin 2α-sin αcos α+2 (2)ααααcos 3sin 5cos sin 3+- 选题意图:考查商数关系和平方关系的应用.解:(1)sin 2α-sin αcos α+25121422431tan 2tan tan 3cos sin cos 2cos sin sin 3222222=++-⨯=++-=++-=αααααααα 653)14()310()14(8)1)(tan 3tan 5()1(tan tan )cos )(sin cos 3sin 5()cos (sin cos sin cos 3sin 5cos sin )2(223222233=+⨯++-=+++-=+++-=+-αααααααααααααααα说明:先通过tan α=2,求出sin α、cos α,再代入求值,需要讨论,运算也较为复杂. [例3]已知51cos sin -=-θθ,求下列各式的值.(1)sin 4θ+cos 4θ(2)tan θ选题意图:考查平方关系的应用.解:(1)由51cos sin -=-θθ,得1-2sin θcos θ=251 ∴2sin θcos θ=2524 sin 4θ+cos 4θ=(sin 2θ+cos 2θ)2-2sin 2θcos 2θ=1-21(2sin θcos θ)2 625337)2524(2112=⨯-= (2)由(1)知sin θcos θ=2512>0, ∴θ为第一或第三象限角 而(sin θ+cos θ)2=1+2sin θcos θ=1+25492524= 若θ在第一象限,则sin θ+cos θ=57与sin θ-cos θ=-51联立求得 ⎪⎪⎩⎪⎪⎨⎧==54cos 53sin θθ 43t a n =∴θ 若θ在第三象限,则sin θ+cos θ=-57与sin θ-cos θ51⎪⎪⎩⎪⎪⎨⎧-=-=53cos 54sin θθ 34t a n =∴θ 说明:通过平方关系可以用sin θ+cos θ或sin θ-cos θ表示sin θ·cos θ以便达到换元的目的.[例4]已知x+y =4-2cos 22θ,x -y=4sin2θ,求证22121=+y x .选题意图:考查三角函数条件等式的证明方法和平方关系的应用.证明:由x +y =4-2cos 22θ,得θ2cos 242=--y x ① 由x -y =4sin2θ得θ2sin 4=-y x ②①+②2得.116)(242=-+--y x y x 即x 2+y 2-2xy -8x -8y +16=0 4xy =x 2+y 2+16-8x -8y +2xy 即4xy =(4-x -y )2 ∴2xy =4-x -y 即x +2xy +y =4 ∴4)(2=+y x 因此22121=+y x说明:可通过⎩⎨⎧=--=+θθ2sin 42cos 242y x y x 求出x 、y ,再代入进行证明.。
三角函数诱导公式练习题 答案

三角函数的引诱公式1一.选择题1.假如|cosx|=cos (x+π),则x 的取值聚集是()A .-2π+2kπ≤x≤2π+2kπ B.-2π+2kπ≤x≤2π3+2kπC .2π+2kπ≤x≤2π3+2kπ D.(2k+1)π≤x≤2(k+1)π(以上k∈Z)2.sin (-6π19)的值是()A .21 B .-21 C .23D .-233.下列三角函数:①sin(nπ+3π4);②cos(2nπ+6π);③sin(2nπ+3π);④cos[(2n+1)π-6π];⑤sin[(2n+1)π-3π](n∈Z).个中函数值与sin 3π的值雷同的是()A .①②B .①③④C .②③⑤D .①③⑤ 4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为()A .-36B .36 C .-26 D .265.设A.B.C 是三角形的三个内角,下列关系恒成立的是()A .cos (A+B )=cosCB .sin (A+B )=sinC C .tan (A+B )=tanCD .sin 2B A +=sin 2C6.函数f (x )=cos 3πx (x∈Z)的值域为()A .{-1,-21,0,21,1} B .{-1,-21,21,1}C .{-1,-23,0,23,1} D .{-1,-23,23,1}二.填空题7.若α是第三象限角,则)πcos()πsin(21αα---=_________.8.sin21°+sin22°+sin23°+…+sin289°=_________.三.解答题9.求值:sin (-660°)cos420°-tan330°cot(-690°).10.证实:1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθθθ. 11.已知cosα=31,cos (α+β)=1,求证:cos (2α+β)=31.12.化简:︒+︒︒︒+790cos 250sin 430cos 290sin 21.13.求证:)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tanθ.14.求证:(1)sin (2π3-α)=-cosα; (2)cos (2π3+α)=sinα.参考答案1一.选择题1.C 2.A 3.C 4.B 5.B 6.B 二.填空题7.-sinα-cosα 8.289三.解答题 9.43+1.10.证实:左边=θθθθ22sin cos cos sin 2-1-- =-θθθθθθθθθθcos sin cos sin )sin )(cos sin (cos )cos (sin 2-+=-++,右边=θθθθθθθθcos sin cos sin tan tan tan tan -+=1-1+=1+-1--,左边=右边,∴原等式成立.11.证实:∵cos(α+β)=1,∴α+β=2kπ.∴cos(2α+β)=cos (α+α+β)=cos (α+2kπ)=cosα=31.12.解:︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21=︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =-1.13.证实:左边=θθθθθθθθθθsin cos cos )sin )(tan ()sin )(cos ()cos()sin()tan(--=-----=tanθ=右边,∴原等式成立.14证实:(1)sin (2π3-α)=sin [π+(2π-α)]=-sin (2π-α)=-cosα.(2)cos (2π3+α)=cos [π+(2π+α)]=-cos (2π+α)=sinα.三角函数的引诱公式2一.选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为() A. 21B. —21 C. 23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为() A.23 B. 21C. 23±D. —233.化简:)2cos()2sin(21-•-+ππ得()2 C.sin2-cos2 D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中准确的是()A.sinα=sinβB. sin(α-π2) =sinβC.cosα=cosβD.cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于(),A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4)二.填空题: 6.cos(π-x)= 23,x∈(-π,π),则x 的值为.7.tanα=m,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ.8.|sinα|=sin(-π+α),则α的取值规模是. 三.解答题: 9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos2(65π-x )的值. 11.求下列三角函数值:(1)sin 3π7;(2)cos 4π17;(3)tan (-6π23);12.求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5;(2)sin [(2n+1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.参考答案21.C 2.A 3.C 4.C 5.A 6.±65π 7.11-+m m 8.[(2k-1) π,2k π]9.原式=)cos (·sin()cos()n s (sin αα)παπα--+--αi =)cos ?(sin )cos (sin 2αααα--= sinα 10.161111.解:(1)sin 3π7=sin (2π+3π)=sin 3π=23.(2)cos 4π17=cos (4π+4π)=cos 4π=22.(3)tan (-6π23)=cos (-4π+6π)=cos 6π=23.(4)sin (-765°)=sin [360°×(-2)-45°]=sin (-45°)=-sin45°=-22.注:应用公式(1).公式(2)可以将随意率性角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.12.解:(1)sin 3π4·cos 6π25·tan 4π5=sin (π+3π)·cos(4π+6π)·tan(π+4π)=(-sin 3π)·cos 6π·tan 4π=(-23)·23·1=-43.(2)sin [(2n+1)π-3π2]=sin (π-3π2)=sin 3π=23.13.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++=θθθθθcos cos 223cos cos 1cos 2223++-+-+=θθθθθcos cos 22)cos (cos 2cos 2223++---=θθθθθcos cos 22)1(cos cos )1(cos 223++--- =θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-=cosθ-1,∴f(3π)=cos 3π-1=21-1=-21.三角函数公式1. 同角三角函数根本关系式sin2α+cos2α=1 sinαcosα =ta nαtanαcotα=12. 引诱公式 (奇变偶不变,符号看象限)(一)sin(π-α)=sinα sin(π+α)=-sinαcos(π-α)=-cosα cos(π+α)=-cosα tan(π-α)=-tanα tan(π+α)=tanα sin(2π-α)=-sinα sin(2π+α)=sinα cos(2π-α)=cosα cos(2π+α)=cosα tan(2π-α)=-tanα tan(2π+α)=tanα(二) sin(π2 -α)=cosα sin(π2+α)=cosαcos(π2 -α)=sinα cos(π2 +α)=- sinαtan(π2 -α)=cotα tan(π2 +α)=-cotαsin(3π2 -α)=-cosα sin(3π2 +α)=-cosαcos(3π2 -α)=-sinα cos(3π2 +α)=sinαtan(3π2 -α)=cotα tan(3π2+α)=-cotαsin(-α)=-sinα cos(-α)=cosα tan(-α)=-tanα3. 两角和与差的三角函数cos(α+β)=cosαcosβ-sinαsinβ cos(α-β)=cosαcosβ+sinαsinβ sin (α+β)=sinαcosβ+cosαsinβ s in (α-β)=sinαcosβ-cosαsinβ tan(α+β)= tanα+tanβ1-tanαtanβtan(α-β)= tanα-tanβ1+tanαtanβ4. 二倍角公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2α tan2α=2tanα1-tan2α5. 公式的变形 (1)升幂公式:1+cos2α=2cos2α 1—cos2α=2sin2α (2)降幂公式:cos2α=1+cos2α2 sin2α=1-cos2α2(3)正切公式变形:tanα+tanβ=tan(α+β)(1-tanαtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)(4)全能公式(用tanα暗示其他三角函数值)sin2α=2tanα1+tan2α cos2α=1-tan2α1+tan2α tan2α=2tanα1-tan2α6. 拔出帮助角公式asinx +bcosx=a2+b2 sin(x+φ) (tanφ= ba )特别地:sinx±cosx= 2 sin(x±π4)7. 熟习情势的变形(若何变形)1±sinx±cosx 1±sinx 1±cosx tanx+cotx 1-tanα1+tanα 1+tanα1-tanα若A.B 是锐角,A+B =π4,则(1+tanA )(1+tanB)=28. 在三角形中的结论若:A +B +C=π , A+B+C 2 =π2则有tanA +tanB +tanC=tanAtanBtanCtan A 2 tan B 2 +tan B 2 tan C 2 +tan C 2 tan A2=1。
三角函数诱导公式练习题-带答案

三角函数的诱导公式(1)一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( )A .-2π+2k π≤x ≤2π+2k π B .-2π+2k π≤x ≤2π3+2k π C . 2π+2k π≤x ≤2π3+2k π D .(2k +1)π≤x ≤2(k +1)π(以上k ∈Z ) 2.sin (-6π19)的值是( ) A . 21 B .-21 C .23 D .-23 3.下列三角函数:①sin (n π+3π4);②cos (2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π]; ⑤sin [(2n +1)π-3π](n ∈Z ). 其中函数值与sin3π的值相同的是( ) A .①② B .①③④ C .②③⑤ D .①③⑤4.若cos (π+α)=-510,且α∈(-2π,0),则tan (2π3+α)的值为( ) A .-36 B .36 C .-26 D .26 5.设A 、B 、C 是三角形的三个内角,下列关系恒成立的是( )A .cos (A +B )=cosC B .sin (A +B )=sin C C .tan (A +B )=tan CD .sin2A B +=sin 2C 6.函数f (x )=cos3πx (x ∈Z )的值域为( ) A .{-1,-21,0,21,1} B .{-1,-21,21,1} C .{-1,-23,0,23,1} D .{-1,-23,23,1} 二、填空题7.若α.8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________.三、解答题9.求值:sin (-660°)cos420°-tan330°cot (-690°).11..12、求证:tan(2π)sin(2π)cos(6π)cos(π)sin(5π)q q qq q-----+=tanθ.三角函数的诱导公式(2)一、选择题:1.已知sin(4π+α)=23,则sin(43π-α)值为( ) A. 21 B. —21 C. 23 D. —23 2.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( ) A. 23 B. 21 C. 23± D. —23 3.化简:)2cos()2sin(21-•-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )A.sinα=sinβB. sin(α-π2) =sinβC.cosα=cosβD. cos(π2-α) =-cosβ5.设tanθ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ), A. 51(4+5) B. 51(4-5) C. 51(4±5) D. 51(5-4) 二、填空题:6.cos(π-x)= 23,x ∈(-π,π),则x 的值为 . 7.tanα=m ,则=+-+++)cos(-sin()cos(3sin(απα)απ)απ . 8.|sinα|=sin (-π+α),则α的取值范围是 .三、解答题:9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin 3π4·cos 6π25·tan 4π5; (2)sin [(2n +1)π-3π2].13.设f (θ)=)cos()π(2cos 23)2πsin()π2(sin cos 2223θθθθθ-+++-++-+,求f (3π)的值.。
三角函数诱导公式练习题(带答案)

三角函数诱导公式检测题1.全国Ⅱ)若sin α<0且tan α>0,则α是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角2.(07·湖北)tan690°的值为( )A .-33 B.33 C. 3 D .- 33.f (sin x )=cos19x ,则f (cos x )=( )A .sin19xB .cos19xC .-sin19xD .-cos19x4.设f (x )=a sin(πx +α)+b cos(πx +β),其中a ,b ,α,β∈R ,且ab ≠0,α≠k π(k ∈Z).若f (2009)=5,则f (2010)等于( )A .4B .3C .-5D .55.(09·全国Ⅰ文)sin585°的值为( )A .-22 B.22 C .-32 D.326.函数y =5sin ⎝⎛⎭⎫25x +π6的最小正周期是( ) A.25π B.52π C.π3 D .5π7.(2010·重庆文,6)下列函数中,周期为π,且在[π4,π2]上为减函数的是( ) A .y =sin(2x +π2) B .y =cos (2x +π2) C .y =sin(x +π2) D .y =cos(x +π2)8.函数y =-2tan ⎝⎛⎭⎫3x +π4的单调递减区间是________.三角函数诱导公式(答案)1.[答案] C2.[答案] A[ 解析] tan690°=tan(-30°+2×360°)=tan(-30°)=-tan30°=-33,选A. 3.[答案] C[解析] f (cos x )=f (sin(90°-x ))=cos19(90°-x )=cos(270°-19x )=-sin19x .4.[答案] C[解析] ∵f (2009)=a sin(2009π+α)+b cos(2009π+β)=-a sin α-b cos β=5, ∴a sin α+b cos β=-5.∴f (2010)=a sin α+b cos β=-5.5.[答案] A[解析] sin585°=sin(360°+225°)=sin225°=sin(180°+45°)=-sin45°=-22. 6.[答案] D[解析] T =2π25=5π. 7.[答案] A[解析] 选项A :y =sin(2x +π2)=cos2x ,周期为π,在[π4,π2]上为减函数; 选项B :y =cos(2x +π2)=-sin2x ,周期为π,在[π4,π2]上为增函数; 选项C :y =sin(x +π2)=cos x ,周期为2π; 选项D :y =cos(x +π2)=-sin x ,周期为2π.故选A. 8. [答案] ⎝⎛⎭⎫k π3-π4,k π3+π12(k ∈Z)[解析] 求此函数的递减区间,也就是求y =2tan ⎝⎛⎭⎫3x +π4的递增区间,由k π-π2<3x +π4<k π+π2,k ∈Z 得:k π3-π4<x <k π3+π12, ∴减区间是⎝⎛⎭⎫k π3-π4,k π3+π12,k ∈Z.。
高一数学 知识点 三角函数 诱导公式 常考题 经典题 50道 含答案和解析

高一数学三角函数诱导公式50道常考题经典题一、单选题1.若角的终边上有一点(-4,a),则a的值是()A. B. C. D.【答案】A【考点】任意角的三角函数的定义,诱导公式一【解析】【解答】由三角函数的定义知:,所以,因为角的终边在第三象限,所以<0,所以的值是。
【分析】三角函数是用终边上一点的坐标来定义的,和点的位置没有关系。
属于基础题型。
================================================================================2.若,则的值是( )A. B. C. D.【答案】C【解析】【解答】即,所以,,=,故选C。
【分析】简单题,此类题解的思路是:先化简已知条件,再将所求用已知表示。
================================================================================3.若,则()A. B. C. D.【答案】C【考点】诱导公式一,同角三角函数间的基本关系【解析】【解答】,故选C.================================================================================4.函数图像的一条对称轴方程是()A. B. C. D.【答案】A【考点】诱导公式一,余弦函数的图象,余弦函数的对称性【解析】【分析】,由y=cosx的对称轴可知,所求函数图像的对称轴满足即,当k=-1时,,故选A.================================================================================5.已知,则()A. B. C. D.【答案】C【考点】诱导公式一,同角三角函数间的基本关系,弦切互化【解析】【解答】因为,所以,可得,故C符合题意.故答案为:C .【分析】利用诱导公式将已知条件化简可求出tan,将中分子分母同时除以cos.================================================================================6.函数()A. 是奇函数B. 是偶函数C. 既是奇函数,又是偶函数D. 是非奇非偶函数【答案】A【考点】奇函数,诱导公式一【解析】【解答】∵,∴,∴是奇函数.故答案为:A【分析】首先利用诱导公式整理化简f(x) 的解析式,再根据奇函数的定义即可得证出结果。
三角函数诱导公式练习题非常经典含有--答案

一、选择题1.如果|cos x |=cos (x +π),则x 的取值集合是( )A.-2π+2k π≤x ≤2π+2k π B .-2π+2k π≤x ≤2π3+2k πC . 2π+2k π≤x ≤2π3+2k πD .(2k +1)π≤x ≤2(k +1)π(以上k ∈Z )2.sin (-6π19)的值是( )A . 21 B .-21C .23 D .-233.下列三角函数:①sin (n π+3π4);②cos(2n π+6π);③sin (2n π+3π);④cos [(2n +1)π-6π];⑤sin [(2n +1)π-3π](n ∈Z ).其中函数值与sinπ的值3相同的是()A.①②B.①③④C.②③⑤D.①③⑤4.若cos(π+α)=-10,5且α∈(-π,0),则tan(2π3+α)2的值为()A.-6B.363C.-6D.2625.设A、B、C是三角形的三个内角,下列关系恒成立的是()A.cos(A+B)=cos C B.sin(A+B)=sin C C.tan (A+B)=tan C D.sin2B A =sin2C 6.函数f(x)=cos3πx(x ∈Z)的值域为()A.{-1,-1,0,21,21} B .{-1,-21,21,1}C .{-1,-23,0,23,1} D .{-1,-23,23,1}二、填空题7.若α是第三象限角,则)πcos()πsin(21αα---=_________.8.sin 21°+sin 22°+sin 23°+…+sin 289°=_________.三、解答题9.求值:sin (-660°)cos420°-tan330°cot (-690°).10.证明:1)πtan(1)π9tan(sin 211cos )πsin(22++-+=--⋅+θθθθθ.11.已知cos α=31,cos(α+β)=1,求证:cos (2α+β)=31.12. 化简:︒+︒︒︒+790cos 250sin 430cos 290sin 21.13、求证:)π5sin()πcos()π6cos()π2sin()π2tan(θθθθθ+-----=tan θ.14. 求证:(1)sin (2π3-α)=-cos α;(2)cos (2π3+α)=sin α.参考答案1一、选择题1.C 2.A 3.C 4.B 5.B 6.B二、填空题7.-sin α-cos α 8.289三、解答题 9.43+1.10.证明:左边=θθθθ22sin cos cos sin 2-1--=-θθθθθθθθθθcos sin cos sin )sin )(cos sin (cos )cos (sin 2-+=-++, 右边=θθθθθθθθcos sin cos sin tan tan tan tan -+=1-1+=1+-1--,左边=右边,∴原等式成立. 11.证明:∵cos (α+β)=1,∴α+β=2k π.∴cos (2α+β)=cos (α+α+β)=cos (α+2k π)=cos α=31.12.解:︒+︒︒︒+790cos 250sin 430cos 290sin 21=)360270cos()70180sin()36070cos()36070sin(21︒⨯+︒+︒+︒︒+︒︒+︒-+=︒-︒︒︒-70sin 70cos 70cos 70sin 21 =︒-︒︒-︒70sin 70cos )70cos 70(sin 2=︒-︒︒-︒70sin 70cos 70cos 70sin =-1.13.证明:左边=θθθθθθθθθθsin cos cos )sin )(tan ()sin )(cos ()cos()sin()tan(--=-----=tan θ=右边,∴原等式成立.14证明:(1)sin(π3-α)2=sin[π+(π-α)]=-sin(2π-2α)=-cosα.(2)cos(π3+α)=cos[π+2(π+α)]=-cos(2π+α)=sinα.2三角函数的诱导公式2一、选择题:1.已知sin(π+α)=23,则4sin(3π-α)值为()4A.1 B. —21 C.223 D. —232.cos(π+α)= —21,23π<α<π2,sin(π2-α) 值为( )A. 23 B. 21 C.23±D. —233.化简:)2cos()2sin(21-∙-+ππ得( )A.sin2+cos2B.cos2-sin2C.sin2-cos2D.± (cos2-sin2)4.已知α和β的终边关于x 轴对称,则下列各式中正确的是( )A.sin α=sin βB.sin(α-π2) =sin βC.cos α=cos βD. cos(π2-α) =-cos β5.设tan θ=-2, 2π-<θ<0,那么sin 2θ+cos(θ-π2)的值等于( ),A. 51(4+5) B. 51(4-5)C. 51(4±5) D. 51(5-4)二、填空题:6.cos(π-x)= 23,x ∈(-π,π),则x 的值为 .7.tan α=m ,则=+-+++)c o s(-s i n ()c o s(3s i n (απα)απ)απ .8.|sin α|=sin (-π+α),则α的取值范围是 .三、解答题: 9.)cos(·3sin()cos()n(s 2sin(απα)παπα)π----+-απi .10.已知:sin (x+6π)=41,求sin ()67x +π+cos 2(65π-x )的值.11. 求下列三角函数值:(1)sin 3π7;(2)cos 4π17;(3)tan (-6π23);12. 求下列三角函数值:(1)sin3π4·cos6π25·tan4π5;(2)sin[(2n+1)π-3π2].13.设f(θ)=)cos()π(2cos23)2πsin()π2(sin cos2223θθθθθ-+++-++-+,求f(3π)的值.参考答案21.C 2.A 3.C 4.C 5.A6.±65π7.11-+m m8.[(2k-1) π,2kπ]9.原式=)cos(·sin()cos()ns(sinαα)παπα--+--αi=)cos?(sin)cos(sin2αααα--=sin α 10.161111.解:(1)sin 3π7=sin(2π+3π)=sin 3π=23.(2)cos 4π17=cos (4π+4π)=cos 4π=22.(3)tan (-6π23)=cos (-4π+6π)=cos 6π=23.(4)sin (-765°)=sin [360°×(-2)-45°]=sin(-45°)=-sin45°=-2.2注:利用公式(1)、公式(2)可以将任意角的三角函数转化为终边在第一象限和第二象限的角的三角函数,从而求值.12.解:(1)sinπ4·cos6π25·tan4π5=sin3(π+π)·cos(4π+6π)·tan(π+4π)3=(-sinπ)·cos6π·tan4π=(-323)·23·1=-43.(2)sin [(2n +1)π-3π2]=sin (π-3π2)=sin 3π=23.13.解:f (θ)=θθθθθcos cos 223cos sin cos 2223++-++=θθθθθcos cos 223cos cos 1cos 2223++-+-+=θθθθθcos cos 22)cos (cos 2cos 2223++--- =θθθθθcos cos 22)1(cos cos )1(cos 223++---=θθθθθθθcos cos 22)1(cos cos )1cos )(cos 1(cos 222++--++-=θθθθθcos cos 22)2cos cos 2)(1(cos 22++++-=cosθ-1,∴f(3π)=cos3π-1=21-1=-1.2三角函数公式1.同角三角函数基本关系式sin2α+cos2α=1sinα=tanαcosαtanαcotα=12.诱导公式(奇变偶不变,符号看象限)(一)sin(π-α)=sinαsin(π+α)=-sinαcos(π-α)=-cosαcos(π+α)=-cosαtan(π-α)=-tanαtan(π+α)=tanαsin(2π-α)=-sinαsin(2π+α)=sinαcos(2π-α)=cosαcos(2π+α)=cosαtan(2π-α)=-tanαtan(2π+α)=tanα(二)sin(π2-α)=cosαsin(π2+α)=cosαcos(π2-α)=sin αcos(π2+α)=- sin αtan(π2-α)=cot αtan(π2+α)=-cot αsin(3π2-α)=-cos αsin(3π2+α)=-cos αcos(3π2-α)=-sin αcos(3π2+α)=sin αtan(3π2-α)=cot αtan(3π2+α)=-cot αsin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanα3.两角和与差的三角函数cos(α+β)=cosαcosβ-sinαsinβcos(α-β)=cosαcosβ+sinαsinβsin (α+β)=sinαcosβ+cosαsinβsin (α-β)=sinαcosβ-cosαsinβtan(α+β)=tanα+tanβ1-tanαtanβtan(α-β)= tanα-tanβ1+tanαtanβ4.二倍角公式sin2α=2sinαcosαcos2α=cos2α-sin2α=2 cos2α-1=1-2 sin2αtan2α=2tanα1-tan2α5.公式的变形(1)升幂公式:1+cos2α=2cos2α1—cos2α=2sin2α(2)降幂公式:cos2α=1+cos2αsin2α=21-cos2α2(3)正切公式变形:tanα+tanβ=tan(α+β)(1-tan αtanβ)tanα-tanβ=tan(α-β)(1+tanαtanβ)(4)万能公式(用tanα表示其他三角函数值)sin2α=2tanα1+tan2αcos2α=1-tan2α1+tan2αtan2α=2tanα1-tan2α6.插入辅助角公式asinx+bcosx=a2+b2sin(x+φ) (tanφ= b a )特殊地:sinx±cosx= 2sin(x±π4 )7.熟悉形式的变形(如何变形)1±sinx±cosx 1±sinx 1±cosxtanx+cotx若A、B是锐角,A+B=π4,则(1+tanA)(1+tanB)=2 8.在三角形中的结论若:A+B+C=π,A+B+C2=π2则有tanA+tanB+tanC=tanAtanBtanCtan A2tanB2+tanB2tan C2+tanC2tanA2=1。
三角函数的诱导公式

三角函数的诱导公式练习题一、知识梳理,双基再现 1.公式一 ,, . 2.公式二 ,, . 3.公式三 ,, . 4.公式四 ,, . 5.公式五 ,, .我们可以用一段话来概括公式一~五:απαπα±-∈⋅+,),(2Z k k 的三角函数值,等于,前面加上一个. 6.公式六 ,, . 7.公式七 ,, .公式六~七可以概括如下:απ±2的正弦(余弦)函数值,分别等于,前面加上一个.利用公式五或公式六,可以实现与的相互转化.二、选择题1. 下列各式不正确的是 ( )A. ααsin )180sin(-=︒+ B .ααcos )180cos(-=︒+ C .ααcos )180cos(=︒+- D .ααsin )180(sin =︒+- 2. 600sin 的值为( ) A .21 B . 21-C .23 D . 23-3. )619sin(π-的值等于( ) A .21 B . 21-C .23 D . 23-4. 对于诱导公式中的角α,下列说法正确的是( ) A .α一定是锐角 B .πα20≤≤C .α一定是正角D .α是使公式有意义的任意角5. 若(),2,53cos παππα<≤=+则()πα2sin --的值是 ( )A . 53B . 53-C . 54D . 54-6. 45tan 625cos 34sinπππ⋅⋅的值是( )A .43-B .43C .43-D .437. )2cos()2sin(21++-ππ等于( )A .2cos 2sin -B .2sin 2cos -C .)2cos 2(sin -±D .2cos 2sin +8. 已知()21sin -=+πα,则()πα7cos 1+的值为 ( )A .332 B . 2- C . 332-D . 332± 9. )2sin(,223,21)cos(αππαπαπ-<<-=+的值为( ) A.23B. 21C. 23±D. 23- 10. 若m -=-++)sin()(sin ααπ, 则)2sin(2)3sin(απαπ-++等于 ( )A .m 32-B .m 23-C .m 32D .m 2311. 已知23)4(sin =+απ,则)43(sin απ-的值为( )A.21 B. 21- C. 23 D. 23- 12. 如果).cos(|cos |π+-=x x 则x 的取值范围是 ( )A .)](22,22[Z k k k ∈++-ππππB .))(223,22(Z k k k ∈++ππππC .)](223,22[Z k k k ∈++ππππ D .))(2,2(Z k k k ∈++-ππππ13. 已知,)1514tan(a =-π那么=︒1992sin ( )A .21||aa + B .21aa + C .21aa +- D .211a+-14. 设角,635πα-=则)(cos )sin(sin 1)cos()cos()sin(222απαπααπαπαπ+--+++--+的值等于 ( ) A .33 B .33-C .3D .3-15. 若,3cos )(cos x x f =那么)30(sin ︒f 的值为 ( )A .0B .1C .1-D .23 16. 在ABC ∆中,若)sin()sin(C B A C B A +-=-+,则ABC ∆必是( )A .等腰三角形B .直角三角形C .等腰或直角三角形D .等腰直角三角形17. 如果βα,满足πβα=+,那么下列式子中正确的是( )A. βαsin sin =B. βαcos cos =C. βαtan tan =D. βαsin sin -= 18. 若C B A ,,分别为ABC ∆的内角,则下列关系中正确的是( ) A.C B A sin )sin(=+ B.A C B cos )cos(=+ C.C B A tan )tan(=+ D.A C B sin )sin(-=+19.)60tan()60sin(240tan 225cos ︒-+︒-+︒+︒的值是( ) A. 2322--B.2322+-C.6322--D.6322+- 20.︒1030cos 等于( )A.︒50cosB.︒-50cosC.︒50sinD.︒-50sin 21.)1920sin(︒-等于( ) A.21 B. 21- C. 23 D.23- 22.32sin 334sin 2)3sin(πππ++-等于( )A .1B.21C. 0D. 1-23.已知41log )sin(8=-απ,且)0,2(πα-∈,则)2tan(απ-的值为( ) A .552-B.552C.552±D.2524.设m =+)5tan(απ,则)cos()sin()cos()3sin(απααππα+---+-的值为( )A.11-+m m B.11+-m m C.1- D.1 25.已知α是三角形的一个内角,下列各式中不一定正确的是( ) A.02tan>αB.ααπsin )sin(-=+C.0cos >αD.01sin >+α26.已知53)sin(=+απ,且α是第四象限角,则)2cos(πα-的值为( )A.54-B.54C.54± D.5327.化简:)2cos()2sin(])12(sin[])12(sin[παπαπαπαn n n n -++-+++得到的结果是( )A .0 B.αcos 2-C.αsin 2D.αcos 228.已知m =75sinπ,则72cos π的值等于( )A.mB.m -C.21m -D.21m -- 29.)22cos()2sin(---ππ化简的结果是( )A .0B.1- C.2sin 2 D. 2sin 2- 30.化简:︒-460sin 12的结果为( )A.︒-80cosB. ︒-80sinC. ︒80cosD. ︒80sin 31.已知53)2cos(-=+απ,且α是第二象限角,则)23sin(πα-的结果是( ) A.54 B. 54- C.54± D.5332.如果C B A ,,为ABC ∆的三个内角,则=+2sin CB ( ) A.2cosA - B. 2sin A C. 2sin A - D. 2cos A 33.设2cos)(xx f =,则下列各式中成立的是( ) A.)()2(x f x f =-π B. )()2(x f x f =+π C.)()(x f x f -=- D. )()(x f x f =-34.已知下列各式:① );tan()tan(πααπ-=+②);cos()cos(απαπ+=- ③);2sin()sin(απαπ-=+④)sin()sin(παα-=-,其中正确命题的个数是( ) A.1 B. 2 C.3 D.435.化简)139tan()63tan()49tan()27tan(βαβα-︒⋅+︒⋅-︒⋅-︒的结果为( ) A.1 B. 1- C.2 D. 2- 36.若),1|(|)6cos(≤=-m m απ则)32(sin απ-等于( ) A.m - B.2m- C . 2m D. m三、填空题1. ︒2010tan 的值为.2. 化简:=--+-+++)(cos )5sin()4sin()3(sin )(cos )4cos(222πθθππθπθπθπθ. 3. 已知()()()()29cos sin 4cos sin 3=+---++απαααπ,则=αtan . 4. 若a =αtan ,则()()=+--απαπ3cos 5sin.5. =+++++76cos 75cos 74cos 73cos 72cos7cosππππππ. 6. 若1312)125(sin =-︒α,则=︒+)55(sin α .7. 设,1234tan a =︒那么)206cos()206sin(︒-+︒-的值为. 8.已知3)tan(=+απ,则=-+)cos()sin(απαπ.9.=︒++︒+︒+︒180cos ......3cos 2cos 1cos . 10.若,2)tan(=-απ则)sin()23sin()25cos()3sin(2απαπαπαπ--+++的值为__________. 11.已知x x f tan )2(=+π,则=)3(πf ,=)65(πf . 四、解答题1. 求︒+︒-1665sin )2640(cos 的值.2. 化简:︒+︒︒︒+790cos 250sin 430cos 610sin 21.3. 已知 3)tan(=+απ,求)2sin()cos(4)sin(3)cos(2a a a a -+-+--πππ的值.4. 若αα,32cos =是第四象限角,求)4cos()cos()cos()3cos()3sin()2(sin πααπαππαπαπα--------+-的值. 5. 已知ααtan 1tan ,是关于x 的方程0322=-+-k kx x 的两实根,且,273παπ<<求)sin()3cos(απαπ+-+的值.6.已知21)tan(-=+απ,求)4sin()2cos(4)sin(3)cos(2αππααπαπ-+-+--的值7.已知α是第三象限角,且)sin()2cos()sin()(πααπαπα----=f(1)化简)(αf ;(2)若51)sin(=+απ,求)(αf ;(3)若︒-=1860α,求)(αf 8.求下列各三角函数值: (1))310sin(π-(2)629cos π(3))855tan(︒- 9.已知,)2cos()3sin(m =++-αππα求证:)(23)2sin(2)27cos(Z k m k ∈=-+-αππα.。
诱导公式练习题答案

诱导公式练习题答案诱导公式是三角函数中常用的公式,主要用于将正弦、余弦等三角函数的角转换为锐角,从而简化计算。
以下是一些诱导公式的练习题及其答案。
# 练习题1:求 \(\sin(90^\circ - x)\) 的值。
答案:根据诱导公式,我们知道 \(\sin(90^\circ - x) = \cos(x)\)。
# 练习题2:计算 \(\cos(180^\circ - x)\)。
答案:根据诱导公式,\(\cos(180^\circ - x) = -\cos(x)\)。
# 练习题3:给出 \(\tan(270^\circ - x)\) 的表达式。
答案:\(\tan(270^\circ - x) = -\cot(x)\)。
# 练习题4:求 \(\sin(360^\circ - x)\) 的值。
答案:\(\sin(360^\circ - x) = -\sin(x)\)。
# 练习题5:计算 \(\cos(90^\circ + x)\)。
答案:\(\cos(90^\circ + x) = -\sin(x)\)。
# 练习题6:给出 \(\tan(180^\circ + x)\) 的表达式。
答案:\(\tan(180^\circ + x) = \tan(x)\)。
# 练习题7:求 \(\sin(270^\circ + x)\) 的值。
答案:\(\sin(270^\circ + x) = -\cos(x)\)。
# 练习题8:计算 \(\cos(360^\circ + x)\)。
答案:\(\cos(360^\circ + x) = \cos(x)\)。
这些练习题涵盖了诱导公式的基本应用,通过这些练习,学生可以更好地理解和掌握诱导公式,提高解决三角函数问题的能力。
三角函数诱导公式经典例题

三角函数诱导公式练习题及答案1.2cos(−θ)+sin(π−θ)cos(π2−θ)+sin(3π2−θ)=4,求tanθ的值 2.已知f(α)=sin(α−3π)⋅cos(2π−α)⋅sin(−α+32π)cos(−π−α)⋅sin(−π−α)(1)化简f(α);(2)若α为第四象限角且sinα=−35,求f(α)的值;(3)若α=−313π,求f(α)。
3.已知sin(α+2022π)−6sin(α−3π2)2cos(α−π)−sinα=−tan 3π4. (1)求tanα的值;(2)求sinα−cosα的值。
4.已知sinα=−35,且α为第三象限角.(1)求cosα和tanα的值;(2)已知f(α)=2sin(π+α)+cos(2π+α)cos(α−π2)+sin(π2+α),求f(α)的值。
5.已知关于x 的方程25x 2−ax +12=0的两根为sinθ和cosθ,其中θ∈(π4,3π4),(1)求a 的值;(2)求2sin(θ+π2)−cos(θ−π2)+sin(θ−π)cos(π+θ)4cos(θ+π2)−1的值。
6.已知f(α)=cos(π−α)sin(−α−π)sin(α−π2)cos(3π2+α)tan(π−α). (1)化简f(α);(2)若角α为第二象限角,且sinα=13,求f(α)的值。
7.已知tanα=2,求cos(π2+α)sin(−α)+cos(2π−α)的值。
8.已知α∈(0,π2),cosα=35,求sin(π2−α)+cos(3π2−α)sin(3π+α)+cos(π−α)的值。
9.(1)化简sin(π−α)sin(π2−α)cos(π+α)cos(π2+α).(2)已知:tanα=2,求sinα+2cosα5cosα−sinα的值.10.化简f(α)=sin(π−α)cos(3π2−α)tan(−π−α)cos(−π2−α)tan(2π+α)11.已知cosα=−√55,α是第三象限角,求: (1)tanα的值;(2)sin(3π2−α)cos(π+α)tan(−α−π)cos(2π−α)sin(π−α)tan(−α)的值. 12.已知tanα=12,求13cos(−α)−2cos(π2−α)sin(π2+α)+3sin(π+α)的值. 13.已知cosα=−45,且tanα>0.(1)求tanα的值;(2)求2sin(π−α)+sin(π2+α)cos(2π−α)+cos(−α)的值. 14.已知3cosα−2sinαsinα+2cosα=−14,cos(π+α)cos(π2+α)sin(3π2−α)cos(3π2−α)sin(3π−α)sin(5π2+α)的值。
正余弦诱导公式练习题

一、选择题 1.下列各式的值等于-sinA 的是( ) . A.sin(π-A) B.sin(k·360°-A) ,k∈Z C.sin(k·360°+A) ,k∈Z D.-sin(-A) 2.如果α+β=180°,那么下列等式中成立的是( ) . A.sinα =-sinβ B.cosα=cosβ C.sinα =sinβ D.cos(α +β )=1 3、下列各式不正确的是 ( ) A. sin(α+180°)=-sinα B.cos(-α+β)=-cos(α-β) C. sin(-α-360°)=-sinα D.cos(-α-β)=cos(α+β) 4、 sin 600 的值为(
11、若 cos ( 2π − α ) =
(
)
A. -
2 3
B.
5 5
D. −
5 5
A.
1 2
B.
−
1 2
C.
3 2
D.
−
3 2
12.已知 sin(π + α ) = A −
5、 sin −
19 π 的值等于( 6
B.
)
4 5
3 , ,则 sin(α − 2π ) 的值为( ) 5 4 4 3 B C ± D 5 5 5
o
A.
2 3 3
B. -2
C. −
2 3 3
D. (
±
2 3 3
)
10、若 cos (α + π ) = A.
3 5
B.
3 , 则 cos ( −α − 2π ) 的值是 5 3 4 − C. 5 5 5 π , 则 sin + α 的值是 5 2 ± 2 3
三角函数 诱导公式专项练习(含答案)

三角函数诱导公式专项练习(含答案) 三角函数诱导公式专项练一、单选题1.sin(-600°)的值为()A。
-√3/2B。
-1C。
1D。
√3/22.cos(11π/3)的值为()A。
-√3/2B。
-13/2C。
√2D。
23.已知sin(30°+α)=√3/2,则cos(60°-α)的值为A。
1/2B。
-1/2C。
√3/2D。
-√3/24.已知cos(π/3+α)=-5/2,且α∈(2π/5,π),则XXX(α-π)=()A。
-34/4B。
-3C。
4D。
35.已知sin(π-α)=-2/√3,且α∈(-2,0),则tan(2π-α)的值为A。
2√5/5B。
-2√5/2√5C。
±5D。
√5/26.已知cos(π/4-α)=√2/2,则sin(α+π/4)=()A。
-3B。
1C。
√2D。
√14/47.已知sinα=3/5,2<α<π/2,则sin(2-α)=()A。
3/5B。
-3/5C。
4/5D。
-4/58.已知tanx=-12/5π,x∈(π/2,π),则cos(-x+3π/2)=()A。
5/13B。
-5/12C。
13D。
-12/139.如果cos(π+A)=-1,那么sin(π/2+A)=A。
-1/2B。
2C。
1D。
-110.已知cos(π/2-α)-3cosα/(sinα-cos(π+α))=2,则tanα=()A。
12/5B。
-3C。
1/2D。
-511.化简cos480°的值是()A。
1B。
-1C。
√3/2D。
-√3/212.cos(-585°)的值是()A。
√2/2B。
√3/2C。
-√3/2D。
-√2/213.已知角α的终边经过点P(-5,-12),则sin(3π/2+α)的值等于()A。
-5B。
-12/13C。
13D。
12/1314.已知cos(π+α)=2/3,则tanα=()A。
√55/2B。
2√5/52.已知cosα=2/5,-2/5<α<0,则tan(α+α)cos(-α)tanα的值为()答案:D解析:由cosα=2/5可得sinα=-√(21)/5,代入公式可得tan(α+α)cos(-α)tanα=-1/√3=-√3/3,故选D。
三角函数诱导公式练习题

三角函数诱导公式练习题三角函数诱导公式练习题三角函数是数学中的重要概念,它们在几何、物理和工程等领域都有广泛的应用。
其中,三角函数诱导公式是三角函数之间的一种重要关系,通过这些公式,我们可以将一个三角函数表示为其他三角函数的组合形式。
在本文中,我们将通过一些练习题来巩固对三角函数诱导公式的理解。
练习题一:已知 sin(x) = 3/5,求 cos(x) 和 tan(x) 的值。
解析:根据三角函数诱导公式sin²(x) + cos²(x) = 1,我们可以得到cos²(x) = 1 - sin²(x)= 1 - (3/5)² = 1 - 9/25 = 16/25。
因此,cos(x) = ±√(16/25) = ±4/5。
由于 sin(x) 和 cos(x) 同号,所以 cos(x) = 4/5。
另外,tan(x) = sin(x) / cos(x) = (3/5) / (4/5) = 3/4。
练习题二:已知 cos(x) = -12/13,求 sin(x) 和 tan(x) 的值。
解析:根据三角函数诱导公式sin²(x) + cos²(x) = 1,我们可以得到sin²(x) = 1 - cos²(x)= 1 - (-12/13)² = 1 - 144/169 = 25/169。
因此,sin(x) = ±√(25/169) = ±5/13。
由于 cos(x) 和 sin(x) 异号,所以 sin(x) = -5/13。
另外,tan(x) = sin(x) / cos(x) = (-5/13) / (-12/13) = 5/12。
练习题三:已知 tan(x) = 4/3,求 sin(x) 和 cos(x) 的值。
解析:根据三角函数诱导公式 tan(x) = sin(x) / cos(x),我们可以得到 sin(x) = tan(x) * cos(x) = (4/3) * cos(x)。
正弦、余弦的诱导公式典型例题

正弦、余弦的诱导公式典型例题正弦、余弦的诱导公式例题讲析例1.求下列三角函数的值(1)sin240º;(2);(3)cos(-252º);(4)sin(-)解:(1)sin240º=sin(180º+60º)=-sin60º=(2)=cos==;(3)cos(-252º)=cos252º=cos(180º+72º)=-cos72º=-0.3090;(4)sin(-)=-sin=-sin=sin=说明:本题是诱导公式二、三的直接应用.通过本题的求解,使学生在利用公式二、三求三角函数的值方面得到基本的、初步的训练.本例中的(3)可使用计算器或查三角函数表.例2.求下列三角函数的值(1)sin(-119º45′);(2)cos;(3)cos(-150º);(4)sin.解:(1)sin(-119º45′)=-sin119º45′=-sin(180º-60º15′)=-sin60º15′=-0.8682(2)cos=cos()=cos=(3)cos(-150º)=cos150º=cos(180º-30º)=-cos30º=;(4)sin=sin()=-sin=.说明:本题是公式四、五的直接应用,通过本题的求解,使学生在利用公式四、五求三角函数的值方面得到基本的、初步的训练.本题中的(1)可使用计算器或查三角函数表.例3.求值:sin-cos-sin略解:原式=-sin-cos-sin=-sin-cos+sin=sin+cos+sin=++0.3090=1.3090.说明:本题考查了诱导公式一、二、三的应用,弧度制与角度制的换算,是一道比例1略难的小综合题.利用公式求解时,应注意符号.例4.求值:sin(-1200º)•cos1290º+cos(-1020º)•sin(-1050º)+tan855º.解:原式=-sin(120º+3•360º)cos(210º+3•360º)+cos(300º+2•360º)-sin(330º+2•360º)]+tan(135º+2•360º)=-sin120º•cos210º-cos300º•sin330º+tan135º=-sin(180º-60º)•cos(180º+30º)-cos(360º-60º)•sin(360º-30º)+=sin60º•cos30º+cos60º•sin30º-tan45º=•+•-1=0说明:本题的求解涉及了诱导公式一、二、三、四、五以及同角三角函数的关系.与前面各例比较,更具有综合性.通过本题的求解训练,可使学生进一步熟练诱导公式在求值中的应用.值得指出的是教材中的诱导公式未介绍正切,因此,计算tan135º的值时应先用商数关系把tan135º改写成,再将分子分母分别用诱导公式进而求出tan135º的值.例5.化简:.略解:原式===1.说明:化简三角函数式是诱导公式的又一应用,应当熟悉这种题型.例6.化简:解:原式====.说明:本题可视为例5的姐妹题,相比之下,难度略大于例5.求解时应注意从所涉及的角中分离出2的整数倍才能利用诱导公式一.例7.求证:证明:左边=====,右边==,所以,原式成立.例8.求证证明:左边===tan3α=右边,所以,原式成立.说明:例7和例8是诱导公式及同角三角函数的基本关系式在证明三角恒等式中的又一应用,具有一定的综合性.尽管问题是以证明的形式出现的,但其本质是等号左、右两边三角式的化简.例9.已知.求:的值.解:已知条件即,又,所以:=说明:本题是在约束条件下三角函数式的求值问题.由于给出了角的范围,因此,的三角函数的符号是一定的,求解时既要注意诱导公式本身所涉及的符号,又要注意根据的范围确定三角函数的符号.例10.已知,求:的值.解:由,得,所以故==1+tan+2tan2=1+.说明:本题也是有约束条件的三角函数式的求值问题,但比例9要复杂一些.它对于学生熟练诱导公式及同角三角函数关系式的应用.提高运算能力等都能起到较好的作用.例11.已知的值.解:因为,所以:==-m由于所以于是:=,所以:tan(=.说明:通过观察,获得角与角之间的关系式=-(),为顺利利用诱导公式求cos()的值奠定了基础,这是求解本题的关键,我们应当善于引导学生观察,充分挖掘的隐含条件,努力为解决问题寻找突破口,本题求解中一个鲜明的特点是诱导公式中角的结构要由我们通过对已知式和欲求之式中角的观察分析后自己构造出来,在思维和技能上显然都有较高的要求,给我们全新的感觉,它对于培养学生思维能力、创新意识,训练学生素质有着很好的作用.例12.已知cos,角的终边在y轴的非负半轴上,求cos的值.解:因为角的终边在y轴的非负半轴上,所以:=,于是2()=从而所以===说明:本题求解中,通过对角的终边在y轴的非负半轴上的分析而得的=,还不能马上将未知与已知沟通起来.然而,当我们通过观察,分析角的结构特征,并将它表示为2()后,再将=代入,那么未知和已知之间随即架起了一座桥梁,它为利用诱导公式迅速求值扫清了障碍.通过本题的求解训练,对于培养学生的观察分析能力以及思维的灵活性和创造性必将大有裨益.。
(完整版)三角函数诱导公式专项练习(含答案)

三角函数 诱导公式专项练习学校:___________姓名:___________班级:___________考号:___________一、单选题1.()sin (‒600∘)=A . B . C .D .‒32‒1212322.的值为( )cos 11π3A . B .C .D .‒32‒1232123.已知,则cos (60°–α)的值为sin(30°+α)=3A . B .12‒12C .D . –32324.已知,且 ,则()cos(π2+α)=‒35α∈(π2,π)tan (α‒π)=A .B .C .D .‒34‒4334435.已知sin(π-α)=-,且α∈(-,0),则tan(2π-α)的值为( )23π2A .B . -C . ±D .255255255526.已知,则=( )cos (π4‒α)=24sin(α+π4)A .B .C .D .‒3414241447.已知,,则()sinα=35π2<α<3π2sin (7π2‒α)=A .B .C .D .35‒3545‒458.已知 ,则( )tanx =‒125,x ∈(π2,π)cos(‒x +3π2)=A .B .-C .D .-513513121312139.如果,那么cos(π+A)=‒12sin (π2+A)=A .-B .C . 1D . -1121210.已知,则( )cos(π2‒α)‒3cosαsinα‒cos (π+α)=2tanα=A .B .C .D . 15‒2312‒5∘A .B .C .D .12‒1232‒3212.的值是( )cos (‒585°)A .B .C .D .2232‒32‒2213.已知角的终边经过点,则的值等于 αP(‒5,‒12)sin (3π2+α)()A .B .C .D .‒513‒1213513121314.已知,则( )cos (π+α)=23tanα=A .B .C .D .52255±52±25515.已知的值为( )cosα=15,‒π2<α<0,则cos (π2+α)tan(α+π)cos (‒α)tanαA .B .C .D . 26‒26‒61261216.已知则 ()sinα=13,α∈(π2,π)cos (‒α)=A .B .C .D .13‒13223‒22317.已知,且是第四象限角,则的值是( )sin(π+α)=45αcos(α‒2π)A .B .C .D .‒3535±354518.已知sin =,则cos =( )A .B .C . -D . -19.已知cos α=k ,k∈R,α∈,则sin(π+α)=( )A . -B .C . ±D . -k20.=( )A . sin 2-cos 2B . sin 2+cos 2C . ±(sin 2-cos 2)D . cos 2-sin 221.的值为sin 585∘A .B .C .D .22‒2232‒3222.( )sin (‒1020°)=1‒13‒323.若,,则的值为( )α∈(0,π)sin(π‒α)+cosα=23sinα‒cosαA .B .C .D .23‒2343‒4324.已知且,则( )α∈(π2,π)sin (π+α)=‒35tan α=A .B .C .D .‒344334‒4325.已知,则()sin(π2+θ)+3cos (π‒θ)=sin (‒θ)sinθcosθ+cos 2θ=A . B . C . D .1525355526.若,且,则( )sinθ‒cosθ=43θ∈(34π,π)sin(π‒θ)‒cos(π‒θ)=A .B .C .D .‒2323‒434327.已知,则( )sin(π2+θ)+3cos (π‒θ)=sin (‒θ)sinθcosθ+cos 2θ=A . B . C . D .1525355528.已知,则的值为( )sin (2015π2+α)=13cos (π‒2α)A .B .C .D .13-1379‒7929.若,,则的值为( )α∈(0,π)sin(π‒α)+cosα=23sinα‒cosαA .B .C .D .23‒2343‒4330.已知,则的大小关系是( )a =tan (‒π6),b =cos (‒23π4),c =sin25π3a,b,c A .B .C .D . b >a >c a >b >c c >b >a a >c >b31.cos 7500=A .B .C .D .3212‒32‒1232.的值等于( )sin (‒236π)A .B .C .D .32‒1212‒3233.的值的( )sin 300°+tan 600°+cos (‒210°)A . B .C .D .‒30‒12+3212+3234.已知,,则等于().α∈(π2,3π2)tan(α‒π)=‒34sinα+cosαA .B .C .D .±15‒1515‒75A .B .C .D . a ‒a 1‒a 2‒1‒a236.点在直角坐标平面上位于( )A (cos 2018∘,tan 2018∘)A . 第一象限 B . 第二象限C . 第三象限D . 第四象限37.如果,那么等于( )sin (π‒α)=13sin (π+α)‒cos (π2‒α)A .B .C .D .‒2323223‒22338.已知角的终边过点,若,则实数α(a,‒2)tan (π+α)=3a =A . B .C .D .6‒23‒62339.cos (2π+α)tan (π+α)sin (π‒α)cos (π2‒α)cos (‒α)=A .B .C .D . 1‒1tan α‒tan α40.已知,则的值为( )sin (‒α)=-53cos (π2+α)A .B .C .D .53‒5323‒23参考答案1.D 【解析】【分析】直接运用诱导公式,转化为特殊角的三角函数值求解。
正,余弦的诱导公式(二)

解:分别求 cos(105° -α),sin(α-105° )的值. cos(105° -α)=cos[180° -(75° +α)] 1 =-cos(75° +α)=- , 3 sin(α-105° )=-sin(105° -α) =-sin[180° -(75° +α)] =-sin(75° +α). 1 ∵cos(75° +α)= >0,又 α 为第三象限角, 3 可知 75° 为第四象限角, +α ∴sin(75° +α)=- 1-cos275° +α 1 2 2 =- 1- 2=- . 3 3 2 2 ∴sin(α-105° )= . 3 则 cos(105° -α)+sin(α-105° ) 1 2 2 2 2-1 =- + = . 3 3 3
9 cos sin 3 sin sin 2
2.导与练P24,7
P y, x
-1
P′(y,x) 2 2 P(x,y) 1 x 0
-1
y 1
yx
公式六 : π sin( α ) cosα , 2 π cos( α ) sinα . 2
公式七 : π sin( α ) cosα , 2 π cos( α ) sinα . 2
公式九: 3π sin( α ) cosα , 2 3π cos( α ) sinα . 2
总结:
公式六,七,八,九口诀:
函数名改变,符号看象限;
正弦、余弦的诱导公式知识精讲试题

正弦、余弦的诱导公式知识精讲一. 本周教学内容:正弦、余弦的诱导公式 二. 重点、难点:掌握诱导公式内容并能纯熟掌握利用诱导公式把任意角的三角函数转化为锐角三角函数。
公式〔一〕:ααπsin )2sin(=+k ααπcos )2cos(=+k 公式〔二〕:ααπsin )sin(-=+ ααπcos )cos(-=+ 公式〔三〕:ααsin )sin(-=- ααcos )cos(=- 公式〔四〕:ααπsin )sin(=- ααπcos )cos(-=- 公式〔五〕:ααπsin )2sin(-=- ααπcos )2cos(=- 以下补充公式六——公式九 公式〔六〕:ααπcos )2sin(=- ααπsin )2cos(=-公式〔七〕:ααπcos )2sin(=+ ααπsin )2cos(-=+ 公式〔八〕:ααπcos )23sin(-=- ααπsin )23cos(-=-公式〔九〕:ααπcos )23sin(-=+ ααπsin )23cos(=+利用诱导公式把任意角的三角函数化为锐角三角函数的步骤。
任意角−−−−−−−→−)()(一或三诱导公式任意正角−−−−−→−)(一诱导公式0到π2的角 −−−−−→−-)()(九二公式锐角三角函数【典型例题】[例1] 化简︒⋅︒+︒-⋅︒+︒⋅︒1110tan 600tan )870cos(930cos 150sin 750sin解:原式)1503602cos()2103602cos(150sin )303602sin(︒+︒⨯⋅︒+︒⨯+︒⋅︒+︒⨯=)303603tan()240360tan(︒+︒⨯︒+︒+︒︒+︒︒+︒⋅︒=30tan 240tan 150cos 210cos 150sin 30sin )30180cos()30180cos()30180sin(30sin ︒-︒⋅︒+︒+︒-︒⋅︒= ︒⋅︒+︒+30tan )60180tan(︒⋅︒+︒-︒-+︒⋅︒=30tan 60tan )30cos )(30cos (30sin 30sin )3090cot(60tan 30cos 30sin 22︒-︒⋅︒+︒+︒= 21160cot 60tan 1=+=︒⋅︒+= [例2] 化简)313cos()313cos(απαπ--+++k k ,Z ∈k 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正余弦的诱导公式
复习要求1:熟练掌握正弦,余弦诱导公式并运用它求任意角的三角函数值,化简,简单三角恒等式的证明。
2:了解把未知问题化归为已知问题的数学思想,提高解题能力。
复习重点:诱导公式及其综合运用。
复习过程: 一:基本公式
1:sin(360k+a)=________________ cos(360k+a)=_______________________
2:sin(180+a)=________________ cos(180+a)=________________________
3:sin(90+a)=__________________ sin(270+a)=_________________________
4:cos(90+a)=__________________ cos(270+a)=________________________
以上四组公式可概括为360k+a,180+a (或90+a, 270+a) 的三角函数值,等于a 的同名(或余名)函数值,前面加上把a 看成锐角时原函数值的符号:简记为:“奇变偶不变,符号看象限。
” 二:公式的主要运用1:任意角的三角函数转化为锐角三角函数。
2:三角函数式的化简。
3:三角恒等式的证明。
三:基础练习〈1〉: tan 0
300+cot(-0405-)的值是
〈2〉: 已知sin(4
π-a)=53 ,则 sin(a-413π)的值等于 〈3〉:设 a 是第三象限角,则)2sin()cos(21a a --+ππ=
〈4〉:已知A=a a k sin )sin(+π+a a k cos )cos(+π (k ∈Z), 则 A 值构成集合 四:例题分析
例1 求 sin315sin(-1260 )+cos570 sin(-840 ) 的值。
例2 已知 tan(π+a)=3 ,求
)
2sin()cos(4)sin(3)cos(2a a a a -+-+--πππ 的值。
例3 已知A,B,C 为三角形的三个内角,求证〈1〉cos(2A+B+C)= --cosA
<2>tan
4B A +=--tan 43C +π
跟踪练习
1:计算 sin
34π cos 625πtan( 43π-)
2:已知 cos(a+75 )=
426- ,a 为第三象限角,求cos(15 –a)+sin(a-15 ) 的值。
3:证明
)5sin()cos()6cos()2sin()2tan(a a a a a ------πππππ=-tana 五:作业
1:设f(n)=cos
2πn ,求f(25)+f(26)+f(27)+…..+f(42)的值
2:化简 sin(
π414-n -a)+cos(a n -+π414),其中n ∈+Z ,a ∈(0,4π)
3:已知sina 是方程52x -7x-6=0的根,求)cot()2
cos()2cos()
2(tan )23sin()23sin(2a a a a a a -+-----ππππππ的
值。
4:在三角形ABC 中,若sin(A+B-C)=sin(A-B+C),试判断三角形ABC 的形状。
