同济高数第七版上册考研数学考纲
《高等数学》(同济第七版)上册知识点归纳总结

《⾼等数学》(同济第七版)上册知识点归纳总结⾼等数学(同济第七版)上册-知识点总结第⼀章函数与极限⼀. 函数的概念1.两个⽆穷⼩的⽐较设0)(lim ,0)(lim ==x g x f 且l x g x f =)()(lim(1)l = 0,称f (x)是⽐g(x)⾼阶的⽆穷⼩,记以f (x) = 0[)(x g ],称g(x)是⽐f(x)低阶的⽆穷⼩。
(2)l ≠ 0,称f (x)与g(x)是同阶⽆穷⼩。
(3)l = 1,称f (x)与g(x)是等价⽆穷⼩,记以f (x) ~ g(x)2.常见的等价⽆穷⼩当x →0时sin x ~ x ,tan x ~ x ,x arcsin ~ x ,x arccos ~ x ,1? cos x ~ 2/2^x , x e ?1 ~ x ,)1ln(x + ~ x ,1)1(-+αx ~ x α⼆.求极限的⽅法1.两个准则准则 1. 单调有界数列极限⼀定存在准则 2.(夹逼定理)设g (x ) ≤ f (x ) ≤ h (x )若A x h A x g ==)(lim ,)(lim ,则A x f =)(lim2.两个重要公式公式11sin lim 0=→x xx公式2e x x x =+→/10)1(lim3.⽤⽆穷⼩重要性质和等价⽆穷⼩代换 4.⽤泰勒公式当x 0→时,有以下公式,可当做等价⽆穷⼩更深层次)()!12()1(...!5!3sin )(!...!3!2112125332++++-+++-=++++++=n n n n nxx o n x x x x x x o n x x x x e )(!2)1(...!4!21cos 2242n n n x o n x x x x +-+++-= )()1(...32)1ln(132n nn x o nx x x x x +-++-=++ )(!))1()...(1(...!1(1)1(2n n x o x n n x x x +---++-++=+ααααααα)(12)1(...53arctan 1212153+++++-+-+-=n n n x o n x x x x x 5.洛必达法则定理1 设函数)(x f 、)(x F 满⾜下列条件:(1)0)(lim 0=→x f x x ,0)(lim 0=→x F x x ;(2))(x f 与)(x F 在0x 的某⼀去⼼邻域内可导,且0)(≠'x F ;(3))()(lim 0x F x f x x ''→存在(或为⽆穷⼤),则这个定理说明:当)()(lim 0x F x f x x ''→存在时,)()(lim 0x F x f x x →也存在且等于)()(lim 0x F x f x x ''→;当)()(lim0x F x f x x ''→为⽆穷⼤时,)()(lim 0x F x f x x →也是⽆穷⼤.这种在⼀定条件下通过分⼦分母分别求导再求极限来确定未定式的极限值的⽅法称为洛必达(H L 'ospital )法则.∞∞型未定式定理2 设函数)(x f 、)(x F 满⾜下列条件:(1)∞=→)(lim 0x f x x ,∞=→)(lim 0x F x x ;(2))(x f 与)(x F 在0x 的某⼀去⼼邻域内可导,且0)(≠'x F ;(3))()(lim 0x F x f x x ''→存在(或为⽆穷⼤),则注:上述关于0x x →时未定式∞∞型的洛必达法则,对于∞→x 时未定式∞∞型同样适⽤.使⽤洛必达法则时必须注意以下⼏点:(1)洛必达法则只能适⽤于“00”和“∞∞”型的未定式,其它的未定式须先化简变形成“00”或“∞∞”型才能运⽤该法则; )(lim)()(lim 00x F x f x F x f x x x x ''=→→)()(lim )()(lim 00x F x f x F x f x x x x ''=→→(2)只要条件具备,可以连续应⽤洛必达法则;(3)洛必达法则的条件是充分的,但不必要.因此,在该法则失效时并不能断定原极限不存在. 6.利⽤导数定义求极限基本公式)()()(lim 0'000x f xx f x x f x =?-?+→?(如果存在)7.利⽤定积分定义求极限基本格式?∑==∞→11)()(1lim dx x f n kf n n k n (如果存在)三.函数的间断点的分类函数的间断点分为两类:(1)第⼀类间断点设0x 是函数y = f (x )的间断点。
高等数学同济第七版上

高等数学同济第七版上一、引言高等数学是理工科学生必修的一门基础课程,对于培养学生的分析和抽象思维能力具有重要的作用。
而《高等数学同济第七版上》是一本经典的教材,为广大学生提供了系统全面的高等数学知识讲解和理解。
本文档将重点介绍《高等数学同济第七版上》这本教材的内容,总计超过1200字。
二、教材概述《高等数学同济第七版上》是由华东师范大学数学科学学院编写的教材,是数学系本科生高等数学课程的教材之一。
该教材详细而全面地介绍了高等数学的各个分支,包括数列、函数、极限、导数、微分、积分和级数等。
三、教材结构《高等数学同济第七版上》共分为十章,涵盖了高等数学的核心内容。
以下是各章节的简要概述:1.微分学基础:介绍微积分的基本概念和原理,包括数列极限、函数极限、连续和导数等内容。
2.微分学进阶:进一步深入讲解导数的应用,包括凹凸性、最值、微分方程和曲线的几何性质等。
3.积分学基础:介绍积分的基本概念和性质,包括定积分、变限积分、不定积分和定积分的几何应用等。
4.积分学进阶:进一步讲解不定积分和定积分的应用,包括换元积分法、分部积分法、定积分的几何应用和空间曲面的面积等。
5.微分方程:介绍微分方程的基本概念和解法,包括一阶微分方程、高阶微分方程、常系数线性微分方程和二阶齐次线性微分方程等。
6.空间解析几何:讲解空间解析几何的基本知识和应用,包括向量、点线面的位置关系、平面和直线的方程等内容。
7.多元函数微分学:介绍多元函数的极限、连续和偏导数等内容,并涉及多元函数的极值和最小二乘法等。
8.重积分学:介绍重积分的基本概念和性质,包括二重积分和三重积分,以及坐标系的选择和变换等。
9.曲线积分学:讲解曲线积分的基本概念和计算方法,包括第一类曲线积分和第二类曲线积分等。
10.曲面积分学:介绍曲面积分的基本概念和计算方法,包括对于向量场的曲面积分和对于标量场的曲面积分等。
四、教学特点《高等数学同济第七版上》具有以下几个教学特点:1.系统性:全面讲解了高等数学的各个分支,内容丰富且涵盖广泛,为学生提供了全方位的学习资源。
数学笔记-同济第七版高数(上)-第二章-导数与微分-函数的微分

数学笔记-同济第七版高数(上)-第二章-导数与微分-函数的微分一、定义y=f(x),(x∈D), x0∈D, x0+Δx∈DΔy=f(x0+Δx)-f(x0)若Δy=AΔx+o(Δx),称y=f(x)在x=x0可微意思是Δy若能表示为一个常数乘以Δx和一个Δx的高阶无穷小的和,就称y=f(x)在x=x0可微称AΔx为y=f(x)在x=x0这点的微分dy|x=x0=AΔx=Adx, dx也是微分二、Notes1、可导 <=> 可微证明:“=>”:设lim(Δx->0)f(x)=A则Δy/Δx=A+α, α->0(Δx->0)Δy=AΔx+Δxα,lim(Δx->0)[Δxα/Δx]=0,即Δxα=o(Δx)所以Δy=AΔx+o(Δx)所以y=f(x)在x=x0点可微“<=”:设Δy=AΔx+o(Δx)Δy/Δx=A+o(Δx)/Δx因为lim(Δx->0)[o(Δx)/Δx]=0所以Δy/Δx=A+α, α->0, (Δx->0)所以y=f(x)在x=x0点可导2、y=f(x),x=x0,Δy=AΔx+o(Δx),则A为f'(x0),A为该点导数3、y=f(x),x=x0,Δy=AΔx+o(Δx),则(dy|x=x0)=AΔx=f'(x0)Δx=f'(x0)dx若y=f(x)可导,dy=df(x)=f'(x)dx如:d(x^3)=(x^3)'dx=3x^2dxd(e^3x)=3e^3xdxx^2dx=d(1/3*x^3+C)1/(1+x^2)*dx=d(arctanx+C)4、若y=f(x)在x=x0可微,则:Δy=f'(x0)Δx+o(Δx), dy|x=x0 = f'(x0)dx=> Δy-dy=o(Δx)5、设y=f(x)在x=x0可微,则dy=f'(x)Δxf'(x)为y=f(x)在x=x0对应点的斜率三、微分的几大工具1、公式d(c)=0d(x^n)=nx^(n-1)dxd(a^x)=a^x*lna*dxd(sinx)=cosxdx, d(cosx)=-sinxdxd(loga(x))=1/(xlna)*dx......2、四则d(u±v)=du±dvd(uv)=dudvd(u/v)=(vdu-udv)/v^23、复合y=f(u)(1)dy=f'(u)du(2)若u=g(x), dy=f'(u)du=f'(u)g'(x)dx四、近似计算设y=f(x)在x=x0可微Δy=f(x0+Δx)-f(x0)=f'(x0)Δx+o(Δx)=>Δy≈f'(x0)Δx=>f(x0+Δx)≈f(x0)+f'(x0)Δx。
新版高等数学(同济第七版)上册-知识点总结-新版-精选.pdf

高等数学(同济第七版)上册-知识点总结第一章函数与极限一. 函数的概念1.两个无穷小的比较设0)(lim ,0)(lim x g x f 且lx g x f )()(lim (1)l = 0,称f (x)是比g(x)高阶的无穷小,记以 f (x) = 0[)(x g ],称g(x)是比f(x)低阶的无穷小。
(2)l ≠ 0,称f (x)与g(x)是同阶无穷小。
(3)l = 1,称f (x)与g(x)是等价无穷小,记以 f (x) ~ g(x) 2.常见的等价无穷小当x →0时sin x ~ x ,tan x ~ x ,x arcsin ~ x ,x arccos ~ x ,1-cos x ~ 2/2^x ,xe -1 ~ x ,)1ln(x ~ x ,1)1(x ~ x二.求极限的方法1.两个准则准则 1.单调有界数列极限一定存在准则 2.(夹逼定理)设g (x ) ≤ f (x ) ≤h (x )若A x h A x g )(lim ,)(lim ,则Ax f )(lim 2.两个重要公式公式11sin limx x x公式2ex xx /10)1(lim 3.用无穷小重要性质和等价无穷小代换4.用泰勒公式当x0时,有以下公式,可当做等价无穷小更深层次)()!12()1(...!5!3sin )(!...!3!2112125332n n nnnxxo n xx x xxx o n x x x x e)(!2)1(...!4!21cos 2242nnnx o n xxxx )()1(...32)1ln(132nnn x o n xxxxx )(!))1()...(1(...!2)1(1)1(2nnx o xn n xx x )(12)1( (5)3arctan 1212153n n n xo n xxxxx 5.洛必达法则定理1 设函数)(x f 、)(x F 满足下列条件:(1)0)(lim 0x f x x,0)(lim 0x F x x;(2))(x f 与)(x F 在0x 的某一去心邻域内可导,且0)(x F ;(3))()(limx F x f xx 存在(或为无穷大),则这个定理说明:当)()(limx F x f xx 存在时,)()(limx F x f xx 也存在且等于)()(limx F x f xx ;当)()(limx F x f x x为无穷大时,)()(limx F x f xx 也是无穷大.这种在一定条件下通过分子分母分别求导再求极限来确定未定式的极限值的方法称为洛必达(H L ospital )法则.型未定式定理2 设函数)(x f 、)(x F 满足下列条件:(1))(lim 0x f xx ,)(lim 0x F xx ;(2))(x f 与)(x F 在0x 的某一去心邻域内可导,且0)(x F ;(3))()(limx F x f xx 存在(或为无穷大),则注:上述关于0x x时未定式型的洛必达法则,对于x 时未定式型同样适用.使用洛必达法则时必须注意以下几点:(1)洛必达法则只能适用于“00”和“”型的未定式,其它的未定式须先化简变形成“00”或“”型才能运用该法则;)()(lim)()(limx F x f x F x f x xx x)()(lim)()(lim 0x F x f x F x f x xxx(2)只要条件具备,可以连续应用洛必达法则;(3)洛必达法则的条件是充分的,但不必要.因此,在该法则失效时并不能断定原极限不存在.6.利用导数定义求极限基本公式)()()(lim0'00x f xx f x x f x (如果存在)7.利用定积分定义求极限基本格式11)()(1limdx x f n kf nnk n(如果存在)三.函数的间断点的分类函数的间断点分为两类:(1)第一类间断点设0x 是函数y = f (x)的间断点。
高等数学(同济第七版)(上册)-知识点

WORD 格式可编辑版
...
第二章 导数与微分 一.基本概念
1.可微和可导等价,都可以推出连续,但是连续不能推出可微和可导。
∈[ a,b] ,有公式
,
, 称为拉格朗日余项 上面展开式称为以0(x) 为中心的n 阶泰勒公式。当 x0 =0 时,也称为n阶麦克劳林
WORD 格式可编辑版
...
公式。 常用公式( 前8个)
WORD 格式可编辑版
...
五.导数的应用
一.基本知识 设函数f ( x) 在 x0 处可导,且 x0 为f ( x) 的一个极值点,则 f '(x0) 0 。 我们称x 满足 f '(x0) 0 的 x0 称为 f (x) 的驻点,可导函数的极值点一定是驻点, 反之不然。极值点只能是驻点或不可导点,所以只要从这两种点中进一步去判断。
二.求导公式
三.常见求导
WORD 格式可编辑版
...
1. 复合函数运算法则 2. 由参数方程确定函数的运算法则
设x =( t) ,y =(t) 确定函数y = y( x) ,其中'(t),'(t) 存在,且'(t) ≠ 0,则 dy '(t)
dx '(t) 3. 反函数求导法则 设y = f ( x) 的反函数x = g( y) ,两者皆可导,且f ′( x) ≠ 0 则 g'( y) 1 1 ( f '(x) 0)
2. 第二充分条件
f (x) 在 x0 处二阶可导,且 f (x0) 0 ,f (x0 ) 0 ,则①若 f (x0 ) 0 , 则 x0 为极大值点;②若 f (x0 ) 0 ,则 x0 为极小值点.
同济高数第七版上册考研数学考纲
做例1~9
数三做
例1~5
P108习题2-4:
1(3),2,3(4)
4(1)(3),5(2),
8(3)数三不用做5,8
由参数方程所确定的
函数的导数
会【重点】(仅数一数二要求)
相关变换率
不作要求
章节
教材内容
考纲要求
必做例题
必做习题
2.5函数的
微分
微分的定义、几何意义
掌握(数一数二)
了解(数三)
例1~6
2(2)(4), 3(2), 4(3),5(1), 7
7.2可分离变量的微分方程
可分离变量的微分方程的
概念及其解法
掌握
例1~4
习题7-2:1(3)(4)(5)(7)
(9), 2(3)(4)
7.3齐次方程
一阶齐次微分方程的形式及其解法
掌握【重点】
例1,2
习题7-3:
1(1)(5), 2(2)
可化为一阶齐次微分方程的
函数极限的性质
掌握(数一数二)
了解(数三)
1.4无穷小与无穷大
无穷小的概念
理解
P37习题1-4:
4,6
无穷大的概念
理解(数一数二)
了解(数三)
1.5极限的预算法则
无穷小的基本性质
理解
例1-8
P45习题1-5:
1(3)(5)(11)(13),
2(1),3,4,5
极限的性质
掌握(数一数二)
了解(数三)
极限的四则运算法则
有理函数的积分
会(仅数一数二要求)
例1~5,
5~8
习题4-4:
4,6,8,12,20,23
可化为有理函数的积分
同济第七版高等数学总复习ppt课件

定理 2
设 y * 是( 2 ) 的一个特解, Y 是与(2)对应
*
的齐次方程(1)的通解, 那么 y Y y 是二阶非
齐次线性微分方程(2)的通解.
7
定理 3
设非齐次方程(2)的右端 f ( x ) 是几个函
i
y C1 e r x C 2 e r x y (C1 C 2 x )e r x y ex (C1 cos x C2 sin x )
1 2
2
9
推广:n 阶常系数齐次线性方程解法
( n ) ( n 1 ) y P y P y P y 0 1 n 1 n
2 2 2 x y z 2 2 1 2 a b c
x2 y2 z 2p 2q
( p与 q 同号 )
x y z
2 2
2
29
4.空间曲线
[1] 空间曲线的一般方程
F(x, y,z) 0 G (x, y,z) 0
[2] 空间曲线的参数方程
x x(t) y y(t) z z(t)
z
旋 转 椭 球 面
o
x
y
22
(1)球面
(2)圆锥面
(3)旋转双曲面
x y z 1
2 2 2
x y z
2 2
2
x y z 2 2 1 2 a a c
2
2
2
2 2 2 2 ( x x ) ( y y ) ( z z ) R 0 0 0
23
2. 柱面
定义:平行于定直线并沿定曲线C移动的直线 L所形成的曲面称之.
高等数学(同济第七版)上册-知识点总结

高等数学(同济第七版)上册-知识点总结第一章 函数与极限一. 函数的概念1.两个无穷小的比较设0)(lim ,0)(lim ==x g x f 且l x g x f =)()(lim(1)l = 0,称f (x)是比g(x)高阶的无穷小,记以f (x) = 0[)(x g ],称g(x)是比f(x)低阶的无穷小。
(2)l ≠ 0,称f (x)与g(x)是同阶无穷小。
(3)l = 1,称f (x)与g(x)是等价无穷小,记以f (x) ~ g(x)2.常见的等价无穷小 当x →0时sin x ~ x ,tan x ~ x ,x arcsin ~ x ,x arccos ~ x ,1− cos x ~ 2/2^x , x e −1 ~ x ,)1ln(x + ~ x ,1)1(-+αx ~ x α二.求极限的方法1.两个准则准则 1. 单调有界数列极限一定存在准则 2.(夹逼定理)设g (x ) ≤ f (x ) ≤ h (x )若A x h A x g ==)(lim ,)(lim ,则A x f =)(lim2.两个重要公式公式11sin lim 0=→x xx公式2e x x x =+→/10)1(lim3.用无穷小重要性质和等价无穷小代换 4.用泰勒公式当x 0→时,有以下公式,可当做等价无穷小更深层次)()!12()1(...!5!3sin )(!...!3!2112125332++++-+++-=++++++=n n n n nxx o n x x x x x x o n x x x x e )(!2)1(...!4!21cos 2242n n n x o n x x x x +-+++-= )()1(...32)1ln(132n nn x o nx x x x x +-++-=++ )(!))1()...(1(...!2)1(1)1(2n n x o x n n x x x +---++-++=+ααααααα)(12)1(...53arctan 1212153+++++-+-+-=n n n x o n x x x x x 5.洛必达法则定理1 设函数)(x f 、)(x F 满足下列条件:(1)0)(lim 0=→x f x x ,0)(lim 0=→x F x x ;(2))(x f 与)(x F 在0x 的某一去心邻域内可导,且0)(≠'x F ;(3))()(lim 0x F x f x x ''→存在(或为无穷大),则 这个定理说明:当)()(lim 0x F x f x x ''→存在时,)()(lim 0x F x f x x →也存在且等于)()(lim 0x F x f x x ''→;当)()(lim 0x F x f x x ''→为无穷大时,)()(lim 0x F x f x x →也是无穷大. 这种在一定条件下通过分子分母分别求导再求极限来确定未定式的极限值的方法称为洛必达(H L 'ospital )法则.∞∞型未定式 定理2 设函数)(x f 、)(x F 满足下列条件:(1)∞=→)(lim 0x f x x ,∞=→)(lim 0x F x x ;(2))(x f 与)(x F 在0x 的某一去心邻域内可导,且0)(≠'x F ;(3))()(lim 0x F x f x x ''→存在(或为无穷大),则 注:上述关于0x x →时未定式∞∞型的洛必达法则,对于∞→x 时未定式∞∞型同样适用.使用洛必达法则时必须注意以下几点:(1)洛必达法则只能适用于“00”和“∞∞”型的未定式,其它的未定式须)()(lim)()(lim 00x F x f x F x f x x x x ''=→→)()(lim )()(lim 00x F x f x F x f x x x x ''=→→先化简变形成“00”或“∞∞”型才能运用该法则; (2)只要条件具备,可以连续应用洛必达法则;(3)洛必达法则的条件是充分的,但不必要.因此,在该法则失效时并不能断定原极限不存在. 6.利用导数定义求极限基本公式)()()(lim 0'000x f xx f x x f x =∆-∆+→∆(如果存在)7.利用定积分定义求极限基本格式⎰∑==∞→101)()(1lim dx x f n kf n n k n (如果存在)三.函数的间断点的分类函数的间断点分为两类:(1)第一类间断点设0x 是函数y = f (x )的间断点。
高等数学(同济第七版)(上册)_知识点总结

...高等数学(同济第七版)上册-知识点总结第一章函数与极限一.函数的概念1.两个无穷小的比较f(x)设l imf(x)0,limg(x)0且llimg(x)(1)l=0,称f(x)是比g(x)高阶的无穷小,记以f(x)=0[g(x)],称g(x) 是比f(x)低阶的无穷小。
(2)l≠0,称f(x)与g(x)是同阶无穷小。
(3)l=1,称f(x)与g(x)是等价无穷小,记以f(x)~g(x)2.常见的等价无穷小当x→0时sinx~x,tanx~x,arcsinx~x,arccosx~x,1-cosx~x^2/2,xe-1~x,ln(1x)~x,(1x)1~x二.求极限的方法1.两个准则准则1.单调有界数列极限一定存在准则2.(夹逼定理)设g(x)≤f(x)≤h(x)若limg(x)A,limh(x)A,则l imf(x)A2.两个重要公式sinx公式11limx0x1/x公式2xelim(1)x03.用无穷小重要性质和等价无穷小代换4.用泰勒公式当x0时,有以下公式,可当做等价无穷小更深层次xe 1x2x2!3x3!...nxn!no(x )sinxx3x3!5x5!... (n1)(2nx2n11)!2no(x1)WORD格式可编辑版...cosx12x2!4x4!... (2nxnox2n1)(2n!)ln(1x)x2x23x3... (nxnox n11)(n)(1x)1x (1)2!2x n ox n(1)...((n1))x...(n!)arctanxx3x35x5... (2n1xnox2n11)(2n11)5.洛必达法则定理1设函数f(x)、F(x)满足下列条件:(1)lim()0fxxx0 ,limF(x)0xx;(2)f(x)与F(x)在x的某一去心邻域内可导,且F(x)0;(3)f(x)limxx0Fx)(f(x)f(x)存在(或为无穷大),则limlimxx0FFx(x)xx()这个定理说明:当f(x)limx0Fxx()存在时,f(x)limxx0Fx()也存在且等于f(x)limxx0F(x);当f(x) limxx()0Fx 为无穷大时,f(x)limx()x0Fx也是无穷大.这种在一定条件下通过分子分母分别求导再求极限来确定未定式的极限值的方法称为洛必达(LHospital)法则.型未定式定理2设函数f(x)、F(x)满足下列条件:(1)lim()fxxx0 ,limF(x)xx;(2)f(x)与F(x)在x的某一去心邻域内可导,且F(x)0;(3)f(x)limx)x0F(x存在(或为无穷大),则f(x)f(x)limlimxx0F(x)x x F(x)注:上述关于x时未定式型的洛必达法则,对于x时未定式型x同样适用.使用洛必达法则时必须注意以下几点:(1)洛必达法则只能适用于“0”和“”型的未定式,其它的未定式须先化简变形成“0”或“”型才能运用该法则;(2)只要条件具备,可以连续应用洛必达法则;(3)洛必达法则的条件是充分的,但不必要.因此,在该法则失效时并不能断定原极限不存在.6.利用导数定义求极限WORD格式可编辑版...f(xx)f(x)00'基本公式()limfx0x0x(如果存在)3.利用定积分定义求极限基本格式1n1klimf()f(x)dxnnnk1(如果存在)三.函数的间断点的分类函数的间断点分为两类:(1)第一类间断点设x是函数y=f(x)的间断点。
高等数学(同济第七版)上册-知识点汇总

高等数学(同济第七版)上册-知识点汇总————————————————————————————————作者:————————————————————————————————日期:高等数学(同济第七版)上册-知识点总结第一章 函数与极限一. 函数的概念1.两个无穷小的比较设0)(lim ,0)(lim ==x g x f 且l x g x f =)()(lim (1)l = 0,称f (x)是比g(x)高阶的无穷小,记以f (x) = 0[)(x g ],称g(x)是比f(x)低阶的无穷小。
(2)l ≠ 0,称f (x)与g(x)是同阶无穷小。
(3)l = 1,称f (x)与g(x)是等价无穷小,记以f (x) ~ g(x)2.常见的等价无穷小当x →0时sin x ~ x ,tan x ~ x ,x arcsin ~ x ,x arccos ~ x ,1− cos x ~ 2/2^x , x e −1 ~ x ,)1ln(x + ~ x ,1)1(-+αx ~ x α 二.求极限的方法1.两个准则准则 1. 单调有界数列极限一定存在准则 2.(夹逼定理)设g (x ) ≤ f (x ) ≤ h (x )若A x h A x g ==)(lim ,)(lim ,则A x f =)(lim2.两个重要公式公式11sin lim 0=→xx x 公式2e x x x =+→/10)1(lim 3.用无穷小重要性质和等价无穷小代换4.用泰勒公式当x 0→时,有以下公式,可当做等价无穷小更深层次)()!12()1(...!5!3sin )(!...!3!2112125332++++-+++-=++++++=n n n n nxx o n x x x x x x o n x x x x e )(!2)1(...!4!21cos 2242n n n x o n x x x x +-+++-= )()1(...32)1ln(132n n n x o nx x x x x +-++-=++ )(!))1()...(1( (2)1(1)1(2n n x o x n n x x x +---++-++=+ααααααα)(12)1(...53arctan 1212153+++++-+-+-=n n n x o n x x x x x 5.洛必达法则定理1 设函数)(x f 、)(x F 满足下列条件:(1)0)(lim 0=→x f x x ,0)(lim 0=→x F x x ; (2))(x f 与)(x F 在0x 的某一去心邻域内可导,且0)(≠'x F ;(3))()(lim 0x F x f x x ''→存在(或为无穷大),则 这个定理说明:当)()(lim 0x F x f x x ''→存在时,)()(lim 0x F x f x x →也存在且等于)()(lim 0x F x f x x ''→;当)()(lim 0x F x f x x ''→为无穷大时,)()(lim 0x F x f x x →也是无穷大. 这种在一定条件下通过分子分母分别求导再求极限来确定未定式的极限值的方法称为洛必达(H L 'ospital )法则.∞∞型未定式 定理2 设函数)(x f 、)(x F 满足下列条件:(1)∞=→)(lim 0x f x x ,∞=→)(lim 0x F x x ; (2))(x f 与)(x F 在0x 的某一去心邻域内可导,且0)(≠'x F ;(3))()(lim 0x F x f x x ''→存在(或为无穷大),则 注:上述关于0x x →时未定式∞∞型的洛必达法则,对于∞→x 时未定式∞∞型同样适用.使用洛必达法则时必须注意以下几点:(1)洛必达法则只能适用于“00”和“∞∞”型的未定式,其它的未定式须先化简变形成“00”或“∞∞”型才能运用该法则; )()(lim )()(lim 00x F x f x F x f x x x x ''=→→)()(lim )()(lim 00x F x f x F x f x x x x ''=→→(2)只要条件具备,可以连续应用洛必达法则;(3)洛必达法则的条件是充分的,但不必要.因此,在该法则失效时并不能断定原极限不存在.6.利用导数定义求极限 基本公式)()()(lim 0'000x f xx f x x f x =∆-∆+→∆(如果存在) 7.利用定积分定义求极限基本格式⎰∑==∞→101)()(1lim dx x f n k f n n k n (如果存在) 三.函数的间断点的分类函数的间断点分为两类:(1)第一类间断点设0x 是函数y = f (x )的间断点。
高等数学同济第七版上册

高等数学同济第七版上册简介《高等数学同济第七版上册》是中国著名的高等教育教材之一,广泛应用于大学高等数学课程中。
本书由来自同济大学的杨传辉等人编写,旨在帮助学生全面掌握高等数学的基本概念和方法。
目录1.函数与极限2.导数及其应用3.微分中值定理与导数的应用4.不定积分5.定积分及其应用6.微分方程与其应用7.空间解析几何8.多元函数微分学9.重积分10.曲线积分与曲面积分11.空间向量与空间直线12.平面及其方程13.空间曲面及其方程内容概要1. 函数与极限本章介绍了函数的概念以及一些常见的函数类型,如多项式函数、指数函数和对数函数。
同时,重点介绍了极限的定义和相关性质,帮助学生理解极限的概念和运算法则。
2. 导数及其应用本章主要讲述了导数的概念和性质,以及如何利用导数解决实际问题。
具体内容包括导数的定义、导数的计算方法、高阶导数、隐函数求导、相关变化率与极值问题等。
3. 微分中值定理与导数的应用本章介绍了微分中值定理及其应用。
主要内容包括罗尔定理、拉格朗日中值定理、柯西中值定理等内容。
同时,通过实际问题的例子,帮助学生理解微分中值定理的意义和应用。
4. 不定积分本章主要介绍了不定积分的概念、性质和计算方法。
包括基本不定积分公式、换元积分法、分部积分法、有理函数的积分等。
同时,引入了定积分的概念,并简要介绍了与不定积分的关系。
5. 定积分及其应用本章深入讲解了定积分的概念和性质。
主要内容包括定积分的定义、计算方法、定积分的几何意义、平均值定理、牛顿-莱布尼茨公式等。
同时,介绍了定积分在物理学、经济学等领域的应用。
6. 微分方程与其应用本章介绍了常微分方程的基本概念和求解方法。
主要内容包括一阶常微分方程、高阶常微分方程、常系数线性齐次微分方程等。
同时,通过一些实际问题的例子,帮助学生理解微分方程的意义和应用。
7. 空间解析几何本章介绍了空间直角坐标系和空间直线的相关知识。
具体内容包括空间直线方程的标准式和一般式、空间直线的位置关系、平面方程等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1(4)(7)(10)(18)
(19)(21)(25)(26)
2,5,6,7(10)(11)(13)
5.4反常积分
无穷限的反常积分
了解概念,会计算反常积分
例1~7
习题5-4:
1(4)(8)(10)
2,3(记住结论),4
无界函数的反常积分
5.5反常积分的审敛法
不作要求
总习题五
总结归纳本章的基本概念、基本定理、基本公式、基本方法
同济高数第七版上册考研数学考纲
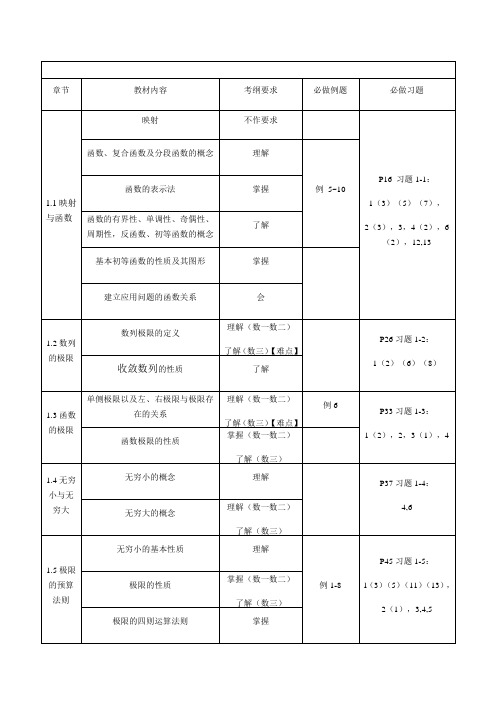
第一章函数与极限(没有第三章)
章节
教材内容
考纲要求
必做例题
必做习题
1.1映射与函数
映射
不作要求
P16习题1-1:
1(3)(5)(7),
2(3),3,4(2),6(2),12,13
函数、复合函数及分段函数的概念
理解
例5~10
函数的表示法
掌握
函数的有界性、单调性、奇偶性、周期性,反函数、初等函数的概念
函数极限的性质
掌握(数一数二)
了解(数三)
1.4无穷小与无穷大
无穷小的概念
理解
P37习题1-4:
4,6
无穷大的概念
理解(数一数二)
了解(数三)
1.5极限的预算法则
无穷小的基本性质
理解
例1-8
P45习题1-5:
1(3)(5)(11)(13),
2(1),3,4,5
极限的性质
掌握(数一数二)
了解(数三)
极限的四则运算法则
1(1)(4)(9),
2(2)(4)
数三不做1(9)
n阶常系数齐次线性微分方程
会(数一数二)
例6~7
7.8常系数非齐次线性微分方程
二阶常系数齐次线性微分方程中自由项为:多项式、指数函数、正弦函数、余弦函数以及它们的和与积
会解【重点】(数三不要求和与积)
例1~4
习题7-8:
1(2)(4)(7)(9)
2(2)(4)
7.2可分离变量的微分方程
可分离变量的微分方程的
概念及其解法
掌握
例1~4
习题7-2:1(3)(4)(5)(7)
(9),2(3)(4)
7.3齐次方程
一阶齐次微分方程的形式及其解法
掌握【重点】
例1,2
习题7-3:
1(1)(5),2(2)
可化为一阶齐次微分方程的
形式及其解法
不作要求
7.4一阶线性微分方程
一阶线性微分方程的
(21)(25)(33)(35)
第五章定积分
5.1定积分的概念与性质
定积分的定义与性质
掌握(数一数二)
了解(数三)(性质6会证明)
例1
习题5-1:
4(4),5,7(4),11
函数可积的两个充分条件
理解【难点】
定积分的近似计算
不作要求
5.2微积分基本公式
积分上限函数及其导数
理解【重点】(定理会证明、会求导)
函数间断点的和、差、积、商的连续性
了解(会利用连续性求极限)
例1
P65习题1-9:
3(3)(5)(7)(8)
4(4)(5)(6)(7)(8)
5
6
反函数与复合函数的连续性
例2~4
初等函数的连续性
例5~8
1.10闭区间上连续函数的性质
有界性与最大值最小值定理,
零点定理与介值定理
理解【重点】(会灵活应用这些性质)
习题5-2:
3,5(2),6,7,8(3)
(8)(11)(12),
11(2),12,13,14,15,16
牛顿-莱布尼茨共识
掌握【重点】
(定理会证明)
例1~4,例6
(记住结论),例7,8
5.3定积分的换元法和分部积分法
定积分的换元法与分部积分法
掌握【重点】
例1~4
例5~7(记住结论),例8~11,
例12(记住结论)
了解
基本初等函数的性质及其图形
掌握
建立应用问题的函数关系
会
1.2数列的极限
数列极限的定义
理解(数一数二)
了解(数三)【难点】
P26习题1-2:
1(2)(6)(8)
收敛数列的性质
了解
1.3函数的极限
单侧极限以及左、右极限与极限存在的关系
理解(数一数二)
了解(数三)【难点】
例6
P33习题1-3:
1(2),2,3(1),4
第四章不定积分
4.1不定积分的概念与性质
原函数与不定积分的概念
理解
例1~3
5~15
P192习题4-1:
1(1),2(5)(8)(13)
(17)(19)(21)(25),
5,7
基本积分表
掌握【重点】(熟记)
不定积分的性质
掌握
4.2换元积分法
第一类换元法(凑微分法)
掌握【重点】(熟记P205公式,双曲代换不作要求)
会(数一数二)
例1~5
习题6-3:
5,11
总习题六
总结归纳本章的基本概念、基本定理、基本公式、基本方法
总习题六:
1,2,4,5,6,7,9
第七章微分方程
7.1微分方程的基本概念
微分方程的阶、解、通解、
初始条件和特解
了解
例1,2
习题7-1:1(3)(4)
2(2)(4),3(2),4(3),5(1),7
数一、二
做例1~9
数三做
例1~5
P108习题2-4:
1(3),2,3(4)
4(1)(3),5(2),
8(3)数三不用做5,8
由参数方程所确定的
函数的导数
会【重点】(仅数一数二要求)
相关变换率
不作要求
章节
教材内容
考纲要求
必做例题
必做习题
2.5函数的
微分
微分的定义、几何意义
掌握(数一数二)
了解(数三)
例1~6
必做例题
必做习题
7.6高阶线性微分方程
线性微分方程的解的结构:齐次线性微分方程与非齐次线性微分方程的解的性质
理解(数一数二)
了解(数三)
【难点】
习题7-6:
1(3)(6),3,4(2),5
7.7常系数齐次线性微分方程
二阶常系数齐次线性微分方程
会解【重点】(特征方程、求通解的步骤)
例1~3
习题7-7:
理解【重点】
例10,11
2.2函数的求导法则
函数的和、差、积、商
的求导法则
掌握
例1~15
P94习题2-2:
2(9),3(3),
6(9)(10),7(8),
8(4),9,10(2),
11(4)(9)
反函பைடு நூலகம்的求导法则
掌握
复合函数的求导法则
掌握【重点】(基本
求导法则与导数公式要非常熟悉)
基本求导法则与导数公式
掌握
章节
教材内容
考纲要求
必做例题
必做习题
1.6极限存在准则,两个重要极限
极限存在的两个准则(夹逼准则、单调有界数列必有极限)
掌握(数一数二)
了解(数三)
P52习题1-6:
1(4)(6),2,4
利用两个重要极限求极限的方法
掌握【重点】
例1~4
柯西审敛原理
不作要求
1.7无穷小的比较
无穷小阶的定义及无穷小量的比较方法
P83习题2-1:
6,7,13,16(2),
17,18,19
导数的物理意义
了解(仅数学一数学二要求)(会用
导数描述物理量)
引例1
导数的几何意义
理解(数一数二)
了解(数三)(会求
平面曲线的切线
方程和法线方程)
例8,9,
引例2
导数的经济意义
了解(仅数三要求)
单侧导数以及单侧可导
与可导的关系
理解
例7
函数的可导性与连续性的关系
掌握【重点】
例1~5
(熟记例1,2的结论)
P55习题1-7:
1,3,4(1),5
一些重要的等价无穷小及其性质
1.8函数的连续性与间断点
函数连续性的概念
(含左连续与右连续)
理解【重点】
P61习题1-8:
3(1),4,5
函数间断点的分类与判别
(第一类间断点与第二类间断点)
会【重点】
例1~5
1.9连续函数的运算与初等函数的连续性
总习题五:
1(1)(2)(4)(5),2,4(2)
5(2),6(1),
11(7)(9)(10),12,13,14
15,18
第六章定积分的应用
章节
教材内容
考纲要求
必做例题
必做习题
6.1定积分的元素法
元素法
理解
6.2定积分在几何学上的应用
平面图形的面积(直角坐标情形、极坐标情形)
会
体积:数学三只要求旋转体的体积
形式及其解法
掌握(熟记公式)
例1,3
习题7-4:
1(3)(5)(8)(10),
2(1)(3),3,7(3)
伯努利方程的形式及其解法
会(仅数一)
例4
8(5)
7.5可降阶的高阶微分方程
用降阶法解下列形式的微分方程:
会(仅数一数二)
例1,3,5,6
习题7-5:
1(3)(4)(7),2(2)
章节
教材内容
考纲要求
会(仅数一数二要求)
例1~5,
5~8
习题4-4:
