上海2020初三数学一模各区几何证明23题集合(供参考)

合集下载

2020年上海市中考数学一模试卷及解析

2020年上海市中考一模试卷数学试卷一、选择题（本大题共6小题，共24分）1.在Rt△ABC中，∠C=90°，如果BC=5，AB=13，那么sin A的值为()A. 513B. 512C. 1213D. 1252.下列函数中，是二次函数的是()A. y=2x−1B. y=2x2C. y=x2+1D. y=(x−1)2−x23.抛物线y=x2−4x+5的顶点坐标是()A. (−2,1)B. (2,1)C. (−2,−1)D. (2,−1)4.如图，点D、E分别在△ABC的边AB、AC上，下列各比例式不一定能推得DE//BC的是()A. ADBD =AECEB. ADAB=DEBCC. ABBD =ACCED. ADAB=AEAC5.如图，传送带和地面所成斜坡的坡度为1：3，它把物体从地面点A处送到离地面3米高的B处，则物体从A到B所经过的路程为()A. 3√10米B. 2√10米C. √10米D. 9米6.下列说法正确的是()A. a⃗+(−a⃗ )=0B. 如果a⃗和b⃗ 都是单位向量，那么a⃗=b⃗C. 如果|a⃗|=|b⃗ |，那么a⃗=b⃗D. 如果a⃗=−12b⃗ (b⃗ 为非零向量)，那么a⃗//b⃗二、填空题（本大题共12小题，共48分）7.已知x=3y，那么x+yx+2y=______．8.已知线段AB=2cm，P是线段AB的黄金分割点，PA>PB，那么线段PA的长度等于______cm．9.如果两个相似三角形对应边之比是2：3，那么它们的对应中线之比是______．10.如果二次函数y=x2−2x+k−3的图象经过原点，那么k的值是______．11.将抛物线y=−3x2向下平移4个单位，那么平移后所得新抛物线的表达式为______．12.如果抛物线经过点A(−1,0)和点B(5,0)，那么这条抛物线的对称轴是直线______．13.二次函数y=−2(x+1)2的图象在对称轴左侧的部分是______.(填“上升”或“下降”)14.如图，在△ABC中，AE是BC边上的中线，点G是△ABC的重心，过点G作GF//AB交BC于点F，那么EFEB=______．15.如图，已知AB//CD//EF，AD=6，DF=3，BC=7，那么线段CE的长度等于______．16.如图，将△ABC沿射线BC方向平移得到△DEF，边DE与AC相交于点G，如果BC=6cm，△ABC的面积等于9cm2，△GEC的面积等于4cm2，那么CF=______cm．17.用“描点法”画二次函数y=ax2+bx+c的图象时，列出了如下的表格：x…01234…y=ax2+bx+c…−3010−3…那么当x=5时，该二次函数的值为．18.在Rt△ABC中，∠C=90°，AC=2，BC=4，点D、E分别是边BC、AB的中点，将△BDE绕着点B旋转，点D、E旋转后的对应点分别为点、，当直线经过点A时，线段的长为______．三、计算题（本大题共1小题，共10分）19.为了测量大楼顶上(居中)避雷针BC的长度，在地面上点A处测得避雷针底部B和顶部C的仰角分别为55°58′和57°，已知点A与楼底中间部位D的距离约为80米，求避雷针BC的长度(参考数据：，，，sin57°≈0.84，tan57°≈1.54)四、解答题（本大题共6小题，共68分） 20. 计算：tan45°−cos60°2sin30∘+cot 260°21. 如图，在平行四边形ABCD 中，点E 在边AD 上，且AE =2ED ，联结BE 并延长交边CD 的延长线于点F ，设BA ⃗⃗⃗⃗⃗ =a ⃗ ，BC⃗⃗⃗⃗⃗ =b ⃗ ． (1)用a ⃗ ，b ⃗ 表示BE⃗⃗⃗⃗⃗ ，DF ⃗⃗⃗⃗⃗ ； (2)先化简，在求作：(−32a⃗ +b ⃗ )+2(a ⃗ −b ⃗ )(不要求写作法，但要写明结论)．22. 如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，且AD =3，AC =6，AE =4，AB =8．(1)如果BC =7，求线段DE 的长；(2)设△DEC 的面积为a ，求△BDC 的面积(用a 的代数式表示)．23.如图，已知△ABC和△ADE，点D在BC边上，DA=DC，∠ADE=∠B，边DE与AC相交于点F．(1)求证：AB⋅AD=DF⋅BC；(2)如果AE//BC，求证：BDDC =DFFE．24.如图，在平面直角坐标系xOy中，抛物线y=−x2+bx+c与x轴的两个交点分别为A(−1,0)，B(3,0)，与y轴相交于点C．(1)求抛物线的表达式；(2)联结AC、BC，求∠ACB的正切值；(3)点P在抛物线上，且∠PAB=∠ACB，求点P的坐标．25.在Rt△ABC中，∠A=90°，AB=4，AC=3，D为AB边上一动点(点D与点A、B不重合)，联结CD，过点D作DE⊥DC交边BC于点E．(1)如图，当ED=EB时，求AD的长；(2)设AD=x，BE=y，求y关于x的函数解析式并写出函数定义域；(3)把△BCD沿直线CD翻折得，联结，当是等腰三角形时，直接写出AD的长．答案和解析1.【答案】A【解析】解：如图：在Rt△ABC中，∠C=90°，BC=5，AB=13，sinA=BCAB =513．故选：A．本题可画出三角形，结合图形运用三角函数定义求解．此题考查了三角函数的定义．可借助图形分析，确保正确率．2.【答案】C【解析】解：二次函数的标准形式为y=ax2+bx+c(a≠0)，∴y=x2+1是二次函数，故选：C．根据二次函数的标准形式y=ax2+bx+c(a≠0)，从选项中直接可以求解．本题考查二次函数的定义；熟练掌握二次函数的定义是解题的关键．3.【答案】B【解析】解：∵y=x2−4x+5=(x−2)2+1，∴顶点坐标为(2,1)，故选：B．利用配方法化成顶点式求解即可．本题考查了二次函数的性质，化成顶点解析式是求抛物线的顶点坐标的一种方法．4.【答案】B【解析】解：∵ADBD =AECE，∴DE//BC，∵ABBD =ACEC，∴DE//BC，∵ADAB =AEAC，∴DE//BC，故选：B．根据平行线分线段成比例定理判断即可．本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．5.【答案】A【解析】解：∵BC：AC=1：3，∴3：AC=1：3，∴AC=9，∴AB=√AC2+BC2=√9+81=3√10，∴物体从A到B所经过的路程为3√10，故选：A．由题意可得物体从A到B所经过的路程为AB的长，根据坡比求出AC的长，再根据勾股定理求出AB的长即可．本题考查了轨迹，解直角三角形，知道坡比的概念是解题的关键．6.【答案】D【解析】解：A、a⃗+(−a⃗ )=0，错误应该等于零向量．B、如果a⃗和b⃗ 都是单位向量，那么a⃗=b⃗ ，错误，模相等，方向不一定相同．C、如果|a⃗|=|b⃗ |，那么a⃗=b⃗ ，错误，模相等，方向不一定相同．D、如果a⃗=−12b⃗ (b⃗ 为非零向量)，那么a⃗//b⃗ ，正确，故选：D．根据平面向量的性质一一判断即可．本题考查平面向量，平行向量等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．7.【答案】45【解析】解：∵x=3y，∴x+yx+2y =3y+y3y+2y=45．故答案为：45．直接利用已知代入原式求出答案．此题主要考查了比例的性质，正确把x代入是解题关键．8.【答案】√5−1【解析】解：根据黄金分割定义，得PA2=AB⋅PB，PA2=2(2−PA)解得PA=√5−1．故答案为√5−1．根据黄金分割的定义：把线段AB分成两条线段AP和BP(PA>PB)，且使AP是AB和BP的比例中项，叫做把线段AB黄金分割，点P叫做线段AB的黄金分割点．本题考查了黄金分割，解决本题的关键是掌握黄金分割定义．9.【答案】2：3【解析】解：∵两个相似三角形对应边之比是2：3，∴它们的对应中线之比是2：3，故答案为：2：3．根据相似三角形对应中线的比等于相似比解答．本题考查的是相似三角形的性质，相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比．10.【答案】3【解析】解：∵二次函数y=x2−2x+k−3的图象经过原点，∴k−3=0，解得k=3，故答案为：3．将原点坐标(0,0)代入二次函数解析式，列方程求k即可．此题考查了二次函数图象上的点与解析式的关系，将点的坐标代入解析式是解题的关键．11.【答案】y=3x2−4【解析】解：∵抛物线y=−3x2向下平移4个单位，∴抛物线的解析式为y=−3x2−4，故答案为：y=−3x2−4．根据向下平移，纵坐标相减，即可得到答案．本题考查了二次函数的图象与几何变换，向下平移|a|个单位长度纵坐标要减|a|．12.【答案】x=2【解析】解：∵抛物线经过点A(−1,0)和点B(5,0)，∴抛物线的对称轴为直线x=−1+52=2．故答案为：x=2．根据点A，B的坐标，利用二次函数的性质可求出抛物线的对称轴，此题得解．本题考查了二次函数的性质，根据抛物线的对称性，找出抛物线的对称轴是解题的关键．13.【答案】上升【解析】解：∵−2<0，∴二次函数的开口向下，则图象在对称轴左侧的部分y随x值的增大而增大，故答案为上升．由函数解析式可知二次函数的开口向下，图象在对称轴左侧的部分y随x值的增大而增大．本题考查二次函数的性质；熟练掌握二次函数的图象及性质是解题的关键．14.【答案】13【解析】解：∵点G是△ABC的重心，∴GE：AG=1：2，∴GE：AE=1：3，∵GF//AB，△EGF∽△EAB，∴EFEB =GEAE=13，故答案为13．由点G是△ABC的重心，可得GE：AG=1：2，则GE：AE=1：3，再GF//AB，得出结论．本题考查了三角形的重心：三角形的重心是三角形三边中线的交点；重心到顶点的距离与重心到对边中点的距离之比为2：1.也考查了相似三角形的判定与性质．15.【答案】72【解析】解：∵AB//CD//EF，AD=6，DF=3，BC=7，∴ADDF =BCCE，即63=7CE，解得：CE=72，故答案为：72根据平行线分线段所得线段对应成比例解答即可．本题主要考查平行线分线段成比例，掌握平行线分线段所得线段对应成比例是解题的关键．16.【答案】2【解析】解：∵AB//DE，∴△ABC∽△GEC，∴S△GECS△ABC =(ECBC)2=49，∴EC6=23∴EC=4cm，∵EF=BC=6cm，∴CF=EF−EC=6−4=2cm．故答案是：2易证△ABC∽△GEC，根据相似三角形的面积的比等于相似比的平方，即可求得EC的长，则CF即可求解．本题考查了平移的性质，以及相似三角形的性质，正确理解性质求得EC的长是关键．17.【答案】−8【解析】解：从表格可知：抛物线的顶点坐标为(2,1)，设y=ax2+bx+c=a(x−2)2+1，从表格可知过点(0,−3)，代入得：−3=a(0−2)2+1，解得：a=−1，即y=−(x−2)2+1，当x=5时，y=−(5−2)2+1=−8，故答案为：−8．从表格可知：抛物线的顶点坐标为(2,1)，抛物线过点(0,−3)，代入求出抛物线的解析式，再把x=5代入函数解析式，即可求出答案．本题考查了二次函数图象上点的坐标特征，二次函数的图象和性质，用待定系数法求二次函数的解析式等知识点，能求出函数的解析式是解此题的关键．18.【答案】2√5或65√5【解析】解：如图1，当点A在的延长线上时，∵∠C=90°，AC=2，BC=4，∴AB=√AC2+BC2=√4+16=2√5，∵点D、E分别是边BC、AB的中点，∴DE//AC，DE=12AC=1，BD=12BC=2，∴∠EDB=∠ACB=90°，∵将△BDE绕着点B旋转，，，，∵在Rt△ABC和中，，AB=BA，∴Rt△ABC≌，，且，∴四边形是平行四边形，且∠ACB=90°，∴四边形是矩形，；如图2，当点A在线段的延长线上时，，，，∵将△BDE绕着点B旋转，，∵BE′AB =12=BD′BC，∽，，，，故答案为：2√5或6√55．分两种情况：①点A在的延长线上时；②点A在线段的延长线上时；然后分类讨论，求出线段BD的长各是多少即可．本题属于三角形综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，矩形的判定和性质，勾股定理等知识，解题的关键是理解题意，正确寻找相似三角形解决问题，属于中考常考题型．19.【答案】解：在Rt△ABD中，∵tan∠BAD=BDAD，∴1.48=BD80，∵AD =80米，∴BD =118.4(米)，在Rt △CAD 中，∵tan∠CAD =CDAD ， ∴1.54=CDAD ，∴CD =123.2(米)，∴BC =CD −BD =4.8(米)．答：避雷针BC 的长度为4.8米．【解析】解直角三角形求出CD ，BD ，根据BC =CD −BD 求解即可．本题考查解直角三角形的应用，解题的关键是熟练掌握基本知识，属于中考常考题型．20.【答案】解：原式=1−122×12+(√33)2=12+13=56．【解析】直接利用特殊角的三角函数值进而分别代入求出答案．此题主要考查了特殊角的三角函数值，正确记忆相关数据是解题关键． 21.【答案】解：(1)∵四边形ABCD 是平行四边形， ∴AD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ =b ⃗ ，AB//CD ， ∵AE =2ED ，∴AE ⃗⃗⃗⃗⃗ =23AD ⃗⃗⃗⃗⃗⃗ =23b ⃗ ，∴BE ⃗⃗⃗⃗⃗ =BA ⃗⃗⃗⃗⃗ +AE ⃗⃗⃗⃗⃗ =a ⃗ +23b ，∵DF ：AB =DE ：AE =1：2， ∴DF =12AB ，∴DF ⃗⃗⃗⃗⃗ =12BA ⃗⃗⃗⃗⃗ =12a ⃗ ．(2)(−32a ⃗ +b ⃗ )+2(a ⃗ −b ⃗ )=−32a ⃗ +b ⃗ +2a ⃗ −2b ⃗ =12a ⃗ −b⃗ ，取AB 的中点H ，连接HC ，HC ⃗⃗⃗⃗⃗⃗ 即为所求．【解析】(1)利用三角形的法则以及平行线分线段成比例定理求解即可．(2)先化简，取AB 的中点H ，连接HC ，HC⃗⃗⃗⃗⃗⃗ 即为所求．本题考查平面向量，平行向量等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．22.【答案】解：(1)∵AEAB =48=12，ADAC=36=12，∴AEAB =ADAC，且∠DAE=∠BAC，∴△ADE∽△ACB，∴ADAC =DEBC=12，∴DE=12BC=12×7=72；(2)∵AE=4，AC=6，∴EC=2=13AC，∴S△ACD=3S△DEC=3a，∵AD=3，AB=8，∴BD=5=53AD，∴S△BDC=53S△ADC=5a．【解析】(1)通过证明△ADE∽△ACB，可求解；(2)由线段的数量关系可求面积关系，即可求解．本题考查了相似三角形的判定和性质，证明△ADE∽△ACB是本题的关键．23.【答案】(1)证明：∵DA=DC，∴∠DAC=∠C，又∵∠ADE=∠B，∴△ABC∽△FDA，∴ABDF =BCAD，∴AB⋅AD=DF⋅BC；(2)证明：∵∠ADE+∠CDF=∠B+∠BAD，∠ADE=∠B，∴∠CDF=∠BAD，∵AE//BC，∴∠E=∠CDF，∠C=∠EAF，∴∠BAD=∠E，又∵∠ADE=∠B，∴△ABD∽△EDA，∴BDAD =ADAE，∵DA=DC，∴∠DAC=∠C，∴∠EAF=∠DAC，即AC平分∠DAE，作FM⊥AD于M，FN⊥AE于N，则FM=FM，∵△ADF的面积△AEF的面积=DFEF=12AD×FM12AE×FN=ADAE，∴BD DC =DFFE ．【解析】(1)由等腰三角形的性质得出∠DAC =∠C ，由已知∠ADE =∠B ，证明△ABC∽△FDA ，得出ABDF =BCAD ，即可得出结论；(2)由三角形的外角性质得出∠CDF =∠BAD ，由平行线的性质得出∠E =∠CDF ，∠C =∠EAF ，证出∠BAD =∠E ，证明△ABD∽△EDA ，得出BDAD =ADAE ，证出∠EAF =∠DAC ，即AC 平分∠DAE ，作FM ⊥AD 于M ，FN ⊥AE 于N ，则FM =FM ，求出△ADF 的面积△AEF 的面积=DF EF=AD AE，即可得出结论．本题考查了相似三角形的判定与性质、等腰三角形的性质、三角形的外角性质、平行线的性质、角平分线的性质等知识；证明三角形相似是解题的关键．24.【答案】解：(1)将点A(−1,0)，B(3,0)代入抛物线y =−x 2+bx +c 中，得{−1−b +c =0−9+3b +c =0，解得，b =2，c =3，∴抛物线的表达式为y =−x 2+2x +3；(2)∵在y =−x 2+2x +3中，当x =0时，y =3， ∴C(0,3)，∴OC =OB =3，∴△OBC 为等腰直角三角形，∠OBC =45°， ∴BC =√2OC =3√2，如图1，过点A 作AH ⊥BC 于H ，则∠HAB =∠HBA =45°， ∴△AHB 是等腰直角三角形， ∵AB =4， ∴AH =BH =√22AB =2√2，∴CH =BC −BH =√2， ∴在Rt △AHC 中，tan∠ACH =AH CH=2√2√2=2，即∠ACB 的正切值为2；(3)①如图2，当∠PAB =∠ACB 时，过点P 作PM ⊥x 轴于点M ，设P(a,−a 2+2a +3)，则M(a,0)，由(1)知，tan∠ACB =2， ∴tan∠PAM =2， ∴PMAM =2， ∴−a 2+2a+3a+1=2，解得，a 1=−1(舍去)，a 2=1， ∴P 1(1,4)；②取点P(1,4)关于x 轴的对称点Q(1,−4)，延长AQ 交抛物线于P 2，则此时∠P 2AB =∠PAM =∠ACB ，设直线PQ 的解析式为y =kx +b ，将A(−1,0)，Q(1,−4)代入，得，{−k +b =0k +b =−4，解得，k =−2，b =−2， ∴y AQ =−2x −2，联立，{y =−2x −2y =−x 2+2x +3，解得，{x =−1y =0或{x =5y =−12，∴P 2(5,−12)；综上所述，点P 的坐标为(1,4)或(5,−12)．【解析】(1)将点A ，B 坐标代入抛物线y =−x 2+bx +c 即可；(2)如图1，过点A 作AH ⊥BC 于H ，分别证△OBC 和△AHB 是等腰直角三角形，可求出CH ，AH 的长，可在Rt △AHC 中，直接求出∠ACB 的正切值； (3)此问需分类讨论，当∠PAB =∠ACB 时，过点P 作PM ⊥x 轴于点M ，设P(a,−a 2+2a +3)，由同角的三角函数值相等可求出a 的值，由对称性可求出第二种情况．本题考查了待定系数法求解析式，锐角三角函数，交点的坐标等，解题关键是第三问要注意分类讨论思想的运用．25.【答案】解：(1)∵ED =EB ， ∴∠EDB =∠B ， ∵CD ⊥DE ，∴∠CDE =∠A =90°，∵∠ACD +∠ADC =90°，∠ADC +∠EDH =90°， ∴∠ACD =∠EDB =∠B ， ∴tan∠ACD =tan∠B ， ∴AD AC =AC AB ，∴AD 3=34， ∴AD =94．(2)如图1中，作EH ⊥BD 于H ．在Rt △ACB 中，∵∠A =90°，AC =3，AB =4， ∴BC =√AC 2+BC 2=√32+42=5， ∵BE =y ，∴EH =35y ，BH =45y ，DH =AB −AD −BH =4−x −45y ， ∵∠A =∠DHE =90°，∠ACD =∠EDH ， ∴△ACD∽△HDE ， ∴ACDH =AD EH ，∴34−x−45y=x35y， ∴y =20x−5x 29+4x(0<x <4)．(3)①如图3−1中，设CB′交AB 于K ，作AE ⊥CK 于E ，DM ⊥CB′于M ，DN ⊥BC 于N∵AC =AB =3，AE ⊥CB′， ∴CE =EB′=12CB′=52，∴AE =√AC 2−CE 2=√32−(52)2=√112，由△ACE∽△KCA ，可得AK =3√115，CK =185，∴BK =AB −AK =4−3√115， ∵∠DCK =∠DCB ，DM ⊥CM ，DN ⊥CB ， ∴DM =DN ， ∴S △CDKS△CDB=DKDB =12⋅CK⋅DM 12⋅BC⋅DN =CKCB =1855=1825，∴BD =2543BK =10043−1543√11，∴AD =AB −BD =4−(10043−15√1143)=7243+15√1143．②如图3−2中，当CB′交BA 的延长线于K 时，同法可得BD =2543BK =10043+15√1143，∴AD =AB −BD =7243−15√1143．【解析】(1)证明∠ACD=∠EDB=∠B，推出tan∠ACD=tan∠B，可得ADAC =ACAB，由此构建方程即可解决问题．(2)如图1中，作EH⊥BD于H.证明△ACD∽△HDE，推出ACDH =ADEH，由此构建关系式即可解决问题．(3)分两种情形：①如图3−1中，设CB′交AB于K，作AE⊥CK于E，DM⊥CB′于M，DN⊥BC于N.利用角平分线的性质定理求出BD即可．②如图3−2中，当CB′交BA的延长线于K时，同法可得BD．本题属于几何变换综合题，考查了解直角三角形，相似三角形的判定和性质，勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考压轴题．。

2020年上海市中考数学一模试卷附答案解析

2020年上海市中考数学一模试卷含答案解析一．选择题（共6小题，每题4分，满分24分）1．函数y＝﹣2x2先向右平移1个单位，再向下平移2个单位，所得函数解析式是（）A．y＝﹣2（x﹣1）2+2B．y＝﹣2（x﹣1）2﹣2C．y＝﹣2（x+1）2+2D．y＝﹣2（x+1）2﹣22．在Rt△ABC中，∠C＝90°，若BC＝3，AC＝4，则sin B的值为（）A．B．C．D．3．下列说法中，正确的是（）A．如果k＝0，是非零向量，那么k＝0B．如果是单位向量，那么＝1C．如果||＝||，那么＝或＝﹣D．已知非零向量，如果向量＝﹣5，那么∥4．如图，在6×6的正方形网格中，联结小正方形中两个顶点A、B，如果线段AB与网格线的其中两个交点为M、N，那么AM：MN：NB的值是（）A．3：5：4B．3：6：5C．1：3：2D．1：4：25．使用家用燃气灶烧开同一壶水所需的燃气量y（单位：m3）与旋钮的旋转角度x（单位：度）（0°＜x≤90°）近似满足函数关系y＝ax2+bx+c（a≠0）．如图记录了某种家用节能燃气灶烧开同一壶水的旋钮的旋转角度x与燃气量y的三组数据，根据上述函数模型和数据，可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度约为（）A．33°B．36°C．42°D．49°6．如图，在正方形ABCD中，△BPC是等边三角形，BP、CP的延长线分别交AD于点E、F，连结BD、DP，BD与CF相交于点H，给出下列结论：①BE＝2AE②△DFP∽△BPH③DP2＝PH•PC；④FE：BC＝，其中正确的个数为（）A．1B．2C．3D．4二．填空题（共12小题，每题4分，满分48分）7．如果tanα＝，那么锐角α的度数是．8．已知f（x）＝，那么f（3）＝．9．已知线段AB＝2，如果点P是线段AB的黄金分割点，且AP＞BP，那么AP的值为．10．已知点A（x1，y1）、B（x2，y2）为抛物线y＝（x﹣2）2上的两点，如果x1＜x2＜2，那么y1y2．（填“＞”“＜”或“＝”）11．如果点A（﹣3，y1）和点B（﹣2，y2）是抛物线y＝x2+a上的两点，那么y1y2．（填“＞”、“＝”、“＜”）．12．抛物线y＝﹣2（x﹣1）2+3在对称轴右侧的部分是的．（填“上升”或“下降”）13．如图，某小区门口的栏杆从水平位置AB绕固定点O旋转到位置DC，已知栏杆AB的长为3.5米，OA的长为3米，点C到AB的距离为0.3米，支柱OE的高为0.6米，那么栏杆端点D离地面的距离为米．14．如图，在菱形ABCD中，O、E分别是AC、AD的中点，联结OE．如果AB＝3，AC＝4，那么cot∠AOE＝．15．如图，在四边形ABCD中，∠B＝∠D＝90°，AB＝3，BC＝2，tan A＝，则CD＝．16．已知在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，⊙C与斜边AB相切，那么⊙C的半径为．17．在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请在边长为1个单位的2×3的方格纸中，找出一个格点三角形DEF．如果△DEF 与△ABC相似（相似比不为1），那么△DEF的面积为．18．如图，在等腰△ABC中，AB＝AC＝4，BC＝6，点D在底边BC上，且∠DAC＝∠ACD，将△ACD沿着AD所在直线翻折，使得点C落到点E处，联结BE，那么BE的长为．三．解答题（共7小题，满分78分）19．计算：3tan30°﹣+cos45°+20．已知：在平行四边形ABCD中，AB：BC＝3：2．（1）根据条件画图：作∠BCD的平分线，交边AB于点E，取线段BE的中点F，联结DF交CE于点G．（2）设＝，＝，那么向量＝；（用向量、表示），并在图中画出向量在向量和方向上的分向量．21．如图1为放置在水平桌面l上的台灯，底座的高AB为5cm，长度均为20cm的连杆BC、CD与AB始终在同一平面上．（1）转动连杆BC，CD，使∠BCD成平角，∠ABC＝150°，如图2，求连杆端点D离桌面l的高度DE．（2）将（1）中的连杆CD再绕点C逆时针旋转，经试验后发现，如图3，当∠BCD＝150°时台灯光线最佳．求此时连杆端点D离桌面l的高度比原来降低了多少厘米？22．如图，梯形ABCD中，AD∥BC，∠ADC＝90°，AD＝2，BC＝4，tan B＝3．以AB为直径作⊙O，交边DC于E、F两点．（1）求证：DE＝CF；（2）求：直径AB的长．23．水城门位于淀浦河和漕港河三叉口，是环城水系公园淀浦河梦蝶岛区域重要的标志性景观．在课外实践活动中，某校九年级数学兴趣小组决定测量该水城门的高．他们的操作方法如下：如图，先在D处测得点A的仰角为20°，再往水城门的方向前进13米至C处，测得点A的仰角为31°（点D、C、B在一直线上），求该水城门AB的高．（精确到0.1米）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）24．已知：在平面直角坐标系xOy中，对称轴为直线x＝﹣2的抛物线经过点C（0，2），与x轴交于A（﹣3，0）、B两点（点A在点B的左侧）．（1）求这条抛物线的表达式；（2）联结BC，求∠BCO的余切值；（3）如果过点C的直线，交x轴于点E，交抛物线于点P，且∠CEO＝∠BCO，求点P 的坐标．25．如图，在△ABC中，AB＝AC＝10，BC＝16，点D为BC边上的一个动点（点D不与点B、点C重合）．以D为顶点作∠ADE＝∠B，射线DE交AC边于点E，过点A作AF ⊥AD交射线DE于点F．（1）求证：AB•CE＝BD•CD；（2）当DF平分∠ADC时，求AE的长；（3）当△AEF是等腰三角形时，求BD的长．参考答案与试题解析一．选择题（共6小题，每题4分，满分24分）1．【分析】先确定物线y＝﹣2x2的顶点坐标为（0，0），再把点（0，0）平移所得对应点的坐标为（1，﹣2），然后根据顶点式写出平移后的抛物线解析式．【解答】解：抛物线y＝﹣2x2的顶点坐标为（0，0），把（0，0）先向右平移1个单位，再向下平移2个单位所得对应点的坐标为（1，﹣2），所以平移后的抛物线解析式为y＝﹣2（x﹣1）2﹣2．故选：B．2．【分析】根据三角函数的定义解决问题即可．【解答】解：如图，在Rt△ABC中，∵∠C＝90°，BC＝3，AC＝4，∴AB＝＝＝5，∴sin B＝＝，故选：A．3．【分析】根据平面向量的性质一一判断即可．【解答】解：A、如果k＝0，是非零向量，那么k＝0，错误，应该是k＝．B、如果是单位向量，那么＝1，错误．应该是||＝1．C、如果||＝||，那么＝或＝﹣，错误．模相等的向量，不一定平行．D、已知非零向量，如果向量＝﹣5，那么∥，正确．故选：D．4．【分析】根据平行线分线段成比例定理得出即可．【解答】解：∵＝，＝，∴AM：MN：NB＝1：3：2，故选：C．5．【分析】根据题意和二次函数的性质，可以确定出对称x的取值范围，从而可以解答本题．【解答】解：由图象可知，物线开口向上，该函数的对称轴x＞且x＜54，∴36＜x＜54，即对称轴位于直线x＝36与直线x＝54之间且靠近直线x＝36，故选：C．6．【分析】由正方形的性质和相似三角形的判定与性质，即可得出结论．【解答】解：∵△BPC是等边三角形，∴BP＝PC＝BC，∠PBC＝∠PCB＝∠BPC＝60°，在正方形ABCD中，∵AB＝BC＝CD，∠A＝∠ADC＝∠BCD＝90°∴∠ABE＝∠DCF＝30°，∴BE＝2AE；故①正确；∵PC＝CD，∠PCD＝30°，∴∠PDC＝75°，∴∠FDP＝15°，∵∠DBA＝45°，∴∠PBD＝15°，∴∠FDP＝∠PBD，∵∠DFP＝∠BPC＝60°，∴△DFP∽△BPH；故②正确；∵∠PDH＝∠PCD＝30°，∠DPH＝∠DPC，∴△DPH∽△CPD，∴，∴DP2＝PH•PC，故③正确；∵∠ABE＝30°，∠A＝90°∴AE＝AB＝BC，∵∠DCF＝30°，∴DF＝DC＝BC，∴EF＝AE+DF＝﹣BC，∴FE：BC＝（2﹣3）：3故④正确，故选：D．二．填空题（共12小题，每题4分，满分48分）7．【分析】直接利用特殊角的三角函数值进而代入求出答案．【解答】解：∵tanα＝，∴锐角α的度数是：60°．故答案为：60°．8．【分析】将x＝3代入f（x）＝计算即可．【解答】解：当x＝3是，f（3）＝＝，故答案为．9．【分析】直接利用黄金分割的定义计算．【解答】解：∵点P是线段AB的黄金分割点，且AP＞BP，∴AP＝AB＝×2＝﹣1．故答案为﹣1．10．【分析】根据二次函数的性质得到抛物线y＝（x﹣2）2的开口向上，对称轴为直线x＝2，则在对称轴左侧，y随x的增大而减小，所以x1＜x2＜2时，y1＞y2．【解答】解：∵y＝（x﹣2）2，∴a＝1＞0，∴抛物线开口向上，∵抛物线y＝（x﹣2）2对称轴为直线x＝2，∵x1＜x2＜2，∴y1＞y2．故答案为＞．11．【分析】根据二次函数的图象和性质得出抛物线的对称轴是直线x＝0，抛物线的开口向上，当x＜0时，y随x的增大而减小，再比较即可．【解答】解：∵y＝x2+a，∴抛物线的对称轴是直线x＝0，抛物线的开口向上，当x＜0时，y随x的增大而减小，∵﹣3＜﹣2＜0，∴y1＞y2，故答案为：＞．12．【分析】根据a＜0，知抛物线开口向下，则在对称轴右侧的部分呈下降趋势．【解答】解：∵a＝﹣2＜0，∴抛物线开口向下，∴对称轴右侧的部分呈下降趋势．故答案为：下降．13．【分析】过D作DG⊥AB于G，过C作CH⊥AB于H，则DG∥CH，根据相似三角形的性质即可得到结论．【解答】解：过D作DG⊥AB于G，过C作CH⊥AB于H，则DG∥CH，∴△ODG∽△OCH，∴＝，∵栏杆从水平位置AB绕固定点O旋转到位置DC，∴CD＝AB＝3.5m，OD＝OA＝3m，CH＝0.3m，∴OC＝0.5m，∴＝，∴DG＝1.8m，∵OE＝0.6m，∴栏杆D端离地面的距离为1.8+0.6＝2.4m．故答案为：2.4．14．【分析】连接OD，根据菱形的性质、勾股定理求出OD，根据三角形中位线定理得到∠AOE＝∠ACD，根据余切的定义计算，得到答案．【解答】解：连接OD，∵四边形ABCD为菱形，∴OD⊥AC，OA＝OC＝AC＝2，由勾股定理得，OD＝＝＝，∵O、E分别是AC、AD的中点，∴OE∥CD，∴∠AOE＝∠ACD，∴cot∠AOE＝cot∠ACD＝＝＝，故答案为：．15．【分析】延长AD和BC交于点E，在直角△ABE中利用三角函数求得BE的长，则EC 的长即可求得，然后在直角△CDE中利用三角函数的定义求解．【解答】解：延长AD和BC交于点E．∵在直角△ABE中，tan A＝＝，AB＝3，∴BE＝4，∴EC＝BE﹣BC＝4﹣2＝2，∵△ABE和△CDE中，∠B＝∠EDC＝90°，∠E＝∠E，∴∠DCE＝∠A，∴直角△CDE中，tan∠DCE＝tan A＝＝，∴设DE＝4x，则DC＝3x，在直角△CDE中，EC2＝DE2+DC2，∴4＝16x2+9x2，解得：x＝，则CD＝．故答案是：．16．【分析】r的长即为斜边AB上的高，由勾股定理易求得AB的长，根据直角三角形面积的不同表示方法，即可求出r的值．【解答】解：Rt△ABC中，∠C＝90°，AC＝3，BC＝4；由勾股定理，得：AB2＝32+42＝25，∴AB＝5；又∵AB是⊙C的切线，∴CD⊥AB，∴CD＝r；∵S△ABC＝AC•BC＝AB•r，∴r＝，故答案为：．17．【分析】根据相似三角形的判定定理得到△DEF∽△ABC，根据三角形的面积公式计算，得到答案．【解答】解：如图，在△DEF中，DE＝，EF＝2，DF＝，则＝，＝＝，＝＝，∴＝＝，∴△DEF∽△ABC，△DEF的面积＝×2×1＝1，故答案为：1．18．【分析】只要证明△ABD∽△MBE，得＝，只要求出BM、BD即可解决问题．【解答】解：∵AB＝AC，∴∠ABC＝∠C，∵∠DAC＝∠ACD，∴∠DAC＝∠ABC，∵∠C＝∠C，∴△CAD∽△CBA，∴＝，∴＝，∴CD＝，BD＝BC﹣CD＝，∵∠DAM＝∠DAC＝∠DBA，∠ADM＝∠ADB，∴△ADM∽△BDA，∴＝，即＝，∴DM＝，MB＝BD﹣DM＝，∵∠ABM＝∠C＝∠MED，∴A、B、E、D四点共圆，∴∠ADB＝∠BEM，∠EBM＝∠EAD＝∠ABD，∴△ABD∽△MBE，（不用四点共圆，可以先证明△BMA∽△EMD，推出△BME∽AMD，推出∠ADB＝∠BEM也可以！）∴＝，∴BE＝＝1．故答案为：1．三．解答题（共7小题，满分78分）19．【分析】代入特殊角的三角函数值即可．【解答】解：原式＝3×﹣+×+＝﹣2+2+﹣1＝2﹣1．20．【分析】（1）首先作∠BCD的平分线，然后作BE的垂直平分线即可；（2）首先判定△GEF∽△GCD，然后根据AB：BC＝3：2，得＝＝，进而得出EF＝CD，CG＝CE，最后根据向量运算即可得结论，即可画出分向量．【解答】解：（1）作∠BCD的平分线，交边AB于点E，取线段BE的中点F，联结DF 交CE于点G．作图如下：（2）∵CE为∠BCD的平分线，∴∠BCE＝∠DCE又∵AB∥CD∴∠DCE＝∠BEC∴△GEF∽△GCD∵AB：BC＝3：2∴＝＝∴EF＝CD，CG＝CE∵＝，＝，∴＝＝，＝＝∵+＝，＝﹣﹣∴＝﹣（+）＝﹣（+）＝﹣﹣同理可得，＝﹣＝（+）＝（﹣）＝﹣）在向量和方向上的分向量，如图所示：故答案为：＝．21．【分析】（1）如图2中，作BO⊥DE于O．解直角三角形求出OD即可解决问题．（2）过C作CG⊥BH，CK⊥DE，由题意得，BC＝CD＝20m，CG＝KH，解直角三角形即可得到结论．【解答】解：（1）如图2中，作BO⊥DE于O．∵∠OEA＝∠BOE＝∠BAE＝90°，∴四边形ABOE是矩形，∴∠OBA＝90°，∴∠DBO＝150°﹣90°＝60°，∴OD＝BD•sin60°＝20（cm），∴DE＝OD+OE＝OD+AB＝（20+5）cm；（2）过C作CG⊥BH，CK⊥DE，由题意得，BC＝CD＝20m，CG＝KH，∴在Rt△CGB中，sin∠CBH＝，∴CG＝10cm，∴KH＝10cm，∵∠BCG＝90°﹣60°＝30°，∴∠DCK＝150°﹣90°﹣30°＝30°，在Rt△DCK中，sin∠DCK＝＝＝，∴DK＝10cm，∴（20+5）﹣（15+10）＝10﹣10，答：比原来降低了（10﹣10）厘米．22．【分析】（1）直接利用垂径定理结合平行线分线段成比例定理得出DH＝HC，进而得出答案；（2）过点A作AG⊥BC，垂足为点G，再利用已知结合勾股定理得出答案．【解答】（1）证明：过点O作OH⊥DC，垂足为H．∵AD∥BC，∠ADC＝90°，OH⊥DC，∴∠BCN＝∠OHC＝∠ADC＝90°．∴AD∥OH∥BC．又∵OA＝OB．∴DH＝HC．∵OH⊥DC，OH过圆心，∴EH＝HF，∴DH﹣EH＝HC﹣HF．即：DE＝CF．（2）解：过点A作AG⊥BC，垂足为点G，∠AGB＝90°，∵∠AGB＝∠BCN＝90°，∴AG∥DC．∵AD∥BC，∴AD＝CG．∵AD＝2，BC＝4，∴BG＝BC﹣CG＝2．在Rt△AGB中，∵tan B＝3，∴AG＝BG•tan B＝2×3＝6．在Rt△AGB中，AB2＝AG2+BG2∴AB＝．23．【分析】在Rt△ABD中可得出BD＝，在Rt△ABC中，可得BC＝，则可得BD﹣BC＝13，求出AB即可．【解答】解：由题意得，∠ABD＝90°，∠D＝20°，∠ACB＝31°，CD＝13，在Rt△ABD中，∵tan∠D＝，∴BD＝＝，在Rt△ABC中，∵tan∠ACB＝，∴BC＝＝，∵CD＝BD﹣BC，∴13＝，解得AB≈11.7米．答：水城门AB的高为11.7米．24．【分析】（1）设抛物线的表达式为y＝ax2+bx+c，将A，B的坐标及对称轴方程代入即可；（2）分别求出点B，C的坐标，直接在Rt△OBC中，根据余切定义即可求出；（3）设点E的坐标是（x，0），求出点E的坐标，再求出CE的解析式，即可求出其与抛物线的交点坐标．【解答】解：（1）设抛物线的表达式为y＝ax2+bx+c，将点C（0，2）、A（﹣3，0）、对称轴直线x＝﹣2代入，得：，解得：，，∴这条抛物线的表达式为；（2）令y＝0，那么，解得x1＝﹣3，x2＝﹣1，∵点A的坐标是（﹣3，0），∴点B的坐标是（﹣1，0），∵C（0，2），∴OB＝1，OC＝2，在Rt△OBC中，∠BOC＝90°，∴；（3）设点E的坐标是（x，0），得OE＝|x|．∵∠CEO＝∠BCO，∴cot∠CEO＝cot∠BCO，在Rt△EOC中，∴，∴|x|＝4，∴点E坐标是（4，0）或（﹣4，0），∵点C坐标是（0，2），∴，∴，或解得和（舍去），或和（舍去）；∴点P坐标是（，）或（，）．25．【分析】（1）根据等腰三角形的性质得到∠B＝∠C，根据三角形的外角性质得到∠BAD ＝∠CDE，得到△BAD∽△CDE，根据相似三角形的性质证明结论；（2）证明DF∥AB，根据平行线的性质得到＝，证明△BDA∽△BAC，根据相似三角形的性质列式计算，得到答案；（3）分点F在DE的延长线上、点F在线段DE上两种情况，根据等腰三角形的性质计算即可．【解答】（1）证明：∵AB＝AC，∴∠B＝∠C，∠ADC＝∠BAD+∠B，∠ADE＝∠B，∴∠BAD＝∠CDE，又∠B＝∠C，∴△BAD∽△CDE，∴＝，即AB•CE＝BD•CD；（2）解：∵DF平分∠ADC，∵∠CDE＝∠BAD，∴∠ADE＝∠BAD，∴DF∥AB，∴＝，∵∠BAD＝∠ADE＝∠B，∴∠BAD＝∠C，又∠B＝∠B，∴△BDA∽△BAC，∴＝，即＝解得，BD＝，∴＝，解得，AE＝；（3）解：作AH⊥BC于H，∵AB＝AC，AH⊥BC，∴BH＝HC＝BC＝8，由勾股定理得，AH＝＝＝6，∴tan B＝＝，∴tan∠ADF＝＝，设AF＝3x，则AD＝4x，由勾股定理得，DF＝＝5x，∵△BAD∽△CDE，∴＝，当点F在DE的延长线上，F A＝FE时，DE＝5x﹣3x＝2x，∴＝，解得，CD＝5，当EA＝EF时，DE＝EF＝2.5x，∴＝，解得，CD＝，∴BD＝BC﹣CD＝；当AE＝AF＝3x时，DE＝x，∴＝，解得，CD＝，∴BD＝BC﹣CD＝；当点F在线段DE上时，∠AFE为钝角，∴只有F A＝FE＝3x，则DE＝8x，∴＝，解得，CD＝20＞16，不合题意，∴△AEF是等腰三角形时，BD的长为11或或．。

word完整版2020年上海静安初三数学一模试卷及答案

E
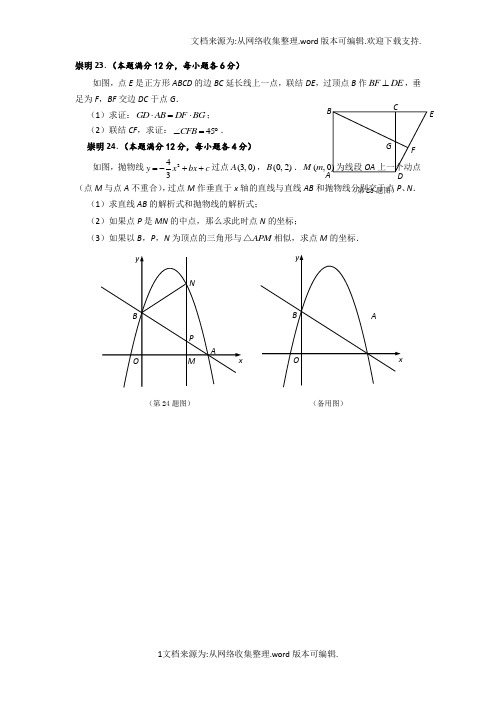
B C F7图4分）4分，第（3）小题（本题满分12分，其中第（1）小题4分，第（2）小题24．2c?bxy?ax?xOy、、b是常数，且c在平面直角坐标系（其中中（如图8a），已知二次函数．AB、AC（、C3，0），联结A0）的图像经过点（0，-3）、B（1，0）a≠1）求这个二次函数的解析式；（y
（C）向左平移4个单位，向上平移5个单位；
（D）向右平移4个单位，向下平移5个单位．
1
4分，满分48分）二、填空题：（本大题共12题，每题2??5xx．7．因式分解：▲
)3f(1(x)?3x?f．．已知=，那么▲8 11x??▲．的根为9．方程 2x?1 3x3x??．10．已知：，那么=▲，且y≠4 4y4y? ．AG=▲AC上的中线AD、BE相交于点G，AD=6，那么11．在△ABC中，边BC、B
M
（2的方向航行，那么该轮船）如果轮船M沿着南偏东30°AB靠岸？请说明理由．能否行至码头≈0.927，0.375（参考数据：sin22°≈，cos22°3≈tan22°0.404，≈1.732．）l
B
A
C
6图
3
分））小题6分，第（2）小题623．（本题满分12分，其中第（1的延长线与AE，点E在线段OB上，与，在梯形ABCD中，AD//BC，ACBD相交于点O如图72．=OB·OEBC相交于点F，OD（1）求证：四边形AFCD是平行四边形；A D，求证：△ABE∽△ACD．=BD，AE·AF=AD·BF（2）如果BCO
（1）找出图中与△ACD相似的三角形，并说明理由；
（2）当DF平分∠ADC时，求DG:DF的值；
（3）如图10，当∠BAC=90°，且DF⊥AE时，求DG:DF的值．
AA
FF

【精品】2020年上海普陀区初三数学一模试卷及答案

78 分）
19．解：原式
2 ( 3)2 1
2
2 ···································································（ 4 分）
( 3) 2 4 2
2
31
2 2 ······················································································（ 3 分） 3 22
．
y y5
2．下列二次函数中，如果函数图像的对称轴是
y 轴，那么这个函数是（ ▲ ）
（ A ） y x2 2x ；（B ） y x2 2 x 1；（C） y x2 2 ；（D ） y ( x 1)2 ．
1 3．已知在 Rt△ ABC 中， C 90 ， sin A ，那么下列说法中正确的是（
3
A
A
A
D
D
B
图6
C
C
17．如图 7，在四边形 ABCD 中， ABC
O B 图8
B 图7
90 ，对角线 AC 、 BD 交于点 O ， AO
C
CO ，
CD BD ，如果 CD 3 ， BC 5 ，那么 AB
▲．
18．如图 8，在 Rt△ ABC 中， C 90 ， AC 5 ，sin B 5 ，点 P 为边 BC 上一点， PC 3 ， 13
∵ DE 5 ，∴ BF 5 ． ·····································································（ 1 分）
∵ DE // BC ，

2024届上海初三一模数学各区23题几何证明题

图9第23题图上海市2024届初三一模数学分类汇编—23题几何证明题【2024届·宝山区·初三一模·第23题】1.（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图9，在正方形ABCD 中，点E 、F 分别在边CD 、BC 上，且CE BF ，DF 分别交AE 、AC 于点P 、Q ．（1）求证：AE DF ；（2）求证：AQ BF DF．【2024届·崇明区·初三一模·第23题】2.（本题满分12分，第（1）小题6分，第（2）小题6分）如图，已知在梯形ABCD 中，//AD BC ，E 是边BC 上一点，AE 与对角线BD 相交于点F ，且2BEEF AE ．（1）求证：DAB AFB ∽；（2）联结AC ，与BD 相交于点O ，若AB OB BC AF ，求证：2AF OD BF ．图123.（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图10，在ABC 中，AB AC ，点D 在边BC 上，已知AFD B ，边DF 交AC 于点E ．（1）求证：AF CE CD FE ；（2）联结AD ，如果AB BC AF DF，求证：2AD AE AC ．【20244.如图12ADC ，2DE DF （1）（2）第23题图图9（本题满分4分）5.（本题满分12分，第（1）小题6分，第（2）小题6分）如图，在平行四边形ABCD 中，AC AD ，过点A 作AE BD ，垂足为E ，再过点C 作CF CD 交直线AE 于点F ．（1）求证：CA CD CB CF ；（2）联结CE ，求证：ACE F ．【2024届·嘉定区·初三一模·第23题】6.（本题满分12分，第（1）小题6分，第（2）小题6分）如图9，在ABC 中，90ACB ，点D 是BC 延长线上一点，点E 是斜边AB 上一点，BC BDBE BA ．（1）求证：AB ED ；（2）联结AD ，在AB 上取一点F ，使AF AC ，过点F 作//FG BC 交AD 于点G ．求证：FG DE ．第23题图第23题图7.（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在四边形ABCD 中，对角线AC 和BD 相交于点O ，BAC BDC ．（1）求证：AOD BOC ∽；（2）过点A 作//AE CD ，AE 交BD 于点E ，求证：AB AD AE BC ．【2024届·静安区·初三一模·第23题】8.（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在ABC 中，AB AC ，D 是BC 中点，点E 在BA 延长线上，点F 在AC 边上，EDF B ．（1）求证：BDE CFD ∽；（2）求证：2DF EF CF ．9.（本题满分12分，第（1）小题6分，第（2）小题6分）如图，在ABC 中，点D 、E 在边AB 上，2AC AD AB ，AC AE ，过点D 作//DF CE 交边AC于点F ．（1）求证：ACD ABC ∽；（2）求证：AE EB AB FC ．【202410.．（1）（2）图11第23题图11.（本题满分12分，第（1）小题5分，第（2）小题7分）已知：如图11，在ABC 中，点D 在边BC 上，ADE B ，EAF FDC ，DE 与AC 交于点F ．（1）求证：AB ADAC AE；（2）联结BF ，如果2AB AF AC ，求证：AD BC AE BF ．【2024届·青浦区·初三一模·第23题】12.（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在ABC 中，点D 、E 分别在边BC 、AB 上，AD 与CE 相交于点F ，CD CF ，2AC AE AB ．（1）求证：ABD ACF ∽；（2）如果2CFD ACF ，求证：AB EF AD AE ．第23题图第23题图13.（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在ABC 中，点D 、E 分别在边AB 、AC 上，//DE BC ，BDC DEC ．（1）求证：ADE ACD ∽；（2）求证：22CD AEBC AC．【2024届·徐汇区·初三一模·第23题】14.（本题满分12分）如图，在ABCD 中，点E 在边AB 上，2DEAE CD ．（1）求证：AD CD CE DE ；（2）当点E 是边AB 的中点时，分别延长DE 、CB 交于点F ，求证：222AB EF ．第23题图第23题图15.（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在等腰梯形ABCD 中，//AD BC ，AB CD ，点E 在边AB 上，AC 与DE 交于点F ，ADE DCA ．（1）求证：AF AC AE CD ；（2）如果点E 是边AB 的中点，求证：22AB DF DE ．【2024届·长宁区·初三一模·第23题】16.（本题满分12分，第（1）小题5分，第（2）小题7分）如图，在ABC 中，点D 、E 分别是BC 、AD 的中点，且AD AC ，联结CE 并延长交AB 于点F ．（1）求证：ABC DCE ∽；（2）求证：4BF EF ．。

2020年上海市青浦区初三中考一模数学试卷及答案 Word含解析

2020年上海市青浦区初三一模数学试卷数学试卷 2020.1（完成时间：100分钟满分：150分）考生注意：1．本试卷含三个大题，共25题．答题时，考生务必按答题要求在答题纸规定的位置上作答，在草稿纸、本试卷上答题一律无效．2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或计算的主要步骤．一、选择题：（本大题共6题，每小题4分，满分24分）[每题只有一个正确选项，在答题纸相应题号的选项上用2B 铅笔正确填涂] 1．如果两个相似三角形对应边之比是1∶2，那么它们的对应高之比是（）A ．1∶2；B ．1∶4；C ．1∶6；D ．1∶8．2．如图，DE ∥AB ，如果CE ∶AE =1∶2，DE =3，那么AB 等于（）A ．6；B ．9；C ．12；D ．13．3．在Rt △ABC 中，∠C =90º，AC =1，AB =3，则下列结论正确的是（）A ．sin B =B ．cos 4B =； C．tan 4B =； D ．cot 4=B ．4．已知非零向量a 、b ，且有2=-a b ，下列说法中，不正确的是（）A ．||2||=a b ；B ． a ∥b ；C ．a 与b 方向相反；D ．20a b +=． 5．如图，在△ABC 中，点D 在边BC 上，点G 在线段AD 上，GE ∥BD ，且交AB 于点E ，GF ∥AC ，且交CD 于点F ，则下列结论一定正确的是（） A ．=AE CFAB CD； B ．=AE DFEB FC； C ．=EG FGBD AC； D ．=AE ADAG AB．6．抛物线2(0)y ax bx c a =++≠上部分点的横坐标x ，纵坐标y 的对应值如下表，那么下列结论中正确的是（）A ．0a >；B ．0b <；C ．0c <；D ．0abc <．二、填空题：（本大题共12题，每小题4分，满分48分） [请将结果直接填入答题纸的相应位置] 7．已知25a b =，那么ab a-的值为 ▲ ． 8．已知线段AB =2，P 是AB 的黄金分割点，且AP > BP ，那么AP= ▲ ．ECAGFEDCBA（第2题图）（第5题图）B 349．已知向量a 与单位向量e 方向相反，且3a =，那么a = ▲ ．（用向量e 的式子表示） 10．如果抛物线21y ax =-的顶点是它的最低点，那么a 的取值范围是 ▲ ．11．如果点A （-3，1y ）和点B （-2，2y ）是抛物线2y x a =+上的两点，那么1y ▲ 2y ．（填“>”、“=”、“<”）． 12．某公司10月份的产值是100万元，如果该公司第四季度每个月产值的增长率相同，都为)0>x x （，12月份的产值为y 万元，那么y 关于x 的函数解析式是 ▲ ． 13．在△ABC 中，∠C =90°，如果tan B =2，AB =4，那么BC = ▲ ．14．小明沿着坡度i =1∶2.5的斜坡前行了29米，那么他上升的高度是 ▲米． 15．点G 是△ABC 的重心，如果AB =AC =5，BC =8，那么AG = ▲ ． 16．如图，在菱形ABCD 中，O 、E 分别是AC 、AD 的中点，联结OE ．如果AB =3，AC =4，那么cot ∠AOE = ▲ ．17．在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请在边长为1个单位的2×3的方格纸中，找出一个格点三角形DEF ．如果△DEF 与△ABC 相似（相似比不为1），那么△DEF 的面积为 ▲ ．18．已知，在矩形纸片ABCD 中，AB =5cm ，点E 、F 分别是边AB 、CD 的中点，折叠矩形纸片ABCD ，折痕BM 交AD 边于点M ，在折叠的过程中，如果点A 恰好落在线段EF 上，那么边AD 的长至少是 ▲ cm ．三、解答题（本大题共7题，满分78分）[请将解题过程填入答题纸的相应位置] 19．（本题满分10分）计算：13tan 3045cos60︒︒︒-+20．（本题满分10分, 第（1）小题5分，第（2）小题5分）如图，在平行四边形ABCD 中，E 为DC 上一点，AE 与BD 交于点F ，DE ∶EC=2∶3．（1）求BF ∶DF 的值；（2）如果AD a =，AB b =，试用a 、b 表示向量AF ．21．（本题满分10分, 第（1）小题5分，第（2）小题5分）如图，在Rt △ABC 中，∠ACB =90º，AC =2，BC =3．点D 为AC 的中点，联结BD ，过点C 作CG ⊥BD ，交AC 的垂线AG 于点G ，GC 分别交BA 、 BD 于点F 、E ．（1）求GA 的长；FE D CBAG F ED CBACBAABCDE O（第20题图）（第17题图）（第16题图）（2）求△AFC 的面积．22．（本题满分10分）水城门位于淀浦河和漕港河三叉口，是环城水系公园淀浦河梦蝶岛区域重要的标志性景观．在课外实践活动中，某校九年级数学兴趣小组决定测量该水城门的高．他们的操作方法如下：如图，先在D 处测得点A 的仰角为20°，再往水城门的方向前进13米至C 处，测得点A 的仰角为 31°（点D 、C 、B 在一直线上），求该水城门AB 的高．（精确到0.1米）（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60 23．（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在△ABC 中，点D 在边BC 上，AE ∥BC ，BE 与AD 、AC 分别相交于点F 、G ， 2AF FG FE =⋅．（1）求证：△CAD ∽△CBG ；（2）联结DG ，求证：DG AE AB AG ⋅=⋅．24．（本题满分12分，其中第（1）小题4分，第（2）小题5分，第（3）小题3分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A 、B 两点，与y 轴交于点C ，对称轴为直线x =2，点A 的坐标为（1，0）．（1）求该抛物线的表达式及顶点坐标；（2）点P 为抛物线上一点（不与点A 重合），联结PC ．当∠PCB=∠ACB 时，求点P 的坐标；（3）在（2）的条件下，将抛物线沿平行于y 轴的方向向下平移，平移后的抛物线的顶点为点D ，点P 的对应点为点Q ，当OD ⊥DQ 时，求抛物线平移的距离．25．（本题满分14分，其中第（1）小题4分，第（2）小题6分，第（3）小题4分）如图，在梯形ABCD 中，AD ∥BC ，BC=BD=10，CD=4，AD=6．点P 是线段BD 上的动点，点E 、QAlEFGD CBA（第22题图）（第23题图）（第24题图）（备用图）（第21题图）分别是线段DA 、BD 上的点，且DE=DQ=BP ，联结EP 、EQ ．（1）求证：EQ ∥DC ；（2）当BP>BQ 时，如果△EPQ 是以EQ 为腰的等腰三角形，求线段BP 的长；（3）当BP=m （0<m<5）时，求∠PEQ 的正切值．（用含m 的式子表示）青浦区2019学年第一学期期终学业质量调研九年级数学试卷参考答案及评分说明2020.1一、选择题：1．A ； 2．B ； 3．C ； 4．D ； 5．A ； 6．D ．二、填空题： 7．23； 81； 9．3-e ； 10．0>a ； 11．>； 12．()21001=+y x ； 13； 14． 15．2； 16； 17．1； 18．三、解答题：19．解：原式=131322⨯-． ······················································· （8分）1． ······················································································ （1分）=1． ······································································································· （1分）20．解：（1）∵四边形ABCD 是平行四边形，∴DC//AB ，DC=AB ， ························································································ （2分） ∴=BF ABDF DE． ······························································································· （1分） ∵DE ∶EC =2∶3，∴DC ∶DE =5∶2，∴AB ∶DE =5∶2， ····························· （1分） ∴BF ∶DF=5∶2． ····························································································· （1分）（2）∵BF ∶DF=5∶2，∴57=BF BD ． ······························································· （1分） ∵=-BD AD AB ，∴=-BD a b ． ·························································· （1分）AB CDE QPDCBA（第25题图）（备用图）∴555777==-BF BD a b ． ········································································· （1分） ∵=+AF AB BF ，∴55527777=+-=+AF b a b a b ． ························· （2分）21．解：（1）∵∠ACB =90°，∴∠BCE +∠GCA =90°．∵CG ⊥BD ，∴∠CEB =90°，∴∠CBE +∠BCE =90°，∴∠CBE =∠GCA ． ··························································································· （2分）又∵∠DCB =∠GAC= 90°，∴△BCD ∽△CAG ． ························································································ （1分） ∴CD BCAG CA=， ······························································································· （1分） ∴132AG =，∴23AG =． ············································································ （1分）（2）∵∠GAC +∠BCA =180°，∴GA ∥BC ． ······················································· （1分）∴GA AFBC FB=． ····························································································· （1分） ∴29AF FB =． ·································································································· （1分） ∴211AF AB =．∴211AFC ABCS S =． ··································································· （1分）又∵12332ABCS=⨯⨯=，∴611AFC S =． ··········································· （1分） 22．解：由题意，得∠ABD =90°，∠D =20°，∠ACB =31°，CD =13． ··························· （1分）在Rt △ABD 中，∵tan ∠=AB D BD ，∴tan 200.36==︒AB ABBD ． ······················· （3分）在Rt △ABC 中，∵tan ∠=AB ACB BC ，∴tan 310.6==︒AB ABBC ． ···················· （3分） ∵CD =BD -BC ， ∴130.360.6=-AB AB． ···························································································· （1分）解得11.7≈AB 米． ······························································································ （1分）答：水城门AB 的高约为11.7米． ········································································ （1分）23．证明：（1）∵2AF FG FE =⋅，∴=AF FEFG AF． ························································ （1分）又∵∠AFG =∠EFA ，∴△FAG ∽△FEA ． ······················································· （1分） ∴∠FAG =∠E ． ······························································································· （1分） ∵AE ∥BC ，∴∠E =∠EBC ． ··········································································· （1分） ∴∠EBC =∠FAG ． ·························································································· （1分）又∵∠ACD =∠BCG ，∴△CAD ∽△CBG ． ·················································· （1分）（2）∵△CAD ∽△CBG ，∴=CA CDCB CG． ···························································· （1分）又∵∠DCG =∠ACB ，∴△CDG ∽△CAB ． ·················································· （1分） ∴=DG CGAB CB． ····························································································· （1分） ∵AE ∥BC ，∴=AE AGCB GC． ········································································· （1分） ∴=AG GC AE CB ，∴=DG AGAB AE， ································································· （1分） ∴⋅=⋅DG AE AB AG ． ·············································································· （1分）24．解：（1）∵A 的坐标为（1，0），对称轴为直线x =2，∴点B 的坐标为（3，0） ··· （1分）将A （1，0）、B （3，0）代入2+=+y x bx c ，得10930.，++=⎧⎨++=⎩b c b c 解得：43.，=-⎧⎨=⎩b c ························································· （2分）所以，243=-+y x x ．当x =2时，2242+3=1=-⨯-y∴顶点坐标为（2，-1） ················································································ （1分）．（2）过点P 作PN ⊥x 轴，垂足为点N ．过点C 作CM ⊥PN ，交NP 的延长线于点M ．∵∠CON =90°，∴四边形CONM 为矩形． ∴∠CMN =90°，CO = MN ．∵243=-+y x x ，∴点C 的坐标为（0，3）···················································· （1分）． ∵B （3，0），∴OB =OC ．∵∠COB =90°，∴∠OCB =∠BCM = 45°， ···················· （1分）．又∵∠ACB =∠PCB ，∴∠OCB -∠ACB =∠BCM -∠PCB ，即∠OCA =∠PCM ． ····· （1分）． ∴tan ∠OCA= tan ∠PCM ．∴13=PMMC．设PM =a ，则MC =3a ，PN =3-a ． ∴P （3a ，3-a ）．······························································································· （1分）将P （3a ，3-a ）代入243=-+y x x ，得()231233-+=-a a a ．解得111=9a ，2=0a （舍）．∴P （113，169）． ···················································· （1分）（3）设抛物线平移的距离为m ．得()221=---y x m ，∴D 的坐标为（2，1--m ）． ···················································································· （1分）过点D 作直线EF ∥x 轴，交y 轴于点E ，交PQ 的延长线于点F ． ∵∠OED =∠QFD =∠ODQ =90°，∴∠EOD+∠ODE = 90°，∠ODE+∠QDF = 90°， ∴∠EOD =∠QDF ，······························································································· （1分）∴tan ∠EOD = tan ∠QDF ．∴=DE QF OE DF ．∴1612911123-++=+-m mm ．解得15=m ．所以，抛物线平移的距离为15． ························································· （1分）25．解：（1）∵AD//BC ，∴∠EDQ =∠DBC ．········································································ （1分）∵1=DE DQ ，1=BDBC，∴=DE BD DQ BC ． ······················································ （1分） ∴△DEQ ∽△BCD ． ························································································ （1分） ∴∠DQE =∠BDC ，∴EQ//CD ． ······································································· （1分）（2）设BP 的长为x ，则DQ =x ，QP =2x -10． ·············································· （1分） ∵△DEQ ∽△BCD ，∴=EQ QD DC CB ，∴25=EQ x ． ································· （1分）（i ）当EQ =EP 时，∴∠EQP =∠EPQ ，∵DE =DQ ，∴∠EQP =∠QED ，∴∠EPQ =∠QED ，∴△EQP ∽△DEQ ，∴EQ QP DE EQ =，∴()222105x x x ⎛⎫=-⋅ ⎪⎝⎭，解得 12523x =，或0x =（舍去）． ······························································ （2分）（ii ）当QE =QP 时， ∴22105x x =-，解得 254x =， ······························································· （1分）。

2020年-上海中考数学一模-23题合集

上海中考数学一模-2020年-23题合集1．（2020•黄浦区一模）已知：如图，在平行四边形ABCD 中，过点C 分别作AD 、AB 的垂线，交边AD 、AB 延长线于点E 、F ．（1）求证：AD DE AB BF = ；（2）联结AC ，如果CF AC DE CD =，求证：22AC AF BC BF=．2．（2020•静安区一模）如图，在梯形ABCD 中，//AD BC ，AC 与BD 相交于点O ，点E 在线段OB 上，AE 的延长线与BC 相交于点F ，2OD OB OE = ．（1）求证：四边形AFCD 是平行四边形；（2）如果BC BD =，AE AF AD BF = ，求证：ABE ACD ∆∆∽．3．（2020•宝山区一模）如图，ABC∆中，AB AC=，AM为BC边的中线，点D在边AC上，联结BD交AM于点F，延长BD至点E，使得BD ADDE DC=，联结CE．求证：（1）2ECD BAM∠=∠；（2）BF是DF和EF的比例中项．4．（2020•安徽一模）如图，在ABC∆中，BD是AC边上的高，点E在边AB上，联结CE交BD于点O，且AD OC AB OD=，AF是BAC∠的平分线，交BC于点F，交DE于点G．求证：（1）CE AB⊥；（2）AF DE AG BC=．5．（2020•普陀区一模）已知：如图，四边形ABCD 的对角线AC 、BD 相交于点O ，AOD BOC S S ∆∆=．（1）求证：DO CO OB OA=；（2）设OAB ∆的面积为S ，CD k AB =，求证：2(1)ABCD S k S =+四边形．6．（2020•青浦区一模）已知：如图，在ABC ∆中，点D 在边BC 上，//AE BC ，BE 与AD 、AC 分别相交于点F 、G ，2AF FG FE = ．（1）求证：CAD CBG ∆∆∽；（2）联结DG ，求证：DG AE AB AG = ．7．（2020•浦东新区一模）如图，已知ABC ∆和ADE ∆，点D 在BC 边上，DA DC =，ADE B ∠=∠，边DE 与AC 相交于点F ．（1）求证：AB AD DF BC = ；（2）如果//AE BC ，求证：BD DF DC FE =．8．（2020•崇明区一模）如图，ABC ∆中，AD BC ⊥，E 是AD 边上一点，连接BE ，过点D 作DF BE ⊥，垂足为F ，且AE DF EF CD = ，联结AF 、CF ，CF 与边AD 交于点O ．求证：（1）EAF DCF ∠=∠；（2）AF BD AC DF = ．9．（2020•长宁金山区一模）如图，在ABC∆中，点D、E分别在边AB、BC上，AE与CD 交于点F，若AE平分BAC∠，AB AF AC AE=．（1）求证：AFD AEC∠=∠；（2）若//EG CD，交边AC的延长线于点G，求证：CD CG FC BD=．10．（2020•杨浦区一模）如图，已知在ABC∆中，AD是ABC∆的中线，DAC B∠=∠，点E 在边AD上，CE CD=．（1）求证：AC BD AB AD=；（2）求证：22AC AE AD= ．11．（2020•徐汇区一模）如图，在ABC ∆中，点D ，E ，F ，G 分别在AB 、AC 、BC 上，3AB AD =，2CE AE =，BF FG CG ==，DG 与EF 交于点H ．（1）求证：FH AC HG AB = ；（2）联结DF ，EG ，求证：A FDG GEF ∠=∠+∠．12．（2020•虹口区一模）如图，在Rt ABC ∆中，90ACB ∠=︒，点D 是边BC 的中点，联结AD ．过点C 作CE AD ⊥于点E ，联结BE ．（1）求证：2BD DE AD = ；（2）如果ABC DCE ∠=∠，求证：BD CE BE DE = ．13．（2020•嘉定区一模）已知：如图，在ABC∆中，点D、E分别在边AB、AC上，//DE BC，ABE C∠=∠．（1）求证：2BE DE BC= ；（2）当BE平分ABC∠时，求证：BD AE BE AB=．14．（2020•奉贤区一模）如图，在平行四边形ABCD中，点E在边AD上，点F在边CB的延长线上，联结CE、EF，2CE DE CF= ．（1）求证：D CEF∠=∠；（2）联结AC，交EF于点G，如果AC平分ECF∠，求证：AC AE CB CG=．15．（2020•松江区一模）已知：如图，点D ，F 在ABC ∆边AC 上，点E 在边BC 上，且//DE AB ，2CD CF CA = ．（1）求证：//EF BD ；（2）如果AC CF BC CE = ，求证：2BD DE BA = ．16．（2020•闵行区一模）已知：如图，ABC ∆中，90ACB ∠=︒，D 在斜边AB 上，DE AC ⊥，DF BC ⊥，垂足分别为E ，F ．（1）当ACD BCD ∠=∠时，求证：四边形DECF 是正方形；（2）当BCD A ∠=∠时，求证：CD CF CA AD=．。

2020上海初三数学一模压轴题汇总各区23~25题

崇明23．（本题满分12分，每小题各6分）如图，点E 是正方形ABCD 的边BC 延长线上一点，联结DE ，过顶点B 作BF DE ⊥，垂足为F ，BF 交边DC 于点G ．（1）求证：GD AB DF BG ⋅=⋅；（2）联结CF ，求证：45CFB ∠=︒．崇明24．（本题满分12分，每小题各4分）如图，抛物线24yx bx c =-++过点(3,0)A ，(0,2)B ．(,0)M m 为线段OA 上一个动点（点N ．（（（△ B DEC G F （第24题图）（备用图）崇明25．（本题满分14分，第(1)小题4分，第(2)小题5分，第(3)小题5分）如图，已知ABC △中，90ACB ∠=︒，8AC =，4cos 5A =，D 是AB 边的中点，E 是AC 边上一点，联结DE ，过点D 作DF DE ⊥交BC 边于点F ，联结EF ．（1）如图1，当DE AC ⊥时，求EF 的长；（2）如图2，当点E 在AC 边上移动时，DFE ∠的正切值是否会发生变化，如果变化请说出变化情况；如果保持不变，请求出DFE ∠的正切值；（3）如图3，联结CD 交EF 于点Q ，当CQF △是等腰三角形时，请直接写出．．．．BF 的长．金山23. （本题满分12分，每小题6分）如图，已知在Rt △ABC 中，∠ACB=90°，AC ＞BC ，CD 是Rt △ABC 的高，E 是AC的中点，ED 的延长线与CB 的延长线相交于点F ．（1）求证：DF 是BF 和CF 的比例中项；（2）在AB 上取一点G ，如果AE ：AC=AG ：AD ，求证：EG ：CF=ED ：DF ．金山24. （本题满分12分，每小题4分）平面直角坐标系xOy 中（如图），已知抛物线23y ax bx 与y 轴相交于点C ，与x 轴正半轴相交于点A ，OAOC ，与x 轴的另一个交点为B ，对称轴是直线1x ，顶点为P ．（1）求这条抛物线的表达式和顶点P 的坐标；（2）抛物线的对称轴与x 轴相交于点M ，求∠PMC 的正切值；（3）点Q 在y 轴上，且△BCQ 与△CMP 相似，求点Q 的坐标．金山25. （本题满分14分，第（1）小题3分，第（2）小题5分，第（3）小题6分）如图，已知在△ABC 中，45,cos 5AB AC B ，P 是边AB 一点，以P 为圆心，PB 为半径的P 与边BC 的另一个交点为D ，联结PD 、AD ．（1）求△ABC 的面积；（2）设PB =x ，△APD 的面积为y ，求y 关于x 的函数关系式，并写出定义域；（3）如果△APD 是直角三角形，求PB 的长．青浦23．（本题满分12分，第（1）小题4分，第（2）小题8分）如图8，已知点D 、E 分别在△ABC 的边AC 、BC 上，线段BD 与AE 交于点F ，且CD CA CE CB ⋅=⋅．（1）求证：∠CAE ＝∠CBD ；（2）若BE AB EC AC=，求证：AB AD AF AE ⋅=⋅．青浦24．（本题满分12分，第（1）小题3分，第（2）小题43）小题5 如图9，在平面直角坐标系xOy 中，抛物线()20y ax bx c a =++>与x 轴相交于点 A （-1，0）和点B ，与y 轴交于点C ，对称轴为直线1x =．（1）求点C 的坐标（用含a 的代数式表示）；（2）联结AC 、BC ，若△ABC 的面积为6，求此抛物线的表达式；（3）在第（2）小题的条件下，点Q 为x 轴正半轴上一点，点G 与点C ，点F 与点A（第25题图1）A BC D F E B DF E C A （第25题图2）B D F EC A （第25题图3） A BDEF 图8关于点Q成中心对称，当△CGF为直角三角形时，求点Q的坐标．图9青浦25．（本题满分14分，第（1）小题5分，第（2）小题5分，第（3）小题4分）如图10，在边长为2的正方形ABCD 中，点P 是边AD 上的动点（点P 不与点A 、点 D 重合），点Q 是边CD 上一点，联结PB 、PQ ，且∠PBC ＝∠BPQ ．（1）当QD ＝QC 时，求∠ABP 的正切值；（2）设AP =x ，CQ =y ，求y 关于x 的函数解析式；（3）联结BQ ，在△PBQ 中是否存在度数不变的角，若存在，指出这个角，并求出它的度数；若不存在，请说明理由．黄浦23、（本题满分12分）如图，BD 是ABC △的角平分线，点E 位于边BC 上，已知BD 是BA 与BE 的比例中项. （1）求证：12CDE ABC ∠=∠ （2）求证：AD CD AB CE ⋅=⋅ 黄浦24、（本题满分12分）在平面直角坐标系xOy 中，对称轴为直线1x =的抛物线28y ax bx =++过点()2,0-.（1）求抛物线的表达式，并写出其顶点坐标；（2）现将此抛物线沿y 方向平移若干个单位，所得抛物线的顶点为D ，与y 轴的交点为B ,与x 轴负半轴交于点A ，过点B 作x 轴的平行线交所得抛物线于点C ，若AC BD ∥，试求平移后所得抛物线的表达式.黄浦25、（本题满分14分）如图，线段5AB =，4AD =，90A ∠=︒，DP AB ∥，点C 为射线DP 上一点，BE 平分ABC ∠交线段AD 于点E （不与端点A 、D 重合）.（1）当ABC ∠为锐角，且tan 2ABC ∠=时，求四边形ABCD 的面积；（2）当ABE △与BCE △相似时，求线段CD 的长；（3）设DC x =，DE y =，求y 关于x 的函数关系式，并写出定义域.松江23．（本题满分12分，每小题6分）已知四边形ABCD 中，∠BAD =∠BDC =90°，2BD AD BC =⋅．（1）求证：AD ∥BC ；（2）过点A 作AE ∥CD 交BC 于点E ．请完善图形并求证：2CD BE BC =⋅．松江24．（本题满分12分，每小题4分）如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++的对称轴为直线x =1，抛物线与x 轴交于A 、B 两点（点A 在点B 的左侧），且AB =4，又P 是抛物线上位于第一象限的点，直线AP 与y 轴交于点D ，与对称轴交于点E ，设点P 的横坐标为t ．（1）求点A 的坐标和抛物线的表达式；（2）当AE :EP =1:2时，求点E 的坐标；（3）记抛物线的顶点为M ，与y 轴的交点为C ，当四边形CDEM图10 Q P D C B A 备用图 A B C D E DCB A是等腰梯形时，求t 的值．松江25．（本题满分14分，第（1）小题4分，第（2）小题5分，第（3）小题5分）如图，已知△ABC 中，∠ACB =90°，AC =1，BC =2，CD 平分∠ACB 交边AB 与点D ,P 是射线CD 上一点，联结AP ．（1）求线段CD 的长；（2）当点P 在CD 的延长线上，且∠P AB =45°时，求CP 的长；（3）记点M 为边AB 的中点，联结CM 、PM ，若△CMP 是等腰三角形，求CP 的长．闵行23．（本题共2小题，每小题6分，满分12分）如图，已知在△ABC 中，∠BAC =2∠B ，AD 平分∠BAC ，DF //BE ，点E 在线段BA 的延长线上，联结DE ，交AC 于点G ，且∠E=∠C ．（1）求证：2AD AF AB =⋅；（2）求证：AD BE DE AB ⋅=⋅．闵行24．（本题共3题，每小题4分，满分12分）抛物线23(0)y ax bx a =++≠经过点A （1-，0），B （32且与y 轴相交于点C ．（1）求这条抛物线的表达式；（2）求∠ACB 的度数；（3）设点D 是所求抛物线第一象限上一点，且在对称轴的右侧，点E 在线段AC 上，且DE ⊥AC ，当△DCE 与△AOC 相似时，求点D 的坐标．闵行25．（共3小题，第（1）小题4分，第（2）小题6分）如图，在Rt △ABC 中，∠ACB =90°，AC =4，BC =3，CD 点F 在边BC 上，且∠EDA =∠FDB ，联结EF 、DC 交于点G ．（1）当∠EDF =90°时，求AE 的长；（2）CE = x ，CF = y ，求y 关于x 的函数关系式，并指出x 的取值范围；（3）如果△CFG 是等腰三角形，求CF 与CE 的比值．浦东23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）如图，已知，在锐角△ABC 中，CE ⊥AB 于点E ，点D 在边AC 上，联结BD 交CE 于点F ，且DF FB FC EF ⋅=⋅. （1）求证：BD ⊥AC ；（2）联结AF ，求证：AF BE BC EF ⋅=⋅.浦东24．（本题满分12分，每小题4分）已知抛物线y ＝ax 2＋bx ＋5与x 轴交于点A (1，0)和点B (5，0)，顶点为M ．点C 在x 轴的负半轴上，且AC ＝AB ，点D 的坐标为(0，3)，直线l 经过点C 、D ．（1）求抛物线的表达式；（2）点P 是直线l 在第三象限上的点，联结AP ，且线段CP 是线段CA 、CB 的比例中项，求tan ∠CPA 的值；（3）在（2）的条件下，联结AM 、BM ，在直线PM 上是否存在点E ，使得∠AEM =∠AMB .若存在，求出点E浦东25．（本题满分14分，其中第（1）小题4 A C E F G （备用图） A B D C （第25题图） A B D C E F G （第24题图） A （第23题图） D E F B C题5分，第（3）小题5分）如图，已知在△ABC 中，∠ACB=90°，BC =2，AC =4，点D 在射线BC 上，以点D 为圆心，BD 为半径画弧交边AB 于点E ，过点E 作EF ⊥AB 交边AC 于点F ，射线ED 交射线AC 于点G ．（1）求证：△EFG ∽△AEG ；（2）设FG =x ，△EFG 的面积为y ，求y 关于x 的函数解析式并写出定义域；（3）联结DF ，当△EFD 是等腰三角形时，请直接．．写出FG 的长度．虹口1、E 、F ，且EF⋅（1；（2=8 虹口1）小题满分4分，第（2）小题满分4分，第（3）小题满分4xOy 中，抛物线与x 轴相交于点A （-2,0）、B （4,0），与y 轴交于点C （0，-4），BC 与抛物线的对称轴相交于点D ．（1）求该抛物线的表达式，并直接写出点D 的坐标；（2）过点A 作AE ⊥AC 交抛物线于点E ，求点E 的坐标；（3）在（2）的条件下，点F 在射线AE 上，若△ADF ∽△ABC ，求点F 的坐标．虹口25．（本题满分14分，第（1）小题满分5分，第（2）小题满分5分，第（3）小题满分4分）已知AB =5，AD =4，AD ∥BM ，3cos 5B =（如图），点C 、E 分别为射线BM 上的动点（点C 、E 都不与点B 重合），联结AC 、AE ，使得∠DAE =∠BAC ，射线EA 交射线CD 于点F ．设BC =x ，AF y AC=．（1）如图1，当x =4时，求AF 的长；（2）当点E 在点C 的右侧时，求y 关于x 的函数关系式，并写出函数的定义域；（3）联结BD 交AE 于点P ，若△ADP 是等腰三角形，直接写出x 的值．普陀23. （本题满分12分）已知：如图9，四边形ABCD 的对角线AC 和BD 相交于点E ，2,AD DC DC DE DB ==⋅．求证：（1）BCE ADE ∽；（2）··AB BC BD BE =．普陀24．（本题满分12分，每小题满分各4分）如图10，在平面直角坐标系中，已知抛物线22y ax ax c +=+（其中a c 、为常数，且0a <）与x 轴交于点A ，它的坐标是()3, 0-，图9AB与y 轴交于点B ，此抛物线顶点C 到x 轴的距离为4．（1）求该抛物线的表达式；（2）求CAB ∠的正切值；（3）如果点P 是抛物线上的一点，且ABP CAO ∠=∠，试直接写出点P 的坐标．普陀25．（本题满分14分，第（1）小题满分3分，第（1）小题满分5分，第（1）小题满分6分）如图11，BAC ∠的余切值为2，AB =D 是线段AB 上的一动点（点D 不与点A B 、重合），以点D 为顶点的正方形DEFG 的另两个顶点E F 、都在射线AC 上，且点F 在点E 的右侧．联结BG ，并延长BG ，交射线EC 于点P ．（1）点D 在运动时，下列的线段和角中，______是始终保持不变的量（填序号）；①AF ； ②FP ； ③BP ； ④BDG ∠； ⑤GAC ∠； ⑥BPA ∠；（2）设正方形的边长为x ，线段AP 的长为y ，求y 与x 之间的函数关系式，并写出定义域；（3）如果PFG 与AFG 相似，但面积不相等，求此时正方形的边长．嘉定23．（本题满分12分，每小题6分）如图6，已知梯形ABCD 中，AD ∥BC ，CD AB =，点E 在对角线AC 上，且满足BAC ADE ∠=∠.（1）求证：BC DE AE CD ⋅=⋅；（2）以点A 为圆心，AB 长为半径画弧交边BC 于点F ，联结AF . 求证：CA CE AF ⋅=2.嘉定24．（本题满分12分，每小题4分）已知在平面直角坐标系xOy （如图7）中，已知抛物线c bx x y ++=232点经过)0,1(A 、)2,0(B .（1）求该抛物线的表达式；（2）设该抛物线的对称轴与x 轴的交点为C ，第四象限内的点D 在该抛物线的对称轴上，如果以点A 、C 、D 所组成的三角形与△AOB 相似，求点D 的坐标；（3）设点E 在该抛物线的对称轴上，它的纵坐标是1，联结AE 、BE ，求ABE ∠sin .嘉定25．（满分14分，第（1）小题4分，第（2）、（3）小题各5分）图6在正方形ABCD中，8=AB，点P在边CD上，43tan=∠PBC，点Q是在射线BP 上的一个动点，过点Q作AB的平行线交射线AD于点M，点R在射线AD上，使RQ始终与直线BP垂直．（1）如图8，当点R与点D重合时，求PQ的长；（2）如图9，试探索：MQRM的比值是否随点Q的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；（3）如图10，若点Q在线段BP上，设xPQ=，yRM=，求y关于x的函数关系式，并写出它的定义域．静安6中，⊥作∠，交DB（1ABE；（2）如果56BCBD=，求BCEBDASS的值．静安24.（本题满分12分，第1小题4分，第2小题8分）在平面直角坐标系xOy中（如图），已知抛物线253y ax bx=+-经过点(1,0)A-、(5,0)B．（1）求此抛物线顶点C的坐标；（2）联结AC交y轴于点D，联结BD、BC，过点C作CH BD⊥，垂足为点H，抛物线对称轴交x轴于点G，联结HG，求HG的长．静安25.（本题满分14分，第1小题4分，第2小题6分，第3小题4分）已知：如图，四边形ABCD中，090,,,BAD AD DC AB BC AC<∠≤==平分BAD∠．（1）求证：四边形ABCD是菱形；（2）如果点E在对角线AC上，联结BE并延长，交边DC于点G，交线段AD的延长线于点F（点F可与点D重合），AFB ACB∠=∠，设AB长度是a（a实常数，且0a>），,AC x AF y==，求y关于x的函数解析式，并写出定义域；（3）在第（2）小题的条件下，当CGE是等腰三角形时，求AC的长．（计算结果用含a 的代数式表示）长宁23．（本题满分12分，第（1）小题6分，第（2）小题6分）如图，在∆ABC中，点D在边BC上，联结AD，∠ADB=∠CDE，AC图8A图9A图10FEADE 交边AC 于点E ，DE 交BA 延长线于点F ，且DF DE AD ⋅=2．（1）求证：BFD ∆∽CAD ∆；（2）求证：AD AB DE BF ⋅=⋅．长宁24．（本题满分12分，每小题4分）在直角坐标平面内，直线221+=x y 分别与x 轴、y 轴交于点A 、C . 抛物线c bx x y ++-=221经过点A 与点C ，且与x 轴的另一个交点为点B . 点D 在该抛物线上，且位于直线AC 的上方．（1）求上述抛物线的表达式；（2）联结BC 、BD ，且BD 交AC 于点E ，如果∆ABE 的面积与∆ABC 的面积之比为4:5，求∠DBA 的余切值；（3）过点D 作DF ⊥AC ，垂足为点F ，联结CD . 若∆CFD 与∆AOC 相似，求点D 的坐标．长宁25．（本题满分14分，第（1）小题3分，第（2）小题6分，第（3）小题5分）已知在矩形ABCD 中，AB =2，AD =4. P 是对角线BD 上的一个动点（点P 不与点B 、D 重合），过点P 作PF ⊥BD ，交射线BC 于点F . 联结AP ，画∠FPE =∠BAP ，PE 交BF 于点E .设PD=x ，EF =y ．（1）当点A 、P 、F 在一条直线上时，求∆ABF 的面积；（2）如图1，当点F 在边BC 上时，求y 关于x 的函数解析式，并写出函数定义域；（3）联结PC ，若∠FPC =∠BPE ，请直接写出PD 的长．徐汇23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图在△ABC 中，AB =AC ，点D 、E 、F 分别在边BC 、AB 、AC 上，且∠ADE =∠B ， ∠ADF =∠C ，线段EF 交线段AD 于点G ．（1）求证：AE =AF ；（2）若DF CF DE AE =,求证：四边形EBDF 是平行四边形．徐汇24．（本题满分12分，第（1）小题满分3分，第（2）小题满分4分，第（3）小题满分5分）如图，在平面直角坐标系xOy 中，直线y =kx （k ≠0）沿着y 轴向上平移3个单位长度后，与x 轴交于点B （3,0），与y 轴交于点C ，抛物线2y x bx c =++过点B 、C 且与x轴的另一个交点为A ．（1）求直线BC 及该抛物线的表达式；（2）设该抛物线的顶点为D ，求△DBC 的面积；备用图第24题图备用图备用图图1 D CB A DC B A F E PD C B A 第25题图（3）如果点F 在y 轴上，且∠CDF =45°，求点F 的坐标．徐汇25．（本题满分14分，第（1）小题3分，第（2）小题7分，第（3）小题4分）已知，在梯形ABCD 中，AD ∥BC ，∠A =90°，AD =2，AB =4，BC =5，在射线BC 任取一点M ，联结DM ，作∠MDN =∠BDC ，∠MDN 的另一边DN 交直线BC 于点N （点N 在点M 的左侧）．（1）当BM 的长为10时，求证：BD ⊥DM ；（2）如图（1），当点N 在线段BC 上时，设BN =x ，BM =y ，求y 关于x 的函数关系式，并写出它的定义域；（3）如果△DMN 是等腰三角形，求BN 的长．杨浦23．（本题满分12分，第（1）小题5分，第（2）小题7分）已知：梯形ABCD 中，AD //BC ，AD =AB ，对角线AC 、BD 交于点E ，点F 在边BC 上，且∠BEF =∠BAC . （1）求证：△AED ∽△CFE ；（2）当EF //DC 时，求证：AE =DE .杨浦24．（本题满分12分，第（1）小题3分，第（2）小题5分，第（3）小题4分）在平面直角坐标系xOy 中，抛物线2221y x mx m m =-+--+交 y 轴于点为A ，顶点为D ，对称轴与x 轴交于点H . （1）求顶点D 的坐标（用含m 的代数式表示）；（2）当抛物线过点（1，-2），且不经过第一象限时，平移此抛物线到抛物线22y x x =-+的位置，求平移的方向和距离；（3）当抛物线顶点D 在第二象限时，如果∠ADH =∠AHO ，求m 的值.杨浦25．（本题满分14分，第（1）、（2）小题各6分，第（3）小题2分）已知：矩形ABCD 中，AB =4，BC =3，点M 、N 分别在边AB 、CD 上，直线MN 交矩形对角线AC 于点E ，将△AME 沿直线MN 翻折，点A 落在点P 处，且点P 在射线CB 上. （1）如图1，当EP ⊥BC 时，求CN 的长；（2）如图2，当EP ⊥AC 时，求AM 的长；（3）请写出线段CP 的长的取值范围，及当CP 的长最大时MN 的长.奉贤23．（本题满分 12 分，每小题满分各 6 分）已知：如图 8，四边形90ABCD DCB ∠=︒，，对角线 BD ⊥AD ，点 E 是边 AB 的中点， CE 与 BD 相交于点 F ，2·BD AB BC =．（1）求证：BD 平分⊥ABC ；（2）求证：··BE CF BC EF ＝．O x y 1 2 3 4 1 23 4 5 -1-2 -3-1 -2 -3 （第24题图）（备用图）（图1） A B C D N P M E （图2） A B C D NP M E （第25题图）A B CD （第23题图）A B C D F E奉贤24. （本题满分 12 分，每小题满分各 4 分）如图9，在平面直角坐标系xOy 中，抛物线238y x bx c =++与x 轴相交于点(2,0)A -和点B ，与y 轴相交于点(0,3)C -，经过点A 的射线AM 与y 轴相交于点E ，与抛物线的另一个交点为点F ，且13AE EF =．（1）求这条抛物线的表达式，并写出它的对称轴；（2）求FAB ∠的余切值；（3）点D 是点C 关于抛物线对称轴的对称点，点 P 是 y 轴上一点，且AFP DAB ∠=∠，求点 P 的坐标．奉贤25．（本题满分 14 分，第（1）小题满分 3 分，第（1）小题满分 5 分，第（1）小题满分 6 分）已知：如图10，在梯形ABCD 中，//,90,2AB CD D AD CD ∠===，点E 在边AD上（不与点A 、D 重合），45,CEB EB ∠=与对角线AC 相交于点F ，设DE x =．（1）用含x 的代数式表示线段CF 的长；（2）如果把CAE 的周长记作CAE C，BAF 的周长记作BAF C ，设CAEBAF Cy C =，求y 关于x 的函数关系式，并写出它的定义域；（3）当ABE ∠的正切值是35时，求AB 的长．宝山23、（满分12分，每小题各6分）如图，ABC 中，AB AC =，过点C 作//CF AB 交ABC 的中位线DE 的延长线于F ，联结BF ，交AC 于点G .（1）求证：AE EG AC CG=；（2）若AH 平分BAC ∠，交BF 于H ，求证：BH 是HG 和HF的比例中项.宝山24、（满分12分，每小题各4分）设,a b 是任意两个不等实数，我们规定：满足不等式a x b ≤≤的实数x 的所有取值的全体叫做闭区间，表示为[],a b ，对于一个函数，如果它的自变量x 与函数值y 满足：当m x n ≤≤时，有m y n ≤≤，我们就此称此函数是闭区间[],m n 上的“闭函数”。

2022年上海市15区中考数学一模考点分类汇编09 几何证明(解答题23题)(讲解版)

2022年上海市15区中考数学一模考点分类汇编专题09 几何证明一．解答题（共15小题）1．（普陀区）已知：如图，在△ABC中，点D、E分别在边AC、BC上，BD＝DC，BD•BC＝BE•AC．（1）求证：∠ABE＝∠DEB；（2）延长BA、ED交于点F，求证：．【分析】（1）由BD•BC＝BE•AC得出＝，BD＝DC得出∠DBC＝∠C，从而得出结论；（2）根据（1）的结论和已知证明△FAD∽△FDB即可．【解答】证明：（1）∵BD＝DC，∴∠DBC＝∠C，∵BD•BC＝BE•AC，∴＝，∴△ABC∽△DEB，∴∠ABC＝∠DEB，即∠ABE＝∠DEB；（2）如图所示：∵△ABC∽△DEB，∴∠CAB＝∠BDE，∴∠FAD＝∠FDB，∵∠F＝∠F，∴△FAD∽△FDB，∴＝，∵∠ABE＝∠DEB，∴FB＝FE，又∵BD＝DC，∴＝．【点评】本题考查相似三角形的判定和性质，关键是找到相似的三角形．2．（崇明区）已知：如图，在Rt△ACB中，∠ACB＝90°，CD⊥AB，垂足为点D，E为边AC上一点，联结BE交CD于点F，并满足BC2＝CD•BE．求证：（1）△BCE∽△ACB；（2）过点C作CM⊥BE，交BE于点G，交AB于点M，求证：BE•CM＝AB•CF．【分析】（1）通过证明△BCD∽△EBC，可得∠CEB＝∠CBD，可得结论；（2）通过证明△BCE∽△ACB，△ACB∽△CDB，△CDM∽△BDF，可得，，，可得结论．【解答】证明：（1）∵BC2＝CD•BE，∴，设＝k，则BC＝k•CD，BE＝k•BC，∴CE＝＝×BC，BD＝＝×CD，∴＝，又∵∠ACB＝∠CDB＝90°，∴△BCD∽△EBC，∴∠CEB＝∠CBD，又∵∠ACB＝∠BCE＝90°，∴△BCE∽△ACB；（2）如图，∵△BCE∽△ACB，∴，∵∠CEB＝∠CBA，∴∠A＝∠CBE，∵∠A+∠ABC＝90°＝∠DCB+∠CBD，∴∠A＝∠DCB，∴∠DCB＝∠EBC，∴CF＝BF，∵∠A＝∠DCB，∠CDB＝∠ACB＝90°，∴△ACB∽△CDB，∴，∵CM⊥BE，∴∠ABE+∠CMD＝90°＝∠CMD+∠MCD，∴∠MCD＝∠ABE，又∵∠CDB＝∠CDM＝90°，∴△CDM∽△BDF，∴，∴，∴BE•CM＝AB•CF．【点评】本题考查了相似三角形的判定和性质，直角三角形的性质，灵活运用相似三角形的性质是解题的关键．3．（嘉定区）如图，已知正方形ABCD和正方形BEFG，点E在边BC上，点G在边AB的延长线上，联结AE，并延长AE交CG于点K．（1）求证：△ABE∽△CKE；（2）如果CG与EF交于点H，求证：BE2＝FH•AB．【分析】（1）由“SAS”可证△ABE≌△CBG，可得∠BAE＝∠ECK，可得结论；（2）通过证明△ABE∽△GFH，可得，可得结论．【解答】证明：（1）∵四边形ABCD是正方形，∴AB＝CB，∠ABC＝90°，∵四边形BEFG是正方形，∴FG＝BG＝BE，∠CBG＝90°，∴∠ABE＝∠CBG＝90°，在△ABE和△CBG中，，∴△ABE≌△CBG（SAS），∴∠BAE＝∠ECK，又∵∠AEB＝∠CEK，∴△ABE∽△CKE；（2）由题意，得∠CEF＝∠F＝∠ABE＝90°，∴FG∥BC，∴∠ECK＝∠FGH，∵∠BAE＝∠ECK，∴∠BAE＝∠FGH，∴△ABE∽△GFH，∴，∵FG＝BE，∴，∴BE2＝FH•AB．【点评】本题考查了相似三角形的判定和性质，正方形的性质，全等三角形的判定和性质，灵活运用这些性质解决问题是解题的关键．4．（宝山区）如图，已知△ABC和△DCE都是等边三角形，点B、C、E在同一直线上，联结BD交AC边于点F．（1）如果∠ABD＝∠CAD，求证：BF2＝DF•DB；（2）如果AF＝2FC，S四边形ABCD＝18，求S△DCE的值．【分析】（1）证明△ABF≌△CAD（ASA），由全等三角形的性质可得出BF＝AD，证明△ADF∽△BDA，由相似三角形的性质得出，则可得出结论；（2）证明△DCF∽△BAF，由相似三角形的性质得出＝，设S△DCF＝x，则S△ADF＝S△BCF＝2x，S△ABF＝4x，由四边形ABCD的面积可得出x+2x+2x+4x＝18，求出x＝2，求出三角形ABC的面积，证明△ABC∽△DCE，由相似三角形的性质得出＝，则可得出结论．【解答】（1）证明：∵△ABC和△DCE都是等边三角形，∴AB＝AC，∠BAC＝∠DCE＝∠ACB＝60°，又∵∠ABD＝∠CAD，∴△ABF≌△CAD（ASA），∴BF＝AD，∵∠ADF＝∠BDA，∠ABD＝∠CAD，∴△ADF∽△BDA，∴，∴AD2＝DF•BD，∴BF2＝DF•BD；（2）解：∵∠ACB＝∠DCE＝60°，∴∠ACD＝60°，∴∠ACD＝∠BAC，∴AB∥CD，∴△DCF∽△BAF，∴＝，∴，，，设S△DCF＝x，则S△ADF＝S△BCF＝2x，S△ABF＝4x，∵S四边形ABCD＝18，∴x+2x+2x+4x＝18，解得x＝2，∴S△ABF＝8，S△BCF＝4，∴S△ABC＝S△ABF+S△BCF＝8+4＝12，∵△ABC和△DCE都是等边三角形，∴△ABC∽△DCE，∴＝，∴S△DCE＝＝×12＝3．【点评】本题考查了等边三角形的性质，相似三角形的判定与性质，全等三角形的判定与性质，证明△DCF∽△BAF是解题的关键．5．（杨浦区）已知，如图，在四边形ABCD中，∠ABC＝∠BCD，点E在边BC上，AE∥CD，DE ∥AB，过点C作CF∥AD，交线段AE于点F，联结BF．（1）求证：△ABF≌△EAD；（2）如果射线BF经过点D，求证：BE2＝EC•BC．【分析】（1）先证AB＝AE，DE＝DC，再证四边形ADCF是平行四边形，得出AF＝CD，进而得出AF＝DE，再由平行线性质得∠AED＝∠BAF，进而证得结论；（2）通过证明△BEF∽△BCD，△DEF∽△BAF，可得，即可得结论．【解答】证明：（1）∵AE∥CD，∴∠AEB＝∠BCD，∵∠ABC＝∠BCD，∴∠ABC＝∠AEB，∴AB＝AE，∵DE∥AB，∴∠DEC＝∠ABC，∠AED＝∠BAF，∵∠ABC＝∠BCD，∴∠DEC＝∠BCD，∴DE＝DC，∵CF∥AD，AE∥CD，∴四边形ADCF是平行四边形，∴AF＝CD，∴AF＝DE，在△ABF和△EAD中，，∴△ABF≌△EAD（SAS）；（2）如图，连接FD，∵射线BF经过点D，∴点B，点F，点D三点共线，∵AE∥DC，∴△BEF∽△BCD，∴，，∵DE∥AB，∴△DEF∽△BAF，∴，∴，∵CD＝AF，∴，∴BE2＝EC•BC．【点评】本题考查了相似三角形的判定和性质，全等三角形的判定和性质，平行四边形的判定和性质，利用相似三角形的性质得到线段的关系是解题的关键．6．（松江区）已知：如图，梯形ABCD中，DC∥AB，AC＝AB，过点D作BC的平行线交AC于点E．（1）如果∠DEC＝∠BEC，求证：CE2＝ED•CB；（2）如果AD2＝AE•AC，求证：AD＝BC．【分析】（1）通过证明△DEC∽△CEB，可得，可得结论；（2）通过证明△BCE∽△ACB，可得，由相似三角形的性质可得，可得，通过证明△ADE∽△ACD，可得＝，可得结论．【解答】证明：（1）∵AC＝AB，∴∠ACB＝∠ABC，∵DC∥AB，∴∠DCE＝∠CAB，∵DE∥BC，∴∠DEC＝∠BCE，∵∠DEC＝∠BEC，∴∠DEC＝∠BCE＝∠BEC＝∠ABC，∴∠BAC＝∠CBE＝∠DCE，BE＝BC，∴△DEC∽△CEB，∴，∴CE2＝DE•BE＝DE•CB；（2）∵∠BAC＝∠CBE，∠ACB＝∠BCE，∴△BCE∽△ACB，∴，∵△DEC∽△CEB，∴，∠CDE＝∠BCE＝∠CED＝∠BEC，∴，CD＝CE，∵AD2＝AE•AC，∴，又∵∠DAE＝∠DAC，∴△ADE∽△ACD，∴＝，∴，∴AD＝BC．【点评】本题考查了相似三角形的判定和性质，熟练运用相似三角形的判定是解题的关键．7．（浦东新区）如图，在△ABC和△ADE中，∠BAC＝∠DAE＝90°，∠B＝∠ADE＝30°，AC 与DE相交于点F，联结CE，点D在边BC上．（1）求证：△ABD∽△ACE；（2）若＝，求的值．【分析】（1）根据相似三角形的判定定理得到△BAC∽△DAE，根据相似三角形的性质得到，求得∠BAD＝∠CAE，根据相似三角形的判定定理得到结论；（2）根据相似三角形的性质和直角三角形的性质即可得到结论．【解答】（1）证明：∵∠ADE＝∠DAE，∠B＝∠ADE，∴△BAC∽△DAE，∴，∵∠BAC＝∠DAE，∴∠BAD＝∠CAE，∴△BAD∽△CAE；（2）解：∵△ABD∽△ACE，∴，∵∠DAE＝90°，∠ADE＝30°，∴＝，∴＝•＝＝3，∵△ADF∽△ECF，∴＝＝3．【点评】本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质定理是解题的关键．8．（徐汇区）如图，已知△ADE的顶点E在△ABC的边BC上，DE与AB相交于点F，∠FEA＝∠B，∠DAF＝∠EAC．（1）求证：AE2＝AF•AB；（2）求证：＝．【分析】（1）利用两个角相等证明△BAE∽△EAF，得，即可证明结论；（2）首先证明△DAE∽△CAB，得，∠D＝∠C，再证明△DAF∽△CAE，得，等量代换即可．【解答】证明：（1）∵∠FEA＝∠B，∠BAE＝∠EAF，∴△BAE∽△EAF，∴，∴AE2＝AF•AB，（2）∵∠DAF＝∠CAE，∠FAE＝∠FAE，∴∠DAE＝∠CAF，∵∠FEA＝∠B，∴△DAE∽△CAB，∴，∠D＝∠C，∵∠DAF＝∠EAC，∴△DAF∽△CAE，∴，∴，∴．【点评】本题主要考查了相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题的关键．9．（金山区）已知：如图，梯形ABCD中，AD∥BC，AB＝DC＝6，E是对角线BD上一点，DE＝4，∠BCE＝∠ABD．（1）求证：△ABD∽△ECB；（2）如果AD：BC＝3：5，求AD的长．【分析】（1）先由AD∥BC得到∠ADB＝∠EBC，然后由∠ABD＝∠ECB得证△ABD∽△ECB；（2）先由AB＝DC得到∠ABC＝∠BCD，再由∠∠ABD＝∠BCE得到∠DBC＝∠DCE，从而得到△DBC∽△DCE，然后利用相似三角形的性质求得BD的长，进而得到BE的长，再由△ABD∽△ECB得到AD的长．【解答】解：（1）∵AD∥BC，∴∠ADB＝∠EBC，又∵∠BCE＝∠ABD，∴△ABD∽△ECB．（2）∵梯形ABCD中，AD∥BC，AB＝DC＝6，∴∠ABC＝∠BCD，又∵∠BCE＝∠ABD，∴∠DBC＝∠DCE∵∠BDC＝∠CDE，∴△BDC∽△CDE，∴，∵DC＝6，DE＝4，∴BD＝9，∴BE＝5，∵△ABD∽△ECB，∴，由AD：BC＝3：5，设AD＝3x，BC＝5x，∴，解得：x＝或x＝﹣（舍），∴AD＝．【点评】本题考查了梯形的性质、相似三角形的判定与性质、平行线的性质，解题的关键是熟练应用等量代换得证∠DBC＝∠DCE．10．（静安区）如图，边长为1的正方形ABCD中，对角线AC、BD相交于点O，点Q、R分别在边AD、DC上，BR交线段OC于点P，QP⊥BP，QP交BD于点E．（1）求证：△APQ∽△DBR；（2）当∠QED等于60°时，求的值．【分析】（1）利用正方形的性质可得∠QAP＝∠BDR＝45°，AC⊥BD，根据已知QP⊥BP，利用同角的余角相等可得∠APQ＝∠DBR，即可解答；（2）由（1）可得△APQ∽△DBR，从而可得＝，根据已知可得∠BEP＝60°，设OE 为a，然后在Rt△OEP中，表示出OP＝a，EP＝2a，从而在Rt△BEP中求出BE＝4a，进而求出OB，然后进行计算即可解答．【解答】（1）证明：∵四边形ABCD是正方形，∴AC⊥BD，OA＝OC＝AC，OB＝OD＝BD，AC＝BD，∠QAP＝∠BDR＝45°，∴∠BOC＝∠DOC＝90°，OA＝OB，∴∠OBP+∠OPB＝90°，∵QP⊥BP，∴∠QPB＝90°，∴∠OPB+∠QPA＝90°，∴∠APQ＝∠DBR，∴△APQ∽△DBR；（2）解：由（1）可得△APQ∽△DBR，∴＝，∵∠QED＝60°，∴∠BEP＝∠QED＝60°，∴∠OPE＝90°﹣∠BEP＝30°，∴PE＝2OE，OP＝OE，设OE为a，则EP＝2a，OP＝a，在Rt△BEP中，BE＝＝＝4a，∴OB＝BE﹣OE＝4a﹣a＝3a，∴BD＝2OB＝6a，∵OA＝3a，OP＝a，∴AP＝OA+OP＝3a+a，∴＝＝，∴＝．【点评】本题考查了正方形的性质，相似三角形的判定与性质，全等三角形的判定与性质，根据题目的已知条件并结合图形分析是解题的关键．11．（虹口区）如图，在梯形ABCD中，∠ABC＝90°，AD∥BC，BC＝2AD，对角线AC与BD交于点E．点F是线段EC上一点，且∠BDF＝∠BAC．（1）求证：EB2＝EF•EC；（2）如果BC＝6，sin∠BAC＝，求FC的长．【分析】（1）先由AD∥BC得到△EAD∽△ECB，从而得到，然后由∠BDF＝∠BAC、∠AEB＝∠DEF得证△EAB∽△EDF，进而得到，最后得到结果；（2）先利用条件得到AC、AB的长，然后利用BC＝2AD得到AD、BD的长，再结合相似三角形的性质得到EB、EC的长，进而得到EF的长和FC的长．【解答】（1）证明：∵AD∥BC，∴△EAD∽△ECB，∴，即，∵∠BDF＝∠BAC，∠AEB＝∠DEF，∴△EAB∽△EDF，∴，∴，∴EB2＝EF•EC．（2）解：∵BC＝6，sin∠BAC＝＝，BC＝2AD∴AC＝9，AD＝3，∵∠ABC＝90°，AD∥BC，∴∠BAD＝90°，∴AB＝＝＝3，∴BD＝＝＝3，∵△EAD∽△ECB，∴，∴EC＝AC＝×9＝6，EB＝BD＝×3＝2，∵EB2＝EF•EC，即（2）2＝6EF，∴EF＝4，∴FC＝EC﹣EF＝6﹣4＝2．【点评】本题考查了直角梯形的性质、相似三角形的判定与性质、勾股定理，解题的关键是熟知“8”字模型相似三角形的判定与性质．12．（奉贤区）根据相似形的定义可以知道，如果一个四边形的四个角与另一个四边形的四个角对应相等，且它们各有的四边对应成比例，那么这两个四边形叫做相似四边形．对应相等的角的顶点叫做这两个相似四边形的对应顶点，以对应顶点为端点的边是这两个相似四边形的对应边，对应边的比叫做这两个相似多边形的相似比．（我们研究的四边形都是指凸四边形）（1）某学习小组在探究相似四边形的判定时，得到如下两个命题，请判断它们是真命题还是假命题（直接在横线上填写“真”或“假”）①梯形的中位线将原梯形分成的两个小的梯形相似；假命题；②有一个内角对应相等的两个菱形相似；真命题．（2）已知：如图1，△ABC是以BC为斜边的等腰直角三角形，以BC为直角边作等腰直角三角形BCD，再以BD为直角边作等腰直角三角形BDE求证：四边形ABDC与四边形CBED相似．（3）已知：如图2，在△ABC中，点D、E分别在边AB、AC上，BE、CD相交于点F，点G在AF的延长线上，联结BG、CG．如果四边形ADFE与四边形ABGC相似，且点A、D、F、E分别对应A、B、G、C．求证：AF•BF＝AG•EF．【分析】（1）根据相似多边形的定义，分别从对应边和对应角两个方面判断即可；（2）由等腰直角三角形的性质可知，两个四边形符合相似四边形的定义；（3）根据相似四边形对应角相等得，∠ADF＝∠ABG，∠AEF＝∠ACG，则CD∥BG，BE∥CG，从而证明四边形BGCF是平行四边形，有BF＝CG，再证明△EAF∽△CAG，则，等量代换即可证明结论．【解答】（1）解：①梯形的中位线将原梯形分成的两个小的梯形满足四个角对应线段，但边不是对应成比例，所以原命题是假命题；②有一个内角对应相等的两个菱形满足四个角线段，对应边成比例，所以是真命题，故答案为：假，真；（2）证明：由题意知，∠A＝∠CBE＝90°，∠ACD＝∠CDE＝135°，∠ABD＝∠BCD＝90°．∠CDB＝∠E＝45°，∴四边形ABDC与四边形CBED的四个角对应相等，设AB＝AC＝x，则CD＝x，BD＝DE＝2x，BE＝2x，∴，∴四边形ABDC与四边形CBED的四边对应成比例，∴四边形ABDC与四边形CBED相似；（3）证明：∵四边形ADFE与四边形ABGC相似，且点A、D、F、E分别对应A、B、G、C．∴∠ADF＝∠ABG，∠AEF＝∠ACG，∴CD∥BG，BE∥CG，∴四边形BGCF是平行四边形，∴BF＝CG，∵∠AEF＝∠ACG，∠EAF＝∠CAG，∴△EAF∽△CAG，∴，∴，∴AF•BF＝AG•EF．【点评】本题是相似形综合题，主要考查了相似四边形的定义，等腰直角三角形的性质，平行四边形的判定与性质，相似三角形的判定与性质等知识，读懂定义，紧扣定义中从边和角两个方面进行考虑是解题的关键．13．（青浦区）已知：如图，在四边形ABCD中，AC、BD相交于点E，∠ABD＝∠CBD，DC2＝DE•DB．（1）求证：△AEB∽△DEC；（2）求证：BC•AD＝CE•BD．【分析】（1）根据已知条件先证明△DCE∽△DBC，可得∠DCE＝∠DBC，进而可以证明结论；（2）结合（1）的结论证明△AED∽△BEC，可得∠ADE＝∠BCE，再证明△BDA∽△BCE，进而可得结论．【解答】证明：（1）∵DC2＝DE⋅DB，∴，∵∠CDE＝∠BDC，∴△DCE∽△DBC，∴∠DCE＝∠DBC，∵∠ABD＝∠DBC，∴∠DCE＝∠ABD，∵∠AEB＝∠DEC，∴△AEB∽△DEC；（2）∵△AEB∽△DEC，∴，∵∠AED＝∠BEC，∴△AED∽△BEC，∴∠ADE＝∠BCE，∵∠ABD＝∠DBC，∴△BDA∽△BCE，∴，∴BC•AD＝CE•BD．【点评】本题考查了相似三角形的判定与性质，解决本题的关键是得到△BDA∽△BCE．14．（徐汇区）如图，已知Rt△ABC中，∠ACB＝90°，射线CD交AB于点D，点E是CD上一点，且∠AEC＝∠ABC，联结BE．（1）求证：△ACD∽△EBD；（2）如果CD平分∠ACB，求证：AB2＝2ED•EC．【分析】（1）根据已知条件先证明△ADE∽△CDB，可得，因为∠ADC＝∠EDB，即可得证；（2）结合（1）证明△EAB是等腰直角三角形，进而可得结论．【解答】证明：（1）∵∠AEC＝∠ABC，∠ADE＝∠BDC，∴△ADE∽△CDB，∴，又∵∠ADC＝∠EDB，∴△ACD∽△EBD；（2）∵△ADE∽△CDB，∴∠DCB＝∠EAB，∵△ACD∽△EBD，∴∠ACD＝∠EBD，∵∠ACB＝90°，∴∠EAB+∠EBD＝∠DCB+∠ACD＝90°，∴∠AEB＝90°，∵CD平分∠ACB，∴∠ACD＝∠BCD＝45°，∴∠EBD＝∠EAB＝45°，∴EA＝EB，∴△EAB是等腰直角三角形，∴∠EAD＝∠ACE，∠AED＝∠CEA，∵△AED∽△CEA，∴＝，∴AE2＝ED•EC，∵AE2+EB2＝AB2，∴2AE2＝AB2，∴AE2＝AB2，∴AB2＝ED•EC，∴AB2＝2ED•EC．【点评】本题考查了相似三角形的判定与性质，等腰直角三角形的判定与性质，勾股定理，解决本题的关键是得到△EAB是等腰直角三角形．15．（黄浦区）已知：如图，在四边形ABCD中，AB∥CD，过点D作DF∥CB，分别交AC、AB点E、F，且满足AB•AF＝DF•BC．（1）求证：∠AEF＝∠DAF；（2）求证：＝．【分析】（1）根据DF∥CB，可得∠B＝∠AFD，根据AB•AF＝DF•BC．证明△ABC∽△DAF，进而可以解决问题；（2）由△DCE∽△FAE，可得＝，所以＝，再由△AFE∽△DFA，可得AF2＝EF•DF，由△AEF∽△ACB，得＝，进而可得结论．【解答】（1）证明：∵AB∥CD，DF∥CB，∴四边形FBCD是平行四边形，∴DC＝FB，DF＝CB，∵AB•AF＝DF•BC．∴＝，∵DF∥CB，∴∠B＝∠AFD，∴△ABC∽△DAF，∴∠ACB＝∠DAF，∵DF∥CB，∴∠AEF＝∠ACB，∴∠AEF＝∠DAF；（2）证明：∵AB∥CD，∴△DCE∽△FAE，∴＝，∴＝，∴＝，∵∠AEF＝∠DAF，∠AFE＝∠DFA，∴△AFE∽△DFA，∴＝，∴AF2＝EF•DF，∴＝＝＝＝，∵DF∥CB，∴△AEF∽△ACB，∴＝，∴＝．【点评】本题考查了相似三角形的判定与性质，解决本题的关键是掌握相似三角形的判定与性质，得到△AEF∽△ACB．。

2020届初三中考数学一诊联考试卷含参考答案 (上海)

2020届**市初三中考一诊联考试卷数学注意事项：1.答卷前，考生务必将自己的姓名、准考证填写在答题卡上。

2.回答客观题时，选出每小题答案后，用2B铅笔把答题卡上对应的答案标号涂黑。

如需改正，必须用橡皮擦擦涂干净，回答非客观题，将答案写在答题卡上，写在试卷上无效。

3.考试结束后，将本试卷和答题卡一并收回。

4.考试时间：120分钟。

一、单选题（共10题，每题3分，共30分，四个选项中只有一项符合题目要求）1．“同吋掷两枚质地均匀的骰子，至少有一枚骰子的点数是3”的概率为（）A．13B．1136C．512D．142．下列各数中是无理数的是（）A．cos60°B．·1.3C．半径为1cm的圆周长D3．如图，在直角坐标系中，Rt△OAB的边OB在y轴上，∠ABO＝90°，AB＝3，点C在AB上，BC＝13AB，且∠BOC＝∠A，若双曲线y＝kx经过点C，则k 的值为（）A B C ．1 D ．24．我国倡导的“一带一路”建设将促进我国与世界一些国家的互利合作，根据规划“一带一路”地区覆盖总人口为4400000000人，这个数用科学记数法表示为( )A ．44×108B ．4.4×108C ．4.4×109D ．4.4×10105．已知点P 为某个封闭图形边界上一定点，动点M 从点P 出发，沿其边界顺时针匀速运动一周，设点M 的运动时间为x ，线段PM 的长度为y ，表示y 与x 的函数图象大致如图所示，则该封闭图形可能是（）A ．B ．C ．D ． 6．已知反比例函数(0)k y k x=<的图象上有两点A （1x ，1y ），B （2x ，2y ），且12x x <，则12y y -的值是（）A ．正数B ．负数C ．非正数D ．不能确定7．在下列命题中，是真命题的是（）A．两条对角线相等的四边形是矩形B．两条对角线互相垂直的四边形是菱形C．两条对角线互相平分的四边形是平行四边形D．两条对角线互相垂直且相等的四边形是正方形8．关于反比例函数y=2x的图象，下列说法正确的是（）A．图象经过点（1，1）B．两个分支分布在第二、四象限C．两个分支关于x轴成轴对称D．当x＜0时，y随x的增大而减小9．按如图所示的运算程序，当输出的y值为0时，x的值是（）A．1B．2C．1±D．2±10．如图，AB是圆O的直径，点C在BA的延长线上，直线CD与圆O相切于点D，弦DF⊥AB于点E，连接BD，CD＝BD＝OE的长度为( )A B．2C．D．4二、填空题（共4题，每题4分，共16分）11．平面直角坐标系xOy中，若抛物线y=ax2上的两点A、B满足OA=OB，且tan∠OAB=12，则称线段AB为该抛物线的通径．那么抛物线y=12x2的通径长为______．12．如图，△ABC的三个顶点分别在直线a、b上，且a∥b，若∠1＝120°，∠2＝80°，则∠3的度数是_____．13．在平面直角坐标系中，规定把一个三角形先沿着x轴翻折，再向右平移2个单位称为1次变换．如图，已知等边三角形ABC的顶点B、C的坐标分别是（﹣1，﹣1）、（﹣3，﹣1），把△ABC经过连续9次这样的变换得到△A′B′C′，则点A的对应点A′的坐标是______．14．已知一元二次方程x2＝0有两个相等的实数根，则nm的值是_____．三、解答题（共6题，总分54分）15．如图，AP平分∠BAC，∠ADP和∠AEP互补．(1)作P到角两边AB，AC的垂线段PM，PN．(2)求证：PD＝PE．16．在直角坐标系中，过原点O及点A（8，0），C（0，6）作矩形OABC、连结OB，点D为OB的中点，点E是线段AB上的动点，连结DE，作DF⊥DE，交OA于点F，连结EF．已知点E从A点出发，以每秒1个单位长度的速度在线段AB上移动，设移动时间为t秒．（1）如图1，当t=3时，求DF的长．（2）如图2，当点E在线段AB上移动的过程中，∠DEF的大小是否发生变化？如果变化，请说明理由；如果不变，请求出tan∠DEF的值．（3）连结AD，当AD将△DEF分成的两部分的面积之比为1：2时，求相应的t 的值．17．为了更好的落实阳光体育运动，学校需要购买一批足球和篮球，已知一个足球比一个篮球的进价高30元，买一个足球和两个篮球一共需要300元．（1）求足球和篮球的单价；（2）学校决定购买足球和篮球共100个，为了加大校园足球活动开展力度，现要求购买的足球不少于60个，且用于购买这批足球和篮球的资金最多为11000元．试设计一个方案，使得用来购买的资金最少，并求出最小资金数．18．据《中国教育报》2004年5月24日报道：目前全国有近3万所中小学建设了校园网，该报为了了解这近3万所中小学校园网的建设情况，从中抽取了4600所学校，对这些学校校园网的建设情况进行问卷调查，并根据答卷绘制了如图的两个统计图：说明：统计图1的百分数＝样本中校园网建设时间在某段时间内的中小学数量×100%；样本数量统计图2的百分数＝样本中校园网建设资金投入在某资金段内的中小学数量×100%．样本容量。

2020届初三中考数学一诊联考试卷含答案解析 (上海)

2020届**市初三中考一诊联考试卷数学注意事项：1.答卷前，考生务必将自己的姓名、准考证填写在答题卡上。

2.回答客观题时，选出每小题答案后，用2B铅笔把答题卡上对应的答案标号涂黑。

如需改正，必须用橡皮擦擦涂干净，回答非客观题，将答案写在答题卡上，写在试卷上无效。

3.考试结束后，将本试卷和答题卡一并收回。

4.考试时间：120分钟。

一、单选题（共10题，每题3分，共30分，四个选项中只有一项符合题目要求）1．在△ABC中，AB=10，BC边上的高AD=6，则另一边BC等于（）A．10 B．8 C．6或10 D．8或102．如图，在Rt△ABC中，∠C＝90°，AB＝10，AC＝6，D、E、F分别是△ABC三边的中点，则△DEF的周长为（）A．24 B．16 C．14 D．123．关于x的一元二次方程(m﹣2)x2﹣4x+1＝0有两个实数解，则实数m的取值范围()A．m≤6 B．m≤6且m≠2 C．m＜6且m≠2 D．m＜64．若a﹣b＝12，则a2﹣b2﹣b的值为（）A．12B．14C．1 D．25．如图，在△ABC中，∠C＝90°，AB＝5cm，BC＝3cm，动点P从点C出发，沿折线CA→AB以3cm/s的速度匀速运动，动点Q从C出发沿CB以1cm/s 的速度匀速运动，若动点P、Q同时从点C出发任意一点到达B点时两点都停止运动，则这一过程中，△PCQ的面积S（cm2）与运动时间t（s）之间的关系大致图象是（）A．B．C．D．6．下列方程，是一元二次方程的是（）①3x 2+x =20，②2x 2-3xy +4=0，③x 2-1x =4，④x 2=0，⑤x 2-3x +3=0 A ．①② B ．①④⑤ C ．①③④ D ．①②④⑤7．如图，在平面直角坐标系中，第二象限内的点P 是反比例函数y ＝kx （k ≠0）图象上的一点，过点P 作P A ⊥x 轴于点A ，点B 为AO 的中点若△P AB 的面积为3，则k 的值为（）A ．6B ．﹣6C ．12D ．﹣128．将一副三角板（∠A ＝30°）按如图所示方式摆放，使得AB ∥EF ，则∠1等于（）A ．75°B ．90°C ．105°D ．115°9．如图，在矩形ABCD 中，4,30AD DAC =∠=，点,P E 分别在,AC AD 上，则PE PD +的最小值是（）A ．2B ．C ．4 D10．若实数m、n满足20m-=，且m、n恰好是等腰△ABC的两条边的边长，则△ABC的周长是（）A．12B．10C．8D．6二、填空题（共4题，每题4分，共16分）11．如图，六边形ABCDEF是⊙O的内接正六边形，若正六边形的面积等于O的面积等于 __________ .12．如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B．小宇同学利用尺规按以下步骤作图：①以点A为圆心，以任意长为半径作弧交AN于点C，交AB于点D；②分别以C，D为圆心，以大于12CD长为半径作弧，两弧在∠NAB内交于点E；③作射线AE交PQ于点F．若AB=2，∠ABP=60°，则线段AF的长为_____．13．分解因式：4m2﹣16n2＝_____．14．如图，PA切⊙O于点A，点B是线段PO的中点，若⊙O，则图中阴影部分的面积为_____．三、解答题（共6题，总分54分）15．小宇想测量位于池塘两端的A、B两点的距离．他沿着与直线AB平行的道路EF行走，当行走到点C处，测得∠ACF=45°，再向前行走100米到点D处，测得∠BDF=60°．若直线AB与EF之间的距离为60米，求A、B两点的距离．16．如图，10×10的网格中，A，B，C均在格点上，诮用无刻度的直尺作直线MN，使得直线MN平分△ABC的周长（留作图痕迹，不写作法）（1）请在图1中作出符合要求的一条直线MN；（2）如图2，点M为BC上一点，BM＝5．请在AB上作出点N的位置．17．某品牌牛奶供应商提供A，B，C，D四种不同口味的牛奶供学生饮用．某校为了了解学生对不同口味的牛奶的喜好，对全校订牛奶的学生进行了随机调查，并根据调查结果绘制了如下两幅不完整的统计图．根据统计图的信息解决下列问题：（1）本次调查的学生有多少人？（2）补全上面的条形统计图；（3）扇形统计图中C 对应的中心角度数是；（4）若该校有600名学生订了该品牌的牛奶，每名学生每天只订一盒牛奶，要使学生能喝到自己喜欢的牛奶，则该牛奶供应商送往该校的牛奶中，A ，B 口味的牛奶共约多少盒？18．一个不透明的口袋中有四个完全相同的小球，把它们分别标号为1，2，3，4.随机摸取一个小球然后放回，再随机摸出一个小球，求下列事件的概率：（1）两次取出的小球标号相同；（2）两次取出的小球标号的和等于4.19．如图，抛物线2y ax bx c =++经过A(-2,0), B(4,0), C(0,-4)三点．点P 是抛物线BC 段上一动点（不含端点(,)B C ，BD BC ⊥与CP 的延长线交于点D（1）求抛物线的解析式．。

(完整word)(完整word版)上海市2020届初三数学一模提升题汇编第23题(几何证明题),推荐文档

【2020长宁金山一模】23.（本题满分12分，第（1）小题5分，第（2）小题7分）如图，在ABC ∆中，点D 、E 分别在边AB 、BC 上，AE 与CD 交于点F ．若AE 平分BAC ∠，AE AC AF AB ⋅=⋅．（1）求证：AEC AFD ∠=∠；（2）若CD EG //，交边AC 的延长线于点G ，求证：BD FC CG CD ⋅=⋅．（长宁金山）23．（本题满分12分，第（1）小题5分，第（2）小题7分）证明：（1）∵AE AC AF AB ⋅=⋅ ∴AFAEAC AB = （1分） ∵AE 平分BAC ∠ ∴CAF BAE ∠=∠ （1分） ∴ABE ∆∽ACF ∆ （1分） ∴ACF B ∠=∠ （1分）又∵BAE B AEC CAF ACF AFD ∠+∠=∠∠+∠=∠,∴AEC AFD ∠=∠ （1分） (2)∵AEC AFD ∠=∠，CFE AFD ∠=∠ ∴AEC CFE ∠=∠ （1分）∴CE FC = （1分） ∵CD EG // ∴CEG DCB ∠=∠ G ACF ∠=∠又∵B ACF ∠=∠ ∴G B ∠=∠ （2分） ∴BCD ∆∽GEC ∆ （1分） ∴CGBDCE CD = （1分） ∴CGBDFC CD = 即BD FC CG CD ⋅=⋅．（1分）第23题图 GAC B ED F【2020杨浦一模】23．（本题满分12分，每小题各6分）如图，已知在ABC △中，AD 是ABC △的中线，DAC B ∠=∠，点E 在边AD 上，CE CD =.（1）求证：AC BDAB AD=；（2）求证：22AC AE AD =⋅.（杨浦）23．证明：（1）∵CD =CE ，∴∠CED =∠CDA . ··········································· （1分） ∴∠AEC =∠BDA . ······················································································ （1分）又∵∠DAC =∠B ，∴△ACE ∽△BAD. ························································· （1分）∴AC CEAB AD=. ···························································································· （1分） ∵AD 是ABC △的中线，∴BD CD =. ····················································· （1分）∵CD =CE ，∴BD CE =.∴AC BDAB AD=. ······················································· （1分）（2）∵∠DAC =∠B ，又∠ACD =∠BCA ，∴△ACD ∽△BCA. ····································· （1分）∴AC CD BC AC=，∴2AC CD CB =?. ································································· （1分） ∵AD 是ABC △的中线，∴2BC CD =，∴222AC CD =. ························ （1分）∵△ACE ∽△BAD ，∴CE AEAD BD=. ·································································· （1分）又∵CD =CE=BD ，∴2CD AD AE =?. ······························································ （1分） ∴22AC AD AE =?. ····················································································· （1分）第23题图 AB CD E【2020徐汇一模】 23．（本题满分12分）如图，在ACB ∆中，点D 、E 、F 、G 分别在边AB 、AC 、BC 上，AD AB 3=，AE CE 2=，CG FG BF ==，DG 与EF 交于点H ．（1）求证： AB HG AC FH ⋅=⋅；（2）联结DF 、EG ，求证：GEF FDG A ∠+∠=∠．（徐汇）23．证明：（1）∵AD AB 3=，AE CE 2=，CG FG BF ==，∴31,31,31,31====BC CG BC BF AC AE AB AD ； ∴BCBFAC AE BC CG AB AD ==,； ∴AC DG //，AB EF //；∴C HGF ∠=∠，B HFG ∠=∠； ∴HFG ∆∽ABC ∆； ∴ABFHAC HG =；即AB HG AC FH ⋅=⋅．（2）∵AB EF //，AC DG //，∴1==FB GF HD GH ，1==GFCGFH HE ； ∴FHHEHD GH =；∴DF EG //； ∴HGE FDG ∠=∠；又HEG HGE FHG ∠+∠=∠，∴HEG FDG FHG ∠+∠=∠； ∵HFG ∆∽ABC ∆，∴A FHG ∠=∠； ∴GEF FDG A ∠+∠=∠．A BC D E F G H （第23题图）【2020松江一模】23．（本题满分12分,第（1）小题5分，第（2）小题7分）已知：如图，点D 、F 在△ABC 边AC 上，点E 在边BC 上，且DE ∥AB ，2CD CF CA =⋅. （1）求证：EF ∥BD ；（2）如果AC CF BC CE ⋅=⋅，求证：2BD DE BA =⋅.23．证明：（1）∵DE ∥AB ∴CD CECA CB=………（1分） ∵2CD CF CA =⋅∴CD CFCA CD =………（1分） ∴CE CF CB CD=………（2分） ∴EF ∥BD ………（1分） (2)∵AC CF BC CE ⋅=⋅ ∴CA CECB CF= ∵∠C =∠C∴△CAB ∽△CEF ………（1分） ∴∠CAB =∠CEF ………（1分） ∵EF ∥BD∴∠CBD =∠CEF ………（1分）∴∠CBD =∠CAB ………（1分）F C BADE (第23题图)F CBAD E (第23题图)FCBAD E (第23题图)∵DE ∥AB ，∴∠BDE =∠DBA ………（1分） ∴△BDE ∽△ABD ………（1分） ∴BD ABDE BD=∴2BD DE BA =⋅………（1分）【2020青浦一模】23．（本题满分12分，第（1）小题6分，第（2）小题6分）已知：如图，在△ABC 中，点D 在边BC 上，AE ∥BC ，BE 与AD 、AC 分别相交于点F 、G ， 2AF FG FE =⋅．（1）求证：△CAD ∽△CBG ；（2）联结DG ，求证：DG AE AB AG ⋅=⋅．23．证明：（1）∵2AF FG FE =⋅，∴=AF FEFG AF．··················································· （1分）又∵∠AFG =∠EFA ，∴△FAG ∽△FEA ． ················································· （1分） ∴∠FAG =∠E ． ························································································· （1分） ∵AE ∥BC ，∴∠E =∠EBC ． ····································································· （1分） ∴∠EBC =∠FAG ． ···················································································· （1分）又∵∠ACD =∠BCG ，∴△CAD ∽△CBG ． ············································· （1分）（2）∵△CAD ∽△CBG ，∴=CA CDCB CG． ······················································· （1分）又∵∠DCG =∠ACB ，∴△CDG ∽△CAB ． ············································· （1分）∴=DG CGAB CB． ······················································································· （1分） ∵AE ∥BC ，∴=AE AGCB GC． ··································································· （1分） ∴=AG GC AE CB ，∴=DG AGAB AE， ··························································· （1分） ∴⋅=⋅DG AE AB AG ． ········································································ （1分）EFGDCBA【2020普陀一模】本题满分12分）23、已知：如图11，四边形ABCD 的对角线AC 、BD 相交于点O ，AOD BOC S S =△△．（1）求证：OACOOB DO =；（2）设△OAB 的面积为S ，k ABCD=，求证：2(1)ABCD S k S =+四边形．（普陀）23．证明：（1）过点A 作AH ⊥BD ，垂足为点H . ·················································· （1分）∵S △AOD =AH DO ⋅⋅21, S △AOB =AH OB ⋅⋅21, ∴OB DOAH OB AHDO S S AOBAOD=⋅⋅⋅⋅=∆∆2121. ··························································· （2分）同理，BOC AOB S COS OA∆∆=． ········································································ （1分） ∵AOD BOC S S =△△， ∵DO COOB OA=． ·············································································· （1分）CDBAO图11（2）∵OACOOB DO =，AOB COD ∠=∠， ∵△OCD ∵△OAB ． ····································································· （1分） ∵CD DO COk AB BO AO===． ································································· （1分） 22k AB CD S S OAB OCD =⎪⎭⎫ ⎝⎛=∆∆． ································································· （1分） ∵△OAB 的面积为S ，∴S k S OCD ⋅=∆2. ··········································· （1分）又∵k OBDOS S OAB AOD ==∆∆，∵S k S AOD ⋅=∆． ··········································· （1分）同理，S k S BOC ⋅=∆. ···································································· （1分） ∴AOB BOC COD DOA ABCD S S S S S =+++△△△△四边形S k S k S k S ⋅+⋅+⋅+=2 S k k ⋅++=)12(2S k 2)1(+=． ······························································· （1分）【2020浦东一模】23．（本题满分12分，其中每小题各6分）如图，已知△ABC 和△ADE ，点D 在BC 边上，DA =DC ，∠ADE =∠B ，边DE 与AC 相交于点F ．（1）求证：AB AD DF BC ⋅=⋅；（2）如果AE ∥BC ，求证：BD DF DC FE =．（浦东）23. 证明：（1）∵DA =DC ，∴∠DCA=∠DAC ．……………………………………（1分）∵∠B=∠ADE ，∴△ABC ∽△FDA ． ……………………………………（3分）∴AB BC FD DA =． ……………………………………………………………（1分） ∴AB DA FD BC ⋅=⋅．………………………………………………………（1分）（2）∵AE // BC ，∴DF DCEF EA =，∠BDA=∠DAE ． ……………………（2分） ∵∠B=∠ADE ，∴△ABD ∽△EDA ．………………………………………（1分） ∴ADBD AE AD =． ……………………………………………………………（1分） ∵DA =DC ，∴AEDCDC BD =．…………………………………………………（1分） ∴FEDF DC BD =． ……………………………………………………………（1分）（第23题图）【2020闵行一模】23．（本题共2小题，每小题6分，满分12分）如图，在△ABC 中，BD 是AC 边上的高，点E 在边AB 上，联结CE 交BD 于点O ，且AD OC AB OD ⋅=⋅，AF 是∠BAC 的平分线，交BC 于点F ，交DE 于点G ．求证：（1）CE ⊥AB ；（2）AF DE AG BC ⋅=⋅．（闵行）23．证明：（1）∵AD OC AB OD ⋅=⋅，∴AD ABOD OC=．………………………………（1分） ∵BD 是AC 边上的高，∴∠BDC = 90°，△ADB 和△ODC 是直角三角形．…………………（1分） ∴Rt △ADB ∽Rt △ODC ．………………………………………………（1分） ∴∠ABD =∠OCD ．……………………………………………………（1分）又∵∠EOB =∠DOC ，∠DOC +∠OCD +∠ODC =180°，∠EOB +∠ABD+∠OEB =180°．∴∠OEB = 90°．…………………………………………………………（1分） ∴CE ⊥AB ．………………………………………………………………（1分）（2）在△ADB 和△AEC 中，∵∠BAD =∠CAE ，∠ABD =∠OCD ，∴△ADB ∽△AEC ．………………………………………………………（2分） ∴AD AB AE AC =，即AD AEAB AC=．…………………………………………（1分）在△DAE 和△BAC 中 ∵∠DAE =∠BAC ，AD AEAB AC=． ∴△DAE ∽△BAC ．………………………………………………………（2分） ∵AF 是∠BAC 的平分线，A BDC（第23题图）EFG O∴AG DEAF BC=，即AF DE AG BC ⋅=⋅．………………………………（1分）【2020静安一模】23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）如图7，在梯形ABCD 中，AD //BC ，AC 与BD 相交于点O ，点E 在线段OB 上，AE 的延长线与BC 相交于点F ，OD 2 = OB ·OE ．（1）求证：四边形AFCD 是平行四边形；（2）如果BC =BD ，AE ·AF =AD ·BF ，求证：△ABE ∽△ACD ．（静安）23．证明：（1）∵OD 2 =OE · OB ，∴OBODOD OE =． ……………………………………………………（1分） ∵AD //BC ，∴OBODOC OA =．……………………………………………………………………（2分） ∴ODOE OC OA =．………………………………………………………（1分） ∴ AF//CD ．………………………………………………………………（1分） ∴四边形AFCD 是平行四边形．……………………………………………（1分）（2）∵AF//CD ，∴∠AED =∠BDC ，BCBFBD BE =．…………………（1分） ∵BC =BD ，∴BE =BF ，∠BDC =∠BCD …………………………………………………………（1分）∴∠AED =∠BCD ．∵∠AEB =180°-∠AED ，∠ADC =180°-∠BCD ，∴∠AEB =∠ADC ．…………………………（1分）∵AE ·AF =AD ·BF ，∴AF ADBF AE =．…………………………………………………………（1分）∵四边形AFCD 是平行四边形，∴AF =CD ．…………………………………………………（1分）图7 A B D C E F O∴DCADBE AE =．………………………………………………………………（1分） ∴△ABE ∽△ADC ．【2020嘉定一模】 23．（本题满分12分，第（1）小题4分，第2小题8分）已知：如图8，在ABC △中，点D 、E 分别在边AB 、AC 上，DE ∥BC ，C ABE ∠=∠. （1）求证：BC DE BE ⋅=2；（2）当BE 平分ABC ∠时，求证：.（嘉定）23.（本题满分12分，第（1）小题4分，第（2）小题8分）证明：（1）∵DE ∥BC ，∴CBE BED ∠=∠. ········································································ 1分又∵C ABE ∠=∠，∴△BDE ∽△CBE . ······································································ 1分 ∴BCBEBE DE =.·········································································································· 1分 ∴BC DE BE ⋅=2. ·································································································· 1分（2）∵DE ∥BC ，∴C AED ∠=∠.又C ABE ∠=∠，∴ABE AED ∠=∠. ······················· 1分又∵BAE EAD ∠=∠，∴△ADE ∽△ABE . ······························································· 1分∴AEADAB AE =. ······································································································· 1分 ∵DE ∥BC ，∴CEAE BD AD =，即CE BDAE AD =. ························································ 1分 ∴CEBDAB AE =. ······································································································· 1分 ∵BE 平分ABC ∠，∴CBE ABE ∠=∠，又∵C ABE ∠=∠，∴C CBE ∠=∠. ······· 1分∴CE BE =. ··········································································································· 1分∴ABAE BE BD =.··········································································································1分ABAEBE BD =B.图8CAED图11 E DCA【2020黄埔一模】 23．（本题满分12分）已知：如图11，在平行四边形ABCD 中，过点C 分别作AD 、AB 的垂线，交边AD 、AB 延长线于点E 、F ．（1）求证：AD DE AB BF ⋅=⋅；（2）联结AC ，如果CF ACDE CD=，求证：22AC AF BC BF =．（黄埔）23．（本题满分12分）（1）∵四边形ABCD 是平行四边形， ∴CD ∥AB ，AD ∥BC ，∴∠CDE =∠DAB ，∠CBF =∠DAB ．∴∠CDE =∠CBF ．……………………………………………………………………（2分） ∵CE ⊥AE ，CF ⊥AF ，∴∠CED =∠CFB =90°．………………………………………………………………（1分） ∴△CDE ∽△CBF ．…………………………………………………………………（1分）∴BC CDBF DE=．…………………………………………………………………………（1分）∵四边形ABCD 是平行四边形，∴BC =AD ，CD =AB ．∴AD ABBF DE=． ∴AD DE AB BF ⋅=⋅．…………………………………………………………（1分）（2）∵CF ACDE CD=，∠CED =∠CFB =90°， ∴ △ACF ∽△CDE ．………………………………………………………（2分）又 ∵ △CDE ∽△CBF ，∴ △ACF ∽△CBF ．………………………………………………………（1分）∴22ACF CBF S AC S BC =V V ．………………………………………………………………………（1分）∵△ACF 与△CBF 等高，∴ACF CBF S AFS BF=V V ．………………………………………………………………………（1分）∴22AC AFBC BF=．………………………………………………………………………（1分）【2020虹口一模】 23．（本题满分12分，第（1）小题满分6分，第（2）小题满分6分）如图11，在Rt △ABC 中，∠ACB =90°，点D 是边BC 的中点，联结AD ，过点C 作 CE ⊥AD 于点E ，联结BE ．（1）求证：2BD DE AD =⋅；（2）如果∠ABC =∠DCE ，求证：BD CE BE DE ⋅=⋅．（虹口）23．证明：（1）∵CE ⊥AD ，∠ACB =90°∴∠ACB =∠CED =90°∵∠EDC =∠CDA∴△EDC ∽△CDA …………………………………………………………………（3分） ∴DE CDCD AD= ∴CD 2=DE ·AD ………………………………………………………………………（2分）∵点D 是边BC 的中点 ∴CD =BD∴BD 2=DE ·AD ………………………………………………………………………（1分）（2）由（1）得DE BDBD AD=且∠EDB =∠BDA ∴△BDE ∽△ADB ……………………………………………………………………（2分） ∴∠ABC =∠BED ……………………………………………………………………（1分） ∵∠ABC =∠DCE ， ∴∠BED =∠DCE ∵∠EBD =∠CBE∴△EBD ∽△CBE ……………………………………………………………………（2分） ∴BD ED BE CE= 即BD CE BE DE ⋅=⋅………………………………………………（1分）D图11 AEC B【2020奉贤一模】23．（本题满分12分，每小题满分6分）已知：如图9，在平行四边形ABCD 中，点 E 在边AD 上，点F 在边CB 的延长线上，联结CE 、EF ，CF DE CE ⋅=2．（1）求证：∠D =∠CEF ；（2）联结AC ，交EF 与点G ，如果AC 平分∠ECF ，求证：CG CB AE AC ⋅=⋅．（奉贤）23．证明：（1）∵CF DE CE ⋅=2，∴CE CFDE CE=． ··································· （1分） ∵四边形ABCD 是平行四边形，∴//AD BC ， ∴DEC ECF ∠=∠． ········ （1分）∴△EDC ∽△CEF ． ····································································································· （2分） ∴∠D =∠CEF ． ········································································································· （2分）（2）∵AC 平分∠ECF ，∴ECG ACB ∠=∠． ∵//AD BC ， ∴DAC ACB ∠=∠．∴ECG DAC ∠=∠． ······························································································ （1分）又∵∠D =∠CEF ，∴△EGC ∽△BAC ． ····································································· （2分）∴CG CEAC CB=． ········································································································· （1分）又AE CE =， ········································································································· （1分） ∴CG AE AC CB =，∴CG CB AE AC ⋅=⋅． ··································································· （1分）ABCDEF图9。

2020上海初三数学各区二模试卷第23几何证明

2020上海各区二模23几何证明2020二模徐汇2020二模青浦2020二模虹口2020二模宝山2020二模普陀2020二模崇明2020二模黄浦23．已知：如图，圆O 是△ABC 的外接圆，AO 平分∠BAC ．（1）求证：△ABC 是等腰三角形；（2）当OA ＝4，AB ＝6，求边BC 的长．2020二模金山23．（本题满分12分，其中第（1）小题5分，第（2）小题7分）如图，已知C 是线段AB 上的一点，分别以AC 、BC 为边在线段AB 同侧作正方形ACDE 和正方形CBGF ，点F 在CD 上，联结AF 、BD ，BD 与FG 交于点M ，点N 是边AC 上的一点，联结EN 交AF 与点H ．（1）求证：AF=BD ；（2）如果AN GMAC GF，求证：AF EN ⊥．（第23题图）NFEHMGDCBA23.（本题满分12分，其中每小题各6分）已知：如图，在平行四边形ABCD 中，对角线AC 与BD 相交于点E ，过点E 作AC 的垂线交边BC 于点F ，与AB 的延长线交于点M ，且AB AM AE AC ⋅=⋅．求证：（1）四边形ABCD 是矩形；（2）2DE EF EM =⋅．2020二模杨浦 23．（本题满分12分，第（1）小题6分，第（2）小题6分）如图，已知在正方形ABCD 中，对角线AC 与BD 交于点O ，点M 在线段OD 上，联结AM 并延长交边DC 于点E ，点N 在线段OC 上，且ON=OM ，联结DN 与线段AE 交于点H ，联结EN 、MN .（1）如果EN //BD ，求证：四边形DMNE 是菱形；（2）如果EN ⊥DC ，求证：2AN NC AC =⋅.第23题图ADCH MONE B23.如图，已知在平行四边形ABCD 中，AE ⊥BC ，垂足为E ，CE=AB ，点F 为CE 的中点，点G 在线段CD 上，联结DF ，交AG 于点M ，交EG 于点N ，且∠DFC=∠EGC ．（1）求证：CG=DG ；（2）求证：2CG GM AG =⋅．2020二模松江23.（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图，已知AB 、AC 是⊙O 的两条弦，且AO 平分∠BAC . 点M 、N 分别在弦AB 、AC 上，满足AM=CN . （1）求证AB=AC ；（2）联结OM 、ON 、MN，求证：.OAOMAB MN =（第23题图）ABCOMN图8EDCABGFH2020二模静安23.（本题满分12分，每小题满分6分）已知：如图8，四边形ABCD 是平行四边形，延长BA 至点E ，使得AE=AB ，联结DE 、AC ．点F 在线段DE 上，联结BF ，分别交AC 、AD 于点G 、H ．（1）求证：BG =GF ；（2）如果AC =2AB ，点F 是DE 的中点，求证：BH GH AH ⋅=2．2020二模嘉定23.（本题满分12分，每小题6分）已知：△ABC ，AC AB =，∠BAC =90°，点D 是边BC 的中点，点E 在边AB 上（点E 不与点A 、B 重合），点F 在边AC 上，联结DE 、DF .（1）如图6-1，当∠EDF =90°时，求证：BE =AF ；（2）如图6-2，当∠EDF =45°时，求证：.CFBEDF DE =22图6-1FD CABE 图6-2EDAF2020二模奉贤23．（本题满分12分，每小题满分6分）已知：如图6，在梯形ABCD 中，CD ∥AB ，∠DAB=90°，对角线AC 、BD 相交于点E ，AC ⊥BC ，垂足为点C ，且CA CE BC ⋅=2．（1）求证：AD=DE ；（2）过点D 作AC 的垂线，交AC 于点F ，求证：AF AE CE ⋅=2．2020二模长宁21. 如图6，已知四边形 A B C D 是矩形，点 E BE ⊥ EF ，且∠ABE +∠CEF =45°. （1）求证：四边形 ABCD 是正方形；（2）联结 BD ，交 EF 于点 Q ，求证： DQ ⋅ BC = CE ⋅ DF .A BCDE图6。

2020年上海市浦东新区初三中考一模数学试卷及答案 Word含解析

2020年上海市浦东新区初三一模数学试卷一、选择题1. 在Rt ABC V 中，∠C =90°，如果BC =5，AB =13，那么sinA 的值为（）A . 513B . 512C . 1213D .1252. 下列函数中，是二次函数的是（） A . 21y x =-B . 22y x =C . 21y x =+D .()221y x x =--3. 抛物线245y x x =-+的顶点坐标是（） A . ()2,1-B . （2,1）C . ()2,1--D . ()2,1-4. 如图，点D 、E 分别在ABC V 的边AB 、AC 上，下列各比例式不一定能推得DE //BC 的是（） A .AD AEBD CE=B .AD DEAB BC=C .AB ACBD CE=D .AD AEAB AC=5. 如图，传送带和地面所成斜坡的坡度为1:3，它把物体从地面点A 处送到离地面3米高的B 处，则物体从A 到B 所经过的路程为（）A .B . 米C .D . 9米6. 下列说法正确的是（）A . ()0a a +-=r rB . 如果a r 和b r 都是单位向量，那么a b =r rC . 如果a b =r r，那么a b =r rD . 如果12a b =-r r （b r为非零向量），那么a r //b r二、填空题7. 已知3x y =，那么2x yx y+=+____________8. 已知线段AB =2cm ，P 是线段AB 的黄金分割点，P A >PB ，那么线段P A 的长度等于____________cm 9. 如果两个相似三角形对应边之比是2:3，那么它们的对应中线之比是____________ 10. 如果二次函数223y x x k =-+-的图像经过原点，那么k 的值是____________11. 将抛物线23y x =-向下平移4个单位，那么平移后所得新抛物线的表达式为____________ 12. 如果抛物线经过点()1,0A -和点B （5,0），那么这条抛物线的对称轴是直线____________ 13. 二次函数()221y x =-+的图像在对称轴左侧的部分是____________（填“上升”或“下降”）14. 如图，在ABC V 中，AE 是BC 边上的中线，点G 是ABC V 的重心，过点G 作GF //AB 交BC 于点F ，那么EFEB=____________ 15. 如图，已知AB //CD //EF ，AD =6，DF =3，BC =7，那么线段CE 的长度等于____________16. 如图，将ABC V 沿射线BC 方向平移得到DEF V ，边DE 与AC 相交于点G ，如果BC =6cm ，ABCV 的面积等于92cm ，GEC V 的面积等于42cm ，那么CF =____________cm17. 用“描点法”画二次函数2y ax bx c =++的图像时，列出了如下的表格：那么当时，该二次函数y 的值为____________18. 在Rt ABC V 中，∠C =90°，AC =2，BC =4，点D 、E 分别是边BC 、AB 的中点，将BDE V 绕着点B 旋转，点D 、E 旋转后的对应点分别为点'D 、'E ，当直线''D E 经过点A 时，线段'CD 的长为____________三、解答题19. 计算：2tan 45cos60cot 602sin 30︒-︒+︒︒20. 如图，在平行四边形ABCD 中，点E 在边AD 上，且AE =2ED ，联结BE 并延长交边CD 的延长线于点F ，设,BA a BC b ==u u u r r u u u r r .（1）用,a b r r 表示,BE DF u u u r u u u r；（2）先化简，再求作：()322a b a b ⎛⎫-++- ⎪⎝⎭r r r r （不要求写作法，但要写明结论）21. 如图，在ABC V 中，点D 、E 分别在边AB 、AC 上，且AD =3，AC =6，AE =4，AB =8. （1）如果BC =7，求线段DE 的长；（2）设DEC V 的面积为a ，求BDC V 的面积（用a 的代数式表示）.22. 为了测量大楼顶上（居中）避雷针BC 的长度，在地面上点A 处测得避雷针底部B 和顶部C 的仰角分别为55°58’和57°，已知点A 与楼底中间部位D 的距离约为80米，求避雷针BC 的长度（参考数据：sin5558'0.83,cos5558'0.56,tan5558' 1.48,sin570.84︒≈︒≈︒≈︒≈)23. 如图，已知ABC V 和ADE V ，点D 在BC 边上，DA =DC ，∠ADE =∠B ，边DE 与AC 相交于点F . （1）求证：AB AD DF BC ⋅=⋅；（2）如果AE //BC ，求证：BD DFDC FE=.24. 如图，在平面直角坐标系xOy 中，抛物线2y x bx c =-++与x 轴的两个交点分别为()()1,0,3,0A B -，与y 轴相交于点C . （1）求抛物线的表达式；（2）联结AC 、BC ，求∠ACB 的正切值；（3）点P 在抛物线上，且∠P AB =∠ACB ，求点P 的坐标.25. 在Rt ABC V 中，∠A =90°，AB =4，AC =3，D 为AB 边上一动点（点D 与点A 、B 不重合），联结CD ，过点D 作DE ⊥DC 交边BC 于点E . （1）如图，当ED =EB 时，求AD 的长；（2）设,AD x BE y ==，求y 关于x 的函数解析式并写出函数定义域；（3）把BCD V 沿直线CD 翻折得'CDB V ，联结'AB ，当'CAB V 是等腰三角形时，直接写出AD 的长.参考答案一、选择题1. A2. C3. B4. B5. A6. D二、填空题7.458. 1 9. 2:3 10. 3 11. 234y x =-- 12. 2x =13. 上升 14. 13 15. 72 16. 2 17. 8- 18.三、解答题19. 原式=56 20.（1）23BE a b =+u u u r r r ，12DF a =u u u r r（2）原式=12a b -r r，作图略21.（1）72（2）5BDC S a =V 22. 约4.8米23.（1）证明略（2）证明略24.（1）223y x x =-++ （2）2（3）点P 坐标为（1,4）或()5,12- 25.（1）94（2）()22050494x x y x x-=<<+（3）7243。

上海初三数学一模各区几何证明23题集合

普陀23．（本题满分12分）已知：如图9，四边形ABCD 的对角线AC 和BD 相交于点E ，AD=DC ，DC 2=DE·DB . 求证：（1）△BCE ∽△ADE ；（2）AB·BC=BD·BE ．静安23. 已知：如图，梯形ABCD 中，AB DC //，BD AD =，DB AD ⊥，点E 是腰AD 上一点，作︒=∠45EBC ，联结CE ，交DB 于点F ．（1）求证：ABE ∆∽DBC ∆；（2）如果65=BD BC ，求BDA BCE S S ∆∆的值．奉贤23.已知：如图，四边形ABCD ，∠DCB =90°，对角线BD ⊥AD ，点E 是边AB 的中点，CE 与BD 相交于点F ，2BD AB BC =⋅ （1）求证：BD 平分∠ABC ；（2）求证：BE CF BC EF ⋅=⋅. CD虹口23．（本题满分12分，第（1）题满分6分，第（2）题满分6分）如图，在△ABC 中，点D 、E 分别在边AB 、AC 上，DE 、BC 的延长线相交于点F ，且EF DF BF CF ⋅=⋅．（1）求证AD AB AE AC ⋅=⋅；（2）当AB =12，AC =9，AE =8时，求BD 的长与△△ADEECFS S 的值．宝山23．（本题满分12分，每小题各6分）如图，△ABC 中，AB ＝AC ，过点C 作CF ∥AB 交△ABC 的中位线DE 的延长线于F ，联结BF ，交AC 于点G ．（1）求证：GAE AC EGC ＝；（2）若AH 平分∠BAC ，交BF 于H ，求证：BH 是HG 和HF 的比例中项．嘉定23．（本题满分12分，每小题6分）如图，已知梯形ABCD 中，AD ∥BC ，CD AB =，点E 在对角线AC 上，且满足BAC ADE ∠=∠.（1）求证：BC DE AE CD ⋅=⋅；（2）以点A 为圆心，AB 长为半径画弧交边BC 于点F ，联结AF . 求证：CA CE AF ⋅=2.闵行23．（本题共2小题，每小题6分，满分12分）如图，已知在△ABC 中，∠BAC =2∠B ，AD 平分∠DF 2AD AF AB =⋅AD BE DE AB ⋅=⋅（1）求证：△AED （2）当EF第23题图（第23题图）松江23．（本题满分12分，每小题6分）已知四边形ABCD 中，∠BAD =∠BDC =90°，2BD AD BC =⋅．（1）求证：AD ∥BC ；（2）过点A 作AE ∥CD 交BC 于点E ．请完善图形并求证：2CD BE BC =⋅．浦东23．（本题满分12分，其中第（1）小题6分，第（2）小题6分）如图，已知，在锐角△ABC 中，CE ⊥AB 于点E ，点D 在边AC 上，联结BD 交CE 于点F ，且DF FB FC EF ⋅=⋅. （1）求证：BD ⊥AC ；（2）联结AF ，求证：AF BE BC EF ⋅=⋅. A （第23题图）DEFBC徐汇23．（本题满分12分，第（1）小题满分5分，第（2）小题满分7分）如图在△ABC 中，AB =AC ，点D 、E 、F 分别在边BC 、AB 、AC 上，且∠ADE =∠B ， ∠ADF =∠C ，线段EF 交线段AD 于点G ．（1）求证：AE =AF ；（2）若DF CFDE AE=,求证：四边形EBDF 是平行四边形．崇明23．（本题满分12分，每小题各6分）如图，点E 是正方形ABCD 的边BC 延长线上一点，联结DE ，过顶点B 作BF DE ⊥，垂足为F ，BF 交边DC 于点G ．（1）求证：GD AB DF BG ⋅=⋅；（2）联结CF ，求证：45CFB ∠=︒．黄浦23．（本题满分12分）（第23题图）ABDECGF（1）求证：∠CDE=12∠ABC；（2）求证：AD•CD=AB•CE.青浦23．（本题满分12分，第（1）小题4分，第（2）小题8分）如图8，已知点D、E分别在△ABC的边AC、BC上，线段BD与AE交于点F，且CD CA CE CB⋅=⋅．（1）求证：∠CAE＝∠CBD；（2）若BE ABEC AC=，求证：AB AD AF AE⋅=⋅．长宁23．（本题满分12分，第（1）小题6分，第（2）小题6分）EC BA图8如图，在∆ABC 中，点D 在边BC 上，联结AD ，∠ADB=∠CDE ，DE 交边AC 于点E ，DE 交BA 延长线于点F ，且DF DE AD ⋅=2．（1）求证：BFD ∆∽CAD ∆；（2）求证：AD AB DE BF ⋅=⋅．金山23．（本题满分12分，每小题6分）如图，已知在Rt △ABC 中，∠ACB=90°，AC > BC ，CD 是Rt △ABC 的高，E 是AC 的中点，ED 的延长线与CB 的延长线相交于点F ．（1）求证：DF 是BF 和CF 的比例中项；（2）在AB 上取一点G ，如果AE ·AC=AG ·AD ，求证：EG ·CF=ED ·DF ．第23题图。