第2.1章传输线理论
合集下载
第2章传输线理论
j z
1 2Z0
(U1
I1Z0 )e
j z
(2―2―14)
同样可以写成三角函数表达式
U (z)
U1 cos z
jZ0
sin z
I
(
z)
j
U1 Z0
sin
z
I1
cos
z
(2―2―15)
第2章 传输线理论
三、入射波和反射波的叠加 由式(2―2―5)和式(2―2―6)两式可以看出,传输线 上任意位置的复数电压和电流均有两部分组成,即有
U (z)
A1e j z
A2e j z
Ui(z) Ur(z)
I
(z)ຫໍສະໝຸດ 1 Z0A1e j z
1 Z0
A2e j z
Ii(z)
Ir(z)
(2―2―16)
第2章 传输线理论
根据复数值与瞬时值的关系,并假设A1、A2为实数, 则沿线电压的瞬时值为
u(z,t) Re[U (Z )e ji ] A1 cos(t z) A2 cos(t z)
式中v0为光速。由此可见,双线和同轴线上行波电
压和行波电流的相速度等于传输线周围介质中的光速,
它和频率无关,只决定周围介质特性参量ε,这种波称为
无色散波。
第2章 传输线理论
(三) 相波长λp
相波长λp是指同一个时刻传输线上电磁波的相位相 差2π的距离,即有
p
2
vp f
vpT
0 r
(2―3―5)
第2章 传输线理论
这种路的分析方法,又称为长线理论。事实上,“场” 的理论和“路”的理论既是紧密相关的,又是相互补充 的。有些传输线宜用“场”的理论去处理,而有些传输 线在满足一定条件下可以归结为“路”的问题来处理, 这样就可借用熟知的电路理论和现成方法,使问题的处 理大为简化。
传输线理论
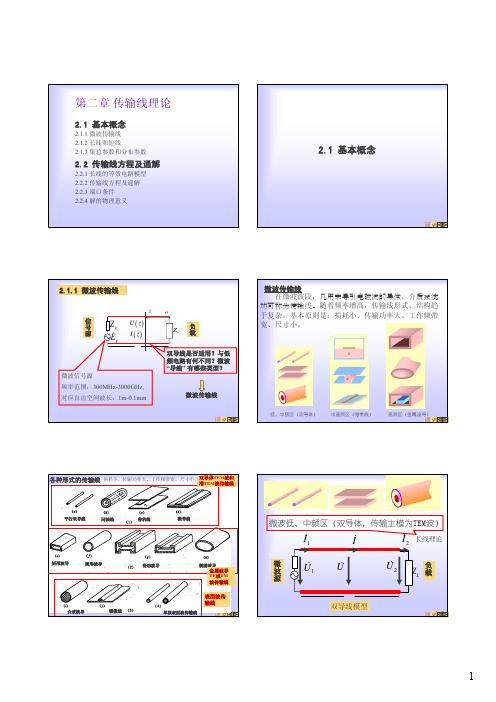
u(z,t) → U (z) i(z,t) → I(z)
∂ → jω, ∂ → d
∂t
∂z dz
∂2 → ( jω )2 = −ω 2
∂t 2
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
∂u ∂z ∂i ∂z
= =
− R0 −G0
⋅
i
−
L0
⋅
∂i ∂t
⋅
u
−
C0dz
`
C0dz
G0dz
dz
z
z + dz
dz
,
t
)
dz → 0
⎧ ⎪⎪ ⎨ ⎪ ⎪⎩
∂u(z,
∂z
t
)
=
− R0
∂i(z,
∂z
t
)
=
−G0
⋅ i(z, t ) ⋅ u(z, t )
− −
L0 C0
⋅ ⋅
∂i(z, t
∂t
∂u(z,
∂t
)
t
)
称为时域传输线方程或电报方程
时域 → 频域
[ ] ⎪⎧u(z,t) = Re U (z)e jωt [ ] ⎪⎩⎨i(z,t) = Re I(z)e jωt
输送市电的电力传输线(f=50Hz, λ = 6000 km)，长达6千 米， l /λ=0.001,为短线；对远距离电力传输线，线路可 能长达几百或几千千米时，则又应视为长线。
在微波技术中，所讨论的传输线都属于长线范畴。
长线和短线有何不同？
l < 0.05λ
“短线”是集总参数电路结构 l ≥ 0.05λ
u(z,t) → U (z), i(z,t) → I(z)，∂ → jω, ∂ → d
∂t
2-传输线理论-1
V R= I
？
E0l l = = = 2.07(Ω/ m) I 2πr0σδs
损耗要增加1500倍 损耗要增加1500倍 1500
R/R0 =1515
使损耗与直流保持相同：？ 使损耗与直流保持相同：？
r0 = 303m .
8
§2.1 引言
总结： 总结：为什么要研究微波传输线 不能称为微波传输线，而应称之为微波传输“ 不能称为微波传输线，而应称之为微波传输“柱” 柱内部几乎物， 柱内部几乎物，并无能量传输 km， 低频电路中，50周市电其 =6000km 线上任一点的电压、 低频电路中，50周市电其λ=6000km，线上任一点的电压、 电流近似为一样。绕地球一圈只有三个波长。 电流近似为一样。绕地球一圈只有三个波长。 λ >> l (短 线） 微波波段， =3cm, 则在l =3cm的线上 的线上U 微波波段， f =10GHz, λ =3cm, 则在 =3cm的线上U、I不 可以近似为一样大。 长线）， 可以近似为一样大。λ < l (长线）， U、I是位置与时间的函 数。 3 在沟通大西洋海底电缆时，开尔芬首先发现了长线效应： 在沟通大西洋海底电缆时，开尔芬首先发现了长线效应： 电报信号的反射。 电报信号的反射。
17
§ 2.3 : 阻抗与驻波
归一化输入阻抗 zin
Z in 1 + Γ z L + j t g ( β z ) = = zin = Z c 1 − Γ 1 + jz L t g ( β z )
λ /2 •？ 的周期性 ？ •？ 的倒置性 ？ λ /4
z L + j t g ( β z + π / 2) zin ( z + λ / 4) = 1 + jz L t g ( β z + π / 2) z L − jct g ( β z ) z L t g ( β z ) − j 1 + jz L t g ( β z ) = = = 1 − jz L ct g ( β z ) t g ( β z ) − jz L zL + j tg(β z)
《传输线理论》课件
阻抗特性
传输线的阻抗决定信号的 匹配和功率传递效率，常 见的阻抗包括50欧姆和75 欧姆。
传输线上的信号传输
传输线上的信号反射和干扰是常见问题，可通过消除信号反射和合理终止传输线来解决。 消除信号反射的方法包括使用终端电阻、滤波器和匹配网络。
传输线的调谐
传输线的等效电路 模型
传输线可用电路模型表示， 包括传输线的电感、电容和 电阻。
传输线用于计算机网络中的局 域网和广域网等数据传输。
总结
1 传输线理论的重要性
传输线理论为电磁信号传输提供了基础理论和实践指导。
2 相关应用领域
传输线广泛应用于通信、雷达、计算机网络等领域。
3 发展趋势及未来展望
随着技术的发展，传输线将继续演进，以满足不断增长的通信需求。
什么是传输线
传输线是传输电磁信号的导体或介质，通常由金属导线、光纤或空气等构成。 传输线可分为平行线、同轴电缆、光纤等多种类型。
传输线的特性
衰减特性
传输线上信号强度随距离 递减，衰减特性决定信号 传输的距离和质量。
相位特性
传输线上的信号会因电磁 波传播速度不同而引起相 位变化，影响信号的时间 同步。
《传输线理论》PPT课件
# 传输线理论 什么是传输线？传输线的定义和分类。 传输线的特性，包括衰减特性、相位特性和阻抗特性。 如何在传输线上进行信号传输？反射与干扰，消除信号反射，传输线的终止方式。 传输线的调谐，包括等效电路模型、调谐方法和在通信系统中的应用。 传输线在通信系统、雷达系统和计算机网络中的应用。 总结传输线理论的重要性，相关应用领域，发展趋势及未来展望。
传输线的调谐方法
通过调节传输线的电性能参 数来实现传输线的谐振和优 化信号传输。
2_传输线理论(2)
V ( z + Δz ) − V ( z ) ⎧ = −( R + jω L) I ( z ) ⎪lim Δz ⎪ Δz →0 ⎨ I ( z + Δz ) − I ( z ) ⎪ = −(G + jωC )V ( z ) lim z Δ ⎪ Δz →0 ⎩
(1)
有
⎧ dV ( z ) ⎪ dz = −( R + jω L) I ( z ) ⎪ ⎨ ⎪ dI ( z ) = −(G + jωC )V ( z ) ⎪ dz ⎩
1 2
vp λp = f
2.3.4 输入阻抗
传输线上任意点z′处的电压与电流之比称为该点的输入阻抗
1 1 (VL + Z 0 I L )eγ z′ + (VL − Z 0 I L )e −γ z′ V ( z ') 2 Z in ( z ') = = 2 1 1 I ( z ') (VL + Z 0 I L )eγ z′ − (VL − Z 0 I L )e −γ z′ 2Z 0 2Z 0
(7)
2.2.4 传输线方程定解
对于终端边界条件场合， 常采用z′(终端出发)坐标系， 即
z′ = L − z,
可表示为
1 1 ⎧ ′) = (VL + Z 0 I L )eγ z′ + (VL − Z 0 I L )e −γ z′ = Vi ( z ′) + Vr ( z ′) ⎪V ( z 2 2 ⎪ (8) ⎨ 1 1 γ z′ ⎪ I ( z ′) = (VL + Z 0 I L )e − (VL − Z 0 I L )e −γ z′ = I i ( z ′) + I r ( z ′) 2Z 0 2Z 0 ⎪ ⎩
(1)
有
⎧ dV ( z ) ⎪ dz = −( R + jω L) I ( z ) ⎪ ⎨ ⎪ dI ( z ) = −(G + jωC )V ( z ) ⎪ dz ⎩
1 2
vp λp = f
2.3.4 输入阻抗
传输线上任意点z′处的电压与电流之比称为该点的输入阻抗
1 1 (VL + Z 0 I L )eγ z′ + (VL − Z 0 I L )e −γ z′ V ( z ') 2 Z in ( z ') = = 2 1 1 I ( z ') (VL + Z 0 I L )eγ z′ − (VL − Z 0 I L )e −γ z′ 2Z 0 2Z 0
(7)
2.2.4 传输线方程定解
对于终端边界条件场合， 常采用z′(终端出发)坐标系， 即
z′ = L − z,
可表示为
1 1 ⎧ ′) = (VL + Z 0 I L )eγ z′ + (VL − Z 0 I L )e −γ z′ = Vi ( z ′) + Vr ( z ′) ⎪V ( z 2 2 ⎪ (8) ⎨ 1 1 γ z′ ⎪ I ( z ′) = (VL + Z 0 I L )e − (VL − Z 0 I L )e −γ z′ = I i ( z ′) + I r ( z ′) 2Z 0 2Z 0 ⎪ ⎩
第2.1章 传输线理论
——→与低频状态完全不同。
第二章 传输线理论
传输线理论 长线理论
传输线是以TEM导模方式传 输电磁波能量。 其截面尺寸远小于线的长度， 而其轴向尺寸远比工作波长大 时，此时线上电压只沿传输线 方向变化。
一维分布参数电路理论
第二章 传输线理论
1）长线理论
传输线的电长度：传输线的几何长度 l 与其上 工作波长l的比值（l/l）。
当f =2GHz时
wLl = 2.3碬 3 / m > > Rl 10 wCl = 1.89S / m > > Gl
可忽略R和G的影响。——低耗线
第二章 传输线理论
P17表2.1-1给出了双导线、同轴线和平行板传输线的 分布参数与材料及尺寸的关系。
同轴线 a：内导体半径 b：外导体半径 m,e：填充介质 L(H/m)
①终端条件解：
边界条件： V (l ) = VL , I (l ) = I L
第二章 传输线理论
将上式代入解中： V = A e- g l + A e g l L 1 2
IL = 1 ( A1eZ0
gl
V ( z ) = A1e- g z + A2 eg z I ( z) = 1 ( A1e- g z - A2eg z ) Z0
第二章 传输线理论
2）时谐均匀传输线方程
a）时谐传输线方程 电压和电流随时间作正弦变化或时谐变化，则
电压电流的瞬时值可用复数来表示：
v ( z , t ) = V0 cos(wt + y v ( z )) = Re 轾 e jwt e jy v ( z ) = Re 轾( z )e j wt V0 V 犏 犏 臌 臌 i ( z , t ) = I 0 cos(wt + y I ( z )) = Re 轾e jwt e jy I ( z ) = Re 轾 z )e j wt I0 I( 犏 犏 臌 臌
传输线理论
传输线理论1 引言传输电磁能量和信号的线路称为传输线。
传输线包括TEM 波传输线、波导传输线和表面波传输线。
本教材讨论TEM 波传输线（如双线、同轴线）的基本理论。
这些理论不仅适用于TEM 波传输线,而且也是研究TEM波传输线的理论基础。
TEM波即横电磁波，其特征是E z=0、H z=0，因此电磁场只有横向分量E T、H T，即TEM波只有垂直于传输方向的横向分量。
但应注意到TEM波的场不是静场，而是随时间t及纵座标z波动变化的场。
研究传输线上所传输电磁波的特性的方法有两种。
一种是“场”的分析方法，即从麦氏方程组出发，解特定边界条件下的电磁场波动方程，求得场量（E和H）随时间和空间的变化规律，由此来分析电磁波的传输特性；另一种方法是“路”的分析方法，它将传输线作为分布参数来处理，得到传输线的等效电路，然后由等效电路根据克希霍夫定律导出传输线方程，再解传输线方程，求得线上电压和电流随时间和空间的变化规律，最后由此规律来分析电压和电流的传输特性。
这种“路”的分析方法，又称为长线理论。
事实上，“场”的理论和“路”的理论既是紧密相关的，又是相互补充的。
1.1 分布参数及其分布参数电路传输线可分为长线和短线，长线和短线是相对于波长而言的。
所谓长线是指传输线的几何长度和线上传输电磁波的波长的比值（即电长度）大于或接近于1。
反之称为短线。
在微波技术中，波长以m或cm计，故1m长度的传输线已长于波长，应视为长线；在电力工程中，即使长度为1000m的传输线，对于频率为50Hz（即波长为6000km）的交流电来说，仍远小于波长，应视为短线。
传输线这个名称均指长线传输线。
有些传输线宜用“场”的理论去处理，而有些传输线在满足一定条件下可以归结为“路”的问题来处理，这样就可以借用熟知的电路理论和现成方法，使问题的处理大为简化。
长线和短线的区别还在于：前者为分布参数电路，而后者是集中参数电路。
在低频电路中常常忽略元件连接线的分布参数效应，认为电场能量全部集中在电容器中，而磁场能量全部集中在电感器中，电阻元件是消耗电磁能量的。
第二章 传输线理论
12:21
电子科技大学电子工程学院
微波技术与天线
第二章 传输线基本理论
传输线的特性参量：
传播常数、特性阻抗、相速和相波长等。
传输线的工作参量：
输入阻抗、反射系数、驻波系数/行波系数等。
12:21
电子科技大学电子工程学院
微波技术与天线
第二章 传输线基本理论
一、传输线输入阻抗 传输线输入阻抗定义： 传输线终端接负载阻抗ZL时，距离终端z处向负载方向看 去的输入阻抗定义为该处的电压U(z)与电流I(z)之比，即
d 2U ( z ) 2 2 U ( z ) 0 ( Z1Y1 ( R1 j L1 )(G1 jC1 )) 2 dz
其通解为：
U ( z) U ( z) U ( z) Ae z Be z
2、电流方程的通解 同理由时谐传输线方程可得： d 2 I ( z) 2 2 I ( z ) 0 ( ( R1 j L1 )(G1 jC1 )) 2 dz 通解：I ( z) I ( z) I ( z)
不仅要考虑传输信号幅度，还需要考虑相位——考虑分布 参数效应——分布参数电路
12:21
电子科技大学电子工程学院
微波技术与天线
第二章 传输线基本理论
2、集肤效应影响
低频传输线 在低频电路中，电流几乎均匀地分布在导线内，能流
集中在导体内部和表面附近。
微波传输线 高频电路中，导体的电流、电荷和场都集中在导体表面
12:21
电子科技大学电子工程学院
微波技术与天线
第二章 传输线基本理论
若已知初始端电压：
U l U0
I l I0
U o I o Z 0 l A e 2
第2章 传输线理论 (1)
也可用矩阵形式表示 cosh( z )
Z0 sinh( z ) U L U ( z ) I ( z ) 1 sinh( z ) cosh( z ) I Z L 0
§2.3 均匀传输线的传输特性
一、均匀传输线的传输特性
第二章 均匀传输线理论
§2.1 均匀传输线
一、基本概念
传输线 引导电磁波能量向一定方向传输的传输系统
均匀传输线 截面尺寸、形状、媒质分布、材料及边界条件 均不变的导波系统。
§2.1 均匀传输线
传输线的分析方法 场的方法 从麦克斯韦方程出发，得到满足边界条件的电 场和磁场的解 路的方法 从传输线方程出发，得到满足边界条件的电压 和电流的解 路的方法，只是一种近似分析方法，在微波的 低频段能满足实际工程的需要；但在微波的高 频段，只能用场的方法来分析
A，B为待定系数，由边界条件确定
( R0 j L0 ) Z 为特性阻抗 Z0 Y (G0 jC0 )
ZY ( R0 j L0 )(G0 jC0 ) j 为传播常数
§2.2 均匀传输线方程及其解
2°解的物理意义
U ( z ) U i ( z ) U r ( z ) Ae z Be z 1 z z I ( z ) I ( z ) I ( z ) Ae Be i r Z0
§2.1 均匀传输线
2°分布参数模型 由于电流流过导线路使导线发热这表明导线本身具 有分布电阻； 由于导线间绝缘不完善而存在漏电流这表明导线间 处处有分布漏电导； 由于导线中通过电流，周围将有磁场因而导线上存 在分布电感的效应； 由于导线间有电压，导线间便有电场，于是导线间 存在分布电容的效应。 分别用R0，G0，L0，C0表示单位长度上的分布电阻,分 布漏电导，分布电感和分布电容
传输线基本理论
≈ ± jω L1C1 (1 + R1 / j 2ωL1 + G1 / j 2ωC1 ) R1 = ± 2
令
16
C1 G1 + 2 L1
L1 C1
+ jω L1C1
γ = α + jβ
则
R1 2
(δ
= ±γ ) L1 C1
(2-2-12)
α=
10
我们用图 2-1-2 所示线上的电压（或电流）随空间位置的分布状况来说 明长、短线的区别。图 a 示出的是半波长的波形图，AB 是线上的一小段， 它比波长小许多倍。由图可见，线段 AB 上各点电压（或电流）的大小和 相位几乎不变，此时的 AB 应视为“短线” 。如果频率升高了，虽然线段长 仍为 AB，但在某一瞬时其上各点电压（或电流）的大小和相位均有很大变 化，如图 b 所示，此时线段 AB 即应视为“长线” 。 前者对应于低频率传输线。它在低频电路中只起连接线的作用，因频率低， 其本身分布参数所引起的效应过错全可以忽略不计，所以在低频电路中只 考虑时间因子而忽略空间效应，因而把电路当作集中参数电路来处于是允 许的。后者对应于微波传输线。因为频率很高时分布参数效应不能再忽视 了，传输线不能仅当作连接线，它将形成分布参数电路，参与整个电路的 工作。因而传输线在电路中所引起的效应必须用传输线理论来研究。
C1 G1 + L1 2
(2-2-13a) (2-2-13b)
β = ω ห้องสมุดไป่ตู้1C1
于是式（2-2-10）的解可以表示为 e −γz 和 e γz 的线性组合，即
U = Ae −γz + Be γz
代入式（2-2-7）可得到电流解为 1 I= ( Ae −γz − Be γz ) Z0 其中
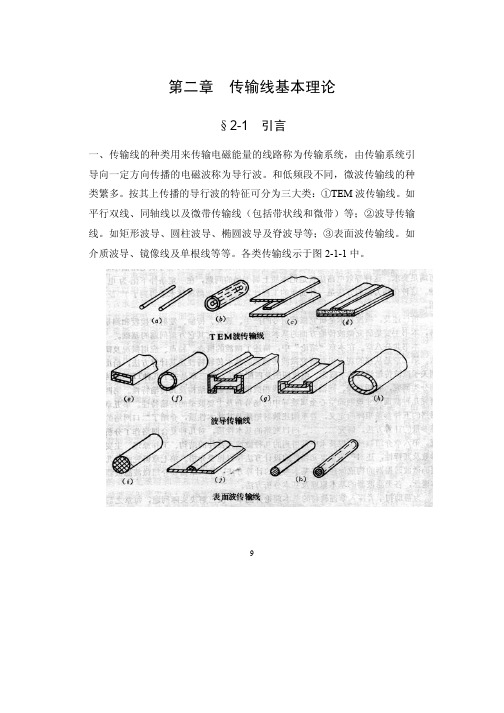
令
16
C1 G1 + 2 L1
L1 C1
+ jω L1C1
γ = α + jβ
则
R1 2
(δ
= ±γ ) L1 C1
(2-2-12)
α=
10
我们用图 2-1-2 所示线上的电压（或电流）随空间位置的分布状况来说 明长、短线的区别。图 a 示出的是半波长的波形图，AB 是线上的一小段， 它比波长小许多倍。由图可见，线段 AB 上各点电压（或电流）的大小和 相位几乎不变，此时的 AB 应视为“短线” 。如果频率升高了，虽然线段长 仍为 AB，但在某一瞬时其上各点电压（或电流）的大小和相位均有很大变 化，如图 b 所示，此时线段 AB 即应视为“长线” 。 前者对应于低频率传输线。它在低频电路中只起连接线的作用，因频率低， 其本身分布参数所引起的效应过错全可以忽略不计，所以在低频电路中只 考虑时间因子而忽略空间效应，因而把电路当作集中参数电路来处于是允 许的。后者对应于微波传输线。因为频率很高时分布参数效应不能再忽视 了，传输线不能仅当作连接线，它将形成分布参数电路，参与整个电路的 工作。因而传输线在电路中所引起的效应必须用传输线理论来研究。
C1 G1 + L1 2
(2-2-13a) (2-2-13b)
β = ω ห้องสมุดไป่ตู้1C1
于是式（2-2-10）的解可以表示为 e −γz 和 e γz 的线性组合，即
U = Ae −γz + Be γz
代入式（2-2-7）可得到电流解为 1 I= ( Ae −γz − Be γz ) Z0 其中
电磁场课件第二章传输线的基本理论
1正弦时变条件下传输线方程
令信源角频率已知 ，线上的电压、电流皆为正弦时变规律（或称为谐变），这样具有普遍性意义。
2 方程的通解
典型波动方程的解 传播常数和波阻抗
3 已知信源端电压和电流时的解
求待定系数
边界条件
解的具体形式
用到的数学公式
4 已知负载端电压和电流时的解
边界条件 求待定系数
信号各频率成分的幅值传输过程中无变化（衰减常数）。
均匀无损耗传输线无频率失真，即为无色散系统。
一般情况，衰减常数及相移常数与频率关系复杂，是色散系统。
均匀无损耗传输特性
行波，没有反射波
驻波，反射波和入射波振幅相同
混合波
相向两列行波叠加结果
3 传输线上任一位置处的输入阻抗
传输线上任一位置处的输入阻抗定义为该点电压和电流的比值。
传输线是用以传输电磁波信息和能量的各种形式的传输系统的总称。
微波传输线是用以传输微波信息和能量的各种形式的传输系统的总称，它的作用是引导电磁波沿一定方向传输, 因此又称为导波系统, 其所导引的电磁波被称为导行波。
一、传输线的概念
1
一般将截面尺寸、形状、媒质分布、材料及边界条件均不变的导波系统称为规则导波系统, 又称为均匀传输线。
考察点位置，实际上和传输线长度有关，
在线电磁波的频率，
外接负载阻抗的阻抗，
传输线的波阻抗（特征阻抗）。
输入阻抗决定因素
输入阻抗和传输线相对长度关系
四分之一波长线：阻抗变换性 二分之一波长线：阻抗不变性 是无损耗传输线的一个重要特性
例2–1 均匀无损耗传输线的波阻抗75Ω，终端接50Ω纯阻负载，求距负载端0.25λ、0.5λ位置处的输入阻抗。若信源频率分别为50MHz、100MHz，求计算输入阻抗点的具体位置。
第二章 传输线理论2.1 2.2(2011完成)1
L Z 1
ZL
C1ZZFG Z来自1I+dIZg Eg
R Z 1
L Z 1
I V
ZL ZF
G Z 1
C1Z
V+dV
Z
整个传输线由许多小线元组成，故整个传输线的等效集总参数电路 可看成由许多线元的 型网络链接而成，如图（b）所示。
对于无耗网络，
R1 0、G1 0
则等效电路如图（c）所示.
1、长线效应
c 3 108 0.03 米＝3厘米， 例如：当 f 10GHz 时， 9 f 10 10
则几厘米的传输线就应视为长线；
c 3 108 6000 千米，即使长为几百米 当 f 50Hz 时， 则 f 50 长的线却仍是短线。 思考题：长度分别 l 104 m和l 0.01cm 为的两根传输线， 是长线，还是短线？
1 6.37 / m 很小。 并联阻抗 X C c
由此可见, X L、X C 不能忽略，也就是说分布参数效应在微波频 率下不能被忽略。
结论： 在微波频率时，传输线的分布参数效应 不能被忽略，而认为传输线的各部分都存在 有电感、电容、电阻和电导，也就是说，这 时传输线和阻抗元件已融为一体，它们构成 的是分布参数电路，即在传输线上处处有贮 能、处处有损耗。也正是如此，在微波下， 传输线的作用除传输信号外还可用于构成各 种微波电路元件。
3 、传输线的分类
（1） 横电磁波（TEM波）传输线，如双导线、同轴线、带状 线等。常用波段米波、分米波、厘米波。
(a)平行双导线
（b）同轴线
（c）带状线
(2）.波导传输线（TE和TM波），如矩形、圆形、脊形和椭圆形 波导等。厘米波、豪米波低端。
电磁波第二章 传输线的基本理论
• 导引电磁波传播的机构通称为传输线，而 传输线具有明确的电路概念。 • 传输线是用以传输电磁波信息和能量的各 种形式的传输系统的总称。 • 微波传输线是用以传输微波信息和能量的 各种形式的传输系统的总称，它的作用是 引导电磁波沿一定方向传输, 因此又称为 导波系统, 其所导引的电磁波被称为导行 波。
z
4 已知负载端电压和电流时的解
边界条件 z l ,U (l ) U L , I (l ) I L
求待定系数
1 e l A1 2 U L Z 0 I L 1 A2 U L Z 0 I L e l 2
1 短线分布参数等效电路
短线分布参数可以用其集总的等效电路 表示。
z
iz, t
iz z, t
u z, t
L0 z R0 z
C 0 z G0 z
z
z
u z z, t
z z
一段传输线实际上就是由无穷多部分网络 链接的系统。
z
为什么高频条件下要考虑电路分布参数
f 0 50Hz
X L 2f 0 L0 2 50 0.99910
9
31410 / mm
3
BC 2f 0 C0 2 50 0.01111012 3.491012 S / mm
f 0 5000MHz
X L 2f 0 L0 2 5000106 0.999109 31.4 / mm
解的具体形式
1 e z 1 U Z I e z U ( z ) U T Z 0 I T T 0 T 2 2 1 U T z 1 U T z I ( z) IT e IT e 2 Z0 2 Z0
z
4 已知负载端电压和电流时的解
边界条件 z l ,U (l ) U L , I (l ) I L
求待定系数
1 e l A1 2 U L Z 0 I L 1 A2 U L Z 0 I L e l 2
1 短线分布参数等效电路
短线分布参数可以用其集总的等效电路 表示。
z
iz, t
iz z, t
u z, t
L0 z R0 z
C 0 z G0 z
z
z
u z z, t
z z
一段传输线实际上就是由无穷多部分网络 链接的系统。
z
为什么高频条件下要考虑电路分布参数
f 0 50Hz
X L 2f 0 L0 2 50 0.99910
9
31410 / mm
3
BC 2f 0 C0 2 50 0.01111012 3.491012 S / mm
f 0 5000MHz
X L 2f 0 L0 2 5000106 0.999109 31.4 / mm
解的具体形式
1 e z 1 U Z I e z U ( z ) U T Z 0 I T T 0 T 2 2 1 U T z 1 U T z I ( z) IT e IT e 2 Z0 2 Z0
传输线基本理论
平行双导线、同轴线的等效电路参数计算公式列于表 2-1。
表 2-1 平行双导线、同轴线的等效电路参数 R'、G'、L'和 C'
参数
同轴线
平行双导线
单位
R'
Rs
2π
1 a
+
1 b
Rs
πa
Ω/m
L'
µ 2π
ln(b
/
a)
µ π
ln (d
/
2a)
+
(d / 2a)2 − 1
H/m
2πσ
G'
ln(b / a)
有耗传输线方程的解
13
对于有损耗的情况，如果传播常数 k 与特征阻抗 Zc（或导纳 Yc）的定义为
jk = (R'+ jωL')(G'+ jωC')
1
Zc
= Yc
=
R'+ jωL' G'+ jωC'
那么传输线方程
dV (z) = −(R'+ jωL')I (z)
dz
dI (z) = −(G'+ jωC')V (z)
将上式代入传输线方程
∂V (z,
∂z
t
)
=
−
R'
I
(z,
t
)
+
L'
∂I
(z,
∂t
t
)
∂I
(z,
∂z
t
)
=
−G'V
(z,
t
)
电信传输原理及应用第二章 传输线理论 1
注：Z从终端起 从终端起
U ( z ) = U 2 chγ z + I 2 Z C shγ z
将A1, A2代入整理后可得 :
I ( z ) = U 2 shγ z + I 2 chγ z ZC
18
第2章 传输线理论
传输线方程的解 3
2. 已知传输线始端电压 1和电流 1，沿线电压电流表达式 已知传输线始端电压U 和电流I 这时将坐标原点z=0选在始端较为适宜。 这时将坐标原点 选在始端较为适宜。将始 选在始端较为适宜 端条件U 代入式， 端条件 (0)=U1, I (0)=I1代入式，同样可得沿线 的电压电流表达式为
其中横电磁波只存在于多导体系统中， 其中横电磁波只存在于多导体系统中，而横磁 波和横电波一般存在于单导体系统中， 波和横电波一般存在于单导体系统中，它们是 色散波。 色散波。
3
第2章 传输线理论
传输线的分类
TEM或准 或准TEM传输线： 传输线： 或准 传输线
4
第2章 传输线理论
13
第2章 传输线理论
均匀传输线的分布参数
14
第2章 传输线理论
均匀传输线方程及其稳态解
把均匀传输线分割成许多小的微元段dz (dz<<λ)， 这样每个微元段可看作集中参数电路，用一个Γ 型网络来等效。于是整个传输线可等效成无穷多 个Γ 型网络的级联
15
第2章 传输线理论
11
第2章 传输线理论
分布参数电路
•某一双线传输线分布电感为 某一双线传输线分布电感为L=1nH/mm，分布电容 某一双线传输线分布电感为 ， 为C=0.01pF/mm。 。 •在低频率f •在低频率f =50Hz 时， 传输线上每毫米引入的串联 在低频率 电抗和并联电纳分别为:X 电抗和并联电纳分别为 L=3.14×10e-7 /mm， × ， Bc=3.14×10e-12 S/mm。可见，低频时分布参数很 × 。可见， 可忽略。 小，可忽略。 •当高频率为 =5×109Hz 时，XL=31.4 /mm， 当高频率为f × 当高频率为 ， Bc=3.14×10e-4 S/mm。显然，此时分布参数不可忽 × 。显然， 略，必须加以考虑。 必须加以考虑。
传输线理论
➢短线：
几何长度l与工作波长λ相比可以忽略不计传输线， 用集总参数进行描述。应用电路理论分析。
分界线可认为是： l / 0.05
2.1.2 分布参数及传输线等效电路模型
Low frequencies(short line) wavelengths >> wire length current (I) travels down wires easily for efficient power transmission measured voltage and current not dependent on position along wire
集 总 参 数 电 路
分 布 参 数 电 路
2.1.2 分布参数及传输线等效电路模型 例
100Km长的高压线，工作频率50Hz，电长度 l / 0.017
---- 短线
1cm长的传输线，工作频率为3GHz，电长度 l / 0.1
---- 长线
2.1.2 分布参数及传输线等效电路模型 分布参数(distributed parameter)
➢可以从场的角度以某种TEM传输线导出 ➢可以从路的角度，由分布参数得到
采用电路理论分析 对时諧情况求通解
得到一般传输线方程 最后根据传输线端接条 件求出传输线方程定解
2.2.1 传输线方程
a.一般传输线方程
按照泰勒级数展开，并忽略高次项
应用基尔霍夫定律
v(z z,t) v(z,t) v(z,t) z z
第二章 传输线理论
本章学习提要：
❖又称一维分布参数电路理论，是微波电路设计 和计算的理论基础。
❖从路的观点研究传输线在微波运用下的传输特 性，讨论用史密斯圆图进行阻抗计算和阻抗匹 配的方法。
几何长度l与工作波长λ相比可以忽略不计传输线， 用集总参数进行描述。应用电路理论分析。
分界线可认为是： l / 0.05
2.1.2 分布参数及传输线等效电路模型
Low frequencies(short line) wavelengths >> wire length current (I) travels down wires easily for efficient power transmission measured voltage and current not dependent on position along wire
集 总 参 数 电 路
分 布 参 数 电 路
2.1.2 分布参数及传输线等效电路模型 例
100Km长的高压线，工作频率50Hz，电长度 l / 0.017
---- 短线
1cm长的传输线，工作频率为3GHz，电长度 l / 0.1
---- 长线
2.1.2 分布参数及传输线等效电路模型 分布参数(distributed parameter)
➢可以从场的角度以某种TEM传输线导出 ➢可以从路的角度，由分布参数得到
采用电路理论分析 对时諧情况求通解
得到一般传输线方程 最后根据传输线端接条 件求出传输线方程定解
2.2.1 传输线方程
a.一般传输线方程
按照泰勒级数展开，并忽略高次项
应用基尔霍夫定律
v(z z,t) v(z,t) v(z,t) z z
第二章 传输线理论
本章学习提要：
❖又称一维分布参数电路理论，是微波电路设计 和计算的理论基础。
❖从路的观点研究传输线在微波运用下的传输特 性，讨论用史密斯圆图进行阻抗计算和阻抗匹 配的方法。
《传输线理论》课件
电流反射系数
Γi (z)
=
Ir (z) Ii (z)
=
-
A2 A1
e- j2β z
=
-Γu (z)
终端反射系数
Γ2
A2 A1
A2 e jφ2 A1
Γ2 e jφ2
传输线上任一点反射系数 与终端反射系数的关系
Γ(z) = Γ2e- j2 β z = Γ2 e j(φ2-2 β z) = Γ2 e jφ
传输线理论
输入阻抗与反射系数间的关系
Z in
(z)
=
U (z) I (z)
=
Ui Ii
(z)[1+ Γ(z)] (z)[1- Γ(z)]
=
Z0
1+ Γ(z) 1- Γ(z)
负载阻抗与终端反射系数的关系
1+ Γ2 ZL = Z0 1- Γ2
上述两式又可写成
Γ(z)
=
Zin(z) - Z0 Zin(z) + Z0
Z0
由此可得行波状态下的分布规律：
(1) 线上电压和电流的振幅恒定不变 (2) 电压行波与电流行波同相，它们 的相位是位置z和时间t的函数 (3) 线上的输入阻抗处处相等，且均 等于特性阻抗
传输线理论
二、驻波状态(全反射情况)
当传输线终端短路、开路或接纯电抗负载时，终端的入射波将被全反射，沿线入
射波与反射波迭加形成驻波分布。驻波状态意味着入射波功率一点也没有被负载吸 阿收，即负载与传输线完全失配。
2
z
)
+
β
2U
(
z
)
=
0
d
2I (z)
dz2
+
《传输线理论详解》课件
VS
详细描述
在高速数字信号处理中，传输线理论被用 于分析信号在传输过程中的特性变化，以 及如何减小信号的延迟和畸变。通过传输 线理论，可以优化信号传输路径和系统参 数，提高信号的传输速度和稳定性，满足 高速数字信号处理的需求。
高频微波系统设计
总结词
传输线理论在高频率微波系统设计中具有重 要应用，有助于实现高频微波信号的高效传 输。
详细描述
传输线的基本特性包括阻抗、传播常数和电磁波的传播速度等。阻抗决定了传输线对信号的负载能力，传播常数 决定了电磁波在传输线中的传播速度和相位变化，而电磁波的传播速度则与传输线的材料和结构有关。这些特性 参数对于传输线的性能和信号完整性至关重要。
传输线的应用场景
总结词
传输线在通信、电子、电力等领域有着广泛的应用， 如信号传输、能量传输等。
详细描述
传输线在许多领域都有着广泛的应用，如通信领域中 的信号传输、电力领域中的能量传输等。在通信领域 中，传输线被用于连接各种通信设备，如电话、电视 和互联网设备，实现信号的传输和接收。在电力领域 中，传输线被用于远距离输电和配电，实现电能的传 输和分配。此外，在电子设备中，传输线还被用于连 接各个组件，实现信号的传输和能量的传递。
当传输线中存在电压或电流 变化时，会在传输线周围产 生电磁场，电磁能量会以辐 射的形式向周围空间传播， 形成电磁辐射。同时，这种 电磁辐射可能会对其他电子 设备产生干扰。
E = -dΦ/dt，H = dA/dt， 其中E是电场强度，H是磁场 强度，Φ是磁通量，A是磁 矢量势。
电磁辐射与干扰可能会对其 他电子设备产生干扰，因此 需要进行电磁兼容性设计和 防护措施。同时，电磁辐射 也可以用于通信和探测等领 域。
传输线的传播特性
第二章传输线理论
如果传播方向为Z，则入射波，反射波
将电压的通解代入时谐传输方程中的第一个式子有
dV ( z ) ( R1 jL1 ) I ( z ) dz 1 dV ( z ) 1 I ( z) [A1e z A2ez ] ( R1 jL1 ) dz ( R1 jL1 ) ( R1 jL1 )(G1 jC1 ) [ A1e z A2ez ] ( R1 jL1 )
信号源和负载条件
(i)终端条件:如图所示已知终端的电压和电流分别为VL，IL
V ( z ) A1e Z A2 eZ V (l ) VL A1e l A2 el 1 I ( z) ( A1e Z A2 eZ ) Z0 1 I (l ) I L ( A1e l A2 el ) I L Z 0 A1e l A2 el Z0 联立求解有： VL Z 0 I L l VL Z 0 I L l A1 e , A2 e 2 2
I (0) I 0
联立求解有： V Z0 I0 V Z0 I0 A1 0 , A2 0 2 2 对于传输线上任意一点 z处的电压和电流可以表 示为： V Z 0 I 0 z V0 Z 0 I 0 z V ( z ) A1e z A2 ez 0 e e 2 2 V Z 0 I 0 z V0 Z 0 I 0 z 1 I ( z) ( A1e z A2 ez ) 0 e e（2.1 14） Z0 2 2
(2)时谐传输线方程： 对于单位电阻，电容，电感、电导不随传输线位置变化的
均匀传输线，其电报方程可以简化。均匀传输线上的电压和
电流可以表示为时谐的形式：
v( z , t ) Re{V ( z )e jt } i ( z , t ) Re{ I ( z )e jt }
将电压的通解代入时谐传输方程中的第一个式子有
dV ( z ) ( R1 jL1 ) I ( z ) dz 1 dV ( z ) 1 I ( z) [A1e z A2ez ] ( R1 jL1 ) dz ( R1 jL1 ) ( R1 jL1 )(G1 jC1 ) [ A1e z A2ez ] ( R1 jL1 )
信号源和负载条件
(i)终端条件:如图所示已知终端的电压和电流分别为VL，IL
V ( z ) A1e Z A2 eZ V (l ) VL A1e l A2 el 1 I ( z) ( A1e Z A2 eZ ) Z0 1 I (l ) I L ( A1e l A2 el ) I L Z 0 A1e l A2 el Z0 联立求解有： VL Z 0 I L l VL Z 0 I L l A1 e , A2 e 2 2
I (0) I 0
联立求解有： V Z0 I0 V Z0 I0 A1 0 , A2 0 2 2 对于传输线上任意一点 z处的电压和电流可以表 示为： V Z 0 I 0 z V0 Z 0 I 0 z V ( z ) A1e z A2 ez 0 e e 2 2 V Z 0 I 0 z V0 Z 0 I 0 z 1 I ( z) ( A1e z A2 ez ) 0 e e（2.1 14） Z0 2 2
(2)时谐传输线方程： 对于单位电阻，电容，电感、电导不随传输线位置变化的
均匀传输线，其电报方程可以简化。均匀传输线上的电压和
电流可以表示为时谐的形式：
v( z , t ) Re{V ( z )e jt } i ( z , t ) Re{ I ( z )e jt }