数学(初二升初三)测试卷-1
初二升初三数学测试题

初二升初三(数学)测试题(30分钟)一、选择题1.已知y 1=x-5,y 2=4x-1,使不等式y 1>y 2成立的x 值中最大整数是( ). A .-2 B .-2 C .-1 D .02.如图1所示,已知OA=OB ,OC=OD ,AD ,BC 相交于E ,则图中全等的三角形的个数是(• ).A .2B .3C .4D .5DACEBO③②①DA C(1) (2) (3) 3.如图2所示,某同学将一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ).A .带①去B .带②去C .带③去D .带①②去 4.已知点(-2,y 1),(-1,y 2),(1,y 3)都在直线y=-13x+b 上,则y 1,y 2,y 3的值的大小关系是( ). A .y 1>y 2>y 3 B .y 1<y 2<y 3 C .y 3>y 1>y 2 D .y 3>y 1>y 25.函数y=kx+b 的图像与函数y=-12x+3的图像平行,且与y 轴的交点为M (0,2),•则其函数表达式为( ). A .y=12x+3 B .y=12x+2 C .y=-12x+3 D .y=-12x+26.如图3,△ABC ≌△BAD ,A 和B ,C 和D 是对应顶点,如果AB=6cm ,BD=5cm ,AD=4cm ,•那么BC 的长是( ). A .4cm B .5cm C .6cm D .无法确定7.若直线y=2x+3与y=3x-2b 相交于x 轴上,则b 的值是( ). A .b=-3 B .b=-32 C .b=-94D .b=6 二、解答题1.某车间有20名工人,每人每天加工甲种零件5个或乙种零件4个,在这20名工人中,派x 人加工甲种零件,其余人加工乙种零件,已知每加工一个甲种零件可获利16元,每加一个乙种零件可获利24元. (1)写出此车间每天所获利润y (元)与x (人)之间的函数关系式.(2)若要使车间每天获利不低于1800元,问至少应派多少人加工乙种零件.2.如图,已知AC=AB ,AE=AD ,∠EAB=∠DAC ,问BD 与EC 相等吗?说明理由.EDA3.(探究题)如图所示,∠ACB=∠ADB=90°,AC=AD ,E 在AB 上,试说明:(1)点A•在∠CBD 的平分线上.(2)CD=DE .DACBE。
初二升初三测试完整卷

数学测试卷一、选择题(本大题共12个小题,每小题2分,共24分)在每小题给出的四个选项中,只有一项是符合题目要求的.1、 25的算术平方根是( )A.5B.-5C.±5D.252.、下列计算正确的是 ( ).(A)3232a a a =+ (B)a a 2121=- (C)623)(a a a -=⋅- (D)a a 221=-3、下列说法错误的结论有( )(1)相等的角是对顶角(2)平面内两条直线的位置是相交,垂直,平行(3)若∠A 与B ∠互补,则B A ∠∠2121与互余,(4)同位角相等 (A )1个(B )2个(C )3个 (D )4个4、对于四舍五入得到的近似数3.20×105,下列说法正确的是( )A 、有3个有效数字,精确到百分位B 、有6个有效数字,精确到个位C 、有2个有效数字,精确到万位D 、有3个有效数字,精确到千位5、在ABC △中,34AC BC ==,,则AB 的长是( )A .5B .10C .4D .大于1且小于76、如图,在Rt △ABC 中,∠BAC=90°,∠B=60°,△''C AB 可以由△ABC 绕点A 顺时针旋转90°得到(点'B 于点B 是对应点,点'C 与点C 是对应点),连结'CC ,则∠''B CC 的度数是( )A .45° B.30°C.25°D.15°7、如果a>b ,那么下列各式中正确的是( )A 、a 3<b 3--B 、a b <33C 、a>b --D 、2a<2b -- 8、如果知道a 与b 互为相反数,且x 与y 互为倒数,那么代数式|a + b| - 2xy 的值为 ( )A. 0B.-2C.-1D.无法确定9、二元一次方程{52323=+=-y x y x 的解是 ( )yx 5 20 21 12 A 、 {01==y x B 、{223==y x C 、{232==y x D 、{17-==y x 10、四边形ABCD 的对角线AC ,BD 相交于点O ,且AD ∥BC ,AD=BC ,如果补上下列条件中的( ),可以使四边形ABCD 为矩形。
初二升初三数学真题试卷

一、选择题(每题5分,共25分)1. 下列数中,不是有理数的是()A. 2.5B. -3C. $\sqrt{2}$D. $\frac{1}{3}$2. 下列方程中,解为整数的是()A. 2x + 3 = 7B. 3x - 4 = 11C. 5x + 2 = 18D. 4x - 5 = 103. 已知等腰三角形的底边长为6cm,腰长为8cm,则该三角形的周长为()A. 20cmB. 21cmC. 22cmD. 24cm4. 若函数y = kx + b(k ≠ 0)的图象经过点(2,3),则k和b的值分别为()A. k = 1, b = 1B. k = 1, b = 2C. k = 2, b = 1D. k = 2, b = 35. 一个长方形的长是宽的2倍,如果长方形的周长是40cm,那么这个长方形的长和宽分别是()A. 20cm和10cmB. 18cm和9cmC. 16cm和8cmD. 15cm和7.5cm二、填空题(每题5分,共25分)6. 若a、b是相反数,则a + b = ________。
7. 已知x = 3,那么2x - 1的值为 ________。
8. 下列数中,最小的有理数是 ________。
9. 一个数的平方根是2,那么这个数是 ________。
10. 一个等腰三角形的底边长为10cm,腰长为12cm,那么该三角形的面积是________cm²。
三、解答题(共50分)11. (15分)解下列方程:(1)2(x - 3) = 5x - 8(2)$\frac{1}{3}y + 2 = 4 - \frac{2}{3}y$12. (15分)已知等腰三角形的底边长为10cm,腰长为12cm,求该三角形的面积。
13. (15分)已知一次函数y = kx + b(k ≠ 0)的图象经过点(-1,2)和(3,0),求该一次函数的解析式。
14. (15分)一个长方形的长是宽的3倍,如果长方形的周长是60cm,求这个长方形的长和宽。
初二升初三上下册数学试卷

考试时间:120分钟满分:100分一、选择题(每题2分,共20分)1. 下列各数中,绝对值最小的是()A. -3B. 0C. 1.5D. -2.12. 若 a > b,则下列不等式中正确的是()A. a + 2 > b + 2B. a - 2 < b - 2C. a + 3 < b + 3D. a - 3 > b - 33. 在直角坐标系中,点P(2,-3)关于x轴的对称点坐标是()A.(2,3)B.(-2,-3)C.(-2,3)D.(2,-3)4. 下列函数中,自变量x的取值范围是全体实数的是()A. y = 2x + 1B. y = √(x - 1)C. y = x² - 4D. y = 1/x5. 若a² = b²,则下列说法正确的是()A. a = bB. a = -bC. a = ±bD. a² = b²6. 下列图形中,中心对称图形是()A. 正方形B. 等边三角形C. 等腰梯形D. 等腰直角三角形7. 若 a、b、c 成等差数列,则下列等式中正确的是()A. a + b + c = 0B. ab + bc + ca = 0C. a² + b² + c² = 0D. a³ + b³ + c³ = 08. 下列各式中,正确的是()A. (a + b)² = a² + b²B. (a - b)² = a² - b²C. (a + b)² = a² + 2ab + b²D. (a - b)² = a² - 2ab + b²9. 若x² + y² = 1,则点(x,y)所在的图形是()A. 线段B. 圆C. 直线D. 双曲线10. 下列函数中,一次函数是()A. y = x² + 2x + 1B. y = 2x + 3C. y = √(x - 1)D. y = 1/x二、填空题(每题2分,共20分)11. 若a² = 9,则 a = _______。
初二升初三数学试卷

一、选择题(每题3分,共30分)1. 下列各数中,正整数是()A. -2B. 0C. 3.5D. -1/22. 下列各数中,无理数是()A. √4B. √9C. √25D. √-13. 下列各数中,平方根为正数的是()A. 4B. -4C. 0D. -94. 下列各数中,立方根为负数的是()A. -8B. -27C. 0D. 645. 下列各数中,能被2整除的是()A. 5B. 10C. 15D. 206. 下列各数中,能被3整除的是()A. 4B. 6C. 8D. 107. 下列各数中,能被5整除的是()A. 3B. 10C. 15D. 208. 下列各数中,能被7整除的是()A. 4B. 14C. 21D. 289. 下列各数中,能被11整除的是()A. 12B. 22C. 32D. 4210. 下列各数中,能被13整除的是()A. 14B. 23C. 34D. 43二、填空题(每题5分,共25分)11. 3的平方根是________,9的立方根是________。
12. 下列各数中,-3的平方是________,-2的立方是________。
13. 下列各数中,能被4整除的是________,能被6整除的是________。
14. 下列各数中,能被8整除的是________,能被9整除的是________。
15. 下列各数中,能被10整除的是________,能被12整除的是________。
三、解答题(每题10分,共30分)16. 简化下列各数:(1)√36 + √64 - √81(2)-√25 + √49 - √10017. 求下列各数的平方根和立方根:(1)√-16(2)√-2718. 求下列各数的倒数:(1)1/2(2)-1/3四、应用题(每题15分,共30分)19. 某市一居民小区共有居民150户,其中50户安装了太阳能热水器,30户安装了空气能热水器,安装了太阳能热水器或空气能热水器的居民共有多少户?20. 某商店销售一批商品,原价为每件200元,打八折后每件商品售价为160元。
第十讲-初二升初三衔接班数学考试试卷(一)

图3相帅炮初二升初三衔接班数学考试试卷(一)一、选择题(每小题4分,共32分)1.如果a 为任意实数,下列根式一定有意义的是:( ) a 2a -21a +21a -2. 用配方法解方程2870x x ++=,则配方正确的是:(A)()249x -= (B)()249x += (C)()2816x -= (D)()2857x +=3.化简)0(||2<<--y x x y x 的结果是( )A .x y 2-B .yC .y x -2D .y -4.若一组数据 -2,-1,3,4的方差是 ( )A .5B .6C .6.5D .13 5、已知点P(x,y)的坐标满足方程|x +1|+y -2 =0,则点P 在( )A 、第一象限B 、第二象限C 、第三象限D 、第四象限6、 点()P a a -+12,在x 轴上,则a 的值为 ( ) A. -1 B. 1 C. 2 D. -27、如图(3)所示的象棋盘上,若帅位于点(1,-2)上,相位于点(3,-2)上,则炮位于点( )A .(-1,1)B .(-1,2)C .(-2,1)D .(-2,2)8.武汉市某中学标准化建设规划在校园内的一块长36米,宽20米的矩形场地ABCD 上修建三条同样宽的人行道,使其中两条与AB 平行,另一条与AD 平行,其余部分种草(如图所示),若使每一块草坪的面积都为96平方米.设人行道的宽为x 米,下列方程:① (36-2x )(20-x )=96×6;② 36×20-2×20x-36x=96×6;③ 36×20-2×20x-36x+2x x=96×6;其中正确的个数为( )(A )0个 (B )1个 (C )2个 (D )3个二、填空题(每小题分,共28分)1、函数y =1x -1中自变量x 的取值范围是2、点P (-1,-3)关于y 轴对称的点的坐标是_____________;关于x 轴的对称的点的坐标是 ____________;3、直线y=3-9x 与x 轴的交点坐标为______,与y 轴的交点坐标为______.4、当m = 时,函数221m m y mx +-=是反比例函数.5、已知32+是关于x 的一元二次方程042=+-m x x 的一个根,则m=6、观察下列各式的规律:①322322+=;②833833+=; ③15441544+=;……则第⑩等到式为____________________ 7、如图, A 、B 为双曲线xk y =(x >0)上两点,AC x ⊥轴于C , BD y ⊥轴于D 交AC 于E ,若矩形OCED 面积为2且A D ∥OE , 则k = .三.解下列各题1、(9分)解下列方程:(1)21x -()-4=0 (2)2x —4x—5=0 (3)2512552x x x +=+-2、(7分)已知21y y y +=,1y 与x 成正比例,2y 与x 成反比例,并且当2=x 时,4-=y ,当1-=x 时,5=y ,求出y 与x 的函数关系式3、(8分)小明家、王老师家、学校在同一条路上,小明家到王老师家的路程为3千米,王老师家到学校的路程为0.5千米,由于小明的父母战斗在抗“非典”第一线,为了使他能按时到校,王老师每天骑自行车接小明上学。
初二升初三数学试题及答案

D CBA 、B 、C 、D 、初二升初三数学测试题一、选择题(每小题有且只有一个答案正确,每小题4分,共40分) 1、如图,两直线a ∥b ,与∠1相等的角的个数为( ) A 、1个 B 、2个 C 、3个 D 、4个2、不等式组x>3x<4⎧⎨⎩的解集是( )A 、3<x<4B 、x<4C 、x>3D 、无解 3、如果a>b ,那么下列各式中正确的是( ) A 、a 3<b 3-- B 、a b<33C 、a>b --D 、2a<2b -- 4、如图所示,由∠D=∠C,∠BAD=∠ABC 推得△ABD ≌△BAC ,所用的的判定定理的简称是( ) A 、AAS B 、ASA C 、SAS D 、SSS5、已知一组数据1,7,10,8,x ,6,0,3,若x =5,则x 应等于( ) A 、6 B 、5 C 、4 D 、26、下列说法错误的是( )A 、长方体、正方体都是棱柱;B 、三棱住的侧面是三角形;C 、六棱住有六个侧面、侧面为长方形;D 、球体的三种视图均为同样大小的图形; 7、△ABC 的三边为a 、b 、c ,且2(a+b)(a-b)=c ,则( ) A 、△ABC 是锐角三角形; B 、c 边的对角是直角; C 、△ABC 是钝角三角形; D 、a 边的对角是直角;8、为筹备班级的初中毕业联欢会,班长对全班学生爱吃哪几种水果作了民意调查,那么最终买什么水果,下面的调查数据中最值得关注的是( )A 、中位数;B 、平均数;C 、众数;D 、加权平均数;9、如右图,有三个大小一样的正方体,每个正方体的六个面上都按照相同的顺序,依次标有1,2,3,4,5,6这六个数字,并且把标有“6”的面都放在左边,那么它们底面所标的3个数字之和等于( )A 、8B 、9C 、10D 、1110、为鼓励居民节约用水,北京市出台了新的居民用水收费标准:(1)若每月每户居民用水不超过4立方米,则按每立方米2米计算;(2)若每月每户居民用水超过4立方米,则超过部分按每立方米4.5米计算(不超过部分仍按每立方米2元计算)。
初二升初三数学试卷及答案

7•如图,点F 是ZZ7ABCD 的边CD 上一点,直线BF 交AD 的延长线于点E,则下列结论错 误的是ED DFB. A ・ ~EA= ~~ABC ・ BC BF D.DEBE角线的交点P ,则该反比例函数关系式是QA. y=-(x>0)B.x 4C ・ y=—(x>0)D.x初二数学试卷一. 选择题 本大题共10小题,每小题3分,共30分・在每小题给出的四个选项中.只有 一项是符合题目要求的,请将选择题的答案写在答题纸相应的位置上. 1.若二次根式圧?有意义.则X 的取值范用是 A ・ x<2 B ・ xH2 C ・ x <2 D ・ x$22.正三角形、正方形、等腰直角三角形、平行四边形中,既是轴对称图形又是中心对称图 形的是A.正三角形B.正方形 C ・等腰直角三角形 D.平行四边形 3・对于函数y =仝,下列说法错误的是xA.它的图像分布在第一、三象限B.C.当x>0时,y 的值随x 的增大而增大D. 4. 下列运算正确的是5. 下列各“根式中与是冋类二次根式的是6. 关于频率与概率有下列几种说法:①"明天下雨的概率是90%”表示明天,下雨的可能性很大:②“抛一枚硬币正而朝上的 概率为土”表示每抛两次就有一次正而朝上:③「“某彩票中奖的概率是1%”表示买10张 该种彩票不可能中奖;④“抛一枚硬币正面朝上的概率为表示随着抛掷次数的增加,“抛出正而朝上”这-事件发生的频率稳定在訓近,正确的说法是它的图像与直线y=-x 无交点当xvO 时,y 的值随x 的增大而减小A_x_y x - v 门 a 】_b' a_bA _____ .______ = ____- x+y x+y •a + bC ・x-l 二 1 1-x 2 "x+TD.a 1 -b ,_ d +Z?(a-by a_bc.A /18D.V30B.②③C.②④D.①③ 8.如图,矩形AOBC 中,顶点C 的坐标(4, y=_L(X>0)X00)⑴底”14. 小丽同学想利用树影测量校园内的树髙,•她在某一时刻测得小树髙为l ・5m 时,其影长 为1.2 m,此时她测量教学楼旁的一棵大树影长为5m,那么这棵大树高约 ▲ m.15. 如图,在Z\ABC 中,ZACB=90° , ZA=35° ,若以点C 为旋转中心,>AABC 旋 转0°到ADEC 的位置,使点B 恰好落在边DE 上,则0值等于 ▲・16. 如图,等r 腰梯形ABQD 中,AD 〃BC, AD=2, BC=4,髙DF=2・腹DC 的长等于 ▲ k17. 如图,点A 、B 在反比例函数y= — (k>0, x>0)的图象上,过点A 、B 作x4由的垂线,x 垂足分别为M 、N,延长线段AB 交x 轴于点C,若OM=MN=NC, S ABNC =2,则k 的值 为▲・ 18. 已知n 是正整数,质亦是整数,则n 的最小值是 ▲三. 解答题本大题共11小题,共76分.把解答过程写在答题纸相对应的位置上.解答时 应写岀必要的讣算过程、推演步骤或文字说明.作图时用2B 铅笔或黑色墨水签字笔. 「19.(本题满分8分,每小题4分)计算:x 2 -6A +9 12-4.丫()l + 4x + 4工 丁 2x + l20. (本题满分8分,每小题4分)计算9. 计算Jll4,-64—502的值为 A ・0B ・25C ・50D ・8010. 如图,在AABC 中,ZC=90° , B 「C=6, D, E 分别在 AB, AC 上, 将△ ADE 沿DE 翻折后,点A 落在点A ,处,若A ,为CE 的中点,则 折痕DE 的长为 A ・1B ・2C ・4D ・6二、填空题 本大题共8小题.每小题3分,共24分.把答案直接填在答题纸相对应的位 置上.211・若分式二-涪意义,则a 的取值范囤是—▲・67 + 112.袋中共有2个红球,2个黄球,4个紫球,从中任取一个球是白球,这个事件是一 ▲ 事 件・a 2 - 4 ci" +A n4 + 兀 c 2x —5 = 兀一1兀一122.(本题满分5分)如图,E. F 分别是Z7ABCD 的边BC 、AD ±的点,且BE=DF(1) 求证:四边形AECF 是平行四边形:(2) 若BC=10, ZBAC=90° ,且四边形AECF 是菱形, 求BE 的长.23・(本题满分5分)如图,“优选1号”水稻的实验田是边长为am(a>l)的正方形去掉一 个边长为lm 的正方形蓄水池后余下的部分;"优选2号”水稻的实验田是边长为(a-l)m 的正方形,两块试验田的水稻都收了 600kg. (1) 优选一 ▲号水稻的单位面积产邑髙:(2) “优选2号”水稻的单位而积产量是“优选1号”水稻的单位而积产量的多少倍?(2) 请补全条形统计•图和扇形统计图;(3) 从这次接受调査的学生中,随机抽查一个学生,则抽到持哪一类态度学生的可能性「大?26. (本题满分8分)已知Vw-3 + V2-7F = O(1)求丄+竺的值;>Jm \/n21. (本题满分5分)解方程:24.(本题满分6分)如图,在口XBCD 中,(1) 求证:AADE^ADEC : (2) 若 AD=6, DE=4,求 BE 的长.25.(本题满分6分)“初中生骑电动 车上学”的现象越来越受到社会 的关注,某校利用“五一”假期, 随机抽査了本校若干名学生和部分 家长对“初中生骑电动车上学” 现象的看法,统计整理制作了的统计图,(1)这次抽查的家长总人数是多少?点 E 在 BC 上,ZCDE=ZDAE.人敦 请回答下列问题:""(第25题)(第22顾)(第23廈)电劲车上”的禺废絨计用100 80 60 40 20 0XWifi 反对(第24題更鳥專蠶鴛口 g长(第26题)(2)将如图等腰三角形纸片沿底边BC上的髙AD剪成两个三角形, 英中AB=AC=m, BC=n.用这两个三角形你能拼成多少种平行四边形?分别求岀它们对角线的长(画出所拼成平行四边形的示意图)27.(本题满分8分)如图,在平而直角坐标系中,双曲线经过点B,连结OB.将OB绕点O按顺时针方向旋转90°并延长至A,使OA=2OB,且点A的坐标为(4, 2).(1)求过点B的双曲线的函数关系式:(2)根据反比例函数的图像,指出当x<-l时,y的取值范围:(3)连接AB,在该双曲线上是否存在一点P,使得S AABP=S AABO,若存在,求出点P坐标;若不存在,请说明理由.28.(本题满分8分)喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100C,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温yCC)与时间x(min) 成一次函数关系;停止加热过了1分钟后,水壶中水的温^度y(°C)与时间x (min)近似于反比例函数关系(如图』. 已知水壶中水的初始温度是20°C,降温过程中水温不低于20a C.(1)分别求岀图中所对应的函数。
数学初二升初三测试卷

暑假(秋季)班 初二升初三数学入学测试卷(1)时间:60分钟 满分:100分姓名: 学校: 联系电话: 成绩: 一、选择题(每题5分,共30分)1.下列分式中,不论x 取何值,都有意义的是 A.152--x x B.112+-x x C.xx 312+ D.12+x x 2.已知点A (2,0)、点B (-12)、点C (0,1),以A 、B 、C 三点为顶点画平行四边形,则第四个顶点不可能在( )A.第一象限B.第二象限C.第三象限D.第四象限3.kx-y)4.如图所示,平行四边形ABCD 中,对角线AC和BD相交于点O ,如果AC=12,BD=10,AB=m ,则m 的取值范围是( )A.10<m<12B.2<m<22C.1<m<11D.5<m<65. 如图,已知矩形ABCD 中,R 、P 分别是DC 、BC 上的点,E 、F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )A.线段EF 的长逐渐增大B.线段EF 的长逐渐减小C.线段EF 的长不改变D.线段EF 的长不能确定6.如图,正方形ABCD 中,AB=4,点E ,F 分别在AD ,DC 上,且△BEF 为等边三角形,则△EDF 与△BFC 的面积比为( )A.2:1B.3:1C.3:2D.5:3二、填空题(每题5分,共30分)7.把分式 中的x 、y 都扩大两倍,则分式的值为 .8.直线b kx y +=与15+-=x y 平行,且经过(2,1),则kb = .9.若0414=----xx x m 无解,则m 的值是 . 10.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩是___________分.11.如图,边长为1的正方形ABCD 绕点A 逆时针旋转30°,得到正方形AB′C′D′,则图中阴影部第5题 第4题第6题分的面积为 .12.如图,?ABCD 中,点E 在AB 边上,将△EBC 沿CE 所在直线折叠,使点B 落在AD 边上的点B′处,再将折叠后的图形打开,若△AB′E 的周长为4cm ,△B′DC 的周长为11cm ,则B′D 的长为 cm .三、简答题(共40分)13.(10分)如图,已知菱形ABCD 的周长是4cm ,∠ABC=120°.(1)求对角线BD 和AC 的长.(2)求菱形的面积.14.(10分)在正方形ABCD 中,P 为对角线BD 上一点,PE ⊥BC ,垂足为E ,PF ⊥CD ,垂足为F ,求证:EF=AP .15.(10分)如图所示,在矩形ABCD 中,AB=12厘米,BC=6厘米.点P 沿AB 边从点A 开始向点B 以2厘米/秒的速度移动,点Q 沿DA 边从点D 开始向点A 以1厘米/秒的速移动,如果P 、Q 同时出发,用t (秒)表示移动的时间(0≤t ≤6),那么:(1)当t 为何值时,△QAP 为等腰直角三角形?(2)求四边形QAPC 的面积,并提出一个与计算结果有关的结论.16.(10分)如图,已知反比例函数(0)k y k x=≠的图像经过点(12,8),直线y x b =-+经过该反比例函数图像上的点Q (4,m ).(1)求上述反比例函数和直线的函数表达式;(2)设该直线与x 轴、y 轴分别相交于A 、B 两点,与反比例函数图象的另一个交点为P ,连接0P 、OQ ,求△OPQ 的面积. 博文教育初二升初三数学入学测试卷(1)答案一、选择题1.B2.C3.B4.C5.C6.A二、填空题7.不变(或2x x y +) 8.-55 9.4 10.82 12.3.5 三、简答题13.解:(1)∵菱形ABCD 的周长是4cm , ∴AB=1412cm ⨯=, ∵∠ABC=120°, ∴∠ABO=12⨯120°=60°, ∵菱形的对角线AC⊥BD,∴∠BAO=90°-60°=30°, ∴BO=1122AB =,由勾股定理得,∴BD=2BO=1cm ,(2)菱形的面积=111222AC BD =⨯=cm 2 14.解:EF=AP .理由:∵PE⊥BC,PF⊥CD,四边形ABCD 是正方形,∴∠PEC=∠PFC=∠C=90°,∴四边形PECF 是矩形,连接PC 、AP ,∴PC=EF,∵P 是正方形ABCD 对角线上一点,∴AD=CD,∠PDA=∠PDC, AD =CD在△PAD 和△PCD 中, ∠PDA=∠PDC , PD =PD∴△PAD≌△PCD(SAS ),∴PA=PC,∴EF=AP .15.解:(1)若△QAP 为等腰直角三角形,则只需AQ=AP ,根据题干条件知AQ=6-t ,AP=2t ,列等式得6-t=2t ,解得t=2秒,即当t=2时,△QAP 为等腰直角三角形;(2)四边形QAPC 的面积=矩形ABCD 的面积-三角形CDQ 的面积-三角形PBC 的面积,设DQ=x .根据题干条件可得四边形QAPC 的面积=72-11126(122)22x x -⨯⨯-=72-36=36, 故可得结论四边形QAPC 的面积是矩形ABCD 面积的一半.16. 解 :(1)把点(12,8)代入反比例函数(0)k y k x =≠,得1842k =⨯=, ∴反比例函数的解析式为4y x =; 又∵点Q (4,m )在该反比例函数图象上,∴4?m=4,解得m=1,即Q 点的坐标为(4,1),而直线y x b =-+经过点Q (4,1),∴1=-4+b ,解得b=5,∴直线的函数表达式为5y x =-+;(2)联立 解得 或 ,∴P 点坐标为(1,4),4y x =, x =4 y=1 x =1 y=4对于5y x =-+,令y=0,得x=5, ∴A 点坐标为(5,0),。
初二升初三数学试卷真题

一、选择题(每题5分,共50分)1. 下列数中,是正整数的是()A. -2B. 0C. 1.5D. 32. 下列各数中,属于有理数的是()A. √2B. πC. 3.1415926...D. 0.101001...3. 下列各数中,绝对值最小的是()A. -2B. 2C. 0D. 34. 下列各数中,是最简二次根式的是()A. √18B. √25C. √50D. √815. 下列函数中,是正比例函数的是()A. y = 2x + 3B. y = 3x^2C. y = 2/xD. y = 3x6. 下列方程中,解得x=3的是()A. x - 2 = 1B. 2x + 1 = 7C. 3x - 2 = 5D. 4x + 3 = 117. 下列不等式中,正确的是()A. 3 > 2B. 4 < 3C. 5 = 4D. 6 ≠ 58. 下列各图形中,是圆的是()A. 正方形B. 矩形C. 菱形D. 圆9. 下列各数中,是勾股数的是()A. 3, 4, 5B. 5, 12, 13C. 6, 8, 10D. 7, 24, 2510. 下列各数中,是同类二次根式的是()A. √8和√18B. √12和√27C. √16和√32D. √20和√36二、填空题(每题5分,共50分)11. 计算:(-2)^3 + 3^2 - 5 = _______12. 若a > 0,b < 0,则a + b的值为 _______13. 下列各数中,是负整数的是 _______14. 若a = -3,则|a|的值为 _______15. 下列函数中,是反比例函数的是 _______16. 解方程:2x - 5 = 3,得x = _______17. 下列不等式中,正确的是 _______18. 下列各图形中,是平行四边形的是 _______19. 下列各数中,是同类二次根式的是 _______20. 若a = 3,b = -2,则a^2 - b^2的值为 _______三、解答题(每题20分,共80分)21. (1)化简下列各二次根式:√36√50(2)计算下列各二次根式的乘积:√3 × √27√8 × √222. (1)解下列方程:2x + 3 = 73x - 2 = 5(2)解下列不等式:3x - 2 > 45 - 2x ≤ 323. (1)画出下列各图形:正方形矩形(2)判断下列各图形是否为圆:正方形等边三角形24. (1)计算下列各数的平方根:√16√81(2)计算下列各数的立方根:√27√6425. (1)求下列函数的值:y = 2x + 3,当x = 2时,y = _______ y = 3x - 2,当x = 1时,y = _______(2)判断下列函数的单调性:y = 2x + 1y = 3x^2 - 2x - 1。
初二升初三测试卷

数学入学测试卷姓名:___________________得分______________________一、选择题(每题4分,共40分)1、在-1,0,1,2这四个数中,既不是正数也不是负数的是( )A .-1B .0C .1D .22、今年“五•一”黄金周,我省实现社会消费零售总额约为94亿元.若用科学记数法表示,则94亿可写为( )A .0.94×109B .9.4×109C .9.4×107D .9.4×1083、如图,已知AB ∥DE ,∠ABC=80°,∠CDE=140°,则∠BCD=( )A 、30°B 、40°C 、50°D 、60°4、下列运算正确的是( )A .234a a a ⋅=B .44(a )a -=C .235a a a +=D .235(a )a =5、一元二次方程x(x -2)=2-x 的根是( )A .-1B .2C .1和2D .-1和26、用两个完全相同的直角三角板,不能拼成下列图形的是( )A 、平行四边形B 、矩形C 、等腰三角形D 、梯形7、某市2008年国内生产总值(GDP )比2007年增长了12%,由于受到国际金融危机的影响,预计今年比2008年增长7%,若这两年GDP 年平均增长率为x%,则x%满足的关系是( )A .12%7%x%+=B .(112%)(17%)2(1x%)++=+C .12%7%2x%+=D .2(112%)(17%)(1x%)++=+8、如图,在△ABC 中,AB=AC=5,BC=6,点M 为BC 中点,MN ⊥AC 于点N ,则MN 等于( )A.65B. 95C. 125D. 1659、下面两个多位数1248624…、6248624…,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位.对第2位数字再进行如上操作得到第3位数字…,后面的每一位数字都是由前一位数字进行如上操作得到的.当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是( )A .495B .497C .501D .50310、甲、乙两个准备在一段长为1200米的笔直公路上进行跑步,甲、乙跑步的速度分别为4m/s 和6m/s ,起跑前乙在起点,甲在乙前面100米处,若同时起跑,则两人从起跑至其中一人先到达终点的过程中,甲、乙两之间的距离y (m )与时间t (s )的函数图象是( )A .B .C .D .二、填空题(每题5分,共20分)11、因式分解2ab 2ab a -+ =____________________12、函数y =12x-的自变量x 的取值范围___________________. 13、如图,直线L 过正方形ABCD 的顶点B ,点A 、C 到直线L 的距离分别是1和2,则正方形的边长是 。
初二升初三数学入学测试卷(含答案)
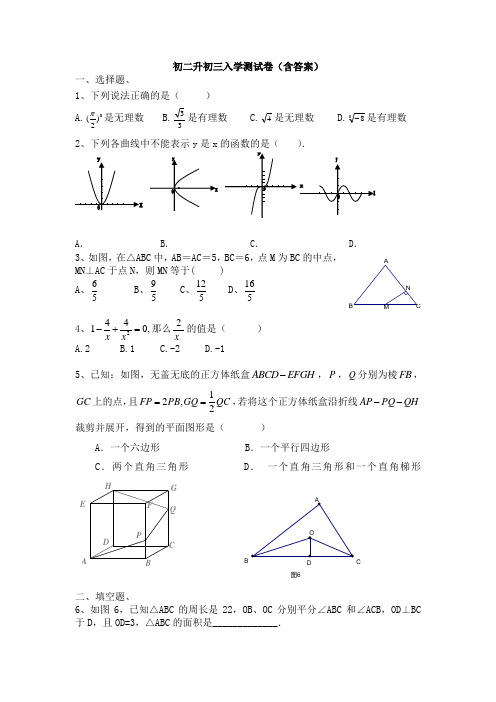
初二升初三入学测试卷(含答案)一、选择题、1、下列说法正确的是( ) A.0)2(π是无理数B.33是有理数 C.4是无理数 D.38-是有理数2、下列各曲线中不能表示y 是x 的函数的是( ).A .B .C .D . 3、如图,在△ABC 中,AB =AC =5,BC =6,点M 为BC 的中点,MN ⊥AC 于点N ,则MN 等于( )A 、65B 、95C 、125D 、1654、,04412=+-x x 那么x2的值是( )A.2B.1C.-2D.-15、已知:如图,无盖无底的正方体纸盒ABCD EFGH -,P ,Q 分别为棱FB ,GC 上的点,且12,2FP PB GQ QC ==,若将这个正方体纸盒沿折线AP PQ QH --裁剪并展开,得到的平面图形是( )A .一个六边形B .一个平行四边形C .两个直角三角形D . 一个直角三角形和一个直角梯形QPHGFED C BA二、填空题、6、如图6,已知△ABC 的周长是22,OB 、OC 分别平分∠ABC 和∠ACB ,OD ⊥BC 于D ,且OD=3,△ABC 的面积是_____________.N MB C A 图6DBC7、.当=m 时,关于x 的方程313292-=++-x x x m 有增根. 8、如图,正方形ABCD 中,AB =6,点E 在边CD 上,且CD =3DE .将△ADE 沿AE对折至△AFE ,延长EF 交边BC 于点G ,连结AG 、CF .下列结论:①△ABG ≌△AFG ;②BG =GC ;③AG ∥CF ;④S △FGC =3.其中正确个数是 。
三、解答题、9、计算:36 -(-2)2 +(214)2+|3.14-π|10、如图,在梯形ABCD 中,DC ‖AB ,AD=BC , BD 平分,60.ABC A ∠∠=o过点D 作DE AB ⊥,过点C 作CF BD ⊥,垂足分别为E 、F ,连接EF ,求证:DEF △为等边三角形.10题图11、如图,直线6y kx =+与x 轴y 轴分别交于点E 、F ,点E 的坐标为(-8,0), 点A 的坐标为(-6,0).(1)求k 的值;(2)若点P (x ,y )是第二象限内的直线上的一个动点,在点P 的运动过程中,试写出△OPA 的面积S 与x 的函数关系式,并写出自变量x 的取值范围;(3)探究:当点P 运动到什么位置时,△OPA 的面积为278,并说明理由.12、以四边形ABCD 的边AB 、BC 、CD 、DA 为斜边分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH .(1)如图1,当四边形ABCD 为正方形时,我们发现四边形EFGH 是正方形;如图2,当四边形ABCD 为矩形时,请判断:四边形EFGH 的形状(不要求证明); (2)如图3,当四边形ABCD 为一般平行四边形时,设∠ADC =α(0°<α<90°), ① 试用含α的代数式表示∠HAE ; ② 求证:HE =HG ;③ 四边形EFGH 是什么四边形?并说明理由.A BCDHEFG(第12题图2)E BFGD HAC(第12题图3)(第12题图1)A BCDH EFG初二升初三数学答案 1~5DBCBB 6、33 7、6或12 8、3个9、解:3.11+π10、证明:因为DC ‖AB ,,60AD BC A =∠=o ,所以60ABC A ∠=∠=o .又因为BD 平分ABC ∠,所以130.2ABD CBD ABC ∠=∠=∠=o因为DC ‖AB ,所以30BDC ABD ∠=∠=o,所以,CBD CDB ∠=∠所以.CB CD =因为CF BD ⊥,所以F 为BD 中点, 又因为DE AB ⊥,所以.DF BF EF == 由30ABD ∠=o,得60BDE ∠=o, 所以DEF △为等边三角形.11、解:(1)把点E 的坐标为(-8,0)代入6y kx =+,得0=-8k+634k =;(2)∵点A 的坐标为(-6,0), ∴OA=6.∵点P (x ,y )是第二象限内的直线上的一个动点,E (-8,0);∴-8<x <0, >0. ∴△OPA 的面积 ∴(3)把S=278代入9184S x =+,得364y x =+364y x =+119366182244S OA y x x ⎛⎫=⨯=⨯⨯+=+ ⎪⎝⎭918(80)4S x x =+-<<132x =-. 再把132x =-代入 ,得98y =∴当P 点的坐标为139,28⎛⎫- ⎪⎝⎭时,△OPA 的面积为278.12、(1)四边形EFGH 是正方形. (2) ①∠HAE=90°+a .在□ABCD 中,AB ∥CD ,∴∠BAD=180°-∠ADC=180°-a ; ∵△HAD 和△EAB 都是等腰直角三角形,∴∠HAD=∠EAB=45°,∴∠HAE=360°-∠HAD -∠EAB -∠BAD =360°-45°-45°-(180°-a )=90°+a .②∵△AEB 和△DGC 都是等腰直角三角形,∴AE=2AB ,DG=2CD ,在□ABCD 中,AB=CD ,∴AE=DG ,∵△HAD 和△GDC 都是等腰直角三角形, ∴∠DHA=∠CDG= 45°,∴∠HDG=∠HAD +∠ADC +∠CDG =90°+a =∠HAE . ∵△HAD 是等腰直角三角形,∴HA=HD ,∴△HAE ≌△HDG ,∴HE=HG . ③四边形EFGH 是正方形.由②同理可得:GH=GF ,FG=FE ,∵HE=HG (已证),∴GH=GF=FG=FE , ∴四边形EFGH 是菱形;∵△HAE ≌△HDG (已证),∴∠DHG=∠AHE , 又∵∠AHD=∠AHG +∠DHG=90°,∴∠EHG=∠AHG +∠AHE =90°, ∴四边形EFGH 是正方形.364y x =+。
初二升初三数学测试卷

初二升初三数学测试卷.d o c(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--初 二 升 初 三 数 学 入 学 测 试 卷 测试时间: 姓名: 成绩:1、若不等式组0,122x a x x +⎧⎨->-⎩≥有解,则a 的取值范围是( )A .1a >-B .1a -≥C .1a ≤D .1a <2、将分式2x x y +中的x 、y 的值同时扩大2倍,则扩大后分式的值( )A 、扩大2倍B 、缩小2倍C 、保持不变D 、无法确定3、某村计划新修水渠3600米,为了让水渠尽快投入使用,实际工作效率是原计划工作效率的倍,结果提前20天完成任务,若设原计划每天修水渠x 米,则下面所列方程正确的是( )A .360036001.8x x = B .36003600201.8x x -= C .36003600201.8x x -= D .36003600201.8x x+= 4、下列命题,正确的是( )A.如果|a |=|b |,那么a=bB.等腰梯形的对角线互相垂直C.顺次连结四边形各边中点所得到的四边形是平行四边形D.平行四边形不是中心对称图形5、在体育课上,八年级2名学生各练习10次立定跳远,要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生立定跳远成绩的 (A)方差 (B)平均数 (C)频率分布 (D)众数6 、如图,已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ,且与直角边AB相交于点C .若点A 的坐标为(6-,4),则△AOC 的面积为 A .12 B .9 C .6 D .4(6题图)DBAyxOC (8题图)7、已知x+y=1,则222121y xy x ++= ;8.如图所示,直线y =x +1与y 轴相交于点A 1,以OA 1为边作正方形OA 1B 1C 1,记作第一个正方形;然后延长C 1B 1与直线y =x +1相交于点A 2,再以C 1A 2为边作正方形C 1A 2B 2C 2,记作第二个正方形;同样延长C 2B 2与直线y =x +1相交于点A 3,再以C 2A 3为边作正方形C 2A 3B 3C 3,记作第三个正方形;…依此类推,则B 3坐标为________,B n 坐标为________, 9、已知线段a,b,d,c 成比例线段,a=3cm,b=2cm,c=6cm 则d= cm 。
人教版八年级升九年级数学测试卷

人教版八年级升九年级数学测试卷一. 选择题(每小题有四个选项,其中只有一个是正确的,请把正确选项的序号填在下表中的相应位置,每小题2分,共20分)1.下列式子不属于分式方程的是 A.21211=++-x x x B.211=+x x C.212131-=++x x D.251=+x x 2.关于x 的一元二次方程02=+k x 有实数根,则 K 的取值范围为3.一元二次方程12)3)(31(2+=-+x x x 化为一般形式为: ,二次项系数为: ,一次项系数为: ,常数项为: 。
4.若方程2x +8x-4=0的两根为1x 、2x 则11x +21x =5.直角三角形的斜边长为10,一直角边长是另一直角边长的3倍,则直角三角形的面积为A.12B.13C.14D.15 6.如图,已知四边形ABCD 是平行四边形,下列结论中不正确的是A.当AB=BC 时,它是菱形B.当AC ⊥BD 时,它是菱形C.当∠ABC=90°时,它是矩形D.当AC=BD 时,它是正方形7.菱形ABCD 的∠DAB=80°,AB 的垂直平分线交对角线AC 于F ,连DF ,则∠CDF=A.50°B.40°C.75°D.60°8.在四边形ABCD 中,O 是对角线的交点,能判定这个四边形是正方形的条件是A .AC=BD ,AD //CD;B .AD ∥BC ,∠A=∠C;C .AO=BO=OC=DO;D .AO=CO=BO=DO ,AB=BC9.已知函数y=kx 中,y 随x 的增大而增大,那么函数y=k x的图像大致是10.为响应承办“绿色奥运”的号召,八年级(1)班全体师生义务植树300棵.原计划每小时植树x 棵,但由于参加植树的全体师生植树的积极性高涨,实际工作效率提高为原计划的1.2倍,结果提前20分钟完成任务.则下面所列方程中,正确的是A .3002030060 1.2x x -= B .300300201.2x x -= C .300300201.260x x x -=+ D .300300201.260x x =- 二、填空题(每小题3分,共24分)D11.x_______时,分式5345x x -+有意义; 12.已知()21213x y -+-与21025z z -+互为相反数,则以x 、y 、z 为边的三角形是 三角形。
八年级升九年级数学测试

八年级升九年级数学考试试题一、选择题(每小题3分,共30分)1、在函数y=1x-3 中,自变量x 的取值范围是 ( )A .3x ≠B .0x ≠C .3x >D .3x =2、下列计算正确的是 ( )A .623x x x= B .()248139x x --= C.1112a a a --= D.()021x +=3、下列说法中错误的是 ( )A .两条对角线互相平分的四边形是平行四边形;B .两条对角线相等的四边形是矩形;C .两条对角线互相垂直的矩形是正方形;D .两条对角线相等的菱形是正方形 4、刘翔为了迎战2008年北京奥运会刻苦进行110米拦训练,教练对他的10次训练成绩进行统计分析,若要判断他的成绩是否稳定,则教练需要知道刘翔这10次成绩的 ( )A .平均数B .中位数C .众数D .方差 5、点P (3,2)关于x 轴的对称点'P 的坐标是 ( ) A .(3,-2) B .(-3,2) C .(-3,-2) D .(3,2)6、下列运算中正确的是 ( )A .1y x x y +=B .2233x y x y +=+C .221x y x y x y +=-- D . 22x y x y x y+=++ 7、如图,已知P 、Q 是△ABC 的BC 边上的两点,且BP=PQ=QC=AP=AQ,则∠BAC 的大小为 ( )A .120°B .110°C .100°D .90°8、如图,在□ABCD的面积是12,点E ,F 在AC 上,且AE =EF =FC ,则△BEF 的面积为 ( )A. 6B. 4C. 3D. 29、小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了骑车的速度继续匀速行驶,下面是行CQ P B AECBDAyxoyxoyxoyxo使路程s (米)关于时间t (分)的函数图象,那么符合这个同学行驶情况的图像大致是 ( )A .B .C .D .10、如图是用若干个全等的等腰梯形拼成的图形,下列说法错误的是( ) A.梯形的下底是上底的两倍 B.梯形最大角是120° C.梯形的腰与上底相等 D.梯形的底角是60°二、填空题(每小题3分,共30分)11、若分式x 2-4x 2-x-2的值为零,则x 的值是 .12、已知1纳米=1109 米,一个纳米粒子的直径是35纳米,这一直径可用科学计数法表示为米.13、如图,已知OA =OB ,点C 在OA 上,点D 在OB 上,OC =OD ,AD 与BC 相交于点E ,那么图中全等的三角形共有 对.14、如图,ACB DFE BC EF ==∠∠,,要使ABC DEF △≌△,则需要补充一个条件,这个条件可以是 .15、已知y 与x-3成正比例,当x=4时,y=-1;那么当x=-4时,y= 。
初二下数学升初三试卷

1. 下列数中,哪个是质数?A. 13B. 12C. 11D. 102. 下列图形中,哪个图形的对称轴最多?A. 矩形B. 正方形C. 圆D. 三角形3. 在等腰三角形ABC中,AB=AC,如果∠B=50°,那么∠A的度数是:A. 40°B. 50°C. 60°D. 70°4. 一个长方形的长是8厘米,宽是5厘米,它的周长是:A. 17厘米B. 20厘米C. 23厘米D. 25厘米5. 下列分数中,哪个是最简分数?A. 3/4B. 4/5C. 5/6D. 6/76. 一个圆的半径增加了50%,那么它的面积增加了:A. 50%B. 100%C. 150%D. 200%7. 下列方程中,哪个方程的解是x=2?A. 2x-1=3B. 3x+2=7C. 4x-3=5D. 5x+4=98. 在一个等腰三角形中,如果底边长为6厘米,腰长为8厘米,那么这个三角形的面积是:A. 24平方厘米B. 28平方厘米C. 32平方厘米D. 36平方厘米9. 下列数中,哪个数是负数?A. -5B. 5C. 0D. 310. 下列图形中,哪个图形是中心对称图形?A. 正方形B. 矩形C. 等腰三角形D. 三角形二、填空题(每题3分,共30分)1. 1/2 + 3/4 = ________2. 5/6 - 2/3 = ________3. 2x - 3 = 7,那么x = ________4. 3(x+2) = 15,那么x = ________5. 下列数中,哪个是正数?A. -3B. 0C. 3D. -26. 下列图形中,哪个图形是轴对称图形?A. 正方形B. 矩形C. 等腰三角形D. 三角形7. 下列数中,哪个数是负数?A. -5B. 5C. 0D. 38. 下列图形中,哪个图形是中心对称图形?A. 正方形B. 矩形C. 等腰三角形D. 三角形9. 一个圆的半径是4厘米,那么它的周长是 ________ 厘米。
初二升初三第一次阶段性测试卷

4
(2)若平行于 AB 的直线与双曲线只有一个公共点,求公共点的坐标.
(图 10)
B 卷(共 50 分) 一、填空题(共 5 个小题,每小题 4 分,共 20 分)
21.点 A 在反比例函数 y= k 的图象上,AB 垂直于 x 轴于 B,若 S△AOB=4,
7.如图 1,在△ABC 中, ÐACB = 90! , CD ^ AB 于 D ,若 AC = 2 3 , AB = 3 2 ,
则 tan ÐBCD 的值为( )
A. 2
B. 2 2
C. 6 3
D. 3 3
8. 在同一直角坐标系中,函数 y = k (k ¹ 0) 与 y = kx + k(k ¹ 0) 的图象大致是( ) x
(图 7)
2
四川天地人教育
(2)若反比例函数的图象 y = 3 与直线 y = ax + 2 另一个交点为 B,求 DAOB 的面积. x
18.如图 8,在 △ABC 中, D 是 BC 边上的一点, E 是 AD 的
中点,过 A 点作 BC 的平行线交 CE 的延长线于 F ,且 AF = BD ,连结 BF . E
C.ax2+bx+c=0 D.x2+2x=x2-1
2.配方法解一元二次方程 x2+8x+7=0,则方程可变形为( ).
A.(x-4)2=9
B.(x+4)2=9 C.(x-8)2=16 D.(x+8)2=57
3.已知 Rt△ABC 中,∠C=90°,AC=2,BC=3,那么下列各式中,正确的是( )
2
x
那么这个反比例函数的解析式为________.
八年级升九年级数学试卷

八年级升九年级数学试卷一、选择题(每题3分,共36分)( )1、若点A (3-m ,m 31-)在第三象限,则m 的取值范围是A .31>m B .3<m C .3>m D . 331<<m ( )2、关于x 的方程5-)1(x a -=x 8-x a )3(-的解为负数,则a 的取值范围A 、4-<aB 、5>aC 、5->aD 、5-<a( )3、如果等腰三角形一个底角是o30,那么顶角是A 、o60 B 、o150 C 、o120 D 、o75( )4、用表示三种不同的物体,现放在天平上比较两次,情况如图所示,那么这三种物体按质量从大到小的顺序排列应为 A . BC . D把不等式组的解集表示在数轴上,正确的是( )5、B 、A 、C 、D 、( )6 在函数23-=x y ,x y -=21 ,231x y +=, 52xy =中,y 随x 的增加而增加的有A 、1个B 、2个C 、3个D 、4个( )7、下列图形分别是桂林、湖南、甘肃、佛山电视台的台徽,其中为轴对称图形的是A 、B 、C 、D 、( )8、反比例函数1y x=的图象位于 b a c a b c a b c a b c ab c 第4题图A .第一、二象限B .第一、三象限C .第二、四象限D .第三、四象限( )9、如图,长方体的底面边长分别为2和4,高为5.若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂蚁爬行的最短路径长为A.13cmB.12cmC.10cmD.8cm ( )10、如图,P (x ,y )是反比例函数xy 3=的图象在第一象限分支上的一个动点,PA ⊥x 轴于点A ,PB ⊥y 轴于点B ,随着自变量x 的增大,矩形OAPB 的面积A . 不变B .增大C .减小D .无法确定( )11、若点(-3,y 1)、(-2,y 2)、(1,y 3)在反比例函数的图像xy 2=上,则下列结论正确的是A .321y y y >>B .312y y y >>C .213y y y >>D .123y y y >>( )12、 二次函数k x x y ++-=22的部分图象如图所示,则关于x 的一元二次方程k x x y ++-=22的一个解31=x ,另一个解=2xA 、1B 、-1C 、-2D 、0、二、填空题(每空2分,共20分)1、一次函数13+-=x y 的图象不经过第 象限.2、抛物线362+-=x x y 的顶点坐标是________.3、小颖同学想用“描点法”画二次函数2(0)y ax bx c a =++≠的图象,取自变量x 的5个值,分别计算出对应的y 值,如下表:… 0 1 2 ……112-125…由于粗心,小颖算错了其中的一个y 值,请你指出这个算错的y 值所对应的=x _ ___. 4、(1)一组数据5 7 7 x 中位数与平均数相等,则x 的值为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
暑假(秋季)班 初二升初三数学入学测试卷(1) 时间:60分钟 满分:100分 姓名: 学校: 联系电话: 成绩:
一、选择题(每题5分,共30分)
1.下列分式中,不论x 取何值,都有意义的是
A.152--x x
B.112+-x x
C.x
x 312+ D.12+x x 2.已知点A (2,0)、点B (-
12)、点C (0,1),以A 、B 、C 三点为顶点画平行四边形,则第四个顶点不可能在( )
(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
3.正比例函数kx y =- k 与反比例函数x k y =
在同一坐标系内的图象为( )
A. B. C. D.
4.如图所示,平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果AC=12,BD=10,AB=m ,则m 的取值范围是( )
<m<12 <m<22 <m<11 <m<6
5. 如图,已知矩形ABCD 中,R 、P 分别是DC 、BC 上的点,E 、F 分别是AP 、RP 的中点,当P 在BC 上从B 向C 移动而R 不动时,那么下列结论成立的是( )
A.线段EF 的长逐渐增大
B.线段EF 的长逐渐减小
C.线段EF 的长不改变
D.线段EF 的长不能确定
6.如图,正方形ABCD 中,AB=4,点E ,F 分别在AD ,DC 上,且△BEF 为等边三角形,则△EDF 与△BFC 的面积比为( )
:1 :1 :2 :3
二、填空题(每题5分,共30分) ( 7.把分式 中的x 、y 都扩大两倍,则分式的值为 .
8.直线b kx y +=与15+-=x y 平行,且经过(2,1),则kb = .
o }
o x o y x y x & x y x 第5题 第4题 2x
x y +第6题
9.若0414=----x
x x m 无解,则m 的值是 . 10.某学生在一次考试中,语文、数学、英语三门学科的平均成绩是80分,物理、化学两门学科的平均成绩为85分,则该学生这五门学科的平均成绩是___________分.
11.如图,边长为1的正方形ABCD 绕点A 逆时针旋转30°,得到正方形AB′C′D′,则图中阴影部分的面积为 .
12.如图,▱ABCD 中,点E 在AB 边上,将△EBC 沿CE 所在直线折叠,使点B 落在AD 边上的点B′处,再将折叠后的图形打开,若△AB′E 的周长为4cm ,△B′DC 的周长为11cm ,则B′D 的长为 cm .
三、简答题(共40分)
…
13.(10分)如图,已知菱形ABCD 的周长是4cm ,∠ABC=120°.
(1)求对角线BD 和AC 的长.
(2)求菱形的面积.
{
14.(10分)在正方形ABCD 中,P 为对角线BD 上一点,PE ⊥BC ,垂足为E ,PF ⊥CD ,垂足为F , 求证:EF=AP .
|
(
第12题
第11题
15.(10分)如图所示,在矩形ABCD 中,AB=12厘米,BC=6厘米.点P 沿AB 边从点A 开始向点B 以2厘米/秒的速度移动,点Q 沿DA 边从点D 开始向点A 以1厘米/秒的速移动,如果P 、Q 同时出发,用t (秒)表示移动的时间(0≤t ≤6),那么:
(1)当t 为何值时,△QAP 为等腰直角三角形?
(2)求四边形QAPC 的面积,并提出一个与计算结果有关的结论.
{
,
16.(10分)如图,已知反比例函数(0)k y k x =
≠的图像经过点(12,8),直线y x b =-+经过该反比例函数图像上的点Q (4,m ).
(1)求上述反比例函数和直线的函数表达式;
(2)设该直线与x 轴、y 轴分别相交于A 、B 两点,与反比例函数图象的另一个交点为P ,连接0P 、OQ ,求△OPQ 的面积.
!
\ 博文教育初二升初三数学入学测试卷(1)答案 一、选择题
二、填空题
7.不变(或2x
x y +) 11.33
3- 三、简答题
13.解:(1)∵菱形ABCD 的周长是4cm ,
∴AB=1
412cm ⨯=,
;
∵∠ABC=120°,
∴∠ABO=1
2⨯120°=60°,
∵菱形的对角线AC ⊥BD ,
∴∠BAO=90°-60°=30°,
∴BO=11
22AB =,
由勾股定理得,AO=2
2223112BO AB -=-=
∴BD=2BO=1cm ,
AC=2AO=3.
(2)菱形的面积=1
1
331222AC BD =⨯⨯=cm 2
14.解:EF=AP .理由:
∵PE ⊥BC ,PF ⊥CD ,四边形ABCD 是正方形,
∴∠PEC=∠PFC=∠C=90°,
∴四边形PECF 是矩形,
连接PC 、AP ,
∴PC=EF ,
∵P 是正方形ABCD 对角线上一点,
∴AD=CD ,∠PDA=∠PDC ,
】
AD =CD
在△PAD 和△PCD 中, ∠PDA =∠PDC,
PD =PD
∴△PAD ≌△PCD (SAS ),
∴PA=PC ,
∴EF=AP. 15.解:(1)若△QAP 为等腰直角三角形,则只需
AQ=AP ,
根据题干条件知AQ=6-t ,AP=2t ,
列等式得6-t=2t ,解得t=2秒,
即当t=2时,△QAP 为等腰直角三角形;
(2)四边形QAPC 的面积=矩形ABCD 的面积-三角形CDQ 的面积-三角形PBC 的面积,
设DQ=x .根据题干条件可得四边形QAPC 的面积=72-11126(122)22
x x -⨯⨯-=72-36=36, 故可得结论四边形QAPC 的面积是矩形ABCD 面积的一半.
16. 解 :(1)把点(
12,8)代入反比例函数(0)k y k x =≠,得1842
k =⨯=, ∴反比例函数的解析式为4y x =; ~
又∵点Q (4,m )在该反比例函数图象上,
∴4•m=4,
解得m=1,即Q 点的坐标为(4,1), 而直线y x b =-+经过点Q (4,1),
∴1=-4+b ,
解得b=5,
∴直线的函数表达式为5y x =-+;
(2)联立 解得 或 ,
∴P 点坐标为(1,4),
对于5y x =-+,令y=0,得x=5,
∴A 点坐标为(5,0),
5y x =-+ 4y x =, x =4 y=1 x =1 y=4。
