算法设计论文-PID算法实例
PID算法程序范文

PID算法程序范文PID控制器是一种常用的反馈控制算法,用于实时地调整控制系统的输出,以使得被控对象的输出尽可能接近设定值。
PID控制器由比例项(P)、积分项(I)和微分项(D)组成,通过对这三个项的调节,可以实现对被控对象的精确控制。
下面是一个简单的PID算法程序的示例,使用C语言编写:```c#include <stdio.h>//定义PID参数#define KP 0.5 // 比例增益#define KI 0.2 // 积分增益#define KD 0.1 // 微分增益//定义全局变量int error = 0; // 当前误差int last_error = 0; // 上一次误差int integral = 0; // 积分项int derivative = 0; // 微分项int output = 0; // 控制器输出//定义被控对象模拟函数int simulate_plant(int control_input)static int actual_output = 0; // 被控对象的输出actual_output += control_input; // 模拟被控对象的响应return actual_output;//PID算法函数int pid_algorithm(int setpoint, int actual_output)error = setpoint - actual_output; // 计算当前误差//计算比例项int proportional = KP * error;//计算积分项integral = integral + error;int integral_term = KI * integral;//计算微分项derivative = error - last_error;int derivative_term = KD * derivative;//计算PID控制器的输出output = proportional + integral_term + derivative_term; //更新上一次误差供下一次计算使用last_error = error;return output;int mai//设置目标值和初始被控对象输出值int setpoint = 50;int actual_output = 0;//模拟实时控制过程,循环100次for (int i = 0; i < 100; ++i)//调用PID算法计算控制器输出int control_input = pid_algorithm(setpoint, actual_output);//更新被控对象的输出actual_output = simulate_plant(control_input);//输出当前相关变量值供调试printf("Error: %d, Control Input: %d, Actual Output: %d\n", error, control_input, actual_output);}return 0;```上述代码中,`KP`、`KI`和`KD`分别表示比例增益、积分增益和微分增益,根据实际控制系统的需求进行调节。
PID算法实例

signed int uk1; //对u[k]四舍五入取整
signed int adjust; //调节器输出调整量
//变量初始化
Kp=4;
Ti=0.005;
T=0.001;
// Ki=KpT/Ti=0.8,微分系数Kd=KpTd/T=0.8,Td=0.0002,根据实验调得的结果确定这些参数
ek=0;
ek1=0;
ek2=0;
uk=0;
uk1=0;
adjust=0;
intpiadjust(float ek) //PI调节算法
{
if( gabs(ek)<0.1 )
adjust=0;
else
{
uk=Kp*(ek-ek1)+Ki*ek; //计算控制增量
ek1=ek;
uk1=(signed int)uk;
{
EvaRegs.CMPR3=EvaRegs.CMPR3+piadjust(ek);//误差较小PID调节稳住
if(EvaRegs.CMPR3>=890)
{
EvaRegs.CMPR3=890; //限制PWM占空比
}
}
PID 算法应用实例
一、PID算法:
比例、积分、微分控制,简称PID控制,又称PID调节;
二、应用环境:
当被控对象的结构和参数不能完全掌握,或得不到精确的数学模型时,控制理论的其它技术难以采用时,系统控制器的结构和参数必须依靠经验和现场调试来确定;
三、PID算法应用实例
四、参数调整
PID控制器参数选择的方法很多,例如试凑法、临界比例度法、扩充临界比例度法等。但是,对于PID控制而言,参数的选择始终是一件非常烦杂的工作,需要经过不断的调整才能得到较为满意的控制效果。依据经验,一般PID参数确定的步骤如下:
PID控制原理的应用论文

PID控制原理的应用论文引言在控制系统中,PID控制算法是一种常用且广泛应用的控制算法。
PID控制器主要由比例、积分和微分三个部分组成,它通过不断调整控制器输出信号,使得控制对象的输出与期望值尽可能接近。
本篇论文主要探讨PID控制原理的应用,并结合实际案例来说明其有效性和优势。
PID控制原理比例控制比例控制基于系统的偏差来调整控制器的输出。
它通过将偏差乘以比例系数来产生输出信号,该输出信号的大小与输入偏差成正比。
比例控制适用于一些偏差较大、但变化较慢的系统。
积分控制积分控制用于补偿系统的累积误差。
它通过将偏差的累积值乘以积分系数,并对其进行积分来产生输出信号。
积分控制可以快速减小系统误差,并且可用于补偿系统的静态误差。
微分控制微分控制用于预测系统未来的行为。
它通过将偏差的变化率乘以微分系数,来产生输出信号。
微分控制可以使系统更加稳定,并且适用于一些快速变化的系统。
PID控制器PID控制器将比例、积分和微分控制结合起来,使得控制器能够更好地适应不同的系统需求。
PID控制器的数学表达式为:u(t) = Kp * e(t) + Ki * ∫e(t) dt + Kd * de(t)/dt其中,u(t)为PID控制器的输出,e(t)为输入偏差,Kp、Ki、Kd分别为比例、积分和微分系数。
实际应用案例为了说明PID控制原理的应用,以温度控制系统为例进行分析。
温度控制系统简介温度控制系统是一个常见的工业控制系统。
在一个温度控制系统中,温度传感器测量当前环境温度,并将数据传递给PID控制器。
PID控制器根据实际温度与期望温度的差异来调整附加设备(如加热器或冷却器)的输出,以使得温度保持在期望值附近。
PID控制器在温度控制系统中的应用在温度控制系统中,PID控制器可以根据温度偏差来控制附加设备的输出。
通过不断调整控制器的输出信号,温度可以稳定在期望值附近。
具体的控制过程包括以下几个步骤:1.温度传感器测量当前温度。
PID控制算法实例_电机_温度
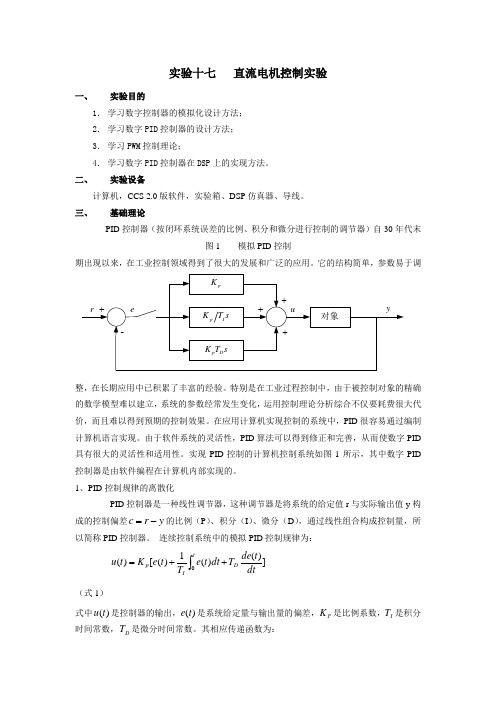
实验十七 直流电机控制实验一、 实验目的1. 学习数字控制器的模拟化设计方法;2. 学习数字PID 控制器的设计方法;3. 学习PWM 控制理论;4. 学习数字PID 控制器在DSP 上的实现方法。
二、实验设备 计算机,CCS 2.0版软件,实验箱、DSP 仿真器、导线。
三、基础理论 PID 控制器(按闭环系统误差的比例、积分和微分进行控制的调节器)自30年代末图1 模拟PID 控制期出现以来,在工业控制领域得到了很大的发展和广泛的应用。
它的结构简单,参数易于调整,在长期应用中已积累了丰富的经验。
特别是在工业过程控制中,由于被控制对象的精确的数学模型难以建立,系统的参数经常发生变化,运用控制理论分析综合不仅要耗费很大代价,而且难以得到预期的控制效果。
在应用计算机实现控制的系统中,PID 很容易通过编制计算机语言实现。
由于软件系统的灵活性,PID 算法可以得到修正和完善,从而使数字PID 具有很大的灵活性和适用性。
实现PID 控制的计算机控制系统如图1所示,其中数字PID 控制器是由软件编程在计算机内部实现的。
1、PID 控制规律的离散化PID 控制器是一种线性调节器,这种调节器是将系统的给定值r 与实际输出值y 构成的控制偏差y r c -=的比例(P )、积分(I )、微分(D ),通过线性组合构成控制量,所以简称PID 控制器。
连续控制系统中的模拟PID 控制规律为:])()(1)([)(0dtt de T dt t e T t e K t u D t I p ++=⎰ (式1)式中)(t u 是控制器的输出,)(t e 是系统给定量与输出量的偏差,P K 是比例系数,I T 是积分时间常数,D T 是微分时间常数。
其相应传递函数为:)11()(s T sT K s G D I p ++= (式2) 比例调节器、积分调节器和微分调节器的作用:(1)比例调节器:比例调节器对偏差是即时反应的,偏差一旦出现,调节器立即产生控制作用,使输出量朝着减小偏差的方向变化,控制作用的强弱取决于比例系数P K 。
pid位置控制算法例题

pid位置控制算法例题PID(比例-积分-微分)控制是一种常用的控制算法,用于控制系统以使其输出接近预期值。
PID控制算法广泛应用于工业自动化、机械系统、电子设备等领域。
本文将为您提供一个关于PID位置控制算法的例题,并详细讨论实现过程。
1. 问题描述假设有一个电动机控制系统,包括电动机和位置传感器。
控制系统的目标是控制电机的位置,使其达到预定的目标位置。
系统的输入是电机的控制信号,输出是电机的位置。
控制器根据目标位置和当前位置之间的误差来调整控制信号,使得误差收敛到0。
现在,我们需要设计一个PID位置控制算法,实现电机位置的精确控制。
2. 算法设计2.1 比例控制比例控制是PID控制算法的核心部分之一。
它根据误差的大小来产生控制信号。
比例控制的计算公式为:\[P = K_p \cdot e(t)\]其中,P是比例控制的输出,Kp称为比例增益,e(t)是目标位置与当前位置之间的误差。
比例增益决定了调节幅度,增大比例增益可加快调节速度,但也可能引入振荡和不稳定性。
2.2 积分控制积分控制用于消除比例控制的静差。
它将误差的累积值乘以积分增益,并将结果添加到控制信号中。
积分控制的计算公式为:\[I = K_i \cdot \int e(t)dt\]其中,I是积分控制的输出,Ki称为积分增益。
积分增益决定了调节的准确性,增大积分增益可减小调节静差,但可能引入过调和不稳定等问题。
2.3 微分控制微分控制用于改善系统的动态响应。
它测量误差的变化率,并将其乘以微分增益,然后将结果与控制信号相加。
微分控制的计算公式为:\[D = K_d \cdot \frac{de(t)}{dt}\]其中,D是微分控制的输出,Kd称为微分增益。
微分增益决定了调节的稳定性,增大微分增益可抑制系统的振荡和不稳定,但也可能降低调节速度。
2.4 PID控制PID控制将比例、积分和微分控制结合起来,形成最终的控制信号。
PID控制的计算公式为:\[u(t) = P + I + D\]其中,u(t)是PID控制的输出,P是比例控制输出,I是积分控制输出,D是微分控制输出。
毕业设计论文——基于模糊PID算法的小型四旋翼无人飞行器控制系统设计

摘要四旋翼飞行器是一种四螺旋桨驱动的、可垂直起降的飞行器,这种结构被广泛用于微小型无人飞行器的设计,可以应用到航拍、考古、边境巡逻、反恐侦查等多个领域,具有重要的军用和民用价值。
四旋翼飞行器同时也具有欠驱动、多变量、强耦合、非线性和不确定等复杂特性,对其建模和控制是当今控制领域的难点和热点话题。
本次设计对小型四旋翼无人直升机的研究现状进行了细致、广泛的调研,综述了其主要分类、研究领域、关键技术和应用前景,然后针对圆点博士的四旋翼飞行器实际对象,对其建模方法和控制方案进行了初步的研究。
首先,针对四旋翼飞行器的动力学特性,根据欧拉定理以及牛顿定律建立四旋翼无人直升机的动力学模型,并且考虑了空气阻力、转动力矩对于桨叶的影响,建立了四旋翼飞行器的物理模型;根据实验数据和反复推算,建立系统的仿真状态方程;在Matlab环境下搭建了四旋翼飞行器的非线性模型。
选取四旋翼飞行器的姿态角作为控制对象,借助Matlab模糊工具箱设计了模糊PID控制器并依据专家经验编辑了相应的模糊规则;通过仿真和实时控制验证了控制方案的有效性,并在此控制方案下采集到了输入输出数据;利用单片机编写模糊PID算法控制程序,实现对圆点博士四旋翼飞行器实物的姿态控制。
本设计同时进行了Matlab仿真和实物控制设计,利用模糊PID算法,稳定有效的对四旋翼飞行器的姿态进行了控制。
关键词:四旋翼飞行器;模糊PID;姿态控制ⅠAbstractQuadrotor UA V is a four propeller driven, vertical take-off and landing aircraft, this structure is widely used in micro mini unmanned aerial vehicle design and can be applied to multiple areas of aerial, archaeology, border patrol, anti-terrorism investigation, has important military and civil value.Quadrotor UA V is a complicated characteristic of the complicated characteristics such as the less drive, the multi variable, the strong coupling, the nonlinear and the uncertainty, and the difficulty and the hot topic in the control field.Research status of the design of small quadrotor UA V were detailed and extensive research, summarized the main classification, research areas, key technology and application prospect of and according to Dr. dot quadrotor actual object, the modeling method and control scheme were preliminary study.First, for the dynamic characteristics of quadrotor UA V, dynamic model of quadrotor UA V is established according to the theorem of Euler and Newton's laws, and consider the air resistance and rotation torque for the effects of blade, the establishment of the physical model of the quadrotor UA V; root according to experimental data and repeated calculation, the establishment of system simulation equation of state; under the MATLAB environment built the nonlinear model of the quadrotor UA V Select the attitude of the quadrotor angle as the control object, with the help of matlab fuzzy toolbox to design the fuzzy PID controller and according to experience of experts to edit the corresponding fuzzy rules; through the simulation and real-time control verify the effectiveness of the control scheme, and this control scheme under the collection to the data input and output; written by SCM fuzzy PID control algorithm, dots, Quad rotor UA V real attitude control. The design of the Matlab simulation and the physical control design, the use of fuzzy PID algorithm, the stability of the four rotor aircraft attitude control.Keywords:Quadrotor UA V;F uzzy PID;Attitude controlⅡ目录摘要(中文) (Ⅰ)摘要(英文) (Ⅱ)第一章概述 (1)1.1 课题背景及意义 (1)1.2 四旋翼飞行器的研究现状 (2)1.3 四旋翼飞行器的关键技术 (5)1.3.1 数学模型 (6)1.3.2 控制算法 (6)1.3.3 电子技术 (6)1.3.4 动力与能源问题 (6)1.4 本文主要内容 (6)1.5本章小结 (7)第二章四旋翼飞行器的运动原理及数学模型 (7)2.1四旋翼飞行器简介 (7)2.2 四旋翼飞行器的运动原理 (8)2.2.1 四旋翼飞行器高度控制 (8)2.2.2 四旋翼飞行器俯仰角控制 (9)2.2.3 四旋翼飞行器横滚角控制 (9)2.2.4 四旋翼飞行器偏航角控制 (10)2.3四旋翼飞行器的数学模型 (11)2.3.1坐标系建立 (11)2.3.2基于牛顿-欧拉公式的四旋翼飞行器动力学模型 (12)2.4 本章小结 (15)第三章四旋翼飞行器姿态控制算法研究 (15)3.1模糊PID控制原理 (15)3.2 姿态稳定回路的模糊PID控制器设计 (16)3.2.1 构建模糊PID控制器步骤 (17)3.2.2 基于Matlab的姿态角控制算法的仿真 (22)3.3 本章小结 (25)第四章四旋翼飞行器飞行控制系统软件设计 (25)4.1 模糊PID控制算法流程图 (25)4.2 系统实验及结果分析 (26)4.3 本章小结 (27)第五章总结与展望 (28)5.1 总结 (28)5.2 展望 (28)参考文献 (28)第一章概述有史以来,人类一直有一个梦想,那就是可以像蓝天上自由翱翔的鸟儿一样。
PID控制算法实例_电机_温度

PID控制算法实例_电机_温度1.电机控制在电机控制中,PID控制算法通常用于控制电机的转速或位置。
PID控制器由比例项(P)、积分项(I)和微分项(D)组成。
具体实现时,可以按照以下步骤进行:第一步,计算误差:将期望的转速或位置信号与实际测量的转速或位置信号做差,得到误差值。
第二步,计算控制量:根据误差值计算控制量,控制量是指控制电机的输出信号。
-比例项:比例项与误差成比例,用于根据误差的大小调节控制量。
大的误差会得到更大的控制量,小的误差会得到更小的控制量。
比例项的作用是尽快将误差减小到零,但可能会引起振荡和超调现象。
-积分项:积分项与误差的累积成正比,用于消除系统静态误差和减小系统的稳态误差。
积分项的作用是逐渐消除误差,但可能会引起超调或者过度响应。
-微分项:微分项与误差的变化率成比例,用于预测误差的变化趋势,减小系统的反应速度和稳定系统。
微分项的作用是减小系统的超调和振荡,但可能会引起系统的抖动。
第三步,更新控制量:将计算得到的控制量应用于电机,调节电机的输出信号。
第四步,循环迭代:重复以上步骤,直到达到期望的转速或位置。
2.温度控制在温度控制中,PID控制算法通常用于控制加热元件或制冷机的输出功率,以维持设定的温度值。
具体实现步骤如下:第一步,测量温度:使用温度传感器或温度计测量当前温度值。
第二步,计算误差:将期望的温度值与实际测量的温度值做差,得到误差值。
第三步,计算控制量:根据误差值计算控制量,控制量是指调节加热元件或制冷机输出功率的信号。
-比例项:比例项与误差成比例,用于根据误差的大小调节控制量。
大的误差会得到更大的控制量,小的误差会得到更小的控制量。
-积分项:积分项与误差的累积成正比,用于消除系统静态误差和减小系统的稳态误差。
-微分项:微分项与误差的变化率成比例,用于预测误差的变化趋势。
第四步,更新控制量:将计算得到的控制量应用于加热元件或制冷机,调节输出功率。
第五步,循环迭代:重复以上步骤,直到达到设定的温度值。
PID算法范文

PID算法范文PID(Proportional-Integral-Derivative)是一种经典的控制算法,广泛应用于工业自动化、过程控制等领域。
PID算法通过调整控制器的输出信号,使被控对象的输出值尽可能接近期望值,从而实现对系统的精确控制。
在PID算法中,比例部分(P部分)根据当前误差计算出一个比例调节量,调节量与误差成正比。
如果误差较大,比例调节量也会较大,从而加快系统响应速度。
但是由于比例调节量只与当前误差有关,无法处理误差累积导致的稳态误差。
为了解决稳态误差的问题,PID算法中引入了积分部分(I部分),该部分根据误差累积值计算出一个积分调节量,调节量与误差累积值成正比。
积分调节量可以消除系统的稳态误差,并且随着误差累积值的增加而增加,从而更好地适应系统变化。
PID算法通过综合比例、积分和微分三部分的调节量来调整控制量,使系统的输出值尽可能接近期望值。
调节量乘以一个系数Kp、Ki和Kd,称为PID的增益。
增益的选择对PID算法的性能影响很大,合理的增益选择可以提高系统的控制性能。
在实际应用中,PID算法还会根据具体需求和系统特性进行调参。
比如通过增大比例增益可以提高系统的响应速度,但同时也容易引发系统的震荡和超调;通过增大积分增益可以减小系统的稳态误差,但过大的积分增益会导致系统的反应迟钝;通过增大微分增益可以提高系统的稳定性,但过大的微分增益会导致系统的抖动。
除了调参外,PID算法还可以进行进一步的改进和优化。
比如基于模型的PID算法(Model-based PID)可以根据系统模型对PID参数进行在线更新,进一步提高系统的控制性能;自适应PID算法(Adaptive PID)可以根据系统的动态特性和工作环境实时调整PID参数,适应系统的变化。
综上所述,PID算法是一种经典的控制算法,具有简单、实用、稳定等特点。
PID算法通过比例、积分和微分三部分的调节来控制系统,实现系统的精确控制。
算法篇(PID详解)

b、特点:
1)增量式算法不需要做累加,控制量增量的确定仅与最近几次偏差采样值有关,计算误差对控制 量计算的影响较小。而位置式算法要用到过去偏差的累加值,容易产生较大的累加误差。 2)增量式算法得出的是控制量的增量,例如在阀门控制中,只输出阀门开度的变化部分,误动作 影响小,必要时还可通过逻辑判断限制或禁止本次输出,不会严重影响系统的工作。 3)采用增量式算法,易于实现手动到自动的无冲击切换。 小结:增量型 PID,是对位置型 PID 取增量,这时控制器输出的是相邻两次采样时刻所计算的位置值 之差,得到的结果是增量,即在上一次的控制量的基础上需要增加(负值意味减少)控制量。
几个需重点理解的概念:
1)基本偏差 e(t):表示当前测量值与设定目标值间的差,设定目标是被减数,结果可为正或负值,正值表 示未达到目标,负值表示超过设定值。 (代表比例) 2)偏差和:∑e(t)=e(t)+e(t-1)+e(t-2)+· · · · · ·+e(1)即每次测量的偏差值总和,注意正负(代表积分) 3)基本偏差的相对偏差:即 e(t)-e(t-1)用本次的基本偏差减去上一次的基本偏差(代表微分)
1)不完全微分 PID 控制算法
问题的提出:对于高频扰动的生产过程,微分作用响应过于灵敏,容易引起控制过程振荡;另外,执行机 构在短时间内达不到应有的开度,会使输出失真。 改进方案: 仿照模拟调节器的实际微分调节器, 在标准 PID 输出后串联一阶惯性环节, 构成不完全微分 PID 控制,以克服完全微分的缺点。 由于完全微分对阶跃信号会产生一个幅度很大的输出信号,并且在一个周期内急剧下降为零,信号变化 剧烈,因而容易引起系统振荡;而不完全微分的 PID 控制中,其微分作用按指数规律逐渐衰减到零,可以延 续多个周期,因而系统变化比较缓慢,故不易引起振荡。从改善系统动态性能的角度看,不完全微分的 PID 算式控制效果更好。
PID算法举例

总所周知,PID算法是个很经典的东西。
而做自平衡小车,飞行器PID是一个必须翻过的坎。
因此本节我们来好好讲解一下PID,根据我在学习中的体会,力求通俗易懂。
并举出PID的形象例子来帮助理解PID。
一、首先介绍一下PID名字的由来:P:Proportion(比例),就是输入偏差乘以一个常数。
I :Integral(积分),就是对输入偏差进行积分运算。
D:Derivative(微分),对输入偏差进行微分运算。
注:输入偏差=读出的被控制对象的值-设定值。
比如说我要把温度控制在26度,但是现在我从温度传感器上读出温度为28度。
则这个26度就是”设定值“,28度就是“读出的被控制对象的值”。
然后来看一下,这三个元素对PID算法的作用,了解一下即可,不懂不用勉强。
P,打个比方,如果现在的输出是1,目标输出是100,那么P的作用是以最快的速度达到100,把P理解为一个系数即可;而I呢?大家学过高数的,0的积分才能是一个常数,I就是使误差为0而起调和作用;D呢?大家都知道微分是求导数,导数代表切线是吧,切线的方向就是最快到至高点的方向。
这样理解,最快获得最优解,那么微分就是加快调节过程的作用了。
二、然后要知道PID算法具体分两种:一种是位置式的,一种是增量式的。
在小车里一般用增量式,为什么呢?位置式PID的输出与过去的所有状态有关,计算时要对e(每一次的控制误差)进行累加,这个计算量非常大,而明显没有必要。
而且小车的PID控制器的输出并不是绝对数值,而是一个△,代表增多少,减多少。
换句话说,通过增量PID算法,每次输出是PWM要增加多少或者减小多少,而不是PWM的实际值。
所以明白增量式PID 就行了。
三、接着讲PID参数的整定,也就是PID公式中,那几个常数系数Kp,Ti,Td等是怎么被确定下来然后带入PID算法中的。
如果要运用PID,则PID参数是必须由自己调出来适合自己的项目的。
通常四旋翼,自平衡车的参数都是由自己一个调节出来的,这是一个繁琐的过程。
PID算法程序范文

PID算法程序范文比例项(P)通过将误差与比例增益相乘,直接将误差的大小线性转换为控制器的输出。
P项对应于调整控制器的灵敏度。
如果P项过大,容易导致控制器输出过冲;如果P项过小,则控制器的反应较迟钝。
积分项(I)通过将误差累加起来,并乘以积分时间进行调整,来消除持续存在的稳态误差。
I项对应于调整控制器的稳定性。
如果I项过大,容易导致控制器输出过冲;如果I项过小,则控制器对系统的纠正能力较弱。
微分项(D)通过将误差的变化率乘以微分时间进行调整,来减小系统的超调和过冲。
D项对应于调整控制器的响应速度。
如果D项过大,容易导致控制器输出的抖动;如果D项过小,则控制器对系统的抑制作用较弱。
实际应用中,根据被控对象的特性和需求,可以根据经验或实验来调整PID算法的参数。
常用的调参方法有手动调参和自动调参两种。
手动调参通过人工观察系统的响应特性,并根据经验来设置参数值。
而自动调参则是通过参数优化方法,如遗传算法、粒子群算法等,来自动最优的参数组合。
下面是一个简单的PID算法的示例程序:```python#PID算法示例程序#定义PID控制器的参数Kp=1.0Ki=0.1Kd=0.01#初始化误差项error = 0last_error = 0integral = 0#循环控制while True:#获取被控对象的实际值actual_value = get_actual_value#计算误差项error = setpoint - actual_value#计算P项P = Kp * error#计算I项integral += Ki * error#计算D项derivative = Kd * (error - last_error) #更新上次误差项last_error = error#计算PID控制器输出output = P + integral + derivative#更新被控对象的控制信号update_control_signal(output)#等待下一次采样```在实际应用中,PID算法不仅可以用于单个被控对象的控制,还可以用于多个被控对象的联合控制,或者用于非线性系统的控制。
PID算法解析范文

PID算法解析范文PID(比例、积分、微分)算法是一种常用的控制算法,常用于工业控制、自动化控制等领域。
它通过比较实际输出值与设定目标值的差别,调整输入信号,达到控制系统的稳定性、快速响应和高精度的控制效果。
PID算法的基本原理是:通过分析实际输出值与目标值之间的误差(偏差),按照比例、积分和微分三种方式调整输入信号。
其中比例控制按照偏差的大小直接调整输入信号,积分控制按照偏差的累计量调整输入信号,微分控制按照偏差的变化率调整输入信号。
三种控制模式的比重可以通过调整各自的系数来控制。
比例控制是最基本的控制模式,按照比例系数Kp将偏差与输出的乘积作为控制信号。
比例控制具有快速响应、让控制器的控制力有一个起始点的作用,但常常出现超调或震荡现象。
积分控制则是通过将偏差累计,按照积分系数Ki调整输入信号。
积分控制可以消除静差,提高稳定性,但容易引起超调、震荡等问题。
微分控制根据偏差的变化率来调整输入信号,减小纠正力。
通过微分系数Kd,使控制器更加稳定、精确。
微分控制可以迅速响应快速变化的控制量,并抑制超调,但容易受到噪声干扰。
PID算法是通过将比例、积分和微分三种控制模式加权组合,综合利用它们的优势,以达到最佳的控制效果。
PID算法的输出是一个调整信号,用于调整控制目标或控制参数。
当输出值与设定目标值接近时,调整信号接近于零,系统趋于稳定。
PID算法的调优是非常重要的,对于不同的系统、不同的控制要求,参数的选择有很大的差异。
常见的调优方法包括试错法、经验法、优化算法等。
试错法是最常用的方法,通过手动调整参数,并观察系统响应特性,不断调整参数以达到最佳控制效果。
经验法则是以经验为基础,根据系统特点和实验经验来选择参数。
优化算法则是利用数学优化方法,通过建立数学模型,自动寻找最佳参数组合。
PID算法的广泛应用使其成为工业控制领域的核心算法。
它具有较为简单的原理和实现方式,在实际应用中反应迅速、稳定性强,容易理解和调试。
算法设计论文-PID算法实例

电子科技大学UNIVERSITY OF ELECTRONIC SCIENCE AND TECHNOLOGY OF CHINA 算法分析与设计结业论文Algorithm analysis and design论文题目PID算法实例分析设计课程名称算法分析与设计上课地点清水河立人楼B106学生姓名范昊洋学号2015170201032年月日PID算法实例分析与设计一,摘要在对机械器件(如电机,电热水器等)进行电子控制的实现时,经常会由于被控制器件的被控制量的变化以及反馈存在一定的机械延迟导致控制的效果不理想,精度不高。
尤其是在控制对于实时系统的控制要求极高的设备,如小车,四轴飞行器,3D打印机等对电机的控制要求非常高,就要求有合适的算法对这些器件进行控制。
PID算法应运而生。
在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器(亦称PID调节器)是应用最为广泛的一种自动控制器。
它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。
PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
控制点包含三种比较简单的PID控制算法,分别是:增量式算法,位置式算法,微分先行。
这三种PID算法虽然简单,但各有特点,基本上能满足一般控制的大多数要求。
本文将以一个具体的用于控制两轮平衡小车的PID算法c语言实例对PID算法进行分析与设计。
本实验中使用的处理器是ST公司的STM32f103C8T6芯片,硬件方面,使用市场上广泛使用的陀螺仪mpu6050作为加速度传感器和方位传感器,使用tb6612芯片制作点击驱动部分,直流减速电机作为小车的电机。
编译器是keil公司的mdk for arm(keil5)。
PID控制算法范文

PID控制算法范文首先,PID控制器由三部分组成:比例控制、积分控制和微分控制。
这三部分分别对应于控制器的比例、积分和微分分量,它们根据控制输入和输出之间的差异来调整控制变量,使其尽可能地接近期望值。
比例控制是根据误差的大小调整控制变量。
误差是指期望值与实际值之间的差异。
比例控制方法将误差乘以一个比例常数Kp,得到比例分量的大小,然后将其加到控制变量上。
这样,当误差较大时,比例分量也会较大,从而加快系统的响应速度。
积分控制是根据误差的累积量调整控制变量。
积分控制方法将误差进行积分,得到误差的累积量,并乘以一个积分常数Ki。
然后将其加到控制变量上。
这样,当误差存在较长时间时,积分分量也会较大,从而减小误差的累积量,提高系统的稳定性。
微分控制是根据误差的变化率调整控制变量。
微分控制方法将误差的变化率乘以一个微分常数Kd,然后将其加到控制变量上。
这样,当误差的变化率较大时,微分分量也会较大,从而及时调整控制变量,提高系统的稳定性。
首先,计算控制变量的过程如下:1.根据实际值和期望值计算误差。
2.根据误差和比例常数Kp计算比例分量。
3.根据误差的累积量和积分常数Ki计算积分分量。
4.根据误差的变化率和微分常数Kd计算微分分量。
5.将比例、积分和微分分量加权求和,得到控制变量。
然后,调整控制器参数的过程如下:1.根据误差的大小,适当调整比例常数Kp,以改变比例控制的强度。
2.根据误差的累积量,适当调整积分常数Ki,以改变积分控制的强度。
3.根据误差的变化率,适当调整微分常数Kd,以改变微分控制的强度。
在实际应用中,PID控制算法被广泛应用于各种控制领域,比如自动化生产线、机器人控制、温度控制等。
通过合理设计和调整PID控制器的参数,可以实现系统稳定性、鲁棒性和精确性的要求。
毕业设计--基于MATLAB的PID控制算法的实现

摘要目前工业自动化水平已成为衡量各行各业现代化水平的一个重要标志。
PID 控制及其控制器已在工程实际中得到了广泛的应用。
本文介绍了PID控制的基础知识和工作原理,并讨论PID控制器的类型以及各种控制器的优缺点,为进行数字PID的算法研究和仿真提供理论基础。
在简单介绍工业过程控制中经常使用到的位置式和增量式PID控制后主要讨论了两种改进的数字PID控制算法:积分分离PID算法与不完全微分PID算法,比较传统控制算法与改进的算法的优缺点,并基于MATLAB对其进行仿真,讨论仿真结果。
仿真结果表明:积分分离控制算法和不完全微分控制算法可以提高控制精度和消除系统高频干扰等。
证明改进的PID控制算法相比一般PID控制算法有很多优点。
关键词:数字PID;积分分离;不完全微分;MATLAB仿真AbstractAt present the level of industrial automation has become an important sign of the modernization of every industries.PID control and controllers now have been worked in a wide range of engineering applications.This paper briefly introduces and discusses the types and the advantages or disadvantages of the PID controllers.These konwledge lay the foundation for the arithmetical research and the simulation.It mainly discusses two improved PID control algorithms: Integral separation PID control algorithm and Not completely differential PID control algorithm after introducing the Incremental PID control and the Position control algorithm used in the industrial process paring the advantage and diadvantage of the traditional PID control algorithm to the improved PID control algorithm and discussing the results of MATLAB simulation.The simulation results show that the Integral separation PID control algorithm and Not completely differential PID control algorithm can improve the control accuracy and eliminate the high frequency interference ,etc.This article proves that the improved PID control algorithm have more advantages than normal PID control algorithm.Key words:digital PID; Integral separation; Not completely differential simulation; MATLAB simulation目录第1章概述 (1)1.1设计的目的和意义 (1)1.2国内外研究发展现状 (1)1.3本次设计的研究内容 (2)第2章 PID控制基本理论 (3)2.1PID的工作原理 (3)2.2PID控制器类型分类 (4)2.4PID控制器参数确定 (6)2.5PID控制器优缺点 (10)2.6本章小结 (10)第3章数字PID控制算法及仿真意义 (11)3.1数字PID控制算法 (11)3.2MATLAB简介 (19)3.3PID仿真的意义 (21)3.4本章小结 (22)第4章改进型PID控制算法及仿真 (23)4.1积分分离式PID控制算法 (23)4.2不完全微分PID控制算法 (27)4.3本章小结 (32)结论 (33)参考文献 (34)致谢 (35)附录 (36)第1章概述1.1 设计的目的和意义PID控制由于结构简单、工作稳定、鲁棒性好等因素在当今的工业过程控制中仍占有主导地位。
PID算法优化(以平衡小车代码为例)

PID算法优化(以平衡小车代码为例)PID控制是一种常用的反馈控制方法,广泛应用于自动控制系统中。
在平衡小车的代码中,PID算法被用于控制小车的平衡。
本文将以平衡小车代码为例,探讨如何优化PID算法。
优化PID算法的第一步是确定合适的初始参数。
可以使用经验法确定初始参数,然后再进行调整。
例如,可以将初始参数都设置为1,然后观察系统的响应情况,根据实际效果逐步调整。
其次,可以使用自适应或自校正的方法来优化PID算法。
自适应PID算法可以根据系统的实时状态动态调整PID参数,从而提高系统的控制效果。
自校正PID算法可以通过系统的实时反馈信息来判断是否需要调整PID参数,从而提高系统的稳定性和鲁棒性。
此外,可以考虑在PID算法中引入限制项,以避免超出系统能够承受的范围。
例如,在平衡小车代码中,可以限制小车的加速度和角度的变化范围,以防止系统过载或翻倒。
在优化PID算法过程中,还需要考虑系统的实时响应速度和稳定性。
必要时,可以进行系统参数的调整,以提高系统的响应速度和稳定性。
例如,可以调整调节参数的时间常数,改变PID算法的响应速度。
另外,可以考虑使用非线性控制方法来优化PID算法。
非线性控制方法可以更好地适应复杂的控制系统,提高系统的性能。
在平衡小车代码中,可以尝试使用基于神经网络的非线性控制方法,从而提高平衡小车系统的控制精度和稳定性。
最后,需要进行系统的实时监测和调试。
通过对系统的实时监测和调试,可以及时发现和解决问题,进一步提高系统的控制效果。
例如,可以使用PID调试工具对系统的实时响应进行监测和调试,从而找到问题的根源,进行相应的调整和优化。
综上所述,通过确定合适的初始参数、使用自适应或自校正的方法、引入限制项、调整系统参数、使用非线性控制方法和进行实时监测和调试,可以对PID算法进行优化,提高系统的控制效果和稳定性。
在平衡小车代码中,这些优化方法可以帮助实现更精确和稳定的平衡控制。
PID控制算法范文

PID控制算法范文一、PID控制算法的基本原理1.比例控制(P控制)比例控制是根据被控对象的偏差信号与设定值之间的差异来调整控制量的大小。
当偏差信号较大时,控制量也会较大,用于缩小偏差;当偏差信号较小时,控制量也会较小,用于稳定系统。
2.积分控制(I控制)积分控制是根据偏差信号的积分累加量来调整控制量的大小。
积分控制可以消除静差,并增强控制系统的稳定性。
但是,过大的积分参数会导致系统的超调和震荡。
3.微分控制(D控制)微分控制是根据偏差信号的变化速率来调整控制量的大小。
微分控制可以减小系统的超调和快速抑制震荡,但是过大的微分参数会带来噪声放大和系统的不稳定。
二、PID控制算法的实现1.离散时间PID控制算法的实现在离散时间下,PID控制算法可以表示为:u(k)=Kp*[e(k)+T*(1/Ti)*∑(e(i))+Td*(e(k)-e(k-1))/T]其中,u(k)为当前时刻的控制量,e(k)为当前时刻的偏差信号,Kp 为比例系数,Ti为积分时间常数,Td为微分时间常数,T为采样周期。
2.连续时间PID控制算法的实现在连续时间下,PID控制算法可以表示为:u(t) = Kp * [e(t) + (1/Ti) * ∫(e(t))dt + Td * de(t)/dt]其中,u(t)为当前时刻的控制量,e(t)为当前时刻的偏差信号,Kp 为比例系数,Ti为积分时间常数,Td为微分时间常数。
三、PID控制算法的优化方法1.参数整定通过分析被控对象的特性,选择合适的比例系数、积分时间常数和微分时间常数。
常用的整定方法有经验整定、频域法和遗传算法等。
2.鲁棒控制为了使PID控制算法对被控对象的参数变化具有鲁棒性,可以采用鲁棒控制方法,如自适应PID控制、模糊PID控制等。
3.先进的控制算法除了传统的PID控制算法,还可以采用一些先进的控制算法来替代PID控制,如模型预测控制、自适应控制等。
综上所述,PID控制算法是一种经典的控制算法,在工业自动化控制系统中得到广泛应用。
【论文】数字PID控制原理及算法

数字PID控制原理及算法自从计算机进入控制领域以来,用数字计算机代替模拟计算机调节器组成计算机控制系统,不仅可以用软件实现PID控制算法,而且可以利用计算机的逻辑功能,使PID控制更加灵活。
数字PID控制在生产过程中是一种最普遍采用的控制方法,在冶金、机械、化工等行业中获得了广泛的应用。
本章主要介绍PID控制的基本原理、数字PID控制算法及其改进算法和几种常用的数字PID控制系统。
1.1 PID控制原理在模拟控制系统中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器是应用最为广泛的一种自动控制器。
图1-1常规PID控制系统原理框图常规PID控制系统原理框图如图1-1所示,系统主要由模拟PID控制器和被控对象组成。
它根据给定值r(t)与实际输出值y(t)构成控制偏差1-11-2 写成传递函数形式:1-3 式中,Kp—比例系数,Ti—积分时间常数,Td—微分时间常数;概括而言,PID控制器的比例、积分和微分三个校正环节的作用如下:比例环节:能迅速反映控制系统的误差,减少稳态误差,但比例控制不能消除稳态误差,比例放大系数的加大,会引起系统的不稳定。
积分环节:主要用于消除系统稳态误差,只要有足够的时间,积分控制将能完全消除误差,使系统误差为零,但积分作用太强会使系统超调加大,甚至使系统产生振荡;积分作用的强弱取决于积分时间常数Ti,Ti越大,积分作用越弱。
微分作用:减少超调量及克服振荡,使系统的稳定性提高,同时加快系统的动态响应速度,减少调整时间,从而改善系统的动态性能。
具体说来,PID 控制器有如下特点:(1)原理简单,实现方便,是一种能够满足大多数实际需要的基本控制器;(2)控制器能适用于多种截然不同的对象,算法在结构上具有较强的鲁棒性,在很多情况下,其控制品质对被控对象的结构和参数摄动不敏感。
但是,PID 控制主要局限性在于它对被控对象的依赖性,一般需预先知道被控对象的数学模型方可进行设计。
PID控制算法范文

PID控制算法范文PID(Proportional-Integral-Derivative)控制算法是一种广泛应用于工业自动化控制系统中的常用控制算法。
它是一种基于反馈原理的控制算法,根据系统的实际输出与期望输出之间的差异来调整控制量,以实现系统的稳定运行和精确控制。
PID控制算法包含三个独立的控制项:比例(Proportional)、积分(Integral)和微分(Derivative)。
它们分别对应对控制量的当前误差、历史误差以及误差变化率的响应。
通过对这三个控制项进行适当的加权组合,可以使系统的响应速度、稳定性和抗干扰能力得到优化。
比例项(P)是PID控制算法中最基本的部分。
它根据当前误差的大小来调整控制量的大小。
具体而言,比例增益参数Kp确定了控制量与误差的线性关系。
增大比例增益可以加快系统的响应速度,但可能导致系统的稳定性下降和抖动增加。
反之,减小比例增益可以提高系统的稳定性,但会使系统的响应速度变慢。
积分项(I)是用来解决系统的静态误差问题。
它通过对历史误差的积累,来逐步减小系统的静态误差。
具体而言,积分增益参数Ki决定了误差积分的速度。
增大积分增益可以加快误差积分的速度,但可能导致系统的超调和过冲。
反之,减小积分增益可以减小系统的超调,但可能会使系统的调节时间变长。
微分项(D)是用来解决系统的动态误差问题。
它通过对误差变化率的响应,来预测系统未来的变化趋势,从而提前调整控制量。
具体而言,微分增益参数Kd决定了对误差变化率的敏感程度。
增大微分增益可以提高对误差变化的敏感性,但可能导致系统的噪声增加。
反之,减小微分增益可以减小噪声的干扰,但可能会使系统的响应速度变慢。
u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt其中,u(t)表示控制量,e(t)表示当前误差,de(t)/dt表示误差变化率,Kp、Ki和Kd分别为比例增益、积分增益和微分增益。
pid算法程序范文

pid算法程序范文PID控制算法是一种常用的控制算法,用于实现对系统输出的精确控制。
PID控制算法的原理是利用比例、积分和微分三个环节对系统输出进行调整,以达到控制目标。
首先,PID控制算法中的比例环节(Proportional)根据系统输出与期望输出之间的差异进行调整。
比例控制的基本思想是系统输出越接近期望输出,对系统的控制力度就越小;反之,系统输出偏离期望输出越远,控制力度就越大。
比例系数Kp用于控制比例环节的调整幅度,大的Kp值会使系统对偏差做出更大的反应,但过大的Kp值可能导致系统震荡。
其次,PID控制算法的积分环节(Integral)用于解决系统存在的持续偏差问题。
积分环节通过对系统输出的偏差进行累加,使系统能够在持续偏差下逐渐调整到期望输出。
积分系数Ki决定了积分环节的调整幅度,大的Ki值会加快系统的调整速度,但过大的Ki值可能导致系统的超调。
最后,PID控制算法的微分环节(Derivative)用于控制系统的响应速度。
微分环节通过对系统输出的变化率进行调整,使系统能够更快地接近期望输出。
微分系数Kd决定了微分环节的调整幅度,大的Kd值会增加系统对输出变化率的敏感度,但过大的Kd值可能导致系统的抖动。
PID控制算法的整体调整可以通过实验和经验进行,也可以通过自动控制算法进行调整。
在实际应用中,通常需要根据具体的系统和控制目标来确定合适的PID参数。
常见的调整方法有经验调整法、Ziegler-Nichols方法和优化算法等。
以下是一个示例的PID控制算法的程序:```python#定义PID控制器class PID:def __init__(self, Kp, Ki, Kd):self.Kp = Kpself.Ki = Kiself.Kd = Kdst_error = 0self.integral = 0def control(self, error):#计算比例项P = self.Kp * error#计算积分项self.integral += errorI = self.Ki * self.integral#计算微分项D = self.Kd * (error - st_error) st_error = error#计算总控制量control = P + I + Dreturn control#示例应用:控制小车的速度target_speed = 50 # 期望速度current_speed = 0 # 当前速度#创建PID控制器pid_controller = PID(0.5, 0.1, 0.2)#模拟控制过程for i in range(10): # 模拟10个控制周期error = target_speed - current_speedcontrol = pid_controller.control(error)#模拟控制信号传递和执行过程current_speed += controlprint("控制量:", control, "当前速度:", current_speed)```以上示例程序演示了使用PID控制算法来控制小车的速度,目标速度为50,初始速度为0。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电子科技大学UNIVERSITY OF ELECTRONIC SCIENCE AND TECHNOLOGY OF CHINA 算法分析与设计结业论文Algorithm analysis and design论文题目PID算法实例分析设计课程名称算法分析与设计上课地点清水河立人楼B106学生姓名范昊洋学号2015170201032年月日PID算法实例分析与设计一,摘要在对机械器件(如电机,电热水器等)进行电子控制的实现时,经常会由于被控制器件的被控制量的变化以及反馈存在一定的机械延迟导致控制的效果不理想,精度不高。
尤其是在控制对于实时系统的控制要求极高的设备,如小车,四轴飞行器,3D打印机等对电机的控制要求非常高,就要求有合适的算法对这些器件进行控制。
PID算法应运而生。
在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器(亦称PID调节器)是应用最为广泛的一种自动控制器。
它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。
PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
控制点包含三种比较简单的PID控制算法,分别是:增量式算法,位置式算法,微分先行。
这三种PID算法虽然简单,但各有特点,基本上能满足一般控制的大多数要求。
本文将以一个具体的用于控制两轮平衡小车的PID算法c语言实例对PID算法进行分析与设计。
本实验中使用的处理器是ST公司的STM32f103C8T6芯片,硬件方面,使用市场上广泛使用的陀螺仪mpu6050作为加速度传感器和方位传感器,使用tb6612芯片制作点击驱动部分,直流减速电机作为小车的电机。
编译器是keil公司的mdk for arm(keil5)。
关键词:PID算法,stm32,平衡小车,mpu6050二,实验设计1.PID算法的初步设计准备在进行实际算法设计之前,首先要进行一些准备工作,确保后续的PID算法设计能够顺利进行。
在此之前首先深入了解PID算法设计思路。
第一要明确设计目的,设计目标是制作一个能够保持平衡的两轮平衡小车,那么首先要保持平衡,其次要能够正常直线行走,再次能实现转向,一个小车就完成了。
所以为了完成这些功能的设计,首先要有一个功能足够的PID体系。
比例(P)控制比例控制是一种最简单的控制方式。
其控制器的输出与输入误差信号成比例关系。
当仅有比例控制时系统输出存在稳态误差(Steady-state error)。
积分(I)控制在积分控制中,控制器的输出与输入误差信号的积分成正比关系。
对一个自动控制系统,如果在进入稳态后存在稳态误差,则称这个控制系统是有稳态误差的或简称有差系统(System with Steady-state Error)。
为了消除稳态误差,在控制器中必须引入“积分项”。
积分项对误差取决于时间的积分,随着时间的增加,积分项会增大。
这样,即便误差很小,积分项也会随着时间的增加而加大,它推动控制器的输出增大使稳态误差进一步减小,直到等于零。
因此,比例+积分(PI)控制器,可以使系统在进入稳态后无稳态误差。
微分(D)控制微分调节就是偏差值的变化率。
例如,如果输入偏差值线性变化,则在调节器输出侧叠加一个恒定的调节量。
大部分控制系统不需要调节微分时间。
因为只有时间滞后的系统才需要附加这个参数。
如果画蛇添足加上这个参数反而会使系统的控制受到影响。
首先看PID的增量型公式:PID=Uk+KP*【E(k)-E(k-1)】+KI*E(k)+KD*【E(k)-2E(k-1)+E(k-2)】由公式可以看出,要实现PID算法的编程,所需的PID变量至少有,KP,KI,KD三个系数。
实验过程中,这三个变量的值就是许多工程师在实际调试过程中要调整的值。
了解这点之后就开始进行实际编码。
2.直立PID的设计两轮平衡小车不同于四轮的小车,开机之后就必须时刻保持直立,否则就会摔倒而无法进行任何操作,所以小车要完成的第一步就是保持直立。
首先解释一下小车保持直立的原理。
小车是一个直立的个体,那么当它要倒下之前,要首先倾斜,但这时如果小车提前预知了这个趋势,并且控制小车的轮子向倾斜的方向运动小段距离,就能保持平衡。
小车只要时刻都保持着这个运动,就可以实现一直保持直立。
考虑到这个过程对于高响应速度的要求以及其依赖于对小车状态趋势的分析,这个过程使用P(比例)D(微分)驱动而不使用I(积分)。
代码如下:int balance(float Angle,float Gyro){floatBias,kp=575,kd=2.7;int balance;Bias=Angle-ZHONGZHI; //求出平衡的角度中值,和机械相关balance=kp*Bias+Gyro*kd; //计算平衡控制的电机PWMreturn balance;}这个函数有两个形参,这两个形参分别是平衡倾角和平衡角速度,由单片机控制的陀螺仪mpu6050实时传回的数据经过卡尔曼滤波计算得出。
关于陀螺仪和卡尔曼滤波的算法与此处的PID算法无关不再叙述。
上面的balance函数是计算PWM值的一个函数,在另一中断函数中,使用该函数为电机PWM赋值。
Balance_Pwm =balance(Angle_Balance,Gyro_Balance);简要说明,PWM在此处指的是单片机通过IO口传出的频率,占空比都可控的方波信号,单片机通过这些方波信号来控制电机的转动与转速,根据电机种类的不同而控制方式也不同。
此处可简要理解为pwm的变量值越大,电机的转速越快。
那么我们来看balance函数的具体内容,函数中的kp为比例系数,kd为微分系数,该值为已经调试好的取值。
输出一个值balance=kp*Bias+kd*Gyro,Angle为平衡倾角,而Bias=Angle-ZHONGZHI 的意思就是求出平衡方向的倾角与实际要控制的值之间的差值,既是被控制量与被控制的值的差值,这个差值与kp的乘积就是比例系数的变量。
然后再看另一个,另一个是平衡倾角角加速度,由加速度传感器直接经过计算而得,也就是现成的平衡倾角(被控制量)的微分变化,与kd的乘积就是微分系数的变量。
两者相加就完成了直立PID的计算。
3.速度PID的设计解决了直立的问题,下一步就要让小车能够自由前行。
既是实现速度PID控制。
int velocity(intencoder_left,intencoder_right){static float Velocity,Encoder_Least,Encoder,Movement;static float Encoder_Integral,Target_Velocity;floatkp=210,ki=1.05;if(1==Flag_Qian) Movement=Target_Velocity/Flag_sudu;else if(1==Flag_Hou) M ovement=-Target_Velocity/Flag_sudu;else Movement=0;Encoder_Least=(encoder_left+encoder_right)-0;Encoder *= 0.8;Encoder += Encoder_Least*0.2;Encoder_Integral +=Encoder;Encoder_Integral=Encoder_Integral-Movement;if(Encoder_Integral>10000) Encoder_Integral=10000;if(Encoder_Integral<-10000) Encoder_Integral=-10000;Velocity=Encoder*kp+Encoder_Integral*ki;return Velocity;}这个函数就是速度PID控制的函数,由于小车本身速度不快(使用直流减速电机),不需要对于很快的动作有过于明显的反应所以舍弃微分D而只使用P和I两个变量进行控制。
Flag_Qian和Flag_Hou两个变量是标志位,若变量为0表示不行进,Flag_Hou=1表示向后走,Flag_Qian=1表示往前走。
函数的两个形参分别是编码器返回值的左轮速度和右轮速度(编码器是用来检测转动圈数的,返回值是单位时间内的转动圈数,也就是速度)。
此处需要说明的是如下语句:Encoder_Least=(encoder_left+encoder_right)-0;Encoder *= 0.8;Encoder += Encoder_Least*0.2;Encoder_Least是当前速度值(两轮速度和),得到当前速度之后,并没有直接把它作为比例量与比例系数相乘,也没有把它的值作为一个时刻的积分量累加,而是让Encoder量自乘0.8,再与Encoder_Least乘0.2的结果相加。
这个处理过程其实是一个低通滤波过程。
由于编码器传回的数据也是直接从机械装置之中检测到的值,偶然事件对该值的影响可能会比较明显,但是这样就会偏离真实的转动量,所以对转动量(速度)这个值进行低通滤波之后再作为变量使用,这样做是为了让小车更加平稳,速度的PID效果更稳定高效。
Encoder_Integral这个变量则是转动量(速度)的积分变量。
积分量每次都加上一个当前变量值,减去该次的速度的目标值,表示速度与目标速度的差值的积分。
其中如下语句:if(Encoder_Integral>10000) E ncoder_Integral=10000;if(Encoder_Integral<-10000) Encoder_Integral=-10000;则是为了防止积分变量过大,当系统处于特殊情况时积分变量不断增大可能会对系统的调整造成很大影响,于是在每次积分变量计算结束之后都对积分变量进行一个上限判断(正值上限与负值上限),如果积分变量超过10000则把它的值限定在10000,这样做增加了系统的稳定性,同时在开发过程中这样的语句也有很大的意义。
最后把积分变量和比例变量相加赋给电机pwm:Velocity=Encoder*kp+Encoder_Integral*ki;这样就能把每一次的计算结果传递给电机,让电机按照指定的计算结果转动,保证电机已给定的控制量方式转动。
4.转向环PID的设计两个电机都赋予了速度之后,小车就能被控制直走了,但是还需要一个转向的指令,这样小车才能够实现正常的功能。
如下为转向PID函数。
