材料力学--简单的超静定问题
材料力学-力法求解超静定结构

力法求解超静定结构时,可以根据计算结果优化结构设计,提高结构的强度和稳定性。
结论与总结
力法是求解超静定结构的有效方法,通过合理应用材料力学基础和力法的原理,我们能够准确求解反力分布并 分析结构的应力情况。
样例分析
结构:桥梁
使用力法求解桥梁上的悬臂梁,计算主梁的支座反 力和悬臂梁的应力分布。
结构:楼房
将力法应用于楼房结构,确定楼板的支座反力并分 析楼梯的受力情况。
实用提示和技巧
1 标定自由度
在应用力法时,正确标定结构的自由度是成功求解反力的重要步骤。
2 验证计算结果
对计算得到的反力进行验证,确保结果的准确性,避免错误的设计决策。
材料力学-力法求解超静 定结构
超静定结构的定义
超静定结构是指具有不止一个不可靠支持反力的结构。它们挑战了传统的结构分析方法,需要使用力法进行求 解。
材料力学基础
材料力学研究材料的受力和变形规律,包括弹性力学、塑性力学和损伤力学。 这些基础理论为力法求解超静定结构提供了必要的工具。
力法的原理
力法是一种基于平衡原理和支座反力法则的结构分析方法。它通过对超静定结构施加虚位移,建立受力平衡方 程,求解未知反力。
超静定结构应用力法求解的步骤
1
确定结构类型
了解结构是否为超静定结构,并确定不
计算反力
2
可靠支持反力的个数。
根据力法原理,建立并求解受力平衡方
程,计算未知反力。
3
验证平衡
通过检查受力平衡方程是否满足等式的
确定应力分布
4
要求,验证计算的反力是否正确。
பைடு நூலகம்
根据已知反力和结构的几何特性,计算 并绘制应力分布图。
材料力学 简单的超静定问题

FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程:由几何方程和物理方程得:
F N 1l1 E1 A1
2
cos a
(5)联解(1)、(2)、(3)式,得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力(支反 力、内力)的问题,称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力(支反 力、内力)的问题,称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固,角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa,弹性模量分别为E1=200GPa 和 E2 =10GPa;求许可载荷P。 解:(1)以压头为研究对象, 设每 个角钢受力为FN1,木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a
材料力学——6简单的超静定问题

M
(x)
X
1
x
X1x, P(x
x l ), 2
l 2
x
l 2
B
l 0
M
(x)M EI
( x)dx
0
如果B处支撑为弹簧 (弹簧系数K) ?
例 P
A
l
l
2
2
BA
P
B
l
l
2
2
X1
解
M
(x)
X1
x
X1x, P(x
x l ), 2
l 2
x
静定基
l 2
x
B
l 0
M (x)M EI
(x)dx
X1 K
求解 线性方程
未知力
以一例说明解法
q
12 3
X1 X2 X3
• 静定基(含未知数)
1 0, 2 0, 3 0
• 位移协调条件
建立方程的过程
以1为例说明
X1 X2 X3
1
M (x)M1(x) dx EI
(M X1 M X2 M X3 M q )M1(x) dx EI
M X1M1 dx M X2 M1(x) dx M X3 M1(x) dx M qM1(x) dx
A
P0 =1 B
M (x) x
解: 协调条件——D截面转
角为零
A
静定基
D
/2
0
M
( )M
EI
()Rd
0
DX
P 2
二、装配应力
1、静定问题无装配应力
B
C
2、静不定问题存在装配应力
1
2
A
下图,3号杆的尺寸误差为,
简单的超静力问题

简单的超静定问题
20
例题 6-2
2. 取1杆和2杆为AB杆的多余约束,FN1和FN2 为多余未知力。得基本静定系如图c。
F
3
AC
B
(c)
材料力学(Ⅰ)电子教案
简单的超静定问题
21
例题 6-2
3. 由变形图(图d)可得变形相容条件为
E
(d) C Dl1 FN1
Δl1 2Δl3 Δl2 2Δl1
F
A
F
FN3
2E F 1A 1F cNo 2 3 l 1sF N E l1 3 3c A 3o s
于是可求出多余未知力FN3 。
材料力学(Ⅰ)电子教案
简单的超静定问题
例2
y
q
A
C
BxA
l/2
l/2
l
8
B
超静定梁
q
A
l/2
FC
l
基本静定系统
B 补充方程为 5ql4 FCl3 0 38E4 I 48EI
材料力学(Ⅰ)电子教案
简单的超静定问题
1
第 6 章 简单的超静定问题
§6-1 超静定问题及其解法 §6-2 拉压超静定问题 §6-3 扭转超静定问题 §6-4 简单超静定梁
材料力学(Ⅰ)电子教案
简单的超静定问题
2
§6-1 超静定问题及其解法
Ⅰ. 关于超静定问题的概述
(b)
材料力学(Ⅰ)电子教案
简单的超静定问题
mm×30 mm的矩形,钢的弹性
模量E=210 GPa,铜的弹性模
量E3=100 GPa。
材料力学(Ⅰ)电子教案
简单的超静定问题
29
例题 6-3
解:1. 装配后有三个未知的装配内力FN1, FN2 , FN3,如 图d所示。但平行力系只有二个独立的平衡方程,
材料力学(I)第六章

(2) 几何方程
L2
( L3 ) cos L1
材料力学(Ⅰ)电子教案
简单的超静定问题
15
(3)、物理方程及补充方程:
FN 1L1 FN 3 L3 ( ) cos E1 A1 E3 A3
(4) 、解平衡方程和补充方程,得:
FN1 FN 2
E1 A1 cos2 L3 1 2 cos3 E1 A1 / E3 A3
FN 1L FN 3 L 得: cos E1 A1 cos E3 A3
5)联立①、④求解:
FN ! F
④
E 3 A3 2 co s E1 A1 co s2
FN 3
F E1 A1 1 2 co s3 E A
材料力学(Ⅰ)电子教案
简单的超静定问题
[例2-19]刚性梁AD由1、2、3杆悬挂,已知三杆材料 相同,许用应力为[σ ],材料的弹性模量为 E,杆长 均为l,横截面面积均为A,试求各杆内力。
5
1.比较变形法 把超静定问题转化为静定问题解,但 必须满足原结构的变形约束条件。
[例2-16] 杆上段为铜,下段为钢杆,
E1 A1
A
1
上段长 1 , 截面积A1 , 弹性模量E1 下段长 2 , 截面积A2 , 弹性模量E2
杆的两端为固支,求两段的轴力。
C
E 2 A2
F
FB
B
2
(1)选取基本静定结构(静定基如图),B 解: 端解除多余约束,代之以约束反力RB
2E1 A1 cos3 FN 3 3 L3 1 2 cos E1 A1 / E3 A3
例2-22
材料力学(Ⅰ)电子教案
材料力学

5 Pa RD a RD a 6 EI 3EI 3EI
如何得到?
A D
P
B
自行完成
C D
RD
例题 6
图示结构AB梁的抗弯刚度为EI,CD杆的抗拉刚度为EA,
已知P、L、a。求CD杆所受的拉力。
D
a
A
C
L
2
L
B
2
P
解:变形协调条件为 wC lCD
D
a
C
FC
A
( P FC ) L wC 48EI FC L lCD EA
温度应力:
FB E t A
6 1 12 . 5 10 碳素钢线胀系数为 C0
温度应力:超静定结构中,由于温度变化,使构
件膨胀或收缩而产生的附加应力。
不容忽视!!!
路、桥、建筑物中的伸缩缝 高温管道间隔一定距离弯一个伸缩节
例题 11
图示阶梯形杆上端固定,下端与支座距离=1mm, 材料的弹性模量E=210GPa,上下两段杆的横截 面面积分别为600平方毫米和300平方毫米。试 作杆的轴力图。
C
A
FA
B
L2
FC
FA FB FC qL 0
L2
M
A
0
FB
变形协调方程
L qL2 FC FB L 0 2 2
3 FB qL 16
FA 3 qL 16
C q C FC 0
7.5kNm
5qL4 FC L3 5 0 FC qL 8 384 EI Z 48EI Z
由于超静定结构能有效降低结构的内力及变形,在 工程上(如桥梁等)应用非常广泛。
●超静定问题的解法:
《材料力学》第6章 简单超静定问题 习题解
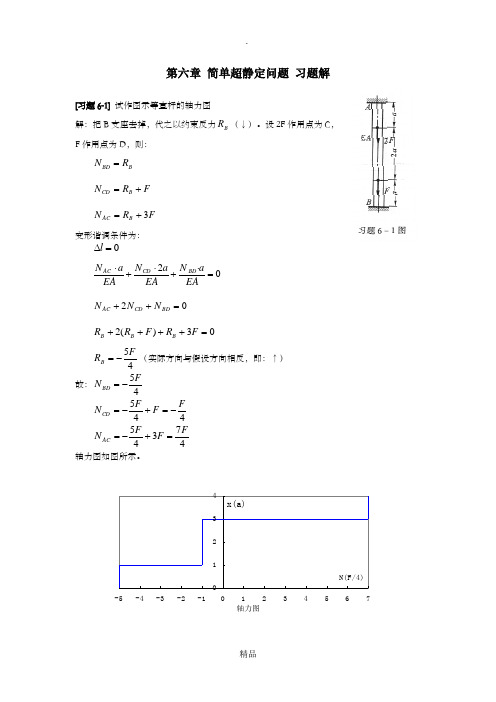
轴力图01234-5-4-3-2-101234567N(F/4)x(a)第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解:把B 支座去掉,代之以约束反力B R (↓)。
设2F 作用点为C ,F 作用点为D ,则:B BD R N =F R N B CD +=F R N B AC 3+=变形谐调条件为:0=∆l02=⋅+⋅+⋅EAa N EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45F R B -=(实际方向与假设方向相反,即:↑) 故:45F N BD-= 445F F F N CD-=+-= 47345F F F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=,1,2,3各杆由同一种材料制成,其横截面面积分别为21100mm A =,22150mm A =,23200mm A =。
试求各杆的轴力。
解:以节点A 为研究对象,其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件:设A 节点的水平位移为x δ,竖向位移为y δ,则由变形协调图(b )可知:00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31,则l l 232= 223311233EA l N EA l N EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得:kN N 45.81=;kN N 68.22=;kN N 54.111=(方向如图所示,为压力,故应写作:kN N 54.111-=)。
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-简单的超静定问题(圣才出品)

8 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
Δl1=FN1l1/EA1=FN1l/(EA1cos30°) Δl2=FN2l2/EA2=FN2l/(EA2) Δl3=FN3l3/EA3=FN3l/(EA3cos30°) 代入式③可得补充方程: FN1l/(EA1sin30°·cos30°)=2FN2l/(EA2tan30°)+FN3l/(EA3sin30°·cos30°)④ (3)求解 联立式①②④,可得各杆轴力:FN1=8.45kN,FN2=2.68kN,FN3=11.55kN。
9 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
MB = 0
FN2 Leabharlann 2 2a+
FN4
2 2
a
+
FN3
2a − F ( 2 a + e) = 0 2
②
根据结构的对称性可得 FN2=FN4③
(2)补充方程
如刚性板的位移图所示,根据几何关系可得:Δl1+Δl3=2Δl2④
由结构对称可知 Δl2=Δl4,其中,由胡克定律可得各杆伸长量:
Δl1=FN1l/EA,Δl2=FN2l/EA,Δl3=FN3l/EA
代入式④,整理可得补充方程:FN1+FN3=2FN2⑤
(3)求解
联立式①②③⑤,解得各杆轴力:
FN1
=
(1 4
−
e )F(压) 2a
FN2
=
FN4
=
F 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简单的超静定问题
1
第六章 简单的超静定问题
§6-1 §6-2 §6-3 §6-4
超静定问题及其解法 拉压超静定问题 扭转超静定问题 简单超静定梁
2
§6-1 超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力(支反 力、内力)的问题,称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力(支反 力、内力)的问题,称为超静定问题。 相应的结构称为超静定结构。
8
[例6-2-3] 刚性梁AD由1、2、3杆悬挂,已知三杆材 料相同,许用应力为[σ],材料的弹性模量为 E, 杆长均为l,横截面面积均为A,试求结构的许可载荷 [F]。
1
2
A
3 D
a
a
a
F
9
解:取刚性梁为研究对象,列 FN1 FN2
静力平衡方程:
MA 0:
受力图 A
a
a
FN1 a FN2 2a FN3 3a F 3a 0
(2)几何方程——变形协调方程:
(2)
A
l2 F l1
l1 l2 l3 cosa
(3)物理方程——胡克定律:
l3
F
FN1l1 E1 A1
l3
FN3l3 E3 A3
(4)补充方程:由几何方程和物理方程得:
aa
FN1l1 FN3l3 cosa
(3)
(1)
变形协调条件:
A
位移图
l2 2l1, l3 3l1
l1
l2
即: FN2l 2 FN1l , EA EA
FN3l 3 FN1l EA EA
FN3
D a
F
D
l3
FN2 2FN1, FN3 3FN1 (2)
10
联立求解(1)和(2), 得:
FN1
3 14
F,
=10GPa;求许可载荷P。 解:(1)以压头为研究对象, 设每
个角钢受力为FN1,木柱受力为FN2.
4FN1 FN2 P 0
4FN1
(2)列变形几何相容方程
FN 2
l1 l2
(3)由物理方程得补充方程:
l1
FN1l1 E1 A1
FN 2l2 E2 A2
l2
12
(4) 解平衡方程和补充方程,得:
14
B
D
C (2) 几何方程
FN2
6 14
F,
FN3
9 14
F
3杆轴力为最大,其强度条件为:
3
FN3 A3
9F 14 A
[ ]
F 14 [ ]A
9
[F] 14 [ ]A
9
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢
加固,角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa,弹性模量分别为E1=200GPa 和 E2
FN 2 A2
[ ]2
0.72 P A2[ ]2
P2
A2 2
0.72
250 2 10 6 12 106 0.72
1042 kN
取 [P] 705.4kN
13
二、装配应力: 杆件尺寸误差引起的应力。
1 静定问题无装配应力。 2 静不定问题存在装配应力。
横截面积A1=A2=A、 A3 ; 弹性模量为:E1=E2=E、E3。
B
外力沿铅垂方向,求各杆的内力。 1
D 3
C 2
aa
A
F
6
B 1
D 3
aa
C 解: (1)以铰A为研究对象,列平衡方程:
F x 0 : FN1 sin a FN2 sin a 0 (1)
2
Fy 0 : FN1 cosa FN2 cosa FN3 F 0
B
D
C [例6-2-5]如图所示3号杆的尺寸误
1
3
aa
2
A0
差为,求各杆的装配内力。 解:(1)取铰A分析,列平衡方程:
A
FN1、 FN2 为压力, FN3为拉力。
FN1 FN3 FN2
A
Fx 0 : FN1 sina FN2 sina 0
Fy 0 : FN1 cosa FN2 cosa FN3 0
A
E1 A1 E3 A3
(5)联解(1)、(2)、(3)式,得:
F
FN1
FN2
E1A1F cos2 a 2E1A1 cos3 a E3 A3
;
FN3
2E1 A1
E3 A3F 7
cos3 a E3 A3
[例6-2-2] 两端固定直杆受轴向外力 F 作用,截面 尺寸如图所示,求两端反力。
A
A
2EA a
C
C
RA 解: 放 松B端,加支反力RA、RB
则,RA RB F 0 (1) 变形协调条件 : l总 0
F 2a
B EA
F
lAC
lCB
F RB a
2EA
RB 2a
EA
0
(2)
B
由(1)、(2)式得
RB
RB
F 5
,
RA
4F 5
(3) 物理关系--列物理方程
(4) 补充方程:由几何方程和物理方程得到
(5) 解由平衡方程和补充方程组成的方程组。 4
静定基、基本静定系(相当系统) 静定基:解除超静定结构的多余约束后得到的静
定结构,称为原超静定系统的静定基,同一问题静定 基可以有不同的选择,主要是便于计算系统的变形和 位移。
F1
FN1 0.07P ; FN 2 0.72P
(5)求结构的许可载荷:
4FN1
角钢面积由型钢表查得: A1=3.086cm2
FN 2
FN 1 A1
[ ]1
0.07 P A1[ ]1
P1
A11
0.07
3.086 10 4 160 106 0.07
705 .4kN
1
2
3
F
1
2
3
3
F
所有超静定结构,都是在静定结构上再加一个或几 个约束,这些约束对于特定的工程要求是必要的,但对 于保证结构平衡却是多余的,故称为多余约束,相应的 有多余未知力。 3. 超静定次数 n :n = 未知力数-独立的平衡方程数 4. 超静定问题的解题方法步骤:
(1) 静力学关系--列静力平衡方程 (2) 几何关系(变形几何相容条件)--列几何方程
F2
F1
F2
F1
F2
R
R
相当系统:在静定基上加上外载荷以及多余约束
力,这样的系统称为原超静定系统的相当系统。
5
§6-2 拉压超静定问题
一、拉压超静定问题解法
对拉压超静定问题,可综合运用静力学关系、物 力关系和几何关系(变形几何相容条件)三方面来求 解。
[例6-2-1] 如图三杆用铰链连接,已知:l1=l2=l、 l3;
